Significance
Visual search is one of the primary tools to study attention in experimental psychology, yet the spatiotemporal behavior of attention during search remains controversial: Does attention focus on one item at a time or several, or even all, items? We used an innovative methodology that relies on simple yet elegant mathematical reasoning and only assumes (like most other attentional studies) that attentional strength is reflected in behavioral performance. We provide evidence against a strict parallel model in space and for an attentional periodicity in time: Attention during a difficult search task was nonuniformly allocated both in space, focusing on one stimulus or subgroup of stimuli at a time, and in time, with this deployment being periodically modulated at ∼7 Hz.
Keywords: visual search, attention, nonuniform, sequential, periodic
Abstract
Difficult search tasks are known to involve attentional resources, but the spatiotemporal behavior of attention remains unknown. Are multiple search targets processed in sequence or in parallel? We developed an innovative methodology to solve this notoriously difficult problem. Observers performed a difficult search task during which two probes were flashed at varying delays. Performance in reporting probes at each location was considered a measure of attentional deployment. By solving a second-degree equation, we determined the probability of probe report at the most and least attended probe locations on each trial. Because these values differed significantly, we conclude that attention was focused on one stimulus or subgroup of stimuli at a time, and not divided uniformly among all search stimuli. Furthermore, this deployment was modulated periodically over time at ∼7 Hz. These results provide evidence for a nonuniform spatiotemporal deployment of attention during difficult search.
Visual search tasks (e.g., to find a target embedded among similar looking distracters) have long been used to investigate the deployment of attention (1–6). Certain tasks are performed “efficiently,” in which case the search time and accuracy are independent of the number of distracters. Other tasks are more difficult, or “inefficient,” characterized by an increase in reaction times (RTs) and/or a decrease in accuracy with the number of distracting elements, a result typically attributed to the need to allocate attention (4–7). For more than 30 y now, since the pioneering study of Treisman and Gelade in 1980 (4), two opposing theories of attention deployment during difficult search have persisted. Attention could either be allocated nonuniformly to the stimuli, such that in some cases it would switch sequentially from one stimulus (or group of stimuli) to another (4, 5), or be divided uniformly to process all of the stimuli in parallel, but with a drop in efficiency for increasing distractor numbers (2, 8–10). To date, neither of these two theories has been unequivocally disproved. Overall performance in the search task itself is not directly informative, because both theories predict an increase in RT with the number of distracters (11, 12). One alternative is to use briefly flashed probes to test for the deployment of attention at a specific location and time. With two probes, it should be possible to differentiate parallel and sequential processing strategies: The strict parallel theory predicts that both probes should receive equal amounts of attention, whereas the sequential theory predicts that one of the probes will receive more attention than the other. Of course, the most attended probe may not be the same one on every trial, but a simple mathematical manipulation, the solution of a quadratic equation, allows us to access this information despite the need to average performance over trials.
In recent years, a second, related, debate has arisen in the literature concerning the temporal behavior of attention. It has been proposed that attention samples visual stimuli periodically rather than continuously (13–18). This question is connected to the uniform vs. nonuniform debate in that the nonuniform (or sequential) model of attention processing maps rather naturally onto a periodic sampling of visual information (with the periodicity reflecting the switching between stimuli). No such relation exists for the parallel uniform model, making it more naturally compatible with continuous processing (although, of course, not incompatible with periodic sampling arising for independent reasons).
Consequently, in this study, we asked whether attention processing during a difficult search task is uniform or nonuniform, both in space and in time. We used a difficult (attention demanding) visual search task consisting of finding a letter T among letter L’s (four stimuli). After a varying delay, we probed two of the four stimulus locations (Fig. 1) and computed performance in reporting both probes correctly (PBOTH) or none of the probes correctly (PNONE). Using the mathematical manipulation described in Methods, we were able to determine that attention was not divided equally between the four search item positions, but focused on one stimulus or subgroup of stimuli at a time. Moreover, we found that the deployment of attention was modulated periodically at theta frequency (∼7 Hz). We conclude that in this difficult search task, attention was deployed nonuniformly both in space and in time.
Fig. 1.
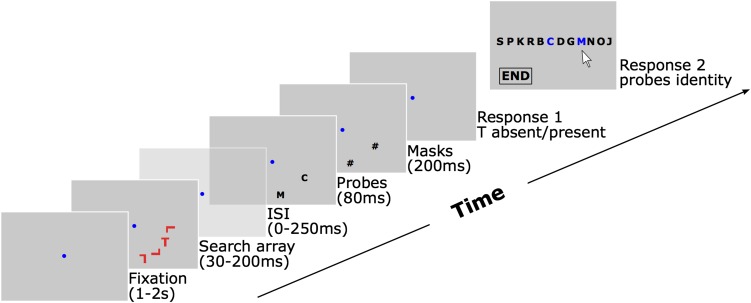
Experimental procedure. One second to 2 s after pressing the space bar, the search array appears for 30–200 ms depending on the randomly chosen SOA for this trial. Observers report the presence or absence of the target stimulus T among distracting L letters. After the variable SOA (from 30–450 ms relative to search array onset), two probe letters appear randomly for 80 ms at two of the four search array locations. For probe onset SOAs greater than 200 ms, an additional empty screen is presented between the search task and the probe detection task (the fixation point is maintained). In other words, if the SOA was shorter than 200 ms, the interstimulus interval (ISI) was zero; otherwise, the ISI was greater than zero. Masks follow probe stimuli for 200 ms. After mask offset, observers first report the presence or absence of the T among L’s, and then the identity of the two probe stimuli by selecting letters from a list, using the computer mouse. A trial ends when observers click on the end button.
Results
Each experimental trial comprised two tasks (Fig. 1): a difficult search task (primary task) and a probe detection task (secondary task). We reasoned that the amount of attention that is deployed in the primary task should translate into correct probe report probability in the secondary task. (This reasoning was indeed supported by evidence of improved probe detection at the location of the search target; SI Text and Fig. S1.) Observers (n = 14) were asked to prioritize the search task to ensure attentional deployment. However, the measure of interest was the probe report probability.
Fig. S1.
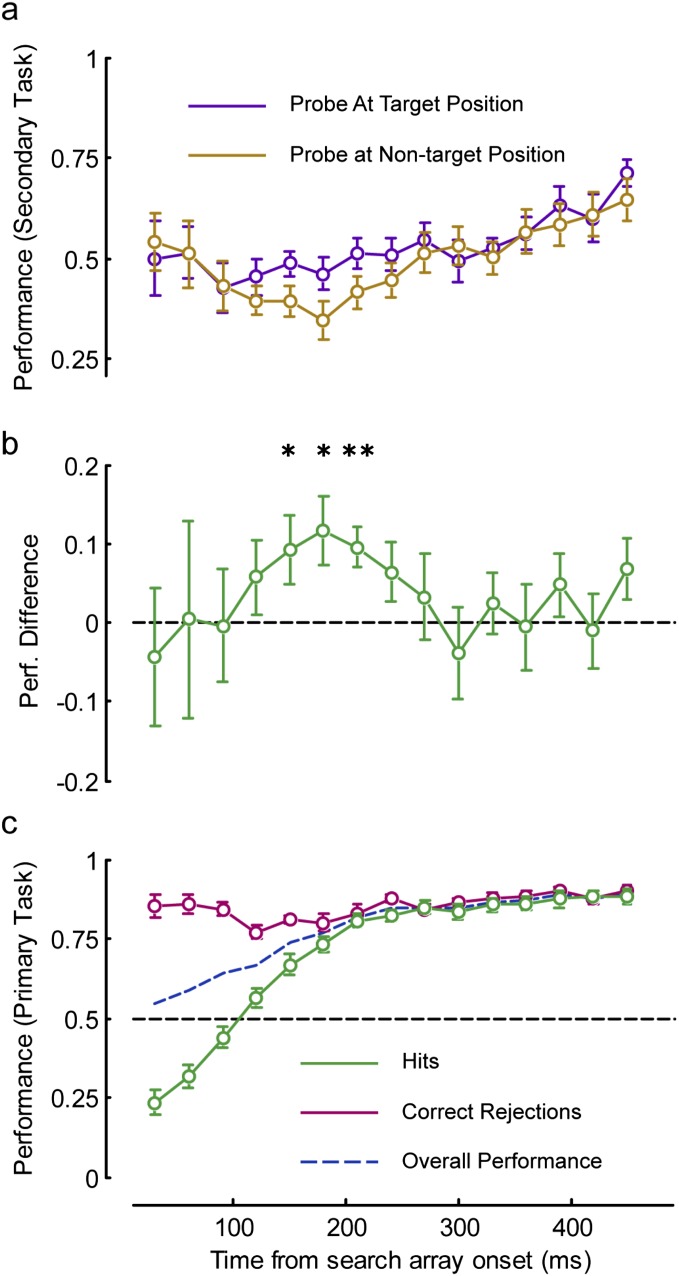
Performance in the probe task is dependent on target position in the primary task. (A) Performance in the secondary task (probe detection), separately for probes at the target and nontarget positions, is presented for only those trials that were “hits” in the primary task (target present, correct response), and where one probe was presented at the same position as the target (n = 14). (B) Difference in probe detection performance (Perf.) at target vs. nontarget positions (target − nontarget ± SEM over subjects, n = 14) is presented. For SOAs from 120 to 270 ms, detection at the target location is greater than at the nontarget location, significantly so at 210 ms [**P = 0.0014 by one-tailed t test, survives false discovery rate (FDR) correction; *P < 0.03, not significant after FDR correction]. (C) Performance in the primary task, with a separate analysis of hits (target present, correct response; these trials are analyzed in A and B) and correct rejections (target absent, correct response), is presented.
Primary Task (L vs. T).
In a preliminary experiment on the same group of observers (n = 14), we verified that each observer used an attention-dependent search strategy in this task by examining search slopes (RT vs. number of search items). We presented the search stimuli (L vs. T) for unlimited durations at constant eccentricity. Set size was randomly drawn between four and eight elements. We computed RT × set size slopes. As expected, search slopes were significantly positive (target present: 21.3 ± 0.1 ms per element, t(13) = 4.94, P < 0.001, confidence interval (ci) = [15.91 40.66]; target absent: 46.7 ± 0.1 ms per element, t(13) = 4.01, P = 0.0015, ci = [20.25 67.43]), generally accepted as an indication that the task requires attentional processing (2, 4, 5).
In the main experiment (Fig. 1), each trial started with the search task (looking for a T among L distractor letters; always four elements). Observers performed well, but not perfectly, on the primary task (average: 78.2% ± 3.7% correct). Thus, the task was challenging enough to keep the observers focused on performing the task and to engage attention, but not so challenging as to demotivate observers.
Secondary Task (Probe Report).
Following the search task, observers performed a probe identification task: At various times after the search array onset, two probes were presented randomly at two of the four previous stimulus locations (Fig. 1). Performance in reporting both probes correctly (PBOTH) or none of them correctly (PNONE) was used to solve a second-degree equation (Methods) aiming at determining the probability of probe report at the most and least attended of our two probed locations on each trial (P1 and P2, respectively). If P1 and P2 were equal, then we would conclude that attention was divided uniformly between all stimuli. However, if these values were not equal, we would then conclude that attention was focused on one stimulus or subgroup of stimuli at a time, thus definitely ruling out a parallel uniform model of attention processing during the search task.
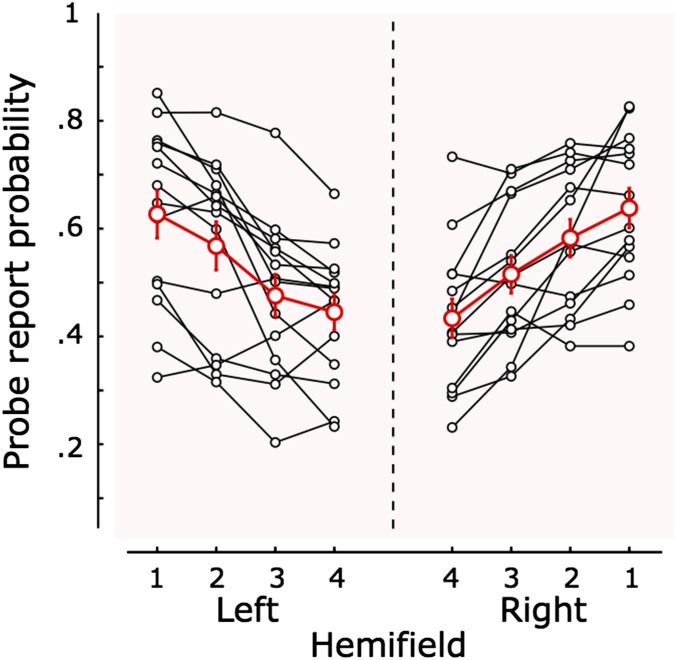
We first tried to identify any confounding, nonattention-dependent biases in probe detection performance that might lead to an erroneous conclusion of focused attention. We did observe a bias due to the position of the probe in the visual field (Fig. 2), such that probes presented in the lower part of the quadrant were, on average, less likely to be reported than probes presented in the upper part of the quadrant [one-way repeated measures ANOVA: F(13,111) = 11.95, P < 0.0001, eta2 = 47.9%]. This effect was observed in both hemifields. This type of visual field asymmetry has been reported previously (19–22). As a result, two probe locations, even adjacent, might present different report probabilities (i.e., P1 > P2) due to a position bias, rather than the kind of attentional effect under investigation here (one might speculate as to whether the position bias is, in turn, due to an attentional effect or some other spatially variable aspect of visual processing, but this question is beyond the scope of this investigation). To avoid including this bias in our analysis and to make sure that any difference in probe report probability is genuinely due to the distribution of attention, for each individual observer and each pair of probe locations, we performed χ2 tests under the null hypothesis that the two probes have an equal probability of being reported (P < 0.05, Bonferroni-corrected for multiple comparisons across the two hemifields and the six possible pairs of probe locations in each hemifield). We then only considered trials in which the probes were located at two positions not significantly different in terms of probe report probability, reducing the possibility of erroneously finding a nonuniformity in attention deployment. As will be seen in the main results below, for some stimulus–probe stimulus onset asynchrony (SOA) conditions, we found performance to be equal across probe locations, so we are confident that this approach has successfully removed any systematic bias in the results (because strictly spatial biases should be present regardless of the stimulus–probe SOA). Finally, only correct trials in which the target was absent were considered in the analysis because the presence of the target could drive attention to its location, artificially inflating P1 relative to P2; this behavior, however, would not be representative of the search process itself.
Fig. 2.
Report probability according to probe position. Curves of performance in probe report for each individual observer as a function of probe position (position numbers 1–4 increase from the horizontal to the vertical meridian), averaged across all SOAs, are shown in black. The curve of the average probabilities over all observers (n = 14) is shown in red. The performance in probe report varies significantly as a function of probe position.
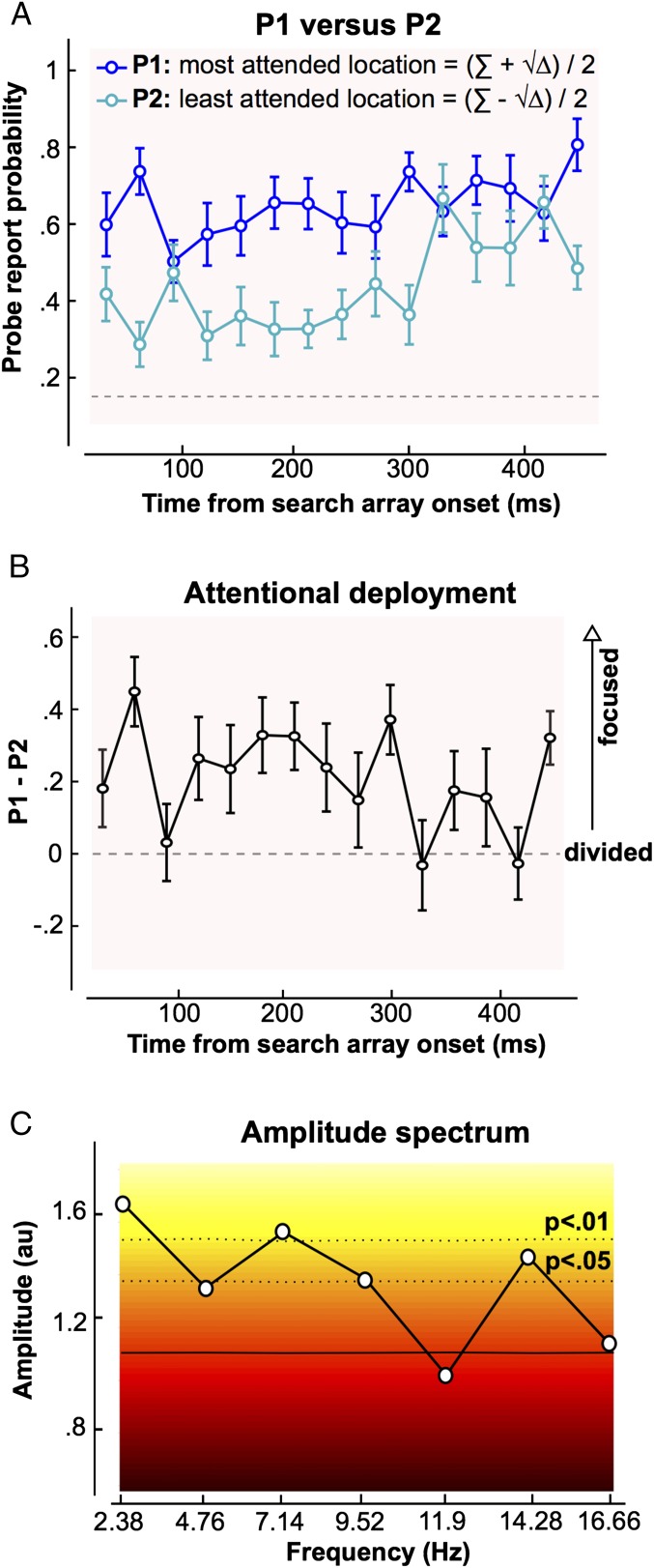
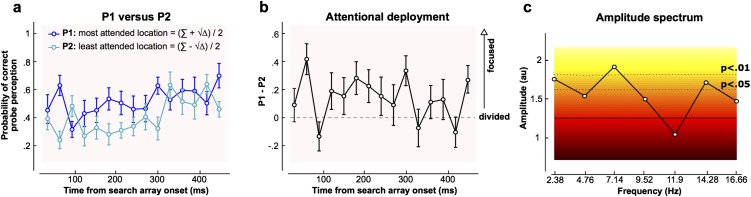
Based on these selected data (of the target-absent, correct response trials, 52% remained after selection based on the probe location, corresponding to an average of 21 trials per SOA condition per observer), we estimated the probabilities PBOTH (i.e., reporting both probes correctly) and PNONE (i.e., reporting none of the probes correctly) for each individual observer. These values allowed us to solve a second-degree equation and estimate P1 and P2 (Methods), (i.e., probabilities of probe report at the most and least attended of the two probed locations respectively, for each SOA) (Fig. 3A). It appears from these results that the spatial distribution of attention critically depends on the delay between search array onset and probe onset. A two-way repeated measures ANOVA indicates a main effect of the delay on probe report probability [F(14,182) = 4.52, P < 0.0001, eta2 = 25.8%], but also of the attention allocated to the probes, (i.e., P1 was significantly higher than P2 [F(1,13) = 22.70, P = 0.0004, eta2 = 63.6%]). We can already conclude that there was a bias of attention for one probe over the other. This finding indicates that attention was not equally divided among the four stimulus positions, but instead focused on one stimulus or subgroup of stimuli (the number of stimuli in the attentional focus is estimated in Results).
Fig. 3.
Dynamics of attentional deployment. (A) P1 (blue curve) and P2 (turquoise curve) are plotted as a function of the delay between search array onset and probe onset. P1 and P2 represent the two solutions of a second-degree equation as given by the equation Σ ± √∆, with Δ being the discriminant of the equation and Σ = 1 + PBOTH − PNONE (Methods). The dashed line represents the chance level (0.1667). A two-way repeated measures ANOVA indicates a significant difference between P1 (probability of probe report at the most attended location) and P2 (probability of probe report at the least attended location) [i.e., attention was not divided equally between positions; the probe report probability fluctuates over time, and there is a significant interaction between the delay and attention (P1/P2) factors]. (B) Difference between P1 and P2 averaged over all observers (n = 14) is represented. When this difference is zero, attention may be divided among all search locations. As this difference increases, attention must be increasingly focused on one or a subset of the search elements. This difference fluctuates significantly over time. (C) Amplitude spectrum obtained with a fast Fourier transform performed on the individual difference between P1 and P2 for each observer, and subsequently averaged, is represented. Background colors represent the significance of a bootstrap statistical test performed under the null hypothesis that the delay between search array onset and probe onset has no effect on P1 and P2. The plain horizontal black line represents the average amplitude spectrum of all the surrogate data obtained with bootstrapping. The dashed lines represent P value boundaries. The significant peaks at 2.4 Hz and 7.1 Hz indicate that the curve in B is periodically modulated at these specific frequencies (note that there is also a peak at 14.3 Hz, which we interpret as a harmonic frequency). au, arbitrary units.
At late delays, well after search array offset (∼300 ms), the difference between P1 and P2 seems to disappear, meaning that the two locations received comparable amounts of attention. Speculatively, at these late delays, observers may have already resolved the primary task and begun to attend to the secondary one. In this case, because probe locations are unpredictable, observers may have divided their attention over the entire area of the search array. It is also conceivable that having resolved the primary task, spatial attention was no longer required and lapsed, so the late performance would reflect a nonattentive level of performance in the probe detection task (i.e., not spatially restricted). The attention division at late delays could thus reflect observers’ strategy in performing both tasks efficiently, rather than a true visual search strategy.
Furthermore, we found a significant interaction between the delay and attention (P1/P2) factors [F(14,182) = 2.22, P = 0.008], meaning that P1 and P2 evolved differently over time. Indeed, it seems that the difference between P1 and P2 was modulated periodically [repeated measures one-way ANOVA: F(1,14) = 1.84, P = 0.036, eta2 = 12.4%], implying that attention oscillated between more focused and more divided modes (Fig. 3B). To determine the frequency of this modulation, we applied a fast Fourier transform on the individual difference between P1 and P2 for each observer, and averaged the subsequent amplitude spectra (Fig. 3C). The Fourier analysis was carried out only on the actual time points measured (i.e., without any zero-padding), yielding a lower frequency limit (and frequency resolution) of 2.38 Hz (1/0.42 s, the total duration analyzed) and an upper frequency limit established by the Nyquist frequency at half of the sampling rate [16.67 Hz (i.e., half of 1/0.030 s)]. Bootstrapping assessed the significance of each frequency component: The simulations were obtained by shuffling the labels of the SOAs, following the null hypothesis that P1 and P2 were independent of the delay between search array onset and probe onset (105 iterations). The 100,000 surrogate amplitude spectra were ranked in ascending order, separately for each delay. The 95,001th value was considered as the limit of the 95% ci [we used a similar procedure before (14)]. An experimentally observed spectral amplitude value was considered significantly different from the corresponding null distribution with P < 0.05 if it exceeded the 95% confidence threshold (and with P < 0.01 above the 99% confidence threshold, and so on). Significant modulation was apparent at three different frequencies (Fig. 3C). A primary oscillatory peak was present at 7.14 Hz [P < 0.01, maintained after false discovery rate correction for multiple comparisons with a P value threshold of 0.014]. A second peak at 14.28 Hz (P < 0.05) was found, which may simply represent a harmonic of the 7.14 Hz activity. Finally, significant modulation occurred at 2.38 Hz (P < 0.01). This last effect, however, must be treated with caution: Because 2.38 Hz is the lower limit of frequencies that we can test, it is impossible to tell whether it reflects a true peak in the spectrum (and thus genuinely periodic activity) or might rather be due to a slow (nonperiodic) trend in performance over the different SOAs, such as the gradual reduction of the P1/P2 difference up to ∼300 ms after search array onset (Fig. 3B). Therefore, we conclude that the P1/P2 report probability difference was modulated periodically at the specific frequency of 7.14 Hz (theta band) in this search task.
How Many Stimuli Are in the Attentional Focus?
Although attention clearly did not encompass all four stimuli simultaneously, how many did it process at any time? Our results only allow us to speculate on this question. At the first peak in attentional focus (Fig. 3B), 60 ms after search array onset, P1 performance was 66% and P2 performance was 32% (Fig. 3A). We already know that attention did not focus on all four stimuli. Consider now the possibility that attention could have encapsulated three stimuli simultaneously (and thus one of the four search items would be unattended on each trial). With only one unattended location, P1 (the most attended among the two probe positions) must directly reflect the performance at an attended location (i.e., P1 = 66% = attended location performance). The unattended location, if probed, would, by definition, be P2, but it would, in fact, only be probed 50% of the time (there were six possible pairs of probe location, three of which would probe a pair of attended locations, with the other three probing one attended location and one unattended location). Thus, the measured performance of 32% for P2 would actually reflect the average of performance at attended and unattended locations; because the attended performance is 66%, the unattended performance would have to be around −2%, well below chance level. It is consequently very unlikely that attention captured three stimuli simultaneously inside its focus. Next, let us consider the possibility that attention could have processed two stimuli simultaneously. Now, for the six possible probe pair combinations, one pair would probe both attended locations, one pair would probe both unattended locations, and the remaining four pairs would probe one attended location and one unattended location. Therefore, P1 would actually be attended in five of six trials, whereas P2 would be unattended in five of six trials. To reach net values of P1 = 66% and P2 = 32%, one would need to assume an attended performance of 74.5% correct and an unattended performance of 23.5% correct, which is perfectly plausible. Finally, is it possible that attention was focused on only one stimulus at a time? In that case, P2 (the least attended among the two probe positions) would directly measure the unattended performance (32%) and P1 would measure an equal mix of attended and unattended performance. To yield the net P1 of 66% would require an attended value of 100%, (i.e., perfect performance). In summary, we surmise that at this particular moment in time (60 ms after search array onset), attention was probably focused on only one or two of the four search elements, but not on three (otherwise, P2 would have been much higher than observed) or four (otherwise, P2 would have been equal to P1). Of course, the preceding section reflects a good deal of speculation, and further experiments would be necessary to investigate the capacity of the focus of attention more directly.
Discussion
In this experiment, observers performed a difficult visual search task (four stimuli). After varying delays, two of the four search locations were briefly probed. Based on the probabilities of reporting both probes and neither probe, we estimated the independent probabilities of reporting the individual probes (without being able to identify which probe is which, we could nonetheless designate a more attended probe and a less attended probe). These probabilities reflect the amount of spatial attention at each of these locations during the visual search. Critically, the results show that the individual probe probabilities were significantly different, ruling out a parallel uniform model of spatial attention deployment during this difficult search task.
In addition, we demonstrated that attentional deployment between the most and least attended locations is modulated periodically in time, with attention switching between more “focused” and more “divided” states at a frequency of ∼7 Hz. Although this temporal alternation is not a direct demonstration of sequential attention sampling (because we do not have a specific tag for each individual item, we cannot ensure that each “focusing” episode is targeted at a distinct item), it is certainly compatible with the idea of sequential search. Note also that we found another significant frequency component at 2.4 Hz (Fig. 3C). With this frequency being the lowest of the range that we could test, however, we cannot tell whether it reflects a true spectral peak (and thus an oscillatory pattern) or rather simply power at low frequencies arising because of a slow monotonic trend in the data. Indeed, we observed a decreasing trend of the attention focus across the different SOAs (Fig. 3C) that could account for the significant modulation at 2.4 Hz.
Previous findings have already demonstrated periodic sampling of visual information, linked to attention. In an electroencephalography experiment, the phase of ongoing oscillations at ∼7 Hz modulated visual perception, but only in the presence of attention (13). More recently, psychophysical studies provided evidence of a periodic and even sequential sampling of visual stimuli by attention at ∼8 Hz (16–18, 23). However, there is little or no experimental evidence from humans supporting the presence of such processing during visual search, or a link between this periodicity and the attentional strategy (i.e., sequential or parallel search). A study in the macaque monkey showed that neurons in the frontal eye field respond sequentially to the items of a difficult search task, at a frequency of 18–25 Hz (24). This finding was the first strong evidence of a link between attentional periodicity and sequential processing in visual search. However, the frequency of such processing is much higher than expected from previous experiments on humans, or indeed the present study. More recently, using human observers, we showed (14, 15) that visual search tasks might be processed periodically by attention at low frequencies (5–10 Hz). This discrepancy between our results and Buschman and Miller’s results (24) might be due to different factors, such as the use of nonhuman primates, the recording of single neurons, or the intrinsic difficulty of the search task. Further work will be necessary to investigate this difference and unequivocally determine the link between the periodic sampling of attention and the sequential processing of visual search tasks.
In this study, by estimating the probabilities of correct probe report at the most and least attended locations, we were able to determine that attention was not divided equally between all stimulus locations, but focused on one stimulus or a subgroup of stimuli. This result rules out a parallel uniform model of attentional processing during this difficult search task, favoring instead a sequential model. Indeed, any spatially nonuniform model of attention deployment will benefit from attentional resources sequentially scanning the environment, lest the search target be stuck in a nonoptimally attended location. Moreover, we have shown that this deployment was periodically modulated at ∼7 Hz, consistent with previous experiments showing periodicity in the sampling of visual stimuli by attention and suggestive of a link between sequential and periodic processing during attentive visual search.
Methods
Observers.
Fourteen observers (eight female) participated in this study. The sample size was determined based on studies in which the same type of task was used to investigate the temporal dynamics of attention [n = 15 (25) and n = 14 (14)]. The age range was 21–35 y. All observers had normal or corrected-to-normal vision. All participants gave written informed consent before the experiment. The study was approved by the local ethics committee “Sud-Ouest et Outre-Mer I” with the protocol number 2009-A01087-50, and was carried out in accordance with the provisions of the World Medical Association Declaration of Helsinki.
Apparatus and Stimuli.
Observers sat 57 cm from a computer screen (600 × 800 pixels, 100-Hz refresh rate) in a dark room. The experiment was programmed using the Psychophysics Toolbox extensions (26) in MATLAB (MathWorks). Each experimental trial comprised two tasks: a difficult search task and a probe detection task. Observers had to respond to both tasks. For the search task, observers had to report the presence or absence of a target shape T embedded among distracting L shapes. For consistency with another series of transcranial magnetic stimulation-EEG experiments suggesting that attentional difficult search is modulated periodically in time (15), the four shapes were presented at constant eccentricity (8.2° of visual angle) in either the bottom-right or bottom-left quadrant of the screen. Having all search items within a single hemifield also prevented the possible use of “independent” attentional resources for each hemifield (27). Each shape (1.8° of visual angle) was randomly presented at one of four orientations (cardinal orientations). The target was present in half of trials, pseudorandomly determined (i.e., the order of target present and target absent trials is random, but the overall number of each trial type is the same). This task was the primary task for observers and served to set the context, a difficult (attentive) visual search. However, our analysis actually concerned the secondary task, whereby observers had to report the identity of two black probe letters (upright orientation; 1.6° of visual angle) flashed randomly at two of the four search-array positions. Probe pairs were randomly chosen from 12 predetermined letters (B, C, D, G, J, K, M, N, P, Q, R, and S; always two different letters on a given trial).
Experimental Procedure.
Each trial was composed of two types of task (Fig. 1). Observers initiated the trial by pressing the space bar on the keyboard, and after a variable delay (1–2 s), the search array appeared randomly at either the bottom-right or bottom-left quadrant of the screen. Observers were asked to search for a T among L’s while maintaining fixation of the central blue dot (target present on 50% of the trials). The search array remained on the screen for 200 ms or until the onset of probe stimuli, whichever occurred first. At variable delays after array onset (15 SOAs from 30 to 450 ms at 30-ms increments), probe stimuli appeared at two positions, randomly chosen from the four search array locations. Probes were replaced after 80 ms by masks (# symbol) of 200-ms duration. Note that interruption of the search array with the probe array was necessary to probe search behavior down to very short delays. We set an upper limit of 200 ms on the search array presentation to somewhat limit the variation in task difficulty across conditions (and therefore optimize observer motivation), as well as to restrict the possibility of ocular exploration of the displays. We did not monitor eye position in this experiment. However, the fixation dot was always present on the screen, the search array was displayed for only a brief duration (always less than 200 ms), the task instructions stressed the importance of maintaining fixation, and all of the observers were well trained in psychophysics experiments. Therefore, we do not believe that eye movements are likely to explain the effects described in this paper. In addition, many of the effects reported above (e.g., nonuniform spatial distribution of attention) are visible at poststimulus times much earlier than normal saccadic latencies (before 120–150 ms).
Observers were instructed to prioritize the search task (primary task) and received auditory feedback in the case of a wrong answer. Subsequently, they had to report which probe letters they had perceived (secondary task). They were instructed to report two probes and to guess if unsure. There was no feedback for this task to ensure that the observers prioritized the first task. The trial ended when observers clicked on the “END” button with the computer mouse. Each observer carried out 1,440 trials in total.
Probability Estimates.
The aim of this experiment was to determine the spatiotemporal behavior of attention during a difficult search task. We adapted an analysis originally developed by Dubois et al. (25) to estimate the probability of probe report at the most and least attended of two locations, through the solution of a second-degree equation.
Models of attention processing propose that the two probe locations receive either equal amounts of attention (parallel model) or different amounts of attention (sequential model). In this study, we assumed that the amount of attention translates into correct probe report probability. In the following, we defined P1 as the probability of reporting the probe at the most attended location and P2 as the probability of reporting the probe at the least attended location (note that this definition refers to the most and least attended locations between the two randomly probed locations, which are not necessarily the most and least attended between the four search locations). We assumed that these probabilities only depend on the amount of attention these locations receive, considering the two events as independent (and constant across trials of comparable conditions). We defined PBOTH as the fraction of trials in which both probes were reported and PNONE as the fraction of trials when neither of the probes was reported.
On any given trial, we do not have access to the identity of the most and least attended locations, even for trials with just one of the two probes correctly reported (a probe can sometimes be detected accurately in the absence of attention, and vice versa, a probe could be missed in the presence of attention); however, we can estimate their probabilities via the solution of a quadratic equation, as detailed below. We were thus able to determine whether attention was equally distributed at both locations (P1 = P2; naturally predicted by the parallel model of attention processing during difficult search tasks) or focused on one location (P1 > P2; naturally predicted by the sequential model of attention). Note that this method, originally developed by Dubois et al. (25), successfully demonstrated that in a situation in which attention is known to be allocated in parallel to multiple locations (28), P1 was indeed equal to P2 (25). This earlier result provides confidence that the method itself does not artificially introduce a difference between P1 and P2.
The probabilities PBOTH and PNONE can be formulated by the following equations:
| [1] |
| [2] |
Eqs. 1 and 2 can be easily rearranged to the following Eq. 3 and Eq. 4
| [3] |
| [4] |
Basic quadratic theory tells us how to find a pair of unknowns, x and y, given that we know their sum (x + y) and product (x * y). More explicitly in this case, knowing that PBOTH and PNONE can be estimated directly from the experimental data, we define Eq. 5 and Eq. 6:
| [5] |
| [6] |
From quadratic theory, our two unknowns, P1 and P2, are the roots of the quadratic Eq. 7:
| [7] |
To solve this equation, we need to calculate its discriminant (Eq. 8):
| [8] |
Finally, Eq. 7 has two solutions:
We can see that the difference between P1 and P2 is given in Eq. 9 as follows:
| [9] |
In a nutshell, for each individual observer, based on his/her experimentally measured PBOTH and PNONE, we were able to estimate the difference in attention at two locations, directly related to Δ. We tested the null hypothesis that attention is equally divided; that is, Δ is not different from zero. Theoretically, because probabilities are real numbers, Δ should be nonnegative. However, with noise and the finite number of experimental measures taken, negative values of Δ could sometimes be obtained. This fact presents no problem as regards our measure of Δ, and, indeed, helpfully enables valid statistical comparison of Δ and zero (i.e., there was no systematic positive bias in the measure of Δ). On the other hand, it does present a problem when recovering the probability values P1 and P2, because the √Δ term yields a nonreal value when Δ is negative. For presentation purposes only, we were obliged to resolve this issue to obtain valid values for P1 and P2. To reflect the full (signed) distribution of Δ values (and because the difference between P1 and P2 is directly related to Δ), we chose to treat the square root of a negative Δ value as a negative number, such that P2 would be greater than P1. This approach reflects the intuitive notion that negative Δ values reinforce the null hypothesis by making Δ closer to zero (i.e., cancelling positive Δ values); similarly, having P2 greater than P1 reinforces the null hypothesis by making the difference between P1 and P2 closer to zero. Explicitly, in Fig. 3 and Fig. S2, we actually present:
Fig. S2.
Dynamics of attentional deployment. (A) P1 and P2 are plotted as a function of the delay between search array onset and probe onset. P1 and P2 represent the two solutions of a second-degree equation as given by the equation Σ ± √∆, with Δ being the discriminant of the equation and Σ = 1 + PBOTH − PNONE (Methods). A two-way repeated measures ANOVA indicates a significant difference between P1 (probability of correct probe perception at the most attended location) and P2 (probability of correct probe perception at the least attended location) (i.e., attention was not divided equally between positions); the probe perception probability fluctuates over time, and there is a significant interaction between the delay and attention (P1/P2) factors. (B) Difference between P1 and P2 averaged over all observers (n = 14) is represented. (C) This difference significantly fluctuates over time. The amplitude spectrum obtained with a fast Fourier transform performed on the individual difference between P1 and P2 for each observer, and subsequently averaged, is represented. Background colors represent the significance of a Monte Carlo statistical test (compare Fig. 3). The significant peak at 7.1 Hz indicates that the curve in B is periodically modulated at this specific frequency (we interpret the peak at 14.3 Hz as a harmonic frequency). au, arbitrary units.
Note that to ensure that any potential effect was not due to the detection of the target per se (i.e., when a target was present and detected, it might have attracted attention, and P1 would thus be significantly different from P2), we restricted the analysis to the half of the total trials in which the target was absent and the observers responded correctly.
Dissociating Probe Detection from Chance Performance.
The probability of correct probe report as defined above actually conflates two factors, the probability of accurately perceiving the probe plus the chance of guessing correctly. As a result, the analysis actually includes a slight approximation, in that the assumption of independence between the two probes (which is evident for the example in Eq. 1) does not hold strictly, given the nature of the task (for “choose two from 12 without replacement,” the chance level of reporting the second probe changes very slightly depending on whether the first probe was correctly identified or not). It is possible to resolve this approximation issue by modifying the analysis to dissociate chance detection from correct perception; we present this approach in SI Text. However, that analysis has the disadvantage of being more difficult for the reader, at least initially, although it can be seen that exactly the same reasoning steps are followed. Given that the results from both analyses are not different, to make the findings more accessible, we present the simpler version.
SI Text
Probability Estimates Dissociating Perception and Chance Performance.
As defined above, P1 and P2, the probabilities of correct probe report, really conflate two factors: actual probe perception plus chance performance (guessing). The analysis then includes a slight approximation because P1 and P2 are not truly independent. Here, we present an analysis that resolves this approximation by defining P1 and P2 instead as the probability of correct probe perception, and separately accounting for chance performance in the calculation. Although the mathematics looks more complicated, the goal and the steps taken are identical [i.e., we have access to the same experimental measures, PBOTH, PNONE, and PONE (the probability of reporting a single probe), and we want to find P1 and P2]. Thus, we express these terms relative to one another, and rearrange them to a form suitable for solution via the quadratic equation (we aim to isolate the terms P1 + P2 and P1 * P2).
Starting with PBOTH:
| [S1] |
It may help to consider that, for example, the expression P1 * (1 − P2) * 1/11 captures the probability of correctly perceiving one probe (P1) and failing to perceive the other (1 − P2) but guessing it correctly nonetheless (1/11), and likewise for the other terms (1/66 is the chance of correctly guessing two items from 12). To isolate the terms (P1 + P2) and (P1 * P2), this equation is rearranged as:
| [S2] |
Carrying out the same process for PONE yields:
| [S3] |
which is rearranged as:
| [S4] |
This pair of simultaneous equations yields:
| [S5] |
| [S6] |
The calculation of the discriminant, Δ, and of P1 and P2 can then proceed as above.
Using the same trial selection as in the first version of the analysis (i.e., based on the position of the probes to account for a probe position bias; Results), we calculated P1 and P2 for each individual and for each SOA (Fig. S2A). As in the first version, it appears that the spatial distribution of attention critically depends on the delay between search array onset and probe onset. A two-way repeated measures ANOVA indicates a main effect of the delay on the probability of correct probe perception [F(14,182) = 4.90, P < 0.0001, eta2 = 27.4%], a main effect of the attention allocated to the probes (i.e., P1 was significantly higher than P2 [F(1,13) = 5.19, P = 0.040, eta2 = 28.5%]), and an interaction [F(14,182) = 2.11, P = 0.013], meaning that P1 and P2 evolved differently over time. Furthermore, the difference between P1 and P2 was modulated periodically [repeated measures one-way ANOVA: F(1,14) = 1.84, P = 0.035, eta2 = 12.4%], implying that attention oscillated between more focused and more divided modes (compare Fig. S2B). Finally, to determine the frequency of this modulation, we applied a fast Fourier transform to compute the amplitude spectrum of the P1/P2 difference modulations observed on each individual (Results, Methods, and Fig. S2C). Again, the modulation of report probability difference at 7.1 Hz (and its harmonic at 14.3 Hz) was found to be highly significant (P < 0.01).
In summary, this more complex analysis yields qualitatively identical conclusions to those conclusions presented above.
Performance in the Probe Task Is Dependent on Target Position in the Primary Task.
Before turning to the main analysis of the probe task, which is the focus of this study, we first asked whether the probe task can actually access attentional behavior in the primary (visual search) task. We reasoned that when subjects correctly detect the target in the primary task, attention should be drawn to that location and be apparent as an advantage for probe detection at that location. Fig. S1 presents an analysis of the relevant subset of trials (target present, correct response, and one probe subsequently presented at the target location; mean of 16.8 trials per SOA condition per observer). Fig. S1A shows the probe detection performance as a function of SOA, separately for the probe at the target location and at the nontarget location. For clarity, Fig. S1B presents the difference between these values (target − nontarget). For all SOAs from 120 to 270 ms, probe detection at the target position is greater than at the nontarget position (although, considering individual time points, only at 210 ms is this difference statistically significant enough to survive correction for multiple comparisons). This apparent attentional advantage at the target location is best interpreted when performance in the primary task is taken into account (Fig. S1C). For early SOAs (and therefore short search array presentation durations) up to 90 ms, target detection is below 50% (i.e., observers cannot reliably detect the target), and it is thus no surprise that we then find no advantage for probes at the target location. For intermediate SOAs (120–270 ms), targets are reliably detected, and observers show an attentional advantage for probes at the target location. At long SOAs, this attentional advantage disappears; we can speculate that observers have typically detected the target before this point in time (performance in the primary task shows minimal improvement beyond 270 ms) and are able to redeploy attention specifically for the secondary probe task, so that no advantage at the target location is apparent. These results establish two important points regarding our further analysis:
-
i)
The secondary probe task does access the deployment of attention during the primary visual search task.
-
ii)
Given that detection of the search target is found to focus attention at that location, if we are to investigate the spatial deployment of attention during the visual search process in an unbiased way, then we must exclude target-present trials from the analysis. That is, all further analyses presented consider only target-absent trials (actually, correct rejection trials only, because even a wrongly detected target could focus attention artificially).
Acknowledgments
We thank Michael S. Landy for his suggestion relative to the probability estimation presented in SI Text and both Michael S. Landy and Marisa Carrasco for their constructive comments on the manuscript. This research was funded by a European Young Investigator Award (to R.V.), by European Research Council Consolidator Grant Perceptual-CYCLES (Grant 614244), and by the European Union’s Seventh Framework Program (Neuro-Bio-Inspired Systems: Spatial Cognition; Grant 600785).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1511331112/-/DCSupplemental.
References
- 1.Nothdurft H-C. Focal attention in visual search. Vision Res. 1999;39(14):2305–2310. doi: 10.1016/s0042-6989(99)00006-1. [DOI] [PubMed] [Google Scholar]
- 2.Palmer J, Ames CT, Lindsey DT. Measuring the effect of attention on simple visual search. J Exp Psychol Hum Percept Perform. 1993;19(1):108–130. doi: 10.1037//0096-1523.19.1.108. [DOI] [PubMed] [Google Scholar]
- 3.Sperling G, Melchner MJ. The attention operating characteristic: Examples from visual search. Science. 1978;202(4365):315–318. doi: 10.1126/science.694536. [DOI] [PubMed] [Google Scholar]
- 4.Treisman AM, Gelade G. A feature-integration theory of attention. Cognit Psychol. 1980;12(1):97–136. doi: 10.1016/0010-0285(80)90005-5. [DOI] [PubMed] [Google Scholar]
- 5.Wolfe JM, Cave KR, Franzel SL. Guided search: An alternative to the feature integration model for visual search. J Exp Psychol Hum Percept Perform. 1989;15(3):419–433. doi: 10.1037//0096-1523.15.3.419. [DOI] [PubMed] [Google Scholar]
- 6.Wolfe JM. Visual search. Curr Biol. 2010;20(8):R346–R349. doi: 10.1016/j.cub.2010.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Busey T, Palmer J. Set-size effects for identification versus localization depend on the visual search task. J Exp Psychol Hum Percept Perform. 2008;34(4):790–810. doi: 10.1037/0096-1523.34.4.790. [DOI] [PubMed] [Google Scholar]
- 8.Cameron EL, Tai JC, Eckstein MP, Carrasco M. Signal detection theory applied to three visual search tasks--identification, yes/no detection and localization. Spat Vis. 2004;17(4-5):295–325. doi: 10.1163/1568568041920212. [DOI] [PubMed] [Google Scholar]
- 9.McElree B, Carrasco M. The temporal dynamics of visual search: Evidence for parallel processing in feature and conjunction searches. J Exp Psychol Hum Percept Perform. 1999;25(6):1517–1539. doi: 10.1037//0096-1523.25.6.1517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Verghese P. Visual search and attention: A signal detection theory approach. Neuron. 2001;31(4):523–535. doi: 10.1016/s0896-6273(01)00392-0. [DOI] [PubMed] [Google Scholar]
- 11.Thornton TL, Gilden DL. Parallel and serial processes in visual search. Psychol Rev. 2007;114(1):71–103. doi: 10.1037/0033-295X.114.1.71. [DOI] [PubMed] [Google Scholar]
- 12.Townsend JT. Serial vs. parallel processing: Sometimes they look like Tweedledum and Tweedledee but they can (and should) be distinguished. Psychol Sci. 1990;1(1):46–54. [Google Scholar]
- 13.Busch NA, VanRullen R. Spontaneous EEG oscillations reveal periodic sampling of visual attention. Proc Natl Acad Sci USA. 2010;107(37):16048–16053. doi: 10.1073/pnas.1004801107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dugué L, Vanrullen R. 2014. The dynamics of attentional sampling during visual search revealed by Fourier analysis of periodic noise interference. J Vis 14(2). pii: 11.
- 15.Dugué L, Marque P, VanRullen R. Theta oscillations modulate attentional search performance periodically. J Cogn Neurosci. 2015;27(5):945–958. doi: 10.1162/jocn_a_00755. [DOI] [PubMed] [Google Scholar]
- 16.Fiebelkorn IC, Saalmann YB, Kastner S. Rhythmic sampling within and between objects despite sustained attention at a cued location. Curr Biol. 2013;23(24):2553–2558. doi: 10.1016/j.cub.2013.10.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Landau AN, Fries P. Attention samples stimuli rhythmically. Curr Biol. 2012;22(11):1000–1004. doi: 10.1016/j.cub.2012.03.054. [DOI] [PubMed] [Google Scholar]
- 18.VanRullen R, Carlson T, Cavanagh P. The blinking spotlight of attention. Proc Natl Acad Sci USA. 2007;104(49):19204–19209. doi: 10.1073/pnas.0707316104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Carrasco M, Talgar CP, Cameron EL. Characterizing visual performance fields: Effects of transient covert attention, spatial frequency, eccentricity, task and set size. Spat Vis. 2001;15(1):61–75. doi: 10.1163/15685680152692015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Talgar CP, Carrasco M. Vertical meridian asymmetry in spatial resolution: Visual and attentional factors. Psychon Bull Rev. 2002;9(4):714–722. doi: 10.3758/bf03196326. [DOI] [PubMed] [Google Scholar]
- 21.Abrams J, Nizam A, Carrasco M. Isoeccentric locations are not equivalent: The extent of the vertical meridian asymmetry. Vision Res. 2012;52(1):70–78. doi: 10.1016/j.visres.2011.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rezec AA, Dobkins KR. Attentional weighting: A possible account of visual field asymmetries in visual search? Spat Vis. 2004;17(4-5):269–293. doi: 10.1163/1568568041920203. [DOI] [PubMed] [Google Scholar]
- 23.VanRullen R. Visual attention: A rhythmic process? Curr Biol. 2013;23(24):R1110–R1112. doi: 10.1016/j.cub.2013.11.006. [DOI] [PubMed] [Google Scholar]
- 24.Buschman TJ, Miller EK. Serial, covert shifts of attention during visual search are reflected by the frontal eye fields and correlated with population oscillations. Neuron. 2009;63(3):386–396. doi: 10.1016/j.neuron.2009.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dubois J, Hamker FH, VanRullen R. Attentional selection of noncontiguous locations: The spotlight is only transiently “split”. J Vis. 2009;9(5):1–11. doi: 10.1167/9.5.3. [DOI] [PubMed] [Google Scholar]
- 26.Brainard DH. The psychophysics toolbox. Spat Vis. 1997;10(4):433–436. [PubMed] [Google Scholar]
- 27.Alvarez GA, Cavanagh P. Independent resources for attentional tracking in the left and right visual hemifields. Psychol Sci. 2005;16(8):637–643. doi: 10.1111/j.1467-9280.2005.01587.x. [DOI] [PubMed] [Google Scholar]
- 28.Bichot NP, Cave KR, Pashler H. Visual selection mediated by location: Feature-based selection of noncontiguous locations. Percept Psychophys. 1999;61(3):403–423. doi: 10.3758/bf03211962. [DOI] [PubMed] [Google Scholar]