The modular and integrative functional architecture of the human brain

Significance

Many complex networks are composed of “modules” that form an interconnected network. We sought to elucidate the nature of the brain’s modular function by testing the autonomy of the brain’s modules and the potential mechanisms underlying their interactions. By studying the brain as a large-scale complex network and measuring activity across the network during 77 cognitive tasks, we demonstrate that, despite connectivity between modules, each module appears to execute a discrete cognitive function relatively autonomously from the other modules. Moreover, brain regions with diverse connectivity across the modules appear to play a role in enabling modules to interact while remaining mostly autonomous. This generates the counterintuitive idea that regions with diverse connectivity across modules are necessary for modular biological networks.

Abstract

Network-based analyses of brain imaging data consistently reveal distinct modules and connector nodes with diverse global connectivity across the modules. How discrete the functions of modules are, how dependent the computational load of each module is to the other modules’ processing, and what the precise role of connector nodes is for between-module communication remains underspecified. Here, we use a network model of the brain derived from resting-state functional MRI (rs-fMRI) data and investigate the modular functional architecture of the human brain by analyzing activity at different types of nodes in the network across 9,208 experiments of 77 cognitive tasks in the BrainMap database. Using an author–topic model of cognitive functions, we find a strong spatial correspondence between the cognitive functions and the network’s modules, suggesting that each module performs a discrete cognitive function. Crucially, activity at local nodes within the modules does not increase in tasks that require more cognitive functions, demonstrating the autonomy of modules’ functions. However, connector nodes do exhibit increased activity when more cognitive functions are engaged in a task. Moreover, connector nodes are located where brain activity is associated with many different cognitive functions. Connector nodes potentially play a role in between-module communication that maintains the modular function of the brain. Together, these findings provide a network account of the brain’s modular yet integrated implementation of cognitive functions.

The principle of modularity, in which a system or process is mostly decomposable into distinct units or “modules,” explains the architecture of many complex systems. Biological systems, including the human brain, are particularly well explained by the principle of modularity (1–7). For example, gene expression in the brain is modular; the transcriptomes of human brain regions are robustly organized into modules of coexpressed genes that reflect the underlying cellular composition of brain tissue (8), and the spatial topography of cortex is also strongly reflected in its genetic topography—the closer two cortical regions, the more similar their transcriptomes (9). Moreover, these genetic divisions corresponded largely to meaningful structural and functional divisions (10, 11). This suggests a modular evolution of the brain, as functions that are adjusted in a modular manner require modular genetic bases (3). Brain regions also exhibit cytoarchitectonic differences (12). A modular structural wiring network (i.e., white matter tracts), with dense connectivity within modules and weak connectivity between modules, has also been consistently found in human brain imaging data (5, 6, 13, 14). Finally, the brain’s functional architecture—how the brain’s modules interact to produce cognition—appears modular (7, 15–17).

One of the most powerful mathematical frameworks for studying the functional architecture of the human brain is the network science (i.e., graph theory) approach (5, 18–21). Network models represent the brain as a graph with a set of nodes, usually around 10¹ to 10⁵ areas of the brain, with edges (i.e., connections) between nodes. Here, edges represent the strength of the correlation between the nodes’ time series of spontaneous neural activity [usually derived from “resting-state” fMRI (rs-fMRI) data where the subject is not administered a cognitive task]. These edges represent “functional connections,” which are not a direct proxy for anatomical connectivity but are largely constrained by anatomical connectivity (13, 22–25). A functional connection between two nodes represents the phase-locking of the two nodes’ low-frequency oscillations, which is associated with the transfer of information between two nodes or the modulation of activity in one node by another node (26, 27). Although not every node and functional connection in the brain is identical, modeling all of the functional connections in the brain as edges between nodes in a network allows for the study of global properties of the brain, such as modularity. This level of analysis complements analyses that measure activity magnitudes within particular brain regions, not connectivity between all regions. These two approaches are not redundant; a brain region can decrease in activity, but increase in connectivity with other brain regions (28). Thus, in this study, we use both types of analyses.

Nodes can be divided into modules by grouping the nodes that are most tightly connected to each other into a single module. When applied to spontaneous neural activity in humans measured via rs-fMRI, this procedure reveals a modular network architecture, in that a large fraction of the edges falls within the modules compared to the expected fraction if edges were distributed at random (7, 16). These modules reflect the underlying structural connectivity architecture of the brain, in that a large number of the functional connections in a module reflect direct anatomical connections (22, 29, 30). Moreover, the spatial organization of these modules corresponds to regions that have more highly correlated gene expression than expected by chance (11). Importantly, the brain’s network architecture during task performance is shaped primarily by the network architecture present during resting state (i.e., spontaneous neural activity), as spontaneous neural activity is likely a prior or constraint on task activity (31, 32). This has been demonstrated in humans using fMRI (33–37), in monkeys using multielectrode recordings (38), and in zebrafish using two-photon Ca²⁺ imaging (39). Thus, predictions regarding the brain’s network structure—and potentially nodes’ activity magnitudes—during tasks can be made based on the brain’s network structure during spontaneous neural activity.

Given a division of nodes into modules, each node’s topological role in the network can be characterized by graph theory metrics that measure the node’s connectivity within its own module and to other modules. A metric called the participation coefficient measures how evenly distributed a node’s edges are across modules, dividing nodes into two classes—connector nodes with many global edges across modules, and local nodes with mostly within-module edges. Connector nodes are thought to have access to information among different modules and thus potentially integrate information across or coordinate connectivity between the modules, whereas local nodes support the specialized function of individual modules (40, 41). A second metric called the within-module–degree z score measures how well connected a node is to nodes in its own module. Thus, connector nodes are further subdivided into “connector hubs” and “satellite connectors” that both have high participation coefficients, but only connector hubs have high within-module–degree z scores. Local nodes are further subdivided into “provincial hubs” and “peripheral nodes” that both have low participation coefficients, but only provincial hubs have high within-module–degree z scores (42–44). These two metrics capture the topological roles of nodes in many large-scale complex networks, such as the mouse brain (45), the cat brain, the macaque brain (46), the Internet, air transportation networks, Arabidopsis thaliana, the protein interactome of Caenorhabditis elegans, and metabolic networks (44). Moreover, in the macaque brain, a brain region’s participation coefficient is positively correlated with its dendritic tree size, spine count, spine density, and layer III pyramidal soma size, suggesting a relationship between a brain region’s topological position in the macroscale brain network and the region’s cytoarchitecture (47). In humans, regions with high participation coefficients are implicated in a diverse range of tasks (41, 48, 49) and are located where many modules are within close physical proximity (40).

The brain’s modular, yet integrated, functional architecture could potentially involve each module executing a discrete cognitive function mostly autonomously or informationally encapsulated from the other modules (3, 50–53), where the computational load in one module is not heavily influenced by processing in the other modules. How discrete the functions of modules are, how dependent the computational load of each module is to the other modules’ processing, and what the precise role of connector nodes is for between-module communication is underspecified. Here, to specify the brain’s modular functional architecture and the role of connector nodes, we measure each node’s connectivity in the network during spontaneous neural activity (measured with rs-fMRI), and then make predictions about those nodes’ activity magnitude probabilities across 9,208 experiments of 77 tasks in the BrainMap database (54). Moreover, we use a highly principled model of cognitive functions—an author–topic (i.e., hierarchical Bayesian) model of the BrainMap database (49)—that provides an ontology of cognitive functions, which are each represented by their probability of engagement in each task in the BrainMap database and the probabilistic spatial distribution of the cognitive function’s activity across the brain. Thus, the model allows for a precise estimate of the number of cognitive functions engaged in each BrainMap task. We refer to the cognitive functions estimated via the author–topic model as cognitive components. In the context of this approach and the large array of cognitive tasks in the BrainMap database, a modular functional architecture with connector nodes makes very specific testable predictions (illustrated in Fig. 1). First, if each module is dedicated to a discrete cognitive function, the cognitive components and modules should exhibit similar spatial distributions in the brain and show similar engagement in each BrainMap task. Second, when more cognitive functions (in our analyses, cognitive components or potentially modules) are engaged in a particular task, more discrete information is generated across the entire brain network and transferred between modules. If the modules’ processing is relatively autonomous (i.e., modular), local nodes (i.e., nodes with mostly within-module connections) should not be required to process more information when more cognitive functions are engaged. Thus, activity at local nodes in each module should not increase during the performance of tasks that engage more cognitive functions. Third, during tasks in which more cognitive functions are engaged, connector nodes should increase activity to maintain modularity while additional information is generated and transferred across the brain, perhaps by integrating information across modules or coordinating the connections between those modules. Finally, connector nodes, to execute the function suggested by the third prediction, should be located where brain activity is associated with many different cognitive components.

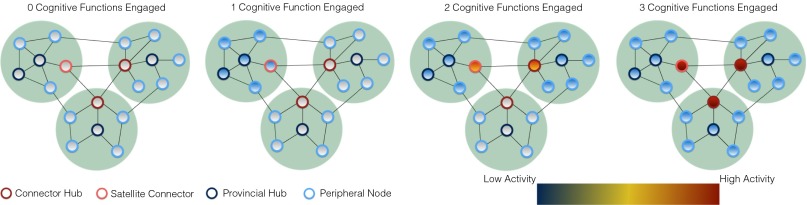
Fig. 1.

Empirical predictions of a modular functional architecture with connector nodes. Each light green circle represents a set of nodes comprising a unique module. The four types of nodes are represented in different colors. Activity is shown from low activity in blue to high activity in dark red. From Left to Right, as the number of cognitive functions (measured in our analysis by modules and cognitive components) engaged in a task varies from 0 to 3, a modular functional architecture predicts that activity will increase at connector hubs and satellite connectors (i.e., connector nodes with high participation coefficients), but not at provincial hubs or peripheral nodes (i.e., local nodes with low participation coefficients).

Results

Overview.

To test the predictions of the brain’s modular functional architecture with connector nodes, we built a network model of the brain by measuring spontaneous neural activity with rs-fMRI and correlated the activity probabilities during each BrainMap task [i.e., how often a region’s blood oxygenation level-dependent (BOLD) activation magnitude was high enough to be reported active across BrainMap experiments for the task] at the four types of nodes in the network with the number of modules or cognitive components engaged in that task. We also compared the spatial distribution of the cognitive components (derived from BrainMap) to the modules (derived from rs-fMRI of spontaneous neural activity), as well as their engagement across BrainMap tasks.

Network Model of the Brain.

Our network model of the brain was built from 24 healthy human subjects. We recorded six separate 10-min blocks of whole-brain spontaneous neural activity with rs-fMRI in each subject (2,610 time points per subject). As there is no agreement regarding the optimal brain atlas to parcellate the brain into nodes in the network, we used four different brain atlases, which we refer to by the name of the first author of the publication. We also validated our results with a publicly available spontaneous neural activity (measured via rs-fMRI) correlation matrix that used a fifth brain atlas (35). Thus, we built five different networks—four with our data using four different atlases to define the nodes in the network [which we refer to as the Shen (55), Power (16), Gordon (56), and Craddock (57) networks], and one with the publicly available data and a fifth brain atlas, which we refer to as the Crossley network. For ease of presentation, only results from the Shen network are presented in Figs. 2 and 3. We chose the Shen network because it has extensive brain coverage, and the number of nodes is common for graph theory analyses of rs-fMRI in humans (16, 56).

Fig. 2.

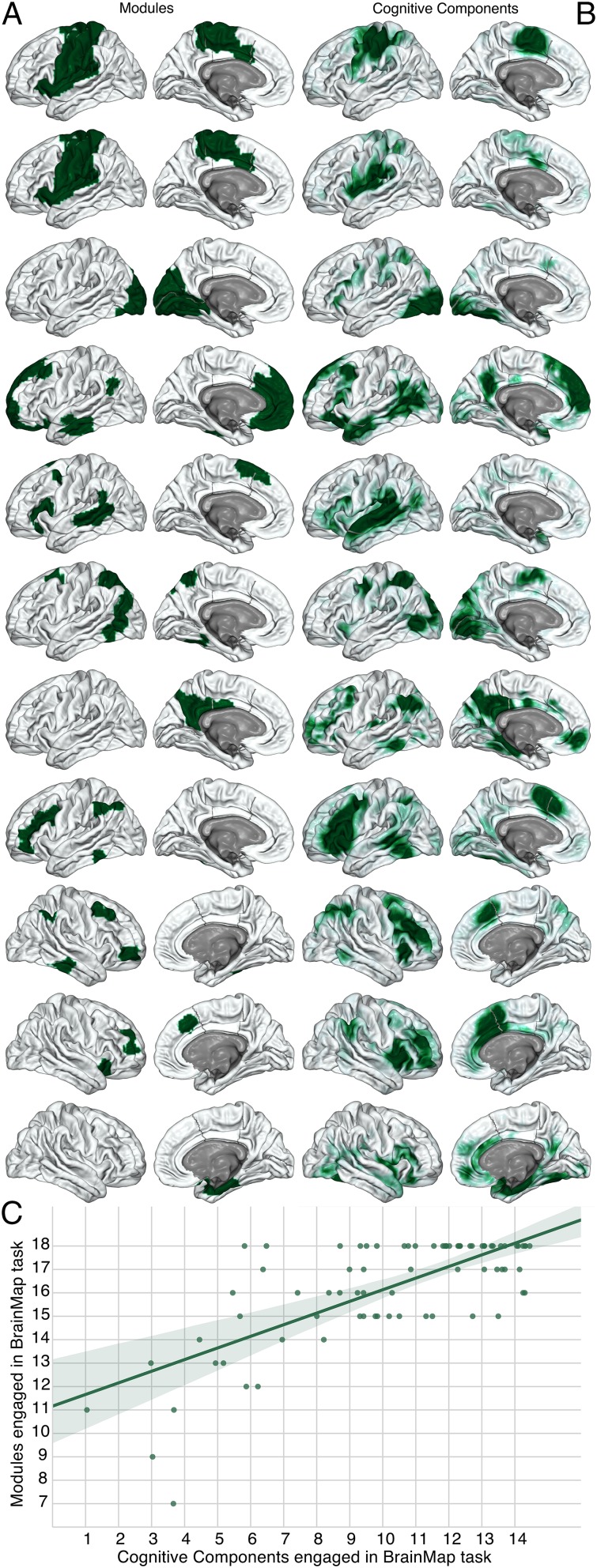
Spatial distribution of network modules and author–topic cognitive components. (A, left column) Modules derived from spontaneous neural activity measured via rs-fMRI with graph theory. (B, right column) Cognitive components derived from the BrainMap database with an author–topic model. Each row comprises a unique module and the cognitive component with the highest probability of activity at voxels in the module. However, the module on the first two rows is a duplicate of the same module, as two different cognitive components had a high probability of activating voxels in it. The spatial distribution of network modules and cognitive components in subcortical regions are presented in Fig. S1. All modules with more than 5 nodes are shown, with the cognitive component that has the highest probability of activating voxels in the module on the same row, to the Right. As a default, the left hemisphere is plotted, unless the module or cognitive component was predominantly located in the right hemisphere. This figure illustrates the high level of shared spatial distribution between modules and cognitive components. (C, Lower) The correlation between cognitive components engaged and modules engaged in each BrainMap task. Each dot represents a BrainMap task. The number of modules and cognitive components engaged in each BrainMap task is strongly correlated.

Fig. 3.

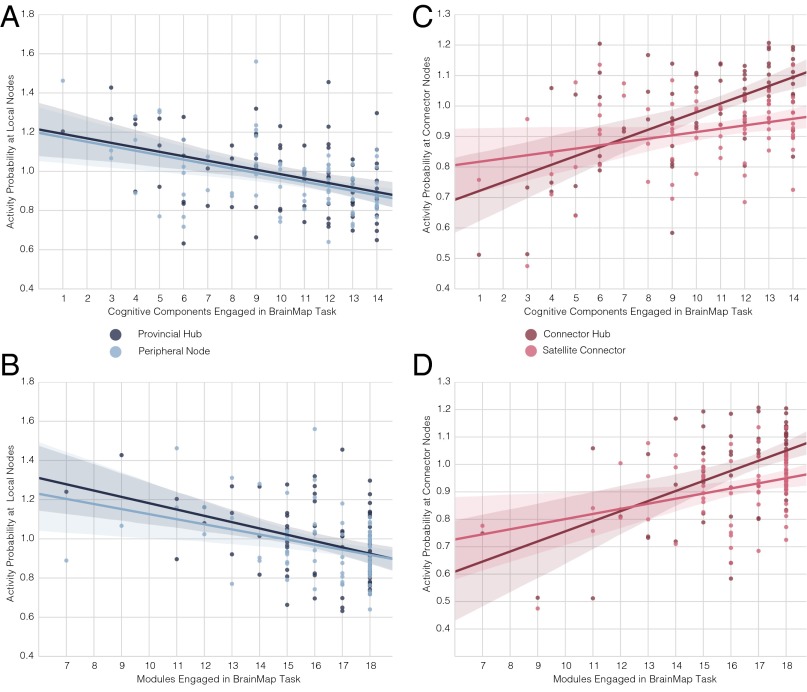
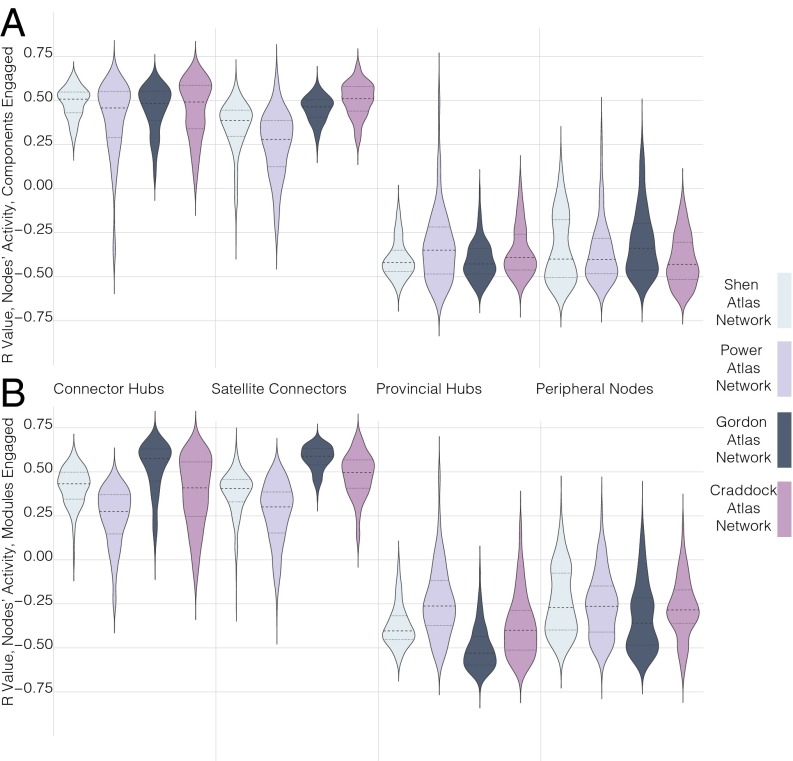
Activity probabilities at different types of network nodes across BrainMap tasks based on the number of modules or cognitive components engaged. Each dot is the mean of activity probabilities in a BrainMap task at the active nodes of interest divided by the mean of activity probabilities across all active brain nodes in the task. In line with predictions from Fig. 1, there is no increase in activity probability at provincial hubs and peripheral nodes (i.e., local nodes) in tasks that engage more components (A) or modules (B), but there is an increase at connector hubs and satellite connectors in tasks that engaged more cognitive components (C) or modules (D).

In each network, two nodes are connected by a weighted edge, with the weight being the Fisher-transformed Pearson correlation value (z) between the time series of activity in the two nodes, if z survives cost thresholding, where a cost of 0.15 retains the strongest 15% of possible edges and their edge weights (i.e., z values) in the network. This cost is reported in the main results (Fig. 3). Modules were identified via consensus clustering (58) based on individual subjects’ networks and the InfoMap algorithm, which decomposes the network into modules based on the probabilistic flow of information through the network. We leveraged individual subjects’ module organization, as group-level averaging often does not accurately represent the topological properties of individuals’ networks (59). For each subject, a consensus matrix (a value of 1 where the two nodes are in the same module and a value of 0 elsewhere) was created by implementing the InfoMap algorithm on the subject’s network. The average of these matrices was used to form a weighted network, to which the InfoMap algorithm was applied. Because individual data are not available for the Crossley network, we ran the InfoMap algorithm on the group-level network. Using this procedure, 11 modules were identified in the Shen network (Fig. 2A and Fig. S1). This division of nodes into modules was then applied to a group-level network, where the edge weights were the average of subjects’ Fisher-transformed correlation matrices, only keeping edges (and their weight values) that survive cost thresholding. Participation coefficients and within-module–degree z scores were then computed for each node. These two metrics were then used to identify the four types of nodes previously defined. Other community detection approaches, the Louvain algorithm, and using motion scrubbed (60) time series yielded similar results (Dataset S1). Moreover, Figs. 4 and 5 and Fig. S2 show results from analyses of costs from 0.05 to 0.2 in 0.01 steps, and Datasets S1–S3 show results based on the average of each nodes' participation coefficient and within-module–degree z score across those costs (61).

Fig. S1.

Subcortical rs-fMRI network module (Top) and BrainMap author–topic cognitive component (Bottom).

Fig. 4.

Correlations between different types of network nodes’ activity probability and the number of cognitive components (A) or modules (B) engaged in the task across atlases and costs in individual subjects. A kernel density plot for each of the four brain networks and four types of nodes is presented. Each kernel represents all subjects at all cost thresholds in the given network for that type of node. The median and the 25th and 75th percentile of Pearson r values are shown in each kernel, with the median as the dashed line, and percentiles as a dotted line.

Fig. 5.

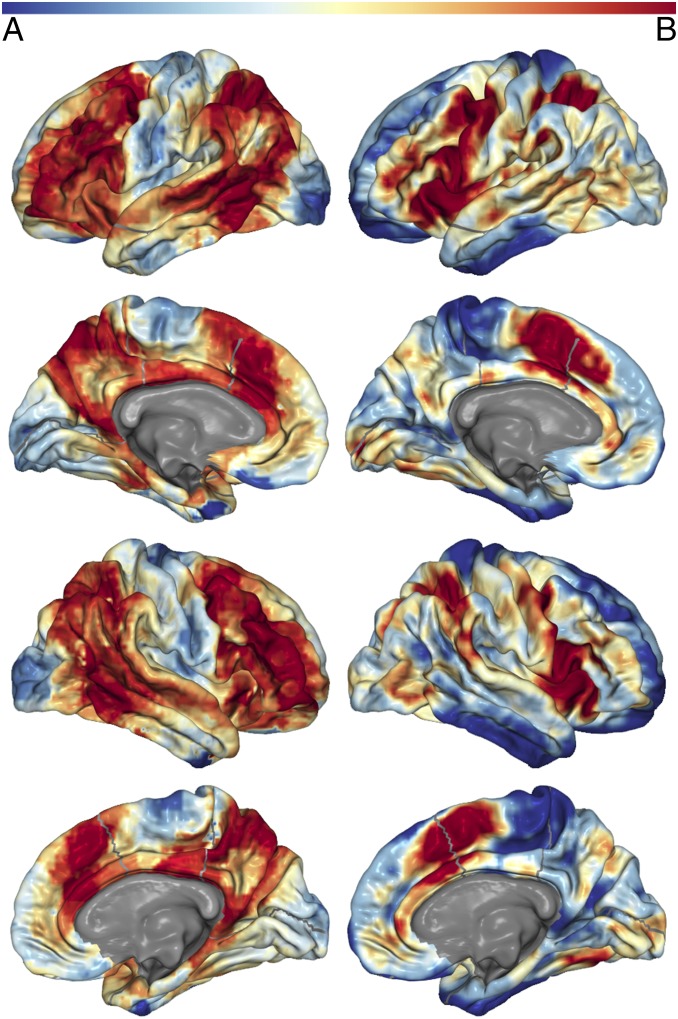
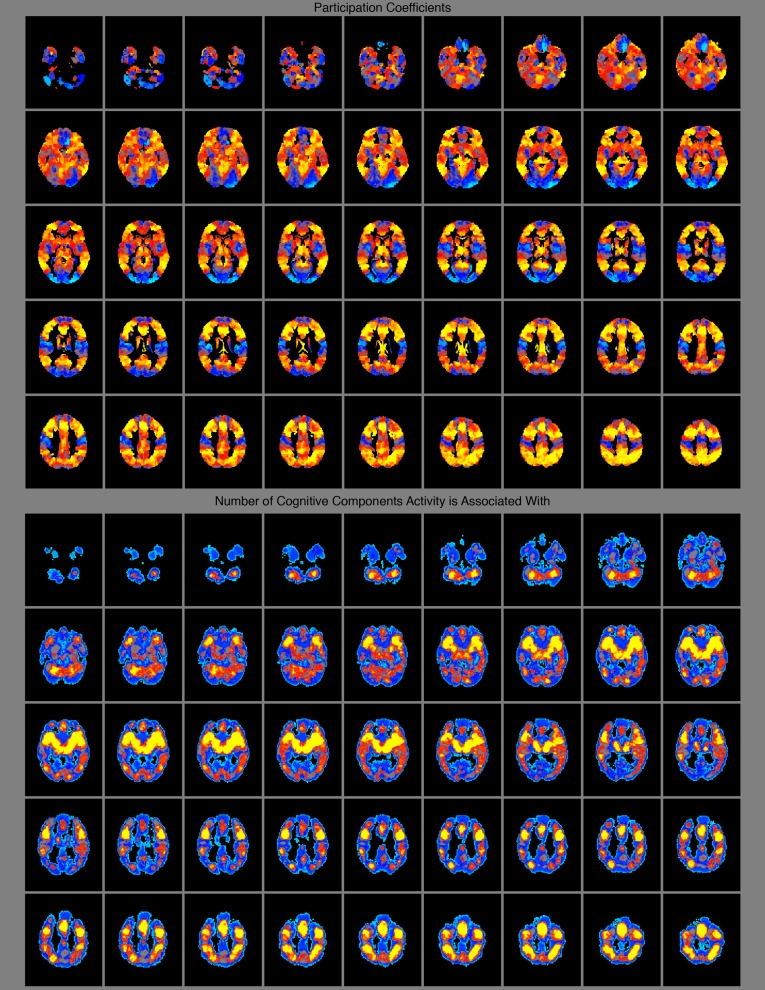
Spatial distribution of connector nodes and areas where many cognitive components have high probability of activity. (A, left column) The mean of each voxel’s participation coefficient across costs for all networks (i.e., atlases) that had coverage at that voxel (i.e., the calculation ignores 0 values if the network did not have a node that covered the voxel). These data are derived from the network model of spontaneous neural activity measured with rs-fMRI. (B, right column) The number of cognitive components that activity at the voxel is associated with above a probability greater than 1e-5. These data are derived from the author–topic model of BrainMap. The color bar is shown at the Top. Values have been normalized to sum to 1 for an accurate comparison across models. Thus, darker red areas represent higher values for both metrics, with lower values in blue. The results from this analysis for subcortical regions is presented in Fig. S3.

Fig. S2.

Correlations between different types of network nodes’ activity and the number of cognitive components (A) or modules (B) engaged in the task across atlases and datasets. A kernel density plot for each of the five brain networks and four types of nodes is presented. Each kernel represents results across cost thresholds, from 0.05 to 0.2 for the Shen, Power, and Gordon atlas networks and 0.01–0.1 for the Craddock atlas network. The median and the 25th and 75th percentiles of Pearson r values are shown in each kernel, with the median as the dashed line, and percentiles as a dotted line.

Author–Topic Model of Cognitive Functions.

To derive an ontology of cognitive functions in the human brain and estimate the number of cognitive functions engaged in each BrainMap task, we used an author–topic (i.e., hierarchal Bayesian) model of the BrainMap database originally built and then validated in an independent dataset (49). Unlike previous attempts to derive an ontology of cognitive functions by applying independent component analysis to the BrainMap database and then mapping the components to tasks post hoc (33, 34), the approach we implemented jointly models the association between brain activation and tasks under the appropriate premise that each task requires a unique number and set of discrete cognitive functions, with each cognitive function being executed by a distinct, but possibly partially overlapping, set of brain regions. In the current model, cognitive functions (referred to as cognitive components) were modeled as latent variables, explaining the relationship between 77 BrainMap tasks and corresponding brain activity. A cognitive component is a cognitive function that generates discrete information (e.g., visual representations of objects, motor movements, attentional biases) required to complete a task. We use the term “cognitive” in this broad sense. Fig. 2B and Fig. S1 show that different cognitive components are executed by different sets of brain regions, and that these cognitive components have a spatial distribution that is qualitatively similar to the modules identified from a network analysis of spontaneous neural activity (Fig. 2).

The author–topic model of cognitive components provides information crucial for our subsequent analyses that previous models of BrainMap data (33–35) were unable to provide. Each BrainMap task has a precise probability of each cognitive component being engaged in that task. This distribution allows for the quantification of the number of cognitive components (i.e., cognitive functions) engaged in each BrainMap task (Methods). This allows for an examination across BrainMap tasks of how task activity probabilities at different types of nodes in the network model of the brain are modulated by the number of cognitive functions engaged in the task. Moreover, each brain region has a probability value for each cognitive component, which allows us to compare the spatial distribution of the cognitive components to the modules derived from network analysis of spontaneous neural activity (Fig. 2 and Fig. S1). Also, we could identify brain regions where the probability values are high (>1e-5) for multiple cognitive components, which means that activity at that region is associated with multiple cognitive components. We reasoned that these regions, similar to connector nodes, likely interact with and have access to information from many cognitive functions. Thus, their spatial distribution was compared with brain areas identified as connector nodes.

Spatial Distribution and Engagement of Cognitive Components and Network Modules.

We first compared the spontaneous neural activity-based network model to the BrainMap based author–topic model. If each network module executes a discrete cognitive function, then the spatial distribution of the modules derived via network analysis of rs-fMRI of spontaneous neural activity should be similar to the author–topic cognitive component model derived from BrainMap task data. Also, there should be a linear relationship between the number of modules and cognitive components engaged in each BrainMap task, in that, as more cognitive components are engaged in a task, more modules are also engaged.

We quantified the similarity of the spatial distribution of modules and cognitive components with normalized mutual information (NMI) (62). To compute this, we assigned each node to the cognitive component that had the highest average probability at the voxels in the node. Thus, we have two divisions of the nodes, one based on the network analysis of spontaneous neural activity, and one based on the author–topic model of BrainMap. If the two divisions are identical, NMI is 1, whereas NMI is 0 if they are completely dissimilar. If NMI is low or there is not a linear relationship between the number of modules and cognitive components engaged in each task, this suggests that modules are not performing discrete cognitive functions. In all networks, we found a high level of NMI between the modules and the cognitive components, suggesting that they share a similar spatial distribution (Shen network NMI = 0.523; Power network NMI = 0.603; Gordon network NMI = 0.542; Craddock network NMI = 0.410; Crossley network NMI = 0.410; P < 1e-323 in every network; see Supporting Information for P value calculation). Fig. 2 and Fig. S1 illustrate this finding. For a relative comparison of NMI values for brain networks, the mean NMI between individual subject partitions and the group partition was 0.41, which is equal to or less than the NMI between the modules and cognitive components in every network. We also verified these results with the z score of the Rand coefficient (Dataset S4), which can be interpreted statistically.

We then quantified the number of modules engaged by a BrainMap task. Given the significant amount of smoothing in the activation images, we considered a module engaged if the activity probability at any voxel in the module was greater than the mean of activity probabilities in all active brain nodes engaged by the task. There was a strong correlation between the number of cognitive components and modules engaged in each task in every network (Fig. 2C; Shen: r = 0.722, P = 1.3e-13; Power: r = 0.577, P = 3.8e-8; Gordon: r = 0.807, P = 8.2e-19; Craddock: r = 0.693, P = 2.9e-12; Crossley: r = 0.598, P = 9.5e-9; df = 75). Together, these results suggest that each module executes a discrete cognitive function.

The Relationship of Nodal Activity Probabilities to Engagement of Cognitive Components and Modules.

The author–topic model allows us to precisely quantify the number of cognitive components engaged in each BrainMap task. With each activation map for each BrainMap task, we quantified the number of modules engaged in each task, as well as activity probabilities at the four different types of nodes. This allows us to test our predictions regarding the modules’ autonomy (Fig. 1) by examining how different types of nodes’ activity probabilities in a task are modulated by the number of cognitive functions (i.e., cognitive components or modules) engaged in the task. For each BrainMap task, we quantified a type of node’s activity probability during the task as the mean of activity probabilities at the active nodes of that type divided by the mean of activity probabilities throughout all active brain nodes during the BrainMap task. Then, across all tasks, we correlated activity probabilities at each type of node in each task with the number of cognitive components or modules engaged in the task.

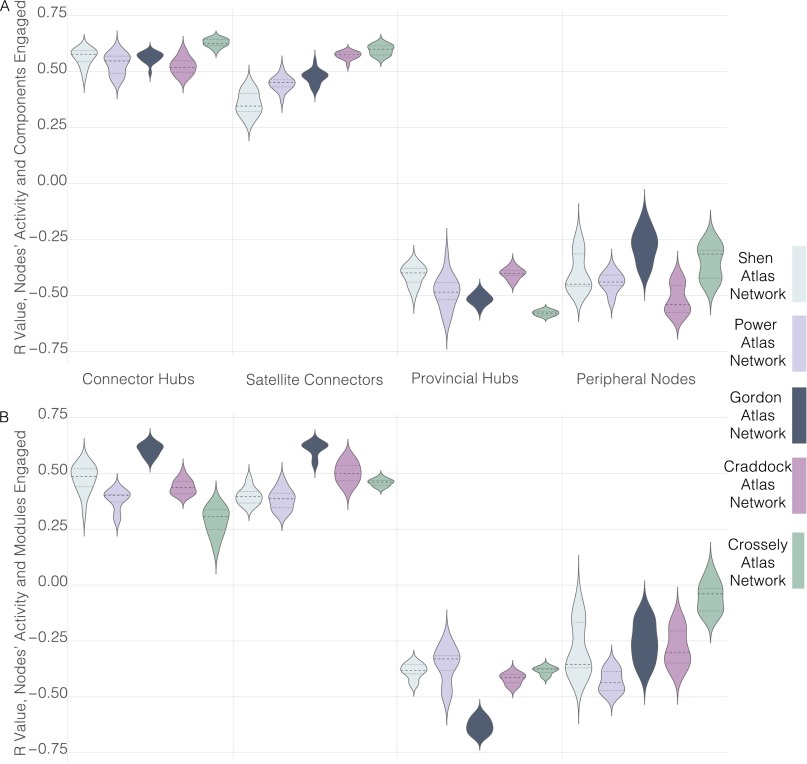
Consistent with predictions from a modular functional brain architecture, we did not observe a positive correlation in any network between provincial hub activity probabilities and the number of cognitive components or modules engaged in a task (Fig. 3A, cognitive components: Shen network: r = −0.395, P = 0.0004; Power network: r = −0.570, P = 6.6e-08; Gordon network: r = −0.530, P = 7.1e-07; Craddock network: r = −0.407, P = 0.0002; Crossley network: r = −0.571, P = 5.8e-08; df = 75; Fig. 3B, modules: Shen network: r = −0.384, P = 0.0006; Power network: r = −0.489, P = 6.2e-6; Gordon network: r = −0.644, P = 2.6e-10; Craddock network: r = −0.415, P = 0.0001; Crossley network: r = −0.374, P = 0.0007; df = 75). We also did not observe a positive correlation in any network between peripheral node activity probabilities and the number of cognitive components or modules engaged in a task (Fig. 3A, cognitive components: Shen network: r = −0.451, 3.9e-5; Power network: r = −0.461, P = 2.4e-5; Gordon network: r = −0.356, P = 0.002; Craddock network: r = −0.567, P = 7.7e-8; Crossley network: r = −0.423, P = 0.0001; df = 75; Fig. 3B, modules: Shen network: r = −0.354, P = 0.002; Power network: r = −0.379, P = 0.0007; Gordon network: r = −0.343, P = 0.002; Craddock network: r = −0.328, P = 0.003; Crossley network: r = −0.116, P = 0.316; df = 75).

In contrast, but consistent with the modular functional brain architecture predictions, in all networks, we observed a positive correlation between connector hub activity probabilities and the number of cognitive components or modules engaged in a task (Fig. 3C, cognitive components: Shen network: r = 0.600, P = 8.3e-9; Power network: r = 0.536, P = 5.1e-7; Gordon network: r = 0.569, P = 6.8e-8; Craddock network: r = 0.512, P = 1.9e-6; Crossley network: r = 0.641, P = 3.2e-10; df = 75; Fig. 3D, modules: Shen, r = 0.528, P = 7.9e-7; Power network: r = 0.409, P = 0.0002; Gordon network: r = 0.616, P = 2.5e-9; Craddock network: r = 0.398, P = 0.0003; Crossley network: r = 0.337, P = 0.002; df = 75). Significant positive correlations between satellite connector activity probabilities and the number of cognitive components or modules engaged in a task were also observed (Fig. 3C, cognitive components: Shen network: r = 0.309, P = 0.006; Power network: r = 0.514, P = 1.7e-6; Gordon network: r = 0.488, P = 6.6e-6; Craddock network: r = 0.593, P = 2.8e-12; Crossley network: r = 0.615, P = 2.7e-09; df = 75; Fig. 3D, modules: Shen network, r = 0.364, P = 0.001; Power network: r = 0.393, P = 0.0004; Gordon network: r = 0.627, P = 1.1e-9; Craddock network: r = 0.527, P = 8.1e-7; Crossley network: r = 0.447, P = 4.5e-05; df = 75).

Although a cost threshold of 0.15 was used in these analyses, to test for the effect of cost thresholds, we ran the same analyses at costs from 0.2 to 0.05. All results were similar and significant across costs (Fig. S2). We also averaged participation coefficients and within-module–degree z scores for nodes across these costs, and results were similar and significant (Dataset S1). Moreover, nodal participation coefficient values are publicly available for the Power network from another cohort of subjects (16, 40). With these data, we found a negative correlation between activity probabilities at local nodes (nodes with low participation coefficients) and the number of cognitive components (r = −0.572, P = 5e-08; df = 75) or modules (r = −0.436, P = 7e-05; df = 75) engaged in a task. We also found a positive correlation between activity probabilities at connector nodes (nodes with high participation coefficients) and the number of cognitive components (r = 0.651, P = 1e-10; df = 75) or modules (r = 0.489, P = 6e-06; df = 75) engaged in a task. For calculating the number of modules engaged in each task in these correlations, we used the division of nodes into modules originally published with the Power atlas and used to derive these participation coefficient values, which are often referred to as the “Power networks” (16). These modules also have a high NMI with the cognitive components (NMI = 0.520).

Individual Subject Analyses.

Although the modular functional brain architecture predictions were confirmed in the group-level networks, we sought to ensure that the network structure of individual subjects’ networks also showed the above pattern of correlations, such that only connector nodes increase activity probabilities in tasks that engage more cognitive functions. Thus, for each subject, for each network (except for the Crossley network, because individual subject data are not available) and cost threshold (0.05–0.2), we used the group-level module division (for example, for the Shen network, the modules in Fig. 2A and Fig. S1), but the edges between nodes in the network were defined by the subject’s Fisher-transformed correlation matrix. We then calculated activity probabilities at the four types of nodes in the network in the BrainMap tasks. Thus, each subject had 60 data points for each type of node: 15 data points for each of the four networks, representing the 15 different cost thresholds. Across subjects, on average, we observed a negative correlation between activity probabilities at local nodes and the number of cognitive components or modules engaged in a task. Across subjects, on average, we also observed a positive correlation between activity probabilities at connector nodes and the number of cognitive components or modules engaged in a task. In Fig. 4, these results are plotted as kernel density estimations with the median and the 25th and 75th percentile of Pearson r values across subjects and costs shown for the particular type of node in that particular network.

Alternative Analyses of Nodal Activity.

Although we did observe a seemingly counterintuitive decrease of activity at local nodes in tasks where more cognitive functions are engaged, follow-up analyses suggest that activity is not decreasing at these nodes but is only increasing at connector nodes. We measured “hub weighted activity” by calculating, for each task, the sum of (each voxel’s activity probability multiplied by that voxel’s participation coefficient or within-module–degree z-score score), divided by the sum of all voxels’ activity probabilities. These calculations only consistently find a strong correlation between participation coefficient weighted activity probabilities and the number of components or modules engaged in the task (cognitive components: Shen: r = 0.571, P = 6e-8; Power: r = 0.330, P = 0.003; Gordon: r = 0.503, P = 3e-6; Craddock: r = 0.498, P = 3.9e-6; Crossley: r = 0.595, P = 1e-8; df = 75; modules: Shen: r = 0.659, P = 7.3e-11; Power: r = 0.290, P = 0.01; Gordon: r = 0.675, P = 1.6e-11; Craddock: r = 0.457, P = 2.8e-5; Crossley: r = 0.444, P = 5.2e-5; df = 75). The relationship between within-module–degree z-score weighted activity probabilities and the number of cognitive components or modules engaged in the task was, overall, very weak (cognitive components: Shen: r = −0.093, P = 0.419; Power: r = −0.163, P = 0.156; Gordon: r = −0.196, P = 0.088; Craddock: r = −0.190, P = 0.09; Crossley: r = −0.275, P = 0.015; df = 75; modules: Shen: r = −0.226, P = 0.05; Power: r = −0.224, P = 0.05; Gordon: r = −0.317, P = 0.005; Craddock: r = −0.417, P = 0.0001; Crossley: r = −0.457, P = 2.8e-5; df = 75).

We also measured activity by computing a Spearman r between task-active voxels’ activity probabilities and the active voxels’ participation coefficients or within-module–degree z scores, and then correlated these r values with the number of cognitive components or modules engaged in the task. This calculation led to similar results. We observed positive correlations between r values of participation coefficients and task activity probabilities and the number of cognitive components or modules engaged in the task (cognitive components: Shen: r = 0.524, P = 1e-6; Power: r = 0.581, P = 3e-8; Gordon: r = 0.555, P = 1e-7; Craddock: r = 0.591, P = 1.5e-8; Crossley: r = 0.592, P = 1e-8; df = 75; modules: Shen: r = 0.480, P = 9.9e-06; Power: r = 0.385, P = 0.0006; Gordon: r = 0.660, P = 6e-11; Craddock: r = 0.439, P = 6.5e-5; Crossley: r = 0.402, P = 0.0003; df = 75). The correlations between r values of within-module–degree z score and task activity probabilities and the number of cognitive components or modules engaged in the task were, overall, very weak (cognitive components: Shen: r = −0.114, P = 0.323; Power: r = 0.184, P = 0.109; Gordon: r = −0.190, P = 0.1; Craddock: r = −0.067, P = 0.559; Crossley: r = −0.025, P = 0.827; df = 75; modules: Shen: r = −0.113, P = 0.328; Power, r = 0.071, P = 0.540; Gordon: r = −0.253, P = 0.027; Craddock: r = −0.165, P = 0.150; Crossley: r = −0.347, P = 0.002; df = 75).

These secondary analyses demonstrate that activity probabilities are not systematically shifting from local nodes to connector nodes, but that, in tasks that require more cognitive components or modules, there is greater activity probabilities at connector nodes. The decrease in activity probabilities at local nodes in tasks that require more cognitive components or modules observed in our main calculation is likely due to an increase in activity probabilities at connector nodes, which increases the mean of activity probabilities in the task relative to local nodes. This suggests that the brain does not obey the law of conservation of energy in network terms, as the total energy of the system does not appear constant.

Location of Connector Nodes and Convergence of Cognitive Components.

If connector nodes are integrating information and coordinating connectivity across modules, and modules are each executing a discrete cognitive function (as evidenced by the above results), then connector nodes should reside in brain areas where activity is associated with many different cognitive components. This location would allow for them to simultaneously interact with brain regions dedicated to multiple cognitive functions with minimal additional wiring costs. Qualitatively, we found that connector nodes reside in brain areas where activity is associated with many different cognitive components (Fig. 5 and Fig. S3). Quantitatively, the number of cognitive components that activity is associated with at a given brain area at greater than a probability of 1e-5 is greater at connector nodes than local nodes (Shen, t = 29.121, P = 7.1e-186, df = 150,520; Power, t = 60.059, P ∼ 0.0, df = 21,383; Gordon: t = 43.4, P ∼ 0.0, df = 56251; Craddock: t = 71.317, P ∼ 0.0, df = 142,999; Crossley: t = 44.006, P ∼ 0.0, df = 160,159). Although we previously showed that the modules and cognitive components share a similar spatial distribution, this finding demonstrates that the spatial distribution of areas that interact with many modules or cognitive components is also very similar.

Fig. S3.

Subcortical spatial distribution of participation coefficients (connector nodes) (Top) and areas where many cognitive components have high probability of activity (Bottom).

Discussion

The Modular Brain.

A detailed argument for the modular function of the brain was first presented over 30 years ago (53), with many versions of the concept presented since then (16, 18, 20, 63–74). A specific account of modularity with empirical support is “massive modularity” (16, 66, 68). Under this view, the brain consists of many modules that each executes a discrete cognitive function relatively autonomously from the other modules. Proponents of massive modularity (e.g., ref. 68) argue that cognitive adaptations to the environment that have evolved are just as likely to have been specific solutions as any other physical adaptation. That is, a discrete module for visual processing is just as likely to have been naturally selected as an opposable thumb is for grabbing. Moreover, proponents argue that a biological system that is composed of mostly autonomous modules with discrete functions will perform more effectively, more efficiently, and adapt faster than a system with a few general functions; thus, a modular functional network architecture is most probable from an evolutionary perspective. Several lines of evidence support this evolutionary argument and the discrete and autonomous nature of modules.

As mentioned in the Introduction, the genetic basis of each module is significantly specialized, a necessary condition for each module to have a discrete function that was shaped modularly by natural selection (3). Moreover, there is a strong spatial correspondence between modules derived from spontaneous neural activity obtained with rs-fMRI and the task-evoked activity in the BrainMap database, and these modules can be linked to broad behavioral domains or to specific groups of related tasks (33–35), suggesting that these modules might be dedicated to discrete cognitive functions. However, these analyses did not empirically derive discrete cognitive functions from the data in BrainMap that could be linked to specific regions in the brain. Here, we observed a strong correspondence between the spatial distribution of the cognitive components derived from the data in BrainMap and modules derived from rs-fMRI of spontaneous neural activity. Given that the cognitive components represent a highly principled model of cognitive functions, our results support the hypothesis that each module executes a discrete cognitive function.

Computational studies have demonstrated that selecting networks based on performance, but not wiring costs (i.e., the number of connections between nodes in the network) produces nonmodular networks that are slow to adapt to new environments. However, adding a selective pressure to minimize wiring costs, or varying the goals of the network, leads to the evolution of modular networks that quickly adapt to new environments (75, 76). Moreover, modular neural networks can be trained to solve problems with less connections than nonmodular networks (77). Thus, when the costs of adding connections is significant in the overall energy budget of an organism, as is likely for the brain, modular networks with weaker connectivity between modules than within the modules are superior to nonmodular networks, as they function as well and adapt faster without consuming as much energy. Moreover, a double dissociation was found between two modules, such that, for both modules, damage to a node in one module only caused dysfunction (i.e., a decrease in functional connectivity) in the damaged module, suggesting their autonomy (78). Finally, empirical functional connectivity studies have shown that modules are weakly functionally connected to each other, likely because their computations are predominantly distinct, suggesting modular function (6, 7, 16, 36, 79). However, connections do occur between modules that transfer information between the modules and influence local activity in the modules, potentially increasing the modules’ computational loads (6, 7, 16, 27, 28, 36, 80–83). Thus, to validate the autonomous nature of modules, it is necessary to demonstrate that, as more modules are engaged simultaneously and more information is generated across the network and transferred between the modules, the modules’ computational loads do not increase (50, 51, 53) (Fig. 1). Here, we used activity magnitude probabilities at the local nodes in each module to measure the computational load on each module—when more information needs to be computed, activity probabilities increase. Given that activity can dissociate from connectivity (28) and no previous analysis has quantified connectivity changes in relation to the number of modules engaged in a task, this type of evidence is not present in previous analyses of connectivity data. If the additional information that is generated and transferred between the modules when more modules are simultaneously engaged does not increase the modules’ computational load, the modules’ local nodes’ activity will not increase. This would suggest that each module, regardless of the information present across the network or transferred to it from other modules, executes a distinct function without an increased computational load (i.e., it is relatively autonomous). On the contrary, if activity does increase, this would suggest important computational dependencies between the modules, and thereby that brain function is potentially not modular (50, 53). We observed the former, demonstrating a decisive characteristic (50, 51, 53) of the human brain’s modular nature.

The Role of Connector Nodes in a Modular Network.

Brain function is often conceptualized as a balance between modular and integrative processing (14, 20, 50, 64, 71–74, 79, 84, 85). The previous results generate an important question regarding this balance—how does the modules’ functioning remain autonomous despite connectivity between the modules and the need for information to be integrated across the modules? One possible mechanism is to have brain regions that integrate across the modules and coordinate connectivity between the modules, keeping the modules’ function mostly autonomous. For example, understanding syntax is likely a discrete cognitive function, supported by a dedicated brain module, whereas getting the gist of a sentence is likely a distributed cognitive process, requiring the combination and integration of various discrete cognitive functions (e.g., vision, attention, semantics, syntax) and processing in multiple modules. Undoubtedly, even a seemingly simple cognitive process likely arises from the simultaneous engagement of multiple modules, which could be orchestrated by connector nodes.

In support of this notion, we found that connector nodes are located where activity is associated with many different cognitive components, and, crucially, activity increases at connector nodes as the number of cognitive functions engaged in a task increases. Thus, unlike local nodes, connector nodes’ increase in activity is proportional to the additional computational load required when many modules are engaged—when more information is generated across the brain that must be integrated and connectivity between many modules must be coordinated without sacrificing the autonomy of the modules’ function (i.e., modularity is maintained). Thus, connector nodes are potentially integrating information across the modules and coordinating connectivity between the modules (i.e., modulating direct connections between modules that are not routed through connector nodes) to ensure modular function, such that information generated in one module does not increase the computational load in the other modules, as we found. An alternative proposal regarding connector nodes is that they are flexible regions that are reused in various ways depending on the current task (48, 86). The connectivity of connector nodes is flexible, in that their connectivity changes based on the particular task demands and modules engaged in the task (41). However, if their function is not relatively fixed, it would be unlikely to observe a strong relationship between their computational load and the number of modules engaged in a task, as the interaction between computational load and the number of modules engaged in a task would be different based on the function they are executing in a given task. Thus, our evidence suggests that connector nodes have a relatively invariable function that becomes more demanding as more modules are engaged in a task.

A wide range of evidence supports this conclusion. It has been proposed that integration across modules occurs via brain regions with strong connectivity across many modules (40, 70, 71). Connector node regions are engaged in a diverse range of tasks (48, 49), because many different tasks require multiple modules, and thus connector nodes’ function. Also, similar to our finding regarding cognitive components, connector nodes are located where many modules are within close physical distance (40); this requires the least amount of physical wiring for maximal or simultaneous interactions across multiple modules. Along with being physically close to many modules, connector nodes appear to change membership to modules often, and this is associated with higher performance and modularity. For example, an fMRI study found that, when switching from a single task to a dual task, nodes changing their module membership was related to both increases and decreases in performance. However, the membership changes of connector node regions (i.e., brain regions identified as connectors in our analysis) was only associated with an increase in performance. Moreover, the high-performing subjects (i.e., subjects with connector nodes that changed module membership) had less connectivity between single-task modules (i.e., more modular) (83). Another fMRI study found that increased module membership changes of 11 regions, 7 of which are connector node regions in our analysis, predicted increased learning rates (87). Moreover, an fMRI study of learning across time showed that, although connectivity between motor and visual modules is broadly evident in all nodes within those modules (not just at connector nodes), motor and visual modules become less connected (i.e., more modular) to each other during learning, and this process appears to be driven by the temporo-parietal junction, entorhinal cortex, and a fronto-cingulate network, all of which contain connector nodes in our analysis (28). Finally, an fMRI study of a visual attention task found that connectivity changes in visual cortex that led to smaller local modules were associated with stronger top-down directional influence from, and stronger connectivity between, the dorsal frontal eye field, the intraparietal sulcus, and the superior parietal lobule, which are all connector nodes in our analysis (32). Together, these studies suggest that the connectivity of connector nodes allows for effective integration across modules and the coordination of between-module connectivity to maintain modularity, which improves performance. This generates the counterintuitive idea that nodes with diverse connectivity across modules might be necessary for modularity in biological networks.

Connectivity changes (measured via fMRI) from spontaneous to task activity also support integrative and coordinative functions for connector nodes. In an analysis of changes in connectivity from spontaneous activity to a range of task-evoked activity, most connections were maintained; however, connector node regions’ connectivity patterns varied as a function of the task (37). In a similar analysis of the connectivity changes from spontaneous activity to task-evoked activity across 64 tasks (36), the network architecture was modular, but there was decreased within-module connectivity during task performance (compared with resting state), with increased between-module connectivity. It is possible that connector nodes are involved in coordinating some of these changes in connectivity. In another analysis of these data, the fronto-parietal network had the highest mean participation coefficient of all of brain networks, exhibited the greatest changes in connectivity with the rest of the brain across tasks out of any network, and the whole-brain connectivity of the fronto-parietal network could predict which task the subject was engaged in. This finding was interpreted as suggesting that the fronto-parietal network can coordinate multiple modules that are engaged in the task (41).

Connector nodes integrating across or coordinating connectivity between task-relevant modules to maintain modular function is also consistent with observations of patients with brain pathology. For example, in patients with focal brain lesions, damage to connector nodes, but not local nodes, decreases the modularity of the global network structure (88). Moreover, transcranial magnetic stimulation to connector regions in two different modules (fronto-parietal and cingulate-opercular) increased global connectivity (likely decreasing modularity) (89). These results are precisely what one would expect if connector nodes’ function plays a role in global connectivity that maintains modularity. Moreover, patients with lesions damaging connector nodes exhibit widespread cognitive deficits, whereas damage to other brain regions (i.e., local nodes) causes specific cognitive deficits (90). Finally, connector node regions have been found to be metabolically demanding (91). Perhaps due to their crucial roles of integration and coordination and high biological cost (extensive wiring and metabolism), abnormal connector node function is associated with nine brain disorders, including schizophrenia and Alzheimer’s disease (92). Thus, the effects of brain damage and dysfunction can be interpreted in the context of our findings derived from brain imaging data in healthy individuals. That is, damage to or dysfunction of local nodes, due to their role in discrete cognitive functions, causes specific impairments without a degradation of the brain’s modular structure, whereas damage to or dysfunction of connector nodes, likely due to their role in the integration and coordination across many modules, which maintains modularity, causes widespread cognitive deficits and a degradation of the brain’s modular structure.

Connector nodes are a single facet of a large network of many complex interactions, and their function must be interpreted in this context. It is unlikely that all cognitive tasks require the engagement of connector nodes. For example, it has been shown that they are not recruited when a task is well learned (17, 28). Crucially, connector nodes are also not involved in all between-module connectivity. Nonconnector node regions play a role as well (28, 87, 93, 94), and, as noted above, increased between-module connectivity that is not routed through connector nodes has been found during many different tasks, and differentiates task connectivity from resting-state connectivity (36). Although the current and previous findings suggest that connector node regions coordinate some of these between-module connections, it is likely that other mechanisms for between-module communication exist that are executed by nonconnector nodes. In line with this, connector nodes are not the only nodes that change module membership during tasks (87, 93). For example, an fMRI study of a 2-back task showed that, although many connector node regions changed module membership and this predicted higher performance, the regions with the most module membership changes were in ventromedial prefrontal cortex, where no connector nodes were located in our analysis (93). Finally, although connector node regions all exhibit the graph theoretic property of a high participation coefficient, these regions do not all have identical cytoarchitecture and their connectivity profiles are to different modules. Thus, each connector node’s function likely has unique properties that are not captured by our graph theory approach. Certainly, the precise type or types of computations that occur at connector nodes, how this varies based on the particular nodes involved in the task, the role of connector nodes’ computations in the global functioning of the brain, and the role of distributed and self-organizing processes that are independent of connector nodes (17) need to be elucidated by future work.

Methods

At the time of analysis, the BrainMap database contained findings from 2,194 journal articles, which contained 83 tasks and 10,449 experimental contrasts and their activation images. BrainMap data were processed identically to the original model’s application (49). For each BrainMap task, we use the average of binary activation reported. For example, if there were 100 experiments for a particular task, and 88 of the experiments reported activity at a voxel, that voxel would have an activity score of 0.88 in our analyses. Thus, activity in our analyses is a probability of activation in a task. For our analyses, we only used tasks with more than 10 experiments, which reduced the number of tasks to 77. The author–topic model has the best cross-validation with 10–14 cognitive components (the cognitive components are estimated based on a random 95% subset of the BrainMap data, and the resulting generalization power is computed on the remaining 5% of the data). Thus, for our analyses, we used the 14-component model, as it has the finest-grained resolution while still obtaining strong cross-validation; however, models with other numbers of cognitive components led to similar results (see Dataset S2 for full results from all calculations with the Shen network).

We calculated the number of cognitive components engaged in each BrainMap task as recommended by the original analysis (49). For each task, the probabilities of cognitive components engaged sums to 1. This probability distribution should be interpreted as the probability of a task recruiting a cognitive component for any activated voxel and not the probability of a task recruiting a cognitive component for the entire task. Thus, the probability (P) for a given cognitive component being engaged in a task is equal to 1 – (1 – X)^Z, where X is the cognitive component’s probability for that task (using the probability from the distribution that sums to 1) and Z is the sum of voxel activity in the task (see ref. 49 for a detailed discussion). We considered a cognitive component engaged in a task if it had at least a P value of 0.9. We also used the original X values (which sum to 1) to quantify the number of cognitive components engaged in a task in three ways. Results were similar to those reported with these alternative calculations (see Supporting Information and Dataset S3 for full results from all calculations with the Shen network).

Spontaneous neural activity was measured in healthy human subjects with BOLD fMRI (Supporting Information). Informed consent was obtained from participants in accordance with procedures approved by the Committees for Protection of Human Subjects at the University of California, Berkeley. Voxel time series were averaged within each node in the atlas. We note that, for the Craddock atlas, we used the 950-node version that, for each node, maximized the similarity of the each voxel’s whole-brain spatial correlation map and used the two-level averaging scheme in which the data of each participant were clustered separately and the results were combined for a group-level parcellation (57). The Shen, Power, Crossley, and Gordon networks had 278, 264, 638, and 333 nodes, respectively. Functional connectivity was assessed in each participant by computing time series Pearson correlations between all pairs of nodes, resulting in a correlation matrix for each participant, which was then Fisher transformed. This correlation matrix was then thresholded, which then served as the basis for defining a weighted, undirected graph. A graph is defined as a set of nodes that are connected by edges, which, in our analyses, represent Fisher z-transformed correlation values between the nodes that survive the cost threshold. We use the term “network” to refer to a graph.

To average individual networks into a group-level network, we applied the InfoMap algorithm to each subject’s network. We chose to use the InfoMap algorithm, because, compared with other algorithms on networks for which the true division of nodes into modules is known, it achieves the most accurate division of nodes into modules (95, 96). Moreover, although most algorithms maximize modularity, InfoMap is based on the probabilistic flow of information through a network, making it principled for use in networks for which information is hypothesized to flow. For each subject, a consensus matrix (a value of 1 where the two nodes are in the same module and a value of 0 elsewhere) was formed on the subject’s network, thresholded at 0.035 in an attempt to achieve a similar number of modules and cognitive components. The average of these matrices was thresholded at the higher cost of 0.07, as all edges in this matrix represented that those two nodes were grouped into the same module, allowing for a less stringent threshold than was applied to the individual subjects’ networks. InfoMap was run on this final matrix, forming a group-level division of nodes into modules. In every iteration, InfoMap was run 5,000 times, with the optimal division (i.e., minimal length of the InfoMap equation) chosen. For the Crossley network, InfoMap was run on the full matrix, which had been previously thresholded based on multiple-comparison correction, resulting in a cost of 0.0916 (35). Other clustering methods and algorithms were used (Supporting Information) and produced very similar results (Dataset S1).

Edges in the group-level network were based on the average of Fisher-transformed Pearson correlations across subjects. Various cost thresholds were used for this network, and all led to similar results (Fig. 4, Dataset S1, and Fig. S2). Results from a cost threshold of 0.15 are presented in the main text for our data, and 0.0916 for the Crossley data. Higher cost thresholds were used for the final networks than for the module detection, as module detection at higher cost thresholds often leads to only three or four large modules (16), and we aimed to compare the modules at the same level of resolution as the cognitive components (i.e., a similar number of modules and cognitive components).

Each node’s topological role in the graph was characterized by measuring the node's participation coefficient and within-module–degree z score (42). Edge weights were used in the calculation instead of a binary count of edges. Although the mean of participation coefficients was 0.52 (for the Shen network at a cost of 0.15), other thresholds for the cutoff of a high participation coefficient (i.e., dividing nodes into connector nodes or local nodes) were tested as well. In the original paper (42), a participation coefficient of 0.62 was proposed—thresholds up to 0.80 also led to similar results (Supporting Information). Dataset S1 shows the mean participation coefficients values for each atlas and clustering method. Results were also robust to variations in the cut off for the within-module–degree z score (Supporting Information).

Given the large variety of experimental and data-processing procedures used across all of the studies in the BrainMap database, a direct comparison of activity scores across tasks is not justifiable. Thus, we calculated the activity in a particular type of node (e.g., connector hubs or provincial hubs) by calculating the mean activity of all voxels within the particular type of node divided by the mean of activity across all nodes. Only active voxels (voxels with nonzero activity scores) were used in this calculation. Thus, our main activity measure reflects the amount of activity at a type of node relative to whole brain activity for the task. We also used two secondary measures (described in the main text) that reflect how well activity aligns with participation coefficients and within-module–degree z scores.

Spontaneous Neural Activity Measured with BOLD fMRI

Twenty-four healthy participants (age range, 18–37 years; mean age, 24 years; 12 males) were studied. All healthy participants were prescreened to exclude individuals with a history of neurologic or psychiatric conditions. Brain images were collected on a 3-T Siemens MAGNETOM Trio MRI scanner using a 12-channel head coil. Structural images were acquired using a T1-weighted magnetization-prepared rapid-acquisition gradient echo [repetition time (TR) = 2,300 ms; echo time (TE) = 2.98 ms; 9° flip angle; 1 × 1 × 1-mm voxels]. For each subject, six blocks of 10 min each of T2*-weighted BOLD sensitive gradient echo echo-planar imaging sequence data (EPI) were analyzed [2,610 time points for each subject; TR = 1,370 ms; TE = 26 ms; 24 3.85-mm-thick axial slices; alt+z2 order (interleaved ascending, beginning at second slice); 2.344 × 2.344 × 3.850-mm voxels; 62° flip angle; field of view = 1,125 × 1,125; percent phase field of view = 100; matrix = 96 × 96]. All participants were instructed to simply stay awake with their eyes open. No other instructions were given.

Construction of the Graph Theory (Network) Model of the Brain

Image preprocessing was carried out in Configurable Pipeline for the Analysis of Connectomes (CPAC). Advanced Normalization Tools (ANTS) was used to register the images to MNI152 (Montreal Neurological Institute, Montreal, QC, Canada). FSL/FAST were used to automatically segment brain images into white matter (pr = 0.96), gray matter (pr = 0.7), and cerebral spinal fluid (pr = 0.96). Boundary-based registration was used to register the EPI values to the anatomical image. This uses the anatomical segmentation outputs to improve the coregistration of EPI images to the anatomical image. Slice timing was used to adjust the time course of voxels in each slice to account for the difference in time between the acquisition of the first and last slice. Volume realignment used the Friston 24-parameter model, which is the six motion parameters of the current volume and the preceding volume, plus each of these values squared. The motion parameters estimated in this set are then included in the general linear model to regress out motion-related artifacts (i.e., regression of motion parameters). The mean white matter and cerebral spinal fluid time series are calculated by averaging signal over all voxels within the white matter or cerebral spinal fluid masks for each time point. Mean white matter and cerebral spinal fluid time series are then used as temporal covariates and, along with linear and quadratic signals, are removed from the time series through linear regression. The time series is also bandpass filtered from 0.009 to 0.08 Hz to remove physiological noise such as cardiac and respiratory artifacts. No spatial smoothing was applied to the image. Although our main analyses do not include the use of motion scrubbing, to ensure that none of our results are impacted by subject motion, analyses were performed after motion scrubbing and average framewise displacement for each subject was not correlated with any of our measures of interest (Supporting Information and Dataset S1).

An Ontology of Cognitive Functions

One common goal of cognitive neuroscience has been to localize cognitive functions. This has been a difficult goal to achieve for numerous reasons (97–104), foremost being the significant challenge of building an ontology of cognitive functions (105). As one scientist eloquently put the challenge: “for example, while we think that ‘working memory’ is a unique function implemented in the brain, it may be the case that there is no such function implemented by the brain and that what we call working memory is in reality a combination of some other functions” (100). Deriving an ontology of the fundamental cognitive functions requires a principled analysis of brain activity across many different cognitive tasks under the appropriate assumptions that each cognitive function is recruited across a variety of cognitive tasks and multiple cognitive functions are recruited in each cognitive task. To our knowledge, the author–topic model is the first mathematical model that formally takes into consideration those two assumptions, and it does not require any assumptions concerning the existence of any particular cognitive function or functions (e.g., “working memory”). The author–topic model was used to build an ontology of cognitive functions by jointly modeling the association between brain activity and 77 cognitive tasks, based on the two assumptions above, across over 9,000 experiments (49). With this approach, the only parameter that must be set is the number of cognitive components; however, from 6 to 16 cognitive components, a nested ontology was found. For example, when changing the model from 11 to 12 components, one cognitive component divides into 2 cognitive components, whereas the other cognitive components remain unchanged. This suggests that each cognitive component is likely composed of more specific, microlevel cognitive functions. Although every microlevel cognitive function is certainly not differentiated by this model, the analyses in this study only depended on an accurate macrolevel description of cognitive functions that are supersets of the microlevel cognitive functions (which is suggested by the observed nested ontology) and a quantification of how many of these macrolevel cognitive functions were engaged in each BrainMap task. Thus, our results apply to a macrolevel description of cognitive functions that are supersets of possible microlevel cognitive functions. Moreover, there is recent evidence that the principle of modularity governs microlevel functioning as well. For example, Aplysia locomotion has been found to be executed by 12 modules that each map onto physically discrete brain regions as well as a particular function during locomotion (15). Future work will bridge the gap between our macrolevel and microlevel understanding of the modular functional architecture of the brain.

Replications

We chose to replicate our findings in a number of ways. We analyzed three different and independent datasets of spontaneous neural activity measured with rs-fMRI. First, we used four different brain atlases to analyze our own dataset. Moreover, we tested our hypotheses at both the individual and group levels. Second, we analyzed a spontaneous neural activity (measured via rs-fMRI) correlation matrix from another group (35) using a fifth brain atlas. Third, we performed our analyses with published graph metrics for nodes, including a module division and participation coefficients from a dataset that averaged across two cohorts (16, 40). This variety of datasets, analyses, and processing pipelines assured that our results are robust and can be fully replicated by other researchers.

Availability of Data and Code

All efforts were made to make our experiment completely reproducible. Analysis, visualization, and plotting code was written in Python using igraph (106), numpy (107), scipy, scikit-learn (108), nibabel, pycortex (109), and seaborn (110). The z score of the Rand coefficient code was executed by MATLAB Engine for Python and was download from NetWiki. Graph theory code and analysis code is available on GitHub upon request and was reviewed in a collaborative code meeting at University of California, Berkeley. The cognitive component model is available via Freesurfer. The original unprocessed rs-fMRI data are available upon request. The rs-fMRI processing pipeline is fully detailed in Methods and can be used to exactly (or not exactly, if one wishes) recreate the data we used for the analysis via CPAC (111), which is also freely available. Thus, this entire analysis can be recreated by anyone with no software purchases or development required.

Alternative Community Detection Methods and Algorithms

To ensure that our results were not dependent on any particular cost, we executed two additional methods that make use of a wide range of costs. First, community detection was run on each subject across a range of costs, from 0.01 to 0.1, in 0.001 steps. Each cost resulted in a consensus style matrix with 1’s between nodes in the same modules and 0’s elsewhere. These matrices are averaged (or, for the Crossley network, we used the group average correlation matrix here), and then community detection is run from 0.1 (0.0916 for the Crossley network) to 0.01 in 0.001 steps, storing a consensus style matrix for each run. The average of these matrices was left unthresholded, and community detection was run 100 times. A consensus-style matrix is stored for each run. If all 100 partitions are identical, the procedure ends. If any partitions are different, the 100 consensus style matrices are averaged and community detection is run again. This is the procedure described in ref. 58. However, a second iteration was never required, because there was enough consensus from the previous community detection techniques to result in a matrix that always leads to the same solution. Results were dramatically similar to our main method. We refer to this as community detection across costs (Dataset S1; “InfoMap Across Costs”).

Second, to further test our community detection procedure, for each subject, we ran community detection at a cost of 0.1. A consensus-style matrix is formed. The cost is then decreased by 0.001, and community detection is run again. The consensus-style matrix is then updated for the new partition, except for rows and columns for which the node has no edges in the current version of the graph or the node is not in a community with at least five nodes. This procedure continues until the cost is equal to 0.01. Thus, for each subject, the consensus-style matrix that is formed represents the community assignments for each pair of nodes at their sparsest level possible (i.e., before they become disconnected from the graph). This method is very similar to previous methods (16, 56). The average of these matrices was then clustered according to the method described above, the only difference being the original subject matrices were formed with this technique instead of averaging across costs. Results were dramatically similar to our main method. We refer to this as the recursive method (Dataset S1).

To make sure that our results were not dependent on the InfoMap algorithm we chose, we used the Louvain community detection in the community detection across costs method. Note, however, that the results from the Louvain community detection were very variable across subjects at lower costs (<0.05), and led to a very large number of modules (>30 in many cases), so we only included costs from 0.1 to 0.05. Again, results were dramatically similar to our main method (Dataset S1; “Louvain Across Costs”).

Note that, in Datasets S1–S3, we report findings based on the average of each node’s participation coefficient and within-module–degree across the original range of costs (0.2–0.05, in 0.01 steps).

Comparison of Modules and Cognitive Components

To calculate a P value, nodes were randomly reassigned to cognitive components and modules, and normalized mutual information (NMI) was recalculated. In this calculation, the number of nodes in each module and cognitive component were kept the same. For example, if module 1 contained 12 nodes, and cognitive component 1 contained 14 nodes, we replaced module 1 with 12 random nodes and cognitive component 1 with 14 random nodes. This was performed 1e8 times, calculating NMI at each iteration. A one-sample t test between the random partition normalized mutual information scores and the real score in every atlas is P < 1e-323.

We also note that the average NMI between individual subjects’ partitions and the group average partition was 0.41. This suggests that the group level partition is usually more similar to the cognitive component model than individual subjects are to the group-level partition.

Finally, we also used the z score of the Rand coefficient to compare the modules to the cognitive component (Dataset S4). This offers a clear statistical interpretation of the values.

Subcortical Views of Modules, Cognitive Components, Participation Coefficients, and Areas Where Activity Is Associated with Multiple Cognitive Components

Figs. 2 and 5 are surface-rendered views of the cortex (i.e., values from the cortical surface and below the cortical surface are projected onto the cortical surface), which do not allow for a view of subcortical brain structures. Thus, Fig. S1 shows the subcortical module (A) and the corresponding cognitive component (B). Fig. S3 shows axial views of the participation coefficients (A) and the areas where activity is associated with multiple cognitive components (B).

Effects of Subject Head Motion

Although our main analyses do not include the use of motion scrubbing, to ensure that none of our results are impacted by subject motion, we removed any frames with framewise displacement greater than 0.05, as well as the frame before and after. For every atlas, NMI between the scrubbed time-series partition and intact time-series partition was greater than 0.90. Participation coefficients and within-module–degree z scores in the scrubbed time-series partition and intact time-series partition all correlated at greater than r = 0.70. Modularity (i.e., Newman’s Q), average participation coefficients, and maximum participation coefficients and within-module–degree z scores were not correlated with subject’s average framewise displacement (P > 0.25 in all cases). Moreover, we ran our main analyses on the scrubbed data using the InfoMap community detection across costs, and the results were very consistent with the unscrubbed data (Dataset S1; “Scrubbed”).

Effects of Cost Thresholds

Given that there is there is no “correct” cost threshold, activity was calculated for the four different types of nodes in the four networks at cost thresholds from 0.05 to 0.20 in 0.01 steps (0.01–0.0916 for the Crossley network). For every network we analyzed, across costs, there were positive correlations between activity at connector nodes and the number of cognitive components or modules engaged in a task, but a nonsignificant or negative correlation between activity at local nodes and the number of cognitive components or modules engaged in a task. Fig. S2 shows these results plotted as kernel density estimations with the median and the 25th and 75th percentile of Pearson r values across cost thresholds shown for the particular type of node in that particular network. This ensures that our findings are not sensitive to the specific definition of the network’s nodes or the densities of the networks constructed based on those nodes. Moreover, we averaged each node’s participation coefficients and within-module–degree z scores across costs, and results were very similar (Dataset S1).

Effects of Cutoffs for Node Type

The values we used were not arbitrary; as the within-module–degree is z scored, the mean is 0.0. However, in the rare case that a node is not assigned to a module (mathematically, it is calculated as belonging to its own module, alone) the within-module–degree z score is 0.0. Thus, to avoid classifying these nodes as provincial hubs or connector hubs, we set the threshold at 1e-5 instead of the mean of the values, as we did with the participation coefficients. However, results were not greatly impacted by changes. For example, with the threshold set to 1 for the Shen atlas [connector hubs, cognitive components (r = 0.518, P = 1.3e-06), modules (r = 0.494, P = 4.9e-06); satellite connectors, cognitive components (r = 0.576, P = 4e-08), modules (r = 0.530, P = 7e-07); provincial hubs, cognitive components (r = −0.151, P = 0.188), modules (r = −0.201, P = 0.079); peripheral nodes, cognitive components (r = −0.502, P = 3.2e-06), modules (r = −0.401, P = 0.0003)]. Higher threshold resulted in less than 5% of nodes that were provincial or connector hubs. The same pattern was observed in the opposite direction; results were significant at −1 [connector hubs, cognitive components (r = 0.561, P = 1.1e-07), modules (r = 0.5033, P = 3e-06); satellite connectors, cognitive components (r = 0.499, P = 3.9e-06), modules (r = 0.523, P = 1e-06); provincial hubs, cognitive components (r = −0.522, P = 1.1e-06), modules (r = −0.455, P = 3.1e-05); peripheral nodes, cognitive components (r = 0.035, P = 0.761), modules (r = 0.0084, P = 0.942)]. Lower thresholds resulted in less than 5% of nodes that were satellite connectors or periphery nodes.

Results were significant up a participation coefficient of 0.80 [connector hubs, cognitive components (r = 0.592, P = 1.4e-08), modules (r = 0.364, P = 0.001); satellite connectors, cognitive components (r = 0.351, P = 0.001), modules (r = 0.295, P = 0.009); provincial hubs, cognitive components (r = −0.281 P = 0.01), modules (r = −0.22, P = 0.04); peripheral nodes, cognitive components (r = −0.41, P = 0.0002), modules (r = 0.22, P = 0.05)]. At higher cutoffs, less than 5% of nodes were characterized as connectors.

Author–Topic Cognitive Component Model with Different Numbers of Cognitive Components

The author–topic model can be applied to estimate a particular number of cognitive components. We ensured that our results are replicable across author–topic models with different numbers of cognitive components by running our main analyses across the model with 10–13 cognitive components. These results are shown in Dataset S2.

Different Methods for Calculating the Number of Cognitive Components Engaged

In addition to the method implemented in the main text, we also used the original probability (X) values (which sum to 1) to quantify the number of cognitive components engaged in a task in three ways. In Dataset S3, we present the results where we quantified the number of cognitive components engaged by the entropy of the distribution of X values (column 1), 1 minus the variance of the distribution of X values (column 2), and the number of cognitive components with an X value greater than 1/14 (column 3). These calculations were significantly correlated with our main method at r = 0.817, r = 0.718, r = 0.439, respectively (4.6e-21 < P > 5e-5).