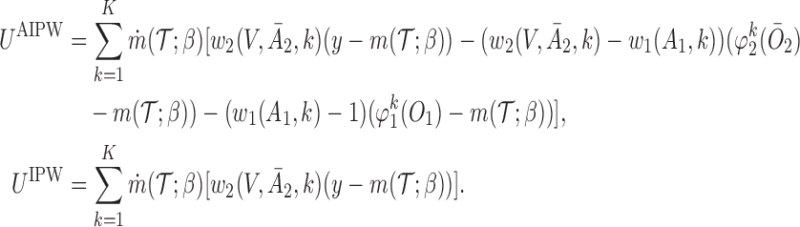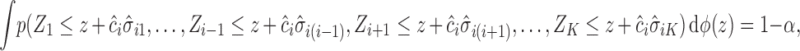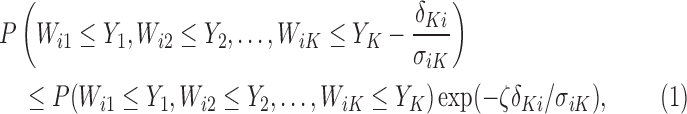Abstract
A dynamic treatment regime (DTR) is a treatment design that seeks to accommodate patient heterogeneity in response to treatment. DTRs can be operationalized by a sequence of decision rules that map patient information to treatment options at specific decision points. The sequential, multiple assignment, randomized trial (SMART) is a trial design that was developed specifically for the purpose of obtaining data that informs the construction of good (i.e. efficacious) decision rules. One of the scientific questions motivating a SMART concerns the comparison of multiple DTRs that are embedded in the design. Typical approaches for identifying the best DTRs involve all possible comparisons between DTRs that are embedded in a SMART, at the cost of greatly reduced power to the extent that the number of embedded DTRs (EDTRs) increase. Here, we propose a method that will enable investigators to use SMART study data more efficiently to identify the set that contains the most efficacious EDTRs. Our method ensures that the true best EDTRs are included in this set with at least a given probability. Simulation results are presented to evaluate the proposed method, and the Extending Treatment Effectiveness of Naltrexone SMART study data are analyzed to illustrate its application.
Keywords: Double robust, Marginal structural model, Multiple comparisons with the best, SMART designs
1. Introduction
A dynamic treatment regime (DTR) is a treatment design that seeks to accommodate patient heterogeneity in response to treatments (Murphy and others, 2001; Murphy, 2003; Robins, 2004). In DTRs the type and or dose of the treatment is adapted over time according to the patient's characteristics and progress in treatment. At each decision point (i.e. specific point in time in which a treatment is to be considered or altered), decision rules are used to map individual characteristics to a specific type of treatment or dosage. Recently, there has been an increased interest in sequential, multiple assignment, randomized trials (SMARTs), which were developed specifically to provide empirical evidence that informs the construction of optimal DTRs (Lavori and Dawson, 2000; Nahum-Shani and others, 2012; Chakraborty and Moodie, 2013; Chakraborty and Murphy, 2014; Laber and others, 2014).
or dose of the treatment is adapted over time according to the patient's characteristics and progress in treatment. At each decision point (i.e. specific point in time in which a treatment is to be considered or altered), decision rules are used to map individual characteristics to a specific type of treatment or dosage. Recently, there has been an increased interest in sequential, multiple assignment, randomized trials (SMARTs), which were developed specifically to provide empirical evidence that informs the construction of optimal DTRs (Lavori and Dawson, 2000; Nahum-Shani and others, 2012; Chakraborty and Moodie, 2013; Chakraborty and Murphy, 2014; Laber and others, 2014).
One scientific question motivating a SMART concerns the comparison of DTRs that are embedded in the design. It aims to identify the best DTR or the set that contains the best DTRs among those that are embedded in the design. In other words, the goal is to screen out ineffective DTRs. This question can be framed as a special case of the general multiple comparison problem.
Methods for multiple comparisons can be used to group sample means, such that within each group, population means are not significantly different (Scheffe, 1953; Tukey, 1953). Current approaches for identifying the set of best DTRs perform all possible comparisons among embedded DTRs (EDTRs). In such a setting, standard multiple comparison approaches used to control for Type I error result in a loss of statistical power (Hsu, 1984; Hsu, 1996). Consequently, important differences between DTRs might go undetected (Saville, 1990; Keselman and others, 1999). Here, we propose a more efficient approach for identifying the set of best DTRs. This approach builds on the work of Hsu (1981), which identifies the best set of means by conducting multiple comparisons with the best (MCB), namely by comparing the best mean with others. Applying this approach will result in fewer comparisons relative to standard approaches, and hence improved power.
The current manuscript will extend the MCB toolbox for analyzing data from SMART studies. The contribution of this paper is two-fold. First, we provide and illustrate, for the first time, a method that can be used to efficiently address an important scientific question that motivates many SMART studies. This question concerns the need to identify the optimal DTR, or several optimal DTRs from a list of DTRs embedded in a SMART study. Enabling researchers to address this scientific question can support clinical decision making, offering clinicians a set of efficacious DTRs to choose from based on other considerations such as cost and patient preferences. The second contribution concerns the correlation structure of the estimators derived from SMART data. The method proposed by Hsu requires a known correlation structure (up to a constant). In SMART, the correlation structure of estimators is not known a priori. Therefore, generalization of the method is warranted.
We briefly introduce SMART designs and explain the structure of SMART data in Section 2. We then present two methods to estimate the mean outcome under each DTR in Section 3. The framework of MCB in SMART settings is introduced in Section 4. We conduct a simulation study in Section 5 to examine the performance of our method. We illustrate the method with analyses of the Extending Treatment Effectiveness of Naltrexone (EXTEND) study in Section 6. The last section contains some concluding remarks. Proofs are given in Appendix A of the supplementary materials available at Biostatistics online.
2. Preliminaries
2.1. Sequential, multiple assignment, randomized trials
The SMART is a clinical trial design in which each individual proceeds through stages of treatments (Lavori and others, 2000; Murphy, 2005; Lei and others, 2012; Nahum-Shani and others, 2012). At each treatment stage, individuals are randomized to one of the available treatment options at that stage, where the subsequent treatment options may depend on an embedded tailoring variable observed at the current stage. For example, in the EXTEND study, at stage 1, patients were randomized to one of two definitions of non-response while receiving naltrexone (NTX): (1) Stringent criterion—a patient is a non-responder if (s)he has two or more heavy drinking days in the first 8 weeks; (2) Lenient criterion—a patient is a non-responder if (s)he has five or more heavy drinking days in the first 8 weeks. At stage 2, non-responders were re-randomized to combined behavioral intervention (CBI)  NTX or CBI alone. Individuals who did not meet their non-response criterion were re-randomized to telephone disease management
NTX or CBI alone. Individuals who did not meet their non-response criterion were re-randomized to telephone disease management  or NTX alone. Thus, in this two-stage design, the embedded tailoring variable is the response
or NTX alone. Thus, in this two-stage design, the embedded tailoring variable is the response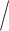 non-response status to initial NTX.
non-response status to initial NTX.
2.2. Data structure
For simplicity, we focus on SMARTs with two stages. The observed data on each individual are given by a trajectory 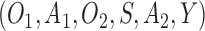 .
.  , for
, for  is a set of covariates available at the beginning of stage
is a set of covariates available at the beginning of stage 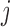 . By
. By 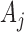 , we denote the treatment options at the beginning of stage
, we denote the treatment options at the beginning of stage 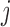 ;
; 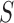 is a binary variable that is coded 1 if an individual has been re-randomized at stage 2, and coded 0 otherwise. Finally,
is a binary variable that is coded 1 if an individual has been re-randomized at stage 2, and coded 0 otherwise. Finally, 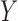 is the continuous primary outcome. The treatment and the covariate history through
is the continuous primary outcome. The treatment and the covariate history through 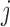 are denoted by
are denoted by 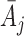 and
and 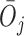 , respectively. We use lowercase letters to refer to the possible values of the corresponding capital letter random variable.
, respectively. We use lowercase letters to refer to the possible values of the corresponding capital letter random variable.
In SMART settings, the stage-2 treatment options may depend on embedded tailoring variables, which are part or all of the observed history up to and including time 2, and we denote them as 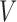 . In the EXTEND study,
. In the EXTEND study, 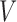 is the response(R)
is the response(R) non-response(NR) status to stage-1 treatment (i.e.
non-response(NR) status to stage-1 treatment (i.e. 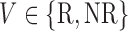 ). Hence, for each individual, we conceptualize a v-treatment trajectory
). Hence, for each individual, we conceptualize a v-treatment trajectory 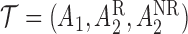 . For responders and non-responders, we set
. For responders and non-responders, we set 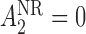 and
and 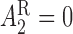 , respectively, with probability 1. This basically means that, for responders,
, respectively, with probability 1. This basically means that, for responders, 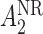 does not apply and vice versa. We use the v-treatment trajectory to model the marginal structural model (MSM) discussed in Section 3. Note, the v-treatment trajectory and treatment history are not necessarily the same. In fact, in this example, the treatment history is 2D, while the v-treatment trajectory is 3D.
does not apply and vice versa. We use the v-treatment trajectory to model the marginal structural model (MSM) discussed in Section 3. Note, the v-treatment trajectory and treatment history are not necessarily the same. In fact, in this example, the treatment history is 2D, while the v-treatment trajectory is 3D.
2.3. Embedded DTRs
An EDTR is one DTR that participants can follow as part of the study design. In the EXTEND study, there are eight EDTRs: (1) start with lenient definition. If the patient is non-responsive, offer NTX+CBI; if the patient is responsive, offer NTX+TDM. (2) Start with lenient definition. If the patient is non-responsive, offer NTX+CBI; if the patient is responsive, offer NTX. (3) Start with lenient definition. If the patient is non-responsive, offer CBI; if the patient is responsive, offer NTX+TDM. (4) Start with lenient definition. If the patient is non-responsive, offer CBI; if the patient is responsive, offer NTX. The other four EDTRs are similar except that they start with stringent definition. Note that a given v-treatment trajectory 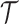 can be consistent with more than one EDTR. For example, a responder to the lenient definition with
can be consistent with more than one EDTR. For example, a responder to the lenient definition with 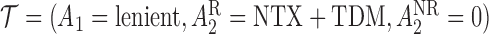 is following both EDTRs (1) and (3).
is following both EDTRs (1) and (3).
3. Estimation
Let 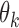 be the population outcome mean under the
be the population outcome mean under the 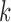 th EDTR for
th EDTR for 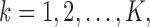 where
where 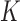 is the number of EDTRs in a SMART. Here, we provide two methods that are based on weighted least squares minimizations and used throughout this paper as tools to estimate the mean outcome under each EDTR. The first approach would be to postulate an MSM
is the number of EDTRs in a SMART. Here, we provide two methods that are based on weighted least squares minimizations and used throughout this paper as tools to estimate the mean outcome under each EDTR. The first approach would be to postulate an MSM 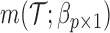 for the outcome given the observed v-treatment trajectory
for the outcome given the observed v-treatment trajectory 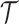 and define
and define 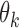 as a known function of
as a known function of 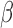 for all
for all 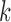 . Let
. Let 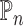 be the empirical average. The parameters of the MSM can be estimated using the following estimating equation:
be the empirical average. The parameters of the MSM can be estimated using the following estimating equation:
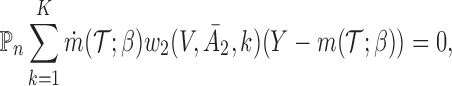 |
(3.1) |
where 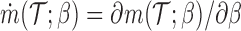 , and
, and
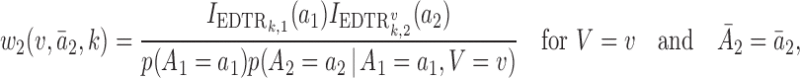 |
where 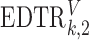 is the treatment option determined by EDTR
is the treatment option determined by EDTR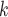 at stage 2 given
at stage 2 given 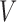 , and
, and 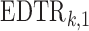 is the treatment option determined by EDTR
is the treatment option determined by EDTR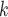 at stage 1. The indicator function selects individuals whose treatment history is consistent with the
at stage 1. The indicator function selects individuals whose treatment history is consistent with the 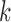 th EDTR given
th EDTR given 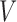 . This method is referred to as inverse probability weighting (IPW) (Robins, 1999; Hernán and others, 2000; Robins and others, 2000). The treatment trajectory is used to define the MSM function. For example, in the EXTEND study, the MSM would be
. This method is referred to as inverse probability weighting (IPW) (Robins, 1999; Hernán and others, 2000; Robins and others, 2000). The treatment trajectory is used to define the MSM function. For example, in the EXTEND study, the MSM would be 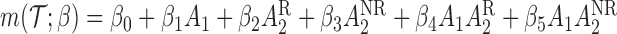 . We denote the solutions of this equation as
. We denote the solutions of this equation as 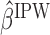 . Hence, the mean outcome under each EDTR can be estimated as
. Hence, the mean outcome under each EDTR can be estimated as 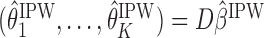 , where
, where  is a
is a 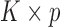 matrix. The
matrix. The 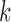 th row of
th row of 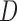 is the contrast corresponding to EDTR
is the contrast corresponding to EDTR (see Section 5).
(see Section 5).
The second approach is based on the augmented IPW (AIPW), which is a more efficient version of IPW developed by Robins and others (2008) and Orellana and others (2010). Let 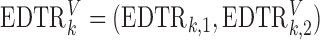 . The corresponding estimating equation for a two-stage design is given by
. The corresponding estimating equation for a two-stage design is given by
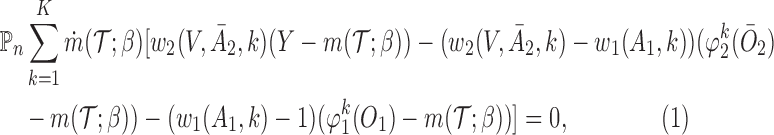 |
(3.2) |
where 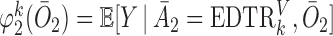 ,
, 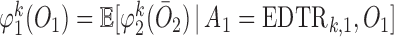 , and
, and
 |
To obtain estimators of  , we postulate parametric models for the unknown functions
, we postulate parametric models for the unknown functions  and
and  parameterized by
parameterized by 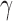 and replace them with their estimated values
and replace them with their estimated values 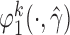 and
and 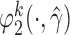 . The estimates may be obtained by fitting two least squares models. We denote the solutions of (3.2) as
. The estimates may be obtained by fitting two least squares models. We denote the solutions of (3.2) as 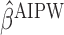 and, similar to the first approach, we define
and, similar to the first approach, we define 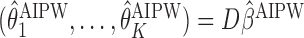 .
.
Estimator (3.2) is double robust in the sense that it results in an unbiased estimate of 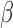 if either
if either 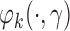 or the treatment assignment probabilities are correctly specified (van der Laan and Robins, 2003; Bang and Robins, 2005; Davidian and others, 2005; Orellana and others, 2010). Although we are focusing on randomized trials and treatment assignment probabilities are known by design, for efficiency we estimate these probabilities non-parametrically using the available data (Robins and others, 1995; Hirano and others, 2003). One may also postulate a parametric model to estimate these probabilities given the observed covariate
or the treatment assignment probabilities are correctly specified (van der Laan and Robins, 2003; Bang and Robins, 2005; Davidian and others, 2005; Orellana and others, 2010). Although we are focusing on randomized trials and treatment assignment probabilities are known by design, for efficiency we estimate these probabilities non-parametrically using the available data (Robins and others, 1995; Hirano and others, 2003). One may also postulate a parametric model to estimate these probabilities given the observed covariate treatment history.
treatment history.
The following proposition provides the asymptotic behaviors of estimators 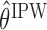 and
and 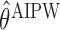 obtained by (3.1) and (3.2), respectively, which is an immediate consequence of (Orellana and others, 2010, Lemma 3). In the proposition, the superscript
obtained by (3.1) and (3.2), respectively, which is an immediate consequence of (Orellana and others, 2010, Lemma 3). In the proposition, the superscript  denotes IPW or AIPW.
denotes IPW or AIPW.
Proposition 3.1. —
Let
, where
is a
matrix with the
th row of
being the contrast corresponding to the
th EDTR. Then, under the standard regularity assumptions,
, where
, and
with
The asymptotic variance 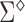 may be estimated consistently by replacing the expectations with expectations with respect to the empirical measure and
may be estimated consistently by replacing the expectations with expectations with respect to the empirical measure and 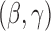 with its estimate
with its estimate 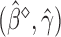 and denoted as
and denoted as 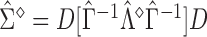 .
.
4. Multiple comparison with the best
Let 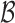 be the true set of best EDTRs and
be the true set of best EDTRs and 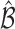 be a set of EDTRs that cannot be differentiated from the best EDTR using the available data. In the previous section, we discussed our procedures to estimate the mean outcome under each EDTR,
be a set of EDTRs that cannot be differentiated from the best EDTR using the available data. In the previous section, we discussed our procedures to estimate the mean outcome under each EDTR, 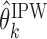 and
and 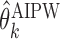 for
for 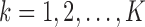 . Since our methodology holds for both IPW and AIPW approaches to estimation, for simplicity of notation, we drop the superscripts IPW and AIPW and refer to the estimator of
. Since our methodology holds for both IPW and AIPW approaches to estimation, for simplicity of notation, we drop the superscripts IPW and AIPW and refer to the estimator of 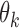 as
as 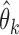 . In this section, we generalize the MCB method introduced by Hsu (1981) to SMART settings. The goal is to find EDTRs that are not significantly different from the EDTR with the maximum outcome, say
. In this section, we generalize the MCB method introduced by Hsu (1981) to SMART settings. The goal is to find EDTRs that are not significantly different from the EDTR with the maximum outcome, say 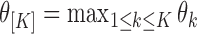 . Hence, a natural criterion would be to include index
. Hence, a natural criterion would be to include index 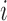 in the set
in the set 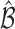 if the standardized difference
if the standardized difference 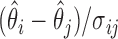 is greater than a constant for all
is greater than a constant for all 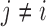 . This can be written as
. This can be written as
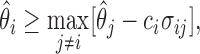 |
(4.1) |
where 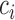 is a constant and
is a constant and 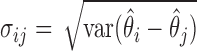 , which can be estimated using the variance formula in Proposition 3.1. The challenge is to find
, which can be estimated using the variance formula in Proposition 3.1. The challenge is to find 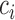 such that
such that 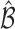 includes the true best EDTR with probability at least
includes the true best EDTR with probability at least 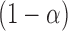 ; that is,
; that is, 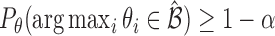 for any
for any 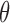 . In cases where there are more than one best EDTR,
. In cases where there are more than one best EDTR, 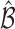 includes each index
includes each index 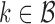 with at least
with at least 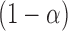 probability. This condition will be satisfied if we find
probability. This condition will be satisfied if we find 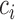 such that under the null hypothesis (i.e. all EDTRs are equally good), the set
such that under the null hypothesis (i.e. all EDTRs are equally good), the set 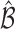 includes each index
includes each index 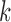 with probability
with probability 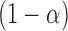 . In other words, when
. In other words, when 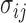 is known,
is known, 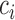 must satisfy
must satisfy
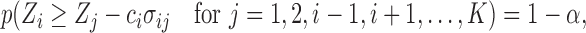 |
(4.2) |
where 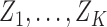 are multivariate normal random variables with mean 0 and covariance matrix
are multivariate normal random variables with mean 0 and covariance matrix 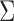 such that
such that 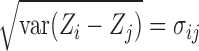 . The above equality can be written as
. The above equality can be written as
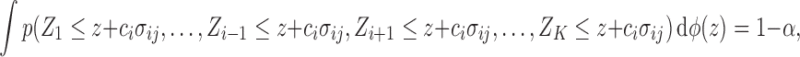 |
where 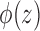 is the marginal cdf of
is the marginal cdf of 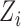 . Note that, for
. Note that, for  , the constant
, the constant 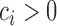 for
for 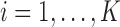 . Hence, in our setting where
. Hence, in our setting where 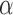 represents the Type I error rate, we can assume that
represents the Type I error rate, we can assume that 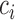 is a positive constant.
is a positive constant.
Hsu (1981) present an equation that can be used to find the constant 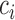 when the structure of the covariance matrix
when the structure of the covariance matrix 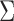 is known up to a constant. This is the case in a standard regression where
is known up to a constant. This is the case in a standard regression where 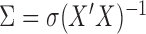 . Note that in this case, given the design matrix,
. Note that in this case, given the design matrix, 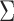 is known up to a constant
is known up to a constant 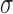 . In Hsu's setting, the constant
. In Hsu's setting, the constant 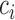 is a function of the correlation matrix and thus it is not a function of
is a function of the correlation matrix and thus it is not a function of 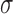 . In the MSM, however, the structure of the design matrix is random because it depends on intermediate outcomes (i.e. variables observed before stage 2 and after stage 1 treatment assignment) that are not included in the design matrix, such as response or non-response status (i.e. embedded tailoring variables). In such a setting, the constant
. In the MSM, however, the structure of the design matrix is random because it depends on intermediate outcomes (i.e. variables observed before stage 2 and after stage 1 treatment assignment) that are not included in the design matrix, such as response or non-response status (i.e. embedded tailoring variables). In such a setting, the constant 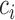 will be a function of an unknown
will be a function of an unknown 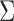 which is estimated by
which is estimated by 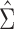 using the observed data. Theorem 4.1 generalizes the idea in Hsu to cases where the structure of the design matrix is unknown. We use the notation
using the observed data. Theorem 4.1 generalizes the idea in Hsu to cases where the structure of the design matrix is unknown. We use the notation 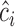 to reflect the dependence of
to reflect the dependence of 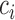 to
to 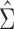 .
.
Theorem 4.1. —
Define the estimated set of best EDTRs as
, where
, and
satisfies
with
being multivariate normal random variables with mean 0 and unknown covariance matrix
, which is estimated by
. Then, asymptotically,
contains the true best EDTR with probability at least
.
Let 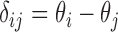 be the difference between the
be the difference between the 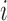 th and the
th and the 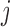 th EDTR. The probability of including an EDTR
th EDTR. The probability of including an EDTR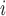 in the estimated set of best EDTRs for any given
in the estimated set of best EDTRs for any given 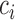 is
is
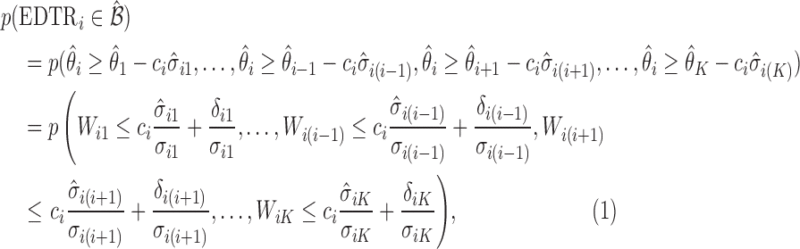 |
(4.3) |
where 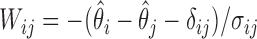 and is distributed as a standard normal random variable. Accordingly, the estimated set size (ESS) of
and is distributed as a standard normal random variable. Accordingly, the estimated set size (ESS) of 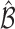 is defined as
is defined as 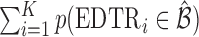 . Note, under the null hypothesis, where all EDTRs are equally good,
. Note, under the null hypothesis, where all EDTRs are equally good, 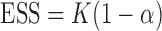 . The following theorem shows that the probability of including an inferior
. The following theorem shows that the probability of including an inferior 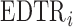 in the estimated set
in the estimated set 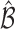 decays to zero exponentially for
decays to zero exponentially for 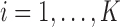 as the difference between the best and the
as the difference between the best and the 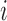 th EDTR increases.
th EDTR increases.
Theorem 4.2. —
Let
follow a multivariate normal distribution with mean zero and unknown variance matrix. Define
for
as non-negative random variables. Let
,
; we have
(4.4) where
is a constant that depends on
and
but is independent of
.
Note that 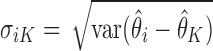 , which decays to zero with rate
, which decays to zero with rate 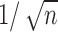 . This implies that, for a fixed
. This implies that, for a fixed 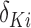 , as
, as 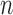 increases the probability of including an inferior
increases the probability of including an inferior 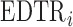 to
to 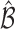 decreases with rate
decreases with rate 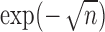 . Also, in the statement of Theorem 4.2, replacing
. Also, in the statement of Theorem 4.2, replacing 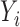 with
with 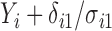 , for
, for 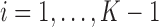 , shows the exponential decay rate in (4.3).
, shows the exponential decay rate in (4.3).
Remark 4.3. —
Let
and
be the covariance matrix of
and
, respectively. Since
, for any fixed sample size and a set of
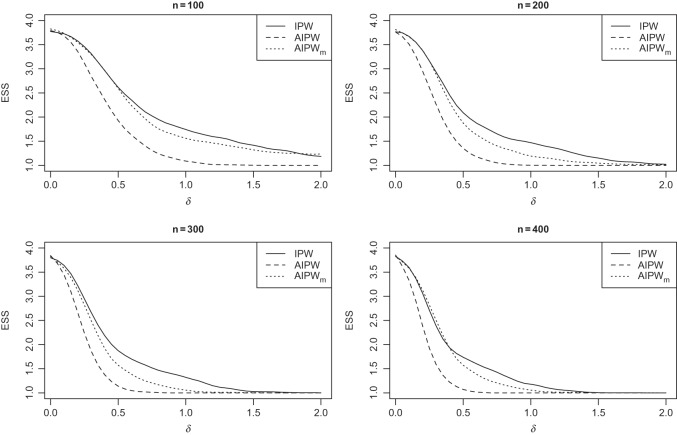
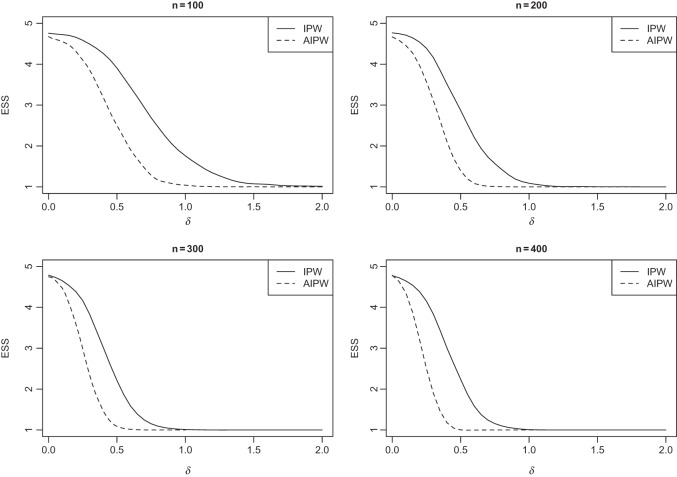
s, the efficient estimator AIPW results in an ESS which is less than or equal to the one obtained by the inefficient estimator IPW (see Figures 1 and 2).
Fig. 1.
Simulation SMART design Example 1: the vertical axes are the estimated set (of best) size (ESS) and horizontal axes are the difference between the best and the second best EDTR.
Fig. 2.
Simulation SMART design Example 2: the vertical axes are the estimated set (of best) size (ESS) and horizontal axes are the difference between the best and the second best EDTR.
5. Simulation study
This section provides empirical evidence for the theoretical results presented in the manuscript. We compare the estimated sets of best obtained by the IPW and AIPW methods and show that the latter method screens out the ineffective EDTRs more efficiently. We examine the performance of the proposed method using two different types of SMART designs. We describe that the form of the MSM 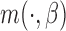 may vary based on the design structure. We also discuss the effect that misspecifying the function
may vary based on the design structure. We also discuss the effect that misspecifying the function 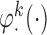 has on estimating the parameters of the MSM and the mean outcome under each EDTR.
has on estimating the parameters of the MSM and the mean outcome under each EDTR.
In all simulation scenarios, baseline variables 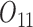 and
and 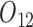 are generated from standard normal, and
are generated from standard normal, and 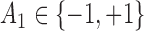 is based on a Bernoulli distribution with probability 0.5. The intermediate outcomes are
is based on a Bernoulli distribution with probability 0.5. The intermediate outcomes are 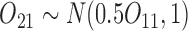 and
and 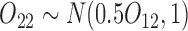 . The estimator IPW and AIPW refer to (3.1) and (3.2), respectively, while AIPW
. The estimator IPW and AIPW refer to (3.1) and (3.2), respectively, while AIPW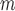 refers to an AIPW estimator where
refers to an AIPW estimator where 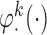 functions are misspecified. Some of the tables and figures corresponding to this section are presented in Appendix C of supplementary material available at Biostatistics online.
functions are misspecified. Some of the tables and figures corresponding to this section are presented in Appendix C of supplementary material available at Biostatistics online.
5.1. SMART design: Example 1
This is a type of SMART design in which just a subset of individuals are re-randomized at stage 2. In our simulation, this subset is non-responders to stage-1 treatment (see Figure 1 of supplementary material available at Biostatistics online). Thus, the embedded tailoring variable 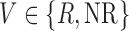 is the indicator of responder or non-responder status, respectively. Four DTRs are embedded in this design depending on v-treatment trajectory
is the indicator of responder or non-responder status, respectively. Four DTRs are embedded in this design depending on v-treatment trajectory 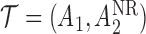 ; these are listed in Table 1 of supplementary material available at Biostatistics online. Note that because there is only one treatment option for responders, the v-treatment trajectory does not include
; these are listed in Table 1 of supplementary material available at Biostatistics online. Note that because there is only one treatment option for responders, the v-treatment trajectory does not include 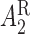 . We generate these SMART data with sample sizes 100, 200, 300, and 400 from the following generative model. The stage-2 treatment option
. We generate these SMART data with sample sizes 100, 200, 300, and 400 from the following generative model. The stage-2 treatment option 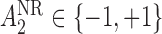 is generated from a Bernoulli distribution with probability 0.5. The outcome is generated from a normal distribution with mean
is generated from a Bernoulli distribution with probability 0.5. The outcome is generated from a normal distribution with mean 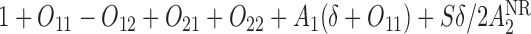 , with variance
, with variance 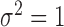 , where
, where 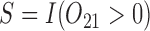 . The main effect of treatment options are parameterized with
. The main effect of treatment options are parameterized with 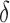 . The true
. The true 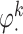 s are given by
s are given by
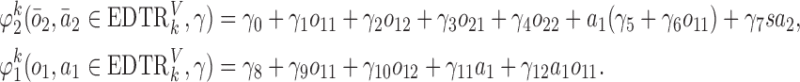 |
Table 1.
Simulation SMART design Example 1: inference about the parameters 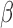 using IPW, AIPW, and AIPW
using IPW, AIPW, and AIPW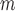 where the latter represents the misspecified scenario
where the latter represents the misspecified scenario
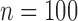 |
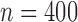 |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IPW |
AIPW |
AIPW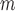 |
IPW |
AIPW |
AIPW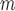 |
|||||||
| Parameter | Bias | SD | Bias | SD | Bias | SD | Bias | SD | Bias | SD | Bias | SD |
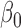 |
0.010 | 0.24 | 0.002 | 0.23 | 0.007 | 0.24 | 0.004 | 0.12 | 0.000 | 0.12 | 0.007 | 0.12 |
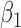 |
0.001 | 0.24 | 0.002 | 0.18 | 0.005 | 0.18 | 0.011 | 0.12 | 0.002 | 0.09 | 0.002 | 0.10 |
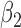 |
0.002 | 0.17 | 0.003 | 0.07 | 0.002 | 0.10 | 0.000 | 0.08 | 0.002 | 0.04 | 0.004 | 0.05 |
 |
0.013 | 0.41 | 0.007 | 0.32 | 0.014 | 0.39 | 0.015 | 0.21 | 0.004 | 0.16 | 0.013 | 0.20 |
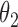 |
0.011 | 0.33 | 0.003 | 0.27 | 0.004 | 0.31 | 0.007 | 0.17 | 0.000 | 0.14 | 0.009 | 0.15 |
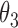 |
0.009 | 0.41 | 0.003 | 0.32 | 0.010 | 0.39 | 0.015 | 0.21 | 0.000 | 0.16 | 0.005 | 0.20 |
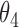 |
0.007 | 0.33 | 0.003 | 0.27 | 0.000 | 0.31 | 0.007 | 0.17 | 0.004 | 0.14 | 0.001 | 0.15 |
We also consider a misspecified scenario where 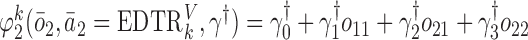 and
and 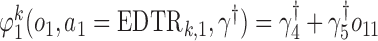 are assumed to be working models. Moreover, the MSM is
are assumed to be working models. Moreover, the MSM is
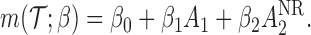 |
Hence, the true parameter value 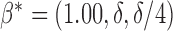 , which means, for
, which means, for 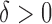 ,
, 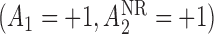 is the true best EDTR and, for
is the true best EDTR and, for 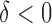 ,
, 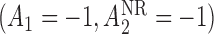 is the true best EDTR. Table 1 presents the point estimate and standard errors of the parameters
is the true best EDTR. Table 1 presents the point estimate and standard errors of the parameters  and
and 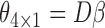 estimated using IPW, AIPW and AIPW
estimated using IPW, AIPW and AIPW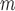 , where
, where
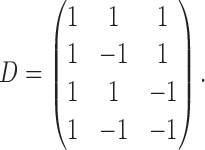 |
The rows of this matrix represent 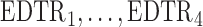 listed in Table 1 of supplementary material available at Biostatistics online. In Table 1, we set
listed in Table 1 of supplementary material available at Biostatistics online. In Table 1, we set 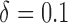 and generated 1000 datasets of sizes 100 and 400. Our results show that AIPW reduces the standard error by up to 60% compared with IPW, and even when
and generated 1000 datasets of sizes 100 and 400. Our results show that AIPW reduces the standard error by up to 60% compared with IPW, and even when 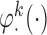 functions are misspecified
functions are misspecified 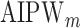 maintains unbiasedness, but some of the standard errors increase. In fact, under our misspecification scenario AIPW still has better performance than IPW. We see a similar pattern in estimation of the mean outcome under different EDTRs.
maintains unbiasedness, but some of the standard errors increase. In fact, under our misspecification scenario AIPW still has better performance than IPW. We see a similar pattern in estimation of the mean outcome under different EDTRs.
Figure 1 shows how fast the size of the set of best 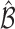 converges to 1 as
converges to 1 as 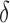 increases when the parameters of each EDTR is estimated using IPW and AIPW. Note that, for
increases when the parameters of each EDTR is estimated using IPW and AIPW. Note that, for 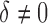 , the true set size
, the true set size 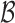 is 1. For each
is 1. For each 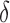 , we generated 500 datasets and defined the ESS as the empirical average of the set sizes for each dataset. This figure shows that when the parameters
, we generated 500 datasets and defined the ESS as the empirical average of the set sizes for each dataset. This figure shows that when the parameters 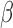 of the MSM are estimated using AIPW, the ESS decreases to 1 faster than when using IPW. This is due to the more efficient estimation of
of the MSM are estimated using AIPW, the ESS decreases to 1 faster than when using IPW. This is due to the more efficient estimation of 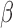 s. Documented R code for this example is available in Appendix B of supplementary material available at Biostatistics online.
s. Documented R code for this example is available in Appendix B of supplementary material available at Biostatistics online.
5.2. SMART design: Example 2
In some SMART designs, stage-2 randomization depends on prior treatment and an intermediate outcome such as response indicator (see Figure 2 of supplementary material available at Biostatistics online). We generate datasets of sizes 100, 200, 300 and 400 from the following generative model. The stage-2 treatment options are generated from a multinomial distribution with probability 0.25 coded as 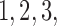 and 4. Let
and 4. Let 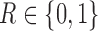 be the non-response and response indicator, respectively. Then, if
be the non-response and response indicator, respectively. Then, if 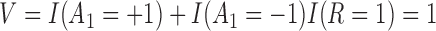 (i.e.
(i.e. 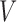 satisfies condition A), there is no randomization, while individuals with
satisfies condition A), there is no randomization, while individuals with 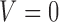 (i.e.
(i.e. 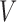 satisfies condition B) will be randomized to one of the four stage-2 treatment options. Hence, the v-treatment trajectory in this example is
satisfies condition B) will be randomized to one of the four stage-2 treatment options. Hence, the v-treatment trajectory in this example is 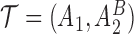 . Five DTRs are embedded in this design depending on the treatment trajectory
. Five DTRs are embedded in this design depending on the treatment trajectory 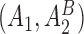 ; these are listed in Table 2 of supplementary material available at Biostatistics online.
; these are listed in Table 2 of supplementary material available at Biostatistics online.
Table 2.
Simulation SMART design Example 2: inference about the parameters 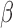 using IPW, AIPW, and
using IPW, AIPW, and  where the latter represents the misspecified scenario
where the latter represents the misspecified scenario
 |
 |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IPW |
AIPW |
AIPW |
IPW |
AIPW |
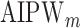 |
|||||||
| Parameter | Bias | SD | Bias | SD | Bias | SD | Bias | SD | Bias | SD | Bias | SD |
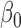 |
0.004 | 0.35 | 0.001 | 0.30 | 0.005 | 0.30 | 0.003 | 0.18 | 0.001 | 0.15 | 0.002 | 0.15 |
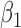 |
0.004 | 0.75 | 0.003 | 0.40 | 0.002 | 0.48 | 0.004 | 0.37 | 0.001 | 0.20 | 0.002 | 0.23 |
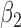 |
0.010 | 0.81 | 0.005 | 0.30 | 0.003 | 0.47 | 0.000 | 0.40 | 0.002 | 0.14 | 0.004 | 0.23 |
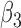 |
0.011 | 0.81 | 0.008 | 0.30 | 0.008 | 0.49 | 0.010 | 0.40 | 0.005 | 0.14 | 0.001 | 0.23 |
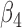 |
0.013 | 0.81 | 0.006 | 0.31 | 0.001 | 0.47 | 0.005 | 0.40 | 0.006 | 0.14 | 0.003 | 0.24 |
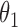 |
0.004 | 0.35 | 0.001 | 0.30 | 0.005 | 0.30 | 0.003 | 0.18 | 0.001 | 0.15 | 0.002 | 0.15 |
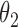 |
0.008 | 0.66 | 0.004 | 0.37 | 0.007 | 0.46 | 0.007 | 0.32 | 0.002 | 0.18 | 0.004 | 0.21 |
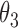 |
0.018 | 0.66 | 0.009 | 0.38 | 0.010 | 0.45 | 0.007 | 0.33 | 0.004 | 0.19 | 0.008 | 0.21 |
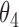 |
0.019 | 0.66 | 0.012 | 0.38 | 0.015 | 0.48 | 0.017 | 0.33 | 0.007 | 0.19 | 0.005 | 0.22 |
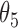 |
0.021 | 0.66 | 0.010 | 0.38 | 0.006 | 0.45 | 0.012 | 0.33 | 0.008 | 0.18 | 0.007 | 0.21 |
The outcome is generated from a normal distribution with mean 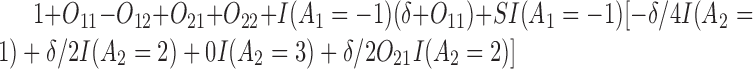 with variance
with variance 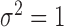 , where
, where 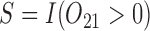 . Thus, the true
. Thus, the true  s are
s are
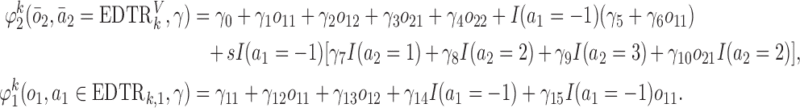 |
We also consider a misspecified scenario where 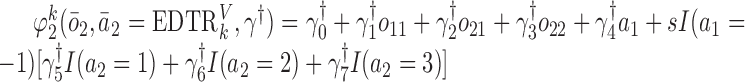 and
and 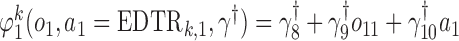 are assumed to be working models. The MSM is
are assumed to be working models. The MSM is
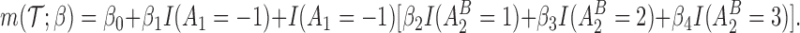 |
Hence, the true parameter value 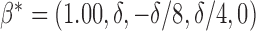 , which means that, for positive and negative
, which means that, for positive and negative 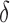 s,
s, 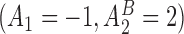 and
and 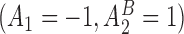 are the best EDTRs, respectively. Table 2 presents the bias and standard errors of the parameters
are the best EDTRs, respectively. Table 2 presents the bias and standard errors of the parameters 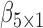 and
and  estimated using IPW, AIPW, and
estimated using IPW, AIPW, and 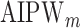 , where
, where
 |
The rows of this matrix represent 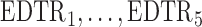 listed in Table 2 of supplementary material available at Biostatistics online. In Table 2, we set
listed in Table 2 of supplementary material available at Biostatistics online. In Table 2, we set 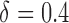 and generated 1000 datasets of sizes 100 and 400. Our results show that AIPW reduces the standard error of
and generated 1000 datasets of sizes 100 and 400. Our results show that AIPW reduces the standard error of 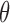 s and
s and 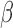 s by up to 55% compared with IPW. The misspecified scenario, where the interaction terms in both
s by up to 55% compared with IPW. The misspecified scenario, where the interaction terms in both 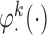 functions are ignored, results in estimators with slightly larger standard errors compared with AIPW.
functions are ignored, results in estimators with slightly larger standard errors compared with AIPW.
Figure 2 shows how fast the size of the set of best converges to 1 as 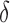 grows when the parameters of each EDTR are estimated using IPW and AIPW. Note that, for
grows when the parameters of each EDTR are estimated using IPW and AIPW. Note that, for 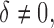 the true set size
the true set size 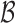 is 1. For each
is 1. For each 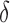 , we generated 500 datasets and defined the ESS as the empirical average of the set sizes for each dataset. This figure shows that when the parameters
, we generated 500 datasets and defined the ESS as the empirical average of the set sizes for each dataset. This figure shows that when the parameters 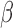 of the marginal model are estimated using AIPW, the ESS decreases to 1 faster than when using IPW. This is due to more efficient estimation of
of the marginal model are estimated using AIPW, the ESS decreases to 1 faster than when using IPW. This is due to more efficient estimation of 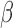 s. The plot of ESS when estimated using
s. The plot of ESS when estimated using 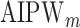 is omitted since it is similar to IPW in this simulation.
is omitted since it is similar to IPW in this simulation.
6. Illustrative data analysis
The EXTEND study was a 24-week, multistage clinical trial that enrolled alcohol-dependent patients (Lei and others, 2012). At stage 1, patients are randomized with probability 0.5 to either the stringent or lenient definitions of non-response while receiving NTX. Participants were assessed weekly for drinking behavior, and starting at week 3, as soon as the participant met his her assigned criterion for early non-response, he
her assigned criterion for early non-response, he she was immediately re-randomized to one of two “rescue” tactics: (1) offering CBI in addition to NTX (i.e.
she was immediately re-randomized to one of two “rescue” tactics: (1) offering CBI in addition to NTX (i.e. 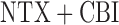 ); or (2) offering CBI alone (i.e. CBI). Participants who did not meet their assigned criterion for early non-response by the end of week 8 (i.e. responders to NTX) were re-randomized at that point (i.e. end of week 8) to one of two “maintenance” tactics: either (1) adding TDM to NTX (i.e. NTX+TDM) or offering NTX alone (NTX). Figure 3 (Appendix C of supplementary material available at Biostatistics online) depicts this two-stage SMART design.
); or (2) offering CBI alone (i.e. CBI). Participants who did not meet their assigned criterion for early non-response by the end of week 8 (i.e. responders to NTX) were re-randomized at that point (i.e. end of week 8) to one of two “maintenance” tactics: either (1) adding TDM to NTX (i.e. NTX+TDM) or offering NTX alone (NTX). Figure 3 (Appendix C of supplementary material available at Biostatistics online) depicts this two-stage SMART design.
For illustration, we focus on a simplified version of this trial. Let the primary outcome 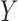 denote the Penn Alcohol Craving Scale (PACS) score over 24 weeks. Lower PACSs are preferable. Let
denote the Penn Alcohol Craving Scale (PACS) score over 24 weeks. Lower PACSs are preferable. Let 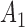 denote the non-response criterion coded as
denote the non-response criterion coded as 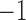 for stringent and
for stringent and 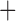 1 for lenient. The embedded tailoring variable
1 for lenient. The embedded tailoring variable 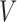 in this design is the response
in this design is the response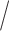 non-response status. The stage-2 treatment options for responders are NTX (
non-response status. The stage-2 treatment options for responders are NTX (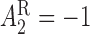 ) and
) and 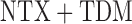 (
(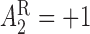 ) and for non-responders the rescue treatment options are CBI (
) and for non-responders the rescue treatment options are CBI (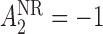 ) and
) and 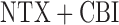 (
(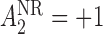 ). Additionally, let
). Additionally, let 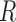 denote the indicator for whether
denote the indicator for whether 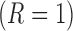 or not
or not 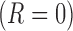 the patient was a responder to the initial NTX treatment. Figure 3 in Appendix C of supplementary material available at Biostatistics online shows the number of patients assigned to each treatment option. By design, there are
the patient was a responder to the initial NTX treatment. Figure 3 in Appendix C of supplementary material available at Biostatistics online shows the number of patients assigned to each treatment option. By design, there are 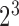 EDTRs in this SMART based on different combinations of
EDTRs in this SMART based on different combinations of  , which are listed in Table 3 of supplementary material available at Biostatistics online.
, which are listed in Table 3 of supplementary material available at Biostatistics online.
Table 3.
Extend trial: inference about the parameters 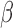 using IPW and AIPW
using IPW and AIPW
| IPW |
AIPW |
|||
|---|---|---|---|---|
| Parameter | Est. | SD | Est. | SD |
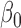 |
8.86 | 0.45 | 8.84 | 0.47 |
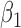 |
 0.99 0.99 |
0.45 |
 0.90 0.90 |
0.44 |
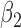 |
 0.24 0.24 |
0.34 |
 0.09 0.09 |
0.27 |
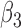 |
 0.07 0.07 |
0.28 |
 0.21 0.21 |
0.13 |
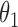 |
7.56 | 0.76 | 7.65 | 0.67 |
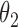 |
7.71 | 0.74 | 8.06 | 0.67 |
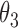 |
8.05 | 0.71 | 7.83 | 0.70 |
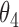 |
8.19 | 0.69 | 8.24 | 0.70 |
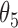 |
9.53 | 0.81 | 9.44 | 0.76 |
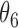 |
9.68 | 0.80 | 9.85 | 0.77 |
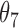 |
10.02 | 0.83 | 9.62 | 0.70 |
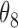 |
10.17 | 0.82 | 10.03 | 0.72 |
Baseline variables include PACS before stage 1 (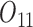 ) and gender (
) and gender (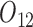 ). The intermediate outcomes are the average PACS during stage 1 (
). The intermediate outcomes are the average PACS during stage 1 (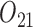 ) and the standard error of the measured PACS during stage 1 (
) and the standard error of the measured PACS during stage 1 (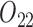 ). We consider the following MSM:
). We consider the following MSM: 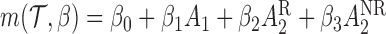 . One may add the interaction terms
. One may add the interaction terms 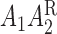 and
and 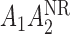 to this model. Also, we consider
to this model. Also, we consider 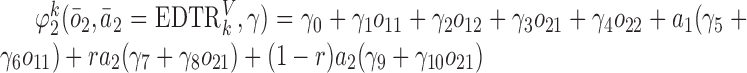 and
and 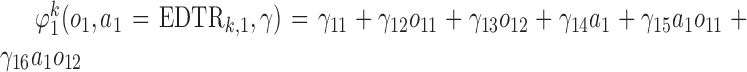 .
.
We estimated the parameter vector 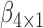 and
and 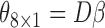 using both the IPW (3.1) and AIPW (3.2) estimators and the results are presented in Table 3, where
using both the IPW (3.1) and AIPW (3.2) estimators and the results are presented in Table 3, where
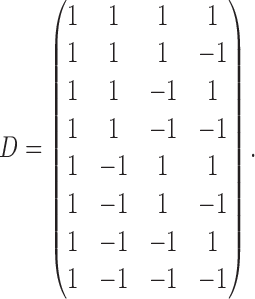 |
The rows of this matrix represent 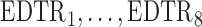 listed in Table 3 of supplementary material available at Biostatistics online. The point estimate and standard errors for
listed in Table 3 of supplementary material available at Biostatistics online. The point estimate and standard errors for  and
and  are very close using both estimators. However, the parameters corresponding to
are very close using both estimators. However, the parameters corresponding to 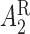 and
and 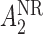 have smaller standard errors when estimated using AIPW. Moreover, our procedure screens out
have smaller standard errors when estimated using AIPW. Moreover, our procedure screens out 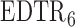 and
and 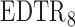 when the parameter vector
when the parameter vector 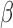 is estimated using AIPW, but using IPW results in keeping all eight EDTRs in the set of best. In other words, when using MCB with the AIPW approach to estimate the mean outcome under each EDTR, results indicated that DTRs that begin with NTX, classifies patients as non-responders by using a stringent criterion, and offers CBI alone to non-responders and NTX or
is estimated using AIPW, but using IPW results in keeping all eight EDTRs in the set of best. In other words, when using MCB with the AIPW approach to estimate the mean outcome under each EDTR, results indicated that DTRs that begin with NTX, classifies patients as non-responders by using a stringent criterion, and offers CBI alone to non-responders and NTX or 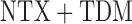 to responders, do not belong to the set of best EDTRs.
to responders, do not belong to the set of best EDTRs.
7. Discussion
An important research question motivating many SMART studies concerns the selection of the best (i.e. most efficacious) DTR among a set of DTRs that are embedded in a SMART. However, this is often not possible due to a small sample size. In this manuscript, we propose a method that can be used to identify the set that contains the best DTR. We frame the problem as a special case of multiple comparison and show that the constructed set of best contains the true best DTR with at least a given probability. We use the AIPW estimator to estimate the mean under each DTR, and our simulation results show that, for any given sample size, the cardinality of the constructed set of best is less than the cardinality obtained by IPW estimators, while maintaining the Type I error rate. Moreover, we prove that the probability of inclusion of an inferior DTR in the constructed set of best decays exponentially as the difference between the best and the inferior DTR grows.
Currently most SMART designs are sized such that an investigator can detect either a given stage-1 or stage-2 treatment effect or a given difference between two DTRs with a given probability. One important extension of this work would be to devise a method that can be used to plan SMART sample sizes such that the constructed set of best includes at most 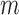 DTRs, for a fixed difference between the best and the worst DTRs, with a given probability. This will be more consistent with the goal of SMART designs in many applications.
DTRs, for a fixed difference between the best and the worst DTRs, with a given probability. This will be more consistent with the goal of SMART designs in many applications.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
This work was supported in part by grants P50 DA010075, R01 AA019092, R01 AA014851, RC1 AA019092, SES 1260782, P01 AA016821 from the National Institute on Drug Abuse (NIDA) and National Science Foundation (NSF).
Supplementary Material
Acknowledgments
The authors are grateful for valuable comments from Professor Susan Murphy and Xi Lu. Conflict of Interest: None declared.
References
- Bang H., Robins (2005). Doubly robust estimation in missing data and causal inference models. Biometrics 614, 962–972. [DOI] [PubMed] [Google Scholar]
- Chakraborty B., Moodie E. (2013) Statistical Methods for Dynamic Treatment Regimes. Berlin: Springer. [Google Scholar]
- Chakraborty B., Murphy S. A. (2014). Dynamic treatment regimes. Annual Review of Statistics and its Application 1, 447–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidian M., Tsiatis A., Leon S. (2005). Semiparametric estimation of treatment effect in a pretest–posttest study with missing data. Statistical Science 203, 261–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernán M. Á., Brumback B., Robins J. M. (2000). Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology 115, 561–570. [DOI] [PubMed] [Google Scholar]
- Hirano K., Imbens G. W., Ridder G. (2003). Efficient estimation of average treatment effects using the estimated propensity score. Econometrica 714, 1161–1189. [Google Scholar]
- Hsu J. (1996) Multiple Comparisons: Theory and Methods. London: Chapman & Hall, CRC Press. [Google Scholar]
- Hsu J. C. (1981). Simultaneous confidence intervals for all distances from the “Best”. The Annals of Statistics 95, 1026–1034. [Google Scholar]
- Hsu J. C. (1984). Constrained simultaneous confidence intervals for multiple comparisons with the best. The Annals of Statistics 123, 1136–1144. [Google Scholar]
- Keselman H., Cribbie R., Holland B. (1999). The pairwise multiple comparison multiplicity problem: an alternative approach to familywise and comparison wise Type I error control. Psychological Methods 41, 58. [Google Scholar]
- Laber E. B., Lizotte D. J., Qian M., Pelham W. E., Murphy S. A. (2014). Dynamic treatment regimes: technical challenges and applications. Electronic Journal of Statistics 81, 1225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavori P. W., Dawson R. (2000). A design for testing clinical strategies: biased adaptive within-subject randomization. Journal of the Royal Statistical Society: Series A (Statistics in Society) 1631, 29–38. [Google Scholar]
- Lavori P. W., Dawson R., Rush A. J. (2000). Flexible treatment strategies in chronic disease: clinical and research implications. Biological Psychiatry 486, 605–614. [DOI] [PubMed] [Google Scholar]
- Lei H., Nahum-Shani I., Lynch K., Oslin D., Murphy S. (2012). A SMART design for building individualized treatment sequences. Annual Review of Clinical Psychology 8, 21–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy S., Van Der Laan M., Robins J. (2001). Marginal mean models for dynamic regimes. Journal of the American Statistical Association 96456, 1410–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy S. A. (2003). Optimal dynamic treatment regimes. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 652, 331–355. [Google Scholar]
- Murphy S. A. (2005). An experimental design for the development of adaptive treatment strategies. Statistics in Medicine 2410, 1455–1481. [DOI] [PubMed] [Google Scholar]
- Nahum-Shani I., Qian M., Almirall D., Pelham W. E., Gnagy B., Fabiano G. A., Waxmonsky J. G., Yu J., Murphy S. A. (2012). Experimental design and primary data analysis methods for comparing adaptive interventions. Psychological Methods 174, 457–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orellana L., Rotnitzky A., Robins J. M. (2010). Dynamic regime marginal structural mean models for estimation of optimal dynamic treatment regimes, part I: main content. The International Journal of Biostatistics 62, 1557–4679. [PubMed] [Google Scholar]
- Robins J., Orellana L., Rotnitzky A. (2008). Estimation and extrapolation of optimal treatment and testing strategies. Statistics in Medicine 2723, 4678–4721. [DOI] [PubMed] [Google Scholar]
- Robins J. M. (1999). Association, causation, and marginal structural models. Synthese 1211, 151–179. [Google Scholar]
- Robins J. M. (2004). Optimal structural nested models for optimal sequential decisions. Proceedings of the Second Seattle Symposium in Biostatistics. Berlin: Springer, pp. 189–326.
- Robins J. M., Hernan M. A., Brumback B. (2000). Marginal structural models and causal inference in epidemiology. Epidemiology 115, 550–560. [DOI] [PubMed] [Google Scholar]
- Robins J. M., Rotnitzky A., Zhao L. P. (1995). Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. Journal of the American Statistical Association 90429, 106–121. [Google Scholar]
- Saville D. J. (1990). Multiple comparison procedures: the practical solution. The American Statistician 442, 174–180. [Google Scholar]
- Scheffe H. (1953). A method for judging all contrasts in the analysis of variance. Biometrika 40(1–2), 87–110. [Google Scholar]
- Tukey J. W. (1953) The Problem of Multiple Comparisons: Introduction and Parts A, B, and C. Princeton: Princeton University. [Google Scholar]
- van der Laan M., Robins J. (2003) Unified Methods for Censored Longitudinal Data and Causality. Berlin: Springer. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.