Abstract
In longitudinal data arising from observational or experimental studies, dependent subject drop-out is a common occurrence. If the goal is estimation of the parameters of a marginal complete-data model for the outcome, biased inference will result from fitting the model of interest with only uncensored subjects. For example, investigators are interested in estimating a prognostic model for clinical events in HIV-positive patients, under the counterfactual scenario in which everyone remained on ART (when in reality, only a subset had). Inverse probability of censoring weighting (IPCW) is a popular method that relies on correct estimation of the probability of censoring to produce consistent estimation, but is an inefficient estimator in its standard form. We introduce sequentially augmented regression (SAR), an adaptation of the Bang and Robins (2005. Doubly robust estimation in missing data and causal inference models. Biometrics 61, 962–972.) method to estimate a complete-data prediction model, adjusting for longitudinal missing at random censoring. In addition, we propose a closely related non-parametric approach using targeted maximum likelihood estimation (TMLE; van der Laan and Rubin, 2006. Targeted maximum likelihood learning. The International Journal of Biostatistics 2(1), Article 11). We compare IPCW, SAR, and TMLE (implemented parametrically and with Super Learner) through simulation and the above-mentioned case study.
Keywords: Inverse probability of censoring weighting, Longitudinal, Marginal structural model, Prediction, Targeted maximum likelihood estimation, Targeted minimum loss-based estimation
1. Introduction
Regression models are often used in the personalized medical literature to estimate the prognostic effect of baseline variables on a health outcome of interest. Longitudinal censoring is a common occurrence, arising from both loss to follow-up and other deviations from the conditions under which the investigator aims to study the population of interest. When the subjects in a study are observed over time, it is possible that time-varying factors affecting the outcome may also influence censoring. Such factors are called time-dependent confounders (Robins, 1986) and in their presence, estimation of the model of interest is complicated.
Inverse probability of censoring weighting (IPCW) is a semiparametric method for estimation of the model of interest that adjusts for censoring that is Missing at Random (MAR), meaning that censoring may depend on the observed past, but not on the future prognosis (Robins and others, 1995). IPCW only requires fitting a model for the probability of censoring, and does not require a specification for the full likelihood. However, standard IPCW is not an efficient semiparametric method, relies on the correct specification of the censoring model, and is sensitive to large weights (Robins and others, 2000), which occur frequently in practice.
Augmented IPCW (AIPCW) (Robins and Rotnitzky, 1992; Scharfstein and others, 1999) can produce double robust estimates, meaning that the estimator is consistent if either the model for censoring or a specific regression model for the outcome process is correctly specified, but not necessarily both. AIPCW estimators, which require a computationally intensive procedure in the longitudinal setting, are semiparametric efficient (under correct specification) for a saturated model of interest. van der Laan and Robins (2003) and Yu and van der Laan (2006) presented a Monte Carlo algorithm for efficient estimation of a history-adjusted marginal structural model. Bang and Robins (2005) developed a (double robust and efficient) variation of the AIPCW methodology where the full data estimating equation was modeled as a sequence of nested regressions. van der Laan and Rubin (2006) introduced targeted maximum likelihood estimation (TMLE), which provides a framework for constructing double robust and efficient substitution estimators, and has been successfully developed for longitudinal and survival data for a treatment-specific mean (Stitelman and others, 2012; van der Laan and Gruber, 2012) and marginal structural models (Schnitzer and others, 2014; Petersen and others, 2014) (the latter three articles using the fundamental theory from Bang and Robins, 2005).
Our theoretical work was inspired by estimation of a prognostic model for an incident clinical event in HIV-positive patients had they all remained on antiretroviral treatment (ART). Even though effective treatment is available, HIV-positive patients are still subject to AIDS-defining morbidities, in addition to being at risk for a disproportionately high number of non-AIDS-defining events, such as liver, cardiovascular and renal disease (Deeks, 2011). Clinical investigators are interested in developing prognostic models to identify patients at a higher risk of these events despite being consistently on treatment. To estimate such a model in a historical cohort, censoring is defined as deviating from the counterfactual scenario: either being lost to follow-up, or interrupting treatment for more than 21 days. Previous work (Lok and others, 2013) used IPCW to estimate a marginal logistic regression model while adjusting for censoring.
In this article, we demonstrate the derivations of two procedures that produce semiparametric efficient and double robust estimation of a non-saturated marginal logistic regression model in the presence of censoring. Previous work (Scharfstein and others, 1999; Bang and Robins, 2005) focused on procedures for the estimation of saturated marginal models. Section 2 defines the setting and notation. Section 3 describes a sequential augmented regression (SAR) procedure that adapts Bang and Robins' method for marginal mean models, and for the logistic regression model in particular. Section 4 details the procedure for fitting a non-parametric TMLE, an approach that allows for more modeling flexibility and therefore additional robustness. Our derivation is a special case of the general theory developed independently and concurrently in Petersen and others (2014). Both of these procedures can be readily implemented with standard software. Section 5 describes a simulation study that compares the properties of IPCW with the estimators described in this article. Section 6 provides the results of the HIV application.
2. Setting and notation
Consider first the full-data setting where all of 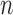 subjects remain uncensored and fully observed over a period of time. Each subject has an independent draw of longitudinal data of the form
subjects remain uncensored and fully observed over a period of time. Each subject has an independent draw of longitudinal data of the form 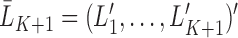 . Each multivariate
. Each multivariate 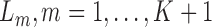 , includes time-dependent variables, and
, includes time-dependent variables, and 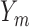 , the monotone indicator of the occurrence of an incident event at or before time point
, the monotone indicator of the occurrence of an incident event at or before time point 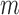 . The event indicator at the final time point,
. The event indicator at the final time point, 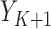 , is the outcome of interest. Although the following procedure applies to any generalized linear model (GLM) on the mean outcome, as a concrete example consider the parameters of interest to be the coefficients of a logistic model with full data. Let
, is the outcome of interest. Although the following procedure applies to any generalized linear model (GLM) on the mean outcome, as a concrete example consider the parameters of interest to be the coefficients of a logistic model with full data. Let 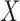 be a column vector that includes the value one (for the intercept) and
be a column vector that includes the value one (for the intercept) and 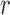 potential predictors of the outcome of interest that are a subset of the baseline variables in
potential predictors of the outcome of interest that are a subset of the baseline variables in 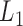 . The logistic regression model of interest is defined by
. The logistic regression model of interest is defined by 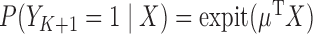 where
where 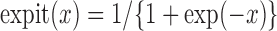 and
and 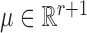 . Fitting this logistic regression based on the full data corresponds to solving the score equations for the logistic regression model. The parameter of interest in this study is
. Fitting this logistic regression based on the full data corresponds to solving the score equations for the logistic regression model. The parameter of interest in this study is 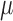 , the column vector of regression model coefficients in the logistic model. The parameter
, the column vector of regression model coefficients in the logistic model. The parameter  satisfies the equations
satisfies the equations
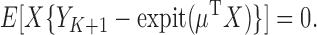 |
(2.1) |
Had complete data been observed, under regularity conditions the empirical solution to the score equations is a consistent, asymptotically normal estimator for 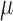 (van der Vaart, 1998).
(van der Vaart, 1998).
The full data may not be observable due to censoring, which can include both drop-out and deviation from a study scenario of interest. In our application, we wish to estimate a prediction model under the counterfactual scenario where all subjects were continuously taking ART. Define the monotone censoring variable 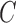 so that if
so that if 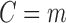 , the subject's data are only observed under the defined protocol until and including time
, the subject's data are only observed under the defined protocol until and including time 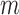 . Assume that the baseline variables
. Assume that the baseline variables 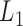 are always observed so that
are always observed so that  for all subjects. If an outcome event is observed before censoring occurs, define
for all subjects. If an outcome event is observed before censoring occurs, define 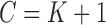 . Therefore, the observed data are
. Therefore, the observed data are 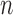 i.i.d. realizations of
i.i.d. realizations of 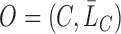 , where
, where 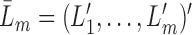 indicates the history of variables measured up until time
indicates the history of variables measured up until time  .
.
The data are assumed to be MAR, meaning that the probability of censoring at a given time only depends on observed past variables and not further on the prognosis of patients, i.e. 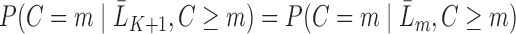 ,
, 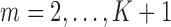 (Robins and others, 1995). Intuitively, this untestable assumption means that “decisions” to exit the study only depend on the past information available to the analyst. Censoring is called “dependent” on past variables when
(Robins and others, 1995). Intuitively, this untestable assumption means that “decisions” to exit the study only depend on the past information available to the analyst. Censoring is called “dependent” on past variables when 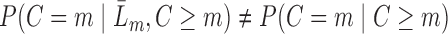 (Robins and Rotnitzky, 1992). We also make the positivity assumption that, for all
(Robins and Rotnitzky, 1992). We also make the positivity assumption that, for all 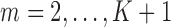 and
and 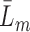 , there is a positive probability of remaining uncensored at each time point, i.e.
, there is a positive probability of remaining uncensored at each time point, i.e. 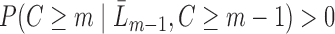 . Intuitively, this means that given past information, no subject is deterministically censored. Let the true conditional probability of being observed at time
. Intuitively, this means that given past information, no subject is deterministically censored. Let the true conditional probability of being observed at time 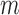 be denoted by
be denoted by 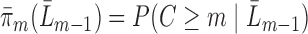 . Under MAR,
. Under MAR, 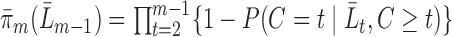 .
.
Define  , and in particular,
, and in particular, 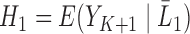 . As shown in Theorem 1 in Section 2 of the Supplementary Material, for
. As shown in Theorem 1 in Section 2 of the Supplementary Material, for 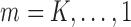 we have that
we have that 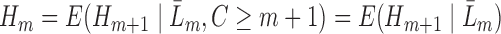 . These quantities are therefore estimable from the data under the described assumptions, by starting with
. These quantities are therefore estimable from the data under the described assumptions, by starting with 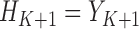 and going backward in time. Recalling that
and going backward in time. Recalling that 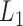 is a superset of
is a superset of 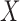 , by taking (1) and applying the property of iterated expectations, we get that
, by taking (1) and applying the property of iterated expectations, we get that
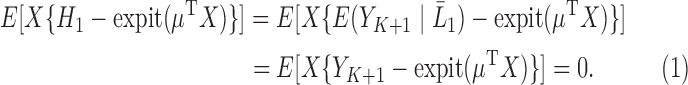 |
(2.2) |
Therefore, 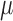 can be represented as a function of
can be represented as a function of 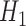 and
and 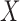 .
.
We can consider our parameter of interest as non-parametrically defined as the solution to (1) if it represents a meaningful summary of the predictive ability of the covariates on the event outcome (Neugebauer and van der Laan, 2007; Petersen and others, 2014). The parameter 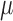 is clinically meaningful as the minimizer of the logistic loss function for the logistic regression model, even if this model is not assumed to partake in the underlying data generation. Therefore, we can treat the underlying data generating function of
is clinically meaningful as the minimizer of the logistic loss function for the logistic regression model, even if this model is not assumed to partake in the underlying data generation. Therefore, we can treat the underlying data generating function of 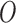 as non-parametric and derive root-
as non-parametric and derive root-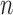 consistent, asymptotically linear and locally efficient estimators for
consistent, asymptotically linear and locally efficient estimators for 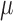 .
.
3. Sequential augmented regression
The SAR procedure is an adaptation of the Bang and Robins (2005) procedure. It uses GLMs to estimate each 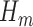 . Starting with an estimate for
. Starting with an estimate for 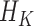 , the models are fit recursively for
, the models are fit recursively for 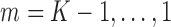 using the identity
using the identity 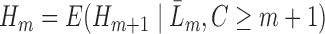 . The key feature of this procedure (and what makes it “double robust” as explained further down) is that each GLM is given an extra covariate (i.e. it is “augmented”); this covariate is the inverse probability of censoring weight for the given time point multiplied by
. The key feature of this procedure (and what makes it “double robust” as explained further down) is that each GLM is given an extra covariate (i.e. it is “augmented”); this covariate is the inverse probability of censoring weight for the given time point multiplied by 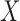 . The estimate of
. The estimate of 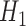 is then directly used to obtain estimates of
is then directly used to obtain estimates of 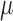 , the coefficients of the logistic regression model of interest. The SAR procedure is as follows:
, the coefficients of the logistic regression model of interest. The SAR procedure is as follows:
-
For each time point
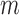 , fit parametric models,
, fit parametric models, 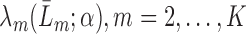 to predict the conditional hazard of censoring at time
to predict the conditional hazard of censoring at time 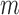 ,
, 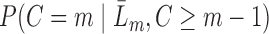 . Let
. Let 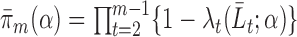 be the parametric model for the conditional probability of being uncensored at time
be the parametric model for the conditional probability of being uncensored at time 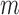 (i.e. the last observation occurs at time
(i.e. the last observation occurs at time 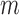 or later), a function of
or later), a function of 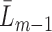 (under MAR). Let
(under MAR). Let 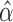 be the maximum likelihood estimate (MLE) for this model so that
be the maximum likelihood estimate (MLE) for this model so that 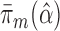 is a parametric estimate of the probability of being uncensored at time
is a parametric estimate of the probability of being uncensored at time 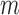 .
.Initialize
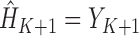 . Recursively, for
. Recursively, for 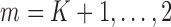 , follow steps (2) and (3).
, follow steps (2) and (3). Using subjects with
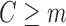 (excepting those with a prior event; see below), fit a GLM for
(excepting those with a prior event; see below), fit a GLM for 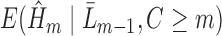 of the form
of the form 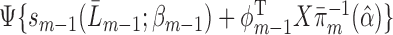 , where
, where  is a known function linear in
is a known function linear in  , and
, and  is the inverse canonical link function for the GLM.
is the inverse canonical link function for the GLM.For all subjects with
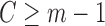 , set
, set 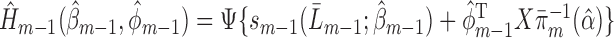 using the parameter estimates for
using the parameter estimates for 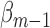 and
and 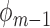 .
.The final
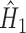 is computed for all subjects as
is computed for all subjects as 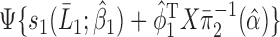 . Then, the double robust estimator
. Then, the double robust estimator 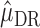 for
for 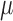 is obtained by running a logistic regression of
is obtained by running a logistic regression of 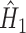 on
on 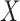 . The estimator
. The estimator 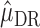 therefore solves the estimating equation
therefore solves the estimating equation 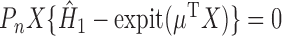 .
.
The GLM in Step (2) will generally correspond with the outcome type. For instance, if 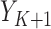 is a binary outcome (such as event-free survival, as in our case) and hence
is a binary outcome (such as event-free survival, as in our case) and hence 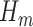 a probability when
a probability when 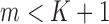 , logistic regression with a logit link would be a natural choice to model
, logistic regression with a logit link would be a natural choice to model 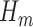 so that
so that 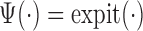 . The linear specification
. The linear specification  corresponds with linear terms
corresponds with linear terms 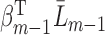 , chosen based on how subject matter experts would specify the complete-data quantity
, chosen based on how subject matter experts would specify the complete-data quantity 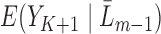 . Note that since the expectation
. Note that since the expectation 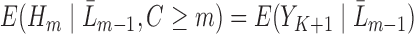 which is modeled in Step (2) is conditional on the entire history
which is modeled in Step (2) is conditional on the entire history 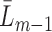 , the occurrence of a previous event sets this expectation to one. Therefore, only subjects who have not experienced a previous event should be used to fit the parameters of
, the occurrence of a previous event sets this expectation to one. Therefore, only subjects who have not experienced a previous event should be used to fit the parameters of 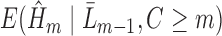 . Note that fitting this GLM by maximum likelihood estimation (or iteratively reweighted least squares) gives vector parameter estimates
. Note that fitting this GLM by maximum likelihood estimation (or iteratively reweighted least squares) gives vector parameter estimates 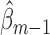 and
and 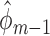 that jointly solve the normal equations:
that jointly solve the normal equations:
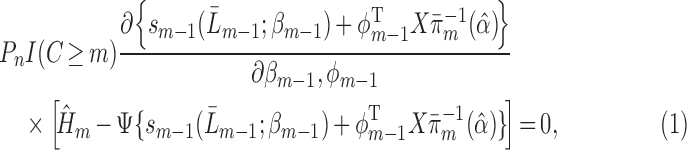 |
(3.1) |
using the notation 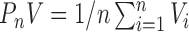 .
.
The estimator 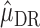 is double robust in the sense that if either all of the censoring models
is double robust in the sense that if either all of the censoring models  (i.e. each hazard of censoring model
(i.e. each hazard of censoring model 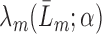 ) or all of the nested outcome models
) or all of the nested outcome models 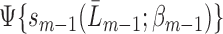 are correct,
are correct, 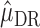 is consistent for
is consistent for 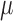 . This is proven directly in Section 4 of the Supplementary Material.
. This is proven directly in Section 4 of the Supplementary Material.
This procedure produces estimates of 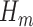 and
and 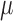 that jointly solve the equation of the empirical mean of the efficient influence function (EIF) set equal to zero. This implies that
that jointly solve the equation of the empirical mean of the efficient influence function (EIF) set equal to zero. This implies that 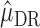 is also locally semiparametric efficient in the class of regular asymptotically linear estimators for
is also locally semiparametric efficient in the class of regular asymptotically linear estimators for 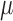 (van der Laan and Robins, 2003; Tsiatis, 2006). As derived in Section 3 of the Supplementary Material, the EIF for
(van der Laan and Robins, 2003; Tsiatis, 2006). As derived in Section 3 of the Supplementary Material, the EIF for 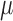 up to a scalar constant is
up to a scalar constant is
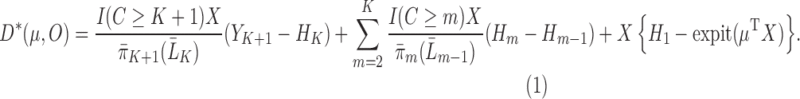 |
(3.2) |
Because 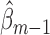 and
and 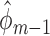 satisfy the normal equations (3) for
satisfy the normal equations (3) for 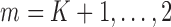 , they also satisfy each summand in the empirical EIF,
, they also satisfy each summand in the empirical EIF, 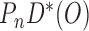 set to 0 (each summand in the EIF is a sub-component of the normal equations in (3) satisfied at step
set to 0 (each summand in the EIF is a sub-component of the normal equations in (3) satisfied at step 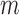 in the procedure).
in the procedure).
To contrast this procedure with Bang and Robins (2005), the authors first define the function 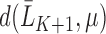 where
where 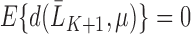 , which corresponds with
, which corresponds with 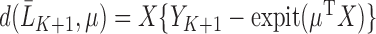 for our parameter of interest. Then, they define
for our parameter of interest. Then, they define 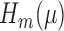 as
as 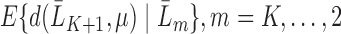 and place a GLM on each conditional expectation of the function
and place a GLM on each conditional expectation of the function 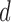 , with
, with 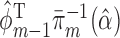 included as the augmentation covariate. At the last step, the estimator is defined as the solution of the estimating equation
included as the augmentation covariate. At the last step, the estimator is defined as the solution of the estimating equation 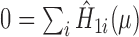 . The limitation in this procedure is that
. The limitation in this procedure is that 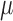 is needed in the first step but it is unknown. A simple procedure cannot be defined when
is needed in the first step but it is unknown. A simple procedure cannot be defined when 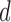 and the link function used in the estimation of
and the link function used in the estimation of 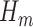 are non-linear, since a GLM is used to directly model
are non-linear, since a GLM is used to directly model 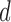 . Our modification of the procedure instead directly imposes a GLM on the quantity
. Our modification of the procedure instead directly imposes a GLM on the quantity 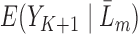 .
.
4. Targeted maximum likelihood estimation
TMLE is an alternative approach to SAR with the same asymptotic properties (double-robustness and local efficiency) but with fewer modeling restrictions. In this section, we focus on the derivation of the TMLE procedure and implementation for the situation where the marginal model of interest is a logistic regression model conditional on baseline covariates, and longitudinal censoring occurs. Section 3 shows that our parameter of interest 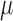 can be identified implicitly through
can be identified implicitly through 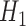 (2), an estimable quantity through our available data. Therefore, by estimating each conditional expectation
(2), an estimable quantity through our available data. Therefore, by estimating each conditional expectation 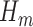 , denoted by
, denoted by 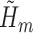 , we can construct a substitution estimator for
, we can construct a substitution estimator for 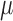 , corresponding to the solution of
, corresponding to the solution of 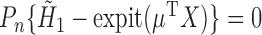 . The TMLE procedure updates the fits of each
. The TMLE procedure updates the fits of each 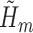 in order to reduce estimation bias. These updates are designed so that the updated estimate for
in order to reduce estimation bias. These updates are designed so that the updated estimate for 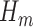 along with the substitution estimate
along with the substitution estimate 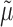 solves the equation of the empirical mean of the EIF set equal to zero. This results in the same efficiency property as SAR.
solves the equation of the empirical mean of the EIF set equal to zero. This results in the same efficiency property as SAR.
The TMLE procedure for an event outcome is as follows:
-
Fit each censoring probability
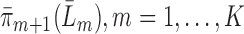 , and denote the predicted values by
, and denote the predicted values by 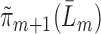 .
.Initialize
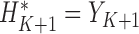 . For
. For 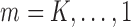 , follow Steps (2) and (3).
, follow Steps (2) and (3). Estimate
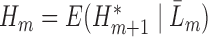 and denote the predicted values by
and denote the predicted values by 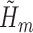 . Note that if an event occurred at or before time
. Note that if an event occurred at or before time 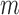 ,
, 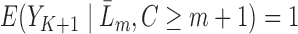 . Therefore, we only model at-risk and uncensored subjects (with no event at or before time
. Therefore, we only model at-risk and uncensored subjects (with no event at or before time 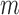 ).
).To update
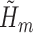 , run a logistic regression with outcome
, run a logistic regression with outcome 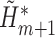 , no intercept, covariates
, no intercept, covariates 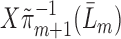 , and offset
, and offset  . This regression is fit using only “at risk” subjects (those with
. This regression is fit using only “at risk” subjects (those with 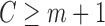 and without an event at or before time
and without an event at or before time 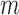 ). Let the coefficient vector estimated in this regression be denoted by
). Let the coefficient vector estimated in this regression be denoted by 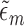 . The prediction for each subject with
. The prediction for each subject with 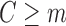 from this logistic regression is then
from this logistic regression is then 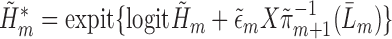 if no event occurred prior to
if no event occurred prior to 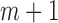 , and
, and 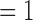 otherwise.
otherwise.When
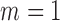 ,
, 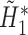 is obtained. Fit a logistic regression of
is obtained. Fit a logistic regression of 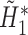 on
on 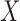 , which is the model of interest. The resulting estimate,
, which is the model of interest. The resulting estimate,  , of the coefficient vector is the TMLE estimate for
, of the coefficient vector is the TMLE estimate for 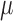 .
.
The above procedure produces asymptotically efficient inference if each 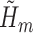 and
and 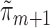 is estimated consistently. The estimate
is estimated consistently. The estimate 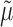 is consistent for
is consistent for 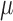 if either all of the
if either all of the  or the
or the 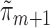 are consistent. In Section 5 of the Supplementary Material, we show that this procedure satisfies the TMLE requirement that the score functions of the update models span the EIF. For intuition, note that the update steps produce fits that solve each component of the empirical mean of the EIF in (4) set equal to zero. The logistic regression in Step (3) produces the estimated
are consistent. In Section 5 of the Supplementary Material, we show that this procedure satisfies the TMLE requirement that the score functions of the update models span the EIF. For intuition, note that the update steps produce fits that solve each component of the empirical mean of the EIF in (4) set equal to zero. The logistic regression in Step (3) produces the estimated 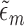 that solves
that solves 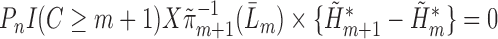 . The final component,
. The final component, 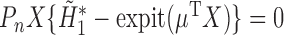 , is directly solved for
, is directly solved for 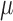 by the final logistic regression of
by the final logistic regression of 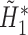 on
on 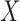 .
.
The TMLE and SAR described above are both asymptotically equivalent under correct specification of the treatment and outcome models. For an understanding of how their construction may lead to different finite-sample estimation even when all models are identically specified, see Section 6 in the Supplementary Material. The construction of SAR requires the usage of GLMs for the specification of the conditional expectations of the outcome. In contrast, TMLE does not predetermine the forms of these models (nor the censoring models). This allows for non-parametric (or data-adaptive) estimation of these quantities using, for example, Super Learner (Polley and van der Laan, 2010). It is recommended to use cross-validation in order to avoid overfitting (van der Laan and Rose, 2011, Chapter 27).
5. Simulation
We conducted a simulation study to compare IPCW and the SAR and TMLE procedures described in the previous sections. We generated datasets of the form 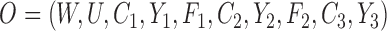 where
where 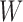 and
and 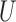 are binary and continuous baseline variables, respectively,
are binary and continuous baseline variables, respectively, 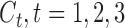 are censoring indicators,
are censoring indicators, 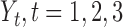 are failure indicators, and
are failure indicators, and 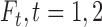 are continuous time-dependent variables. If
are continuous time-dependent variables. If 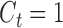 , then
, then 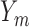 is unobserved for
is unobserved for 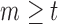 . If a failure is observed, there is no subsequent censoring (by definition). See Table 1 for details about the data generation. The marginal model of interest is
. If a failure is observed, there is no subsequent censoring (by definition). See Table 1 for details about the data generation. The marginal model of interest is 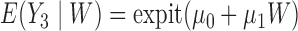 . Given the data generation, the true values of the coefficients (calculated using numerical integration) are
. Given the data generation, the true values of the coefficients (calculated using numerical integration) are 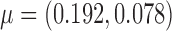 .
.
Table 1.
Simulation study data generation
| Baseline | ||
 |
 |
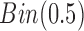 |
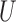 |
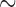 |
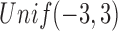 |
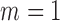 | ||
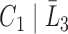 |
 |
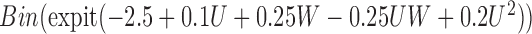 |
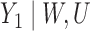 |
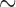 |
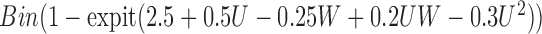 |
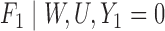 |
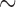 |
 |
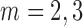 | ||
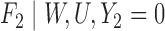 |
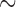 |
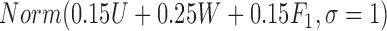 |
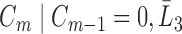 |
 |
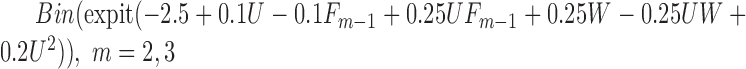 |
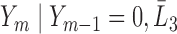 |
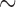 |
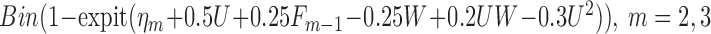 where where 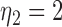 and and 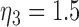
|
| Marginal probabilities of censoring | ||
 |
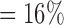 , , |
the probability that no 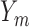 s are observed s are observed |
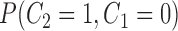 |
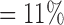 , , |
the probability that only 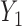 is observed is observed |
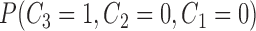 |
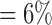 , , |
the probability that only 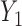 and and 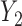 are observed are observed |
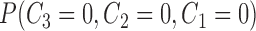 |
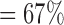 , , |
the probability that all 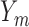 s are observed s are observed |
Data were independently sampled for each individual according to the above distributions using the random number generator in R. The notation  represents the full data.
represents the full data.
IPCW was implemented with logistic regressions to estimate the weights. SAR was implemented with logistic regressions to estimate each 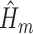 (henceforth referred to as the “outcome models”). A semiparametric version of the TMLE (TMLE-BIN) was implemented with logistic regression to estimate each
(henceforth referred to as the “outcome models”). A semiparametric version of the TMLE (TMLE-BIN) was implemented with logistic regression to estimate each 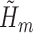 . The same IPCW weights were used in all of the above methods. Lastly, non-parametric TMLE (TMLE-SL) was implemented using Super Learner (Polley and van der Laan, 2010) to fit each
. The same IPCW weights were used in all of the above methods. Lastly, non-parametric TMLE (TMLE-SL) was implemented using Super Learner (Polley and van der Laan, 2010) to fit each 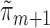 and
and 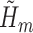 . Super Learner runs a library of candidate models, combining their predictions based on each method's cross-validated risk. Using the CRAN package SuperLearner (Polley and Van der Laan, 2011), three libraries were used: all methods (referred to as “all”), data-adaptive methods (“adapt”), and several logistic regression models (“par”). See Table 2 for details. Each of the above methods was used to estimate
. Super Learner runs a library of candidate models, combining their predictions based on each method's cross-validated risk. Using the CRAN package SuperLearner (Polley and Van der Laan, 2011), three libraries were used: all methods (referred to as “all”), data-adaptive methods (“adapt”), and several logistic regression models (“par”). See Table 2 for details. Each of the above methods was used to estimate 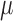 , the parameter of interest. For the non-parametric TMLE, the Super Learner was given all of the parent variables of the outcome being modeled. For the other methods, we considered four different scenarios: (1) where both the models for censoring and outcome included the correct interactions and non-linear terms, (2) where the outcome models included the correct terms and the censoring models contained only the main terms, (3) where the censoring models included the correct terms and the outcome models contained only the main terms, and (4) where both sets of models used only the main terms. Even when the outcome models included the correct terms, the models for
, the parameter of interest. For the non-parametric TMLE, the Super Learner was given all of the parent variables of the outcome being modeled. For the other methods, we considered four different scenarios: (1) where both the models for censoring and outcome included the correct interactions and non-linear terms, (2) where the outcome models included the correct terms and the censoring models contained only the main terms, (3) where the censoring models included the correct terms and the outcome models contained only the main terms, and (4) where both sets of models used only the main terms. Even when the outcome models included the correct terms, the models for 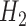 and
and 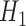 were not correctly specified since the true functional forms of
were not correctly specified since the true functional forms of 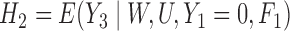 and
and 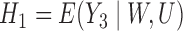 do not correspond with logistic regressions despite being modeled as such. (To see this, note that
do not correspond with logistic regressions despite being modeled as such. (To see this, note that  and
and  are expectations of the outcome conditional on an incomplete history.) However,
are expectations of the outcome conditional on an incomplete history.) However,  was correctly specified in this scenario.
was correctly specified in this scenario.
Table 2.
Simulation study: Methods included in the Super Learner library
| TMLE-SL | “all” |
“adapt” |
“par” |
|||
|---|---|---|---|---|---|---|
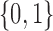 |
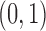 |
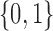 |
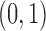 |
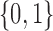 |
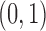 |
|
| Method | ||||||
| Logistic regression—main terms | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Logistic regression—interactions | ✓ | ✓ | ✓ | ✓ | ||
| Logistic regression—squared terms | ✓ | ✓ | ✓ | ✓ | ||
| Multivariate adaptive regression spline models | ✓ | ✓ | ✓ | ✓ | ||
| Random forests | ✓ | ✓ | ||||
| k-Nearest neighbors (KNN) | ✓ | ✓ | ||||
| Multivariate adaptive polynomial spline regression | ✓ | ✓ | ||||
Each implementation of TMLE must model both binary (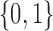 ) and probability (
) and probability ( ) outcomes. Some methods are not available for non-categorical outcomes, which is why they were excluded when modeling probabilistic outcomes. Models for censoring and
) outcomes. Some methods are not available for non-categorical outcomes, which is why they were excluded when modeling probabilistic outcomes. Models for censoring and 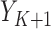 had binary outcomes, whereas models for
had binary outcomes, whereas models for 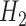 and
and 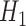 had
had 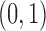 outcomes.
outcomes.
Table 3 contains the results of the simulation study. For all scenarios, IPCW had slightly higher mean standard error (as using the influence function-based sandwich estimator) than TMLE or SAR. When the censoring models were correct and the outcome models were conditional on the correct variables, all methods had similarly low MSE, near zero bias, and optimal coverage. When the censoring model was misspecified, only IPCW had a higher MSE and bias, and poor coverage. When the censoring model was correct, but the outcome models were only fit with main terms, TMLE-BIN and SAR had minimal MSE and bias, as did IPCW, because it does not utilize estimates of  . When all models were misspecified, TMLE-BIN gave highly biased results with a large MSE and poor coverage for the intercept. SAR maintained low MSE but was biased for the intercept. When TMLE was implemented with Super Learner, the procedures produced low MSE and bias, and near optimal coverage regardless of the library. When this simulation study was repeated for
. When all models were misspecified, TMLE-BIN gave highly biased results with a large MSE and poor coverage for the intercept. SAR maintained low MSE but was biased for the intercept. When TMLE was implemented with Super Learner, the procedures produced low MSE and bias, and near optimal coverage regardless of the library. When this simulation study was repeated for 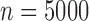 , the coverage improved for both TMLE-SL implementations when adaptive models were included in the Super Learner library. Extended results for
, the coverage improved for both TMLE-SL implementations when adaptive models were included in the Super Learner library. Extended results for 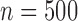 and two strengths of dependent censoring are summarized in the Supplementary Material, Section 7.
and two strengths of dependent censoring are summarized in the Supplementary Material, Section 7.
Table 3.
Simulation results. Estimates taken over 1000 generated datasets. Each dataset has 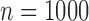 observations. True values for the intercept and the coefficient of
observations. True values for the intercept and the coefficient of 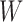 are
are 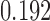 and
and 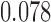 , respectively
, respectively
|
Intercept |
Coefficient |
|||||||
|---|---|---|---|---|---|---|---|---|
| Method | MSE | Bias | SE | % Coverage | MSE | Bias | SE | % Coverage |
| Correct censoring and outcome model variables | ||||||||
| IPCW | 13.6 | 1.4 | 119.6 | 95.9 | 25.3 | 1.1 | 169.6 | 96.0 |
| SAR | 13.5 | 2.7 | 108.9 | 93.5 | 24.5 |
 1.1 1.1 |
152.5 | 94.7 |
| TMLE-BIN | 13.3 | 1.7 | 110.6 | 94.7 | 24.3 | 0.8 | 154.3 | 95.3 |
| Misspecified censoring, correct outcome model variables | ||||||||
| IPCW | 18.0 |
 74.0 74.0 |
110.2 | 89.7 | 29.1 |
 66.0 66.0 |
158.2 | 93.7 |
| SAR | 12.8 | 1.9 | 104.7 | 94.0 | 23.7 | 0.0 | 150.6 | 94.7 |
| TMLE-BIN | 12.6 | 2.6 | 104.7 | 94.7 | 23.6 |
 2.1 2.1 |
150.6 | 94.4 |
| Misspecified outcome, correct censoring model variables | ||||||||
| IPCW | 13.6 | 1.4 | 119.6 | 95.9 | 25.3 | 1.1 | 169.6 | 96.0 |
| SAR | 13.8 | 9.6 | 111.8 | 94.9 | 25.5 |
 2.5 2.5 |
155.7 | 94.6 |
| TMLE-BIN | 13.6 |
 0.2 0.2 |
114.6 | 94.9 | 24.9 | 3.3 | 158.9 | 95.3 |
| Misspecified censoring and outcome model variables | ||||||||
| IPCW | 18.0 |
 74.0 74.0 |
110.2 | 89.7 | 29.1 |
 66.0 66.0 |
158.2 | 92.7 |
| SAR | 14.5 |
 38.1 38.1 |
105.1 | 91.1 | 23.6 | 9.5 | 151.0 | 94.6 |
| TMLE-BIN | 25.6 |
 117.0 117.0 |
106.4 | 80.5 | 23.3 | 24.5 | 152.1 | 94.6 |
| TMLE-SL(all) | 12.6 |
 11.4 11.4 |
100.8 | 92.9 | 23.4 | 9.2 | 143.9 | 93.7 |
| TMLE-SL(adapt) | 13.6 |
 32.4 32.4 |
96.4 | 89.1 | 23.4 | 14.1 | 136.5 | 92.1 |
| TMLE-SL(par) | 12.7 |
 11.3 11.3 |
104.7 | 93.9 | 23.5 | 7.5 | 150.4 | 94.7 |
All values (except coverage) are given as 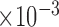 .
.
MSE: mean squared error; SE: the square-root of the mean sandwich estimator variance; TMLE-BIN:TMLE with logistic regressions for censoring and outcome models; TMLE-SL: TMLE with Super Learner, (all) with the complete SL library, (adapt) with only main terms logistic regression in addition to the adaptive methods, and (par) with only logistic regression implementations.
The data generation resulted in no practical positivity violations, but occasional large weights were observed. Increasing the sample size to 5000 created better controlled weights (rarely over 20) and otherwise produced comparable results. R functions for the data generation, SAR, TMLE-BIN, and TMLE-SL are available online (see Section 8).
6. Case Study: Prognostic factors of clinical events in HIV-positive patients
Our data were obtained from patients previously enrolled in four AIDS Clinical Trials Group (ACTG) clinical trials, all of whom were ART naïve at enrollment (see Lok and others, 2013 for a complete description of the data and exclusion criteria). A subset of 1036 patients included all subjects who were virologically suppressed 1 year after ART initiation (defined as the baseline time period) and who had data on CD8 T-cell activation at that time. Eleven subjects were excluded because they had an event within 84 days prior to the year one measurement. We used up to 4 years of follow-up data (after the year one measurement) collected from the 1025 remaining patients. HIV RNA and CD4 cell count measurements were planned at least every 16 weeks. Loss to follow-up was defined by the absence of an HIV RNA measurement over six consecutive months. The data were divided into 28-day periods, and CD4 cell counts and HIV RNA levels were carried forward through these periods when unavailable.
The outcome of interest was the occurrence of a clinical event in years 2–5 after ART initiation. Clinical events included both AIDS-defining (as defined by the Centers for Disease Control, 1992) and non-AIDS-defining (as defined in previous ACTG projects; Overton and others, 2013). Non-AIDS-defining events included non-accidental death, hepatic end organ disease, cardiovascular end organ disease, serious renal disease, non-AIDS cancers, hip, spine or wrist fractures, diabetes mellitus, and serious bacterial infections. A total of 104 events were observed, and by the end of year five, 318 patients were still event-free, in follow-up and on treatment throughout.
Interest lies in determining the baseline predictors for an outcome event over the 4 years of follow-up, had all subjects remained in follow-up and without ART interruption. However, the patients in the study did not consistently remain on ART. Patients were considered censored at a given time point when they were either lost to follow-up or interrupted ART for longer than 21 days. Lok and others (2013) estimated the coefficients of a logistic model with square-root of CD4 cell count, % CD8 T-cell activation, and age as the prognostic factors of interest. Additional work was deemed necessary to determine whether there was a true prognostic association.
We estimated the coefficients of the same marginal logistic regression model as Lok and others (2013). As in the original analysis, the conditional probabilities of censoring at each time point were estimated using two models: one for loss to follow-up and the other for remaining on ART. Both of these models pooled over all periods, and adjusted for baseline variables, variables at the previous time point, period and period squared. We also implemented the augmented regression procedure from Section 3, and the TMLE procedure from Section 4. The TMLE was implemented in two ways: the first with weights and 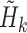 estimated using logistic regressions and the second using Super Learner for these models. Following Lok and others (2013), the potential baseline confounders adjusted for in all analyses were age, age squared, sex, CD8 T-cell activation, and whether the patient was ever an injection drug user. The time-dependent variables (also measured at baseline) adjusted for were square-root of CD4 cell count, whether the HIV-RNA level was <50 copies/mL, and study stage (clinical trial, end of clinical trial, or enrolled in a subsequent observational study). It is believed that sequential ignorability for treatment and loss to follow-up holds conditional on the baseline variables and the most recently reported values of the time-dependent variables. This is because treatment decisions were generally made based on the most recently available measures of the disease state.
estimated using logistic regressions and the second using Super Learner for these models. Following Lok and others (2013), the potential baseline confounders adjusted for in all analyses were age, age squared, sex, CD8 T-cell activation, and whether the patient was ever an injection drug user. The time-dependent variables (also measured at baseline) adjusted for were square-root of CD4 cell count, whether the HIV-RNA level was <50 copies/mL, and study stage (clinical trial, end of clinical trial, or enrolled in a subsequent observational study). It is believed that sequential ignorability for treatment and loss to follow-up holds conditional on the baseline variables and the most recently reported values of the time-dependent variables. This is because treatment decisions were generally made based on the most recently available measures of the disease state.
As is common in survival settings with events registered on a fine grid, it became a challenge to model  due to the sparsity of events in a single period. Therefore, for both SAR and TMLE, we estimated
due to the sparsity of events in a single period. Therefore, for both SAR and TMLE, we estimated 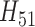 using a pooled model across all time points, adjusting for period and period squared as in the censoring models. All subsequent steps for fitting the SAR and TMLE were followed as given in Sections 3 and 4. All analyses used R statistical software version 2.15.1. Super Learner was fit using the SuperLearner package and implemented with the same library used in the simulation study (with both parametric and adaptive methods). The Random Forests algorithm often failed (due to memory issues) and was removed from all models. The results from the four methods are given in Table 4. The IPCW results corresponded with the results obtained in Lok and others (2013). Using the sandwich estimator for variance, SAR concluded a significant odds ratio for CD8 T-cell activation and generally smaller confidence intervals. TMLE implemented with logistic regression or Super Learner gave similar results to IPCW. TMLE produced only slightly smaller confidence intervals than IPCW, when the confidence intervals were obtained using the EIF sandwich estimator.
using a pooled model across all time points, adjusting for period and period squared as in the censoring models. All subsequent steps for fitting the SAR and TMLE were followed as given in Sections 3 and 4. All analyses used R statistical software version 2.15.1. Super Learner was fit using the SuperLearner package and implemented with the same library used in the simulation study (with both parametric and adaptive methods). The Random Forests algorithm often failed (due to memory issues) and was removed from all models. The results from the four methods are given in Table 4. The IPCW results corresponded with the results obtained in Lok and others (2013). Using the sandwich estimator for variance, SAR concluded a significant odds ratio for CD8 T-cell activation and generally smaller confidence intervals. TMLE implemented with logistic regression or Super Learner gave similar results to IPCW. TMLE produced only slightly smaller confidence intervals than IPCW, when the confidence intervals were obtained using the EIF sandwich estimator.
Table 4.
Odds ratios and 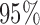 CI for the marginal model per x unit increase
CI for the marginal model per x unit increase
| Method | CD8 activation year 1 % per 10 units | square-root CD4 year 1 Per 3 units | Age year 1 Per 10 years |
|---|---|---|---|
| CIs constructed using the influence function sandwich estimator | |||
| IPCW | 1.16 (0.98,1.36) | 1.10 (0.95, 1.27) | 1.86 (1.44, 2.40) |
| SAR | 1.15 (1.00,1.32) | 1.09 (0.97, 1.22) | 1.81 (1.44, 2.27) |
| TMLE-BIN | 1.11 (0.97,1.29) | 1.08 (0.97, 1.22) | 1.86 (1.47, 2.35) |
| TMLE-SL(all) | 1.11 (0.96,1.28) | 1.08 (0.96, 1.21) | 1.87 (1.48, 2.37) |
| CIs constructed using the non-parametric bootstrap | |||
| IPCW | 1.16 (0.97,1.36) | 1.10 (0.95, 1.28) | 1.86 (1.47, 2.41) |
| SAR | 1.15 (0.86,1.38) | 1.09 (0.88, 1.27) | 1.81 (0.92, 2.46) |
| TMLE-BIN | 1.11 (0.87,1.30) | 1.08 (0.85, 1.29) | 1.86 (1.30, 2.46) |
The 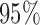 confidence intervals presented in the top part of Table 4 used the variance of the influence function to estimate the standard errors of the estimators. The validity of this approach relies on the correct specification of all
confidence intervals presented in the top part of Table 4 used the variance of the influence function to estimate the standard errors of the estimators. The validity of this approach relies on the correct specification of all 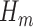 and
and 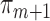 models, and a large sample size. However, if only the
models, and a large sample size. However, if only the 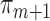 are consistent, the EIF sandwich estimator is an asymptotically conservative estimator of the asymptotic variance (van der Laan and Rose, 2011, Section 5.2.7). The bottom part of Table 4 contains the non-parametric bootstrap confidence intervals for the three less computationally intensive methods. We used 2000 resamples with replacement of the patient IDs with a resample size of 1025. The bootstrap confidence intervals were calculated using the 2.5th and 97.5th percentiles of the resulting estimates. For IPCW, the bootstrap and sandwich estimator confidence intervals for the three odds ratios were very similar. For SAR and TMLE, the bootstrap intervals were much wider than their sandwich estimator counterparts. By plotting the quantiles of the bootstrap estimates against the quantiles of the standard normal (i.e. a quantile–quantile plot), the bootstrapped estimates for IPCW appeared to be approximately Gaussian, but the bootstrapped estimates for SAR and TMLE did not. Throughout the analysis, the inverse weights did not exceed a value of 15, and remained similarly small when bootstrapping.
are consistent, the EIF sandwich estimator is an asymptotically conservative estimator of the asymptotic variance (van der Laan and Rose, 2011, Section 5.2.7). The bottom part of Table 4 contains the non-parametric bootstrap confidence intervals for the three less computationally intensive methods. We used 2000 resamples with replacement of the patient IDs with a resample size of 1025. The bootstrap confidence intervals were calculated using the 2.5th and 97.5th percentiles of the resulting estimates. For IPCW, the bootstrap and sandwich estimator confidence intervals for the three odds ratios were very similar. For SAR and TMLE, the bootstrap intervals were much wider than their sandwich estimator counterparts. By plotting the quantiles of the bootstrap estimates against the quantiles of the standard normal (i.e. a quantile–quantile plot), the bootstrapped estimates for IPCW appeared to be approximately Gaussian, but the bootstrapped estimates for SAR and TMLE did not. Throughout the analysis, the inverse weights did not exceed a value of 15, and remained similarly small when bootstrapping.
7. Discussion
This article presented methods for estimating the parameters of a marginal mean model in the presence of dependent censoring. In particular, we derived SAR, an adaptation of the Bang and Robins' estimator for the coefficients of a marginal logistic regression model. We then presented a corresponding TMLE that can optionally be fit with non-parametric methods such as Super Learner. Both methods easily generalize to estimate the coefficients of any marginal mean model (such as GLMs conditional on baseline covariates) for any outcome type and unlike the procedure given in Bang and Robins (2005), can be readily implemented for non-linear marginal mean models. These methods were compared in a simulation study where their double robustness property was numerically confirmed. Finally, these methods were used in a case study to estimate a prognostic model for AIDS and non-AIDS events in HIV-positive patients in the presence of dependent censoring.
Since SAR is defined as a sequence of nested GLMs, it may be more susceptible to bias caused by model misspecification (van der Laan and Rose, 2011). Because TMLE does not predetermine a parametric form for these models, non-parametric modeling can instead be used.
In the simulation study, when TMLE was implemented non-parametrically, the Super Learner library with a collection of parametric models produced the best results overall. This study demonstrated that even when the analyst is ignorant of the true data generating form, TMLE with Super Learner can perform about as well as IPCW, SAR, or TMLE with correct parametric model specification. For larger sample sizes, adding methods to the Super Learner library did not appear to impede performance. Therefore, an implementation of TMLE with Super Learner might be more likely to be successful with a more inclusive library of methods. Similar results were observed in Porter and others (2011) in their cross-sectional simulation study. Due to the reliance on the asymptotic linearity of the estimators, the standard error estimates may be invalid for smaller sample sizes.
In the case study, the discord between the confidence intervals obtained using sandwich estimation versus non-parametric bootstrap for SAR and TMLE points to an instability in variance estimation. This may have been due to the low number of outcome events. Recent investigation by Petersen and others (2014) indicates that variance estimation in cases of event sparsity might lead to incorrect variance estimates, whether by using bootstrap or large sample theory (i.e. with a sandwich estimator) for both IPCW and longitudinal TMLE. In addition, a drawback of inverse-weighting methods is small-sample instability (Robins and others, 2007).
In the case study, IPCW, SAR, and both implementations of TMLE produced very similar results. The sandwich-estimated confidence intervals for TMLE and SAR were only marginally smaller than for IPCW. SAR estimated a significant odds ratio for CD8 activation (using sandwich estimation of the variance). Because the non-parametric TMLE was implemented with an inclusive Super Learner library and was therefore more robust to model form misspecification, we are inclined to believe those results, which confirm, in this case, the original IPCW results.
8. Software
Software in the form of R functions and complete documentation are available online at http://www.mireilleschnitzer.com/double-robust-estimation-of-marginal-models.html.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
This work was supported by the National Institutes of Health [R01AI100762 to J.J.L. supporting M.E.S.] and by the ACTG which is sponsored by the National Institutes of Health [grant numbers AI 38858, AI 68636, AI 38855, AI 68634].
Supplementary Material
Acknowledgments
We are indebted to the subjects who volunteered for ACTG 384, ACTG 388, ACTG A5014, ACTG A5095, and subsequently to ALLRT, the ACTG sites, and the study teams. We would like to thank Doug Kitch, Evelyn Zheng, and Kunling Wu for database and analytic support. We also thank our clinical collaborators Peter Hunt, Ann Collier, Constance Benson, Mallory Witt, Amneris Luque, and Steven Deeks for their valuable input on this project. M.E.S. would like to acknowledge very helpful discussions with Iván Díaz, Susan Gruber, Samuel Lendle, Jamie Robins, and Andrea Rotnitzky. Conflict of Interest: None declared.
References
- Bang H., Robins J. M. (2005). Doubly robust estimation in missing data and causal inference models. Biometrics 61, 962–972. [DOI] [PubMed] [Google Scholar]
- Centers for Disease Control. (1992). Revised classification system for HIV infection and expanded surveillance case definition for AIDS among adolescents and adults. Morbidity and Mortality Weekly Report 41(RR-17), 1–19. [PubMed] [Google Scholar]
- Deeks S. G. (2011). HIV infection, inflammation, immunosenescence, and aging. Annual Review of Medicine 62, 141–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lok J. J., Hunt P. W., Collier A. C., Benson C. A., Witt M. D., Luque A. E., Deeks S. G., Bosch R. J. (2013). The impact of age on the prognostic capacity of CD8+ t-cell activation during suppressive antiretroviral therapy. AIDS 27(13), 2101–2110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neugebauer R., van der Laan M. J. (2007). Nonparametric causal effects based on marginal structural models. Journal of Statistical Planning and Inference 137(2), 419–434. [Google Scholar]
- Overton E. T., Kitch D., Benson C. A., Hunt P. W., Stein J. H., Smurzynski M., Ribaudo H. J., Tebas P. (2013). Effect of statin therapy in reducing the risk of serious non-AIDS-defining events and nonaccidental death. Clinical Infectious Diseases 56(10), 1471–1479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen M., Schwab J., Gruber S., Blaser N., Schomaker M., van der Laan M. (2014). Targeted maximum likelihood estimation for dynamic and static longitudinal marginal structural working models. Journal of Causal Inference 2(2), 147–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polley E. C., van der Laan M. J. (2010). Super learner in prediction. U.C. Berkeley Division of Biostatistics Working Paper Series (Working Paper 266).
- Polley A. C., Van der Laan M. J. (2014). SuperLearner: Super Learner Prediction. R package version 2.0-15. http://CRAN.R-project.org/package=SuperLearner.
- Porter K. E., Gruber S., van der Laan M. J., Sekhon J. S. (2011). The relative performance of targeted maximum likelihood estimators. The International Journal of Biostatistics 7(1), Article 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins J. M. (1986). A new approach to causal inference in mortality studies with a sustained exposure period – application to control of the healthy worker survivor effect. Mathematical Modelling 7, 1393–1512. [Google Scholar]
- Robins J. M., Hernán M. A., Brumback B. (2000). Marginal structural models and causal inference in Epidemiology. Epidemiology 11(5), 550–560. [DOI] [PubMed] [Google Scholar]
- Robins J. M., Rotnitzky A. (1992). Recovery of information and adjustment for dependent censoring using surrogate markers. AIDS Epidemiology – Methodological Issues 297–331. [Google Scholar]
- Robins J. M., Rotnitzky A., Zhao L. P. (1995). Analysis of semiparametric regression models for repeated outcomes under the presence of missing data. Journal of the American Statistical Association 90, 106–121. [Google Scholar]
- Robins J. M., Sued M., Lei-Gomezand Q., Rotnitzky A. (2007). Comment: performance of double-robust estimators when “inverse probability” weights are highly variable. Statistical Science 22(4), 544–559. [Google Scholar]
- Scharfstein D. O., Rotnitzky A., Robins J. M. (1999). Adjusting for nonignorable drop-out using semiparametric nonresponse models. Journal of the American Statistical Association 94(448), 1096–1120. [Google Scholar]
- Schnitzer M. E., van der Laan M. J., Moodie E. E. M., Platt R. W. (2014). Effect of breastfeeding on gastrointestinal infection in infants: a targeted maximum likelihood approach for clustered longitudinal data. Annals of Applied Statistics 8(2), 703–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stitelman O. M., De Gruttola V., van der Laan M. J. (2012). A general implementation of TMLE for longitudinal data applied to causal inference in survival analysis. International Journal of Biostatistics 18(1), Article 26. [DOI] [PubMed] [Google Scholar]
- Tsiatis A. A. (2006). Semiparametric Theory and Missing Data. Springer Series in Statistics Berlin, New York, Heidelberg: Springer. [Google Scholar]
- van der Laan M. J., Gruber S. (2012). Targeted minimum loss based estimation of causal effects of multiple time point interventions. The International Journal of Biostatistics 8(1), Article 9. [DOI] [PubMed] [Google Scholar]
- van der Laan M. J., Robins J. M. (2003). Unified Methods for Censored Longitudinal Data and Causality. Springer Series in Statistics New York: Springer. [Google Scholar]
- van der Laan M. J., Rose S. (2011). Targeted Learning: Causal Inference for Observational and Experimental Data. Springer Series in Statistics Berlin, Heidelberg, New York: Springer. [Google Scholar]
- van der Laan M. J., Rubin D. (2006). Targeted maximum likelihood learning. The International Journal of Biostatistics 2(1), Article 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Vaart A. W. (1998). Asymptotic Statistics, Mathematics. Cambridge: Cambridge University Press. [Google Scholar]
- Yu Z., van der Laan M. J. (2006). Double robust estimation in longitudinal marginal structural models. Journal of Statistical Planning and Inference 136(3), 1061–1089. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


