Abstract
Screening and surveillance are routinely used in medicine for early detection of disease and close monitoring of progression. Motivated by a study of patients who received a human tissue valve in the aortic position, in this work we are interested in personalizing screening intervals for longitudinal biomarker measurements. Our aim in this paper is 2-fold: First, to appropriately select the model to use at the time point the patient was still event-free, and second, based on this model to select the optimal time point to plan the next measurement. To achieve these two goals, we combine information theory measures with optimal design concepts for the posterior predictive distribution of the survival process given the longitudinal history of the subject.
Keywords: Decision making, Information theory, Personalized medicine, Random effects
1. Introduction
Decision making in medicine has become increasingly complex for patients and practitioners. This has resulted from factors such as the shift away from physician authority toward shared decision making, unfiltered information on the Internet, new technology providing additional data, numerous treatment options with associated risks and benefits, and results from new clinical studies. Within this context, medical screening procedures are routinely performed for several diseases. Most prominent examples can be found in cancer research, where, for example, mammographic screening is performed for the detection of breast cancer in asymptomatic patients, and prostate-specific antigen levels are used to monitor the progression of prostate cancer in men who have been treated for the disease. In general, the aim of screening procedures is to optimize the benefits, i.e. early detection of disease or deterioration of the condition of a patient, while also balancing the respective costs. In this paper, we are interested in optimizing screening intervals for asymptomatic or symptomatic patients that are followed-up prospectively (the latter possibly after a medical procedure). The setting we focus on is better explained via Figure 1. More specifically, this figure depicts a hypothetical patient who has been followed up to time point 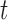 , and has provided a set of longitudinal biomarker measurements. Using this information, physicians are interested in events occurring within a medically relevant time interval
, and has provided a set of longitudinal biomarker measurements. Using this information, physicians are interested in events occurring within a medically relevant time interval 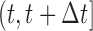 . If the probability of surviving beyond
. If the probability of surviving beyond 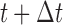 is lower than the pre-specified constant
is lower than the pre-specified constant 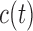 , then the physician is supposed to immediately take action to improve the prospects for this patient. However, when the chance of surviving until
, then the physician is supposed to immediately take action to improve the prospects for this patient. However, when the chance of surviving until 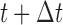 is higher than
is higher than 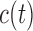 , then the physician may not initiate treatment or require an invasive test, and instead wishes to gain a better understanding of the disease progression using additional biomarker measurements. The decision to request an additional measurement requires careful weighing of the potential benefits and costs to the patient and health care system. Hence, we are interested in carefully planning the timing of the next measurement in order to maximize the information we can gain on disease progression, and at the same time minimize costs and patient burden.
, then the physician may not initiate treatment or require an invasive test, and instead wishes to gain a better understanding of the disease progression using additional biomarker measurements. The decision to request an additional measurement requires careful weighing of the potential benefits and costs to the patient and health care system. Hence, we are interested in carefully planning the timing of the next measurement in order to maximize the information we can gain on disease progression, and at the same time minimize costs and patient burden.
Fig. 1.
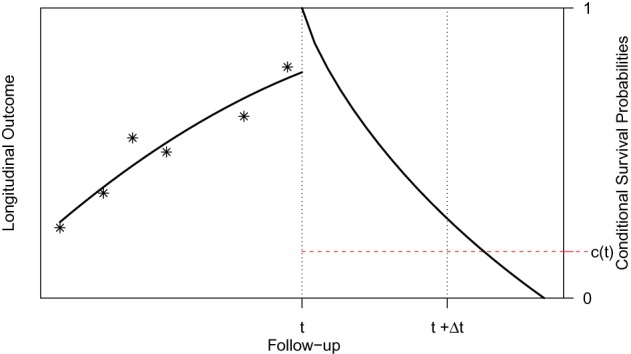
Illustration of a patient's longitudinal profile up to time 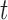 , and conditional
survival function for whom we wish to plan an extra measurement. Physicians
are interested in events occurring within the time interval
, and conditional
survival function for whom we wish to plan an extra measurement. Physicians
are interested in events occurring within the time interval 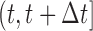 . Constant
. Constant 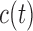 defines the
threshold above which the physician requires extra information before making a
decision.
defines the
threshold above which the physician requires extra information before making a
decision.
Statistical methods for optimizing medical screening strategies have flourished in the past years. These methods have been primarily based on Markov and multistate models (Parmigiani, 1993, 1998, 1999, 2002; Lee and Zelen, 1998; Schaefer and others, 2004). The appealing feature of these models is that they can simultaneously handle different medical options and select the one that provides the most gains at an acceptable cost (cost-effectiveness). Here we will instead work under the framework of joint models for longitudinal and time-to-event data (Tsiatis and Davidian, 2004; Rizopoulos, 2012). An advantageous feature of joint models is that they utilize random effects and therefore have an inherent subject-specific nature. This allows one to better tailor decisions to individual patients, i.e. personalize screening, rather than using the same screening rule for all. In addition, contrary to the majority of screening approaches that are based on a dichotomized version of the last available biomarker measurement to indicate the need for a further medical procedure (e.g. prostate-specific antigen greater than 4.0 ng/mL), joint models utilize the whole longitudinal history to reach a decision without requiring dichotomization of the longitudinal outcome. Our methodological developments couple joint models with information theory quantities and optimal design concepts. In particular, our aim in this paper is 2-fold: First, to appropriately select the joint model to use at time 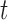 , i.e. the time point the subject of interest is still event-free, and second, based on this model to select the optimal time point
, i.e. the time point the subject of interest is still event-free, and second, based on this model to select the optimal time point 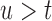 to plan the next measurement. We measure optimality by the amount of information gained for the survival process given the history of the subject of interest that includes both baseline information and his/her accumulated longitudinal measurements.
to plan the next measurement. We measure optimality by the amount of information gained for the survival process given the history of the subject of interest that includes both baseline information and his/her accumulated longitudinal measurements.
The motivation for this research comes from a study conducted by the Department of Cardio-Thoracic Surgery of the Erasmus Medical Center in the Netherlands. This study includes 285 patients who received a human tissue valve in the aortic position in the hospital from 1987 until 2008 (Bekkers and others, 2011). Aortic allograft implantation has been widely used for a variety of aortic valve or aortic root diseases. Major advantages ascribed to allografts are the excellent hemodynamic characteristics as a valve substitute; the low rate of thrombo-embolic complications, and, therefore, absence of the need for anticoagulant treatment and the resistance to endocarditis. A major disadvantage of using human tissue valves, however is the susceptibility to degeneration and the concomitant need for re-interventions. The durability of an aortic allograft is age-dependent, leading to a high lifetime risk of re-operation, especially for young patients. Re-operations on the aortic root are complex, with substantial re-operative risks, and mortality rates in the range of 4–12%. A timely well-planned re-operation has lower mortality risks compared with urgent re-operative surgery. It is therefore of great interest for cardiologists and cardio-thoracic surgeons to plan in the best possible manner echocardiographic assessments that will inform them about the future prospect of a patient with a human tissue valve in order to optimize medical care, carefully plan re-operation, and minimize valve-related morbidity and mortality.
The rest of the paper is organized as follows. Section 2 briefly presents the joint modeling framework and the information theory quantities that can be used to select the joint model at a particular follow-up time, and Section 3 the corresponding quantities for planning the next longitudinal measurement. Section 4 illustrates the use of these information measures in the Aortic Valve study, and Section 5 presents the results of a cost-effectiveness simulations study.
2. Choosing the model to use at time 
We start with a short introduction of the joint modeling framework we will use in our following developments. Let 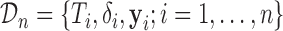 denote a sample from the target population, where
denote a sample from the target population, where 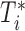 denotes the true event time for the
denotes the true event time for the 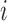 th subject,
th subject, 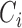 the censoring time,
the censoring time, 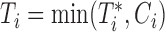 the corresponding observed event time, and
the corresponding observed event time, and 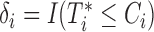 the event indicator, with
the event indicator, with 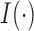 being the indicator function that takes the value 1 when
being the indicator function that takes the value 1 when 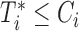 , and 0 otherwise. In addition, we let
, and 0 otherwise. In addition, we let 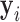 denote the
denote the 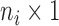 longitudinal response vector for the
longitudinal response vector for the 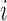 th subject, with element
th subject, with element 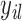 denoting the value of the longitudinal outcome taken at time point
denoting the value of the longitudinal outcome taken at time point 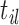 ,
, 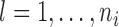 .
.
To accommodate different types of longitudinal responses, we postulate a generalized linear mixed-effects model. In particular, the conditional distribution of 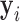 given a vector of random effects
given a vector of random effects 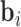 is assumed to be a member of the exponential family, with linear predictor given by
is assumed to be a member of the exponential family, with linear predictor given by
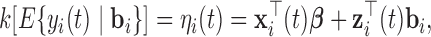 |
(2.1) |
where 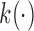 denotes a known one-to-one monotonic link function, and
denotes a known one-to-one monotonic link function, and 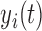 denotes the value of the longitudinal outcome for the
denotes the value of the longitudinal outcome for the 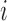 th subject at time point
th subject at time point 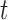 ,
, 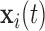 and
and 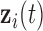 denote the time-dependent design vectors for the fixed effects
denote the time-dependent design vectors for the fixed effects 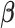 and for the random effects
and for the random effects 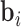 , respectively. The random effects are assumed to follow a multivariate normal distribution with mean zero and variance–covariance matrix
, respectively. The random effects are assumed to follow a multivariate normal distribution with mean zero and variance–covariance matrix  . For the survival process, we assume that the risk for an event depends on a function of the subject-specific linear predictor
. For the survival process, we assume that the risk for an event depends on a function of the subject-specific linear predictor 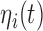 and/or the random effects:
and/or the random effects:
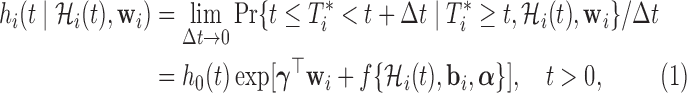 |
(2.2) |
where 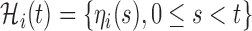 denotes the history of the underlying longitudinal process up to
denotes the history of the underlying longitudinal process up to 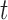 ,
, 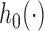 denotes the baseline hazard function,
denotes the baseline hazard function, 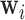 is a vector of baseline covariates with corresponding regression coefficients
is a vector of baseline covariates with corresponding regression coefficients 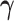 . Function
. Function 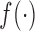 , parameterized by vector
, parameterized by vector 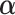 , specifies which components/features of the longitudinal outcome process are included in the linear predictor of the relative risk model. Some examples, motivated by the literature (Rizopoulos and Ghosh, 2011; Rizopoulos, 2012; Taylor and others, 2013; Rizopoulos and others, 2014) are:
, specifies which components/features of the longitudinal outcome process are included in the linear predictor of the relative risk model. Some examples, motivated by the literature (Rizopoulos and Ghosh, 2011; Rizopoulos, 2012; Taylor and others, 2013; Rizopoulos and others, 2014) are:
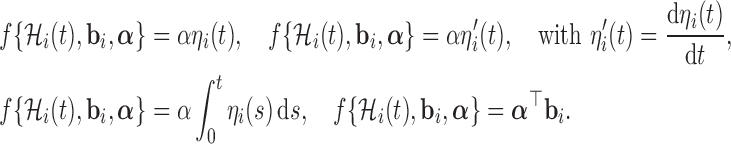 |
These formulations of 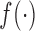 postulate that the hazard of an event at time
postulate that the hazard of an event at time 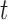 may be associated with the underlying level of the biomarker at the same time point, the slope of the longitudinal profile at
may be associated with the underlying level of the biomarker at the same time point, the slope of the longitudinal profile at 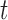 , the accumulated longitudinal process up to
, the accumulated longitudinal process up to  , or the random effects alone. Finally, the baseline hazard function
, or the random effects alone. Finally, the baseline hazard function 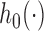 is modeled flexibly using a B-splines approach, i.e.
is modeled flexibly using a B-splines approach, i.e.
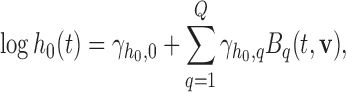 |
(2.3) |
where 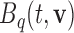 denotes the
denotes the 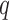 th basis function of a B-spline with knots
th basis function of a B-spline with knots  and
and 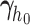 the vector of spline coefficients. To avoid the task of choosing the appropriate number and position of the knots, we include a relatively high number of knots (e.g. 15–20) and appropriately penalize the B-spline regression coefficients
the vector of spline coefficients. To avoid the task of choosing the appropriate number and position of the knots, we include a relatively high number of knots (e.g. 15–20) and appropriately penalize the B-spline regression coefficients 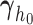 for smoothness using the differences penalty (Eilers and Marx, 1996). For the estimation of joint model's parameters, we use a Bayesian approach—more details can be found in Section 1 of supplementary material available at Biostatistics online.
for smoothness using the differences penalty (Eilers and Marx, 1996). For the estimation of joint model's parameters, we use a Bayesian approach—more details can be found in Section 1 of supplementary material available at Biostatistics online.
As motivated in Section 1, our aim is to decide the appropriate time point to plan the next measurement for a new subject 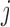 from the same population (i.e. with
from the same population (i.e. with 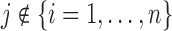 ), whose survival chance at a particular time point
), whose survival chance at a particular time point 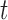 lies within the interval
lies within the interval 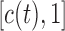 (see Figure 1). In general, and as we have just seen, defining a joint model entails choosing an appropriate model for the longitudinal outcome (i.e. baseline covariates and functional form of the time effect), an appropriate model for the time-to-event (i.e. baseline covariates), and how to link the two outcomes using function
(see Figure 1). In general, and as we have just seen, defining a joint model entails choosing an appropriate model for the longitudinal outcome (i.e. baseline covariates and functional form of the time effect), an appropriate model for the time-to-event (i.e. baseline covariates), and how to link the two outcomes using function 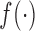 . Hence, a relevant question is which model to use for deciding when to plan the next measurement of subject
. Hence, a relevant question is which model to use for deciding when to plan the next measurement of subject 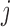 . Standard approaches for model selection within the Bayesian framework include the deviance information criterion (DIC) and (pseudo-) Bayes factors. However, a potential problem with these methods is that they provide an overall assessment of a model's predictive ability, whereas we are interested in the model that best predicts future events given the fact that subject
. Standard approaches for model selection within the Bayesian framework include the deviance information criterion (DIC) and (pseudo-) Bayes factors. However, a potential problem with these methods is that they provide an overall assessment of a model's predictive ability, whereas we are interested in the model that best predicts future events given the fact that subject 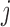 was event-free up to time point
was event-free up to time point 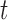 . To identify the model to use at
. To identify the model to use at 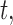 we follow similar arguments as in Commenges and others (2012), and focus on the conditional density function of the survival outcome given the longitudinal responses and survival up to
we follow similar arguments as in Commenges and others (2012), and focus on the conditional density function of the survival outcome given the longitudinal responses and survival up to 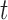 . More specifically, we let
. More specifically, we let 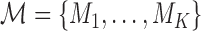 denote a set of
denote a set of 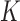 joint models fitted to the original dataset
joint models fitted to the original dataset 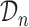 . Due to the fact that the choice of the optimal model in
. Due to the fact that the choice of the optimal model in 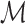 is based on a finite sample, an important issue we need to address is overfitting. Hence, to obtain an objective estimate of the predictive ability of each model based on the available data
is based on a finite sample, an important issue we need to address is overfitting. Hence, to obtain an objective estimate of the predictive ability of each model based on the available data 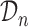 , we will use the cross-validatory posterior predictive conditional density of the survival outcome. For model
, we will use the cross-validatory posterior predictive conditional density of the survival outcome. For model 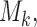 this is defined as
this is defined as 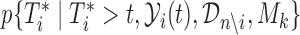 , where
, where 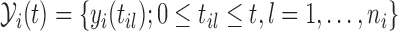 and
and 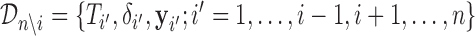 denotes the version of the dataset that excludes the data for the
denotes the version of the dataset that excludes the data for the 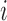 th subject. Similarly, we can define the same distribution under model
th subject. Similarly, we can define the same distribution under model 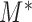 , which denotes the model under which the data have been generated (
, which denotes the model under which the data have been generated (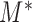 is not required to be in
is not required to be in 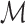 ). Using conventional quantities of information theory (Cover and Thomas, 1991), we select the model
). Using conventional quantities of information theory (Cover and Thomas, 1991), we select the model 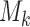 in the set
in the set 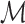 that minimizes the cross-entropy:
that minimizes the cross-entropy:
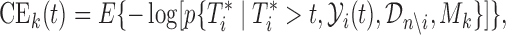 |
where the expectation is taken with respect to 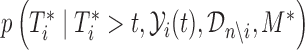 . An estimate of
. An estimate of 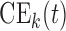 that accounts for censoring can be obtained using the available information in the sample at hand. We term this estimate the cross-validated Dynamic Conditional Likelihood:
that accounts for censoring can be obtained using the available information in the sample at hand. We term this estimate the cross-validated Dynamic Conditional Likelihood:
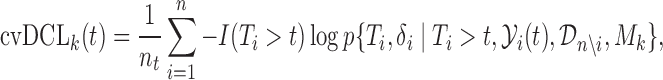 |
(2.4) |
where 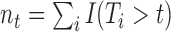 . In turn, a consistent estimate of
. In turn, a consistent estimate of 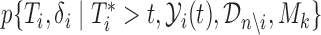 can be obtained from the MCMC sample of model
can be obtained from the MCMC sample of model 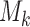 by utilizing a similar computation as for the conditional predictive ordinate statistic (Chen and others, 2008; condition on
by utilizing a similar computation as for the conditional predictive ordinate statistic (Chen and others, 2008; condition on 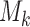 is assumed but is dropped in the following expressions):
is assumed but is dropped in the following expressions):
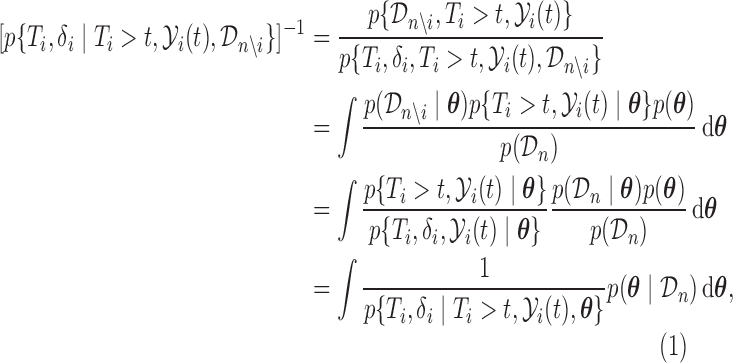 |
(2.5) |
where 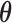 includes here both the parameters of the joint model
includes here both the parameters of the joint model 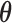 and the random effects. Hence, based on the MCMC sample from
and the random effects. Hence, based on the MCMC sample from 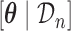 and identity (2.5) we can obtain a Monte Carlo estimate of (2.4) as
and identity (2.5) we can obtain a Monte Carlo estimate of (2.4) as
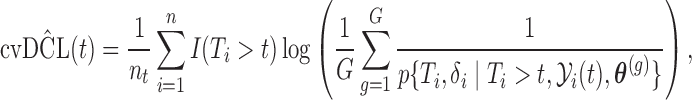 |
(2.6) |
where 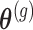 denotes here the
denotes here the 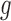 th realization from the MCMC sample
th realization from the MCMC sample 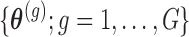 . Calculation of
. Calculation of 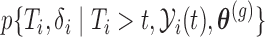 follows in a similar manner as the calculations we will illustrate in the following section, and due to space limitations we do not show them here.
follows in a similar manner as the calculations we will illustrate in the following section, and due to space limitations we do not show them here.
3. Scheduling patterns based on information theory
3.1. Planning of the next measurement
Having chosen the appropriate model to use at time  , our aim next is to decide when to plan the following measurement of subject
, our aim next is to decide when to plan the following measurement of subject 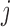 . Similarly to the previous section, the quantity that we will use for making this decision is the posterior predictive distribution. This distribution effectively combines the two sources of information we have available, namely, the observed data of the
. Similarly to the previous section, the quantity that we will use for making this decision is the posterior predictive distribution. This distribution effectively combines the two sources of information we have available, namely, the observed data of the 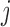 th subject
th subject 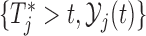 with the original dataset we used to fit the joint model
with the original dataset we used to fit the joint model 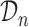 , and still maintains a cross-validatory flavor because
, and still maintains a cross-validatory flavor because 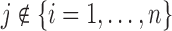 . We let
. We let 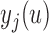 denote the measurement of the longitudinal outcome at the future time point
denote the measurement of the longitudinal outcome at the future time point 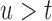 . For the selection of the optimal
. For the selection of the optimal 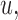 we would like to maximize the information we gain by measuring
we would like to maximize the information we gain by measuring 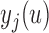 at this time point, provided that the patient was still event-free up to
at this time point, provided that the patient was still event-free up to 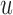 . That is, if the event occurs before taking the measurement for subject
. That is, if the event occurs before taking the measurement for subject 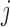 , then there is no gain in information. To achieve this, we suitably adapt and extend concepts from Bayesian optimal designs (Verdinelli and Kadane, 1992; Clyde and Chaloner, 1996) to our setting. More specifically, we propose to select the optimal time
, then there is no gain in information. To achieve this, we suitably adapt and extend concepts from Bayesian optimal designs (Verdinelli and Kadane, 1992; Clyde and Chaloner, 1996) to our setting. More specifically, we propose to select the optimal time 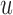 by maximizing the utility function (conditioning on baseline covariates
by maximizing the utility function (conditioning on baseline covariates 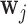 is assumed in the following expressions but is dropped for notational simplicity):
is assumed in the following expressions but is dropped for notational simplicity):
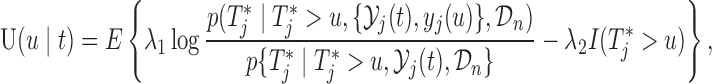 |
(3.1) |
where 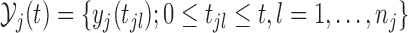 and the expectation is taken with respect to the joint predictive distribution
and the expectation is taken with respect to the joint predictive distribution 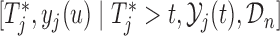 . The first term in (3.1) is the expected Kullback–Leibler divergence between the posterior predictive conditional distributions with and without this extra measurement, namely
. The first term in (3.1) is the expected Kullback–Leibler divergence between the posterior predictive conditional distributions with and without this extra measurement, namely
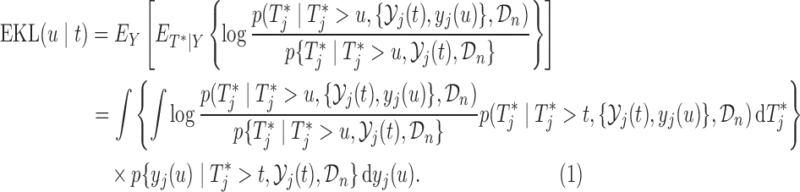 |
(3.2) |
The larger this divergence is, the more information we expect to gain by measuring the longitudinal outcome at 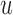 . However, when the true event actually occurs before
. However, when the true event actually occurs before 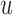 , i.e.
, i.e. 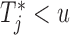 , then expression
, then expression 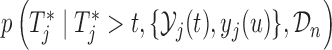 becomes
becomes 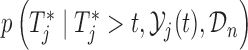 , and hence
, and hence 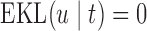 . On the other hand, when
. On the other hand, when 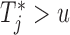 , then, heuristically, as
, then, heuristically, as 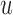 is set further away from the last time point a longitudinal measurement was taken, the more information we would expect to gain regarding the shape of the longitudinal profile of subject
is set further away from the last time point a longitudinal measurement was taken, the more information we would expect to gain regarding the shape of the longitudinal profile of subject 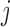 . The value of
. The value of 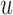 that maximizes this information gain will depend on the characteristics of the subject's profile. Another aspect we need to account for is the “cost” of waiting. In particular, as we just saw,
that maximizes this information gain will depend on the characteristics of the subject's profile. Another aspect we need to account for is the “cost” of waiting. In particular, as we just saw, 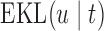 penalizes against selecting
penalizes against selecting  ; however, the fact that we still need to wait up to time
; however, the fact that we still need to wait up to time 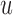 when
when 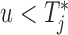 also means that we inevitably increase the risk that the patient will experience the event. Because we would not like to wait up to a point that it would be too late for the physician to intervene, we need to further penalize for waiting up to
also means that we inevitably increase the risk that the patient will experience the event. Because we would not like to wait up to a point that it would be too late for the physician to intervene, we need to further penalize for waiting up to 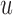 . This explains the inclusion of the second term in (3.1). The expectation with respect to this second term gives the conditional survival probability
. This explains the inclusion of the second term in (3.1). The expectation with respect to this second term gives the conditional survival probability
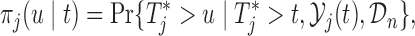 |
which has been used in the context of dynamic individualized predictions (Yu and others, 2008; Rizopoulos, 2011, 2012; Taylor and others, 2013).
The purpose of the non-negative constants 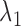 and
and 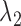 is to weigh the contribution of the conditional survival probability as opposed to the information gain, and to take into account that these two terms have different units. In practical applications, elicitation of these constants for trading information units with probabilities can be difficult. To overcome this, we can suitably utilize the equivalence between compound and constrained optimal designs (Cook and Wong, 1994; Clyde and Chaloner, 1996). More specifically, it can be shown that for any
is to weigh the contribution of the conditional survival probability as opposed to the information gain, and to take into account that these two terms have different units. In practical applications, elicitation of these constants for trading information units with probabilities can be difficult. To overcome this, we can suitably utilize the equivalence between compound and constrained optimal designs (Cook and Wong, 1994; Clyde and Chaloner, 1996). More specifically, it can be shown that for any 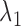 and
and 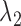 , there exists a constant
, there exists a constant 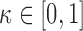 for which maximization of (3.1) is equivalent to maximization of
for which maximization of (3.1) is equivalent to maximization of 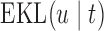 subject to the constraint that
subject to the constraint that 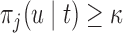 . Under this equivalent formulation elicitation of
. Under this equivalent formulation elicitation of 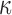 is relatively easier; for example, a logical choice is to set
is relatively easier; for example, a logical choice is to set 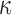 equal to the constant
equal to the constant 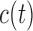 , introduced in Figure 1, for deciding whether the physician is supposed to intervene or not. In turn, a choice for
, introduced in Figure 1, for deciding whether the physician is supposed to intervene or not. In turn, a choice for 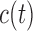 can be based on medical grounds (e.g. physicians are not willing to allow survival probabilities to drop below a specific threshold value) or on time-dependent receiver operating characteristic analysis. Then, the optimal value of
can be based on medical grounds (e.g. physicians are not willing to allow survival probabilities to drop below a specific threshold value) or on time-dependent receiver operating characteristic analysis. Then, the optimal value of 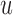 can be found by maximizing
can be found by maximizing 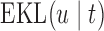 in the interval
in the interval 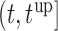 , where
, where 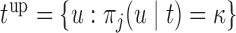 . In practice, it also may be reasonable to assume that there is an upper limit
. In practice, it also may be reasonable to assume that there is an upper limit 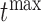 of the time interval the physician is willing to wait to obtain the next measurement, in which case
of the time interval the physician is willing to wait to obtain the next measurement, in which case 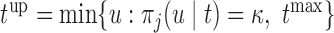 .
.
3.2. Estimation
Estimation of (3.1) proceeds by suitably utilizing the conditional independence assumptions presented in Section 1 of supplementary material available at Biostatistics online. More specifically, the density of the joint distribution 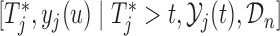 can be written as the product of the predictive distributions,
can be written as the product of the predictive distributions,
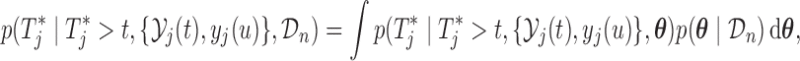 |
and
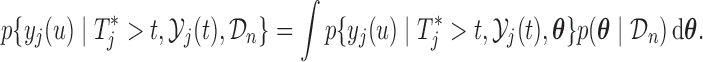 |
Analogously, the first term in the right-hand side of each of the above expressions can be written as expectations over the corresponding posterior distributions of the random effects of subject 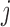 ,
,
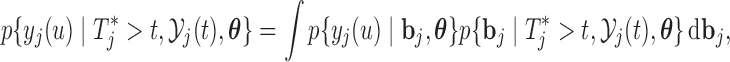 |
and
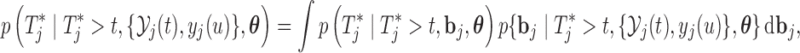 |
respectively. In a similar manner, the predictive distribution  is written as:
is written as:
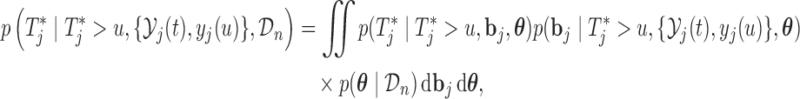 |
with
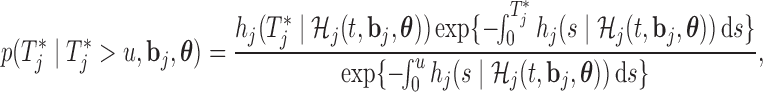 |
and the hazard function is given by (2.2), in which we have explicitly noted that the history of the longitudinal process 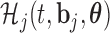 is a function of both the random effects and the parameters, because it is estimated from the mixed model (2.1). By combining the above equations, we can construct a Monte Carlo simulation scheme to obtain an estimate of (3.1) for a specific value of
is a function of both the random effects and the parameters, because it is estimated from the mixed model (2.1). By combining the above equations, we can construct a Monte Carlo simulation scheme to obtain an estimate of (3.1) for a specific value of 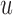 . This scheme contains the following steps that should be repeated
. This scheme contains the following steps that should be repeated 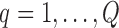 times:
times:
Step  Simulate
Simulate  ,
, 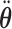 , and
, and 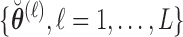 independently from the posterior distribution of the parameters
independently from the posterior distribution of the parameters 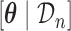 .
.
Step 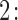 Simulate
Simulate 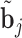 from the posterior of the random effects
from the posterior of the random effects 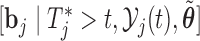 .
.
Step 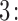 Simulate
Simulate 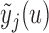 from
from 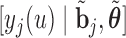 .
.
Step  Simulate
Simulate  and
and  independently from the posterior of the random effects
independently from the posterior of the random effects 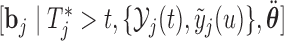 and
and 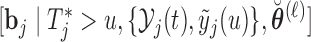 , respectively.
, respectively.
Step 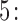 Simulate
Simulate 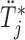 from
from 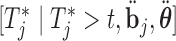 .
.
Step 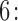 If
If 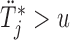 , compute
, compute 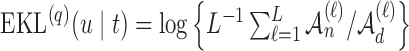 , where
, where
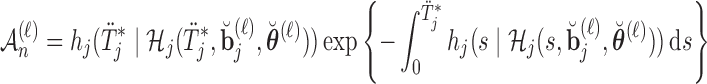 |
and
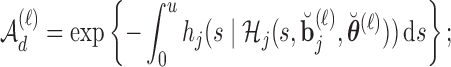 |
otherwise set 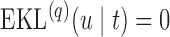 .
.
The sample mean over the Monte Carlo samples provides the estimate of 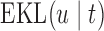 , i.e.
, i.e. 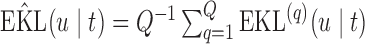 . The posterior distribution of the random effects in Steps 2 and 4 is not of a known form, and therefore the realizations
. The posterior distribution of the random effects in Steps 2 and 4 is not of a known form, and therefore the realizations 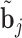 ,
, 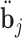 , and
, and 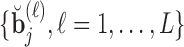 are obtained using a Metropolis–Hastings algorithm, with proposal distribution a multivariate Student's-
are obtained using a Metropolis–Hastings algorithm, with proposal distribution a multivariate Student's-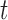 distribution with mean
distribution with mean 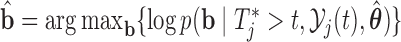 , variance–covariance matrix
, variance–covariance matrix 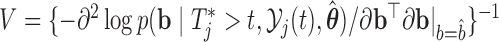 , and four degrees of freedom, where
, and four degrees of freedom, where 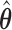 denotes the posterior means based on
denotes the posterior means based on 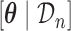 . Step 3 just entails simulating a realization from the mixed-effects model. In Step 5 again, the distribution
. Step 3 just entails simulating a realization from the mixed-effects model. In Step 5 again, the distribution 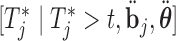 is not of standard form, and hence we simulate the realization
is not of standard form, and hence we simulate the realization 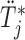 using the inversion method, i.e. first we simulate
using the inversion method, i.e. first we simulate 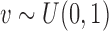 , and then using a line-search method we find the
, and then using a line-search method we find the 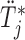 for which
for which 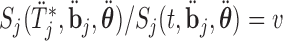 , with
, with 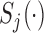 denoting the subject-specific survival function (Equation (7) in supplementary material available at Biostatistics online). Finally, in Step 6 it is sufficient to compute the numerator of (3.2) to obtain the optimal
denoting the subject-specific survival function (Equation (7) in supplementary material available at Biostatistics online). Finally, in Step 6 it is sufficient to compute the numerator of (3.2) to obtain the optimal 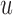 . An estimate of
. An estimate of 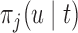 can be obtained from a separate Monte Carlo scheme, i.e.
can be obtained from a separate Monte Carlo scheme, i.e.
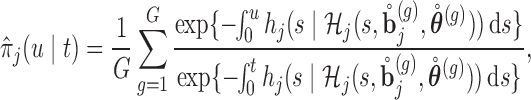 |
with 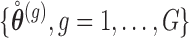 a sample from
a sample from 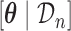 , and
, and 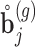 a sample from
a sample from  . Based on the Monte Carlo sample of
. Based on the Monte Carlo sample of 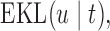 a 95% credible interval van be constructed using the corresponding Monte Carlo sample percentiles. Using this simulation scheme, we take as optimal
a 95% credible interval van be constructed using the corresponding Monte Carlo sample percentiles. Using this simulation scheme, we take as optimal 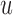 the value
the value 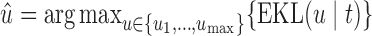 , subject to the constraint that
, subject to the constraint that 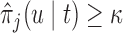 , with
, with 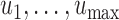 denoting a grid of values in
denoting a grid of values in 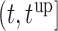 .
.
4. Analysis of the Aortic Valve dataset
We return to the Aortic Valve dataset introduced in Section 1. Our aim is to use the existing data to build joint models that can be utilized for planning the visiting patterns of future patients from the same population. In our study, two surgical implantation techniques were employed, with 77 (27%) patients receiving a sub-coronary implantation and the remaining 208 patients a root replacement. These patients were followed prospectively over time with annual telephone interviews and biennial standardized echocardiographic assessment of valve function until July 8, 2010. Echo examinations were scheduled at 6 months and 1 year postoperatively, and biennially thereafter, and at each examination, echocardiographic measurements were taken. By the end of follow-up, 1262 assessments have been recorded, with an average of 4.3 measurements per patient (s.d. 2.4 measurements), 59 (20.7%) patients had died, and 73 (25.6%) patients required a re-operation on the allograft. Here we are interested in the composite event re-operation or death, which was observed for 125 (43.9%) patients.
For our analysis, we will focus on aortic gradient, which is the primary biomarker of interest for these patients. We start by defining a set of joint models for the square root transform of aortic gradient. A preliminary analysis suggested that many patients exhibit profiles for aortic gradient. To account for this feature, we postulate the linear mixed model:
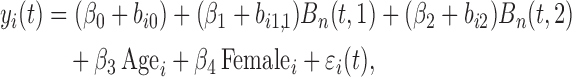 |
where 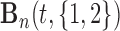 denotes the B-spline basis for a natural cubic spline with boundary knots at baseline and 19 years and one internal knot placed at 3.7 years (i.e. the median of the observed follow-up times), Female denotes the dummy variable for females. For the survival process, we consider five relative risk models with different association structures between the two outcomes:
denotes the B-spline basis for a natural cubic spline with boundary knots at baseline and 19 years and one internal knot placed at 3.7 years (i.e. the median of the observed follow-up times), Female denotes the dummy variable for females. For the survival process, we consider five relative risk models with different association structures between the two outcomes:
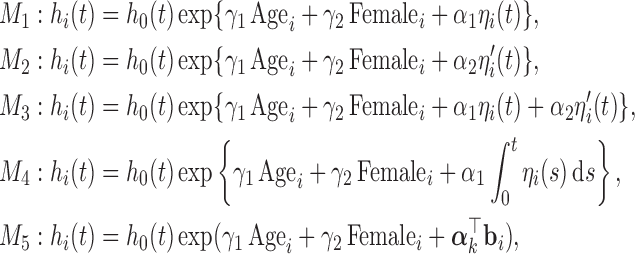 |
where the baseline hazard is approximated using penalized B-splines. For all parameters, we took standard prior distributions. In particular, for the vector of fixed effects 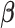 , the regression coefficients
, the regression coefficients 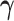 , the spline coefficients
, the spline coefficients 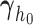 , and for the association parameter
, and for the association parameter 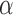 we used independent univariate diffuse normal priors. For the variance of the error terms
we used independent univariate diffuse normal priors. For the variance of the error terms 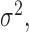 we took an inverse-Gamma prior, while for
we took an inverse-Gamma prior, while for 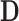 we assumed an inverse Wishart prior.
we assumed an inverse Wishart prior.
Tables 1 and 2 in Section 2 of supplementary material available at Biostatistics online present the posterior means and 95% credible intervals of the parameters of the joint models to the Aortic Valve data. With respect to the parameters of the longitudinal component, we do not observe great differences between the fitted joint models for both aortic gradient. For the relative risk submodels, we see that when the terms 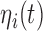 and
and 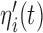 are independently included in the model both of them are related to the risk of re-operation/death, however, when both of them are included in the model, the slope term
are independently included in the model both of them are related to the risk of re-operation/death, however, when both of them are included in the model, the slope term 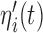 does not seem to be associated with the hazard of the event anymore. We continue by investigating the performance of the fitted joint models with respect to predicting future events after different follow-up times. Table 1 shows the DIC and the value of
does not seem to be associated with the hazard of the event anymore. We continue by investigating the performance of the fitted joint models with respect to predicting future events after different follow-up times. Table 1 shows the DIC and the value of 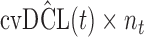 for
for 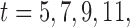 and 13 years. We observe that models
and 13 years. We observe that models 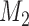 and
and 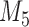 have almost identical DIC values but according to
have almost identical DIC values but according to 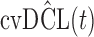 model
model 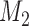 provides the best predictions for future events.
provides the best predictions for future events.
Table 1.
DIC and 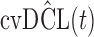 evaluated at five time points for the fitted joint models
evaluated at five time points for the fitted joint models
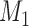 |
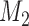 |
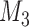 |
 |
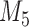 |
|
|---|---|---|---|---|---|
| DIC | 7237.26 | 7186.18 | 7195.57 | 7268.45 | 7186.34 |
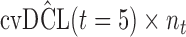 |
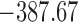 |
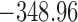 |
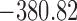 |
 |
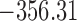 |
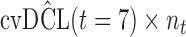 |
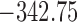 |
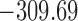 |
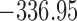 |
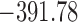 |
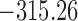 |
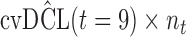 |
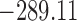 |
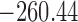 |
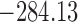 |
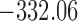 |
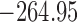 |
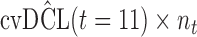 |
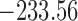 |
 |
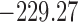 |
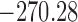 |
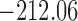 |
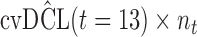 |
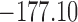 |
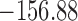 |
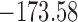 |
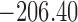 |
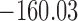 |
Table 2.
The values of 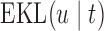 (i.e. the first term of (3.1)),
(i.e. the first term of (3.1)), 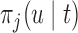 (i.e. the second term of (3.1)), for Patient 7 computed in a dynamic manner, after each of his longitudinal measurements (i.e. time point
(i.e. the second term of (3.1)), for Patient 7 computed in a dynamic manner, after each of his longitudinal measurements (i.e. time point 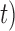 , and for
, and for 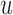 set in the interval
set in the interval 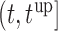
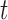 |
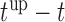 |
 |
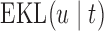 |
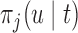 |
|
|---|---|---|---|---|---|
| 3.5 | 5 | 4.5 | 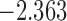 |
0.983 | |
| 5.5 | 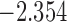 |
0.964 | |||
| 6.5 | 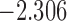 |
0.943 | |||
| 7.5 | 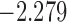 |
0.919 | |||
| 8.5 | 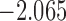 |
0.892 | * | ||
| 4 | 5 | 5.0 | 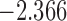 |
0.982 | |
| 6.0 | 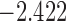 |
0.963 | |||
| 7.0 | 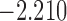 |
0.941 | |||
| 8.0 | 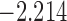 |
0.915 | |||
| 9.0 | 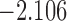 |
0.886 | * | ||
| 5 | 5 | 6.0 | 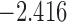 |
0.981 | |
| 7.0 | 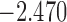 |
0.959 | |||
| 8.0 | 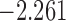 |
0.933 | |||
| 9.0 | 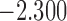 |
0.904 | |||
| 10.0 | 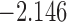 |
0.872 | * | ||
| 5.7 | 5 | 6.7 | 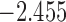 |
0.979 | |
| 7.7 | 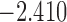 |
0.956 | |||
| 8.7 | 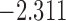 |
0.928 | |||
| 9.7 | 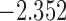 |
0.897 | |||
| 10.7 | 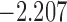 |
0.861 | * | ||
| 6.7 | 5 | 7.7 |  |
0.976 | |
| 8.7 | 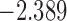 |
0.949 | |||
| 9.7 | 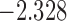 |
0.917 | |||
| 10.7 | 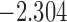 |
0.882 | |||
| 11.7 | 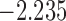 |
0.841 | * | ||
| 7.7 | 5 | 8.7 | 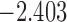 |
0.973 | |
| 9.7 | 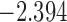 |
0.941 | |||
| 10.7 | 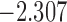 |
0.906 | |||
| 11.7 | 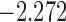 |
0.865 | |||
| 12.7 | 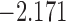 |
0.819 | * | ||
| 9.1 | 4.3 | 9.9 | 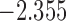 |
0.971 | |
| 10.8 | 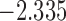 |
0.939 | |||
| 11.7 | 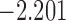 |
0.903 | |||
| 12.5 | 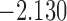 |
0.863 | |||
| 13.4 | 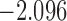 |
0.817 | * | ||
| 11.3 | 3.1 | 11.9 | 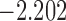 |
0.969 | |
| 12.5 | 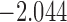 |
0.935 | |||
| 13.1 | 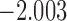 |
0.897 | |||
| 13.8 | 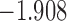 |
0.856 | * | ||
| 14.4 | 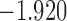 |
0.810 | |||
| 13.5 | 1.9 | 13.9 | 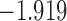 |
0.968 | |
| 14.3 | 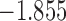 |
0.933 | |||
| 14.7 | 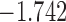 |
0.897 | |||
| 15.1 | 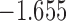 |
0.858 | * | ||
| 15.4 | 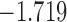 |
0.817 | |||
| 15.1 | 1.4 | 15.4 | 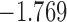 |
0.968 | |
| 15.7 | 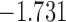 |
0.934 | |||
| 15.9 | 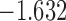 |
0.899 | |||
| 16.2 | 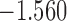 |
0.862 | |||
| 16.5 | 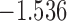 |
0.824 | * |
The last column denotes which time point is selected to plan the next measurement.
To illustrate the use of the methodology developed in Section 3 for selecting the next screening time point, we focus on the continuous marker and two patients from the Aortic Valve dataset, namely Patient 81 who is a male of 39.8 years old, and Patient 7 who is a male of 46.8 years old and neither had an event (Patient 81 was still event-free 11.6 years after the operation, while Patient 7 was also event-free after 20.1 years). The longitudinal trajectories of these patients are shown in Figure 1 of supplementary material available at Biostatistics online. More specifically, Patient 7 exhibits a slightly increasing trajectory of aortic gradient indicating that he remained in relatively good condition during the follow-up, whereas Patient 81 showed an increasing profile of aortic gradient indicative of a deterioration of his condition. We should note that in accordance with a realistic use of (3.1) for planning the next measurement, the joint models presented above have been fitted in the version of the Aortic Valve dataset that excluded those two patients. Tables 2 and 3 show the values of 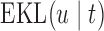 (i.e. the first term of (3.1)), and of
(i.e. the first term of (3.1)), and of 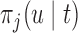 (i.e. the second term of (3.1)) for these two patients computed in a dynamic manner, namely, after each of their longitudinal measurements (i.e. time point
(i.e. the second term of (3.1)) for these two patients computed in a dynamic manner, namely, after each of their longitudinal measurements (i.e. time point 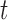 ). The upper limit
). The upper limit 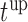 of the interval
of the interval 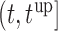 was set as the minimum of
was set as the minimum of 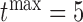 years and the time point
years and the time point 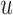 for which
for which 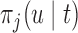 was equal to
was equal to 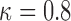 . Then the optimal
. Then the optimal 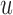 was taken as the point that maximizes
was taken as the point that maximizes 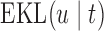 in a grid of five equidistant values in the interval
in a grid of five equidistant values in the interval 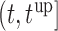 . All calculations have been based on joint model
. All calculations have been based on joint model 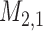 . For Patient 7, who remained relatively stable during the first period of his follow-up, we observe that
. For Patient 7, who remained relatively stable during the first period of his follow-up, we observe that 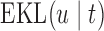 always suggests waiting the full 5 years up to measurement seven; however, after the seventh measurement and because his profile started to slightly increase and his relative older age, the length of the interval
always suggests waiting the full 5 years up to measurement seven; however, after the seventh measurement and because his profile started to slightly increase and his relative older age, the length of the interval 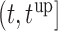 for finding the optimal
for finding the optimal 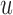 decreases, which in turn suggests to wait after each visit less time before requesting the next echocardiography. For Patient 81 on the other hand, we observe that for the first two visits, where he exhibited relatively low levels of aortic gradient,
decreases, which in turn suggests to wait after each visit less time before requesting the next echocardiography. For Patient 81 on the other hand, we observe that for the first two visits, where he exhibited relatively low levels of aortic gradient, 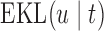 suggests to wait for a longer period years before requesting the next measurement. In accordance,
suggests to wait for a longer period years before requesting the next measurement. In accordance, 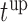 is set to 5 years because the probability that he will survive more than 5 years was higher than
is set to 5 years because the probability that he will survive more than 5 years was higher than 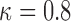 . After the third measurement however, when it starts to become clear that the condition of this patient deteriorates,
. After the third measurement however, when it starts to become clear that the condition of this patient deteriorates, 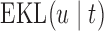 recommends to wait less time to request the next echocardiography. Accordingly from the fourth measurement onwards, the length of the interval
recommends to wait less time to request the next echocardiography. Accordingly from the fourth measurement onwards, the length of the interval 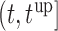 decreases and in the last measurement is set to 1.7 years that also indicates the deterioration of the patient.
decreases and in the last measurement is set to 1.7 years that also indicates the deterioration of the patient.
Table 3.
The values of 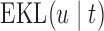 (i.e. the first term of (3.1)),
(i.e. the first term of (3.1)), 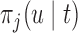 (i.e. the second term of (3.1)), for Patient 81 computed in a dynamic manner, after each of his longitudinal measurements (i.e. time point
(i.e. the second term of (3.1)), for Patient 81 computed in a dynamic manner, after each of his longitudinal measurements (i.e. time point 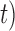 , and for
, and for 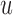 set in the interval
set in the interval 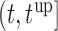
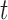 |
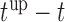 |
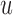 |
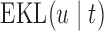 |
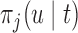 |
|
|---|---|---|---|---|---|
| 0.3 | 5 | 1.3 | 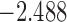 |
0.989 | |
| 2.3 | 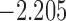 |
0.977 | |||
| 3.3 | 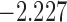 |
0.963 | |||
| 4.3 | 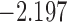 |
0.948 | |||
| 5.3 | 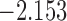 |
0.933 | * | ||
| 1.3 | 5 | 2.3 | 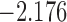 |
0.987 | |
| 3.3 | 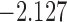 |
0.973 | |||
| 4.3 | 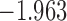 |
0.957 | |||
| 5.3 | 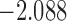 |
0.940 | |||
| 6.3 | 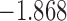 |
0.922 | * | ||
| 3.3 | 5 | 4.3 | 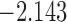 |
0.978 | |
| 5.3 | 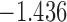 |
0.956 | * | ||
| 6.3 | 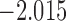 |
0.932 | |||
| 7.3 | 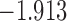 |
0.905 | |||
| 8.3 | 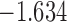 |
0.875 | |||
| 5.3 | 3.9 | 6.1 |  |
0.968 | |
| 6.9 | 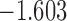 |
0.935 | * | ||
| 7.6 | 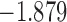 |
0.900 | |||
| 8.4 | 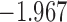 |
0.864 | |||
| 9.2 | 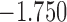 |
0.827 | |||
| 7.1 | 2.1 | 7.5 | 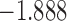 |
0.969 | * |
| 7.9 | 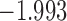 |
0.937 | |||
| 8.4 | 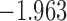 |
0.906 | |||
| 8.8 | 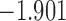 |
0.875 | |||
| 9.2 | 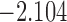 |
0.844 | |||
| 10.6 | 1.7 | 11.0 | 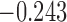 |
0.970 | |
| 11.3 |  |
0.940 | * | ||
| 11.6 | 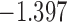 |
0.910 | |||
| 12.0 | 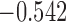 |
0.880 | |||
| 12.3 | 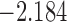 |
0.849 |
The last column denotes which time point is selected to plan the next measurement.
5. Cost-effectiveness simulation study
The analysis of the Aortic Valve dataset illustrated that the utility function 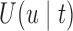 effectively adapts screening intervals depending on the characteristics of the patients' longitudinal trajectories. However, due to the fact in this dataset the data have been already collected under a fixed-planning design, we cannot directly assess the advantages of planning measurements using the framework of Section 3. To this end, we have performed a simulation study to evaluate the cost-effectiveness of
effectively adapts screening intervals depending on the characteristics of the patients' longitudinal trajectories. However, due to the fact in this dataset the data have been already collected under a fixed-planning design, we cannot directly assess the advantages of planning measurements using the framework of Section 3. To this end, we have performed a simulation study to evaluate the cost-effectiveness of 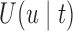 . In the context of screening, and assuming that the monetary cost of each examination remains (roughly) the same during follow-up, we would prefer a procedure that requires the fewest possible screenings. On the other hand, of course, we would also like to get as close as possible to the optimal time point at which a medical action is required. Under these considerations, the setting of our simulation study is motivated by the Aortic Valve dataset. In particular, we assume that patients undergo a valve transplantation and we follow their progression after this operation using the longitudinal outcome (aortic gradient). The aim is to effectively plan re-operations. We assume that the patient population has a level of homogeneity such that the decision of the cardiologists to request a re-operation can be solely based on the aortic gradient levels and how these are translated to survival probabilities (no need to correct for any baseline covariates or other longitudinal outcomes). In addition, we assume that at any particular follow-up time
. In the context of screening, and assuming that the monetary cost of each examination remains (roughly) the same during follow-up, we would prefer a procedure that requires the fewest possible screenings. On the other hand, of course, we would also like to get as close as possible to the optimal time point at which a medical action is required. Under these considerations, the setting of our simulation study is motivated by the Aortic Valve dataset. In particular, we assume that patients undergo a valve transplantation and we follow their progression after this operation using the longitudinal outcome (aortic gradient). The aim is to effectively plan re-operations. We assume that the patient population has a level of homogeneity such that the decision of the cardiologists to request a re-operation can be solely based on the aortic gradient levels and how these are translated to survival probabilities (no need to correct for any baseline covariates or other longitudinal outcomes). In addition, we assume that at any particular follow-up time 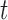 , the cardiologist will request a re-operation if the conditional survival probability
, the cardiologist will request a re-operation if the conditional survival probability 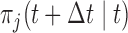 falls under a specific threshold
falls under a specific threshold 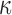 . We used
. We used 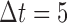 and
and 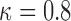 . The goal is to select the screening strategy that follows each individual patient both efficiently (i.e. with the fewest measurements possible) and effectively (i.e. request re-operation as soon as
. The goal is to select the screening strategy that follows each individual patient both efficiently (i.e. with the fewest measurements possible) and effectively (i.e. request re-operation as soon as 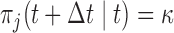 ). For each iteration of the simulation study, we proceeded as follows:
). For each iteration of the simulation study, we proceeded as follows:
We simulate data for 450 patients from a joint model that has the same structure as model
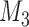 fitted to the Aortic Valve dataset (the parameter values we used can be found in Section 3 of supplementary material available at Biostatistics online). From those patients, we randomly chose 400 for the training dataset and 50 for the test dataset. Similarly to the Aortic Valve dataset, all patients have measurements at baseline, 6 months, 1 year, and biannually thereafter. For the patients in the test dataset, we only keep their first three measurements. The reason why we fix the screening times of the first three measurements is that it is not medically advisable to request a re-operation within a year from the first operation. Then the model is fit in the training dataset.
fitted to the Aortic Valve dataset (the parameter values we used can be found in Section 3 of supplementary material available at Biostatistics online). From those patients, we randomly chose 400 for the training dataset and 50 for the test dataset. Similarly to the Aortic Valve dataset, all patients have measurements at baseline, 6 months, 1 year, and biannually thereafter. For the patients in the test dataset, we only keep their first three measurements. The reason why we fix the screening times of the first three measurements is that it is not medically advisable to request a re-operation within a year from the first operation. Then the model is fit in the training dataset.For each patient in the test dataset, we first find her true optimal time point
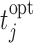 to plan the re-operation. This is the time point at which her true conditional survival function
to plan the re-operation. This is the time point at which her true conditional survival function 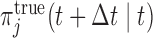 equals
equals 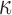 . To locate this point, we calculate
. To locate this point, we calculate 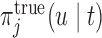 using the true values of the parameters and random effects for a fine grid of values
using the true values of the parameters and random effects for a fine grid of values 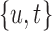 with
with 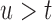 and
and 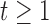 . Note that due to the fact that we use the true values of the random effects and under the conditional independence assumptions (Section 1 of supplementary material available at Biostatistics online), no longitudinal measurements are required for the calculation of
. Note that due to the fact that we use the true values of the random effects and under the conditional independence assumptions (Section 1 of supplementary material available at Biostatistics online), no longitudinal measurements are required for the calculation of 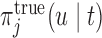 .
.From year 1 onwards, our aim next is to compare two strategies, namely, (S1) with fixed visits every 2 years (as in the Aortic Valve dataset), and (S2) with the personalized screening of Section 3. For each patient and any time point
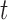 up to which we have longitudinal measurements, the
up to which we have longitudinal measurements, the  th strategy (
th strategy (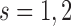 ) proposes to take the next measurement at time
) proposes to take the next measurement at time  (e.g. S1 sets the first
(e.g. S1 sets the first 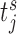 at 3 years for all patients). Then, for each strategy we simulate a longitudinal measurement using the true values of the parameters and random effects at the corresponding
at 3 years for all patients). Then, for each strategy we simulate a longitudinal measurement using the true values of the parameters and random effects at the corresponding 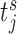 . Using this measurement, we estimate
. Using this measurement, we estimate 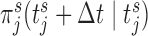 based on the joint model fitted to the training dataset. For each patient
based on the joint model fitted to the training dataset. For each patient 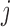 and strategy
and strategy 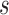 , we keep repeating this procedure until
, we keep repeating this procedure until 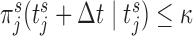 , and when this condition is satisfied we set as the optimal re-operation time point for the
, and when this condition is satisfied we set as the optimal re-operation time point for the 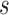 th strategy
th strategy 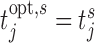 .
.
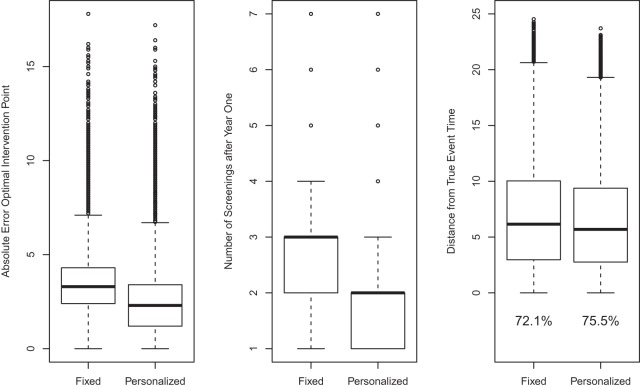
The above scheme has been repeated 500 times and the results are summarized in Figure 2. The left panel of Figure 2 shows boxplots of the absolute errors 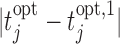 and
and 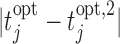 for the fixed and personalized screening strategies, respectively, from all the
for the fixed and personalized screening strategies, respectively, from all the 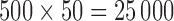 test subjects. Analogously, the middle panel of Figure 2 shows boxplots of the number of screenings for the two strategies again from all test subjects. We can clearly observe that the personalized strategy requires fewer screenings and reaches the optimal intervention time point with less absolute error. As an extra comparison between the two strategies, the right panel of Figure 2 shows the boxplot of the errors
test subjects. Analogously, the middle panel of Figure 2 shows boxplots of the number of screenings for the two strategies again from all test subjects. We can clearly observe that the personalized strategy requires fewer screenings and reaches the optimal intervention time point with less absolute error. As an extra comparison between the two strategies, the right panel of Figure 2 shows the boxplot of the errors 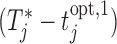 and
and 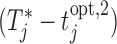 for the number of cases (shown under the boxplots) for which
for the number of cases (shown under the boxplots) for which 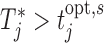 ,
, 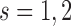 , with
, with 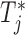 denoting the true event time. Again we observe that the personalized screening strategy performs a little bit better than the classic fixed-planning design.
denoting the true event time. Again we observe that the personalized screening strategy performs a little bit better than the classic fixed-planning design.
Fig. 2.
Simulation results based on 500 datasets comparing the fixed-planning and personalized screening strategies. Left panel: absolute error between the optimal intervention time point and the time point suggested by the two screening strategies. Middle panel: number of screenings after year 1 required by the two strategies. Right panel: positive distances between the true event time of each patient and the intervention point suggested by each strategy; below the boxplots the percentage of positive differences is shown (i.e. the percentage of patients for whom the intervention time was earlier than the true event time).
6. Discussion
In this paper, we have presented two measures based on information theory that can be used to dynamically select models in time and optimally schedule longitudinal biomarker measurements. Contrary to standard screening procedures that require all patients to adhere to the same screening intervals, the combination of the framework of joint models for longitudinal and time-to-event data with these two measures allows one to tailor screening to the needs of individual patients and dynamically adapt during follow-up. The advantageous feature of our approach is that the optimal 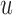 is found by conditioning on both the baseline characteristics
is found by conditioning on both the baseline characteristics 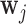 and accumulated longitudinal information
and accumulated longitudinal information 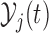 of subject
of subject 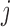 . This allows one to better tailor screening to the subject's individual characteristics compared with approaches that only use the baseline covariates and the last available longitudinal measurement (Markov assumption). We should note that due to the fact that the timing of each next visit depends on the collected longitudinal responses of each subject, the recorded data should be analyzed under an approach that accounts for this feature (e.g. a full likelihood-based method).
. This allows one to better tailor screening to the subject's individual characteristics compared with approaches that only use the baseline covariates and the last available longitudinal measurement (Markov assumption). We should note that due to the fact that the timing of each next visit depends on the collected longitudinal responses of each subject, the recorded data should be analyzed under an approach that accounts for this feature (e.g. a full likelihood-based method).
In this work, we have concentrated on a single endpoint. Nevertheless, using recent extensions of joint models (Andrinopoulou and others, 2014) the same ideas can be relatively easily extended to multiple endpoints (competing risks) or intermediate states combined with one or several endpoints (multistate settings). In such settings, the first term of (3.1) will remain the same, but the second term 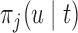 will need to be replaced by the corresponding event-specific cumulative incidence functions.
will need to be replaced by the corresponding event-specific cumulative incidence functions.
Finally, to facilitate the computation of 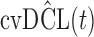 and
and 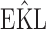 we have implemented them in functions cvDCL() and dynInfo(), respectively, available in package JMbayes (version 0.7-3) for the R programming language (freely available at http://cran.r-project.org/package=JMbayes). An example on the use of these functions can be found in supplementary material available at Biostatistics online.
we have implemented them in functions cvDCL() and dynInfo(), respectively, available in package JMbayes (version 0.7-3) for the R programming language (freely available at http://cran.r-project.org/package=JMbayes). An example on the use of these functions can be found in supplementary material available at Biostatistics online.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
This research was partially supported by the Netherlands Organisation for Scientific Research VIDI grant 016.146.301 (D. Rizopoulos) and US National Institutes of Health grant CA129102 (J.M.G. Taylor).
Supplementary Material
Acknowledgments
The authors would like to thank Professor Daniel Commenges for useful discussions with regard to the development of the 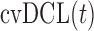 . Conflict of Interest: None declared.
. Conflict of Interest: None declared.
References
- Andrinopoulou E. R., Rizopoulos D., Takkenberg J., Lesaffre E. (2014). Joint modeling of two longitudinal outcomes and competing risk data. Statistics in Medicine 33, 3167–3178. [DOI] [PubMed] [Google Scholar]
- Bekkers J., Klieverik L., Raap G., Takkenberg J., Bogers A. (2011). Re-operations for aortic allograft root failure: experience from a 21-year single-center prospective follow-up study. European Journal of Cardio-Thoracic Surgery 40, 35–42. [DOI] [PubMed] [Google Scholar]
- Chen M.-H., Huang L., Ibrahim J., Kim S. (2008). Bayesian variable selection and computation for generalized linear models with conjugate priors. Bayesian Analysis 3, 585–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clyde M., Chaloner K. (1996). The equivalence of constrained and weighted designs in multiple objective design problems. Journal of the American Statistical Association 91, 1236–1244. [Google Scholar]
- Commenges D., Liquet B., Proust-Lima C. (2012). Choice of prognostic estimators in joint models by estimating differences of expected conditional Kullback–Leibler risks. Biometrics 68, 380–387. [DOI] [PubMed] [Google Scholar]
- Cook D., Wong W. K. (1994). On the equivalence of constrained and compound optimal designs. Journal of the American Statistical Association 89, 687–692. [Google Scholar]
- Cover T., Thomas J. (1991) Elements of Information Theory. New York: Wiley. [Google Scholar]
- Eilers P., Marx B. (1996). Flexible smoothing with b-splines and penalties. Statistical Science 11, 89–121. [Google Scholar]
- Lee S., Zelen M. (1998). Scheduling periodic examinations for the early detection of disease: applications to breast cancer. Journal of the American Statistical Association 93, 1271–1281. [Google Scholar]
- Parmigiani G. (1993). On optimal screening ages. Journal of the American Statistical Association 88, 622–628. [Google Scholar]
- Parmigiani G. (1998). Designing observation times for interval censored data. Sankhya: The Indian Journal of Statistics 60, 446–458. [Google Scholar]
- Parmigiani G. (1999). Decision model in screening for breast cancer. In: Bernardo, J. M., Berger, J. O., Dawid, A. P. and Smith, A. F. M. (editors), Bayesian Statistics 6. Oxford: Oxford University Press, pp. 525–546.
- Parmigiani G. (2002) Modeling in Medical Decision Making: A Bayesian Approach. New York: Wiley. [Google Scholar]
- Rizopoulos D. (2011). Dynamic predictions and prospective accuracy in joint models for longitudinal and time-to-event data. Biometrics 67, 819–829. [DOI] [PubMed] [Google Scholar]
- Rizopoulos D. (2012) Joint Models for Longitudinal and Time-to-Event Data, with Applications in R. Boca Raton: Chapman & Hall/CRC. [Google Scholar]
- Rizopoulos D., Ghosh P. (2011). A Bayesian semiparametric multivariate joint model for multiple longitudinal outcomes and a time-to-event. Statistics in Medicine 30, 1366–1380. [DOI] [PubMed] [Google Scholar]
- Rizopoulos D., Hatfield L., Carlin B., Takkenberg J. (2014). Combining dynamic predictions from joint models for longitudinal and time-to-event data using Bayesian model averaging. Journal of the American Statistical Association 109, 1385–1397. [Google Scholar]
- Schaefer A., Bailey M., Shechter S., Roberts M. (2004). Modeling medical treatment using Markov decision processes. In: Brandeau, M., Sainfort, F. and Pierskalla, W. (editors), Operations Research and Health Care. Berlin: Springer, pp. 593–612.
- Taylor J. M. G., Park Y., Ankerst D., Proust-Lima C., Williams S., Kestin L., Bae K., Pickles T., Sandler H. (2013). Real-time individual predictions of prostate cancer recurrence using joint models. Biometrics 69, 206–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsiatis A. A., Davidian M. (2004). Joint modeling of longitudinal and time-to-event data: an overview. Statistica Sinica 14, 809–834. [Google Scholar]
- Verdinelli I., Kadane J. B. (1992). Bayesian designs for maximizing information and outcome. Journal of the American Statistical Association 87, 510–515. [Google Scholar]
- Yu M., Taylor J. M. G., Sandler H. (2008). Individualized prediction in prostate cancer studies using a joint longitudinal-survival-cure model. Journal of the American Statistical Association 103, 178–187. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.