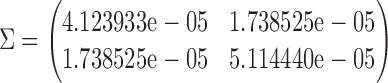Large sample inference for a win ratio analysis of a composite outcome based on prioritized components

Abstract

Composite outcomes are common in clinical trials, especially for multiple time-to-event outcomes (endpoints). The standard approach that uses the time to the first outcome event has important limitations. Several alternative approaches have been proposed to compare treatment versus control, including the proportion in favor of treatment and the win ratio. Herein, we construct tests of significance and confidence intervals in the context of composite outcomes based on prioritized components using the large sample distribution of certain multivariate multi-sample 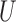-statistics. This non-parametric approach provides a general inference for both the proportion in favor of treatment and the win ratio, and can be extended to stratified analyses and the comparison of more than two groups. The proposed methods are illustrated with time-to-event outcomes data from a clinical trial.

1. Introduction

Clinical trials provide the general framework for evaluating the effect of an intervention or new therapy versus control with respect to several clinically important outcomes (also inappropriately called endpoints). These outcomes can be analyzed separately, or combined into a univariate composite outcome, usually defined as the time to the first event to which standard survival analysis techniques can be applied (Pocock, 1997). However, Pocock and others (2012) have proposed an alternate simple approach, the win ratio, based on an ordering of outcomes by priority or importance.

Analyzing the outcomes separately may provide low power due to possibly lower incidence for (some) individual outcomes, and the need for multiplicity adjustments required to control the type-I error probability. Different modern members of the closed testing procedure family (e.g. gatekeeping methods, Demidenko and others, 2008; fallback procedures, Wiens and Demidenko, 2005) were proposed to overcome the loss in power due to the multiplicity adjustments (Alosh and others, 2013; Huque and others, 2011).

While using a composite outcome may help in terms of the power to detect treatment differences, the effect of the intervention on the individual outcomes is lost. In addition, although only outcomes that share a common directional effect should be combined together, not all of them may have the same clinical relevance or importance for the patient. For example, the usual outcome for cardiovascular disease (CVD) trials is a major adverse cardiovascular (CV) event, which is the time to the first of either CV death, non-fatal stroke (stroke) or non-fatal myocardial infarction (MI). Clearly, CV death is more important than stroke. Without taking this into account, an intervention with a strong effect on stroke but no effect on CV death may appear to be preferable over an intervention with a moderate effect on both CV death and stroke. Further discussions and examples appear in the literature (Freemantle and others, 2003; Neaton and others, 2005). Standard statistical methods do not distinguish between event types when dealing with composite outcomes (e.g. time to the first event), and the need to move beyond this paradigm has been recognized (Claggett and others, 2013).

Several approaches have been proposed to address the difference in the clinical relevance of the individual outcomes that define a composite outcome. Pocock and others (2012) introduced the win ratio. The individual outcomes are ordered from the most severe to the least severe one (e.g. CV death followed by MI and then by stroke), and a partial ordering is introduced between the subjects in the study as follows. Two participants, one from each group, are compared based on the most severe individual outcome; if that is inconclusive (e.g. neither of them have an event of that type), then the comparison is based on the second worst event type, and so on. When comparing two participants, each subject can either be a winner or a loser, or the comparison can be inconclusive.

For simplicity, consider a matched study (similar ideas apply to unmatched designs). Then the win ratio is the ratio of the number of pairs where the subject receiving the new treatment was a winner, to the number of pairs where the subject receiving the new treatment was a loser. A value of 1 corresponds to the null hypothesis of no difference between the two groups, while a value larger than one is evidence that the new treatment is beneficial relative to the comparator. A similar measure, called the proportion in favor of treatment, was proposed in Buyse (2010), which is the difference in the proportion of winners and proportion of losers. An attractive feature of this partial ordering approach is that it allows the construction of composite outcomes using individual components on different scales. For example, Finkelstein and Schoenfeld (1999) describe an analysis of mortality and longitudinal CD4 values in AIDS prophylaxis and pediatric trials.

Statistical inference in this context was based on a randomized test (Finkelstein and Schoenfeld, 1999) for inference regarding the win ratio, and on a random permutation test for the proportion in favor of treatment parameter (Buyse, 2010). However, these approaches do not provide expressions for confidence intervals, and one has to rely on the bootstrap instead, which turns out to be very computationally intensive (Rauch and others, 2014).

Another proposed approach (Bakal and others, 2012) is based on an aggregate analysis of all of the possible outcomes using a priori specified weights. All individual events are considered for each participant, with the score of each event reduced multiplicatively based on the weights of the previous events for that particular subject. One can then obtain weighted versions of the Kaplan–Meier survival curve, which can be used in Aalen–Gill type tests for comparing the treatment groups (cf. Lachin, 2011).

Herein, we further characterize the large sample distribution of the sample estimates of the win ratio and the proportion in favor of treatment parameters in the context of composite outcomes based on prioritized components that yields large sample tests and confidence intervals. It is shown that both sample estimates can be obtained using certain multivariate multi-sample 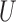-statistics, and statistical tests and confidence intervals can be obtained using large sample asymptotics.

Under random censoring, it is further shown that the win ratio and the win difference depend on censoring only through the total hazards of censoring, and that the null values of these parameters correspond to the null hypothesis of no treatment difference even with different censoring distributions between groups. Besides providing valid tests and confidence intervals, another strength of the proposed approach is that it can be easily extended to stratified studies and the comparison of more than two groups.

Recently, Luo and others (2015) also used 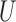-statistics to derive the distribution of these estimators in the restricted case of semi-competing risks data (Fine and others, 2001) with only two individual outcomes, one of them being an absorbing state (competing risk). The results herein apply more generally to multiple outcomes that can be measured on any scale (binary, ordinal, etc.) with or without competing risks.

The performance of the proposed methods is evaluated using simulations. The methods developed herein are then illustrated for multiple event-time outcomes in the context of a prior CV outcomes study, the Prevention of Events with Angiotensin Converting Enzyme Inhibition (PEACE) study (The PEACE Trial Investigators, 2004). The article is concluded with a brief discussion.

2. A large sample test

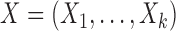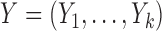Let and denote the 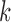possible outcomes for two subjects, one from each group, ordered based on their clinical relevance, starting with the most severe. A given outcome could be measured on any scale, e.g. 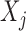could be a binary variable, ordinal variable, quantitative measure, etc. Herein, we principally focus on the case where all of the outcomes represent event times that could include an absorbing state. The comparison of the two participants is based on the most severe component measures 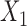and 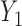. If it is not possible to determine a winner (the other loser), then the comparison is based on the second most severe components 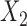and 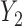(if possible), and so on.

More formally, introduce the partial ordering (Rauch and others, 2014),

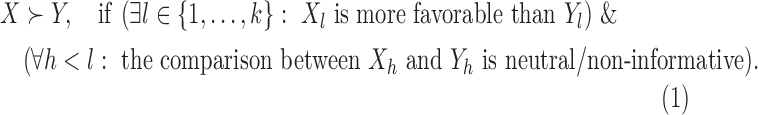(2.1)

If 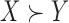, then 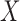is called a winner, while 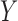a loser. Similarly, one can define 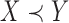( 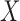is a loser), or 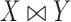(the comparison is inconclusive). Let 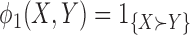and 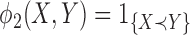then represent binary variables to indicate whether the member of group 1 or group 2, respectively, is a winner, and let 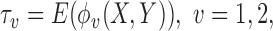denote the corresponding probabilities.

The precise definition of more favorable depends on the type of outcomes compared. For example, for binary and continuous outcomes, 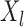is more favorable than 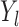if 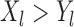, where it is assumed that larger values are more beneficial. The comparison of time-to-event outcomes is more complicated due to censoring, and it is described in detail in Section 3.

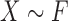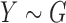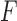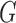Consider the two-sample problem , and , where and denote the joint distributions of the 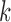outcomes in the two groups. Then, given two subjects, one from each group, 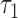is the probability that the subject in the first group is a winner. Under the null hypothesis of no difference between the two groups (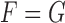), one has 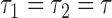, where 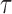may be less than 0.5 if 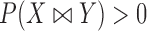. The latter can occur as a result of censoring for time-to-event outcomes, or missing values for outcomes measured on other scales. Two statistics have been proposed to test this null hypothesis, one based on their difference 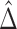with expectation 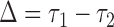, and the other on their ratio 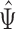with expectation 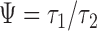(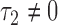), where 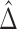is the proportion in favor of treatment (Buyse, 2010), and 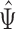is called the win ratio (Pocock and others, 2012).

Consider two random samples 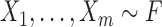, and 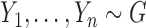, where 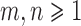, 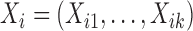for 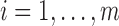, and let 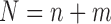denote the total sample size.

The permutation test proposed in Buyse (2010) for inference regarding the proportion in favor of treatment is based on the empirical distribution of 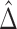obtained using random permutations of the group labels. In principle, although more efficient approaches may be possible, one needs to compare the 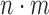pairs for each permutation, which is very computationally expensive.

The randomization test used in Pocock and others (2012) for inference regarding the win ratio parameter was first proposed in Finkelstein and Schoenfeld (1999). All pairs of subjects are compared, regardless of group, and a score 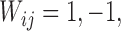or 0 is assigned to the pair 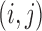depending on whether subject 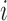was a winner, a loser, or the comparison was inconclusive. The test statistic is 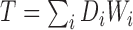, where 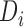is the indicator variable for the treatment and 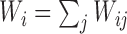. Under the null distribution of no treatment effect, 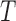is asymptotically normally distributed with mean 0 and variance 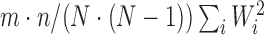; see Pocock and others (2012) and Finkelstein and Schoenfeld (1999) for details.

However, the tests of Buyse (2010) and Finkelstein and Schoenfeld (1999) are both based on a non-parameteric estimate of the variance of the respective statistic under the null, not the unrestricted alternative, and a confidence interval is not provided for either f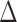or or .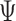

The proposed approach herein is based on the observation that an unbiased estimator for 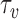can be obtained using the 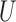-statistic:

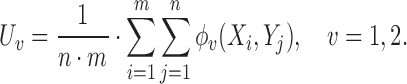Inference regarding the proportion in favor 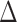and the win ratio 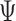will be based on the joint distribution of 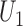and 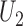. Using Lehmann's theorem for multivariate multi-sample 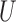-statistics (Lehmann, 1963), the joint distribution of 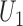and 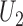is asymptotically normal,

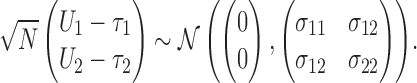(2.2)

The components of the variance–covariance matrix are given by

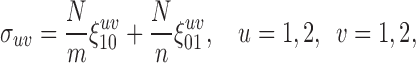(2.3)

with

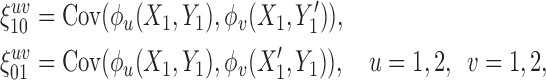where 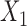and 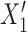refer to values of 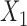for two different subjects, 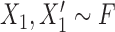, and likewise 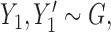all independent.

These terms can be further simplified, for example,

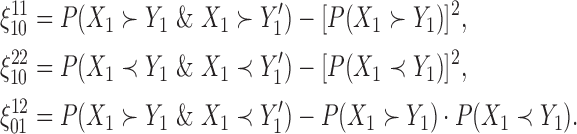(2.4)

Details on the estimation of the various probability terms in (2.4) are provided in Appendix A of supplementary material available at Biostatistics online, and these estimates are then used in (2.3).

It follows that

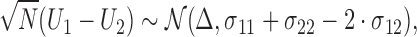(2.5)

and statistical tests and confidence intervals for the proportion in favor parameter 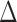can be easily obtained.

Similarly, statistical tests and confidence intervals for the win ratio parameter 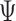can be obtained using the delta method on the log scale, and one obtains

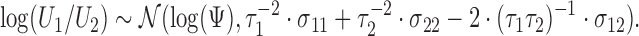(2.6)

Alternatively, one can use Fieller's theorem, which is based on the following distributional result:

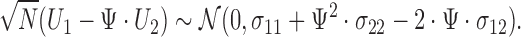Fieller's confidence interval for 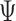is obtained by inverting the following inequality:

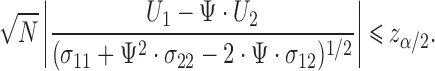(2.7)

This can be a finite interval, the complement of a finite interval or even 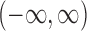, depending on the roots of the quadratic equation 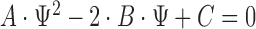, where 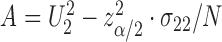, , 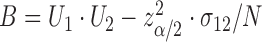and .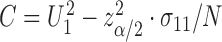

Note that the above approach can be applied for any set of outcomes on possibly different scales, such as the example in Finkelstein and Schoenfeld (1999) that used time to death and longitudinal CD4 counts as two ordered outcomes.

Pocock and others (2012) also considered the win ratio parameter for a matched pairs analysis and the test is then based on a normal approximation for the binomial distribution. One can easily show that in this case, the test in Pocock and others (2012) is equivalent to the large sample test proposed herein.

3. Survival outcomes

The standard approach for comparing time-to-event composite outcomes is to consider the time to the first event, and then to use a univariate test (e.g. logrank test) to compare the two groups. Drawbacks of this approach can be illustrated using a simple example. Consider a composite outcome with components CV death and stroke, both exponentially distributed with parameters 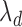and 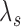(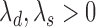). Assuming that the two events are independent, the time to the first event is again exponentially distributed with parameter 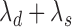. This approach will not be able to distinguish between a treatment that decreases 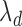by 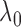(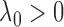) but increases 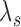by 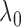, and another treatment that increases 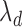by 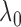but decreases 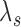by 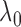, although clearly the first one is preferable.

The comparison of time-to-event outcomes based on prioritized components was proposed to address this issue. Due to censoring, the determination of the partial ordering (2.1) is more complicated than in the simple binary case. We assume that censoring is at random but perhaps with a different distribution in the two groups.

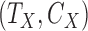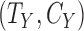Start with only one outcome (such as CVD death), and let and denote the time of the event and time of censoring (not both of them observed) for the two subjects, one from each group. Then 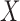is more favorable than 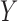if

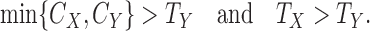(3.1)

Similarly, one can show that the comparison is non-informative if

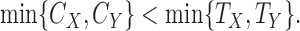(3.2)

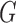Now consider the case of a composite outcome defined based on individual outcomes. In the two-sample problem, let and denote the distribution functions of 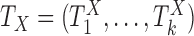and 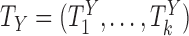, respectively, assumed, for simplicity, absolutely continuous with pdf's 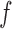and 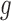. From (2.1), using (3.1) and (3.2), one obtains

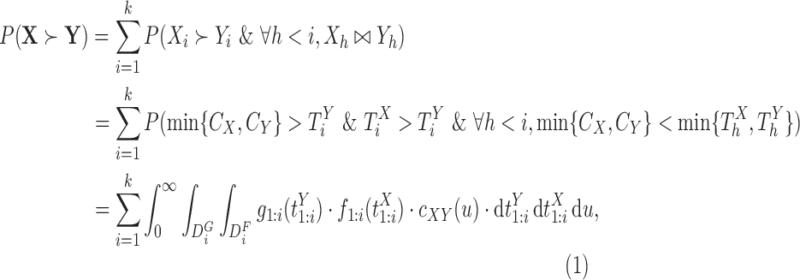(3.3)

where 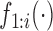denotes the marginal pdf of 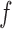corresponding to the first 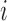components, 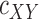is the density of 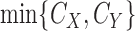, , 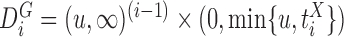and 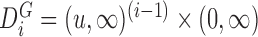, with 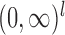the 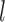times Cartesian product of 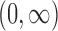with itself.

A similar representation can be derived for 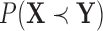, which will provide closed form expressions for 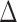and .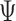

Several comments are in order. First note from (3.1–3.3) that the two parameters of interest depend on censoring only through the distribution of their minimum, or equivalently, through the sum of the two hazards of censoring. The second remark is that if the two true multivariate event times are equal (i.e. 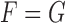), then regardless of the pattern or censoring in the two groups, 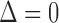and .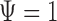

The proposed approach based on the large sample asymptotic result (2.2) is easy to implement. Its performance is evaluated through simulations and it is illustrated using data from a randomized trial.

Simulation: The performance of the proposed methods is evaluated using the same simulation model used in Luo and others (2015). It consists of three different bivariate distributions: exponential with Gumbel–Hougaard copula, exponential with bivariate normal copula, and the Marshall–Olkin distribution for semi-competing risks data subject to censoring. We refer the reader to Luo and others (2015) for details regarding these distributions and the parameter values employed.

The proposed methods are evaluated in terms of coverage probabilities at nominal levels of 80%, 90%, and 95%. Numerical results assuming different censoring between groups (with a log hazard ratio of 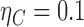) and various combinations of log hazard ratios for the non-fatal endpoint (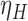) and the fatal endpoint (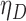) are reported in Table 1 using the method of Luo and others (2015), the Delta Method (2.6), and the Fieller method (2.7). All methods provide very accurate results.

Table 1.

Simulated coverage probabilities (using 5000 simulations) for the different confidence intervals for the win ratio parameter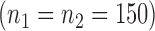

				Luo and others			Delta method			Fieller
			log(WR)	80%	90%	95%	80%	90%	95%	80%	90%	95%
GH	0.0	0.0	0.00	0.8058	0.9056	0.9520	0.8030	0.9026	0.9500	0.8018	0.9012	0.9478
GH	0.2	0.5	0.29	0.8092	0.9092	0.9528	0.8054	0.9074	0.9516	0.8030	0.9046	0.9502
GH	0.3	0.3	0.30	0.8146	0.9082	0.9548	0.8112	0.9064	0.9530	0.8104	0.9044	0.9510
GH	0.5	0.2	0.38	0.7906	0.8950	0.9492	0.7882	0.8932	0.9470	0.7872	0.8910	0.9424
BN	0.0	0.0	0.00	0.7982	0.8976	0.9544	0.7947	0.8948	0.9536	0.7936	0.8914	0.9510
BN	0.2	0.5	0.28	0.7986	0.8982	0.9494	0.7952	0.8956	0.9478	0.7946	0.8912	0.9460
BN	0.3	0.3	0.29	0.8036	0.9074	0.9532	0.7996	0.9060	0.9510	0.7984	0.9040	0.9506
BN	0.5	0.2	0.38	0.7980	0.9004	0.9500	0.7966	0.8984	0.9480	0.7936	0.8946	0.9436
MO	0.0	0.0	0.00	0.8030	0.9028	0.9454	0.7977	0.9004	0.9438	0.7956	0.8980	0.9416
MO	0.2	0.5	0.13	0.8046	0.9022	0.9506	0.8016	0.9008	0.9480	0.7992	0.8992	0.9454
MO	0.3	0.3	0.14	0.7998	0.9040	0.9504	0.7972	0.9034	0.9492	0.7946	0.9012	0.9470
MO	0.5	0.2	0.19	0.8032	0.9012	0.9476	0.7977	0.8996	0.9464	0.7977	0.8974	0.9432

GH, Gumbel–Hougaard bivariate exponential; BN, bivariate exponential with bivariate normal copula; MO, Marshall–Oklin bivariate exponential. See Luo and others (2015) for details on the simulation setups.

Example 3.1 (the PEACE Study) —

The PEACE study (The PEACE Trial Investigators, 2004) was a double-blind, placebo controlled study that investigated the therapeutic benefit of adding an ACE inhibitor versus placebo to conventional therapy in terms of reducing CV outcomes. A total of 8290 patients were enrolled in the study, with 4158 subjects randomized to the ACE arm, and 4132 subjects to placebo. The study results were negative with respect to the primary, a priori-defined composite outcome defined as the time to CV death, MI, or coronary revascularization, whichever occurred first. Other CV outcomes were also reported in the study, and, a composite outcome based on CV death, MI and stroke is considered herein for illustration, in order of severity. The -value (two-sided) using the logrank test in a time to the first event analysis was 0.304, which is not significant. The corresponding value was 1.0279.

The proposed large sample approach is illustrated for both the proportion in favor of treatment and the win ratio. The censoring time distribution was not statistically different between the two groups for any of the three CV outcomes (results not shown). The parameters of the asymptotic joint distribution (2.2) are estimated by 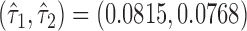, and

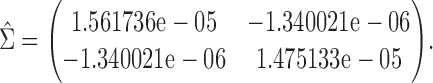The win ratio estimate is 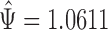. Using the Delta method, its standard error is 0.0770, and a 95% confidence interval for 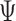is given by (0.9101,1.2120). The 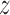-score for testing 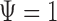is 0.7934, which is not significant. Using Fieller's theorem, a 95% confidence interval is given by (0.9201,1.2243), while the 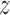-score in (2.7) is 0.8173, which is again not significant. The randomization-based test in Pocock and others (2012) yields a 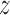-score of 0.8172, but this test does not provide a confidence interval.

The estimate of the proportion in favor of treatment is 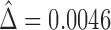, and using (2.5), a 95% CI is given by (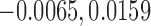), again, not significant.

Note that the standard composite logrank test gave a larger 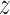score than the tests based on the estimate of the win ratio or proportion in favor of treatment. It turned out that, when analyzed separately, stroke had a 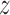-score of 1.81, while the 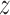-score for the CV death was 1.14. Since a time-to-first-event analysis treated all individual outcomes equally, the least severe outcome played a stronger role than using prioritized outcomes.

The proposed approach can be easily extended to stratified analyses with a fixed number of strata and large sample sizes within each strata; see Appendix B of supplementary material available at Biostatistics online for details and an example.

4. More than two groups

The proposed approach also allows testing the equality of more than two groups, as illustrated for three groups with distributions 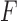, , 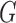and .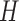

Define

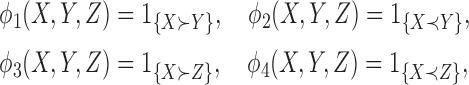and

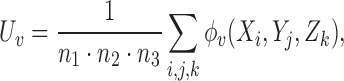(4.1)

where , , and 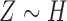are independent, 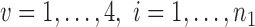, , 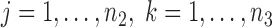and let 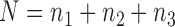. Then one has, asymptotically,

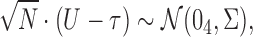(4.2)

where 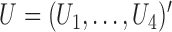, , 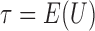and 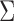has elements as shown in the Appendix. Further details are provided in Appendix C of supplementary material available at Biostatistics online.

Example 4.1 —

As a simple example, the subjects in the PEACE study were divided based on the tertiles of age (, 60–68, ), which resulted in three groups with sizes 2938, 2667, and 2685. Then , and the variance–covariance matrix of is estimated by

The test of 67.1986 with is highly significant (), so, as expected, the time to the composite CVD outcome differed by age tertiles.

5. Discussion

Composite outcomes are commonly used in clinical trials as an attempt to quantify the treatment effect on the burden of disease with respect to several individual outcomes. In addition, they usually provide more statistical power to detect the difference in treatment effects than analyzing the outcomes separately. The standard statistical approach uses the time to the first observed individual component, and therefore considers all outcomes as equal, which is rarely the case. Alternative approaches that take into account the clinical priority of each possible outcome are of interest. They include defining the composite outcome based on prioritized components (Buyse, 2010; Pocock and others, 2012), and using a weighted analysis with weights a priori defined in terms of the relative importance of the standard outcomes (Bakal and others, 2012).

Recently, we describe a simple one-directional test of the equality of groups for multiple outcomes based on a simple 1 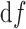(univariate) linear combination of the treatment group coefficient estimates for each outcome in a Cox PH model (Lachin and Bebu, 2015). We show that this analysis can have greater power than the composite approach when the treatment tends to provide a beneficial effect on all outcomes. While this test may be more powerful, the results may not be as clinically meaningful as those of the approaches described herein.

A general criticism of the composite outcome analysis is the lack of transparency in the assessment of the treatment effect on the individual components (Freemantle and others, 2003). More specific criticisms are about how to define the weights in weighted analyses, and the dependence on censoring when defining composite outcomes based on prioritized components (Rauch and others, 2014). As shown herein, although valid statistical tests can be obtained under the null hypothesis of no difference between groups, both the win ratio and proportion in favor of treatment parameters depend on the censoring distributions under the alternative hypothesis. Clearly, a general solution is not possible, and careful consideration of these issues is needed when defining the primary outcome of a trial. Acknowledging these limitations, the goal of this paper was not to recommend the use of one approach over another. We rather remark that these new methods for composite outcomes have already been employed in several studies (Bakal and others, 2015; Pocock and others, 2012; Kwawaja and others, 2014; Kirtane and Leon, 2012), and the interest in these new approaches is further illustrated by a number of recent editorials (Ciolino and Carter, 2015; Claggett and others, 2013; Freemantle and others, 2003). Therefore, sound statistical methods are needed to guide their use.

This paper describes statistical inference for two parameters of interest in the context of composite outcomes based on prioritized components. The large sample distribution of a multivariate multi-sample 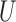-statistic (Lehmann, 1963) was employed to provide a unifying approach for constructing tests and confidence intervals for both the proportion in favor of treatment and the win ratio. Moreover, this approach can be easily extended in a number of ways, including inference for stratified studies and the comparison of more than two groups, and can also be applied to mixtures of outcomes measured on different scales.

Supplementary material

Supplementary material is available online at http://biostatistics.oxfordjournals.org.

Funding

This work was supported with funding from NIDDK, NIH for the Glycemia Reduction Approaches in Diabetes: A Comparative Effectiveness (GRADE) Study through grant U01-DK-098246, John M. Lachin and David M. Nathan (Massachusetts General Hospital) co-Principal Investigators; and for the study of the Epidemiology of Diabetes Interventions and Complications (EDIC) through grant U01-DK-094176, John M. Lachin, PI.