The perceptual processing capacity of summary statistics between and within feature dimensions

Abstract

The simultaneous–sequential method was used to test the processing capacity of statistical summary representations both within and between feature dimensions. Sixteen gratings varied with respect to their size and orientation. In Experiment 1, the gratings were equally divided into four separate smaller sets, one of which with a mean size that was larger or smaller than the other three sets, and one of which with a mean orientation that was tilted more leftward or rightward. The task was to report the mean size and orientation of the oddball sets. This therefore required four summary representations for size and another four for orientation. The sets were presented at the same time in the simultaneous condition or across two temporal frames in the sequential condition. Experiment 1 showed evidence of a sequential advantage, suggesting that the system may be limited with respect to establishing multiple within-feature summaries. Experiment 2 eliminates the possibility that some aspect of the task, other than averaging, was contributing to this observed limitation. In Experiment 3, the same 16 gratings appeared as one large superset, and therefore the task only required one summary representation for size and another one for orientation. Equal simultaneous–sequential performance indicated that between-feature summaries are capacity free. These findings challenge the view that within-feature summaries drive a global sense of visual continuity across areas of the peripheral visual field, and suggest a shift in focus to seeking an understanding of how between-feature summaries in one area of the environment control behavior.

Introduction

Our experiences and memories are established in part through the interactions of our visual system with the visual information present in the external world. Supporting the extraction of relevant information in the world are specialized mechanisms, called statistical summary representations, which represent the statistical properties of groups of similar items (Ariely, 2001; Balas, Nakano, & Rosenholtz, 2010; Chong & Treisman, 2003, 2005a, 2005b; Im & Chong, 2009; Peterson & Beach, 1967; Pollard, 1984; Rosenholtz, 2011). A highway of cars during rush hour, for instance, may be represented in terms of their mean direction and mean speed at the expense of individual representations of each car alone (Corbett & Oriet, 2011; Haberman & Whitney, 2007; Parkes, Lund, Angelucci, Solomon, & Morgan, 2001). Such representations may inform routine decisions such as which lane to use, which lanes to avoid, and what speed to travel.

Visual perception, in general, may critically depend on the integration of coarse summary representations that are established across the peripheral visual field, as well as on more detailed representations of information sampled at the fovea (Chong & Treisman, 2003; Haberman & Whitney, 2009). These broad classes of representations provide a complementary analysis of the external environment; while foveal representations sacrifice generality for more specific analysis, summary representations sacrifice specifics for generality (e.g., Corbett & Oriet, 2011). Because summary statistics allow the system to remain sensitive to behaviorally relevant events that appear outside areas of focus, it is hypothesized that the function of these statistical representations is to reduce the complexity of information in the environment in a way that optimizes processing for our limited perceptual and cognitive systems (e.g., Alvarez, 2011; Alvarez & Oliva, 2009). Under this view, the subjective impression that we see more than is truly possible (“Grand Illusion”; e.g., Noë, 2002; Noë, Pessoa, & Thompson, 2000) is produced by no more than coarse summaries inducing the perception of visual continuity.

Consistent with the view that summary representations reflect a fundamental aspect of visual perception are reports that summaries underlie a wide range of low- and high-level tasks and phenomena from crowding to visual search to scene perception. Also consistent are reports of superior averaging performance over an impressive range of simple visual features and complex object properties (Ackermann & Landy, 2014; Ariely, 2001; Balas, Nakano, & Rosenholtz, 2010; Brady & Alvarez, 2011; Cavanagh, 2001; Chong, Joo, Emmanouil, & Treisman, 2008; Corbett & Melcher, 2013; Gillen & Heath, 2014; Rosenholtz, 2011; Whitney, 2009; Whitney, Haberman, & Sweeny, 2014). The breadth of tasks benefitted by statistical extraction, and the expansive range of properties over which summaries are formed, suggest that the inclusion of statistical summaries are necessary for theories of early visual processing as well as for understanding how we develop unified, coherent visual percepts.

Between-feature summary representations

Summary statistics are proposed to “… precede the limited capacity bottleneck …” (Chong & Treisman, 2005b, p. 899; see also Alvarez, 2011; Alvarez & Oliva, 2008; Ariely, 2001; Brady & Alvarez, 2011; Chong & Treisman, 2003, 2005b; Dakin & Watt, 1997; Demeyere, Rzeskiewicz, Humphreys, & Humphreys, 2008; Oriet & Brand, 2013; Robitaille & Harris, 2011; Rosenholtz, 2011). This view predicts that summary representations are established through unlimited-capacity processes, which is to say that they unfold independently (i.e., without interference) of the number of items to be processed.

Because collections of objects in the environment are most often comprised of combinations of multiple different feature properties, the view that summary representations play a critical role in abstracting the vast amount of information in the visual world depends partially on demonstrating that summaries can be established independently between different feature dimensions. Stated another way, accurate scene perception would suffer if behavior could only be guided by a single feature representation at any given time. Rather, it is necessary that the system establish all or most feature representations that define a particular collection of items.

Emmanouil and Treisman (2008) used a pre–post cueing paradigm to determine whether statistical averages could be generated for multiple dimensions without interference. Observers saw two sets of circles, separated on the left and right sides of the display. The circles varied in both the size and speed at which they moved. On each trial, observers were cued to perform one of two tasks: report which set (left or right) had the larger mean size or the larger mean speed. When the cued dimension was precued, occurring prior to stimulus onset, observers could average over the relevant feature while the displays were present and ignore the noncued feature. Performance was based on the statistical extraction of only one feature in this case. In contrast, when the cued dimension was postcued, occurring after stimulus offset, observers had to average over both feature dimensions in order to successfully perform the task because they could not know which of the two they would have to report. According to the logic of this method, if statistical extraction for both dimensions unfolds in parallel without interference, then performance should be equal between the pre- and postcue conditions. It should be possible to average two features just as well as one. Alternatively, if averaging one dimension interferes with averaging the other, then performance should be better in the pre-cue than the postcue condition. The results were consistent with this latter alternative; performance was better when the to-be-reported dimension was precued than when it was postcued.

Although Emmanouil and Treisman (2008) claim that establishing summary representations of multiple different features incurs a performance cost, it is possible that this cost derived from having to establish multiple summaries within a given dimension. This is because in the post-cued conditions, observers had to summarize size for both sets and speed for both sets. Two within-dimension summaries were therefore required for the size task and another two for speed. It is unclear, therefore, whether the precue advantage reflects limited within-dimension averaging, limited between-dimension averaging, or both. Indeed, using the pre–post cue method, Poltoratski and Xu (2013) found a performance decrement in the postcue condition for two within-feature summaries, indicating that selection of the relevant set beforehand could improve performance (see also Brand, Oriet, & Tottenham, 2012). Results from our lab using a different method were also consistent with the view that forming multiple within-dimension summaries causes interference. Specifically, we used an extended version of the simultaneous–sequential method (Scharff, Palmer, & Moore, 2011; Shiffrin & Gardner, 1972) to test the perceptual processing capacity of mean size and mean orientation summaries. Those studies revealed that no more than a single summary could be established independently within either dimension (Attarha & Moore, 2015; Attarha, Moore, & Vecera, 2014). We use that method in the current study, and therefore turn now to a description of it.

The extended simultaneous–sequential method

The simultaneous–sequential method was developed to test the capacity limitations of perceptual processing (Eriksen & Spencer, 1969; Shiffrin & Gardner, 1972). On each trial a target among three distractors is presented (see Figure 1). In the simultaneous condition, all stimuli onset concurrently in a single frame and must be processed at the same time to perform the task. In contrast, in the sequential condition, half of the same display is presented across two temporally separated frames, and therefore fewer stimuli require processing at any given time. Importantly every display is presented for the same amount of time in the simultaneous and sequential conditions. The quick exposure duration of the critical displays and their subsequent masks serve to minimize eye movements. A direct comparison of accuracy performance between the simultaneous and sequential conditions, therefore, can then be made because the amount of time available for processing each item is constant between conditions and because the overall viewing time is low enough to limit performance.

Figure 1.

Trial events for the (A) simultaneous, (B) sequential, and (C) repeated conditions in Experiment 1. Observers saw four sets of gratings in which the items of each set varied in their orientation and size. In the case of orientation, the mean of the target set was tilted either left or right relative to the other three roughly vertical distractor sets. In the case of size, the mean of the target set was either smaller or larger than the other three similarly sized distractor sets. Observers were asked to establish a representation of the mean orientation and mean size for each set. Observers reported the tilt direction (left or right) and size (large or small) of the oddball sets. The correct response is “left and small” in this example.

The simultaneous–sequential method tests the independence/dependence of processing multiple relevant stimuli. Unlimited-capacity models (i.e., independence) predict equal accuracy across the simultaneous and sequential conditions. This follows because if processing unfolds completely independently across multiple stimuli, then it should make no difference how many stimuli require processing. The quality or speed of processing will be constant. In contrast, limited-capacity models predict an advantage in accuracy for sequential over simultaneous presentation because the sequential condition allows fewer stimuli to engage the process at any one time. Processing is compromised by having to process additional items at the same time.

An extended version of the simultaneous–sequential method, developed by Scharff et al. (2011), includes a repeated condition that presents the entire array of items twice across two temporal frames. Assuming there is room for improvement over what can be processed during the single simultaneous display, performance should be better in the repeated condition when each item is available for twice the duration. The addition of the repeated condition provides two advantages over the original simultaneous–sequential design. First, in the event that processing is unlimited capacity, this condition allows us to confirm that an effect could be obtained if it were there (i.e., there was room for improvement). The negative finding between the simultaneous and sequential conditions, in the context of better performance in the repeated condition, raises confidence that observers could have taken advantage of the sequential condition if processing was limited. Second, in the event that processing is limited capacity, performance in the repeated condition allows us to test among a specific type of limited-capacity model, called the fixed-capacity model. This model assumes that only a fixed amount of visual information can be processed at any given moment (e.g., Shaw, 1980). A fixed-capacity model predicts that performance in the sequential condition will be better than the simultaneous condition and equal to performance in the repeated condition. Scharff et al. (2011) has formulized these predictions.

Scharff et al. (2011) derived the unlimited- and fixed-capacity predictions using models based on signal detection theory (Green & Swets, 1966) and then compared the output of these models to behavioral data on various tasks. The models use the principles of statistical sampling to assume that the accuracy of an internal representation rests upon the number of perceptual samples collected from the corresponding external stimulus, with greater samples improving the precision of the representation and with the total number of samples limited by the amount of time the display remains available for viewing.

The assumptions of the unlimited-capacity model state that a random variable is assigned to every stimulus to reflect the degree to which the stimulus represents a target or distractor item. These values are obtained from their respective target or distractor distributions, the centers of which are separated by the degree of discriminability (i.e., difficulty) between targets and distractors. Each value is determined independently of one another. Critically, the values of the random variables are assigned to the stimuli at the same time without a time delay (i.e., in parallel) and independently of the number of items presented (i.e., there exists no effect of divided attention; processing is unlimited capacity). The item whose value most closely resembles that of the target by exceeding the value of the distractors is chosen by the perceptual observer.

As discussed previously, the unlimited-capacity model predicts equal performance between the simultaneous and sequential conditions. The quality of representation for each stimulus is assumed equal between the simultaneous and sequential conditions because the perceptual samples that are collected from each stimulus unfold independently, and therefore insofar as the items are displayed for the same duration (which they are), the number of average number of samples obtained will be the same. Therefore, the predicted percent correct, or the probability that the chosen stimulus is in fact the target, is modeled using the same function. The output of this function is then identical, producing an equality prediction between the simultaneous and sequential conditions for the unlimited-capacity model.

The fixed-capacity model is based on the same assumptions that underlie the unlimited model with an exception. The number of samples that can be collected for each stimulus is inversely related to the number of items that are concurrently displayed—the greater the number, the fewer the samples. With fewer samples, the variance of the random variables increase, effectively producing a positive correlation between variance and display size. When the simultaneous and sequential conditions are modeled by a probability function that includes the difference in variance between conditions, predicted percent correct improves in the sequential condition relative to simultaneous. This follows because variance doubles in the simultaneous condition when all items are presented at once compared to the sequential condition where only half the number of items are presented at a time. In addition to predicting a sequential over simultaneous advantage, the fixed-capacity model also predicts equal performance between the sequential and repeated conditions. This equality emerges because the variance of the random variables in repeated and sequential conditions is halved relative to simultaneous. That is, in the repeated display, when twice the number of samples can be collected for each stimulus across the double displays, variance is reduced by half that of the simultaneous condition, just as it is in the sequential condition.

In the current study, we used the extended version of the simultaneous–sequential method developed by Scharff et al. (2011) to reexamine the question of whether multiple between-feature summary representations unfold independently.

Motivation of the current study

Summary statistic representations may be hierarchically established within separate pathways of the visual system (Haberman & Whitney, 2009, 2012; Whitney et al., 2014). To paraphrase Whitney et al. (2014), summaries of basic visual features—such as brightness (Bauer, 2009) and orientation (Dakin, 2001)—may be generated by mechanisms in early visual stages that pool the output from various feature-selective cells (Suzuki, 2005; Whitney et al., 2014). On the other hand, more complex summaries that require the integration of multiple component feature populations—such as size (Ariely, 2001) and motion (Watamaniuk, Sekular, & Williams, 1989)—may be generated further along the ventral or dorsal pathways, or even after the convergence of these streams as the case may be for summaries based on biological motion (Sweeny, Haroz, & Whitney, 2013). Brady and Alvarez (2011) provide additional support for the hierarchical model by showing that the representation of individual items from a collection of items that vary in color and size is biased toward the average of those features. These results suggest that representations are formed at different levels of visual processing, ranging from the individual to the collective and across the features to which the items engage.

Based on the hierarchical model of summary formation, any interference for establishing multiple between-feature summaries should be reduced to the extent that those summaries are generated in nonoverlapping visual stages (see also Cohen, Konkle, Rhee, Nakayama, & Alvarez, 2014). We used the extended version of the simultaneous–sequential method to test this prediction for mean orientation and mean size in Experiment 3, after demonstrating significant costs in establishing multiple within-feature summaries in Experiment 1. To preview the results, we found that within-feature summaries depend on limited-capacity processes and that between-feature summaries depend entirely on unlimited-capacity processes. These results are inconsistent with the conclusion that the visual system cannot generate summary representations for multiple different features without cost (Emmanouil & Treisman, 2008).

Experiment 1

Method

Observers

A power analysis based on a pilot run of the experiment with two subjects indicated that at least four observers were needed to achieve at least 80% power (N*; Cohen, 1988). We increased this number to six in order to be consistent with the number of observers needed to satisfy the full sequence of counterbalanced conditions in subsequent experiments. All volunteers were from University of Iowa's psychology department (four male, two female, age range: 18–31 years, none left-handed). The experiment was conducted in accordance with the University of Iowa Internal Review Board (IRB) approved policies and procedures.

Equipment

Stimuli were displayed on a cathode ray tube monitor (19-in. ViewSonic G90fB) controlled by a Macintosh Pro (Mac OS X) with a 512MB NVIDIA GeForce 8800 GT graphics card (1024 × 768 pixels, viewing distance of 61.5 cm, refresh rate of 100 Hz). Stimuli were generated using the Psychophysics Toolbox Version 3.0.11 (Brainard, 1997; Pelli, 1997) for MATLAB (Version 8.2, Mathworks, Natick, MA). Observers sat in a height-adjustable chair and used an adjustable chin rest to maintain a constant viewing distance from the monitor. The room was brightly lit to enhance visibility of the response keys.

Stimuli

Sixteen sinusoidal gratings that varied in both orientation and size were equally divided into four sets and presented on a neutral gray background (37.14 cd/m²; Figure 1). The gratings had a spatial frequency of four cycles and were presented at the maximum contrast that could be produced by the monitor (50.06 cd/m²). On every trial, the orientations and diameters of items within each set were determined using independent sampling procedures. The orientations of the gratings within three randomly selected sets were randomly chosen from a Gaussian distractor distribution (μ = 0°; σ = 8°), while the orientations of items within the remaining target set were randomly chosen equally from either a Gaussian tilted-left distribution (μ = −15°; σ = 8°) or a Gaussian tilted-right distribution (μ = 15°; σ = 8°). Vertical was 0°. In addition, the diameters of gratings within three randomly selected sets were randomly chosen from a Gaussian distractor distribution (μ = 1.86°; σ = 0.28°), while the diameters of gratings within the remaining target set were equally chosen from either a Gaussian small-target distribution (μ = 1.40°; σ = 0.28°) or a Gaussian large-target distribution (μ = 2.33°; σ = 0.28°).

Each of the four sets were centered on a corner of an imaginary square approximately 5.59° from fixation. The center of the grating closest to fixation was 3.26° away, while the center of the grating furthest from fixation was 7.91° away. A distance of 7.91° separated the sets horizontally and vertically, center to center.

Procedure

Observers completed one 45-min session. The session began with three practice blocks of 10 randomly selected trials, each of which presented the critical displays at increasingly shorter exposure durations: 1000, 300, and 100 ms, respectively. The practice block was followed by six experimental blocks of 48 trials each (96 observations per display type, 288 experimental observations per subject). Practice trials were excluded from all analyses.

All trials began with a black, centrally located fixation dot for 500 ms (3 cd/m²; 2-pixel diameter). Observers were instructed to maintain central fixation throughout the experiment. In the simultaneous condition, the fixation display was followed by the four sets of gratings (Figure 1). Each grating was subsequently masked by a square-shaped grating patch that was oriented horizontally for 100 ms (3.07° × 3.07°). A blank screen with a question mark (?) at fixation followed the mask display and remained on the screen until a response was made (Figure 1A). In the sequential condition, fixation was followed by two sets of gratings presented along either the positive or negative diagonal, masks for 100 ms, a blank interstimulus interval (ISI) of 1200 ms, the other two sets of gratings presented along the opposite diagonal, masks again for 100 ms, and a blank screen with a question mark until response (Figure 1B). The repeated condition was the same as the sequential condition except that all four sets appeared in both of the two displays (Figure 1C). Written feedback (correct/incorrect) was given at fixation following each response for 500 ms. Feedback may alter averaging performance, perhaps by reducing training time within the first several dozen trials of an experiment (e.g., Fan, Turk-Browne, & Taylor, 2013; see also Bauer, 2009). The next trial automatically began 1000 ms after the feedback display.

The initial exposure duration of the critical displays for the first block of the main experiment was set to the duration of the practice block that yielded above-chance performance. The average initial duration across observers was 200 ms (see Attarha & Moore, 2015; see also Whiting & Oriet, 2011). In addition, a coarse tracking procedure altered the exposure duration throughout the main experiment, block-by-block, on the basis of performance in the simultaneous condition only. If performance in the simultaneous condition was within 10% of perfect performance on a given block, then the exposure duration for the simultaneous, sequential, and repeated conditions was decreased by 10 ms on the next block. Moreover, if performance was only 10% above chance (or lower) in the simultaneous condition, then the exposure duration in all three conditions increased by 10 ms. Chance performance was 25% in this four alternative forced-choice task (4AFC). The average adjusted exposure duration across all subjects was 240 ms.

Design

The full factorial combination of display type (simultaneous, sequential, repeated), orientation target type (left, right), and size target type (large, small) were randomly mixed within blocks of trials and appeared equally often. The target positions for the orientation and size target sets were sampled randomly from the following four possible positions: upper left, upper right, lower left, or lower right. Which of the two diagonally opposite positions were presented first in the sequential display was constant for a given observer but varied across observers. Odd-numbered subjects saw sets of gratings that first appeared along the negative diagonal and then along the positive diagonal. Even-numbered subjects saw sets of gratings that appeared positive to negative. We kept the presentation of diagonal orders constant within an observer to eliminate uncertainty of the presentation positions.

Task

Observers performed a dual task in which they reported the tilt direction (leftward or rightward) and size (larger or smaller) of the oddball sets. Observers pressed the 1, 4, 3, and 6 keys on the number pad of a standard keyboard using their index and middle fingers depending on whether the targets were “left and small,” “left and large,” “right and small,” or “right and large,” respectively. Observers were instructed to respond as accurately as possible. Speed was not emphasized.

General method of analysis

We filtered the small percentage of trials in which the stimulus response led to an incorrect feedback message. In Experiments 1 and 2, this meant that either the mean orientation of a distractor set was, by chance, tilted either more leftward (or rightward) than the mean orientation of the target set, or that the mean size of a distractor set was smaller or larger than the target set. The set that appeared to be the target was in fact a distractor on these trials. A total of 10 and 18 out of 1,728 experimental trials across all six observers were filtered in Experiments 1 and 2, respectively. In Experiments 3A–C, we filtered trials in which (3A) the mean orientation of the entire set of 16 items was not tilted in the intended direction relative to vertical; (3B) the mean diameter of the entire set was not smaller or larger than the mean of the distractor distribution; or (3C) either the mean orientation or mean size were the incorrect tilt or size. A total of 44, 51, and 91 out of 1,728 experimental trials across all six observers in Experiments 3A–C were filtered, respectively. The elimination of these trials did not change the pattern of results.

After filtering, the accuracy data were transformed to arcsin values to normalize their distributions and the underlying assumptions of the repeated-measures ANOVA were confirmed. Assumptions of normality and sphericity were confirmed using the Shapiro-Wilk test (Shapiro & Wilk, 1965) and Mauchly's test (Mauchly, 1940), respectively. When violations of sphericity were found, p values were adjusted based on the Greenhouse-Geisser epsilon correction on degrees of freedom (Jennings & Wood, 1976). Two follow-up paired t tests, one between the simultaneous and sequential conditions, and another between the sequential and repeated conditions, were used after significance of the final model was verified. An alpha level of 0.05 was used to determine significance for all statistical tests.

Results and discussion

Figure 2 shows mean percent correct as a function of display, collapsed across all observers. Error bars are within-subject standard errors (Cousineau, 2005; Morey, 2008). Dashed lines in Figure 2 define both the unlimited- and fixed-capacity predictions. According to the logic of the simultaneous–sequential method, if performance in the sequential condition falls on the line determined by the simultaneous condition, then the unlimited-capacity model is supported. In contrast, if performance in the sequential condition falls on the line determined by the repeated condition, then the fixed-capacity model is supported. More formal accounts of specific versions of these models are offered in a previous paper (Scharff et al., 2011, appendix).

Figure 2.

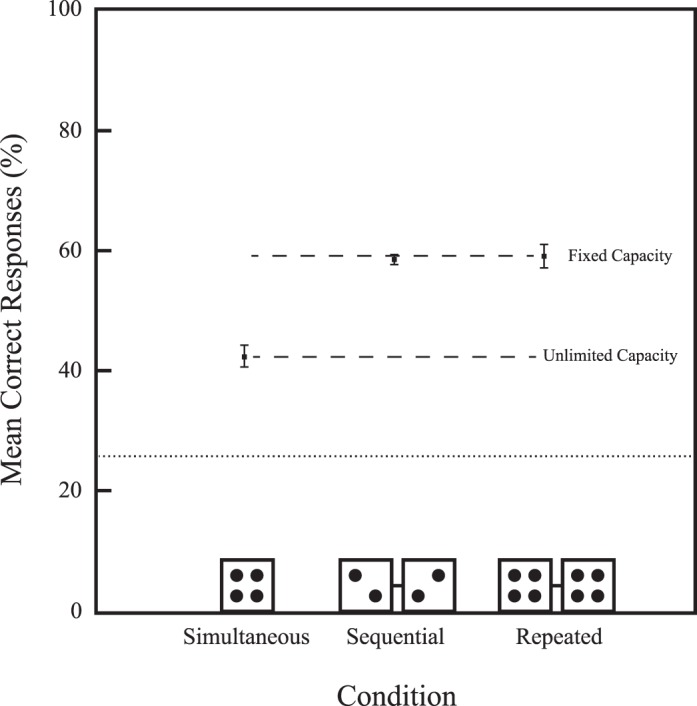
Mean correct responses (%) as a function of display collapsed across observers in Experiment 1. Consistent with the fixed-capacity model, performance in the sequential condition was better than performance in the simultaneous condition and equal to performance in the repeated condition. These results suggest that generating summaries for two features is mediated by a fixed-rate bottleneck if those summaries appear in different sets. Error bars are within-subject standard errors (Cousineau, 2005; Morey, 2008). The dotted line indicates chance performance.

In Experiment 1, we found that performance in the sequential condition was statistically equal to that in the repeated condition and that performance was reliably worse in the simultaneous condition. This pattern of results is inconsistent with an unlimited-capacity model and consistent with a fixed-capacity model. Arcsin transformed values of mean percent correct were submitted to a one-way repeated-measures ANOVA with display type as the within-subjects factor. The final model was significant, F(2, 10) = 32.05, p < 0.001, pη² = 0.865, MSE = 0.002 (all Shapiro-Wilk p > 0.089; Mauchly's p = 0.234). As predicted by fixed-capacity processing, performance in the sequential condition (58% ± 0.83%) was significantly greater than performance in the simultaneous condition (42% ± 1.74%), t(5) = 9.85, p < 0.001. Performance between the repeated (59% ± 2.03%) and sequential conditions were equal, t(5) = 0.37, p = 0.727. We conclude that establishing multiple within-feature summaries undergoes quite a bit of interference and is therefore highly limited in processing capacity (see Scharff et al., 2011).

It is worthwhile to note that the simultaneous and sequential conditions differ in two critical ways. The first is with respect to the number of sets that must undergo statistical extraction at any given time (two or four in this particular experiment). However, a second difference between these conditions is how close in time the target appeared before observers were allowed to enter their response. In the simultaneous condition, the target always appeared in the frame immediately preceding response, while in the sequential condition, the target could appear in either the first or second frame. A memory disadvantage for first-frame targets in the sequential condition may have biased performance. We tested this possibility by comparing accuracy between both frames. Performance was statistically equal regardless of whether targets appeared first (58%) or second (62%), t(5) = 0.70, p = 0.516 (Shapiro-Wilk p = 0.489). These data suggest that targets presented further in time from response did not suffer from greater memory loss.

Potential limitation

Averaging performance decreases when set size is small and when the variance between items is large (Marchant, Simons, & de Fockert, 2013; Robitaille & Harris, 2011). For example, Dakin (2001) showed that averaging thresholds increase when the standard deviation of the distribution was greater than 8, especially when the number of items per set was low. There may therefore be concern that Experiment 1 supports a fixed-capacity model only because means had to be extracted from only four heterogeneous items. Under this view, evidence of unlimited capacity may have been obtained had each set been composed by a larger number of items. In previous work we responded to this concern by increasing the number of items per set from four to nine. Like the four-item experiment, the nine-item experiment yielded evidence of limited-capacity processing (Attarha & Moore, 2014, 2015). Assuming that nine items per set is sufficient for statistical extraction, we conclude that using a larger set size or a smaller variance would not have eliminated the observed limitation in Experiment 1.

Experiment 2

In Experiment 1, we concluded that generating multiple summaries within two different feature dimensions, in that case mean orientation and size, produced significant interference. However, successful completion of the task in Experiment 1 required more than just statistical averaging. The involvement of other mechanisms with limited capacity, such as a limited-capacity comparison process, might have contributed to the observed advantage in the sequential condition. That is, the comparison of multiple summaries may undergo less interference in the sequential condition, when the representations from only two sets require comparison at any given time, than in the simultaneous condition, when all four sets require comparison at once. Under this view, statistical extraction itself could be unlimited but appear limited experimentally due to the need to compare sets. We tested this possibility in Experiment 2. Observers were required to perform the task from Experiment 1 but now without averaging. Specifically, all gratings within a given set were identical and reflected the mean orientation and mean size of their respective set. Observers could exploit this redundancy and compare individual gratings within each set in order to circumvent the averaging process. If the limited-capacity results from Experiment 1 are due to averaging and nothing else, then eliminating the need to generate averages should support an unlimited-capacity model. This follows because all aspects of the task, including the number of comparisons between sets, remain the same.

Method

All aspects of the method were identical to Experiment 1, with the exceptions noted below.

Observers

Six new undergraduate volunteers from the University of Iowa participated in exchange for course credit (three male, three female, age range: 18–23 years, one left-handed).

Stimuli

After the orientations and sizes of the gratings within each of the four sets were randomly chosen from their appropriate target or distractor distributions, the means of both features were calculated and every item within a given set was adjusted to the mean of their respective set prior to presentation (Figure 3). The gratings within each set were therefore the exact same orientation and size.

Figure 3.

Trial events for the (A) simultaneous, (B) sequential, and (C) repeated conditions in Experiment 2. The orientations and sizes of items within each set were adjusted according to the mean of their respective set and were therefore identical. Since the mean of the sets was provided directly, summary statistics are no longer necessary to perform the task. The task was otherwise the same to that of Experiment 1. The correct response is “right and small” in this example.

Procedure

As before, the exposure duration of the critical displays on block one of the main experiment was based on the duration of the practice block that yielded above-chance performance. The average initial duration for all subjects was 300 ms. The average adjusted exposure duration after tracking was 310 ms.

Results and discussion

Figure 4 shows the mean percent correct as a function of display collapsed across all observers. In contrast to Experiment 1, the pattern of results in Experiment 2 is consistent with an unlimited-capacity model and inconsistent with a fixed-capacity model.

Figure 4.

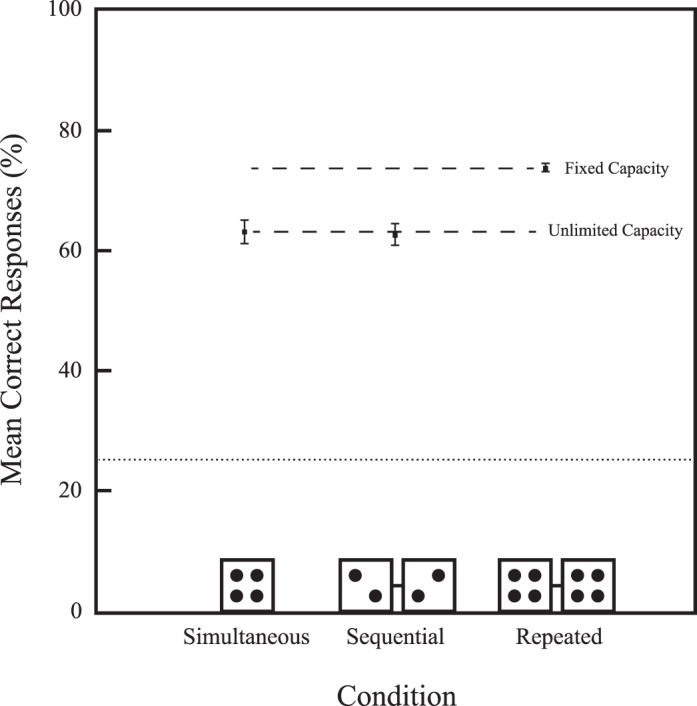
Mean correct responses (%) as a function of display collapsed across observers in Experiment 2. Consistent with the unlimited-capacity model, performance in the sequential condition was equal to the simultaneous condition and reliably worse than performance in the repeated condition. Error bars are within-subject standard errors (Cousineau, 2005; Morey, 2008). The dotted line indicates chance performance.

Arcsin transformed values were submitted to a one-way repeated-measures ANOVA with display as the within-subjects factor. The final model was significant, F(2, 10) = 17.19, p = 0.001, pη² = 0.776, MSE = 0.002 (all Shapiro-Wilk p > 0.294; Mauchly's p = 0.134). As predicted by unlimited-capacity processing, accuracy was not reliably greater in the sequential condition (62% ± 1.88%) than in the simultaneous condition (63% ± 1.88%), t(5) = 0.19, p = 0.861. However, performance in the repeated condition (74% ± 0.77%) was significantly higher than performance in the sequential condition, t(5) = 6.54, p = 0.001.

We again compared performance within sequential trials for when the target was presented in the first frame versus the second frame. Performance across both frames were statistically equal, 67% (first frame) versus 66% (second frame); t(5) = 0.28, p = 0.794 (Shapiro-Wilk p = 0.153). Targets presented closer in time to response were not remembered better.

The critical difference between Experiments 1 and 2 is whether the task can be performed with or without the generation of summary representations. We found evidence of fixed-capacity processing when summaries were required (Experiment 1) and evidence of unlimited-capacity processing when summaries were not required (Experiment 2). These results increase confidence in the conclusion that limited averaging processes produced the observed capacity limitation in Experiment 1.

In addition to ruling out the possibility that the pattern of results in the first experiment was caused by a limited comparison process, Experiment 2 also addresses the issue that differences in mean variability between the experiments limited performance. It may be argued that the mean difference between the target and distractor sets may have been too small a discrimination. Notice, though, that the mean values for the target and distractor sets were identical across Experiments 1 and 2 and yet we obtained evidence of fixed-capacity processing in one case and unlimited-capacity processing in the other. We conclude that the source of the limitation in Experiment 1 was due to generating multiple mean representations across multiple sets.

Experiments 3A–C

In previous studies, we have shown that capacity limitations differ with respect to whether summaries are generated over multiple sets of items, or over many items within a single set. It appears that multiset summaries, which require multiple within-feature representations, undergo mutual interference whereas single-set summaries, no matter how large the set, unfold independently (Attarha & Moore, 2015; Attarha et al., 2014; see also Poltoratski & Xu, 2013). These studies tested mean orientation and mean size summary statistics alone. In Experiments 3A–C, we tested whether the system can independently generate summaries between dimensions over items of a single set.

We used identical stimuli for Experiments 3A, B, and C, but we altered the task instructions for each experiment (see Figure 5). There were three tasks. In the report orientation task, observers reported whether the mean orientation of the entire set was tilted left or right relative to vertical. In the report size task, observers reported whether the mean size of the entire set was larger or smaller than the size of a probe circle. The size of the probe was set to the mean diameter of the distractor distribution. (The probe was presented only during practice trials and did not appear during the main experiment.) Finally, in the report orientation and size task, observers reported both the tilt direction and size of the whole set.

Figure 5.

Trial events for the (A) simultaneous, (B) sequential, and (C) repeated conditions in Experiment 3. The items from Experiment 1 were respaced to produce a single set of 16 items. Observers participated in three experimental sessions using these displays, each of which had a different task. In the report orientation task, observers were told to ignore size and report whether the mean orientation of the entire set is tilted left or right relative to vertical. The correct answer is “right” in this example. In the report size task, observers ignored orientation and reported whether the mean size of the entire set was larger or smaller than the size of a probe circle (not shown) that was set to the mean diameter of the distractor distribution. The probe circle was only presented on practice trials. In the report orientation and size task, observers reported both features. The correct answer is “right and large.”

If simultaneously forming a single summary of both orientation and size is a limiting factor of statistical extraction, then a limited-capacity model should be supported. Support of this model would be consistent with the results of Emmanouil and Treisman (2008). However, unlike the task in Emmanouil and Treisman, the current task only requires a representation of one summary per dimension and therefore cannot be limited by having to establish multiple summaries within both dimensions. With this change, it is possible that we will find evidence of concurrent summary processing between dimensions. An unlimited-capacity model should be supported in this case.

Method

All aspects of the method were identical to Experiment 1, with the exceptions noted below.

Observers

Six new volunteers from University of Iowa's psychology department participated in three sessions performed on separate days (three male, three female, age range: 21–32 years, none left-handed).

Stimuli

The items from Experiment 1 were placed on an evenly spaced grid centered at fixation (Figure 5). The gratings and masks were separated horizontally and vertically by 3.26° center to center. The size of the whole display was approximately 12° × 12°.

Procedure

The same observers participated in three experimental sessions, one for each of the following task types: report orientation, report size, and report orientation and size. As before, each session began with three practice blocks of 10 trials each. A slight modification was made to all practice trials in which an estimation of mean size was required. After each of these trials, a black probe disc, adjusted to the mean diameter of the distractor distribution, appeared on the response screen at central fixation (3 cd/m²; 1.86°). The probe disc was omitted from the main study to keep the trial events consistent across experiments. Each session lasted approximately 45 min and was performed on separate days in complete counterbalanced order.

The average initial exposure durations for the report orientation and report size experimental sessions were both 100 ms, while the initial duration for the report orientation and size task was 200 ms. The average adjusted exposure durations for these sessions was 60, 90, and 230 ms, respectively.

Task

In the report orientation session, observers determined whether the mean orientation over the entire set of 16 items was tilted left (pressing 1) or right (pressing 6) from vertical (two alternative forced-choice task [2AFC]). In the report size session, observers reported whether the mean diameter of the set was larger (pressing 4 ) or smaller (pressing 3) than the size of the probe circle that was presented on the practice trials (2AFC). In the report orientation and size session, observers reported both orientation and size using the same response-key mapping described in the task section of Experiment 1 (4AFC).

Results and discussion

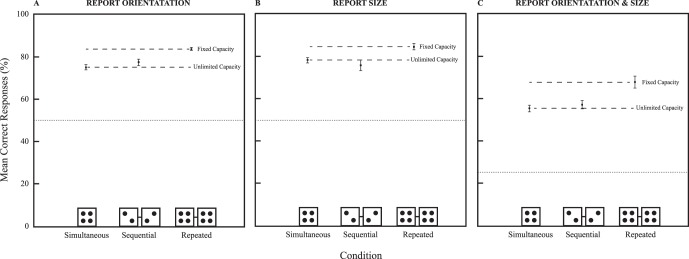
Figure 6 shows the mean percent correct as a function of condition collapsed across observers. Across all three experimental sessions—report orientation (Figure 6A), report size (Figure 6B), and report both (Figure 6C)—the data were consistent with an unlimited-capacity model and inconsistent with a limited-capacity model.

Figure 6.

Mean correct responses (%) as a function of display collapsed across observers in Experiments 3A–C. Across all three task types—report orientation, report size, report both orientation and size—performance was equal across the simultaneous and sequential conditions and there was a reliable advantage in the repeated condition. These results are consistent with the unlimited-capacity model. Error bars are within-subject standard errors (Cousineau, 2005; Morey, 2008). Dotted lines indicate chance performance. The orientation and size tasks were 2AFC for 50% chance and the dual task.

Arcsin transformed values were submitted to a one-way repeated-measures ANOVA with condition as the within-subjects factor. The final model was significant for all three task types; orientation: F(2, 10) = 12.34, p = 0.002, pη² = 0.712, MSE = 0.002, all Shapiro-Wilk p > 0.053, Mauchly's p = 0.201; size: F(2, 10) = 6.38, p = 0.016, pη² = 0.561, MSE = 0.003, all Shapiro-Wilk p > 0.073, Mauchly's p = 0.188; both: F(2, 10) = 9.34, p = 0.005, pη² = 0.651, MSE = 0.003, all Shapiro-Wilk p > 0.220, Mauchly's p = 0.199. As predicted by unlimited-capacity processing, accuracy was not reliably greater in the sequential condition (orientation: 77% ± 1.50%; size: 75% ± 2.51%; both: 57% ± 1.95%) than in the simultaneous condition (orientation: 75% ± 1.34%, t[5] = 1.01, p = 0.359; size: 77% ± 1.37%, t[5] = 0.84, p = 0.440; both: 55% ± 1.53%, t[5] = 0.97, p = 0.376). However, performance in the sequential condition was significantly lower than performance in the repeated condition (orientation: 83% ± 0.65%, t[5] = 3.82, p = 0.012; size: 84% ± 1.60%, t(5) = 2.77, p = 0.039; both: 68% ± 2.82%, t(5) = 2.81, p = 0.037). We conclude that the establishment of multiple between-feature summary representations depends entirely on parallel, unlimited-capacity processes.

In order to test whether targets presented in the second frame of the sequential condition had an advantage over targets presented in the first frame, performance across both frames were compared for each of the three sessions. Performance across the sequential frames was statistically equal in both the report orientation task, 71% (first frame) versus 82% (second frame), t(5) = 2.20, p = 0.079 (Shapiro-Wilk p = 0.687; see also Attarha & Moore, 2015), and the report orientation and size task, 56% (first frame) versus 61% (second frame), t(5) = 0.85, p = 0.435 (Shapiro-Wilk p = 0.700). However, targets presented closer in time to response were remembered better than targets that appeared first in the report size task, 70% (first frame) versus 81% (second frame), t(5) = 2.79, p = 0.038 (Shapiro-Wilk p = 0.635). This finding suggests that, in the case of mean size, memory differences may have contributed to lower performance in sequential condition (but see Attarha et al., 2014, who did not observe this difference for mean size using the same task and similar stimuli).

Alternative explanations

In our displays, each set consisted of multiple items. Our goal from the outset was to ensure that observers were establishing a representation of the mean that incorporated all (or most) of these items rather than engaging in an alternative strategy in which they simply based their response on information contained within the most distinct local item. To this end, we used distributions with a large degree of overlap. The target and distractor distributions had a mean separation of 15° and a standard deviation of 8°. As a result, the most distinct item on any given trial may have originated from a distractor set, rather than a target set. Observers would thus obtain an incorrect response if their response were based on the identity of the outlier. This would render a strategy based on individual items, rather than on the set of items, unreliable. Furthermore, the results of Experiment 3 provide evidence against this account of the results. In this third experiment, the same 16 items from Experiment 1 were presented in a single set (instead of in four separate sets). The task was otherwise the same. If the observed limited-capacity results in Experiment 1 were caused by how efficiently observers could process individual items, then that limitation should have persisted in Experiment 3. This follows because the items—specifically the degree of target-distractor heterogeneity and the assumed local target item—are identical across both experiments. Instead, we find evidence consistent with an unlimited-capacity model in this case.

Another alternative to the formation of summary representations, in the context of orientation-averaging task in particular, would be to use the overall difference in the pattern of orientations across sets to direct attention to the most likely target set. Over the course of the experiment, the items belonging to a distractor set will typically consist of items tilted to the left and right of vertical, whereas the items composing the target set will typically slant in the same direction (see Figure 1). Observers may arrive at the correct answer by exploiting these pattern discontinuities. However, it is worthwhile to note that Huang, Pashler, and Junge (2004) have shown that this sort of pattern detection engages only unlimited-capacity processes. Given that we obtained evidence consistent with a fixed-capacity model—the opposite processing extreme reported by Huang et al. (2004)—we conclude that observers did not use this strategy in Experiment 1. In addition, performance levels in the size-only and orientation-only tasks were quite similar, even though such pattern discontinuities do not exist in the size task (Experiments 3A–B). This finding increases confidence in the view that one task type did not benefit from some strategy that was unavailable in the other task.

Considering the issues mentioned above, it seems unlikely that the evidence of limited statistical extraction for multiple within-dimension summaries is attributed to pattern detection or to the limited processing of local items.

General discussion

It has been proposed that in order to provide a sense of visual completeness in the periphery, the visual system is equipped with specialized mechanisms that represent statistical properties of groups of like items (Ariely, 2001; Balas et al., 2010; Chong & Treisman, 2003, 2005a, 2005b; Im & Chong, 2009; Peterson & Beach, 1967; Pollard, 1984; Rosenholtz, 2011). These summary processes are thought to unfold across the visual field very early in the stream of visual processing via parallel, unlimited-capacity processes. Once established, these representations purportedly serve as a foundation for the operation of more complex processes.

Since it is a general rule that multiple different features define the objects available in the world, a useful summary representation would require that multiple between-feature summaries be established without limitation, at least for the features that define a particular collection of items. Emmanouil and Treisman (2008) found evidence against this hypothesis. In their study they reported what looked like a cost to averaging over two different feature dimensions at the same time. Based on the current study, we suggest that their observed limitation was not due to a need to establish multiple between-feature summary representations but rather to the need to establish multiple within-feature representations, which the specific task used in that study required. We used an extended version of the simultaneous–sequential method to reexamine the perceptual processing capacity of establishing multiple between- and within-feature summaries of mean orientation and size. The results indicate that multiple within-dimension summary representations are mediated through at least some limited-capacity processes (Experiment 1) whereas between-dimension summaries are mediated entirely through unlimited-capacity processes (Experiment 3). Notice that the stimuli across these two experiments were nearly identical and yet we obtained evidence of both processing extremes: maximally limited processing in the first experiment and maximally unlimited processing in the third. These findings contrast those reported by Emmanouil and Treisman (2008).

By demonstrating that the extraction of within-feature summaries involves limited-capacity processes and that between-feature summaries do not, we hope to, first, challenge the current dominant view that within-feature summaries drive a global sense of visual continuity in separate areas of the peripheral visual field, and to, second, encourage a shift in focus to understanding the functional role that between-feature summaries play in the control of behavior.

On the limitations of within-feature summaries in visual perception

Central to the dominant view that statistical summaries reflect a fundamental aspect of early visual processing is the claim that the system can generate more than one mean within the same dimension without cost (e.g., Emmanouil & Treisman, 2008). The results of the current study as well as those from other recent work (e.g., Brand et al., 2012; Jacoby, Kamke, & Mattingley, 2013; Marchant et al., 2013; Myzczek & Simons, 2008) challenge the claim that within-dimension summaries unfold independently of attention and other cognitive processes.

Implicit in discussions of summary representations serving a functional role of reducing complex information across the visual field is often the idea that they are formed automatically. Brown, Gore, and Carr (2002) outlined several generally accepted criteria that a given process should meet in order to be considered automatic. First, the process in question should be insensitive to capacity demands. However, summaries do appear to be constrained by such demands. Summary performance is sensitive to input at stages beyond the initial registration of features such as object-substitution masking and visual working memory (Jacoby et al., 2013; Myzczek & Simons, 2008; Poltoratski & Xu, 2013; see also Im & Chong, 2014), and susceptible to set size manipulations when homogeneity is minimized (Marchant et al., 2013). Furthermore, in the current study, we demonstrate that summaries are generated via fixed-capacity processes and therefore are not immune to interference with respect to within-feature averaging (see also Brand et al., 2012).

A second proposed criterion of automaticity is that processing should be established quickly enough to avoid serial shifts of attention. Initial studies reported that summary extraction occurs in as little as 50 ms (Chong & Treisman, 2003). But these displays were never masked. When observers can no longer rely on sensory memory to inform their estimates of the mean, the amount of time required to achieve adequate performance increases to 200 ms (Whiting & Oriet, 2011; see also Attarha et al., 2014), which suggests that summaries cannot be processed nearly as fast as originally proposed.

Finally, a third proposed criterion that defines a basic perceptual process is evidence of involuntarily processing. The issue of whether summaries are obligatory remains a matter of debate in our opinion. A concern with the studies espousing the view that summaries are formed beyond the focus of selective attention use tasks in which the observers are required to report properties of the unattended information. Statistical processing in these studies, therefore, is not tested under condition of inattention and so the question of whether summary representations are truly attention free, we believe, remains to be seen. Also related to the criterion of involuntary processing is the finding that statistical estimates improve with feedback (e.g., Fan et al., 2013). This finding is consistent with our conclusion that averaging is not a passive, automatic process that is impenetrable to top-down learning and observer goals, as is often the claim. Rather, across-trial learning may play an important role in forming averages with high precision.

Together, these recent studies present a challenge to the hypothesis that the functional role of within-feature summaries is to reduce complex information across multiple areas of the visual field to support later processes and the sense of perceptual continuity. This follows because such summary representations are limited as well.

On the role of between-feature summaries in visual perception

The results of Experiment 3 contribute to the discussion of whether there exists a general-purpose mechanism for summary extraction or more specialized mechanisms (see Haberman, Brady, & Alvarez, 2015, for a discussion of this issue). The hierarchical view of summary statistics, which states that different statistical summaries are established in separate visual pathways, predicts that it should be possible to form summaries between dimensions insofar as each summary type engages different subsets of processes. Following this logic, we conclude that summaries of orientation and summaries of size are generated in separate processing streams.

According to the hierarchical view, any between-feature averaging processes that do not overlap in terms of processing resources, should not interfere, and therefore should unfold with unlimited capacity. While summary representations may be more spatially constrained than previously thought, they may be perceptually richer in localized, behaviorally relevant regions of space. After all, a summary representation of the leaves on a single tree, for example, may include the average color, size, and shape of the leaves and would be potentially more useful than representations of size alone for all visible trees. The results of Experiment 3 should therefore encourage a shift in focus to understanding how behavior is controlled by multiple summary representations in one area of the environment (see Halberda, Sires, & Feigenson, 2006 and Poltoratski & Xu, 2013, who also include single sets in their experiments). It may be the case that between-feature summaries of a single collection of items, rather than within-feature summaries of multiple collections, are the critical factor in theories of visual perception.

Future work should determine whether the claim that all between-feature summaries are capacity free requires qualification. The current paper only demonstrates processing independence with respect to orientation and size. Haberman, Brady, and Alvarez (2015) tested another form of independence across a wide range of averaging tasks by using an individual differences method that correlated performance among those tasks. For between-feature summaries, they found no correlation for orientation and emotional expression, but a significant correlation for orientation and color. The difference in results that were observed as a function of which summary tasks were contrasted was attributed to which visual processing level(s) the tasks were believed to engage. Multiple between-feature representations of low- and high-level summaries (such as orientation and facial expression) may have been independent because they engaged different processing and/or neural resources (e.g., Cohen et al., 2014; Haberman & Whitney, 2012). In contrast, multiple between-feature representations of low-level summaries (or high-level summaries) were dependent perhaps because they were close in representational space. Applying this interpretation to the results of the current project suggests that summaries of orientation and size either belong to different processing levels, or that they reflect an exception to the interference rule when averaging within the same processing level. Further testing is needed to determine the degree of independence across different summary representations, both high and low, in order to help elucidate the internal architectural organization to which statistical processing seemingly adheres.