Evaluating real-time image reconstruction in diffuse optical tomography using physiologically realistic test data

Abstract

In diffuse optical tomography (DOT), real-time image reconstruction of oxy- and deoxy-haemoglobin changes occurring in the brain could give valuable information in clinical care settings. Although non-linear reconstruction techniques could provide more accurate results, their computational burden makes them unsuitable for real-time applications. Linear techniques can be employed under the assumption that the expected change in absorption is small. Several approaches exist, differing primarily in their handling of regularization and the noise statistics. In real experiments, it is impossible to compute the true noise statistics, because of the presence of physiological oscillations in the measured data. This is even more critical in real-time applications, where no off-line filtering and averaging can be performed to reduce the noise level. Therefore, many studies substitute the noise covariance matrix with the identity matrix. In this paper, we examined two questions: does using the noise model with realistic, imperfect data yield an improvement in image quality compared to using the identity matrix; and what is the difference in quality between online and offline reconstructions. Bespoke test data were created using a novel process through which simulated changes in absorption were added to real resting-state DOT data. A realistic multi-layer head model was used as the geometry for the reconstruction. Results validated our assumptions, highlighting the validity of computing the noise statistics from the measured data for online image reconstruction, which was performed at 2 Hz. Our results can be directly extended to a real application where real-time imaging is required.

1. Introduction

In diffuse optical tomography (DOT), cerebral haemodynamics can be monitored non-invasively using light in the red and near-infrared range [1–3]. Sources placed on the subject’s head emit light that travels diffusely through the underlying tissues, with some back-scattered to detectors positioned several centimetres from the source. Each tissue (e.g. scalp, skull, grey matter (GM), etc.) has a characteristic absorption and scattering coefficient. When functional activation or any pathophysiological change in haemodynamics occurs, a change in absorption is induced, while scattering is usually assumed to remain constant. The modified Beer-Lambert Law links the change in absorption to a change in oxy-(HbO) and deoxy-(HbR) haemoglobin concentration, which are the molecules absorbing light at this wavelength range, while all other tissues are relatively transparent. These concentration changes can either reflect functional brain activity or spontaneous baseline physiological trends or pathological changes in brain haemodynamics. An example of the latter is the dramatic changes in oxygen saturation and therefore oxy/deoxy-haemoglobin concentration that can occur during epileptic seizures [4,5]. Hence, from the difference in measured light intensity it is possible to infer the concentration changes of HbO and HbR occurring in the underlying cortical tissue [6–10]. Unlike in near-infrared spectroscopy (NIRS), where haemoglobin changes are examined on a channel-by-channel basis, DOT aims to recover three-dimensional images of haemoglobin variations. For this reason, DOT uses overlapping and multi-distance channels to increase spatial resolution and to obtain depth information, since photons detected at larger source-detector separations will (on average) have travelled to deeper regions of the head [7,11,12].

DOT has been applied both in clinical environments [2,4] and in studies of functional activation [1,2,13], where the growing number of applications is fuelling the continuous development of DOT methodology. Hardware advances have allowed an increasing number of sources and detectors to be used during the same acquisition, but this can slightly restrict the portability of the technique [2]. Portable, wireless devices are likely to extend the range of DOT applications in the near future [14]. Furthermore, developments in computing power and the growing number of DOT reconstruction packages has led to increased opportunities for sophisticated image reconstruction [15–17].

The ability to provide real-time, 3D images of HbO and HbR concentration changes is an essential step in the development of DOT techniques. Images can be interpreted more naturally than channel-wise data, since one image can summarise the whole measured data set. However, there are a number of obstacles that must be overcome before the technique can become commonplace: channel-wise signals must be pre-processed and fed to a reconstruction software package able to recover and display images in real-time, which is a computationally expensive process. Real-time reconstruction within 1 s has been demonstrated in the rat brain measuring data from 24 channels and using Graphic Processing Units (GPU) to parallelize the computations [18].

The process of recovering absorption or concentration changes in DOT is a non-linear, ill-posed inverse problem [8,9]. First, a model of how light propagates through the tissues (given the location of the optical sources and detectors), is required to relate changes in optical properties to changes in the measured signals. This forward problem is typically solved using either Finite Element Method (FEM) approaches (e.g. Toast [17] or Nirfast [19]) or with Monte Carlo methods (e.g. the mesh-based MMC [20] or the voxel-based MCX [16]). Whichever method is used, a geometric representation of the target object is required. Many studies have used simple homogeneous slab [21], hemi-spherical [7] or 2D circular [22] geometries to model the target object. However, a more accurate representation will allow a more accurate image to be reconstructed. Ideally, subject-specific, multi-layered, anatomically accurate head models would be used, where sources and detectors can be precisely located [12,23,24]. If a subject-specific model is not available, an atlas head model can be registered to the subject’s cranial landmarks [25]. Wavelength specific and tissue specific optical properties can then be assigned and the forward problem can be solved in a geometry that is as close as possible to the real case.

Image reconstruction requires the inversion of the solution to the forward problem. This step is a computationally expensive, under-determined, ill-posed inverse problem. Non-linear methods (e.g. Newton methods or gradient methods) can be used, but these are computationally unfeasible for real-time applications [8]. Under the hypothesis that the measured change in absorption is small, the reconstruction can be linearized [8,9]. In this context the inverse problem principally consists of forming and inverting the Jacobian matrix of partial derivatives of the measurement with respect to the chromophore concentrations. Several linear techniques exist to invert the Jacobian and they mainly differ in the type of regularization they apply [26,27]. Regularization is required to improve the conditioning of the inverse problem and to cope with noise amplification that can occur in the inversion process due to the small singular values of the Jacobian matrix. Perhaps the most commonly used inversion technique is the Tikhonov regularized least-square solution [9].

The reduced computational burden of linear approaches to the inverse problem render them highly suitable for real-time imaging. Furthermore, data are usually noisier in real-time processing because offline data processing methods (e.g. averaging of the response to repetitions of the same stimulus) cannot be applied. Furthermore, motion artifacts and drifts are more difficult to detect and correct in real-time applications, adding to the noise present in the data. For this reason, it is extremely important that the best regularization strategy and noise statistics are employed for real-time reconstruction. Whilst investigators commonly assume the noise level to be constant across different channels [7,28,29], a more reasoned approach considers the actual noise statistics present in the data.

DOT reconstruction algorithms are usually tested in simulation (often in simplified geometries and often with homogeneous optical properties) by introducing a focal change in absorption coefficient and adding random (Gaussian) noise [22,30]. However, in practice, optical measurements are influenced by physiological factors in addition to the cerebral event of interest (e.g. a functional response to stimulation), such as blood volume oscillations due to the cardiac and respiratory cycles [31–33]. In the context of image reconstruction, these factors can be considered to contribute noise. In offline applications it is possible either to record many responses to the same stimulation and average them to characterise the noise contamination or to isolate the pathological event of interest and apply targeted filtering; however, this is not possible in real-time applications. When testing real-time reconstruction algorithms it is, therefore, important to use data that closely mimics real data, and contains real physiologic noise. In functional NIRS studies, researchers have generated test data by adding simulated haemodynamic responses to real, resting-state data [32]. This results in a controlled test data set with realistic noise characteristics. The same idea can be applied to imaging [28], but in the imaging domain the process is more complex because it is essential that the relative absorption changes between channels is maintained.

The aim of this paper is to compare three fast reconstruction approaches that differ in the matrix used to weight the contribution of the data from different channels. We tested these approaches using data that were created by adding a simulated change in absorption to real, resting-state DOT data. Three different weighting matrices were used: the identity matrix; the covariance matrix with null off-diagonal elements (i.e. the variance matrix); and the full covariance matrix. From a theoretical perspective, the use of the full covariance matrix should provide the best solution; however, the true covariance matrix cannot be measured in practice in real-time due to the presence of dynamic physiological components in the data. A secondary aim of this paper is to compare the reconstruction of data after online and offline signal filtering.

2. Material and methods

2.1 Head model

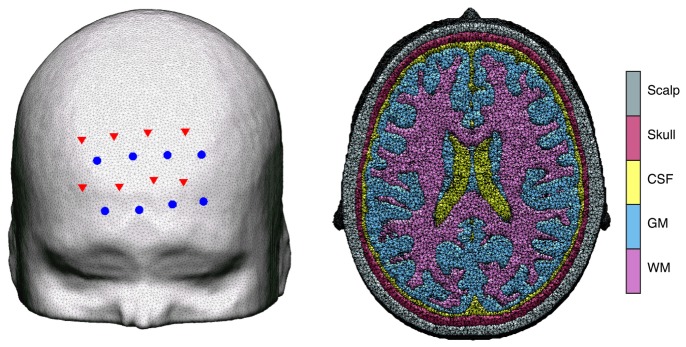
For synthetic data generation, a high-resolution adult head model created by segmenting an MR atlas into five tissue types (scalp, skull, cerebrospinal fluid (CSF), grey matter (GM) and white matter (WM)), was constructed as described in [34,35]. A tetrahedral finite element mesh was generated using the iso2mesh toolbox [36] with the maximum element volume set to 2 mm³ (Fig. 1 ). The total number of nodes and elements was 460323 and 2712451, respectively.

Fig. 1.

Probe placement. Left: sources (red triangles) and detectors (blue circles) overlaid on the adult head model. Right: cross section of the head mesh, showing the 5 different tissue types.

For image reconstruction, the same adult head model was re-meshed with the maximum element volume set to 3 mm³, which resulted in a mesh with 218165 nodes and 1272212 elements.

2.2 Jacobian computation

A source-detector array with 8 sources and 8 detectors, which is an extension of the array geometry used in [37], was simulated and overlaid on the forehead in the head mesh (Fig. 1). Data could be acquired from five source-detector distances with this array (18.0 mm, 33.5 mm, 46.1 mm, 52.2 mm and 71.6 mm) for a total of 51 channels. The optical properties assigned to the head model are reported in Table 1 [35,38–41].

Table 1. Optical properties assigned to the head model.

	absorption coefficient µa (mm−1)	reduced scattering coefficient µ’s (mm−1)			refractive index
Scalp	0.018		0.69	1.3
Skull	0.017		0.92	1.3
CSF	0.003		0.12	1.3
GM	0.018		0.75	1.3
WM	0.019		1.10	1.3

The Jacobian was computed with the Toast++ software [17], which solves the diffusion light transport model for continuous wave data (CW) using a Finite Element Method (FEM) forward solver:

$$J_{i,j}^{mesh}=\frac{\partial y_i}{\partial {\mu }_a^i}$$ (1)

where i is a particular source-detector pair, j is a given node in the mesh, y are the log amplitude CW data, μ_a is the absorption coefficient and ∂ denotes the partial derivate. J^mesh is computed on the volumetric head mesh.

The forward model solution J^mesh (i.e. the Jacobian) was projected into a regular grid basis of 50 × 60 × 50 voxels (hereafter, J) for reconstruction, using a linear transform computed by Toast++ . The size of the voxels was ∼3.6 × 3.6 × 3.6 mm. A finer grid basis (of 100 x 120 x 100 voxels) was used by Toast++ as an intermediate grid to optimize the mapping between the mesh and the grid basis. Sources were simulated with Neumann boundary conditions and a Gaussian profile with a 2 mm standard deviation. Detectors were also simulated as Gaussian profiles with standard deviation of 2 mm. The forward solution was computed with a stabilised bilinear conjugate gradient (BiCGSTAB) iterative solver.

2.3 Synthetic data creation

2.3.1 Real resting state data

CW resting state data were acquired in four subjects using the same array configuration shown in Fig. 1. The UCL Optical Imaging System [37] was used to acquire the data, at two wavelengths (780 nm and 850 nm) with a sampling frequency of 10 Hz. However, since the aim of this study is to recover absorption changes, only wavelength 780 nm was employed to generate the synthetic data. A custom-made Velcro probe holder was constructed to couple the source and detector fibres to the forehead of the subjects. Subjects were asked to remain still for the duration of the 10 minute acquisition.

2.3.2 Simulated change in absorption

Baseline log amplitude data, y_b, were simulated using Toast++ [17] on the higher density head model with the same optical properties used to compute the Jacobian.

A sequence of absorption perturbations was inserted into the model in order to simulate brain activation, first centered in the right frontal hemisphere at a depth of 13.5 mm and then in the left frontal hemisphere at a depth of 17.75 mm (Fig. 2 ). The perturbations in absorption were simulated as three-dimensional Gaussian distributions with 5 mm standard deviation and an amplitude varying from 101% of the GM absorption coefficient to 136% of GM absorption coefficient and back to 101% of GM absorption coefficient in steps of 5%. The change in perturbation was forced to be confined to GM nodes. Perturbation log amplitude data, y_p, were created for each of the added perturbations in absorption with Toast++ [17]. The only difference between the left and right hemisphere perturbations was the topological location of the centre of the perturbation and hence, its depth, given the asymmetric head model used.

Fig. 2.

Simulated absorption changes projected on the GM surface mesh.

2.3.3 Final synthetic data

Each 5% step in the simulated perturbation had a duration of 1 s in the simulated data time-course. The whole perturbation therefore lasted 16 s in each hemisphere. Baseline periods of 10 s were added before, after, and between the perturbations, providing a total sequence of 62 s in duration (Fig. 3 ). The change in intensity due to the perturbation (ΔI_pert) can be obtained by dividing the simulated intensity data (computed as e^yp) by the simulated intensity baseline data (computed as e^yb). A spline interpolation was then applied to up-sample the simulated change in intensity due to perturbation to a 10 Hz sampling frequency.

Fig. 3.

Schematic of the synthetic data time line.

The change in intensity due to physiological noise (ΔI_phy) for each subject and channel can be obtained by dividing the real resting state data by their mean. Physiological noise is considered to be any change in physiology that is not dependent on the task, e.g. heartbeat, respiration, vasomotion. Resting state data are usually a good representation of physiological, but also measurement, noise, since no task related changes are present in these data. For each subject, 62 seconds of resting state data were selected in order to match the length of the simulated data.

Simply adding the simulated change in intensity to the change in intensity due to physiological noise would be incorrect, since these changes are almost certain to be of different scales. Therefore, the change in intensity due to physiological noise was scaled by a factor β, to make it comparable to the change in intensity due to perturbation:

$$\Delta Isyn=\Delta Ipert+(\beta \ast \Delta Iphy-\beta )$$ (2)

with

$$\beta =\frac{1}{\alpha }\ast \frac{A\Delta Ipert}{A\Delta Iphy}$$ (3)

where A_ΔIpert and A_ΔIphy are the peak-to-peak amplitude in ΔI_pert and ΔI_phy respectively and α is a tuning parameter (here set to vary between 0.1 and 1 in steps of 0.05) that can be employed by the user to increase or decrease the Signal to Noise Ratio (SNR) in the final synthetic data ΔI_syn. The peak-to-peak values were computed as the difference between the maximum and minimum values of the change in intensity at the shorter separation channels (18 mm separation). This was performed in order to optimize the SNR of the data in these channels, which should have the best measured physiological signal. The same scaling factor β was then applied to all channels at all source-detector distances in the same subject so that all channels maintained their relative amplitudes. Note that the perturbation was not scaled here, so that the recovered perturbation can directly be compared with the original simulated image, whilst the scaling of the physiological noise allows the SNR to vary. Another way to modify the SNR of the synthetic data would have been to keep the physiological noise data constant and run the forward modelling many times to create the perturbation data with different percentage increases in the GM absorption coefficient. However, not only would this be less computationally efficient, but it would cause the SNR of the final synthetic data to be dependent on the array arrangement and position of the simulated absorption change. The approach proposed in this study is therefore more controlled, and the SNR of the synthetic data can be varied by changing only the scale of the added physiological noise. These final synthetic data can be freely download at [41].

Since image reconstruction is usually performed on the difference between activation data and baseline data, it was necessary to select 30 seconds of real resting state data as a baseline for each subject. The intensity values were converted to changes in intensity by dividing by their mean. The same scaling factor β was applied to these baseline data in order to match the amplitudes of the synthetic data. The synthetic data and baseline data were finally converted into log changes (hereafter called optical density), and difference data Δy were computed by subtracting, in each channel, the mean of the baseline optical density from each time point of the synthetic optical density data.

2.4 Image reconstruction

Image reconstruction was performed by solving the linear problem Δy = J*Δx, where Δx is the change in absorption coefficient to be estimated. Reconstruction was performed on the head model with three different techniques used to invert the matrix J and with two different approaches to filter the data Δy, as described in the following sections.

2.4.1 Inverse problem

The Tikhonov regularized least-square solution was used to invert the matrix J [8,9]:

$$J^{*}=\Sigma u\ast J^T\ast {(J\ast \Sigma u\ast J^T+\Sigma v\ast \lambda )}^{-1}$$ (4)

where ∑_u was set to the identity matrix and λ = λ₁ * trace(J*∑_u*J^T)/trace(∑_v). In this study, λ₁ was set to 0.1. The regularization parameter was chosen by inspection of the reconstructed images for each subject and then λ₁ was fixed for all reconstructions. The matrix ∑_v was selected to be one of the three following matrices: 1) the noise covariance matrix, computed as the covariance of the 30 s of baseline optical density, 2) a matrix with the variance of the 30 seconds of baseline optical density on the diagonal and zeros in all off-diagonal elements, or 3) the identity matrix. The inversion process was implemented in Matlab without the use of GPUs and was performed offline once, since it is not dependent on the acquired data.

2.4.2 Data filtering

Synthetic data were filtered in two different ways to test both offline and online image reconstruction scenarios. For the ‘online’ approach, synthetic data were filtered with a moving average approach with a 4 s window applied only to samples immediately before the sample to be imaged. Offline synthetic and baseline data were filtered with a 3rd order Butterworth low-pass filter with 0.2 Hz as cut-off frequency. Baseline data were carefully chosen for each subject in the offline approach, while the first 30 seconds of acquired data were selected for the online approach.

2.4.3 Reconstruction

Image reconstruction was performed every 0.5 s on the head model, multiplying the matrix J*, which is defined on the regular voxel grid, with the difference data Δy. The resulting images were therefore defined on the same regular grid of voxels as the matrix J. To visualize the reconstructed absorption changes in the mesh, the voxel-based image was mapped back onto the irregular volumetric head mesh.

A further step is needed to visualize images on the GM surface mesh. The volumetric head mesh-based image was projected to the GM surface mesh by assigning a value to each node on the GM boundary surface that is equal to the mean value of all the volumetric mesh node values within a 3 mm radius [34].

2.5 Metrics

A set of metrics was defined to compare images reconstructed with the different approaches and to thoroughly assess image quality. Four metrics were computed on the GM surface mesh image, while one was computed on the volumetric mesh. These metrics were designed to quantify image SNR, image resolution on the surface, image resolution in the volume, and accuracy in peak localization and recovered value.

A good reconstructed image should present an increase in absorption around the position where the actual change in absorption occurred and will display a small amount of background noise, i.e. a good reconstructed image should achieve a high SNR. To identify the region where the reconstructed change in absorption took place, the peak value in the images reconstructed when the highest absorption change was added in each hemisphere (i.e. t = 18 s and t = 44 s for right and left hemispheres respectively) was identified (Fig. 3). Regions of interest (ROI_Active), were then defined as the regions where the values of the reconstructed image were greater than half of their peak value. This can be interpreted as an area which is analogous to the full width at half-maximum, i.e. Area_FWHM. Two further ROIs (ROI_Background) were identified on the same two images as the regions where the values within the reconstructed image were smaller than one tenth of the peak value. To confine ROI_Background to cover only cortical areas sensitive to the measurement array, only nodes having a sensitivity value higher than 0.1% of the maximum of sum over rows of J were kept in ROI_Background. To test the quality of the reconstructed images, the SNR_image metric was then defined for each image as:

$$SN{R}_{image}^i=\frac{\overline{\Delta {\mu }_a^i}|{}_{ROIActive}}{{\sigma }_{\Delta \mu a}^i|{}_{ROIBackground}}\hspace{0.17em}\text{with}\hspace{0.17em}i=\mathrm{1..}n$$ (5)

where $\overline{\Delta {\mu }_a^i}$ is the mean of the recovered absorption changes in the i^th image computed in the region defined by ROI_active, ${\sigma }_{\Delta {\mu }_a}^i$is the standard deviation of the recovered absorption changes in the ith image computed in the region defined by ROI_Background, and n is the total number of reconstructed images, one for each time step (every 0.5 s; n can be considered the number of samples at a 2 Hz sampling frequency). Note that the SNR_image metric for each of the simulated absorption changes is computed on the same area for all images. The ROI_Active and ROI_Background computed on the image recovered at t = 18s were used for all images corresponding to activation of the right frontal cortex, while the ROI_Active and ROI_Background computed on the image recovered at t = 44s were used for all images corresponding to activation of the left frontal cortex (Fig. 3). A higher SNR_image should indicate a higher quality reconstructed image.

Image resolution on the surface was tested by identifying a ROI_Active area on each reconstructed image, computing the Area_FWHM metric and comparing it with the true area. The latter was computed as the area covered by the simulated absorption change projected to the GM surface mesh with values between 50% and 100% of the true peak value.

The accuracy in peak localization and recovered value was tested for each reconstructed image computing the maximum value in ROI_active (peak_FWHM) and comparing it to the true peak value. The latter was computed by projecting the simulated change in absorption on the GM surface mesh with the same procedure used to project the volumetric reconstructed images to the GM surface mesh. For each image, the error in peak localization was defined as the Euclidean distance between the true location of the simulated absorption change and the coordinates of peak_FWHM.

The image resolution in the volume was defined on the volumetric reconstructed images before their projection to the GM surface mesh. GM nodes were selected and the maximum recovered absorption change was found. A 3D ROI_active area, constrained to the GM, was defined as the region exhibiting a recovered absorption change with values greater than half of the maximum absorption change. The volume of 3D ROI_active for each image was found (Vol_FWHM) and compared to the true volume of the simulated absorption change.

Area_FWHM, peak_FWHM, the error in peak localization and Vol_FWHM metrics were calculated only when a change in absorption had been added (from 10 to 26 s and from 36 to 52 s) and not during the baseline periods.

3. Results

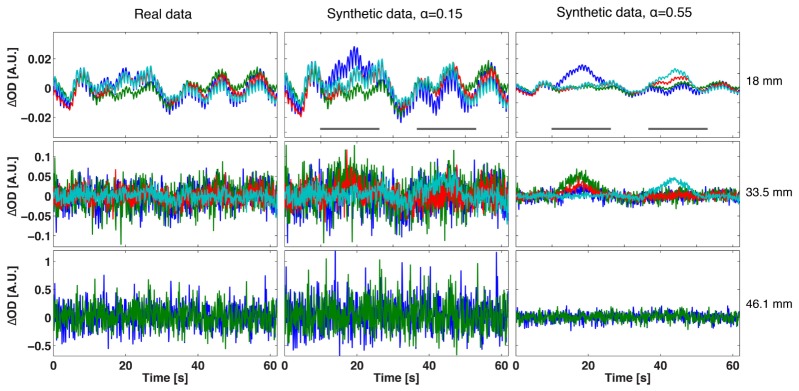
Figure 4 shows examples of synthetic data at two different values of the tuning parameter α. In the first column, the original physiological data are shown. For small values of α, the synthetic data are very similar to the original physiological data and no clear activation can be observed. As α is increased, the SNR of the synthetic data increases, and a clear activation can be seen in the data at short separations from 10 to 26 s and 36-52 s. Note, however, that the background physiological noise maintains the same characteristic pattern. The amplitude of the synthetic optical density data Δy decreases as α increases because physiological noise amplitude is reduced, while the added activation remains constant, increasing the SNR of the simulated data.

Fig. 4.

Original physiological optical density data in one of the subject (first column) and examples of synthetic optical density data at two different α values (in the last two columns). Signals have been divided according to source-detector separation for visualization purposes and only the first 3 distance ranges are shown. For each source-detector separation, 4 channels (each with a different colour) showing activation either in the left or right hemisphere have been selected and displayed. Grey lines indicate when perturbation changes were added in the synthetic data and are shown for visualization purposes only in the first row.

In Fig. 5 examples of reconstructed images using the head model and the data from Fig. 4 are displayed. Three time points were reconstructed: one during baseline (at t = 9s), just before the start of the first simulated absorption change; one half way between the start of the simulated absorption change in the right hemisphere and its peak (t = 14s, half-peak time); and one at the peak change (t = 18s) (Fig. 3). At low SNR values (i.e. small α), the reconstructed images appear noisier, and exhibit bilateral changes in absorption during both baseline and at the half-peak time. At the peak time, a clear but broad change in absorption is correctly recovered in the right hemisphere, but a lot of background noise is still apparent. At higher signal SNR values (larger α), background noise is reduced, with no visible changes in absorption during baseline, a localized change in absorption in the right hemisphere at half-peak time and a clear and focal change in absorption in the right hemisphere at peak time.

Fig. 5.

Examples of reconstructed absorption changes images on the GM surface mesh for the data displayed in Fig. 4 (α = 0.15 in the first row and α = 0.55 in the second) for one of the subject. These images were recovered using the variance as weighting matrix in the inversion of the Jacobian. Three time points of the signal were reconstructed: t = 9s (first column) where no absorption change was added, t = 14s (second column), which is half way between resting state and time of peak and t = 18s, which is the time of peak of the absorption change added in the right hemisphere.

As is expected, when α increases, the computed SNR_image metric also increases (Fig. 6 ). During baseline periods, SNR_image has a very small value, oscillating around zero with little variability among subjects and no variability between data sets with different values of α (as each channel is scaled by the same factor, the relative changes and therefore SNR_image remain the same). From 10 seconds for the right hemisphere and from 36 seconds for the left (Fig. 3), the SNR_image metric starts to increase in all subjects for both values of α, reaching a peak at the time point when the maximum change in absorption was simulated. For the higher value of α, the SNR_image metric appears to respond faster, as can be seen also from the reconstructed images of Fig. 5.

Fig. 6.

Examples of computed SNR_image values for the reconstructed images on the GM surface mesh. Images were reconstructed from data scaled with two different values of α (α = 0.15 in blue crosses and α = 0.55 in red circles) at each time step. The crosses/circles give the mean between subjects while the error bars present the standard deviation. Absorption changes were added between 10 and 26 s in the right hemisphere and between 36 and 52 s in the left one, as in indicated by the grey bars.

Both the computed Area_FWHM and Vol_FWHM from the reconstructed images are highly overestimated. The Area_FWHM computed on the GM surface mesh for the true added activation was 133.1 mm² and 75.3 mm² for the right and left simulated absorption change, while the Vol_FWHM was 570.2 mm³ and 762.1 mm³, respectively. Figure 7(a), 7(b) shows Area_FWHM and Vol_FWHM for the periods of simulated activation. For both metrics, as α increases, the metric decreases in value and reaches a plateau approximately at α = 0.5. The standard deviation between subjects also decreases as α increases. The variability between subjects and the estimated values of these two metrics are higher for the images reconstructed at the starting time of the simulated absorption changes.

Fig. 7.

Examples of metric values for two synthetic data series (α = 0.15 in blue crosses and α = 0.55 in red circles). Images were recovered for each time step in the head model using the variance matrix to weight the inversion of J. a) Area_FWHM, b) Vol_FWHM, c) Peak_FWHM and d) Euclidean distance between the position of the true peak in absorption change and that recovered from the image. The black arrow indicates whether the true value was lower or larger than the estimated one.

While the area and volume of the reconstructed absorption changes are highly overestimated, the actual peak value of the reconstructed absorption change (peak_FWHM) is underestimated. The true simulated peak changes in absorption measured on the GM surface mesh during the activation periods were between 1.2 × 10⁻⁴ and 5.7 × 10⁻³ mm⁻¹. As α increases, the estimated peak decreases, but the variability between subjects also decreases leading to a more reliable estimate (Fig. 7(c)). In Fig. 7(d), the Euclidean distance between the true and recovered peak positions of the change in absorption are displayed, showing that as the signal SNR increases, the position of the maximum change is recovered more precisely and the variability between subjects decreases. The biggest error in the recovery of the peak position is achieved at the starting points of the simulated absorption change.

3.1 Variance vs. Covariance vs. Identity matrix reconstruction

In Fig. 8 the mean SNR_image values, averaged across subjects, obtained using the three different weighting matrices are displayed as a function of α. The values refer to images reconstructed at the time of peak of the simulated change in absorption in the right and left hemispheres. The variance and covariance matrix approaches recover higher quality images than the identity matrix approach.

Fig. 8.

Mean SNR_image across subjects as a function of α obtained reconstructing images with the variance approach (black squares), the covariance approach (magenta triangles) and the identity matrix approach (blue circles). The values obtained at the time of peak of the added absorption change in the left and right hemisphere are displayed. The shaded areas represent the standard deviation among subjects.

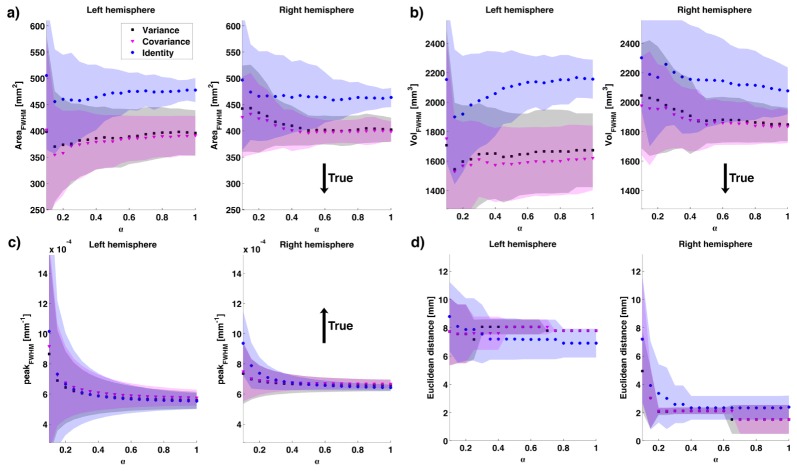
In Fig. 9 the mean Area_FWHM, the mean Vol_FWHM, the mean peak_FWHM and the mean Euclidean distance between the true peak of change in absorption and the recovered one across subjects are displayed as a function of α for the three weighting matrices approaches. Again, values refer to images corresponding to the peak in simulated absorption. All methods overestimate the area and volume of the recovered absorption change. However, the variance and covariance approaches demonstrate improved spatial resolution compared to the identity matrix approach. All approaches underestimate the value of the recovered absorption change, with the covariance matrix approach displaying a slightly higher recovered value than the other methods. The error in the recovery of the position of the maximum absorption change varies between hemispheres, due to the asymmetric brain template (Fig. 9(d)). Here, variance and covariance approaches perform similarly in both hemispheres, but have a better performance than the identity matrix approach in the right hemisphere and a worse performance in the left hemisphere. At small α values, however, the performance of the variance and covariance approaches exceeds that of the identity matrix approach in both hemispheres. The step changes in Euclidean distance values in Fig. 9(d) are likely to be caused by the low resolution of the GM surface mesh.

Fig. 9.

a) Mean Area_FWHM across subjects, b) mean Vol_FWHM across subjects, c) mean peak_FWHM across subjects and d) mean Euclidean distance across subjects between the true peak change in absorption and that recovered from the images. The variance approach results are shown in black squares, the covariance in magenta triangles and the identity matrix in blue circles. The shaded areas represent the standard deviation among subjects. The black arrow indicates whether the true value was lower or larger than the estimated one.

An example of reconstructed images with the three reconstruction approaches is displayed in Fig. 10 .

Fig. 10.

Examples of reconstructed images on the GM surface mesh with α = 0.15 at t = 18s (time of peak of the simulated absorption change in the right hemisphere). From left to right, the images recovered using the variance matrix approach, the covariance matrix approach and the identity matrix approach.

3.2 Online vs offline reconstruction

In Fig. 11 the mean SNR_image across subjects computed on the images recovered using data filtered with the online and offline approaches is displayed as a function of α. The displayed values refer to the images reconstructed at the time of peak of the added change in absorption in the right and left hemisphere using the variance matrix approach. The performances of the online and offline approaches are very similar.

Fig. 11.

Mean SNR_image across subjects for the online (in black squares) and offline (in green triangles) reconstruction. The values obtained at the time of peak of the added absorption change in the left and right hemisphere are displayed. The shaded areas represent the standard deviation among subjects.

In Fig. 12 the mean Area_FWHM, the mean Vol_FWHM, the mean peak_FWHM and the mean Euclidean distance between the true location of the peak change in absorption and the recovered location across subjects are displayed as a function of α for both the online and offline reconstructions. The performances of both filtering methods are very similar for all metrics.

Fig. 12.

a) mean Area_FWHM across subjects, b) mean Vol_FWHM across subjects, c) mean peak_FWHM across subjects and d) mean Euclidean distance between true and recovered location of maximum change in absorption for the online (black squares) and the offline (green triangles) reconstruction. The values obtained at the time of peak of the added absorption change in the left and right hemisphere are displayed. The shaded areas represent the standard deviation among subjects.

4. Discussion

Achieving real-time image reconstruction is essential if DOT is to fulfil its potential for clinical monitoring. Images that display cerebral haemodynamics in real-time could provide physicians with valuable insight into the functional state of the patient’s brain and alert them to pathological events including desaturations [42], seizures [4] and strokes [43].

In this study, we compared three different approaches to handling noise that are all suitable for online reconstruction. Both the covariance matrix approach and the variance matrix approach outperform the identity matrix approach in all metrics. These two approaches are able to better recover the simulated absorption change, and they also reduce the background noise, which is important to reduce the risk of false-positives. This is particularly important in real-time applications, where interpreting spurious absorption changes as true could compromise clinical care. The covariance and variance matrix approaches perform similarly, with the variance approach performing slightly better than the covariance approach in the SNR_image metric, whereas the opposite is true in the Area_FWHM and Vol_FWHM metrics. This suggests that it is important to use information coming from the measured data when inverting the Jacobian, but that the most valuable information is the variance of the measured channels. The information stored in the covariance between channels does not noticeably improve the reconstructed image but it does not deteriorate it. This is likely to be because the variance (which is also the diagonal of the covariance matrix) is at least 2 orders of magnitude larger than the covariance between channels, which are the off-diagonal elements of the covariance matrix (Fig. 13 ). Whether the off-diagonal elements are zero or just very small does not heavily influence the reconstruction.

Fig. 13.

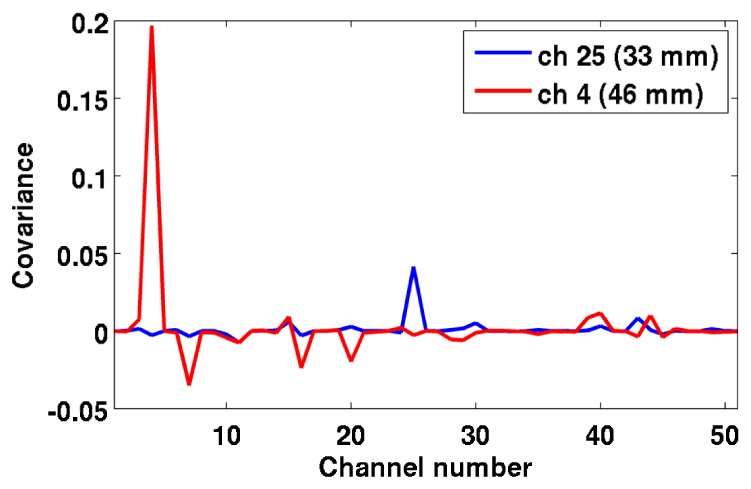
Example of two rows of the covariance matrix in one of the subject. The blue line refers to channel 25, which is a 33 mm channel, while the red line to channel 4, which is a 46 mm channel. In both cases, the peak of the plot corresponds to the channel number itself, showing that the covariance of the channel with itself (hence the variance of that channel) is larger than the covariance of the selected channel with all other channels. Furthermore, the amplitude of the variance increases with source-detector distance.

The topological location of the centre of perturbation and their different depths inevitably influences the reconstruction results, with differences in the computed metrics and their standard deviation between hemispheres. The worse performance in the left hemisphere is likely to be attributed to the deeper location of the simulated absorption change. However, the general performance of the techniques (i.e. variance and covariance approaches outperforming the identity matrix approach) is stable irrespective of topological location of the perturbation, indicating that these results might be extended to other brain regions.

One of the most important result of this study is that the performances of online and offline reconstruction are similar, with no dramatic differences in the computed metrics. In this study, both online and offline reconstructions are performed on a single trial. Although this will always be the case for online applications, for the majority of offline applications it is possible to collect multiple responses to the same stimulus type, average them and reconstruct the mean response to the stimulus. This is clearly true in the study of functional activation, but is also the case in the study of certain pathology, for example inter-ictal epileptic events [44]. The averaging procedure will inevitably reduce the background noise and therefore it is highly likely that the recovered image will be more accurate. However, some situations may require single trial responses with offline reconstructions, such as oxygenation changes after a seizure, or in brain-computer-interface applications. Here, we decided to compare the performance of offline and online reconstructions for single trial responses. It is worth noting that recovering small single trial functional changes is also very challenging for an offline approach. Instead, a single large pathological change is easier to recover for both online and offline approaches. Therefore, it is not surprising that the performance of online and offline approaches for single trials estimation is very similar. The largest difference between online and offline reconstruction performance was found in the metrics computed in the first and last seconds of the period of simulated activation. In the online case the computed metrics do not show a symmetric behaviour (Fig. 7), and reveal larger error at the start of the period of simulated activation. In the offline case the metrics show a symmetric pattern, with an increased error at both the start and end of the activation period. The moving average applied to the online data is the likely cause of this behaviour. These online approaches therefore experience more difficulties in recovering accurate images at the starting point of the stimulation. More complex online techniques able to cope with this problem should be developed. Nevertheless, it is likely that our main results will not be affected by using a different online algorithm to filter the data.

While online image reconstruction is limited in its choice of filtering method compared to offline reconstruction, there is a similar restriction in the availability of baseline data. Such data for offline reconstruction can be carefully chosen by examining the entire data series, which is not possible when online reconstruction is performed. To simulate this difference, baseline data were carefully chosen for each subject in the offline reconstruction approach, while three different baseline data were compared in the online reconstruction approach: a) the first 30 s of measured data, b) 30 s of measured data before the data chosen for the reconstruction and c) the same reference data chosen for the offline reconstruction. The results presented above are for online reconstruction employing the first 30 s of measured data as baseline (choice a). The results of online reconstruction using the three approaches were indistinguishable (results not shown). Furthermore, it is difficult to predict the SNR that a pathological event would produce. Therefore, for signals with low SNR, more complex offline processing than that presented here might be required to adequately isolate the haemodynamics of the pathological event. It should be noted that the real resting-state data we acquired did not contain major motion artifacts. Clearly the performance of offline and online reconstruction approaches will differ when motion artifacts are present. New techniques are needed for online filtering that should be able to detect and correct motion artifacts, remove noisy channels and reduce physiological contamination. When developing these new techniques one should consider not only the difficulties of working in real-time and in many channels in parallel, but also their computational burden.

In this study, reconstruction techniques were tested on realistic synthetic data, where simulated absorption changes were added to real physiological noise. Reconstruction algorithms should be tested on data that can replicate a real experiment as closely as possible, while also providing a known target image that is controlled and quantifiable [28]. The proposed method to create synthetic data does not modify the simulated absorption change and therefore the recovered absorption change image can be directly compared to the true change. Furthermore, changing the scaling of the real physiological noise allows data sets with different SNRs to be created. Usually, simulated data are created by adding a known change in absorption coefficient to Gaussian random noise; the mean and the standard deviation of the Gaussian distribution are varied to create simulated data with different SNR to test the algorithm in several scenarios. Here, we used this same procedure, scaling the real physiological noise, without modifying its pattern. The approach proposed in this study is straightforward and easy to replicate, and the SNR of the final data can be easily controlled.

5. Conclusion

In this study, a new approach to creating synthetic data with real physiological noise and varying SNR is demonstrated. This approach can be readily applied by others to create realistic data to test image reconstruction algorithms. Real-time reconstruction with online filtering of the data has been validated and more accurate images were reconstructed when using the variance or covariance matrix approaches as compared to the identity matrix. Our results also imply that using the covariance matrix has little impact compared to using the variance only. These results are important since any practical experiment will be limited to using real data to compute the noise statistics. We suggest that head-model based reconstruction should be used with the variance matrix for the inversion of the Jacobian for real-time diffuse optical tomography.