Abstract
Optical based methods for non-invasive measurement of regional blood flow tend to incorrectly assess cerebral blood flow, due to contribution of extra-cerebral tissues to the obtained signal. We demonstrate that spectral analysis of phase-coded light signals, tagged by specific ultrasound patterns, enables differentiation of flow patterns at different depths. Validation of the model is conducted by Monte Carlo simulation. In-vitro experiments demonstrate good agreement with the simulations' results and provide a solid validation to depth discrimination ability. These results suggest that signal contamination originating from extra-cerebral tissue may be eliminated using spectral analysis of ultrasonically tagged light.
OCIS codes: (170.1065) Acousto-optics, (170.4090) Modulation techniques, (280.2490) Flow diagnostics, (170.7170) Ultrasound, (170.1470) Blood or tissue constituent monitoring, (170.3660) Light propagation in tissues
1. Introduction
Monitoring cerebral blood flow (CBF) is crucial, since inadequate perfusion might lead, in a matter of minutes, to brain damage or even death. It is critical for managing patients who are unconscious or anesthetized, as it provides an indication whether the brain is receiving an adequate amount of nutrients (such as oxygen or glucose). Thus, significant research efforts are directed at developing reliable monitoring tools that will enable continuous, simple and cost-effective monitoring of CBF [1].
Among the most accurate methods for measurement of CBF are the different imaging techniques [2], i.e. Computed Tomography (CT Perfusion), Magnetic Resonance Imaging (DW-MRI), SPECT, etc. Although these methods can provide an accurate, direct measurement of cerebral blood flow, they are not continuous and do not provide real time measurement. Moreover, they are often expensive and sometime require exposure to radioactive isotopes and ionizing radiation. Transcranial Doppler ultrasound (TCD) [3], on the other hand, can provide real-time continuous measurement of blood flow velocity in large vessels (assuming a constant angle of insonation during the measurement), however it is not easy to use and requires the operator's proficiency in applying the sensors. Another less frequently used technique is based on thermal diffusion [4], which suffers from the inherent disadvantage of being invasive as it involves drilling into the skull in order to reach the brain tissue.
Optical methods, which provide non-invasive blood flow related measurement, are particularly attractive since they are simple to use, inexpensive and do not require ionizing radiation of radioactive agents.
Among these optical techniques is Laser Doppler Flowmetry. Laser Doppler probes are often used for measuring skin perfusion non-invasively, or are directly inserted into the tissue to measure microcirculatory blood flow in deeper tissue [5, 6]. Yet, due to its operation principle which is based on single scattering, the penetration depth of the Laser Doppler systems is limited to up to few millimeters only.
Photoacoustic (PA) signals, which result from absorption of light by intrinsic chromophores, have also been shown to spatially assess blood flow in-vitro [7] and in-vivo [8]. It should be noted that it is difficult to obtain reliable PA tomographic signals in human brains, due to absorption and aberrations of the generated acoustic signals through the thick human skull [9].
Diffused Correlation Spectroscopy (DCS) [10, 11] enables deeper penetration depths, and the extraction of data from brain tissue. Still, the measurement is not specific to brain tissue since light travels through both cerebral and extra-cerebral tissues, which affect the obtained signal. To mitigate this difficulty, it was suggested to apply pressure on the probe, greater than the peak systolic pressure, thereby causing a reduction in scalp flow at the vicinity of the probe, thus relatively increasing the cortical contribution to the measured DCS signal [12]. Nonetheless, one cannot be certain that the scalp blood flow is indeed suppressed, and there may be undesired physiological consequences to such long continuous blood suppression to the tissue. Moreover, due to the rapid decay of light when diffusing through highly scattering media, only a small portion of the backscattered light can interact with deeper layers, while most of it will be affected by shallower, irrelevant tissue layers.
Dye densitometry methods, such as the use of Indocyanine green (ICG) [13], are also affected by perfusion through extra-cerebral layers. The dye is inhaled or injected intravenously and migrates systemically throughout body vasculature, including the brain. Thus, when measuring non-invasively, the origin of the obtained clearance curve is uncertain. Again, flow measurement might be contaminated [14, 15] as the signal may originate from both extra cerebral and cerebral regions.
In conclusion, all existing optically based CBF measurement methods are contaminated by extra-cerebral signal. This contamination, which is dependent on the ratio between the optical path-length in brain compared with the total optical path-length [16], cannot be eliminated and certainly cannot be neglected. Computer modeling of NIR light propagation has shown that in adult head, approximately 20% to 30% of the typical volume of tissue examined by conventional Near Infrared Spectroscopy (NIRS) equipment is actually brain, while 70% to 80% is extra-cerebral, i.e., scalp and skull [17]. Thus, even though the blood flow in the scalp and skull regions might be expected to be only about 10-15% that in the cortex [18], its contribution to the optical signals can be significant and can lead to incorrect interpretation of physiological responses in deeper brain tissue [12]. Hence, there is an evident need to reduce the contamination of the brain related signal by extra-cerebral regions and provide a signal that is correlated primarily to brain tissue perfusion. However, solving the important problem of determining the depth at which blood flow is measured and whether it is superficial (extra-cerebral) or deeper (cerebral) blood flow, is still pending as far as optical methods are concerned.
Herein we present a novel non-invasive method for measurement of deep tissue blood flow based on coherent NIR light scattering and the acousto-optic effect, named Ultrasound Tagged Light (UTL) [19]. This is a hybrid technique which combines ultrasonic resolution with optical contrast, thus enabling better spatial resolution of the tissue optical properties. We demonstrate that this approach is depth sensitive, thus may distinguish blood flow patterns at different depths. Using such a method, one could reduce the contamination by superficial flow, through extra-cerebral tissues, and enable a direct, non-invasive measurement of cerebral perfusion in a desired predetermined specific depth, while benefitting from all the advantages of light based technologies.
2. Methods
2.1 Flow calculation
Backscattered light emanating from a coherent light source and propagating through a highly scattering medium results in an interference pattern, on the surface of the detection plane, usually referred to as a 'speckle pattern'. It is a well established fact that in the case that scatterers in the sample undergo movement (e.g. flow), the obtained light speckle pattern fluctuates, and its de-correlation time is proportional to the inverse of the average velocity [20–22].
Laser Doppler systems exploit speckle fluctuations to measure blood flow parameters. A tissue volume is illuminated with a monochromatic (single-frequency) coherent light. Moving red blood cells scatter the light, generating “Doppler” frequency shifts and a total spectral broadening of the light. The frequency distribution of the backscattered light is analyzed to obtain an estimate of blood perfusion. In its most simple form, continuous wave Doppler systems offer velocity information without any depth resolution and are therefore used mainly for the evaluation of superficial structures [23].
In acousto-optic systems [24–26], coherent monochromatic laser light illuminates a tissue volume while irradiating the same tissue volume with an ultrasound beam simultaneously. As the ultrasound beam propagates through the tissue, the local scattering centers are periodically displaced by the acoustic signals. When light propagates through the modulated tissue volume, its phase is “tagged” (modulated). This causes the speckle intensity of the scattered light to be modulated in correlation with the ultrasound signal. When further scattered by moving blood cells, the tagged light undergoes slight Doppler shifts relative to the original acoustic signal. Hence, the spectral distribution of the US tagged light around the US frequency exhibits an additional spectral broadening, which is proportional to the averaged velocity [23, 27, 28].
Spectral analysis was applied for light intensity modulated by continuous-wave ultrasound radiation in phantoms and live tissue [29, 30]. The broadening of the otherwise sharp spectrum is related to the velocity distribution of the scatterers in a tested sample. Due to the nature of light propagation within tissue, the obtained spectrum width is an accumulative parameter which is influenced by the entire photon path. At each scattering site along this path, the optical wave acquires a certain amount of phase change due to movement of scatterers. The overall spectral width is a result of many such phase changing events along the optical path. Hence, the spectral width itself lacks range discrimination.
When using the acousto-optic effect with a continuous US beam that modulates the whole sample, the resulting spectrum is affected by scatterers from all depths. The obtained spectrum is a coherent weighted sum of amplitudes contributed by different optical paths travelling in the sample. It suggests that frequency changes resulting from movement of scatterers in specific layers in the sample can hardly be discriminated. If, however, it would be possible to modulate by US only a specific slice as a function of depth (localized), then data from this specific slice could be extracted and discriminated (Fig. 1(B) - lower panel). This localized modulation (“Tagging”) might be done by a narrow ultrasound pulse such that only a specific layer is spatially modulated at given time. As the US pulse propagates through the tissue, different depths are modulated with corresponding time delays. Hence, in principle, different time delays yield spectra (sometimes termed “ambiguity function”) which correspond to different depths in the sample. In an actual experimental setup, the modulation of a specific depth can be obtained using other techniques, such as the use of continuous pseudo random coded US waves or a coded wave with a narrow autocorrelation (such as a Golay code) [31]. For reasons of simplicity, we focus the discussion here on a propagating short US pulse.
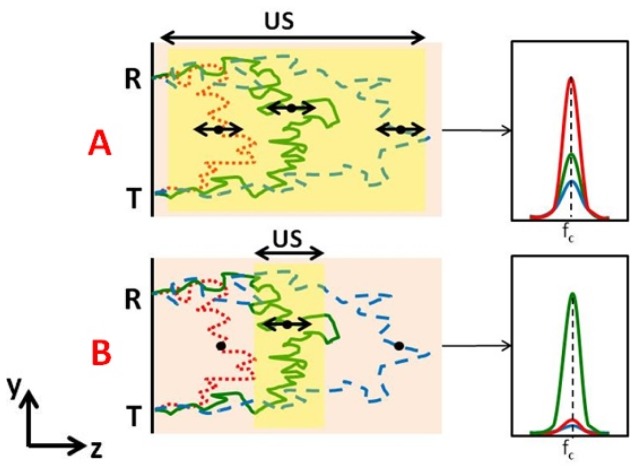
Fig. 1.
Different light paths propagate thorough different depths inside the sample (examples in red, green, blue) and their corresponding spectra around US frequency (fc). Black points designate typical scattering sites along the different paths. T & R stands for the light transmission and reception points, respectively. (A): The red path represents the most probable path for the given geometric configuration. As paths get longer, their probability gets smaller (green) and smaller (dashed blue). When a continuous ultrasound (US) wave is used for modulating the entire tissue volume of the “banana” defined by the transmission and reception points - the overall spectral distribution which is sum of three spectra “types” (colors) will normally be dominated by “red” type paths (right). (B): In the case where an US pulse modulates only a specific volume (overlapping mainly with “green” type paths), then the spectrum is dominated by these paths. Shorter “red” type are almost not modulated while longer “blue” type will be less expressed due to their relatively smaller probability and smaller US overlap.
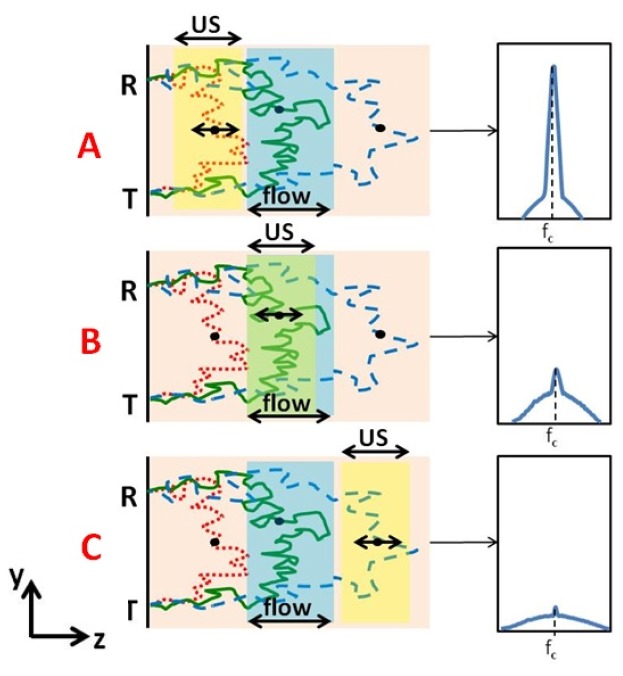
To find out what is expected in case of a flow pattern through a specific volume (or layer) located inside the tested sample, we examine three types of relative positioning of the US pulse and the flow layer (Fig. 2 ). The first type is when US excitation is shallower than the flow layer. Shallower optical paths (marked in red) pass through the US modulated layer but not through the flow layer. In such case the spectrum is going to be relatively narrow as there is almost no broadening of the light signal around the US frequency inside the tagged volume. In addition, the spectrum will also contain a broadened “pedestal” part caused by the longer “green” and “blue” type photon paths which pass both through US modulated layer and flow volume. This case is depicted in panel A of Fig. 2. In panel B, the US modulated layer overlaps with the flow layer, therefore spectra of modulated “green” and “blue” trajectories are broadened due to the effect of flow on their phase. In that case, “red” trajectories are not modulated nor are they broadened as they are shallower than both flow and US modulated layers. In the lower panel (C), the US modulated layer is deeper than the flow layer, thus, although the total number of trajectories is smaller (long path means less probability to get back to detector), the spectrum is broadened as “blue” paths traveled also through the flow volume.
Fig. 2.
Each layer is modulated (by Ultrasound) at a different time. In panel A the spectrum (schematically illustrated on the right panel) is narrow around the US carrier frequency (fc) as “red type” trajectories, which are not broadened by flow, are dominant. At panel B the US layer overlaps with the flow layer such that the US modulated trajectories are also broadened by flow. In panel C the US modulated layer is deeper than the flow layer, and although the total number of trajectories is small (a longer path means less probability to get back to detector), it is still broadened as it traveled through the flow layer as well.
Yet, as explained above, this ability to associate spectral width to a specific depth is still contaminated by incremental contributions from all the intermediate layers between this depth and the transmission-reception plane. Spectral broadening resulting from flow pattern at a given depth is deduced by subtracting spectral widths of adjacent layers (adjacent time delays). This subtraction provides us with the net broadening caused by the desired tissue layer, termed “local broadening”, and reduces the influence of shallower layers. Therefore, in order to get both location and amplitude of flow patterns, the differential spectral width should be determined instead of the spectral width. The delay at which changes in the spectral width occur are attributed to location (depth), while the broadening – to volumetric flow rate, which is termed flow index (FI).
To validate our method's depth discrimination ability, both computerized simulations and in-vitro experiments were conducted. All aimed to prove that by using the acousto-optic effect of a localized pulse, one can isolate flow patterns at a given depth in the target sample.
2.2 Simulations
Our acousto-optic method was implemented in a computerized Monte-Carlo simulation using Matlab® environment (Matlab 8.3.0.532 R2014a). The exact specifics are detailed elsewhere [32]. In summary, light emanating from a coherent point source is transmitted towards a highly scattering medium (tissue). The back reflected light is collected on a detector located at a predetermined distance from the source. The tissue is defined by its optical properties (scattering coefficient, absorption coefficient and anisotropy factor) which govern the photons' diffusion through it. A Monte-Carlo approach was utilized to produce photon trajectories within the tissue, which were subjected to scatterer motion caused by blood flow or US field (see Fig. 3(A) ). The simulated motion produced a change in scatterers' positions within the same trajectories (i.e. the identity of these trajectories was kept during their deformation). Each motion type was defined by a characterizing scatterer displacement expression that was applied to specific scatterers, thus changing the overall photon optical paths and causing a corresponding phase shift. The total phase increment of each trajectory was calculated as the sum of all individual phase shifts of moving scatterers in each trajectory using the following equation:
| (1) |
Where represents the wave vector ( ) difference between consecutive scattering events (i and i + 1) of the optical path ( , see Fig. 3(A) - right), and represents the position change of the ith scatterer due to the motion within the tissue [30]. N is the number of scatterers in trajectory .
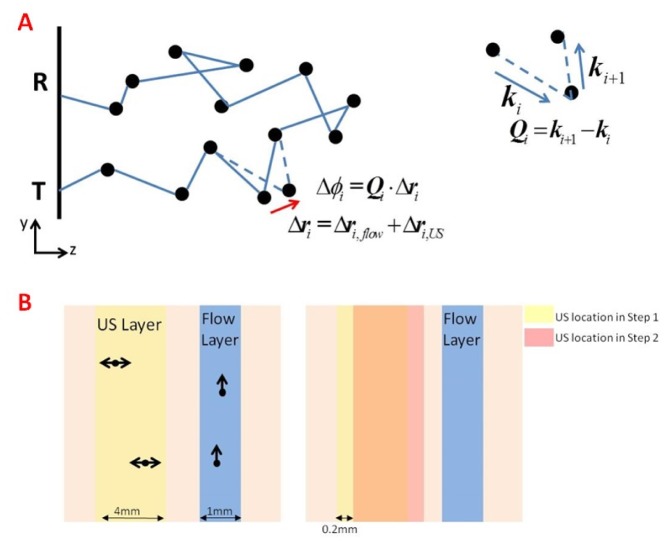
Fig. 3.
(A) An illustration of one photon trajectory obtained from transmission to reception point. Black spheres represent scatterers along the trajectory. The ith scatterer is shifted by both flow and US field. This phase shift would be summed up with phase shifts of other scatterers of this trajectory to get the overall phase increment along the path. On the right – an illustration of Qi. (B) The simulation setup. The pink square represents the tissue, characterized by its optical properties. Black spheres denote scatterers, moved by the characterizing displacement (due to flow or US). On the left, one can observe the different layers. In the blue layer photons encounter moving scatterers due to flow, and its depth is kept constant throughout the specific simulation (it is changed between different simulations). In the yellow layer photons are tagged by the US. In order to create the full picture of pulse propagation, this layer is shifted in 0.2mm increments to scan the whole tissue. The right side represents the US layer locations in two consecutive steps (yellow – step 1, red – step 2), and the shift is apparent.
Then, for each time step, the overall interference at the detector was determined, using Eq. (2)
| (2) |
where denotes the weight or “absorption” behavior of the path (taken into account in the MC simulation). represents the phase due to the optical path, which changes with time due to the scatterers' motion, and is the sum of an initial phase, and a phase increment, which is due to the deformation of the trajectory ( ). The corresponding intensity signal was then obtained, according to the following Eq. (3)
| (3) |
Blood flow was modeled as directional flow (parallel to the transmission plane) with constant velocity amplitude V. The displacement expression over time for the ith scatterer is given by:
| (4) |
where is a unit vector in the flow direction, V is the velocity and t is time.
The US field was modeled as a continuous and sinusoidal field (with a confined spatial width). Its effect on scatterers is modeled by a periodical motion along the transmission axis (z) at the US central frequency. The displacement is therefore described by the following expression:
| (5) |
where is maximal amplitude of the scatterer displacement due to the applied US field, is the US angular frequency, and is the US phase for the ith scatterer. The US field exhibits a different phase for each scatterer due to its different position along the z axis (modulated by the US wave at a different delay). is a unit vector in the z direction to represent a displacement along the US propagation axis.
The simulation was modularly built to enable observation of the effect of each motion source (and direction) separately, as well as the cumulative effect of all of them together (or any desired combination). While the simulation can also accommodate Brownian motion [32], for simplicity reasons, it was neglected and we considered only flow patterns and US fields as the sources of motion of scatterers within the tissue.
As the intent of this study is to discriminate between flow patterns at different depths, we implemented a flow pattern only in a certain layer (1 mm width). That is to say that only scatterers located in that specific layer were exposed to displacement caused by flow. Then, we changed the depth of this layer several (3) times and compared the results.
For each depth of flow pattern we modeled an US pulse propagating through the tissue. We chose a certain layer thickness (4 mm), which was tagged by US (by the corresponding scatterers motion). Then, this layer was shifted deeper, as the US pulse is propagating deeper, with increments of 0.2mm (see Fig. 3(B) (right)). Each US location within the tissue corresponds to different time delay from its transmission. The depth of the flow layer was kept constant throughout the US propagation. For each US location, the intensity temporal pattern on the area of the detector was obtained (as aforementioned by Eq. (3)), and the corresponding power spectrum (PS) was calculated, using
| (6) |
Prior to FFT (Fast Fourier Transform) calculation, the signal was smoothed by Blackman window to reduce ringing effects originating from the software's zero padding while calculating the FFT. Stacking the obtained power spectra (corresponding to different US layer depths) one next to the other yielded a 2D spectrogram (ambiguity function).
To estimate the spectral width, two parameters were calculated for each US depth, the area under the spectrum curve (AUC) in a predetermined bandwidth (BW) around the central US frequency, and the PS amplitude at the central US carrier frequency (A(fUS)). The spectral width (SW) was then given by
| (7) |
Local broadening, which is the Flow Index (FI) as explained before, was determined by the first derivative of the spectral width according to the depth (Eq. (8)).
| (8) |
2.3 In-vitro experiments
In order to validate our depth discrimination technique, we constructed a laboratory phantom experiment. We used a previously designed phantom that mimics blood flow in tissues [33]. The phantom is made of UltraFlex (Douglas & Sturgess Inc) which is a synthetic polymer matrix soaked with oil. TiO2 particles (0.1% by weight) were added as light scattering agents. The optical and acoustic properties of the phantom are similar to those of tissue, as detailed in Table 1 .
Table 1. Optical and acoustic properties of the phantom and the tissue [34, 35].
| Property | Tissue – muscle/brain | Phantom |
|---|---|---|
| Light Effective decay coefficient | 2.17/2.12 cm−1 | 2.2 ± 0.2cm−1 |
|
| ||
| Sound Velocity | 1.5 ·105 cm/s | 1.43 ·105 cm/s |
|
| ||
| Acoustic impedance | 150-170 Kg/cm2∙s | 149 Kg/cm2∙s |
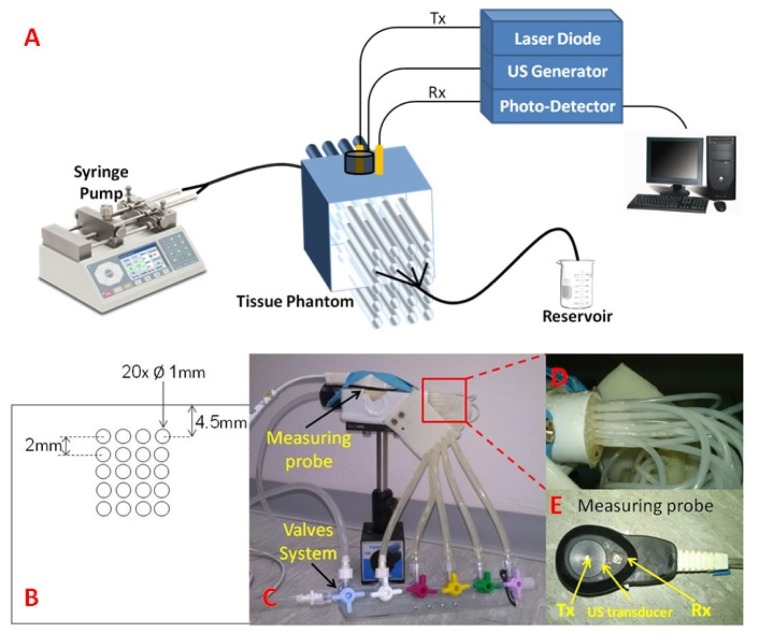
The UltraFlex slab contains 20 hollow parallel channels with an outer diameter of 1mm. Those channels are arranged in 5 rows of 4 channels each, as depicted in Fig. 4(B) , and connected to silicon tubes (each channel separately - Fig. 4(D)). Each row of channels is connected to a separate valve, as seen in Fig. 4(C), thus enabling control of it separately (turn on/off).
Fig. 4.
(A) Schematic illustration of the experimental setup. (B) A cross section of the flow phantom detailing the channels structure. Five rows, corresponding to five different depths, each containing four flow channels. The geometric sizes are given as well. (C) Overview on the flow phantom including the controlling valves system and the measuring probe, (D) Zoom in on the channels connection to the silicon tubes, and (E) A closer look on the measuring probe, including the transmitting (Tx) and receiving (Rx) fibers and the US transducer.
A schematic diagram of the experimental set-up is presented in Fig. 4(A). Light from a long coherence length (>3m) laser diode (808nm, 100mW, IPS, USA) was delivered towards the phantom through an optical fiber (62.5µm, NA 0.27). Backscattered light was collected with a second optical fiber (bundle of 12*200µm fibers, NA = 0.22), and delivered to an APD photo-detector (Hamamatsu Si APD s12023). An US transducer (Custom made Flat circular wide band transducer, Sonomed), which transmitted pressure sequence (0.3MPa, 7Hz repetition rate) into the medium, was placed on the transmission plane, such that the transmitting fiber (Tx) passed through a hole in its center. The light collecting fiber (Rx) was positioned aside the transducer such that the Tx-Rx distance was 12 mm. The two optical fibers and the US transducer were assembled together in a measuring probe (see Fig. 4(E)).
A calibrated computer-controlled syringe pump (Chemix, Model Infusion 100) was used to generate flow patterns. It was controlled using a designated LabView® program and enabled accurate and reproducible generation of desired flow rates. To generate flow patterns in different depths, all channels were filled with white scattering fluid, while enabling flow in one row of channels at a time. Measurements were repeated for flow at 3 different rows (depths). For each depth, data was recorded for 10 minutes. The liquid flowing through the channels was collected into a drain reservoir. The flow rate was arbitrarily chosen (1000µl/min). A setup in which two rows of channels, shallow and deep, were activated simultaneously was also investigated.
The US sequence was generated using a computer controlled function generator. The optical fibers and the US transducer were placed such that the flow channels are within the sampled volume of the system. The diameter of the acoustic beam was 4mm (FWHM at −3dB), and the central ultrasound carrier frequency was 1MHz. The photodetector’s signals were sampled with an A/D converter. Data analysis was performed using a custom MATLAB program.
3. Results
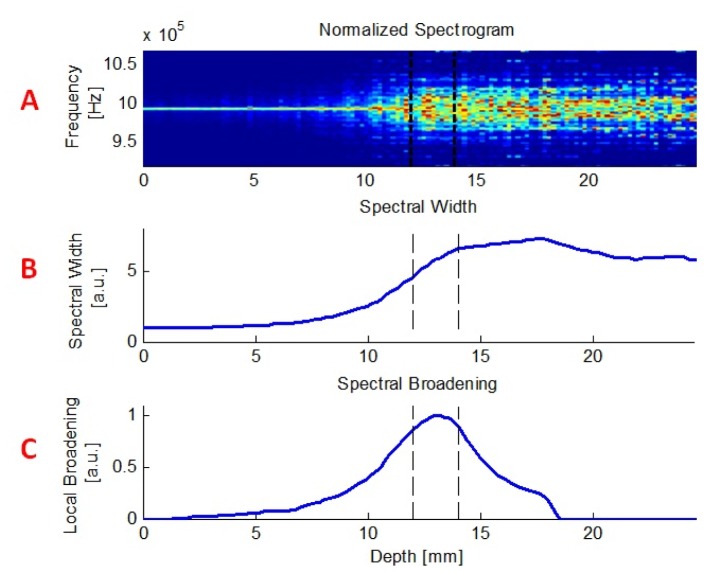
The ability to discriminate flow patterns at different depths was investigated using both computerized simulations and in-vitro experiments. Figure 5 shows the simulation's output for one representing case of a flow pattern through a specific layer. In this case, the flow layer was between 13 and 14mm, velocity was set to 5mm/sec and US pulse width was 4mm with increments of 0.2mm (as explained previously). The upper panel (A) exemplifies a normalized spectrogram, which is a visual representation of the light spectrum around the US carrier frequency (exactly in the middle) as it varies over time. The middle panel (B) includes the corresponding spectral width as a function of depth, showing narrower spectrum obtained from shallower depths and a significant broadening as the US pulse propagates, overlaps the flow layer and passes it. The “local broadening”, which is the flow index FI, as previously defined, is presented in the lower panel (C) of that figure. As opposed to the spectral width, the local broadening exhibits an increase only around the flow layer, and an equivalent decrease immediately thereafter.
Fig. 5.
An example of the simulation's output. Upper panel (A) demonstrates a normalized spectrogram. X axis corresponds to depth, Y axis represents the frequency, and color stands for amplitude in arbitrary units. Spectra obtained at different depths are plotted one next to another, thus creating the 2D image presented here. The middle panel (B) contains the matching spectral width, and the lower one (C), the obtained local broadening (FI).
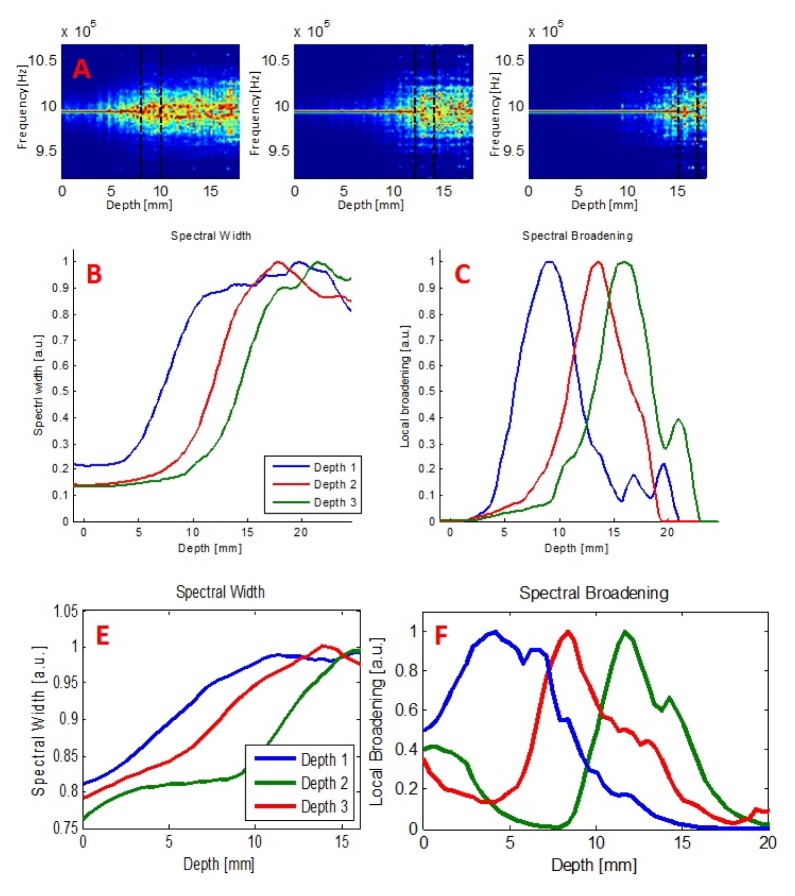
The simulation was repeated three times, corresponding to three flow layers at different depths (9-10mm, 13-14mm, 15-16mm) and yielded the following results, presented in Fig. 6(A)-6(C) .
Fig. 6.
(A-C) Simulation results for 3 different depths of the 1mm wide flow layer. Spectrograms (A), spectral width (B) and spectral broadening (C) curves exhibit apparent depth discrimination ability. (D-E) Experimental results obtained for flow patterns taking place at 3 different depths. Spectral width (D) and local broadening (E) both indicate a distinct depth discrimination.
Depth discrimination is clearly apparent, as the spectral broadening occurred at different depths, as expected.
The same experiments were performed in-vitro. In each case, only one row of channels (corresponding to the same depth relative to the surface as in the simulation) was operated, demonstrating flow in a specific layer only (depths 5.5mm, 9.5mm and 13.5mm respectively). Other channels (in other depths) were filled with static fluid to avoid air bubbles. Figure 6(E)-6(F) shows both the spectral width and its corresponding spectral broadening data. Similarly to the simulation, a distinct separation between flow patterns at different depths is clearly seen.
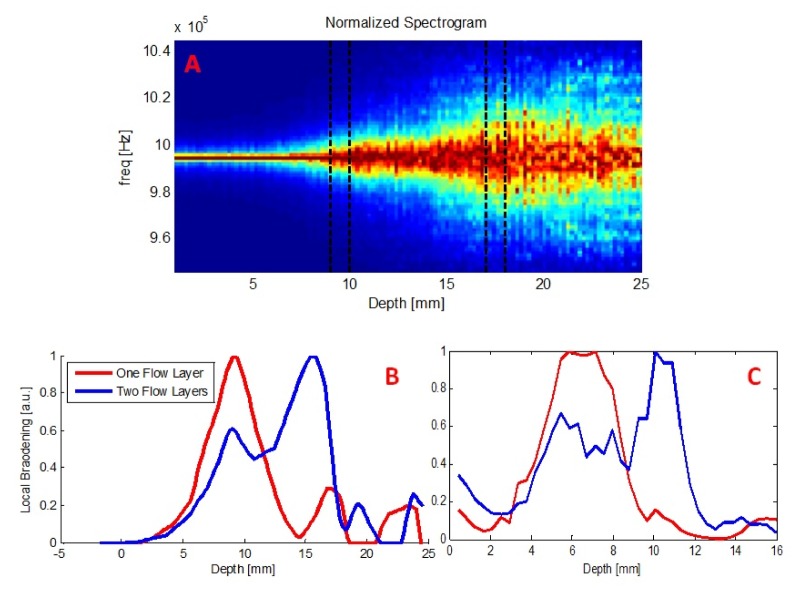
In addition to the ability to identify flow patterns at different depths illustrated in Fig. 6, we wanted to examine the ability to distinguish between simultaneous flow patterns at two depths. Thus, we further modeled a supplementary case, in which flow patterns were generated in two disparate layers within the sample, shallower and deeper, concurrently. Figure 7 shows the normalized spectrogram obtained by the simulation in this state. Dashed black lines represent the two flow layers at 9-10mm and 17-18mm. The flow velocities were chosen to be 2mm/sec and 5mm/sec, respectively, though a similar effect was observed when identical velocities were chosen for the different depths as well.
Fig. 7.
(A) Normalized spectrogram obtained by the simulation for two flow layers in parallel. Dashed black lines represent both flow layers. A noticeable spectral broadening is apparent in each flow layer. Simulation's (B) and experimental (C) results for parallel flow in two layers, shallow and deep. Red curves represent results obtained for one, shallow, flow layer only. Blue curves depict the case of shallow and deep flow patterns concurrently, providing an evidence for the ability to distinguish between those two.
Flow index (which is the local broadening parameter) results from both the simulation (B) and in-vitro experiment (C) are presented in Fig. 7. Red curves depict the case of flow patterns only in a shallow layer, whereas the blue ones show two simultaneous flow patterns.
One may note a clear identification and localization of both flow layers, suggesting that discrimination and elimination of shallower (superficial) flow effect is indeed feasible and achievable.
4. Discussion
NIRS based methods can provide a continuous, non-invasive tool for measuring cerebral blood flow. However, these techniques are usually affected and contaminated by artifacts originating in extra-cerebral tissues, through which light diffuses before and after propagating through the brain. Here we presented a novel technique, based on the acousto-optic effect that can extract flow patterns from a specific depth within a sample. Depth discrimination was demonstrated using both computerized simulation and in-vitro experiments. In addition, identification of two parallel flow patterns located at different depths, shallow and deep, was also clearly presented, suggesting that using such methods one can effectively reduce contamination of blood flow through the extra-cerebral layers on the obtained signals, and specifically extract cerebral flow data.
Figure 6 demonstrate local spectral broadening (flow) curves obtained in computerized simulation and in-vitro experiments. They both display 3 differentiated peaks, corresponding to 3 different depths of the flow patterns. These curves exhibit a rather wide range of depths and a fairly slow rise and decay times, rather than a very localized peak surrounding the flow channel. As mentioned above, the simulated flow layer width was 1mm (marked with dashed black lines in Fig. 5(A)), while the measured range of non-zero flow is larger than 1mm. It practically means that this technique has lower spatial resolution than the flow layer’s actual physical dimension. We associate this increased range to the behavior of light scattering in the tissue and the scatterer distribution along the photon paths (we discuss only the optical resolution as the acoustic resolution is better and not the limiting factor here. Under other conditions, acoustic pulse width may also affect the peak resolution). However, despite lower resolution, it provides much better depth discrimination than pure optical techniques based on NIRS or laser Doppler flowmetry, which are unable to discriminate between the two layers using a single wavelength of illumination [36]. In fact, preliminary simulations demonstrated that the optical properties of the “tissue” affect the broadening function. Further study should investigate the properties of the trajectories' and the different parameters which may influence the spatial resolution in the presented flow measurement.
Different improvements and modifications involve the possible use of a focused US beam, to target the measurement into one specific depth within the sample. Since the US beam will be directed to a certain depth, it can enhance the depth resolution. By doing so, we might also be able to shorten the required sampling time. Yet, to enable blood flow measurement in multiple depths, some kind of scanning procedure would have to be applied.
The agreement between the simulation and in-vitro experiments provided here implies that this simulation models correctly the phenomena involved in the acousto-optic effect. Thus, it may provide insight as to the occurring processes and serve as a tool for investigators in this field to answer different questions arising while adapting this technique. For example, using the simulation one can mimic different shapes of US beams (such as focused beam which was discussed before) and evaluate its contribution to the obtained signals or to the depth discrimination ability. It may assist in the optimization of system design and in the understanding of photon trajectories properties. It can be also used to simulate different flow protocols and examine the system performance and capabilities. Use of this platform with different velocity values may provide absolute quantification to the relation between spectral broadening and flow parameters as well.
The flow phantom described here has several limitations which have to be taken into account. First, it models only directional flow rather than flow in random directions such as in the microvasculature flow in tissue. Second, though having optical and acoustical properties similar to those of a tissue (as depicted in Table 1), the phantom's background decorrelation time differs from that of a living tissue. The Ultraflex which is used to construct the phantom has a longer scatterer decorrelation time. In addition, the phantom does not perfectly mimic tissue absorption. Finally, if cerebral blood flow is to be investigated, the phantom should include an additional component mimicking the skull that is known to significantly attenuate the US signal and of course affect the related UTL signal. However, considering the fact that the UTL technique was already proved to be able to monitor microvasculature flow in the brain [37], we believe that applying the algorithm described here, depth discrimination can be obtained in in-vivo environment as well. This should be further investigated in the future using an improved phantom which better mimics random flow direction in different depths along with skull modeling component.
While the proposed algorithm was validated in simulation and laboratory experiments, it should be further investigated in in-vivo experiments and clinical trials using manipulations which change cerebral blood flow only (rather than systemic ones which are prone to change the extra-cerebral blood flow as well). Our depth discriminative measurement can be compared to a superficial blood flow measurement, obtained by laser Doppler for instance, emphasizing the expected difference between the two. Those experiments will enable to assess the algorithm ability to reduce the influence of extra-cerebral tissue and specifically concentrate on cerebral blood flow measurements. It will further clarify the influence of real blood on the obtained signal (different optical properties from the used fluid, higher absorption, etc.). Previous studies carried with this technique showed that deep signals originating from the brain could indeed be obtained [37]. It was also showed that similar signals could not be obtained using other NIRS method [38], which may imply that using UTL technique as depicted here, depth discrimination could potentially be validated in-vivo as well.
Finally, a novel algorithm combining ultrasonic resolution with optical contrast, thus allowing identification of flow patterns as a function of depth within a sample, was introduced and validated. The inherent advantages of being continuous, non-invasive, and easy to use make this US Tagged NIRS (UT-NIRS) device very promising. The depth discrimination ability presented here is a powerful added value, not existing today, distinguishing this unique device from other available NIRS devices.
Acknowledgments
This work is supported by Ornim Medical LTD.
References and links
- 1.Steiner L. A., Andrews P. J., “Monitoring the injured brain: ICP and CBF,” Br. J. Anaesth. 97(1), 26–38 (2006). 10.1093/bja/ael110 [DOI] [PubMed] [Google Scholar]
- 2.Griffiths P. D., Hoggard N., Dannels W. R., Wilkinson I. D., “In vivo measurement of cerebral blood flow: a review of methods and applications,” Vasc. Med. 6(1), 51–60 (2001). 10.1177/1358836X0100600109 [DOI] [PubMed] [Google Scholar]
- 3.Aaslid R., Markwalder T.-M., Nornes H., “Noninvasive transcranial Doppler ultrasound recording of flow velocity in basal cerebral arteries,” J. Neurosurg. 57(6), 769–774 (1982). 10.3171/jns.1982.57.6.0769 [DOI] [PubMed] [Google Scholar]
- 4.Vajkoczy P., Roth H., Horn P., Lucke T., Thomé C., Hubner U., Martin G. T., Zappletal C., Klar E., Schilling L., Schmiedek P., “Continuous monitoring of regional cerebral blood flow: experimental and clinical validation of a novel thermal diffusion microprobe,” J. Neurosurg. 93(2), 265–274 (2000). 10.3171/jns.2000.93.2.0265 [DOI] [PubMed] [Google Scholar]
- 5.Nilsson G. E., Tenland T., Oberg P. A., “Evaluation of a laser Doppler flowmeter for measurement of tissue blood flow,” IEEE Trans. Biomed. Eng. 27(10), 597–604 (1980). 10.1109/TBME.1980.326582 [DOI] [PubMed] [Google Scholar]
- 6.Obeid A. N., Boggett D. M., Barnett N. J., Dougherty G., Rolfe P., “Depth discrimination in laser Doppler skin blood flow measurement using different lasers,” Med. Biol. Eng. Comput. 26(4), 415–424 (1988). 10.1007/BF02442302 [DOI] [PubMed] [Google Scholar]
- 7.Sheinfeld A., Gilead S., Eyal A., “Simultaneous spatial and spectral mapping of flow using photoacoustic Doppler measurement,” J. Biomed. Opt. 15, 066010 (2010). [DOI] [PubMed] [Google Scholar]
- 8.Yao J., Maslov K. I., Shi Y., Taber L. A., Wang L. V., “In vivo photoacoustic imaging of transverse blood flow by using Doppler broadening of bandwidth,” Opt. Lett. 35(9), 1419–1421 (2010). 10.1364/OL.35.001419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yao J., Wang L. V., “Photoacoustic brain imaging: from microscopic to macroscopic scales,” Neurophotonics 1(1), 011003 (2014). 10.1117/1.NPh.1.1.011003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kim M. N., Durduran T., Frangos S., Edlow B. L., Buckley E. M., Moss H. E., Zhou C., Yu G., Choe R., Maloney-Wilensky E., Wolf R. L., Grady M. S., Greenberg J. H., Levine J. M., Yodh A. G., Detre J. A., Kofke W. A., “Noninvasive measurement of cerebral blood flow and blood oxygenation using near-infrared and diffuse correlation spectroscopies in critically brain-injured adults,” Neurocrit. Care 12(2), 173–180 (2010). 10.1007/s12028-009-9305-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Durduran T., Yu G., Burnett M. G., Detre J. A., Greenberg J. H., Wang J., Zhou C., Yodh A. G., “Diffuse optical measurement of blood flow, blood oxygenation, and metabolism in a human brain during sensorimotor cortex activation,” Opt. Lett. 29(15), 1766–1768 (2004). 10.1364/OL.29.001766 [DOI] [PubMed] [Google Scholar]
- 12.Mesquita R. C., Schenkel S. S., Minkoff D. L., Lu X., Favilla C. G., Vora P. M., Busch D. R., Chandra M., Greenberg J. H., Detre J. A., Yodh A. G., “Influence of probe pressure on the diffuse correlation spectroscopy blood flow signal: extra-cerebral contributions,” Biomed. Opt. Express 4(7), 978–994 (2013). 10.1364/BOE.4.000978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Patel J., Marks K., Roberts I., Azzopardi D., Edwards A. D., “Measurement of cerebral blood flow in newborn infants using near infrared spectroscopy with indocyanine green,” Pediatr. Res. 43(1), 34–39 (1998). 10.1203/00006450-199801000-00006 [DOI] [PubMed] [Google Scholar]
- 14.Keller E., Froehlich J., Muroi C., Sikorski C., Muser M., “Neuromonitoring in intensive care: a new brain tissue probe for combined monitoring of intracranial pressure (ICP) cerebral blood flow (CBF) and oxygenation,” in Early Brain Injury or Cerebral Vasospasm (Springer, 2011), pp. 217–220. [DOI] [PubMed] [Google Scholar]
- 15.Gora F., Shinde S., Elwell C. E., Goldstone J. C., Cope M., Delpy D. T., Smith M., “Noninvasive measurement of cerebral blood flow in adults using near-infrared spectroscopy and indocyanine green: a pilot study,” J. Neurosurg. Anesthesiol. 14(3), 218–222 (2002). 10.1097/00008506-200207000-00008 [DOI] [PubMed] [Google Scholar]
- 16.Owen-Reece H., Elwell C. E., Harkness W., Goldstone J., Delpy D. T., Wyatt J. S., Smith M., “Use of near infrared spectroscopy to estimate cerebral blood flow in conscious and anaesthetized adult subjects,” Br. J. Anaesth. 76(1), 43–48 (1996). 10.1093/bja/76.1.43 [DOI] [PubMed] [Google Scholar]
- 17.Hiraoka M., Firbank M., Essenpreis M., Cope M., Arridge S. R., van der Zee P., Delpy D. T., “A Monte Carlo investigation of optical pathlength in inhomogeneous tissue and its application to near-infrared spectroscopy,” Phys. Med. Biol. 38(12), 1859–1876 (1993). 10.1088/0031-9155/38/12/011 [DOI] [PubMed] [Google Scholar]
- 18.Ohmae E., Ouchi Y., Oda M., Suzuki T., Nobesawa S., Kanno T., Yoshikawa E., Futatsubashi M., Ueda Y., Okada H., Yamashita Y., “Cerebral hemodynamics evaluation by near-infrared time-resolved spectroscopy: correlation with simultaneous positron emission tomography measurements,” Neuroimage 29(3), 697–705 (2006). 10.1016/j.neuroimage.2005.08.008 [DOI] [PubMed] [Google Scholar]
- 19.Ron A., Racheli N., Breskin I., Metzger Y., Silman Z., Kamar M., Nini A., Shechter R., Balberg M., “Measuring tissue blood flow using ultrasound modulated diffused light,” in Proc. of SPIE Vol, 2012), 82232J. 10.1117/12.906349 [DOI] [Google Scholar]
- 20.Briers J. D., Webster S., “Laser speckle contrast analysis (LASCA): a nonscanning, full-field technique for monitoring capillary blood flow,” J. Biomed. Opt. 1(2), 174–179 (1996). 10.1117/12.231359 [DOI] [PubMed] [Google Scholar]
- 21.Dunn A. K., Bolay H., Moskowitz M. A., Boas D. A., “Dynamic imaging of cerebral blood flow using laser speckle,” J. Cereb. Blood Flow Metab. 21(3), 195–201 (2001). 10.1097/00004647-200103000-00002 [DOI] [PubMed] [Google Scholar]
- 22.Bonner R., Nossal R., “Model for laser Doppler measurements of blood flow in tissue,” Appl. Opt. 20(12), 2097–2107 (1981). 10.1364/AO.20.002097 [DOI] [PubMed] [Google Scholar]
- 23.Burns P. N., “The physical principles of Doppler and spectral analysis,” J. Clin. Ultrasound 15(9), 567–590 (1987). 10.1002/jcu.1870150903 [DOI] [PubMed] [Google Scholar]
- 24.Ramaz F., Forget B., Atlan M., Boccara A.-C., Gross M., Delaye P., Roosen G., “Photorefractive detection of tagged photons in ultrasound modulated optical tomography of thick biological tissues,” Opt. Express 12(22), 5469–5474 (2004). 10.1364/OPEX.12.005469 [DOI] [PubMed] [Google Scholar]
- 25.Mahan G. D., Engler W. E., Tiemann J. J., Uzgiris E., “Ultrasonic tagging of light: theory,” Proc. Natl. Acad. Sci. U.S.A. 95(24), 14015–14019 (1998). 10.1073/pnas.95.24.14015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yao G., Wang L. V., “Theoretical and experimental studies of ultrasound-modulated optical tomography in biological tissue,” Appl. Opt. 39(4), 659–664 (2000). 10.1364/AO.39.000659 [DOI] [PubMed] [Google Scholar]
- 27.Bascom P. A., Cobbold R. S., Roelofs B. H., “Influence of spectral broadening on continuous wave Doppler ultrasound spectra: a geometric approach,” Ultrasound Med. Biol. 12(5), 387–395 (1986). 10.1016/0301-5629(86)90196-1 [DOI] [PubMed] [Google Scholar]
- 28.Newhouse V. L., Bendick P. J., Varner L. W., “Analysis of transit time effects on Doppler flow measurement,” IEEE Trans. Biomed. Eng. 23(5), 381–387 (1976). 10.1109/TBME.1976.324648 [DOI] [PubMed] [Google Scholar]
- 29.Wang L. V., Ku G., “Frequency-swept ultrasound-modulated optical tomography of scattering media,” Opt. Lett. 23(12), 975–977 (1998). 10.1364/OL.23.000975 [DOI] [PubMed] [Google Scholar]
- 30.Lev A., Sfez B., “In vivo demonstration of the ultrasound-modulated light technique,” J. Opt. Soc. Am. A 20(12), 2347–2354 (2003). 10.1364/JOSAA.20.002347 [DOI] [PubMed] [Google Scholar]
- 31.Metzger Y., Rokni M., Pery-Shechter R., “System and method for noninvasively monitoring conditions of a subject,” (Google Patents, 2009). [Google Scholar]
- 32.A. Tsalach, Y. Metzger, I. Breskin, R. Zeitak, and R. Shechter, “Ultrasound modulated light blood flow measurement using intensity autocorrelation function: a Monte-Carlo simulation,” in SPIE BiOS (Proc. SPIE 8943 Photons Plus Ultrasound: Imaging and Sensing 2014), pp. 89433N–89433N–89411. [Google Scholar]
- 33.N. Racheli, A. Ron, Y. Metzger, I. Breskin, G. Enden, M. Balberg, and R. Shechter, “Non-invasive blood flow measurements using ultrasound modulated diffused light,” in SPIE BiOS, (International Society for Optics and Photonics, 2012), 82232A–82232A–82238. [Google Scholar]
- 34.Cheong W.-F., Prahl S. A., Welch A. J., “A review of the optical properties of biological tissues,” IEEE J. Quantum Electron. 26(12), 2166–2185 (1990). 10.1109/3.64354 [DOI] [Google Scholar]
- 35.Christensen D., Ultrasonic Bioinstrumentation (Wiley, 1988). [Google Scholar]
- 36.Obeid A. N., Barnett N. J., Dougherty G., Ward G., “A critical review of laser Doppler flowmetry,” J. Med. Eng. Technol. 14(5), 178–181 (1990). 10.3109/03091909009009955 [DOI] [PubMed] [Google Scholar]
- 37.Schytz H. W., Guo S., Jensen L. T., Kamar M., Nini A., Gress D. R., Ashina M., “A new technology for detecting cerebral blood flow: a comparative study of ultrasound tagged NIRS and 133Xe-SPECT,” Neurocrit. Care 17(1), 139–145 (2012). 10.1007/s12028-012-9720-2 [DOI] [PubMed] [Google Scholar]
- 38.Schytz H. W., Wienecke T., Jensen L. T., Selb J., Boas D. A., Ashina M., “Changes in cerebral blood flow after acetazolamide: an experimental study comparing near-infrared spectroscopy and SPECT,” Eur. J. Neurol. 16(4), 461–467 (2009). 10.1111/j.1468-1331.2008.02398.x [DOI] [PMC free article] [PubMed] [Google Scholar]