Abstract
Intraoperative 5- aminolevulinic acid induced-Protoporphyrin IX (PpIX) fluorescence guidance enables maximum safe resection of glioblastomas by providing surgeons with real-time tumor optical contrast. However, visual assessment of PpIX fluorescence is subjective and limited by the distorting effects of light attenuation and tissue autofluorescence. We have previously shown that non-invasive point measurements of absolute PpIX concentration identifies residual tumor that is otherwise non-detectable. Here, we extend this approach to wide-field quantitative fluorescence imaging by implementing spatial frequency domain imaging to recover tissue optical properties across the field-of-view in phantoms and ex vivo tissue.
OCIS codes: (110.0110) Imaging systems; (110.0113) Imaging through turbid media; (170.6510) Spectroscopy, tissue diagnostics
1. Introduction
The extent of resection of glioma is a significant prognostic factor [1]. Specifically, complete or near-complete tumor resection, removing >98% of the gadolinium-enhancing tumor seen on MRI, increases patient survival and improves the efficacy of adjuvant radiotherapy and chemotherapy [1]. 5-aminolevulinic acid (ALA)-induced protoporphyrin IX fluorescence guided resection (PpIX-FGR) helps define tumor margins without disrupting the surgical work flow [2]. 5-ALA is administered orally at~3h prior to surgery. After removing the bulk tumor, the surgical field is illuminated with violet-blue light, whereupon residual tumor tissue is visualized by the red PpIX fluorescence. PpIX-FGR has shown increased complete resection rates (65% vs. 36%) and prolonged progression-free survival (16.7 vs. 11.8 months) [3]. However, the technique remains qualitative and subjective.
Since tissue is highly scattering, the measured fluorescence signal at the tissue surface is distorted, depending on the wavelength-dependent reduced scattering coefficient, and absorption coefficient, , at the excitation and emission wavelengths. This results in loss of sensitivity to detect residual tumor [4]. The PpIX fluorescence signal is also seen on a background of tissue autofluorescence [5]. These confounding factors limit the sensitivity of direct visual fluorescence guidance [6]. We have shown that quantitative assessment of the true fluorophore concentration, [PpIX], can improve residual tumor detection [6] using a contact fiber-optic probe that measures both the tissue fluorescence and diffuse reflectance spectra at two source-detector separations. Applying a spectrally-constrained diffusion model, the intrinsic optical properties are uncoupled from the fluorescence signal, yielding absolute measurement of [PpIX] with an accuracy of ± 10% down to ~10 ng/g. Ongoing clinical trials have demonstrated increased sensitivity and specificity for high-grade glioma and extension of FGR to low-grade disease [6]. However, this quantitative fluorescence spectroscopy (qFS) technique samples the resection surface only point-by-point. Hence, we are pursuing several approaches to wide-field quantitative fluorescence imaging, qFI [7]. One approach uses a semi-empirical ratiometric correction algorithm based on hyperspectral florescence and diffuse reflectance imaging [7]. Here we present the first results of a more rigorous, model-based algorithm using spatial frequency domain imaging (SFDI) in diffuse reflectance mode to map the wavelength-dependent tissue optical properties, which are then applied on a pixel-by-pixel basis to correct the measured fluorescence image.
SFDI determines and as 2D maps by projecting sinusoidal patterns of different spatial frequencies onto the tissue surface [8], which acts as a low-pass filter. The degree of blurring at a given spatial frequency depends on the tissue optical properties, as well as the modulation transfer function of the illumination-detection system. After compensating for the latter, a standard diffusion theory approximation (SDA) or a Monte Carlo (MC)-based look-up table (LUT) is then used to solve the inverse problem and extract the optical properties.
The system uses multi-wavelength excitation and a liquid crystal tunable filter (LCTF) coupled to a 14-bit CCD, enabling hyperspectral SFDI. The system integrates quantitative diffuse reflectance imaging and hyperspectral fluorescence imaging to produce quantitative maps of [PpIX]. While others have used multi-wavelength SFDI to correct fluorescence images in the visible domain [9] or to obtain near-infrared chromophore concentrations [10], we have extended SFDI to extract optical properties in both the diffusive and sub-diffusive regime, where the transport albedo, = /( + ), can be as low as 0.2 in glioma at 405 nm [4]. Here we report the capability to recover tissue optical properties in these regimes and then apply the qFI model to obtain quantitative fluorescence images in both tissue-simulating phantoms and ex vivo tissues. Finally, the derived [PpIX] values are compared to those measured by the “gold standard” of qFS.
2. Methodology
2.1 SFDI system and experimental setup
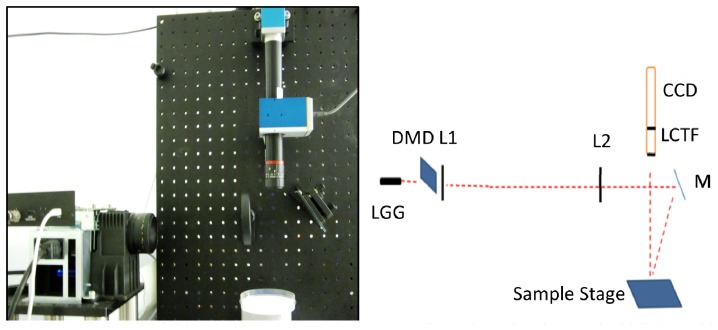
The SFD-enabled qFI system is shown in Fig. 1 . The DLP light engine (0.55XGA Series 450 DMD, Texas Instruments, Dallas, Tx) was customized for this application. The standard DLP white light source was replaced by 6 LEDs (Spectra X, Lumencor, Beaverton, OR) at 390, 438, 475, 512, 586 and 632 nm. The light is focused onto the micromirror array by a 3 mm liquid light guide (LGG0338, ThorLabs, Montreal, Canada). Specular reflection is limited by illuminating slightly off normal incidence. In front of the 14-bit CCD (Pixelfly, PCO AG, Kelheim, Germany), a C-mount lens couples the CCD to the visible-range liquid crystal tunable filter (LCTF: varispec-07-02, Perkin Elmer. Inc, Waltham, MA). The 20 cm working distance and 4x4 cm field-of-view approximate the neurosurgical microscope.
Fig. 1.
(a) Photograph of the SFDI qFI system; (b) corresponding schematic with the liquid light guide (LGG), digital micromirror device (DMD), lenses (L1, L2), mirror (M1), liquid crystal tunable filter (LCTF), charge-coupled device (CCD) and the sample stage.
2.2 SFDI implementation
In SFDI, the structured light patterns illuminating the surgical field are sinusoids of the form:
| (1) |
, where is the illumination source intensity, is the spatial frequency, is the modulation depth and is the spatial phase. The diffuse reflected intensity image is also a superposition of spatially modulated illumination ( ) and planar illumination ( ), where has the form:
| (2) |
, where is the modulation amplitude and . We choose to recover by projecting the same pattern three times with phase shifts of and applying a time-domain amplitude demodulation scheme over applying the Hilbert transform on a single phase intensity image, because the Hilbert transform results in poor image quality from ringing effects in the frequency domain [8]:
| (3) |
, while the DC reflectance amplitude, , is obtained from the average of three phase-shifted images for the same :
| (4) |
The calibrated demodulated reflectance, is formed from the ratio of the demodulated intensity measured on the sample, to that on a reference standard of known optical properties, multiplied by the diffuse reflectance, , of the standard:
| (5) |
2.3 Quantitative reflectance imaging
While most studies have applied SFDI in the near- infrared with SDA as the light transport model [8,11], MC-based LUTs have also been constructed for the visible range where the diffusion model starts to break down [12,13]. Since the reported tissue optical properties in glioma ( ~3 mm−1 and ~1 mm−1) at the excitation wavelength are in the sub-diffusive regime [4], MC is the more appropriate model. However, we present optical properties in the diffusive regime as well as the sub-diffusive regime derived by SDA only, because our previous results show that SDA derived optical properties in the sub-diffusive regime better compare to their expected values with a relative error similar to those reported for scattering dominant tissue-like phantoms [14].
2.3.1 Diffusive regime
To validate the performance of the system, three liquid phantoms were made from 20% Intralipid (Fresenius Kabi, Sweden) as the scatterer and India ink as the absorber, varying the concentrations to produce and values similar to glioma at the PpIX fluorescence emission peak ~635 nm as exemplified in Table 1 and reported in [4]. The phantoms were imaged at 632 nm for fx between 0 and 1.7 mm−1, each for 25 ms integration time. The modulated images were collected with the LCTF set to 640 nm. Eqs. (3), (4), (5) were applied to generate images (fx). For each pixel, these measurements were then fitted to the spatially-resolved diffuse reflectance predicted by SDA in the frequency domain [8]. Each measurement was repeated in triplicate.
Table 1. Summary of phantom optical properties used to test the qFI model in order of increasing transport albedo, each used with 5 µg/ml PpIX concentration.
|
(mm−1) |
(mm−1) |
a’ |
|---|---|---|
| 6.0 | 1.5 | 0.20 |
| 6.0 | 2.0 | 0.25 |
| 4.0 | 1.5 | 0.27 |
| 4.0 | 2.0 | 0.33 |
| 1.4 | 1.0 | 0.41 |
| 2.0 | 1.5 | 0.42 |
| 3.0 | 2.3 | 0.43 |
| 2.0 | 2.3 | 0.54 |
2.3.2 Sub-diffusive regime
Since we are interested in extracting maps of and at the PpIX excitation wavelength of 405 nm, SFDI will be implemented on absorption-dominant tissue, where the diffusion model is expected to break down ( / <3) [8]. In addition, the source-detector separation for diffusive conditions should be > 3/ , which corresponds to fx< 0.33( + ). Although < at 405 nm, we justify the use of SDA to recover both the optical properties by extending the SFDI frequency up to 1.7 mm−1, thereby still satisfying the condition fx< 0.33 . Using higher spatial frequencies is particularly useful in the sub-diffusive domain, since it better separates the effects of tissue absorption from scattering on the modulated reflectance image. This is because higher absorption causes the diffuse reflectance to attenuate more slowly with spatial frequency. Therefore, the upper limit, while still satisfying the above condition, is chosen by determining the spatial frequency that reduces (fx) to half its maximum value ( (fx = 0)) for a given range of and . Here the average and values in the sub-diffusive regime are 4 and 2 mm−1, respectively, so that is around 1.7 mm−1. In principle, projecting higher spatial frequencies is possible because higher retains the higher frequency patterns, thus keeping the modulated signal above background noise.
In order to simulate tissue absorption at 405 nm, yellow food dye was added at varying concentrations producing optical properties with from 0.2 to 0.6. The same spatial frequencies as above were used and were collected from 420 to 720 nm. The raw images were sharper than the first set of phantoms but required a longer acquisition time of 100 ms to achieve comparable signal-to-noise. The reference Intralipid–dye phantom had and both equal to 1 mm−1. The true values were obtained from a spectrophotometer with a standard error of ± 2%. The expected value was derived empirically by Michels et al. and had a 2-4% uncertainty for a given Intralipid batch [15].
2.4 Quantitative Fluorescence Imaging
2.4.1 Fluorescence model
Recovering the true [PpIX] distribution is equivalent to accurately measuring the intrinsic PpIX fluorescence intensity, , defined as:
| (6) |
where , and are, respectively, the PpIX fluorescent quantum yield, wavelength-dependent absorption coefficient and extinction coefficient. Subscripts x and m refers to the excitation and emission wavelengths. Hence, measuring and knowing and should yield [PpIX]. However, due to light scattering, the detected fluorescence is not the true fluorescence and is modulated by tissue’s absorption and scattering coefficients at both the excitation and emission wavelength. For excitation at 400-440 nm, where the PpIX and hemoglobin absorption are high, the remitted fluorescent photons, ,detected at 600-720 nm can be assumed to travel similar path lengths to those for the diffuse reflectance signal, , in the same wavelength range. Hence, is proportional to multiplied by the fraction of excitation photons absorbed by PpIX and producing fluorescence. Thus [16],
| (7) |
where is the predicted total diffuse reflectance at the excitation wavelength and is the measured wavelength-dependent diffuse reflectance at the emission band 600-720 nm. is obtained by fitting the measured to the predicted SDA-based spatially-resolved with the spectral shapes of and as constraints. Rearranging to solve for wide field , the model becomes:
| (8) |
where and are the demodulated diffuse reflectance values.
In addition to producing a 2D map of , SFDI produces the demodulated and calibrated total diffuse reflectance images and using Eq. (5) as input to the modified qF model:
| (9) |
and are then the average of the DC reflectance images (see Eqs. (4,5) calculated for all frequencies.
2.4.2 Phantom studies
In fluorescence mode, the SFDI system projects a violet-blue uniform field (fx = 0). The raw fluorescence is captured from 600 to 720 nm in steps of 10 nm. The acquisition time varies from 0.5 to 2s depending on the optical properties. In reflectance mode, SFDI was implemented in both the violet-blue and red bands. The reflectance images from 420 to 720 nm were collected for 100 ms per wavelength.
PpIX (Sigma-Aldridge) was dissolved at 5µg/ml in dimethyl sulfoxide (DMSO), this being representative of the PpIX tissue concentration in high-grade glioma [4]. This was mixed with Intralipid and yellow dye of different concentrations to simulate tissue absorption at 405 nm. The resulting phantoms had = 0.2 to 0.6 with absorption coefficients as high as 6 mm−1, as summarized in Table 1. One phantom was used as the reference. The raw fluorescence and reflectance images were flat-field corrected and the modified qF model was applied using Eq. (9). qfx,m(λ) was scaled using the published PpIX fluorescence quantum yield of 0.5% [17]. As an additional comparison, the flat-field corrected fluorescence images were also normalized to the demodulated diffuse reflectance, Rx, to evaluate the performance of correcting the fluorescence images simply by the common Born normalization method.
2.4.3 Ex vivo tissue studies
As an intermediate step towards in vivo qFI, we used a tissue model comprising ground beef or chicken in a 3 cm deep petri dish. The center portion was mixed with 1.0 µg/ml and 3.0 µg/ml of PpIX in the chicken and beef, respectively. Polarizing filters were added to the illumination and detection to further limit specular reflection. Planar fluorescence images were collected from 600 to 720 nm and SFD images from 420 to 720 nm at fx = 0-1.49 mm−1. For SFDI analysis, two regions were selected per sample: the PpIX-rich central zone region and the PpIX-free surrounding zone. The recovered and 2D maps were used as inputs to the qFI model. [PpIX] was then calculated from the quantitative hyperspectral fluorescence images using the known basis spectrum and the built-in Matlab function lsqnonneg for nonnegative least-squares curve fitting. Since no significant autofluorescence was detected, PpIX and its photoproducts were considered as the only fluorophores. As an independent method, tissue was also sampled with the qFS probe.
3. Results and discussion
3.1 Quantitative reflectance imaging
3.1.1 Diffusive regime
The known and recovered optical coefficients are shown in Table 2 . The average standard deviation for each measurement performed in triplicate and normalized to the mean was ± 1.1%. These measurements were made on the same phantom at different times within 2 days. The expected error in preparing a new set of phantoms from Intralipid and India ink is estimated to be ± 2% [18].
Table 2. Accuracy in recovering phantom optical properties in the diffusive regime at 635 nm.
| True (mm−1) | True (mm−1) | SDA-derived (mm−1) (COVa) | SDA-derived (mm−1) (COV) | RMS |
|---|---|---|---|---|
| 0.002 | 0.87 | 0.0021 (5%) | 0.89 (2%) | 3.8% |
| 0.004 | 1.14 | 0.0043 (7.5%) | 1.19 (5%) | 6.4% |
| 0.006 | 1.42 | 0.0059 (1.7%) | 1.34 (5%) | 3.7% |
aCOV: coefficient of determination, relative difference between the true and SFDI-derived values. RMS: root mean square error
3.1.2 Sub-diffusive regime
Table 3 summarizes the results for recovering optical properties in the sub-diffusive regime. The combined RMS error increased from 5% for = 0.5 to 30% for = 0.3, attributed to the increasing breakdown of SDA. Interestingly, the average error in recovering is twice as high as that in recovering probably due to the uncertainty in the true scattering coefficient. Nevertheless, there is a systemic increase in the error when <0.35. While in principle, Monte Carlo simulations should be used for solving in the sub-diffusive domain, we have shown that SDA-derived optical properties have a relative error similar to that reported for scattering-dominant phantoms [14]. This may be due to selecting a standard phantom with properties also in the sub-diffusive regime as well as sampling at higher spatial frequencies.
Table 3. Accuracy in recovering phantom optical properties in the sub-diffusive regime.
| True (mm−1) | True (mm−1) | SDA-derived (mm−1) (COV) |
SDA-derived
(mm−1) (COV) |
RMS (%) |
|---|---|---|---|---|
| 2.00 | 1.50 | 2.13 (6.5%) | 1.25 (17%) | 12.9 |
| 2.00 | 2.00 | 2.15 (7.5%) | 2.07 (3.5%) | 5.85 |
| 2.00 | 2.50 | 2.05 (2.5%) | 2.29 (8.4%) | 6.20 |
| 4.00 | 1.50 | 4.47 (12%) | 1.28 (15%) | 13.6 |
| 4.00 | 2.00 | 3.60 (10%) | 1.91(4.5%) | 7.75 |
| 4.00 | 3.37 | 3.79 (5.3%) | 3.22 (4.5%) | 4.92 |
| 6.00 | 1.50 | 4.67 (22%) | 1.09 (27%) | 24.6 |
| 6.00 | 2.00 | 5.90 (1.7%) | 1.38 (31%) | 22.0 |
| 6.00 | 2.50 | 5.45 (9.2%) | 1.46 (42%) | 30.4 |
3.2 Quantitative fluorescence imaging
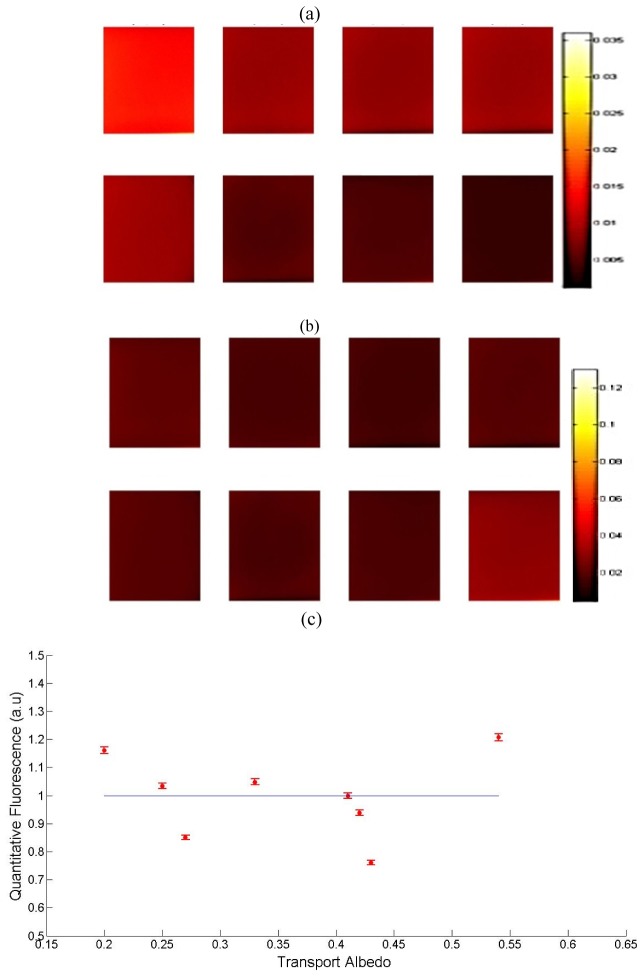
Figure 2(a) demonstrates the strong dependence of the raw fluorescence images on the optical properties. Figure 2(b) shows that the derived images have more constant intensity when qFI is applied, but with some overestimate for the lowest albedo phantom. Figure 2(c) shows the variation in the quantitative fluorescence images, plotting the mean intensities (and corresponding standard deviations) from each phantom shown in 2(b) after normalization to the mean fluorescent intensity across all eight phantoms. The standard deviation for each phantom indicates small variations in the derived fluorescence across the whole image. The mean relative standard deviations from all eight phantoms are summarized in Table 4 . Simply normalizing the measured fluorescence images to the reflectance images reduces the variance from 108% to 36% but applying the qFI model gives a much greater (6-7 fold) reduction. The largest error in the SFDI-derived values also corresponds to the lowest albedo case, suggesting that the modified qFI model still has a residual ( ) dependence on the tissue optical properties, which deteriorates for very low albedos. The relative standard deviation in [PpIX] for similar optical properties is when qFS is used [16].
Fig. 2.
(a) Raw fluorescence images for tissue phantoms with [PpIX] = 5µg/ml; (b) Derived fluorescence images after applying the qFI model. The phantom optical properties are shown in Table 1 and the images are displayed in order of increasing transport coefficient, µTR, (c) Corresponding plot of the mean quantitative fluorescent intensity of each image normalized to the mean fluorescent intensity. The error bars denote the standard deviation across each image relative to its mean intensity.
Table 4. Comparison of the relative and maximum standard deviation values for the PpIX phantoms, normalized to the mean in each case, using 3 different algorithms.
| Correction method | Relative standard deviation (%) | Maximum standard deviation (%) |
|---|---|---|
| Measured fluorescence | 107 | 303 |
| Born-normalized fluorescencea | 35.7 | 102 |
| qFI | 15.4 | 24.2 |
| qFSb | 10.1 | 15.2 |
Figures 3(a), 3(b) show the raw PpIX fluorescence image and the model-corrected fluorescence image from the chicken tissue sample detected at 640 nm. It is recognized that these ex vivo model tissues likely do not have the identical optical properties as glioma and normal brain tissue and in particular are likely less scattering. However, they are still highly diffusive, and so provide a reasonable proof-of-principle test of the correction algorithm. Indeed, the corrected fluorescence image does show a larger extent of PpIX signal compared to the raw fluorescence image, and this corresponds to the real situation. It is also known that the spatial distribution of PpIX near the tumor margin is not necessarily sharply defined, as it is in the model used here, since gliomas tend to be infiltrative. However, this should not markedly affect the accuracy of the correction algorithm.
Fig. 3.
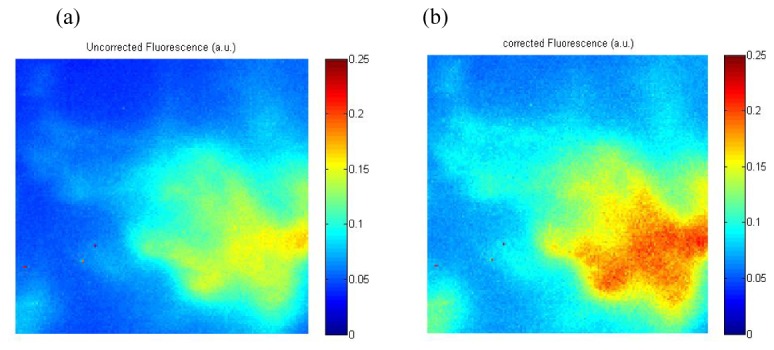
(a) Raw fluorescence image at 640 nm for the chicken sample with [PpIX] = 1µg/ml; (b) Derived fluorescence images after applying the qFI model.
Table 5 compares the mean values for tissue optical properties and the derived [PpIX] values obtained by applying the qFI to the same parameters obtained by the qFS probe. The value of (white) chicken tissue was measured as less than that of the more pigmented ground beef, which should not be the case. This is likely due to altered scattering properties due to the different tissue handling prior to measurements (frozen & thawed versus fresh, resp.). Marked effects on scattering by freeze/thaw have been reported elsewhere [19]. The mean [PpIX] derived by qFI for each sample correlates well with the true value (within 20%), as well as with that derived from qFS.
Table 5. Comparison of SFD-qFI derived optical properties (mm−1) and [PpIX] (µg/ml) with those derived by qFS. The known [PpIX] added to chicken and beef were 1.0 µg/l and 3.0 µg/l.
| Tissue |
qFI |
[PpIX] |
qFS |
[PpIX] | ||
|---|---|---|---|---|---|---|
| chicken | 0.74 ± 0.17 | 0.74 ± 0.09 | 0.81 ± 0.02 | 0.81 ± 0.27 | 1.11 ± 0.04 | 0.99 ± 0.37 |
| beef | 1.43 ± 0.19 | 1.21 ± 0.42 | 2.56 ± 0.30 | 1.25 ± 0.38 | 1.36 ± 0.76 | 2.56 ± 0.21 |
astd is the standard deviation in the recovered optical parameters and [PpIX] across the region of interest in Fig. 3
As regards to sensitivity, preliminary data suggest that [PpIX] down to ~20 ng/g in tissues with as high as 8.8 mm−1 can be measured, but the uncertainty in this is yet to be determined. Clinically, [PpIX] found in biopsy sampled glioma patients varied from 3.6 to 4523 ng/g for tumor grades 1 to 4, respectively [6]. Hence, although we expect the sensitivity of the intraoperative probe (10 ng/g) to be superior to that of SFD-based wide-field qF imaging, a sensitivity of 20 ng/g is still clinically relevant for higher-grade patients. Additionally, the sensitivity of the semi-empirical ratiometric approach is reported to be 100 ng/ml ± 10% when the same CCD presented here is used [7]. This sensitivity is reduced to 20 ng/ml ± 20% when a CMOS based camera is used [7]. The lower limit for detecting and quantifying the PpIX concentration in tissue will also be affected by the level of tissue autfluorescence. Ongoing work includes evaluating the accuracy of qFI to estimate [PpIX] in vivo using an intracranial tumor-bearing rat model. Our previous semi-empirical quantitative fluorescence imaging studies have shown that the corrected fluorescence spectrum can be spectrally decomposed into the contributions from PpIX, PpIX photoproducts (generated during surgical exposure of the tissue) and tissue autofluroescence, and this approach should be equally valid using the correction algorithms developed here [7].
4. Conclusions
In summary, the performance of a novel multi-wavelength, spectrally-resolved SFD-based system for quantitative wide-field fluorescence imaging has been evaluated in tissue-simulating phantoms and in an ex vivo tissue model. This is an extension to the current point qFS probe that is in clinical trials and an alternative to our previously-reported semi-empirical ratiometric technique [7]. The transport albedo range of the tissue optical properties tested spans the diffusive as well as the sub-diffuse regime. The errors (2-30%) in the SDA-derived optical properties in the sub-diffusive regime are within the range of errors reported by SDA-derived optical properties in the diffusive regime when compared to MC [8]. This was made possible by calibrating the system with a standard of similar albedo, as well as sampling at higher spatial frequencies to better separate absorption and scattering.
As for the fluorescence model, the relative standard deviation of the corrected fluorescence images across a wide range of tissue phantom optical properties (Table 1) compares well with that evaluated by qFS (15% vs. 10%). [PpIX] values derived by SFD-qFI from ex vivo tissue are within 20% the absolute [PpIX]. This is compared to the calculated [PpIX] from qFS, which are within 14% of the true [PpIX]. Even though current acquisition times do not allow for real-time imaging and analysis, video-rate imaging should be possible after automating the sequence for patterned illumination and optimizing the inverse solver. Additionally, substituting the CCD with a CMOS based camera may not only improve the accuracy and sensitivity of quantifying fluorescence images as discussed above, but will significantly reduce acquisition times. Moreover, a replica of this benchtop SFDI system is being modified to mount on a surgical microscope for first clinical trials in glioma surgery [20]. Finally, structured-light profilometry via the SFDI system is being implemented to account for the curved surface of the tumor resection bed at craniotomy [20].
Acknowledgments
This work was supported by the National Institutes of Health (US): grant # R01 NS052274.
References and links
- 1.Colditz M. J., Jeffree R. L., “Aminolevulinic acid (ALA)-protoporphyrin IX fluorescence guided tumour resection. Part 1: Clinical, radiological and pathological studies,” J. Clin. Neurosci. 19(11), 1471–1474 (2012). 10.1016/j.jocn.2012.03.009 [DOI] [PubMed] [Google Scholar]
- 2.Colditz M. J., Leyen K., Jeffree R. L., “Aminolevulinic acid (ALA)-protoporphyrin IX fluorescence guided tumour resection. Part 2: Theoretical, biochemical and practical aspects,” J. Clin. Neurosci. 19(12), 1611–1616 (2012). 10.1016/j.jocn.2012.03.013 [DOI] [PubMed] [Google Scholar]
- 3.Stummer W., Pichlmeier U., Meinel T., Wiestler O. D., Zanella F., Reulen H. J., ALA-Glioma Study Group , “Fluorescence-guided surgery with 5-aminolevulinic acid for resection of malignant glioma: a randomised controlled multicentre phase III trial,” Lancet Oncol. 7(5), 392–401 (2006). 10.1016/S1470-2045(06)70665-9 [DOI] [PubMed] [Google Scholar]
- 4.Valdés P. A., Kim A., Leblond F., Conde O. M., Harris B. T., Paulsen K. D., Wilson B. C., Roberts D. W., “Combined fluorescence and reflectance spectroscopy for in vivo quantification of cancer biomarkers in low- and high-grade glioma surgery,” J. Biomed. Opt. 16(11), 116007 (2011). 10.1117/1.3646916 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Marcu L., Jo J. A., Butte P. V., Yong W. H., Pikul B. K., Black K. L., Thompson R. C., “Fluorescence lifetime spectroscopy of glioblastoma multiforme,” Photochem. Photobiol. 80(1), 98–103 (2004). 10.1562/2003-12-09-RA-023.1 [DOI] [PubMed] [Google Scholar]
- 6.Valdés P. A., Leblond F., Kim A., Harris B. T., Wilson B. C., Fan X., Tosteson T. D., Hartov A., Ji S., Erkmen K., Simmons N. E., Paulsen K. D., Roberts D. W., “Quantitative fluorescence in intracranial tumor: implications for ALA-induced PpIX as an intraoperative biomarker,” J. Neurosurg. 115(1), 11–17 (2011). 10.3171/2011.2.JNS101451 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Valdés P. A., Jacobs V. L., Wilson B. C., Leblond F., Roberts D. W., Paulsen K. D., “System and methods for wide-field quantitative fluorescence imaging during neurosurgery,” Opt. Lett. 38(15), 2786–2788 (2013). 10.1364/OL.38.002786 [DOI] [PubMed] [Google Scholar]
- 8.Cuccia D. J., Bevilacqua F., Durkin A. J., Ayers F. R., Tromberg B. J., “Quantitation and mapping of tissue optical properties using modulated imaging,” J. Biomed. Opt. 14(2), 024012 (2009). 10.1117/1.3088140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yang B., Sharma M., Tunnell J. W., “Attenuation-corrected fluorescence extraction for image-guided surgery in spatial frequency domain,” J. Biomed. Opt. 18(8), 080503 (2013). 10.1117/1.JBO.18.8.080503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Saager R. B., Cuccia D. J., Saggese S., Kelly K. M., Durkin A. J., “Quantitative fluorescence imaging of protoporphyrin IX through determination of tissue optical properties in the spatial frequency domain,” J. Biomed. Opt. 16(12), 126013 (2011). 10.1117/1.3665440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Laughney A. M., Krishnaswamy V., Rice T. B., Cuccia D. J., Barth R. J., Tromberg B. J., Paulsen K. D., Pogue B. W., Wells W. A., “System analysis of spatial frequency domain imaging for quantitative mapping of surgically resected breast tissues,” J. Biomed. Opt. 18(3), 036012 (2013). 10.1117/1.JBO.18.3.036012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Erickson T. A., Mazhar A., Cuccia D., Durkin A. J., Tunnell J. W., “Lookup-table method for imaging optical properties with structured illumination beyond the diffusion theory regime,” J. Biomed. Opt. 15(3), 036013 (2010). 10.1117/1.3431728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lin A. J., Ponticorvo A., Konecky S. D., Cui H., Rice T. B., Choi B., Durkin A. J., Tromberg B. J., “Visible spatial frequency domain imaging with a digital light microprojector,” J. Biomed. Opt. 18(9), 096007 (2013). 10.1117/1.JBO.18.9.096007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sibai M., Veilleux I., Eliott J. T., Leblond F., Roberts D. W., Wilson B. C., “Quantitative fluorescence imaging enabled by spatial frequency domain optical-property mapping in the sub-diffusive regime for surgical guidance,” Proc. SPIE 93110, 93110C (2015). [Google Scholar]
- 15.Michels R., Foschum F., Kienle A., “Optical properties of fat emulsions,” Opt. Express 16(8), 5907–5925 (2008). 10.1364/OE.16.005907 [DOI] [PubMed] [Google Scholar]
- 16.Kim A., Khurana M., Moriyama Y., Wilson B. C., “Quantification of in vivo fluorescence decoupled from the effects of tissue optical properties using fiber-optic spectroscopy measurements,” J. Biomed. Opt. 15(6), 067006 (2010). 10.1117/1.3523616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kepshire D. S., Gibbs-Strauss S. L., O’Hara J. A., Hutchins M., Mincu N., Leblond F., Khayat M., Dehghani H., Srinivasan S., Pogue B. W., “Imaging of glioma tumor with endogenous fluorescence tomography,” J. Biomed. Opt. 14(3), 030501 (2009). 10.1117/1.3127202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Spinelli L., Botwicz M., Zolek N., Kacprzak M., Milej D., Sawosz P., Liebert A., Weigel U., Durduran T., Foschum F., Kienle A., Baribeau F., Leclair S., Bouchard J. P., Noiseux I., Gallant P., Mermut O., Farina A., Pifferi A., Torricelli A., Cubeddu R., Ho H. C., Mazurenka M., Wabnitz H., Klauenberg K., Bodnar O., Elster C., Bénazech-Lavoué M., Bérubé-Lauzière Y., Lesage F., Khoptyar D., Subash A. A., Andersson-Engels S., Di Ninni P., Martelli F., Zaccanti G., “Determination of reference values for optical properties of liquid phantoms based on Intralipid and India ink,” Biomed. Opt. Express 5(7), 2037–2053 (2014). 10.1364/BOE.5.002037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mesradi M., Genoux A., Cuplov V., Abi Haidar D., Jan S., Buvat I., Pain F., “Experimental and analytical comparative study of optical coefficient of fresh and frozen rat tissues,” J. Biomed. Opt. 18(11), 117010 (2013). 10.1117/1.JBO.18.11.117010 [DOI] [PubMed] [Google Scholar]
- 20.Angulo-Rodrigues L. M., Jermyn M., Kolste K. K., Valdes P. A., Pichette J., Gosselin Y., Sibai M., Mok K., Petrecca K., Roberts D. W., Paulsen K. D., Wilson B. C., Leblond F., “A surgical microscope combining real-time surface reconstruction and spectroscopic fluorescence imaging with a light transport model to quantify visible and near-infrared fluorescent molecular markers,” Proc. SPIE 9313, 9313C (2015). [Google Scholar]