Birefringence imaging of posterior eye by multi-functional Jones matrix optical coherence tomography

Abstract

A clinical grade prototype of posterior multifunctional Jones matrix optical coherence tomography (JM-OCT) is presented. This JM-OCT visualized depth-localized birefringence in addition to conventional cumulative phase retardation imaging through local Jones matrix analysis. In addition, it simultaneously provides a sensitivity enhanced scattering OCT, a quantitative polarization uniformity contrast, and OCT-based angiography. The probe beam is at 1-μm wavelength band. The measurement speed and the depth-resolution were 100,000 A-lines/s, and 6.6 μm in tissue, respectively. Normal and pathologic eyes are examined and several clinical features are revealed, which includes high birefringence in the choroid and lamina cribrosa, and birefringent layered structure of the sclera. The theoretical details of the depth-localized birefringence imaging and conventional phase retardation imaging are formulated. This formulation indicates that the birefringence imaging correctly measures a depth-localized single-trip phase retardation of a tissue, while the conventional phase retardation can provide correct single-trip phase retardation only for some specific types of samples.

1. Introduction

Polarization-sensitive optical coherence tomography (PS-OCT) is a functional extension of OCT that measures the polarization properties of samples. Conventional PS-OCT measures the cumulative phase retardation, which originates from tissue birefringence [1–3], and has been applied in several medical fields, including cardiology [4, 5], dentistry [6, 7], dermatology [8–10], and oncology [11, 12].

There are various tissues in the eye with birefringent characteristics. PS-OCT has been used to investigate these characteristics in both the anterior [13–17] and the posterior segments [3, 18–20]. The main source of birefringence in biological tissue is fibrous tissues such as the collagenous intercellular matrix, smooth muscles, and nerve fibers. The collagen largely exists in the sclera [21] and the lamina cribrosa [22]. Smooth muscle is a main component of vessel walls [23] which are abundant in the choroid.

PS-OCT has been used for qualitative observation and quantitative measurements in ophthalmology. Qualitative observation was performed for both the posterior eye [19, 20, 24] and the anterior eye [13, 25]. Quantitative measurements have been performed for the nerve fiber layer (NFL) [26–30], Henle’s fiber layer [31], the cornea [32], the anterior sclera [33], and filtration blebs in trabeculectomy [34].

While PS-OCT has been widely used for eye imaging, the clinical utility and validity are not widely accepted. This is partially because of a fundamental limitation of cumulative phase retardation imaging in that it is based on a strong hypothesis about the optic axis orientation of the tissue; this will be discussed in detail in Section 2.2. In contrast, Jones-matrix-based birefringence imaging [35], which is also denoted as local phase retardation imaging, does not use this hypothesis. Birefringence imaging is thus a promising method for the investigation of tissue polarization property, and has been used for several tissues, including the anterior eye segment [17, 35] and the coronary artery [36].

While birefringence imaging is a promising method, there are two outstanding problems with the application of this method to posterior eye imaging. The first is the low signal-to-noise ratio (SNR) of birefringence measurement. The birefringence is a local phase retardation that occurs in a small depth region, and it is significantly smaller than cumulative phase retardation. In contrast, the amount of phase retardation noise is identical for both local and cumulative phase retardation measurements. As a result, the SNR of phase retardation decreases as the depth region, in which the local phase retardation is defined, becomes smaller, i.e., as the resolution of the birefringence measurements increases. This is particularly problematic for clinical posterior eye imaging, because the SNR of the OCT signal is low in general, and thus the phase retardation noise is high. Several methods have been developed to increase the SNR, including adaptive Jones averaging [37, 38], complex Gaussian averaging [17], and intensity averaging [39].

While these methods have significantly improved the overall image quality, there is another problem for the quantification of tissue birefringence. The mean estimation is one of commonly utilized estimators to quantify the cumulative and local phase retardations, but it is strongly biased if the SNR of the OCT signal, and not the SNR of the phase retardation, is low. It is because the distribution of repeatedly measured phase retardations, even at a single location, is not centered at the true phase retardation and is skewed. This distortion of the distribution becomes severer with lower SNR [35, 40]. Typically, an effective SNR of around 25 dB is required to obtain reliable phase retardation [35,40], but this level is hardly achieved for posterior eye measurements as the typical reflectivity of the retina is only around 10⁻³ to 10⁻⁵ [41]. Kasaragod et al. overcame this issue by using a maximum a-posteriori (MAP) estimator for birefringence [42]. Quantitative birefringence imaging of the anterior eye was demonstrated using a combination of adaptive Jones matrix averaging and the MAP estimator [42]. However, clinically meaningful posterior birefringence imaging using this method has not been demonstrated to date.

In this paper, we demonstrate clinical birefringence imaging of the posterior eye using multifunctional Jones-matrix optical coherence tomography (JM-OCT). A single JM-OCT scan provides scattering OCT, birefringence imaging, quantitative degree-of-polarization uniformity (Makita DOPU, or M-DOPU) imaging [43], and vasculature imaging based on Jones matrix correlation [44, 45]. First, we formulate the theories of cumulative phase retardation and local phase retardation (birefringence) imaging. This allows us to clarify the limitations of cumulative phase retardation imaging in detail. A JM-OCT prototype based on 1-μm swept source OCT (SS-OCT) technology is presented. This system is ready to be used in a clinic as it has a compact footprint similar to a commercially available OCT, the high stability, and an easy interface enabling operation by a non-engineering specialist. The clinical utility of birefringence imaging is then examined by measuring both normal and pathologic eyes.

2. Theory of local polarization property imaging

In this section, we first formulate the theory of conventional cumulative phase retardation (cPR) imaging. This formulation reveals the implicit assumption that is used in cPR, which limits the accuracy of the conventional birefringence measurement method that is based on cPR. We then introduce local phase retardation imaging based on local Jones matrices; this method uses less strict assumptions than cPR imaging, and thus provides a more rational estimate of birefringence for practical biological and medical samples.

The notations used in this and later sections are summarized in Appendix B.

2.1. Cumulative Jones matrix and cumulative phase retardation

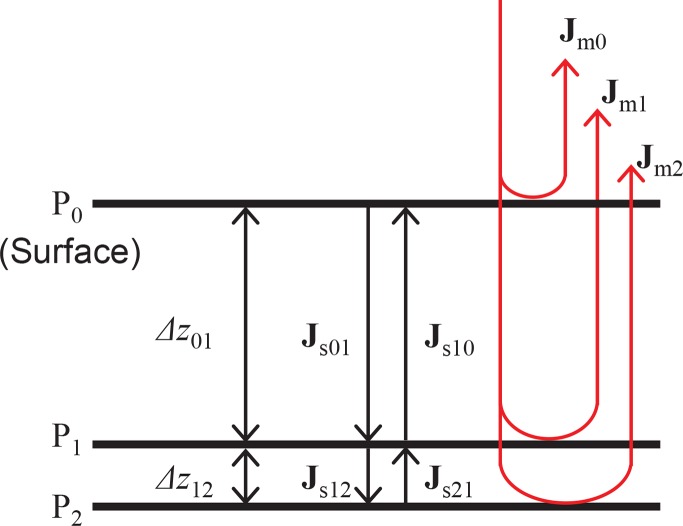
Figure 1 shows the Jones matrix model of a multi-layered sample. P_i represents the i-th depth position. More specifically, P₀ represents the position of the tissue surface. J_mi is the raw measured Jones matrix at the depth position P_i and J_sij is the single-trip Jones matrix from P_i to P_j. In the following formulation, L_ij denotes a tissue layer located between P_i and P_j. Δz_ij is the distance between P_i and P_j, i.e., it is the thickness of L_ij.

Fig. 1.

The Jones matrix model of multi-layered tissue.

By scanning the sample, JM-OCT primarily provides a raw measured Jones matrix, which is called as the raw measured Jones matrix. Each entry of the raw measured Jones matrix is a complex OCT image where the columns of the matrix correspond to the two incident polarization states and the rows represent two detection polarization states [38, 46]. Specifically, the raw measured Jones matrix at P_i becomes

$${\mathbf{J}}_{\text{m}i}={\mathbf{J}}_{\text{out}}{\mathbf{J}}_{\text{r}0i}{\mathbf{J}}_{\text{in}},$$ (1)

where J_out and J_in are the Jones matrices of the collection and illumination optics, respectively. For retinal imaging, the collection and illumination optics are considered to include ocular optics. J_r0i is the round-trip Jones matrix from the sample surface to P_i and J_r0i = J_si0J_s0i = J_s0i^TJ_s0i, where we used the fact that J_si0 = J_s0i^T. The superscript T indicates a transpose.

By assuming that the reflection at the sample surface is specular, the measured Jones matrix at the surface becomes

$${\mathbf{J}}_{\text{m}0}={\mathbf{J}}_{\text{out}}{\mathbf{J}}_{\text{in}}.$$ (2)

A cumulative Jones matrix that represents the polarization property from the surface to a specified depth position is then obtained by multiplying the inverse of the surface measured Jones matrix by the measured Jones matrix of that depth position. This means that the cumulative Jones matrix at P_i is

$${\mathbf{J}}_{\text{c}i}\equiv {\mathbf{J}}_{\text{m}i}{{\mathbf{J}}_{\text{m}0}}^{-1}={\mathbf{J}}_{\text{out}}{\mathbf{J}}_{\text{r}0i}{{\mathbf{J}}_{\text{out}}}^{-1},$$ (3)

where J_ci represents the cumulative Jones matrix at P_i. As shown by the equation, J_ci is a similar matrix of the round-trip sample Jones matrix J_r0i, and thus they have the same eigenvalues.

The cPR is then obtained by calculating the phase difference between the two eigenvalues of the cumulative Jones matrix. Because the cumulative Jones matrix has the same eigenvalues as the round-trip sample Jones matrix, the cPR is identical to the round-trip phase retardation (rPR) of the sample, and this rPR is the phase retardation that is measured by conventional PS-OCT. For example, the rPR obtained from J_ci is the rPR between P₀ and P_i.

2.2. Round-trip and single-trip phase retardation

While we can measure the rPR, a single-trip phase retardation (sPR) would more appropriately represent the polarization property of the sample. And hence, the sPR is the focus of our interest. In this subsection, we formulate the relationship between the rPR and the sPR and clarify the conditions under which the sPR can be obtained from the rPR.

Consider the round-trip Jones matrix J_r02, which is decomposed into two components by eigendecomposition in the form of

$${\mathbf{J}}_{\text{r}02}={\mathbf{V}}_{\text{r}02}{\mathrm{\Lambda }}_{\text{r}02}{{\mathbf{V}}_{\text{r}02}}^{-1}$$ (4)

where V_x is an eigenvector-matrix with columns that are eigenvectors of a Jones matrix J_x. Λ_x is an eigenvalue-matrix of J_x and is $\left[\begin{array}{lll}{\lambda }_x^{(1)}\hfill & 0;0\hfill & {\lambda }_x^{(2)}\hfill \end{array}\right]$ with ${\lambda }_x^{(1)}$ and ${\lambda }_x^{(2)}$ as the two eigenvalues of J_x.

Because the phase retardation is the phase difference between these two eigenvalues, the rPR from the surface to P₂ is obtained from Λ_r02 as $\text{arg}\left[{\lambda }_{r02}^{(1)}{\lambda }_{r02}^{(2)*}\right]$, where arg[ ] gives phase angle and the superscript * represents the complex conjugate.

Similarly, the corresponding single-trip Jones matrix J_s02 can be decomposed as

$${\mathbf{J}}_{\text{s}02}={\mathbf{V}}_{\text{s}02}{\mathrm{\Lambda }}_{\text{s}02}{{\mathbf{V}}_{\text{s}02}}^{-1}.$$ (5)

J_r02 can also be decomposed into the eigenvalue- and eigenvector- matrices of the single-trip Jones matrix J_s02 in the form

$$\begin{array}{lll}{\mathbf{J}}_{\text{r}02}\hfill & =\hfill & {{\mathbf{J}}_{\text{s}02}}^{\text{T}}{\mathbf{J}}_{\text{s}02}\hfill \\ \hfill & =\hfill & {\left({{\mathbf{V}}_{\text{s}02}}^{-1}\right)}^{\text{T}}{\mathrm{\Lambda }}_{\text{s}02}{{\mathbf{V}}_{\text{s}02}}^{\text{T}}{\mathbf{V}}_{\text{s}02}{\mathrm{\Lambda }}_{\text{s}02}{{\mathbf{V}}_{\text{s}02}}^{-1}.\hfill \end{array}$$ (6)

The equation shows that J_r02 has no evident similarity to Λ_s02. Therefore, the sPR cannot be obtained from the round-trip Jones matrix, which in turn means that the sPR cannot be measured by cPR-based PS-OCT.

Because of this unclear relationship between the sPR and the rPR, it is also impossible to obtain the local phase retardation from the rPR. For example, the sPR and the rPR between P₁ and P₂ cannot be determined from the rPR values obtained at P₁ and P₂. This issue is discussed extensively and in detail in Section 6.1.

While the sPR cannot be measured under general conditions, it can however be measured under the specific condition where the eigenvector-matrix V_s02 is an orthogonal matrix. Under this condition, V_s02^T = V_s02⁻¹ and Eq (6) is reduced to

$${\mathbf{J}}_{\text{r}02}={\mathbf{V}}_{\text{s}02}{\mathrm{\Lambda }}_{\text{s}02}^{\text{2}}{{\mathbf{V}}_{\text{s}02}}^{-1}.$$ (7)

Because J_r02 is similar to a squared eigenvalue-matrix of a single-trip Jones matrix, the rPR becomes the double the sPR. Therefore, the sPR is determined and is found to be half the rPR. Conventional cPR-based PS-OCT can thus only measure the sPR if this orthogonality condition is satisfied.

This orthogonality condition is satisfied if and only if the following two physical conditions are satisfied; (1) the eigen-polarizations of the tissue from the sample surface to the measurement point (P₂ in this example) must be linear polarizations and (2) the eigen polarizations must be orthogonal to each other (see Appendix A for details). In practical tissue samples, these conditions are interpreted as follows: (i) the eigen-polarizations of each small depth region from the surface to the measurement point must be linear polarizations (the local linearity condition, or LL-condition); also, (ii) the optic axis orientations of all small depth regions must be identical (the uniform orientation condition, or UO-condition). These conditions, and particularly the UO-condition, are not likely to be satisfied for most practical tissues, except for certain special types of tissue, such as the retinal nerve fiber layer (RNFL).

In summary, the cPR when measured by PS-OCT and JM-OCT, is a cumulative rPR that represents the cumulative and the round-trip polarization effect between the sample surface and the measurement point. Although the sPR is more directly related to the tissue property than the rPR, the sPR cannot be obtained from the measured cPR unless both the LL-condition and the UO-condition are satisfied. Thus, in practice, cPR is hard to be clearly interpreted for general tissues except for some special types of tissues. Similarly, depth-localized polarization information cannot be obtained from cPR measurements (see also Section 6.1).

2.3. Local Jones matrix and local phase retardation

In order to obtain a physically meaningful phase retardation, our JM-OCT method first computes the local Jones matrix, and then computes its phase retardation (local phase retardation; lPR).

Here, we consider a thin layer L₁₂ to be the tissue of interest and then measure its phase retardation. In general, the local Jones matrix at L_ij is defined as J_Lij = J_cjJ_ci⁻¹ [35]. For example, the local Jones matrix at L₁₂ is obtained from the cumulative Jones matrices of J_c1 and J_c2 in the form

$$\begin{array}{lll}{\mathbf{J}}_{\text{L}12}\hfill & =\hfill & {\mathbf{J}}_{\text{c}2}{{\mathbf{J}}_{\text{c}1}}^{-1}\hfill \\ \hfill & =\hfill & \left({\mathbf{J}}_{\text{out}}{\mathbf{J}}_{\text{s}10}{\mathbf{J}}_{\text{s}21}{\mathbf{J}}_{\text{s}12}{\mathbf{J}}_{\text{s}01}{{\mathbf{J}}_{\text{out}}}^{-1}\right){\left({\mathbf{J}}_{\text{out}}{\mathbf{J}}_{\text{s}10}{\mathbf{J}}_{\text{s}01}{{\mathbf{J}}_{\text{out}}}^{-1}\right)}^{-1}\hfill \\ \hfill & =\hfill & {\mathbf{J}}_{\text{out}}{\mathbf{J}}_{\text{s}10}{\mathbf{J}}_{\text{r}12}{\mathbf{J}}_{\text{s}10}{{\mathbf{J}}_{\text{s}10}}^{-1}{{\mathbf{J}}_{\text{out}}}^{-1}.\hfill \end{array}$$ (8)

This local Jones matrix is evidently similar to the round-trip Jones matrix at layer L₁₂. Therefore, J_L12 provides the rPR at L₁₂.

In a similar manner to Eq. (4), J_L12 can be further decomposed as

$${\mathbf{J}}_{\text{L}12}={\mathbf{J}}_{\text{out}}{\mathbf{J}}_{\text{s}10}{\left({{\mathbf{V}}_{\text{s}12}}^{-1}\right)}^{\text{T}}{{\mathrm{\Lambda }}_{\text{s}12}}^{\text{T}}{{\mathbf{V}}_{\text{s}12}}^{\text{T}}{\mathbf{V}}_{\text{s}12}{\mathrm{\Lambda }}_{\text{s}12}{{\mathbf{V}}_{\text{s}12}}^{-1}{{\mathbf{J}}_{\text{s}10}}^{-1}{{\mathbf{J}}_{\text{out}}}^{-1}.$$ (9)

If the eigenvector-matrix V_s12 is orthogonal, i.e., V_s12^T = V_s12⁻¹, this equation is then reduced to

$${\mathbf{J}}_{\text{L}12}=\mathbf{A}{\mathrm{\Lambda }}_{\text{s}12}^2{\mathbf{A}}^{-1},$$ (10)

where A ≡ J_outJ_s10V_s12. Here we utilized Λ_s12^T = Λ_s12. Evidently, J_L12 is similar to ${\mathrm{\Lambda }}_{\text{s}12}^2$, and thus the phase retardation of J_L12 is twice the sPR of the tissue at L₁₂.

The above discussion implies that the condition that enables the sPR measurement at L₁₂ is the orthogonality of V_s12. Similar to the case of J_r02 [Eq. (7)], this condition is interpreted as being the LL- and UO-conditions of the tissue at L₁₂. However, unlike that case, the separation between P₁ and P₂ can be set to be sufficiently small, and these two conditions are thus significantly more easily satisfied, even in realistic tissue. This implies that the phase of the local Jones matrix provides the sPR as one half of the lPR.

Additionally, if the tissue can be regarded as being homogeneous within this thin region, then the birefringence of the tissue can also be obtained as

$$b_{ij}=\frac{l{\text{PR}}_{ij}}{2k_0\mathrm{\Delta }{z}_{ij}},$$ (11)

where b_ij is the birefringence at L_ij, lPR_ij is the round-trip PR between P₁ and P₂, k₀ is the center wavenumber of the JM-OCT and Δz_ij is the thickness of L_ij.

To summarize this section, our JM-OCT method obtains the lPR via the local Jones matrix measurements. The sPR is then obtained from the lPR by assuming that the LL- and UO-conditions are satisfied in the local layer, which is typically set to have a thickness of a few tens of micrometers in our particular implementation. Because this local layer is thin, these conditions are far more easily satisfied than in the cPR imaging case.

One possible drawback of lPR imaging is the low SNR of the phase retardation [35,40]. This is because, on the one hand, the cumulative nature of phase retardation means that the phase retardation of a thin layer is small. On the other hand, the noise energy of the phase retardation measurement is independent of the layer thickness. This drawback is overcome by using a MAP estimator for the birefringence [42] in the present JM-OCT method, as described in Section 4.

Notably, the local Jones matrix can also be obtained directly from the measured Jones matrices as J_m2J_m1⁻¹, which gives the same form with the last line of Eq. (8). Note that a numerical algorithm based Eq. (8) should first compute the cumulative Jones matrixes from the measured Jones matrices and then computes the local Jones matrix from the cumulative Jones matrixes. On the other hand, the present equation derives the local Jones matrix directly from the measured Jones matrices. So, it is computationally less intense and would be more appropriate for practical JM-OCT implementation.

3. Jones matrix OCT system

A clinical prototype of the posterior JM-OCT system based on a passive-component-based JM-OCT method [17, 37, 38, 46, 47] was built. The system’s optical components, apart from the retinal scanning unit, are packed in an optical component box with dimensions of 55 cm (width) × 31 cm (depth) × 33 cm (height) as shown in Fig. 2(a). The prototype uses a three-layer stacking structure to reduce the overall footprint of the system. All system components, including the optical component box, the retinal scanner, and a personal computer (PC) can be assembled on a table with a footprint of 100 cm (width) × 55 cm (depth) as shown in Fig. 2(b).

Fig. 2.

Clinical prototype of the JM-OCT system. (a) Optical component box without a cover; (b) complete system on a table.

A light source and a JM-OCT interferometer are implemented in the component box. The light source is a wavelength sweeping laser (Axsun Technologies, Massachusetts, USA) with a scanning frequency of 100 kHz, a center wavelength of 1048 nm, a sweeping wavelength range of 110 nm, a duty cycle of 47%, and average output power of 26.5 mW.

The light from the light source goes into a single-mode-fiber-based interferometer as shown in Fig. 3 [38]. A 99 : 1 fused coupler is used to split the beam from the light source. The 99% portion of the beam is directed into the JM-OCT interferometer. The remaining 1% of the beam goes to a fiber Bragg grating with a reflection wavelength at 995.8 nm and reflectivity of 56.9% (FBG, FBG-SMF (1060)-995.8-55-0.1-A-2 60F/E, L = 1M, Tatsuta Electric Wire & Cable Co., Ltd, Osaka, Japan). The reflection from the FBG is received by a photo detector (C5331-03, Hamamatsu, Shizuoka, Japan). The output from the photo detector is then delivered to the trigger channel of a digitizer (ATS9350, Alazar Technologies, Quebec, Canada) which is equipped with a PC.

Fig. 3.

Schematic diagram of JM-OCT system. Abbreviated terms: FBG: fiber Bragg grating; APD: avalanche photo detector; FC: fiber collimator; PC: polarization controller; LP: linear polarizer; PBS: polarizing beam splitter; NPBS: non-polarizing beam splitter; BPD: balanced photo detector.

The JM-OCT interferometer consists of a reference arm, a passive polarization delay unit (PP-delay unit), a polarization diversity detection unit (PD-detection unit), a probe arm, and a phase calibration mirror. The PP-delay unit and the PD-detection unit are implemented with compact optical designs [17]. 20% of the light from the 99 : 1 coupler passes through the reference arm which includes a variable delay line with a 75-mm travel distance (150-mm optical distance, VDL-06-50-H-M-A-2-L-1, Advanced Fiber Resources, Hong Kong) and is then directed into the PD-detection unit.

The remaining 80% of the light from the 99 : 1 coupler is guided into the PP-delay unit in the probe arm. In the PP-delay unit, the incoming light is then split into two orthogonal polarization states by a polarization beam splitter (PBS), after it passes through a linear polarizer (LP) with a 45-degree orientation. Each beam travels through different passes with different lengths; a 3-mm delay is applied to the P-polarization component but not to the S-polarization component. The two components are then recombined by the PBS. This results in the multiplexing of the incident polarization states in depth [37, 38, 48].

The light from the PP-delay unit output port is then split by a 20 : 80 coupler. The 80% portion of the light from the coupler is directed to the phase calibration mirror, while the remaining 20% is guided to the probe arm. The probe arm is connected to a retinal scanner with a motorized alignment feature. The retinal scanner consists of an OCT scanner, a complementary metal-oxide-semiconductor (CMOS) camera-based anterior eye monitor, a fixation target, a motorized focusing lens, and a motorized alignment stage. The OCT scanner is equipped with a two-axis galvanometric scanning mirror (6200H, Cambridge Technology Inc, Massachusetts, USA), which is controlled by an analogue output board (PCIe-6323, National Instruments, Texas, USA) that is equipped with a PC. The optical design of the scanning head allows transverse measurement range of up to 14 mm. Transverse scanning ranges of 3, 6, and 12 mm can be selected using our custom software configuration. These scanning ranges are correspond to scanning angles of 14.3, 28.7, 57.3 degrees, respectively. The motorized focusing lens enables the correction of large refractive errors of the target eye, ranging from −25 to +10 diopters (D). The power on the cornea is 1.4 mW, which satisfies the American National Standards Institude (ANSI)-defined safety standard [49]. The sensitivities measured at each polarization channel were 93.0 dB, 93.3 dB, 87.7 dB, and 90.2 dB at 0.5 mm from the zero-delay position under 1.4-mW probe power. The sensitivity roll-off was −0.63 dB/mm over the depth range from 0.5 mm to 2.5 mm.

The backscattered light from the sample and the reflected light from the phase calibration mirror are guided towards the PD-detection unit, in which the interference signals of the two orthogonal polarizations (i.e., horizontal and vertical) are detected independently by two balanced photo detectors (BPDs; PDB471C, Thorlabs, Inc., NJ).

The outputs from these BPDs pass through 1-MHz high pass filters and 250-MHz low pass filters (HP1CH3-0S and LP250CH3-0S, respectively, 7th-order type-I Chebyshev, R & K, Shizuoka, Japan), and are directed to the sampling channels of the digitizer. Each input to the digitizer is digitized with 12-bit resolution at a sampling rate of 500 MS/s with an internal clock. Each spectrum interference signal is sampled with 2,560 data points; this process defines a depth measurement range of 6 mm. Because the two input polarizations are multiplexed in terms of depth, the maximum measurable depth range becomes 3 mm. The sampled signal is numerically resampled and is then rescaled into the k-domain with a wavelength range of 104.7 nm by a predefined resampling parameter [50–52]. Jittering shift of spectra among A-scans is numerically corrected [38]. A depth pixel separation was 4.9 μm in air which corresponds to 3.8 μm in tissue. The depth-resolution was 8.9 μm in air which corresponds to 6.6 μm in tissue, which was measured at 1.5-mm depth which is the center of depth range.

The sub-pixel delay between OCT images of two incident polarization states are corrected to form an accurate Jones matrix tomography. For this purpose, non-delayed and delayed polarization-insensitive OCT images are obtained by adding each of the non-delayed signals and the delayed signals with zero-padding. The distance between the non-delayed and delayed OCT images is then obtained by maximum cross-correlation in sub-pixel order. The sub-pixel delay is then compensated. After the sub-pixel correction process, the intensity image, the cumulative phase retardation image, the birefringence image, M-DOPU image, and a vascular image based on the Jones correlation are obtained.

4. Image formation

Four repetitive B-scans were obtained at the same position in our scanning protocol. A sensitivity-enhanced scattering OCT image is obtained by coherent composition of these repetitive B-scans (Section 3.8 of [38]). The cPR is computed by a method described in [38]. The low signal region that having SNR less than +5 dB from the noise floor was masked and appeared as gray in cPR images.

To obtain high quality birefringence and M-DOPU images, the adaptive Jones matrix averaging process is first applied (Section 3.4 of [38]). Then, a MAP estimation of the birefringence and its reliability is computed [42]. In our implementation, the depth separation Δz_ij of Eq. (11), which is the depth dimension of the local Jones matrix, is 9 pixels (equivalent to 33 μm in tissue). The MAP estimation was performed using an estimation kernel size of 2 (transverse) by 2 (depth) pixels, where the estimated birefringence was finally assigned to the pixel at the top-left of the kernel. The estimated birefringence and its reliability are then combined with the scattering intensity to yield a pseudo-color composite OCT image. The composite image is formed using the three parameters as follows: the birefringence was used to define the hue, the scattering intensity was used for the pixel brightness and the reliability of the birefringence estimation determines the color saturation of each pixel [42].

An en face maximum birefringence projection was created to ease understanding of both the sample structure and the birefringence distribution. The maximum birefringence value at each en face position is defined as follows. The top 20 pixels with the highest birefringence are selected for each A-line. The mean of these pixels is then used as the maximum birefringence at the en face position.

DOPU with noise correction (i.e., M-DOPU) [43] is used for the polarization uniformity imaging process. M-DOPU is computed using a 3 pixel (transverse) by 3 pixel (depth) kernel size. Because the polarization uniformity becomes low at tissues containing melanin [53], retinal pigment epithelium (RPE) [18] and choroid [43] both show low M-DOPU.

Vasculature imaging is obtained by computing the complex correlation of the Jones matrix, which is called correlation mapping OCT angiography (cmOCA) [44, 45]. The correlation was computed between successive B-scans among the four repetitive B-scans. The details of this method are described elsewhere [44, 45].

5. Results

We discuss the clinical applications of birefringence imaging, DOPU imaging, cmOCA imaging, and scattering OCT in this section. Qualitative comparisons are also presented among birefringence imaging, scattering OCT, and cPR imaging.

Areas of 3 mm × 3 mm, 6 mm × 6 mm, or 12 mm × 12 mm are scanned with 512 A-lines (horizontal) × 4 repetitive scans at each vertical position × 256 vertical positions in 6.6 s.

5.1. Normal eye

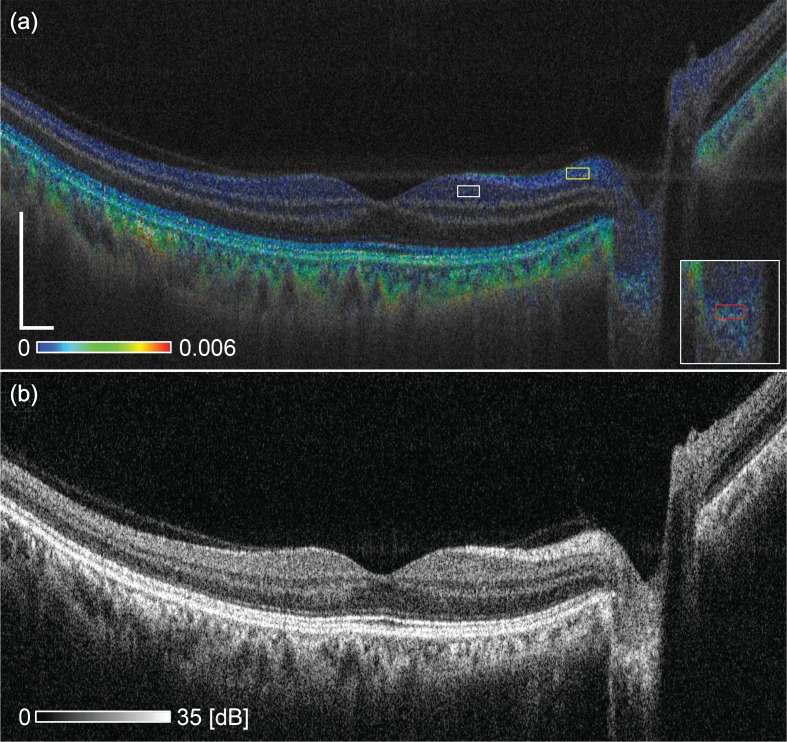
Figure 4 shows a typical case of a normal eye. The subject is a 56-year-old male with an emmetropic eye. The cross-sectional image is extracted from a volumetric OCT data covering 12 mm × 12 mm.

Fig. 4.

(a) Cross-sectional birefringence image of a normal eye and (b) scattering OCT image of the same eye. The scale bar represents 0.5 mm × 0.5 mm.

In the birefringence image [Fig. 4(a)], the NFL shows moderate birefringence (light blue). The mean and the mode of the birefringence in the box in Fig. 4(a) were 4.1 × 10⁻⁴ and 2.1 × 10⁻⁴, respectively. These results are consistent with the NFL birefringence measured by PS-OCT in previous studies, such as those in the ranges from 2.2 × 10⁻⁴ to 4.8 × 10⁻⁴ [27], from 0.5 × 10⁻⁴ to 3.3 × 10⁻⁴ [28], from 1.2 × 10⁻⁴ to 6.3 × 10⁻⁴ [29], from 1.6 × 10⁻⁴ to 3.3 × 10⁻⁴ [30]. The wavelength used in the previous studies listed above was 840 nm, while the center wavelength of the present JM-OCT was 1048 nm. As a reference, the mean and the mode of birefringence around the ganglion cell layer (GCL) and inner plexiform layer (IPL) [at the region indicated by white box in Fig. 4(a)] were 2.0 × 10⁻⁴ and 3.0 × 10⁻⁵, respectively. The mean birefringence can be positively biased because of asymmetrical distribution of measured birefringence. So the mode would be more rational for this region.

The choroid shows higher birefringence than the NFL (green). This higher birefringence appearance was found in four out of five normal eyes, while the other eye did not show sufficient signal penetration to the choroid. Because the choroid consists of densely-packed small vessels, this high birefringence is likely to originate from the vessel wall.

The lamina cribrosa (LC) shows high scattering in the scattering OCT [Fig. 4(b)] and moderate birefringence in the birefringence image [Fig. 4(a)]. The mean and the mode of birefringence of LC at the red rectangle region in the inset of Fig. 4(a) were 1.1×10⁻³ and 2.4×10⁻⁵, respectively. The inset is a magnified image of the LC region. The mean is significantly larger than the mode by the same reason with GCL-IPL, and mode would be more reliable also in this region. The birefringence of the lamina cribrosa will be discussed in detail with reference to a glaucoma suspect patient case in the next subsection.

5.2. Glaucoma suspect patient

Figures 5 and 7 show the optic nerve head (ONH) of a glaucoma suspect patient. The subject is a 48-year-old male with a refractive error of −2.75 diopters (D). The transverse scanning area is 3 mm × 3 mm.

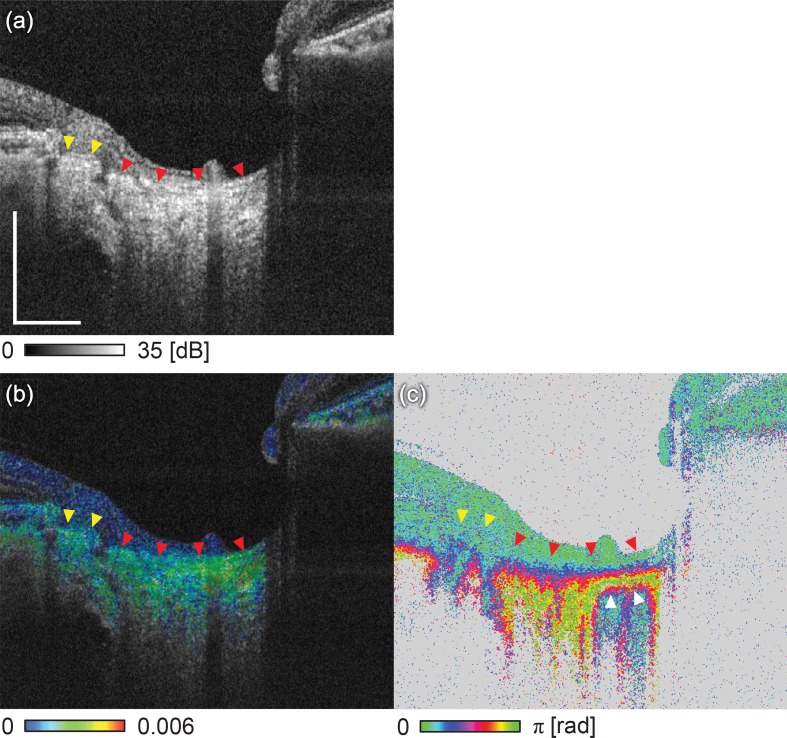
Fig. 5.

Comparison of multifunctional OCT images of glaucoma suspect patient. (a) scattering OCT, (b) birefringence, and (c) cumulative phase retardation B-scan images. The scale bar represents 0.5 mm × 0.5 mm.

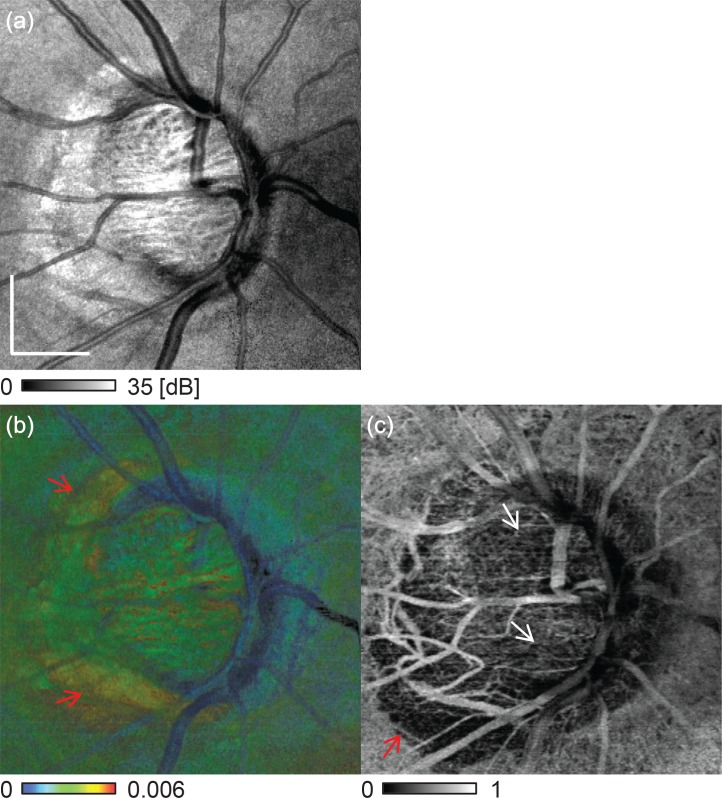
Fig. 7.

En face projection images of (a) scattering OCT, (b) birefringence, and (c) vasculature. (a) is the en face averaging of the scattering OCT, (b) is the maximum birefringence projection and (c) is the averaged cmOCA. The scale bar represents 0.5 mm × 0.5 mm.

The boundary between the LC and the pre-lamina cribrosa (PLC) was manually delineated using scattering OCT [indicated by the red arrowheads in Figs. 5(a), 5(b), and 5(c)]. The LC showed higher birefringence than the PLC in Fig. 5(b). The nasal region of the LC showed higher birefringence than the temporal region. The cPR image shows the rapid alteration in the LC region, which is constantly low (blue) in the PLC region [Fig. 5(c)]. Notably, the LC-PLC boundary is unclear in the cPR image. The cPR of the right region of the LC [indicated by the white arrowheads in Fig. 5(c)] becomes blue in the deep region, while the colors continue to vary from red to yellow in the left region. This difference in contrast in the deep region was caused by the cumulative effect of the phase retardation. Namely, the birefringence of a superior tissue, i.e., LC, affected the appearance of this region. The higher LC birefringence on the right region thus altered the cPR more strongly while causing the cPR below the LC to alias into low cPR values. Therefore, this clear regional difference of cPR beneath the LC would be a shadowing artifact and would thus mislead the clinical interpretation.

The sclera at the peripapillary atrophy (PPA) region (indicated by the yellow arrowheads) shows high scattering in the scattering OCT [Fig. 5(b)] and moderately high birefringence (green) in the birefringence image [Fig. 5(b)]. Despite this moderately high birefringence, this region does not show depth-oriented alteration of the cPR in Fig. 5(c).

Figure 6 shows the en face slices of the ONH at different depths, where the columns running from left to right indicate the direction from anterior to posterior. The first, second and third rows are the scattering OCT images, birefringence images and cPR images, respectively. The depth positions are indicated by the white arrows in the B-scan birefringence images located in the fourth row [Figs. 6(j) and 6(k)]. The locations of the B-scan birefringence images are indicated by the white arrowheads in Fig. 6(f).

Fig. 6.

Comparison of multifunctional OCT images of glaucoma suspect patient. C-scan images of (a)–(c) scattering OCT, (d)–(f) birefringence, and (g)–(i) cPR. C-scan images in the same column are taken at same depth indicated by the white arrows in the cross-sectional birefringence images (j) and (k). The columns from left to right indicate the position of anterior to posterior position. The locations of the B-scan images are indicated by the white arrows in (f). The scale bar represents 0.5 mm × 0.5 mm.

The scattering OCT slices [Figs. 6(a)–6(c)] show that the LC pores located at the superior and inferior regions are larger than those located at the temporal and nasal regions. This appearance is consistent with a previous study [54]. The birefringence slices [Figs. 6(d)–6(f)] show the low birefringence (blue) at the superior and inferior regions of the LC, and the high birefringence (green) at the temporal and nasal regions. While the cPR slices [Figs. 6(g)–6(i)] also show regional differences, their morphological patterns (indicated by the white arrowheads) are not identical to those of the birefringence slices. This inconsistency comes primarily from the cumulative nature of cPR imaging and secondarily from the inaccuracy of cPR imaging caused by violation of the LL- and UO-conditions.

The sclera at the superotemporal and inferotemporal PPA regions show very high birefringence, as indicated by the red arrows in the C-scan birefringence images [Figs. 6(d)–6(f)] and also in B-scan birefringence images [Figs. 6(j) and 6(k)]. In particular, the sclera at the inferotemporal PPA regions show complex birefringence distribution changes with depth [Fig. 6(k)]. Birefringence differences with depth are also observed in the next subject. This subtle regional difference is hard to see in the scattering OCT images [Figs. 6(a)–6(c)].

Figure 7 shows non-depth-resolved en face images of (a) scattering, (b) birefringence, and (c) vasculature. The scattering image is a depth-oriented average of the scattering, the birefringence image is the maximum birefringence projection, and the vasculature image is formed by depth-oriented averaging of a cmOCA volume.

An appearance shown in the maximum birefringence projection [Fig. 7(b)] is consistent with that of depth-resolved en face birefringence slices [Figs. 6(d)–6(f)]. The temporal and nasal LC regions both show higher birefringence than the superior and inferior regions. The superotemporal and inferotemporal PPA regions show also high birefringence as indicated by the red arrows in Fig. 7(b).

In the en face vasculature image [Fig. 7(c)], lower vasculature signals are observed in the superior and inferior regions of the optic disk as indicated by the white arrows in Fig. 7(c). These regions roughly collocate with the low-birefringence regions of the en face birefringence image. The vasculature density is low at the peripapillary region, which indicates choroidal atrophy in this region. The inferotemporal region of the PPA shows extremely low vascular density, and is collocated with the high birefringence region.

5.3. Myopic choroidal neovascularization with choroidal atrophy

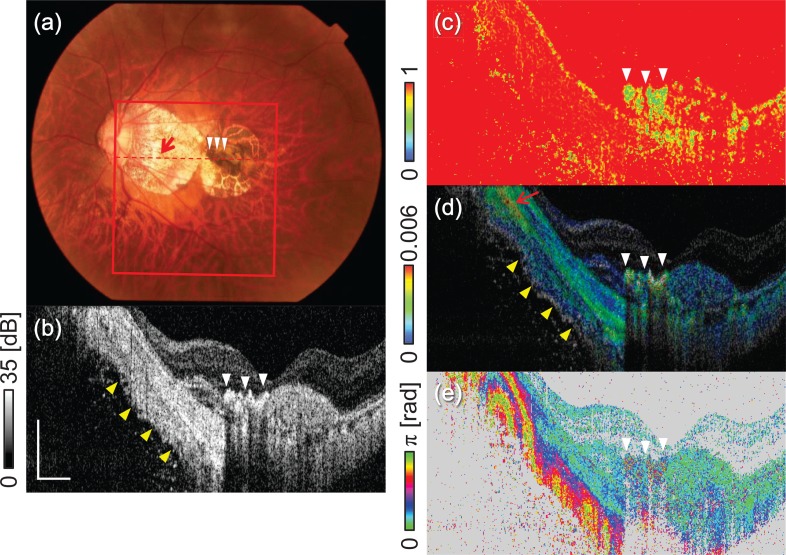
Figure 8 shows a case of myopic choroidal neovascularization (mCNV). The subject is a 40-year-old female with a refractive error of −4.0 D. The measurement is performed on a transverse area of 6 mm × 6 mm that is indicated by a red square in the color fundus [Fig. 8(a)].

Fig. 8.

Multifunctional OCT images of mCNV. (a) Color fundus, (b) scattering OCT, (c) M-DOPU image, (d) birefringence image, and (e) and cPR image. The red square in (a) indicates the measurement area. The red dashed line in (a) indicates the location of the images in parts (b)–(e). The scale bar represents 0.5 mm × 0.5 mm.

The color fundus shows a pigmented region [indicated by the white arrowheads in Fig. 8(a)] at the macula, and a hyper-scattering region that indicates choroidal atrophy. Scattering OCT [Fig. 8(b)] shows the hyper-scattering at the pigmented region. This region shows a low DOPU appearance (yellow) [Fig. 8(c)], which would be caused by the pigmentation. The pigmented region shows high birefringence (colored green to red) in the birefringence image [Fig. 8(d)], which indicates that the fibrosis occurs in this region. Notably, there is no marked appearance in this region in the cPR image (light blue) [Fig. 8(d)]. This inconsistency may be because of violation of the LL- and UO-conditions in the fibrosis region.

The sclera shows homogeneous hyper scattering in the atrophic region [indicated by the yellow arrowheads in Fig. 8(b)]. In contrast, the birefringence image visualized a layered structure as indicated by yellow arrowheads in Fig. 8(d). In this region, three layers with different birefringence properties are observed: arranged from the anterior to the posterior, we see a high birefringence layer (green), a low birefringence layer (blue), and then another high birefringence layer again at the bottom. The cPR image [Fig. 8(e)] also shows consistent rapid alternation along the depth direction, but the layered pattern can hardly be seen.

An extremely high birefringence region is observed at the peripapillary sclera [indicated by the red arrow in Fig. 8(d)]. This high birefringence originate from the dura mater that is known to extend from the ONH towards the temporal direction in highly myopic eyes [55, 56].

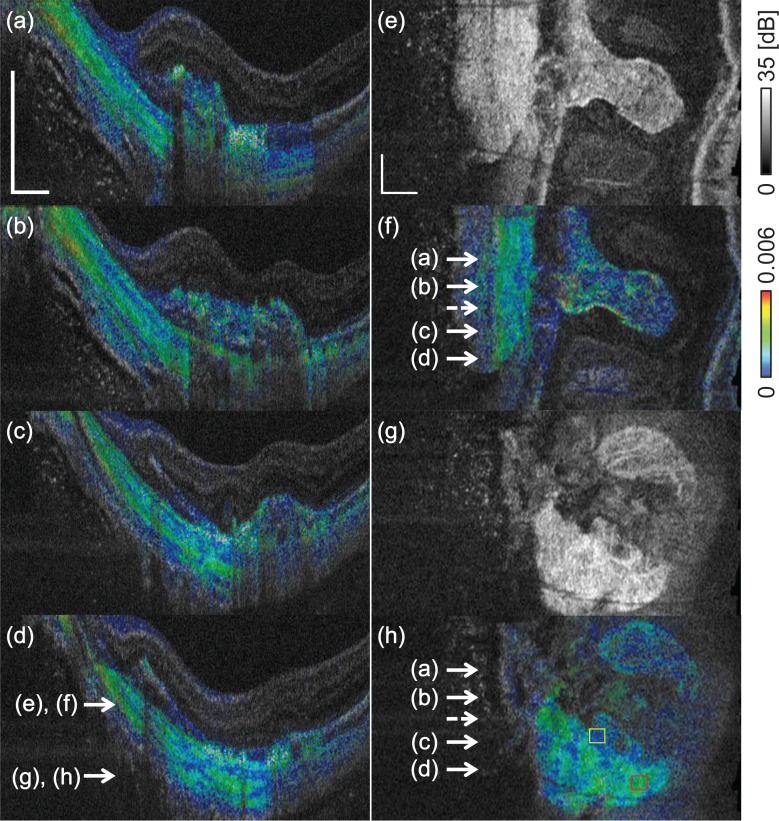
Figures 9(a)–9(d) show the cross-sectional scleral birefringence at several locations. Figures 9(e) and 9(g) are the en face slices of the scattering OCT at the depth position indicated in Fig. 9(d). Figures 9(f) and 9(h) are the en face birefringence slices at the same locations as those in Figs. 9(e) and 9(g), respectively. The locations corresponding to the cross-sectional birefringence images are indicated by the white arrows in Figs. 9(f) and 9(h). The layered pattern in the sclera is observed in all cross-sectional images [Figs. 9(a)–9(d)]. Figure 9(e)–9(h) show comparisons of the en face slices of scattering OCT and the birefringence images. The scleral in the yellow and red boxes in Fig. 9(h) showed the mean birefringence of 7.2 × 10⁻⁴ and 2.2 × 10⁻³, respectively. The birefringent structures in the sclera also can be seen in the en face birefringence slices, while they can not be seen in the corresponding scattering OCT slices.

Fig. 9.

Birefringence cross-sections (a)–(d) show the layered birefringence structure of the sclera. (e) and (g) show en face scattering OCT slices, and (f) and (h) are the corresponding birefringence slices, respectively. The transverse positions of the cross-sectional images are indicated by the solid arrows in (f) and (h). The dashed arrow indicates the position corresponding to Figs. 8(b)–(e). The depth positions of the en face images are indicated by the arrows in (d). The scale bar represents 0.5 mm × 0.5 mm.

6. Discussion

6.1. Limitations of phase retardation slope and differential phase retardation imaging

Traditionally, the depth-oriented differentiation of the cPR, which is also known as a phase retardation slope, was regarded as being proportional to the birefringence. In this section, the difference between the phase retardation slope and the lPR, and the limitations of the phase retardation slope measurements are discussed.

Consider the phase retardation between two points, P₁ and P₂, which are close to each other in depth. To simplify this problem, we consider here the difference between the cPRs at P₁ and P₂ as an alternative to the phase retardation slope, and this is called the differential phase retardation (dPR), Note that dPR is equal to the phase retardation slope as long as P₁ and P₂ are sufficiently close in depth. Therefore, the current discussion can also be applied to the phase retardation slope in practice.

As discussed earlier in Section 2.3, the local Jones matrix between P₁ and P₂ is ${\mathbf{J}}_{\text{L}12}=\mathbf{A}{\mathrm{\Lambda }}_{\text{s}12}^2{\mathbf{A}}^{-1}$ [Eq. (10)]. Hence, the lPR becomes double the sPR of L₁₂.

In contrast, as discussed in Section 2.2, there is no clear relationship between the sPR and the cPR at L₀₁ (from the surface to P₁) and at L₀₂ (from the surface to P₂) unless the orthogonality condition is satisfied (see the last paragraph of Section 2.2 for details). Therefore, the dPR between P₁ and P₂ does not show a clear relationship to the sPR at L₁₂, even if these two points are close in terms of depth.

This means that the dPR and, similarly, the phase retardation slope do not have a clear physical interpretation unless the orthogonality condition is satisfied, and the orthogonality condition is less likely to be satisfied for general tissue.

It should be noted here that the NFL is an exceptional case, in which the orthogonality condition is satisfied, and thus the dPR and the phase retardation slope are proportional to the sPR.

6.2. Computational time and its acceleration

The total processing time for the entire set of multifunctional OCT images is approximately 98 min for a volume with 512 A-scans × 1024 B-scans when using a custom-built program in LabVIEW 2013 (National Instruments, Texas, USA) on a Windows 8.1 PC with an Intel Core i7-4930K processor (six cores, 3.4-GHz clock frequency) and 32-GB of random access memory (RAM). There are two computationally intense processes. The first process involves obtaining four complex OCT signals corresponding to the four entries of Jones matrix, which takes approximately 47 min. This long OCT reconstruction time is mainly related to the requirement for numerical correction of spectral jitters among A-scans. It should be noted that this process can be eliminated in future versions by using a high-frequency k-clock interferometer [17].

The second process is the MAP estimation of the birefringence, which takes approximately 31 min.

6.3. Limitations of present birefringence imaging method

The present birefringence imaging method has three potential limitations. The first limitation is about its depth resolution. The birefringence is determined through a local phase retardation measurement, and the local region corresponding to the local retardation has a significant depth-extent, such as 33 μm in our specific case. Since it is typically larger than OCT resolution, the resolution of birefringence imaging is worse than that of a corresponding scattering OCT imaging.

The second limitation is about the accuracy of birefringence measurement. The present method is based on an assumption that the LL- and UO-conditions are satisfied in the local tissue region. But this assumption is not always true. If the tissue birefringence is not homogeneous in the local region, these conditions are not likely to be satisfied. This problem is similar to the limitation of the cumulative phase retardation measurement, which requires LL- and UO-conditions for the entire depth region from the tissue surface to the point of interest. Since the local region is thinner than that of the entire depth region, LL- and UO-conditions are more likely satisfied in the birefringence measurement than the cumulative phase retardation measurement. However, it should be noted that some inaccurate measurements may still occur.

The imperfect tissue homogeneity leads to another limitation. The birefringence can be obtained from the lPR only if the tissue is homogeneous in the local tissue region. Namely, although the LL- and UO-conditions are satisfied, the obtained birefringence becomes inaccurate if the tissue is inhomogeneous. This potential inaccuracy should be considered especially for applications requiring quantitative birefringence measurement.

A possible solution for the tissue inhomogeneity problem is superpixel methods [57]. The superpixel method is a clustering algorithm for pixels in general color images. It generates groups of pixels, so called as superpixels, based on the spatial and color similarity of pixels. This method has been modified and applied to JM-OCT [58]. This modified version has clustered JM-OCT pixels based on its spatial similarity and similarities of optical properties. Since each cluster, i.e, superpixel, is more likely to be homogeneous than arbitrarily defined depth region utilized in the present study, the accuracy of birefringence measurement may be improved by computing local Jones matrix and birefringence within the superpixels. However, it should also be noted that the application of the superpixel to birefringence measurement is not straightforward and is still an open and active research issue.

6.4. Visualization of layered structure in sclera by birefringence imaging

Electron microscopy studies have shown that the diameters of fibrils vary along the depth direction [59] and that the sclera has a lamellar collagen structure [21]. Nadkarni et al. investigated the birefringence of the atherosclerotic plaques and found a positive correlation between the proportion of thick collagen fibers and the birefringence [4]. These previous studies suggested that the lamellar structures in sclera with different collagen fiber diameter distributions would be the cause of the layered birefringence structure shown in Section 5.3.

6.5. Clinical utility of multifunctional OCT imaging

Conventional angiographies such as fluorescein angiography (FA) and indocyanine green angiography (ICGA) visualize not only vascular structure but also the abnormality of RPE through the dynamic change such as leakage, pooling, staining, and window defect. While the recently developed OCT-based angiography (OCT-A) [60–63] visualizes the vascular structure, it has no sensitivity to RPE abnormalities. In contrast, the multifunctional OCT presented here visualizes both RPE and pigmentation abnormalities through DOPU in addition to the vascular structure abnormalities through cmOCA. Therefore, this method would provide more information that was comparable with the results of FA and ICGA than OCT-A.

JM-OCT has measured the birefringence properties of the choroid, the lamina cribrosa, and the sclera, which have not previously been obtained by conventional PS-OCT based on cPR imaging. It was reported that the scleral birefringence was positively correlated with its mechanical stiffness [33]. The mechanical properties of the posterior sclera play an important role in maintaining the structure of an eye globe and also would have a significant effect on the mechanical properties of the ONH against the mechanical stress produced by internal ocular pressure (IOP). It was also reported that the myopia progression is associated with the mechanical property of sclera, and the thinning of scleral collagen fiber bundle and fibril [64]. Therefore, in vivo birefringence imaging is likely to be useful for the understanding and detection of both myopia and glaucoma.

7. Conclusion

In this paper, the theoretical details and clinical utility of both posterior birefringence and multifunctional imaging were investigated. The theoretical investigation showed the limitations of conventional cPR imaging and the legitimacy of local Jones matrix based birefringence imaging. A clinical grade JM-OCT prototype was built and used to investigate both normal and pathologic eyes. This investigation revealed several previously unknown birefringence properties of the in vivo ocular tissues, including the layered structure of the sclera and the high birefringence of both the choroid and the LC. In addition to these birefringence properties, JM-OCT can also reveal abnormalities in the vasculature and the RPE. JM-OCT is therefore set to become a powerful non-invasive diagnostic tool for posterior eye diseases.

Appendix

A. Orthogonality condition of eigenvector-matrix of physically admissible Jones matrix

For a physically admissible Jones matrix, the eigenvector-matrix of the Jones matrix becomes an orthogonal matrix if and only if the Jones matrix has two linearly polarized eigen polarizations that are orthogonal to each other. This appendix shows the proof of this condition.

The eigen polarizations of a physically admissible Jones matrix fall into one of the following six classes.

1. Both of the eigen polarizations are linear and are orthogonal to each other.

2. Both eigen polarizations are linear but are not orthogonal to each other.

3. Both eigen polarizations are not linear, i.e., they are circular or elliptic, and are orthogonal to each other.

4. Both eigen polarizations are not linear and are not orthogonal to each other.

5. One of the eigen polarizations is linear while the other is not linear. They are not orthogonal to each other by necessity.

6. Only one eigenpolarization exists, i.e., the Jones matrix is a full diattenuation matrix such as that of a polarizer.

In the following proof, the Jones vectors of the eigen polarizations, i.e., the eigenvectors of the Jones matrix, are denoted by v₁ and v₂. These eigenvectors are assumed to be normalized without any loss of generality, i.e., v₁^Tv₁^* = 1 and v₂^Tv₂^* = 1. The eigenvalue-matrix is thus expressed as

$$\mathbf{V}=\left[\begin{array}{ll}{\mathbf{v}}_1\hfill & {\mathbf{v}}_2\hfill \end{array}\right],$$ (12)

where the right-hand-side means that the first and second columns of the matrix are v₁ and v₂, respectively. Similarly, the transpose of V is

$${\mathbf{V}}^{\text{T}}=\left[\begin{array}{ll}{{\mathbf{v}}_1}^{\text{T}};\hfill & {{\mathbf{v}}_2}^{\text{T}}\hfill \end{array}\right],$$ (13)

where the right-hand-side means that the first and second rows are the transposes of v₁ and v₂, respectively.

The orthogonality condition of V is written as

$${\mathbf{V}}^{\text{T}}\mathbf{V}=\left[\begin{array}{ll}{{\mathbf{v}}_1}^{\text{T}}{\mathbf{v}}_1\hfill & {{\mathbf{v}}_1}^{\text{T}}{\mathbf{v}}_2\hfill \\ {{\mathbf{v}}_2}^{\text{T}}{\mathbf{v}}_1\hfill & {{\mathbf{v}}_2}^{\text{T}}{\mathbf{v}}_2\hfill \end{array}\right]=\mathbf{I},$$ (14)

where I is an identity matrix.

For the first class, because the eigen polarizations are linear, v₁ and v₂ are real vectors, i.e., v₁ = v₁^* and v₂ = v₂^*. Additionally, v₁ and v₂ are orthogonal to each other. Therefore, the off-diagonal entries of V^TV [Eq. (14)] becomes v₁^Tv₂ = v₁^Tv₂^* = 0 and v₂^Tv₁ = v₂^Tv₁^* = 0. Because v₁ and v₂ are normalized, the diagonal entries all become unity. This can be summarized as V^TV = I. Therefore, V is an orthogonal matrix and the orthogonality condition is satisfied for this class.

For the second class, because the eigen polarizations are linear, v₁ and v₂ are also real vectors. However, they are not orthogonal to each other. Therefore, v₁^Tv₂ = v₁^Tv₂^* ≠ 0 and v₂^Tv₁ = v₂^Tv₁^* ≠ 0. The off-diagonal entries are thus not zero and V^TV ≠ I. This suggests that the orthogonality condition is not satisfied for this class.

For the third class, because the eigen polarizations are not linear but are orthogonal to each other, both v₁ and v₂ are complex vectors and are orthogonal to each other. The orthogonality leads to v₁^Tv₂^* = 0 and v₂^Tv₁^* = 0, but the complex nature of these vectors suggests that v₁^Tv₂ ≠ v₁^Tv₂^* and v₂^Tv₁ ≠ v₂^Tv₁^*. Therefore, the off-diagonal entries of V^TV are not zero. Similarly, v₁^Tv₁ ≠ v₁^Tv₁^* = 1 and v₂^Tv₂ ≠ v₂^Tv₂^* = 1, and thus the diagonal entries of V^TV are not unity. Consequently, V^TV ≠ I and the orthogonality condition is not satisfied for this case.

For the forth class, because the eigen polarizations are not linear, v₁ and v₂ are complex vectors. Therefore, v₁^Tv₁ ≠ v₁^Tv₁^* = 1 and v₂^Tv₂ ≠ v₂^Tv₂^* = 1, and thus the diagonal entries of V^TV are not unity. This suggests that V^TV ≠ I and that the orthogonality condition is not satisfied for this class.

For the fifth class, one of the eigen polarization is linear and the other is not linear. v₁ can be assumed to be the real vector and v₂ is the complex vector without loss of generality for this case. Naturally, these vectors not orthogonal to each other. The (1, 1)-entry of V^TV is v₁^Tv₁ = v₁^Tv₁^* = 1. However, the other diagonal entry [(2, 2)-entry] is v₂^Tv₂ ≠ v₂^Tv₂^* = 1. One of the off-diagonal entries [(1, 2)-entry] v₁^Tv₂ ≠ v₁^Tv₂^*, and thus is unknown. The other off-diagonal entry [(2, 1)-entry] is not zero as v₂^Tv₁ = v₂^Tv₁^* ≠ 0. Therefore, V^TV ≠ I and the orthogonality condition is not satisfied for this case.

For the sixth class, because there is only one eigen polarization, rank(V) = 1 and V⁻¹ is not determined. Therefore, V cannot be an orthogonal matrix. The orthogonality condition is thus not satisfied for this class.

In summary, a physically admissible Jones matrix falls into one of the six classes and the orthogonality condition is satisfied by only the first of the six classes. Therefore, the orthogonality condition of a physically admissible Jones matrix is satisfied if and only if the Jones matrix is in the first class, where the eigen polarizations are both linear polarizations and they are orthogonal to each other.

B. List of notations

	Tissue model
Pi	The i-th depth position
P0	The position of a tissue surface
Lij	The tissue layer between Pi and Pj
Δzij	The distance between Pi and Pj, same as the thickness of Lij
bij	The birefringence of Lij
	Variants of phase retardation
sPR	Single-trip phase retardation
rPR	Round-trip phase retardation
cPR	Round-trip cumulative phase retardation
lPR	Local round-trip phase retardation
lPRij	The local round-trip phase retardation from Pi to Pj
dPR	Depth-differentiation of cPR
	Variants of Jones matrix
Jin	The Jones matrix of illumination optics
Jout	The Jones matrix of collection optics
Jmi	The raw measured Jones matrix measured at the depth position Pi
Jsij	The single-trip Jones matrix from Pi to Pj
Jrij	The round-trip Jones matrix from Pi to Pj
Jci	The cumulative Jones matrix at Pi
JLij	The local round-trip Jones matrix from Pi to Pj
	General notations relating to Jones matrix
${\lambda }_x^{(i)}$	The i-th eigenvalue of a Jones matrix Jx
Λx	The eigenvalue-matrix of Jx defined as $\left[\begin{array}{llll}{\lambda }_x^{(1)}\hfill & 0;\hfill & 0\hfill & {\lambda }_x^{(2)}\hfill \end{array}\right]$
Vx	The eigenvector-matrix whose columns are eigenvectors of Jx
	System parameter
k0	The center wavenumber of a probe beam