From genome-scale data to models of infectious disease: a Bayesian network-based strategy to drive model development

Abstract

High-throughput, genome-scale data present a unique opportunity to link host to pathogen on a molecular level. Forging such connections will help drive the development of mathematical models to better understand and predict both pathogen behavior and the epidemiology of infectious diseases, including malaria. However, the datasets that can aid in identifying these links and models are vast and not amenable to simple, reductionist, and univariate analyses. These datasets require data mining in order to identify the truly important measurements that best describe clinical and molecular observations. Moreover, these datasets typically have relatively few samples due to experimental limitations (particularly for human studies or in vivo animal experiments), making data mining extremely difficult. Here, after first providing a brief overview of common strategies for data reduction and identification of relationships between variables for inclusion in mathematical models, we present a new generalized strategy for performing these data reduction and relationship inference tasks. Our approach emphasizes the importance of robustness when using data to drive model development, particularly when using genome-scale, small-sample in vivo data. We identify the use of appropriate feature reduction combined with data permutations and subsampling strategies as being critical to enable increasingly robust results from network inference using high-dimensional, low-observation data.

1 Introduction

The proliferation of genome-scale experimental analysis techniques – proteomics, transcriptomics, metabolomics, and others – brings with it numerous challenges in data analysis. With many more measurements (or variables) than observations, it is complex (both conceptually and computationally) to identify those variables that are most important in determining the phenotype or outcome of a system, as well as how these variables interact with each other. The identification of these variables and interactions is a crucial step in most downstream work, whether the development of diagnostics or the detailed study and modeling of a biological system.

Modeling of infectious diseases is a particularly salient and important example of where addressing this challenge is critical. The mechanisms, presentation, and transmission of infectious disease are quite complex and depend on a number of factors including the host, the pathogen, the environment, and potentially even the vector.

Malaria, for example, is a disease caused by five different species of Plasmodium, and each of these pathogens can cause different clinical presentations and degrees of severity of the disease. Plasmodium vivax infections are typically characterized by fever spikes every 48 h, but the shorter life cycle of P. knowlesi typically manifests as a daily spike in fever [1]. Around 10% of P. falciparum infections result in severe malaria, with somewhere between 10% and 50% of those severe cases being fatal [2], while P. vivax infections may more rarely cause severe malaria [3]. Within the same species, specific strains of the parasite can be quite different, causing (for example) varying efficiencies of vector infection (and thus of disease transmission) [4] or strain-specific resistance to certain classes of drugs [5; 6]. All of these parasite variations are on the backdrop of host variations, which can have a tremendous impact on the presentation of the disease even between different individuals infected by isogenic parasites. Complicating the situation even further is that all of the above factors (whether related to host, parasite, or vector) are only things already known to be key in the disease, with potentially numerous additional critical factors that we just have not discovered yet.

With such complex dependence on different aspects of the host and pathogen, varying phenotypic effects after infection, and the general uncertainty about what all of the controlling factors in disease progression are, creation of mathematical models of infectious diseases is obviously quite difficult. One critical question, even if by virtue of its primacy in the process of developing models, is: what variables should be included in the model? As suggested above, a wealth of proteomics, metabolomics, and other measurements can provide the data that can help to build an effective model, but sifting through the large volume of measurements that do not correlate to the phenomenon of interest to identify the ones that do is a monumental task requiring appropriate statistical treatment. Even supposing that the right variables to include in a mathematical model could be identified, the notion of how to include these variables is the next significant task. One may know that a specific gene is important in a process, but that does not sufficiently inform the mathematical model. Does that gene affect only one other molecule (variable) in the system? If so, which variable does it affect? If it affects multiple variables, how many does it affect, and which ones? And then beyond this, if one knows which interactions to include, there is still the open question of the appropriate functional form to represent this interaction.

Thus, the ability to use modern high-throughput, high-information content, genome-scale data effectively will be essential in developing models for infectious diseases. These models may be on a molecular scale, indicating transcriptional or other regulation within a pathogen or indicating the interactions between host and pathogen biology. They may also be on a much larger scale, capturing epidemiological dynamics as a function of key aspects of the hosts, pathogens, and vectors. In either case, it is crucial that the methods used to identify the variables and relationships to be included in the model are as robust and accurate as possible. This is particularly relevant for cases where taking a large number of samples is not feasible, particularly in vivo clinical studies involving infected humans in need of treatment and non-human primate experiments where both cohort size and sampling frequency are limited on ethical grounds. One must extract as much information as possible in as reliable a way as possible with a comparatively small number of observations.

Here, we will first briefly review some of the common approaches to whittle genome-scale data into candidate knowledge for inclusion in mathematical models. We will then focus on one specific and promising approach to achieve this goal, Bayesian networks, and address some of the difficulties inherent in using this approach. We consider this task particularly in the context of systems where we expect to have a fairly small number of observations with significant biological variability. We present a unique approach that uses clustering to reduce the dimensionality of a dataset, concatenation of clustered genes to increase the effective number of observations, and permutation and cross-validation analysis to ensure that the results of network inference are trustworthy for the purposes of modeling and not disproportionately influenced by random variation. Taken together, this represents an efficient and reasonable approach to drive the generation or improvement of mathematical models in infectious disease research.

2 Background

Multivariate dimensional reduction, classification, and visualization approaches are often used as first-line analyses in the interpretation of high-variable, low-observation genome-scale datasets. Methods include principal component analysis (PCA), partial least squares discriminant analysis (PLS-DA), and numerous variations thereof that reduce the original variable space to a few composite variables [7; 8]. In the ideal case, samples from the same group are close to each other in the reduced feature space, and the weight of the original variables in these key composite variables can be used to drive further downstream interpretation and analysis, including ontological analyses like enrichment analysis. Other methods for group classification tasks (e.g., support vector machines or artificial neural networks) can create classifiers capable of separating two sample classes, though with potentially increased difficulty in interpreting the biological meaning of the mathematical representations in the inferred classifier.

What such classification and dimensional reduction approaches largely do not permit is the ability to discover new interactions between variables. Much richness in biological systems is driven by the complexities of regulation, which manifests itself by the apparent correlation of biomolecules across time or experimental conditions. The ability to identify interactions between variables is a valuable tool to learn more about the molecular level of novel or understudied complex biological systems, and in particular it is valuable for knowing what variables should be included in mathematical models of such systems.

As discussed in Section 1, the process of reducing genome-scale data to a form that can be integrated into mathematical models can be broadly divided into three steps: feature selection, identification of candidate interactions between features, and mathematical formulation of those candidate interactions.

2.1 Feature selection

Feature selection is the process of reducing a larger set of variables to a subset for use in model construction or further analysis. This is due to the expectation (quite appropriate for genome-scale data) that a significant fraction of the measured variables are either not relevant to the task at hand or are redundant. The latter is a particularly troubling problem for the construction of mathematical models, as the inclusion of redundant variables will greatly increase the computational complexity of estimating parameters in the mathematical model, and may in fact prevent many parameters from being identifiable. Feature selection methods may be independent filters, they may be search-and-score approaches that select subsets of features and assess the accuracy of the model derived from those features (“wrapper” methods), or they may be directly embedded into (and specific to) the model development [9]. A set of common methods to perform this task is described herein; while representative, this list is by no means exhaustive.

Common embedded methods include recursive feature elimination (RFE) and Lasso (the least absolute shrinkage and selection operator). RFE is an embedded approach often used in the development of support vector machines (SVMs), a powerful tool for classification problems [10; 11; 12]. In this approach, variables deemed unimportant in early model development are considered candidates for elimination from the model, with progressively more parsimonious models developed. Lasso can be embedded in regression models to minimize the number of parameters included [13]: a full regression model built on all variables is decreased in complexity by using smaller constraint parameters in the Lasso, eliminating variables with insignificant impact on the regression. Both of these methods address the relevance as well as the redundancy of the candidate variables.

Numerous filters can be used for feature selection, though these typically only address feature relevance, not redundancy. Univariate statistical tests can be used to identify features that distinguish two sample groups (t-test) or that are different across multiple sample groups (F-test or ANOVA). Thresholds can then be set (with consideration to multiple hypothesis testing) on the statistical significance of each variable to identify the putatively important variables for further analysis. Correlation-based filters [14] can also be constructed based on the correlation or mutual information between a variable and the output or phenotype.

Clustering methods can also be used for feature selection by identifying similar, and thus putatively redundant, features. For example, in hierarchical clustering [15; 16], variables are organized in a tree structure, with more similar variables being closer to each other on the tree. By applying a cutoff threshold to the edges in the tree, dissimilar groups can be disconnected from each other, leaving distinct clusters. A number of other clustering methods (e.g., k-means clustering [17]) are widely used for the same task. Aside from identifying potentially redundant features, clusters may also be candidates for further detailed modeling, particularly if a cluster is enriched for some well-characterized subset of variables but also contains a small number of surprising members that could represent as-yet unknown members of that subset.

2.2 Identification of candidate interactions

In accordance with the difficulty and importance of identifying regulatory interactions, there are scores of candidate approaches for this task. A representative sampling of the breadth of approaches can be accessed by surveying the results of the most recent DREAM (Dialogue for Reverse Engineering Assessment of Methods) challenge [18], where gene regulatory network inference is a recurring challenge. (In graphical networks, variables are represented by vertices and edges represent the “interactions” that we are looking to identify between those variables.) Below are three common classes of approaches (with attention when possible to methods that have been applied in the context of the systems biology of infectious diseases), but this is again by no means an exhaustive listing of approaches.

One widely-used class of methods involves the use of mutual information to infer relationships between variables. Mutual information between two random variables X and Y is defined as

$$I(X,Y)=\sum _{y\in Y}\sum _{x\in X}p(x,y)\log \left(\frac{p(x,y)}{p\left(x\right)p\left(y\right)}\right)$$

where p(x,y) is the joint probability distribution of X and Y, while p(x) and p(y) are the marginal probability distributions of X and Y, respectively. Essentially, this combines a measure of entropy or information content with a measure of the correlation between the variables X and Y to determine how much information is provided about one variable by knowing the value of the other.

There are a wide variety of mutual information-based approaches currently used [19]. CLR, or context likelihood of relatedness [20], has been used in multiple systems biology studies of infectious disease [21; 22; 23]. This approach calculates mutual information between variables and identifies as most important those pairs of variables where the mutual information between those variables is statistically significant compared to the background distribution of all mutual information values involving either of the variables in the pair. ARACNE [24], or Algorithm for the Reconstruction of Accurate Cellular Networks, also uses mutual information to determine interactions, but uses a combination of permutation tests to identify significant values with the “data processing inequality” to eliminate interactions that are putatively indirect. MRNET [25] uses mutual information in a feature selection step with the maximum relevance/minimum redundancy (MRMR [26; 27]) approach, considering each gene as a starting point in parallel to identify highly-ranked genes to be retained in the network along with their putative interactions.

Partial correlation networks [28; 29] (also known by a variety of other names) are another frequently used approach to infer interactions between variables. Whereas a standard correlation network will capture both direct and indirect interactions between variables based on Pearson or Spearman correlation coefficients, a partial correlation network looks to remove indirect relationships by calculating partial correlation coefficients, which are obtained by finding the correlation between the residuals of two variables after they are independently regressed on some other variable(s):

$${\rho }_{XY\mid Z}=\frac{{\rho }_{XY}-{\rho }_{XZ}{\rho }_{YZ}}{\sqrt{(1-{\rho }_{XZ}^2)(1-{\rho }_{YZ}^2)}}$$

where ρ_XY|Z is the partial correlation coefficient of the variables X and Y given the variable Z and the ρ_IJ terms represent the correlation coefficients of the variables I and J. Ideally one would be able to determine the partial correlation of any two variables conditioned on all possible subsets of other variables, but this is computationally intractable. As such, a variety of different approaches [30; 31; 32] and approximations have been developed to estimate partial correlation networks from datasets with many variables and few observations (as is typical with genome-scale data).

Bayesian networks are directed acyclic graphs where edges represent conditional probability relationships. (The directed nature of the network allows one to identify the “parents” of a given node X as all of the nodes with connected edges that end at X.) Thus, in a Bayesian network, a variable is independent of all variables to which it is not connected when conditioned on all of its parent nodes. This approach was one of the earliest to be applied to genome-scale data [33; 34], and has been used many times over [35]. Again, there are a number of variations on Bayesian networks, including dynamic Bayesian networks that allow for certain kinds of cycles in temporal data [36], as well as a number of algorithms available to infer these networks from experimental data [33; 37; 38]. The directional flow of information makes them attractive for biological interpretation and perceived closeness to representing causality, each of which are extremely useful for mathematical model development.

2.3 Mathematical formulation of interactions

Defining a functional form for candidate interactions is also crucial in moving towards new or revised mathematical models that benefit from genome-scale data. These will often be specific to the type of mathematical model being derived. At any rate, there are a variety of widely-used functional forms with biological relevance, including Hill-type equations [39], logistic equations [40], and power-law models [41]. While this step is certainly pivotal to model development, it is not unique to the task of exploiting genome-scale data, and so no further consideration will be given of it herein.

2.4 Importance of data processing and assumptions

Again, the ultimate goal of these efforts is to identify the key interactions between variables that should be included in mathematical models of disease processes or epidemiology. What must be appreciated, though, is that the processing of the data and the implementation details of each of these approaches can have just as big an impact on the interactions identified from genome-scale data as the selections made for how to infer interactions. Using one normalization or clustering scheme versus another could affect not only the robustness of the computed results with respect to missing data or perturbations in the data, but also the specific conclusions that one may draw from such work. It is these conclusions that form the bedrock of downstream modeling, and so it is important that the robustness and believability of the inferences made is as high as possible for any set of data processing selections.

To demonstrate this point, we will analyze in depth the impact of a number of decisions in the process of identifying key interactions for a host-pathogen interaction model. We will consider specifically the case of using clustering as a feature selection technique, with the resulting clusters being used in Bayesian network inference to identify relationships between the variables in those clusters. This ultimately leads to our Bayesian network-based strategy for inferring networks from large-scale data under the constraint of few observations.

3 Methods

3.1 Selected data processing methods

We choose to work with Bayesian networks based on their benefits as related to driving the development of mathematical models. Bayesian networks explicitly look to rule out indirect relationships, thus providing detailed and focused information on the relationships between the variables under study. The directed nature of the network allows easy visualization and interpretation of information flow very close to a “causal” interpretation, even though that is typically beyond the scope of what one can confidently and strictly interpret from an inferred Bayesian network. These directed relationships are quite amenable to inclusion in mathematical models, as they give a reasonable starting point for how to include a set of relationships in a model. However, our selection of Bayesian networks does have some significant drawbacks based on the type of data to which we will apply them. First, Bayesian networks can be computationally expensive to infer for large numbers of variables; in the limit of tens of thousands of variables, they may be nearly intractable. Moreover, for datasets with few observations (as is often the case in genome-scale study), it may be difficult to reliably infer correct networks even for relatively few variables.

To this end, we also choose to use clustering methods as part of our analysis workflow. Clustering as feature selection enables significant reduction in the scale of the model to be analyzed, making the Bayesian network inference problem much more reasonable (both in terms of computational time and in relationship to the number of observations available). We note a key choice in the use of these clusters: rather than using the clusters as starting points within which we would infer networks of relationships, we will instead use them as a way to separate out diverse sets of variables which can be treated as one “node” in the network inference problem. In this way, we minimize the redundancy between variables and hopefully maximize the relevance of inferred relationships. Nonetheless, interesting clusters (those found to have relationships with other clusters) could also be pursued later for detailed network analysis within those clusters.

3.2 Representative genome-scale dataset

The dataset we will use for our analyses (available on Gene Expression Omnibus as GSE58340) is from an experiment designed, generated, and previously published as a pilot experiment prior to subsequent studies involving malaria infections [42]. This experiment consisted of seven time point (TP) samples of peripheral blood and bone marrow from five rhesus macaques (Macaca mulatta). At the beginning of the experiment, the animals were injected with a preparation of Anopheles dirus salivary gland material, analogous to that which would be used to inject Plasmodium sporozoites into the animals. The experiment was designed for 100 days, mimicking the anticipated course of a malaria infection, with a baseline measurement immediately prior to the inoculation and samples taken for analysis at several time points representing possible predicted peaks of parasitemia had the animals been actually infected (days 21, 52, and 90). Treatment with the antimalarial pyrimethamine followed each of these time points, and additional samples were taken for analysis approximately one week after each drug administration.

The peripheral blood and bone marrow samples were ultimately to be used for parallel transcriptomics, proteomics, metabolomics, lipidomics, and immune profiling. Here, we consider only the results of the transcriptional analyses, and focus in particular on the bone marrow transcriptomics data. These transcriptional datasets were the best-annotated of the data initially obtained in this experiment, allowing for reasonable post hoc biological interpretation and analysis if necessary, and thus were the focus of our initial analyses. This dataset also provides one of the largest numbers of measured features, particularly relevant for the challenges we look to address.

After appropriate data processing and normalization, ANOVA was used to determine for which variables there was a difference between the pre-treatment (TP 1 and 2), immediately post-treatment (TP 3, 5, and 7), and “between-treatment” (TP 4 and 6) measurements. Animal identity was considered a random effect to remove as much impact of animal-specific differences as possible. Based on the resulting F statistics at a false discovery rate (FDR [43; 44; 45]) of 0.05, over 6000 genes were identified as being statistically significantly different across the measurements. (As described in section 4.1, ultimately we used only the top 1000 most significant of these variables due to a limitation in the implementation in one of the clustering methods used.) As the input data have no missing values, and are already in their normalized format, we omitted the preprocessing step (Step 1) indicated in Figure 1. A heatmap of the data for the top 1000 most significant genes is presented in Figure S1.

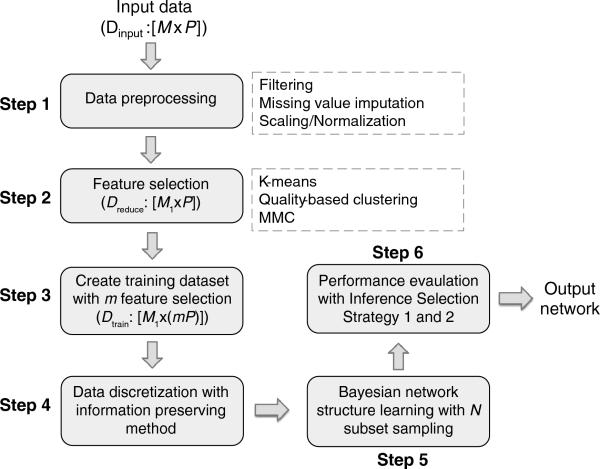
Figure 1. Diagram of the proposed pipeline for analyzing datasets with small sample size and many features.

D_input represents the original input data matrix with M features and P observations (M >> P). D_reduce represents the input data with its feature space reduced to M₁, where M₁ << M. D_train is created by selecting m features from each reduced feature and concatenating their observations together, where m = 1, 2, 3, ... The default value of m is 10.

3.3 Data processing scheme

To move towards solving the issues caused by the “high dimensionality” of omic-scale biological datasets, we have proposed an analysis workflow that identifies key interactions between variables with limited sample observations, and assesses the robustness of the inferred interactions. As illustrated in Figure 1, six main steps are involved, with the final output of the workflow being a learned network with maximal robustness and confidence.

The input experimental data is organized into an M×P matrix where M (the number of features or variables) is much larger than P (the number of observations). Any relevant data-preprocessing step (Step 1 in Figure 1), typically specific to the experimental technique generating the data matrix (e.g., transcriptomics vs. metabolomics), must first be performed. Depending on the data, such steps may include filtering outlier or low-confidence data, imputation of missing data, and scaling or normalization of the data to make them more suitable and uniform for later analysis. The preprocessed data then pass through the feature selection step (Step 2). As stated above, we choose to focus on clustering methods to reduce the feature space. Many algorithms could be selected, including K-means clustering [17], hierarchical clustering [15; 16], quality-based or quality-threshold clustering [46; 47], modulated modularity clustering (MMC [48]), or others. In Section 4.1, we describe in more detail why we choose to use quality-based clustering for our feature selection. After clustering, the original high-dimensional feature space is reduced from M features to M₁ clusters, where M₁ << M. A training dataset is then created by selecting m features as representatives from each cluster (Step 3). If m = 1, only one feature is selected to represent each cluster and the training dataset is an M₁×P matrix. If m > 1, the observations of these m features will be concatenated together and the training dataset will be an M₁×(mP) matrix. We hypothesize that this feature concatenation is reasonable because the variables found in a given cluster are highly correlated with each other and have very similar temporal profiles; they can thus be considered to be separate observations of the profile represented by that cluster. (The use of quality-based clustering in Step 2 further supports the validity of this hypothesis.) As the data are usually continuous rather than discrete, a data discretization step (Step 4) is applied to facilitate fast and efficient Bayesian network structure inference.

Data discretization is obviously a lossy process, where one must balance minimizing the loss of information content with the required or preferred simplicity of the discretized data for downstream analyses. Simple methods such as quantile or interval discretization usually consider and discretize each individual variable separately. Information regarding the relationship between variables thus is not taken into account in these methods, and may be a likely casualty of the discretization process. However, in the context of the applications described here, it is these very dependencies between variables that we seek. It thus is important to retain as much information as possible regarding the information flow between variables during discretization, and so we choose to use a more complex discretization method, namely information-preserving discretization [49], so that the variables are not considered in isolation. Specifically, a set of real-valued variables is initially discretized into D discretization levels where D is a large number (for instance, D = P if P ≤ 100, or D = 100 if P > 100, for the purposes of saving computational cost). The discretization level D is then reduced to a much smaller number in an iterative fashion. We use the total mutual information (TMI) for each variable i, defined as:

$$\begin{array}{cc}\hfill TMI\left(variabl{e}_i\right)& =\sum _{j\ne i}I(variabl{e}_i,variabl{e}_j)\hfill \\ \hfill =& \sum _{j\ne i}\sum _{y\in variabl{e}_i}\sum _{x\in variabl{e}_j}p(x,y)\log \left(\frac{p(x,y)}{p\left(x\right)p\left(y\right)}\right)\hfill \end{array}$$

where I is the mutual information as previously defined. At each iteration, for each variable we select the interval to be coalesced with its next-highest interval so as to minimize the total pairwise mutual information lost for that variable:

$$\arg \underset{n<D}{\min }TMI\left(variabl{e}_i\right)-TMI\left(variabl{e}_{i,n}\right)$$

where D is the current number of discretization levels and variable_i,n is the discretization of variable i that results from coalescing interval n with interval n + 1. The optimal n for this step is determined for each variable individually, and only then do all variables have their optimal intervals coalesced simultaneously. The coalesced intervals need not be the same across all variables during any given iteration. Iterations are continued until D = 1. Figure S2 gives an example of the plot of total mutual information (TMI) across all variables as a function of the number of discretization levels remaining during the discretization level coalescence algorithm, a monotonically increasing function in D. The TMI starts at 0 when the discretization level is 1, increases dramatically with increasing C for small values, and remains relatively unchanged at large C values. The optimal discretization level is typically selected as the “elbow” point in such a plot. A brief discussion of the impact of the selection of C is provided in Section 4.4.

After the discretization step, the discrete data matrix is then analyzed with a Bayesian network structure inference algorithm (Step 5). To evaluate robustness, a subset sampling strategy is applied: for each subset, 10% of the samples are randomly omitted, and the remaining 90% are used for Bayesian network inference. The process is repeated independently N times (in our case, N = 1000). Then, the relative likelihood of an inferred connection can be assessed based on how frequently the connection was inferred:

$$L\left(E_{ij}\right)=\frac{1}{N}\sum _{k=1}^N\delta (E_{ij},k)$$

where E_ij is an edge between variables i and j, and δ(E_ij, k) is a function that equals 1 if E_ij is in the graph for subset k and 0 otherwise. Accordingly, a likelihood value of 0 means a connection was never inferred in any of the N simulations and is thus unlikely to be a true connection, while a value of 1 indicates the connection was found in all independent simulations and is thus a robust and believable connection.

To assess the impact of slightly different information content in the datasets provided to the Bayesian inference step, we use an additional analysis step (Step 6) with two different possible strategies (Inference Selection Strategy 1 and 2). Inference Selection Strategy 1 applies a threshold of connection likelihood to individual datasets separately, and then considers only whether a given edge meets that threshold for each member of a group of similar datasets:

$$IS{S}_1\left(\alpha \right)=\{E_{ij}\mid \forall m\in M{L}_m\left(E_{ij}\right)>\alpha ,\}$$

where M is the set of datasets being considered, L_m(E_ij) is the value of L(E_ij) in dataset m, and α is the minimum likelihood threshold. This approach allows for an intuitive, but perhaps overly conservative (due to thresholding effects), way to find common interactions among different datasets. In contrast, Inference Selection Strategy 2 averages the existing likelihood value for each possible connection among the datasets being compared:

$$IS{S}_2\left(\alpha \right)=\left\{E_{ij}\mid \sum _{m\in M}\frac{L_m\left(E_{ij}\right)}{\mid M\mid }>\alpha ,\right\}$$

After averaging, the number of common connections can be plotted as a function of the cut-off parameter (see the example in Figure 4), with the analogous value to the above-described application of Inference Selection Strategy 1 being the percentage conserved at a cut-off value of α. This approach allows for simple visualization of the simulation results of different implementations on the same plot, identification of the impacts of different cut-offs, as well as other possible benefits discussed in Section 4.5.

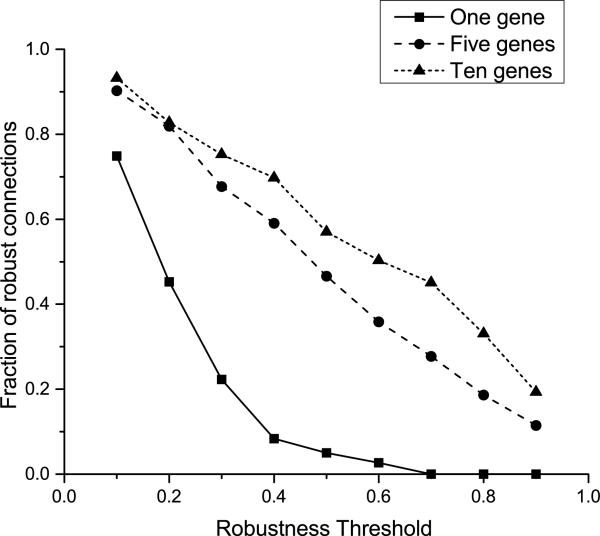
Figure 4. Percentage of connections conserved across subset samples and permutations at different probability cut-offs for Inference Selection Strategy 2.

The y-axis represents the percentage of robust connections, which is calculated as the total number of edge occurrences found across all subsamples that are retained at a given threshold, expressed as a percentage of all edge occurrences ever observed in the subsampling scheme for a given cluster representation scheme and for all relevant datasets, even if inferred for only one subsample for one dataset. The solid line represents the inference results using the single-gene representation of clusters, for Datasets 1 through 4; the dashed and dotted lines represent using 5 and 10 genes, respectively, for each cluster to form pseudo-genes for use in network inference and using Datasets 11 through 14 and 5 through 8, respectively. For any cutoff enforcing reasonably robust results across resampling replicates, the multiple-gene representation of clusters is far more reliable.

4 Results and Discussion

4.1 Clustering as a feature reduction method

We first consider the task of feature selection and opt to use clustering to perform this task. As indicated above, clustering provides the benefit of reducing the variable space by identifying highly correlated or similar features that could potentially be encapsulated in some reduced representation. In addition, those clusters can be used for further detailed network modeling later, whether models of each cluster of variables individually, or some combination of clusters identified by other analyses as likely to be interdependent. We consider the use of three different approaches to clustering: k-means, MMC, and quality-based clustering. Again, we note that these are by no means an exhaustive list of clustering methods nor necessarily what the community would agree to be the universally “best” methods, but a reasonable representation of different types of methods that are commonly used.

For the purposes of feature reduction to identify variables for inclusion in detailed mathematical models, the ideal clustering method is computationally efficient, has few adjustable parameters, is robust to small perturbations in the data, and returns biologically meaningful results. Typically there is a tradeoff between computational complexity and the level of detail that can be used in calculations to determine clusters. Of the three algorithms defined above, the online implementation of MMC has a threshold of 1000 variables for the clustering, so we use the top 1000 significant (as determined by F statistics) variables for the clustering for all three methods.

k-means clustering is a widely-used and straightforward approach to generating clusters from data. Given some parameter k, the algorithm looks to identify k distinct clusters of variables that minimize the within-cluster sum of squares distances:

$$\arg \underset{\mathit{S}}{\min }\sum _{i=1}^k\sum _{\mathbf{x}\in S_i}{\Vert \mathbf{x}-{\mu }_{\mathit{i}}\Vert }^2$$

where x is the vector of all observations for a given variable, S_i is a cluster (set) of variables, S is the set of all S_i, and μ_i is the vector mean of the variables in cluster S_i across each sample. That is, it looks to make k clusters that are as compact in the full-dimensional space as possible. Though this is an np-hard problem, there are a variety of tools available for heuristic or approximate solutions of the problem. One of the key difficulties, though, is defining k in cases where there is no a priori justification for the selection of a specific k value. It is thus common practice to do the clustering with multiple values of k and use a scalar quantity called the Figure Of Merit (FOM) to indicate how “good” the current clustering is [50]. This FOM is calculated in a jackknife fashion by applying the clustering to all but one experimental conditions (samples) in a dataset and using the left-out observation to assess the predictive power of the current clustering. For an individual sample e being left out and the remaining variables being clustered into k clusters, the figure of merit for that subsample is:

$$FOM(e,k)=\sqrt{\frac{1}{n}\sum _{i=1}^k\sum _{x\in C_i}{\left(R(x,e)-{\mu }_{C_i}\left(e\right)\right)}^2}$$

where C_i is the set of variables in a cluster when sample e is omitted from the clustering, n is the total number of variables being clustered, R(x,e) is the level of variable x under condition e in the original data matrix, and μ_Ci(e) is the average value in sample e of all of the variables in cluster C_i. The total figure of merit for finding k clusters across all subsamplings where a single sample is omitted is thus defined as:

$$tFOM\left(k\right)=\sum _{e=1}^{m}FOM(e,k)$$

where m is the total number of samples. The adjusted FOM is calculated as the total FOM multiplied by a factor that takes into account a statistical bias when many clusters are used:

$$aFOM=tFOM\sqrt{\frac{n}{n-k}}$$

k is then often selected as an approximate elbow-point in the plot of FOM versus k, where an increase in the value of k provides diminishing returns in terms of the FOM. A disadvantage of standard k-means clustering is that every variable must be in some cluster, often leading to the inclusion of disparate variables in the same cluster.

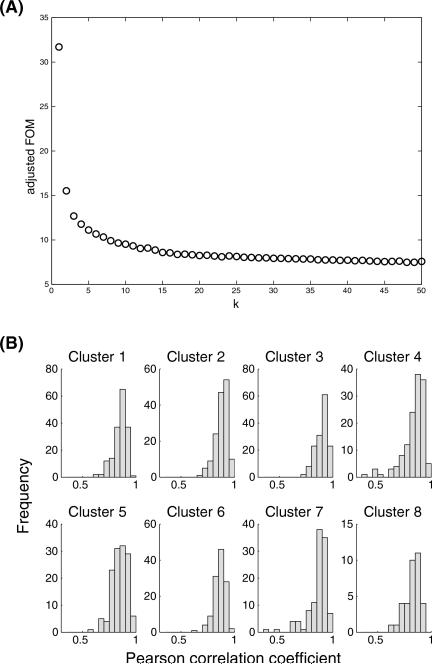
In our case, a plot of the FOM versus k values indicated no clear “elbow point” in the curve but suggests that k = 8 may be the optimal value of k (see Figure 2a). This was viewed negatively for a variety of reasons. First, based on our knowledge of the underlying data, it seemed unlikely that there were only 8 distinct transcriptional profiles and that all of the genes fit into one of those clusters. Second, as indicated, the elbow point of the curve was unclear, suggesting that the selection of k = 8 was, at best, approximate. Finally, the distribution of pairwise correlations among all members of each cluster suggested that the clusters can be quite heterogeneous (see Figure 2b). This heterogeneity defeats the purpose of using these clusters to identify “representative” variables, as there is no truly good representative of the entire cluster. This, again, is ultimately due to the fact that standard k-means clustering necessarily requires all variables to be added to a cluster.

Figure 2. Results of k-means clustering as a candidate method for feature selection.

(a) Plot of the FOM vs. different number of clusters k, where the location of an “elbow point” typically identifies the optimal value of k. (b) Distribution of correlations (Pearson) between each gene and the cluster centroid for all clusters in the case of k = 8. Internal similarity within each cluster is variable and often includes a number of outliers.

Turning to MMC clustering, we found that this lacks robustness to small perturbations in the input dataset. We found that not only could removing a small number of input genes substantially affect the clustering, but even changing the order of the input affected the clustering substantially. This level of sensitivity is expected to have sizable impacts on downstream network inference and thus ultimate inclusion in mathematical models, and so the MMC method was not considered any further.

Quality-based clustering provided robust results that were relatively insensitive to perturbations to the input dataset and input parameters. The parameter driving the clustering in this method is d, a metric that defines how similar two profiles must be to be clustered together. Of particular note here is that the algorithm does not take as input the number of clusters; rather, the algorithm dynamically determines the appropriate number of clusters from the data and the distance parameter d by enforcing a minimum degree of similarity between all members of the cluster based on d. Accordingly, there can be many singleton clusters, giving the effect of not forcing each variable to be added into a larger cluster. The selection of d still remains a task, but there is evidence that a heuristic of d = 0.3 may work well for unit-normalized data. Accordingly, we began with that value and performed slight perturbations.

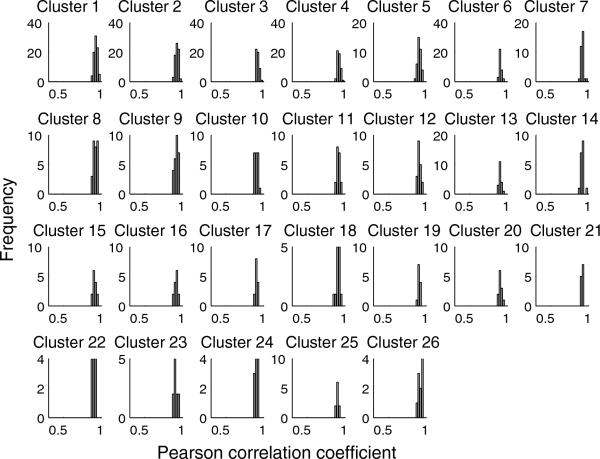
With the default value of d = 0.3, 26 clusters were identified, each containing at least 10 genes per cluster. There were 143 clusters overall, including 43 singleton clusters that will be disregarded from further analysis (but could be incorporated into network modeling if desired). The identified clusters consist of very tightly regulated transcripts based on the required similarity metric, with the correlation distance of each transcript within one cluster to the cluster centroid ranging from 0.87 to 0.98 (detailed correlation distance histograms for the 26 large clusters are given in Figure 3). We note that the presence of these clusters is not merely an artifact of the algorithm. Clustering a dataset where all measurements within a variable are permuted returned zero clusters. Clustering a dataset where for each variable, the time points for each animal were permuted returned only one non-singleton cluster containing two variables. This stands in contrast to k-means clustering, where k clusters will always be found no matter what data is provided as input. These results strongly suggest that the identified clusters are statistically significant.

Figure 3. Distribution of correlations (Pearson) between each gene and the cluster centroid.

Histograms are shown for all clusters with at least ten genes, as found by quality-based clustering with d = 0.3. All clusters have extremely high internal correlation with few or no outliers; x-axis scale is the same as in Figure 2.

To assess the sensitivity of the clustering results to the similarity parameter d, we also performed the clustering with d = 0.4 and 0.5. Increasing the value of d is expected to return larger but looser clusters, while decreasing the value of d will search for smaller but tighter clusters. Identification of many small clusters containing only a few transcripts will not significantly reduce the feature space, and so only more permissive values of d are considered here (this is also more analogous to the results of the k-means clustering). With d = 0.4 or 0.5, 22 or 18 clusters were identified with at least 10 genes per cluster, not too different than the results for d = 0.3. The largest cluster for each of these parameter runs contains 83, 129, and 189 transcripts when d = 0.3, 0.4, and 0.5, respectively. Among them, 79 transcripts (~95% of the largest cluster found with d = 0.3) overlap across the largest clusters found with three different d values. Larger clusters with higher d were often formed by the merger of clusters (or substantial fractions of clusters) found using lower d values. These results suggest reasonable robustness to parameter selection. Accordingly, all further network inference analyses will use only quality-based clustering with d = 0.3 as the feature selection step.

The importance of applying this feature reduction step becomes evident when considering the results of the alternative. Not using feature reduction makes the scale of the network inference problem intractable for Bayesian network modeling (in terms of computational time, robustness, and identifiability), and thus necessitates the use of a different class of models or algorithms to identify relationships in the data. We will consider as a representative example the CLR method, briefly explained in Section 2.2, and previously used in multiple systems biology studies of pathogens [21; 22; 23]. We have run CLR with the original data (1000 features × 35 observations), assuming all features as the possible “transcription factors” in the algorithm, meaning that any gene can have a connection to any other gene. With an FDR threshold of 0.05, over a thousand interactions are found. Using different background estimating functions, CLR returned different interaction networks: 6143 interactions found using the “normal” function (shown in Figure S3.a), 6084 interactions found using the “beta” function, 6847 interactions found using the heuristic strategy described in Gardner's paper [20], and 1087 interactions found using the “epanechnikov” (finite support) kernel density estimator (shown in Figure S3.b). The dependence of the number of connections on the background estimating function is not ideal, but is fairly robust in all but the “epanechnikov” case. More important, though, is the scale of the network: with over 1000, and usually over 6000, interactions discovered, the generated information is still too voluminous to use in driving the development of mathematical models. This analysis would at best be a first step before further, likely graph topology-based, analysis of the results to continue to search for the few most important variables and connections in the system. (We note that using CLR on the feature-reduced dataset is not successful; at the same FDR threshold, there are no significant connections in the network for any of the background estimating functions, presumably due to insufficient sampling to form a background distribution from which to distinguish true connections.)

4.2 Inferred Bayesian network structures are sensitive to single-gene representation of clusters

We now consider the task of network inference using single-gene representation of the clusters identified in the feature reduction step. We have reduced the original large feature space (M = 1000 transcripts) to a few important clusters (M₁ = 26 large clusters for d = 0.3 using quality-based clustering). Each cluster becomes one feature, which requires selecting a representative for the cluster. Previous methods using clustering as a feature selection step have used an average or centroid gene as a representative of the cluster, or the gene closest to the centroid, so as to ensure that “real” data is being used rather than synthetic data that is not present in the original dataset [51]. To investigate the effect of choosing different representatives, we created 4 different datasets by choosing the centroid (Dataset 1), the closest gene to the centroid (Dataset 2), the second closest gene to the centroid (Dataset 3), and the third closest gene to the centroid (Dataset 4) as the representative of each cluster. Each dataset consists of 26 features with 35 observations (where m = 1 and P = 35 in the data processing workflow of Figure 1). The four different datasets then in turn went through the same data discretization step (Step 4) and BN structure learning step (specifically, the sparse candidate method [37] for network inference in Step 5)) with the same subset sampling strategy (N = 1000). The learned networks for each dataset were then screened and evaluated with the aforementioned Inference Selection Strategies 1 & 2 (Step 6). One might reasonably expect these inferred networks to be very similar.

Using Inference Selection Strategy 1, only connections frequently inferred from each dataset's subsamples (e.g., present in more than half of inferences for each dataset) were retained, thus focusing on the most consistent (and presumably strongest or most likely) connections in the data. As shown in Table 1, there are 13 to 20 connections found in at least half of the sampling subsets for each individual dataset. However, these connections are not consistent across the datasets. Between using the centroid of a cluster (Dataset 1) and the real gene closest to the centroid of the cluster (Dataset 2), which one may expect to yield similar results, only 10% of the connections in Dataset 1 are present in Dataset 2. Using the second- and third-closest genes to the centroid also yields similarly divergent results. Moreover, of all of the connections found in these four otherwise similar datasets, there are no connections found in all datasets. The results are even worse when a higher probability cutoff (e.g. 0.8) is used to determine the most likely connections.

Table 1.

Summary of Bayesian network inference results with single-gene representation of clusters and Inference Selection Strategy 1.

Data	# of connections with at least 50% existence in N simulations	# of connections with at least 80% existence in N simulations
Dataset 1	20	9
Dataset 2	18	4
Dataset 3	18	2
Dataset 4	13	1
Dataset 1 & 2	2 (10%)	2 (22.2%)
Dataset 1 & 3	1 (5%)	1 (11.1%)
Dataset 1 & 4	4 (20%)	1 (11.1%)
Dataset 1, 2, 3 & 4	0 (0%)	0 (0%)
Average Prob.	8.75%*	11.1%*

Note: Datasets 1, 2, 3 & 4 have 26 features and 35 observations. N = 1000 for all cases. Percentages are calculated as the number of common connections found in two (or more) datasets at a given threshold divided by the number of connections found in Dataset 1 at the same threshold. Percentages marked with an asterisk (*) are an exception, and are calculated as the average of all preceding percentages in a given column.

Using Inference Selection Strategy 2 (where instead of thresholding the probability of interactions at 0.5 for each set individually, the average probability across all datasets is calculated, averaged, and then thresholded) does not change the results substantially. For instance, there are only 2 connections present at a threshold probability of 0.5 averaged across all datasets. Compared to the overall set of learned connections for all datasets (with non-zero probability), less than 5% of connections remained at the threshold of 0.5 (see Figure 4).

In summary, even though the identified clusters are very tight based on pairwise correlation distances of cluster genes to the cluster centroid (shown in Figure 3), choosing one feature per cluster as a representative does not result in consistent learning using BN structure learning algorithms.

4.3 Creating pseudo-genes comprised of multiple features allows more robust network inference

One possible cause of the non-robust network learning using a single-gene representation of clusters is the small sample size of the dataset (35 observations), known to be challenging for Bayesian network inference [52; 53]. For typical proof-of-principle approaches for Bayesian network inference algorithms, the number of samples used is typically hundreds or thousands; for instance, a previous study using the K2 inference algorithm explored the use of sample sizes from 100 to 10,000, concluding that 3,000 was sufficient to reproduce the results of having all 10,000 observations [33]. For the case of in vivo experiments in general, and non-human primate experiments in particular, sample sizes that large are experimentally and ethically infeasible. As a result, random noise in the representative genes seems to drive the identification of connections between clusters rather than the signal that those genes are supposed to represent. To compensate for sample size limitations, we selected multiple features from each cluster and concatenated their observations together to create pseudo-genes with greatly increased numbers of observations.

For our first analyses, we chose to use ten genes per cluster, yielding for each cluster a new feature with 35 × 10 = 350 “observations” instead of the single representative gene with 35 observations previously used for network inference. We chose to use 10 genes since this would be the maximum number of genes possible for all of our 26 large clusters; in addition, the resultant number of observations is more in line with sample sizes previously demonstrated to be reasonably effective for Bayesian network inference.

Based on the previous results indicating overfitting of the model to the single-gene datasets, we then sought to control for overfitting by comparing the results of multiple instantiations of the 10-gene pseudo-genes. Dataset 5 was created by concatenating the ten genes closest to the centroid, in order. Dataset 6 took the same sets of 10 genes and permuted their order of concatenation for each cluster's pseudo-gene independently, controlling for fitting to random noise in the data. Dataset 7 used the second-closest to eleventh-closest genes to the centroid in each cluster, controlling for small changes in the information content of each pseudo-gene. Similarly, Dataset 8 used the third-closest to twelfth-closest genes to the centroid. (For clusters with fewer than eleven or twelve genes, the ten genes furthest from the centroid were used for Datasets 7 and 8, respectively.) Dataset 9 uses the ten features furthest from the centroid, to assess the impact of more significant changes in the information content of the pseudo-genes. Finally, Dataset 10 used ten features picked randomly and independently for each cluster, again to control for the impact of more significant changes in information content. As in the single-gene representative analyses, these datasets were then all processed through Steps 4, 5, and 6 of our pipeline with all parameter settings unchanged.

The summary of simulation results using Inference Selection Strategy 1 is given in Table 2. When any single dataset is considered, there are approximately 20 connections inferred from at least half of the subsamples of the dataset (N = 1000), similar to the single-gene representation. The overlap among the discovered interactions across datasets has increased markedly, though. Nearly 80% of the connections identified in Dataset 5 are present in its permuted version, Dataset 6, substantially better than the best overlap from the single-gene case, which was 20%. This result suggests that the network inference is not sensitive to gene order in the pseudo-gene. Moreover, there is substantial overlap between Dataset 5 and Datasets 7 and 8, suggesting that small changes in the information content do not substantially affect the inferred networks. Dataset 9 exhibits the least amount of overlap with Dataset 5; this outcome is intuitive, as the features are not only the least representative of each cluster, but also the least similar to each other, thus adding the most noise to the data. However, this worst-case scenario is still better than the best example from the single-gene representative analysis, indicating the improved robustness imparted by using multiple genes as representatives of a cluster. The results from randomly-selected genes in each cluster, accounting for both feature order and gene selection variability, represent a challenging but reasonable scenario that still shows almost 50% overlap with Dataset 5.

Table 2.

Summary of Bayesian network inference results with the ten-gene representation of clusters and Inference Selection Strategy 1.

Data	# of connections with at least 50% existence in N simulations	# of connections with at least 80% existence in N simulations
Dataset 5	23	13
Dataset 6	23	14
Dataset 7	24	13
Dataset 8	19	14
Dataset 9	18	7
Dataset 10	19	6
Dataset 5&6	18 (78.3%)	10 (76.9%)
Dataset 5&7	17 (73.9%)	9 (69.2%)
Dataset 5&8	13 (56.5%)	7 (53.9%)
Dataset 5&9	7 (30.4%)	2 (15.9%)
Dataset 5&10	11 (47.8%)	3 (23.1%)
Dataset 5, 6, 7 & 8	12 (52.2%)	6 (60%)
Average Prob.	56.5%*	49.8%*

Note: Datasets 5, 6, 7, 8, 9, & 10 have 26 features and 350 observations. N = 1000 for all cases. Percentages are calculated as the number of common connections found in two (or more) datasets at a given threshold divided by the number of connections found in Dataset 5 at the same threshold. Percentages marked with an asterisk (*) are an exception, and are calculated as the average of all preceding percentages in a given column.

Also worth noting is the conservation across multiple related datasets. Looking across Datasets 5, 6, 7, and 8, more than 50% of the interactions found in Dataset 5 are found in all of these datasets. More specifically, all but one of the interactions shared between Datasets 5 and 8 are also in Datasets 6 and 7, speaking to the robustness of the results to noise and information content.

Using Inference Selection Strategy 2 (shown by the dotted line in Figure 4), the percentage of frequently-detected connections relative to all detected connections has increased significantly by using ten-feature pseudo-genes instead of single-gene representations. For example, at a cutoff of 0.5 (interactions detected across more than 50% of the subsamples from Datasets 5, 6, 7, and 8 combined), 17 connections (approximately 50% of all connections ever found for a group of datasets) are retained, which is over 10-fold greater than the results of the single-gene representation. In summary, for either inference selection strategy, selecting ten features improved the robustness of BN structure learning across multiple subsamples and permutations of the original data.

It may be too restrictive to require at least ten features for each cluster for general application of this approach. For example, datasets starting with a smaller number of features may have an insufficient number of large clusters to apply the approach as described above. Smaller clusters of genes may be expected to be important in the underlying biology in some cases, motivating their inclusion in the network inference step. Accordingly, we implemented another round of network inference using pseudo-genes containing five genes per cluster to see if fewer features in a pseudo-gene could still provide robust network inference. To compare the performance of the five-gene representation to that of the ten-gene representation, we generated six more analogous datasets by using the five features closest to the cluster centroid (Dataset 11), the five features closest to the cluster centroid with the feature order randomly shuffled per cluster (Dataset 12), the second- through sixth-closest genes to the cluster centroid (Dataset 13), the third- through seventh-closest genes to the cluster centroid (Dataset 14), the five genes furthest from the centroid (Dataset 15), and five randomly selected genes (Dataset 16). For these datasets, there were originally 52 clusters with at least five transcripts per cluster. In order to generate results as directly comparable as possible with the ten-gene representation, we have restricted the newly created 6 datasets to only the 26 largest clusters.

The summary of results for the five-gene representation using Inference Selection Strategy 1 is given in Table 3. Clearly, using five representative genes per cluster also yields more robust learned networks than using only one representative gene. The average probability of common connections has been increased almost four-fold (from less than 10% to almost 40%), and randomizing the order of the five genes or replacing 20% of the data with different representatives still yields almost two-thirds of the same inferred connections. Inference Selection Strategy 2 indicates the same (Figure 4): a significant increase in robustness compared to a single-gene representation, though short of the robustness of a ten-gene representation. These five-gene results support the conclusion that using multiple features as cluster representatives for regulatory network inference in datasets with a quite limited sample size could be a valuable strategy to drive the development of mathematical models, while also allowing for the inclusion of more (smaller) clusters in the network inference.

Table 3.

Summary of Bayesian network inference results with the five-gene representation of clusters and Inference Selection Strategy 1.

Data	# of connections with at least 50% existence in N simulations	# of connections with at least 80% existence in N simulations
Dataset 11	23	12
Dataset 12	23	12
Dataset 13	23	15
Dataset 14	21	8
Dataset 15	19	10
Dataset 16	18	8
Dataset 11&12	15 (65.2%)	8 (66.7%)
Dataset 11&13	13 (56.5%)	6 (50%)
Dataset 11&14	10 (43.5%)	4 (33.3%)
Dataset 11&15	2 (8.7%)	2 (16.7%)
Dataset 11&16	8 (34.8%)	5 (41.7%)
Dataset 11, 12, 13 & 14	6 (26.1%)	2 (26.1%)
Average Prob.	39.2%*	39.1%*

Note: Datasets 11, 12, 13 & 14 have 26 features and 175 observations. N = 1000 for all cases. Percentages are calculated as the number of common connections found in two (or more) datasets at a given threshold divided by the number of connections found in Dataset 11 at the same threshold. Percentages marked with an asterisk (*) are an exception, and are calculated as the average of all preceding percentages in a given column.

4.4. Discretization cutoff values are less important than representation of clusters

Small changes in the selected value of the discretization parameter C may at times have an impact on the robustness of the downstream results (see Figure S4, analyzed with Inference Selection Strategy 2, and Table S1 and S2, analyzed with Inference Selection Strategy 1, for detailed results in two specific cases analyzed using the ten-gene and single-gene representation approach, respectively). We observed that an increase in the final C value had little impact on robustness, while a decrease in C had a substantial negative impact, presumably due to loss of mutual information between variables, as shown in Figure S4. At reasonable threshold values for subsample robustness (greater than 0.5), though, the impacts of slight changes in C in either direction are still less important than those resulting from the gene representation strategy used.

4.5 Comparison of inference selection strategies

In all of the aforementioned analyses, two different inference selection strategies were considered to assess the robustness of the inference results and find the connections that are most likely given the data. While Inference Selection Strategy 1 ensures that each candidate connection is highly likely given each subsample or permutation of the data, it is necessarily subject to threshold effects: a connection may be present, for example, in the inference for 51% of the subsamples in a given dataset, but given some small perturbation may dip down to 49% in one permutation. This very small relative change in probability would likely not significantly affect one's expectation of whether this is a real connection, but would have the effect of completely eliminating it from consideration in further analyses. If multiple permutation datasets are being considered, then each permutation would carry the risk of eliminating a possibly real interaction through a relatively small change and a threshold effect. While this would certainly indicate that such connections may rank as less likely than the more conserved inferred connections, it seems undesirable to exclude more connections from further considerations due strictly to the effects of noise near a threshold border. This is particularly true in the context of all of the effort already expended to identify higher-confidence connections, combined with the need to provide as thorough an exploration of network space as possible in order to drive the development of accurate mathematical models. In these cases, Inference Selection Strategy 2, which averages the probabilities across all datasets being compared, may be desirable for being reasonably inclusive but still selective for highly likely interactions.

To assess the impacts of using the two different inference selection strategies, we first created two new permuted versions of Dataset 5, yielding four versions overall: Datasets 5, 6, 6’, and 6’’. We processed all of the datasets through the same working pipeline indicated in Figure 1. As listed in Table 4, the performances of the four datasets with the feature order randomly shuffled are quite similar. However, it is evident that adding small perturbations to the data as induced by the feature order permutation method may cause different connections to be removed via thresholding for different pairs of datasets. Accordingly, when looking at the intersection of all datasets, only 14 of the connections originally present in Dataset 5 remain in the analysis, even though there are quite a few more connections that may have just barely missed the threshold in only one of the permutations. The connections present in all four permuted datasets are represented by the solid edges in the network in Figure 5. Using Inference Selection Strategy 2, on the other hand, identifies 19 connections as consistent across all of the permutations. The additional five edges, represented in Figure 5 with dotted lines, compensate for any potential threshold effect in one dataset by even higher likelihood of presence in other datasets. So, while Inference Selection Strategy 1 may be useful if a more restrictive set of connections is desired, we believe that the second strategy provides a better balance of restrictiveness with inclusiveness and is potentially a more useful candidate network for downstream biological inference and future modeling purposes.

Table 4.

Summary of Bayesian network inference results with the ten-gene representation of clusters and Inference Selection Strategy 1 for shuffled gene orders.

Data	# of connections with at least 50% existence in N simulations	# of connections with at least 80% existence in N simulations
Dataset 5	23	13
Dataset 6	23	14
Dataset 6’	21	13
Dataset 6’’	23	13
Dataset 5 & 6	18 (78.3%)	10 (76.9%)
Dataset 5 & 6’	17 (73.9%)	8 (61.5%)
Dataset 5 & 6’’	15 (65.2%)	9 (69.2%)
Dataset 5, 6, 6’ & 6’’	14 (60.8%)	4 (30.7%)
Average Prob.	69.6%*	59.6%*

Note: Datasets 5, 6, 6’ & 6’’ have 26 features and 350 observations. N = 1000 for all cases. Percentages are calculated as the number of common connections found in two (or more) datasets at a given threshold divided by the number of connections found in Dataset 5 at the same threshold. Percentages marked with an asterisk (*) are an exception, and are calculated as the average of all preceding percentages in a given column.

Figure 5. The learned network using the proposed pipeline.

Numbers in vertices represent the numbers assigned during clustering and are consistent with Figure 3. This network was generated using the ten-gene representation of clusters. Connections with dotted lines are only found with Inference Selection Strategy 2, not with Strategy 1. The connections with solid lines are found with both strategies.

5 Conclusions

While the high dimensionality of feature space in large-scale biological datasets allows for wide-ranging, untargeted discovery of new phenomena in biological systems, when coupled with typically small numbers of sample observations, these features present a major computational and analytical problem. If a key downstream goal of these analyses is to develop mathematical models for the entire system (or some subsystem) that can help to increase our understanding of the system, then identifying the key biological players as well as their network interactions is a critical step. Although some computational methods (e.g. CLR) can efficiently learn networks from large genome-scale datasets, the identified networks are usually far too large and dense to directly inform later mathematical modeling. The necessity of developing approaches for exacting a concise and meaningful network that could benefit mathematical modeling becomes imperative for such large-scale datasets. Aiming at this issue, we have proposed a six-step workflow as depicted in Figure 1 that can infer robust and high-confidence networks for a dataset with many more measured features than observations. Depending on the available data, step 1 (data preprocessing) may or may not be needed.

We focused on clustering methods to reduce the dimension of measured features. After comparing three representative clustering methods, namely k-means, MMC, and quality-based clustering, we adopted the last one in our pipeline as it returns tight, robust clusters and does not force every feature to a cluster. The only parameter associated with the clustering method, the similarity metric d, has some effect on the final clustering result, but yields high overlap between computed clusters and thus allows for reasonably robust interpretability across downstream results.

We identified that the perhaps intuitive approach to use the median of a cluster as the cluster representative will not yield robust results for network inference when applied to a small-sample dataset. We have used the strategy of creating composite “pseudo-genes” by concatenating some small number of genes closest to the cluster's centroid as ideal representatives of a cluster's pattern. Choosing multiple features from each cluster greatly improves the robustness of Bayesian network learning results, with more features (e.g. m = 10) performing slightly better than fewer features (e.g. m = 5). However, choosing fewer features allows more clusters to be considered, so there is a compromise between the learning robustness and the breadth of the analysis.

We then used a combination of subset sampling and permutation analyses to identify the most likely connections between clusters based on a discretized version of the reduced dataset. Discretization maintains the structure of the data and has the effect of reducing the “resolution” of the data from its original form, but it also reduces the number of samples required for effective Bayesian network inference. We used a more complex discretization method than the commonly-used equal-interval or equal-quantile discretization so as to maintain as much mutual information in the dataset as possible. For the network learning step, we used a subset sampling strategy with 10% of the samples randomly omitted for N independent but overlapping subsets (e.g. N = 1000). We then used permutations of the pseudo-gene construction to identify the connections least susceptible to individual-gene noise and thus most likely to be real, and identified two similar inference selection strategies that provide slightly different levels of conservatism in selecting the most likely connections.

There are certainly limitations to the system described herein. First, we restrict ourselves to only clusters of at least a certain size, and not every critical gene may have so many similarly regulated genes. This limitation is ultimately a result of the selection of Bayesian networks as a modeling approach: Bayesian networks require significant numbers of observations for reliable inference and became less computationally tractable as they get bigger. These limitations are significant, particularly in light of the obviously limited number of samples (observations) available from genome-scale experiments. However, this tradeoff was viewed as reasonable in comparison to the limitations of full genome-scale networks, which are often dense and difficult to interpret. Other limitations of our work include incomplete consideration of all of the factors that may affect downstream results. For transcriptome sequencing, for example, assumptions in mapping reads to genes, splice isoforms, or other transcriptional units may affect the information content of the data and ultimately the inference. For other types of data, the methods used for missing value imputation may also be a significant factor. It is critical to consider these steps as well when defining an overall data analysis and interpretation pipeline. Finally, we have not yet considered the task of biological interpretation of the results. Enrichment analyses might be used to characterize which of the candidate interactions are most likely given previous biological knowledge or to confirm that the overall network seems reasonable. We have restricted focus here to only the statistical treatment of the data, with the expectation that robust results are more likely to be real rather than artifacts.

Taken together, the approach we have described represents a promising strategy for use in what will likely be a growing field: the application of systems biology approaches to pathogenic diseases and epidemiology. Such applications will ultimately be best informed and driven by developing mathematical models that capture our knowledge of the system and make predictions to guide future experiments. The framework presented here is a useful, efficient, and reasonable way to help identify the most relevant information from genome-scale experimental datasets that can help drive both the modeling and later experimental follow-ups necessary to validate our understanding of the system. Specifically, we believe that the proposed method will be useful to identify the factors that may impact infectious disease, whether in the host or the pathogen, and will help lead to improved models and understanding of infectious disease, whether on a molecular or an epidemiological level.

Highlights.

• A generalized workflow for driving model development based on large-scale datasets.

• Network inference for omic-scale datasets with few observations.

• Robust Bayesian network learning from few samples using resampling and permutation.

Abbreviations

ANOVA

Analysis of variance

ARACNE

Algorithm for reconstruction of accurate cellular networks

BN

Bayesian network

CLR

Context likelihood of relatedness

DREAM

Dialogue for reverse engineering assessment of methods

FDR

False discovery rate

FOM

Figure of merit

MI

Mutual information

MMC

Modulated modularity clustering

MRMR

Maximum relevance/minimum redundancy

MRNET

Minimum redundancy networks

PCA

Principal component analysis

PLS-DA

Partial least squares discriminant analysis

RFE

Recursive feature elimination

SVM

Support vector machine

TMI

Total mutual information