Is Mathematical Anxiety Always Bad for Math Learning: The Role of Math Motivation

Abstract

The linear relations between math anxiety and math cognition have been frequently studied. However, the relations between anxiety and performance on complex cognitive tasks have been repeatedly demonstrated to follow a curvilinear fashion. Given the lack of attention to the possibility of such complex interplay between emotion and cognition in the math learning literature, the current study aimed to address this gap via exploring the relations between math anxiety, math motivation, and math cognition. The current study consisted of two samples. One sample included 262 pairs of young adolescent twins and the other included 237 adult college students. Participants self-reported their math anxiety and math motivation. Math cognition was assessed using a comprehensive battery of mathematics tasks. In both samples, results showed inverted-U relations between math anxiety and math performance in students with high intrinsic math motivation, and modest negative associations between math anxiety and math performance in students with low intrinsic math motivation. However, this pattern was not observed in tasks assessing student’s nonsymbolic and symbolic number estimation. These findings may help advance our understanding of mathematics learning processes and may provide important insights for treatment programs that target improving mathematics learning experiences and mathematical skills.

Math anxiety (MA) is defined as a feeling of tension, worry, and fear in situations involving math-related activities (Suinn & Winstson, 2003). It has significant conceptual overlap with general academic affect such as test anxiety and academic self-confidence (Devine, Fawcett, Szucs, & Dowker, 2012), but also captures affective experiences unique to mathematic situations (Hembree, 1990). The relations between math anxiety (MA) and math cognition have been frequently studied, and the negative associations between the two have been observed at multiple levels of mathematical processing ranging from simple counting (Maloney, Risko, Ansari, & Fugelsang, 2010) to complex math problem solving (Ramirez, Gunderson, Levine, & Beilock, 2013), and is evident across various developmental stages (Maloney et al, 2010; Ramirez et al., 2013).

However, to conclude that MA uniformly impairs the development of math cognition might not fully capture the potentially complex interplay between emotion and cognition. A long tradition in the animal learning and cognitive psychology literatures demonstrated complex relations between stress, emotional arousal, and cognitive performance. These studies revealed that an intermediate level of stress produced optimal learning efficiency of complex tasks in rats, whereas both extremely low and high levels of stress produced poor learning efficiency (Yerkes & Dodson, 1908). This inverted-U law has since been extended to the relation between negative emotions such as anxiety and performance in complex memory and attention tasks that rely heavily on prefrontal cortex functioning in primates (Andreano & Cahill, 2006; Aston-Jones, Rajkowski, & Cohen, 2000; Mendl, 1999). At the behavioral level, a moderate level of anxiety is believed to heighten alertness and focused attention, which facilitates complex cognitive functioning, whereas high anxiety impairs performance by diverting resources away from cognitive performance. More recent studies have demonstrated that central neurochemical activities (e.g., catecholamine release and signaling) may underlie the observed curvilinear relationship between anxiety and complex cognitive performance (Arnsten, 2009; Diamond, Campbell, Park, Halonen, & Zoladz, 2007). Therefore, given that these complex cognitive functions are crucial to mathematical processing (Ashcraft, 2002), it is plausible that a quadratic curvilinear relation between math performance and specific anxiety about math would be observed. Two previous studies have provided some preliminary evidence suggesting facilitative effects of moderate levels of MA on math performance in adults and mathematically gifted children (Evans, 2000; Tsui & Mazzocco, 2006). Thus, the first aim of the current study was to examine whether math performance varies as a quadratic curvilinear function of MA in a normal-achieving student population.

Another important affective aspect involved in math cognition is motivation (Middleton & Spanias, 1999; Vallerand et al, 1992). Math motivation (MM) captures the extent to which individuals embrace math challenges, value the importance of math abilities, and are motivated to perform well in math (Gottfried, Marcoulides, Gottfried, Oliver, & Guerin, 2007). MA and MM are two related but distinct dimensions of math affect. MA captures nervousness and discomfort in math experiences, but offers little information on how individuals approach math-related activities to relieve these negative feelings. MM defines approach versus withdrawal-oriented response tendencies toward math. MA and MM are related in the sense that they both capture some hedonic (i.e., negative vs. positive) aspects of math experience, and are shown to be modestly negatively correlated (Chiu & Henry, 1990). MA and MM are distinct constructs in that items measuring MA and MM are shown to load on separate factors (Bai, Wang, Pan, & Frey, 2009; Krinzinger, Kaufmann, & Willmes, 2009). Some highly math anxious individuals are more avoidant in math, whereas others invest more efforts and recruit more cognitive resources in math problem solving (Lyons & Beilock, 2012; Wigfield & Meece, 1988). Such a multi-dimensional conceptualization of math-related affect is also consistent with the emotion literature that points to the bidimensionality in affective evaluative space (Norris, Gollan, Berntson, & Cacioppo, 2010) and the distinction between motivational direction and affective valence (Harmon-Jones, Gable, & Peterson, 2010).

Importantly, MA and MM together improves prediction of math learning behaviors and achievement outcomes as compared to either one alone (Lyons & Beilock, 2012; Wigfield & Meece, 1988). In particular, one recent study showed that high activations in brain regions involved in motivating behaviors dampen the negative effects of high MA on math performance, suggesting that math performance not only varies as a function of MA, but also on how individuals approach math-related situations (Lyons & Beilock, 2012). However, given the exclusive focus on extremely high and low MA in this study, it is ultimately unclear how motivation interacts with MA across the full range of MA in predicting performance. This question is of particular importance in the present context where a linear relation between MA and math cognition is no longer assumed. Therefore, the second aim of this study was to examine the potential complex interaction between MA and MM in relation to math cognition. Specifically, we investigated whether the quadratic relations between MA and math performance would further vary as a function of MM. It is possible that while intermediate levels of anxiety can facilitate attention focusing and mobilization of cognitive resources, this facilitative effect of MA on math performance may only be observed in individuals with high MM who are motivated to overcome challenges and relieve discomfort in math situations via active approach. To the contrary, given the avoidance tendencies in individuals who are not motivated in math, increasing levels of fear and discomfort in these individuals may be associated with more withdrawal of efforts resulting in even poorer performance. Therefore, we hypothesized that the quadratic curvilinear relations between MA and math performance would only be observed in individuals with high MM, whereas a negative linear relation would be observed in those with low MM. We tested our hypotheses in two independent samples.

Study 1

Methods

Participants

Data were collected from 262 pairs of same-sex twin siblings (58% female) that participate in the ongoing longitudinal Western Reserve Reading and Math Projects (WRRMP; Hart, Petrill, Thompson, & Plomin, 2009). Annual assessments for these projects began in kindergarten or first grade, and have continued across a maximum of ten waves. The current study examined data collected when siblings were 12.25 years old on average (SD = 1.20 years; Range = 8.75 to 15.33 years). The race composition of the sample was: 91% White, 5% African American, and 2% Asian. Parent education varied widely: 20% had some postgraduate education, 42% had a bachelor degree, 16% had attended some college, 10% had a high school education or less, and 12% did not specify.

Procedure

The current study was approved by the Office of Responsible Research Practice at The Ohio State University and the Institutional Review Board at Case Western Reserve University. The current study included data collected on two separate 3-hour home visits that occurred within one month of each other. Parental consent and child assent were obtained at the beginning of each home visit. Each child was evaluated by a separate tester in a separate room on a series of cognitive assessments. In addition, children completed a series of questionnaires. Each family received a $100 honorarium for their participation in each visit.

Measures

Mathematical Anxiety

Children reported their own MA using the Revised Mathematics Anxiety Rating Scale of Elementary Students (MARS-E; Suinn, Taylor, & Edwards, 1988). The 26 items in MARS-E are rated on a 5-point Likert type scale (1 = not at all nervous; 5 = very very nervous) that captures how tense or worried children feel during math-related activities. The MARS-E has good internal consistency with a Cronbach’s α of .94.

General Anxiety

The general anxiety subscale of the Spence Children’s Anxiety Scale (Spence, 1997) was used to measure children’s general anxiety. This subscale consists of 6 items that are rated on a 4-point Likert type scale (1 = never; 4 = always). This scale has adequate internal consistency with a Cronbach’s α of .71.

Mathematical Motivation

Children self-reported their MM using 3 items from the scale developed by Chiu and Zeng (2008). These items are rated on a 4-point Likert type scale (1 = strongly disagree; 4 = strongly agree), and measure children’s beliefs about the value of math as well as their interest in math. The Cronbach’s α for this scale is .78, indicating adequate internal consistency.

Mathematics Performance

The Dots Task captures individual differences in the approximate number system. It measures individual’s ability to represent numerical quantities nonverbally (Halberda, Mazzocco, & Feigenson, 2008). The Dots task was administered on a laptop. In this task, participants were shown a series of pictures of intermixed blue and yellow dots of different sizes and quantities. Participants had to decide whether there were more blue dots or yellow dots for each trial. The total number of dots in each trial was randomized within the range of 5 to 16. Four possible ratio bins were presented across trials: 1:2, 3:4, 5:6, and 7:8. To each participant, two sessions were administered with 10 practice trials and 10 test trials per ratio bin per session. The Weber fraction that has been corrected for guessing was used as the outcome variable of interest. Larger Weber fractions represent less accurate non-symbolic number estimation.

Number-Line Estimation Task captures individuals’ ability to represent and estimate numerical quantities spatially (Siegler & Opfer, 2003). Participants were shown a series of blank number lines approximately 24cm long, with the label “0” at one end, and “1000” at the other end. Each blank number line was presented in the center on a separate piece of paper, together with a number displayed above the number line. Participants were asked to estimate where that number would be on the number line using a pencil mark. Each participant was first given a practice trial of placing “500” on the number line. Subsequently, 22 test trials were administered in the same order for all participants. To obtain the actual number represented by the mark given by each participant, the length from “0” to the mark on the line was measured and then divided by the total length of the line and multiplied by 1000. To measure each participant’s estimation accuracy, the average of the 22 absolute difference scores between the participant’s answers and the corresponding target numbers were obtained and used as the outcome of interest. Larger scores represent less accurate estimation.

Composing and Decomposing Numbers Task (CDNT) is a timed measure of the automaticity of composing and decomposing numbers (Mazzocco & Hanich, 2010). The CDNT was administered using pencil and paper. There were four blocks in this task. The first block was a practice block in which participants were asked to compose as many numerical pairs as possible which sum to 19. In the second and third blocks, participants were presented with 49 pairs of numbers per block, and were asked to circle sets of numbers which sum to 19. For each block, 21 pairs of numbers sum to 19 and 28 pairs do not sum to 19 (i.e., foil pairs). In the fourth block, participants were asked to circle sets of numbers which sum to 19 and cross out pairs of numbers which sum to more than 23, again among 49 pairs of numbers. There were 21 pairs of numbers that sum to 19 and 7 pairs that sum to greater than 23. Participants were encouraged to work as quickly as possible without skipping, and they were given 60s to work on each block. Response time was defined as the time between the start and the end of a block (a maximum of 60s), and was recorded by the tester using a stop watch. The number of correct responses was computed as the total circles over the pairs which sum to 19 and uncircled foil pairs evaluated in 60s or less. In addition, the number of pairs that was correctly crossed out was counted as correct responses for the fourth block. Efficiency scores were computed for each block by dividing the number of correct responses by response time (seconds). A mean efficiency score was computed by averaging the efficiency scores across the last three blocks, and was the outcome variable of interest for this task.

Problem Verification Task was developed as a measure of math calculation fluency and metacognition (Rinne & Mazzocco, 2014). We relied on the calculation fluency component of this measure in the present study. Participants were shown a series of two-operand arithmetic problems on a laptop including addition, subtraction, multiplication, division, and equivalency of fractions. Each arithmetic problem included a solution that was correct or incorrect, and participants were asked to indicate whether the solution is “right”, “wrong”, or “don’t know” as quickly as possible without calculating. Participants were also asked to indicate whether they were “positively sure”, “kind of sure”, or “not sure” of their answer after each item. Each item was presented for a maximum of 10s. If no response was given within 10s, the program would proceed to the next item. In total, participants were given 4 practice items followed by 88 test items. Among all test items, 64 were easy items (e.g., single digit arithmetic, common-denominator fraction, and far-foils) and 24 were hard items (e.g., double-digit arithmetic, uncommon-denominator fraction, and close-foils). Reaction time (seconds) was defined as the time between stimulus onset and response and was recorded by the computer for each item. For the current analyses, an efficiency score was used and was calculated by dividing the percent of total correct responses by the mean reaction time across all items.

Calculation

The Calculation subtest of the Woodcock Johnson III Tests of Achievement (Woodcock, McGraw, & Mather, 2001) is a test of mathematical computation ability. This test was administered using paper and pencil. Participants were asked to solve a series of arithmetic problems. These arithmetic problems include addition, subtraction, multiplication, and division of positive and negative numbers, whole numbers, percentages, decimals, and fractions. Unlike the Problem Verification task, the Calculation Test is an untimed measure. It requires participants to do the actual calculation rather than to simply retrieve math facts. In addition, the complexity and difficulty level of the arithmetic problems in the Calculation test increase across items and far exceed those in the Problem Verification task. W-scores were used in the current study. W-scores are obtained based on item response theory, and all scores have equal measurement intervals.

Applied Problems

The Applied Problems subtest of the Woodcock Johnson III Tests of Achievement (Woodcock et al., 2001) measures participant’s ability to integrate math knowledge, quantitative reasoning, and calculation skills in problem solving. The Applied Problems test was administered using paper and pencil. Participants were presented with a series of math story problems presented both orally and visually. Participants decided which mathematical operation to use and completed the calculations. W-scores were used for the current analyses.

Results

Descriptive and correlational analyses were conducted using SPSS 22.0 (SPSS IBM, NY). Descriptive statistics are shown in Table 1. All main study variables were distributed widely across their respective scales. Most variables were distributed normally, with the exception of Dots task, Number-Line task, and Problem Verification task. Subsequently, log transformations were performed on the skewed variables. Transformation successfully produced variables that more closely approximated normal distributions. In addition, to maintain scale consistency across all math cognition tasks and to facilitate interpretation, scores from the Dots task and Number-Line task were reverse-scored so that higher scores also represent better performance.

Table 1.

Descriptive Statistics of the Main Study Variables

	N	Mean	SD	Skewness	Kurtosis	Min	Max
General Anxiety	391	5.42	2.78	.61	.42	.00	15.00
Math Anxiety	506	48.77	16.44	.92	.95	14	126
Math Motivation	389	2.59	.75	.00	−.43	1.00	4.00
Dots Task	506	.34	.25	4.89	36.25	.06	2.95
Number-Line	504	83.62	79.96	2.84	9.14	16.23	523.45
CDNT	511	.48	.20	.78	.98	.11	1.31
Problem Verification	505	16.41	6.71	1.12	2.65	2.82	55.63
Calculation	493	518.98	16.62	−.17	.09	462	567
Applied Problems	509	526.87	18.65	−.26	1.58	449	597

Note. The N for general anxiety and math motivation questionnaire is lower because they belong to the last part of the testing battery and was not administered to some participants due to time constraints. CDMT = Composing and Decomposing Numbers Task.

Correlations between study variables are shown in Table 2. To account for the biased standard errors arising from sibling non-independence, significance tests for the correlations were adjusted according to the method outlined by Griffin & Gonzalez (1995). Generally, MA and MM did not differ as a function of child age. However, older children exhibited better performance on all math tasks, except for the Dots task. Child sex (0 = female, 1 = male) was negatively associated with both general anxiety and MA, indicating higher general and math anxiety level for girls. Boys out-performed girls on four out of six tasks including Number-Line task, Composing and Decomposing Numbers task, Problem Verification task, and Applied Problems task. Additionally, general anxiety was minimally correlated with math task performance whereas MA was modestly negatively correlated with math performance. MM was positively correlated with the Calculation and Applied Problems tasks, but was not correlated with performance on other math tasks. Finally, performance on all math tasks was positively correlated.

Table 2.

First Order Correlations between the Main Study Variables

	1. Age	2	3	4	5	6	7	8	9	10
2. Sex	.07
3. General Anxiety	−.01	−.14a
4. Math Anxiety	−.04	−.19c	.38c
5. Math Motivation	−.11	.00	−.05	−.35c
6. Dots Task	.08	−.02	−.02	−.07	.05
7. Number Line	.32c	.19 c	−.04	−.19c	.03	.23c
8. CDNT	.39c	.21c	−.09	−.25c	.11	.21c	.40c
9. Problem Verification	.41c	.15b	−.14a	−.23c	.07	.10a	.33c	.59c
10. Calculation	.39c	.09	−.04	−.29c	.18b	.30c	.43c	.62c	.49c
11. Applied Problems	.33c	.15b	−.10	−.33c	.20c	.33c	.56c	.64c	.47c	.70c

Note. CDNT = Composing and Decomposing Numbers Task.

^ap < .05.

^bp < .01.

^cp < .001.

Subsequently, structural equation modeling (SEM) with interchangeable dyads (Olsen & Kenny, 2006) was employed using Amos 22.0 (SPSS IBM, NY) to examine the two research questions. SEM with interchangeable dyads was preferred over multiple regression because the former approach was more flexible, such that it is possible to analyze data from both siblings within the same family together to enhance statistical power while controlling for biased standard errors arising from sibling non-independence at the same time (Olsen & Kenny, 2006).

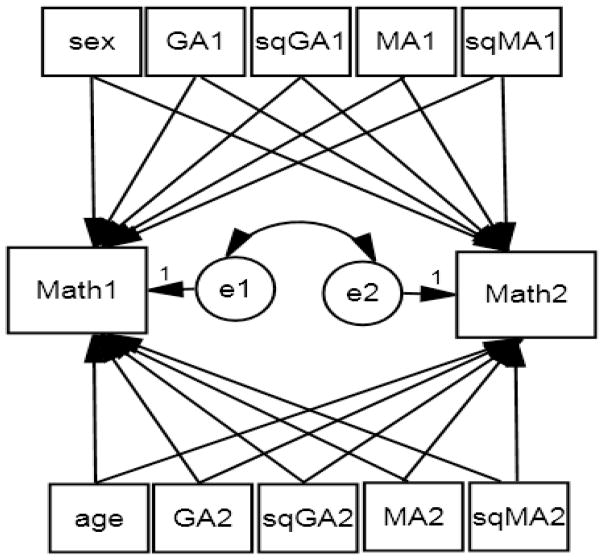
Figure 1 presents the SEM model with interchangeable dyads that was used to examine the first research question regarding the quadratic curvilinear relations between MA and performance on math tasks. Sibling data were first organized in a pairwise fashion prior to model fitting such that each sibling was entered twice, once as sibling1 and once as sibling2. This model was symmetrically structured and contained two identical parts, one for sibling1 and one for sibling2 as indicated by the numbers “1” and “2” at the end of each variable. For each sibling, math performance was entered in the model as a manifest outcome. Child age and sex were the same for both siblings, and thus were included only once in the model as statistical covariates. The linear and quadratic effects of general anxiety (i.e., general anxiety and its squared term) were entered as manifest covariates in the model for each sibling to control for the possibility that the relations between math performance and MA are due to general anxiety, not specific anxiety about math. Lastly, the linear (MA) and quadratic effects (squared MA) of MA were entered as manifest predictors of math performance for each sibling. Additionally, parameters (including means, variances, intercepts, regression weights, and correlations) for each sibling were constrained to be equal to their counterparts for the other sibling. The correlations between covariates and predictors were all estimated in the model, but are not shown in Figure 1 for clarity of presentation. Each math task was examined in a separate model, resulting in a total of six models. Note that MA, MM, and general anxiety were standardized and centered prior to model fitting in order to compute the interaction and higher-order terms. All outcome variables were also standardized to maintain scale consistency and interpretability across all math tasks.

Figure 1.

SEM with interchangeable dyads examining the quadratic curvilinear relation between math anxiety and math performance. The correlations between covariates and predictors are not shown in the figure for clarity of presentation. MA= math anxiety; GA= general anxiety; sqMA=squared math anxiety; sqGA=squared general anxiety.

To estimate parameters as well as their confidence intervals, bootstrapping was performed on 1000 samples using the maximum likelihood estimator for each model. In order to perform bootstrapping in Amos, missing values were first computed and replaced in the dataset using linear interpolation method. Parameters and their bias-corrected 95% confidence intervals are reported in Table 3. Due to various degrees of missing data, models were rerun using different methods of handling missing data in order to test for potential bias yielded by linear interpolation. Results remained essentially the same when missing data were handled using both listwise deletion and full information maximum likelihood estimation. Because these are all saturated models, χ² values and degrees of freedom were all zero. As shown in Table 3, total variance (i.e., total R²) in each of the six tasks explained by this set of predictors ranged from .02 to .25, with less variance explained in the Dots and Number-Line tasks compared to the other math tasks. After controlling for the effects of the covariates, MA was negatively associated with all tasks. In addition, after controlling for the linear effects of MA, the quadratic term was significantly associated with the performance on the Problem Verification and Calculation tasks.

Table 3.

Quadratic Relations between MA and Math Performance: Standardized Parameter Estimates (95% Confidence Interval) and Squared Multiple Correlation

		Dots Task	Number-Line	CDNT	Problem Verification	Calculation	Applied Problems
Covariate	Age	.07(−.01, .13)	.29(.21, .35)b	.35(.28, .42)b	.36(.30, .42)c	.35(.28, .42)b	.29(.21, .36)b
	Sex	−.02(−.10, .05)	.13(.07, .20)b	.13(.07, .20)b	.07(.00, .13)a	−.00(−.07, .07)	.07 (−.00, .14)
	GA	−.01(−.09, .06)	.02(−.05, .09)	.02(−.04, .07)	−.01(−.08 .06)	.06(−.02, .13)	.05(−.01, .11)
	GA2	−.03(−.10, .03)	.00(−.05, .06)	−.03(−.08, .02)	−.04(−.09, .02)	−.00(−.06, .06)	−.05(−.10, .00)
	ΔR2	.02	.13	.20	.20	.15	.13
Linear	MA	−.05(−.14, .05)	−.13(−.19, −.06)b	−.18(−.25,−.11)b	−.10(−.17,−.03)b	−.23(−.31,−.16)b	−.29(−.34,−.23)b
	ΔR2	.01	.02	.02	.02	.08	.10
Quadratic	MA2	−.04(−.11, .03)	−.03(−.13, .06)	−.03(−.08, .03)	−.11(−.17, −.04)b	−.09(−.16,−.03)b	.01(−.07, .09)
	ΔR2	.00	.00	.01	.01	.01	.00
Total R2		.02	.16	.24	.23	.25	.23

Note. CDNT = Composing and Decomposing Number task. GA = general anxiety; MA = math anxiety; ΔR² = change in squared multiple correlation.

^ap < .05.

^bp < .01.

^cp < .001.

To further examine these two significant quadratic curvilinear relations, post-hoc analyses were conducted to examine the relations between MA and performance on the two math tasks at different levels of MA (i.e., 3, 2, and 1 SD below and above the mean and the mean of MA; Table 4) using methods outlined in Aiken & West (1991). Overall, MA was increasingly negatively associated with math performance on these two tasks as levels of MA increased, a pattern that was inconsistent with our prediction.

Table 4.

Post Hoc Analyses: Standardized Parameter Estimates (95% Confidence Interval) of the Statistical Predictive Effects of MA on Math Performance at Different Levels of MA

MA level	3SD below	2SD below	1SD below	Mean	1SD above	2SD above	3SD above
Problem Verification	.09(−.06, .25)	.03(−.10, .15)	−.04(−.13,.05)	−.10(−.17, −.03)	−.16(−.23, −.11)	−.23(−.30, −.16)	−.29(−.40, −.20)
Calculation	−.06(−.24, .10)	−.12(−.26 .01)	−.17(−.28, −.08)	−.23(−.31, −.16)	−.29(−.35, −.23)	−.34(−.40, −.27)	−.40(−.48, −.30)

Note. MA = math anxiety.

To examine the second research question regarding whether the quadratic relations between MA and math task performance would be further moderated by MM, three more manifest predictors were added for each sibling in each of the original six models. These predictors included a linear effect of MM (MM), an interaction term (MA*MM), and a moderated quadratic interaction term (MA²*MM). Results of these models are shown in Table 5. In addition to the original six predictors, MM was positively associated with all math tasks. After controlling for the covariates, linear effects of MA and MM, and all lower-order interaction terms, the moderated quadratic term (i.e., MA²*MM) was significantly related to four math tasks but were not significantly related to the Dots and Number-Line tasks. These significant moderated quadratic effects persisted with the sequential Bonferroni correction. Overall, the covariates as a set explained a major proportion of variance in these math outcome variables, whereas the main effects of MA and MM and their interactive effects together only added incremental effects in predicting math performance.

Table 5.

Moderated Quadratic Relations between MA, MM, and Math Performance: Standardized Parameter Estimates (95% Confidence Interval) and Squared Multiple Correlation

		Dots Task	Number-Line	CDNT	Problem Verification	Calculation	Applied Problem
Covariate	Age	.07(−.00, .13)	.30(.23, .37)b	.36(.29, .43)b	.37(.31, .43)c	.36(.30, .43)b	.31(.23, .39)b
	Sex	−.02(−.10, .05)	.13(.06, .19)b	.13(.07, .20)b	.07(.00, .14)a	.00(−.06, .07)	.07 (−.00, .14)
	GA	−.02(−.09, .06)	.02(−.05, .09)	.01(−.05, .06)	−.02(−.09 .05)	.05(−.03, .11)	.03(−.03, .09)
	GA2	−.03(−.10, .03)	.01(−.05, .07)	−.03(−.08, .02)	−.04(−.10, .02)	−.00(−.06, .06)	−.04(−.08, .01)
	ΔR2	.02	.15	.21	.20	.15	.14
Linear	MA	−.03(−.12, .05)	−.12(−.19, −.05)b	−.14(−.23, −.07)b	−.06(−.13, −.00)a	−.18(−.26, −.11)c	−.24(−.31, −.18)c
	MM	.08 (.00, .16)a	.03(−.06, .12)	.17(.10, .25)b	.12(.05, .20)b	.20(.13, .28)b	.21(.14, .29)c
	ΔR2	.01	.02	.04	.02	.10	.10
2-way	MA2	−.04(−.11, .03)	−.06(−.14, .04)	−.04(−.10, .02)	−.10(−.17, −.01)a	−.12(−.17, −.05)b	−.03(−.09, .04)
	MA*MM	.02(−.06, .10)	−.08(−.15, −.02)a	.07(.00, .15)a	.14(.07, .22)b	.08(.02, .15)a	.02(−.04, .09)
		.00	.02	.00	.02	.01	.00
3-way	MA2*MM	−.04(−.12, .05)	−.04(−.13, .06)	−.11(−.21, −.03)b	−.09(−.19, −.01)a	−.15(−.24, −.06)b	−.17(−.26, −.07)b
	ΔR2	.00	.00	.01	.01	.01	.02
Total R2		.03	.18	.26	.25	.28	.27

Note. CDNT = Composing and Decomposing Number task; GA = general anxiety; MA = math anxiety; MM = math motivation; ΔR² = change in squared multiple correlation.

^ap < .05.

^bp < .01.

^cp < .001.

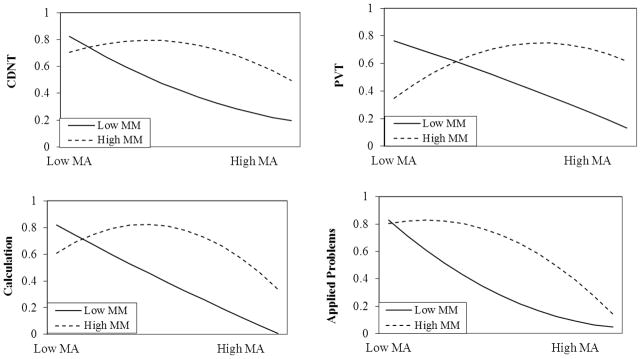
To further examine the four significant moderated quadratic effects, statistical moderators were re-centered to examine the predictive effects of MA at different levels of MA and MM (Aiken & West, 1991). Specifically, MM was re-centered at low (i.e., 1SD below the mean) and high (i.e., 1SD above the mean) levels to examine the relations between MA and math performance across a wide range of MA (i.e., 3SD, 2SD, and 1SD below the mean, the mean, and 1SD, 2SD, and 3SD above the mean of MA) at these two different levels of MM. These results are shown in Table 6 and Figure 2. Overall, the findings were consistent with our prediction. At low levels of MM, MA was modestly negatively associated with task performance across all levels of MA (top portion of Table 6 and solid lines in Figure 2). At high levels of MM, there was an inverted-U curvilinear relation between MA and each of these four tasks, such that performance peaked at an intermediate level of MA and decreased as levels of MA deviated from this optimal intermediate level (bottom portion of Table 6 and dashed lines in Figure 2). However, compared to the other tasks, performance on the Applied Problems task peaked at relatively lower levels of MA.

Table 6.

Post Hoc Analyses: Standardized Parameter Estimates (95% Confidence Interval) of the Statistical Predictive Effects of MA on Math Performance at Different Levels of MA and MM

		CDNT	Problem Verification	Calculation	Applied Problem
1SD below MM	3SD below MA	−.26(−.51, −.02)	−.13(−.36, .10)	−.22(−.44, .00)	−.39(−.60, −.15)
	2SD below MA	−.24(−.44, −.06)	−.15(−.32, .03)	−.23(−.40, −.06)	−.34(−.51, −.16)
	1SD below MA	−.22(−.37, −.08)	−.16(−.29, −.03)	−.24(−.37, −.12)	−.30(−.42, −.17)
	mean of MA	−.20(−.30, −.10)	−.18(−.28, −.09)	−.25(−.34, −.16)	−.25(−.34, −.16)
	1SD above MA	−.18(−.24, −.11)	−.20(−.27, −.13)	−.25(−.33, −.19)	−.20(−.28, −.14)
	2SD above MA	−.16(−.22, −.07)	−.22(−.31, −.14)	−.27(−.36, −.18)	−.16(−.26, −.08)
	3SD above MA	−.14(−.24, −.00)	−.24(−.38, −.13)	−.27(−.42, −.10)	−.11(−.27, .01)
1SD above MM	3SD below MA	.16(−.08, .40)	.33 (.07, .55)	.31 (.09, .53)	.08(−.14, .27)
	2SD below MA	.09(−.12, .27)	.24 (.04, .41)	.17 (.01, .35)	−.01(−.18, .13)
	1SD below MA	.01(−.14, .15)	.15(−.00, .27)	.04 (−.08, .17)	−.10(−.22, .01)
	mean of MA	−.07(−.18, .03)	.05(−.06, .14)	−.10(−.19, −.01)	−.19(−.28, −.11)
	1SD above MA	−.14(−.22, −.07)	−.04(−.13, .04)	−.24(−.32, −.16)	−.28(−.36, −.20)
	2SD above MA	−.22(−.32, −.14)	−.14(−.24, −.02)	−.37(−.47, −.29)	−.37(−.47, −.25)
	3SD above MA	−.30(−.42, −.18)	−.23(−.36, −.04)	−.51(−.63, −.38)	−.46(−.60, −.30)

Note. MA = math anxiety; MM = math motivation; CDNT = Composing and Decomposing Numbers task.

Figure 2.

Relations between MA and math performance as a function of MA and MM. All math performance outcomes have a SD = 1. The scale of the Y axis is in standard deviation units. CDNT = Composing and Decomposing Numbers Task; PVT = Problem Verification Task; MA = math anxiety; MM = math motivation.

Given the complexity of the three-way interaction and the small effect sizes, we conducted a replication study in another sample (i.e. college students) in order to examine whether this moderated quadratic effect between MA and MM on math cognition was replicable and generalizable to another developmental period.

Study 2 (Replication Study)

Methods

Participants

Data were collected from 237 undergraduate students (56% female) from The Ohio State University using the online survey platform Qualtrics 2013 (Qualtrics, Provo, UT). Undergraduate students who took the Introductory Psychology course were recruited in the current study on a voluntary basis, and were compensated with research credits. Eighteen participants were excluded from the analyses due to either technical problems (2) or random responses (16). Participants were on average 19.53 (SD = 2.01; range = 18 to 39) years old. Participants’ grade level varied: 57% freshman, 24% sophomore, 10% junior, and 8% senior. Participants were from diverse majors, including 5% arts and humanities, 31% social sciences, 28% natural sciences, 13% engineering, 12% pre-medicine, and 12% undecided. The current study was approved by the Office of Responsible Research Practice at The Ohio State University.

Measures

Mathematical Anxiety

Participants self-reported MA using the Mathematics Anxiety Rating Scale-Brief (MARS-B; Suinn & Winston, 2003). The 30-item MARS-B is widely used to measure mathematical anxiety in adults. Items are rated are on a 5-point Likert type scale (1 = not at all nervous; 5 = very very nervous). The MARS-B has good internal consistency with a Cronbach’s α of .94.

General Anxiety

The trait subscale from the State-Trait Anxiety Inventory (Spielberger, 1983) was used to measure participants’ general anxiety. This subscale consists of 20 items that are rated on a 4-point Likert type scale (1 = almost never; 4 = almost always). This scale has adequate internal consistency with a Cronbach’s α of .94.

Mathematical Motivation

Participants self-reported their MM using 3 items from the scale developed by Chiu and Zeng (2008). Description of this measure can be found under the Methods section for Study 1. The Cronbach’s α for this scale is .82, indicating adequate internal consistency.

Mathematics Performance

Problem Verification Task (Rinne & Mazzocco, 2014) was used to measure participants’ math calculation fluency. Description of this task can be found under the Methods section for Study 1. Because the 64 easy items were far too easy for undergraduate students (mean accuracy = .93, SD = .06), we chose to focus on the 24 hard items which had wider performance variability (mean accuracy = .85, SD = .13), and was therefore a more proper measure of individual differences in math calculation fluency in college students. An efficiency score was used and was calculated by dividing the percent of total correct responses by the mean reaction time across all items.

Results

All analyses were conducted using SPSS 22.0 (SPSS IBM, NY). Descriptive statistics are shown in Table 7. All main study variables were distributed widely and normally across their respective scales. Correlations between main study variables are shown in Table 8. None of the main study variables vary as a function of age. Sex (0 = female, 1 = male) was positively associated with performance on the Problem Verification task and was negatively correlated with MA. Additionally, general anxiety was not related to math performance. Finally, MA was negatively associated with math performance whereas MM was positively associated with math performance.

Table 7.

Descriptive Statistics of the Main Study Variables

	N	Mean	SD	Skewness	Kurtosis	Min	Max
General Anxiety	219	2.13	.56	.41	−.42	1.05	3.55
Math Anxiety	219	2.35	.57	.17	−.02	1.00	4.03
Math Motivation	219	3.09	.92	−.24	−.46	1.00	5.00
Problem Verification	219	.20	.06	−.96	1.53	.07	.45

Table 8.

Correlations between the Main Study Variables

	1. Age	2	3	4	5
2. Sex	−.13
3. General Anxiety	−.09	−.12
4. Math Anxiety	−.12	−.21b	.40c
5. Math Motivation	.09	.12	.00	−.28c
6. Problem Verification	−.11	.34c	.02	−.19b	.10

Note.

^ap < .05.

^bp < .01.

^cp < .001.

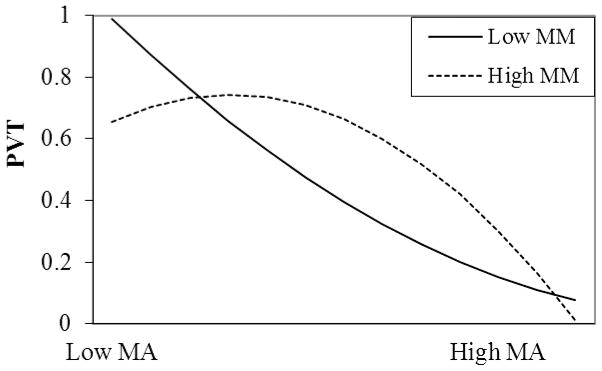
Subsequently, hierarchical regression analysis was used to examine the main research question. Specifically, performance on the Problem Verification Task was statistically predicted from: step 1, study covariates including age, sex, and linear and quadratic terms of general anxiety; step 2, linear term of MM and MA; step 3, quadratic term of MA (MA²) and the interaction between MA and MM (MA*MM); step 4, moderated quadratic interaction term between MA and MM (MA²*MM). MA, MM, and general anxiety were standardized and centered prior to analyses in order to compute the interaction and higher-order terms. The outcome variable was also standardized to maintain consistency across the two studies. Results of the hierarchical regression analyses are shown in Table 9. Overall, age and sex both negatively predicted task performance, indicating that younger and male participants performed better on average, with a larger effect size for the latter. General anxiety did not predict math performance. MA negatively predicted math performance after controlling for the effects of the covariates. Finally, after controlling for all the linear and 2-way interaction effects, the moderated quadratic interaction between MA and MM was statistically significant, and added incremental predictive effects on math performance. To further examine the moderated quadratic effects, post-hoc analyses were conducted to examine the predictive effects of MA at different levels of MA and MM using the procedures described in Study 1. Results are shown in Table 10 and Figure 3. The findings were consistent with results from Study 1. At low levels of MM, MA was modestly negatively associated with task performance across all levels of MA. At high levels of MM, there was an inverted-U curvilinear relation between MA and task performance.

Table 9.

Unstandardized Coefficients and Explained Variance for Hierarchical Regression Equations Predicting Performance on the Problem Verification Task

		Step1	Step2	Step3	Step4
Covariate	Age	−.10(−.19, −.02)a	−.11(−.19, −.02)a	−.11(−.19, −.02)a	−.10(−.18, −.01)a
	Sex	−.73(−.98, −.47)c	−.67(−.92, −.41)c	−.67(−.92, −.41)c	−.61(−.87, −.35)c
	GA	.10(−.14, .34)	.23(−.03, .49)	.23(−.03, .49)	.23(−.03, .49))
	GA2	−.03(−.13, .08)	−.04(−.15, .07)	−.03(−.14, .08)	−.06(−.17, .05)
Linear	MA	-	−.18(−.33, −.04)a	−.18(−.32, −.03)a	−.26(−.42, −.10)b
	MM	-	.02(−.11, .15)	.02(−.11, .15)	.13(−.03, .30)
2-way	MA2	-	-	.03(−.10, .17)	.05(−.09, .18)
	MA*MM	-	-	−.01(−.12, .10)	−.04(−.16, .07)
3-way	MA2*MM	-	-	-	−.10(−.19, −.01)a
ΔR2		.14c	.03a	.00	.02a
ΔF		8.64(4,214)	3.66(2,212)	.26(2,210)	5.18(1,209)

Note:

^ap < .05;

^bp < .01;

^cp < .001.

Table 10.

Post Hoc Analyses: Unstandardized Regression Coefficients (95% Confidence Interval) of the Predictive Effects of MA on Math Performance at Different Levels of MA and MM

	Problem Verification		Problem Verification
1SD below MM		1SD above MM
3SD below MA	−.49 (−1.02, .04)	3SD below MA	.23 (−.21, .66)
2SD below MA	−.43 (−.84, −.02)	2SD below MA	.08 (−.22, .38)
1SD below MA	−.37 (−.66, −.07)	1SD below MA	−.07 (−.27, .14)
mean of MA	−.30 (−.51, −.10)	mean of MA	−.21 (−.43, −.00)
1SD above MA	−.24 (−.42, −.07)	1SD above MA	−.36 (−.67, −.05)
2SD above MA	−.18 (−.41, .05)	2SD above MA	−.51 (−.96, −.06)
3SD above MA	−.12 (−.44, .20)	3SD above MA	−.65 (−1.25, −.05)

Note. MA = math anxiety; MM = math motivation.

Figure 3.

Relations between MA and math performance as a function of MA and MM. Math performance outcomes have a SD = 1. The scale of Y axis is in standard deviation units. PVT = Problem Verification Task; MA = math anxiety; MM = math motivation.

Discussion

Research in the animal learning and cognitive psychology literatures has demonstrated that emotion and cognition are related in a complex fashion (Arnsten, 2009; Diamond et al., 2007). The current study extended this literature in the specific context of math performance via exploring the interplay between math anxiety and math motivation in relation to different types of mathematical behaviors, and demonstrated that the transactions between math-related emotions and cognitions were far more complex than simple linear and additive relations.

Consistent with our hypothesis, an inverted-U relation between MA and math performance was observed in students who are more intrinsically motivated in math, whereas a negative linear relation was observed in those who are less motivated. This observation emerged among both adolescents and adults. Importantly, this pattern was observed in the four math tasks that required generating or evaluating number combinations (i.e., CDNT, PVT, Calculations, Applied Problems), but not in the symbolic or nonsymbolic number estimation tasks (i.e., the Dots and the Number-Line tasks). It is possible that the math-specific affect-cognition transaction may function through enhancing or impairing general cognitive processes that are more likely to be engaged during computation, such as executive attention and working memory. These executive skills are less involved in more primary mathematical abilities such as those assessed in the number estimation tasks (Geary, 2007). The general cognitive literature has shown that moderate levels of anxiety help enhance focused attention and working memory whereas extremely high or low levels of anxiety are associated with insufficient cognitive resources allocated to the tasks (Arnsten, 2009; Diamond et al., 2007). The current findings indicate that in the specific context of math learning, an area in which students have abundant experiences and well-developed attitudes, the facilitative/debilitative effects of MA on math performance vary not only across different levels of MA, but also as a function of how motivated children are to perform well. It is only in students with high MM that moderate MA had a facilitative effect on performance. In individuals with low MM, higher MA consistently demonstrated a debilitative effect on math performance. This pattern potentially points to the importance of MM in mobilizing cognitive resources and regulating the effects of negative affect during math problem solving, and is consistent with contemporary fMRI research that highlights the links between brain activations involved in motivating behaviors and cognitive control in improving performance in math anxious adults (Lyons & Beilock, 2012).

The four tasks that assessed higher levels of mathematical processing in the current study were similar to those encountered in students’ math classes and math tests. Thus, it is possible that the observed relations between math affect and math performance capture more than just the transient distribution of cognitive resources, and also reflect long-term transactions between math-related affect and math behaviors. Students with high MM who are motivated to perform well on math may be more willing to overcome challenges via active approach (Middleton & Spanias, 1999; Vallerand et al, 1992). Therefore, it is possible that the intermediate levels of worrying or discomfort implicate such challenges during math activities which in turn motivates students with high MM to invest more efforts leading to better math outcomes over time (Wigfield & Meece, 1988). On the contrary, given the avoidance tendencies in students who are not motivated in math (Middleton & Spanias, 1999), higher levels of negative affect and discomfort in situations involving math may threat them further away from active engagement which ultimately leads to poorer math outcomes. This is in line with previous findings which demonstrated that the effects of stress response on math performance depend on whether individuals interpret math situations as positive and challenging or negative and threatening (Mattarella-Micke, Mateo, Kozak, Foster, & Beilock, 2011).

Although such complex curvilinear relations were not found between math-related affect and performance on the two number estimation tasks, the current findings showed that MA was negatively correlated with performance on the symbolic number estimation task (i.e., Number-Line task), suggesting the possibility that poorer math performance in high MA children may capture deficits in basic numerical processing beyond transient reduction in attentional and working memory resources (Nunez-Pena & Suarez-Pellicioni, 2014). On the contrary, MA was not related to the nonsymbolic number estimation task (i.e., Dots task). Because the nonsymbolic number estimation task does not explicitly present numerical symbols, concepts, or operations, it is possible that such tasks are not particularly anxiety-provoking to math anxious individuals.

Math learning is a prolonged and accumulative process. Given that the magnitude and etiology of the relations between math-related affect and cognition may differ across various developmental stages (Krinzinger et al., 2009), longitudinal studies spanning multiple developmental stages are needed to address how MA and MM interact in relation to the development of math skills in the context of daily math learning.

These findings should not be interpreted as evidence of a unidirectional causal relation between math-related emotion and math cognition. Rather, our goal is to explore the complex interplay between emotion and cognition in the context of math learning, and to highlight the potential significance of these findings regarding their educational implications in improving math learning experiences and outcomes. In particular, MA may not universally impair the development of math abilities (Lyons & Beilock, 2012; Wigfield & Meece, 1988), and clinical efforts that simply target lowering MA levels may not prove to be effective to all students. The current findings suggest that moderate levels of MA seem to be beneficial rather than detrimental to intrinsically motivated children. Therefore, it may be better for some students to maintain moderate levels of MA, potentially through making their learning and testing materials moderately challenging. Such a combination of moderate MA and high intrinsic motivation may help drive students to work harder in math learning and enjoy the stimulation and fun in this process at the same time. These findings support mathematical educational efforts to identify appropriate challenge levels for students by taking into account students’ math-related abilities and affect.