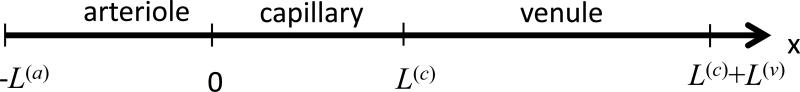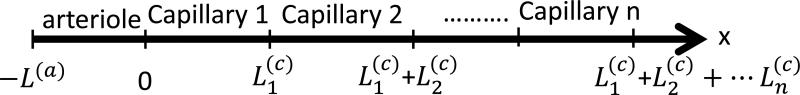Nonlinear extension of a hemodynamic linear model for coherent hemodynamics spectroscopy

Abstract

In this work, we are proposing an extension of a recent hemodynamic model (Fantini, 2014 a), which was developed within the framework of a novel approach to the study of tissue hemodynamics, named coherent hemodynamics spectroscopy (CHS). The previous hemodynamic model, from a signal processing viewpoint, treats the tissue microvasculature as a linear time-invariant system, and considers changes of blood volume, capillary blood flow velocity and the rate of oxygen diffusion as inputs, and the changes of oxy-, deoxy-, and total hemoglobin concentrations (measured in near infrared spectroscopy) as outputs. The model has been used also as a forward solver in an inversion procedure to retrieve quantitative parameters that assess physiological and biological processes such as microcirculation, cerebral autoregulation, tissue metabolic rate of oxygen, and oxygen extraction fraction. Within the assumption of “small” capillary blood flow velocity oscillations the model showed that the capillary and venous compartments “respond” to this input as low pass filters, characterized by two distinct impulse response functions. In this work, we do not make the assumption of “small” perturbations of capillary blood flow velocity by solving without approximations the partial differential equation that governs the spatio-temporal behavior of hemoglobin saturation in capillary and venous blood. Preliminary comparison between the linear time-invariant model and the extended model (here identified as nonlinear model) are shown for the relevant parameters measured in CHS as a function of the oscillation frequency (CHS spectra). We have found that for capillary blood flow velocity oscillations with amplitudes up to 10% of the baseline value (which reflect typical scenarios in CHS), the discrepancies between CHS spectra obtained with the linear and nonlinear models are negligible. For larger oscillations (~50%) the linear and nonlinear models yield CHS spectra with differences within typical experimental errors, but further investigation is needed to assess the effect of these differences. Flow oscillations larger than 10-20% are not typically induced in CHS; therefore, the results presented in this work indicate that a linear hemodynamic model, combined with a method to elicit controlled hemodynamic oscillations (as done for CHS), is appropriate for the quantitative assessment of cerebral microcirculation.

1. Introduction

Hemodynamic models are needed in order to interpret the signals measured in neuroimaging techniques, in terms of the underlying physiological dynamics of blood flow, blood volume and metabolic rate of oxygen. This interpretation is usually facilitated by hemodynamic models that include both of the following two categories: a) models focusing on the intrinsic dynamic relationship between physiological parameters in several conditions; b) models that are dedicated to understand how the dynamics of physiological parameters are linked to the dynamics of measured signals. For example, a model that explains the coupling or uncoupling between blood flow and oxygen metabolism belongs to the first category. A model dedicated to finding the relationship between the blood oxygen level dependent (BOLD) signal measured in functional magnetic resonance imaging (fMRI), or the optical signal measured in near infrared spectroscopy (NIRS), and the dynamics of blood flow and oxygen metabolism, belongs to the second category. While the models in the first category are general (and therefore usable by different neuroimaging techniques), those in the second category are specific to each neuroimaging modality. Historically, several hemodynamic models have been proposed for interpreting the signal measured in BOLD fMRI or in Positron Emission Tomography (PET). We remind briefly two of the major models that were originally proposed for fMRI, and that had a large impact also for other neuroimaging modalities. Buxton and Frank (Buxton and Frank, 1997) proposed an oxygen diffusion limitation model in order to explain the large imbalance (often observed in PET experiments) between changes in blood flow and oxygen consumption during brain activation. They showed that such an imbalance could be consistent with tight coupling between flow and metabolism in presence of a limitation in oxygen availability. Their model provided a static relationship between the oxygen extraction fraction (a metabolic parameter) and blood flow (a hemodynamic parameter) that could be used to interpret the BOLD signal. Originally, they considered only the extravascular component of the BOLD signal and concluded that if flow and metabolism were coupled, BOLD signal could be used as a robust estimator of flow changes. Later, Buxton (Buxton et al., 1998) in order to explain the BOLD signal when both the intra- and extravascular components were considered, proposed the “balloon model” for the relationship between deoxyhemoglobin concentration and blood volume in the venous compartment. The balloon model used typical mass conservation properties in order to obtain a system of coupled differential equation linking blood volume and deoxyhemoglobin concentration. The temporal trend of blood flow entering the venous compartment was assumed as the typical boxcar function used for brain activation. The blood flow exiting the venous compartment was modeled as a power law of the venous blood volume, extending improperly a static property, the Grubb's law (Grubb et al., 1974) to a dynamic situation. Mandeville (Mandeville et al., 1999), based on experimental observations of different temporal dynamics of blood flow (measured with laser Doppler flowmetry) and blood volume (measured with MRI) during forepaw stimulation in rats, proposed a windkessel model for the relationship between flow and volume which was mathematically given by coupled partial differential equations having the dynamic trends of flow and volume as unknown. The authors derived this system of partial differential equation by using more basic physiological principles, such as the fact that blood flow in the capillary and venous compartments is modulated by changes in blood pressure due to changes in arteriolar resistance, and that veins (due to the presence of muscle cells) respond to an increase in pressure with a delayed compliance, as observed in vivo (Porciuncula et al., 1964). In the original windkessel model (Mandeville et al., 1999), the capillary and venous compartments were lumped in a single compartment (windkessel compartment), but the authors also proposed a serial windkessel model where the volume contributions from these two compartments could be separated. The windkessel model also had a large impact in NIRS. A first example is found in the work of Boas (Boas et al; 2003), where the authors used the windkessel model in order to assess the ratio between the changes in cerebral metabolic rate of oxygen (CMRO₂) and the changes in blood flow during a finger tapping task. Their model used thirteen parameters to fit the changes of oxy-, deoxy-, and total hemoglobin concentrations measured on the subjects during a finger tapping task. Six of these parameters where held fixed, whereas the remaining seven were varied in an optimization scheme. Among the parameters retrieved by the fit, four parameters characterized the dynamics of the arteriolar resistance and the windkessel transit time (comprising the transit time in the capillary and venous compartments). Expanded (three compartments) windkessel models have also been proposed (Zheng et al., 2005; Huppert et al., 2007; Huppert et al., 2009). Huppert (Huppert et al., 2007) extended the three compartments windkessel model proposed by Zheng (Zheng et al., 2005), by introducing the concept of capillary compliance and allowing oxygen extraction to occur also in the arterioles and small veins. The authors used multimodal optical imaging, combining the information of laser speckle imaging and NIRS in order to measure the changes in blood flow and hemoglobin concentration in tissue during a rat whisker stimulation protocol. The coupled partial differential equations for blood volume and flow, and also for oxygen extraction, were solved based on the optimization of fourteen state variables that were retrieved by the inversion procedure. Seven of these parameters were used to model the dynamic arteriolar expansion and the dynamic change of CMRO₂ in tissue. Other parameters retrieved by the model were the vascular transit time, the pial vessel transit time and the baseline hemoglobin saturations in the three compartments (showing an interesting possibility of the model, to retrieve absolute baseline values from relative optical intensity measurements). One of the results of this work was that a three compartment windkessel model could fit the experimental data better than a single compartment windkessel model. The windkessel model, together with a model of oxygen dynamics and exchange with tissue, has also been used for more complicated vascular networks, comprising thirty-two arterioles, thirty-two venules and sixty-four capillaries (Boas et al., 2008). This study was an important step toward the modeling of more realistic vascular networks. However, the model proposed was used only as a “forward” solver in order to predict the distribution of blood flow velocity, pressure, and hemoglobin saturation along the network for a steady state response to localized arterial dilation, and also during transient arterial dilation and oxygen consumption. The changes in the concentration of oxy-, deoxy-, and total hemoglobin were also calculated and averaged in the arterioles, capillaries and venules. Finally, we mention the work of Diamond (Diamond et al., 2009), where the authors developed a complex multi-compartment model (comprising thirteen different compartments) in order to model the baseline fluctuations of intensity measured in NIRS. In summary, most of the hemodynamic models found in the literature, and described briefly above, are based on the solution of a system of partial differential equations in order to retrieve physiological information during different conditions.

Recently, our group proposed a novel technique to study tissue hemodynamics, named coherent hemodynamic spectroscopy (CHS) (Fantini, 2014 a; Fantini, 2014 b). The technique is based on inducing controlled and stable hemodynamic oscillations by a forcing mechanism (e.g. paced breathing, cyclic thigh cuff inflation/deflation etc.) at different frequencies. The oscillations are induced during hemodynamic and metabolic “equilibrium” states of a tissue under investigation in order to measure some underlying physiological parameters (like the capillary and venous transit times and the autoregulation cutoff frequency). For this purpose, a hemodynamic model was also proposed in order to interpret the induced oscillations in optical intensity measured by NIRS in terms of blood flow, blood volume, and metabolic dynamics. From a signal processing viewpoint, the model treats the microvasculature as a linear time-invariant system, and considers changes of blood volume, capillary blood flow velocity, and oxygen consumption as inputs, and changes of oxy-, deoxy-, and total hemoglobin concentrations as outputs. The advantage of such a model is that it is analytical and therefore does not involve any system of complex partial differential equations. The model depends on eleven baseline or static parameters, such as the capillary and venous blood transit times, the cutoff frequency of the autoregulation process, the blood volume in the three vascular compartments, the concentration of total hemoglobin in blood, the rate constant of oxygen diffusion, etc.. The independent parameters reduce to six if we consider ratios of changes in the concentrations of hemoglobin species, as we have shown in a previous study (Kainerstorfer et al., 2014). The model has been tested during several experimental conditions, including a paced breathing protocol (Pierro et al., 2014 a), a hyperventilation study (Kainerstorfer et al., 2015) and a clinical study on patients undergoing hemodialysis (Pierro et al., 2014 b). The model predicts that the capillary and venous compartments respond to a “small” perturbation in blood flow velocity as low-pass filters, characterized by two distinct impulse response functions. In this work we have relaxed this constraint on the amplitude of blood flow velocity perturbation and we propose a general method to solve the full partial differential equation governing the spatio-temporal behavior of hemoglobin saturation in capillaries and veins. We refer to this extended hemodynamic model, including the general solution for hemoglobin saturation, as a nonlinear model. We report some preliminary comparisons both in time domain, and frequency domain, between the linear and the nonlinear models.

2. General formulation of the problem

2.1 Blood oxygen saturation for a simple vascular topology: a sequence of one arteriole, one capillary and one venule

In this section, we describe and solve the time-dependent equations for blood oxygen saturation when arbitrary temporal dynamics of blood flow velocities are considered in the ideal blood vessels of Fig.1. In order to understand the origin of these equations we will start from the capillary.

Fig.1.

Schematic sequence of three blood vessels, i.e. arteriole, capillary and venule, which represents an arbitrary path followed by blood in the microcirculation. The “x” coordinate, indicates any curvilinear coordinate along the “path” of blood in three blood vessels. The blood flow velocities are: c^(a)(t), c^(c)(t), c^(v)(t), for the arteriole, capillary and venule, respectively. The origin of the coordinate system is chosen at the beginning of the capillary. L^(a), L^(c) and L^(v) are the lengths of the arteriole, capillary and venule, respectively.

a) Dynamic equation for the oxygen saturation in the capillary

The dynamic equation in the capillary originates from the static equation when we consider that the speed of blood flow is allowed to vary arbitrarily with time. The static equation in the capillary is usually written for the total concentration of oxygen in blood ([O₂]^(blood) in units of mol_O2/l_blood) (Fantini, 2002):

$$c^{\left(c\right)}\frac{d{\left[O_2\right]}^{\left(blood\right)}\left(x\right)}{dx}=-{\alpha }_{\stackrel{.}{o}}{\left[O_2\right]}^{\left(blood\right)}\left(x\right)$$ (1)

where c^(c) is the speed of blood flow in the capillary (assumed constant in the steady state case), x is the coordinate along the capillary, and ${\alpha }_{\stackrel{.}{o}}$ is the rate constant for oxygen diffusion from blood to tissue (units of s⁻¹):

$${\alpha }_{\stackrel{.}{o}}=k\frac{{\left[O_2\right]}^{\left(plasma\right)}-{\left[O_2\right]}^{\left(tissue\right)}}{{\left[O_2\right]}^{\left(blood\right)}}$$ (2)

In Eq.(2) k is the probability per unit time for a molecule of oxygen in plasma to cross the capillary wall (Buxton and Frank, 1997), [O₂]^(plasma) is the concentration of oxygen in plasma and [O₂]^(tissue) is the concentration of oxygen in tissue. Even though more complex static models have been proposed (Hyder et al., 1998; Jespersen and Østergaard, 2012) which make use of the oxyhemoglobin dissociation curve, here we are adopting the simpler model that ${\alpha }_{\stackrel{.}{o}}$ is a constant along the capillary length. This simpler model has been adopted in the literature by several authors (Zheng et al, 2002; Fantini, 2002; Kocsis et al. 2006; Buxton and Frank, 1997). In particular, we note that Buxton and Frank carried out calculations of the oxygen extraction fraction as a function of percentage changes in blood flow for different models of oxygen exchange in capillaries, including the model used in this work and more complex models based on the oxygen dissociation curve of hemoglobin (Buxton and Frank, 1997). The results of their calculations showed negligible differences among the models for a wide range of changes in blood flow, from −50% to +100%. It is well known that the oxygen bound to hemoglobin accounts for about 97-99% of [O₂]^(blood), therefore [HbO₂]^(blood) ≈ ¼[O₂]^(blood) (Fantini, 2002). Therefore Eq.(1) can be rewritten for [HbO₂]^(blood) and by dividing the left and right sides of the equation by ctHb^(c) which is the total hemoglobin concentration in capillary blood, assumed to be constant) we derive the static equation for the oxygen saturation of capillary blood, S^(c):

$$c^{\left(c\right)}\frac{d{S}^{\left(c\right)}\left(x\right)}{dx}=-{\alpha }_{\stackrel{.}{o}}{S}^{\left(c\right)}\left(x\right)$$ (3)

When the capillary flow velocity is allowed to change arbitrarily as a function of time (c^(c)(t)) we obtain the dynamic equation by adding a time-derivative term to Eq.(3):

$$c^{\left(c\right)}\left(t\right)\frac{\partial S^{\left(c\right)}(x,t)}{\partial x}+\frac{\partial S^{\left(c\right)}(x,t)}{\partial t}=-{\alpha }_{\stackrel{.}{o}}{S}^{\left(c\right)}(x,t)$$ (4)

Eq.(4) represents the substantial or material derivative (also called Lagrangian derivative) of the saturation given in terms of Eulerian (or fixed point) variables. Eq.(4) is a case of damped unidirectional wave equation (Zauderer, 1989) with a time dependent capillary blood flow velocity. When c^(c) is constant, Eq.(4) reduces to Eq.(3), having the Crone-Renkin expression as its solution (Fantini, 2002; Buxton and Frank, 1997; Jespersen and Østergaard, 2012). When c^(c) is time dependent, in order to solve Eq.(4) we have to resort to some standard numerical methods, like the finite difference method. Here, we propose a general method that can be particularly useful for CHS, where a sinusoidal behavior of c^(c)(t) is considered. Since the parameters measured in CHS are related to the spatial average of the capillary saturation (〈S^(c)〉(t)), the complexity of the problem can be further reduced. In fact, one can prove that 〈S^(c)〉(t)) can be calculated by solving one transcendental equation at each time point. First, we address the general solution of Eq.(4) which is solved with the boundary condition: S^(c)(x = 0, t) = S^(a) is the arterial saturation. In order to solve Eq.(4), we introduce the concept of partial capillary transit time, $t_p^{\left(c\right)}(x,t)$, which is defined for any time t and coordinate x along the capillary as the variable which satisfies the equation:

$$x={\int }_{t-t_p^{\left(c\right)}(x,t)}^t{c}^{\left(c\right)}\left(\tau \right)d\tau$$ (5)

The partial capillary transit time represents the time necessary for an infinitesimal blood element to travel from the origin of the capillary to the coordinate x (x ∈ [0, L^(c)]) time t. We can prove (appendix A) that the general solution of Eq.(4) with the boundary condition stated above is given by:

$$S^{\left(c\right)}(x,t)=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{o}}{t}_p^{\left(c\right)}(x,t)}$$ (6)

Eq.(6) shows how the transit time is the fundamental parameter that characterizes the desaturation at a certain field point x and time t, regardless of the complexity of the blood flow velocity dynamics. Also, if we consider the spatially averaged capillary saturation 〈S^(c)〉(t), we can prove (appendix B) that it can be calculated as:

$$\langle S^{\left(c\right)}\rangle \left(t\right)=\frac{1}{L^{\left(c\right)}}{\int }_0^{L^{\left(c\right)}}{S}^{\left(c\right)}(x,t)dx=\frac{S^{\left(a\right)}}{L^{\left(c\right)}}{\int }_{t-t^{\left(c\right)}\left(t\right)}^t{e}^{-{\alpha }_{\stackrel{.}{O}}(t-\tau )}{c}^{\left(c\right)}\left(\tau \right)d\tau$$ (7)

In Eq.(7), the total capillary transit time t^(c)(t) is defined as: $t^{\left(c\right)}\left(t\right)=t_p^{\left(c\right)}(L^{\left(c\right)},t)$. Even though the theory described is valid for general dynamics of blood flow velocity in the capillary (c^(c)(t)), in this work we will consider a sinusoidal oscillation: $c^{\left(c\right)}\left(t\right)=c_0^{\left(c\right)}+c_1^{\left(c\right)}\sin \left(\omega t\right)$. Sinusoidal hemodynamics are directly relevant for CHS. If we substitute the sinusoidal expression of c^(c)(t) in Eq.(5) and we solve for x=L^(c) we obtain the transcendental equation for the total transit time t^(c)(t):

$$L^{\left(c\right)}=-\frac{c_1^{\left(c\right)}}{\omega }\left\{\cos \left(\omega t\right)-cos\left[\omega \left(t-t^{\left(c\right)}\left(t\right)\right)\right]\right\}+c_0^{\left(c\right)}{t}^{\left(c\right)}\left(t\right)$$ (8)

Once Eq.(8) is solved for t^(c)(t) at any time t, the average capillary saturation 〈S^(c)〉(t) is calculated from Eq.(7). Note that even though c^(c)(t) is sinusoidal, t^(c) (t) is not, as it will be shown in the results section. The full spatio-temporal profile of the capillary saturation S^(c)(x, t) is found by solving Eq.(8) for $t_p^{\left(c\right)}(x,t)$ instead of t^(c)(t). In this case, the left side of Eq.(8) is a generic value of the x coordinate along the capillary. The full spatio-temporal profile can be calculated numerically by dividing the entire time span of observation and capillary length in “small” intervals and studying the rate of convergence of S^(c)(x, t) as we increase the number of intervals.

b) Dynamic equation for the oxygen saturation in the arteriole

In the arteriole, since there is no oxygen exchange with tissue, the dynamic equation reduces to:

$$c^{\left(a\right)}\left(t\right)\frac{\partial S^{\left(a\right)}(x,t)}{\partial x}+\frac{\partial S^{\left(a\right)}(x,t)}{\partial t}=0$$ (9)

which is also a unidirectional (undamped) wave equation with c^(a)(t) arbitrary dynamics of blood flow velocity in the arteriole. A trivial solution of this equation which satisfies the boundary condition at the capillary side is: S^(a)(x, t) = S^(a), therefore the saturation in the arteriole is constant.

c) Dynamic equation for the oxygen saturation in the venule

Even in the venule, as in the arteriole, there is no oxygen exchange with tissue. However, the venule is downstream with respect to the capillary, therefore any temporal change of the capillary speed of blood flow, which affects the dynamic of S^(c)(x, t), will affect also the dynamic of the venule saturation S^(v)(x, t), The equation for the venule saturation is the unidirectional wave equation (undamped):

$$c^{\left(v\right)}\left(t\right)\frac{\partial S^{\left(v\right)}(x,t)}{\partial x}+\frac{\partial S^{\left(v\right)}(x,t)}{\partial t}=0$$ (10)

where c^(v)(t) is the venule blood flow velocity. The solution for S^(v)(x, t) is built in a straightforward way if we also make use of the concept of partial venous transit time: $t_p^{\left(v\right)}(x,t)$ which is defined by the equation:

$$x=L^{\left(c\right)}+{\int }_{t-t_p^{\left(v\right)}(x,t)}^t{c}^{\left(v\right)}\left(\tau \right)d\tau$$ (11)

where x ∈ [L^(c), L^(c)+ L^(v)] (see Fig.1). The venule partial transit time represents the time necessary for an infinitesimal blood element to travel from the end of the capillary (i.e. the beginning of the venule) to the coordinate x in the venule (x ∈ [L^(c), L^(c)+ L^(v)]) at time t. We can prove (Appendix C) that the general solution of Eq.(10) which satisfies the boundary condition at the capillary side is given by:

$$S^{\left(v\right)}(x,t)=S^{\left(c\right)}\left(L^{\left(c\right)},t-t_p^{\left(v\right)}(x,t)\right)=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{o}}{t}_p^{\left(c\right)}\left(L^{\left(c\right)},t-t_p^{\left(v\right)}(x,t)\right)}=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}^{\left(c\right)}\left(t-t_p^{\left(v\right)}(x,t)\right)}$$ (12)

Eq.(12) states that the oxygen saturation at a point x within the venule at time t, is the saturation that was found at the end of the capillary at a previous time:t – $t_p^{\left(v\right)}(x,t)$. In Eq.(12) we have used both Eq.(6) and the definition of venule partial transit time (Eq.11). The average venule saturation which is the relevant parameter we are interested in can be written as:

$$\langle S^{\left(v\right)}\rangle \left(t\right)=\frac{1}{L^{\left(v\right)}}{\int }_{L^{\left(c\right)}}^{L^{\left(c\right)}+L^{\left(v\right)}}{S}^{\left(v\right)}(x,t)dx=\frac{S^{\left(a\right)}}{L^{\left(v\right)}}{\int }_{t-t^{\left(v\right)}\left(t\right)}^t{e}^{-{\alpha }_{\stackrel{.}{O}}{t}^{\left(c\right)}\left(\tau \right)}{c}^{\left(v\right)}\left(\tau \right)d\tau$$ (13)

The derivation of Eq.(13) is similar to that for Eq.(7), therefore the reader is referred to Appendix B. In Eq.(13), we have used the definition of total transit time for both capillary (t^(c)(t)) and venule $(t^{\left(v\right)}\left(t\right)=t_p^{\left(v\right)}(L^{\left(c\right)}+L^{\left(v\right)},t))$. The theory described for the venule, in particular Eq.(13), is valid for arbitrary dynamics of flow velocity c^(v)(t). However, if we assume a sinusoidal oscillation, $c^{\left(v\right)}\left(t\right)=c_0^{\left(v\right)}+c_1^{\left(v\right)}\sin \left(\omega t\right)$, the total transit time is defined (as it was defined for the capillary) by solving the following transcendental equation:

$$L^{\left(v\right)}=-\frac{c_1^{\left(v\right)}}{\omega }\{\cos \left(\omega t\right)-cos\left[\omega (t-t^v\left(t\right))\right]\}+c_0^{\left(v\right)}{t}^{\left(v\right)}\left(t\right)$$ (14)

Note that if $c^{\left(c\right)}\left(t\right)=c_0^{\left(c\right)}$ and $c^{\left(v\right)}\left(t\right)=c_0^{\left(v\right)}+c_1^{\left(v\right)}\sin \left(\omega t\right)$, then $t^{\left(c\right)}\left(t\right)=L^{\left(c\right)}∕c_0^{\left(c\right)}$ and, from Eq.(12), $S^{\left(v\right)}(x,t)=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{o}}{L}^{\left(c\right)}∕c_0^{\left(c\right)}}$. Therefore if a change in the flow velocity occurs only in the venule, the saturation along the venule will not be affected. Note also that the solutions given by Eq.(6) and Eq.(12) for the capillary and vein, respectively, are correct for a general case including transients.

2.2 Blood oxygen saturation for more complex vascular topologies

In this section we show how the method based on the partial and total blood transit times can be extended to derive expressions for the solutions of oxygen saturation in more complex vascular topologies for arbitrary dynamics of speed of blood flow. The proofs of the solutions provided in this section are omitted since they can be obtained by following the guidelines of Appendix A and C.

a) Dynamic equation for the oxygen saturation for a sequence of one arteriole and two capillaries

The solution for the oxygen saturation in the first capillary of Fig.2 ($S_1^{\left(c\right)}(x,t)$, where the subscript “1” indicates the first capillary) is the same as the one given in Eq.(6). For the second capillary, the equation to be solved is still Eq.(4) with $c_2^{\left(c\right)}\left(t\right)$ instead of c^(c)(t). For this case the boundary condition at $x=L_1^{\left(c\right)}$ imposes the continuity of oxygen saturation. If we consider a point x within the second capillary $(x\in [L_1^{\left(c\right)},L_1^{\left(c\right)}+L_2^{\left(c\right)}])$ and a time t, the solution for oxygen saturation is:

$$S_2^{\left(c\right)}(x,t)=S_1^{\left(c\right)}\left(L_1^{\left(c\right)},t-t_{p2}^{\left(c\right)}(x,t)\right)e^{-{\alpha }_{\stackrel{.}{0}}{t}_{p2}^{\left(c\right)}(x,t)}=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}_1^{\left(c\right)}\left(t-t_{p2}^{\left(c\right)}(x,t)\right)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}_{p2}^{\left(c\right)}(x,t)}$$ (15)

In Eq.(15), $t_1^{\left(c\right)}\left(t\right)=t_{p1}^{\left(c\right)}(L_1^{\left(c\right)},t)$ is the total transit time in the first capillary and $t_{p2}^{\left(c\right)}(x,t)$ is the partial transit time in the second capillary defined by the Eq.(16) and (17), respectively:

$$L_1^{\left(c\right)}={\int }_{t-t_1^{\left(c\right)}\left(t\right)}^t{c}_1^{\left(c\right)}\left(\tau \right)d\tau ;x\in \left[0,L_1^{\left(c\right)}\right]$$ (16)

$$x=L_1^{\left(c\right)}+{\int }_{t-t_{p2}^{\left(c\right)}(x,t)}^t{c}_2^{\left(c\right)}\left(\tau \right)d\tau ;x\in \left[L_1^{\left(c\right)},L_1^{\left(c\right)}+L_2^{\left(c\right)}\right]$$ (17)

Eq.(15) says that the oxygen saturation in a point x in the second capillary at a time t, is calculated by considering the desaturation at the end of the first capillary at an anterior time $(t-t_{p2}^{\left(c\right)}(x,t))$ times the desaturation which occurred in the second capillary, which involves the partial transit time $t_{p2}^{\left(c\right)}(x,t)$. By inspection of Eq.(15) we can easily conclude that the boundary condition at $x=L_1^{\left(c\right)}$ is satisfied. In fact at $x=L_1^{\left(c\right)}$, we have that $t_{p2}^{\left(c\right)}(L_1^{\left(c\right)},t)=0$ and Eq.(15) coincides with Eq.(6). Also, one can prove that the spatially averaged oxygen saturation in the second capillary is given by:

$$\langle S_2^{\left(c\right)}\rangle \left(t\right)=\frac{1}{L_2^{\left(c\right)}}{\int }_0^{L_2^{\left(c\right)}}{S}_2^{\left(c\right)}(x,t)dx=\frac{S^{\left(a\right)}}{L_2^{\left(c\right)}}{\int }_{t-t_2^{\left(c\right)}\left(t\right)}^t{e}^{-{\alpha }_{\stackrel{.}{O}}{t}_1^{\left(c\right)}\left(\tau \right)}{e}^{-{\alpha }_{\stackrel{.}{O}}(t-\tau )}{c}_2^{\left(c\right)}\left(\tau \right)d\tau$$ (18)

In Eq. (18), without loss of generality, we have redefined the coordinate system with its origin at the beginning of the second capillary. In this case, the definition of partial transit time (Eq.(17)), does not include the term $L_1^{\left(c\right)}$.

Fig.2.

Schematic of a sequence of three blood vessels: one arteriole, and two capillaries. The blood flow velocities are: $c^{\left(a\right)}\left(t\right),c_1^{\left(c\right)},c_2^{\left(c\right)}\left(t\right)$ for the arteriole and the two capillaries, respectively. The origin of the coordinate system is chosen at the beginning of the first capillary. $L^{\left(a\right)},L_1^{\left(c\right)},L_2^{\left(c\right)}$ are the lengths of the arteriole and the two capillaries, respectively.

b) Dynamic equation for the oxygen saturation for a sequence of one arteriole two capillaries and one venule

The solution for the oxygen saturation in the two capillaries are those given in the previous sections (see Eq.(6) and Eq.(15) for the full spatio-temporal profile and Eq.(7) and Eq.(18) for the spatially averaged saturation).

For the solution of the partial differential equation in the venule (Eq.(10)), we reason as in section 2.1.c. The saturation at a point a x within the venule at time t is the saturation found at the end of the second capillary at the anterior time $t-t_p^{\left(v\right)}(x,t)$:

$$\begin{array}{cc}\hfill & S^{\left(v\right)}(x,t)=S_2^{\left(c\right)}\left(L_2^{\left(c\right)},t-t_p^{\left(v\right)}(x,t)\right)=\hfill \\ \hfill & =S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}_1^{\left(c\right)}\left(t-t_p^{\left(v\right)}(x,t)-t_2^{\left(c\right)}(t-t_p^{\left(v\right)}(x,t))\right)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}_2^{\left(c\right)}\left(t-t_p^{\left(v\right)}(x,t)\right)}\hfill \end{array}$$ (19)

where $t_p^{\left(v\right)}(x,t)$ is the venule partial transit time defined by:

$$x=L_1^{\left(c\right)}+L_2^{\left(c\right)}+{\int }_{t-t_p^{\left(v\right)}(x,t)}^t{c}^{\left(v\right)}\left(\tau \right)d\tau$$ (20)

We note that Eq.(19) makes use also of Eq.(15). Eq.(19) tells us that the amount of desaturation occurring in both capillaries is calculated by considering both total transit times, $t_1^{\left(c\right)}$ and $t_2^{\left(c\right)}$. $t_2^{\left(c\right)}$ (transit time in the second capillary) is calculated at the anterior time $t-t_p^{\left(v\right)}(x,t)$, while $t_1^{\left(c\right)}$ (transit time in the first capillary) is calculated at the anterior time $t-t_p^{\left(v\right)}(x,t)-t_2^{\left(c\right)}(t-t_p^{\left(v\right)}(x,t))$. Note that the boundary condition for the saturation at $x=L_1^{\left(c\right)}+L_2^{\left(c\right)}$ is satisfied. The spatially averaged saturation in the venule is calculated by the expression:

$$\langle S^{\left(v\right)}\rangle \left(t\right)=\frac{1}{L^{\left(v\right)}}{\int }_0^{L^{\left(v\right)}}{S}^{\left(v\right)}(x,t)dx=\frac{S^{\left(a\right)}}{L^{\left(v\right)}}{\int }_{t-t^{\left(v\right)}\left(t\right)}^t{e}^{-{\alpha }_{\stackrel{.}{O}}{t}_1^{\left(c\right)}(\tau -t_2^{\left(c\right)}\left(\tau \right))}{e}^{-{\alpha }_{\stackrel{.}{O}}{t}_2^{\left(c\right)}\left(\tau \right)}{c}^{\left(v\right)}\left(\tau \right)d\tau$$ (21)

As in Eq.(18) we have redefined the origin of the system so that its origin coincides at the beginning of the venule.

c) Dynamic equation for the oxygen saturation for an arteriole and a sequence of “n” capillaries

We can generalize the reasoning applied in the previous sections and calculate the solution for oxygen saturation in a network of capillaries (see Fig.4). In particular, the solution for a point x in the n-th capillary at time t is given by:

$$S_n^{\left(c\right)}(x,t)=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}_{pn}^{\left(c\right)}(x,t)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}_{n-1}^{\left(c\right)}\left({\tau }_{n-1}(x,t)\right)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}_{n-2}^{\left(c\right)}\left({\tau }_{n-2}(x,t)\right)}\dots e^{-{\alpha }_{\stackrel{.}{0}}{t}_j^{\left(c\right)}\left({\tau }_j(x,t)\right)}\dots e^{-{\alpha }_{\stackrel{.}{0}}{t}_1^{\left(c\right)}\left({\tau }_1(x,t)\right)}$$ (22)

Eq.(22) can be more concisely rewritten as follows:

$$S_n^{\left(c\right)}(x,t)=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}_{pn}^{\left(c\right)}(x,t)}{\prod }_{k=1}^{n-1}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}_k^{\left(c\right)}\left({\tau }_k\right)}=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}_{pn}^{\left(c\right)}(x,t)}{e}^{-{\alpha }_{\stackrel{.}{0}}{\sum }_{k=1}^{n-1}{t}_k^{\left(c\right)}\left({\tau }_k(x,t)\right)}$$ (23)

In Eq.(23) $t_{pn}^{\left(c\right)}(x,t)$ is the partial transit time in the n-th capillary, and $t_j^{\left(c\right)}$ is the total transit time in the j-th capillary, which is calculated at a specific time, τ_j(x, t), anterior to the observation time t.

Fig.4.

Schematic of a sequence of n+1 blood vessels: one arteriole, and n capillaries. The blood flow velocities are: $c^{\left(a\right)}\left(t\right),c_1^{\left(c\right)}\left(t\right),c_2^{\left(c\right)}\left(t\right),\dots c_n^{\left(c\right)}\left(t\right)$ for the arteriole, and the n capillaries, respectively. The origin of the coordinate system is chosen at the beginning of the first capillary. $L^{\left(a\right)},L_1^{\left(c\right)},L_2^{\left(c\right)},\dots .L_n^{\left(c\right)}$ are the lengths of the arteriole, and the n capillaries, respectively.

The variables τ_j(x, t) are defined by the recurrence relationship:

$${\tau }_{n-1}(x,t)=t-t_{pn}^{\left(c\right)}(x,t);{\tau }_j(x,t)={\tau }_{j+1}(x,t)-t_{j+1}^{\left(c\right)}\left({\tau }_{j+1}(x,t)\right);j=1,\dots ..n-2$$ (24)

The expression given in Eq.(23) solves Eq.(4) in the n-th capillary and satisfies the boundary conditions with the previous capillary (n-1). A physical interpretation of Eq.(23) is that a j-th capillary has contributed to the desaturation of a blood element found in a point x in the n-th capillary (downstream with respect to the capillary j) at time t, according to an exponential temporal decay involving the total transit time in the j-th capillary at a specific anterior time τ_j(x, t). The total desaturation of the blood element is given by an exponential temporal decay law involving the total transit time along the particular path chosen in the capillary network from the arteriole to the n-th capillary. Note that the transit times in the single capillaries and the total transit time, depend on the observation time t and the point x within the n-th capillary. The fact that desaturation depends on the total transit time in the capillary network is not surprising. In fact, if one adopts a Lagrangian viewpoint for studying the process of desaturation along the capillary network, one has to solve the simple ordinary differential equation:

$$\frac{d{S}_L^{\left(c\right)}\left(t\right)}{dt}=-{\alpha }_{\stackrel{.}{o}}{S}_L^{\left(c\right)}\left(t\right)$$ (25)

In Eq.(25) $S_L^{\left(c\right)}\left(t\right)$ is the saturation along the motion of a particular infinitesimal blood element (the subscript L in this case indicates the Lagrangian viewpoint) and t represents the transit time in the network. The solution of Eq.(25) is:

$$S_L^{\left(c\right)}\left(t\right)=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{o}}t}$$ (26)

Eq.(26) is the Lagrangian representation of Eq.(23), while Eq.(23) is the Eulerian or field view representation of Eq.(26). The reason why a field view description of the process of desaturation is often necessary is because, since we don't need to keep track of each blood element as it flows along the vascular network, it is easier to calculate the spatially averaged saturation in the capillaries at a given observation time t, which is the fundamental parameter for calculating the dynamics of oxy and deoxy-hemoglobin concentrations in tissue. The expression of the spatially averaged saturation in the n-th capillary of Fig.(4) is:

$$\langle S_n^{\left(c\right)}\rangle \left(t\right)=\frac{1}{L_n^{\left(c\right)}}{\int }_0^{L_n^{\left(c\right)}}{S}_n^{\left(c\right)}(x,t)dx=\frac{S^{\left(a\right)}}{L_n^{\left(c\right)}}{\int }_{t-t_n^{\left(c\right)}\left(t\right)}^t{e}^{-{\alpha }_{\stackrel{.}{0}}(t-\tau )}{\prod }_{j=1}^{n-1}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}_j^{\left(c\right)}\left(T_j\left(\tau \right)\right)}{c}_n^{\left(c\right)}\left(\tau \right)d\tau$$ (27)

In Eq.(27), the transit time in the j-th capillary $\left(t_j^{\left(c\right)}\right)$ is calculated at time T_j(τ), which is defined by a recurrence relation:

$$T_{n-1}\left(\tau \right)=\tau ;T_j\left(\tau \right)=T_{j+1}\left(\tau \right)-t_{j+1}^{\left(c\right)}\left(T_{j+1}\left(\tau \right)\right);j=1,\dots ..n-2$$ (28)

2.3 Dynamics of oxy- and deoxy-hemoglobin concentrations in tissue

In the previous sections, we have shown how the method based on the capillary transit times can be used to derive solutions for the temporal trend of blood oxygen saturation in a network of capillaries and venules. We have calculated the spatio-temporal changes in blood oxygen saturation along a path of the capillary and venules network due to the dynamics of capillary speed of blood flow. Even though the capillaries and venules in a real network feature different lengths and speed of blood flow dynamics (hence different transit times), in this work in order to translate our results into macroscopic (measurable) parameters like the concentrations of oxy- and deoxy-hemoglobin in tissue, we will assume that all the capillaries and venules are characterized by the same lengths and speed of blood flow (hence, a single time resolved transit time; i.e. we will adopt the schematic of Fig.1). Therefore, our multi-compartmental model is a “lumped parameters” model, since the complex network of arterioles, capillaries and venules is described by a few parameters per each compartment.

a) Baseline concentrations of oxy- and deoxyhemoglobin in tissue

According to the previous model (Fantini, 2014 a) the baseline concentrations of oxy- and deoxy-hemoglobin in tissue are referred to a baseline (i.e. constant) value of speed of blood flow in the capillaries and constant blood volumes in the three compartments:

$$O_0=ctHb\left[{\varphi }^{\left(a\right)}{S}^{\left(a\right)}+{\varphi }^{\left(c\right)}{F}^{\left(c\right)}\langle S_0^{\left(c\right)}\rangle +{\varphi }^{\left(v\right)}{S}_0^{\left(v\right)}\right]$$ (29)

$$D_0=ctHb\left[{\varphi }^{\left(a\right)}(1-S^{\left(a\right)})+{\varphi }^{\left(c\right)}{F}^{\left(c\right)}(1-\langle S_0^{\left(c\right)}\rangle )+{\varphi }^{\left(v\right)}(1-S_0^{\left(v\right)})\right]$$ (30)

In Eq.(29) and Eq.(30) O_o and D_o are the baseline concentrations of oxy- and deoxyhemoglobin in tissue. F^(c) is the Fåhraeus factor (ratio of capillary to large vessel hematocrit), ctHb is the concentration of total hemoglobin in arterial and venous blood, S^(a), $\langle S_0^{\left(c\right)}\rangle$ and $S_0^{\left(v\right)}$ are the “baseline” oxygen saturations in the arterial, capillary and venous compartments, respectively. ϕ^(a), ϕ^(c), ϕ^(v) are the volume fractions of arterial, capillary, and venous blood in tissue (units of ml_blood/ml_tissue). Eq.(29) and (30) are used also in the nonlinear model.

b) Changes of oxy- and deoxy-hemoglobin concentrations in tissue due to changes in capillary blood flow velocity

When we solve Eq.(4) and Eq.(10) for a step function (i.e. for a step change in the speed of blood flow at t=0 from $c_0^{\left(c\right)}$ to $c_1^{\left(c\right)}$ and from $c_0^{\left(v\right)}$ to $c_1^{\left(v\right)}$, for the capillary and venule, respectively) we can find explicit solutions for 〈S^(c)〉(t) and 〈S^(v)〉(t) (Fantini, 2014 a; appendices B and C). The dynamic change in saturations 〈S^(c)〉(t) – 〈S^(c)〉(t = 0) and 〈S^(v)〉(t) – S^(v)(t = 0) can be expressed in terms of the normalized step amplitude f: $f=(c_1^{\left(c\right)}-c_0^{\left(c\right)})∕c_0^{\left(c\right)}$. By inspection of these expressions (not shown) it is clear that the capillary and venule do not respond as linear time invariant systems, (where f is the input of the systems and the change in saturations the outputs) otherwise f would appear as a factor in the expression of the output. However in the limit of “small” f it can be shown that the capillary and venule indeed respond as linear time invariant systems and the impulse response functions for capillary and venule were given as in the following Eq.(31) and Eq.(32), respectively (Fantini, 2014 a):

$$h_{RC-LP}^{\left(c\right)}\left(t\right)=H\left(t\right)\frac{1}{{\tau }^{\left(c\right)}}{e}^{-t∕{\tau }^{\left(c\right)}}$$ (31)

$$h_{G-LP}^{\left(v\right)}\left(t\right)=\frac{1}{t_r^{\left(v\right)}}{e}^{-\pi {(t-t_{0.5})}^2∕{\left(t_r^{\left(v\right)}\right)}^2}$$ (32)

Eq.(31) is the expression of an RC (resistor-capacitor) low-pass filter where H(t) is the Heaviside unit step function (H(t) = 0 for t < 0; H(t) =0.5 for t=0; H(t) = 1 for t > 0) and ${\tau }^{\left(c\right)}=L^{\left(c\right)}∕\left(e{c}_0^{\left(c\right)}\right)=t_0^{\left(c\right)}∕e$). Eq. (32) is the expression of a shifted Gaussian low pass filter with $t_r^{\left(v\right)}\sim 0.6(L^{\left(v\right)}∕c_1^{\left(v\right)}+L^{\left(c\right)}∕c_0^{\left(c\right)})=0.6(t_0^{\left(v\right)}+t_0^{\left(c\right)})$ and $t_{0.5}=(5∕6)t_r^{\left(v\right)}$. The fixed parameters $t_0^{\left(c\right)}$ and $t_0^{\left(v\right)}$, which have a fundamental role in the linear model, are the capillary and venous transit times. The changes in oxy- and deoxyhemoglobin concentrations due to flow changes (f(τ)) are given as (Fantini, 2014 a):

$$\Delta O_F^{\left(lin\right)}\left(t\right)=ctHb{F}^{\left(c\right)}{\varphi }^{\left(c\right)}\left(\langle S_0^{\left(c\right)}\rangle -S_0^{\left(v\right)}\right)\left[h_{RC-LP}^{\left(c\right)}\left(\tau \right)\ast f\left(\tau \right)\right]\left(t\right)+ctHb{\varphi }^{\left(v\right)}{S}_0^{\left(v\right)}{\alpha }_{\stackrel{.}{\mathrm{O}}}{t}_0^{\left(c\right)}\left[h_{G-LP}^{\left(c\right)}\left(\tau \right)\ast f\left(\tau \right)\right]\left(t\right)$$ (33)

$$\Delta D_F^{\left(lin\right)}\left(t\right)=-\Delta O_{flow}^{\left(lin\right)}\left(t\right)$$ (34)

In Eq.(33) and Eq.(34) the symbol $\Delta O_F^{\left(lin\right)}\left(t\right)$ and $\Delta D_F^{\left(lin\right)}\left(t\right)$ are the changes of oxy- and deoxyhemoglobin concentrations (calculated with the linear model), respectively, due to changes in capillary speed of blood flow, and “*” represents the convolution operator. Also, $\langle S_0^{\left(c\right)}\rangle$ and $S_0^{\left(v\right)}$ are the “baseline” oxygen saturations in the capillary and venules, respectively, which are associated to the baseline transit time $t_0^{\left(c\right)}$ (Fantini, 2014 a):

$$\langle S_0^{\left(c\right)}\rangle =\frac{S^{\left(a\right)}\left[1-e^{-{\alpha }_{\stackrel{.}{O}}{t}_0^{\left(c\right)}}\right]}{{\alpha }_{\stackrel{.}{O}}{t}_0^{\left(c\right)}}$$ (35)

$$S_0^{\left(v\right)}=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{O}}{t}_0^{\left(c\right)}}$$ (36)

For the sinusoidal blood flow velocity oscillations which are studied in this work $(c^{\left(c\right)}\left(t\right)=c_0^{\left(c\right)}+c_1^{\left(c\right)}\sin \left(\omega t\right))$ the baseline transit time $t_0^{\left(c\right)}$ is calculated from the capillary length and the average capillary speed of blood flow: $t_0^{\left(c\right)}=L^{\left(c\right)}∕c_0^{\left(c\right)}$. We can also say that $t_0^{\left(c\right)}$ is associated with a steady state or unperturbed capillary speed of blood flow. By using the nonlinear method we obtain:

$$\Delta O_F^{\left(nlin\right)}\left(t\right)=ctHb\left[{\varphi }^{\left(c\right)}{F}^{\left(c\right)}\left(\langle S^{\left(c\right)}\rangle \left(t\right)-\langle S_0^{\left(c\right)}\rangle \right)+{\varphi }^{\left(v\right)}\left(\langle S^{\left(v\right)}\rangle \left(t\right)-S_0^{\left(v\right)}\right)\right]$$ (37)

$$\Delta D_F^{\left(nlin\right)}\left(t\right)=-\Delta O_F^{\left(nlin\right)}\left(t\right)$$ (38)

In Eq.(37) and Eq.(38) $\Delta O_F^{\left(nlin\right)}\left(t\right)$ and $\Delta D_F^{\left(nlin\right)}\left(t\right)$ are the changes of oxy- and deoxyhemoglobin concentrations (calculated with the nonlinear model), respectively, due to changes in capillary speed of blood flow. 〈S^(c)〉(t) and 〈S^(v)〉(t) are given by Eq.(7) and Eq.(13), respectively.

c) Changes of oxy- and deoxy-hemoglobin concentrations in tissue due to changes in blood volume

The concentrations of oxy- and deoxy-hemoglobin in tissue can change also because of blood volume changes. In the previous work (Fantini, 2014 a) these changes were described by the following expressions:

$$\Delta O_V^{\left(lin\right)}\left(t\right)=ctHb\left[{\varphi }^{\left(a\right)}{S}^{\left(a\right)}{v}^{\left(a\right)}\left(t\right)+{\varphi }^{\left(v\right)}{S}_0^{\left(v\right)}\left(t\right)v^{\left(v\right)}\left(t\right)\right]$$ (39)

$$\Delta D_V^{\left(lin\right)}\left(t\right)=ctHb\left[{\varphi }^{\left(a\right)}(1-S^{\left(a\right)})v^{\left(a\right)}\left(t\right)+{\varphi }^{\left(v\right)}\left(1-S_0^{\left(v\right)}\left(t\right)\right)v^{\left(v\right)}\left(t\right)\right]$$ (40)

In Eq. (39) and Eq.(40), $\Delta O_V^{\left(lin\right)}\left(t\right)$ and $\Delta D_V^{\left(lin\right)}\left(t\right)$ are the changes in oxy- and deoxy-hemoglobin concentrations (calculated with the linear model), respectively, due to the changes in blood volume. Eq.(39) and Eq.(40) were derived under the assumption of no capillary recruitment (i.e. the capillary blood volume remains constant), and v^(a)(t) and v^(v)(t) are the changes of arterial and venous blood volumes normalized to their baseline values. For the nonlinear model, since we are solving directly for 〈S^(v)〉(t), we obtain the following expressions:

$$\Delta O_V^{\left(nlin\right)}\left(t\right)=ctHb\left[{\varphi }^{\left(a\right)}{S}^{\left(a\right)}{v}^{\left(a\right)}\left(t\right)+{\varphi }^{\left(v\right)}\langle S^{\left(v\right)}\rangle \left(t\right)v^{\left(v\right)}\left(t\right)\right]$$ (41)

$$\Delta D_V^{\left(nlin\right)}\left(t\right)=ctHb[{\varphi }^{\left(a\right)}(1-S^{\left(a\right)})v^{\left(a\right)}\left(t\right)+{\varphi }^{\left(v\right)}(1-\langle S^{\left(v\right)}\rangle \left(t\right))v^{\left(v\right)}\left(t\right)]$$ (42)

In Eq.(41) and Eq.(42) $\Delta O_V^{\left(nlin\right)}\left(t\right)$ and $\Delta D_V^{\left(nlin\right)}\left(t\right)$ are the changes of oxy- and deoxyhemoglobin concentrations (calculated with the nonlinear model), respectively, due to the changes in blood volume. We note that according to the linear model the contributions to $\Delta O_V^{\left(lin\right)}\left(t\right)$ (or $\Delta D_V^{\left(nlin\right)}\left(t\right)$) from the arterial and venous compartments are always synchronous (or in phase) as long as v^(a)(t) and v^(v)(t) are in phase. This result is not true for the nonlinear model, however the mismatch between the two contributions is negligible in all the cases investigated in this work.

d) Relationship between changes in blood volume and changes in blood flow

Even though the comparison of the linear and nonlinear models can be carried out also by assuming arbitrary and independent dynamics of perturbations in blood volume and flow (v^(a), v^(v)(t), f(t), respectively), in this work we will assume the relationship that derives from the mechanism of cerebral autoregulation (Fantini, 2014 a):

$$f\left(t\right)=k{h}_{RC-HP}^{\left(\mathrm{AR}\right)}\left(t\right)\ast v\left(t\right)$$ (43)

In Eq.(43) k is the inverse of the modified Grubb's exponent, while $h_{RC-HP}^{\left(\mathrm{AR}\right)}\left(t\right)$ is the RC high-pass impulse response function with cutoff frequency $f_c^{\left(\mathrm{AR}\right)}$ that describes the effect of autoregulation:

$$h_{RC-HP}^{\left(\mathrm{AR}\right)}\left(t\right)=-\frac{1}{\tau }{e}^{-\frac{t}{\tau }}+\delta \left(t\right)$$ (44)

In Eq.(44), $\tau =1∕\left(2\pi f_c^{\left(\mathrm{AR}\right)}\right)$ and δ is the Dirac delta function. As for v(t) in Eq.(43) we have assumed that v(t) = v^(a)(t) = v^(v)(t). Note that if $f_c^{\left(\mathrm{AR}\right)}=0$, $h_{RC-HP}^{\left(\mathrm{AR}\right)}\left(t\right)=\delta \left(t\right)$.

2.4 Definition of the relevant parameters in Coherent Hemodynamics Spectroscopy (CHS) and computational details

In coherent hemodynamic spectroscopy (CHS) (Fantini, 2014 a; Fantini, 2014 b; Kainerstorfer et al., 2014; Kainerstorfer et al., 2015; Pierro et al., 2014 a; Pierro et al., 2014 b; Sassaroli et al., 2015), one is interested in blood pressure oscillations at several distinct frequencies. The blood pressure oscillations induce blood flow and blood volume oscillations, therefore for the calculations of the parameters relevant to CHS we will use the expressions for ΔO and ΔD obtained from the two models (linear and nonlinear) described in sections 3.c and 3.d when v(t, ω) = v₀ sin (ωt). Based on Eq.(43) the blood flow oscillations will be:

$$f(t,\omega )=a\sin \left(\omega t\right)+bcos\left(\omega t\right);$$ (45)

with a and b given by the expressions:

$$a=k{v}_0\left[1-\frac{{\left({\omega }_c^{\left(AR\right)}\right)}^2}{{\omega }^2+{\left({\omega }_c^{\left(AR\right)}\right)}^2}\right];b=k{v}_0\left[\frac{\omega {\omega }_c^{\left(AR\right)}}{{\omega }^2+{\left({\omega }_c^{\left(AR\right)}\right)}^2}\right]$$ (46)

where ${\omega }_c^{\left(AR\right)}=2\pi f_c^{\left(\mathrm{AR}\right)}$, $f_c^{\left(\mathrm{AR}\right)}$ being the autoregulation cutoff frequency. Note that for a nonautoregulated system (i.e. $f_c^{\left(\mathrm{AR}\right)}=0$), Eq.(45) simplifies into f(t, ω) = kv₀ sin(ωt). For the case of the linear model f(t, ω) and v(t, ω) are the inputs of the system, and $\Delta O^{\left(lin\right)}(t,\omega )=\Delta O_V^{\left(lin\right)}(t,\omega )+\Delta O_F^{\left(lin\right)}(t,\omega )$, and $\Delta D^{\left(lin\right)}(t,\omega )=\Delta D_V^{\left(lin\right)}(t,\omega )+\Delta D_F^{\left(lin\right)}(t,\omega )$ are the outputs, which are calculated from Eqs.(33), (34) and Eqs.(39), (40), respectively. For the case of the nonlinear model the knowledge of f(t, ω) does not suffice for solving the transcendental equation for t^(c)(t) (see Eq.(8)), and also the baseline capillary speed of blood flow is needed. For autoregulated systems (i.e. $f_c^{\left(\mathrm{AR}\right)}>0$) the transcendental equation for t^(c)(t) becomes:

$$\begin{array}{cc}\hfill L^{\left(c\right)}=& \frac{a{c}_0^{\left(c\right)}}{\omega }\left\{-\cos \left(\omega t\right)+cos\left[\omega \left(t-t^{\left(c\right)}\left(t\right)\right)\right]\right\}+\hfill \\ \hfill & +\frac{b{c}_0^{\left(c\right)}}{\omega }\left\{\sin \left(\omega \mathrm{t}\right)-sin\left[\omega \left(t-t^{\left(c\right)}\left(t\right)\right)\right]\right\}+c_0^{\left(c\right)}{t}^{\left(c\right)}\left(t\right)\hfill \end{array}$$ (47)

where $c_0^{\left(c\right)}$ is the baseline capillary speed of blood flow. Eq.(47) reduces to Eq.(8) for nonautoregulated systems. For the nonlinear model we will use $\Delta O^{\left(nlin\right)}(t,\omega )=\Delta O_V^{\left(nlin\right)}(t,\omega )+\Delta O_F^{\left(nlin\right)}(t,\omega )$ and $\Delta D^{\left(nlin\right)}(t,\omega )=\Delta D_V^{\left(nlin\right)}(t,\omega )+\Delta D_F^{\left(nlin\right)}(t,\omega )$ calculated from Eq.(37), Eq.(38), and Eq.(41), Eq.(42). In both models we also define the change of total hemoglobin concentration as: ΔT^(lin)(t, ω) = ΔO^(lin) (t, ω) + ΔD^(lin)(t, ω), and ΔT^(nlin)(t, ω) = ΔO^(nlin)(t, ω), + ΔD^(nlin)(t, ω), for the linear and nonlinear models, respectively. We further proceed by using the method of the analytic signal to associate time varying phasors to the changes of oxy- deoxy- and total hemoglobin concentrations (Boashash, 1992). The method of the analytic signal is more general than a Fourier Transform, since it can be used also for nonlinear, non stationary systems. We define the phasors associated to ΔO^(x)(t, ω), ΔD^(x)(t, ω) and ΔT^(x)(t, ω) as O^(x)(ω), D^(x)(ω) and T^(x)(ω), respectively, where “x” indicates either the linear or the nonlinear model. Once these eight basic phasors are defined we consider the ratios:

$$\frac{{\mathbf{D}}^x\left(\omega \right)}{{\mathbf{O}}^x\left(\omega \right)}=\frac{\mid {\mathbf{D}}^x\left(\omega \right)\mid }{\mid {\mathbf{O}}^x\left(\omega \right)\mid }{e}^{i\{\mathrm{Arg}\left[{\mathbf{D}}^x\left(\omega \right)\right]-\mathrm{Arg}\left[{\mathbf{O}}^x\left(\omega \right)\right]\}}$$ (48)

$$\frac{{\mathbf{O}}^x\left(\omega \right)}{{\mathbf{T}}^x\left(\omega \right)}=\frac{\mid {\mathbf{O}}^x\left(\omega \right)\mid }{\mid {\mathbf{T}}^x\left(\omega \right)\mid }{e}^{i\{\mathrm{Arg}\left[{\mathbf{O}}^x\left(\omega \right)\right]-\mathrm{Arg}\left[{\mathbf{T}}^x\left(\omega \right)\right]\}}$$ (49)

One of the objectives of this work was to carry out a comparison between the four spectra |D^x(ω)|/|O^x(ω)|, Arg[D^x(ω)] – Arg[O^x(ω)], |O^x(ω)|/|T^x(ω)|, and Arg[O^x(ω)] – Arg[T^x(ω)] for different amplitudes of blood volume and capillary blood flow oscillations. More in details, we defined ten different (equally spaced) angular frequencies ω_i = 2πf_i where f_i ∈ [0.02, 0, 2]Hz is the frequency of oscillation. This frequency range is typically used in CHS studies. For each frequency f_i we divided the period of oscillation T_i = 1/f_i in time steps Δ(Δ=5 ms). The capillary (t^(c)(t)) and venous (t^(v)(t)) transit times were calculated at the discrete time points t_i = iΔ by solving the transcendental equations Eq.(8),(14), respectively. The integrals defining 〈S^(c)〉(t_i, ω) (Eq.(7)) and 〈S^(v)〉(t_i, ω) (Eq.(13)) that were used for the nonlinear model were calculated numerically by dividing the integration intervals in 1000 time steps. We also used Eq.(37), Eq.(38) and Eq.(41), Eq.(42) for calculating ΔO^(nlin)(t,_i, ω) and ΔD^(nlin)(t_i, ω), respectively, and Eq.(33), Eq.(34), and Eq.(39), Eq.(40) for calculating ΔO^(lin)(t_i, ω) and ΔD^(lin)(t_i, ω), respectively. Afterwards, the temporal profiles of ΔO^(x)(t_i, ω) and ΔD^(x)(t_i, ω) (where x stands for the linear or the nonlinear model) were down sampled to 0.25 s and we defined extended temporal profiles by connecting 65 periods. This was necessary (for computational economy) in order to apply a finite impulse response (FIR) filter according to the Parks-Mcclellan algorithm (MATLAB function “firpmord”) with a relative narrow bandwidth. The characteristics of the filters were: pass band edges defined by f_i ± 0.005 Hz, stop band edges f_i ± 0.01 Hz, passband ripple 0.05, and stopband attenuation 0.05. The order of the filter was n=856. In order to avoid temporal shifts the coefficients of the filter were input in the MATLAB function “filtfilt”. Afterwards the phasors of Eq.(48) and Eq.(49) were defined by taking the Hilbert transform of the filtered temporal profiles. The accuracy of this procedure was tested for the linear model by comparing its results with those obtained by using directly the formulas in the frequency domain (Fantini, 2014). The comparison yielded discrepancies in the parameters |D^lin(ω)|/|O^lin(ω)| and |O^lin(ω)|/|T^lin(ω)| less than 1%; the discrepancies in the parameters Arg[D^lin(ω)] – Arg[O^lin(ω)] and Arg[O^lin(ω)] – Arg[T^lin(ω)] were less than 1.2°. The consistency of the nonlinear calculations was studied by tweaking several parameters used for the numerical calculations, like using a finer time step (Δ=1 ms) or doubling the partition of the integration interval in Eq.(7) and (13) for the calculations of the spatially averaged capillary and venous saturations.

3. Comparison of linear and nonlinear models

3.1 Oscillatory hemodynamics

Before comparing the spectra obtained with the linear and nonlinear models, we will compare the models in the “time domain” for sinusoidal oscillations of both capillary and venous speed of blood flow: $c^x\left(t\right)=c_0^{\left(x\right)}+c_1^{\left(x\right)}\sin \left(\omega t\right)$, where the superscript “x” indicates either the capillary or the venous compartment. We considered a case of “small” (10%) and a case of “large” (50%), flow perturbations, corresponding (according to our model and choice of the parameter k =5) to volume oscillations of 2% and 10%, respectively. In the discussion we will provide more details about this choice in reference to flow changes found in the literature. The calculations were run by fixing the following baseline parameters: ϕ^(a) = ϕ^(v) = 0.05, ϕ^(c) = 0.015, ctHb = 2.3 mM, S^(a) = 0.98, F^(c) = 0.8, ${\alpha }_{\stackrel{.}{o}}$ = 0.8, k = 5, $f_c^{\left(\mathrm{AR}\right)}=0$ = 0, ω = 2π/T (T=10 s). For the small oscillation regime we fixed $c_0^{\left(c\right)}=1mm∕s$, $c_1^{\left(c\right)}=0.1mm∕s$, which corresponds, according to the blood volume-flow relationship (Eq.(43)), to a blood volume oscillation amplitude of 2% (v₀ = 0.02). For the venule flow speed we fixed $c_0^{\left(v\right)}=2mm∕s$. $c_1^{\left(v\right)}=0.2mm∕s$. Therefore, in both capillary and venule the perturbation in blood flow velocity is 10%. The baseline transit times for capillary and venous compartments are defined by $t_0^{\left(x\right)}=L^{\left(x\right)}∕c_0^{\left(x\right)}$ where the subscript “x” indicates either capillary (c) or venous (v) compartments. The lengths of the blood vessel was chosen as L^(c) = 0.5 mm and L^(v) = 4 mm, for the capillary and venule, respectively, which yields the transit times $t_0^{\left(c\right)}=0.5s$ (capillary) and $t_0^{\left(v\right)}=2s$ (venous).

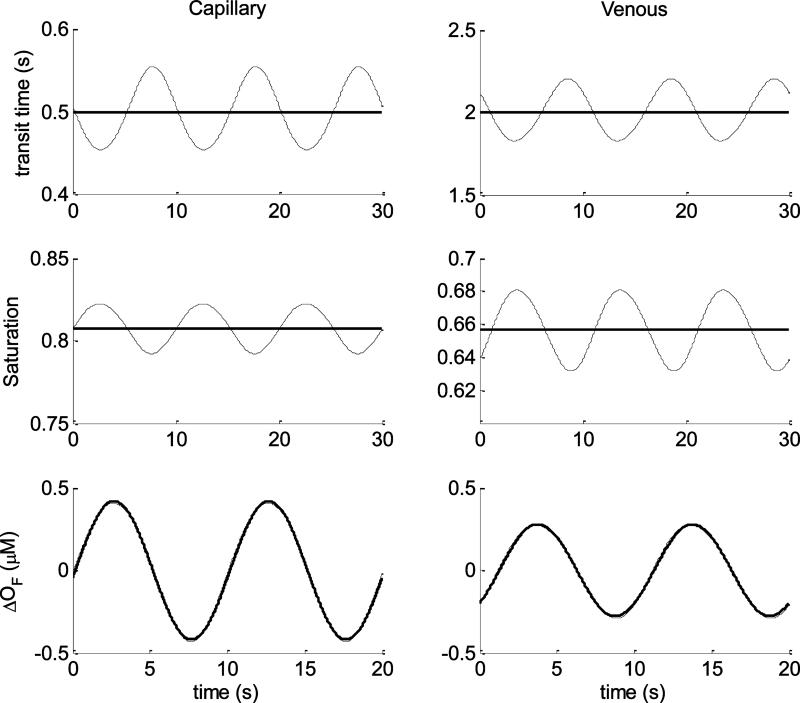
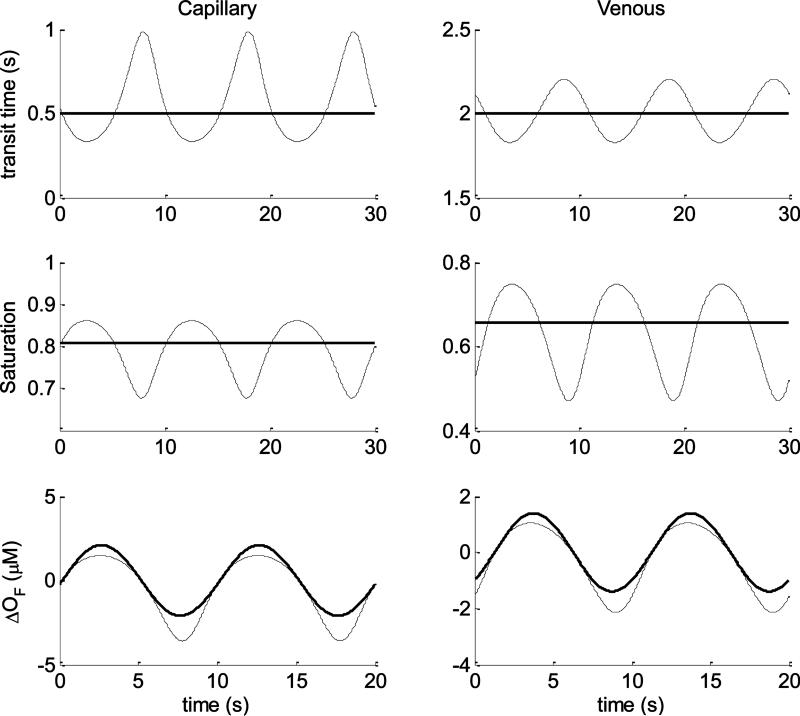
In Fig.5 are plotted some comparisons between parameters of the linear (thick lines) and nonlinear (thin lines) models. The top row refers to the capillary (left plots) and venous (right plots) transit times. As we have discussed (see section 2.3.b) the linear model assumes constant values for these two parameters which define the impulse response functions of the capillary and venous compartments. The changes in oxy and deoxyhemoglobin concentrations are calculated by performing the convolution (see Eq.(33) and Eq.(34)) between the impulse responses and the normalized capillary flow oscillations: $f(t,\omega )=\frac{c_1^{\left(c\right)}}{c_0^{\left(c\right)}}\sin \left(\omega t\right)=kv(t,\omega )=k{v}_0\sin \left(\omega t\right)$. On the contrary, in the nonlinear model, both capillary and venous transit times are time dependent, and for relatively small flow oscillations they are quasi-sinusoidal temporal profiles. The center row in Fig. 5 refers to the spatially averaged oxygen saturations for capillary (left plots) and venous (right plots) compartments. The linear model assumes constant values for these two parameters which are uniquely defined by the capillary transit time (section 2.3.b). On the contrary the nonlinear model directly solves for these two parameters which are time dependent, and for “small” flow oscillations they are quasi-sinusoidal temporal profiles. The last row of Fig.(5) refers to the changes of oxy-hemoglobin concentration due to flow changes only (ΔO_F), in the capillary (left plots) and venous (right plots) compartments. Despite the different approach followed by the two models for these calculations, we can appreciate that they yield results with negligible differences. In Fig.6, the comparisons between linear and nonlinear models are carried out for the same baseline parameters but for a wider volume oscillation v₀ = 0.1 which yield a capillary flow oscillation of 50%. Also the venous flow oscillation was changed by fixing $c_1^{\left(v\right)}=1mm∕s$, therefore both compartments are characterized by flow oscillations having amplitudes 50% of their baseline values. In this case, all the time resolved parameters (transit times, saturations and changes in oxy-hemoglobin) calculated by the nonlinear model clearly deviate from sinusoidal oscillations. Notice in particular the differences between the changes in oxy-hemoglobin concentration calculated by the two models. The nonlinear model yields asymmetric (non-sinusoidal) oscillations for both capillary and venous compartments with minima wider than the maxima.

Fig.5.

Time domain comparisons between linear (thick lines) and nonlinear (thin lines) models for sinusoidal capillary and venous blood flow velocities oscillations (having periods T=10 s). The amplitudes of the oscillations is 10% of the baseline values. Left column refers to the capillary while the right column to the venous compartment. Top row represents the transit times, center row the oxygen saturation, bottom row the changes of oxyhemoglobin due to flow changes only. The baseline parameters used for the computation are listed in the text.

Fig.6.

Time domain comparisons between linear (thick lines) and nonlinear (thin lines) models for sinusoidal capillary and venous blood flow velocities oscillations (having periods T=10s). The amplitude of the oscillations is 50% of the baseline values. Left column refers to the capillary while the right column to the venous compartment. Top row represents the transit times, center row the oxygen saturation, bottom row the changes of oxy-hemoglobin concentration due to flow changes only. The baseline parameters used for the computation are listed in the text.

The calculation of oxyhemoglobin changes for the venous compartment shows also a slanted profile with clear temporal shifts (both at the points of maximum and minimum) with respect to the linear model. We also compared the changes of oxy-hemoglobin concentration associated with blood volume changes and we found negligible differences between the two models (results not shown).

3.2 CHS spectra

Since the CHS spectra are defined by the ratios of phasors associated with oscillations of oxy-, deoxy-, and total hemoglobin concentrations, we can predict that the discrepancies between the parameters calculated by the two models will be less than for the time domain case. We ran two sets of calculation by using the same baseline parameters used in the previous section. Even for the CHS spectra we considered one case of “small” (10% of the baseline value) and one case of “large” (50% of the baseline values) flow capillary and venous oscillations.

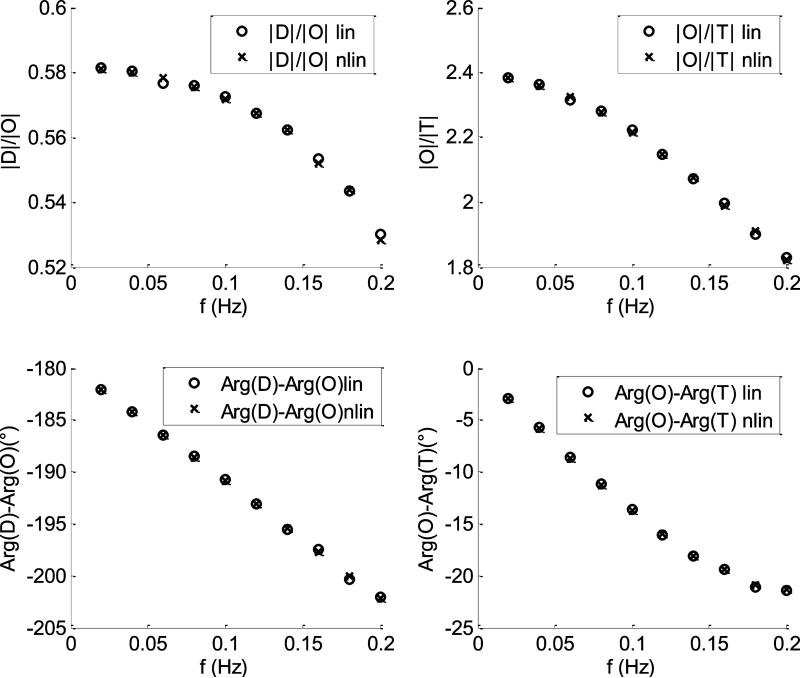
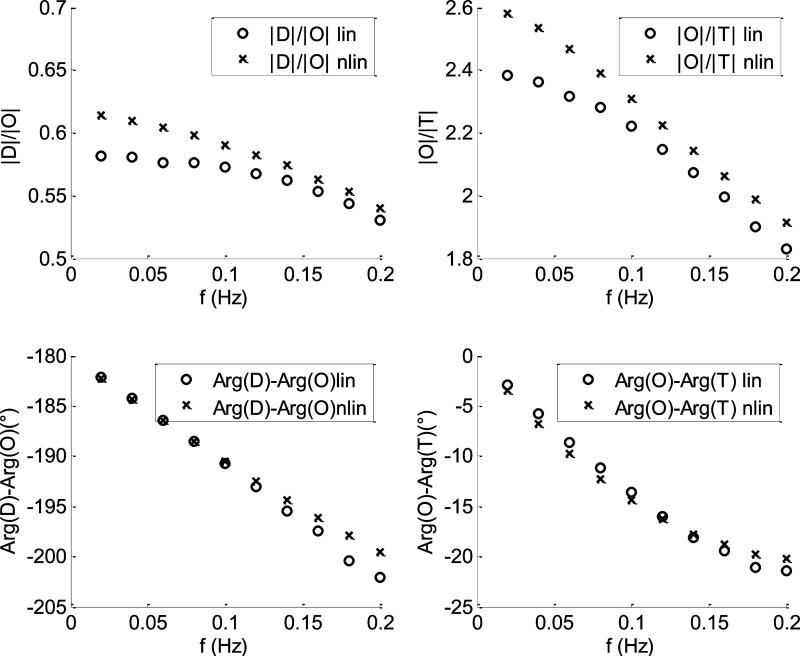
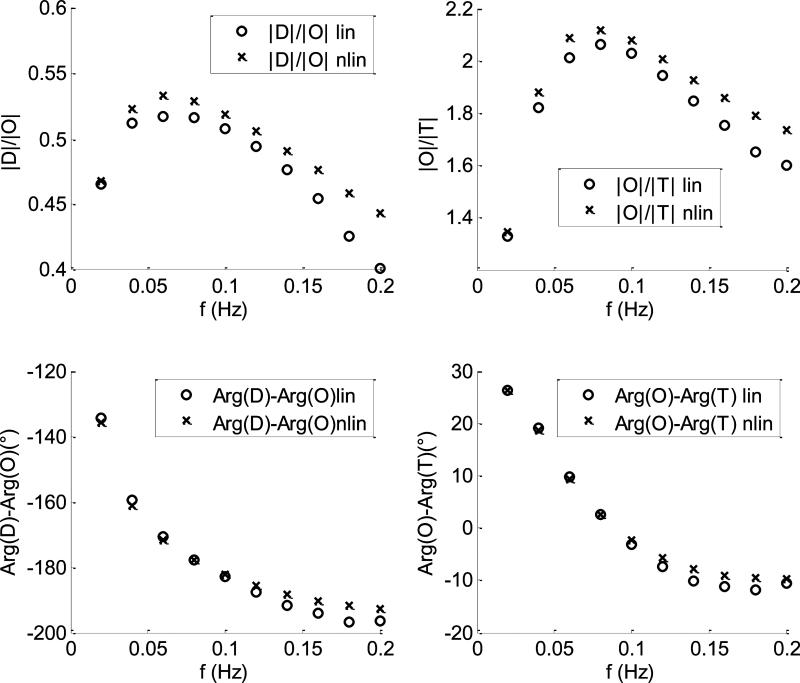
In Fig.7 are shown the comparisons between the CHS spectra calculated with the linear (empty circles) and nonlinear (crosses) models for the case of 10% flow oscillations in both capillary and venous compartments. The baseline parameters used by the two models are listed in section a). For this case the two models yield the same spectra with negligible discrepancies for all the four parameters. In Fig.8 the comparison between linear and nonlinear model was repeated by using the same baseline parameters of Fig.(7) for a case of 50% flow fluctuations in both capillary and venous compartments. For this case the two models start diverging: the discrepancies between |D|/|O| and |O|/|T| are less than 6% and 8%, respectively; the discrepancies between arg(D) – arg(O) and arg(O) – arg(T) are less than 3° and 2°, respectively. In Fig.9, we repeated the calculations of Fig(4) by changing the length and the transit time in the venous compartment $(L^{\left(v\right)}=6mm,t_0^{\left(v\right)}=3s)$ and the autoregulation cutoff frequency $f_c^{\left(\mathrm{AR}\right)}=0.04\mathrm{Hz}$. As we can see, the discrepancies between the two models are similar to those found in Fig.(8).

Fig.7.

CHS spectra calculated at ten different oscillations frequencies. The capillary and venous amplitudes of flow oscillations are 10% of their baseline values. The crosses and the empty circles refer to the nonlinear and the linear models, respectively. The baseline parameters of the models are listed in section a).

Fig.8.

CHS spectra calculated at ten different oscillations frequencies. The capillary and venous amplitudes of flow oscillations are 50% of their baseline values. The crosses and the empty circles refer to the nonlinear and the linear models, respectively. The baseline parameters of the models are listed in section a).

Fig.9.

CHS spectra calculated at ten different oscillations frequencies. The capillary and venous amplitudes of flow oscillations are 50% of their baseline values. The crosses and the empty circles refer to the nonlinear and the linear models, respectively. The baseline parameters of the models are those listed in section a) with the exception of $t_0^{\left(v\right)}=3s$, L^(v) = 6 mm, and $f_c^{\left(\mathrm{AR}\right)}=0.04\mathrm{Hz}$.

Discussion and conclusions

Coherent hemodynamic spectroscopy (CHS) is a promising new method for investigating physiological properties of living tissues which can be used by different neuroimaging modalities (Fantini 2014). In our previous studies (Fantini, 2014 a; Fantini, 2014 b) we have also proposed a hemodynamic model for the interpretation of the dynamics of oxy- and deoxy-hemoglobin concentrations in tissue measured by NIRS, in terms of changes in blood flow, blood volume and cerebral metabolic rate of oxygen. The proposed hemodynamic model is analytical, therefore less computationally cumbersome than other hemodynamic models proposed in NIRS.

The model was derived in the limit of “small” perturbations in capillary blood flow velocity and cerebral metabolic rate of oxygen. In this work we have relaxed the first assumption and extended the hemodynamic model, by proposing a general method for solving the partial differential equation governing the spatio-temporal behavior of hemoglobin saturation in a capillary and in a venule given arbitrary perturbations of the capillary and venous blood flow velocities. We refer to this extended model as the nonlinear model. The nonlinear model is based on the concept of time resolved partial transit time, which is a variable parameter defined at each coordinate x along the capillary (or venule) and at each observation time t. It defines the transit time spent by an infinitesimal blood element, which is found at time t at x, in the capillary (or venule). By using the concept of partial transit time it is possible to write in a concise way the general solution of the partial differential equation for hemoglobin saturation in the capillary and venule. Along the capillary, the hemoglobin saturation is described by an exponential decay law of the partial transit time, whereas, in the venule, the saturation changes only as the effect of the changing capillary blood flow velocity. However, each blood infinitesimal element that leaves the capillary and enters the venule is characterized by a constant value of the hemoglobin saturation. We have shown that the spatially averaged hemoglobin saturation in the capillaries and veins, which are directly connected with the concentration of hemoglobin in tissue, are expressed in a concise form by using the total time resolved transit times in capillaries and veins. We have also shown that, at least in principle, the concept of time resolved transit time can be used for expressing the dynamic of hemoglobin saturation in more complex topologies of blood vessels. For example, the hemoglobin saturation calculated in a point x which belongs to an n-th capillary, at the observation time t, depends on the transit times spent in the previous (upstream) capillaries calculated at specific times anterior to the observation time. This result is easily understood if we use a Lagrangian viewpoint of the desaturation process: if we calculate the hemoglobin saturation associated with an infinitesimal blood element moving along the capillary network we will find that it decays exponentially based only on the transit time spent in the capillaries, regardless of the topological intricacy of the network.

One of the purposes of this work was to carry out some preliminary comparison between the linear and nonlinear models both for “time domain data” (i.e. by comparing the temporal evolution of oxy- and deoxyhemoglobin concentration, given a sinusoidal capillary and venous blood flow velocities) and in the frequency domain by comparing the CHS spectra. More specifically, we wanted to test the performance of the linear model for a range of amplitude of perturbations in blood flow velocities. We restate that flow oscillations in CHS are due to induced systemic oscillations in blood pressure, therefore they differ from flow oscillations induced during brain activation, in terms of both origin and extent. During brain activation flow oscillations occur due to the mechanism of neurovascular coupling and it is not unlikely to measure flow changes in the range 30-50% (Fox and Raichle, 1986). However in CHS, blood volume oscillations are usually less than 2-4% (Kainerstorfer et al., 2015), therefore flow oscillations are less than 10-20% according to flow-volume relationship given by the autoregulation process. Also, we remind that the systemic pressure/flow oscillation in CHS are induced during equilibrium states of the tissue investigated (which can be either a baseline state or an “activation” state), in order to determine some underlying physiological properties in each state. Therefore, if we wanted to measure the “altered” physiological parameters during a brain activation state where blood flow has increased 50% with respect to the baseline value (therefore a shorter capillary transit times will be measured by our model), we would induce systemic flow oscillations (on top of the existing 50% flow oscillations) of a lesser extent. The amplitude of these induced oscillations (which is usually estimated less than 20%) should be used to test the linear versus the nonlinear model. Based on these arguments, the results presented in this work related to flow oscillations of 10% represent a typical situation found in CHS, while the results obtained for the case of 50% flow oscillations represent an extreme case (beyond what is induced in CHS) that we have studied in order to estimate a threshold in flow changes when the linear model shows discrepancies with respect to the nonlinear model. We have found that the performance of the linear model is different depending if we are studying the time domain parameters evolution (section 3.1) or the CHS spectra (section 3.2). In the time domain, where we compare the absolute changes of oxy- and deoxyhemoglobin oscillations, the discrepancies between the two models are already visible for perturbations larger than 10%. For example from Fig.6 (where the flow perturbation is 50%) we can see a discrepancy of about 40% for the change in oxy-hemoglobin concentration contributed by the capillaries and a noticeable phase shift of about 30° for the change in oxy-hemoglobin concentration contributed by the venules. These differences between the two models become much less pronounced when we compare the CHS spectra. This result is rather intuitive, since the parameters calculated in CHS are the ratios of amplitudes of oscillations of hemoglobin species and their phase shifts. In Fig.7, which is related to flow oscillations of 10% (typically found in CHS) we can see negligible differences between the linear and nonlinear models. From Fig.8 and Fig.9 it is clear that even for flow oscillations up to 50% (which are largely outside the range of CHS) the discrepancies between the two models are within experimental errors. We note that these discrepancies, as we can see from Fig.8 and Fig.9, are not random, therefore the linear and the nonlinear models might yield significantly different results when used as forward solvers in an inversion procedure.. Our inversion procedure (based on the linear model) retrieves six physiological parameters (Kainerstorfer, 2014), including the capillary and venous transit times, the autoregulation cutoff frequency and other static and dynamic parameters involving the blood volume in the three compartments and their perturbations. Therefore, we are planning more quantitative tests by using the linear model for the retrieval of these six parameters. For example the performance of the linear model can be tested by using a model-mismatched reconstruction: we generate CHS spectra by using the nonlinear model and we “invert” the data (in order to retrieve the six parameters) by using the linear model. For typical values of blood flow oscillations induced in CHS (~10%), based on the results presented in this work there are strong indications that the linear model would be adequate for retrieving the underlying physiological parameters. However, if the amplitude of induced hemodynamic oscillations exceeds the region of linearity, the proposed nonlinear model can be used in an inversion procedure and provides a more general solution to the quantitative analysis of CHS spectra.

Our novel CHS method, combined with the linear model for data analysis, has already shown encouraging results in human studies in vivo. For example, one of the physiological parameters retrieved by our inversion procedure is the autoregulation cutoff frequency (f_c; Eqs. (43) and (44)), which provides a quantitative measure of cerebral autoregulation. It is well known that hyperventilation induces hypocapnia and enhances the level of autoregulation in healthy and diseased human subjects (Steiner et al., 2005; Strauss et al., 1998; Møller et al., 2000), as well as in animal models (Ma et al., 2000). In a study on healthy human subjects, we have demonstrated that by using CHS and the linear model for data analysis not only could we retrieve values of the autoregulation cutoff frequency that are consistent with results reported with Doppler ultrasound (Diehl et al., 1995; Reinhard et al., 2006), but we also measured higher cutoff frequencies during hyperventilation, which is indicative of the expected enhancement in autoregulation (Kainerstorfer et al., 2015). Moreover we stress that, unlike measurements with Doppler ultrasound, our measurements of autoregulation reflect local autoregulation at the microcirculation level. These results are extremely promising and show the potential of CHS combined with the linear model of data analysis for assessing cerebral autoregulation. This method could have a significant impact on the management of patients with brain injury, which are affected by unpaired autoregulation (Steiger, 2005), and our work reported here provides a mathematical framework to extend our previous results to cases that may fall outside the limit of validity of the linear model for the analysis of CHS spectra. Other two directions of future investigations will focus on the effect of the rate of oxygen diffusion (α) which is mistakenly assumed constant by the current models. More refined models would have to consider that this parameter is not only spatially dependent (due to the hemoglobin saturation dissociation curve), but also temporally dependent on the dynamics of oxygen concentration in blood, which varies according to the dynamics of blood flow. However, since CHS spectra are based on relative measurements, it is likely that even a constant rate of oxygen diffusion (as assumed in this work) is an adequate approximation for modeling the CHS spectra. Finally, both the linear and nonlinear models can in principle be applied also for brain activation studies, as it is shown in our previous work (Fantini, 2014 a), where the changes in oxy- and deoxy-hemoglobin concentrations depend also on the cerebral metabolic rate of oxygen, which usually increases during brain activation. However during brain activation the relationship between blood volume and flow derived from the autoregulation mechanism (currently used by both models) may not hold, therefore other relationships will be investigated.

In summary, we have presented a non-linear extension to our mathematical model that aims to provide a deeper physiological and biological insight from in vivo NIRS data. Despite the enormous success of imaging techniques such as functional magnetic resonance imaging (fMRI) and NIRS, their measured quantities (the blood-oxygenation level dependent, BOLD, signal in fMRI, or the concentrations of oxy- and deoxy-hemoglobin in NIRS) are only indirect indicators of the physiological and biological processes of interest in the examined tissue (blood flow, blood volume, metabolic rate of oxygen, oxygen extraction fraction, autoregulation, etc.). In this work, we present a key step in our quest toward the translation of measurable signals with NIRS (and also fMRI) into the underlying biological and physiological processes that are really the target of biomedical imaging measurements. We have extended our original linear model for CHS to address two critical questions: “What is the range of validity of the linear model?”; “Can our proposed CHS approach be applied beyond the limit of validity of the linear model?”. The answers to these questions, as presented here, allow for the identification of the conditions of applicability of the linear model and provide a solution for the cases that fall outside of the linear approximation. Ultimately, this work paves the way for the practical application of our CHS technique in a variety of scenarios to better ascertain the physiological and biological meaning of NIRS data.

1. Coherent hemodynamics spectroscopy (CHS) quantifies hemodynamic oscillations

2. Near-infrared spectroscopy can measure CHS spectra in a variety of tissues

3. A linear hemodynamic model yields biological meaning of CHS spectra

4. A nonlinear model is presented here to treat cases beyond the linear approximation

5. Cerebral autoregulation and blood flow are among the processes assessed by CHS

Fig.3.

Schematic of a sequence of four blood vessels: one arteriole, two capillaries and one venule. The blood flow velocities are: $c^{\left(a\right)}\left(t\right),c_1^{\left(c\right)}\left(t\right),c_2^{\left(c\right)}\left(t\right),c^{\left(v\right)}\left(t\right)$ for the arteriole, the two capillaries, and the venule, respectively. The origin of the coordinate system is chosen at the beginning of the first capillary. $L^{\left(a\right)},L_1^{\left(c\right)},L_2^{\left(c\right)},L^{\left(v\right)}$ are the lengths of the arteriole, the two capillaries and the venule, respectively.

APPENDIX A

We want to prove that:

$$S^{\left(c\right)}(x,t)=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{o}}{t}_p^{\left(c\right)}(x,t)}$$ (A.1)

is the general solution of:

$$c^{\left(c\right)}\left(t\right)\frac{\partial S^{\left(c\right)}(x,t)}{\partial x}+\frac{\partial S^{\left(c\right)}(x,t)}{\partial t}=-{\alpha }_{\stackrel{.}{o}}{S}^{\left(c\right)}(x,t)$$ (A.2)

with the boundary condition: S^(c)(x = 0, t) = S^(a).

Let's calculate the partial derivatives of (A1) with respect to x and t. The derivative with respect to x includes $\frac{\partial t_p^{\left(c\right)}}{\partial x}$, which is the inverse of $\frac{\partial x}{\partial t_p^{\left(c\right)}}$. The latter can be calculated by using the definition of partial transit time $t_p^{\left(c\right)}(x,t)$ (Eq.(5)), and the definition of derivative as limit of the incremental ratio. By doing so, we obtain:

$$\frac{\partial t_p^{\left(c\right)}(x,t)}{\partial x}=\frac{1}{c^{\left(c\right)}(t-t_p^{\left(c\right)}(x,t))}$$ (A.3)

For the calculation of the derivative $\frac{\partial t_p^{\left(c\right)}}{\partial t}$, we fix the spatial coordinate x = x₀ and we use the rule of differentiation of the implicit function. In fact:

$$F\left(t,t_p^{\left(c\right)}\right)=x_0-{\int }_{t-t_p^{\left(c\right)}(x_0,t)}^t{c}^{\left(c\right)}\left(\tau \right)d\tau =0$$ (A.4)

Eq. (A.4) defines the implicit function $t_p^{\left(c\right)}(x_0,t)$. We rewrite Eq.(A.4) as:

$$F\left(t,t_p^{\left(c\right)}\right)=x_0-G\left(t,t_p^{\left(c\right)}\right)=0$$ (A.5)

where:

$$G\left(t,t_p^{\left(c\right)}\right)={\int }_{t-t_p^{\left(c\right)}}^t{c}^{\left(c\right)}\left(\tau \right)d\tau$$ (A.6)

By the rule of the differentiation of the implicit function we have:

$$\frac{\partial t_p^{\left(c\right)}}{\partial t}=-\frac{\frac{\partial G\left(t,t_p^{\left(c\right)}\right)}{\partial t}}{\frac{\partial G\left(t,t_p^{\left(c\right)}\right)}{\partial t_p^{\left(c\right)}}}$$ (A.7)

We have already calculated the denominator of Eq.(A.7) (which was done for calculating Eq.(A.3)):

$$\frac{\partial G\left(t,t_p^{\left(c\right)}\right)}{\partial t_p^{\left(c\right)}}=c^{\left(c\right)}(t-t_p^{\left(c\right)})$$ (A.8)

The numerator can be calculated by using the definition of derivative, as it was done for deriving Eq.(A.3):

$$\frac{\partial G\left(t,t_p^{\left(c\right)}\right)}{\partial t}=c^{\left(c\right)}\left(t\right)-c^{\left(c\right)}\left(t-t_p^{\left(c\right)}\right)$$ (A.9)

Therefore:

$$\frac{\partial t_p^{\left(c\right)}}{\partial t}=-\frac{c^{\left(c\right)}\left(t\right)-c^{\left(c\right)}\left(t-t_p^{\left(c\right)}\right)}{c^{\left(c\right)}\left(t-t_p^{\left(c\right)}\right)}=1-\frac{c^{\left(c\right)}\left(t\right)}{c^{\left(c\right)}\left(t-t_p^{\left(c\right)}\right)}$$ (A.10)

If now we substitute Eq.(A.1) into Eq.(A.2) and we consider the derivatives of $t_p^{\left(c\right)}$ with respect to x and t (Eq.(A.3), (A.10), we will find that Eq.(A.2) is satisfied.

APPENDIX B

We want to find a more convenient way to express the spatially averaged capillary saturation:

$$\langle S^{\left(c\right)}\rangle \left(t\right)=\frac{1}{L^{\left(c\right)}}{\int }_0^{L^{\left(c\right)}}{S}^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{o}}{t}_p^{\left(c\right)}(x,t)}dx$$ (B.1)

We define $t_p^{\left(c\right)}(x,t)=T$, therefore $\frac{dx}{c^{\left(c\right)}(t-t_p^{\left(c\right)})}=dT$. The lower and upper bounds of the integral are easily recalculated by considering that: x(T = 0) = 0 and x(T = t^(c)) = L^(c). Therefore Eq.(B.1) becomes:

$$\langle S^{\left(c\right)}\rangle \left(t\right)=\frac{1}{L^{\left(c\right)}}{\int }_0^{t^{\left(c\right)}}{S}^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{o}}\tau }{c}^{\left(c\right)}(t-T)dT$$ (B.2)

If we define a new variable: τ = t – T we obtain:

$$\langle S^{\left(c\right)}\rangle \left(t\right)=\frac{S^{\left(a\right)}}{L^{\left(c\right)}}{\int }_{t-t^{\left(c\right)}\left(t\right)}^t{e}^{-{\alpha }_{\stackrel{.}{O}}(t-\tau )}{c}^{\left(c\right)}\left(\tau \right)d\tau$$ (B.3)

APPENDIX C

We want to prove that:

$$S^{\left(v\right)}(x,t)=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}^{\left(c\right)}\left(t-t_p^{\left(v\right)}(x,t)\right)}$$ (C.1)

is the general solution of:

$$c^{\left(v\right)}\left(t\right)\frac{\partial S^{\left(v\right)}(x,t)}{\partial x}+\frac{\partial S^{\left(v\right)}(x,t)}{\partial t}=0$$ (C.2)

where the coordinate x belong to the venule: (x ∈ [L^(c), L^(c)+ L^(v)]) and the boundary condition is: $S^{\left(v\right)}(x=L^{\left(c\right)},t)=S^{\left(a\right)}{e}^{-{\alpha }_{\stackrel{.}{0}}{t}^{\left(c\right)}\left(t\right)}$. The total transit time in the venule and the partial transit time in the capillary are defined by Eq.(5) and Eq.(11), that here we rewrite as Eq.(C.3) and Eq.(C.4), respectively:

$$L^{\left(c\right)}={\int }_{t-t^{\left(c\right)}\left(t\right)}^t{c}^{\left(c\right)}\left(\tau \right)d\tau$$ (C.3)

$$x=L^{\left(c\right)}+{\int }_{t-t_p^{\left(v\right)}(x,t)}^t{c}^{\left(v\right)}\left(\tau \right)d\tau$$ (C.4)

We define $T(x,t)=t-t_p^{\left(v\right)}(x,t)$, therefore we have to calculate:

$$\frac{\partial t^{\left(c\right)}(x,T(x,t))}{\partial x}=\frac{\partial t^{\left(c\right)}(x,T(x,t))}{\partial T}\frac{\partial T(x,t)}{\partial x}$$ (C.5)

and

$$\frac{\partial t^{\left(c\right)}(x,T(x,t))}{\partial t}=\frac{\partial t^{\left(c\right)}(x,T(x,t))}{\partial T}\frac{\partial T(x,t)}{\partial t}$$ (C.6)

By using the formulas derived for APPENDIX A, we have that:

$$\frac{\partial t^{\left(c\right)}(x,T(x,t))}{\partial x}=-\left[1-\frac{c^{\left(c\right)}(t-t_p^{\left(v\right)}(x,t))}{c^{\left(c\right)}(t-t_p^{\left(v\right)}(x,t)-t^{\left(c\right)}\left(t\right))}\right]\frac{1}{c^{\left(v\right)}(t-t_p^{\left(v\right)}(x,t))}$$ (C.7)

$$\frac{\partial t^{\left(c\right)}(x,T(x,t))}{\partial t}=\left[1-\frac{c^{\left(c\right)}(t-t_p^{\left(v\right)}(x,t))}{c^{\left(c\right)}(t-t_p^{\left(v\right)}(x,t)-t^{\left(c\right)}\left(t\right))}\right]\frac{c^{\left(v\right)}\left(t\right)}{c^{\left(v\right)}(t-t_p^{\left(v\right)}(x,t))}$$ (C.8)

If we insert Eq.(C.1) into Eq.(C.2) and we use Eq.(C.7) and (C.8) we can prove our statement.