Multi-atlas Learner Fusion: An efficient segmentation approach for large-scale data

Abstract

We propose Multi-atlas learner fusion (MLF), a framework for rapidly and accurately replicating the highly accurate, yet computationally expensive, multi-atlas segmentation framework based on fusing local learners. In the largest whole-brain multi-atlas study yet reported, multi-atlas segmentations are estimated for a training set of 3,464 MR brain images. Using these multi-atlas estimates we (1) estimate a low-dimensional representation for selecting locally appropriate example images, and (2) build AdaBoost learners that map a weak initial segmentation to the multi-atlas segmentation result. Thus, to segment a new target image we project the image into the low-dimensional space, construct a weak initial segmentation, and fuse the trained, locally selected, learners. The MLF framework cuts the runtime on a modern computer from 36 hours down to 3-8 minutes – a 270× speedup – by completely bypassing the need for deformable atlas-target registrations. Additionally, we: (1) describe a technique for optimizing the weak initial segmentation and the AdaBoost learning parameters, (2) quantify the ability to replicate the multi-atlas result with mean accuracies approaching the multi-atlas intra-subject reproducibility on a testing set of 380 images, (3) demonstrate significant increases in the reproducibility of intra-subject segmentations when compared to a state-of-the-art multi-atlas framework on a separate reproducibility dataset, (4) show that under the MLF framework the large-scale data model significantly improve the segmentation over the small-scale model under the MLF framework, and (5) indicate that the MLF framework has comparable performance as state-of-the-art multi-atlas segmentation algorithms without using non-local information.

Graphical Abstract

Introduction

Magnetic resonance (MR) imaging of the brain is an essential diagnostic method in clinical investigation and an effective quantitate method in neurology and neurological research. To explore the complicated relationships between biological structure and clinical diagnosis as well as brain function, segmentation of anatomical structure on MR images has been widely used. Expert manual delineation (Crespo-Facorro et al., 1999; Tsang et al., 2008) has been regarded as “gold standard”. However, since manual segmentation is extremely resource consuming, automatic methods have been proposed to get robust and accurate segmentation (Cocosco et al., 2003; Van Leemput et al., 1999; Wells et al., 1996). Atlas-based segmentation, which uses a pairing of structural MR scans and corresponding manual segmentation, is one of the most prominent approaches.

In atlas-based segmentation models, an existing dataset (atlas) is spatially transferred to a previously unseen target image through deformable registration. Single-atlas segmentation has been successfully applied on some applications (Gass et al., 2013; Guimond et al., 2000; Wu et al., 2007). Yet, more recent approaches employ a multi-atlas paradigm as the de facto standard atlas-based segmentation framework (Heckemann et al., 2006; Rohlfing et al., 2004b). In multi-atlas segmentation, the typical framework is: (1) a set of labeled atlases are non-rigidly registered to a target image (Avants et al., 2008; Klein et al., 2009; Ourselin et al., 2001; Zitova and Flusser, 2003), and (2) the resulting label conflicts are resolved using label fusion (Aljabar et al., 2009; Artaechevarria et al., 2009; Asman et al., 2014; Asman and Landman, 2013; Coupé et al., 2011; Heckemann et al., 2006; Isgum et al., 2009; Sabuncu et al., 2010; Wang et al., 2013; Warfield et al., 2004).

Recently, learning based multi-atlas segmentation has emerged from the multi-atlas segmentation as a new family of methods. One field of study deals with the generation of a template library based on the limit set of manual segmentation such as the LEAP algorithm (Wolz et al., 2010) and the MAGeT Brain (Chakravarty et al., 2013). Other approaches used groupwise registration and iterative groupwise segmentation such as the MABMIS algorithm (Jia et al., 2012). A new algorithm exploited the strengths of both label fusion and statistical classification to get more robust segmentations (Weisenfeld and Warfield, 2011). Meanwhile, the widely used supervised machine learning algorithms have also been successfully employed - including, but not limited to, SVMs (Hao et al., 2014; Morra et al., 2010; Powell et al., 2008), random forest(Han, 2013; Zikic et al., 2014), artificial neural networks (Magnotta et al., 1999; Powell et al., 2008), logistic LASSO (Liao et al., 2012) and boosting (Morra et al., 2010).

Unfortunately, this robustness of multi-atlas segmentation comes at the cost of computational complexity (CC) since both typical multi-atlas approaches and the learning based methods rely on expensive non-rigid registrations or non-local correspondences calculation. Concisely, we define these two types of computational complexity as (1) the computational complexity of conducting non-rigid registrations (CCNR), and (2) the computational complexity of capturing non-local correspondences (CCNC).

To decrease overall computational complexity without compromising segmentation quality, new approaches have emerged to minimize CCNR. One of the most common methods is the atlas selection (Aljabar et al., 2009; Langerak et al., 2013; Langerak et al., 2010; Rohlfing et al., 2004a), which reduces the CCNR by keeping the most representative atlases. In recent years, researchers have even tried to eliminate the CCNR by employing non-local label fusion methods (Asman and Landman, 2013; Coupé et al., 2011; Rousseau et al., 2011; Wang and Yushkevich, 2013; Wang et al., 2013). However, the reduction of CCNR is typically accompanied with the large increase of CCNC. To minimize the CCNC further, other researchers have attempted to use the learning based scheme, which grasps the non-local correspondences offline (Han, 2013; Hao et al., 2014; Magnotta et al., 1999; Morra et al., 2010; Powell et al., 2008; Zikic et al., 2014). Once the model is well trained, it is able to be applied on the target image efficiently. However, these learning-based algorithms are still limited since the learning based model are applied and tested on homogenous small-scale dataset (typically less than 200 subjects from the same resource) without using a great deal of available heterogeneous data (from different resources e.g. different studies and scanners). As the results, the previous learning based schemes are mostly applied on segmenting single anatomical region or subcortical regions rather than whole brain. When applied on whole brain, non-rigid registration (high CCNR) is still essential to compensate the large inter-subject variation for the small size of the dataset.

In this paper, to eliminate both CCNR and CCNC, we propose the multi-atlas learner fusion (MLF) framework. Due to the large amount of training atlases used in our framework, we are able to provide more candidates for atlases selection and a larger training pool during the learning step, which leads to dramatically reduction of the total computational complexity when segmenting a target image. Particularly, the MLF framework has the following important characteristics.

1. 1. Efficient framework by using large-scale dataset. When the training dataset is large and representative enough (3464 images from 6 projects), the MLF framework is able to find the close trained AdaBoost learners (“close” means with the similar anatomy) for the target image. As a result, the MLF provides a high-speed learning based segmentation framework that only requires 3-8 minutes to segment a target image by totally eliminating the CCNR and CCNC.

2. 2. The elements of the framework are designed for the large-scale scenario. The PCA is used for low-dimensional projection, which eliminates the computational expensive pairwise similarity measurements (typically required by manifold learning approaches) for thousands of training data (even on larger data sets). The AdaBoost, combined with decision tree, has proved to be an extremely successful in two-class classification (the case this paper is investigating) and even described as the “best off-the-shelf classifier in the world”(Breiman, 1998). After the training procedure, 3464 AdaBoost learners were trained and a group of the closest learners (with smallest Euclidean distance on PCA low-dimensional space) were applied on each target image.

3. 3. Application of whole brain segmentation. The framework is trained and applied on the whole brain segmentation (133 labels) which is much more complicated than segmenting single anatomical region or subcortical regions.

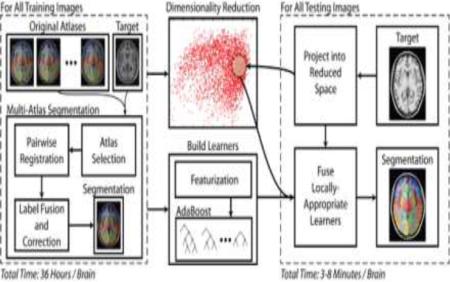
In the rest of the paper, we propose a whole-brain (133 labels) multi-atlas segmentation framework using a large-scale data paradigm. Building on seminal works in machine learning (e.g., AdaBoost (Freund and Schapire, 1995) and Principal Component Analysis – PCA), we use a learning-based approach to emulate the accuracy of a premier multi-atlas segmentation framework while dramatically lessening the computational burden. Given a large collection of training data which was pre-processed using a state-of-the-art multi-atlas segmentation procedure, we: (1) construct a low-dimensional representation of our training data for computing neighborhood relationships and (2) optimize an AdaBoost classifier for each training image that maps a weak segmentation estimate (e.g., a majority vote of the local neighbors) to the expensive, yet highly accurate, multi-atlas segmentation estimate. Thus, when a new target image needs to be segmented we simply need to (1) project the image into the low-dimensional space, (2) construct a weak initial segmentation, and (3) fuse the locally selected learners from the training phase. We refer to the algorithm as multi-atlas learner fusion (MLF) – Figure 1

Figure 1.

Flowchart demonstrating the multi-atlas learner fusion (MLF) framework. A large collection of training images are processed offline using a typical multi-atlas segmentation pipeline. The dimensionality of the training images is then reduced, and learners are constructed to map a weak initial estimate to the multi-atlas segmentation. Finally, for a new testing image, the image needs to be projected into the low-dimensional space and the locally appropriate learners can be fused to efficiently and accurately estimate the final segmentation.

Data and Pre-Processing

Herein, the complete data aggregates 7 unique datasets covering a wide range of demographics, ages, and neurological states (Table 1). Data from 1000 Functional Connectome (fcon_1000)(Biswal et al., 2010), Information eXtraction from Images (IXI), Open Access Series on Imaging Studies (OASIS)(Marcus et al., 2007) and Multi-Modal MRI Reproducibility Resource (MMMRR)(Landman et al., 2011) are publicly available. The Baltimore Longitudinal Study on Aging (BLSA) is the study of aging whose data are collected by the National Institute of Aging (Kawas et al., 1997). The Deep Brain Stimulation (DBS) data is obtained from the DBS project at Vanderbilt University (D'Haese et al., 2012). The Tennessee Twin Study (TTS) is an ongoing study that examines the health and wellbeing of twins born in Tennessee between 1984 and 1995 (Tackett et al., 2013). In total, a set of 3,505 subjects were scanned resulting in a total of 3,886 T1-weighted MR whole-brain volumes. For validation, the data was separated into three groups: training, testing, and reproducibility. First, the MMMRR dataset was used in its entirety as the reproducibility set as it consists of 21 subjects identically scanned twice. The remaining datasets were split 90%/10% into the training/testing cohorts. Note, all intra-subject scans were placed accordingly in the same training/testing group.

Table 1.

Data summary. Each value is represented by: number of subjects (number of images)

	Training	Testing	Repro.
1000 Functional Connectome (fcon_1000)a	1055 (1055)	117 (117)
Baltimore Longitudinal Study on Aging (BLSA)	578 (883)	64 (94)
Information eXtraction from Images (IXI)b	523 (523)	58 (58)
Deep Brain Stimulation (DBS)	493 (493)	54 (54)
*Open Access Series on Imaging Studies (OASIS)c	375 (392)	41 (44)
Tennessee Twins Study (TTS)	113 (118)	13 (13)
Multi-Modal MRI Reproducibility Resource (MMMRR)d			21 (42)
Total:	3137 (3464)	347 (380)	21 (42)

^ahttps://www.nitrc.org/projects/fcon_1000/

^bhttp://www.oasis-brains.org/

^chttp://biomedic.doc.ic.ac.uk/brain-development/

^*With OASIS, 6 subjects are used for simulation and 5 subjects are used for empirical validation.

In addition, 50 MPRAGE images (from unique subjects) from OASIS dataset were manually labeled with 133 labels by NeuroMorphometrics with BrainCOLOR protocol (Klein et al., 2010). 45 images (from 50 MPRAGE images) were used as the original atlases in multi-atlas segmentation (Marcus et al., 2007). Meanwhile, 6 randomly selected images (from 45 MPRAGE images) were used for a simulation test. Lastly, the 5 unused images (from the 50 MPRAGE images) were used for an empirical evaluation.

For all 3,886 images, a state-of-the-art multi-atlas segmentation was performed. For consistency, all images were affinely registered (Ourselin et al., 2001) to the MNI305 atlas (Evans et al., 1993). Practically, 10-20 atlases are sufficient for a good multi-atlas segmentation (Aljabar et al., 2009). Thus, also based on our experience, for each image, the 15 closest atlases were selected (using a naïve PCA projection), pairwise registered (Avants et al., 2008; Ourselin et al., 2001), fused (Asman and Landman, 2012, 2013), and corrected through implicit error modeling (Wang et al., 2011). On average, this process took 36 hours on a modern computer.

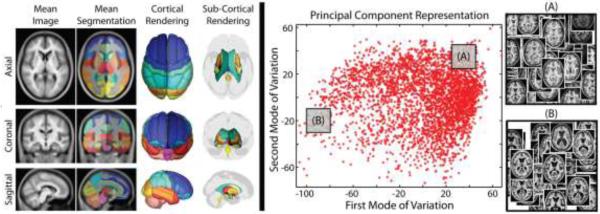
Finally, for all 3464 training images, a low-dimensional representation was computed using PCA. Briefly, whole brain anatomical images were down-sampled to 2mm isotropic resolution and only the non-background voxels were used for the PCA analysis. Such voxels were extracted from a non-background mask whose probability of non-background is greater than 0.8. The non-background probability is represented by a probabilistic map which is obtained by averaging the segmentations (set all non-background regions to 1 and background to 0) defined by the multi-atlas segmentation estimates. Local distances, the pairwise Euclidian distances between any two subjects on low-dimensional PCA domain, are computed using the projection weights onto the first 15 modes of variation (representing 15.33% of the total variation). Notice that the remaining variation (84.67%) might be introduced by the registration error and the large inter-subject variance of brain anatomy. The results of the pre-processing framework are summarized in Figure 2.

Figure 2.

Summary of the training data processed through multi-atlas segmentation and their corresponding representation in the estimated low-dimensional space. The inlays in (A) and (B) illustrate that the PCA distance metric leads to reasonable clustering of anatomical features.

Multi-Atlas Learner Fusion Theory

The theory presented below builds on the foundation for learning-based error correction presented in (Wang et al., 2011). For training image j , we assume that we are given (1) the target image, ${\mathit{I}}_j\in {\mathbb{R}}^N$, (2) the initial weak segmentation, Ψ_j ∊ L^N , and (3) the multi-atlas segmentation, ω_j ∊ L^N , where N is the total number of voxels, and L is the set of possible labels (herein, |L| = 133). As in (Wang et al., 2011), the AdaBoost training procedure is computed for all of the labels independently. For each label, let B_l , such that l ∊ L, be the collection of voxels for which any of the training images observe label l .

For the classifier, let the feature matrix be defined as ${\mathit{X}}^l\in {\mathbb{R}}^{M\times F}$, such that each element,$X_{mf}^l$, is the feature value for feature f at sample m and label l , where F is the number of features, and M ≤ |B_l| is the number of samples (or voxels). For simplicity, we define the features at each sample the same way as (Wang et al., 2011). Briefly, these consist of the voxel coordinates, the observed labels (i.e., all Ψ_ji s.t.i ∊ R_m), the target intensities (i.e., all I_ji s.t.i ∊ R_m), and the corresponding spatial correlations – where R_m is the collection of voxels within the feature window defined for sample (herein, a 5mm isotropic window centered at the current sample). This feature collection strategy results in a total number of features of F = 1009. Finally, we define the class vector as, Y^l ∊ {−1, 1}^M , where each element $Y_m^l=1$ if Ω_jm = l, and $Y_m^l=-1$ otherwise.

For the AdaBoost training, let ${\mathit{D}}_{jl}^{\left(t\right)}\in {\mathbb{R}}^M$, be the distribution of relative weights for all samples at iteration t ≤ (where $D_{jlm}^{\left(0\right)}=\frac{1}{M}$ initially). The goal of the training process at iteration t is to optimize the weak learner, h_jlt , where $h_{jlt}\left[X_m^l\right]\in \{-1,1\}$

$$h_{jlt}=\underset{h_{jlt}}{\arg \max }\mid 0.5-\sum _m{D}_{jlm}^{\left(t\right)}(1-\delta (h_{jlt}\left[X_m^l\right],Y_m^l))\mid$$ (1)

where, $\delta (\cdot ,\cdot )$ is the Kronecker delta function. Note, herein, the weak learner in (1) is a decision tree and optimization of this learner is addressed later in the manuscript. Next, the weight associated with the current iteration, ${\alpha }_{jlt}\in \mathbb{R}$, is defined as

$${\alpha }_{jlt}=\frac{1}{2}\ln \frac{1-{\sum }_m{D}_{jlm}^{\left(t\right)}(1-\delta (h_{jlt}\left[X_m^l\right],Y_m^l))}{{\sum }_m{D}_{jlm}^{\left(t\right)}(1-\delta (h_{jlt}\left[X_m^l\right],Y_m^l))}$$ (2)

and the sample weight can be updated with

$$D_{jlm}^{(t+1)}=\frac{1}{Z}\exp \left({\alpha }_{jlt}\delta (h_{jlt}\left[X_m^l\right],Y_m^l)\right)$$ (3)

where Z is a partition function ensuring that ${\sum }_m{D}_{jlm}^{(t+1)}=1$ This process is then iterated until we have reached the desired number of iterations, T (herein, T = 50).

Once the training process has been performed on all training images, we can then approximate the desired multi-atlas segmentation through fusing the trained AdaBoost learners associated with the corresponding locally selected training images. If we let J be the set of selected training images, and Ω* ∊ L^N be the approximated multi-atlas segmentation, then ${\Omega }_i^{\ast }$ (i.e., the estimated label at voxel i) is computed as

$${\Omega }_i^{\ast }=\underset{l\in L}{\arg \max }\sum _{j\in J}\sum _t{\alpha }_{jlt}{h}_{jlt}\left[X_i^l\right]$$ (4)

where the feature matrix, X, is defined in exactly the same way for the testing image as it was previously defined for the training images.

Methods and Results

Throughout, all segmentation comparisons are assessed with the mean Dice Similarity Coefficient (DSC) (Dice, 1945) across the 132 non-background labels, and all claims of statistical significance are made using a Wilcoxon signed rank test (p < 0.01) (Wilcoxon, 1945). In Figures 1 to 6, the DSC values were calculated in MNI305 space. To compare the label fusion results (in MNI305 space) with the manually labels images (in original space), in Figures 7 and 8, the DSC values were calculated in original space by affinely transferred the label fusion results to each subject's original space. Here, the 4×4 affine matrices were the inverse matrices which were generated during the affine registration in preprocessing.

low-dimensional representation

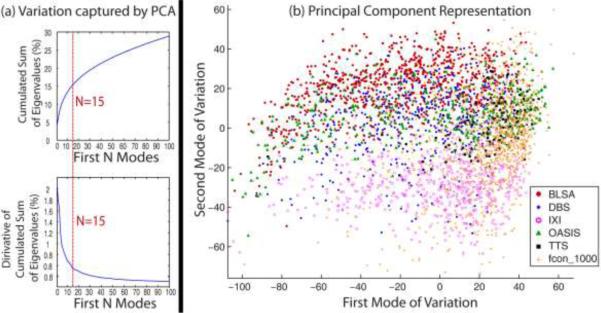
For the large-scale framework, it is time-consuming to find the closest leaners by calculating the similarity measurements between every testing subject and 3464 training images in the original image space. Thus, the low-dimensional representation is used for computational efficiency. In the MLF framework, we need to find the close (anatomically similar) trained learners for a target image by a low-dimensional representation of high-dimensional MRI image data. Linear models such as principle component analysis (PCA) (Pearson, 1901) and Multidimensional Scaling (MDS) (Torgerson, 1958) have been widely used to address this problem. In recent years, non-linear manifold learning algorithms like Isomap (Tenenbaum et al., 2000), Laplacian Eigenmaps (Belkin and Niyogi, 2003) and Local Linear Embedding (LLE) (Roweis and Saul, 2000) have also been successfully used in addressing the low-dimensional projection (Aljabar et al., 2008; Gerber et al., 2010; Wolz et al., 2010; Wolz et al., 2011). However, the typical non-linear methods require the computational expensive pairwise similarity measurements which is a heavy burden for datasets with thousands, or more, 3D images. Thus, to accommodate the large-scale scheme, the PCA is employed in the MLF framework. The first 15 modes of variation in the PCA are used as the low-dimensional representation as it offers a practical / pragmatic choice that has shown stable performance for the MLF framework. The chosen number of components represents a balance between capturing more variations and avoiding over-fitting (Figure 3A). However, we do not claim the optimality of the number of PCA low-dimensional representation from Figure 3A. To validate the usage of PCA, the widely used Laplacian Eigenmaps method is also evaluated in this paper. The comparisons are shown in the section “Empirical Validation”.

Figure 3.

(a) Total variation captured by first N modes from the PCA projection. The upper left figure shows the total variation captured by first N modes from the PCA. It's got from the percentage of the cumulated sum of the first N eigenvalues among all eigenvalues. The lower left figure shows the derivative of the upper left figure. (b) Coordinate embedding of 3464 training dataset from 6 projects. The first two modes in the PCA low-dimensional space are shown.

The first two modes of variation for PCA applied to the 3464 training images are shown in Figure 3B. As shown in the figure, the training images are densely distributed in the Eigenspace .As the results, locally closer trained learners are able to be found for a target image by the large-scale framework than the small-scale framework. Moreover, the images from different studies distributed differently in the Eigenspace, which means these studies are not redundant. Thus, a more representative training dataset is provided by the heterogeneous datasets.

Parameter Optimization and Sensitivity

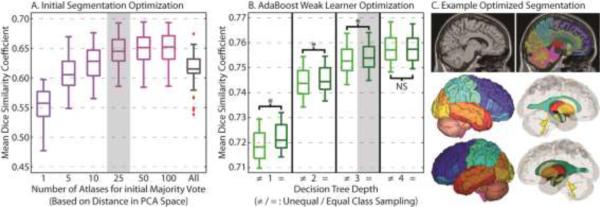
First, we optimize the number of locally selected atlases for the initial weak segmentation (via a majority vote). For optimization, the desired parameters were swept across an appropriate range for a random subset of 50 training images. The results can be seen in Figure 4. The Dice similarity values in the Figure 4 are computed by comparing the 50 segmentations from the AdaBoost classifier with the corresponding multi-atlas segmentations. For the initial majority vote accuracy (Figure 4A), using too few (e.g., 5) or too many (e.g., all available training data) results in sub-optimal accuracy. Additionally, there is marginal return when increasing the number of selected atlases beyond 25. Thus, as computation time is of primary concern, the closest 25 training images were used for all subsequent analysis.

Figure 4.

Parameter optimization and sensitivity for the number of atlases fused for the initial majority vote (A), and the type of weak learner used for the AdaBoost classifiers (B). A representative segmentation using the optimized parameters can be seen in (C). Note, on (B), “*” indicates statistically significant difference, and “NS” indicates no significant difference.

Second, we optimize the weak learner (decision tree) used in AdaBoost classifier. The decision tree works as the weak learner h_jlt for the image j, label i and iteration t. At iteration t, The decision tree is built based on the Classification And Regression Tree (CART) method (Breiman et al., 1984). Each node can be split into two child and the splits are determined by the maximizing the classification rate(Hastie et al., 2009; Quinlan, 1993). For the AdaBoost weak learner optimization (Figure 4B), we consider decision trees with depths ranging from 1 (i.e., a “decision stump”) to 4. Additionally, we consider two sampling methods, unequal and equal. For each label, the samples are the feature voxels from the training data (matrix X) and the corresponding true values (matrix Y) within pre-calculated regional masks. Each regional mask extracts the voxels with probability larger than 0 from its regional probabilistic atlas, which is obtained by averaging the regional segmentations from all the 3464 training segmentation images. For unequal sampling, all available voxels within the mask were used for each label, regardless of the resulting class imbalance between the positive class (Y = 1) and negative class (Y =-1). For equal sampling, a random subset from the larger class was selected to enforce class balance (the same number of samples in positive and negative class). Here, it is evident that (1) increasing the decision tree depth improves training accuracy, and (2) equal class sampling provides a marginal, yet significant, improvement in segmentation accuracy. Given the marginal return and dramatic runtime increase of a depth 4 decision tree, a depth 3 decision tree with equal class sampling was used for all subsequent experiments.

Testing Data Accuracy and Assessment

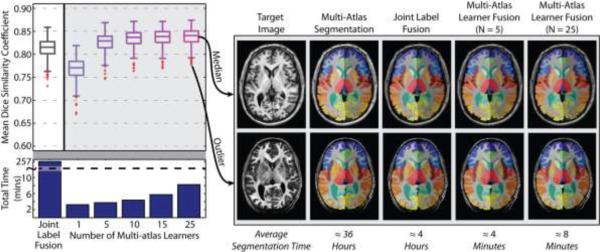
Next, we quantify our ability to replicate the expensive multi-atlas segmentation result using the MLF framework. Using the multi-atlas segmentation estimate on our testing data (380 images) as a “silver standard” we applied the MLF framework with varying numbers of local learners (from 1 to 25). The “silver standard” is the multi-atlas segmentations using both rigid and non-rigid registration (Avants et al., 2008; Ourselin et al., 2001) and Non-local Spatial Staple label fusion (Asman and Landman, 2013). As a benchmark, we consider fusing the 25 nearest training images using the premier joint label fusion (JLF) algorithm (Wang et al., 2013). More specifically, the multi-atlas segmentation uses typical “non-rigid registration + fusion” framework to (1) generate the training images, and (2) demonstrate the state-of-the-art multi-atlas segmentation performance with non-local information. Once we get the trained framework, the MLF only requires an affine registration when applying new subjects to the trained AdaBoost learners. To compare with the MLF, the benchmark JLF also uses “affine registration + fusion” framework, which guarantees the MLF and the JLF are in the exactly same condition except the label fusion. The results of this experiment across the 380 testing images (Figure 5) demonstrate: (1) increasing the number of local learners results in an improved ability to replicate the multi-atlas segmentation result, (2) using at least 5 learners results in significant and substantial improvement over the JLF benchmark, and (3) increasing the number of learners from 1 to 25 increases the total segmentation time from approximately 3 minutes to approximately 8 minutes – which remains a speedup of ≈30× over the JLF benchmark and ≈270× over the multi-atlas framework (shown in Table 2). In Table 2, we show the time consumed by registration and label fusion as well as the total time required for each framework. For multi-atlas segmentation, 15 non-rigid registrations were conducted for each testing subject. However, for the JLF and MLF, only 1 affine registration was required since all the training data and the trained AdaBoost learners had already been aligned to MNI space. The qualitative results support the quantitative accuracy analysis for both the worst and median cases from the testing set.

Figure 5.

Mean accuracy assessment for the defined testing data using the multi-atlas segmentation estimate as a “silver standard”. The results demonstrate (1) the MLF framework provides a dramatic decrease in total segmentation time, (2) increasing the number of fused learners has valuable benefits in terms of segmentation accuracy, and (3) when fusing more than 5 local learners the MLF framework provides substantial and significant accuracy benefits over the joint label fusion baseline.

Table 2.

Runtime of each method on an Intel Xeon W3550 4 Core CPU (64 bit Ubuntu Linux 12.04)

Methods	Time Consumed
	Registration	Fusion	Total
Multi-Atlas segmentation (with majority vote)	≈ 22 hours	≈ 5 min	≈ 22 hours
Multi-Atlas segmentation (with SS)	≈ 22 hours	≈ 2 hours	≈ 24 hours
Multi-Atlas segmentation (with NLSS)	≈ 22 hours	≈ 14 hours	≈ 36 hours
Joint Label Fusion framework	≈ 2 min	≈ 4 hours	≈ 4 hours
Multi-Atlas Learner Fusion framework (with 5 learners)	≈ 2 min	≈ 2 min	≈ 4 min
Multi-Atlas Learner Fusion framework (with 25 learners)	≈ 2 min	≈ 6 min	≈ 8 min

Reproducibility Data Accuracy and Assessment

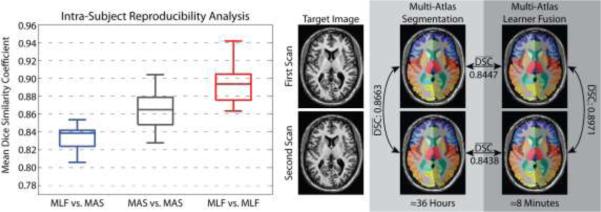
Then, we assess the reproducibility of the MLF framework using the MMMRR dataset (see Table 1). Within this dataset, all 21 subjects were scanned twice with exactly the same scanning parameters. All subjects are healthy without history of neurological disease. This dataset is intended to be a resource for statisticians and imaging scientists to quantify the reproducibility of their imaging methods using data available from a generic session at 3T. The intra-subject reproducibility was assessed by comparing the mean DSC for: (1) the MLF result vs. the corresponding multi-atlas result, (2) the intra-subject multi-atlas estimates, and (3) the intra-subject MLF framework estimates. The results (Figure 6) demonstrate: (1) the MLF similarity to the multi-atlas segmentation result approaches the intra-subject reproducibility for multi-atlas segmentation, and (2) MLF is significantly more reproducible than multi-atlas segmentation with a mean intra-subject DSC improvement of 0.0288.

Figure 6.

Reproducibility analysis on the MMMRR dataset. Note, (1) the MLF similarity to the multi-atlas segmentation result approaches the intra-subject reproducibility for multi-atlas segmentation, and (2)MLF is significantly more reproducible than multi-atlas segmentation on this dataset.

Efficacy of Large-scale Data Model

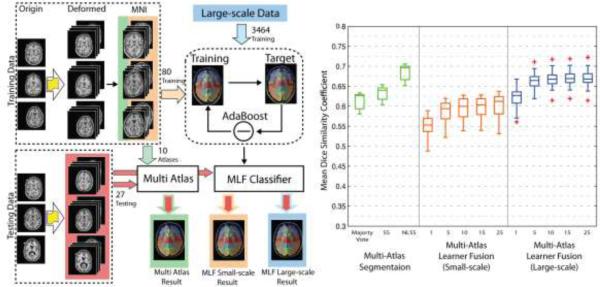
Next, we compare the efficacy of the large-scale data model with a small-scale model via a simulation. The purpose of doing simulation is to compare the performance using large-scale heterogeneous dataset with using small-scare homogenous dataset. Moreover, more independent training and testing datasets can be generated from the limited number of available truth atlases (with manual segmentations). To generate simulated data, we randomly selected 6 subjects from 45 atlases and divided them to 3 training subjects and 3 testing subjects. Then, a deformation was applied on the 3 training subjects to generate 90 deformed images and labels (30 for each subject) by sampling a sixth-order Chebyshev polynomial with random coefficients (Asman and Landman, 2013). In these 90 image-label pairs, 10 were used as atlases in multi-atlas segmentation for three label fusion algorithms: (1) majority vote (MV), (2) Spatial Staple (SS) (Asman and Landman, 2012) and Non-local Spatial Staple (NLSS) (Asman and Landman, 2013) while the rest 80 were used as training data for the MLF framework. Note that the multi-atlas segmentation (majority vote, SS and NLSS) uses the non-local registration while the MLF framework does not. Lastly, the 3 testing subjects were deformed to 27 testing images using the same method as 3 training subjects.

After getting the simulated data, we (1) applied multi-atlas segmentation algorithms on 27 simulated testing images using 10 simulated atlases, (2) trained the MLF framework by 80 simulated training image-label pairs and tested the MLF framework by 27 simulated testing images, and (3) evaluated the large-scale data model by running the 27 simulated testing images under the MLF framework which was trained by 3464 images (see Table 1). When testing the large-scale data model, for each testing subject, the same subject in large-scale training dataset was excluded to keep the testing procedure unbiased.

The results (Figure 7) show: (1) increasing the number of training data from 80 to 3464 results in significant improvement on the DSC, (2) with small-scale training data, the MLF framework performs worse than any of multi-atlas segmentation algorithms (majority vote, SS and NLSS), (3) with large-scale training data, the MLF framework (with 25 learners) provides significant improvement not only over the small-scale model but also over majority vote and SS, (4) the MLF framework with 25 learners performs less accurately than NLSS since the MLF framework does not use the non-local information which NLSS used. Therefore, the large-scale data model improves the performance of the MLF framework and achieves acceptable accuracy.

Figure 7.

Summary of the simulation and results. The flowchart shows the framework of the simulation: (1) 3 images were deformed to 90 simulated images and converted to MNI space by affine registration. (2) 10 of them were used as atlases for multi-atlas segmentation while 80 of them were used as training data for the MLF framework. (3) 3 images were deformed to 27 testing images for comparing the Multi-Atlas segmentation, small-scale model and big data model. The results demonstrate (1) the performance of the MLF framework is significantly improved when using big data model (3464 training images) and (2) the MLF framework under big data model provides the better performance than majority vote and SS even without using non-local information.

Empirical Validation

Lastly, we compare the performance of MLF framework with state-of-the-art multi-atlas segmentation algorithms by an empirical validation. To conduct the empirical validation, we employed 5 manually labeled subjects (with the same protocol as atlases but have not been used as atlases) from the 50 MPRAGE images as unbiased testing data. Note that these were obtained from the human raters after the conclusion of the algorithm training and development process. Since the testing dataset has the size n=5, all claims of statistical significance in this section are made using a Wilcoxon signed rank test (p < 0.05) which is the smallest significant level for n=5 (Wilcoxon, 1945).

Briefly, we conducted four types of analyses called Test-1, Test-2, Test-3 and Test-4. In Test-1, the multi-atlas segmentation pipeline is applied to 5 MPRAGE images with different label fusion algorithms: majority vote (MV), SS and NLSS (use 15 atlases from 45 MPRAGE images). In Test-2, the 25 nearest training images were selected by Laplacian Eigenmaps and then fused by the majority vote and JLF algorithm. Test-3 is the same as Test-2 except using the PCA for low-dimensional projection. Lastly, Test-4 applied the MLF framework with varying numbers of local learners (from 1 to 25). Note that Test-2, Test-3 and Test-4 use the same 3464 training images.

Overall, Test-1 has the highest CCNR among 4 groups. Test-2 is employed to compare the non-linear low-dimensional projection with the PCA used in Test-3. Test-3 serves as the benchmark to evaluate the performance of the MLF framework in Test-4.

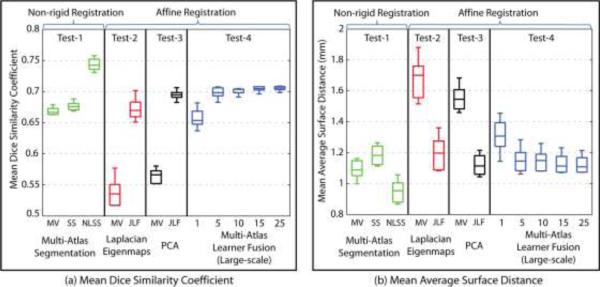
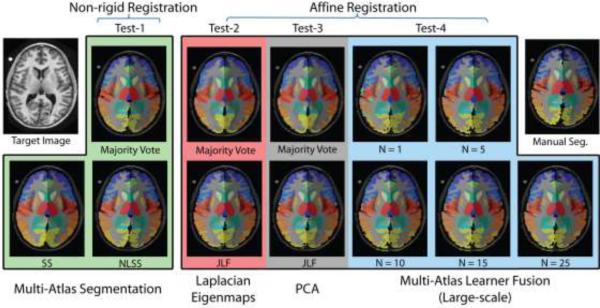
While providing a speedup of ≈30× over the JLF benchmark (Test-3) and ≈270× over the multi-atlas framework (Test-1), the segmentation quality of MLF framework (Test-4) is comparable with other methods. Dice similarity is used as the main metric of segmentation quality (Figure 8A). Meanwhile, the average surface distance (ASD) is used as a supplementary metrics (Figure 8B). Figure 9 compares different methods (same as Figure 8) by showing the same axial slice from one subject in the testing dataset. Here, we discuss the Dice similarity first.

1. Test-1 vs Test-4. We compare the MLF framework (Test-4) with three non-rigid registration based multi-atlas segmentation algorithms, majority vote, SS and NLSS (Test-1). The mean Dice similarity coefficients of the MLF framework (with 25 learners) are significantly higher than majority vote and SS. Meanwhile. Meanwhile, as shown in the simulation, the MLF framework with 25 learners performs less accurately than NLSS, which uses both non-rigid registration (high CCNR) and non-local correspondence (high CCNC). The results demonstrate the MLF framework (without CCNR and CCNC) provides significant improvement on Dice similarity over majority vote and SS (high CCNR) without using time-consuming non-rigid registration algorithms.

2. Test-3 vs Test-4. The comparison is conducted between the MLF framework (Test-4) and two benchmarks, majority vote and JLF (Test-3) which both use the same affine registration. Notice that the majority vote here is applied on the 25 atlases selected from 3464 training data (without CCNR). It is different from the majority vote in the multi-segmentations, which fuse the 15 non-rigid registered manual segmentations (in Test-1 with high CCNR). The MLF framework has significantly higher Dice similarity than the majority vote benchmark and has statistically indistinguishable Dice values comparing with the JLF benchmark. It proves that the MLF framework (without CCNR and CCNC), significantly outperforms the majority vote benchmark (without CCNR and CCNC) with the similar computational complexity. In addition, it has the comparable performance of JLF benchmark, which requires high CCNC to find non-local correspondences.

3. Test-2 vs Test-3, we compare the non-linear manifold learning method (Test-2) with the PCA method (Test-3) used in the MLF framework. The dataset used in Laplacian Eigenmaps is exactly the same as the one used for the PCA described in former sections. The closest subjects are selected based on the Euclidian distance of first 15 features in the Laplacian Eigenmaps. The Laplacian Eigenmaps is generated from the pairwise similarity measurements (normalized mutual information) between whole brain anatomical images. The results show that PCA performs significantly better than Laplacian Eigenmaps, which validates the usage of the PCA scheme. Even as validated, we do not claim any optimality of the PCA projection. Investigation into alternative low-dimensional projection methods could provide improvements.

Figure 8.

Results of empirical evaluation. The results indicate: without using non-local information, the MLF framework (large-scale) provides better performance than two multi-atlas segmentation algorithms (majority vote and SS) and has comparable performance as the JLF benchmark. Note that, the multi-atlas segmentation used “non-rigid registration + fusion” framework while the JLF and the MLF used “affine registration + fusion” framework.

Figure 9.

Example for one subject, which corresponds to the different methods in Figure 8. The anatomical and the manual segmentation of the target image are also provided.

The average surface distance (ASD) measurement repeats the finding in the Dice similarity except: (1) the smaller value is better for ASD, which is different from the Dice similarity, and (2) the mean ASD is not significantly smaller than majority vote in multi-atlas segmentation. However, it is still better than the SS. The similar results from the surface distance provide a more robust comparison than using Dice similarity only.

To summarize, (1) the empirical validation repeats the results in the simulation, (2) the MLF framework (without CCNR and CCNC) outperforms majority vote and SS in Dice similarity coefficients without using non-rigid registration (high CCNR), (3) the MLF framework has comparable performance as JLF benchmark without using resource consuming non-local correspondences (high CCNC), and (4) PCA and the Laplacian Eigenmaps have similar performance and PCA is a valid method under large-scale scenario.

Discussion and Conclusion

We present multi-atlas learner fusion (MLF), a framework for replicating the robust and accurate multi-atlas segmentation model, while dramatically lessening the computational burden. Using a training set of 3464 images, we estimate a low-dimensional representation of brain anatomy for selecting nearest appropriate example images, and build AdaBoost learners that map weak initial segmentations to the more accurate multi-atlas segmentation result. By completely bypassing the deformable atlas-target registrations, the MLF framework, cuts the runtime on a modern computer from 36 hours down to 3-8 minutes – a speedup that could be further enhanced through GPU-based optimization. Specifically, we: (1) describe a technique for optimizing the initial segmentation and the AdaBoost learning parameters (Figure 4), (2) quantify the ability to replicate the multi-atlas result with mean DSC of approximately 0.85 on a testing set of 380 images (Figure 5), (3) demonstrate accuracies that are approaching the intra-subject multi-atlas reproducibility on a separate reproducibility dataset, and show significant increases in MLF reproducibility (Figure 6), (4) show the advantage of large-scale data model by comparing small-scale training data with large-scale training data (Figure 7), and (5) indicate the performance of MLF is better than majority vote and SS and is comparable to state-of-the-art multi-atlas segmentation algorithm (the JLF framework) without using non-local information (Figure 8).

The results show the advantages of using large-scale data. Compared with the MLF framework under small-scale, the large-scale scheme improves the segmentation accuracy significantly. Compared with other state-of-the-arts multi-atlas segmentation methods, the MLF framework (without CCNR and CCNC) outperforms the typical multi-atlas frameworks (majority vote and SS) without using the resource consuming non-rigid registrations (high CCNR). Meanwhile, the MLF framework has comparable performance with the JLF benchmark (high CCNC). As a result, the MLF framework surpasses the expensive CCNR and CCNC, which speeds up the segmentation to 3-8 minutes without compromising on segmentation accuracy. With the availability of more training data (even the big data) the performance of the learning based large-scale framework could be further enhanced.

In the interest of brevity, all of our comparisons have been against the standard pairwise registration framework for multi-atlas segmentation, and have not included the more recent advancements in groupwise registration (e.g., (Jia et al., 2012)). The primary reason for not directly including this comparison is: (1) groupwise registration is still a very active area of continuing research, and (2) the MLF framework is, in its essence, a machine learning perspective on the groupwise registration model. Meanwhile, since the simulated data and empirical data were manually labeled by the same protocol (BrainColor), the effect of inter-protocol comparison has not been discussed in this paper.

The MLF framework is designed for the large-scale scenario so it does not perform well on small-scale dataset such as the 80 training dataset in the simulation. Meanwhile, although outside the scope of this paper, applying the MLF framework on other applications (e.g., spinal cord segmentation and abdominal organ segmentation) would be interesting research topics in the future. As the soft tissues structures are not well constrained by bone and tend to exhibit higher inter-individual variation, we cannot make the conclusion that the proposed method is able to be applied on abdomen organ segmentation directly. However, this learning based large-scale processing framework might trigger new methods in organ segmentation with more representative training images and more powerful registration and label fusion tools for whole abdomen.

In the end, while the MLF framework shows great promise for rapid and accurate multi-atlas segmentation, there are certainly areas for which further investigation is warranted. Namely, first, we used a naïve PCA projection to model the neighborhood relationships between the training images. The proposed method is an open framework, which is able to incorporate with other algorithms. For example, the PCA and the AdaBoost algorithms could be replaced by any other low-dimensional projection methods and other two-class classifiers. More recent advancements in the manifold learning literature (e.g., (Gerber et al., 2010)) present fascinating opportunities for more accurately modeling these relationships. Second, while highly successful, we do not claim any optimality of our AdaBoost-based learners. Investigation into alternative classification techniques (e.g., (Criminisi et al., 2013)) could provide valuable improvements in segmentation modeling without dramatically altering the MLF framework.

Highlights.

• We build the multi-atlas learner fusion (MLF) framework for mapping weak initial segmentations to the more accurate multi-atlas segmentation.

• The MLF framework cuts the runtime from 36 hours down to 3-8 minutes.

• We demonstrate significant increases in the reproducibility of intra-subject segmentations

• We show the large-scale data model significantly improve the segmentation over the small-scale model under the MLF framework

• The MLF framework has comparable performance as state-of-the-art multi-atlas segmentation algorithms without using non-local information