Right-Sizing Statistical Models for Longitudinal Data

Abstract

Arguments are proposed that researchers using longitudinal data should consider more and less complex statistical model alternatives to their initially chosen techniques in an effort to “right-size” the model to the data at hand. Such model comparisons may alert researchers who use poorly fitting overly parsimonious models to more complex better fitting alternatives, and, alternatively, may identify more parsimonious alternatives to overly complex (and perhaps empirically under-identified and/or less powerful) statistical models. A general framework is proposed for considering (often nested) relationships between a variety of psychometric and growth curve models. A three-step approach is proposed in which models are evaluated based on the number and patterning of variance components prior to selection of better-fitting growth models that explain both mean and variation/covariation patterns. The orthogonal, free-curve slope-intercept (FCSI) growth model is considered as a general model which includes, as special cases, many models including the Factor Mean model (FM, McArdle & Epstein, 1987), McDonald's (1967) linearly constrained factor model, Hierarchical Linear Models (HLM), Repeated Measures MANOVA, and the Linear Slope Intercept (Linear_SI) Growth Model. The FCSI model, in turn, is nested within the Tuckerized factor model. The approach is illustrated by comparing alternative models in a longitudinal study of children's vocabulary and by comparison of several candidate parametric growth and chronometric models in a Monte Carlo study.

Longitudinal research is increasingly prevalent given the ease with which multiple assessments may be collected using palm pilots, physiological measurements in the time domain, internet-based assessments, diary studies, and large-scale, frequently epidemiological longitudinal studies (see, e.g., the updated list at Longitudinal Study, 2015). In response, many statistical models have been developed for characterizing the timing and chronicity of change or growth. The sheer variety of available models, however, presents the researcher with challenges because there is often little guidance as to how to select the models most appropriate to the data at hand. Choosing models only because they demonstrate a favored effect, are the latest “cutting edge approaches” or have been traditionally employed in an area seem poor justifications. At the other extreme, some researchers appear to believe that model selection must occur prior to data collection and that any exploration of alternative models risks undue capitalization on chance. Such researchers often acknowledge but effectively ignore model misfit and focus discussion on the magnitude or statistical significance of particular parameters of the model. This approach is also less than optimal because it ignores the possibilities of either discovering more appropriate models or that the statistical significance of individual model parameters may be an artifact of fitting an inappropriate model.

By contrast, the structural equation models (SEMs) reported by researchers have often been not only selected, but changed during the course of analysis. This is especially true if the initially chosen model fits poorly, yields an improper solution, or is empirically under-identified. These changes often take the form of a (hopefully) small number of ad hoc modifications (Kenny, Kashy & Bolger, 1998; Kenny & Milan, 2013). Such approaches have their critics (e.g., MacCallum, 1986; Wood & Jackson, 2013), given the capitalization on chance involved when several modifications are employed. Additionally, ad hoc modifications overlook the existence of different classes of preferable alternative models.

Finally, some researchers have responded to this embarrassment of modeling riches by reporting only those effects which appear demonstrable across several statistical models. Such “vote by statistical model majority rule” ignores the possibility that a more complex model may permit more accurate estimation, possess greater statistical power or make more reasonable assumptions of the data. The “candidate field” of published statistical models, by contrast, is a far from systematically representative pool and several, if not most, of the candidate models may fit poorly.

Identification of a member of an appropriate class of models may be more informative than evaluation of one initially-chosen model. For example, Hussong, Curran, Moffitt, and Caspi (2008) wished to compare a “general deviance” model with prospective “snare” and “launch” models of problem behaviors in a prospective study of young men. The linear slope “general deviance” model they fit to the data fit poorly even after ad hoc modification, which they interpreted as evidence against the existence of a general deviance factor in favor of the prospective “snare” and “launch” models. Wood and Jackson (2013) re-analyzed the data and found that when the data were analyzed as trait factors model with estimated mean effects not only were the solutions proper, they fit the data better than the proposed “snare” and “launch” models. Sometimes exploration of alternative models may seem obvious in benefit of hindsight. For example, in a reanalysis of Partridge and Lerner's (2007) longitudinal study of difficult infant temperament, Wood (2011) found that a nonlinear trajectory over time revealed a developmentally limited “terrible twos” period of difficult temperament for some children which fit the data better than the originally proposed model. By contrast, individual ad hoc modifications of model parameters may overlook the possibility of a simpler class of statistical models that provides a better summary of patterns of covariation consistent with the data.

There is No “Right” Model, but We May Determine Which Models are “Better.”

Consideration of more or less complex classes of alternative models highlights the importance of balancing the interplay of parsimony and fit in the process of modeling data, a process Rodgers (2010) has termed the “quiet methodological revolution.” As some of the hesitancy to explore alternative, possibly unanticipated, models appears to stem from philosophical, rather than statistical considerations, some philosophical comment appears warranted. As Karl Popper (1959; 1963; 1994) noted, we cannot inductively validate our models by gathering repeated observational data consonant with our theory nor can we prove our theories true by deducing observational systems from first principles. Rather, our awareness and definition of any problem (itself a “theory soaked” enterprise to use Popper's term) results in a tentative theoretical proposal or model. Our statistical models, as with any other class of scientific theory, are merely conjectures which have survived our initial attempts at critical counterargument or experimental attempts at refutation which may be refined or refuted in the presence of superior alternatives in the future (Wood, 2014).

The Evolutionary Epistemology of Statistical Models

The scientific value of considering radically different models is not new. Donald Campbell (1974) used the term “evolutionary epistemology” to refer to the “natural selection” process of successive conjectures and refutations of a theory and for the proposal, refinement, and eventual replacement of models in favor of better alternatives. Campbell argued for a broad search of candidate models, rather than minor ad hoc modifications, as a broad search increases the odds that a well-fitting, but radically different statistical model “mutation” will be identified. Within adversarial science, such novel, well-fitting models may also be initial conjectures in service of new theories of change and growth or may also be useful as an operationalization of an alternative narrative proposed by a reasonable skeptic. Before going into specifics regarding a strategy for comparison of classes of models, it is necessary to survey the historical and more recent development of growth curve and other longitudinal models.

Review of Growth Curve Models and Their Relation to Other Longitudinal Models

It is difficult to adequately acknowledge both the history and breadth of growth curve models given that they are so frequently considered in statistical research; see, however, Bollen's (2007) historical overview. Historically, early work was proposed by Potthoff and Roy (1964), Rao (1958), Scher, Young and Meredith (1960), and Tucker (1958). Subsequent work noted the relationship of growth models to earlier factor models (Browne, 1993; Chan, 1998; McArdle & Epstein, 1987; Meredith & Tisak, 1984; 1990). Several papers have noted that specific choices regarding the scaling of time permits the expression of growth curve models as longitudinal hierarchical linear models (HLM's) and that choice of numerical values for this scaling affects the estimated covariance between slope and intercept factors (Biesanz, Deeb-Sossa, Aubrecht, Bollen, & Curran, 2004; Curran, 2003; Mehta & Neale, 2005; Meredith & Tisak, 1990; Muthén & Curran, 1997; Rovine & Molenaar, 1998; Stoel & van den Wittenboer, 2003).

Expression of longitudinal statistical models as SEMs is also an informative way for understanding how measurement and error structure vary across models. Voelkle (2007) expresses several models (t-tests, repeated measures anova, and MANOVA) as structural models. This paper, and others (e.g., Liu, Rovine, & Molenaar, 2012; Meredith & Horn, 2001; Meredith & Tisak, 1990; Rovine & Molenaar, 2000) have noted that repeated measures analysis of variance can be expressed as an SEM.

Finally, recent work using SEMs to model growth has led to development of models which either integrate growth models with other SEMs or which propose new parametric growth models. For example, Alessandri, Caprara and Tisak (2012) propose structural models that merge latent curve analysis with state-trait models. Grimm and Ram (2009) represent the Richards, logistic and Gompertz parametric curve models using nonlinear constraints on the growth factor while including a random intercept component. Viewed broadly, SEMs for longitudinal data have historically highlighted equivalencies and extensions of traditional approaches while recent work extends such models to more refined articulations of the growth process.

“Right-Sizing Models”

The wide variety of statistical models for longitudinal data to be considered below represent different operationalizations of change and growth. This paper seeks to survey many of these with a formal emphasis on model comparison and articulation of model assumptions. At its most general level, models may be collectively considered (and at times directly compared) based on examination of a.) the number of latent variables (i.e., variance components) thought to underlie the data, b.) the patterning of factor loadings associated with the identified latent variables, and c.) the assumed measurement model relating the factors to the manifest variables of the study. Given that models of growth involve statements of level as well as covariation, this last step involves explicit operationalization of mean effects in the model. Some of the growth models considered are expressed in an equivalent orthogonal form, making it easier to compare such models with nested alternatives. Organization of statistical models according to these three aspects could be used as the basis for a general model search.

Three additional advantages are also evident from such an exposition. First, some promising alternatives appear to have fallen into unmerited disuse over the years (such as McDonald's 1967 linear factor model). Second, new models are identified which are intermediary between existing models and are as yet unexplored. Third, the strategy of imposing nonlinear constraints can be extended to accommodate a greater variety of parametric forms which, in addition to being yet more parsimonious, may lead to the conjecture of new theories of the growth process itself. Although all models considered here are based on longitudinal assessments with fixed measurement occasions, similar model comparison approaches could be adapted to research designs with unequally-spaced lagged assessments (McArdle & Woodcock, 1997), time-varying covariates (e.g., McCoach & Kaniskan, 2010), or unequally spaced assessments across individuals (e.g., Dang, Anderson, Tan, & Mazumdar, 2005).

Matrix Notation for Structural Models

Parameter estimates of the latent and measured variables of the model formulations presented below may be obtained from the observed means and covariances matrices of the data or from the raw data. Using Sörbom's (1974) conventions regarding Greek notation, the factor model including mean effects at the level of the ith individual observation is represented in the following two equations:

$$x_i=\mu +\Lambda {\xi }_i+{\epsilon }_i.$$ (1)

and

$${\xi }_i=\theta +{\eta }_i.$$ (2)

x_i is a column vector associated with a manifest variable across k measurement occasions for one individual. μ is a k by 1 column vector of intercepts (which take the same values across all individuals) that scale the manifest variables to their zero points, Λ is a k by f matrix of factor loadings (assumed to be the same across all individuals), ξ_i is an f by 1 vector of latent variable values, and ε_i is a column vector of k errors of measurement. θ is a column vector of f factor means (again assumed the same across individuals), and η_i is a column vector of f latent variable scores for the individual expressed as deviations from their respective factor means. Traditionally, the variance/covariance matrix Σ based on this model is given as (Sörbom, 1974, p. 230):

$$\Sigma =\mathrm{E}\left[(x_i-\mu -\Lambda \theta ){(x_i-\mu -\Lambda \theta )}^{\prime }\right]=\Lambda \Phi {\Lambda }^{\prime }+\Psi .$$ (3)

Φ represents the variance/covariance matrix of the latent variables and Ψ is a matrix of variances and covariances of the errors of measurement. Expected values of the observed manifest variables are given by:

$$E\left(x\right)=\mu +\Lambda \theta .$$ (4)

The factor model in equations 1 and 2 is not identified unless constraints are imposed on the variance components and intercepts. Although discussed in more detail in Sörbom (1974) and Jöreskog (1971), at a minimum, f² restrictions across Λ and Φ must be imposed to secure an identified solution. These may be accomplished by fixing a factor variance for each factor to 1, fixing the factor loading of a different manifest variable to 1 for each latent variable and, in the case of multiple factors, setting factor covariances to zero, setting selected loadings to equality, or setting an additional loading to zero for each successive factor beyond the first one. Additionally, the mean matrices μ and θ can accommodate at most k freely estimated parameters.

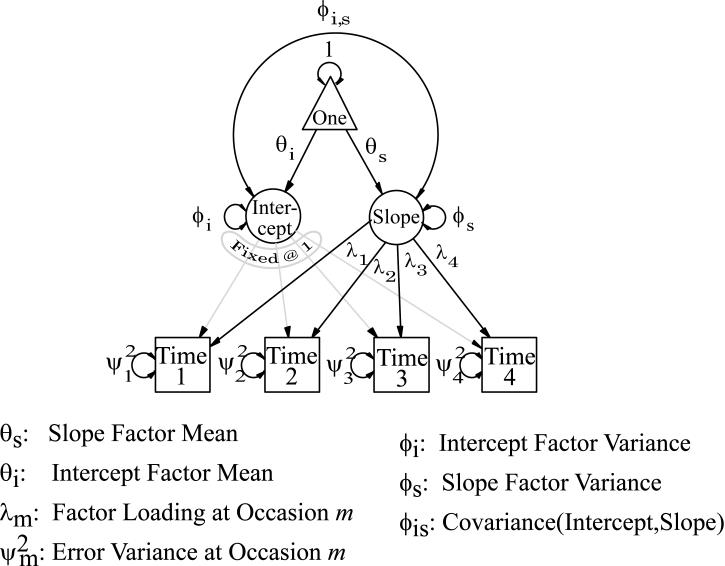
By patterning the Λ, Φ, Ψ, μ and θ matrices appropriately, a variety of structural models can be generated. For example, Figure 1 shows how this notation may be patterned for a class of models termed Slope Intercept models for those more familiar with path diagrams. At the most general level, models vary only in terms of the number of variance components needed to account for variation and covariation. At a more refined level, the possibility of further model parsimony is investigated by exploring whether specific patterns in the covariance components can be achieved by imposing functional forms or other constraints on the Λ, ϕ, or conceivably, Ψ matrices. At a third level, the possibility of yet more parsimony is explored by considering whether mean level effects over time can be patterned as well (either by patterns identical to that imposed on the variance components or via functional forms or constraints on the model intercepts, μ). These three sequential levels of analysis are consonant with the argument that model misfit due to covariance structure alone may be profitably considered separate from model misfit due to both mean and covariance structure (Liu et al., 2012; Wu, West, and Taylor, 2009). This hierarchy of model complexity may be used to identify specific “nearest neighbor” models to an initially selected model or, under Campbell's “distant relative” approach, may be used to navigate an hierarchical “family tree” of models from the top down.

Figure 1.

Path Diagram for Slope Intercept Growth Models.

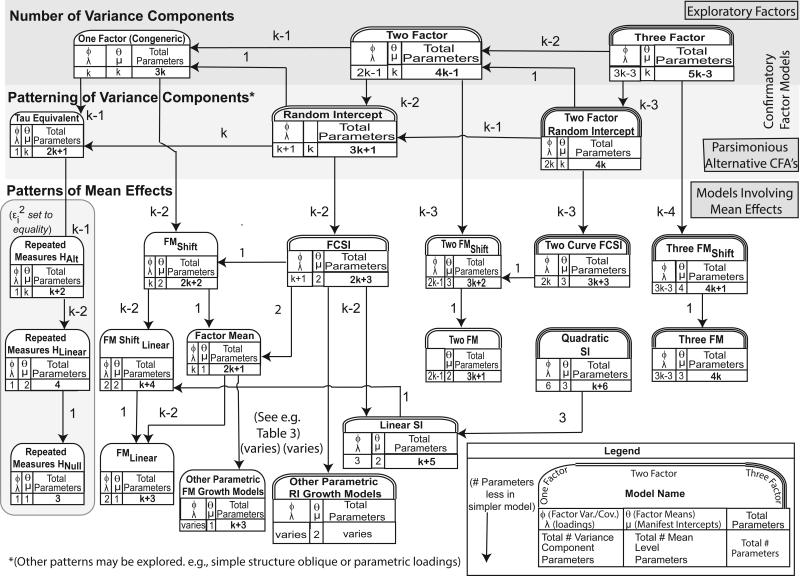
Specifically, Figure 2 shows how decisions about the appropriate SEM for longitudinal data can be divided into questions of the number of variance components, the patterning of loadings associated with these components, and the patterning of mean level effects in the data. For each model, the total number of parameters associated with the variance components (ϕ and λ) and the total number of parameters associated with mean level (θ and μ) are shown. Ψ is assumed to be a freely estimated diagonal matrix except for the repeated measures models, in which case the diagonal elements of Ψ are constrained to equality.

Figure 2.

Relationships Between Longitudinal Models.

Figure 2 can be used, then, to guide a three-step approach to “right-sizing” growth models when the researcher either wishes to explore the existence of other plausible well-fitting models or is simply agnostic about the form of growth. In the first step, only the dimensionality of the longitudinal data is explored via orthogonal confirmatory factor models. In the second, the researcher considers whether the dimensionality identified in the first step can be parsimoniously patterned (by considering, for example, oblique simple structure models or, alternatively, random intercept factor models [described below]). In the third step, the researcher considers whether these factors with patterned loadings can be used to model mean level effects by estimating mean level effects at the latent variable level with and without an estimated additive shift. We highlight this process of navigation in the real-world example discussed in the next section but mention again that if researchers wish instead to consider nearby neighbor to an initially chosen model, they can proceed by locating their chosen model in Figure 2 and fit alternatives which are slightly more or less complex.

Confirmatory Factor Models

If θ is defined as a zero vector and the vector μ freely estimated, suitable patterning of Λ, Φ, and Ψ results in an identified confirmatory factor model. As shown in the top row of Figure 2, at a basic level such models may vary in terms of the number of variance components which explain patterns of covariation in the data. For example, one way to express the single confirmatory factor model is to fix Φ to unity and freely estimate the k loadings, k (diagonal) error variances in θ, and k intercepts (μ), for a total of 3k estimated parameters. Other identification strategies involving Λ and Φ are possible that use the same number of estimated parameters (e.g., fixing a loading in Λ to 1 and allowing Φ to be freely estimated). The model labeled “One Factor” in the top row of Figure 2 summarizes the number of free variance component parameters in Φ and Λ, and number of mean level effects in μ and ν. The sum of these two numbers, plus the number of error variances in θ estimated yields the total number of parameters for the model. The Two Factor model (in the middle of the top row of Figure 2) can be estimated by fixing a loading in the second column of Λ to zero and Φ as a 2 × 2 identity matrix (yielding f² constraints, i.e., the fixed zero loading, and the three fixed values of the symmetric Φ matrix). The one-factor model is nested within this two-factor model with k-1 df, as shown in the arrow between these two models. Higher dimensional factor models such as the three-factor model shown at the right of the top row of the figure can, in turn, be estimated by extending this identification process of constraining successively more loadings in Λ to zero, and specifying Φ to be an identity matrix of suitable dimension.

Parsimonious Alternatives: Tau Equivalent, Random Intercept and Simple Structure Factors

Random Intercept factors are an alternative form of parsimonious patterning of Λ that is a component of many longitudinal models. Conceptually, models consisting of a single random intercept factor represent the measurement process as being in the same scale over occasions as operationalized by the equality of factor loadings. For the case of a single confirmatory factor, such a model corresponds to the familiar tau equivalent factor model (Lord & Novick, 1968) and is labeled as such in the left-most model of the second row of Figure 2. In this model, the k μ and k diagonal entries of Ψ are estimated as before. This results in k-1 fewer parameters than the One Factor model, as shown by the arrow. If Λ is fixed to unity with Φ freely estimated, an equivalent form results that more closely corresponds to one of the conditions for the compound symmetry assumption of repeated measures analysis of variance model.

It is also possible to consider whether a random intercept factor constitutes a parsimonious alternative model nested within the orthogonal Two-factor model described above. This model is termed the Random Intercept factor model (Maydeu-Olivares & Coffman, 2006), and consists of specification of both the single factor and tau-equivalent factor model that, for identification purposes, are assumed orthogonal. This model has k+1 freely estimated elements in Λ, k intercepts and k diagonal elements of Ψ making a total of 3k+1 freely estimated parameters. As shown in Figure 2, it has k-2 fewer free parameters than the Two Factor model. The One Factor and Tau Equivalent Factor model are nested within the Random Intercept model, with 1 and k degrees of freedom difference, respectively. When loadings associated with the random intercept factor are constrained to 1 and the variance of the intercept factor is freely estimated, the random intercept model is more readily related to growth curve models considered below.

This logic can be extended to specification of a Two Factor Random Intercept model (shown on the right of the second row of Figure 2) by either adding a Tau Equivalent factor to the two factor model or by suitably restricting a Three Factor model. As shown by the arrows, the Two Factor model is nested within the Two Factor Random Intercept model by a single degree of freedom and is in turn nested within the Three Factor model by k-3 degrees of freedom.

Alternatively, the researcher may wish to consider simple structure rotations of the factors as parsimonious factor models. Though the criterion of simple structure is often criticized in longitudinal models (see the discussion of the 2 FM model below), in some situations this may be appropriately made part of model comparisons. Although confirmatory factor models may be useful for assessing whether patterns of variation and covariation have been parsimoniously well-characterized, they make no assumptions about the patterning of mean change over time. The best fitting confirmatory factor model leads to conjectures as to whether such variance components can also be used to characterize mean level across occasions. We therefore turn now to models that achieve their parsimony by the number and patterning of both mean level and variation.

Models That Parsimoniously Explain Mean Effects

The models below the second row of factor models in Figure 2 seek (with the exception of the Repeated Measures H_Alt models) to achieve additional parsimony by estimating fewer than k mean parameters (θ and μ). As we will see, nested relationships between some models can be understood by equivalent re-parameterizations of a given model.

Repeated Measures Analysis of Variance

The presentation of repeated measures analysis of variance as an SEM has already been noted elsewhere (e.g., Meredith & Tisak, 1990; Rovine and Molenaar, 2000; Voelkle, 2007) and so will not be extensively discussed here except to note that it involves specification of a random intercept factor and equality of error variances across measurement occasions (as noted in the footnotes to Table 1 and Figure 2). The shaded vertical block of Figure 2 identifies those models which make this assumption. The alternate hypothesis of unequal means in repeated measures anova (“Repeated Measures H_Alt” in Figure 2) is nested within the Tau-Equivalent model with k-1 degree of freedom difference (due to the error variance equality assumption). An example of matrix specification for the case of a four-measurement study is shown in the fourth row of Table 1.

Table 1.

Matrix Notation and Parameters for Various Growth Models^a

Row	Model	Matrices
		Λ (factor loadings)	θ (factor means)	Φ (factor Var/Co var)	μ (Manifest variable Intercepts)
1	One Factor Model	$\left[\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_2\hfill \\ \hfill {\lambda }_3\hfill \\ \hfill {\lambda }_4\hfill \end{array}\right]$	[0]	[1]	$\left[\begin{array}{c}\hfill {\mu }_1\hfill \\ \hfill {\mu }_2\hfill \\ \hfill {\mu }_3\hfill \\ \hfill {\mu }_4\hfill \end{array}\right]$
2	Random Intercept	$\begin{array}{cc}\hfill 1\hfill & \hfill {\lambda }_1\hfill \\ \hfill 1\hfill & \hfill {\lambda }_2\hfill \\ \hfill 1\hfill & \hfill {\lambda }_3\hfill \\ \hfill 1\hfill & \hfill {\lambda }_4\hfill \end{array}$	$\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]$	$\left[\begin{array}{cc}\hfill {\varphi }_I\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$	$\left[\begin{array}{c}\hfill {\mu }_1\hfill \\ \hfill {\mu }_2\hfill \\ \hfill {\mu }_3\hfill \\ \hfill {\mu }_4\hfill \end{array}\right]$
3	Tau Equivalent/Repeated Measures HAltb	$\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \end{array}\right]$	[0]	[θI]	$\left[\begin{array}{c}\hfill {\mu }_1\hfill \\ \hfill {\mu }_2\hfill \\ \hfill {\mu }_3\hfill \\ \hfill {\mu }_4\hfill \end{array}\right]$
4	Respecified Repeated Measures HAltb	$\left[\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_1\hfill \\ \hfill {\lambda }_1\hfill \\ \hfill {\lambda }_1\hfill \end{array}\right]$	[0]	[1]	$\left[\begin{array}{c}\hfill {\mu }_1\hfill \\ \hfill {\mu }_2\hfill \\ \hfill {\mu }_3\hfill \\ \hfill {\mu }_4\hfill \end{array}\right]$
5	Repeated Measures HAlt Estimated Means Relative to Time 1b	$\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \end{array}\right]$	[θI]	[ϕI]	$\left[\begin{array}{c}\hfill 0\hfill \\ \hfill {\mu }_2\hfill \\ \hfill {\mu }_3\hfill \\ \hfill {\mu }_4\hfill \end{array}\right]$
6	Repeated Measures HLinearb	$\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \end{array}\right]$	[0]	[1]	$\left[\begin{array}{c}\hfill {\mu }_1\hfill \\ \hfill {\mu }_1+\frac{Tim{e}_t-Tim{e}_i}{Tim{e}_t-Tim{e}_1}({\mu }_t-{\mu }_i)\hfill \\ \hfill \cdots \hfill \\ \hfill {\mu }_t\hfill \end{array}\right]$ For Osborne & Suddick data: $\left[\begin{array}{c}\hfill {\mu }_1\hfill \\ \hfill (0.81{\mu }_1+0.19{\mu }_4)\hfill \\ \hfill (0.42{\mu }_1+0.58{\mu }_4)\hfill \\ \hfill {\mu }_4\hfill \end{array}\right]$
7	Repeated Measures HNullb	$\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 1\hfill \end{array}\right]$	[θI]	[ϕI]	$\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]$
8	Factor Mean (FM)	$\left[\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_2\hfill \\ \hfill {\lambda }_3\hfill \\ \hfill {\lambda }_4\hfill \end{array}\right]$	[θS]	[1]	$\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]$
9	Factor Mean Linear (FMLinear)	$\left[\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_1+\frac{Tim{e}_t-Tim{e}_i}{Tim{e}_t-Tim{e}_1}({\lambda }_t-{\lambda }_i)\hfill \\ \hfill \cdots \hfill \\ \hfill {\lambda }_t\hfill \end{array}\right]$ For Osborne & Suddick data: $\left[\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill (0.81{\lambda }_1+0.19{\lambda }_4)\hfill \\ \hfill (0.42{\lambda }_1+0.58{\lambda }_4)\hfill \\ \hfill {\lambda }_4\hfill \end{array}\right]$	[θS]	[1]	$\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]$
10	Factor Mean Shift (FM-Shift)	$\left[\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_2\hfill \\ \hfill {\lambda }_3\hfill \\ \hfill {\lambda }_4\hfill \end{array}\right]$	[θS]	[1]	$\left[\begin{array}{c}\hfill {\mu }_1\hfill \\ \hfill {\mu }_1\hfill \\ \hfill {\mu }_1\hfill \\ \hfill {\mu }_1\hfill \end{array}\right]$
11	Equivalent FM-Shift	$\left[\begin{array}{cc}\hfill 1\hfill & \hfill {\lambda }_1\hfill \\ \hfill 1\hfill & \hfill {\lambda }_2\hfill \\ \hfill 1\hfill & \hfill {\lambda }_3\hfill \\ \hfill 1\hfill & \hfill {\lambda }_4\hfill \end{array}\right]$	$\left[\begin{array}{c}\hfill {\theta }_I\hfill \\ \hfill {\theta }_S\hfill \end{array}\right]$	$\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$	$\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]$
12	Factor Mean Shift Linear (FM-ShiftLin)	$\left[\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_1+\frac{Tim{e}_t-Tim{e}_i}{Tim{e}_t-Tim{e}_1}({\lambda }_t-{\lambda }_i)\hfill \\ \hfill \cdots \hfill \\ \hfill {\lambda }_t\hfill \end{array}\right]$ For Osborne & Suddick data: $\left[\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill (0.81{\lambda }_1+0.19{\lambda }_4)\hfill \\ \hfill (0.42{\lambda }_1+0.58{\lambda }_4)\hfill \\ \hfill {\lambda }_4\hfill \end{array}\right]$	[θS]	[1]	$\left[\begin{array}{c}\hfill {\mu }_1\hfill \\ \hfill {\mu }_1\hfill \\ \hfill {\mu }_1\hfill \\ \hfill {\mu }_1\hfill \end{array}\right]$
13	Free Curve Slope Intercept (FCSI)	$\left[\begin{array}{cc}\hfill 1\hfill & \hfill {\lambda }_1\hfill \\ \hfill 1\hfill & \hfill {\lambda }_2\hfill \\ \hfill 1\hfill & \hfill {\lambda }_3\hfill \\ \hfill 1\hfill & \hfill {\lambda }_4\hfill \end{array}\right]$	$\left[\begin{array}{c}\hfill {\theta }_I\hfill \\ \hfill {\theta }_S\hfill \end{array}\right]$	$\left[\begin{array}{cc}\hfill {\varphi }_I\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$	$\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]$
14	Orthogonal Linear SI	$\left[\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill {\lambda }_1+\frac{Tim{e}_t-Tim{e}_i}{Tim{e}_t-Tim{e}_1}({\lambda }_t-{\lambda }_i)\hfill \\ \hfill \cdots \hfill \\ \hfill {\lambda }_t\hfill \end{array}\right]$ For Osborne & Suddick data: $\left[\begin{array}{c}\hfill {\lambda }_1\hfill \\ \hfill (0.81{\lambda }_1+0.19{\lambda }_4)\hfill \\ \hfill (0.42{\lambda }_1+0.58{\lambda }_4)\hfill \\ \hfill {\lambda }_4\hfill \end{array}\right]$	$\left[\begin{array}{c}\hfill {\theta }_I\hfill \\ \hfill {\theta }_S\hfill \end{array}\right]$	$\left[\begin{array}{cc}\hfill {\varphi }_I\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$	$\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]$
15	Equivalent Linear SI	$\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0.88\hfill \\ \hfill 1\hfill & \hfill 2.734\hfill \\ \hfill 1\hfill & \hfill 4.724\hfill \end{array}\right]\left(\text{Linear Growth}\right)$ $\left[\begin{array}{cc}\hfill 1\hfill & \hfill 6.066\hfill \\ \hfill 1\hfill & \hfill 6.946\hfill \\ \hfill 1\hfill & \hfill 8.80\hfill \\ \hfill 1\hfill & \hfill 10.79\hfill \end{array}\right]{\left(\mathrm{HLM}\right)}^{\mathrm{c}}$	$\left[\begin{array}{c}\hfill {\theta }_I\hfill \\ \hfill {\theta }_S\hfill \end{array}\right]$	$\left[\begin{array}{cc}\hfill {\varphi }_I\hfill & \hfill {\varphi }_{IS}\hfill \\ \hfill {\varphi }_{IS}\hfill & \hfill {\varphi }_S\hfill \end{array}\right]$	$\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]$

^aFor N observations, k measurement occasions (matrix examples show specification for k=4) and f factors.

^bFor Repeated Measures models, diagonal elements ψ assumed equal. For remaining models (including Tau Equivalent) diagonal elements of y assumed freely estimated

^c(Assuming Age at first measurement occasion is 1)

As Voelkle (2007) notes, it is also possible within such models to specify that the pattern of means follows a linear form, as shown in the model “Repeated Measures H_Linear” in Figure 2). In addition to Voelkle's strategy of using fixed numerical values, one can also fit this model by freely estimating two intercepts (say the first and final measurement occasion) and constraining the intercepts associated with measurement occasions between these two occasions to be time-scaled proportions of the elapsed difference between these two loadings. The sixth row of Table 1 illustrates this for the case of four equally-spaced measurement occasions.

The Repeated Measure H_Null model is a yet more restrictive repeated measures model fit by specifying that the intercepts are equal. The model may also be equivalently expressed by, for example, by imposing the additional constraint that the freely estimated Λ of the Repeated Measures H_Linear model are equal to each other or that the μ are zero but the θ is now freely estimated as shown in the seventh row of Table 1, making it nested within the Repeated Measures H_Linear model with 1 df.

Factor Means Model (FM)

The FM factor model is a One Factor Model in which μ are fixed to 0 and a factor mean, θ, is estimated instead. Although factor models with means are implicit in McDonald's (1967) linear factor model (discussed below), they were formally introduced to the field of psychology by Jöreskog (1971) and Sörbom (1974) and applied to growth by McArdle and Epstein (1987), who termed this the CURVE model. This model is also the single factor exploratory structural equation growth model considered by Grimm et al. (2013) as a follow-up to exploratory Tuckerized growth curve analysis. As noted by McArdle and Epstein (1987), it is possible to further constrain the FM model by imposing linearity constraints in Λ (their “Linear” model, p. 121). This may be accomplished either by fixing the Λ to numeric values and freeing the factor variance or, equivalently, fixing the factor variance to 1, freeing initial and final loadings and imposing linearity constraints on the remaining loadings as explained for the Repeated Measures H_Linear model above. This is shown in the ninth row of Table 1 and clarifies the nested relationship (with k-2 degrees of freedom) of the linear FM model within the FM model as shown in Figure 2.

In the FM model, the mean level at any given measurement occasion is explained only by the product of the factor mean and loading for that occasion. As such, it assumes that measurements have been conducted at a common ratio level of measurement, i.e., that a measurement occasion with a factor loading of zero must correspond to an observed mean of zero. Given that the scaling of continuous manifest variables in psychology is often somewhat arbitrary and that having “none” of the construct of interest may correspond to a non-zero number due to floor effects of assessment or coding, this model would seem unreasonable in many contexts.

Note also that the FM model cannot be used to document patterns of differential decline in scales consisting of positive numbers (i.e., decreases in mean level associated with increasing variability across individuals). By contrast, the FM_Shift (discussed below) and other random intercept models do not share this limitation as these models will be fit identically under addition of a constant across all individuals and occasions. Examples of such differential decline exist in the literature, however. For example, longitudinal studies of general psychological distress among undergraduates have found that entering freshmen report high average levels of psychological distress. Although average level of distress declines on subsequent occasions, much greater inter-individual variability in scores is observed as well (e.g., Sher, Wood, & Gotham, 1996). Such a pattern of differential decline can only be assessed with the FM model if scores are suitably transformed to negative values beforehand or estimated with the FM_Shift model described next.

Factor Mean with Shift (FM _Shift )

The FM_Shift model was originally termed the “Linear Factor Model” by McDonald (1967) who explained it as a traditional factor model with estimated θ in which each element of Λ consisted of a common parameter across all measurement occasions (an intercept) in addition to the usual λ for each manifest variable, thus making each loading appear similar to a linear regression model (i.e., the loading for the ith variable is expressed as λ+κ). The model can be estimated in this original form with any structural equation program that can accommodate nonlinear constraints. We refer to this model as the FM_Shift model, however, because it can also be thought of as a measurement model in which the manifest variables consist of ratio level measurements (i.e., measurements with a zero point) shifted by an unknown constant (κ in McDonald's notation). This shift can be estimated by constraining the μ to equality across variables, as shown in the tenth row of Table 1, a form which demonstrates the nested relationship (with k-2 df) of the FM_Shift model within the One Factor model. Alternatively, this shift can be estimated using a phantom intercept variable (i.e., an intercept latent variable with zero variance, but freely estimated mean), as shown in the eleventh row of Table 1. As shown in the twelfth row of Table 1, one can also equivalently express the FM_Shift model by constraining the loadings to be linear over time, resulting in the FMShift_Linear Model, a model intermediary between the FM_Shift and FM_Linear models.

Free Curve Slope Intercept (FCSI) Growth

The FCSI growth model is identical to the Random Intercept Factor Model described above, except that μ is assumed to be a zero vector and θ is freely estimated. It was, to our knowledge, first proposed by Meredith and Tisak (1984, 1990) where it was referred to as a “simple two curve model” (p. 115) and elsewhere as a “latent basis model” (e.g., Bollen & Curran, 2006; Grimm et al., 2013). To distinguish it from the other curve models considered here, we use the term “Free Curve Slope Intercept” as most descriptively accurate. It is worth noting that the FM_Shift model is nested within the FCSI by 1 degree of freedom (by excising the ϕ_i as shown in the eleventh row of Table 1). As noted by Meredith and Tisak, it is possible to specify this model via two equally well-fitting models. In its orthogonal form (shown in the 13th row of Table 1), no covariance between the random intercept and factor is assumed, meaning that the intercept factor mean is an estimate of overall level across all measurement occasions. Alternatively, one may specify an oblique form of the model by constraining one of the slope loadings in Λ to be zero with the covariance between the intercept and slope factors freely estimated. The resulting model then estimates the variability of a random intercept component at the ith measurement occasion and the estimated covariance between the intercept at that occasion and the growth factor. Other equivalent constraints for the model are also possible (e.g., McArdle & Woodcock, 1997).

Linear Slope Intercept Growth (Linear SI)

The Linear SI Growth model represents possibly the currently most widely used growth model. As with the FCSI model, μ is assumed to be a zero vector and the vector θ freely estimated. Often this model is estimated as an oblique model in which fixed numeric values are assigned to the column of Λ associated with the factor and the random intercept factor loadings are fixed to 1 as well. The factor variance, random intercept variance, and the covariance between them are specified as free elements in Φ (as shown in the fourteenth row of Table 1). This model can be seen as a special case of the FCSI model, however, if it is parameterized as the FCSI model described above, but with nonlinear constraints imposed on loadings to reflect the linear interpolation of intermediary measurement occasions between the two endpoints of assessment, as shown in the 15th and final row of Table 1. The Linear SI model is nested within the FCSI (with k-2 df) and, in turn, the FMShift_Linear model is nested within the Linear SI model (with 1 df) as shown in Figure 2.

Two Factor Growth Models

The Two Factor Mean with Shift (Two FM_Shift) model can be estimated by patterning the Λ and Φ as for the two factor confirmatory model, constraining the μ to equality across all measurement occasions, and freely estimating the vector θ. As with the FM_Shift model, the Two FM_Shift model assumes variables are measured in a common interval scale. To our knowledge, this model has not been used in any prospective study, but its use would seem warranted, given the dependence of the FM and Two FM models on the assumption of ratio level measurement. This model can be seen as nested within the two factor confirmatory model if the mean effects of the original two factor model are specified as composed of a μ set to equality across measurement occasions, θ freely estimated, and a phantom variable composed of a fixed zero variance and freely estimated loadings to k-3 of the manifest variables.

The Two FM model can be estimated by patterning the Λ and Φ as for the two factor confirmatory model, specifying the μ as zero, and freely estimating θ. This model is the two factor exploratory growth model considered by Grimm et al. (2013). Although confirmatory models are often specified parsimoniously in a simple structure, in which the manifest variables have loadings on only one factor, some (e.g., Tucker, 1958) have argued against simple structure as a criterion for factor loadings in prospective data. Wood (1992) has written a suite of SAS macros that can be used to rotate such solutions and Grimm et al. (2013) have illustrated use of these macros in two example data sets. As with the factor mean model with a single factor, however, this model cannot be used to document differential decline unless appropriately scaled to negative numbers (by estimating it as an FM_Shift or FCSI model with two rather than one slope factors).

Three Factor Models

The Three Factor Model is specified by freely estimating μ, λ's associated with the first factor freely estimated, λ's associated with the second factor having one zero loading and λ's for the third having two zero loadings, Ψ diagonal and freely estimated, Φ a three by three identity matrix and θ set to zero. The Three FM_Shift model is specified in identical fashion except that μ is constrained to equality, and θ is freely estimated. The Two Factor Random Intercept model has the same form of specification in Λ, Φ and Ψ as the Random Intercept Model, except that Λ contains a third column which is freely estimated except for one entry that is fixed to zero. The corresponding Two Curve FCSI is estimated the same way as the Two Factor Random Intercept model, except that μ is constrained to zero, with θ freely estimated. Degree of freedom differences between these models are shown in Figure 2.

The quadratic growth curve model has often been used as a (three factor) more complex alternative to the (two factor) linear growth slope intercept model. Although this is usually estimated by specifying fixed numeric values for the intercept, linear and quadratic loadings, it is possible to specify it using the nonlinear constraint strategy for linear forms outlined above, preserving a zero covariance between the intercept and slope factors, and specifying a third factor with free variance in which free covariances are estimated between it and the intercept and linear slope factors. This model fits the data as well as the traditional method, but makes it clearer that it is an elaboration of the Linear SI model with nonlinear constraints specified earlier. It is not, however, covariance nested within the orthogonal three factor model, due to the specification of freely estimated covariances of the quadratic factor with the intercept and slope factors and the constrained pattern of loadings in Λ. Analogous cubic polynomial models can also be specified as discussed in the Monte Carlo simulation below.

Other Variations

Although several models have been described above, they are only heuristic of a larger variety of similar models. One could, for example, explore whether the assumption of equality of measurement errors over time is warranted by the data or, as already noted, whether other error structures such as an autoregressive error structure, provide plausible alternatives (Braun, Kuljanin, and DeShon, 2013). Other parametric forms for growth may suggest themselves once the factor loadings are estimated as noted in Figure 2. We now turn to a brief examination of how this approach can be used to compare models in a real-world example.

Example: Longitudinal Change in Children's Vocabulary

Osborne and Suddick's (1967, 1972) longitudinal study of intellectual ability in 204 children is an apt exemplar for the model approach described here given its use in earlier analyses for the FM (McArdle & Epstein, 1987), SI growth, and more elaborate non-linear mixed models such as latent change models (Ferrer, Hamagami & McArdle, 2004; Ghisletta & McArdle, 2012). Briefly, data are selected from an original base of 110 African-American and 163 Caucasian children assessed on the Wechsler Intelligence Scale for Children ([WISC], Wechsler, 1949) during their first, second, fourth, and sixth grade years with the focal variable being the total WISC–R score at each of the four occasions. Average chronological ages of the children at each wave are shown below in the first column of Table 2. More information on these data is available from the original source and from McArdle and Epstein (1987).

Table 2.

Structural Models of Growth for Vocabulary Data^d

Parametere		Nested Growth Curves			Oblique FCSIf	Orthogonal SILinearc	SILinearc	HLMc	RMAlt	Random Interceptg	Linear Random Intercept
		FM	FM-Shift	FCSId
Factor Loadings	λ 1(Age=6.066)	4.08	5.44	3.61	0.00	5.21	0.00	6.07	0.00	3.35	3.85
	λ 2(Age=6.946)	5.72	6.42	4.84	1.23	5.90	0.88	6.95	7.77	4.73	4.66
	λ 3 (Age=8.80)	7.69	7.59	6.32	2.70	7.37	2.73	8.80	17.20	5.56	6.37
	λ 4(Age=10.79)	10.11	9.03	8.12	4.51	8.95	4.72	10.79	28.56	8.69	8.21
Factor Means	θ I	0.00	−24.69	−4.15	18.79	−18.63	19.94	−15.72	18.78	0.00	0.00
	θ S	4.67	7.99	6.35	6.35	7.41	5.88	5.88	1.00	0.00	0.00
Factor Variances	Φ I	0.00	0.00	18.55	31.59	3.28	30.37	3.43	51.27	21.39	17.95
	Φ S	1.00	1.00	1.00	1.00	1.00	0.63	0.63	0.00	1.00	1.00
Factor Covariances	ΦIS (corrIS)	0.00	0.00	0.00	3.61 (0.64)	0.00	3.83 (0.67)	0.31 (0.21)	0.00	0.00	0.00
Error Variances	ψ12=ψ22	12.30	9.70	8.30	8.30	12.22	12.20	12.20	13.81	8.11	8.52
	ψ 3 2	5.81	6.54	6.90	6.90	5.72	5.72	5.72	13.81	7.96	6.82
	ψ 4 2	17.23	18.86	15.89	15.89	18.35	18.35	18.35	13.81	10.54	15.79
Selected Fit Statistics
χ2 (df)		64.82 (6)	13.74 (5)	7.72 (4)	7.72 (4)	79.74 (6)	79.49 (6)	79.49 (6)	184.94 (8)	0.16 (2)	10.19 (4)
prob(χ2|Ho)		0.00	0.02	0.10	0.10	0.00	0.00	0.00	0.00	0.92	0.04
TLI		0.93	0.99	0.99	0.99	0.91	0.91	0.91	0.84	1.01	0.99
CFI		0.93	0.99	1.00	1.00	0.91	0.91	0.91	0.79	1.00	0.99
RMSEA (90% CI)		0.22 (0.17-0.27)	0.09 (0.04-0.15)	0.07 (0.0-0.14)	0.07 (0.0-0.14)	0.25 (0.20-0.30)	0.25 (0.20-0.30)	0.25 (0.20-0.30)	0.33 (0.29-0.37)	0.00 (0.00-0.05)	0.09 (0.02-0.16)
PRMSEA<=0.05		0.00	0.10	0.28	0.28	0.00	0.00	0.00	0.00	0.95	0.14
AIC		4917.58	4868.50	4864.48	4864.48	4932.50	4932.24	4932.24	5033.70	4860.92	4866.95

^dUnderlines denote fixed parameters in the model. Error variances for Waves 1 and 2 set to equality because of their near equivalence.

^eAverage age at testing given in parentheses. N=110

^fλ_S for slope factor shown, λ_i for intercept factor set to 1

^gManifest variable intercepts for Times 1-4=18.78, 26.55, 35.98, and 47.34, respectively.

Proposed Three-Step Approach

Given that only four measurement occasions were assessed, it is not possible to explore many confirmatory factor models for these data. The fit, though, of confirmatory one and two factor models to these data seem acceptable (CFI's and TLI's for both models >.99). Given the relatively small number of measurement occasions, in this context one of the analytic goals of model comparison is to assess whether psychometrically more complex or simpler models fit the data as well as the growth models traditionally proposed for the data. The random intercept factor model represents a statistically significant improvement over the single factor confirmatory model (χ²_diff(1)=8.29, p=.004) and its associated BIC (4900.74) is lower than that found for the single or two factor models (4903.71 and 4911.21, respectively), suggesting that a growth curve model which includes a random intercept component may be appropriate. If a parsimonious patterning of the random intercept factor model is further explored by constraining its factor loadings to follow a linear form, fit of the resulting linear random intercept factor model is worse (χ²_diff(2)=10.03, p=.007), however the BIC for the model is slightly better than the unconstrained random intercept model (4900.13), suggesting that the researcher may wish to entertain both the linear and unconstrained loading patterns as structures for explaining mean levels. Estimated parameters and other fit statistics for the Random Intercept and Linear Random Intercept models are shown in the right-most columns of Table 2. Under the general three step process outlined above the researcher would therefore next consider the Linear SI and FCSI models as candidate growth models. However, in order to the fit of “nearest neighbors” to the models originally proposed for the data we turn now to the FM and FM_Shift models.

Factor Mean (FM) Growth Model

The FM model was originally proposed for these data by McArdle and Epstein (1987) with parameter specification shown in the eighth row of Table 1 with resulting estimates and associated fit statistics shown in the column of Table 2 labeled “FM.” These values are similar to those reported by McArdle and Epstein; however, the model fits slightly better than reported there as it was decided here to free the error variances associated with times 3 and 4. As can be seen, the χ² statistic (χ²(6)=64.50, p<.0001) and other fit statistics indicate that the FM model fits poorly.

FM_Shift Model

As noted earlier, the FM_Shift model investigates whether adjusting the scores by an estimated additive constant would significantly improve fit. The matrix model for fitting the FM_Shift model to these data is shown in the tenth row of Table 1 with estimated parameters in the corresponding column of Table 2. This model represents a substantial improvement in fit over the FM model (χ_diff²(1)=51.08; p<.00001), although the χ² associated with the model is still statistically significant (χ²(5)=13.74; p<.02, as shown in Table 2). Given the sensitivity of the χ² test to non-normality, some might argue that values obtained for the CFI, TLI (both 0.99) indicate acceptable fit, however. Inspection of the parameter estimates associated with the FM_Shift model in Table 2 indicates that the value of the shift parameter needed to bring the scale into a ratio level scale is equal to −24.69 which suggests a score of 24.69 as a psychometric zero point of verbal ability for the scale. Factor loadings from the two models seem largely similar, although slightly larger in the FM_Shift model at the two earlier measurement occasions and slightly smaller at the last two times of measurement.

Free Curve Slope Intercept Model

Can it be thought that shifts in measurements at the individual level are a source of inter-individual differences, i.e., does the shift parameter itself vary from individual to individual? If, for example, some vocabulary items are more familiar to children from some ethnic or economic backgrounds than others, children may be likely to correctly answer such questions based on their background and not because of their verbal ability per se. Alternatively, some children may be uniformly more disposed to guess at answers across all measurement occasions than others or may score systematically higher across all occasions because of the fixed effect of level of some other variable such as maternal education. These possibilities correspond to Maydeu-Olivares and Coffman's (2006) interpretation of the intercept factor as a “method factor” in random intercept factor models which, in this case, appears responsible for differences in overall level across all measurement occasions. To some extent, the researcher may be able to further investigate the covariates responsible for these components or the identification of method effects provided suitable additional variables are available.

Recall that the FCSI model (row 13 of Table 1) is identical to the random intercept factor model (row 2 of Table 1) except that μ are constrained to zero and θ are freely estimated. For these data, the FCSI model appears to fit well, with a non-significant χ² statistic and the other fit statistics shown in the bottom half of the table. A χ² difference test comparing the FCSI with the FM_Shift model supports this conclusion as well (χ₁²=6.01; p=0.01). The AIC and BIC values are very similar to those obtained for the FM_Shift model, but slightly lower, indicating a marginally better fit. The p-value associated with the RMSEA was, as with the FM_Shift model not statistically significant (p=0.28) and the 90% confidence interval brackets 0. Taken together, although the fit indices of the FM_Shift and FCSI models are very similar, a reasonable skeptic may hold that variability exists in the intercept factor, indicating a preference for the FCSI model over the FM_Shift. As with the FM and FM_Shift models, recovered factor loadings (λ_i) in the FCSI model increase as a function of measurement occasion.

When the slope loadings from the FCSI are squared and added to the intercept variance, it is possible to calculate the proportion of variability in the manifest variable at each measurement occasion explained by the latent variables in the model. For these data, it appears that the proportion of variability due to the intercept and slope factors increases over the waves of the study (79.18%, 83.49%, 89.43%, and 84.17% for Waves 1 through 4 respectively). Similarly, the proportion of variability in the model which appears due to the slope relative to that explained by the intercept and slope factors also increases across measurement occasions (41.28%, 55.82%, 68.23%, and 78.05% across Waves 1 through 4, respectively).

Oblique FCSI Models

Researchers may wish, for conceptual reasons, to designate a specific measurement occasion as a reference point to mark a particular point of the developmental process under investigation. Under such models, it is assumed that all systematic variability between individuals at the referent measurement occasion represents differences conceptually distinct from the change processes represented by the growth trajectory. In this case, Φ₁₁, the variance of the intercept factor, is an estimate of the variation between scores at the measurement occasion associated with the zero slope loading in Λ.

The fit of the oblique FCSI in Table 2 is identical to that of the original FCSI model, which is unsurprising, given that it represents an oblique rotation of the orthogonal FCSI model. Obtained values for the slope variable are now different than the orthogonal FCSI model, however, due to the assumption that this slope represents change subsequent to the first measurement occasion. When the total predicted amount of variability due to the latent variables at each measurement occasion is calculated, the resulting proportions are identical to those of the orthogonal FCSI. Proportions of variability accounted for by the Slope factor are, however, much smaller, given that change is now defined as change relative to the observed variability between individuals at the first measurement occasion instead of the point of minimum intercept variability as in the FCSI (3.65%, 8.91%, and 18.01% for Waves 2 through 4, respectively).

Functional Form

More parsimonious models can be constructed from either the FM_Shift or FCSI models by assuming a parametric form for the loadings. Although the pattern of means does not suggest a pattern of growth similar to linear, quadratic or negative exponential curves, the small sample and small number of measurement occasions suggest that it may be profitable to consider whether it is reasonable to consider a model in which individuals’ growth follows a linear form. When the Linear Slope Intercept model is fit to these data (as shown in the column labeled “Orthogonal Linear” in Table 2), the fit of the model is poor, however. As pointed out in several of the articles mentioned above, this model is mathematically equivalent to the traditional Linear SI, and HLM, which are reported in their respective columns in Table 2. The RM_Alt Model, shown in column so labeled in Table 2 appears to represent the poorest fitting candidate model. As such, it seems that the FCSI or FM_Shift models appear most appropriate for these data based on examination of fit.

Monte Carlo Examination of Model Comparison

Although many models can be compared in terms of their parsimony and structure, this is no guarantee that such comparisons will necessarily succeed given differences in statistical power due to number of measurement occasions and sample size. Additionally, as noted earlier, the pattern of estimated factor loadings may be suggestive of one (or more) parametric forms, corresponding to a conjecture regarding the functional form of growth over time. To this end, we present results from a brief Monte Carlo study to illustrate how the proposed approach can be used to identify the correct dimensionality and form of change over time. Although the suite of Monte Carlo simulations presented here is of limited generalizability, the psychometric properties and effect sizes are chosen to be roughly illustrative of that found in studies of growth in order to make the following points: a.) The search procedure advocated here can be used to identify the psychometric form and dimensionality in the data; b.) Once the dimensionality is identified, a variety of more parsimonious parametric models can be compared; c.) as with structural modeling in general, use of larger samples and greater measurement precision enables better discrimination between candidate models and fewer estimation problems such as non-convergence.

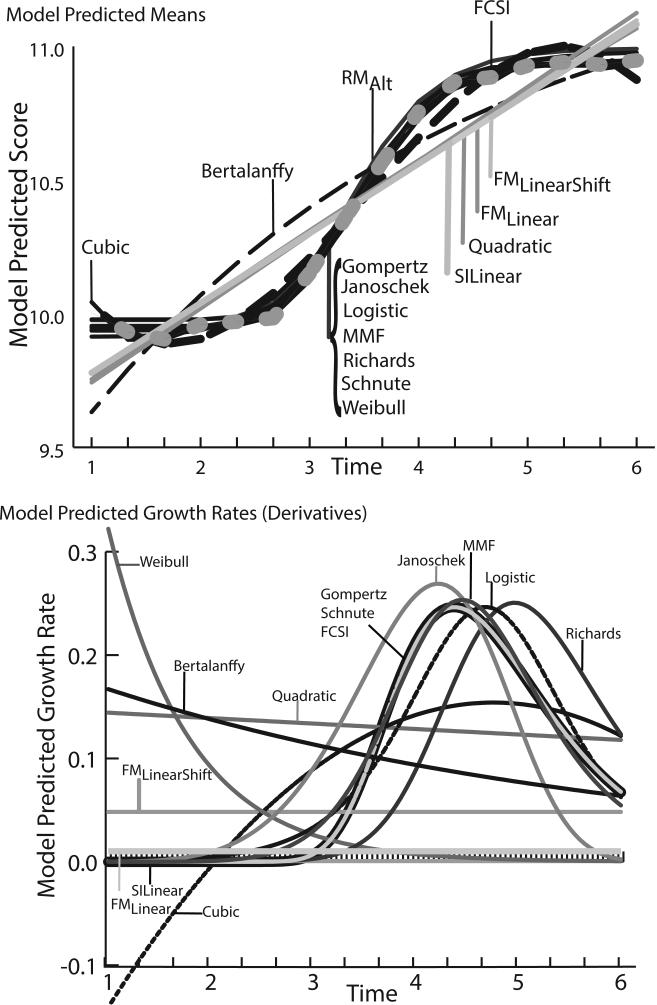
The top half of Figure 3 shows the random intercept Gompertz reference curve (Grimm and Ram, 2009) used to generate the data for our simulation as well as several other curves fit to the generated data. The Gompertz curve as the following form as a function of time t:

$$y_t=e^{-e^{-\alpha (t-\lambda )}}$$ (5)

with λ indicating the time at which maximum growth occurs, and α indicating a rate of change. We refer the reader to Grimm and Ram for a comparison of substantive merits of the Gompertz relative to other parametric curves other than to note that it contains an inflection point, indicating the maximum rate of growth over time and that the curve is asymmetric about this inflection point with 1/e of the total growth (about 37%) occurring before the inflection point with the remainder occurring afterward. The curve has found application, for example, in growth populations with confined space or limited nutrients. Masuyama, for example, (1979; 1985; 1988; 1991; 1992) notes that several growth processes including human stature appear to be “biphasic” with some individuals demonstrating an initially slower rate of growth accompanied by more rapid growth at later ages and vice versa. As such, the pattern of growth is different than for the more widely used logistic curve, which has a symmetric inflection point.

Figure 3.

Illustrative Candidate Growth Curves and Corresponding Growth Rates. FM = factor mean; FCSI = free curve slope intercept; MMF Morgan-Mercer-Flodin.

The several curves shown in top half of Figure 3 are fit to a single data set of 700 observations. Clearly, some of the curves do not show correspondence with the underlying curve, such as the SI_Linear, quadratic, and Bertalanffy growth curves, an observation supported by the fact that RMSEA fit for the models is greater than 0.10. Additionally, the cubic polynomial model also has an RMSEA greater than .05.

Such a visual examination, though, is insufficient to judge model fit, as it fails to consider patterns of predicted covariation over time. For example, despite the close pattern of predicted means, the FM_Shift, RM_Alt, and FM models all have RMSEA values in excess of 0.10, possibly because the assumptions regarding the structure of covariation are not met. Differences between the predicted growth rates of the various models are more evident when model predicted growth rates are considered (i.e., the derivative of each growth model with respect to a given time). These are shown in the bottom half of Figure 3 and show, for this single data set, that growth rates for the (true) Gompertz curve seem quite similar to that of the MMF, Schnute and FCSI, with the Janoschek, logistic and Richards curves being somewhat similar in form, and the von Bertalanffy, cubic, quadratic, and Weibull growth rates appearing quite different, visually. The remaining (linear) growth curves also appear dramatically different in form. This example suggests comparison of growth curves as SEMs is preferable to examination based on patterns of mean level alone.

To show how the factors of sample size and reliability of assessment are related to estimate candidate models and identify the correct model, we considered a study composed of six measurement occasions in which the intra-class correlation (ICC) of each time of measurement ranged from low to high (0.30, 0.55, 0.80, and 0.95). (The 0.80 scenario is somewhat similar to the WISC data, where the proportion of variability explained by the latent variables in the estimated FCSI model ranged from 0.80 to 0.89 across measurement occasions). The ICC = .95 scenario is similar to the reliability of the measurement of stature. The amount of change over time was chosen to reflect a one standard deviation change over the course of the study, an effect somewhat similar in magnitude to the amount of cognitive change over the undergraduate years (Pascarella & Terenzini, 2005) and indicative of what many would call a “large” effect size. Note that this is only approximately one quarter of that observed for the vocabulary data considered above, if the standard deviation of the initial measurement is used as a reference.

Individual random intercept Gompertz curves were generated in which the asymptote slope (a) was 1, the horizontal displacement (b) was −60, and the growth rate (c) set to −.6. θ_I was set to 10, θ_S to 1, and ϕ_I and ϕ_S were set to 1, and ϕ_IS to zero, resulting in manifest variables that demonstrated an average mean of 10 at the first time of measurement and average mean of 11 at the last time of measurement. Sample sizes were generated, some of which were small (N=25; 50) and others more moderate (from 100 to 700 in increments of 50.) To assure an adequate number of replications, 1000 data sets were generated in each condition. A variety of psychometric models were considered including traditionally used models (e.g., the SI Linear and Quadratic models), the psychometric and chronometric models proposed above (the FCSI, FM, FM_Shift, FMShift_Linear, FM_Linear, and Repeated Measures Null and Alternate models), and various nonlinear parametric models (described below). The parametric models were chosen from among several described by Panik (2014) commonly used in biology, demography, and ecology.

Rates of Non-Convergence

For ICC values of .5 or higher, convergence rates for these models across sample size and internal consistency were generally high, with solutions converging more than 80% of the time. For the lowest internal consistency condition (ICC=.3), the Richards curve converged only about 60% of the time, and, although the cubic curve specified with fixed loadings converged across all conditions, the orthogonal specification of the model converged only slightly over 80% of the time across conditions, suggesting the approach may be prone to local minima if internal consistency is low. For sample sizes of 25 and 50, convergence rates were slightly higher than 70% for the Linear SI, FM_Shift, FMShift_Linear, and Bertalanffy models. In terms of estimation, there is some reason for optimism that the FCSI model and associated nested models can be fit to longitudinal data using sample sizes typically employed in longitudinal research at least for large effect sizes. If extremely internally consistent constructs are assessed (e.g., ICC = 0.95), even very small sample sizes may be considered.

Model Comparison via BIC

Although comparisons of the FCSI model with other traditionally used longitudinal models appeared adequate for this scenario, the FCSI model may be criticized as being unparsimonious. The data were, after all, generated from a nonlinear parametric model (the Gompertz curve) with a random intercept component and, as such, were generated from a function with fewer parameters than the freely estimated loadings and associated parameters of the FCSI. This brings up the question of whether comparison of the FCSI model would be correctly rejected as unparsimonious relative to a more parsimonious parametric curve and whether the correct parametric form could be correctly identified from a plausible candidate field. Use of FCSI loadings to suggest a parametric form of growth was proposed in an example analysis by Meredith and Tisak (1990) in which loadings from a simulated unknown process were inspected to (correctly) conjecture the functional form (specifically a negative exponential curve, a form of the von Bertalanffy curve to be introduced shortly). In Table 3, we present a variety of such parametric growth models used in biology, ecology, agriculture, and medicine. In addition to the Gompertz curve, these include the Janoschek, Logistic, Morgan-Mercer-Flodin, Richards, Schnute, von Bertalanffy, and Weibull curves. In the interests of brevity, we will not discuss their merits and uses except to note that one important difference between models concerns whether they characterize growth as having an inflection point (a measurement occasion associated with change in the direction of curvature) and whether the rate of growth before and after the inflection point is symmetric. Some of these models are general cases of other models; For example, the Richards curve has, as special cases, the logistic and Gompertz curves; the Schnute model contains the von Bertalanffy, Richards, Logistic, Gompertz, and exponential growth curves as special cases. Other models have been advanced as particularly appropriate to growth when nutritional resources are in short supply (e.g., Morgan-Mercer-Flodin and Gompertz). Still other models, such as the Janoschek, are simply mathematically tractable ways of expressing a sigmoid shape. Note also in Figure 3 that the polynomial growth curves (SI_Linear, quadratic, and cubic) represent successively increasing approximations of the sigmoid form.

Table 3.

Sigmoid Growth Curves^h

Model	Matrices
	Model	Point of Inflection	Constrainti
Gompertz Curvej	$x_t=L_{\infty }{e}^{e^{-k(t-L0)}}$	Age at L	${\lambda }_t=e^{e^{-k(t-L)}}$
Janoschek	$\begin{array}{c}\hfill x_t=L_{\infty }+(L_{\infty }-L_0)e^{e^{-k{t}^{\delta }}}\hfill \\ \hfill (\delta >1)\hfill \end{array}$	${\left(\frac{\delta -1}{\delta k}\right)}^{\frac{1}{\delta }}$	${\lambda }_t=1-(1-L_0)e^{e^{-k{t}^{\delta }}}$
Logistic Curve	$x_t=\frac{L_{\infty }}{1+e^{-k(t-I)}}$	$\frac{L_{\infty }}{2}$	${\lambda }_t=\frac{1}{1+e^{-k(t-I)}}$
Morgan-Mercer-Flodin	$x_t=L_{\infty }-\frac{L_{\infty }-L_0}{1+{\left(kt\right)}^{\delta }}$	$\delta \sqrt{\frac{\delta -1}{\delta +1}}$	${\lambda }_t=1-\frac{1}{1+{\left(kt\right)}^{\delta }}$
Richardsk	$x_t=L_{\infty }\sqrt[1-\delta ]{1+(\delta -1)e^{-k(t-\gamma )}}$	γ	${\lambda }_t=\sqrt[1-\delta ]{1+(\delta -1)e^{-k(t-\gamma )}}$
Schnute	$x_t-L_{\infty }{(1-\delta e^{-at})}^{\frac{1}{b}}$	$\frac{1}{a}\left(ln\frac{\delta }{b}\right)$	${\lambda }_t={(1-e^{-at})}^{\frac{1}{b}}$
von Bertalanffyl	$x_t=L_{\infty }(1-e^{k(t-t_0)})$	None.	λt = 1 - ek(t)
Weibull	$x_t=L_{\infty }-\frac{L_{\infty }-L_0}{e^{{\left(kt\right)}^{\delta }}}$	$\left(\frac{1}{k}\right)\delta \sqrt{\frac{\delta -1}{\delta }}$	${\lambda }_t=1-\frac{1}{e^{{\left(kt\right)}^{\delta }}}$

^hupper asymptote, k=growth rate, I=age at inflection point, t₀ is age at which growth is zero, L₀ is lower asymptote.

ⁱAssuming L₀=0 and L_∞ = 1.

^jSame as von Bertalanffy curve, except that ln(x) replaces x in the derivative of the function.

^kNote if δ is zero, this becomes von Bertalanffy curve.

^lNote that for the case of a final growth value of 1 and an age of zero indicating a zero size, the von Bertalanffy curve is equal to the negative exponential. This curve is also equal to the Brody curve if initial size is zero and terminal size is 1.

Comparison with Linear SI, quadratic and cubic growth

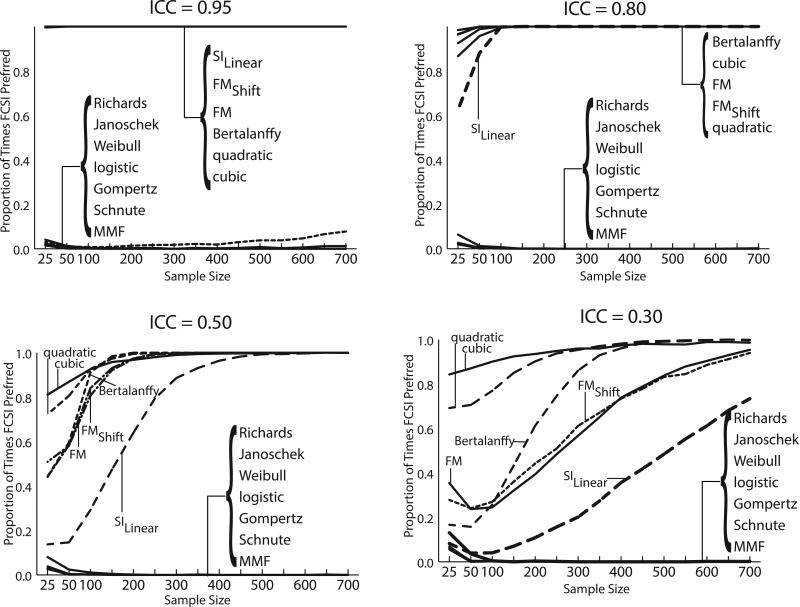
Figure 4 shows that comparison of BIC values also identifies the FCSI curve as a better fitting alternative to several of the models presented in Figure 2 but that the ability to discriminate between models depends on how reliably growth is measured. For the ICC = 0.8 and ICC = 0.95 conditions, sample sizes of 50 are sufficient to (correctly) favor the functional form suggested by the FCSI more than 80% of the time. For the ICC = 0.5 condition, approximately 250 observations are required to reject the SI_Linear model, with only 100 required for the remainder. For the low reliability condition (ICC = 0.3), 700 observations are required and, even then, the SI_Linear model is rejected only 73% of the time. Relative to the parametric curves, the FCSI is identified as a superior alternative to the Bertalanffy curve (which has no inflection point), although requiring a sample size of at least 300 in the ICC = 0.3 condition. It should be noted that if χ² difference tests are used instead of the BIC to compare the subset of models nested with the FCSI (specifically the FM, FM_Shift, FM_Linear, FMShift_Linear, and SI_Linear models), the ability to correctly reject these models is slightly better than the BIC for the smaller sample conditions (between 100 and 200) for the lower reliability conditions (ICC=0.5 and 0.3). The FCSI is not identified as a superior alternative to the remaining curves (Gompertz, Janoschek, logistic, MMF, Richards, Schnute, or Weibull), however.

Figure 4.

Proportion of BIC Favoring FCSI Model. ICC = intraclass correlation; FCSI = free curve slope intercept; MMF Morgan-Mercer-Flodin.

Comparison of Gompertz with Other Parametric Sigmoid Curves

If the researcher had originally (correctly) conjectured that growth followed a Gompertz curve, would a comparison of parametric growth curves reveal this? To examine this, we then compared the BIC difference scores of the remaining parametric models relative to the Gompertz curve. These are shown in Supplemental Figure 1 for the four internal consistency conditions. As shown in the figure, the Richards and cubic curves appear appreciably worse than the Gompertz curve. Across all conditions, the Schnute model fits the data as well as the Gompertz model. This is unsurprising, given that, as noted above and in the footnote for the model in Table 3, the Schnute model is a Gompertz curve if a>0 and b=0. For example, for the sample size 700 condition with an ICC of .95, the average a value across replications was 1.79 and the average b value was 0.0028. That the MMF model fits about as well as the FCSI model, though, is somewhat surprising and suggests that it might have some use as a less-elaborate alternative for modeling growth or, alternatively, that it may overfit data to any given functional form. For the high internal consistency condition (ICC = 0.9), the Gompertz curve is identified as superior more than 80% of the time for samples greater than 200 (Janoschek and Weibull) or 350 (logistic). For ICC = 0.8 the pattern appears to vary more directly with sample size, with even a sample size of 700 resulting in rejection of the Janoschek, logistic and Weibull curves occurring between only 69% to 77% of the replications. For the ICC = 0.3 condition, only the Richards and cubic models are rejected consistently.

Taken together, the results of this simulation study, though limited in its generalizability illustrate that it is feasible in practice to right-size a longitudinal model relative to many alternative statistical models. Designs with more or fewer occasions, differently spaced assessments, with different or varying internal consistency over time and/or different magnitudes of change over time will of course are differently powered for model estimation and comparison and are the object of further needed research.

Discussion

This paper argues for more general comparison of classes of statistical models for longitudinal data in addition to models originally considered. Consideration of such alternatives informs both the research area and reasonable skeptics of the plausibility of alternative explanations for the data and may result in identification of better fitting models for use in future research. Model comparison of structural models involving only general trait factors nicely complements other work by Molenaar (2003) which shows that such models can also be equivalently modeled as time-bound autoregressive processes absent any latent variables at all.

The three step approach for model exploration proposed here is not prescriptive, however; We acknowledge that a researcher who has selected a particular model may choose to consider models which are minor but systematic modifications of the original. Such a decision may be based on the “collective research expertise” regarding the appropriateness of the technique for an area of inquiry or the increased ease with which a slightly modified model can be communicated to the research community. Conversely, researchers may also elect to retain and report a more complex model for theoretical reasons or comparability with other studies. Regardless of the outcome of the model comparisons, we believe that researchers should report the alternative models entertained both as a way of investigating whether alternatives make more reasonable assumptions of the data, to inform the area as to whether particular effects continue to be found and to alert the research community of the possible ad hoc nature of a newly discovered well-fitting model.

Although several models are considered here, these are only heuristic of several which could be specified. For example, parametric growth curves presented here contained a random intercept factor but it is also be possible to consider shifted parametric models as well. Such a shifted Gompertz model, for example, was proposed by Winsor (1932). Growth models considered can be employed as the basis of mixture models either by specifying free curve loadings across the latent groups, as described by Wood (2011), for example. Alessandri et al. (2012) and Tisak and Tisak (2000), by contrast, integrate growth models with notions of trait stability over time.

FCSI as a Starting Point

Because many psychological processes appear to contain a random intercept component, the FCSI model may well be an initial model which is preferable to the models of linear or quadratic growth frequently used. As noted, several of the psychometric and factor models presented here are special cases of the model, and extension of the model to more complex parametric forms is straight-forward. This observation for growth data is consonant with the approach of Ram and Grimm's (2009) approach to mixture modeling in which the FCSI model was first fit to the data to determine the common functional form underlying the finite mixtures.

Have HLM, Repeated Measures Anova and Linear SI Models Been Poor Factor Models All Along?

While the renewed emphasis on model comparison may result in more use of the FCSI model, it may also stimulate researchers to explore other parameterizations for the data such as the alternative factor models or parametric growth curves presented in the Monte Carlo study. As a result, this may lead over time to decreased use of some models such as HLM, Repeated Measures, and Linear SI models as researchers conclude that such models make overly restrictive assumptions regarding the functional form of growth. It is not necessarily the case, though, that researchers are obligated to blindly accept a model with superior fit.

Specifically, any new model must itself undergo skeptical evaluation. Skeptical counterarguments could be based on the presence of influential or outlying observations, for example. Alternatively, the researcher may choose to operationalize measurement differently in order to improve fit of the initial model. This may be done by scoring the manifest variables differently, or by appeal to a different psychometric model (such as using a latent response variable model for ordered categorical variables; e.g., Cho, Wood, & Heath, 2009; Millsap & Yun Tein, 2004).

Alternatively, better fitting models may be indicative of phenomena initially unanticipated by the researcher. Under this possibility, the researcher may adopt the new model, but, in describing it, interpret these loadings as representing an admixture of more than one longitudinal process. (See Alessandri et al.'s [2012] point that free curve loadings may also be indicative of several, rather than one source of stability and change over time which may also include environmental effects, age-related effects, or turning points.) Growth curve models, like factor models, may thus be subject to the same “naming problem” found in latent variables in general in that they do not represent the constructs initially intended. Remedies for such possibilities may include collection of additional variables or other types of data.

Some may believe that the model comparison approach advocated here risks over-capitalization on chance and that, by not building a firm connection between a priori theory and the data, the researcher risks not using the “true” correct model. Such a perspective seems curious, given that it is exactly the observation of unexpected systematic regularities that spurs proposal of a new model or theory and the fact that the alternatives identified may be skeptical counterarguments to the initial model. Although a general model comparison approach is described here, researchers are free to consider and justify more limited subsets, as was done for the real-world example presented here. In other situations, changing to a better fitting class of models given obvious shortcomings in the initial model (such as poor fit, improper, or unidentified solutions) seems preferable to incremental modification of individual parameters of the initial model. Our models (initial or otherwise) need not be true, only (as yet) unrefuted. As Popper (1959; 1963) noted even if a “single correct” theory was proposed, we have no way to identify it as such and scientists often use models they know to be wrong. Technically speaking, any model is a false picture of the facts because our models are oversimplifications of the facts. The failure to find the “true model” is not a fatal flaw. It is the cost of doing business in science.

MANOVA as Unrestrictive Structural Equation Model

Given the possible model comparisons and their controversial nature, a researcher may wonder whether it is best to simply not assume structured variance components. If the sole question of interest is whether mean level changes over time, the MANOVA model may be preferable to any structural equation model, as it only tests a null model of equal means over time against a model in which means are free to vary and assumes no structured variance components. If statistical power is adequate, this may be the least controversial statistical model even though the H_alt MANOVA model, expressed as an SEM, is a just identified model with 0 degrees of freedom. If, however, MANOVA is not well-powered or if researchers in the area agree as to the existence of specific variance components, the models described here may be thought of as intermediately parsimonious alternatives between the (perhaps overly) restrictive repeated measures analysis of variance model and the MANOVA model.

Limitations

Research Design

Model comparisons are limited by study design. For example, a FCSI model with unequal error variances cannot be estimated from data consisting of three times of measurement and the Two Factor Mean model cannot be estimated from four measurement occasions. The problem of “too much” unanticipated model complexity is not “solved,” though, by entertaining only data which do not allow for the testing of more complicated models, however. Researchers must simply admit that a given data set is agnostic as to whether a particular more complex model actually underlies the data. This problem, though, is a general one affecting the estimation of all structural models. The random intercept model cannot be estimated from three items per construct, for example.

Even when the number of measurement occasions proves deficient or ill-timed, well-fitting growth models may be useful, provided the researcher is cognizant of the limitations of the data. This situation is somewhat analogous to the low reliability condition of the Monte Carlo simulation: If measurement error is substantial, the “straight line” of the SI_Linear model may be all we can “say” about growth with the six measurement occasions at hand. However, just as the “dots” used in photographs within newspapers are useful representations when looked at superficially but cannot stand closer inspection with a magnifying glass, the somewhat coarser assessments of growth studies may provide a general patterning suggestive of design of a future more refined assessment.

The timing and frequency of assessments also affects the informativeness of model comparisons. For example, assessments designed to assess behavior close to a possible inflection point in growth should provide more ability to adjudicate between the types of candidate parametric growth models considered in the Monte Carlo study. Although the importance of appropriately timed assessments is well-understood by developmental researchers (e.g., Boker & Nesselroade, 2002) longitudinal research which includes intensive “measurement bursts” may be especially informative of the nature of change over time during critical developmental periods (Ram & Gerstorf, 2009).

None of the Above: Criticisms Based on Ergodic Theory

All models considered here may be inappropriate because individuals may possess unique, qualitatively different trajectories over time. Although the question of whether growth curves can be aggregated across individuals is an old one (Estes, 1956; Merrill, 1931; Tucker, 1966), more recently Molenaar and colleagues have formally summarized the conditions under which aggregate or even cross-sectional data is generalizable to individual change patterns using the language of ergodic theory (Molenaar & Campbell, 2009; Molenaar, 2003, 2004; Molenaar, Huizenga & Nesselroade, 2003). Ergodic theory criticisms are a critical imitation of all of the models presented here, although it may be noted that the individual level state space models proposed by Molenaar and colleagues may require their own “right-sizing” as well.

Conclusion

The approach described here may be seen as part of a larger evolution of the identification, discovery, and proposal of statistical models that can withstand challenges of reasonable skeptics. If patterned inter-individual variability exists, this implies that corresponding constructs also “exist” in some real fashion and are not arbitrary mathematical conveniences, a position is grounded in philosophical realism as summarized by Borsboom, Mellenbergh and van Heerden (2004) who note “...a test is valid for measuring an attribute if and only if (a) the attribute exists and (b) variations in the attribute causally produce variations in the outcomes of the measurement procedure” (p. 1061).

The model exploration and comparisons described here do not guarantee success, and there may indeed be no “Goldilocks” model which is neither oversimple nor overly complex for a given data set. The model comparisons described here are, however, a useful exercise in examining how model assumptions affect research conclusions. The current strategy of reporting only initially chosen statistical models do not appear to “survive” very well either, given the larger concerns that the “statistical truth” of research effects which appear to “wear off” upon replication (Ioannidis, 2005; Lehrer, 2010). Neither need we forego statistical inference because the “state of the art is uncertain” as some have suggested (Trafimow and Marks, 2015). It is hoped that by evaluating and reporting plausible models that a more optimistic picture of research replication can emerge, resulting in a systematic critical evaluation consonant with Popperian notions of adversarial science.