Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Dec 16;5:18373. doi: 10.1038/srep18373

Dimpled elastic sheets: a new class of non-porous negative Poisson’s ratio materials

Farhad Javid 1, Evelyne Smith-Roberge 1, Matthew C Innes 2, Ali Shanian 2, James C Weaver 3, Katia Bertoldi 1,4,a
PMCID: PMC4680965  PMID: 26671169

Abstract

In this study, we report a novel periodic material with negative Poisson’s ratio (also called auxetic materials) fabricated by denting spherical dimples in an elastic flat sheet. While previously reported auxetic materials are either porous or comprise at least two phases, the material proposed here is non-porous and made of a homogeneous elastic sheet. Importantly, the auxetic behavior is induced by a novel mechanism which exploits the out-of-plane deformation of the spherical dimples. Through a combination of experiments and numerical analyses, we demonstrate the robustness of the proposed concept, paving the way for developing a new class of auxetic materials that significantly expand their design space and possible applications.

The Poisson’s ratio, ν, defines the ratio between the lateral and axial strains in a material under uniaxial loading. Theoretically, in linear isotropic materials, the Poisson’s ratio can range between −1 and 1/2. A material with ν = 1/2 shears easily and resists volumetric deformations due to its vanishing shear (G = 0) and infinite bulk (K → ∞) modulus. Conversely, a material with ν = −1 resists shear (G → ∞), but easily undergoes volumetric deformations (K = 0). Outside this range, either the shear or bulk modulus of the material is negative, which is impossible due to thermodynamic stability1.

Although the traditional belief is that the Poisson’s ratio of elastic materials must be positive (so that they shrink/expand laterally when stretched/compressed axially), since 1980s many 2D and 3D structures and materials with negative Poisson’s ratio have been reported2,3,4,5,6. Auxetic behavior was first realized in 2D re-entrant honeycomb structures that unfold and expand laterally when uniaxially stretched7,8. The same concept was later exploited by Lakes to design and fabricate the first 3D polymeric foam with isotropic auxetic behavior9. Subsequently, a number of geometries were proposed to achieve negative Poisson’s ratio through rotation of the stiffer components in the microstructure. These include chiral honeycombs10,11, networks of rigid rotating units12,13,14,15, and elastomeric porous structures in which instabilities are exploited to trigger the rotation of stiff domains16,17,18. Finally, negative Poisson’s ratio was realized in non-porous systems either by embedding an auxetic network within a compliant matrix19,20 or by using angle-ply laminates21,22,23,24,25,26.

Till now, the majority of materials designed to have negative Poisson’s ratio are porous and this significantly limits the potential applications of auxetic materials. Although low porosity auxetic sheets comprising an array of elongated holes have been recently designed15, porosity is still crucial for inducing negative Poisson’s ratio in these systems and, hence, their auxetic response disappears if made non-porous. Auxetic composites can overcome this limitation due to their non-porous structure. However, since their response highly depends on the contrast between the material properties of their different phases, a limited set of engineering materials and manufacturing techniques can be used for their fabrication, making them unsuitable for many industrial applications. Here, we introduce a new class of auxetic materials that are non-porous and are easily fabricated out of any elastic sheet using conventional manufacturing techniques.

Dimpled Elastic Sheets

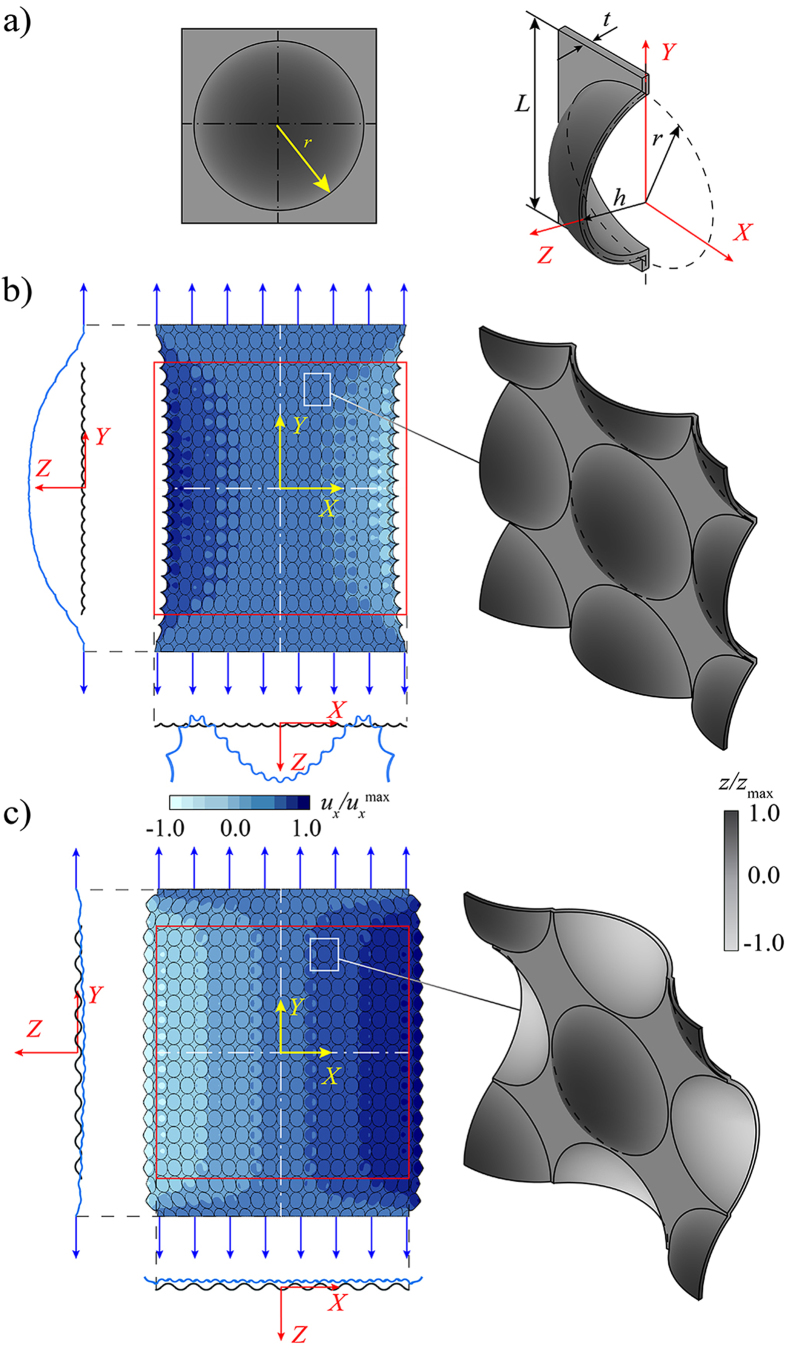
As shown in Fig. 1a, the building block of the proposed material consists of a square flat sheet with edge L and constant thickness t dented with a spherical dimple of height h. Each dimple is a sector of a thin spherical shell which forms a circle of radius r when intersecting the flat sheet. The geometry of the dimpled elastic sheets is then characterized by three dimensionless parameters: the dimple aspect ratio, h/r, the normalized thickness, t/r, and the dimple density,

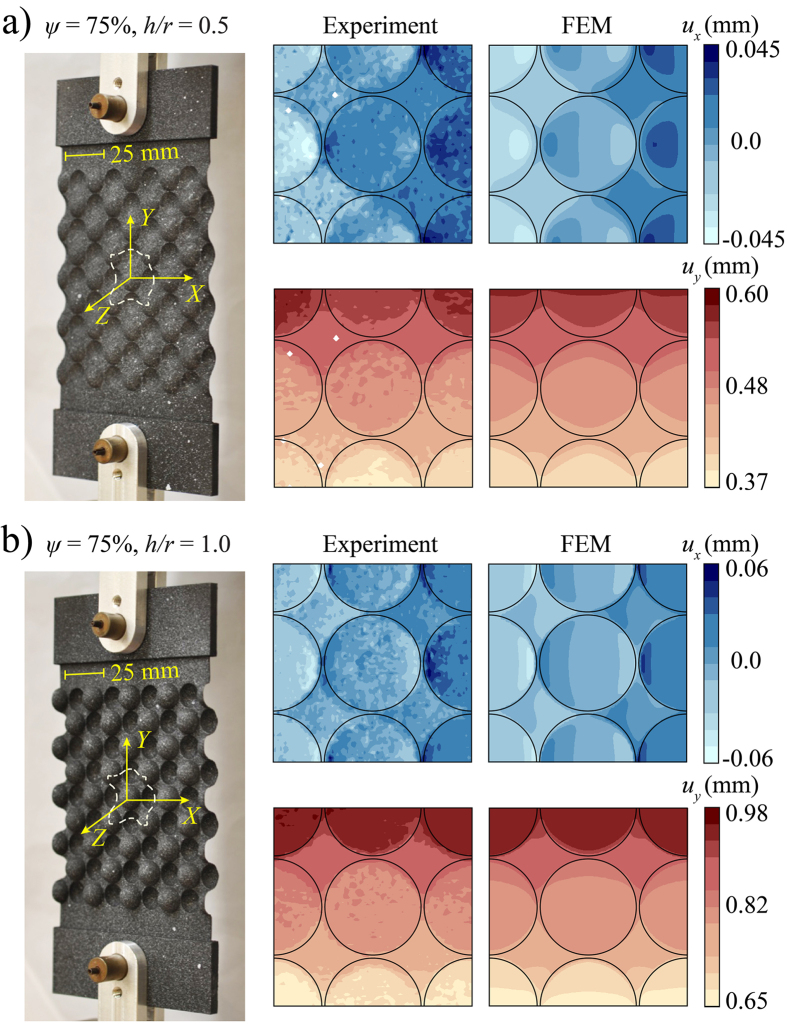
Figure 1. Deformation mechanism of dimpled elastic sheets.

Figure 1

Open in a new tab

(a) The building block of the proposed auxetic material comprises a flat sheet dented with a spherical dimple. (b) Numerical results showing the deformation under uniaxial tension of an elastic sheet with a square array of 20 × 20 dimples dented on one side of the sheet (we assume ψ = 75%, h/r = 0.5 =  and t/r = 0.08). The analysis reveals that this structure bends out of plane and contracts laterally. (c) The out-of-plane bending of the structure can be prevented by denting the dimples on both side of the flat sheet to form a checkerboard pattern. Such structure expands when stretched and, thus, is characterized by negative Poisson’s ratio. Note that the results shown in (b,c) have been magnified 600 times to better visualize the deformations.

graphic file with name srep18373-m1.jpg

To realize a 2D auxetic material, we arrange the dimples on a square lattice and investigate the response of the system both numerically and experimentally.

We study the behavior of the dimpled structures numerically using the commercial finite element (FE) package ABAQUS/Standard (Simulia, Providence, RI) and investigate the response of the system under uniaxial tension (see Numerical techniques in the Methods section for details of the FE analysis). We first focus on an elastic sheet with all dimples dented on one side (see Fig. 1b-right). In particular, we choose h/r = 0.5 and ψ = 75% and consider a finite-size domain comprising a square array of 20 × 20 dimples. For such structure, we find that the applied uniaxial stretch causes out-of-plane bending (see side views in Fig. 1b). Moreover, the contour map for the horizontal component of the displacement (ux), shown in Fig. 1b-left, indicates that the system contracts laterally, resulting in a positive value of the in-plane macroscopic Poisson’s ratio (i.e. 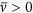Inline graphic). However, it is important to note that the out-of-plane bending of the structure can be suppressed by balancing the system in z direction. This is achieved by denting the dimples on both sides of the flat sheet to form a checkerboard pattern (see Fig. 1c-right). Remarkably, in such balanced structure, all dimples flatten toward the structure mid-plane under an applied uniaxial tension, resulting in lateral expansion of the system (see Fig. 1c-left) and, therefore, an auxetic response (i.e. 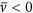Inline graphic). Finally, we note that, although the results reported in Fig. 1 are for a sheet comprising a square array of 20 × 20 dimples, the response of the system is not affected by the finite size of the structure (see Supplementary Information for details).

Results

Numerical models

Having demonstrated that an elastic sheet with spherical dimples dented on both sides can exhibit auxetic behavior, we now numerically investigate the effect on the macroscopic Poisson’s ratio of such structure, 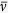Inline graphic, of the dimple aspect ratio, h/r, the dimple density, ψ, the thickness of the elastic sheet, t/r, and the Poisson’s ratio of the bulk material, ν. To ensure the results are not affected by the boundary effects, we focus on an infinite periodic system and study the response of a 2 × 2 unit cell (see inset in Fig. 2a) with periodic boundary conditions27,28. We stretch the unit cell uniaxially by applying a homogenized strain in vertical direction, 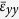Inline graphic, and measure the transverse strain in horizontal direction, 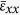Inline graphic. The Poisson’s ratio of the dimpled sheet is then calculated as 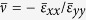Inline graphic. In Fig. 2a, we report the evolution of 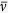Inline graphic as a function of h/r for different values of ψ (45–75%), while t/r and ν are kept constant. First, the results indicate that, as h/r increases, 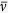Inline graphic initially drops, reaches a minimum value and then increases. Moreover, we find that the macroscopic Poisson’s ratio monotonically decreases as the dimple density increases and eventually becomes negative. Interestingly, for t/r = 0.08 and ν = 0.35, all structures with ψ ≥ 55% exhibit auxetic behavior for a range of dimple aspect ratios, demonstrating that by controlling ψ and h/r dimpled structures with 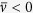Inline graphic can be designed. Furthermore, we find that the response of the system is moderately affected by t and ν. In fact, the data reported in Fig. 2b,c show that the auxetic response of the dimpled sheet can be enhanced by decreasing the structure thickness and the Poisson’s ratio of the bulk material. Finally, we should note that, although the results reported in Fig. 2 are for uniaxial tension, we expect the Poisson’s ratio of the structure to remain identical under compressive loading, since we are exploiting a linear elastic effect.

Figure 2. Effect of h/r, ψ, t and ν on the macroscopic Poisson’s ratio of the dimpled elastic sheet, 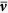Inline graphic.

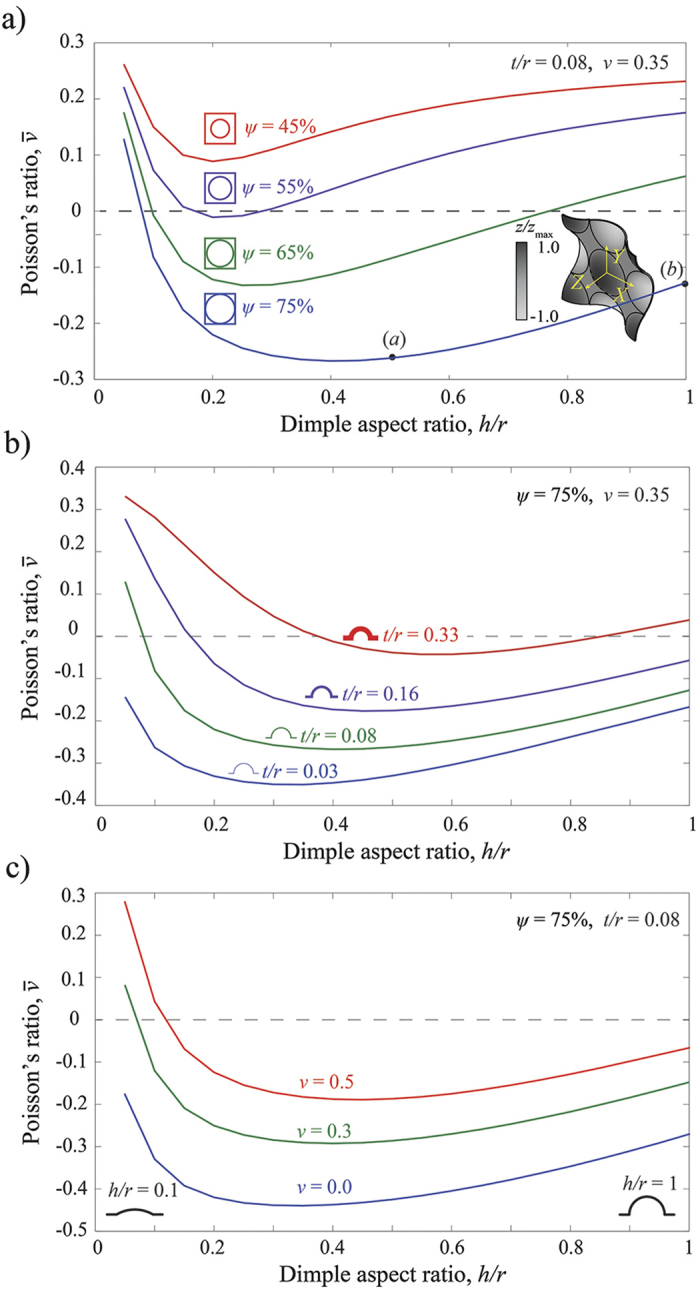
Figure 2

Open in a new tab

Evolution of 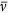Inline graphic as a function of h/r is shown in (a) for four different values of ψ (assuming t/r = 0.08 and ν = 0.35), in (b) for four different values of t/r (assuming ψ = 75% and ν = 0.35), and in (c) for four different values of ν (assuming ψ = 75% and t/r = 0.08).

Experiments

We proceed to verify the numerical predictions experimentally. Two specimens are fabricated using a 3D printer (Connex 500 available from Objet, Ltd.) from VeroClear material (product number: RGD840) with Young’s modulus E = 1.5 GPa and Poisson’s ratio ν = 0.35 (see Supporting Information for the mechanical properties of VeroClear material). Each specimen comprises an array of 9 × 9 dimples (with L = 12.5 mm). In particular, we focus on two structures characterized by (a) h/r = 0.5 and (b) h/r = 1.0 (highlighted by circular markers in Fig. 2a), while we keep ψ = 75% and t/r = 0.08 fixed. The specimens are tested under uniaxial tension in an Instron testing machine and the displacement fields are visualized using a digital image correlation (DIC) technique29,30. In Fig. 3, we report the experimental contour maps for the horizontal (ux) and vertical (uy) components of the displacement fields obtained for a grip displacement of ugrip = 1.0 mm (Fig. 3a - resulting in a longitudinal strain of 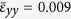Inline graphic in the central part of the sample) and 1.625 mm (Fig. 3b - resulting in a longitudinal strain of 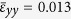Inline graphic in the central part of the sample). To minimize the boundary effects, we focus on the central unit cell (highlighted with white dashed lines in Fig. 3a,b at left) and compare the results with the numerical predictions for the corresponding infinite periodic structure, showing a very good agreement. Importantly, the contour maps for ux show that both structures expand laterally when uniaxially stretched, confirming their auxetic behavior.

Figure 3. Contour maps for the horizontal (ux) and vertical (uy) components of the displacement fields.

Figure 3

Open in a new tab

Experimental (left) and numerical (right) results are quantitatively compared for two structures characterized by (a) ψ = 75%, h/r = 0.5 and (b) ψ = 75%, h/r = 1.0. Snapshots of the deformed samples are shown on the left, with the central unit cell highlighted by white dashed lines.

Next, we use the experimentally measured displacement fields, shown in Fig. 3, to quantify the macroscopic Poisson’s ratio of the dimpled sheets. We first calculate the average displacement components along each of the four boundaries of the central unit cell, 〈ux〉R, 〈ux〉L, 〈uy〉T, and 〈uy〉B (R, L, T, and B denoting the right, left, top, and bottom edges of the unit cell, respectively), from which the average strain values for the unit cell are obtained as

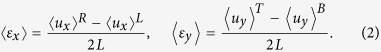graphic file with name srep18373-m13.jpg

Finally, the macroscopic Poisson’s ratio is calculated as

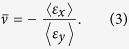graphic file with name srep18373-m14.jpg

For the two specimens characterized by h/r = 0.5 (Fig. 3a) and h/r = 1.0 (Fig. 3b), we find that 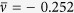Inline graphic and −0.126, respectively, in excellent agreement with the FE predictions for the corresponding infinite periodic structures (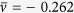Inline graphic and −0.128). Note that we also simulate the response of finite-size structures (see Supplementary Information for details) and find that the results are very close to those obtained for the infinite domains, indicating that the effect of the boundaries is not pronounced.

Discussion

In the previous section, we focused on dimples arranged to form a square array and showed that having a balanced number of them dented on both sides of a flat sheet is a crucial condition to achieve auxetic behavior. However, it is important to realize that both the direction of the applied load, θ, and the arrangement of the dimples affect the macroscopic Poisson’s ratio of the sheets. Focusing on the effect of the loading direction, in Fig. 4a we report the evolution of 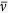Inline graphic as a function of θ for a structure with dimples arranged to form a checkerboard pattern (blue line). These numerical results indicate that the dimpled sheet is characterized by 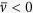Inline graphic only when loaded approximately in horizontal (i.e. θ ~ 0°) and vertical (i.e. θ ~ 90°) directions. Large positive values of 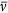Inline graphic are instead found for θ = 45°. In Fig. 4a, we also report results for a structure in which the dimples are still dented on both sides of the flat sheet, but to form a stripe pattern (red line). Although this system is also characterized by an equal number of dimples dented on each side of the sheet, no auxetic behavior is observed, demonstrating the important role played by the arrangement of the dimples. To further confirm this point, we investigate the response of a flat sheet with a triangular array of dimples dented on both sides (inset in Fig. 4b - note that this is the only triangular arrangement characterized by an equal number of dimples dented on both sides of the sheet.). As shown in Fig. 4b, the balanced triangular array of dimples is characterized by auxetic behavior for specific loading directions. In particular, for the considered structure characterized by ψ = 86%, h/r = 0.5 and t/r = 0.08, 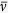Inline graphic is negative for 174° < θ < 36° and 84° < θ < 126° and reaches a minimum (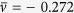Inline graphic) for θ ~ 15° and 105°.

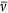Figure 4. Effect of loading direction, θ, and dimples arrangement on Inline graphic.

Figure 4

Open in a new tab

(a) Evolution of Inline graphic as a function of θ for an elastic sheet with a square array of dimples dented to form a checkerboard (blues line) and a stripe (red line) pattern. For this set of simulations, we assume ψ = 75%, h/r = 0.5, t/r = 0.08 and ν = 0.35. (b) Evolution of Inline graphic as a function of θ for an elastic sheet with a triangular array of dimples dented on both sides. Here, we assume ψ = 86%, h/r = 0.5, t/r = 0.08 and ν = 0.35.

Finally, it is important to note that 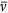Inline graphic is also affected by the magnitude of the applied deformation. To highlight this point, we numerically evaluate the evolution of the macroscopic Poisson’s ratio, 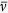Inline graphic, under large deformations (we consider values of 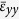Inline graphic up to 0.1 and conduct a non-linear FE analysis) for an infinite dimpled sheet characterized by ψ = 75%, h/r = 0.5, and t/r = 0.08. As shown in Fig. 5a, by increasing the applied strain the macroscopic Poisson’s ratio of the structure monotonically increases (i.e. the auxetic behavior weakens). This is because as 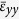Inline graphic increases, the dimples gradually flatten (see contour maps for uz in Fig. 5c) and their ability to push the flat sheet in the lateral directions diminishes (see contour maps for ux in Fig. 5b).

Figure 5. Effect of large applied deformations on the macroscopic Poisson’s ratio of the dimpled elastic sheet.

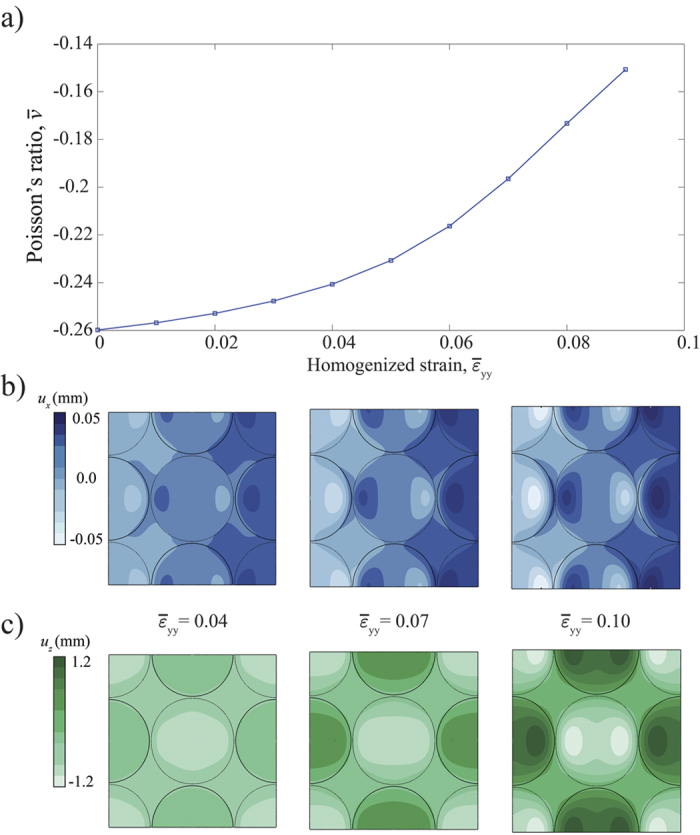
Figure 5

Open in a new tab

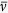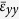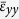(a) Numerical results showing the evolution of Inline graphic as a function of Inline graphic. (b,c) Contour maps for (b) the in-plane lateral (ux) and (c) the out-of-plane (uz) components of the displacement fields at different levels of strain, Inline graphic.

In this study, we demonstrated a fundamentally new approach to generate non-porous periodic materials with negative Poisson’s ratio by denting a homogeneous and uniform elastic sheet with an array of dimples. Through a combination of numerical analysis and experiments, we showed that the Poisson’s ratio of the system can be easily tuned and altered by controlling the arrangement of the dimples. In particular, we found that having an arrangement with a balanced number of dimples dented on the two sides of the flat sheet is crucial to generate auxetic behavior. Importantly, the system we explored can be easily fabricated and has a robust behavior, pointing to a novel and practical method for producing non-porous negative Poisson’s ratio materials.

Methods

Numerical techniques

The numerical analysis are performed using the commercial FE package ABAQUS/Standard (Simulia, Providence, RI). The response of both finite-size and unit cell dimpled sheets are investigated under uniaxial tension throughout this work. All models are generated by quadratic tetrahedral elements (ABAQUS element type C3D10M). We should note that we also built FE shell models, but we found that the stress distribution around the dimple edges is not accurate, unless a very refined mesh is used which significantly increases the computational time. In all simulations, we model the response of the bulk material as linear elastic with Young’s modulus E = 1.5 GPa and Poisson’s ratio ν = 0.35. Moreover, since we focus on the linear response of the structure, we do not account for non-linearities in the simulations.

Finite-size models (see Fig. 1b,c) are initially studied to verify the auxetic behavior in dimpled structures, while the unit cells models (see Figs 2 and 3) are used to ensure the qualitative results are not affected by the boundary effects. In finite-size structures, the uniaxial loading in vertical direction is applied by fixing all nodes on their top and bottom surfaces in x and z directions and uniformly displacing them in y direction while in unit cell models, the loading is applied as a homogenized strain in vertical direction, 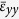Inline graphic. To this end, periodic boundary conditions are applied on all lateral edges of an infinite periodic structure of a 2 × 2 unit cell27,28.

Experiments

Picture of our experimental setup is shown in Fig. 6. An Instron uniaxial testing machine with a 50 kN load cell is used for applying uniaxial tension to the samples. The samples are connected to the machine using two custom-made adapters. To improve the samples alignment, pinned grips are used for connection. A uniaxial vertical displacement (uy) is applied to the upper grip of the Instron machine, while the lower grip is fixed. To quantify 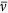Inline graphic, the in-plane deformation of the samples is monitored by taking images at different levels of applied displacement using a high-resolution digital camera (Nikon D90 camera with a 50 mm f/2.8 lens). The images are then analyzed to quantify the in-plane deformation of the specimens using a digital image correlation (DIC) package29,30. To increase the images contrast, the samples are first coated in black and then speckled with a white spray paint (Krylon Products Group, Cleavland, OH) prior to the test. The speckle pattern generates a density of approximately 2–9 pixels per speckle which, given our experimental setup, leads to a displacement accuracy of 800 nm31.

Figure 6. Experimental setup: the camera, the sample, and its connection to the Instron machine are identified on the figure.

Figure 6

Open in a new tab

A total displacement of 2 mm is applied to each sample at the low rate of 0.25 mm/min to ensure quasi-static conditions (note that the contour maps shown in Fig. 3a,b are obtained for an applied grip displacement of ugrip = 1.0 and 1.625 mm, respectively). The sample, the adapters to connect the samples to the grips, the grips, and the camera are all identified on Fig. 6. Two large stand lamps are also used to better light the samples during the tests, which are not shown in Fig. 6.

Additional Information

How to cite this article: Javid, F. et al. Dimpled elastic sheets: a new class of non-porous negative Poisson's ratio materials. Sci. Rep. 5, 18373; doi: 10.1038/srep18373 (2015).

Supplementary Material

Supplementary Information
srep18373-s1.pdf (9.1MB, pdf)

Acknowledgments

This work has been funded by Rolls-Royce Energy and Siemens ADGT. The authors also acknowledge support by the Materials Research Science and Engineering Center under National Science Foundation (NSF) Award No. DMR-1420570, NSF CMMI-1149456-CAREER award, and the support of the Kavli Institute at Harvard University. The authors thank Dr. Anas Chalas and Elaine Kristant at Harvard Active Learning Lab for providing us the experimental setup. We also thank Prof. William T. Freeman and Donglai Wei at the Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, for their great help and directions in DIC analyses.

Footnotes

The authors declare no competing financial interests.

Author Contributions M.C.I. and A.S. suggested the idea. F.J. and E.S.R. performed the numerical studies, while F.J. conducted all the experiments. J.C.W. fabricated the samples. The manuscript was written by F.J. and K.B. and was reviewed by all coauthors before submission. All the work was supervised by K.B.

References

  1. Truesdell C. & Noll W. The Non-Linear Field Theories of Mechanics. Springer-Verlag, Berlin, third edition (2003). [Google Scholar]
  2. Evans K. E. & Alderson A. Auxetic materials: Functional materials and structures from lateral thinking! Adv. Mater. 12(9), 617–628 (2000). [Google Scholar]
  3. Yang W., Li Z. M., Shi W., Xie B. H. & Yang M. B. Review on auxetic materials. J. Mater. Sci. 39(10), 3269–3279 (2004). [Google Scholar]
  4. Greaves G. N., Greer A., Lakes R. S. & Rouxel T. Poisson’s ratio and modern materials. Nat. Mater. 10(11), 823–837 (2011). [DOI] [PubMed] [Google Scholar]
  5. Hou X. & Silberschmidt V. V. Metamaterials with negative poisson’s ratio: A review of mechanical properties and deformation mechanisms. In Silberschmidt V. V. & Matveenko V. P. (eds), Mechanics of Advanced Materials, Engineering Materials, pages 155–179. Springer International Publishing (2015). [Google Scholar]
  6. Lim T. C. Auxetic Materials and Structures. Springer, (2015). [Google Scholar]
  7. Gibson L. J., Ashby M. F., Schajer G. S. & Robertson C. I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. A. 382(1782), 25–42 (1982). [Google Scholar]
  8. Almgren R. F. An isotropic three-dimensional structure with poisson’s ratio = −1. J. Elasticity 15(4), 427–430 (1985). [Google Scholar]
  9. Lakes R. S. Foam structures with a negative poisson’s ratio. Science 235(4792), 1038–1040 (1987). [DOI] [PubMed] [Google Scholar]
  10. Prall D. & Lakes R. S. Properties of a chiral honeycomb with a poisson’s ratio of −1. Int. J. Mech. Sci. 39(3), 305–314 (1997). [Google Scholar]
  11. Scarpa F. et al. Elastic buckling of hexagonal chiral cell honeycombs. Compos. Part A-Appl. S. 38(2), 280–289 (2007). [Google Scholar]
  12. Grima J. N., Alderson A. & Evans K. E. Auxetic behaviour from rotating rigid units. Phys. Status Solidi B 242(3), 561–575 (2005). [Google Scholar]
  13. Attard D. & Grima J. N. Auxetic behaviour from rotating rhombi. Phys. Status Solidi B. 245(11), 2395–2404 (2008). [Google Scholar]
  14. Grima J. N., Farrugia P. S., Caruana C., Gatt R. & Attard D. Auxetic behaviour from stretching connected squares. J. Mater. Sci. 43(17), 5962–5971 (2008). [Google Scholar]
  15. Taylor M. et al. Low porosity metallic periodic structures with negative poisson’s ratio. Adv. Mater. 26(15), 2365–2370 (2014). [DOI] [PubMed] [Google Scholar]
  16. Bertoldi K., Reis P. M., Willshaw S. & Mullin T. Negative poisson’s ratio behavior induced by an elastic instability. Adv. Mater. 22, 361–366 (2010). [DOI] [PubMed] [Google Scholar]
  17. Overvelde J. T. B., Shan S. & Bertoldi K. Compaction through buckling in 2D periodic, soft and porous structures: Effect of pore shape. Adv. Mater. 24, 2337–2342 (2012). [DOI] [PubMed] [Google Scholar]
  18. Babaee S. et al. 3d soft metamaterials with negative poisson’s ratio. Adv. Mater. 25(36), 5044–5049 (2013). [DOI] [PubMed] [Google Scholar]
  19. Milton G. W. Composite materials with poisson’s ratios close to −1. J. Mech. Phys. Solids. 40(5), 1105–1137 (1992). [Google Scholar]
  20. Jang K. et al. Soft network composite materials with deterministic and bio-inspired designs. Nat. Commun. 6, 6566, doi: 10.1038/ncomms7566 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Bjeletich J. G., Crossman F. W. & Warren W. J. The influence of stacking sequence on failure modes in quasi-isotropic graphite-epoxy laminates. Failure Modes in Composites–IV, Cornie J. R. & Crossman F. W. (editors), American Institute of Mining, Metallurgical and Petroleum Engineers, New York, NY (1979). [Google Scholar]
  22. Herakovich C. T. Composite laminates with negative through-the-thickness poisson’s ratios. J. Compos. Mate. 18, 447–456 (1984). [Google Scholar]
  23. Hahn H. T. & Tsai S. W. Introduction to Composite Materials. Technomic Publishing Co. (1980). [Google Scholar]
  24. Donoghue J. P. & Evans K. E. Composite laminates with enhanced indentation and fracture resistance due to negative poisson’s ratios. in Proc. ICCM 8 (eds Tsai S. W. & G. S.Springer) (1991). [Google Scholar]
  25. Clarke J. F., Duckett R. A., Hine P. J., Hutchinson I. J. & Ward I. M. Negative poisson’s ratios in angle-ply laminates: theory and experiment. Composites. 25(9), 863–868 (1994). [Google Scholar]
  26. Hine P. J., Duckett R. A. & Ward I. M. Negative poisson’s ratios in angle-ply laminates. J. Mater. Sci. Lett. 16(7), 541–544 (1997). [Google Scholar]
  27. Danielsson M., Parks D. M. & Boyce M. C. Three-dimensional micromechanical modeling of voided polymeric materials. J. Mech. Phys. Solids. 50(2), 351–379 (2002). [Google Scholar]
  28. Bertoldi K., Boyce M. C., Deschanel S., Prange S. M. & Mullin T. Mechanics of deformation-triggered pattern transformations and superelastic behavior in periodic elastomeric structures. J. Mech. Phys. Solids. 56(8), 2642–2668 (2008). [Google Scholar]
  29. Jones E. M. C., Silberstein M. N., White S. R. & Sottos N. R. In situ measurements of strains in composite battery electrodes during electrochemical cycling. Exp. Mech. 54(6), 971–985 (2014). [Google Scholar]
  30. Jones E. M. C. MATLAB central file exchange: improved digital image correlation (DIC), url: http://www.mathworks.com/matlabcentral/fileexchange/43073-improved-digital-image-correlation-dic- (2013) (updated 05/22/2015).
  31. Sutton M. A., Orteu J. J. & Schreier H. Image Correlation for Shape, Motion and Deformation Measurements:Basic Concepts,Theory and Applications. Springer (2009). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep18373-s1.pdf (9.1MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES