A proposed route to independent measurements of tight junction conductance at discrete cell junctions

Abstract

Direct recording of tight junction permeability is of pivotal importance to many biologic fields. Previous approaches bear an intrinsic disadvantage due to the difficulty of separating tight junction conductance from nearby membrane conductance. Here, we propose the design of Double whole-cell Voltage Clamp - Ion Conductance Microscopy (DVC-ICM) based on previously demonstrated potentiometric scanning of local conductive pathways. As proposed, DVC-ICM utilizes two coordinated whole-cell patch-clamps to neutralize the apical membrane current during potentiometric scanning, which in models described here will profoundly enhance the specificity of tight junction recording. Several potential pitfalls are considered, evaluated and addressed with alternative countermeasures.

Abbreviations

a

nanopore inner radius (eqn. 2-3)

BE

balance electrode

CE

counter electrode

C_ma

apical membrane capacitance

C_mb

basolateral membrane capacitance

C_S

capacitance of patch clamp pipet

d

nanopore diameter (Fig. 4B caption)

D_ps

probe-surface distance

DVC-ICM

double whole-cell voltage clamp ion conductance microscopy

E

electric field (eqn.1)

E_rest

resting membrane potential

G

conductance (eqn.1)

GND

electrical ground

h

cylindrical nanopore length (Fig. 4B caption)

I

current across C_mb1 (eqn. 5-6)

i.d.

inner radius

i_BE

balance electrode current

i_GJ

gap junctional current

i_ma

apical membrane current

i_mb

basolateral membrane current

i_para

paracellular current

i_trans

transcellular current

JAMs

Junctional Adhesion Molecules

MDCK

Madin-Darby canine kidney

PE

pipet electrode

P-SICM

potentiometric scanning ion conductance microscopy

r

distance from the axis of symmetry (eqn.3)

RC

resistor capacitor circuit or product of resistance and capacitance

RE

reference electrode

R_GJ

gap junction resistance

R_L

leak resistance (or seal resistance)

R_ma

apical membrane resistance

R_mb

basolateral membrane resistance

R_pore

nanopore resistance (Fig. 4B caption)

R_S

series resistance

R_TE

transepithelial resistance

R_TJ

tight junction resistance

S/N

signal-to-noise ratio

SICM

scanning ion conductance microscopy

TEER

transepithelial electrical resistance

TJs

tight junctions

UE

potential electrode

V

command voltage at balance electrode

V’

actual intracellular potential (holding potential)

V_TE

transepithelial potential

WE

working electrode

ΔV

potential deflection (eqn.1)

z

normal distance from the pore (eqn.2-4)

Δz

pipet vertical displacement (eqn. 1)

ξ, η

rotational elliptic coordinates (eqn. 2-4)

ρ

specific resistance of bath electrolyte (eqn. 1 Fig. 4B)

Φ

potential at a certain position above nanopore (eqn. 4)

Φ₀

potential at the nanopore surface (eqn.4)

Figure 4.

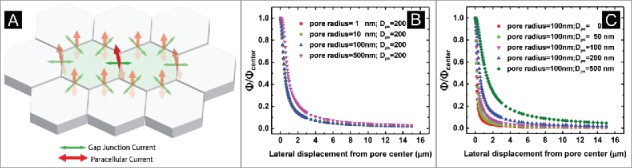
(A) Illustration of possible current flow between the two cells involved in DVC-ICM measurements (green cells in the middle) and their neighboring cells (gray cells in the periphery). Gap junctional currents flow within the epithelial cell layer (green arrow) and paracellular currents flow through tight junctions perpendicular to the cell layer (red arrow). (B) Lateral distribution of relative potential field (normalized to the potential amplitude over nanopore center) at 200 nm above a nanopore for nanopores with inner radius of 1, 10, 100 and 500 nm. The pore resistance (R_pore) of a cylindrical nanopore can be calculated by the following equation: ${\text{R}}_{pore}=p·\frac{4h}{\pi ·d^2}$, in which p represents the solution resistivity, d represents the pore diameter, and h represents the pore length. (C) Lateral distribution of relative potential field (same as in (B)) at different heights above a radius 100 nm nanopore (D_ps = 0, 20, 100, 200, and 500 nm).

Tight Junctions

Tight junctions (TJs) form a continuous paracellular seal between adjacent epithelial cells and control solute transport between apical and basolateral fluids. In thin section electron microscopy, TJs appear as series of direct membrane contacts, where membranes from adjacent cells fuse together,¹ and freeze-fracture electron microscopy has further revealed TJs to exist as extended protein strands that form transmembrane networks.² Known integral membrane proteins of the tight junction include occludin,³ Junctional Adhesion Molecules (JAMs),⁴ and claudins.⁵ Claudins have been shown to confer ion selectivity to tight junctions. For instance, claudin-4, -5, -8, -11 and -14 selectively decrease cation permeability,^6-10 whereas claudin-15 and -17 are anion selective.^11,12 Permeability studies suggest paracellular channels 4-7 Å in diameter are formed from claudins at tight junction contacts and are responsible for the selectivity in ion transport.^13,14 The first crystal structure of claudin has recently been published,¹⁵ which primes the field to study the structure and function relationship of tight junction. The present study offers a new approach for assessing the conductive properties of tight junction with unprecedented resolution.

Measurement of Tight Junction Conductance

Tight junction permeability is often experimentally assessed by electrical measurements of transepithelial ion transport. For instance, in the classic Ussing chamber,^16-20 the transepithelial electrical resistance (TEER) is measured to determine the transepithelial resistance (R_TE, inverse of epithelial conductance) of tissue slices and the dilution potential is recorded to determine the ion selectivity of the conductive pathways. This approach can also be translated to cells cultured on polymer membranes, where hundreds to thousands of cells can be measured in a single TEER measurement, with R_TE values recorded that are typically in the range of 10-1000s of Ω∙cm². Although useful, TEER measurements represent the aggregate response of all ion-conductive pathways, which include transcellular ion channels as well as paracellular channels. Approaches to separate the two conductivity pathways (transcellular, paracellular) are difficult to achieve experimentally. Two-path impedance spectroscopy²¹ has been perhaps most successful in distinguishing between paracellular and transcellular conductances, but still lacks local information for studying heterogeneously conductive epithelium. In particular, delineation of paracellular conductance from an epithelium proves especially challenging. If we consider patch-clamp techniques²² as the “gold standard” to measure ion transport of protein channels in the transcellular pathway, no comparable approach exists to study components of paracellular conductance. Patch–clamp approaches appear unsuitable for direct measurement of tight junctions because of the inability to form gigaohm seals between pipet and the cell perimeter where the tight junction resides.

Frömter and co-workers pioneered a little used, but particularly intriguing method to separate paracellular and transcellular conductances through voltage scanning (or conductance scanning) technique, in which local voltage deflections over individual cell junctions are measured.^23,24 Voltage scanning makes use of a pair of microelectrodes that are positioned in space above a cell or tissue monolayer. With application of a pulsed current across the epithelial cell layer, the microelectrodes can be used to record spatially resolved conductance. However, limitations of this technique exist due to lack of accurate electrode position control and low signal-to-noise ratios (S/N), making voltage scanning only applicable to very flat epithelia and cases where tight junction conductance differs significantly from the transcellular conductance. We have adapted the general conductance scanning concepts of Frömter into scanning ion conductance microscopy (SICM)²⁵ with a goal of improving resolution through better probe control and experimental flexibility. SICM utilizes an ion conductance feedback mechanism to scan an electrolyte filled nanopipet over a surface.  SICM provides relatively high-resolution surface topography (<100 nm), which is then used to position the nanopipet probe accurately over cell-cell junctions. Additionally, the robust feedback control of SICM allows precise control of probe-cell surface distance (at the nanometer scale) during measurement and not only flat but also rough epithelial surfaces to be studied. To record tight junction conductance with SICM, the nanopipet is positioned over a tight junction and local ion current is recorded as a transepithelial potential is applied across the epithelium. To compensate for limits in S/N in the current-based measurement due to the high resistance of the probe, we introduce an additional electrode that measures the potential at the pipet tip, in an SICM mode we termed potentiometric scanning ion conductance microscopy (P-SICM).²⁶

Potentiometric Scanning Ion Conductance Microscopy (P-SICM)

P-SICM utilizes a dual barrel nanopipet to scan and measure epithelial cell layers grown on a filter mounted between 2 chambers of a perfusion well (Fig. 1). The tip diameter of each barrel of the pipet typically ranges from 10 - 100 nanometers, as determined with scanning electron micrographs. The pipet electrode (PE, biased at 100 mV vs. reference electrode (RE)) present in one barrel monitors the probe-surface distance (D_ps) dependent ion current to control probe position. A potential electrode (UE) in the second barrel measures the local potential deflection (also with respect to RE). A platinum counter electrode (CE) drives the majority of transepithelial current to avoid potential fluctuations of RE when a transepithelial potential (V_TE) is applied at the working electrode (WE) placed in the bottom chamber. V_TE drives ion current through cell-cell junctions as well as membrane channels and results in a potential gradient in the vicinity of these ion conductive pathways. Local potential variations captured by UE can then be used to determine apparent local conductance (G) values from Equation 1.^27,28

$$G=\left(\frac{E}{\rho ·V_{TE}}\right)=\left(\frac{\left(\Delta V_{0.2\mu \text{m}}- \Delta V_{12.5\mu m}\right)/\Delta z}{\rho ·V_{TE}}\right)$$ (1)

Figure 1.

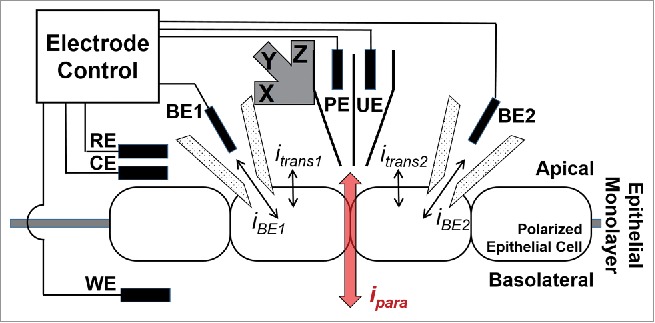
Illustration of the DVC-ICM setup. Double barrel pipet for topographical mapping (PE) and local potential measurement (UE) is attached to a piezo positioner. Reference electrode (RE), counter electrode (CE) and working electrode (WE) are controlled with home-built electrode controller to apply transmembrane potential across the epithelial monolayer. Two balance electrodes (BE1 and BE2) are used to control the intracellular potentials of 2 patched cells and to record the current flowing from or to BE1 or BE2 (i_BE1 or i_BE2) respectively. Upon the application of transmembrane potential, ion current flows across the epithelial cell layer through both paracellular pathways (i_para) and transcellular pathways (i_trans1 and i_trans2), and both i_trans are undesired background signal for the measurement of  paracellular conductance.

In this equation, E represents the electric field (potential gradient) induced by transepithelial potential V_TE and ρ is the specific resistance of the bath electrolyte. In P-SICM measurements, UE records local potentials at two D_ps (typically 0.2 µm and 12.5 µm above the cell junction or cell body), which are then used to calculate the electric field, knowing the pipet vertical displacement (Δz = 0.2 µm to 12.5 µm). To avoid polarization of the cell plasma membrane, an alternating transepithelial potential (V_TE) is utilized, at a frequency (typically 1 Hz) selected to minimize capacitive contributions. The magnitude of V_TE is usually held to less than 50 mV to avoid cell damage and disruption of the cell membrane.^29,30

We have previously shown that P-SICM results in significantly enhanced S/N of approximately an order of magnitude for potential measurement (compared to current measurement).^26,31 We have also demonstrated P-SICM as a sensitive tool to distinguish small differences in paracellular and transcellular conductance in cell monolayers and proposed that P-SICM can be utilized in leaky epithelia that cannot be measured by other techniques.

Double Whole-cell Voltage Clamp Ion Conductance Microscopy (DVC-ICM)

Despite advantages in tight junction recordings with P-SICM, the multitude of competing conductance pathways and the use of a nonzero probe-surface distance (D_ps) may result in systematic errors that arise from transcellular conductance artifacts. To be specific, in the P-SICM configuration, the application of transepithelial potential (V_TE) drives ions to move across the cell layer through both paracellular (cell junctions) and transcellular (membrane ion channels) pathways. The resultant currents are indicated as i_para and i_trans in Figure 1. An unknown fraction of i_trans (mainly from the two cells forming the cell junction under study) will inevitably be picked up by the pipet (or from the potential gradient point of view, i_trans can interfere with local gradients at cell-cell junctions), especially at a D_ps of ∼12.5 µm, where background conductance is measured (Equation 1). To more accurately record tight junction conductance, the background signal - i_trans from neighboring cells, has to be subtracted either through pharmacologic inhibition or mathematical deduction. However, pharmacologic inhibition would likely affect natural physiological processes, while the exact contribution from transcellular transport within neighboring cells of the measured tight junction needs to be known for the mathematical deduction approach, which turns out to be very difficult.

Here, we propose a new method to electrically offset contributions of i_trans from neighboring cells by coupling double whole-cell patch-clamps (commonly referred to as a double whole-cell patch-clamp)^32,33 with P-SICM measurements. The general idea of this method is to “zero out” the driving force for i_trans (due to the application of V_TE) by controlling the intracellular potential (membrane potential) of cells on either side of the tight junction with whole-cell patch-clamps. One reasonable assumption of this method is that i_trans from the two adjoining cells making the tight junction contribute to the major background signal in the previous P-SICM measurements at cell-cell junction compared to other cells that are further away from the junction (see detailed discussion below in “practical concerns” section).

Instrumentation

Figure 1 illustrates adaptation of the P-SICM instrumentation we have previously developed^26,31 to incorporate the double whole-cell patch-clamp. As in the previous P-SICM configuration, a double barrel pipet controls the probe position through the pipet electrode (PE) and measures local potential deflection at the potential electrode (UE). V_TE is applied to working electrode (WE) located on the basolateral side of the cell layer and a counter electrode (CE) close to the reference electrode (RE) drives the majority of the bulk ion current. The major instrumental advance is the addition of two micropipets that are patched to the two adjacent cells forming the cell junction being measured with P-SICM. We term these patched electrodes as “balance electrodes” (BEs). Each BE is controlled with a patch-clamp amplifier operating in voltage-clamp mode. During measurement, BE holds the intracellular potential at the resting membrane potential (E_rest) by providing a counter current (i_BE) through BE to eliminate the changes in intracellular potential due to the application of V_TE.

Equivalent circuit analysis

The origin of i_trans is the V_TE driven ion movement, which disrupts the natural resting membrane potential, which maintains a net i_trans of zero (although cellular processes generate a nonzero flux of specific ions). Therefore, the effect of V_TE on cell membranes must be “zeroed out” to eliminate the i_trans signal. To achieve this, DVC-ICM will clamp the membrane potential at E_rest value during the application of V_TE.

Figure 2A shows a proposed equivalent electric circuit for the DVC-ICM. Cell 1 and cell 2 are two adjoining cells that form a tight junction. At the cell junction, paracellular ion transport that occurs perpendicular to the epithelial cell layer is mediated through the tight junction, and the resistance of the TJ is represented as R_TJ. Gap junctions are also located in the cell junction and provide the primary path for ion transport between 2 cells. The resistance of the gap junction is R_GJ. For the cells, resistance of the apical membrane is indicated with R_maj (j=1 or 2, refers to cell 1 and cell 2 respectively) and resistance of the basolateral membrane is indicated by R_mbj (j=1 or 2). For each patch pipet, a series resistance R_Sj (j=1 or 2), which consists of the resistances of BE and the broken membrane patch, exists. Depending on the pipet geometry and electrolyte conductivity, R_S is typically on the order of 1-10 MΩ and draws a non-negligible voltage drop when current is passed through the patch pipet. The voltage drop across R_S causes V_j’ (j=1 or 2), the actual intracellular potential or so-called holding potential, to differ from the command voltage at BE (V₁ and V₂ in Figure 2A). Current flowing through each resistor is labeled with the same subscript as shown in Figure 2B.

Figure 2.

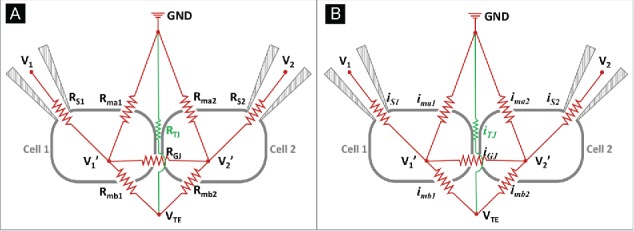
(A) Equivalent circuit of the DVC-ICM system. Here, tight junction conductance (reciprocal of tight junction resistance, R_TJ) of the junction formed by cell 1 and cell 2 is being measured with P-SICM (electrodes not shown). Cell 1 and cell 2 are voltage-clamped with two patch clamp pipets controlled with an individual patch clamp amplifier respectively. The intracellular potential of cell 1 (cell 2) is held at V₁’ through BE1 (BE2), where the holding voltage by patch clamp amplifier is V₁ (V₂). Series resistance R_S1 (R_S2) consists the resistances of BE and broken membrane patch from cell 1 (cell 2). Apical membrane resistance and basolateral membrane resistance are indicated separately with R_ma1 and R_mb1 for cell 1 and R_ma2 and R_mb2 for cell 2. R_GJ refers to the gap junction resistance through which ion current can pass between cell 1 and 2. (B) Ion current passing each resistor in (A) is labeled with the same subscript.

To simplify the circuit, R_GJ is omitted from the discussion, because the intracellular potential of cell 1 is considered to be equal to that of cell 2 in a uniform epithelial cell layer. Furthermore, the effects on the intracellular potentials of both cells from V_TE should be equivalent if 2 cells are considered “electrically” the same (gap junctional reversal potential is not considered here). Therefore i_GJ = 0 always holds, which means R_GJ can be considered an open circuit, and can be neglected in further circuit analysis.

With no external driving force - V_TE, the balance electrode potentials at patch pipets (V₁ and V₂) and the intracellular potentials remain at resting membrane potential value (E_rest, ∼ −70 mV) and the net ion currents across cell membranes (i_ma1, i_ma2, i_mb1, i_mb2) are zero. In this circuit, with the application of V_TE, ion movement will take place either through the paracellular pathway (R_TJ) or the transcellular pathway (R_mb1+ R_ma1, and R_mb2+ R_ma2). The value of V₁′ (or V₂′) will deviate from E_rest due to the non-zero i_mb1 (or i_mb2) driven by V_TE, and result in transmembrane current at the apical membrane side (i_ma1 and i_ma2). This is the case for previous conductance scanning and P-SICM measurements. In the DVC-ICM configuration, the two patch pipets inject compensating currents through the BEs to clamp V₁′ and V₂′ at E_rest in the voltage clamp feedback loop of the patch clamp amplifiers. Since V₁′ = V₂′ = E_rest, the driving force for i_ma1 and i_ma2 due to the application of V_TE is eliminated and hence i_ma1 = i_ma2 = 0. Under this condition, the P-SICM probe positioned over this “electrically isolated” cell-cell junction will only measure the signal generated from the paracellular conductive pathway. Another way of analyzing current flow in the circuit is shown in Figure 3. The two BEs that provide compensation current can be viewed as much less resistive pathways in the circuit, which serves to shunt the majority of current flow (compared to the apical membranes) coming from the basolateral membrane.

Figure 3.

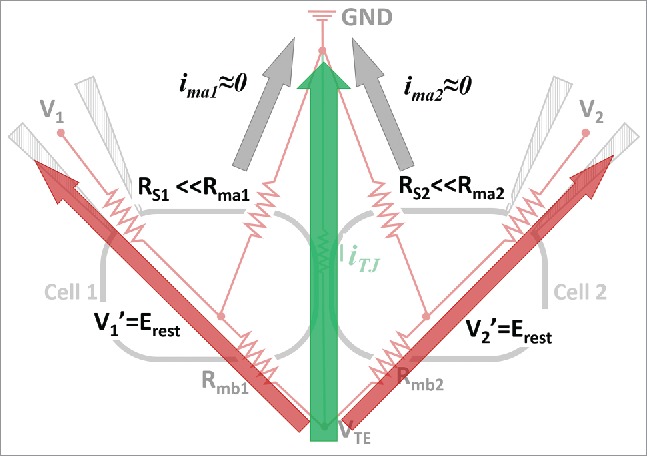
Intracellular potentials (V₁’ and V₂’) for both cell 1 and cell 2 are held at their E_rest to yield zero transmembrane current at the apical membranes (i_ma1 and i_ma2) during the application of transmembrane potential V_TE. Majority of V_TE induced basolateral membrane current (i_mb1 and i_mb2) is drawn through BE1 and BE2 (red arrows). Note: R_GJ is omitted from this circuit because V₁’ and V₂’ are always kept the same and there is no current through R_GJ.

Practical Concerns

Effects from neighboring cell-cell junctions

In the equivalent circuit shown in Figure 2A, only the resistance of the measured cell junction and the membrane resistance for 2 cells (cell 1 and cell 2) involved in forming this junction are considered. In a confluent epithelial cell layer, neighboring cells that are coupled to cell 1 and cell 2 by gap junctions will inevitably induce current flow to or from these 2 cells (Fig. 4A, green arrows). Additionally, the paracellular current at cell-cell junctions formed by cell 1 (or cell 2) with the neighboring cells (Fig. 4A, red arrows) may also be picked up by the P-SICM UE and hence contribute to background noise and unwanted signal for P-SICM measurements. Influence from these 2 effects is discussed here.

During P-SICM measurement, when a transepithelial potential (V_TE) is applied to the working electrode (WE, placed in the bottom chamber of the perfusion well) the intracellular potential for all cells in the epithelial layer will be altered by V_TE. In the proposed DVC-ICM model, only the two cells forming the junction under study are voltage-clamped at E_rest, which results in a difference in intracellular potential between either of the clamped cells (central green cells in Figure 4A, V₁′ or V₂′ in Figure 2A) and their closest neighbors (gray cells in the periphery in Figure 4A). Such intracellular potential differences may induce current flow through gap junctions (indicated with light green arrows around the 2 central cells in Figure 4A), which may interrupt V₁′ or V₂′ in a manner similar to i_mb1 or i_mb2 discussed above. Nevertheless, these effects will be detected and compensated by the patch clamp amplifiers connected to the BEs. In other words, the BEs will eventually offset additional gap junctional current flow between cell 1 and cell 2, as V₁′ and V₂′ are always held at E_rest. Therefore, the gap junction current through neighboring cells will not contribute to i_trans in the proposed DVC-ICM model. The junctional reversal potential due to any type of asymmetry (e.g., voltage gating property of connexins) is not considered here but may also be eliminated by clamping V₁′=V₂′ at E_rest.

Another possible effect arises from the paracellular ion current at tight junctions formed by either cell 1 or cell 2 with other cells adjacent to them. These paracellular currents are indicated with light red arrows (vs. the dark red arrow at the cell 1-cell 2 junction) oriented perpendicular to the epithelial layer in Figure 4A. Although the paracellular channel density may vary at different cell-cell junctions to result in intrinsic variation of the measured conductance, the signals from neighboring junctions would have to be estimated and minimized to make the recording as accurate and localized as possible. First, UE is held over the center of a bicellular cell junction ("vs". the edge or corner of junctions) where the lateral distance between UE and the closest neighboring cell junctions is the largest (e.g., ∼5-10 µm for epithelial cells such as MDCK). To estimate the relative potential field strength 5-10 µm away from versus at the field center (in this case, the tight junction), a previous mathematical model for calculation of potential distribution above a disk electrode is used.³⁴ Here, the tight junction channel at one individual cell-cell junction is treated as ideal nanopore geometry for simplicity. In this model, rotational elliptic coordinates $\xi$, $\eta$ and $a$ (nanopore inner radius) are used to express $z$ (the normal distance from the pore) and $r$ (distance from the axis of symmetry) as shown in Equations (2-3).

$$z=a\xi \eta$$ (2)

$$r=a\sqrt{\left(1+{\xi }^2\right)\left(1-{\eta }^2\right)}$$ (3)

The potential $\text{Φ}$ at a certain position can be determined as a function of $\xi$ (Equation 4, ${\text{Φ}}_0$ is the potential at the nanopore surface).

$$\frac{\Phi }{{\Phi }_0}=1- \frac{2}{\pi }ta{n}^{-1}\xi$$ (4)

Figure 4B shows the relative potential distribution (normalized to the potential value above nanopore center) at D_ps of 200 nm above the surface for different sized nanopores (pore radii are 1, 10, 100, 500 nm). Generally, the shape of the curve is not influenced by nanopore radius and the potential drops rapidly (by ∼90%) through distances within 2 µm from the nanopore center. At 5-10 µm from the pore center, the potential gradient changes very little and is approximately equal to the baseline value for the potential measured at a farther away distance (D_ps = 12.5 µm, simulation results not shown). Thus, at scales and potentials described here, we expect that contributions from nearby cell-cell junctions can be negligible. Controlling D_ps provides an additional route to minimize the signal from neighboring cell-cell junctions. As shown in Figure 4C, as D_ps decreases, the potential gradient above a 100 nm radius pore becomes sharper and results in a much more localized potential field.

Voltage-Gated Membrane Channels

Voltage-gated membrane channels are transmembrane ion channels that allow ion transport in response to changes in the membrane potential.^35-37 In P-SICM, V_TE is typically swept from -50 mV to +50 mV at 1 Hz. From previous studies, this potential range (at least at +50 mV) is sufficient to excite many types of voltage-gated channels, which will also contribute to i_trans. Because 1 Hz (the frequency V_TE is swept at) is much slower than the frequency needed to activate voltage-gated channels,³⁸ clamping the cell intracellular potentials at resting membrane potential (E_rest) can effectively avoid activation of voltage-gated membrane channels in the apical membrane and hence minimize the i_trans from these channels.

How Effectively can V1′ and V2′ be Clamped?

The equivalent electric circuit in Figure 2A includes key resistance components in the DVC-ICM system, other resistors and capacitors are added in Figure 5 and need to be considered to evaluate the accuracy and response speed in clamping the intracellular potentials of the two cells (V₁′ and V₂′).

Figure 5.

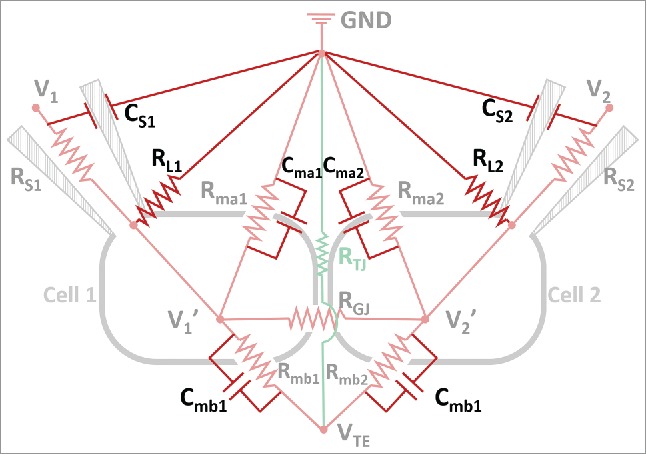
A more complete equivalent circuit of DVC-ICM system. C_S1 and C_S2 represent the capacitance of the patch clamp pipets glass wall. R_L1 and R_L2 are the “gigaohm seal” resistances at the sealed spaces between patch pipets and cell membranes. The cell membrane capacitances are indicated with C_ma1, C_ma2 (for apical membrane) and C_mb1, C_mb2 (for basolateral membrane).

First, the voltage drop across R_S1 (or R_S2) due to current flow through BE causes a difference between V₁ (or V₂), the amplifier command voltage, and V₁′ (or V₂′), the actual intracellular potential. This effect becomes more significant when R_S1 (or R_S2) is larger and cell membrane resistance becomes smaller. For instance, typical values for R_S1 (or R_S2) are on the order of 1-10 MΩ, and the cell membrane resistance can range from GΩ³⁹ to tens of MΩ,^40-42 dependent on the cell type. One way to accurately hold V₁′ (or V₂′) at E_rest is to set the value of V₁ (or V₂) as the sum of E_rest and the voltage drop across BE. To do this, the value of R_S1 (or R_S2) and the BE current need to be known.  Ion current at each BE is constantly monitored under V-clamp mode by the patch clamp amplifiers, while R_S1 (or R_S2) can be obtained by application of a test pulse of known amplitude between BE and RE (GND in Figure 5) and measurement of the corresponding current before and after formation of the gigaohm seal.

Second, in principle, the resistance of the sealed space (between pipet tip and cell membrane) should be infinite to guarantee no leakage current from the seal. In practice, however, the seal resistance (or leak resistance as R_L1 and R_L2 in Figure 5) is on the order of GΩ or hundreds of MΩ for a poor seal. R_L1 and R_L2 are in parallel with cell membrane resistances as shown in circuit in Figure 5. For highly resistive cell membranes, the seal resistances become comparable to membrane resistances and may need to be considered when setting the holding potential values. R_L1 and R_L2 can be measured in a manner similar to that described for R_S1 and R_S2 through the application of a test pulse.

Third, the RC response of the system, or the speed at which potentials are built up in the equivalent circuit should be evaluated. For example in cell 1, the changes in V_TE induce changes in V₁′, which is clamped by V₁ through the patch pipet R_S1. As shown in Figure 5, circuit components involved in this current path include V₁, R_S1, V₁′, R_mb1, C_mb1 and V_TE (capacitances for Ag/AgCl BEs are omitted because capacitive charging current is negligible for Ag/AgCl electrode). The response speed of the abovementioned current path is dominated by the RC circuit formed by R_S1 and C_mb1. R_mb1 is not included in the estimation of response speed because R_mb1 is a purely resistive path for ion current flow and hence the time-dependent current across basolateral membrane due to the sweeping of V_TE passes through C_mb1 instead of R_mb1. Consider R_S1 = 10 MΩ and C_mb1 = 30 pF, the RC time constant can be calculated by the product of R_S1 and C_mb1, which yields 0.3 ms. V_TE is swept at 1 Hz in P-SICM measurement and as such is much slower than the response speed of this RC circuit.

An alternative way to estimate the rate-dependent effect exerted on V₁′ by sweeping V_TE is to calculate the potential change on V₁′. Initially before any potential is applied to WE, V₁ and V₁′ are held at E_rest. As V_TE starts to change, a time-dependent current passes through C_mb1 and this current (I) can be calculated from the fundamental description of a capacitor and Equation 5 below.

$$\Delta V_{TE}·C_{mb1}=I\cdot \Delta t$$ (5)

In Equation 5, the product of the capacitance and voltage difference across a capacitor equals the charge on the capacitor. In this case, changes in V_TE ($\Delta V_{TE}$) during time $\Delta t$ induce the voltage difference across C_mb1 from the initial state, with $I$ representing current through C_mb1. Rearrangement of Equation 5 yields:

$$\frac{\Delta V_{TE}}{\Delta t}·C_{mb1}= I$$ (6)

where $\frac{\Delta V_{TE}}{\Delta t}$ represents the sweeping rate of V_TE. As described previously, V_TE is swept from −50 mV to +50 mV at 1 Hz and therefore 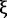$\frac{\Delta V_{TE}}{\Delta t}=0.2V/s$ . The current 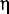$I$ is calculated to be 6 pA according to Equation 6 if 30 pF is used for C_mb1. The current $I$ then flows through R_S1 to the amplifier and V₁ = V₁′ no longer holds. If R_S1 = 10 MΩ, a 60 µV ($I·R_{S\mathit{1}}$) voltage difference is induced by V_TE through the RC circuit, which is small enough to be compensated by patch clamp amplifier. One thing worth mentioning is that, the patch clamp amplifier response speed in controlling V₁ is not discussed because the frequency of V_TE is much smaller than the upper limit of signal frequency (tens to hundreds of kHz) accessible by most patch clamp amplifiers.

Conclusion

We have described an approach to isolate and measure paracellular ionic permeability, with minimal contributions from transcellular pathways. The approach is based on previous developments in potentiometric scanning ion conductance microscopy and voltage clamp methods. Ultimately, we expect the approach described here will lead to definitive measurements of ion permeation through tight junctions, especially at nanometer scales, and with the potential of identifying discrete conductance events of the paracellular ion channels. This new approach will allow revealing previously unknown aspects of the tight junction in physiological and pathophysiological processes.

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Acknowledgment

We acknowledge Andy Alexander of Indiana University EIS for enlightening discussions.

Funding

This work is supported by grants from National Institute of Diabetes and Digestive and Kidney Diseases - RO1DK084059 and Department of Defense - HDTRA1-11-16-BRCWMD-BAA.