Phase Resetting Behavior in Human Gait is Influenced by Treadmill Walking Speed

Abstract

Gait is often modeled as a limit cycle oscillator. When perturbed, this type of system will reset its output in a stereotypical manner, which may be shifted in time with respect to its original trajectory. In contrast to other biological oscillators, relatively little is known regarding the phase resetting properties for human gait. Because humans must often reset their gait in response to perturbation, an improved understanding of this behavior may have implications for reducing the risk of fall. The purpose of this study was to further evaluate phase resetting behaviors in human gait with particular emphasis on 1) variance of the phase resetting response among healthy individuals, and 2) the sensitivity of this response to walking speed. Seventeen healthy subjects walked on a treadmill at 2.0 mph, 2.5 mph, and 3.0 mph while their right limb was perturbed randomly every 12–20 strides. Discrete, mechanical perturbations were applied by a rope that was attached to each subject’s ankle and actuated by a motorized arm. Perturbations were applied once during a select stride, always at a different point in the swing phase, and the amount of phase shift that occurred on the subsequent stride was recorded. A subset of 8 subjects also walked at their preferred walking speed for 3 additional trials on a separate day in order to provide an estimate of within-subjects variability. The results suggested that phase resetting behavior is relatively consistent among subjects, but that minor variations in phase resetting behavior are attributable to walking at different treadmill speeds.

INTRODUCTION

Unintentional falls are a significant public health problem among aging and diseased populations. Unexpected perturbations are an important cause of falls that occur during walking [1, 2]. Effective solutions to fall prevention may therefore be related to an improved understanding of the human locomotor response to perturbation.

A promising approach to understanding gait stability involves modeling gait as a limit cycle oscillator [3, 4]. During human gait, oscillator dynamics arise from a variety of mechanisms, including the biomechanical properties of limbs (i.e. passive dynamic walking [3, 4]) and the output of the central pattern generator (CPG) [5]. This approach is convenient because a limit cycle oscillator responds to perturbations in a stereotypical manner and this behavior can help to explain how unanticipated events might contribute to falling. For example, when a healthy person stumbles, they quickly reset their limit cycle in a predictable manner and continue walking [6–9]. While there is some debate as to whether gait can be considered a true limit cycle oscillator, several previous investigations have demonstrated the utility of this approach for understanding locomotor control (e.g. [3, 4, 6, 9, 10]).

The response of a limit cycle oscillator to perturbation can be characterized by examining its phase resetting properties. These properties have been studied extensively in several biological systems, including neurons [11–13], circadian rhythms [14], and cardiac cells [15]. This behavior is succinctly described in terms of a phase resetting curve (PRC), which represents the transient change in the cycle period of an oscillator induced by a perturbation that is a function of the phase in which it is received [16, 17]. This curve is often established by perturbing a system at different phases and measuring the amount of phase shift that occurs when the cycle is reset. Once established, the PRC for a biological oscillator can be a valuable and rich source of information.

There are good reasons to suspect that the measurement of the PRC for human gait holds implications for understanding the risk of falling. For example, Nomura et al. (2009) utilized a walking simulation to demonstrate that the probability of falling in response to a small perturbation is related to the phase reset [6, 7, 9, 18]. These simulations were designed using a PRC that had been recorded previously in walking humans by introducing a brief stimulus that resisted motion of the swing leg [9]. The results suggested that a phase resetting response that deviated from the observed PRC in healthy humans is likely to place an individual at greater risk for fall. Other observations suggest that phase resetting in response to perturbation is abnormal in older adults. These include video motion capture of falls [1] and responses to lateral perturbations (i.e. slip) of the walking surface [19–21]. Moreover, additional data suggest that a phase-dependent modulation of the limit cycle is typical of human walking, and effective use of positive (lengthened) or negative (shortened) resetting dynamics can reduce a person’s risk for fall [8, 22–25].

In comparison to other biological phenomena, the PRC for human gait is currently not well defined. Several studies have demonstrated that, in general, perturbations applied early during the swing phase of gait result in a flexor response, which prolongs swing and results in a delay of the onset of the next step. In contrast, perturbations that occur later during swing result in an extensor response, which shortens swing and results in an advance of the next step [8, 22, 23]. However, this behavior has only recently been studied under the paradigm of the PRC [13]. In addition, this behavior may not be consistent for individuals with impairment or those walking under less than ideal conditions.

Several questions remain regarding the nature of phase resetting behavior in human walking. For example, one previous study in neurons reported that different cells exhibit different PRC’s, and the shape of these PRC’s was sensitive to changes in the baseline firing rate of the neuron [13]. These results imply that the PRC for human gait may also vary among healthy individuals and these curves may be affected by an individual’s walking speed (analogous to baseline firing frequency in a neuron). Therefore, the purpose of this experiment was to examine the phase resetting curve among young healthy walkers to determine if 1) differences exist between individuals, and 2) phase resetting responses are altered by changes in treadmill walking speed. In addition, an analysis of the number of cycles (i.e. strides) required for an individual to return to their normal cycle length following perturbation is provided.

METHODS

Subjects

A convenience sample of 17 healthy male and female subjects was recruited from the local student population (age 25.6±4.9yr, mass 66.0±14.8kg, height 1.7±0.1m). All subjects were free of musculoskeletal or neurological conditions that may have affected gait. Approval for these procedures was obtained through the Institutional Review Board at California State University, San Marcos, and all subjects gave their informed consent before participation.

Apparatus

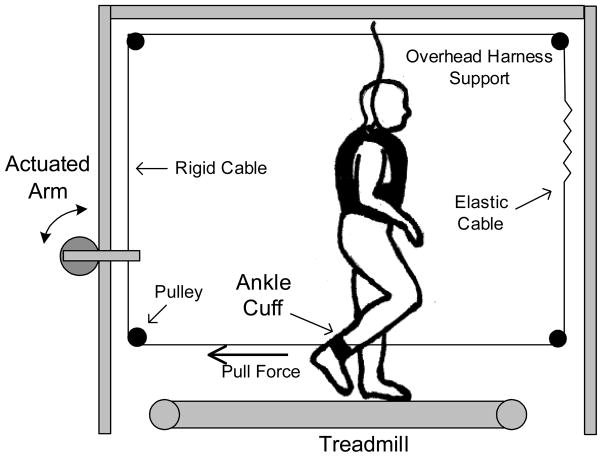
Subjects walked on a treadmill with both side rails and control panel removed. Both ends of a lightweight rope were attached to their right ankle (Fig 1). This rope was routed through a loop via low friction pulleys, beginning from behind the subject’s ankle, through a mechanical arm mounted behind the treadmill, overhead, and then to the front of the subject where it attached again on the anterior aspect of the same ankle. A small section of this loop in front of the subject was elastic to allow the ankle to move in three dimensions, as occurs normally during swing. This loop was under a small amount of tension to ensure that it remained taut. With each step, the rope was pulled forward and backward along its loop by the action of the stepping subject. This configuration provided very little resistance to normal movement of the ankle in the sagittal plane.

Fig. 1.

Experimental Setup.

Perturbations were applied directly to a section of the rope that was highly inelastic. A ¼ Hp DC electric motor (Bison Gear & Engineering Corp.) was used to actuate a mechanical arm, which performed discrete pulls on the rope from behind the subject with a peak force up to 180 N and an average rise time of 0.125 seconds. An overhead harness system was used to ensure safety but did not provide any support of body weight. Specialized harnesses were used to avoid any interference with lower extremity motion (Maine Anti-Gravity Systems, Inc.).

Control of the apparatus was provided by a custom program written in Matlab’s xPC Target (Natick, MA). Each walking trial was completely automated using feedback received from specialized insoles worn by subjects in their right shoe (B&L Engineering). These insoles were instrumented with foot switches at the heel, base of the 1^st and 5^th metatarsals, and the great toe, and these sensors were used to determine the onset and end of swing. Once a trial was initiated, the system was programmed to apply a single, discrete perturbation in a pseudorandom fashion every 12–20 strides. The within-stride timing of perturbations followed a simple algorithm in which each pull advanced in time by 5% of the subject’s average swing duration (determined during warm-up). The trial ended after 19 pulls, ensuring that perturbations were applied throughout the entire swing phase. This yielded an average of 300 strides per trial, and each trial was approximately 5–6 minutes in duration. All pulls occurred during the swing phase of the perturbed limb. No perturbations were applied during the stance phase as it was previously demonstrated that phase shift is minimal during stance for this type of perturbation [7].

Data Collection and Analysis

Prior to data collection, subjects were asked to walk on the treadmill for a period of 2 minutes in order to become familiar with the harness, treadmill, insole, and ankle cuff. Each subjects’ preferred walking speed (average: 2.56±0.23 mph) was determined during this 2 minute warm-up. Subjects then performed 3 different trials at 3 different treadmill speeds: 2.0 mph, 2.5 mph, and 3.0 mph. A subset of subjects (n=8) also performed 3 additional trials at their preferred walking speed (2.54±0.12 mph) on a separate day in order to provide an estimate of within-subject variability. Preferred walking speed trials followed the automated procedure outlined above.

The following analysis is consistent with standard pulse-PRC methods [26]. Custom routines in Matlab were developed to analyze data offline by calculating the amount of phase shift (in seconds) that occurred immediately following perturbation. In other words, did the step immediately following perturbation arrive ahead or behind schedule? The amount of phase reset was calculated using

$$\mathrm{\Delta }\varphi =\varphi -{\varphi }^{\prime }=\frac{T^{\prime }}{T}-1$$

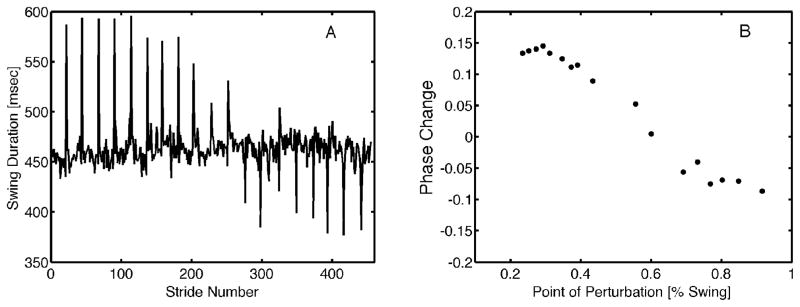
where T′ is the period of the perturbed cycle, T is the period of the original cycle, ϕ is the phase of the original cycle in which the perturbation was applied, and ϕ′ refers to the new phase (after perturbation). This notation assumes that phase is defined between 0 and 1. A negative phase reset indicates that the cycle was shifted forward in time (i.e. the next step arrived early), while a positive phase reset indicates that the cycle was shifted backward in time (i.e. the next step was delayed). Sample data from a single subject for a single trial are provided in Figure 2. The PRC was defined in terms of swing cycle percentage, beginning at toe off (0%) and ending at heel strike (100%).

Fig. 2.

A) Sample PRC from a representative subject. The high amplitude changes in swing duration are the strides when the perturbation was applied. B) Phase advance or delay (ΔΦ) is plotted vs. the point in swing at which the perturbation was applied. In this context, 0 = toe off and 1 = heel strike.

Differences between PRCs were calculated as follows. To explore whether differences existed between subjects (i.e. analogous to different PRCs for different neurons), the variance observed between subjects was compared to the variance observed within subjects. Variance was calculated in each case by finding the RMS difference of each individual PRC with respect to a PRC criterion, and then calculating the coefficient of variance of this RMS difference across subjects (for between subjects variance) or across walking trials (within subjects variance). Within-subjects variance was calculated specifically as the coefficient of variance of the RMS difference across the 3 preferred walking speed trials for 8 subjects. The criterion PRC used in all cases was a 6-degree polynomial that was fit to the aggregate data from the first trial of the subset of 8 subjects that completed trials at their preferred walking speed.

To determine whether differences existed across different walking speeds, two approaches were used. First, the data for all subjects were combined to create an aggregate PRC for each walking speed. Within the PRC for each speed, data were separated into epochs of 5% based on the point in swing at which the perturbation was applied. Means and standard deviations were calculated for each epoch, and data points contained within each epoch were compared statistically with data points contained within the same epoch for a different walking speed. A Mann-Whitney U test was used to determine if differences existed. A second, within-subjects analysis was also utilized. Here, each subject’s performance at each walking speed was compared to the same criterion PRC used above by calculating the RMS difference. The mean RMS difference for all subjects was then compared across walking speeds using a Mann-Whitney U test.

Finally, the amount of time required for subjects to return to their “normal” cycle length following perturbation was analyzed by comparing 1) their average swing time for 4 strides just prior to perturbation, 2) the average swing time for the perturbed stride, and 3) the average swing time for each of the next 6 strides following perturbation. For each subject, perturbations that occurred early in swing (causing phase delay) were analyzed separately from those that occurred late in swing (causing phase advance). Differences in average swing time between baseline (prior to perturbation) and each step after perturbation were compared using a Mann-Whitney U test. Due to the high number of statistical comparisons required for this analysis, the Bonferroni correction was applied to reduce the chance of type 1 error resulting from multiple comparisons (α = 0.05/20).

RESULTS

The sinusoidal shape of the aggregate PRC curve shown in Figure 3 has been observed for a number of limit cycle oscillators [26] and in particular is similar to the PRC reported by Kobayashi et al. (2000) for the right limb. The PRC was Type II because it contains both a phase advance and phase lag at different points in the curve. Further, the magnitude of phase shifts observed here were comparable to those reported by others [9]. There was no evidence that the PRC varied across participants. The variance in phase resetting behavior within the same subjects across multiple trials was similar to the variance that was measured between subjects for any of the walking trials (mean coefficient of variance of 22% between subjects vs 28% within subjects).

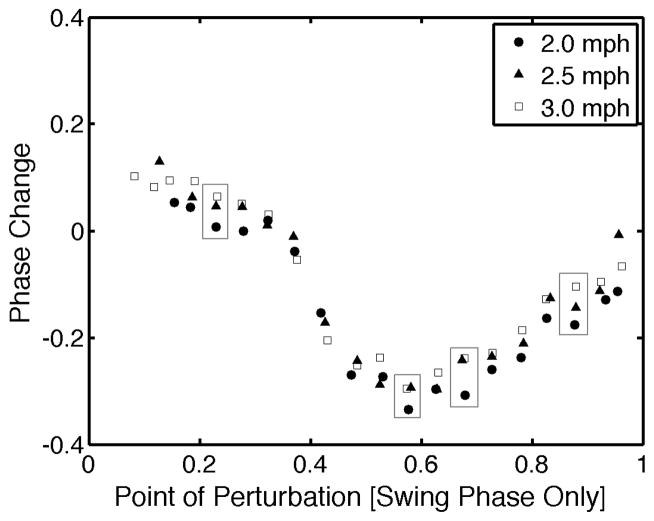
Fig. 3.

Epoch means for all 17 subjects walking at 3 different treadmill speeds. Large boxes indicate epochs where mean phase shift at 2.0 mph was significantly different from at least one of the other treadmill speeds.

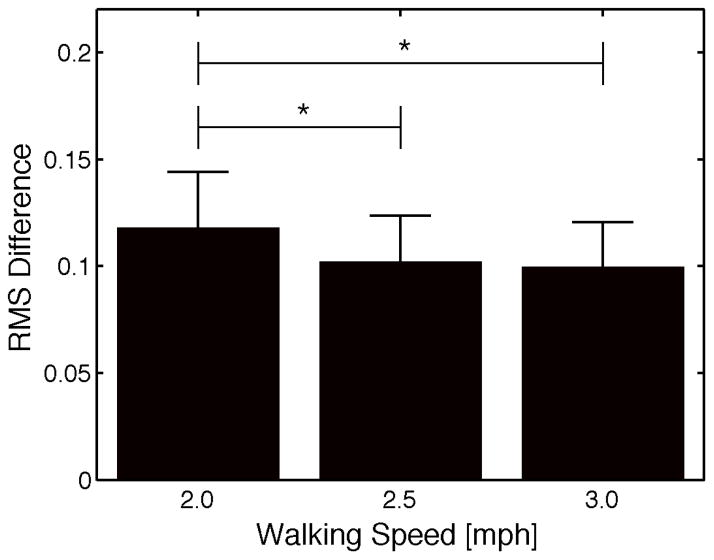
However, there were differences in the phase resetting response for multiple epochs, or regions of the PRC, when different walking speeds were compared. Generally speaking, subjects tended to demonstrate less of a phase lag and more of a phase advance to perturbations while walking at 2.0 mph compared to 2.5 or 3.0 mph. Figure 3 illustrates the 4 epochs where a significant difference was noted between the average phase change at 2.0 mph and at least one of the other walking speeds. No significant differences were found for any epochs between the 2.5 mph and 3.0 mph trials. In addition, subjects demonstrated significantly greater deviation from the “criterion” PRC during the 2.0 mph trial when compared to both the 2.5 mph and 3.0 mph trial (Fig 4, p<0.001).

Fig. 4.

Comparison of the mean RMS difference from a criterion PRC at each treadmill speed. Trials at 2.0 mph demonstrated significantly greater RMS differences than those observed at 2.5 and 3.0 mph. Bars represent standard error of the mean.

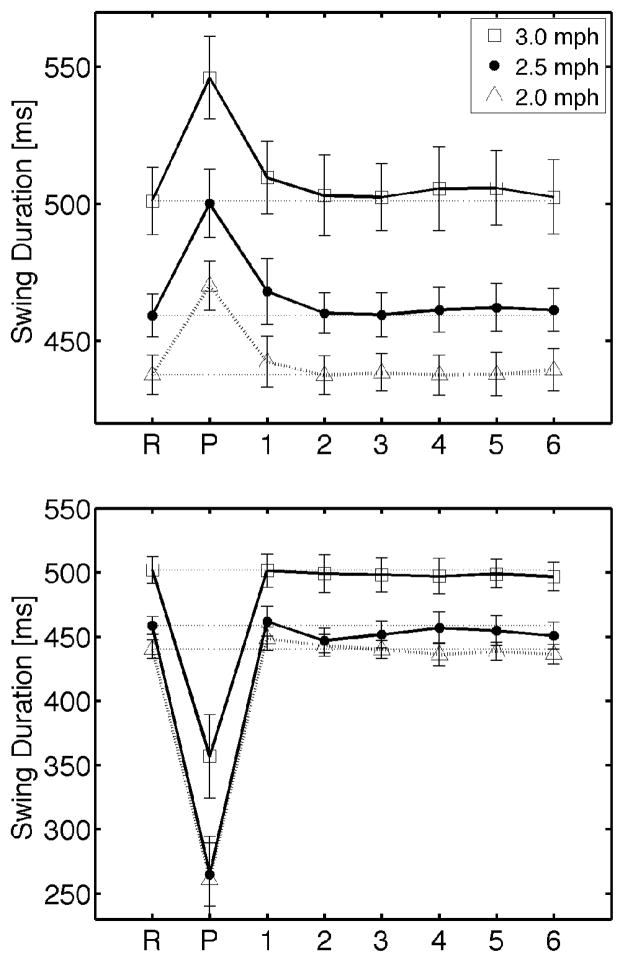
There were significant differences in average swing duration when strides just prior to perturbation were compared to the perturbed stride for all walking speeds (Mann-Whitney U test, p<0.001). Swing duration did not appear to return to baseline by the stride immediately following perturbation (Figure 5), though no significant differences in stride duration were observed (Mann-Whitney U test, range of p=0.055 to 0.92).

Fig. 5.

Mean swing duration before, during, and after discrete ankle perturbation for three walking speeds. R: reference swing duration taken from strides immediately before perturbation, P: perturbed stride, 1–6: strides following perturbation. TOP: perturbations that occurred in early swing resulting in a lengthening of the swing phase. BOTTOM: perturbations that occurred in late swing resulting in a shortening of the swing phase. Bars represent standard error of the mean.

DISCUSSION

The results of this experiment suggest that the PRC for human gait is relatively consistent among healthy adults while walking at the same treadmill speed. However, phase resetting behavior appears to be affected by one’s walking speed. In particular, walking at a treadmill speed slower than one’s preferred speed led to a reduction in phase delay for perturbations delivered early during swing and an increase in phase advance in response to perturbations delivered in later swing (Fig 3). These results may be limited by the fact that perturbations were not applied at random points during swing. However, there was a relatively high number of strides between perturbations and the strides selected for perturbation were randomized. Though these results were obtained in healthy subjects, they provide some context from which the PRC might be evaluated in other populations including older adults or those with neurological impairment.

Previous research suggests that even subtle variations in the PRC can place an individual at greater risk for fall [7]. Therefore, it is not surprising that there should be a relatively consistent PRC across healthy individuals age 20–40. However, the current data also suggest that phase resetting behavior varies with changes in walking speed. This result is consistent with several other aspects of gait, including changes in statistical persistence (detrended fluctuation analysis) of stride length and time [27] and maximal Lyapunov exponents of lower limb kinematics [28]. In particular, Jordan et al (2007) reported that statistical persistence of multiple variables was greater at 80% than at 100% of one’s preferred walking speed and suggested that this may reflect a decrease in the adaptability of gait when walking at slower speeds. Others have also suggested that humans are less flexible at non-preferred speeds [29], and it is therefore not surprising that the PRC might also be modified at different treadmill speeds. Modifications in the PRC might be a type of compensation for changes in adaptability, or may be the direct result of a reduction in the number of possible solutions to the movement problem of advancing the leg in a stable manner. In addition, increased risk of fall may be related to an inability to quickly determine the most effective response to a perturbation, particularly if it were to occur at a point near the interface between a phase delay or phase advance response (around 35% of swing in the current data).

When fast and slow walking speeds are compared, the current data suggest that slower walking speeds lead to greater deviation from the PRC at one’s preferred walking speed. This idea may be related to the time required for the system to return to its unperturbed cycle length. Other investigators have suggested that the speed at which an oscillator returns to its unperturbed cycle length may affect measurement of the PRC [16, 30]. Though no significant differences were noted in the current data, when subjects’ baseline swing duration was compared to that of the stride immediately following perturbation, the difference at 2.0 mph was greater than that observed for the other speeds (e.g. 501±43ms vs 510±46ms swing duration, p=0.055 for 2.0 mph). This difference may approach significance with additional subjects. Alternatively, it is possible that cycle length is restored at some point within the stride immediately following the perturbation, and an analysis that involves finer resolution of the phase in the gait cycle may help to determine more precisely the point at which phase reset is most often completed.

In summary, phase resetting behavior appears to be consistent across healthy individuals yet is sensitive to changes in walking speed. These results may have implications for multiple areas of study, most notably in an individual’s risk for fall. Further application can be found in gait entrainment, which involves a constant monitoring of the difference between one’s stepping and that of an external signal. Because gait must be reset often in order to maintain a desired phase relationship between walking pairs, synchronization may be characterized as a function of the PRC of each individual. This analytical approach has been used to model and predict behavior in synchronizing neurons [13]. The PRC may also have application in the design and control of bipedal walking robots that must also respond appropriately to external perturbation [6, 7].

Highlights.

• We applied mechanical perturbations during swing and measured stride cycle reset.

• Stride reset varied as perturbations were applied at different points during swing.

• This behavior was consistent across healthy adults.

• However, stride-resetting behavior was altered at different treadmill speeds.

• Fall risk may be related to stride cycle reset following unexpected perturbation.