Abstract
Background: Abdominal aortic aneurysm (AAA) growth is a complex process that is incompletely understood. Significant heterogeneity in growth trajectories between patients has led to difficulties in accurately modeling aneurysm growth across cohorts of patients. We set out to compare four models of aneurysm growth commonly used in the literature and confirm which best fits the patient data of our AAA cohort. Methods: Patients with AAA were included in the study if they had two or more abdominal ultrasound scans greater than 3 months apart. Patients were censored from analysis once their AAA exceeded 5.5 cm. Four models were applied using the R environment for statistical computing. Growth estimates and goodness of fit (using the Akaike Information Criterion, AIC) were compared, with p-values based on likelihood ratio testing. Results: Of 510 enrolled patients, 264 met the inclusion criteria, yielding a total of 1861 imaging studies during 932 cumulative years of surveillance. Overall, growth rates were: (1) 0.35 (0.31,0.39) cm/yr in the growth/time calculation, (2) 0.056 (0.042,0.068) cm/yr in the linear regression model, (3) 0.19 (0.17,0.21) cm/yr in the linear multilevel model, and (4) 0.21 (0.18,0.24) cm/yr in the quadratic multilevel model at time 0, slowing to 0.15 (0.12,0.17) cm/yr at 10 years. AIC was lowest in the quadratic multilevel model (1508) compared to other models (P < 0.0001). Conclusion: AAA growth was heterogeneous between patients; the nested nature of the data is most appropriately modeled by multilevel modeling techniques.
Keywords: Abdominal aortic aneurysm, Growth rate, Quadratic, Multilevel modeling
Introduction
An abdominal aortic aneurysm (AAA) is a focal dilatation of the abdominal aorta, greater than 3 cm in diameter or 1.5 times the diameter of the adjacent normal aorta. In clinical practice and in the UK AAA National Screening Programme (http://aaa.screening.nhs.uk), once the infrarenal aorta reaches 3.0 cm in its maximal anteroposterior (AP) diameter, it is classified as aneurysmal. The event(s) that trigger AAA development remain unknown. Important clinical risk factors include male sex, smoking, hypertension, and a family history of the condition [1]. Once established, AAA progressively evolves toward rupture, which confers high mortality.
Rupture risk is positively associated with aneurysm size. Presently, the mainstay of clinical management involves active monitoring, smoking cessation therapies, and cardioprotective medication, with prophylactic repair once the annual risk of rupture outweighs the mortality risk of intervention. This intervention threshold is currently set at 5.5 cm (on abdominal ultrasonography) in otherwise fit patients, based on randomized trial data [2]. Aneurysm screening is effective at reducing mortality from AAA rupture in men and is being increasingly adopted in many developed countries [3]. The recent report from the RESCAN collaborators suggests surveillance intervals could be safely increased, with significant cost savings [4].
Aneurysm growth is a complex process that is not necessarily linear and remains a relatively poorly explored area in the literature. Many authors have noted significant heterogeneity in aneurysm growth patterns between patients [5–7]. This has led to difficulties in attempts to report pooled growth estimates for patient cohorts [7]. A variety of growth modeling strategies have been reported previously [8], but direct comparisons within a single-center patient cohort are lacking. The aims of this study were (1) to compare a range of models to estimate aneurysm growth and (2) to confirm the most appropriate modeling strategy for estimating growth in a cohort of patients by testing the goodness-of-fit of each model to data derived from our patient cohort.
Materials and Methods
Patients
Consecutive patients referred to our institution, a university hospital vascular surgery unit, serving a local population of 800,000 in the United Kingdom with a diagnosis of AAA between January 1, 2003 and April 31, 2010 were invited to participate in the Leeds Aneurysm Development Study (LEADS) on a voluntary basis. The inclusion and exclusion criteria for LEADS have previously been reported [9–11]. Ethical approval was given by the institutional ethics committee (Project Reference: 03/142). At recruitment, all patients gave written, informed consent and completed a standardized health questionnaire which was administered face-to-face by a research nurse (A.J.).
Imaging
Maximal aortic diameter in the anteroposterior plane was measured with B mode abdominal ultrasound (USS) using an Acuson Antares scanner (Siemens Healthcare, Malvern PA, USA). Calipers were placed on the outer wall of the sac, producing outer wall- to-outer wall (OTO) maximal aneurysm diameter measurements, which reflected departmental practice during the study period. Scanning intervals were based on the UK Small Aneurysm Trial [12], arranged by the clinician in charge of the patient's care. Enrollment in the study had no impact on normal clinical care. Patients received surveillance until they underwent aortic repair, died, or withdrew from the study. Scans performed in our department prior to recruitment were also included, with patient consent, and thus the earliest imaging study dates from February 1994. All USS were performed by experienced vascular sonographers; variability for the department has been previously reported [13].
Inclusion and Exclusion Criteria
Patients from LEADS were included in the present study if they had an infrarenal abdominal aortic aneurysm (defined as an infrarenal aortic diameter ≥ 3 cm or 1.5 times the diameter of the adjacent aorta) and agreed to participate in the study [10,11]. We only included imaging data from patients with two or more USS performed a minimum of 3 months apart, while the aneurysm was ≤ 5.5 cm in maximal diameter for the modeling comparisons. Patient data were censored from the analysis once the aneurysm exceeded the 5.5 cm intervention threshold on USS, as it is possible that growth patterns in large aneurysms, above the intervention threshold, differ from those beneath it, and this falls outside the remit of the present study.
Statistics
We applied four growth models to the data: (1) simple growth/time analysis, (2) ordinary linear regression model, (3) linear multilevel model (MLM), and (4) quadratic MLM. All models were constructed by a biostatistician (P.B., T.J.) using the R environment for statistical computing (www.R-project.org).
Simple growth/time analysis (1) involved dividing the difference between the first and last aortic diameters (centimeters) by the length of time between the two measurements (years). An ordinary linear regression model (2) [14] was fitted with aortic diameter as the response element and time from the initial scan as the predictor. A parametric, linear MLM (3) with two levels and measurements nested within patients [15,16] was fitted by full maximum likelihood, with aortic diameter as the response element and time from the initial scan as the fixed predictor. A random, normally distributed intercept term and a random, normally distributed slope term were added for each patient. A quadratic MLM (4) [15,16] was also fitted using the same basic structure as the linear MLM, with the addition of both a fixed effect and a random, normally distributed slope term that were quadratic in time (modeled up to 10 years).
Model comparisons were conducted using the Akaike Information Criterion (AIC) together with p-values based on likelihood ratio testing. Lower values of AIC represent a more parsimonious fit of the model to the data set and provide a measure of how well the model represents the patient data on which it is based. Data are presented as mean (95% confidence intervals) or mean ± standard deviation unless otherwise stated. A p-value <0.05 was set as the predetermined level of statistical significance.
Results
Study Population
Five hundred and ten patients with AAA were enrolled in LEADS during the study period. Of these, 264 met the inclusion criteria for the present analysis. Data were available from 1861 suitable imaging studies for modeling comparison. Each patient contributed an average of 7 ± 3 USS measurements to the study during 932 cumulative years of surveillance (mean 3.5 ± 2.5 years/patient). The mean aneurysm size at recruitment to the study was 3.8 ± 0.7 cm, increasing to 4.7 ± 0.7 cm at the end of the study period. The mean age of the study population was 74 ± 2 years at recruitment; 81% were men. The results of the medical questionnaire are provided in Table 1. As expected, there was a high proportion of hypertensive ex-smokers (mean pack years smoked, 43) with a range of cardiovascular comorbidities. Of these, 197 of 264 (74.6%) were receiving antiplatelet therapy, 175 of 264 (66.3%) statins, and 181 of 264 (68.6%) at least one antihypertensive medication (beta blockers, angiotensin converting enzyme inhibitors, angiotensin II receptor antagonists, or calcium channel blockers).
Table 1.
Clinical Characteristics of the Study Population
| n | % | |
|---|---|---|
| Ever smoker | 238 | 90.2 |
| Hypertension | 157 | 59.5 |
| Peripheral vascular disease | 86 | 32.6 |
| Myocardial infarction | 69 | 26.1 |
| Current smoker | 66 | 25.0 |
| Cerebrovascular disease | 53 | 20.1 |
| Diabetes mellitus | 37 | 14.0 |
| CABG | 28 | 10.6 |
| Family history AAA | 16 | 6.1 |
| DVT/PE | 15 | 5.7 |
Hypertension was defined as a clinical history of the condition or the use of antihypertensive medication. Peripheral vascular disease was defined as a clinical history of claudication or an ankle-brachial pressure index of < 0.8. Myocardial infarction was defined as a known clinical history of the condition or q waves on the recruitment ECG. Cerebrovascular disease included both completed stroke and transient ischemic attack. CABG = coronary artery bypass grafting, DVT = deep venous thrombosis, PE = pulmonary embolism.
Growth Modeling Estimates
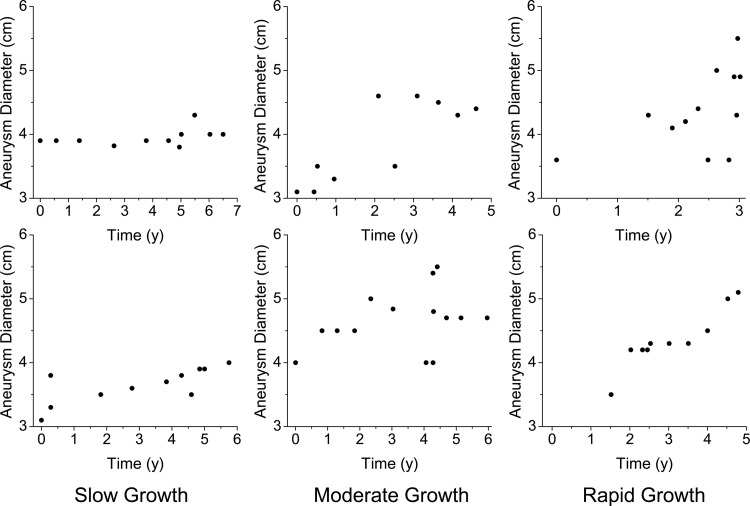
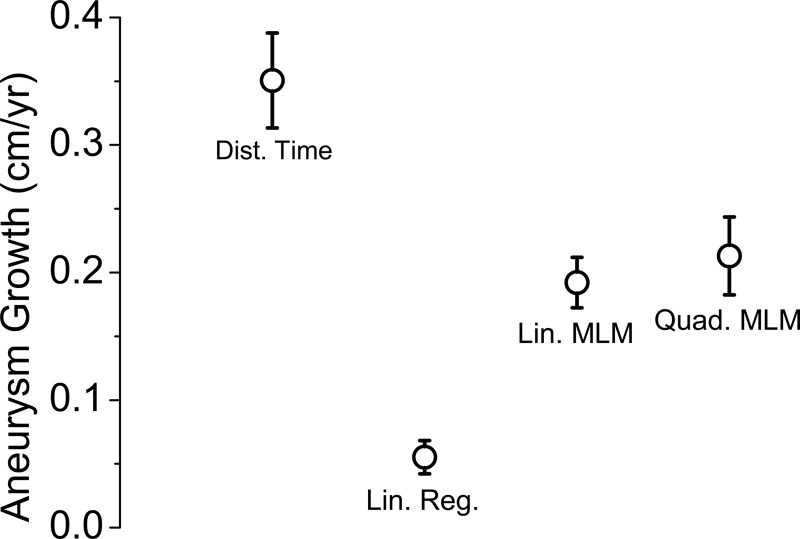
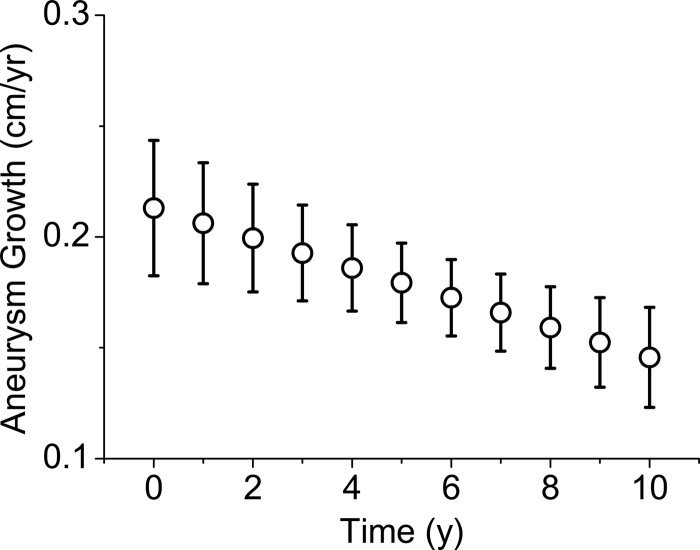
As expected, aneurysm growth was heterogeneous across the study population. Illustrative scatter plots of patients exhibiting slow, moderate, and rapid aneurysm growth are provided in Figure 1. Overall growth estimates for the cohort by model were: (1) simple growth/time model: 0.35 (0.31,0.39) cm/yr, (2) ordinary linear regression model: 0.056 (0.042,0.068) cm/yr, (3) linear MLM: 0.19 (0.17,0.21) cm/yr, and (4) quadratic MLM: 0.21 (0.18,0.24) cm/yr, at time zero (see Fig. 2), slowing to 0.15 (0.12,0.17) by year 10 (see Fig. 3). The residuals were normally distributed for models (2), (3), and (4).
Figure 1.
Example growth trajectories of patients with slow growth (left), moderate growth (center), and rapid growth (right).
Figure 2.
Comparison plot of growth estimates by model. Each point represents growth estimate with 95% confidence intervals. Dist. Time = (1) growth/time calculation, Lin. Reg. = (2) ordinary linear regression model, Lin. MLM = (3) linear multilevel model, Quad. MLM. = (4) quadratic multilevel model (estimate at time zero).
Figure 3.
Aneurysm growth estimates for the quadratic multilevel model plotted at annual intervals over a 10 year quadratic growth model. Each point represents growth estimate with 95% confidence intervals.
Goodness-of-Fit Analysis
It is not possible to calculate the AIC for the simple growth/time model (1). For the ordinary linear regression model (2), AIC: 3819. For the linear MLM (3), AIC: 1527, P < 0.0001 compared to model (2). For the quadratic MLM (4), AIC: 1508, P < 0.0001 compared to model (2) and P < 0.0001 compared to model (3).
Discussion
In this study, we have modeled aneurysm growth in a cohort of 264 patients with infrarenal AAA below or at the intervention threshold and compared four statistical modeling approaches which have been previously used in the literature. We have demonstrated that the four different models applied to our data produced heterogeneous estimates of aneurysm growth.
The simple growth/time calculation produced an overestimate of growth compared to the MLM estimate. We relate this to the observation that the last scan in the series is more likely to be an overestimate (due to observer variability in measurement) that triggered intervention and hence was never corrected by further scans. When used as the second of two data points to calculate growth, this leads to bias in favor of overestimation. It is also possible that negative growth rates could be produced by this method; however, we did not observe this in our analysis. Further, the method is significantly weakened by the fact that it ignores the majority of the data points (71.6% of data points in our study are ignored by this method, for example). AIC cannot be calculated for this method of growth estimation as there is no statistical model underlying the growth process that can be tested.
When applied to our data, an ordinary linear regression model underestimated growth as compared to all other models with heavily autocorrelated residuals. We hypothesize that this may be related to the differences in individual growth trajectories that are attenuated when trajectories are pooled across patients, coupled with the fact that the model ignores the multilevel structure of these data. Patients with slow-growing AAA tend to have a larger number of scans in total, which may compound bias in the model toward slow growth. Using a linear regression model does include all data, in contrast to the growth/time calculation, but analyzes all scan data for all patients together. This represents a statistical error; the assumptions of the model are not met by these data, as scans from the same patient are related through growth and thus are not independent, as is required for simple linear regression analysis. We suggest that this is therefore an invalid method of modeling this type of data, the growth estimate of which is completely inaccurate and should be ignored.
In MLM, each patient contributes to the overall growth estimate, but an individual regression line is modeled for each patient. The effects of covariates can then be added as interactions with the overall growth estimate observed (although this covariate analysis requires a large number of patients). MLM better represents the correlated nature of these data, and an improved AIC is apparent for the linear MLM as compared to a linear regression model. However, a linear MLM still presumes aneurysm growth to be a linear process, and this is not necessarily the case [17]. We therefore also tested a quadratic basis to the MLM. In our patient cohort, a quadratic basis to MLM demonstrated a small but significant improvement in AIC when compared to a linear MLM. Both the linear and quadratic MLM demonstrated significantly improved AIC compared to the ordinary linear regression model. It is noteworthy that the growth estimate in the quadratic MLM slows over time. This is not suggesting that aneurysm growth slows in individual patients, but rather reflects the observation in the fixed effects part of the model, that patients with slower growing aneurysms will remain in the cohort for longer time periods, whereas those with rapidly growing aneurysms will leave the cohort to undergo repair.
Our data support the notion that AAA growth exhibits significant variation between patients, is not necessarily linear, and is more suitably represented by MLM techniques. Our AIC data suggest that quadratic as opposed to linear modeling strategies most accurately represent the growth of AAAs within a cohort of patients over time. However, it is difficult to be certain if the quadratic MLM provides a more accurate growth estimate than a linear MLM or simply better detects the selection effects introduced by slow-growing aneurysms persisting in the data set for a longer time. Our data add weight to the previous work using MLM techniques, and we suggest that future studies aiming to identify factors which may influence growth must use MLM to reach valid conclusions. Relatively few groups have previously used MLM [5,18–21], possibly because this requires access to a suitably experienced biostatistician, which is not always possible. Reassuringly, the MLM generated growth estimates for our patient cohort which were similar to previous high-quality reports using large patient numbers with linear MLM [17,19].
There are clear limitations to this work. We have used a cohort of patients from a single center in the UK. Our findings are therefore specific to this cohort of patients, which may differ compared to other AAA patient groups around the globe. While the overall sample size was relatively small, it was large enough to estimate the fixed effects of the model [22]. It would have been beneficial to include relevant clinical risk factors for AAA (e.g., gender, smoking, hypertension) in the model; however, the sample was likely underpowered for looking at interaction terms, as would be required for subgroup analysis, so this was not possible. It is noteworthy that a proportion of patients recruited to the study were excluded from the growth modeling analysis (48%). These patients tended to have an incidental large aneurysm detected with a single scan that went straight for intervention; thus no growth data were available. Another problem is the fact that patients with fast-growing aneurysms are selected out of the data (to go for intervention) and thus have fewer data points included. Joint modeling [23,24] is an appealing approach to try to broach this problem, as it would allow correction for this selection effect. Joint modeling allows the analysis of the data taking into account both the autocorrelation in the repeated measures as well as the time-to-event outcome (aortic intervention). We chose to censor any measurement data from AAAs above the traditional intervention threshold of 5.5 cm. Very little is known about the growth patterns of these large AAAs and it is possible that these aneurysms exhibit a growth pattern different from smaller aneurysms which would require an alternative modeling technique. This is an important, separate area for further study. We also set a minimum standard of scans required to meet inclusion criteria (two or more USS which were at least 3 months apart). This approach was taken to ensure enough data were available to estimate a growth trajectory for each patient. Few patients contributed only the minimum number of scans (n = 16, 6% of the study population), with the average contribution being 7 scans per patient. It has been established that USS aneurysm measurement from inner wall to inner wall (ITI) is more reproducible than OTO [25]. As our study began in 2003, we have used OTO measurements for the purposes of the present analysis. The data used for analysis reflect the duration of OTO measurement policy in our department. All patients now receive ITI measurements as per the UK National AAA Screening Programme (http://aaa.screening.nhs.uk), but none of these measurements were included in the present analysis.
Conclusion
AAA growth is a complex process that varies significantly patient-to-patient. Between 3.0 and 5.5 cm, the heavily nested structure of the data is best represented with multilevel modeling techniques. Further work should focus on joint modeling approaches and on aneurysms above the intervention threshold.
Acknowledgments
Acknowledgments
This work was supported by funding from The Garfield Weston Trust for Medical Research into Diseases of the Heart and The Circulation Foundation (UK). This work was presented at the Society for Academic and Research Surgery Jan 2012, Nottingham, UK and the International Workshop on Statistical Modelling July 2013, Palermo, Italy. The authors confirm that the work is all their own and has not been submitted for publication or previously published in any other journal. D.J.A.S. is a RESCAN collaborator. No authors have any conflict of interest to declare. M.A.B., K.J.G., and K.I.B. are British Heart Foundation funded Clinical Research Training Fellows; S.S. is a National Institute of Health Research funded Clinical Lecturer.
References
- 1. Vardulaki KA, Walker NM, Day NE, Duffy SW, Ashton HA, Scott RA. Quantifying the risks of hypertension, age, sex and smoking in patients with abdominal aortic aneurysm. Br J Surg. 2000;87:195–200. 10.1046/j.1365-2168.2000.01353.x [DOI] [PubMed] [Google Scholar]
- 2. Filardo G, Powell JT, Martinez MA, Ballard DJ. Surgery for small asymptomatic abdominal aortic aneurysms. Cochrane Database Syst Rev. 2012;3:CD001835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Thompson SG, Ashton HA, Gao L, Buxton MJ, Scott RA. Final follow-up of the Multicentre Aneurysm Screening Study (MASS) randomized trial of abdominal aortic aneurysm screening. Br J Surg. 2012;99:1649–1656. 10.1002/bjs.8897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Bown MJ, Sweeting MJ, Brown LC, Powell JT, Thompson SG. Surveillance intervals for small abdominal aortic aneurysms: a meta-analysis. JAMA. 2013;309:806–813. 10.1001/jama.2013.950 [DOI] [PubMed] [Google Scholar]
- 5. Brady AR, Thompson SG, Fowkes FG, Greenhalgh RM, Powell JT. Abdominal aortic aneurysm expansion: risk factors and time intervals for surveillance. Circulation. 2004;110:16–21. 10.1161/01.CIR.0000133279.07468.9F [DOI] [PubMed] [Google Scholar]
- 6. Darwood R, Earnshaw JJ, Turton G, Shaw E, Whyman M, Poskitt K, et al. Twenty-year review of abdominal aortic aneurysm screening in men in the county of Gloucestershire, United Kingdom. J Vasc Surg. 2012;56:8–13. 10.1016/j.jvs.2011.12.069 [DOI] [PubMed] [Google Scholar]
- 7. Dunne JA, Bailey MA, Griffin KJ, Sohrabi S, Coughlin PA, Scott DJ. Statins: the holy grail of abdominal aortic aneurysm (AAA) growth attenuation? A systematic review of the literature. Curr Vasc Pharmacol. 2012. [DOI] [PubMed] [Google Scholar]
- 8. Bailey MA, Charnell AM, Griffin KJ, Czoski-Murray CJ, Sohrabi S, Rashid ST, et al. A systematic review of the methodology employed to calculate abdominal aortic aneurysm (AAA) growth rate. Ultrasound. 2011;19:197–202. 10.1258/ult.2011.011040 [DOI] [Google Scholar]
- 9. Bailey MA, Griffin KJ, Sohrabi S, Whalley DJ, Johnson AB, Baxter PD, et al. Plasma thrombin-antithrombin complex, prothrombin fragments 1 and 2, and D-dimer levels are elevated after endovascular but not open repair of infrarenal abdominal aortic aneurysm. J Vasc Surg. 2013;57:1512–1518. 10.1016/j.jvs.2012.12.030 [DOI] [PubMed] [Google Scholar]
- 10. Parry DJ, Al-Barjas HS, Chappell L, Rashid ST, Ariëns RA, Scott DJ. Markers of inflammation in men with small abdominal aortic aneurysm. J Vasc Surg. 2010;52:145–151. 10.1016/j.jvs.2010.02.279 [DOI] [PubMed] [Google Scholar]
- 11. Parry DJ, Al-Barjas HS, Chappell L, Rashid T, Ariëns RA, Scott DJ. Haemostatic and fibrinolytic factors in men with a small abdominal aortic aneurysm. Br J Surg. 2009;96:870–877. 10.1002/bjs.6632 [DOI] [PubMed] [Google Scholar]
- 12. Powell J, Brown LC, Forbes JF, Fowkes FG, Greenhalgh RM, Ruckley CV, et al. Final 12-year follow-up of surgery versus surveillance in the UK Small Aneurysm Trial. Br J Surg. 2007;94:702–708. 10.1002/bjs.5778 [DOI] [PubMed] [Google Scholar]
- 13. Foo FJ, Hammond C, Goldstone A, Abuhamdiah M, Rashid S, West R, et al. Agreement between computed tomography and ultrasound on abdominal aortic aneurysms and implications on clinical decisions. Eur J Vasc Endovasc Surg. 2011;42:608–614. 10.1016/j.ejvs.2011.07.003 [DOI] [PubMed] [Google Scholar]
- 14. Draper NR, Smith H. Applied regression analysis, 3rd edition Chichester: Wiley Interscience; 1998. [Google Scholar]
- 15. Goldstein H. Multilevel statistical models, 4th edition Chichester: Wiley Interscience; 2011. [Google Scholar]
- 16. Pinheiro JC, Bates DM. Mixed-effects models in S and S-PLUS. New York: Springer-Verlag; 2000. [Google Scholar]
- 17. Powell JT, Sweeting MJ, Brown LC, Gotensparre SM, Fowkes FG, Thompson SG. Systematic review and meta-analysis of growth rates of small abdominal aortic aneurysms. Br J Surg. 2011;98:609–618. 10.1002/bjs.7465 [DOI] [PubMed] [Google Scholar]
- 18. Sweeting MJ, Thompson SG, Brown LC, Greenhalgh RM, Powell JT. Use of angiotensin converting enzyme inhibitors is associated with increased growth rate of abdominal aortic aneurysms. J Vasc Surg. 2010;52:1–4. 10.1016/j.jvs.2010.02.264 [DOI] [PubMed] [Google Scholar]
- 19. Sweeting MJ, Thompson SG, Brown LC, Powell JT. Meta-analysis of individual patient data to examine factors affecting growth and rupture of small abdominal aortic aneurysms. Br J Surg. 2012;99:655–665. 10.1002/bjs.8707 [DOI] [PubMed] [Google Scholar]
- 20. Thompson A, Cooper JA, Fabricius M, Humphries SE, Ashton HA, Hafez H. An analysis of drug modulation of abdominal aortic aneurysm growth through 25 years of surveillance. J Vasc Surg. 2010;52:55–61.e2. [DOI] [PubMed] [Google Scholar]
- 21. Thompson AR, Cooper JA, Ashton HA, Hafez H. Growth rates of small abdominal aortic aneurysms correlate with clinical events. Br J Surg. 2010;97:37–44. 10.1002/bjs.6779 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Bell BA, Morgan GB, Schoeneberger JA, Loudermilk BL, Kromrey JD, Ferron JM. Dancing the sample size limbo with mixed models: how low can you go? SAS Global Forum; Seattle, Washington: 2010;1–11. [Google Scholar]
- 23. Diggle PJ, Sousa I, Chetwynd AG. Joint modelling of repeated measurements and time-to-event outcomes: the fourth Armitage lecture. Stat Med. 2008;27:2981–2998. 10.1002/sim.3131 [DOI] [PubMed] [Google Scholar]
- 24. Henderson R, Diggle P, Dobson A. Joint modelling of longitudinal measurements and event time data. Biostatistics. 2000;1:465–480. 10.1093/biostatistics/1.4.465 [DOI] [PubMed] [Google Scholar]
- 25. Hartshorne TC, McCollum CN, Earnshaw JJ, Morris J, Nasim A. Ultrasound measurement of aortic diameter in a national screening programme. Eur J Vasc Endovasc Surg. 2011;42:195–199. 10.1016/j.ejvs.2011.02.030 [DOI] [PubMed] [Google Scholar]