Distributed and Dynamic Neural Encoding of Multiple Motion Directions of Transparently Moving Stimuli in Cortical Area MT

Abstract

Segmenting visual scenes into distinct objects and surfaces is a fundamental visual function. To better understand the underlying neural mechanism, we investigated how neurons in the middle temporal cortex (MT) of macaque monkeys represent overlapping random-dot stimuli moving transparently in slightly different directions. It has been shown that the neuronal response elicited by two stimuli approximately follows the average of the responses elicited by the constituent stimulus components presented alone. In this scheme of response pooling, the ability to segment two simultaneously presented motion directions is limited by the width of the tuning curve to motion in a single direction. We found that, although the population-averaged neuronal tuning showed response averaging, subgroups of neurons showed distinct patterns of response tuning and were capable of representing component directions that were separated by a small angle—less than the tuning width to unidirectional stimuli. One group of neurons preferentially represented the component direction at a specific side of the bidirectional stimuli, weighting one stimulus component more strongly than the other. Another group of neurons pooled the component responses nonlinearly and showed two separate peaks in their tuning curves even when the average of the component responses was unimodal. We also show for the first time that the direction tuning of MT neurons evolved from initially representing the vector-averaged direction of slightly different stimuli to gradually representing the component directions. Our results reveal important neural processes underlying image segmentation and suggest that information about slightly different stimulus components is computed dynamically and distributed across neurons.

SIGNIFICANCE STATEMENT Natural scenes often contain multiple entities. The ability to segment visual scenes into distinct objects and surfaces is fundamental to sensory processing and is crucial for generating the perception of our environment. Because cortical neurons are broadly tuned to a given visual feature, segmenting two stimuli that differ only slightly is a challenge for the visual system. In this study, we discovered that many neurons in the visual cortex are capable of representing individual components of slightly different stimuli by selectively and nonlinearly pooling the responses elicited by the stimulus components. We also show for the first time that the neural representation of individual stimulus components developed over a period of ∼70–100 ms, revealing a dynamic process of image segmentation.

Introduction

Natural scenes often contain multiple entities. The ability to segregate visual scenes into distinct objects and surfaces, referred to as image segmentation, is fundamental to vision. Although a great deal has been learned about the neural mechanisms underlying image segmentation, how the visual system segments two entities that differ only slightly remains an important open question.

Visual motion provides a potent cue for image segmentation. When two stimuli overlap in space and move in different directions, the primate visual system can segment them into distinct, transparent surfaces based on visual motion cues alone. The extent of “separation” between two transparently moving stimuli can be conveniently controlled by manipulating the angular difference between the motion directions. In primates, neurons in the extrastriate middle temporal (MT) cortex are direction selective (Maunsell and van Essen, 1983). Area MT is also important for image segmentation pertinent to visual motion signals (Allman et al., 1985; Snowden et al., 1991; Stoner and Albright, 1992; Qian and Andersen, 1994; Britten, 1999, 2003; Born et al., 2000; Born and Bradley, 2005; Huang et al., 2007, 2008).

MT neurons are broadly tuned to motion in a single direction, with a mean tuning width of ∼100° (Albright, 1984). Broad direction tuning can be useful for integrating motion signals (Braddick, 1993; Rust et al., 2006), but it can also limit the ability to distinguish two “slightly different” directions that are separated by an angle less than the tuning width to unidirectional stimuli. Previous studies have examined neural mechanisms underlying transparent motion (Snowden et al., 1991; Qian and Andersen, 1994; Treue et al., 2000; Rosenberg et al., 2008; Krekelberg and van Wezel, 2013; McDonald et al., 2014). However, it remains unclear how MT neurons encode visual stimuli moving transparently in slightly different directions. It has been shown that the response of an MT neuron elicited by two stimuli presented simultaneously tends to follow the average of the responses elicited by the stimulus components presented alone (Qian and Andersen, 1994; Recanzone et al., 1997). Given the broad tuning of MT neurons to unidirectional stimuli, averaging the component responses elicited by two slightly different directions would give rise to a unimodal tuning curve to the bidirectional stimuli. The response peak of the tuning curve is reached when the vector-averaged direction is aligned with a neuron's preferred direction. Indeed, it has been shown that, when visual stimuli are moving transparently in two directions separated by <90°, the population-averaged tuning curve of MT neurons contains only a single response peak (Treue et al., 2000; McDonald et al., 2014). Such a scheme of response averaging would make the segmentation of slightly different directions challenging. In contrast, humans can segment transparently moving stimuli separated by an angle much smaller than the tuning width of MT neurons (Braddick et al., 2002).

We hypothesized that, although, on average, MT neurons appear to perform a linear response averaging, different subgroups of neurons may be informative about slightly different component directions by selectively pooling the response elicited by one of the stimulus components and by performing nonlinear operations that emphasize the differences between the stimulus components. We trained two monkeys to perform either a fixation task or a perceptual discrimination task and presented overlapping random-dot stimuli moving transparently in two different directions. We measured the psychophysical performance of the monkeys in discriminating a bidirectional stimulus from a unidirectional stimulus and characterized the tuning curves of MT neurons to the bidirectional stimuli. We also characterized the time course of the response tuning. The monkeys were able to perform the discrimination task well. Our results confirmed the hypotheses described above and further showed that the neural representation of component directions developed gradually over time. Our findings revealed important neural processes underlying image segmentation and provide new insights into how the visual system segments two stimuli even when the stimulus separation is smaller than the tuning width to a single stimulus.

Materials and Methods

Subjects and neural recording.

Two adult male rhesus monkeys (Macaca mulatta) were used in the neurophysiological experiments. Experimental protocols were approved by the local Institutional Animal Care and Use Committee and followed the National Institutes of Health's Guide for the Care and Use of Laboratory Animals. Procedures for surgical preparation and electrophysiological recording were routine and similar to those described previously (Huang et al., 2008; Huang and Lisberger, 2009). During sterile surgery with the animal under isoflurane anesthesia, a head post and a recording cylinder were implanted to allow recording from neurons in cortical area MT. Eye position was monitored using a video-based eye tracker (EyeLink SR Research) at a rate of 1000 Hz.

We used tungsten electrodes (∼1–3 MΩ; FHC) for electrophysiological recordings from neurons in area MT. We identified area MT by its characteristically large portion of directionally selective neurons, small receptive fields (RFs) relative to those of neighboring medial superior temporal cortex (area MST), and its location at the posterior bank of the superior temporal sulcus. Electrical signals were amplified and single units were identified with a real-time template-matching system and an offline spike sorter (Plexon).

Visual stimuli and experimental procedure.

Stimulus presentation, the behavioral paradigm, and data acquisition were controlled by a real-time data acquisition program (https://sites.google.com/a/srscicomp.com/maestro/). Visual stimuli were presented on a 25 inch CRT monitor at a viewing distance of 63 cm. Monitor resolution was 1024 × 768 pixels and the refresh rate was 100 Hz. Visual stimuli were generated by a Linux workstation using an OpenGL application that communicated with an experimental control computer. The output of the video monitor was measured with a photometer (LS-110; Minolta) and was gamma corrected.

Visual stimuli were achromatic random-dot patterns presented within a stationary, circular aperture that was 7.5° across. Each dot was a square of 2 pixels, extending 0.08° on a side. The dot density of a single random-dot pattern was 3.4 dots/deg² and all dots of a random-dot pattern moved in the same direction at the same speed (i.e., had a motion coherence of 100%). The luminance levels of the dots and the background were 15.3 and 1.9 cd/m², respectively, giving rise to a Michelson contrast of 0.78. The SD of the luminance intensity of the random-dot pattern was 1.95 cd/m², which reflects the root mean square contrast (Moulden et al., 1990; Peli, 1990). The bidirectional stimuli contained two overlapping random-dot patterns translating in different directions. Each random-dot pattern is referred to as a “stimulus component.” In the main experiment, the angle separation between the two component directions was 60°. In a subset of experiments, four direction separations (DS's) of 45°, 60°, 90°, and 135° were interleaved randomly. At each DS, we varied the vector-averaged (VA) direction of the bidirectional stimuli across 360° to characterize the response tuning, typically in an even step of 15°. In some experiments, we used a fine-sampling step of 10° within ±90° of the recorded neuron's preferred direction (PD) and a step of 45° beyond.

We also used plaid stimuli consisting of superimposed sinusoidal gratings to characterize the pattern- and component-direction selectivity of MT neurons. The plaids and gratings were presented within a circular aperture that was 7.5° across. The component gratings were separated by 135° in orientation. Grating was presented at 50% contrast, with a mean luminance of 15.3 cd/m². The spatial frequency was 0.8 cycles/° and the temporal frequency was between 4 and 16 cycles/s. The plaids and grating were sampled in a step of 22.5° or 15°. Gratings were first turned on and stationary for 200 ms and then drifted for 500 ms.

In each experiment, we first characterized the direction selectivity of a neuron by interleaving trials of 30 × 27° random-dot patches moving at 10°/s in different directions at 45° steps. Directional tuning and the PD of the neuron were evaluated on-line using MATLAB (The MathWorks). We next characterized the speed tuning of the neuron using random-dot patches moving at different speeds of 1, 2, 4, 8, 16, 32, 64, or 128°/s in the PD. The speed tuning curve was fitted using a cubic spline and the speed that gave rise to the highest firing rate in the fitted tuning curve was taken as the preferred speed (PS) of the neuron. The mean PS of our neuron population was 24°/s (SD = 16°). We then mapped the RF of the neuron by recording responses to a series of 5 × 5° patches of random dots that moved in the PD and at the PS of the neuron. The location of the patch was varied randomly to tile the screen in 5° steps without overlap and to cover an area of 35 × 25°. The raw map of the RF was interpolated and the location yielding the highest firing rate was taken as the center of the RF. In the following experiments, testing stimuli were centered on the RF. The mean RF size of our neuron population was 12.8° in diameter (SD = 6.6°). The RF size was calculated as the square root of the area where the baseline-subtracted neural activity exceeded the half-maximal response (Womelsdorf et al., 2006). If the RF only occupied a small portion of a mapping patch, then the area of the whole patch would be considered as part of the RF.

Behavioral paradigms.

The experiments were conducted while the monkeys performed either a fixation task or a discrimination task. All visual stimuli were presented in individual trials while the animals fixated on a spot of light within a 1.5° × 1.5° window to receive juice rewards. In the fixation paradigm, visual stimuli were first turned on but remained stationary for 200 ms before moving for 1000 ms. This allowed us to separate the neuronal response elicited by stimulus motion from stimulus onset. The animals maintained fixation for another 250 ms after the stimulus offset. Trials containing a single stimulus component of the bidirectional stimuli were randomly interleaved with trials of the bidirectional stimuli. Trials that sampled all tested directions around 360° once were grouped in a random sequence into a “block of trials.” A new block of trials was initiated only after the previous block was successfully completed. Each stimulus direction was repeated an average of 10 times (SD = 3.6).

In the discrimination paradigm, the monkeys were trained to distinguish the bidirectional stimulus that had a DS of 60° from a unidirectional stimulus. The unidirectional stimulus contained two overlapping random-dot patterns that moved in the same direction and had the same dot density as the bidirectional stimulus. We trained two monkeys on two variants of the task. For monkey GE, a bidirectional (or a unidirectional) stimulus was centered on a neuron's RF and the corresponding unidirectional (or bidirectional) stimulus was presented at the other half of the visual field symmetric to the RF location relative to the fixation spot. Visual stimuli moved for 1500 ms. After the stimulus offset, two spots of light were presented at the two stimulus centers. Once the fixation spot turned off, the monkey was required to make a saccadic eye movement to the spot of light at the center of the bidirectional stimuli to receive juice rewards. In half of the trials, the bidirectional stimuli were placed on the RFs and, in the other half, the unidirectional stimuli were placed on the RFs. All trials were randomly interleaved. In 41 of a total of 48 experiments, visual stimuli started to move as soon as they were turned on. In the remaining seven experiments, visual stimuli remained stationary for 200 ms before moving.

For monkey BJ, only one stimulus, either bidirectional or unidirectional, was centered on the RF and presented in a given trial. Trials containing bidirectional and unidirectional stimuli were randomly interleaved. In all 37 experiments, visual stimuli were turned on and remained stationary for 200 ms and then moved for 1000 ms. After the stimulus offset, two reporting targets were turned on. The monkey was required to make a saccadic eye movement to the target located at the right (or left) side of the fixation spot when a bidirectional (or unidirectional) stimulus was presented in a given trial to receive juice rewards.

In addition to using the percentage of correct trials to measure the behavioral performance, we also used the discriminability index (d′) = norminv (hit rate) − norminv (false alarm rate). norminv is a MATLAB function that calculates the inverse of the normal cumulative distribution function, with the mean and SD set to 0 and 1, respectively.

Analysis of response tuning.

We calculated the firing rate for each unidirectional stimulus and each VA direction of the bidirectional stimuli based on the spike count during the 1000 ms motion interval and averaged the response across repeated trials. Based on the experiments in which the motion onset was separated from the stimulus onset in time, we found that the transient neuronal response elicited by the stimulus onset lasted, on average, <150 ms. In a subset of the experiments of the discrimination paradigm, motion onset was not separated from the stimulus onset and the stimulus duration was 1500 ms. For these experiments, we calculated the firing rate based on the response 150–1150 ms after the stimulus onset.

We constructed the response tuning curves to unidirectional stimuli and to bidirectional stimuli and fitted the raw direction tuning curves using cubic splines at a resolution of 1°. For each VA direction, we determined the responses elicited by the bidirectional stimuli and the constituent unidirectional stimulus components. To average the direction tuning curves across neurons, we rotated the spline-fitted tuning curve elicited by the bidirectional stimuli such that the VA direction of 0° was aligned with the PD of each neuron. We then normalized neuronal responses by each neuron's maximum bidirectional response and averaged the aligned, normalized tuning curves across cells.

When the sampling step of the VA direction in a block of trials was 15°, the unidirectional stimuli sampled all possible component directions across different VA directions. However, when a neuron was tested with the sampling steps of a mixture of 10° and 45°, the unidirectional stimuli did not fully sample the component directions. For those neurons, we first used a cubic spline to fit the neuronal responses elicited by the unidirectional stimuli and then resampled the tuning curve to obtain the responses elicited by the component directions.

We fitted the response tuning curves elicited by the bidirectional stimuli using a linear weighted summation (LWS) model (Eq. 1), and a summation plus nonlinear interaction (SNL) model (Eq. 2) (Sanada et al., 2012; Xiao et al., 2014) by minimizing the sum of squared error as follows:

where R_pred is the model predicted response to the bidirectional stimuli, R₁ and R₂ are the measured component responses elicited by the two unidirectional motion components, and w₁ and w₂ are the weights for the component responses, respectively. “C” in the LWS model is a constant and “b” in the SNL model is referred to as the “nonlinear interaction coefficient” that determines the sign and strength of the multiplicative interaction between the component responses.

We also fitted the responses to the bidirectional stimuli using a power-law summation (PWS) model (Eq. 3) after Britten and Heuer (1999). We allowed the response weights w₁ and w₂ for the two stimulus components to be different. The parameter n is a positive exponent and C is a constant as follows:

To evaluate the goodness-of-fit of each model, we computed the percentage of variance (PV) accounted for by a model fit as follows:

where SSE is the sum of squared errors between a model fit and the data and SST is the sum of squared differences between the data and the mean of data (Morgan et al., 2008). When occasionally SSE exceeded SST and gave rise to a negative PV, we forced the PV to be zero.

To compare the goodness-of-fit between models and take the number of free parameters into consideration, we calculated the Akaike information criterion (AIC) (Akaike, 1973) for each model fit as follows:

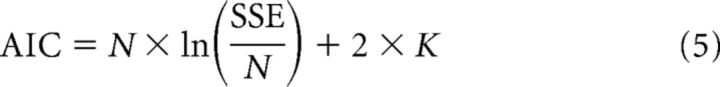where N is the number of data points, SSE is the sum of squared errors, and K is the number of free parameters of the model. Between two models, the one that gives a smaller AIC provides a better goodness-of-fit.

For each neuron, we also fitted its responses to the unidirectional stimuli first by a cubic spline at a step of 1° and then fitted the spline-fitted tuning curve using the von Mises function, similar to a circular Gaussian function as follows:

where θ is the motion direction of the unidirectional stimulus, θ_c is the direction where the tuning curve reaches its peak, a and b determine the magnitude and bandwidth of the tuning curve, respectively, and C is a positive constant. First fitting the tuning curve using a spline at a fine step allowed the following Gaussian-like fit to accurately capture the response tuning, especially when the tuning curve's bandwidth was narrow. The full width at the half-height of the fitted tuning curve by Equation 6 was taken as the “tuning width” for a given neuron. For a neuron to be selected for further data analyses, we required the goodness of fit (PV) of a neuron's unidirectional tuning curve by Equation 6 to be >90%. A small number of neurons that had irregular or multimodal tuning curve to the unidirectional stimuli were rejected by this criterion (see Results).

To calculate the skewness of a neuron's response tuning curve to a unidirectional stimulus, we used a measure of Pearson's first skewness coefficient, defined as follows: (mean − mode)/SD. The mean, mode, and SD were calculated from the unidirectional tuning curve of each neuron elicited by a random-dot stimulus.

Classification of response tuning curves.

We classified neurons into different classes based on the tuning curves in response to the bidirectional stimuli. To determine whether a tuning curve contained only a single peak or at least two peaks, we first located the global peak, a candidate second peak, and a “trough” in between based on the spline-fitted and smoothed tuning curve of the trial-averaged responses. The smoothing was done using a second-order, seven-point Savitzky–Golay filter. To qualify as a candidate second peak, a response at a given VA direction had to be a local maximum within the neighborhood of ±10° along the spline-fitted tuning curve. A candidate trough was determined as the minimum between the global peak and a candidate second peak and had to be within ±40° from VA direction of 0° when the DS of the bidirectional stimuli was 60°. More generally, at a DS that was not >135°, a candidate trough had to be within an angle range of ±2 × DS/3 centered on VA direction 0°. If the response at the candidate trough was significantly smaller than the global peak and the candidate second peak, then the tuning curve was considered to contain two peaks. If these criteria were not met after searching through all candidate second peaks, the tuning curve was considered to contain one peak.

We used the bootstrap method (Efron and Tibshirani, 1994) to determine whether a candidate trough was significantly smaller than the global peak or a candidate second peak. Specifically, for each spline-fitted but not smoothed tuning curve determined by a single trial across different VA directions, the responses at the locations of the global peak, a candidate second peak, and a trough were taken and the difference between a peak and the trough was calculated. If the difference between a peak and a trough was >1.5 times of the SEM difference (i.e., 87% of confidence interval), then the trough was considered significantly smaller than the peak. The SEM difference was estimated by bootstrapping (200 times) the difference between the responses at the peak and trough locations from individual trials. Note that the peak and trough locations were determined by the trial-averaged tuning curve and were not necessarily peaks and trough for a tuning curve based on a single set of trials.

To determine whether a trial-averaged tuning curve of the responses elicited by the bidirectional stimuli was significantly biased toward one motion component (i.e., showed “side bias”), we used the SNL model to fit each tuning curve determined by a single trial across different VA directions. Across the repeated trials, we obtained trial-by-trial model fits of the response weights for the two components w₁ and w₂. We conducted a permutation test (50,000 times) to determine whether w₁ was significantly greater than w₂ (p < 0.05) or vice versa.

Time course analysis of response tuning.

To compute the time course of the response tuning to the bidirectional stimuli, we calculated the tuning curve using trial-averaged firing rates within a 50 ms time window and sliding at a 10 ms step for each neuron. The responses were normalized by the maximum firing rate across all time windows and averaged across neurons. For the time course analysis, we excluded the experiments in which the visual stimuli started to move as soon as they were turned on and therefore the motion onset was not separated from the stimulus onset. When analyzing the time course of the response tuning from neurons that showed side bias, we pooled the results from neurons that showed side bias to the component directions at the clockwise side (C-side; i.e., Dir. 2 in the diagram in Fig. 1) and the counterclockwise side (CC-side; i.e., Dir. 1 in the diagram in Fig. 1) together. To do so, we first horizontally flipped the tuning curves to the bidirectional and unidirectional stimuli of neurons that showed side bias to the C-side, along the axis of VA direction 0°. We then averaged the flipped tuning curves together with the tuning curves from the neurons that showed side bias to the CC-side.

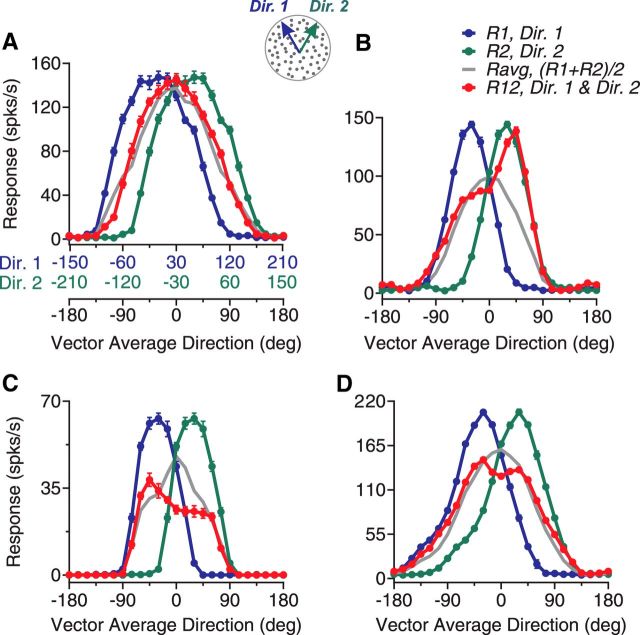
Figure 1.

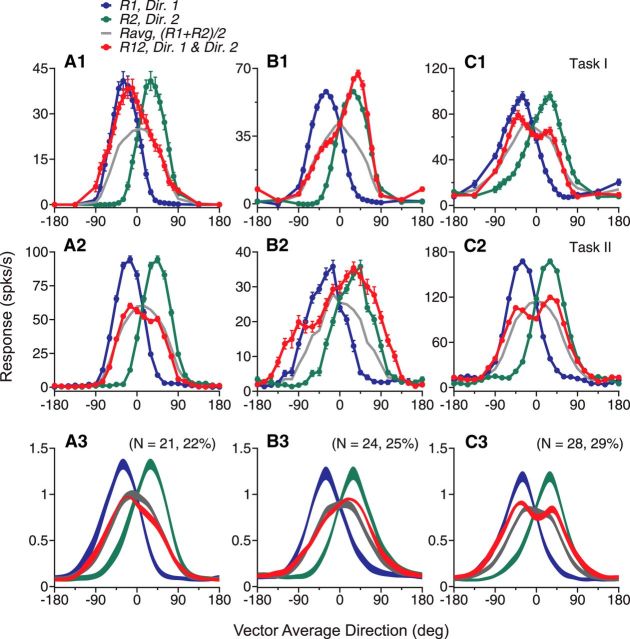
Direction tuning curves of four example neurons elicited by bidirectional stimuli separated by 60° and constituent unidirectional stimulus components. A, Diagram illustration of the visual stimuli and the response tuning curves of an example neuron. Gray dots in the diagram indicate two overlapping, achromatic random-dot patterns moving in two directions separated by 60°. Colors were used for illustration purposes only. The component direction shown in blue (Dir. 1) moved at the CC-side of the other component direction shown in green (Dir. 2). The abscissas in blue and green show unidirectional components Dir. 1 and Dir. 2, respectively, of the corresponding bidirectional stimuli for which the VA direction is shown by the black abscissa. The blue and green axes are shifted by 60° relative to each other. A VA direction of 0° is aligned with the neuron's PD. For this neuron, the responses elicited by the bidirectional stimuli approximately followed the average of the responses elicited by the stimulus components. B, C, D, Response tuning curves of another three example neurons. Error bars indicate SE and they are sometimes smaller than the symbol size (e.g., as in D).

Stimulus discrimination using a classifier.

To evaluate whether the responses of populations of neurons in MT carry sufficient information about the bidirectional and unidirectional stimuli, we used a linear variant of the support vector machine (SVM) (Vapnik, 2000; Schölkopf et al., 2002; Graf et al., 2011; Chen et al., 2015) to discriminate the bidirectional stimuli from unidirectional stimuli and between bidirectional stimuli that had different angular separations. In our experiments, we did not record the responses from a population of neurons simultaneously. To convert the direction tuning curve of a single neuron into the response pattern of a population of neurons, we assumed that, for each neuron in our dataset, there was a family of “cloned” neurons that had the same tuning curve but different PDs evenly spanning 360°. Each presentation of a visual stimulus would generate a pattern of population response across the cloned neurons, as well as across other neurons with different direction tuning curves and their cloned neurons. The procedure of classification follows.

For each neuron, we calculated the “single-trial” direction tuning curve based on the neural responses from one randomly selected block of trials. We fitted the single-trial tuning curve using a cubic spline at a resolution of 1° and duplicated and shifted the tuning curve in a step of 7.5°. This generated the tuning curves of 48 cloned neurons with PDs that were evenly distributed. We took the numbers of spikes of the cloned neurons elicited by a unidirectional stimulus moving at 0° or a bidirectional stimulus that had a VA direction of 0° as the “single-trial population neural response.” The procedure was repeated 10 times with replacement for a given neuron. Using a data sample of N recorded neurons, the SVM classifier was trained to discriminate the population response elicited by two different visual stimuli based on the responses from N − 1 “training” neurons and, for each training neuron, 10 randomly chosen single-trial tuning curves, i.e., a total of 10 × (N − 1) pairs of single-trial population responses. The classifier was then used to classify a pair of the single-trial population responses from the remaining “testing neuron” elicited by two stimuli. For a given testing neuron, the single-trial response was randomly selected 10 times with replacement. The selection of the testing neuron was repeated across all N neurons. The performance of the classifier was measured using d′ = norminv (hit rate) − norminv (false alarm rate), as for measuring the behavioral performance of the animals. The hit and false alarm rates were calculated over the classifications of 10 × N pairs of single-trial population responses of the testing neurons. When the hit or false alarm rate occasionally reached 1, d′ was calculated using a modified formula: d′ = norminv{[(100 × hit rate) + 1]/102} − norminv{[(100 × false alarm rate) + 1]/102} (Chen et al., 2015). We only needed to use the modified d′ twice in all calculations and those occasions were for the neuronal population that showed two response peaks. The SVM was implemented using the MATLAB function fitcsvm.

We also trained the classifier based on the responses from N neurons and a total of 10 × N − 1 pairs of single-trial population responses by leaving one pair of single-trial population responses out as the testing patterns. The procedure was repeated across 10 randomly picked testing patterns for each neuron and across N neurons. We found similar results using this method as the method of leaving one neuron out described above. Because the left-out pattern from one neuron was similar to the rest of the patterns from the same neuron, we chose to use the stricter method of leaving all the patterns from one neuron out (i.e., leaving one neuron out).

Analysis of pattern and component direction selectivity.

We used the methods of Movshon et al. (1985) and Smith et al. (2005) to quantify the pattern- and component-direction selectivity of MT neurons. The pattern prediction was determined by the responses to gratings drifting in the pattern directions and the component prediction was the sum of the responses elicited by the component gratings. We calculated the partial correlations R_pp and R_pc for the pattern and component predictions, respectively, as follows:

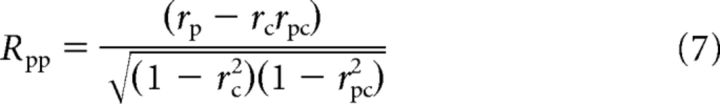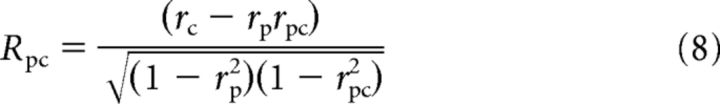where r_p and r_c are the correlations between the neuronal responses to plaid and the pattern and component prediction, respectively, and r_pc is the correlation between the two predictions. We converted each value of R_pp and R_pc to a Z-score designated as Z_p and Z_c respectively using Fisher's r-to-Z transformation (Smith et al., 2005). For a neuron to be judged as pattern-direction selective, Z_p had to exceed Z_c by a value of 1.28 (or 0 if Z_c was negative), equivalent to a probability of 0.9, and vice versa for a neuron to be judged as component-direction selective. Otherwise, the cell was considered unclassified.

Results

To gain a better understanding of the fundamental neural process of image segmentation, we asked the question of how simultaneously presented and slightly different motion directions are represented by neurons in extrastriate area MT. To address this question, we first presented overlapping random-dot stimuli moving in two directions separated by 60° and characterized the tuning curves of MT neurons in response to the bidirectional stimuli. We next used bidirectional random-dot stimuli that had different DS's of 45°, 60°, 90°, and 135° to determine whether the tuning curves showed a consistent trend across DS's. We also characterized the time courses of the tuning curves in response to the bidirectional stimuli. Finally, we compared the tuning properties of MT neurons in response to our random-dot stimuli with the pattern- and component-direction selectivity characterized by plaid stimuli. We recorded from 290 neurons in area MT of two macaque monkeys as they performed either a simple fixation task or a perceptual discrimination task. A majority of the recorded neurons (N = 267, 92%, 131 from monkey GE and 136 from monkey BJ) passed our selection criteria for the direction tuning curve to a unidirectional stimulus and were included in our dataset (see Materials and Methods).

MT direction tuning to bidirectional stimuli separated by 60°

We set the DS between two stimulus components to 60° and varied the VA direction of the bidirectional stimuli to characterize the direction tuning curve. In this experiment, the monkeys performed a fixation task. The data sample of this experiment contained 202 neurons (107 from GE and 95 from BJ). The mean eccentricity of the RFs was 7.1° (SD = 3.7°). We chose to use a DS of 60° for two reasons. First, at this DS, both humans (Gaudio and Huang, 2012) and monkeys (see below) can reliably segment the two component directions of our stimuli. Second, for a majority of MT neurons, the average of the responses elicited by two motion components separated by 60° contains only a single response peak because the tuning curves of MT neurons elicited by unidirectional stimuli have a mean width of ∼100° (Albright, 1984). The peak response occurs when the VA direction is aligned with a neuron's PD, which imposes a challenge for the neural encoding of two separate component directions.

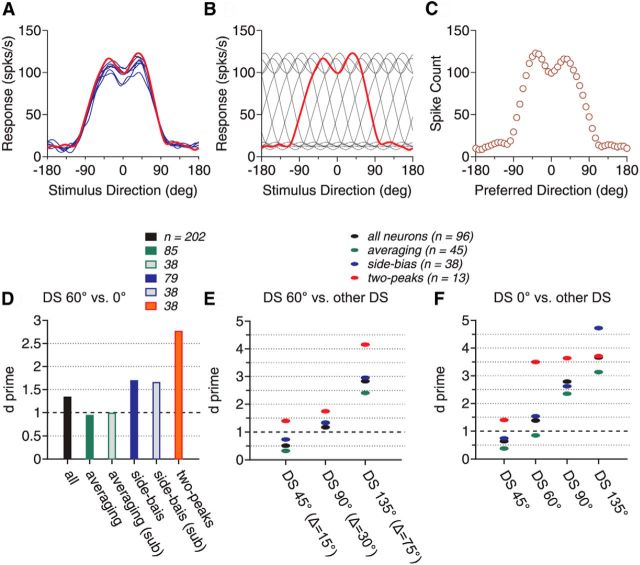
Figure 1 shows the direction tuning curves of four representative MT neurons. The neuron shown in Figure 1A had a tuning curve elicited by the bidirectional stimuli (R₁₂, shown in red) approximately following the average of the component responses (R_avg, shown in gray). However, we also found that many MT neurons showed tuning curves that deviated significantly from the response average. For the second neuron shown in Figure 1B, the response elicited by the bidirectional stimuli was the strongest when the motion component at the C-side of the two directions (i.e., Dir. 2) was near the neuron's PD, but not when the CC-side component (i.e., Dir. 1) was near the PD. We refer to this response bias toward the stimulus component at a specific side of two motion directions as “side bias.” The third neuron had a side bias toward the CC-side of the two component directions (Fig. 1C). Approximately 40% of the neurons showed the side bias. Last, the fourth neuron showed two separate response peaks that were reached when either stimulus component moved in a direction near the neuron's PD even though the average of the component responses only contained a single peak located when the VA direction was at the PD (Fig. 1D). Approximately 20% of the neurons showed this type of tuning curve.

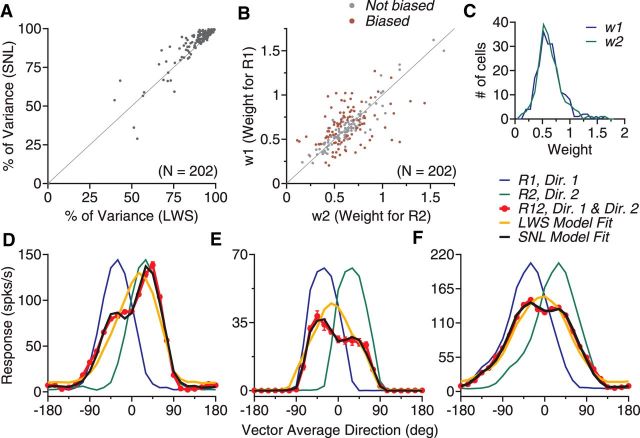
We fitted the response tuning curves using a LWS model (see Materials and Methods, Eq. 1) and a SNL model (Eq. 2). Each model has three free parameters. The SNL model accounted for, on average, 92.4% of the response variance (SD = 12.0%), whereas the LWS model accounted for 90.8% of the response variance (SD = 11.8%). The SNL model provided a significantly better fit than the LWS model (N = 202, one-tailed paired t test, p < 10⁻⁶; Fig. 2A). Figure 2, D–F, demonstrates this by comparing the SNL and LWS model fits with three of the example neurons shown in Figure 1. We therefore used the SNL model to fit the data in the rest of our analyses.

Figure 2.

Model fits of the response tuning curves elicited by bidirectional stimuli separated by 60°. A, PV accounted for by the LWS and the SNL model. B, Weights for the component responses obtained using the SNL model fit. Each dot in A and B represents data from one neuron. Colored dots in B indicate that the two response weights are significantly different. C, Distribution of the response weight for each stimulus component. D–F, Direction tuning curves and their model fits of three example neurons. These neurons are the same as those shown in Figure 1B–D.

We obtained the response weights w₁ and w₂ for the two component responses, respectively, using the SNL model fit (Eq. 2). When averaged across all neurons in the sample, the mean w₁ and w₂ were 0.64 and 0.63, respectively (SD = 0.23 for both), suggesting sublinear summation. The two response weights were not significantly different from each other (paired t test, p > 0.8). The distributions of the two response weights w₁ and w₂ are shown in Figure 2C. However, many individual neurons (N = 94, 47%) had significantly different response weights for the two stimulus components (permutation test, p < 0.05; Fig. 2B), consistent with the observation that the tuning curves of many MT neurons showed the side bias.

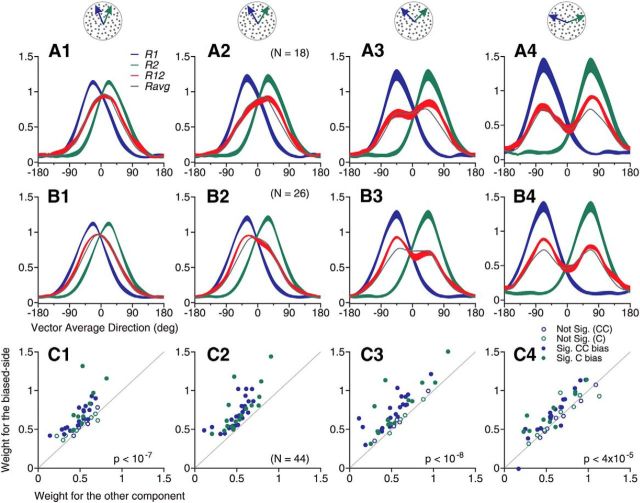
To classify the response tuning curves elicited by the bidirectional stimuli, we used an algorithm to determine whether a tuning curve contained a single response peak or two separate peaks based on a bootstrap method. We also classified neurons as “side biased” if the response weights for the two stimulus components were significantly different based on a permutation test (see Materials and Methods). Figure 3 shows the response tuning curves averaged across the whole population and subgroups of neurons. The tuning curve averaged across all neurons in the population is very similar to the average of the component responses but is slightly broader (Fig. 3A). The tuning curve contains only a single response peak located when the VA direction was in the PD. Among 202 neurons, 85 neurons (42%) showed a single response peak and no side bias. The response tuning curves of these neurons were similar to the average of the component responses (Fig. 3B). We referred to these neurons as “averaging” cells. In contrast, the response tuning curves of other subgroups of neurons appear to be informative about the component directions. Another 79 neurons (39%) showed a single response peak and side bias to one side of the two component directions (Fig. 3C,D). On average, these neurons were most active when a component direction at a specific side of the two motion directions was near the PD, but not when the other component direction was near the PD. In other words, these neurons showed selectivity, not only to the motion direction of a stimulus component, but also to which side the component direction was situated relative to the other component direction.

Figure 3.

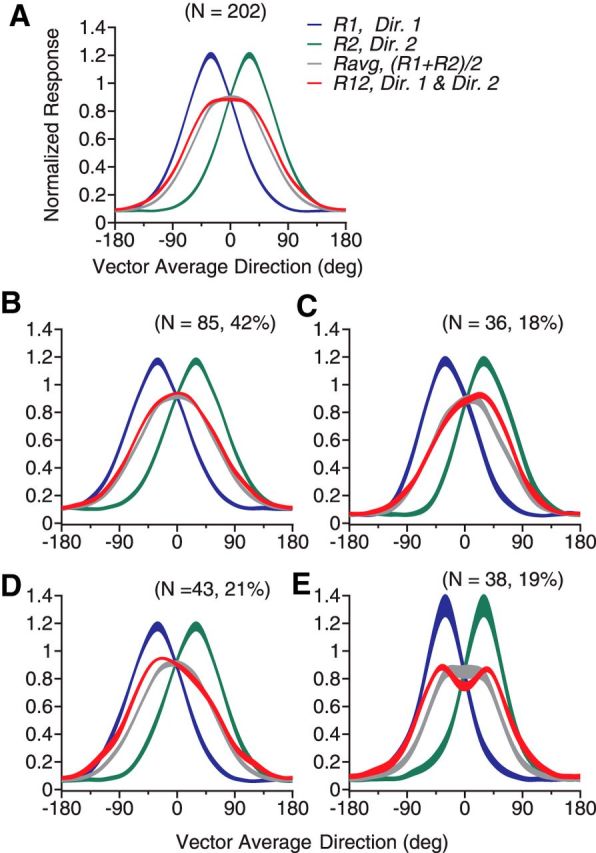
Population-averaged tuning curves elicited by bidirectional stimuli separated by 60° and by constituent unidirectional components. A, Tuning curves averaged across all neurons in the sample. B, Averaged across neurons that showed a single response peak and no side bias to the bidirectional stimuli. C, Neurons that showed side bias toward the stimulus component at the C-side of the two component directions (i.e., Dir. 2). D, Neurons that showed side bias toward the CC-side component (i.e., Dir. 1). E, Neurons that showed two response peaks. The convention of the abscissa is the same as that in Figure 1. Abscissas for component Dir. 1 and Dir. 2 are not plotted for simplicity. The width of each curve indicates SE.

Another 38 neurons (19%) showed two response peaks (Fig. 3E). The peaks were located when either component direction was near the PD. In other words, these neurons were informative about the direction of a stimulus component regardless of which side the component direction was situated on relative to the other stimulus component. Compared with the average of the component responses R_avg (shown in gray), the two response peaks appear to be shaped by facilitation at the outer flanks of the tuning curve and suppression near VA 0° (Fig. 3E). Consistent with the observation that suppression occurred when the VA direction was near the PD, for neurons that showed two response peaks, the mean value of the nonlinear interaction coefficient b of the SNL model fit (Eq. 2) was significantly smaller than 0 (Table 1; one-tailed t test, p < 0.001). This indicates that the multiplicative interaction between the component responses had a suppressive effect on the neuronal response. In contrast, for neurons that showed a single response peak with or without a side bias, the mean values of b (Table 1) were not significantly different from 0 (Student's t test, p > 0.2).

Table 1.

Parameters of the model fits and tuning widths of subgroups of neurons

Cells	No. of cells	Nonlinear interaction coefficient b of SNL model fit (mean ± SD)	Exponent n of PWS model fit (median, no. of cells)	Tuning width to unidirectional stimuli (mean ± SD)
All	202 (100%)	−0.007 ± 0.058	1.5 (n = 201)	99 ± 22°
Averaging	85 (42%)	−0.004 ± 0.028	1.2 (n = 84)	105 ± 18°
Side-biased	79 (39%)	0.001 ± 0.079	1.7 (n = 79)	99 ± 19°
2-peak	38 (19%)	−0.03 ± 0.052	3.7 (n = 38)	85 ± 27°

Notably, neurons that showed two response peaks in the tuning curves had a narrower tuning width to unidirectional stimuli than other subgroups of neurons (one-tailed two-sample t test, p < 0.002, after Bonferroni correction for multiple comparisons; Table 1). The mean tuning width of the side-biased neurons was marginally smaller than that of the averaging neurons (one-tailed two-sample t test, p = 0.02). Between any two subgroups of averaging, side-biased and two-peaked neurons, we did not find significant difference in the RF eccentricity, RF size, or PS (Wilcoxon rank-sum test, p > 0.14). The RF locations of the three subgroups of neurons largely overlapped with each other.

The SNL model outperformed the LWS model due to the inclusion of a nonlinear interaction term between the component responses. We asked whether a model involving a different type of response nonlinearity could account for the response tuning curves to the bidirectional stimuli. We fitted our data using a nonlinear summation model (Britten and Heuer, 1999). The PWS model (Materials and Methods, Eq. 3) fitted the data well and accounted for, on average, 93.2% of the response variance (N = 201, SD = 10.6%). The model was unable to fit the response from one neuron. Note that the PWS model has one additional free parameter than the LWS and SNL model. We used the AIC to take the number of model parameters into consideration and compared the goodness-of-fit between the models (Akaike, 1973; Burnham and Anderson, 2002; Chen et al., 2011). For 119 neurons (59%), the AIC of the SNL model fit was smaller (and better) than that of the PWS model. For the rest of the neurons, the AIC of the PWS model was smaller. Across the population, the average AIC for the SNL model was not significantly different from that of the PWS model (paired t test, p = 0.67), indicating that the goodness-of-fits of the SNL and PWS model were comparable. Between the PWS and LWS model, the PWS model was better. The AIC of the PWS model was smaller for 174 neurons (87%) and the average AIC of the PWS model was significantly smaller than that of the LWS model (one-tailed paired t test, p < 10⁻²⁸).

Across the neuron population, the median of the exponent parameter n of the PWS model fit was 1.5. The median n of the neurons that showed two response peaks was 3.7 and significantly greater than that of the averaging neurons and the side-biased neurons (one-tailed Wilcoxon rank-sum test, p < 0.001, after Bonferroni correction; Table 1). This indicates that neurons showing two response peaks are more likely to perform a soft MAX-like operation (Britten and Heuer, 1999; Riesenhuber and Poggio, 1999; Kouh and Poggio, 2008) than other subgroups of neurons. The median n of the side-biased neurons was also significantly greater than that of the averaging neurons (one-tailed Wilcoxon rank-sum test, p < 0.01).

Comparison of response tuning curves across different angular separations

As characterized above, some MT neurons showed side bias in the response tuning curves to the bidirectional stimuli separated by 60°. We asked whether the side bias was consistent across different angular separations. In this experiment, we randomly interleaved experimental trials of four angular separations of 45°, 60°, 90°, and 135° and varied their VA directions to characterize the response tuning curves. The monkeys performed a fixation task and our data sample included 96 neurons.

We found that MT neurons showed consistent side bias across different angular separations (Fig. 4). We classified side-biased neurons based on their responses to bidirectional stimuli separated by 60°. For neurons showing side bias to one side of two component directions at a DS of 60° (Fig. 4A2,B2), their tuning curves tended to bias to the same side at other angular separations (Fig. 4A1,A3,A4,B1,B3,B4). Figure 4C shows the response weights obtained using the SNL-model fit. We pooled together the response weights of 44 neurons (46% of the data sample) that showed side bias to the C-side (Fig. 4A) and the CC-side (Fig. 4B) at 60° DS. Although the “biased-side” was only determined by the response tuning to the DS of 60°, at the DS's of 45°, 90°, and 135°, the mean response weight for the component direction at the “biased-side” defined at 60° DS was significantly greater than the response weight for the other stimulus component (one-tailed paired t test, p < 0.00012, after Bonferroni correction; Fig. 4C).

Figure 4.

Consistent side bias of response tuning curves across different angular separations. A, Averaged response tuning-curves across 18 neurons that showed side bias to the C-side component of the bidirectional stimuli separated by 60°. B, Averaged response tuning curves across 26 neurons that showed side bias to the CC-side component of the bidirectional stimuli separated by 60°. The width of each curve indicates SE. C, Response weights obtained using the SNL model fit for the combined 44 neurons that showed side bias to the bidirectional stimuli separated by 60°. The “biased-side” in the ordinate was determined by the response to 60° DS. Each dot represents data from one neuron. Solid dots indicate that the response weight for one stimulus component was significantly greater than the other component (permutation test, p < 0.05). The mean weight for the component response to the “biased-side” defined at 60° DS was significantly greater than the weight to the other stimulus component at angular separations of 45°, 90° and 135°. p-values are the results of one-tailed paired t test. A1–C1, 45° DS; A2–C2, 60° DS; A3–C3, 90° DS; A4–C4, 135° DS. Note that we allowed the side-biased neurons to have either a single response peak or two response peaks in this analysis.

Relationship between the shapes of tuning curves to bidirectional and unidirectional stimuli

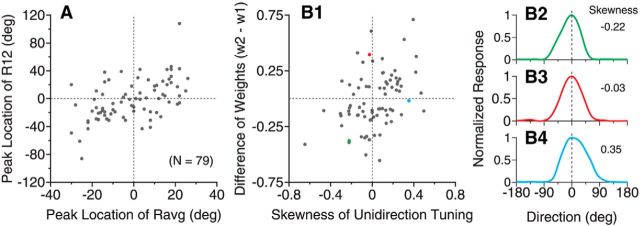
For neurons that showed side bias in the response tuning to the bidirectional stimuli (i.e., R₁₂) separated by 60° (Fig. 3C,D, red curves), the mean component response averaged across the same subpopulation of neurons (i.e., R_avg, Fig. 3C,D, gray curves) had the response peak slightly shifted toward the same side as that of R₁₂. We asked whether the side bias of R₁₂ was linked to a shift of peak location in R_avg. We found that the peak location of R₁₂ of the side-biased neurons in response to the bidirectional stimuli separated by 60° was correlated with that of R_avg (Spearman's ρ = 0.54, p < 10⁻⁶, N = 79; Fig. 5A). However, the side bias in R₁₂ cannot be explained simply by the bias in R_avg. For some neurons, as shown in the second and fourth quadrants, the peak locations of R₁₂ and R_avg were at opposite sides of VA direction 0° (Fig. 5A). When we determined the “biased-side” by the response weights of the SNL model fit, the shift of the peak location in R₁₂ toward the biased side (mean = 17°) was significantly greater than the shift of the peak location to the same side in R_avg (mean = 5°; one-tailed t test, p < 10⁻⁵).

Figure 5.

Relationship between the shapes of response tuning curves to bidirectional and unidirectional stimuli. The results were from 79 neurons that showed side bias in their tuning curves to the bidirectional stimuli separated by 60°. A, Relationship between the peak locations of the response tuning to the bidirectional stimuli R₁₂ and the average of the responses elicited by individual stimulus components R_avg = (R₁ + R₂)/2. The peak location is represented as the VA direction of the bidirectional stimuli. B1, Relationship between the difference of the response weights for the two stimulus components obtained from the SNL model fit of R₁₂ and the skewness of the unidirectional tuning curve (see Materials and Methods). w₂ and w₁ correspond to the response weights for Dir. 2 and Dir. 1, respectively (Fig. 1 diagram). B2–B4, Response tuning curves to the unidirectional stimuli of three neurons that had negative (B2), near zero (B3), and positive skewness (B4). These neurons are marked in B1 using the corresponding colors. The neuron shown in B3 is the same example neuron shown in Figure 1B.

The peak location of R_avg is related to the shape, specifically the skewness of the tuning curve to the unidirectional component. The peak location of R_avg would shift to the right (or left) side of VA direction 0° if a neuron's tuning to unidirectional stimuli has a positive (or negative) skewness. Because the peak location of R₁₂ was correlated with that of R_avg, we asked whether the side bias in R₁₂ of a neuron was linked to the skewness of its tuning curve to the unidirectional stimuli. We found that the difference between the response weights for the two stimulus components obtained from the SNL model fit of R₁₂ had a weak but significant correlation with the skewness of the tuning curve to the unidirectional stimuli (Spearman's ρ = 0.38, p < 0.001, N = 79; Fig. 5B). Despite this correlation, the side bias in the response tuning to the bidirectional stimuli cannot be explained simply by a neuron's tuning property to unidirectional stimuli. For some neurons, as shown in the second and fourth quadrants of Figure 5B1, the skewness of the tuning curve to unidirectional stimuli mismatched the side bias in R₁₂. Furthermore, for neurons that had a symmetric tuning curve to unidirectional stimuli (e.g., the neuron shown in Figs. 5B3, 1B), they nevertheless showed side bias to either the C-side or CC-side (Fig. 5B1).

Time course of response tuning to bidirectional stimuli

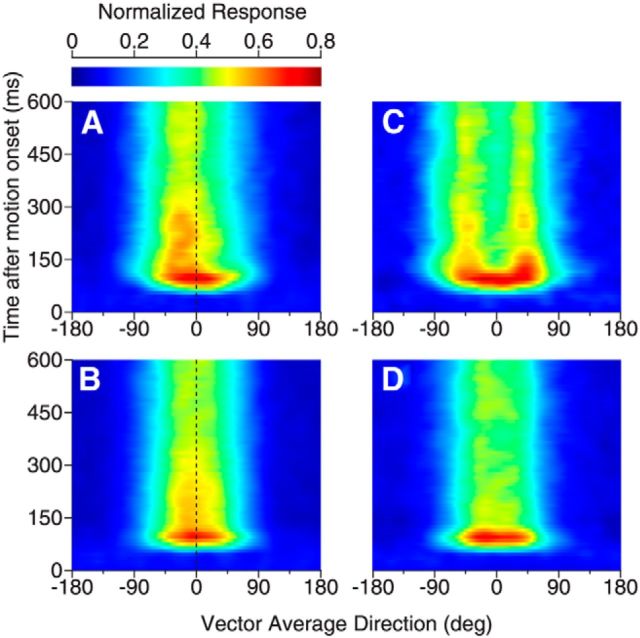
We found that the side bias and two response peaks in MT response tuning to the bidirectional stimuli evolved over time. When the angular separation between the two component directions was small, the tuning curve initially followed the average of the component responses and gradually changed to better represent the constituent component directions. To measure the time course of the response tuning, we characterized the direction tuning curves using a time window of 50 ms and sliding at a step of 10 ms.

Figure 6 shows the time course of the response tuning curve elicited by the bidirectional stimuli separated by 60°. For neurons that showed the side bias (79 of 202 neurons), the initial response tuning had a symmetric single peak located near the VA direction at 0° (Fig. 6A, black curve). Over time, the response peak gradually shifted toward one side of the tuning curve (Fig. 6A,B). In contrast, the average of the component responses elicited by the two component directions (i.e., R_avg) had an approximately symmetric single peak throughout the motion response period with only a slight bias (Fig. 6C). Taking the difference between the response tuning curves elicited by the bidirectional stimuli (i.e., R₁₂) and R_avg revealed strong facilitation at the biased side and suppression at the other side of the tuning curve (Fig. 6D).

Figure 6.

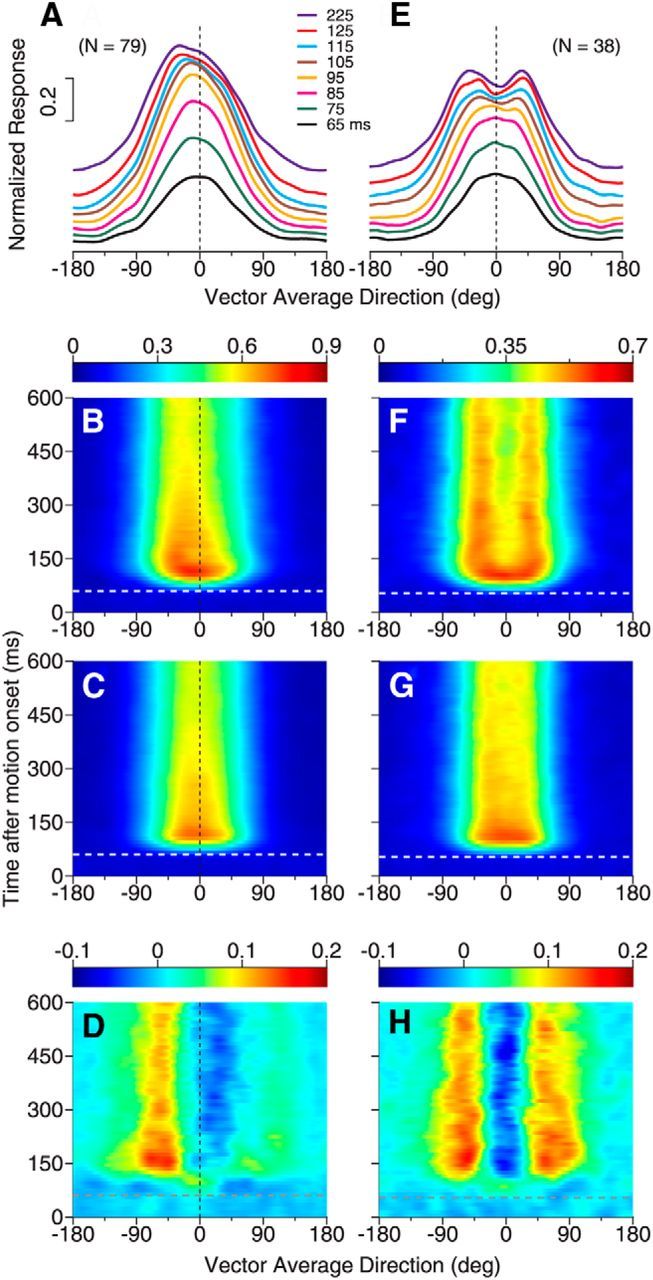
Time course of response tuning to bidirectional stimuli separated by 60°. A–D, Responses of neurons showing side bias to bidirectional stimuli. E–H, Responses of neurons showing two peaks to bidirectional stimuli. A, E, Subpopulation-averaged response tuning curves to bidirectional stimuli at different time epochs after the stimulus motion onset. The duration of each time epoch is 50 ms. The tuning curves of later epochs are stacked on earlier ones. The number in figure legends indicates the middle point of each time epoch. B, F, Time course of the subpopulation-averaged response tuning to bidirectional stimuli (i.e., R₁₂). Ordinates indicate the middle point of each time epoch. C, G, Time course of the average of the component responses (i.e., R_avg), averaged across neurons in each subpopulation. D, H, Difference between the response to bidirectional stimuli shown in B and F and the average of the component responses shown in C and G, respectively. In A–C, we pooled the results from neurons that showed side bias to the component directions at the C-side (i.e., Dir. 2) and CC-side (i.e., Dir. 1) together by first flipping the bidirectional and unidirectional tuning curves of neurons that showed the side bias to Dir. 2 along the axis of VA direction 0°. The white and gray horizontal lines in B–D and F–H indicate the neuronal response onset to the stimulus motion. In D and H, the deviation from the average of the component responses emerged later than the neuronal response onset.

For neurons that showed two response peaks (38 of 202 neurons), the initial response tuning also had a single, symmetric peak near VA 0° (Fig. 6E,F) similar to the average of the component responses (Fig. 6G). Over time, the response elicited by the bidirectional stimuli split into two separate peaks (Fig. 6E,F), whereas the average of the component responses remained a single peak (Fig. 6G). The difference between the bidirectional response and the average of the component responses indicated response facilitation at the two outer flanks of the tuning curve and response suppression near VA 0° (Fig. 6H). For both groups of neurons that showed the side bias and two response peaks, the facilitatory and suppressive effects occurred after a delay following the onset of the neuronal response (Fig. 6D,H).

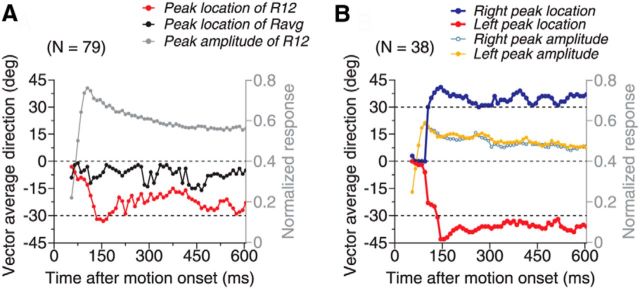
The peak locations in the response tuning curves of the side-biased neurons and those showing two separate peaks were approximately aligned with the directions of the stimulus components (Fig. 7). For neurons that showed the side bias, the peak location of R₁₂ was initially near VA direction 0° and progressively shifted to near −30° over a period of 80–100 ms (Fig. 7A, red curve). At VA direction −30°, the two component directions were 0° (i.e., the PD of the neuron) and −60°, respectively. In other words, these neurons responded most strongly when one component direction was near the PD. After the initial, progressive shift, the peak location fluctuated to some extent, but returned to VA −30° at times. In contrast, the peak location of R_avg (Fig. 7A, black curve) had a much smaller bias and the fluctuation started in the very beginning of the neural response. These results suggest that the side bias is not a byproduct of randomly sampling two response weights from a given distribution, but rather may be functionally important in representing slightly different stimulus components.

Figure 7.

The temporal evolution of the response peak(s) in the tuning curve to bidirectional stimuli separated by 60°. A, Location and amplitude of the response peak of neurons that showed a single peak and side bias. We pooled neurons that showed side bias to the C-side (i.e., Dir. 2) and CC-side (i.e., Dir. 1) together as in Figure 6, A and B. B, Peak locations and amplitudes of neurons that showed two response peaks to bidirectional stimuli. Right side and left side refer to the peaks seen in Figure 6, E and F. The peak location and magnitude were calculated based on averaged response tuning curves across neurons in each subgroup. The tuning curve was calculated within a 50 ms time epoch, sliding at a 10 ms step. Abscissa indicates the middle point of each time epoch.

For neurons that showed two response peaks, the peaks did not separate until 30–40 ms after the response onset and it took another 40–50 ms for the two peaks to separate to the farthest angles of near VA directions of ±40° (Fig. 7B, red and blue curves). After this initial, farthest separation, the two response peaks returned and remained near VA directions of ±35° (i.e., a DS of ∼70°). The overshoot of the peak separation from the veridical 60° separation may be related to the perceptual phenomenon of direction repulsion reported by human subjects (Marshak and Sekuler, 1979). When human subjects viewed visual stimuli similar to those used in our neurophysiological experiments, they also reported direction repulsion (Gaudio and Huang, 2012).

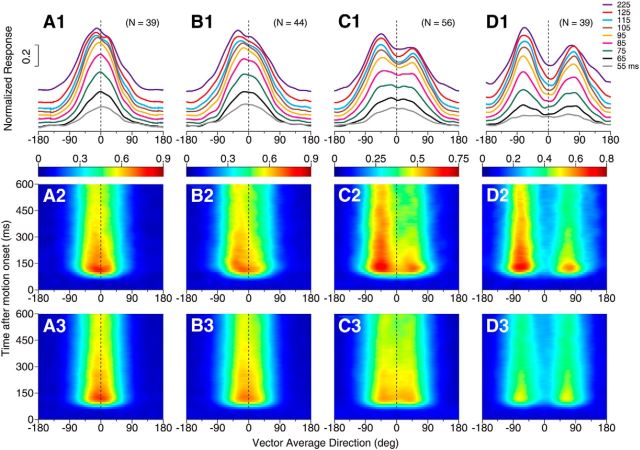
At other angular separations, the response tuning for neurons with side bias also shifted gradually from initially following the average of the component responses to later being biased toward one side of the tuning curve. Moreover, the side bias appeared to develop slightly slower at the smaller angular separation. Figure 8 shows the results of the neurons that displayed side bias at the DS of 45°, 60°, 90°, and 135°, respectively. At the DS of 45°, the average of the component responses contained a single response peak centered near VA 0° throughout the motion response period (Fig. 8A3). The bidirectional responses initially showed a single response peak centered near VA 0° (Fig. 8A1, gray, black, green, and pink curves), but over a period of ∼50 ms, the response peak shifted to a side (Fig. 8A1,A2). At the DS of 90°, the average of the component responses showed a broad but approximately symmetric tuning curve (Fig. 8C3). The bidirectional response of the same group of neurons initially showed a broad and symmetric tuning curve peaked near VA 0°. Over a period of ∼40 ms, the response peak shifted ∼45° in the VA direction and was reached when one component direction was near a neuron's PD (Fig. 8C1,C2). At the DS of 135°, the average of the component responses contained two separate but symmetric peaks (Fig. 8D3). The bidirectional response tuning showed two symmetric peaks in the early response. However, over a period of ∼30 ms, one response peak evolved to be higher than the other peak and the whole response tuning curve was biased toward one side (Fig. 8D1,D2). The temporal development of the side bias was delayed relative to the response onset and the transition occurred slightly earlier at the larger angular separations (Fig. 8A1–D1, A2–D2).

Figure 8.

Temporal development of side bias in the response tuning curves elicited by bidirectional stimuli at different angular separations. A1–A3, Responses elicited by bidirectional stimuli separated by 45°. B1–B3, 60° DS. C1–C3, 90° DS. D1–D3, 135° DS. A1–D1, Subpopulation-averaged tuning curves of responses at different time epochs elicited by bidirectional stimuli. The duration of each time epoch is 50 ms. A2–D2, Time course of the response tuning to bidirectional stimuli averaged across side-biased neurons at each DS. Classification for the side-biased neurons was based on the responses to the bidirectional stimuli at each DS. A3–D3, Time course of the average of the component responses. Conventions are the same as for Figure 6, A–C. The results from neurons that showed side bias to the component directions at the C-side and CC-side were pooled together. This analysis included side-biased neurons that showed either a single response peak or two peaks at each DS.

Neuronal response tuning obtained during a perceptual discrimination task

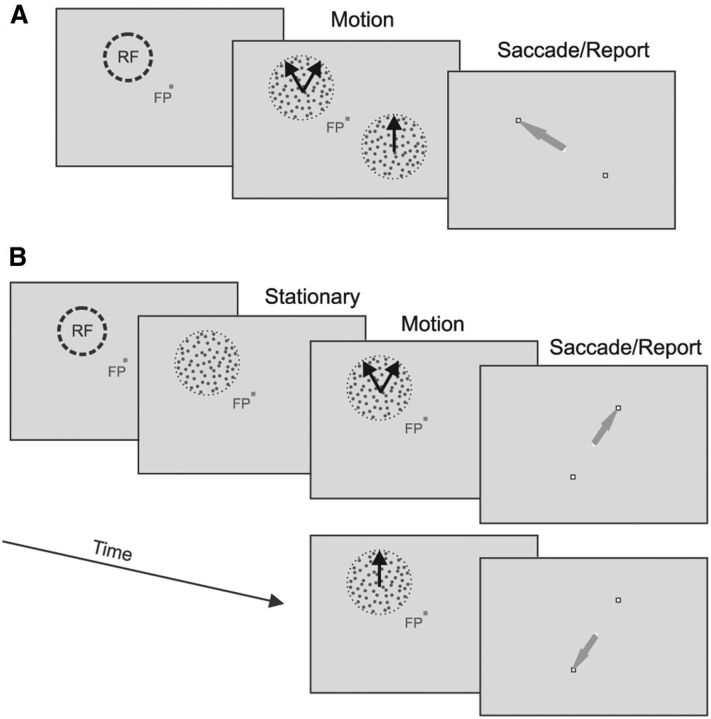
The results reported so far were obtained while the monkeys performed a simple fixation task and viewed the visual stimuli passively. We asked whether MT neurons showed similar patterns of response tuning when monkeys performed a behavioral task to actively discriminate bidirectional stimuli from unidirectional stimuli (see Materials and Methods). The DS of the bidirectional stimuli was set to 60°. For monkey GE, a bidirectional stimulus and a unidirectional stimulus moving in the VA direction were presented simultaneously at locations symmetric to the fixation spot. One of the two stimuli was centered on a neuron's RF. After viewing the moving stimuli for 1.5 s, the monkey was required to make a saccadic eye movement to the location of the bidirectional stimulus to receive a juice reward (referred to as Task I; Fig. 9A). The behavioral performance of monkey GE was, on average, 83% correct (SD = 7.1%) across 48 recording sessions, during which 51 neurons were recorded. The corresponding d′ was 1.9. As in the fixation task, when the monkey performed this task, we found that some MT neurons showed the side bias in their response tuning curves (Fig. 10A1,B1) and some neurons showed tuning curves containing two separate peaks (Fig. 10C1), although the average of the component responses had only a single peak.

Figure 9.

Illustration of two perceptual discrimination tasks. A, In Task I, a bidirectional stimulus and a unidirectional stimulus were presented simultaneously. The animal was required to make a saccadic eye movement after the stimulus offset toward the location where a bidirectional stimulus was presented. The stimulus centered on the RF was either bidirectional or unidirectional. B, In Task II, only one stimulus, either bidirectional or unidirectional, was presented in a given trial and centered on the RF. The animal was required to make a saccadic eye movement after the stimulus offset toward one reporting target if the stimulus was bidirectional or the other target if the stimulus was unidirectional.

Figure 10.

Direction tuning curves obtained while the animals performed the perceptual discrimination tasks. The DS of the bidirectional stimuli was 60°. A1–C1, Three example neurons recorded while monkey GE performed Task I. A2–C2, Three example neurons recorded while monkey BJ performed Task II. A3–C3, Direction tuning curves averaged across subpopulations of neurons from the two animals. A, Neurons showing side bias to the CC-side. B, Neurons showing side bias to the C-side. C, Neurons showing two separate peaks in the response tuning curves.

To perform Task I, however, the monkey may shift its attention back and forth between the RF stimulus and the other stimulus at the opposite side of the visual field. To better control the spatial allocation of attention, we trained a second monkey (BJ) on a modified task, in which only one stimulus, either bidirectional or unidirectional, was presented in a given experimental trial and centered on the RF. The monkey's task was to discriminate whether the presented stimulus was unidirectional or bidirectional (referred to as Task II; Fig. 9B). Trials containing the bidirectional stimuli and those containing the unidirectional stimuli were interleaved randomly. To perform this task well, the animal needed to direct its attention toward the RF. Across 37 recording sessions during which 44 neurons were recorded, monkey BJ correctly identified the bidirectional stimuli at a rate of 90% (SD = 3.8%) and correctly identified the unidirectional stimuli at a rate of 92% (SD = 5.9%). The corresponding d′ was 2.7.

Again, we found that some MT neurons showed side bias (Fig. 10A2,B2) or two response peaks (Fig. 10C2) in their tuning curves while the monkey performed this task. Because we found similar results across Tasks I and II, we pooled the data to calculate the population-averaged tuning curves. MT neurons showed similar patterns of response tuning curves when the monkeys performed the perceptual discrimination tasks (Fig. 10A3–C3) as when they performed the fixation task (Fig. 3C–E). Notably, a higher percentage of neurons showed two response peaks when the monkeys performed the discrimination tasks (29% of 95 neurons) than when they performed the fixation task (19% of 202 neurons). To characterize the tuning curves obtained during the discrimination tasks, we used all of the experimental trials, including those that had correct and incorrect behavioral reports, because the correct rates of the animals' performance were high and our algorithm classifying tuning curves into different subgroups required equal number of trials at different VA directions. In addition to this analysis, we first classified a neuron's tuning curve into one of three subgroups based on all trials and recalculated the tuning curve based on only the correct trials. The direction tuning curves constructed based on only the correct trials were very similar to those based on all trials (results not shown).

When the monkeys performed the perceptual discrimination task, the time course of MT response tuning to the bidirectional stimuli also evolved from initially following the average of the component responses to later showing the side bias or two response peaks, as found using the fixation paradigm. Figure 11 shows the results from monkey BJ while it performed Task II, in which the stimulus motion onset was separated in time from the stimulus onset (see Materials and Methods).

Figure 11.

Time course of the direction tuning curves obtained while an animal performed a perceptual discrimination task. The DS of the bidirectional stimuli was 60°. Results were recorded while monkey BJ performed Task II, during which the onset of visual motion was separated from the stimulus onset (see Materials and Methods). A, B, Averaged responses from 25 neurons that showed side bias to the bidirectional stimuli. C, D, Averaged responses from 14 neurons that showed two peaks in the tuning curves to the bidirectional stimuli. A, C, Response tuning curves to the bidirectional stimuli. Ordinates indicate the middle point of each time epoch of 50 ms. B, D, Average of the component responses.

Stimulus discrimination using a classifier of SVM

To evaluate whether the population of recorded neurons contained sufficient information to discriminate a bidirectional stimulus from a unidirectional stimulus and to discriminate between two bidirectional stimuli that had different angular separations, we used the SVM to classify different visual stimuli (see Materials and Methods). We assumed that, for each neuron in our dataset, there was a family of “cloned” neurons that had the same tuning curve but different PDs evenly spanning 360° (Fig. 12A,B). The inclusion of the cloned neurons in the population allowed an unbiased representation of all motion directions and the conversion of the direction tuning curve of a single neuron (Fig. 12A) to the responses of a population of the cloned neurons elicited by a given stimulus (Fig. 12C).

Figure 12.

Stimulus discrimination using a classifier of support vector machine (SVM). A–C, Procedure of constructing a “single-trial population neural response” based on the direction tuning curve. D–F, Discrimination performance of the classifier. A, Trial-by-trial tuning curves of one example neuron in response to the bidirectional stimuli of 60° DS. A tuning curve based on one block of trials (red) was picked. B, The picked single-trial tuning curve from A (red) was duplicated and shifted in a step of 7.5° to create the tuning curves of 48 “cloned” neurons. For clarity, only the cloned neurons that had PDs in a step of 30° are shown (black). C, Single-trial population neural response of the cloned neurons elicited by a bidirectional stimulus moving at VA direction 0°. D, Discrimination between the bidirectional stimuli of 60° DS and the unidirectional stimulus moving at the same VA direction. Stimulus classification was based on the neural responses of all neurons in the dataset (black) or one of three subgroups of neurons (green, blue, and red). The label “sub” in the abscissa means a subset of randomly selected neurons within the groups of averaging and side-biased neurons. E, Discrimination between a bidirectional stimulus of 60° DS and another bidirectional stimulus that had a DS of 45°, 90°, and 135°, respectively, and moving at the same VA direction. When discriminating between DS 60° and 90°, the performances of the side-biased neurons and the averaging neurons were nearly identical. In this analysis, the side-biased neurons only contained a single response peak to the bidirectional stimulus of 60° DS, so the side-biased and two-peaked neuron populations did not overlap. F, Discrimination between a unidirectional and a bidirectional stimulus. The classifications of averaging, side-biased, and two-peaked neurons were based on the responses to DS 60°.

The classifier was capable of discriminating a bidirectional stimulus of 60° DS from a unidirectional stimulus moving at the same VA direction (Fig. 12D). Based on the responses of all 202 neurons in the dataset shown in Figure 3, the discrimination performance of the classifier, measured in d′, was 1.3. The performances of the classifier based on the responses of the two-peaked neurons (N = 38) and the side-biased neurons (N = 79) were better than the averaging neurons (N = 85) (Fig. 12D). The d′ based on the responses of the averaging neurons merely reached 1 (Fig. 12D, solid green bar), whereas the d′ based on the side-biased neurons and the two-peaked neurons was 1.7 and 2.8, respectively (Fig. 12D, solid blue and red bars), similar to the behavioral performance of the two monkeys. This difference in classification was not due to different pool sizes of three subgroups of neurons. We randomly picked 38 neurons from 85 averaging neurons and from 79 side-biased neurons and repeated the procedure 100 times. The averaged classification performance based on 38 subsampled neurons was similar to that based on all averaging neurons or side-biased neurons (Fig. 12D, open green and blue bars). The mean d′ based on 38 subsampled averaging neurons was significantly smaller than that based on 38 side-biased neurons (t test, N = 100, p < 10⁻⁷⁴) and both were significantly smaller than the d′ value of 2.8 based on 38 two-peaked neurons (t test, p < 10⁻⁸⁴). These results support the idea that the two-peaked neurons and the side-biased neurons carry more information about the bidirectional stimuli of 60° DS than the averaging neurons.

The classifier was also capable of discriminating a bidirectional stimulus of 60° DS from another bidirectional stimulus moving at the same VA direction (Fig. 12E) based on the 96 neurons shown in Figure 4. As expected, the classification performance increased as the difference between the DS's of two stimuli increased from 15° to 75°. Among the three subgroups of neurons, classification based on the two-peaked neurons gave the best performance. For the most difficult discrimination between DS 60° and DS 45°, the classification based on all 96 neurons and the averaging neurons was poor and had a d′ of 0.51 and 0.33, respectively. In contrast, the classification based on the two-peaked neurons had a d′ of 1.4. The d′ based on the side-biased neurons was 0.74, which was better than the d′ based on the averaging neurons (Fig. 12E).

The two-peaked neurons classified based on the tuning curves to the bidirectional stimuli of 60° DS provided good classification between a unidirectional stimulus and a bidirectional stimulus with various DS's, suggesting that this group of neurons were informative about bidirectional stimuli in general (Fig. 12F). Classification based on the side-biased neurons was better than the averaging neurons (Fig. 12F). Note that, at DS 135°, all side-biased neurons showed two response peaks, which may explain why the d′ value based on the side-biased neurons was the largest. At DS 45°, although not all 13 two-peaked neurons classified at DS 60° showed two response peaks, they nevertheless supported reliable discrimination between DS 45° and 0°, giving a d′ value of 1.4 (Fig. 12F). The d′ based on the side-biased neurons was 0.75, better than the d′ of 0.38 based on the averaging neurons (Fig. 12F).

Based on the response tuning curves to DS 45°, 42 of the 96 neurons were classified as the side-biased neurons with a single response peak and seven neurons were classified as the two-peaked neurons. When discriminating between DS 45° and 0°, the classifier gave the largest d′ of 0.90 based on the 42 side-based neurons. The d′ based on the 7 two-peaked neurons was smaller and had a value of 0.58, which may be caused by the small sample size of the two-peaked neurons at DS 45°. In comparison, the d′ based on the 47 averaging neurons was 0.41. These results suggest that, at a DS of 45° or smaller, the side-biased neurons may be important for representing the bidirectional stimuli.

Comparison of direction tuning curves elicited by overlapping random-dot stimuli and plaid stimuli

It has been well established that, when tested with overlapping sinusoidal gratings (i.e., plaid stimuli) drifting in widely different directions, some MT neurons are selective to the pattern-motion direction of the plaid, whereas some other neurons are selective to the directions of the component gratings (Movshon et al., 1985; Rodman and Albright, 1989; Smith et al., 2005; Rust et al., 2006). McDonald et al. (2014) showed recently that pattern cells in area MT of marmosets represented component directions of transparently moving random-dot stimuli that had a large DS of 120°, whereas component cells tended to represent the VA direction.

We examined the relationship between the pattern- and component-direction selectivity to plaid and the types of response tuning curves elicited by overlapping random-dot stimuli moving in slightly different directions. A total of 102 neurons were tested with both plaid stimuli that had a large DS of 135° and random-dot stimuli that had a DS of 60°. Among them, 99 neurons were tested with component gratings moving at the same speed as the random-dot patterns. The classification of neurons as pattern- or component-direction selective relies on the “pattern prediction” and the “component prediction” to be significantly different from each other (see Materials and Methods), which only holds true when the DS of plaid stimuli is large. We therefore chose to use plaid stimuli that had a DS of 135° rather than 60°. The monkeys performed a fixation task when tested with the plaid stimuli and performed either a fixation task or the perceptual discrimination tasks as mentioned earlier when tested with the random-dot stimuli. Because we found that the response tuning curves elicited by the random-dot stimuli were qualitatively similar when the monkeys performed the fixation task (60 neurons recorded) and the perceptual discrimination tasks (42 neurons recorded), we pooled the results of these neurons together.

We did not find a significant relationship between the properties of the response tuning curves to the random-dot stimuli and the pattern/component selectivity to the plaid stimuli. Neurons that showed each of the three types of tuning curves—side bias, two response peaks, and response-averaging to random-dot stimuli that had a DS of 60°—could be either pattern selective or component selective to our plaid stimuli. Across the population of 102 neurons, the “averaging” neurons included a higher percentage of pattern cells than did the side-biased and two-peaked neurons, whereas the two-peaked neurons included a slightly higher percentage of component cells than did the side-biased and averaging neurons (Fig. 13, Table 2). Examining the difference between Z-transformed pattern correlation (Zp) and component correlation (Zc; see Materials and Methods) revealed that the median value of Zp − Zc was positive and the largest for the averaging neurons, indicating that these neurons tended to be more pattern selective, whereas the median value of Zp − Zc was negative for the two-peaked neurons, indicating that these neurons tended to be more component selective (Table 2). However, the median values of Zp − Zc were not significantly different between any two subgroups of averaging, side-biased, and two-peaked neurons (Wilcoxon rank-sum test, p > 0.18). We found the same result when we constrained our dataset to the 99 neurons that were tested with the plaid and random-dot stimuli moving at the same speed.

Figure 13.

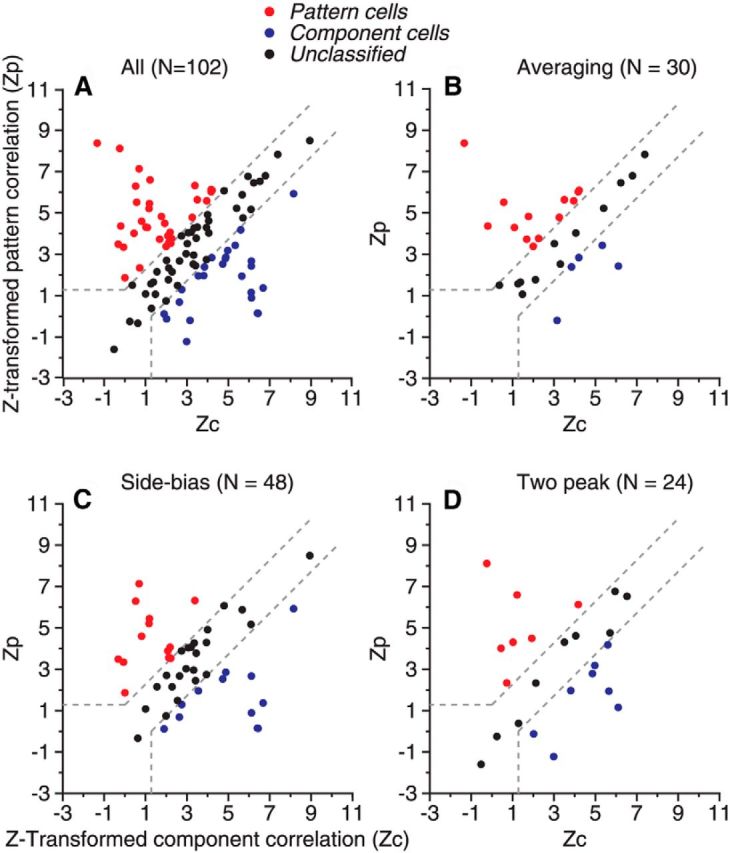
Z-transformed pattern and component correlation between the responses elicited by 135° plaid and pattern/component predictions. Each dot represents results from one neuron. A, Results from overall neuron population. B, Results from neurons approximately followed the average of the component responses when responding to the bidirectional random-dot stimuli that had a DS of 60°. C, Neurons with responses to the random-dot stimuli that showed side bias. D, Neurons with responses to the random-dot stimuli that showed two response peaks.

Table 2.

Relationship between the properties of response tuning to random-dot stimuli (RDS) and plaid stimuli

Cells	No. of neurons	Pattern- selective	Component- selective	Unclassified	Zp − Zc (median)	Zp − Zc (mean)	Zp − Zc (SD)
RDS 60°/Plaid 135°
All	102	32%	25%	43%	0.25	0.36	2.78
Averaging	30	43%	17%	40%	0.47	0.96	2.57
Side-biased	48	27%	25%	48%	0.14	0.087	2.76
2-peak cells	24	29%	33%	38%	−0.24	0.15	3.04
RDS 135°/Plaid 135°
All	46	39%	26%	35%	0.22	0.46	3.47
Averaging (1-peak)	1	0	0	100%	0.50	0.50	—
Averaging (2-peak)	23	39%	17%	44%	0.23	0.74	2.76
Side-biased (2-peak)	22	41%	36%	23%	0.07	0.16	4.20

We also tested 46 neurons with both the plaid stimuli and random-dot stimuli that had the same DS of 135°. We did not find a significant relationship between the tuning properties to the random-dot stimuli and the pattern/component selectivity even when the DS was matched. In response to the random-dot stimuli, most of these neurons (45/46) showed two response peaks because the DS was large. Twenty-three (23) of the two-peaked neurons followed the average of the component responses and 22 neurons showed side bias. Only one of the 46 neurons showed a single response peak. This cell was classified as an averaging neuron. Based on the responses to the plaid stimuli, the median values of Zp − Zc were not significantly different between the two-peaked averaging neurons (N = 23) and the two-peaked side-biased neurons (N = 22) (Wilcoxon rank-sum test, p = 0.59; Table 2).

Smith et al. (2005) have shown that it takes longer for the pattern-direction selectivity of the pattern cells to develop than the component-direction selectivity of the component cells. Our data obtained using the plaid stimuli confirmed this finding. Among 102 neurons in this dataset, the pattern selectivity of 33 pattern cells emerged later than the component selectivity of 25 component cells. A neuron showing a longer buildup of the pattern selectivity (consistent with motion integration) depended on whether the neuron was a pattern cell regardless of the neuron's tuning property to the random-dot stimuli. All three types of tuning curves characterized based on the response to the random-dot stimuli: two-peaked, side-biased, and averaging neurons showed a longer buildup of pattern selectivity with the plaid stimuli as long as they were also pattern cells (results not shown). Interestingly, for neurons that were pattern cells and also showed two response peaks or side bias to the bidirectional random-dot stimuli with a small DS, the temporal evolution of the response tuning to bidirectional stimuli was stimulus dependent and switched from a gradual buildup of segmentation (as shown in Fig. 6) to a buildup of integration when the visual stimuli changed from random dots to plaids. This adaptive change of the temporal property of response tuning is akin to the stimulus-dependent change of surround antagonism and integration found in area MT (Huang et al., 2007, 2008). Future study is needed to understand the neural mechanism underlying such adaptive change of direction tuning over time.

Discussion

We found that many neurons in area MT were capable of representing component directions of transparently moving stimuli even when the angular difference between two directions was smaller than the tuning width to unidirectional stimuli. We also discovered that the neural representation of component directions developed over time. The tuning curves of some neurons initially followed the average of the component responses and later showed side bias or two response peaks. The early neuronal responses better represented the VA direction of slightly different stimuli, whereas the late responses were informative about the component directions.

Previous studies show that the neuronal response elicited by two stimuli within the RF can be described as a weighted sum of the responses elicited by the individual stimulus components (Qian and Andersen, 1994; van Wezel et al., 1996; Recanzone et al., 1997; Britten and Heuer, 1999; Zoccolan et al., 2005). Consistent with the model of response normalization (Carandini and Heeger, 2012), the response weight is greater for the stimulus component that has a stronger signal strength, as found in area V1 (Busse et al., 2009; MacEvoy et al., 2009), MT (Xiao et al., 2014) and MST (Morgan et al., 2008; Fetsch et al., 2012). In the current study, the stimulus components had the same signal strength. Although, as expected, the population-averaged response weights for the two stimulus components with a DS of 60° were identical, we found that, for many neurons, the response weight for one stimulus component was significantly greater than the other. This unequal pooling of the component responses allows a neuron to selectively represent the direction at a specific side of two motion vectors. To the best of our knowledge, this finding establishes for the first time the selectivity of MT neurons for the side relationship of two motion directions.

Ni et al. (2012) suggest that response normalization is tuned, meaning that different visual stimuli contribute differently to normalization (also see Carandini et al., 1997; Rust et al., 2006). Tuned normalization can explain why, for some MT neurons, the response to the bidirectional stimulus follows the average of the component responses whereas, for others, the response follows the stronger (or weaker) component response or anywhere in between. At its current form, however, tuned normalization cannot explain the side bias found in our study. Taking the neuron in Figure 1B as an example, this neuron showed response averaging when the component direction at the CC-side was closer to the PD and winner-take-all when the C-side component was closer to the PD. The two component stimuli contributed equally to normalization at one side of the tuning curve, but contributed differently at the other side of the tuning curve. The extent of tuned normalization itself is tuned to the visual stimuli.

We speculate that recurrent interactions among MT neurons may be involved in shaping the side bias because the side bias developed over time and emerged later in the tuning curve. Feedback connections from higher-order areas may also be involved. Area MT receives feedforward inputs from direction-selective neurons in V1 (Movshon and Newsome, 1996). If feedforward connections between V1 neurons and a target MT neuron have an asymmetric distribution of the synaptic weights in relation to whether the PD of a V1 neuron is at the C-side or CC-side of the PD of the MT neuron (Fig. 14A), then the MT neuron's response to the bidirectional stimuli would show side bias. However, it is unlikely that feedforward connections alone can explain the time course of the side bias. Alternatively, the side bias may arise due to asymmetric recurrent connections between MT neurons (Fig. 14B). It is also possible that a slight asymmetry in the feedforward connections is amplified by recurrent interactions (Fig. 14C). Future studies are needed to understand the neural circuit mechanisms underlying the side bias, possibly involving an attractor network (Knierim and Zhang, 2012).

Figure 14.

Illustration of possible circuit mechanisms underlying the side bias. Each circle represents one neuron in area MT or V1. The arrow inside each circle represents the PD of that neuron. The width of the connection line and the diameter of the solid circle at the end of each line indicate the strength of the synaptic connection. A, Asymmetric feedforward connections between V1 neurons and a MT neuron. The connection between a V1 neuron with a PD that is at the C-side of the PD of the MT neuron is stronger than the connection between a V1 neuron with a PD that is at the CC-side of the MT neuron. B, Symmetric feedforward connections and asymmetric recurrent connections among MT neurons. Recurrent connections between the center MT neuron and the MT neurons that have PDs at the C-side are stronger than those at the CC-side. For clarity, only one way of the recurrent connections are shown. C, Slightly asymmetric feedforward connections coupled with asymmetric recurrent connections. Except for the center MT neuron, only the feedforward connections between V1 neurons and MT neurons that have matching PDs are illustrated for simplicity. Recurrent interactions between MT neurons may include both excitatory and inhibitory connections (not differentiated in the illustration).

Some MT neurons showed two response peaks to the bidirectional stimuli even when the average of the component responses was unimodal. This result suggests that stimulus components interact nonlinearly within the RF. One possible mechanism involves response suppression proportional to the product of the component responses (Xiao et al., 2014). Another possibility involves a soft MAX-like operation (Riesenhuber and Poggio, 1999; Lampl et al., 2004) in which the neuronal response elicited by two stimuli is close to the stronger component response. The suppressive mechanism involving multiplicative interaction and the soft MAX-like operation may work synergistically to allow neurons to represent slightly different stimulus components.

Treue et al. (2000) previously investigated how bidirectional random-dot stimuli were represented by neurons in area MT. Recently, McDonald et al. (2014) studied the response tuning of MT neurons in marmosets using similar stimuli. Consistent with these studies, we found that the tuning curve averaged across all neurons in response to the bidirectional stimuli with a small DS approximately followed the average of the component responses and showed a symmetric, unimodal shape (Fig. 3A). It is unclear whether the individual neurons in these previous studies also showed the side bias or two response peaks that deviated from response averaging. Moreover, these previous studies did not examine the time course of the tuning curve. In the study of Treue et al. (2000), the random-dot stimuli moved on a circular path (Schoppmann and Hoffmann, 1976). Although this method of stimulus presentation is efficient for measuring direction tuning, the constant change of stimulus direction could make it difficult to reveal the time course of response tuning to the bidirectional stimuli.

Perceptually, lowering luminance contrast benefits motion integration rather than segmentation (Murakami and Shimojo, 1993). Response normalization in area MT is also contrast dependent (Heuer and Britten, 2002). The response tuning to the bidirectional random-dot stimuli may become less supportive of segmentation when luminance contrast is reduced. Furthermore, the perceived angle separation between two component directions of random-dot stimuli varies with motion coherence (Gaudio and Huang, 2012). As the coherence level is lowered, the perceived angle shifts from repulsion to attraction, consistent with a change from motion segmentation to integration. The response tuning to the bidirectional stimuli therefore may also depend on the coherence level of the random dots. Future studies are needed to test these hypotheses.

Attention can bias the neuronal response elicited by multiple stimuli in the RF (Ferrera and Lisberger, 1997; Reynolds et al., 1999; Treue and Martínez-Trujillo, 1999; Recanzone and Wurtz, 2000; Li and Basso, 2005). Wannig et al. (2007) showed that attention directed to one of two transparently moving surfaces could alter the responses of MT neurons in favor of the direction of the attended surface. In that study, attention was cued to one of two already segregated surfaces. In contrast, the two slightly different stimuli in our experiments had not been rendered in advance as separate surfaces and no visual cue was given for attention selection. It is unlikely that our finding of the side bias was due to an attentional bias. For the side bias to be caused by attention, attention had to be directed to the stimulus component at a specific side (e.g., the C-side) of the two component directions across different VA directions. Without an attention cue, such a specific and consistent attention selection is unlikely to occur. The fact that we found similar results when the animals performed a passively viewing fixation task and performed two variants of a perceptual discrimination task also suggests that the side bias was not caused by an attentional bias. Under our experimental conditions, the visual system may have to solve the problem of segmentation first, at least at a primitive level, before attention can be directed to one of the stimulus components. Although attention selection may occur during the later portion of the stimulus presentation, it is unlikely to be specific to one side of the bidirectional stimuli.

A recent theoretical study shows that having heterogeneous response weights and response nonlinearity in “stimulus mixing” benefits the neural coding of multiple stimuli (Orhan and Ma, 2015). Our findings of the side-biased and two-peaked neurons in area MT provide experimental evidence that the visual system uses these strategies to encode slightly different stimuli. The existence of the side-biased neurons toward the stimulus component at the C-side or CC-side and the two-peaked neurons suggest that information regarding slightly different moving stimuli is distributed across subpopulations of neurons in area MT. The visual system may take the distributed neural code of multiple stimuli into consideration to fully use such information.

Previous studies show that direction tuning curves of MT neurons undergo dynamic changes during the process of motion integration related to the solution of the aperture problem (Pack and Born, 2001) and the emergence of pattern-motion selectivity (Smith et al., 2005). Here, we show that, during the process of motion segmentation, the direction tuning curves of the side-biased and two-peaked neurons evolve over time to better represent the component directions. Our results suggest that segmenting different stimuli is a dynamic process and may involve recurrent interactions within the neuronal network. Together, our findings put new constraints on neural models of visual motion processing and have implications for understanding the neural mechanisms underlying image segmentation in general.