A Surrogate Measure of Cortical Bone Matrix Density by Long T₂-Suppressed MRI

Abstract

Magnetic resonance has the potential to image and quantify two pools of water within bone: free water within the Haversian pore system (transverse relaxation time, T₂ > 1 ms), and water hydrogen-bonded to matrix collagen (T₂ ~ 300–400 µs). While total bone water concentration quantified by MRI has been shown to scale with porosity, greater insight into bone matrix density and porosity may be gained by relaxation-based separation of bound and pore water fractions. The objective of this study was to evaluate a recently developed surrogate measurement for matrix density, single adiabatic inversion recovery (SIR) zero echo-time (ZTE) MRI, in human bone.

Specimens of tibial cortical bone from 15 donors (27–97 y/o, eight female and seven male) were examined at 9.4T field strength using two methods: (1) ¹H ZTE MRI, to capture total ¹H signal, and (2) ¹H SIR-ZTE MRI, to selectively image matrix-associated ¹H signal. Total water, bone matrix, and bone mineral densities were also quantified gravimetrically, and porosity was measured by micro-CT.

ZTE apparent total water ¹H concentration was 32.7±3.2 M (range: 28.5–40.3 M), and was correlated positively with porosity (R² = 0.80) and negatively with matrix and mineral densities (R² = 0.90 and 0.82, respectively). SIR-ZTE apparent bound water ¹H concentration was 32.9±3.9 M (range: 24.4–39.8 M), and its correlations were opposite to those of apparent total water: negative with porosity (R² = 0.73) and positive with matrix density (R² = 0.74) and mineral density (R² = 0.72). Porosity was strongly correlated with gravimetric matrix density (R² = 0.91, negative) and total water density (R² = 0.92, positive). The strong correlations of SIR-ZTE-derived apparent bound water ¹H concentration with ground-truth measurements suggest that this quantitative solid-state MRI method provides a nondestructive surrogate measure of bone matrix density.

1. Introduction

Bone is composed of apatite-like mineral, collagen, and water arranged in a complex manner over several size scales⁽¹⁾. These three components contribute to the tissue’s mechanical properties in unique ways: mineral is responsible for bone’s compressive strength and rigidity⁽²⁾, collagen matrix provides tensile strength and elasticity⁽³⁾, and water serves as a medium for transport of nutrients and is responsible for bone’s viscoelasticity⁽⁴⁾, a property which increases toughness⁽⁵⁾.

Standard clinical assessment of bone health is most commonly performed using dual energy x-ray absorptiometry (DXA), which expresses areal bone mineral density (BMD), or mineral mass per total cross-sectional area of bone, as a T-score relative to that of a young, healthy adult⁽⁶⁾. Though this method is in widespread use, it is insensitive to bone matrix and water content and fails to explain a significant portion of the increased fracture risk that occurs with aging⁽⁷⁾. However, density and hydration state of bone matrix collagen are important determinants of bone quality⁽⁸⁾, and measurements of these properties can provide complementary (and potentially superior) information on bone strength^(5,9–11).

Over the past decade, various solid-state magnetic resonance imaging (MRI) methods have emerged that allow detection and quantification of bone water, which, due to its short transverse relaxation time (T₂), is invisible to conventional MRI methods. Ultrashort echo time (UTE) MRI has been shown to visualize and quantify the short-T₂ ¹H signal of bone water^(12–14), and a similar technique, zero echo-time (ZTE) imaging, has also shown promise to detect extremely short-T₂ signals^(15–19).

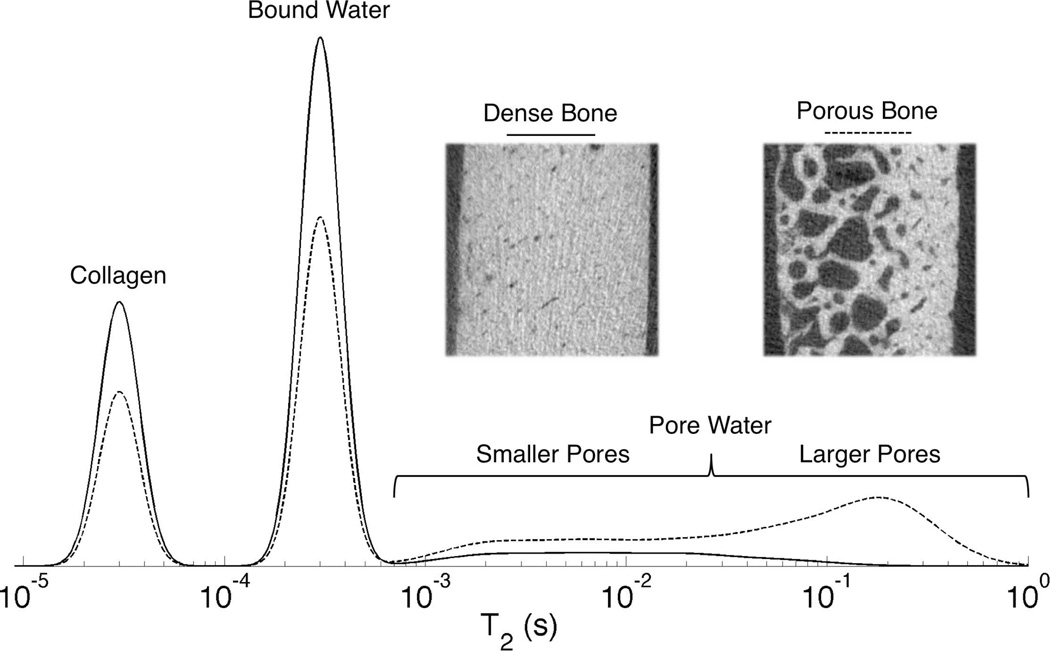
Bone water exists in two major pools that are visible to solid-state MRI: water diffusing freely within the Haversian pore system⁽²⁰⁾, and water that is hydrogen-bonded to matrix collagen^(21–23). These two pools differ significantly in their ¹H nuclear magnetic resonance (NMR) relaxation properties. Pore water has long T₂ > 1 ms at 4.7T, while bound water has T₂ ~ 300–400 µs⁽²¹⁾. A separate ¹H NMR signal fraction with extremely short T₂ ~ 60 µs is also visible with specialized spectroscopic hardware, and has been postulated to arise from ¹H nuclei in bone matrix collagen. These signal pools are diagrammed in a schematic T₂ spectrum shown in Figure 1.

Figure 1.

Schematic T₂ relaxation spectrum diagramming the three major ¹H NMR signal pools in bone. Pore water has T₂ > 1 ms and is broadly distributed, while bound water has T₂ ~ 300–500 µs. Collagen and macromolecular signal, at T₂ ~ 40–60 µs, is below the detection limit at clinical field strengths, but becomes visible using micro-imaging and spectroscopic hardware. As porosity increases, as shown in the inset µCT images of bone specimens from 27 y/o and 83 y/o female donors (dense and porous bone, respectively) collagen and bound water content decrease while pore water content increases and shifts to longer T₂ values due the smaller surface-to-volume ratio of enlarged pores.

The aforementioned differences in relaxation properties between bone ¹H signal components can be exploited to distinguish the matrix-associated short-T₂ fraction from longer-T₂ signal arising from pore water. MRI of matrix-bound water has been studied by several groups in recent years as a possible surrogate for collagen bone matrix^(24–34).

There are two general approaches to pore water suppression taken in prior work: bi-component effective transverse relaxation time (T₂*) fitting of a free-induction decay (FID) or a series of images obtained at multiple echo times (TE)^(25,27,28), and T₂-selective magnetization preparation using either a long, low-amplitude radiofrequency (RF) saturation pulse^(24,26,33) or an adiabatic inversion pulse followed by an inversion-recovery delay time (TI)^{(29–32,34,35)}.

The major difference between T₂* and T₂, in general, is that T₂* relaxation encompasses all mechanisms responsible for T₂ relaxation, as well as an additional contribution due to magnetic field inhomogeneity on a sub-voxel scale. The large difference in volume magnetic susceptibility (χ_v) between water (χ_v = −8.9 ppm) and bone tissue (χ_v = −11.3 ppm⁽³⁶⁾) and the complex arrangement of these two phases in bone leads to strong internal magnetic field gradients within the pore spaces. These gradients cause significant additional attenuation in pore water ¹H signal, especially in small pores, reducing the T₂* of pore water nearer to that of bound water⁽³⁷⁾, whose T₂ and T₂* relaxation are both dominated by dipolar relaxation. The T₂ of pore water remains long, due to rephasing of isochromats by the 180° pulses.

The single adiabatic inversion-recovery (SIR) method, therefore, has the potential to outperform T₂*-based methods of pore water suppression. While duration and bandwidth are inversely proportional in non-adiabatic pulses, they are less strictly linked in adiabatic RF pulses. Such a pulse can therefore simultaneously possess a long duration and broad bandwidth. The long duration allows it to saturate short-T₂ signal while inverting long-T₂ signal, and the broad bandwidth encompasses the broad frequency distribution of pore water within the inhomogeneous internal magnetic field environment of bone pores.

The objective of the present study was to measure zero echo time (ZTE)-derived apparent total water (aTW) and SIR-ZTE-derived apparent bound water (aBW) ¹H concentrations in human cortical bone, and to evaluate the hypothesis that aBW ¹H concentration parallels bone matrix density and scales inversely with porosity. These concentrations are termed ‘apparent’ in that systematic measurement errors may cause overestimation of true bone water ¹H concentration. This work thus may provide a foundation upon which to build a two-part non-invasive in vivo examination of true bone tissue mineralization density (also referred to as ‘degree of mineralization of bone’⁽³⁸⁾) consisting of bone matrix and mineral densities by ¹H SIR-ZTE and ³¹P ZTE, respectively. Such an examination could potentially aid in the differentiation of bone-demineralizing disorders from osteoporosis.

2. Materials and Methods

2.1. Specimens and Scanners

The tissue examined consisted of cortical bone specimens taken from the tibial mid-shaft of seven male and eight female human donors, aged 27–97 years (National Disease Research Interchange, NDRI). Specimens were harvested within 30 hours of death and immediately frozen. Time between tissue harvest and this study was 8–11 years. This set ranges from young, dense bone to severely porous bone due to age-related bone loss. Donors with bone-demineralizing disorders were excluded.

A 4-mm slice was sectioned from each thawed tibia with a rotating blade at the region of maximum cortical bone thickness, 38% of the length of the tibia from the medial malleolus to the medial condyle. Then, a rectangular beam with its long axis perpendicular to the osteonal axis was cut from each slice and trimmed to fit inside a 5-mm NMR tube. Specimens ranged from 15 to 35 mm in length. The direction of the osteonal axis of the bone was indicated on the end of each beam by cutting a notch parallel to the bone’s osteonal axis, and specimens were stored individually in phosphate-buffered saline.

All scanning was performed in a 9.4T vertical-bore NMR spectrometer and micro-imaging scanner (Avance III, Bruker, Billerica, MA). For measurement of relaxation times, a broad-band inverse (BBI) probe with a one-axis z-gradient was used, and for imaging, a 20-mm quadrature birdcage probe in a three-axis microimaging gradient set was used. Bones were imaged in the presence of an intensity reference sample consisting of a 20-mm column of 10 mM MnCl₂ in 90% D₂O/10% H₂O in a 5-mm NMR tube. This sample had a ¹H concentration of 11.1 M, T₂ = 530 µs, and T₁ = 12.7 ms.

2.2. Measurement of Relaxation Times

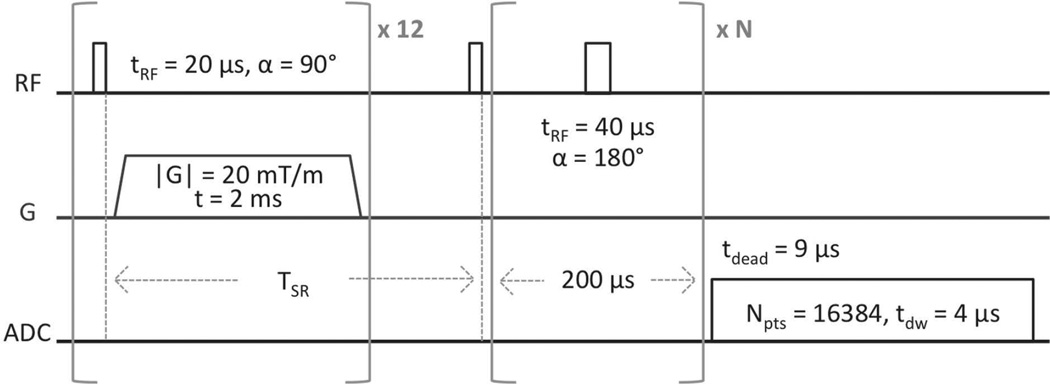
Prior to imaging, all bones were scanned using a saturation recovery (SR)-prepared Carr-Purcell-Meiboom-Gill (CPMG) pulse sequence (Figure 2) to measure the T₁, T₂, and T₂* relaxation times of the bound and pore water fractions. Knowledge of these relaxation times is necessary for subsequent conversion of raw MR image intensities to ¹H concentration. The fitting of these SR-CPMG data to bi-exponential functions is illustrated in Figure 3 and described in detail in the Appendix.

Figure 2.

SR-CPMG pulse sequence. Saturation-recovery times (T_SR) were arrayed logarithmically in 12 steps from 3 ms to 6 s, the number of refocusing pulses, N, was arrayed logarithmically from 0 to 5000 in 20 steps, and one signal acquisition was performed.

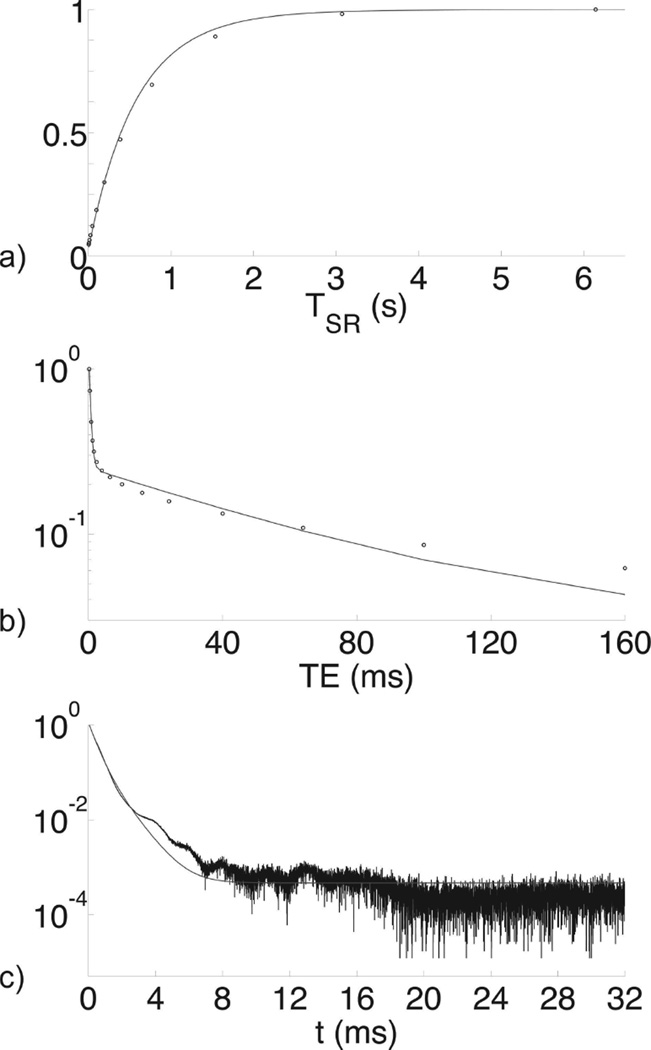
Figure 3.

NMR data (points) from a bone specimen from a 53-year-old male with bi-component fits (curves). Panel (a) shows a T₁ fit of saturation-recovery data, (b) shows a T₂ fit of CPMG echo amplitudes, and (c) shows a T₂* fit of a FID. Although only one-dimensional data are shown, fits were performed using the two-dimensional methods given in the methods section (a,b: T₁–T₂; c: T₂-T₂*). Vertical axes are normalized to M₀.

2.3. Zero Echo-Time Imaging

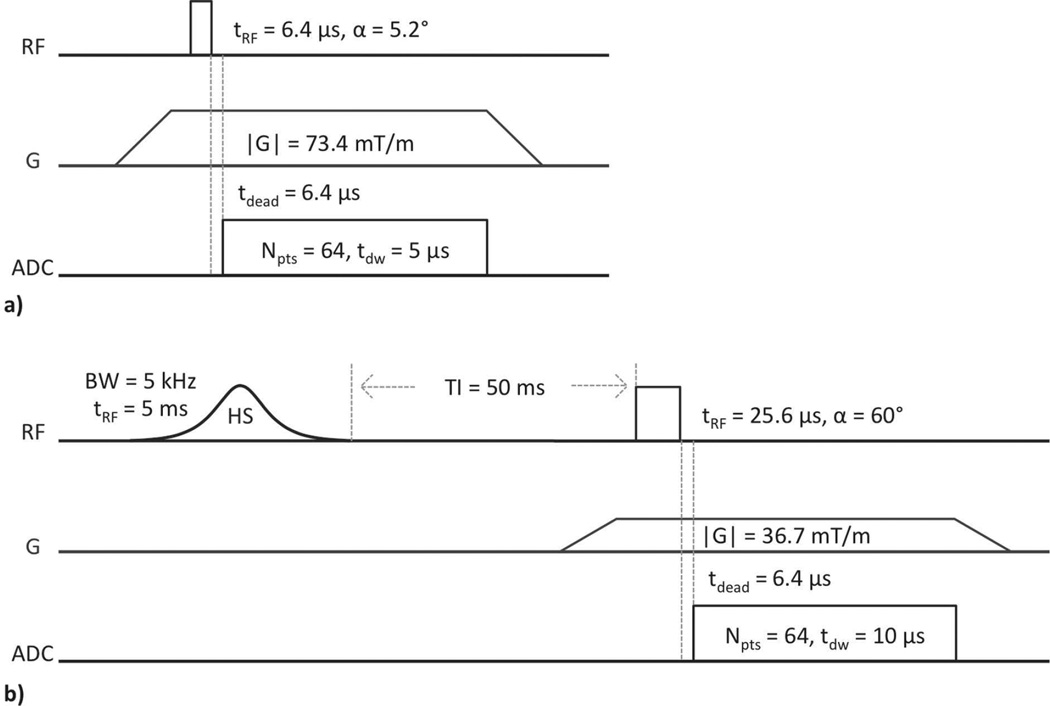
Imaging and reconstruction were performed using the standard Bruker ZTE pulse sequence (Figure 4a), and a modified form of this sequence incorporating a single adiabatic inversion preparation and delay time (SIR-ZTE, Figure 4b). ZTE was chosen due to its superior SNR performance to UTE in samples with extremely short T₂*⁽³⁹⁾. Gradient amplitude was limited to 73.4 mT/m by two simultaneous requirements of the reconstruction method⁽⁴⁰⁾: (1) that the field of view (FOV) fully enclose all sources of signal, including the plastic support structure of the NMR probe, and (2) that the readout bandwidth be low enough (i.e., that the dwell time be long enough) so as not to lose more than ~2 readout points during the hardware-dependent transmit/receive switching dead time. Due to this finite dead time, the ZTE sequence does not actually acquire signal beginning at TE = 0; the minimum delay time is instead equal to the transmit/receive switching time of 6.4 µs. Though greater than zero, this dead time is negligible for bound and pore water signal having T₂ > 300 µs.

Figure 4.

ZTE (a) and SIR-ZTE (b) imaging pulse sequences. ZTE parameters: 51896 projections, TR = 2 ms, 1 min 43 sec scan time. SIR-ZTE parameters: 6588 projections, TR = 200 ms, 21 min 58 sec scan time. FOV = 64 mm isotropic, resolution = 500 µm isotropic, and 1 signal acquisition for both. The pre-excitation portion of the readout gradient and the short T₂* of bound and pore water ¹H signal serve to effectively spoil residual transverse magnetization created by the adiabatic pulse.

First, each specimen was scanned with the reference sample using ZTE without adiabatic inversion recovery. Then, each specimen was immediately scanned again using SIR-ZTE. The adiabatic inversion pulse, with bandwidth of 5 kHz and duration of 5 ms, selectively saturates the longitudinal magnetization, M_z, of the short-T₂ protons in matrix-bound water (M_z = 0) while inverting long-T₂ signal arising from pore water and marrow fat (M_z < 0)^{(29,35,41–43)}. The T₂ response of M_z to this pulse was calculated by Bloch equation simulation. Following an appropriately chosen inversion-recovery time, the long-T₂ magnetization will be nulled as it passes through zero, and the short-T₂ magnetization will have recovered by longitudinal relaxation to M_z > 0. A ZTE imaging module applied at this time will thus selectively image short-T₂ signal. SIR-ZTE was performed with a repetition time (TR) of 200 ms and inversion time (TI) of 50 ms, and in both of these sequences, FOV was 64 mm and resolution was 500 µm (both isotropic). Readout bandwidth in both sequences was adequate to render unnecessary any correction for signal loss due to attenuation of high spatial frequencies.

2.4. Density Quantification

To convert raw image intensity to ¹H concentration, each image was corrected for longitudinal and transverse relaxation, including transverse relaxation during RF pulses. Each image was imported into Matlab (Mathworks, Natick, MA), and volumes of interest (VOIs) were drawn to fully enclose the bone and the reference sample. Then, within each VOI, the image intensity was corrected by solving Equation 3 for ρ (see Appendix), using the average relaxation times for the set of bone specimens and the measured relaxation times of the reference sample. Next, the bone and reference VOIs were refined by automatic thresholding⁽⁴⁴⁾, and, finally, the ¹H concentration ([¹H]) within the bone was calculated as the ratio of the mean corrected intensity within the bone to that of the reference, multiplied by the known ¹H concentration, [¹H] = 11.1 M, within the reference sample.

2.5. Micro-CT Imaging

Bone specimens were imaged using a Scanco µCT35 scanner (Scanco, Brüttisellen, Switzerland) at 18.5-µm isotropic voxel resolution. Bone boundaries were masked by 3D active snakes using ITK-SNAP⁽⁴⁵⁾. Pores were then segmented within these bone masks by automated thresholding, and porosity was calculated as pore volume divided by total bone volume.

2.6. Gravimetry

Bone specimens were removed from phosphate-buffered saline, blotted dry, and weighed to determine their fully hydrated mass. The bones were then placed in tared crucibles and dried at 105°C for 110 hr to remove all bound and pore water. Completion of drying was verified by observing no change in mass over a 24-hour period. The bones were again weighed, and their dry mass was recorded. Finally, the bones were incinerated at 600°C for 30 hr to burn off all organic material, and the residue was weighed. Total water mass was calculated as the difference between hydrated and dry masses, matrix mass was the difference between dry and ash masses, and mineral mass was equal to the residual ash mass. These masses were divided by total bone volume (the volume of the µCT bone boundary mask) to yield total water, matrix, and mineral densities^(24,46).

3. Results

3.1. Gravimetry and µCT

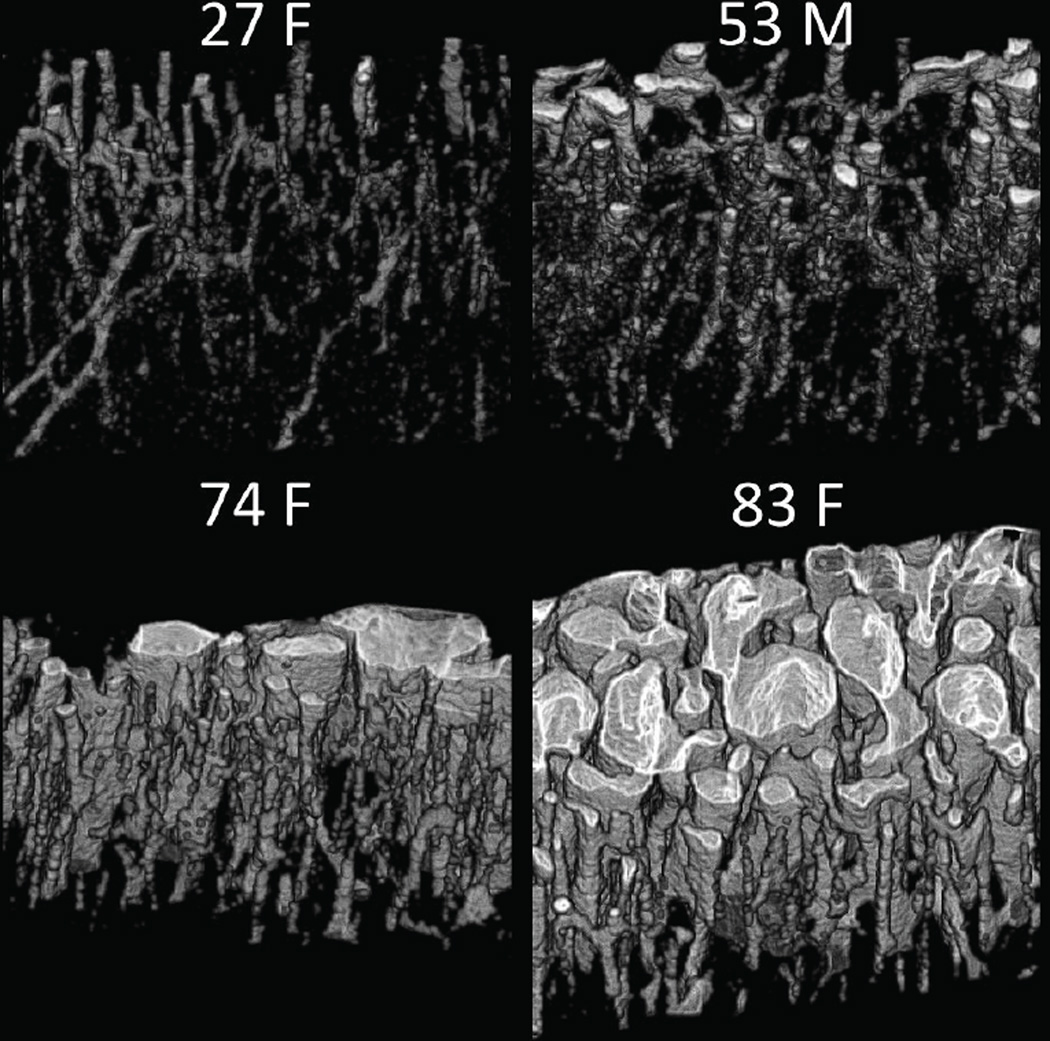
All bone measurement results, both from MRI and validation methods, are given in Table 1. Mean porosity across the 15 donors was 8.96±8.61% (3.06–33.5%); all data expressed in this format are mean ± standard deviation (min-max). Volume renderings of the pore spaces of four representative bone specimens are shown in Figure 5. Gravimetric mineral density was 1118±130 mg/cc (751–1219 mg/cc), matrix density was 503.7±24.3 mg/cc (437.0–527.5 mg/cc), and total water density was 326.2±48.4 mg/cc (281.4–435.6 mg/cc) bone tissue (i.e. 32.6% v/v or 36.1 M). The mineralization mass ratio, which is the unitless ratio of gravimetric mineral density to matrix density, was 2.212±0.173 (1.719–2.367), and bone mineralization, which is the bone mineral density normalized by bone volume fraction (1 - porosity), was 1225±36 mg/cc (1130–1286 mg/cc).

Table 1.

Apparent total water (aTW) and apparent bound water (aBW) ¹H concentration measurements by MRI, and reference measurements by µCT, gravimetry, and ¹H NMR. Sample labels indicate age and gender.

Bone	aTW [1H] (M)	aBW [1H] (M)	µCT Porosity (%)	Mineral Density (mg/cc)	Matrix Density (mg/cc)	Water Density (mg/cc)	T1–T2 Bound Fraction (%)	Mineralization Mass Ratio	Bone Mineralization (mg/cc)
27F	29.5	39.8	3.70	1197	525.2	287.4	86.6	2.280	1243
30F	28.5	38.0	3.06	1208	520.7	292.3	86.2	2.320	1246
37M	34.6	33.5	4.77	1163	494.9	316.2	78.4	2.351	1222
49M	30.2	34.2	4.08	1207	514.3	281.4	83.8	2.346	1258
53M	31.7	33.4	5.56	1159	513.1	294.6	82.9	2.258	1227
53F	29.6	35.4	3.78	1192	527.5	294.8	86.6	2.260	1239
65F	32.2	34.9	5.57	1161	513.0	297.3	81.2	2.263	1229
69M	32.8	34.7	5.18	1172	511.2	302.7	79.3	2.293	1236
74F	36.7	26.7	20.4	930.7	472.4	405.0	62.4	1.970	1169
75M	33.4	32.2	4.51	1175	510.3	298.8	80.1	2.303	1230
82F	35.5	30.6	17.3	1015	479.0	394.5	66.4	2.119	1227
83F	40.3	24.4	33.5	751.2	437.0	435.6	55.4	1.719	1130
83M	31.0	32.3	4.94	1159	520.1	317.2	77.3	2.228	1219
93M	30.7	31.8	5.18	1219	515.2	318.7	77.6	2.367	1286
97F	34.6	31.0	12.9	1058	501.2	356.2	71.4	2.110	1215
Mean	32.7	32.9	8.96	1118	503.7	326.2	77.0	2.212	1225
StDev	3.2	3.9	8.61	130	24.3	48.4	9.3	0.173	36

Figure 5.

Volume rendering of the pore spaces (in white) within four representative bone specimens. Note the increased number and size of pores in bone specimens from elderly female donors.

Porosity was strongly correlated with gravimetric mineral density (R² = 0.98, negative), matrix density (R² = 0.91, negative), and total water density (R² = 0.92, positive). Matrix and mineral densities were also strongly positively correlated (R² = 0.91). The mineralization mass ratio, however, was strongly positively correlated with mineral density (R² = 0.96) and negatively correlated with porosity (R² = 0.94).

3.2. MRI-Derived Density

ZTE-derived aTW ¹H concentration was 32.7±3.2 M (28.5–40.3 M), and SIR-ZTE-derived aBW ¹H concentration was 32.9±3.9 M (24.4–39.8 M). MRI quantifies the electromagnetic signal emitted by ¹H nuclei within a voxel, so these measurements are properly expressed in molar concentrations of ¹H nuclei, rather than mass densities in mg/cc.

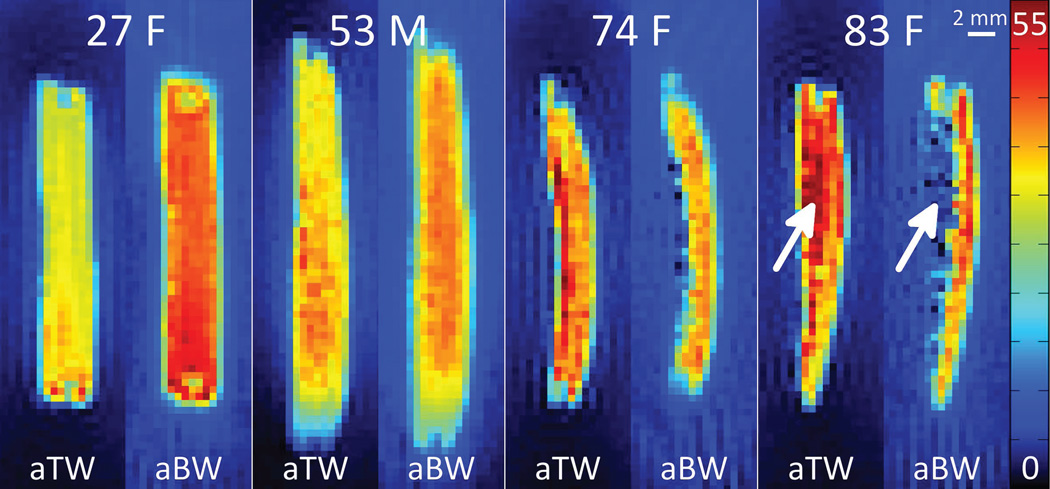
¹H concentration maps of aTW and aBW in four representative bone specimens are given in Figure 6. As age and porosity increase, aTW increases and aBW decreases. Note especially the region of extreme structural degradation (indicated by white arrows), with high aTW and commensurately lower aBW ¹H concentration.

Figure 6.

Maps of apparent total water (aTW) and apparent bound water (aBW) ¹H concentrations, in mol/L, in bone specimens from four representative donors. Age and gender of the donors are given within each quadrant, and the endosteal surface of each specimen faces left. Arrows indicate a region of high porosity, which has elevated total water and reduced matrix densities, and correspondingly increased aTW and decreased aBW. Non-zero background signal surrounding the bone specimen arises from extremely short-T₂ signal contributed by the plastic body of the RF probe.

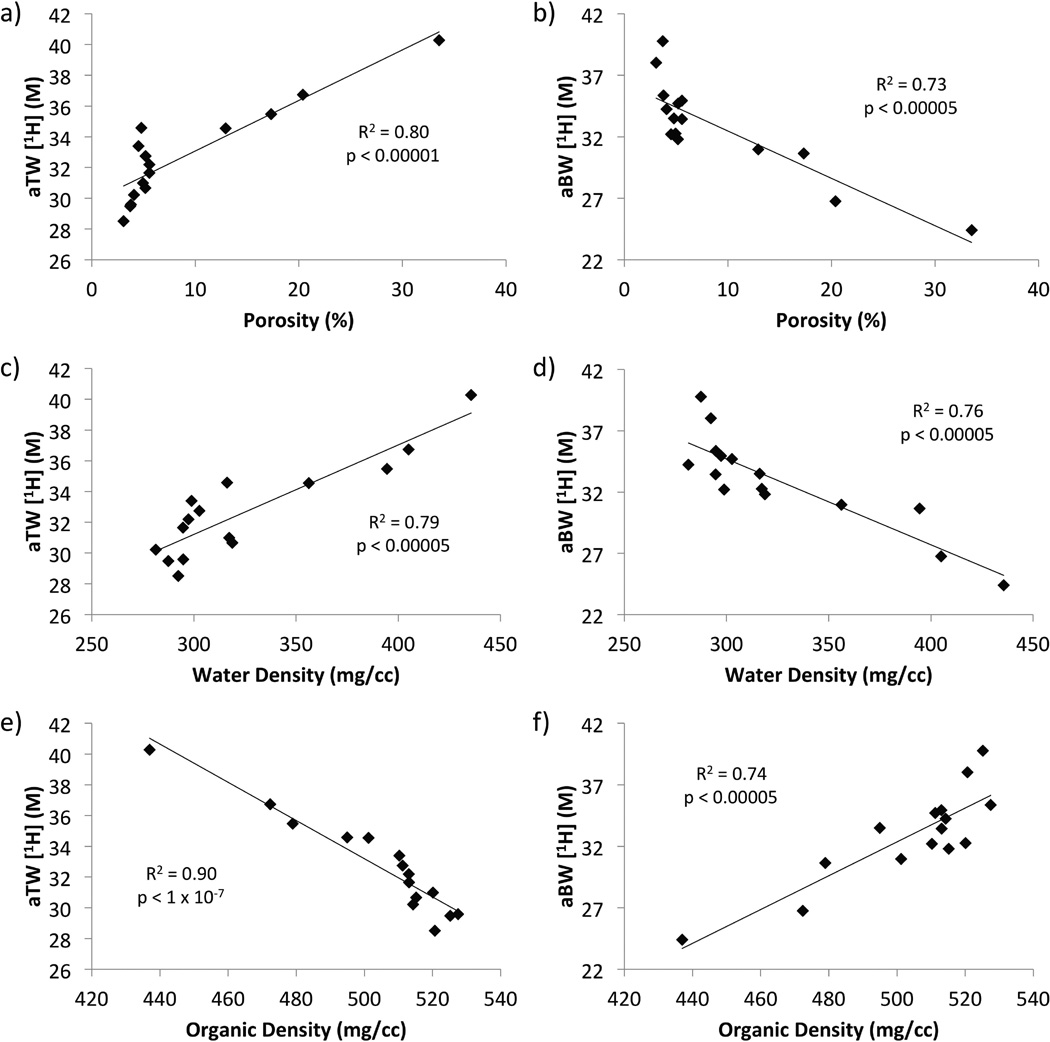
Apparent total water concentration was correlated positively with porosity and gravimetric water density (R² = 0.80 and 0.79, respectively), and negatively with matrix density and mineral density (R² = 0.90 and 0.82, respectively). Apparent bound water correlations were opposite those of aTW; aBW was correlated negatively with porosity and total water density (R² = 0.73 and 0.76, respectively), and positively with matrix density and mineral density (R² = 0.74 and 0.72, respectively). Scatter plots of aTW and aBW ¹H concentration versus porosity, water density, and organic matrix density are given in Figure 7. All relevant correlation coefficients between parameters are given in Table 2.

Figure 7.

Scatter plots displaying the correlations of apparent total water (aTW, a,c,e) and apparent bound water (aBW, b,d,f) ¹H concentrations versus µCT porosity (a,b), gravimetric water density (c,d), and gravimetric organic matrix density (e,f). Apparent total water ¹H concentration is positively correlated with porosity and gravimetric water density and negatively with matrix density, while aBW correlations show the opposite behavior.

Table 2.

Inter-parameter correlations (R²) of measured bone properties. All correlations are statistically significant (p < 0.05).

	µCT Porosity (%)	Matrix Density (mg/cc)	Mineral Density (mg/cc)	Water Density (mg/cc)	Mineralization Mass Ratio	Bone Mineralization (mg/cc)	T1–T2 Bound Fraction (%)	aBW [1H] (M)
aTW [1H] (M)	0.80	0.90	0.82	0.79	0.69	0.71	0.86	0.77
aBW [1H] (M)	0.73	0.74	0.72	0.76	0.64	0.54	0.86
T1–T2 Bound Fraction (%)	0.90	0.89	0.88	0.96	0.79	0.63
Bone Mineralization (mg/cc)	0.73	0.70	0.84	0.62	0.84
Mineralization Mass Ratio	0.94	0.78	0.96	0.82
Water Density (mg/cc)	0.92	0.86	0.90
Mineral Density (mg/cc)	0.98	0.91
Matrix Density (mg/cc)	0.91

3.3. Relaxation Times

The short-T₂ ¹H fraction had T₁ = 480±80 ms (320–560 ms), T₂ = 540±150 µs (430–980 µs), T₂* = 400±50 µs (330–520 µs), and accounted for 77.0±9.3% (55.4–86.6%) of total signal by 2D bi-component T₁–T₂ fitting. The long-T₂ fraction had T₁ = 1210±300 ms (880–1910 ms), T₂ = 55000±38000 µs (17000–161000 µs), T₂* = 940±230 µs (600–1540 µs), and accounted for 23.0±9.3% (13.4–44.6%) of the signal.

Short-T₂ fraction by 2D T₁–T₂ bi-component fitting was strongly negatively correlated with aTW (R² = 0.86) and strongly positively correlated with aBW (R² = 0.86). Short-T₂ fraction was also very strongly correlated with porosity (R² = 0.90, negative) and gravimetric matrix density (R² = 0.89, positive).

4. Discussion

In this study, we presented non-invasive, non-destructive MRI-based measurements of apparent total and bound water ¹H concentrations in human cortical bone, and compared these results to gravimetric bone density measurements and µCT porosity. The strong correlations of aBW with both gravimetric matrix density and µCT porosity support the applicability of this method as a surrogate measurement of bone matrix density. This measurement may later be combined with a previously established ³¹P MRI-based examination of bone mineral density^(24,31) to investigate bone tissue mineralization.

Although aTW is a surrogate for bone porosity^(32,47,48), it is not positively associated with the density of bone’s collagen matrix; rather, it is representative of the voids within that matrix (i.e. pore volume fraction). On the other hand, aBW is positively correlated with matrix density. It is this positive association that renders aBW a useful surrogate for matrix density, and facilitates its future pairing with a measurement of bone mineral density to create a measurement of bone mineralization; specifically, the ratio of mineral density to aBW.

Apparent total water ¹H concentration (32.7±3.2 M, 28.5–40.3 M) in this work is greater than the 24 M⁽⁴⁹⁾ and 19.3–31.8 M⁽⁴⁷⁾ found in previous ¹H UTE work at 3T, but the results are more consistent with the 29–41 M measured more recently by Horch et al.⁽²⁹⁾ using a 4.7T micro-imaging system. This may be due to the improved abilities of the ZTE pulse sequence and experimental (i.e. non-clinical) hardware to image the shortest-T₂ components in bone. The aTW image likely contains signal not only from water, but also the extremely short-T₂ signal fraction illustrated in Figure 1, which does not appear in UTE images obtained on clinical scanners.

Likewise, the aBW ¹H concentration of 32.9±3.9 M (24.4–39.8 M) found in the present study using SIR-ZTE is also higher than the 12–24 M found by Horch et al.⁽²⁹⁾ or 12–23 M by Manhard et al.⁽³⁰⁾ using SIR-UTE, but these differences may also be explained by the greater ability of ZTE to capture the shortest-T₂ signal present in bone. Long-range blurring of the extremely short-T₂* signal arising from the plastic body of the RF probe, which appears as an increased (but constant) background signal level, and is more severe in aBW images than aTW due to lower readout gradient strength, also causes an additional systematic error in aBW values not present in aTW. The strengths of the correlations of aBW to porosity and matrix density in the present work, however, are consistent with Horch’s reported correlations versus peak stress⁽²⁹⁾ and CPMG-derived short-T₂ pool fraction^(29,30).

4.1. Sensitivity to Relaxation Times

All conversions of image intensity to density in this work were performed using average relaxation times for the set of 15 bone specimens, rather than individually measured relaxation times for each specimen. This ensures that the strengths of the correlations observed between the measured MRI ¹H concentrations and reference measurements are translatable to eventual in vivo use, where measurement of relaxation times in each subject would not be practical. Under this constraint, the correlations of aBW with porosity and matrix density remain strong (R² > 0.7, p < 0.00005).

If the T₁ value used in Equations 3–6 is longer than the true T₁ in the specimen, ¹H concentration will be overestimated. A ±5% deviation in T₁ results in ±3.0% error in calculated aTW and ±5.2% error in aBW. Variation in T₂* will have very little effect on the calculated aTW: the same ±5% error in T₂* results in error of approximately ±0.022%. However, due to the T₂-selectivity of the adiabatic inversion pulse, a ±5% change in T₂ will cause an appreciable error of ±3.8% in aBW.

In Equations 3–5, such errors may artificially amplify the true differences in aTW; greater porosity is associated not only with higher total water content, but also longer T₁ and T₂* due to decreased surface interaction and susceptibility effects in larger pores⁽⁴⁹⁾. Equations 4–6, however, suggest that these same errors may slightly reduce the sensitivity of aBW to true bound water content in the case of perfect long-T₂ suppression, but this possible effect is alleviated by the fact that, while pore water relaxation properties are very strongly affected by bone porosity, bound water relaxation times are relatively constant⁽²¹⁾. Only the stable bound water T₁ and T₂* values are used in quantification.

The assumption of perfect long-T₂ nulling by SIR-ZTE in all specimens, however, is not realistic for a single TI applied to both dense and porous bones. In porous bone, although bound water relaxation times are stable, pore water T₁ and T₂ are longer than in dense bone: T₁ of long-T₂ pore water (T_1L) by bi-component 2D T₁–T₂ fitting (see Equation 1) ranges from 880 to 1910 ms, and is positively correlated with porosity (R² = 0.70, p < 0.0001). The long T₂ relaxation time (T_2L) ranges from 17 ms to 161 ms and is strongly positively correlated with porosity (R² = 0.91, p < 10^-7). These relaxation times vary because free water near the surface of a pore experiences an additional contribution to its transverse (1/T₂) and longitudinal (1/T₁) relaxation rates due to interaction with the surface, typically termed surface relaxation⁽²⁰⁾. The contribution of surface relaxation to the relaxation times of the entire pore water pool, therefore, scales with the surface to volume ratio (S/V) of the pore spaces. In very porous bones, cortical pores are large and the S/V ratio is small; however, in young, dense bone, cortical pores are very small and the S/V ratio is large, leading to an increased effect of surface relaxation and more rapid transverse and longitudinal relaxation.

In empirically choosing TI for a set of specimens such that pore water is nulled, TI is biased toward optimal nulling of pore water in more porous bones; these bones have more pore water to be nulled, so proper inversion is more important. In dense bones, with shorter T_1L and T_2L, pore water magnetization may be incompletely inverted during the adiabatic inversion pulse (i.e., M_z > −1) due to transverse relaxation during the pulse, and will undergo significantly faster longitudinal relaxation after inversion, thus overshooting the null point (M_z > 0) during the inversion-recovery delay. Some of this pore water magnetization in dense bone will therefore also be imaged, along with bound water magnetization, by SIR-ZTE. This additional contribution of pore water in dense bones is partially responsible for the overestimation of bound water density (which is 60–80% of total bone water^(21,22)) by SIR-ZTE, causing average aBW ¹H concentration (32.9±3.9 M, 24.4–39.8 M) to be slightly greater than average aTW (32.7±3.2 M, 28.5–40.3 M). This overestimation, however, does not diminish the strength of the positive correlation of aBW with bone matrix density, or the negative correlation with porosity. In fact, this phenomenon may enhance the sensitivity of aBW to changes in matrix density and porosity. The remainder of this overestimation is due to the previously discussed signal contributed by the plastic body of the RF probe. This issue could be remedied by using proton-free polymers for coil construction.

4.2. Bone Mineralization

The strong positive correlation (R² = 0.91) between matrix and mineral densities measured by gravimetry confirms that the degree of mineralization in these bones is not the primary determinant of bulk bone mineral density; changes in mineral density are primarily a result of structural degradation rather than a deficit of mineralization. The mineralization mass ratio, which is defined as gravimetric mineral density divided by matrix density, however, was strongly negatively correlated with porosity (R² = 0.94), consistent with the notion that bone mineralization is decreased due to rapid bone turnover in age-related bone loss.

Tissue mineralization density calculated in this work, 1225±36 mg/cc matrix (1130–1286 mg/cc matrix), was similar to previous microradiographic measurements by Boivin et al.⁽⁵⁰⁾ (1082±17 mg/cc). Gravimetric densities are also consistent with gravimetric measurements performed by Cao et al.⁽²⁴⁾ in rat bone.

4.3. Translatability to the Clinic

This work has established aBW ¹H concentration as a surrogate for matrix density. This examination, in combination with a ³¹P ZTE examination of bone mineral density⁽³¹⁾, could be developed into a non-invasive in vivo MRI assessment of bone mineral and matrix densities, and their ratio, the degree of mineralization of bone. If reduced to practice, this MRI method would allow clinicians to discriminate between age-related macroscopic bone loss and impairment of bone mineralization. Such an examination is not possible using standard x-ray-based screening methods.

This study benefitted from the enhanced performance of experimental versus clinical hardware. The 9.4T scanner used in this work is equipped with much stronger gradients than clinical scanners, narrowing the point spread function and, thus, reducing blurring. This allows for better delineation of bone margins, and even enables visualization of individual pore spaces in severely porous bones (see Figure 5, panel 83F). The use of a 20-mm RF probe and very high field strength also yields higher SNR than is achievable using clinical hardware.

Although the maximum achievable gradient strength is limited on clinical scanners, and image blurring due to signal decay during readout will be increased, this issue will be mitigated by the larger size of bones in human subjects compared to the small specimens studied in this work, and the longer T₂* of both bound and pore water at lower B₀. In previous work using these methods at 3T⁽³¹⁾, point-spread function blurring was minimal. Also, at clinically relevant field strengths, such as 3T, the difference in T₁ between the bound and pore water signal components is much greater (145 ms and 880 ms, respectively, at 3T, versus 480 ms and 1210 ms at 9.4T)⁽³⁷⁾, so the bound water selectivity of the SIR-ZTE method would be enhanced.

5. Conclusion

Based on the strong correlations of aBW ¹H concentration with gravimetric matrix density and porosity, long T₂-suppressed solid-state MRI is a promising surrogate for bone matrix density.

Appendix

7.1. Measurement of Relaxation Times

Saturation recovery times (T_SR) in the SR-CPMG sequence (Figure 2) were arrayed logarithmically in 12 steps from 3 ms to 6 s, and the number of refocusing pulses, N, was arrayed logarithmically from 0 to 5000 in 20 steps, resulting in TEs ranging from zero to 1 s, although the 9-µs transmit/receive dead time must be added to the beginning of each sampled echo. The duration of the refocusing RF pulse, 40 µs, is one order of magnitude less than the shortest relevant T₂ relaxation time, so no corrections for incomplete refocusing are necessary. One signal acquisition was performed, and scan time for this sequence was 29 minutes. All other relevant pulse sequence parameters are given within the pulse sequence diagram in Figure 2.

Two-dimensional bi-component T₁–T₂ fitting was performed by fitting a sum of two exponential functions in two dimensions,

$$f(T_{SR},TE)=M_S(1-e^{\frac{-T_{SR}}{T_{1S}}})e^{\frac{-TE}{T_{2S}}}+M_L(1-e^{\frac{-T_{SR}}{T_{1L}}})e^{\frac{-TE}{T_{2L}}}+n,$$ [1]

to the array of SR-CPMG echo amplitudes. Here, the magnetizations of the short- and long-T₂ components are given by M_S and M_L, respectively. These terms are converted to short- and long-T₂ fractions by dividing by their sum, i.e. M_S/(M_S+M_L) and M_L/(M_S+M_L). Longitudinal (T₁) relaxation times are given by T_1S and T_1L, T₂ relaxation times by T_2S and T_2L, and the noise level by n. This fitting process yields the sizes of each of the two pools and their characteristic T₁ and T₂ relaxation times.

T₂* values for the pools were also obtained by fitting a similar equation,

$$f(TE,t)=M_S{e}^{\frac{-TE}{T_{2S}}}{e}^{\frac{-t}{T_{2S}^{*}}}+M_L{e}^{\frac{-TE}{T_{2L}}}{e}^{\frac{-t}{T_{2L}^{*}}}+n,$$ [2]

to the two-dimensional array of FIDs beginning at the center of each CPMG echo. Here, t is the time within the FID after each echo. These data were taken from the SR-CPMG data set after the longest T_SR of 6 seconds, which satisfies the condition of full longitudinal relaxation. This process yields two pools characterized by T₂ and T₂* relaxation times, rather than T₁ and T₂. Fitting was performed in two dimensions, rather than one, for improved accuracy and stability⁽⁵¹⁾. All fitting was performed in Matlab (Mathworks, Natick, MA). Example data from bone from a 53-year-old male donor, along with bi-component fits, are shown in Figure 3.

7.2. Density Quantification

The steady-state signal acquired in the ZTE sequence (Figure 4a) is given in Equation 3:

$$S(\overrightarrow{r})\propto \rho (\overrightarrow{r})\frac{1-\text{exp}(-TR/T_1)}{1-f_z\text{exp}(-TR/T_1)}{f}_{xy}\text{exp}(-TE/T_2^{*}),$$ [3]

where ρ is aTW ¹H concentration. Because ZTE measures total water signal, single-component exponential fitting of SR-CPMG data was performed to determine total water T₁, T₂, and T₂* relaxation times, which were then incorporated into this equation. Also, e^−TE/T2* ≈ 1 because this pulse sequence has an echo time of approximately zero. The f_xy and f_z terms represent the response of the transverse and longitudinal magnetization, respectively, to rectangular RF pulses in the general case, where the pulse is not infinitesimally short relative to T₂*⁽⁵²⁾:

$$f_{xy}=\text{exp}(-\tau /2T_2)\alpha \text{sin}\mathrm{c}\left(\sqrt{{\alpha }^2-{(\tau /2T_2)}^2}\right)$$ [4]

and

$$f_z=\text{exp}(-\tau /2T_2)\left[\text{cos}\right(\sqrt{{\alpha }^2-{(\tau /2T_2)}^2})+(\tau /2T_2)\text{sin}\mathrm{c}(\sqrt{{\alpha }^2-{(\tau /2T_2)}^2}\left)\right],$$ [5]

where τ is RF pulse duration and α = γB₁τ is the nominal flip angle.

Quantification of aBW ¹H concentration in the SIR-ZTE images is similar, except for three important differences. First, the contribution of the adiabatic inversion pulse was added to Equation 3:

$$S(\overrightarrow{r})\propto \rho (\overrightarrow{r})\frac{1+(f_{HS}-1)\text{exp}(-TI/T_1)-f_{HS}\text{exp}(-TR/T_1)}{1-f_{HS}{f}_z\text{exp}(-TR/T_1)}{f}_{xy}\text{exp}(-TE/T_2^{*}),$$ [6]

where f_HS, the response of the longitudinal magnetization to the adiabatic inversion pulse, was calculated for the bone and reference by Bloch equation simulation based on their respective relaxation times. Also, because long-T₂ signal is nulled in SIR-ZTE, the short T₁, T₂, and T₂* relaxation times measured by bi-component fitting of SR-CPMG data were used in Equation 6 for relaxation correction, rather than the single-component relaxation times used in Equation 3. Finally, to maintain consistency, the VOIs obtained by automatic thresholding in the ZTE images were carried over for SIR-ZTE correction. Apart from these two changes, quantification of aBW is performed in the same manner as aTW.