Exercise activates compensatory thermoregulatory reaction in rats: a modeling study

Abstract

The importance of exercise is increasingly emphasized for maintaining health. However, exercise itself can pose threats to health such as the development of exertional heat shock in warm environments. Therefore, it is important to understand how the thermoregulation system adjusts during exercise and how alterations of this can contribute to heat stroke. To explore this we measured the core body temperature of rats (T_c) running for 15 min on a treadmill at various speeds in two ambient temperatures (T_a = 25°C and 32°C). We assimilated the experimental data into a mathematical model that describes temperature changes in two compartments of the body, representing the muscles and the core. In our model the core body generates heat to maintain normal body temperature, and dissipates it into the environment. The muscles produce additional heat during exercise. According to the estimation of model parameters, at T_a = 25°C, the heat generation in the core was progressively reduced with the increase of the treadmill speed to compensate for a progressive increase in heat production by the muscles. This compensation was ineffective at T_a = 32°C, which resulted in an increased rate of heat accumulation with increasing speed, as opposed to the T_a = 25°C case. Interestingly, placing an animal on a treadmill increased heat production in the muscles even when the treadmill speed was zero. Quantitatively, this “ready-to-run” phenomenon accounted for over half of the heat generation in the muscles observed at maximal treadmill speed. We speculate that this anticipatory response utilizes stress-related circuitry.

to compensate for overall lifestyle-induced decrease of exercise (26), millions of people around the world participate in various sports. Many of these people choose to exercise and compete outdoors. Since outdoor running occurs most frequently in the warmer months of the year, the participants are at risk for developing heat-related illnesses. The most devastating heat-related illness is exertional heat stroke. Occurring in otherwise healthy people, heat stroke affects people at the most productive times of their lives. Between 1990 and 2010 an average of 2 high school and college football players died each year due to heat stroke (3). The U.S. Centers for Disease Control and Prevention estimates that each year 660 heat related-deaths occur (1). Along with the risk for death, those suffering heat stroke lose the ability to work or perform normal activities and may suffer life-long medical complications even after recovery. As the number of marathoners in the U.S. exceeds a half-million (35), the ability to predict who is prone to heat stroke could benefit thousands of people. The dynamics of the body temperature is a major determinant of heat stroke (14), so the ability to predict a heat stroke is largely an ability to predict changes in body temperature.

Mammals have developed multiple thermoregulatory mechanisms to maintain their core body temperature within a relatively narrow range. In cold environments, the body produces heat through nonshivering thermogenesis and decreases heat dissipation through cutaneous vasoconstriction (34). Correspondingly, in warm environments, nonshivering thermogenesis is shut off and excess heat is dissipated by increasing blood flow near the skin and, in humans, through evaporative heat loss through sweat.

During exercise an additional heat is produced by contractions of the skeletal muscles. Unlike “classical” heat stroke where the primary cause of heat stroke is ineffective dissipation of heat in hot and/or humid environment, exertional heat stroke develops due to excessive production of heat from work/exercise. In these cases, heat stroke is produced by heat production outstripping maximal heat dissipation. It is logical to hypothesize that during exercise heat production unrelated to exercise would be suppressed (for review, see 21). However, activity-thermoregulatory heat substitution had not been analyzed in terms of resulting body temperature dynamics. Thermoregulatory processes affecting heat production during exercise are difficult to study, as the corresponding experimental paradigms require measuring the metabolism in, and heat exchange between, different body compartments in conscious running animals. In this study, we use mathematical modeling to characterize thermoregulatory processes from easy-to-measure body temperature dynamics observed at different ambient temperatures and exercise intensities.

METHODS

Animals and experimental design.

Male Sprague-Dawley rats (280-350 g) were individually housed with a 12:12-h light-dark cycle at a room temperature of 23–25°C with free access to food and water. All animals for which data are reported remained in good health throughout the course of surgical procedures and experimental protocols as assessed by appearance, behavior, and maintenance of body weight. All procedures described here were approved by the Indiana University Institutional Animal Care and Use Committee and followed NIH guidelines.

Rats were anesthetized with 1.5–2% isoflurane in oxygen. The concentration of isoflurane was adjusted as needed, and we have monitored heart rate and oxygen saturation during surgery using a Pulse Oximeter monitor (model LS1P-10R, Nonin, Plymouth, MN). To measure core body temperature TA-F40 telemetric transmitters (DSI, St. Paul, MN) were implanted intraperitoneally. Briefly, animals were placed in a dorsal recumbent position with abdominal skin shaved along midline. A longitudinal medial skin incision (∼2 cm) was made, followed by a longitudinal incision of the muscular wall along the white line. The body of the transmitter was placed into the abdominal cavity, and the muscle was sutured followed by the skin. Animals were returned to their cage for at least 1 wk before being familiarized to the treadmill.

All rats were familiarized to running on the treadmill. Mild electric stimulus at the back of the treadmill chamber promoted learned running behavior. On the first day of familiarization the rats were placed on the treadmill at standby and were given 10 min to explore the surroundings. After 10 min the treadmill was activated at 6 m/min for 5 min. In two consecutive days rats were familiarized with running in 5-min sessions at increasing speeds.

Two series of experiments were performed in two separate groups of rats: running at room temperature (T_a = 25°C, N = 6) and running at high ambient temperature (T_a = 32°C, N = 4). Each rat was subjected to four experiments: stayed on the idle treadmill belt (0 m/min with zero incline) or ran on the treadmill at one of three speeds (6, 12, and 18 m/min with zero incline). The experiments were performed every other day with a speed which was selected using a random number generator. We did not use higher speeds (e.g., 24 m/min), because not all rats were able to keep such speeds for 15 min without getting excessive prodding electric stimuli.

Baseline temperatures were recorded for at least 20 min in the home cage at room temperature. Then the animal was transferred to the treadmill, equilibrated at ambient temperature, and the belt was activated. Animals ran for 15 min at set speed, while body temperature was recorded; then the treadmill was inactivated. During the run no rat received more than 3 consecutive prodding shocks. After the run the rats were immediately transferred back to the home cage for recovery.

Data processing.

The running on the treadmill created momentary artifacts (<5 ms) on the temperature signal from the probe recorded by the telemetric system. When animals were not running, there were no artifacts. Artifacts were also absent when the electrical motor was working at a speed needed for the highest treadmill speed used in described experiments (18 m/min) with the clamp connecting the shaft of the motor to the treadmill belt removed, so the rat was resting. When an animal was running at the highest speed, the mean value could be significantly affected by artefacts. Therefore, we could not rely on the mean value collected by hardware every data acquisition cycle. Instead, every minute we have recorded a 10-s “waveform” signal at intrinsic 250 Hz, and used a median of collected 2,500 points as a value for this minute. The artifacts constituted less than 10% of all samples, so the median was a robust statistic and reliable measure. To calculate the median, we have exported “waveform” data to an ASCII file, which was then filtered by the program developed by one of the authors (YIM). Further processing of experimental data was performed using Microsoft Excel. Results were compared using a one-way ANOVA with repeated measures followed by a Fisher's LSD post hoc test, where appropriate. A value of P < 0.05 was considered to indicate a significant difference in all comparisons.

Model design.

The time constant of telemetric probe measured by us was relatively small (0.96 ± 0.01 min), which allowed us to neglect the inertia of measurements in the model.

In a model containing only one compartment any additional heat production due to running will result in immediate increase of body temperature. This contradicts the dynamics of body temperature in the first minutes after an initiation of running, when body temperature does not change or can even slightly decrease. Therefore, we excluded one-compartment models from further consideration.

Our working mathematical model contained two compartments which generate heat, aptly named core body and muscles. We considered that muscles perform the physical work, and are producing heat during exercise. Muscles are insulated from the environment, and as such can dissipate heat only to the core. Biologically we expect the heat generated by the muscles to be transferred to the core proportionately to the difference of temperature between the two compartments. In turn changes of heat production in the core are not a direct result of performing the physical work, and are of regulatory origin. The core can also dissipate heat to the environment with heat loss proportionate to the difference between core body and ambient temperatures.

In rats, the bones and muscles together constitute 45–50% of body weight (11), while skeleton comprises only ∼3% (9). Therefore, we explicitly assumed that two compartments of the model (core body and muscles) have equal heat capacities. We introduced net heat accumulation in the core P₀ as the difference between overall heat production in the core and dissipation to the environment. We assumed that at rest all heat is generated in the core. Based on the experimental data (13) the temperature of the muscles was considered equal to the temperature of the core without exercise as an initial condition. P_m was defined as the additional heat produced by the muscles due to exertion. Both P₀ and P_m were considered constant throughout exercise. Initial model fitting was performed by varying the parameters P₀ and P_m to check the basic validity and the ability to reproduce experimental data.

Differential equations describing the change in temperature for each compartment were written as follows. The rate of change in the temperature of the core over time (dT_c/dt,°C/min) is affected by the net heat accumulation in the body and the heat transfer from muscles:

$$\frac{\text{d}{T}_{\text{c}}}{\text{d}t}={\text{P}}_0+\eta \left(T_{\text{m}}-T_{\text{c}}\right)$$ (1)

where η is a heat transfer coefficient, which indicates the percent of temperature differential transferred from the muscles to the core per minute (and is measured in min⁻¹). We found that η = 0.125 min⁻¹ provided an average value of the rate of heat transfer that best reproduced the data.

Correspondingly, the rate of change in temperature of the muscles (dT_m/dt,°C/min) was affected by heat produced due to running and heat exchange with the core.

$$\frac{\text{d}{T}_{\text{m}}}{\text{d}t}={\text{P}}_{\text{m}}-\eta \left(T_{\text{m}}-T_{\text{c}}\right)$$ (2)

At equilibrium we know that the temperature is not changing, indicating that

$$\text{d}{T}_{\text{c}}/\text{d}t=\text{d}{T}_{\text{m}}/\text{d}t=0$$ (3)

At initial resting conditions, there is no additional heat generated by exercise, P_m = 0, and the net heat accumulation in the core P₀ = 0. To satisfy condition 3 and considering resting conditions, we set the initial temperature of the muscles equal to the initial temperature of the core T_m(0) = T_c(0) = T₀. This temperature is higher than ambient temperature due to baseline heat production by the organism. Any baseline heat production in muscles before the exercise is considered as a part of the P₀, while the P_m reflects only the heat produced from exercise.

The explicit solution of the system of equations can be found for any given time t as:

$$T_{\text{c}}=T_{\text{0}}+{\text{P}}_{\text{0}}\left(\frac{t}{2}+\frac{1-e^{-2\eta t}}{4\eta }\right)+{\text{P}}_{\text{m}}\left(\frac{t}{2}-\frac{1-e^{-2\eta t}}{4\eta }\right)$$ (4)

$$T_{\text{m}}=T_{\text{0}}+{\text{P}}_{\text{0}}\left(\frac{t}{2}-\frac{1-e^{-2\eta t}}{4\eta }\right)+{\text{P}}_{\text{m}}\left(\frac{t}{2}+\frac{1-e^{-2\eta t}}{4\eta }\right)$$ (5)

Model parameter estimation.

A temperature time-series for each running speed at each ambient temperature consisted of 16 points for each rat (15 min running), which were calculated by obtaining medians for corresponding time intervals as described in Data processing. For each ambient temperature T_a and speed j we calculated the mean temperature among rats at time t as ${\left\{T_t^j\right\}}_{t=0}^{15}$. Also, we denote the predicted value of T_c from our model using Eq. 4 at time t as T(P₀,P_m,T₀,t).

For a fixed speed j, we considered T_t^j of the time series ${\left\{T_t^j\right\}}_{t=0}^{15}$ as independent identically distributed normal random variables with mean T(P₀,P_m,T₀,t) and variance σ² = ${\displaystyle {\sum }_{t=0}^{15}}{s}_t^2/16$, where s_t² is the sample variance found for each time t = 0,1,. . .,15, i.e., T_t^j ∼ N[T(P₀,P_m,T₀,t),σ²].

Then, the likelihood function, the conditional joint probability density function, is given by the product of the conditional distributions as noted: ${\prod }_{t=0}^{15}f\left({\left\{T_t^j\right\}}_{t=0}^{15}|T_0,{\text{P}}_0,{\text{P}}_{\text{m}}\right)$. The likelihood function can be calculated as recommended in Refs. 20a, 31, and 32:

$$L\left({\left\{T_t^j\right\}}_{t=0}^{15}|T_0,{\text{P}}_0,{\text{P}}_{\text{m}}\right)=\frac{1}{{\left(2\pi \right)}^{\frac{16}{2}}{\sigma }^{16}}\exp \left\{-\frac{1}{2{\sigma }^2}{\displaystyle {\sum }_{t=0}^{15}}{\left[T_t^j-T\left({\text{P}}_0,{\text{P}}_{\text{m}},T_0,t\right)\right]}^2\right\}$$ (6)

where j = 0,6,12,18 (m/min).

Model reduction and analysis.

By maximizing the likelihood (Eq. 6) we obtained a best-fit set of parameter values (P₀,P_m,T₀) for each speed at two different ambient temperatures, 25°C and 32°C. Then by assuming that the likelihood (Eq. 6) represents a Bayesian posterior probability distribution for the model parameters, we calculated the 95% confidence regions of parameter estimates on the (P₀,P_m)-plane, which demonstrated strong negative correlation between estimates of these two parameters. This correlation results in large variability of estimate for individual parameters. This also indicated that any independent prior limitations on the value of one of the parameters could significantly improve the precision of the estimates for both of them.

To formulate the prior restrictions on the parameters, we considered two hypotheses. First, we hypothesized that the heat production in the core at high ambient temperature is at its minimum, and hence cannot be further lowered by exercise, while heat dissipation remains constant. Mathematically this means that the net heat production in the core P₀ at T_a = 32°C remains equal to 0 for all treadmill speeds. The statistical analysis confirmed that the estimate for P₀ is not statistically significantly different from 0 for any speed. Second, we hypothesized that the heat production in the muscles P_m is independent of T_a and depends only on the intensity of the exercise (speed of the treadmill). Following these hypotheses, at T_a = 32°C, we fixed P₀ = 0 for all speeds, and used the likelihood function to determine the best-fit P_m values for each speed. Then, these P_m values were substituted into the model for T_a = 25°C, which was used to obtain the distribution of P₀ values for different speeds at 25°C.

RESULTS

Body temperature dynamics.

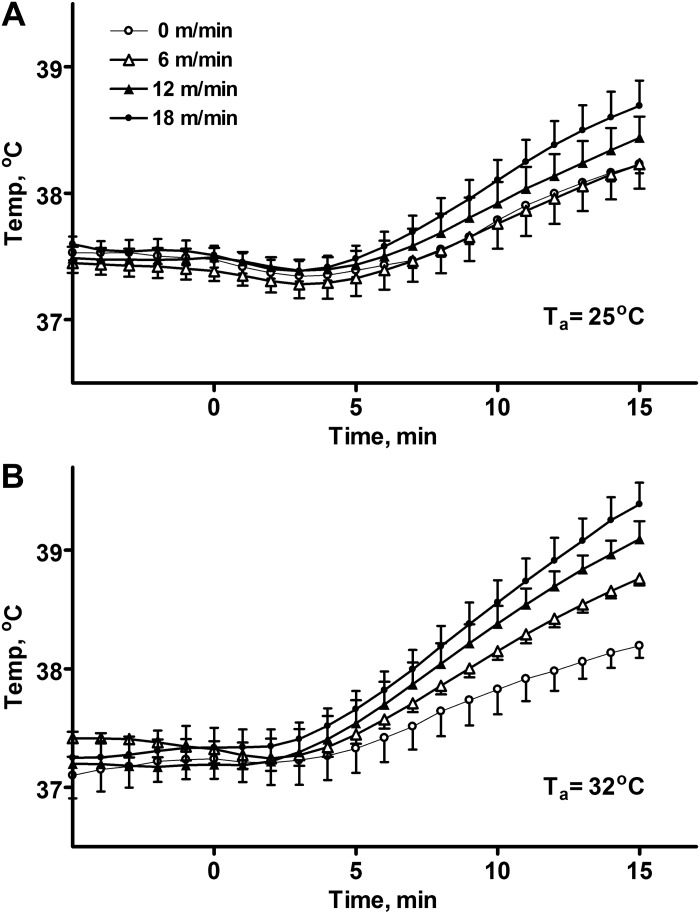
All rats were kept in home cages at room temperature before being placed on the treadmill. The time during which the baseline temperature was recorded was sufficient to achieve uniform values of core body temperature in all groups within 37.3 ± 0.2°C. No statistical differences between baseline temperatures in all experiments (for various ambient temperatures and speeds) were found. The dynamics of the average temperature for each group is shown in Fig. 1. The temperature in all groups eventually rose, including animals on the idle belt (Fig. 1, 0 m/min). In a room temperature environment, T_a = 25°C, the core temperature decreased slightly before starting to rise; this decrease was observed at all running speeds (Fig. 1A). In the warm environment, T_a = 32°C, the body temperature did not decrease initially; however, the temperature did not start to increase for at least 3 min (Fig. 1B). After 5 min body temperatures were increasing in a linear fashion in all groups until the end of the run (15 min total, Fig. 1, A and B).

Fig. 1.

Experimental data: the average and standard deviations of the core body temperature of rats running on a treadmill for 15 min at various speeds in two environments: at 25°C (A) and at 32°C (B). Rats were in their home cages before the run, transferred to the treadmill at t = 0 min, and the belt was set to the actual speed in 30 s.

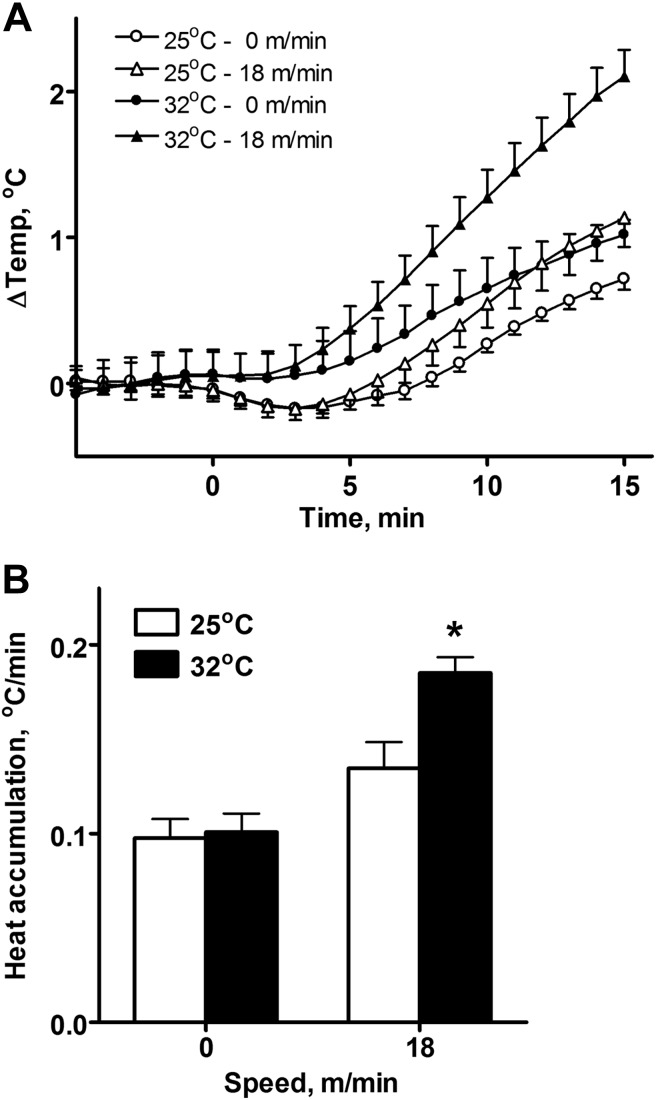
The presence of a “hypothermic” phase is more obvious when experimental data for both ambient temperatures are plotted together (Fig. 2A). We have used the estimate of the rate of change in the core temperature from 6 to 11 min to determine the rate of heat accumulation. In the control group which was placed on an idle treadmill, the rate of change of the core temperature was almost identical for both ambient temperatures (Fig. 2B). However, at 25°C running at the speed of 18 m/min subtly increased the rate of heat accumulation, whereas at 32°C running at 18 m/min led to almost twofold faster increase in temperature (Fig. 2B).

Fig. 2.

Comparison of the body temperature dynamics (A) and heat accumulation rate (B) between animals at two ambient temperatures which were either running at 18 m/min or staying on the idle belt. Heat accumulation rate was calculated as an average rate of the body temperature change between 6 and 11 min. *Statistically significant difference with staying on the idle belt (P < 0.05).

After analysis of the experimental data we can summarize a few qualitative observations and phenomena characterizing short-term running on a treadmill as follows. First, the running at the treadmill results in increases in body temperatures which do not appear immediately, but rather after a delay. Second, increases in temperature are preceded by slight decreases at room temperature, while no initial change in temperature is observed in the warm environment. Finally, the rate of heat accumulation is not significantly different between animals running with different speeds at room temperatures. In a warm environment, however, the increase in the running speed correlates with the rate of heat accumulation.

The model with unrestricted parameter values.

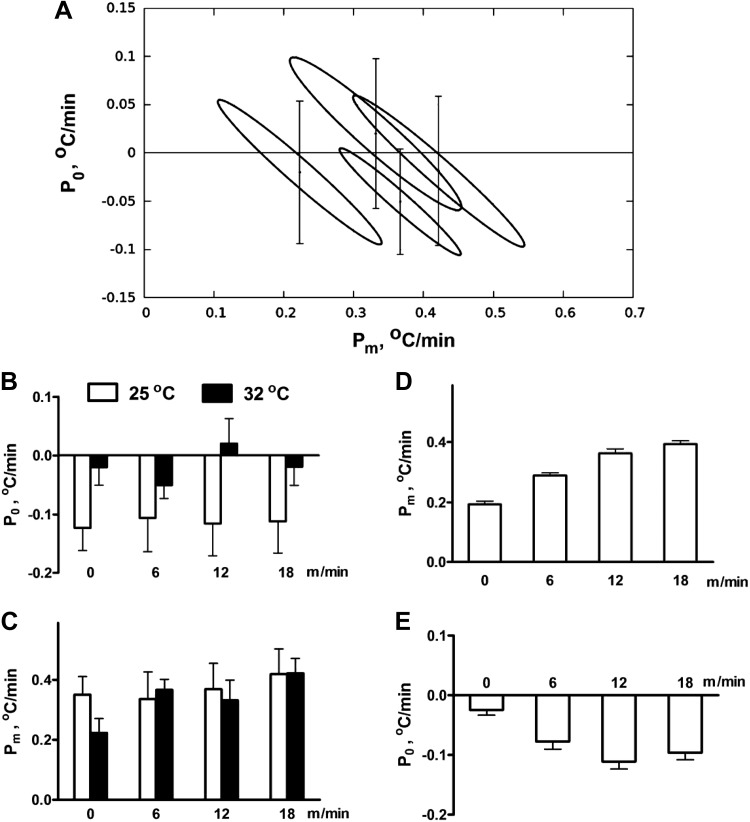
At first, we utilized the likelihood function (Eq. 6) to find the confidence regions for all model parameters in all groups as described in methods. The analytically calculated (for the high ambient temperature) 95% confidence regions on the (P_m,P₀)-parameter plane have an elliptical shape and are shown in Fig. 3A. Figure 3, B and C, represents the best-fit estimates and standard errors for P₀ and P_m, respectively.

Fig. 3.

A: confidence regions on the (P₀,P_m)-plane for each of the four studied speeds (0, 6, 12, and 18 m/min) at 32°C. B and C: parameter estimates before the model reduction for two ambient temperature, 25°C and 32°C: P₀ vs. speed (B) and P_m vs. speed (C). D and E: parameter estimates after model reduction: P_m vs. speed at T_a = 32°C after P₀ is set to 0 for the experiments at 32°C (D), and P₀ estimates at different speeds of running at 25°C with P_m values from D under an assumption that heat generation in the muscles does not depend on the ambient temperature (E).

The P₀ and P_m estimates appear strongly correlated. This suggests that the model with unrestricted parameter values is overdetermined. Practically, it means that the model with higher heat production in the muscles and accordingly lower net heat production in the core can describe the same temperature curve equally well. Consequently, while the ellipses in Fig. 3A are largely separated, their projections onto P_m and P₀ axes (which represent the confidence intervals for each parameter individually) heavily overlap. Accordingly, no conclusion can be drawn about exercise intensity-dependent changes in individual parameters, as those changes appear statistically insignificant due to large standard errors.

The standard approach to overcome the problem of the overdetermined model is to introduce appropriate prior restrictions on its parameter values. In this regard, we formulated two biologically plausible hypotheses and verified that none of them contradicted our modeling results with unrestricted parameter values.

First, Fig. 3B shows that at room temperature P₀ drops to negative values for all speeds, whereas this is not observed in a warm environment. Such a drop in P₀ represents a decrease in the core metabolism. With an increase in ambient temperature, the core metabolism is decreasing to maintain the appropriate body temperature until metabolism reaches a minimum value. Our first hypothesis is that at T_a = 32°C this limit is reached, and accordingly the exercise cannot lead to any further thermoregulatory decrease in the core heat production. Mathematically, this hypothesis states that for all speeds at high ambient temperature, P₀ remains equal to 0. Statistical analysis indeed shows that at T_a = 32°C, none of the P₀ estimates for different speeds are statistically different from 0. This fact is reflected in Fig. 3A as confidence regions of P₀ for each speed contained P₀ = 0.

Our second hypothesis follows that the heat production in the muscles correlates with exercise and its intensity, and does not depend on the ambient temperature. In support of this idea no statistically significant differences were found between P_m values for different ambient temperatures, at identical treadmill speeds (Fig. 3C).

The restricted model.

The first condition that we applied to the model was fixing P₀ = 0 at the high ambient temperature. As expected, this restriction allowed calculation of P_m with much better precision (Fig. 3D). Increasing the treadmill speed resulted in progressive increases in heat production by the muscles. Interestingly, just placing an animal on the treadmill resulted in heat production in the muscles comparable to the nonzero speeds. Specifically, the heat production at zero speed is approximately one half of the heat produced at the highest running speed of 18 m/min.

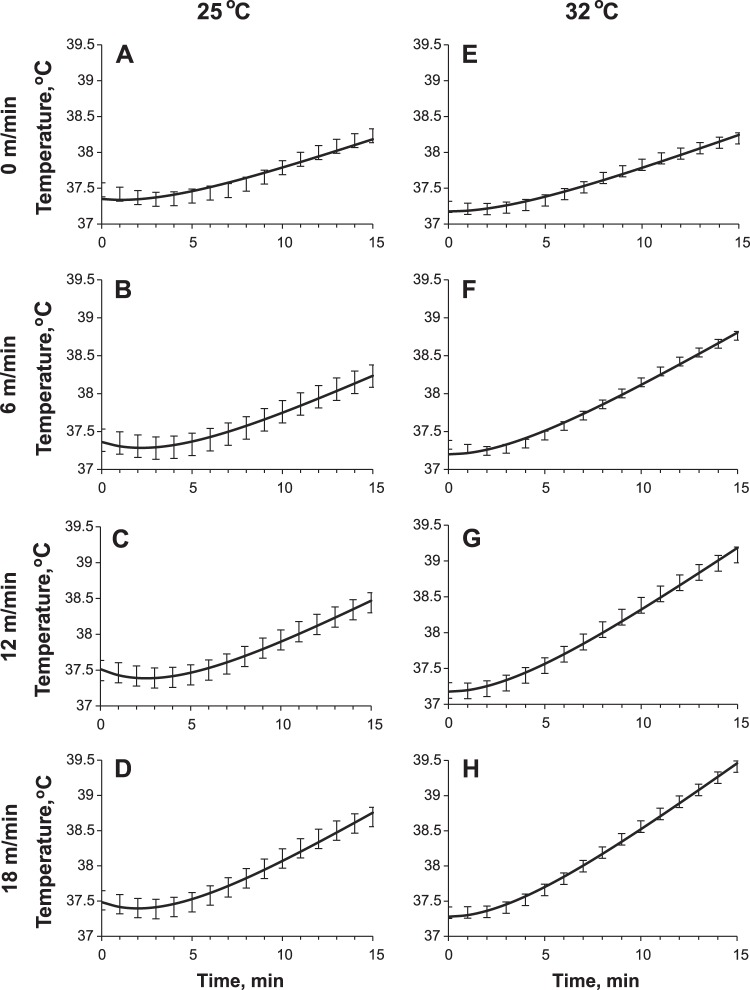
Following the second hypothesis that P_m depends on speed, but not on ambient temperature, we used the P_m values shown in Fig. 3D to define changes of P₀ for the ambient temperature T_a = 25°C (Fig. 3E). Overall, the model reproduced experimental temperature dynamics: calculated values were within one standard deviation (Fig. 4). The dynamics of the predicted temperature of the muscles is shown at the Fig. 5.

Fig. 4.

Comparison of the experimental data (error bars) and the core temperature curves as generated by the model (solid lines) using the parameter estimates represented in Fig. 3, D and E. The error bars show means ± one SD of the core body temperature over a group of rats. Rows of graphs correspond to different speeds of running (A and E: 0 m/min; B and F: 6 m/min; C and G: 12 m/min; D and H: 18 m/min as marked on the left). Columns of graphs correspond to different ambient temperatures (25°C, left column; 32°C, right column).

Fig. 5.

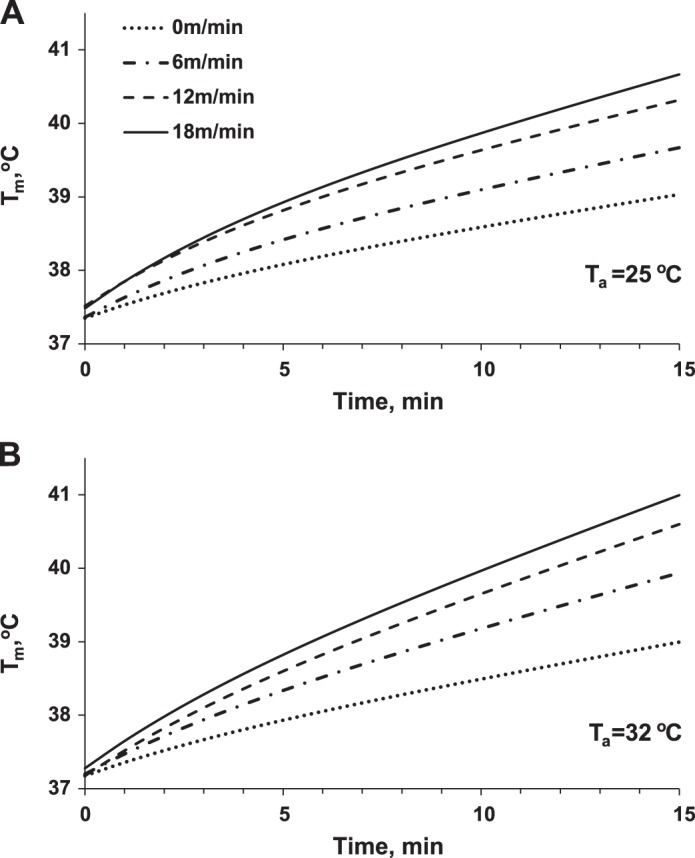
Muscle temperatures (T_m) as predicted by the model at T_a = 25°C (A) and at T_a = 32°C (B).

Placing the animal on a treadmill (speed 0 m/min) resulted in a small but significant decrease of core heat production. As the running speed increased, the decrease in core heat production became more significant. This decrease was not able to fully compensate for the production of heat in muscles. At the highest running speed, the increase in muscle heat generation was ∼0.4°C/min, while P₀ dropped by only 0.1°C/min. The difference between P_m values for 0 and 18 m/min was ∼0.2°C/min. This resulted in significant increases in overall heat accumulation at the ambient temperature of 32°C (Fig. 2B). At room temperature the heat produced by muscles was half-compensated by the reduced core heat generation. This led the increase in heat accumulation to be not significant (see Fig. 2B).

DISCUSSION

Treadmill exercise results in the steady production of heat in animals (16). Our objective was to mathematically model core body temperature changes as a result of exercise as a first step in building a model to predict the expected core body temperature at any given point in time given a specific running speed and ambient temperature. We also attempted to model physiological and metabolic responses, which are difficult to directly measure in exercising animals: muscle temperature, and both muscle and core heat generation.

Relationship between various parameters characterizing heat production.

Temperature changes in the body occur because metabolic processes generate heat. Increases in temperature occur when heat production is greater than dissipation into the environment, and decreases occur when it is less. In our model, heat production is separated into exercise-related, which occurs in muscles (P_m), and exercise-independent, which we assume to occur in the core. The heat production in the core was combined with the heat dissipation from the core, indicating overall net heat change in the core, and it was quantified as P₀.

Heat generation and dissipation is commonly expressed as power (P, energy divided by time) and is measured in units of energy per unit of time (e.g., W = J/s). Heat accumulation is directly connected with changes in body temperature through heat capacity as dT/dt = P/heat capacity (15). Both heat production during running and heat capacity are proportional to the body weight; therefore changes of body temperature are independent of body weight and are reflecting heat production per unit of weight. In this study the heat production/accumulation is always expressed in degrees Centigrade per minute, which can be translated to the power by multiplying by the heat capacity of the body.

As will be discussed below, we accepted heat dissipation approximately constant throughout these experiments, because the body temperature is not changed strongly enough to activate thermoregulatory responses. Therefore, P₀ provides an estimate of the changes in heat production mediated by the core, and a sum (P₀ + P_m) can be considered an estimate of a change in total heat production in the organism.

At room temperature rats can run at the maximal speed used in this study, 18 m/min, for extended periods of time. We have noticed that rats will run for more than an hour at room temperature (unpublished observation). This means that at this speed, heat is generated by oxidative processes without significant accumulation of metabolic by-products such as lactic acid. In this case the generated heat is proportional to oxygen consumption, because the differences related to metabolic substrate comprise less than 7% per unit of oxygen: if the substrate is carbohydrates, the energy generated from 1 liter of O₂ is 21.13 kJ, and it is 19.69 kJ if the substrate is fat (28). Considering this, in the following discussion we will draw connections between studies that used various end points: body temperature, heat production, or oxygen consumption.

Via modeling, we have quantified several key phenomena. While some of those phenomena may appear counterintuitive, we found multiple evidence supporting our observations.

Delay in body temperature increase.

When animals began running, their body temperature did not increase immediately. Instead there was a several minute long delay prior to the temperature elevation. Even more, there was a decrease in the temperature observed at the beginning of the run at room temperature. A graph of abdominal temperature vs. running time revealed a delay in the temperature change at the beginning of the run in the study by Fuller et al. (12). Hasegawa et al. (19) also observed a similar delay in the experiment in which the rat was allowed to adapt to the idle treadmill first, and the treadmill belt was activated after body temperature reached new baseline. When a rat was transferred from a home cage to an idle treadmill, there were at least two data points, shown in 5-min time increments, before the slope of the temperature curve became positive (see Fig. 2 in Ref. 19). Upon activation of a treadmill, there was an immediate temperature increase; however, the maximum slope was reached only after a 10-min delay (19). In a separate study from the same group a similar delay was shown (see Fig. 2 in Ref. 20).

The mechanism of this delay at the beginning of the run is explained by our model. As soon as exercise begins, contracting muscles begin to produce heat, yet this heat is not transmitted to the core immediately. Until muscles become physically warmer than the core, there is no net transfer of the heat to the core, and no changes in the core body temperature occur. The rate of heat transfer from the muscles to the core is proportional to the difference in temperatures between the core and the muscles and the heat transfer coefficient η which defines the inertia of this process. Therefore, the delay in the core temperature increase is concerned with the time needed for sufficient heat accumulation in muscles to activate the heat transfer from muscles to the core. When a larger time scale (1 h or longer) is considered, this delay would be hardly noticeable; however, on a time scale of 15 min, this delay is an important part of the system's dynamics.

A decrease in temperature in the beginning of the run at room temperature.

A slight decrease in body temperature in the beginning of each run was clearly present at room temperature; this was absent at high ambient temperature. We speculate that the mechanism of this “hypothermia” may be a compensatory adjustment of heat production in the body core, which is not yet compensated by heat transfer from the muscles. It takes some time for the produced heat to increase temperature of the muscles, and only after can that additional heat be transferred to the core. During this time, the heat produced in the core by the decrease of heat accumulation is less than the amount of heat dissipated to the environment. This results in a transient decrease of the body temperature. That decrease is significantly smaller or nonexistent in hot environments due to low baseline heat production and a smaller difference between the temperatures of the environment and the core. An anticipatory decrease of heat accumulation in the core occurs at all speeds including 0. So the very fact of the transfer of an animal to the treadmill evokes preparation for the exercise.

Relative independence of body temperature changes on exercise intensity at room temperature.

This phenomenon is best demonstrated by a linear increase in body temperature in graded exercise studies. An experimental protocol of Balthazar et al. (2) had an initial speed of 10 m/min with 5% incline and increased the speed every 3 min by 1 m/min. In this protocol of graded exercise, body temperature increases were virtually linear. Despite increasing speed (the maximal speed was 16 m/min) the increase of body temperature was so close to linear that the authors calculated the average slope over the whole run. The rate of change of the body temperature measured by Hasegawa et al. (18) was also independent of the work load with speeds between 10 and 26 m/min (see Fig. 1 in Ref. 18).

In experiments presented in the present study, during the linear part of the temperature increase the slope of heat accumulation in rats running at 18 m/min is significantly higher than in rats on the idle belt of the treadmill in the hot environment but not at room temperature (Fig. 2B). This slope is dependent on both P₀ and P_m with (P₀ + P_m)/2 providing a good estimate. At high ambient temperatures P₀ = 0 and it cannot be decreased with increasing speed. Accordingly, the slope increases as P_m increases (Fig. 3D). As a result, the slope is higher in running rats compared with idle rats (Fig. 2B). In contrast, at room temperature, P₀ decreases with the increasing speed (Fig. 3E), while P_m has the same dependence on the speed as in the hot environment. This means that at room temperature an increase of the temperature slope with an increase in treadmill speed is partially offset by decreasing heat accumulation in the core (Fig. 2). As a result, due to variability present in all biological systems, the increase in the slope does not reach statistical significance (Fig. 2B).

At first glance, this independence contradicts not only common sense, but also experimental data demonstrating that at higher speeds body temperatures of rats are higher (see, for example, Ref. 38). To interpret this contradiction, it is important to consider a time frame of the experiments: Tanaka et al. (38) explicitly stated that they measured the rectal temperature at the steady state (after 30 min of running). In the referenced study, the cutaneous dissipation of heat is not effective in the beginning of the run, and body temperature rises due to the increased heat production. As soon as body temperature reaches cutaneous vasodilation threshold, the steady state is established. In other words, the steady state is defined by a thermoregulatory threshold of cutaneous vasodilation, which is increasing with the running speed. Correlation between thermoregulatory threshold and running speed is the reason for higher body temperature at higher speeds. We argue below that in the time frame of our experiments the thermoregulatory heat dissipation is not activated.

Alternatively, in studies showing initial phases of temperature increases in rats running at various speeds, the slopes of temperature are impressively similar (Figs. 2 and 6 in Ref. 25). The temperature dynamics in different groups separates dramatically only after the (brain) temperature exceeds heat dissipation threshold, and when thermoregulatory heat loss responses are activated (25).

Transfer to a treadmill accounts for a large part of the temperature change during exercise.

When animals were placed on a treadmill and stayed at least 30 min, Hasegawa et al. (19) found that their body temperature rose by 1°C and remained elevated without any trend to return to baseline. After stabilization of the increased temperature, running at 10 m/min raised the temperature by an additional 0.5°C in 15 min when it again reached a plateau. So placing the animal on the idle treadmill accounted for approximately two-thirds of the total increase of the body temperature. From Eqs. 2 and 3, it follows that the additional overall heat accumulation (P₀ and P_m in our study) is proportional to the change in equilibrium temperature after sufficient time. The sum (P₀ + P_m) when staying on the idle belt was ∼0.17°C/min (see Fig. 3, D and E), while at a treadmill speed of 12 m/min (closest to the speed used in Ref. 19) it is ∼0.25°C/min, so a transfer to the belt accounts for approximately the same two-thirds of the increase in the rate of heat accumulation in the whole body during running at 12 m/min.

Further increases in speed do not dramatically increase heat production. Brooks and White (4) reported that oxygen consumption was 50 ml·kg⁻¹·min⁻¹ when running at 15 m/min speed on a treadmill with 1% incline, and increased only to ∼65 ml·kg⁻¹·min⁻¹ at 45 m/min with the same incline.

Suppression of thermoregulatory metabolism by exercise.

In our study we showed that rats exposed to exercise exhibited a decrease in their core heat production. Similar effects of thermoregulation suppression were described in the study by Guimaraes et al. (17). When rats were exposed to 12°C, their core body temperature went up [a well-known phenomenon from other studies (22)]. However, when the animals were forced to run at the same temperature, their body temperature was lower than at rest. Running at progressively colder temperatures resulted in lower body temperatures at equilibrium, which were achieved after 15–30 min of exercise. Similar observations were presented in Ref. 10. Assuming that running produces the same amount of heat regardless of the ambient temperature, one can conclude that in colder environments the exercise suppresses the thermoregulatory heat production more in absolute values. In fact, Makinen et al. (29) observed that exercise at 0°C did not increase oxygen consumption relative to exercise at 22°C, which means that intense thermoregulatory heat production in cold-exposed rats was substituted by thermogenesis induced by exercise.

Two compartments are necessary to explain complex temperature dynamics.

In a model with a single compartment, the increase of heat generation would result in an immediate growth of the body temperature. In contrast, we observed a clear delay between the beginning of an exercise and the temperature rise. Therefore, a single-compartmental model is not able to accurately describe changes in body temperature during running.

It appears that a two-compartment model reproduces experimental data with a sufficient level of precision. For simplicity's sake we named the additional heat produced from exercise as the heat produced by muscles, P_m. It is important to note that this variable can include heat produced by other organs as well (e.g., the heart or brain), and disregards any heat produced by the muscles at rest. In fact, an immediate increase of brain temperature during exercise (8, 10) is a feature of “muscle temperature” in our model, and indicates that additional heat production in the brain during the exercise contributes to the “muscle” compartment of our model. The rate of the initial temperature change in the second compartment (the core) is defined by the difference between overall heat production in the core and dissipation to the environment, P₀. Later during the run, the rate of temperature change in the core will be also modified by heat transfer from warmer “muscles” in addition to P₀. Note again that the use of P₀ is a simplification to refer to any heat produced by the body that is not directly related to additional heat resulting from exercise. It also allows us to disregard different forms of heat dissipation from the body by combining them in a single term.

Prior restrictions on model parameters.

Parameter confidence regions on the (P₀,P_m) plane appeared to be ellipses strongly extended in a certain direction (see Fig. 3A). As a result, the model parameter estimates had large standard errors and, hence, did not differ statistically significantly between various speeds and ambient temperatures. As described in methods, our findings became much more conclusive when additional restrictions were applied. Two reasonable hypotheses were formulated and proved to not contradict the initial estimates of the parameters of the model. First, we hypothesized that in hot environment there was no room to decrease heat generation in the core, supported by the fact that 95% P₀ confidence regions for each speed in T_a = 32°C included 0 (Fig. 3A). Therefore, we assumed that the amount of heat generated in the core body was at its minimum level and it could not be further reduced to compensate the additional heat coming from the muscles. This hypothesis is firmly footed in the concept of a thermoneutral zone (TNZ). T_a = 32°C is just exceeding the estimate of the upper border of the TNZ for rats (34). This means that at T_a = 32°C, the rat does not generate heat to keep its core temperature steady. Instead the only heat that the rat generates is in the process of sustaining normal bodily functions.

Next, we hypothesized that heat generation in the muscles, P_m, at given running speed is independent of the ambient temperature. Figure 3C represents the P_m estimates for 0, 6, 12, and 18 m/min speed of treadmills at both values of T_a. There is no statistically significant difference between values for matching speeds, which is compatible with the above idea.

Using these two restrictions provided more precise estimates of the model parameters (compare Fig. 3, B and C, with Fig. 3, D and E). This allowed us to conclude that the heat generated by the muscles increases with the speed, but this increase saturates as speed is increased. As soon as we used the P_m estimates obtained by fixing P₀ = 0 for the models with the high ambient temperature (T_a = 32°C) as priors for the model with the ambient temperature T_a = 25°C, we were able to calculate changes in the core heat production at T_a = 25°C with much better accuracy (Fig. 3E). Again the compensatory decrease in the core heat generation appeared statistically significant even when the animal was placed on the idle treadmill, and saturated at the speed of 12 m/min.

Role of heat dissipation.

There are two ways in which the net heat accumulation P₀ can be decreased by exercise. It can be due to suppression of thermogenesis, which is used to keep body temperature constant in relatively cold environment, or it can occur through increased heat dissipation. The major mechanism responsible for controlling heat dissipation in mammals is cutaneous blood flow. Cordeiro et al. (7) recorded the body temperature of rats running at 18 m/min at 5% incline simultaneously with the tail temperature, a marker of heat dissipation. The tail temperature reached its maximum at ∼20 min, and this moment corresponded to the beginning of plateau phase of body temperature at ∼38.5°C. The experimental setup for our study with the highest speed was the same except we did not impose the incline. Running time in our experiment was 15 min, and we did not observe plateauing of the body temperature. Hasegawa et al. (18) also confirmed that at body temperatures below 38°C, the tail is not dissipating heat effectively. Cutaneous heat loss threshold temperature in running rats is at or above 38.5°C in other studies as well (27, 39). Tanaka et al. (38) also demonstrated that the threshold for cutaneous vasodilation increases with increasing speeds and exceeded 39°C when running required above 70% of maximal oxygen consumption (V̇o_{2 max}), which approximately corresponds to the maximal running speed in our experiments (40). This let us consider that at least for most of the experimental time we did not reach conditions for significant cutaneous vasodilation resulting in noticeable additional heat loss. As a result, the changes in P₀ account for alterations in the thermoregulatory heat generation.

Biological implications.

In this study we quantitatively describe a particular thermoregulatory mechanism concerned with partial compensation of heat overproduction during exercise. This mechanism is based on the reduction of regulatory thermogenesis. We hypothesize that the impairments of this mechanism may lead to faster overheating and hence may underlie heat injury/stroke in some cases.

For example, heat illness is typically observed in individuals exercising in a hot environment. However, there are multiple occasions when it affects competitors in events in moderate climate, when a majority of participants appears to be not prone to this medical condition. Surprisingly, the correlation with running speed is often significant but fails to reliably explain more than a fraction of the variability in body temperatures (6, 30). In modeling terms it means that high body temperature is not a direct consequence of extreme amounts of heat due to the intensity of running. Less effective suppression of baseline thermoregulatory heat production could be one of the mechanisms which results in overheating in some athletes.

Are changes in metabolism specific to exercise?

One could interpret the increase in body temperature at the idle belt as a stress response, which remains despite rat familiarization to running on a treadmill. However, one can also notice that this increase is a part of a pattern: the core heat production drops while the heat production in muscles increases. The same phenomenon was observed in rats that were actually running. This allows formulating a hypothesis that muscular metabolic engagement and a compensatory decrease in the core heat production are not a response to exercise per se, but an anticipatory response to the need to run. In some situations this demand may never actualize (when the speed is 0).

Can we distinguish between anticipation of exercise and stress? The very definition of general adaptation syndrome by Selye as “a generalized effort of the organism to adapt itself to new conditions” (37), suggests that reactions to exercise could be considered as responses to stress. It is noteworthy that stress is typically associated with locomotion, and helps to prime the organism for fight-or-flight (5).

Temperature of muscles as a critical physiological end point.

It is difficult to measure muscle temperature in humans and animals while they are exercising without negatively affecting their ability to run. In those experiments where researchers placed temperature probes adjacent to muscles of exercising animals (13), similar values to what we predict (Fig. 5) were observed (39°C adjacent to muscles after 15 min at 9 m/min in Ref. 13 vs. 39.5°C in the muscle after same time at 12 m/min in our model at room temperature).

In our model the heat was dissipated from muscles to the core only, supposedly by the means of blood flow. This property of the model is based on the fact that in the beginning of the exercise the temperature of the muscles is the same as the temperature of the core, which is supported by experimental observations in rats (13). However, some authors suggest that in certain conditions, such as extreme exposure to cold environment (36) or in specific muscles in humans (23), the dissipation from muscles can occur directly to the environment. To describe such conditions the model needs to be modified appropriately. The physiological parameter, which is most sensitive to such dissipation, will be the temperature of the muscles. Obviously, at ambient temperatures lower than body temperature, it will be shifted down at all times, including the baseline.

Our modeling shows that the temperature in muscles when running with the fastest speed, 18 m/min, reaches 41°C and approaches the levels (41–42°C) at which the muscle tissue can be damaged (24). Avoiding this damage is important for selection of appropriate training regimens, especially in highly competitive athletes. Modeling may serve as an effective tool to determine if specific exercise regimens and conditions can result in thermal injury.

Energy production as a marker of substrate utilization.

Heat production is a measure of substrate utilization during exercise, and as such is directly linked to weight loss induced by exercise. Therefore, knowing heat production during exercise is important from a public health viewpoint. The finding that energy expenditure is relatively independent of the exercise load could have quite far-reaching considerations for fitness practitioners. In our experimental conditions, the most important factor associated with calorie expenditure was that exercise was occurring; the intensity of the exercise appears to have had a minor influence.

Conclusions.

Our study serves as a step towards a comprehensive mathematical model of thermoregulation during exercise. Inclusion of both thermogenesis and heat dissipation together with corresponding control mechanisms are needed to predict adverse temperature in exercising individuals. In this paper we have studied in rodents an “activity for free” phenomenon (21), which is a significant thermoregulatory mechanism activated by exercise. The phenomenon is relatively obvious biologically: when additional heat is produced by exercise, the generation of heat aimed at maintaining body temperature can be reduced. The energy which was used for maintaining body temperature is now used for locomotion (thus the name “activity for free”). However, for the first time we characterized this phenomenon quantitatively. At room temperature, rats are able to save from one-quarter to one-half of energy used for running. This compensatory suppression of metabolism is saturated with the low load. At running speeds as low as 12 m/min with zero incline the drop of metabolic activity in the core is already maximal. We predict that in colder conditions, which induce significant levels of metabolic support for homeothermy, this compensation could be more substantial.

GRANTS

The research reported in this publication was supported by National Institute on Drug Abuse Grant R01-DA-026867, iM²CS-GEIRE, and Research Support Funds Grants (RSFG) to Y. I. Molkov and D. V. Zaretsky, and a Purdue Research Foundation Award to Y. I. Molkov. Furthermore, this work was conducted in a facility constructed under support from National Center for Research Resources Grant C06-RR-015481-010.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: Y.Y., M.L., H.K., A.B., D.E.R., Y.I.M., and D.V.Z. analyzed data; Y.Y., M.L., H.K., M.V.Z., A.B., D.E.R., Y.I.M., and D.V.Z. interpreted results of experiments; Y.Y., M.L., Y.I.M., and D.V.Z. prepared figures; Y.Y., M.L., H.K., M.V.Z., A.B., Y.I.M., and D.V.Z. drafted manuscript; Y.Y., M.L., H.K., M.V.Z., A.B., D.E.R., Y.I.M., and D.V.Z. edited and revised manuscript; Y.Y., M.L., H.K., M.V.Z., A.B., D.E.R., Y.I.M., and D.V.Z. approved final version of manuscript; H.K., M.V.Z., and D.V.Z. performed experiments; Y.I.M. and D.V.Z. conception and design of research.

Glossary

dT_c/dt

Rate of change in core temperature over time,°C/min

dT_m/dt

Rate of change in temperature of muscles over time,°C/min

P₀

Difference between overall heat production in core and dissipation to environment, °C/min

P_m

Additional heat produced by muscles due to exertion,°C/min

T

Time, min

T_a

Ambient temperature,°C

T_c

Core body temperature from the mathematical model,°C

T_m

Temperature in muscles from the mathematical model,°C

T_t^j

Averaged core body temperature at time t (min) of rats running on the treadmill with speed j (m/min),°C

{T_t^j}¹⁵_t=0

Series of averaged core body temperature at every minute for 15 min of rats running on the treadmill with speed j (m/min),°C

T(P₀,P_m,T₀,t)

Core body temperature as a function of four parameters (P₀,P_m,T₀,t),°C

s_t² (s_t)

Sample variance (SD) of the experimental measurement of core body temperature at time t (min) of rats running on the treadmill with speed j (m/min),°C

η

Heat transfer coefficient between muscles and core, min⁻¹

σ² (σ)

Averaged value of sample variance s_t² (square root of averaged value of the sample variance s_t²),°C