Electrically Tunable Selective Reflection of Light from Ultraviolet to Visible and Infrared by Heliconical Cholesterics

Development of materials capable to dynamically control transmission and reflection of visible light and near infrared (IR) radiation is one of the most important directions of research with potential applications such as energy-saving smart windows,[1] transparent displays, communications, lasers,[2] etc. The most challenging problem is to formulate materials in which the transmission of light, or, more generally, electromagnetic radiation, can be performed dynamically and independently for different spectral bands, preferably by controlling reflection (as opposed to absorption). Among the oldest known materials capable of selective reflection of light are the so-called cholesteric liquid crystals (LCs) formed by chiral elongated organic molecules in a certain temperature range between a solid crystal and an isotropic melt.[2–8] The molecules are packed into a periodic structure in which the local orientation of molecules, called the director 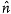, rotates around a helicoidal axis, remaining everywhere perpendicular to it, Figure 1a. The pitch P₀ of the resulting right-angle helicoid is typically in the range (0.1–10) μm. The cholesteric separates the light traveling along the helicoidal axis into right-handed and left-handed circularly polarized components. One component, of the same handedness as the cholesteric, is reflected, and the other is transmitted. The selective reflection is observed in the spectral range Δλ = (n_e – n_o)P₀ determined by the pitch and the ordinary n_o and extraordinary n_e refractive indices. The band is centered at 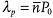, where 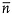is the average refractive index. The selectively reflected colors are highly saturated, they add like colored lights and produce a color gamut greater than that obtained with inks, dyes, and pigments.[4]

Figure 1.

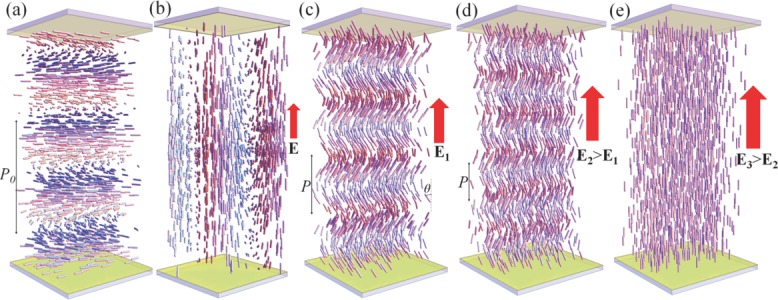
Field induced behavior of cholesterics structures. a) Right-angle helicoidal cholesteric with a large bend constant and a positive local dielectric anisotropy in a planar cell. b) Sufficiently strong vertical electric field E realigns the cholesteric axis perpendicularly to itself, causing light-scattering fingerprint texture. c) Heliconical structure in a cholesteric with a small bend constant and positive dielectric anisotropy stabilized by the vertical electric field E₁. d) The pitch P and tilt angle θ of the field-induced heliconical state both decrease as the electric field increases, E₂ > E₁. e) As the field increases further, to some E₃ > E₂, it unwinds the helical structure completely and forms a homeotropic nematic state. The figures are not to scale, as the experimental cell thickness is typically 20–50 times larger than the cholesteric pitch P₀.

The pitch P₀ and thus the wavelength λ_p of reflected light can be controlled by exposure to a variety of stimuli including electric/magnetic field, heat, and light,[9] thus enabling applications such as temperature indicators,[3] sensors of minute quantities of gases,[10,11] and optical switchable reflectors.[12,13] However, the most desirable mode to control light reflection, by an electric field applied parallel to the helicoidal axis, Figure 1a, has so far been elusive. The reason is that the field applied parallel to the axis, instead of changing the pitch while keeping the cholesteric axis intact to reflect light, rotates this axis perpendicularly to itself, as dictated by the dielectric anisotropy of the LC,[14] causing a light scattering structure called a “fingerprint texture,” Figure 1b. A limited range of electric tuning of right-angle cholesterics is still possible, with the help of special electrode geometry[15] or photopolymerization technique,[16–19] at the expense of reduced levels of reflection and relatively high electric field. Because of these difficulties in electric tuning of the standard cholesterics, their use as materials for electrically tunable large-area smart windows, mirrors, filters, displays, and lasers are not currently feasible.

In this work, in order to produce electrically tunable selective reflection, we use the so-called oblique helicoid structure of the cholesteric under low driving electric field, Figure 1c,d, as opposed to the right-angle helicoid shown in Figure 1a. In the oblique helicoid, the director is tilted, making some angle θ < π/2 with the helicoid axis. The electric field acting along the axis, realigns the molecules along itself and thus changes the pitch P without reorienting the helicoid axis, Figure 1c,d.

The oblique helicoidal (heliconical) state has been predicted by Meyer and de Gennes to occur in the applied electric field in a cholesteric in which the elastic constant of bend K₃ is much smaller than the elastic constant of twist.[20,21] For a long time, the effect could not be explored because of lack of materials with the needed elastic properties. Recently, it was suggested[22] that the novel dimeric LCs, representing two rigid rod-like units connected by a flexible chain with an odd number of links, might have a small value of K₃, which was confirmed experimentally.[23–25] The heliconical state of the corresponding cholesterics was observed in Raman–Nath diffraction experiments,[26] in which light propagates perpendicularly to the axis, and in Bragg reflection geometry,[27] but only at very high temperatures above 100 °C and for a relatively short tuning range of the reflection band. In this work, by designing the cholesteric mixture with a broad temperature range of stability (that embraces the room temperatures) and with a small K₃ that assures the existence of the oblique helicoidal state, we demonstrate that the selective reflection of light can be tuned by relatively low electric fields (a few V μm⁻¹) within an exceptionally wide spectral range, from UV to near IR.

We formulated the broad temperature range cholesterics with the small K₃ by mixing two dimeric LCs (1′,7′-bis(4-cyanobiphenyl-4′-yl)heptane (CB7CB) and 1-(4-cyanobiphenyl-4′-yl)-6-(4-cyanobiphenyl-4′-yloxy)hexane (CB6OCB)), and a standard LC pentylcyanobiphenyle (5CB) (Merck). The mixtures were doped with a left-handed chiral additive S811 (Merck) that determines P₀. Three mixtures were used, with composition CB7CB:CB6OCB:5CB:S811 (in weight units) being 30:20:46:4 (mixture M₁, cholesteric phase in the range 20–66.5 °C); 30.1:20:45.9:4 (M₂, 22–68 °C); and 29:20:49:2 (M₃, 21–69.5 °C). All mixtures demonstrated electrically tunable light reflection in the cholesteric phase at temperatures up to 45 °C; at higher temperatures, the effect disappears as K₃ in dimeric materials increases with temperature.[23–25] All data reported below were obtained at 25 °C.

In the experiments, the cholesteric is sandwiched between two glass plates with transparent indium tin oxide (ITO) electrodes. When a sufficiently strong electric field is applied, the material is switched into a uniform nematic with the director parallel to the field, Figures 1e and 2a. Such a state is dark when viewed between crossed linear polarizers. When the field is decreased, the LC shows a sequence of changing wavelength of reflection, from UV to visible blue, then green, orange, red, and, finally, near IR, Figure 2b–g and Supporting Information, Video S1. Below 0.7 V μm⁻¹, the LC transforms into the light scattering texture, Figure 2h.

Figure 2.

Electric field induced textures in cholesteric mixture M₁. Polarizing optical microscope textures of field induced a) unwound nematic; b–g) heliconical states with reflected (b) blue, (c) green, (d) orange, and (e) red colors, (f,g) two IR-reflective states; h) fingerprint state. The RMS amplitude of the electric field is indicated on the figures.

Figure 3 presents reflection spectra, peak wavelength, and bandwidth of reflection at various field strengths that further demonstrate a very broad range of controlled reflectance, from UV to IR, covering the entire range of visible light. As the field decreases, the peak wavelength shifts to IR, Figure 3a,b and Supporting Information, Video S2. The reflection coefficient R was measured to be 41% for the reflection peak at 632 nm (field 1.1 V μm⁻¹). By controlling the chemical composition of the mixture, one can optimize the reflection efficiency for any given pitch, and adjust the bandwidth that narrows down at higher electric field, Figure 3b.

Figure 3.

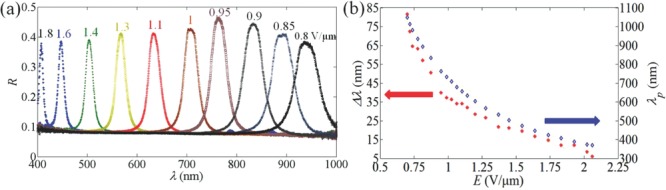
Selective light reflection in M₁ cell. a) Typical reflection spectra of M₁ cell for different amplitudes of the electric field, shown underneath the spectra in V μm⁻¹ units. b) Electric field dependencies of the wavelength and bandwidth of the selective reflection peak.

An important goal in the field of smart windows is to block visible and near-IR light selectively and independently, by varying the applied voltage.[28,29] Such a task can be performed by multilayered stacks of oblique helicoidal cholesterics with different concentration of chiral additive, since the materials are not absorbing. To demonstrate the principle, we stack the cells with short-pitch M₂ and long-pitch M₃ on top of each other, Figure 4. The spectral tuning range is exceptionally wide, 360–1520 nm for M₃, and somewhat shorter, 360–800 nm, for M₂, Figure 4a. Depending on the applied fields, the stack produces a variety of states: a state (I) transparent in the visible region and reflecting in IR (a stronger voltage is applied to M₂ as compared to M₃ cell), Figure 4b; (II) transparent in IR and reflecting in the visible (stronger voltage applied to M₃ cell), Figure 4c; (III) reflecting in both visible and IR (moderate voltages), Figure 4d; (IV) transparent in both the visible and IR part (high voltages). Importantly, the electric field not only switches the two reflection bands on and off (as in standard cholesterics), it also tunes their spectral position, Figure 4a. Using the rich arsenal of techniques developed previously for standard cholesterics, one can broaden the reflected bands by polymerization of the material,[8,14,16,19] or increase the reflectivity to 100% by using optical compensators.[4]

Figure 4.

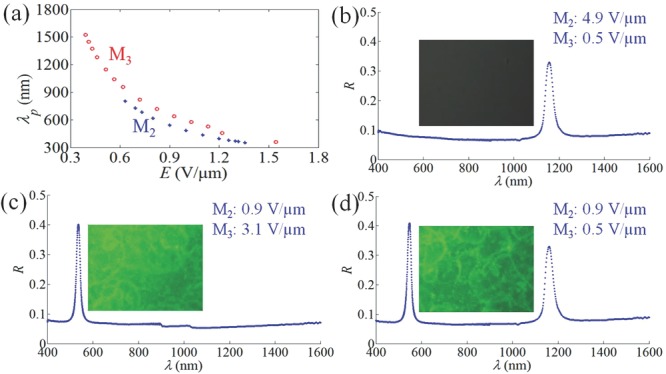
Selective light reflection in double cell. a) Reflection wavelength versus electric field for M₂ and M₃ cells. b) State (I) transparent in visible and reflecting in IR. The electric field 4.9 V μm⁻¹ acts on M₂ cell and 0.5 V μm⁻¹ on M₃ cell; c) state (II) transparent in IR and reflecting in visible; 0.9 V μm⁻¹ at M₂ cell and 3.1 V μm⁻¹ at M₃ cell; d) state (III) reflecting in two different parts of spectrum; 0.9 V μm⁻¹ at M₂ cell and 0.5 V μm⁻¹ at M₃ cell. The textures are taken under a reflective optical microscope with crossed polarizers.

Experimental results on the field dependence of λ_p, Figure 3b, support the theoretical model[20] in which P ∝ 1/E. For full description of the dependency λ_P(E) one also needs to take into account a somewhat weaker field dependency of the refractive indices. For light propagating along the axis, the effective birefringence depends on the tilt angle θ: 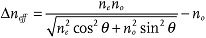. As demonstrated in ref. [26], θ decreases as the field increases, so that Δn_eff becomes smaller. This is why, for a given material, the reflectivity is typically weaker at high fields; it is also weaker at low fields, as the number of cholesteric layers in the cell of a fixed thickness decreases as the pitch increases, Figure 3a.

When the light beam is not strictly perpendicular to the cell, the oblique helicoid produces reflection not only at 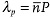, but also at 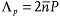, since the molecules separated by P/2 are tilted in opposite directions.[30] In the presented experiments with normally incident beams of small divergence, the peak at 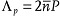, although observable, was about 10 times weaker than the main peak at .

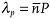To change the color, the pitch needs to adjust to the field, either through slippage at the bounding plates or through nucleation and propagation of dislocations; some of these defect lines are seen in Figure 2b–e. An important advantage of the heliconical cholesteric over similar structures in smectics is absence of positional order in molecular packing, which allows the system to adapt easily and reversibly to the changes of period; all the color changes observed in our experiments are fully reversible and relatively fast. For example, the homeotropic state (at 5 V μm⁻¹) switches into the heliconical state with saturated (90% of the maximum reflection) reflective red color (1.1 V μm⁻¹) within 0.8 s; the time was measured by monitoring the transmission intensity of the He–Ne laser beam, Supporting Information, Figure S1. The Supporting Information, Video S2, shows that the range (400–890) nm is swept within about 19 s, with an average rate 26 nm s⁻¹; the reflection coefficient increases from about 20% at 400 nm to 28% at 633 nm and then reduces to about 20% at 890 nm. Transition from the scattering state that exists at zero field, to the heliconical state with saturated (90% of the maximum reflection) red color reflection (1.1 V μm⁻¹) takes much longer time, about 2 min. The reasons are that this transformation implies complete restructuring through dynamics of multiple defects. It necessitates glide of dislocations, which is hindered in chiral structures.[31] The transition from the scattering state (zero field) to the homeotropic state (5 V μm⁻¹) is faster, 60 ms, since the applied field is strong; thus the preferred mode of switching might involve the homeotropic and color-reflecting states.

To conclude, we describe an electrically tunable selective reflection of light in UV, visible and IR by the heliconical cholesteric state that exists in a broad temperature range including the room temperatures. The tunable structural color is achieved in a simple sandwich geometry, in which the cholesteric is confined between two plates with transparent electrodes, thus implying a low cost and easy fabrication process. The color change occurs over the entire electrode area that can be designed as a desired pattern suitable, for example, for “see-through” color displays. The electrically tunable colors can be additionally controlled by the cholesteric composition and by employing reflective stacks. The effect can be tuned to practically any spectral regions in UV, visible and IR by chiral additives of different twisting power or concentrations. The regular right-angle cholesterics are known to provide structural colors of certain birds, beetles,[32] and plants;[33] it would be of interest to explore whether the oblique helicoidal states occur in the natural world.

Experimental Section

The main component of the explored mixtures that yields the necessary smallness of K₃ is CB7CB.[18,22] It shows a uniaxial N phase in the range (103–116) °C between the isotropic and the twist-bend nematic phase N_tb. At the field frequency 10 kHz, the dielectric permittivities parallel and perpendicular to the director were measured to be ε_|| = 7.3 and ε_⊥ = 5.9, respectively; the dielectric anisotropy of the material is thus positive,[18] so that the director prefers to align parallel to the electric field. At 106 °C, the elastic constants are K₁ = 5.7pN, K₂ = 2.6pN and K₃ = 0.3pN,[26] while the refractive indices are measured in our laboratory by the wedge cell technique[34] to be n_e = 1.73 ± 0.01 and n_e = 1.58 ± 0.01 (at λ = 632 nm). CB6OCB is also of positive dielectric anisotropy; it shows a uniaxial N phase in the range 110–157 °C.

The temperature was controlled by a hot stage LTS350 with a controller TMS94 (both Linkam Instruments) with 0.01 °C accuracy. All cells in the selective reflection experiments were addressed with the AC electric field of frequency 3 kHz (square wave). Flat cells were formed by glass plates with transparent ITO electrodes and alignment polyimide PI-1211 (Nissan); the thickness of cholesteric layers was d = 50 ± 2 μm. Selective light reflection was characterized by two complementary approaches. First, the field-induced color changes were visualized under the polarizing microscope (Optiphot2-pol, Nikon) with two crossed linear polarizers, in the reflection mode, Figure 2. Second, we measured the reflection spectra of the cholesteric heliconical structure using Ocean Optics spectrometers USB2000 (visible) and NIRQuest256 (near-IR). Note that the reflection of light can be tuned in cells thinner than 50 μm; however, the coefficient of reflection gradually decreases as d becomes smaller.

The reflection coefficient R at λ_p = 632 nm was determined by measuring the transmitted intensity I_trans and reflectance I_reflect of a linearly polarized He–Ne laser beam of diameter 1.5 mm with intensity I_in (λ = 632 nm) through the cell. The incident beam was tilted by 1° from the normal to the cell. We first characterized the cell in which the material was melted into the isotropic phase, to obtain the coefficient of reflection R_glass = I_reflect/I_in = 0.064 associated with the glass interfaces and transmission I_trans/I_in = 0.923. For the heliconical state with red color reflection, we measured I_reflect/I_in = 0.41 and I_reflect/I_in = 0.564, which implies that the coefficient of reflection caused exclusively by the periodic heliconical structure is R_hc = 0.35 (or 35%) and that the losses due to the light scattering are not significant, about 2.6%. The value of reflection coefficient caused by both the interfaces and heliconical structure, R = 0.41, measured at 632 nm, was used to renormalize the reflection data measured by spectrometers for other wavelengths in Figures 3 and 4.

Supporting Information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

Supplementary

Supplementary