DNA Brushing Shoulders: Targeted Looping and Scanning of Large DNA Strands

Abstract

We present a nanouidic device for targeted manipulations in the quarternary structure of single DNA molecules. We demonstrate the folding and unfolding of hairpin-shaped regions, similar to chromatin loops. These loops are stable for minutes at nanochannel junctions. We demonstrate continuous scanning of two DNA segments that occupy a common nano-volume. We present a model governing the stability of loop folds, and discuss how the system achieves specific DNA configurations without operator intervention.

DNA stretches to a large fraction of its contour length when it is confined to long nanochannels with a cross-section on the order of 100 × 100 nm².¹ Over the last decade or so, simulations^2–5 and experiments^1,6–9 have addressed the equilibrium statistical mechanics of single DNA molecules confined in straight nanochannels.¹⁰ Such understanding has been useful for developing analytical tools that take advantage of single molecule extension.^11,12

There is less known about molecules that overlap along the nanochannel axis.^13–15 Particularly little is known about the forces arising from hydrodynamic flow fields within nanochannels that contain two polymer strands.¹⁶ Part of the bottleneck for experimentalists lies in the challenge of forming and maintaining overlapping strands of DNA. As a step toward this end, we investigate the steady-state dynamics of nanoconfined DNA loops in a device containing Y-junctions (Fig. 1).

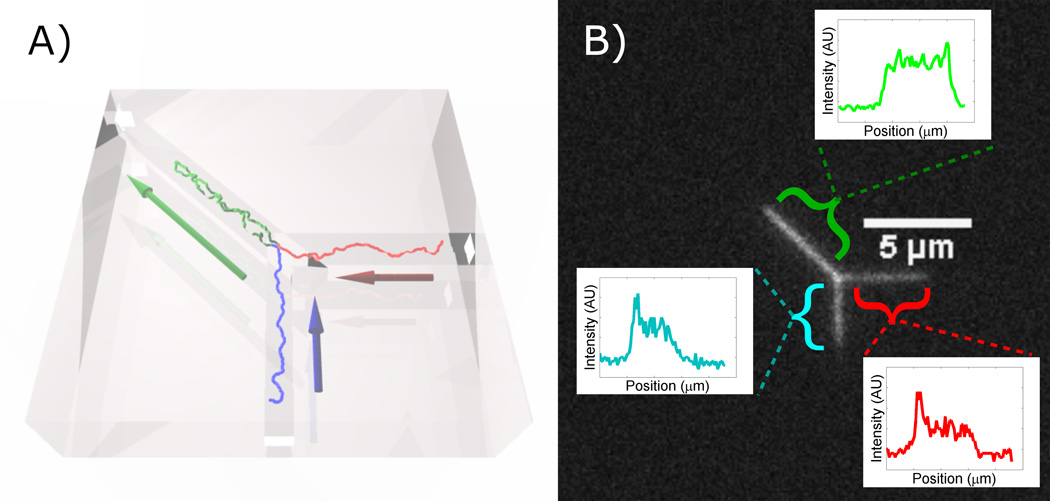
Figure 1.

A simulated DNA molecule trapped at a Y-junction. Arrows indicate direction of pressure driven buffer liquid flow. (B) Fluorescence micrograph of looped DNA at Y-junction. The insets show the fluorescence intensity profiles along the three channels axes: the loop (l), the vertical leg (υ), and the horizontal leg (h).

A loop within a DNA molecule establishes the possibility of testing long-range DNA interactions. Previous methods to test these interactions through DNA co-location were based on chemical modifications with protein bridges,¹⁷ or manipulation with magnetic or optical tweezers. In order to force DNA to interact, the latter require grafting DNA molecules onto colloids and lead to little orientational control of DNA strands.^18–20 In contrast, the plectonemes formed by twisting DNA with magnetic tweezers facilitate long range interactions, which are likely important to biological search.^21–23 However, efficient site-specific DNA-DNA interactions can only be tested with molecules up to a few kilobasepair in length, which limits the obtainable insights relevant for the long-range interactions within nuclear domains and dense chromatin.²⁴ We believe that directed colocation of multiple genomic regions provides a more realistic window into in vivo DNA interactions.

In this letter, we present a device with a Y-shaped junction of three nanochannels (Fig. 1). Our device enables the stable formation and manipulation of complex DNA configurations. We first show loops that are stable for minutes at a time. The two strands comprising such stable loops are an ideal platform for experiments that require two strands of DNA to run parallel to each other over large distances with a small separation and frequent contacts. We develop a mean-field model for DNA that is subject to hydrodynamic forces and the free energy of confinement at the Y-junction.

We then explore advanced applications of the device. First, we configure the fluid flow to scan the two genomic regions comprising the loop past each other. We then extend this procedure to colocate and scan two individual strands of DNA independently of each other. Lastly, we hold a DNA molecule stationary while exposing multiple regions to different buffer conditions.

Nanofuidic devices were fabricated from fused silica using a previously-reported electron beam lithography process.¹ λ-DNA and its multimers were suspended in 1/8×TBE buffer, and stained with the intercalating YOYO-1 dye at a ratio of 1 dye per 5 basepairs (Supplement S1). DNA was observed using a fluorescence microscope with an oil-immersion objective coupled to an EMCCD camera. DNA was illuminated by a strobed laser with illumination times of 10 ms.⁹

In Fig. 1 we show both a schematic and a fluorescence micrograph of a λ-DNA dimer (97 kbp) trapped at the junction of three channels by steady liquid flow. The contour of the single DNA molecule is stored in the three nanochannels. Each nanochannel defines an axis along which the DNA’s extended length is projected. We analyze looped DNA in terms of the length of each nanochannel that the DNA occupies (Fig. 1b). The extended length in the diagonal channel, vertical branch, and horizontal branch channels are labeled as l, υ, and h, respectively. For full functionality of the device, we have chosen the l (105 nm) marginally wider than the υ and h (95 nm) channels while all channels have the same depth (85 nm). Note that the choice of relatively low salt strength and relatively narrow channels places us in a regime in with a relatively high spring constant, which lowers both the amplitude of length fluctuations and the compressibility und sedimentation-like flows when compared to recent examples in the literature.²⁵ We point out that the insets in Fig. 1b confirms that incompressibility, and that the bright end of the h and υ traces is the transition from single to double occupancy at the junction, and not a compression of a singly-occupied channel. The image analysis is described in Supplement S2. We are able to apply independent pressures to the nanochannel ends, and thus can set flow rates through the channels independently up to a mass-conservation constraint. In order to trap the molecule in the shown configuration, flows in the vertical and horizontal channels are equal and face toward the junction, while the flow in the diagonal channel faces away from the junction.

In Fig. 2 we show the time evolution of molecules at low, intermediate, and high steady flow rates. For each flow condition, we show kymographs of the vertical branch, Fig. 2(A, D, K), the horizontal branch, Fig. 2(B, E, L), and of the diagonal channel, Fig. 2(C, F, M). The kymographs are formed by plotting the intensity along each nanochannel for each frame, and assembling them so that the position along the channel run horizontal, and the time runs vertical. The location of the junction is the fixed bright point on the left of each panel, and bright regions indicate DNA occupying the nanochannels. As long as DNA occupies the junction, this fixed point must be bright in all kymographs.

Figure 2.

Kymographs of DNA under steady, equal flows toward the junction in the vertical and horizontal channels, and flow away from the junction in the diagonal channel. Panels (A–C) show low flow $(\approx 0.1\frac{\mu m}{s})$, (D–F) show medium flow $(\approx 0.3\frac{\mu m}{s})$, and (K–M) show high flow $(\approx 0.5\frac{\mu m}{s})$. In each flow regime, there is a kymograph of the horizontal leg (A, D, K), the vertical leg (B, E, L), and the loop (C, F, M). (G–J) are instantaneous micrographs from the intermediate flow dataset (D–F) at the times indicated by the arrows. The frames in (G–I) do not show loops, but do have different lengths in the vertical and horizontal legs. (J) shows a frame with a loop.

In Fig. 2(A–C), the DNA is under low flow $(\approx 0.1\frac{\mu m}{s})$. The kymograph of the diagonal channel (Fig. 2C) shows only the fixed bright point described above, indicating little loop formation. At the same time, the length of the horizontal and vertical legs fluctuate (Fig. 2(A, B)). The molecule in Fig. 2(D–F) is under intermediate flow $(\approx 0.3\frac{\mu m}{s})$, and shows strong variations in the occupied length in all three channels. This variation of leg lengths is illustrated in Fig. 2(G–J), which show instantaneous frames from dataset that generated Fig. 2(D–F). Fig. 2F shows three events where a large bright region forms, indicating frequent formation of a transient loop. Under high flow $(\approx 0.5\frac{\mu m}{s})$ in Fig. 2(K–M), the loop (Fig. 2M) is stable, and fluctuates around a characteristic length. The vertical and horizontal legs (Fig. 2(K, L)) fluctuate around their flown equilibrium lengths.

We develop a model by assuming that the system is in a regime with strong viscous damping, and that only confinement, self-avoidance, and flow forces act on the polymer. The full derivation is given in Supplement S4. Briefly, the energy penalty per unit length for confining two DNA double helices instead of one is noted as Δα. In our device, loops are expelled from the l channel in absence of flow, which implies Δα > 0. We find a pseudopotential for the hydrodynamic drag force U_Drag by considering the DNA to be quasi-stationary. The drag force F_Drag is given by the local liquid velocity ϕ, and a interaction parameter between DNA and the liquid, ξ. ξ depends on the channel width and the number of occupying strands, and thus F_{Drag, i} = ξ_sϕ_i(i) (i is either υ or h) for the singly occupied channels, and F_{Drag, l} = ξ_dϕ_ll for the doubly occupied diagonal channel. Depending on the degree of screening of hydrodynamic interactions and the detailed hydrodynamic profile, we anticipate ξ_s ≤ ξ_d ≤ 2ξ_s, where Khorshid’s results suggest that we are at the bottom of this range. We further introduce $\beta =\frac{{\xi }_d\nu }{{\xi }_s{\gamma }^2}$, the ratio of flow forces per unit length of singly to doubly occupying polymer. γ is the ratio in polymer extension between singly-occupied vertical/horizontal branch and the doubly occupied diagonal channel. Importantly, γ is not to be confused with the ratio of extension and contour length, and is a function of both the change of transition from single to double occupation, and the difference in channel widths between the υ, h and l channels. In Supplement S3 we find γ ≃ 1. $\nu =\frac{{\varphi }_l}{{\varphi }_h+{\varphi }_{\upsilon }}\approx 1$ is the ratio of fluid velocity in the diagonal channel to the sum of those in the branch channels. For equal nanochannel widths mass conservation would demand ν = 1.

In the Supplement S3 we show that DNA in our system has a very high spring constant for axial compression,⁷ which leads to the constraint equation L = υ + h + 2γl. L is not the contour length, but rather the length that the molecule occupies when it is in an unfolded equilibrium configuration in the υ and h channels. At considerably higher flow velocities or higher salt, compression/expansion of the polymer at the junction would lead to a violation of the L constraint, and a more complicated model. The constraint makes the (υ, h, l) coordinate system overdetermined. We can reduce the number of variables by taking the viewpoint of a naive observer without knowledge of the linear topology of the molecule, who could consider the legs as a continuous distribution of singly occupying polymer with a doubly-occupying segment protruding from it. We know that in reality the linear contour runs from singly-occupied legs through the loop to the other singly-occupied leg. This naive observer could define the center of mass of the polymer within the singly-occupied legs as, $X_{\mathrm{C}\mathrm{M}}=\frac{\upsilon -h}{2}$. This choice of variable decouples key terms of the resulting effective potential

$$U_{\text{Total}}=\frac{{\xi }_s({\varphi }_{\upsilon }+{\varphi }_h)}{2}{X}_{CM}^2+(1-\beta )\frac{{\gamma }^2{\xi }_s({\varphi }_{\upsilon }+{\varphi }_h)}{2}{l}^2+[\mathrm{\Delta }\alpha -\frac{1}{2}{\xi }_s({\varphi }_{\upsilon }+{\varphi }_h)L\gamma ]l+{\xi }_s({\varphi }_{\upsilon }+{\varphi }_h)\gamma l{X}_{CM}+\frac{{\xi }_s({\varphi }_{\upsilon }+{\varphi }_h)L}{2}{X}_{CM}+\text{const}.$$ (1)

We can link U_Total to the observed probabilities p(l, X_CM) of molecular configurations by using the Smoluchowski equation and assuming steady state. Thus, $p(l,X_{CM})~\text{exp}(-\frac{U_{\text{Total}}}{kT})$, and we expect a Gaussian probability surface in two dimensions. Note that the steady-state probabilities are not affected by the choice of coordinates (or presumed topology).

The quadratic term in X_CM (Eq. 1) contains physical parameters related only to the vertical and horizontal branch channels, which are singly occupied. Therefore a Gaussian fit to the configuration probability surface along the X_CM direction allows us to extract ξ_s(ϕ_υ + ϕ_h) (Supplement S4 for details). Considering the quadratic term in l, we see that a similar fit along the l direction allows determination of (1 − β)γ². This factor hence governs whether the potential landscape is concave or convex in l, and thus determines whether steady flow results in stable loops (β < 1), or whether they are suppressed (β > 1). β can experimentally be chosen by varying the relative widths of vertical/horizontal (single-occupied) channels and the diagonal (loop) channel. Our device has β < 1 because the diagonal channel is wider than the branch channels. Further inspection of Eq. 1 shows that an assumption of symmetric flow across the legs (ϕ_υ = ϕ_h) decouples the X_CM and l terms completely. With the fourth and fifth terms removed from consideration, the third term, linear in l, governs whether a local minimum of U_Total is physically accessible at $0<l<\frac{\gamma L}{2}$. We note that this term is dependent both on the confinement energy penalty of loop formation, and on the contour length of the polymer.

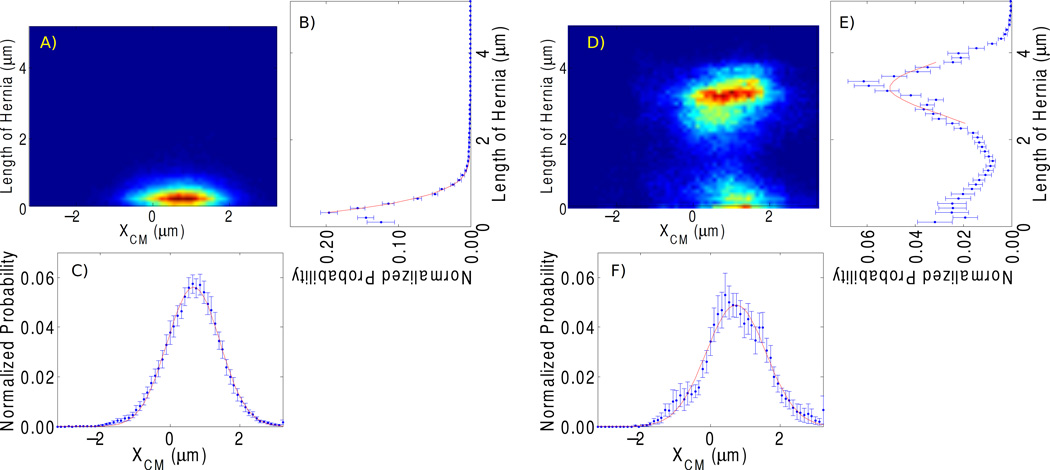
Indeed, we noted a different behavior for long DNA (λ-DNA multimers and concatamers of λ-DNA with its fragments), which formed loops, and shorter DNA (λ-DNA monomers and fragments), which did not form loops. This is demonstrated in Fig. 3, which shows experimental p(l, X_CM) maps for short (Fig. 3A) and long (Fig. 3D) molecules. We also show the marginal probabilities p(l) and p(X_CM) that are the projections of the configuration probabilities on the l and X_CM axes. Supplement S5 details such maps on a single-molecule basis.

Figure 3.

Average histograms from all molecules in the short and long dataset. (A, D) 2D histogram of lengths of short and long molecules, respectively. (B, E) Probability distributions with respect to l obtained by summing and normalizing the 2D histrograms in (A, D) along the X_CM-axis. (C, F) Probability distributions with respect to X_CM obtained by summing and normalizing the 2D histrograms in (A, D) along the l-axis.

In Supplement S4 we show that this transition between non-loop forming and loop-forming regimes can be explained as a transition of the global minimum of U_Total from l > 0 to l < 0 by varying the molecule length. By considering the impact of the flow rate, we find that for sufficiently long molecules and high flow speeds, the ratio of loop length and contour length becomes invariant. This implies that the device will function as a length-dependent “filtering trap”, and that loops can be formed without real-time control of junction flows after the molecule has been brought into the area of interest. Note that in both parts of Fig. 3, the location of maximum X_CM ≠ 0, and that the principal axes of the paraboloid probability surface are not fully aligned with the l and X_CM axes. Both effects are caused by the fourth and fifth terms in Eq. 1 that depend on ϕ_υ − ϕ_h, and thus are due to small asymmetries in the flow impedances of our chip design.

The coefficients of the paraboloid in Eq. 1 can be determined from Gaussian fits to p(h) and p(X_CM) in Fig. 3. For the “short” molecules (Fig. 3(A–C)) we find σ_CM = 0.76 ± 0.08 µm (σ_h undefined in absence of hernia). The corresponding widths for the “long” molecules (Fig. 3(D–F)) are σ_XCM = 0.86 ± 0.09 µm and σ_h = 0.59 ± 0.06 µm. Eq. 1 predicts σ_CM independent of L, and we believe that the agreement found here is well within the bounds of sampling depth and the finite sampling time per molecule.

We can test the plausibility of our model by comparing the ξ_s implicated by σ_XCM to values found from length fluctuations.^6,9 By observing short DNA fragments (< 1µm) and assuming that they drift with velocity equal to the average liquid velocity, we use the σ_CM determined above to find ${\xi }_s=3.8\times {10}^{-4}\frac{\mathrm{k}\mathrm{g}}{\mathrm{m}·\mathrm{s}}$. This value is consistent, to within an order of magnitude, with ${\xi }_s=1.7\times {10}^{-4}\frac{\mathrm{k}\mathrm{g}}{\mathrm{m}·\mathrm{s}}$ obtained from equilibrium length fluctuations of extended λ-DNA molecules residing in the branch channels by using the equipartition and fluctuation dissipation theorems, see Supplement S6. However, in comparing the two values, it is important to note that they are drawn from experiments in two different flow scenarios. The first case, introduced in this paper, is one where the DNA is stationary and fluid is flowing through it. In the second case, there are no external flow stresses and length fluctuations occur around an equilibrium configuration. The fluid is on average stationary as the DNA fluctuates through it. Thus the ξ_s’s obtained from both methods should differ by a factor of order unity. The drag is lower than theoretically predicted,²⁶ but we note that the values entering the analysis are within earlier publications.⁶

Having established the Y-geometry’s ability to form stable loops, we note that the full capabilities of the device arises from the possibility of programmed strand manipulation under real-time observation. In the following section, we demonstrate three applications of the Y-junction device: intramolecular scanning within the loop of a single molecule; intermolecular scanning between two independent molecules; and the selective exposure of multiple regions of a single molecule to reagent gradients. While there are many questions of non-equilibrium polymer physics that can be probed using the device, we will highlight the potential for biophysical analysis.

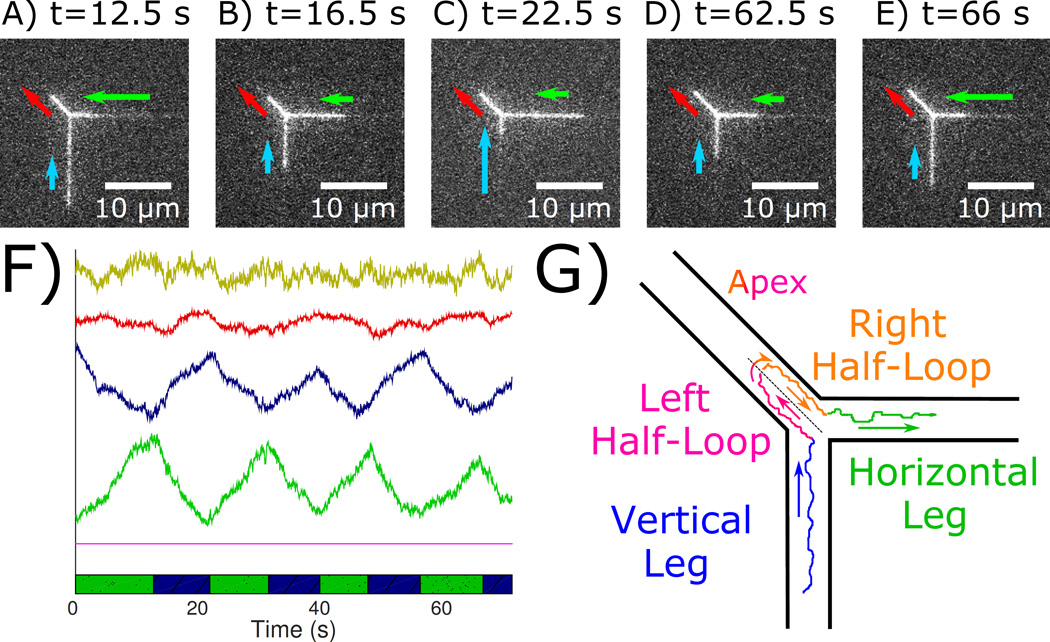
The unique property of device-induced loops is the colocation of two genetically distant regions of a single DNA within the diagonal channel, which allows testing of (protein-mediated) DNA-DNA interactions that are the basis of three-dimensional genome organization.²⁴ The first principal mode of strand manipulation to test such interactions is to force the two strands composing the loop in opposite directions relative to each other while keeping the loop length stationary. The intramolecular scanning procedure in Fig. 4 uses a pre-stabilized, looped DNA. An asymmetric pressure is applied so that the flow in the horizontal branch (green arrow) is initially higher than flow in the vertical branch (blue arrow). Under this flow configuration, the horizontal leg (green) shrinks as the vertical leg (blue) grows continuously over time. This occurs as the loop (red) maintains its steady-state length. The pressures are then reversed, and the scanning proceeds in the opposite direction.

Figure 4.

Intramolecular scanning of genetically distant regions of a molecule via spatial colocation in the loop. (A–E) Micrographs of the looped molecule at select times. (F) Lengths of the horizontal leg (green), vertical leg (blue), and loop (red) versus time. The yellow curve is the sum of the green, blue, and red curves. (G) Schematic of internal dynamics. Contour in the vertical leg (blue) passes into the left half-loop (red-blue), through the apex, then into the right half-loop (red-green), and exits into the horizontal leg (green). Contour flowing in the left and right half-loops potentially interact.

As it travels, the contour in the two strands constituting the loop scan past each other, making frequent contact.²⁷ For an application that tests site-specific intramolecular interactions mediated by proteins, the rate of making specific DNA-DNA contacts limits the ability to probe their properties. The rate of making contacts is proportional to the square of the local DNA concentration.²⁸ In typical free solution interactions, the concentration of monomers within a single, unconfined coil is ≲40µg/mℓ. For the diagonal channel, however, a back of the envelope calculation yields an effective concentration of >1000 µg/mℓ, two orders of magnitude above the concentration within a single, unconfined coil. Therefore, the likelihood of interaction in the diagonal channel is greatly amplified.

To underscore this point, we consider the J-factor (J(s)), which is the probability that two loci, spaced apart by some genetic distance, s, occupy a volume that is small enough for a chemical reaction to occur. J(s) = (2πsl_k/3)^−3/2 for a large, unconfined, Gaussian coil (l_k is the Kuhn length).²⁹ For a typical λ-DNA with a contour length l_c ≈ 16 µm, J(s = l_c) = 8.5 × 10⁻¹⁰ M, where J(s = l_c) is the cyclization probability when the two ends of the DNA come into contact. In a nanochannel device, however, the interaction volume is a DeGennes blob of 100 × 100 × 100 nm³. Within a blob, the DNA behaves like the ideal Gaussian chain described above with an effective stored contour on the order of 6l_k. We can thus ascribe a J(s = 6l_k) = 3.0 × 10⁻⁷ M to a blob, which is nearly three orders of magnitude greater than it is for unconfined DNA. Incidentally, J(6l_k) is also in the range of the optimum cyclization probability.³⁰ While J ~ s^−3/2 and continues to decrease for an unconfined polymer that is larger than a DeGennes blob, our device enables the optimal J(6l_k) for any two loci separated by s ≫ l_k as long as these loci that are genetically separated along the DNA are colocated within the volume of a DeGennes blob. This is achieved within the loop formed by our device.

The hydrodynamically driven search in our device also proceeds faster, on average, than a random search in an unconfined coil in three dimensions. We base this statement on two observations: a random search cannot occur faster than the relaxation time scales of Rouse modes in a randomly fluctuating coil, where the slowest mode scales with the square of the contour length, i.e. τ ≈ L².²⁸ The search time must then scale with the same, if not higher, power. In contrast, the DNA confined in our device can be actively scanned at a fixed rate. Therefore, the time required for two sites to “find” each other is directly proportional to the contour length. Moreover, the molecules travel effectively in one dimension, along the axis of the nanochannels. Berg, et. al. describes an analogous search of a protein for a locus while it is loosely bound to a DNA strand.³¹ The random spatial search in three dimensions is sped up to the facilitated one-dimensional diffusion of the protein as it “slides” along the backbone. This is effectively a one dimensional search. Hence, the colocation of the multiple strands in the loop can also be viewed as the facilitated diffusion of one strand along the other.

As useful as intramolecular scanning in a loop is in facilitating interactions within a single molecule, it is not as powerful a procedure as colocating and flowing two independent molecules past each other. Such a system would set the ideal stage for DNA hybridization, DNA recombination, and DNA-proteins-DNA complex formation, all of which are ubiquitous functions of DNA existence in eukaryotes.³² Studying these phenomena in real-time would yield insight into not only how they occur naturally, but also how to control and manipulate them for the desired purpose. The procedure for DNA scanning between two independent strands is illustrated in Fig. 5. An overlap of two molecules is established through independent loading of two DNA molecules followed by controlled motion. In essence, the tactic is to apply pressures such that one DNA molecule (green) is held stationary in the vertical and diagonal channel, while owing a second molecule (red) from the horizontal channel into the vertical channel that is already occupied by the green molecule. The manipulation is enabled by the fact that the flows in the diagonal and horizontal channels can be varied independently, and that molecules that occupy only one of the two channels is largely unaffected by the flow in the other channel. Note that our argument concerning the extraordinarily high local DNA concentrations and high interaction probabilities applies to this scanning strategy as well.

Figure 5.

A)–C) Intermolecular scanning of two DNA molecules via spatial colocation. Schematics and corresponding images of two λ-DNA molecules, one stained with YOYO-1 (green), the other with YOYO-3 (red), being scanned past each other. Inlet pressures are regulated to force the DNA into the desired configurations. D)–F) DNA is regioselectively exposed to fluorescent dye (S640) that is introduced through the υ channel and leaves through the l channel. DNA is green, S640 is red, and we show both individual color images (D,F) and the composite image (E).

Whatever intermolecular events we can facilitate by colocating two strands, we can increase the benefits even further by exposing a stationary molecule locally to a reagent, or even to general chemical gradients. We demonstrate the ability of the Y-junction device to establish such chemical gradients spanning an extended molecule by exposing each of two legs of a stationary DNA molecule at a channel junction to a chemical gradient of the fluorescent dye S640 (Fig. 5B). In this figure dye-free and dye-carrying buffers enter through the horizontal and vertical channels, respectively. A continuous gradient forms in both, while the diagonal loop channel carries a single concentration. The slope of the gradient is given by the ratio of diffusivity of dye and flow speed squared. Since S640 (MW ≈ 630 g/mol) is much more diffusive than a typical 1,000 amino acid protein (MW ≈ 100, 000 g/mol), the gradients in Fig. 5B are lower bounds on what we can create for proteins. In the future, we believe that selective exposure of different parts of a single molecule to different chemical gradients will enable multiple reactions to occur on the same molecule. For instance, one can establish a protein gradient over one leg and a cofactor gradient over the other. Then, by adjusting the flow asymmetries for a desired X_CM, we can facilitate a protein-mediated event on an arbitrary location on the molecule.

In summary, the Y-junction device enables the formation of a variety of stable DNA configurations. Under various flow strategies, we maintain stable loops and use them to scan different contour regions past each other, colocate two molecules, and selectively expose multiple regions to different reagents. The techniques developed with this tool can be used to facilitate experiments with the interactions of DNA with itself, with other DNA, with proteins, with reagents, etc. Self-interactions can shed light on broader questions of polymer entanglement. Future experiments would use the Y-geometry to explore basic questions of polymer physics as well as to develop methods of targeted manipulation at the submolecular level.