Transient β-hairpin formation in α-synuclein monomer revealed by coarse-grained molecular dynamics simulation

Abstract

Parkinson’s disease, originating from the intrinsically disordered peptide α-synuclein, is a common neurodegenerative disorder that affects more than 5% of the population above age 85. It remains unclear how α-synuclein monomers undergo conformational changes leading to aggregation and formation of fibrils characteristic for the disease. In the present study, we perform molecular dynamics simulations (over 180 μs in aggregated time) using a hybrid-resolution model, Proteins with Atomic details in Coarse-grained Environment (PACE), to characterize in atomic detail structural ensembles of wild type and mutant monomeric α-synuclein in aqueous solution. The simulations reproduce structural properties of α-synuclein characterized in experiments, such as secondary structure content, long-range contacts, chemical shifts, and ³J(H_NH_Cα)-coupling constants. Most notably, the simulations reveal that a short fragment encompassing region 38-53, adjacent to the non-amyloid-β component region, exhibits a high probability of forming a β-hairpin; this fragment, when isolated from the remainder of α-synuclein, fluctuates frequently into its β-hairpin conformation. Two disease-prone mutations, namely, A30P and A53T, significantly accelerate the formation of a β-hairpin in the stated fragment. We conclude that the formation of a β-hairpin in region 38-53 is a key event during α-synuclein aggregation. We predict further that the G47V mutation impedes the formation of a turn in the β-hairpin and slows down β-hairpin formation, thereby retarding α-synuclein aggregation.

I. INTRODUCTION

Parkinson’s disease, similar to many other severe pathologies associated with protein aggregation, is attributed to the misfolding and aggregation of a 140 amino acids (a.a.) presynaptic protein, named α-synuclein.^1–5 An α-synuclein monomer contains three regions with distinct compositions of a.a. (Fig. 1(a)): (i) an amphipathic N-terminal region (region 1-60) that tends to form α-helical structure; (ii) a non-amyloid-β component (NAC) region (region 61-95) that is hydrophobic and tends to form β-sheet structure; (iii) an unstructured C-terminal region (region 95-140) including 14 acidic a.a.^6–14 In solution, monomeric α-synuclein does not assume a well-defined structure.^{6–8,10,15,16} Under pathological conditions, α-synuclein undergoes disorder-to-order structural transitions, forming partially structured oligomers, and eventually self-assembles into highly ordered amyloid fibrils exhibiting cross-β-sheet structure.^4,9,17–20 Formation of α-synuclein amyloid fibrillar aggregates is a hallmark of Parkinson’s disease.^17,21–23

FIG. 1.

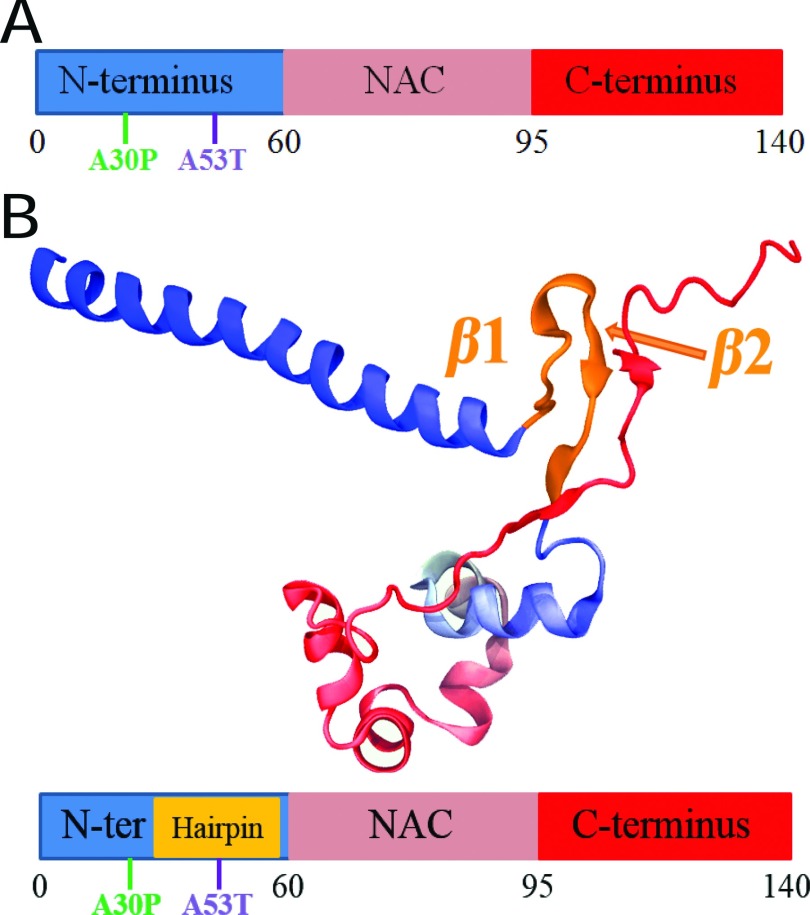
Overall structural features of α-synuclein monomer. (a) Schematic depiction of α-synuclein structure. N-terminus, NAC region, and C-terminus are colored blue, pink, and red, respectively. Starting and ending residue ID for N-terminus, NAC region, and C-terminus are labeled. The locations of point mutations, A30P and A53T, are labeled in green and blue, respectively. (b) Representative structure of α-synuclein conformations containing β-hairpins. The representative structure is chosen from the center structure of all sampled α-synuclein conformations with the β-hairpin conformations, such that the backbone of each member of the β-hairpin conformations in the group falls within a RMSD distance of 6 Å to the center structure. N-terminus, NAC region, and C-terminus are colored blue, pink, and red, respectively. Part of the C-terminus forms a β-strand attached to the β-hairpin. The first two regions involved in the fibril core are labeled β1 (region 38-44) and β2 (region 47-53). The coloring scheme used is applied throughout the further figures of this study. Shown beneath the structure is a schematic depiction of the β-hairpin. The coloring scheme is the same as that in panel (a) except for the gold part denoting the β-hairpin region. The schematic depiction serves as a structural guide of α-synuclein in further figures.

The formation of the α-synuclein fibril is a complex process, involving various intermediates, including oligomeric species arising at early stages of the aggregation and in protofibrils preceding fibril formation.^7,24–27 Monomeric α-synuclein plays a key role during the course of the aggregation process, being involved in formation of small oligomers at early stages and growth of fibrils at late stages.^5,28–30 During the two processes, α-synuclein monomers undergo substantial structural transitions from their solution conformations to structures enriched in β-sheet.^30,31 Conformations of α-synuclein monomer could play essential roles in these structural transitions, defining the starting points of transitions and perhaps facilitating the aggregation process through special structural features. Therefore, conformational sampling of monomers in solution is needed to provide mechanistic insight into the aggregation processes.

Numerous experimental studies have focused on resolving the conformational features of α-synuclein monomers.^32–41 Due to the heterogeneity of α-synuclein conformations, experimental techniques like NMR and CD spectroscopy can only characterize structures of α-synuclein monomers as ensemble averages.^{32–37,42,43} These experiments revealed that α-synuclein monomers assume an ensemble of disordered conformations, including both extended conformations and conformations exhibiting transient tertiary structure,^{32–37,39,42–49} such as those involving the interactions formed between C-terminus and NAC regions that could explain the protective effect of the C-terminal region against aggregation.^{34,39,44–49} Experimental data generated from NMR or EPR spectroscopy have also been combined with all-atom simulations to explore efficiently the conformational space of α-synuclein, generating in atomic detail conformational ensembles that are consistent with experimental observations.^44,50–55 These conformational ensembles revealed specific residues involved in the contacts formed between C-terminus and NAC regions as well as essential interactions involved.^44,53–55 Apart from the conformational features of α-synuclein monomers, their conformational dynamics has also been investigated using single-molecule techniques such as fluorescence resonance energy transfer and atomic force microscopy, indicating that α-synuclein monomers exhibit dynamic conformational exchange on time scales ranging from nanoseconds to micro-seconds.^{13,36,37,39,54,56–64}

Given the heterogeneous and dynamic conformational ensemble of α-synuclein monomers, it is critical to identify the key structural elements and overall conformational states of α-synuclein that are essential for the aggregation processes. At the level of secondary structure, the occurrence of multiple β-strand regions has been proposed through sequence analysis, simulations, and ingeniously designed experiments.^39,53,55,65 Furthermore, it has been suggested that one type of β-structure, namely, β-hairpin states, could play a critical role in α-synuclein aggregation.^66–69 Several lines of evidence from prior studies appear to support the importance of β-hairpin states. Reagents that are known to stabilize β-hairpins can promote the aggregation of α-synuclein;⁶⁹ peptides that presumably recognize β-hairpins can also capture monomeric α-synuclein and block the α-synuclein aggregation.^67,68 In addition, numerous experimental and computational studies have proved directly that β-hairpin-like structures are indeed metastable states of other aggregation-prone proteins, such as amyloid-β peptides (Aβ) and Islet amyloid-polypeptide (Iapp), likely participating in both oligomer formation and fibril growth.^17,70–80

In the present study, we seek to investigate the formation of β-hairpin structure and its possible role in aggregation of α-synuclein. Unlike short peptides such as Aβ and Iapp that could readily access local β-hairpin structures by exploring a small conformational space,^{17,70,72,74,76,79,80} α-synuclein has a much longer sequence (140 a.a.) and thus exhibits a much larger conformational space. In this regard we ask, how does β-hairpin structure arise in α-synuclein? Is a particular part of α-synuclein playing a decisive role for β-hairpin formation? How does the remainder of the protein influence local β-hairpin formation? In addition, a possible link between formation of β-hairpin conformations and bio-activity of α-synuclein needs to be explored.

In particular, point mutations A30P and A53T, with their location illustrated in Fig. 1(b), were found to be associated with an increase of α-synuclein aggregation and with familial Parkinson’s disease.^4,81–83 An altered conformational ensemble was ascribed to the A30P and A53T mutations compared to the wild type (WT) α-synuclein one.^40,41 We thus ask what effect do the two mutations have on the β-hairpin structure? Moreover, the C-terminal region protects the NAC region from interactions that lead to aggregation.^{34,39,44–49} Does the C-terminal region play its protective role by affecting formation of β-hairpin structure?

For intrinsically disordered proteins, conformational dynamics has been explored by molecular dynamics simulations in atomic-level detail.^74,84–88 A major challenge in simulating α-synuclein arises from the accessible conformational space that is too large to be explored sufficiently through all-atom MD simulations. Combining a description of protein at the atomic level and solvent at a coarse-grained (CG) level, the Proteins with Atomic details in Coarse-grained Environment (PACE) model developed by the authors’ group⁸⁰ provides the simulation power for sampling sufficiently protein conformational space for thermodynamic and kinetic information, while protein structures are provided in atomic detail. In particular, to achieve a proper conformational balance between structured and disordered parts of proteins, residue-specific conformational potentials and special interactions between side chain and backbone were designed and optimized for PACE,⁸⁹ permitting PACE’s application both in simulating protein folding^89,90 and in characterizing structural change of disordered proteins.⁸⁰

In fact, we present here microsecond-long PACE simulation of α-synuclein monomer in solution along with simulations of its mutants and of protein segments. All the systems were explored through unbiased simulations without restraints. The simulations reveal that region 38-53 indeed brings about a formation of a β-hairpin structure spontaneously and repeatedly. A comparison with simulations of the same region isolated from α-synuclein reveals further that the formation of β-hairpin is an intrinsic property of region 38-53 and can be slowed down significantly by the region’s interaction with the remainder of α-synuclein. In particular, the C-terminal region can interact with region 38-53 when the β-hairpin is present, likely preventing the β-hairpin from interaction with other molecules and, thus, explaining the protective (against fibril formation) role of the C-terminal region seen in experiments.^{34,39,44–49} Moreover, the simulations show that the familial mutations, namely, A30P and A53T, accelerate greatly the rate of β-hairpin formation, further suggesting that the latter is closely linked to α-synuclein aggregation.

II. METHODS

A. Hybrid-resolution model PACE

Table I lists size and time scale of the simulations carried out for the present study and demonstrates the long-time scale needed for computational exploration of α-synuclein conformations. Such computations were achieved by employing a hybrid-resolution model, namely, PACE (www.ks.uiuc.edu/~whan/PACE/PACEnew/).^80,89,90 By representing proteins at a united-atom level of resolution, PACE provides a correct description of structural details essential for both secondary and tertiary structures of proteins, such as packing of side chains and geometry and directionality of hydrogen bonding interactions; by coarse-graining environmental components such as solvent and lipids that account for the majority of computation carried out in all-atom simulations, PACE accelerates greatly conventional simulations.^89,91,92

TABLE I.

Simulations performed in the present study. The aggregated simulation time is 186 μs.

Simulation	Description	Time	Atoms (K)
WT	Wild type α-synuclein equilibration, 10 simulations for 3 μs each, starting from 10 conformations.	3 μs × 10	12
A30P	A30P mutant equilibration same as in case of WT.	3 μs × 10	12
A53T	A53T mutant equilibration, same as in case of WT.	3 μs × 10	12
Hairpin	Wild type α-synuclein β-hairpin region (region 36-55) equilibration, 10 simulations for 3 μs each, starting from each from a separate conformation.	3 μs × 10	3.6
Hairpin with salt	Wild type α-synuclein β-hairpin region (region 36-55) equilibration in the presence of 0.15M NaCl salt, same as in case of hairpin.	3 μs × 10	3.6
HairpinG47V	G47V mutant β-hairpin region (region 36-55) equilibration, same as in case of hairpin.	3 μs × 10	3.6
InteractionWT	Wild type α-synuclein equilibration, starting from the center structure of the conformational ensemble containing the β-hairpins (region 38-53) in contact with C-terminus (1B) (region 118-130, VDPDNEAYEMPSE)	0.2 μs × 10	12
InteractionA30P	A30P mutant equilibration, same as in case of InteractionWT.	0.2 μs × 10	12
InteractionA53T	A53T mutant equilibration, same as in case of InteractionWT.	0.2 μs × 10	12

A key feature of PACE is that it was designed and optimized to ensure a balanced preference for different secondary structure types as well as disordered structures. The complete description of PACE and its optimization in this regard has been described elsewhere.⁸⁹ Briefly, to achieve the balance, the potential functions of PACE relevant to backbone dihedral angles ϕ and ψ and side chain dihedral angle χ was optimized, through iterative free energy simulations, by fitting to a library of statistical potentials derived according to PDB structures of proteins.⁹³ As the statistical analysis of the PDB structures was performed only on each residue in coil regions of proteins rather than in the regions containing any regular secondary structure that relies also on contribution from other residues, the potentials derived thus can reflect intrinsic conformational preference of the residue type studied. Moreover, the same statistical analysis reveals that the backbone conformational preference does not only vary for different residual types but does also couple tightly with rotameric states of side chains. To reproduce these conformational preferences, the PACE parameters for backbone and side chain potentials (ϕ, ψ, and χ) were optimized separately for each residual type.^89,91 More importantly, extra parameters were introduced to describe the non-bonded interactions between certain atoms of side chain and adjacent backbone. Such parameters permit PACE to reproduce the dependence of backbone conformational preference on side chain rotamers.^89,91

Having been optimized as described above, PACE has been demonstrated to be able to fold proteins with various structural motifs^89,90 and to describe structural features of disordered proteins, e.g., amyloid-β peptide, reproducing chemical shifts, ³J(H_NH_Cα)-coupling constants, and secondary structure contents measured by NMR and CD experiments.⁸⁰ Interestingly, our approach taken in developing PACE has also been adopted recently in further optimization of the AMBER99SB all-atom force field.⁹⁴ The resulting force field turned out to be significantly improved, being capable of reproducing ³J(H_NH_Cα)-coupling constants for a large number of two-residue peptides.⁹⁵

B. Model and simulation setup

To obtain initial random structures of α-synuclein, the protein in an all-atom model was equilibrated in a TIP3 water solvent⁹⁶ and adopting a CHARMM27 force field with CMAP correction.^97–99 The simulation started from a stretched conformation at high temperature (700 K) and was carried out for 3 ns. Ten structures were randomly chosen from the last 1 ns of the simulation as initial starting structures of α-synuclein simulations, referred to as WT simulations. We ensured that these initial structures were free from β-sheet structures (Fig. S1)¹⁰⁰ to avoid initial bias that could affect the interpretation of β-hairpin formation (Table I).

Each α-synuclein monomer was represented as a PACE united atom model and solvated in a box of water, the latter described at a CG level with MARTINI solvent,¹⁰¹ leading to a system of ∼12 000 particles. After 5000 steps of energy minimization, the resulting system was equilibrated for 500 ns before production simulations were carried out. For the simulations of A30P and A53T mutants (Table I, A30P and A53T), the corresponding mutations were introduced with the Mutator plugin of VMD.¹⁰² The mutant systems were prepared with the same procedure as employed for the WT simulations (Table I and Fig. S1).¹⁰⁰ To assess the stability of long-range contacts between C-terminus and β-hairpin region, we simulated the α-synuclein from the center structure with β-hairpin (Fig. 1(b)). For each WT α-synuclein and its A30P and A53T mutants, ten independent simulations were performed (Table I, InteractionWT, InteractionA30P and InteractionA53T), again with the same procedure as employed for the WT simulations (Table I).

Apart from the entire α-synuclein, the protein segment containing region 36-55 was isolated from α-synuclein and simulated alone to see whether the sequence does fold into β-hairpins by itself. Ten structures were randomly chosen from the last 1 ns of the simulations at 700 K as initial starting structures of further simulations, referred to as hairpin simulations (Table I). Each α-synuclein monomer was solvated in a box of MARTINI water¹⁰¹ leading to a system of ∼3600 particles, and simulated with the same procedure as employed for the WT simulations (Table I). To assess the effect of salt on β-hairpin formation, we have also simulated region 36-55 isolated from α-synuclein in physiological salt concentration (0.15M NaCl).^90,103 For the simulations of G47V mutant (Table I, HairpinG47V), the corresponding mutation was introduced, employing again the Mutator plugin of VMD.¹⁰² The mutant system was prepared with the same procedure as used for the hairpin simulations (Table I).

All simulations were conducted as NPT ensembles; temperature was maintained at 320 K through a Langevin thermostat with a damping coefficient γ = 0.2 ps⁻¹;¹⁰⁴ pressure was maintained at 1 atm with a Langevin-piston barostat with a damping time of 2 ps. Short-range non-bonded interactions were cut off smoothly between 0.9 and 1.2 nm; simulations were performed with an integration time step of 4 fs. All simulations employed the program NAMD 2.9¹⁰⁵ modified for PACE simulations.⁸⁰

C. Cluster analysis of α-synuclein conformational ensemble

To analyze intrinsically disordered proteins over a long-time scale, a cluster analysis^80,106 based on principle component analysis (PCA) was employed to examine protein conformations. In this analysis, a set of pairwise-distance parameters, namely, C_α-C_α distances between every 3 residues of α-synuclein, were employed to describe the conformations of the α-synuclein monomer. In addition, a distance cutoff of 20 Å was enforced for the monitoring of all C_α-C_α distances variation to ensure that the conformational space to be investigated is manageable such that the cluster analysis can generate meaningful results. The pairwise-distance parameters were then calculated from 3 × 10⁵ conformations selected every 0.1 ns from the 30 μs simulations and were accounted for in the PCA analysis. The most significant 100 principal components, which account for over 85% of conformational variance, are presented in Fig. S2.¹⁰⁰ Finally, the clustering algorithm described earlier⁸⁰ was employed to cluster the 3 × 10⁵ conformations into meta-states based on chosen principal components.

The center structure from the largest cluster of the WT α-synuclein β-hairpin region (region 38-53) was selected as a representative structure for WT α-synuclein. Representative structures of A30P and A53T mutant α-synuclein were obtained with the same procedure as employed in case of the WT simulations.

D. Description of folding kinetics

In order to examine the kinetics of β-hairpin formation in α-synuclein, we characterized the folding time of β-hairpins. These times were determined as the inverse of the folding rates k, which were estimated from the observed number of folding events n in trajectories. The folding rates were derived in two different ways depending on frequency of β-hairpin formation. In the case that formation of β-hairpin arises infrequently in the simulations of α-synuclein, namely, not more than once in any simulation, the β-hairpin formation events can be treated as a two-state Poisson process. The folding rate, k, of β-hairpins can thus be estimated by fitting the observed first passage time of folding to the expression¹⁰⁷

$${\displaystyle 〈n〉={\int }_0^{t}d{t}^{\prime }\hspace{0.17em}M\left(t^{\prime }\right)\hspace{0.17em}k\hspace{0.17em}exp[-M\left(t^{\prime }\right)\hspace{0.17em}k{t}^{\prime }],}$$ (1)

where t is the simulation time for each trajectory, M(t) is the number of simulations that reach time t determined from the simulations, k is the to be fitted folding rate and 〈n〉 is the average probability for each simulation to make a folding transition till time t, determined from the simulations. The equation basically connects the 〈n〉 from multiple uncoupled parallel simulations to the folding rate constant k by assuming that the folding transitions arise between two states and that the rate is both low and constant with time. One can write Eq. (1) as

$${\displaystyle 〈n〉=1-exp[-M\left(t\right)\hspace{0.17em}kt],}$$

$${\displaystyle k=-ln(1-〈n〉)/\left[M\left(t\right)\hspace{0.17em}t\right].}$$

An example for the use of this equation is M(t) = 10 and 〈n〉 = 1/10 = 0.1, i.e., one out of ten trajectories folded into a β-hairpin, t = 3 μs, which yield k = 0.003 512 μs⁻¹ and a folding time of 1/k = 1/0.003 512 μs = 284.74 μs.

In the case that folding into a β-hairpin occurs frequently, on average more than once in a folding simulation, the folding rate can be estimated by dividing the accumulated simulation time by the number of β-hairpin folding events. Standard errors are obtained via a standard bootstrapping procedure with population size of 5. A β-hairpin folding event is defined as a transition of the β-hairpin region (region 38-53) from an unfolded state (RMSD > 5 Å) to a folded state (RMSD < 3.25 Å) (see Figs. S4 and S6).¹⁰⁰ Root mean square deviation (RMSD) values were calculated with respect to the center structure of the largest clusters of WT α-synuclein or its A30P, A53T mutants. The center structures of WT α-synuclein and its A30P, A53T mutants are similar to each other, with a RMSD value of 2.6 Å between WT and A30P center structures and a RMSD value of 3.3 Å between WT and A53T center structures. Backbone atoms of the β-hairpin region (region 38-53) were selected as reference atoms for alignment and RMSD calculation. More details of the analysis method have been described earlier.⁸⁰

E. Analysis of structural properties of α-synuclein

Furthermore, to compare our structural ensemble with experimental results, we analyzed three experimentally well-characterized structural properties of α-synuclein monomers, namely, secondary structure content,^{6,9,20,37,60,66,108–113} chemical shifts of α-carbons (C_α), amide nitrogens (N), hydrogen atoms attached to α-carbons (H) and carbonyl carbons (C) from NMR data,¹¹⁴ and ³J(H_NH_Cα)-coupling constants between protons attached to backbone nitrogen and C_α atoms measured in NMR spectroscopy.¹¹⁵ Chemical shifts were calculated with SHIFTX2.¹¹⁶ All analysis and visualization were performed using VMD.¹⁰²

III. RESULTS

In the present study, we investigate the possibility of α-synuclein forming β-hairpin conformations and the possible role of β-hairpin formation in α-synuclein aggregation. We first seek β-hairpin conformations of α-synuclein monomers from a conformational ensemble sampled through tens of microseconds of unbiased simulations. The ensemble obtained is validated through comparison with experimental measurements. We then repeat simulations for two disease-related, aggregation-prone mutants (A30P and A53T) to examine whether the two mutations affect the formation of β-hairpins. Finally, the detailed mechanisms of the folding of β-hairpins are characterized, based on which an aggregation-inhibiting mutation is proposed.

A. Extensively sampled conformational ensemble of α-synuclein is consistent with experimental measurements

To characterize the conformational ensemble of WT α-synuclein monomers, we performed ten 3-μs simulations to sample the conformations of α-synuclein monomers arising in aqueous environment (Table I, WT). The resulting conformational ensemble reproduces several key structural features of α-synuclein monomers reported in prior experiments. The radius of gyration of α-synuclein monomers is 3.14 ± 0.70 nm, within the range of experimental values of 2.7 nm–4.0 nm.^{12,42,117–120} The overall α-helix, turn and β-sheet contents, as shown in Fig. 2, are 27%, 40%, and 2%, respectively. The corresponding experimental values, though varying depending on measurement conditions and techniques employed, are within 10%-48%, 17%-41%, and 0%-20%, respectively.^{6,9,20,37,60,66,108–113} Hence, the simulation results are qualitatively consistent with experimental measurements.

FIG. 2.

Residual secondary structure content in WT α-synuclein and its A30P and A53T mutants. Fractions of α-helix, β-sheet, and turn are shown in the top, middle, and bottom panels, respectively. The traces for WT α-synuclein and its A30P and A53T mutants are colored red, green, and purple, respectively. The five regions involved in the core of α-synuclein fibrils, as suggested earlier,⁷ are shaded in grey. The x-axis giving residue numbers is also shown as a chain of blue, gold, pink, and red bars as defined in Fig. 1.

The secondary structure content determined from the simulations (Fig. 2) is not distributed uniformly along the α-synuclein sequence. The residual α-helical content decreases towards the C-terminus; the turn and β-sheet content follow the opposite trend. The secondary structure distributions agree with biochemical and structural studies which showed that the N-terminal region tends to form helices while NAC and C-terminal region are unstructured.^6–10 Although the entire α-synuclein has a small chance to form β-sheet structures (1.11%), region 38-53 exhibits higher probability (6%-8%) of forming β-sheet, overlapping well with the regions reported to exhibit high β-sheet propensities as reported in prior studies.^{7,55,65,67,121}

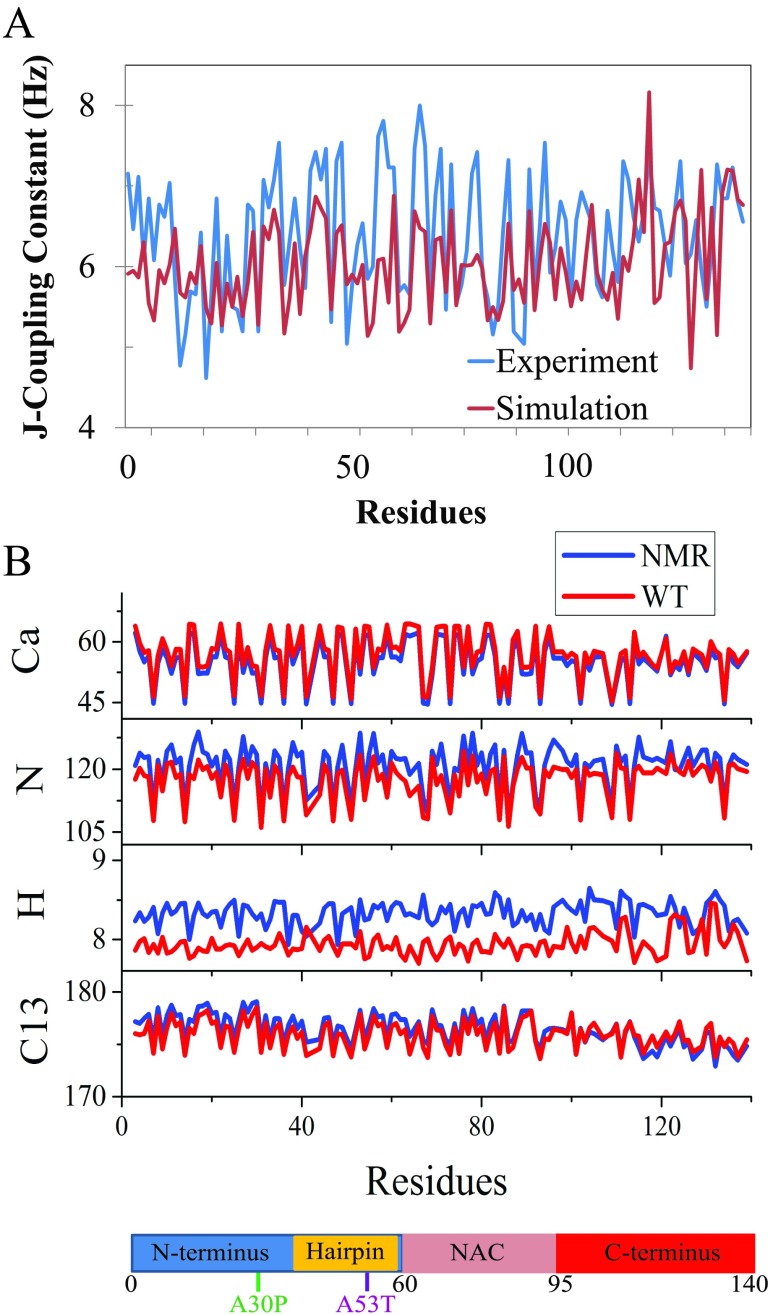
Apart from the overall secondary structure content, we examined also whether the generated conformational ensemble of α-synuclein reproduces the experimental structural features at the residue level (Fig. 3). In particular, we back-calculated ³J(H_NH_Cα) constants that are related to backbone dihedral angles ϕ of individual amino acids (see Sec. II) and compared the calculated constants with those reported in NMR experiments. The correlation of ³J(H_NH_Cα) data between simulations and experiments was quantified by a Pearson correlation coefficient (PCC).¹²² The PCC was calculated to be 0.6. Although we are unaware of any prior computational study that made an identical comparison of ³J(H_NH_Cα) constants for α-synuclein, a similar comparison made in earlier computational studies of Aβ^123–125 did suggest that a PCC of 0.6 indicates a satisfactory agreement between simulations and experimental measurements.

FIG. 3.

(a) ³J(H_NH_Cα)-coupling constants of WT α-synuclein from experiment (blue)¹¹⁵ and simulation (red). (b) Chemical shifts of α-carbons (C_α), amide nitrogens (N), hydrogen atoms attached to α-carbons (H), and carbonyl carbons (C) of WT α-synuclein from NMR (blue)¹¹⁴ and simulation (red). The x-axis giving residue numbers is also shown as a chain of blue, gold, pink, and red bars as defined in Fig. 1.

To further validate our α-synuclein ensembles, we computed NMR chemical shifts for α-carbons (C_α), amide nitrogens (N), hydrogen atoms attached to α-carbons (H), and carbonyl carbons (C). Chemical shifts obtained from simulation ensembles reproduce values obtained from NMR¹¹⁴ (Fig. 3), with an average difference of 3.1%, 2.8%, 4.7%, and 0.4% and Pearson’s correlation coefficients of 0.99, 0.95, 0.45, and 0.88 for C_α, N, H, and C, respectively. We noticed that H chemical shifts were consistently underestimated (Fig. 3). The underestimation may be due to a systematic error in experimental data or classical force fields.¹²⁶ All classical force fields underestimate H chemical shifts, possibly due to lack of polarization on alpha hydrogens.¹²⁶

We conclude from our analysis of ³J(H_NH_Cα) and chemical shift data that the conformational ensemble sampled in the present study captures realistically the major structural features of individual residues of α-synuclein monomers.

We next investigate the heterogeneity of α-synuclein conformations through conformational cluster analysis. Specifically, the sampled conformations were projected onto principal component (PC) space and clustered employing PCs as a measure of similarity between conformations as described in Sec. II. Fig. S3¹⁰⁰ shows the representative structures of clusters with the highest probabilities that altogether account for 55% of sampled conformations. The remaining 45% of the α-synuclein conformational ensemble is described by more than 400 clusters. The clusters shown in Fig. S3¹⁰⁰ exhibit distinct structural features. For example, cluster 1 is mainly composed of extended conformations showing little tertiary structure, while clusters 2-4 exhibit local tertiary contacts in distinct regions of α-synuclein. Interestingly, the tertiary contact observed in cluster 2 is involved in β-hairpin conformations formed in region 38-53. The importance of the β-hairpins will be addressed in Secs. III B–III E.

Close examination of structures in the largest cluster, cluster 1, revealed that its radius of gyration is 4.27 ± 0.59 nm, 38% larger than the average radius of gyration 3.14 ± 0.70 nm over the entire ensemble and consistent with the extended structural features of the cluster (Fig. S5).¹⁰⁰ As for secondary structures, the α-helical content of cluster 1 is higher than that of WT α-synuclein in water while the β-sheet content of cluster 1 shows the opposite trend, indicating the helical conformations are enriched in cluster 1.

B. α-synuclein and its mutants form β-hairpin in region 38-53

Having confirmed that the conformational ensemble generated in the α-synuclein simulations is consistent with experimental data, we checked for β-hairpin conformations in this conformational ensemble. Our cluster analysis revealed that cluster 2 exhibits β-hairpin conformations spanning region 38-53, indicating that β-hairpins indeed arise in the α-synuclein conformational ensemble. To further examine the statistical significance of the formation of β-hairpin conformations, the RMSD to the β-hairpin conformations were evaluated over all trajectories of the WT simulations, using the β-hairpin observed in cluster 2 as reference (Fig. S4).¹⁰⁰ The analysis revealed three β-hairpin folding events, each arising in a different trajectory, suggesting that the observations of the β-hairpins are statistically robust. In addition, by counting all frames involving the β-hairpin conformations, it turned out that ∼8% of the frames contain such β-hairpin conformations, more than the population of cluster 2. Thus, β-hairpin conformations arise also in other conformational clusters, indicating that the β-hairpins formed in region 38-53 are not specific to any α-synuclein conformation. In one of the 10 WT simulations (simulation 7), β-hairpin formed starting from the random coil conformation in the pre-equilibration stage and unfolded at 2.1 μs. The long-lasting folding-unfolding event might be attributed to the interaction of the C-terminus with the β-hairpin region, which also caused an elevation of β-sheet structure in the C-terminal region (Fig. 2). The importance of this interaction on folding events in the β-hairpin region is discussed below.

To examine structural elements essential for a β-hairpin formed in region 38-53, all sampled conformations with the local β-hairpin conformations were grouped together. A center structure of the group was chosen such that the major part of the β-hairpin conformations in the group falls within a RMSD distance of 6 Å to the center structure (Fig. 1(b)). Visual inspection on the center structure revealed that the β-hairpins exhibit a well-defined pattern of hydrogen bonding (HB) interactions involving mainly uncharged residues across two β-strands, β1 (L-38YVGSKT-44) and β2 (V-47GHVVG-53).

To examine whether mutations affect the formations of the β-hairpins, we performed simulations (Table I, A30P and A53T) of two familial mutants of α-synuclein, namely, A30P and A53T. The RMSD to the same β-hairpin structure as discussed above was calculated for the mutant simulations, showing that the β-hairpins indeed arise in the A30P and A53T mutants for 8 and 9 times, respectively. Hence, the β-hairpins formed in region 38-53 seem to be a general structural feature for both α-synuclein and its mutants.

C. β-hairpin folds faster when isolated from α-synuclein or upon A30P or A53T mutation

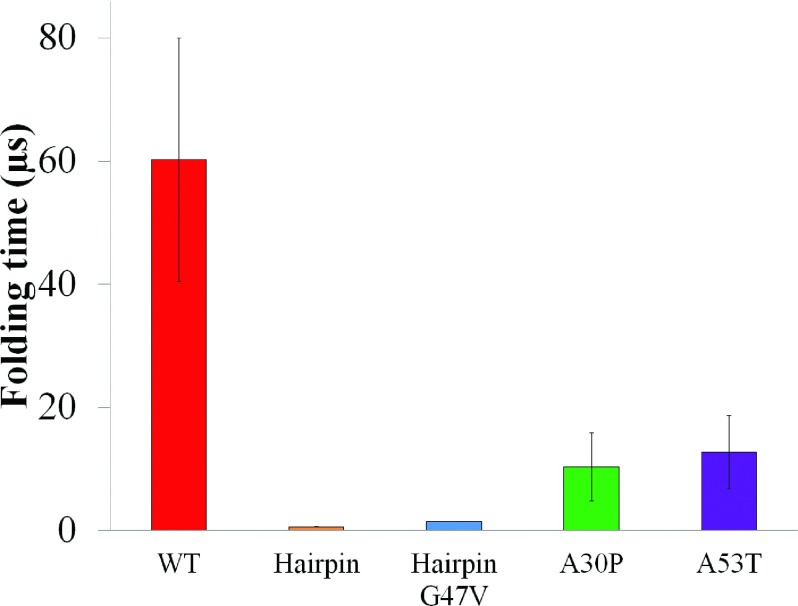
As the β-hairpins form only in a small segment (16 a.a.) of a much longer (140 a.a.) peptide, the question arises whether the formation of the β-hairpin is due to an intrinsic propensity of the segment or if it requires the involvement of the remainder of the peptide. To address this question, we isolated the β-hairpin region (region 36-55) from α-synuclein and performed ten folding simulations of this region starting from unfolded structures (Table I, hairpin). During these simulations, 50 folding- and unfolding-events occurred. Since folding into a β-hairpin occurs on average more than once in an independent folding simulation in isolated β-hairpin region, the folding time was estimated by dividing the accumulated simulation time by the number of β-hairpin folding events. The analysis of the simulations for the isolated β-hairpin region yields a β-hairpin folding time of 0.60 ± 0.03 μs, much shorter than the times needed for the same segment to achieve β-hairpin structure in WT full-length α-synuclein (60.23 ± 19.82 μs) (Fig. 4). Taken together, the analysis suggests that formation of β-hairpin is an intrinsic property of region 38-53 that is determined by the local sequence and is slowed down significantly in the context of full-length α-synuclein.

FIG. 4.

Folding times of β-hairpins in region 38-53. The β-hairpin folding for the isolated β-hairpin region or for the A30P and A53T mutants of full-length α-synuclein is faster than that of WT full-length α-synuclein. The time (in μs) needed to achieve a β-hairpin structure in WT full length α-synuclein (Table I, WT), isolated β-hairpin region (hairpin), isolated β-hairpin region with G47V mutation (HairpinG47V), A30P mutant (A30P), and A53T mutant (A53T) of full-length α-synuclein is shown in red, gold, blue, green and purple, respectively. Standard errors are shown as vertical error bars. In the analysis, a folding event is described as a two-state Poisson process arising during independent folding simulations. Formation of β-hairpin arises infrequently in the simulations of α-synuclein, usually not more than once in any simulation. In such case, the β-hairpin formation events can be treated as a two-state Poisson process. The folding times of β-hairpins can thus be estimated by fitting the observed first passage time of folding to Eq. (1) ¹⁰⁷ (see Sec. II). In case that folding into a β-hairpin occurs on average more than once in a folding simulation, the folding time was estimated by dividing the accumulated simulation time by the number of times the β-hairpin folds. The folding events were identified according to change of the RMSD with respect to the center structure of the β-hairpin ensemble identified for WT α-synuclein and its A30P, A53T mutants, respectively (Fig. S4).¹⁰⁰ Backbone atoms of the β-hairpin region (region 38-53) were selected as reference atoms for alignment and RMSD calculation. A β-hairpin folding event starts with a RMSD value above 5 Å and ends when the RMSD value falls below 3.25 Å (Figs. S4 and S6).¹⁰⁰ The folding time of the isolated β-hairpin region is 0.60 ± 0.03 μs, much shorter than the times needed for the same segment to achieve β-hairpin structure in WT full-length α-synuclein (60.23 ± 19.82 μs). The G47V mutation increased the folding time of the isolated β-hairpin region 2.4-fold, namely, to 1.43 ± 0.05 μs. Two mutations of full-length α-synuclein, A30P and A53T, decreased the folding times of WT full-length β-hairpin 5.83- and 4.75-fold to 10.32 ± 5.56 μs and 12.67 ± 5.98 μs.

We extended the approach described to estimate the β-hairpin folding rates for the A30P and A53T mutants (Table I, A30P and A53T). These two mutants are known to accelerate α-synuclein aggregation, having a close link to early onset of Parkinson’s disease.^4,81–83 If the β-hairpins are indeed important for aggregation, their formation should be facilitated by the mutations. Indeed, the β-hairpin folding times for the A30P and A53T mutants of full-length α-synuclein were found to be 10.32 ± 5.56 μs and 12.67 ± 5.98 μs, respectively, a 5- to a 7-fold increase in the folding rate as compared to that of WT full-length α-synuclein (Fig. 4).

D. C-terminus interacts with β-hairpin in α-synuclein

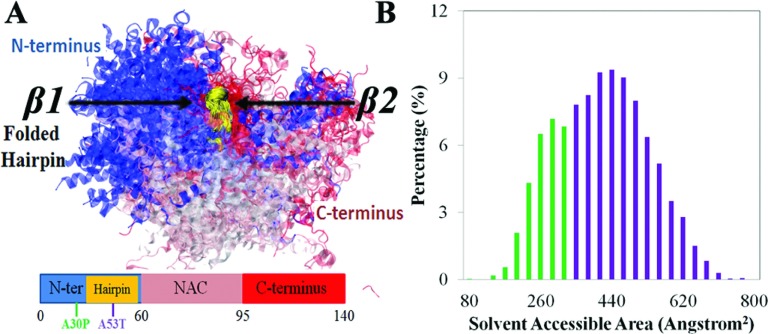
An analysis of the folding in the β-hairpin region (region 38-53) reveals that the other regions of α-synuclein can affect β-hairpin formation by interacting directly with the β-hairpin region. To probe such interaction, we selected all β-hairpin-containing conformations of α-synuclein and superimposed them in the β-hairpin region (region 38-53). The superposition of the structures, as shown in Fig. 5, reveals that the N-terminus is more localized around the β-hairpin region than is the C-terminus, owing to the shorter distance in sequence between N-terminus and β-hairpins in region 38-53. Yet, one can recognize that there are a group of conformations in which the C-terminus is more likely to cluster around β2 (region 47-53) of the β-hairpin region, indicating that there arises a strong interaction between C-terminus and forming β-hairpins. The interactions involving the C-terminus were further confirmed by a contact map of the α-synuclein conformational ensemble (Fig. S7)¹⁰⁰ which clearly shows long-range contacts between region 38-53 (β-hairpin) and region 118-130 (C-terminus). Notably, these contacts are the only noticeable long-range contacts seen in our α-synuclein simulations.

FIG. 5.

β-hairpin interacting with α-synuclein C-terminus. (a) Overlay of structures of simulated α-synuclein containing β-hairpin formed in region 38-53. The structures are aligned at the β-hairpin region shown in gold (region 38-53). N-terminus, β-hairpin region, NAC region, and C-terminus are colored blue, gold, pink, and red, respectively. Shown beneath the structure is a schematic depiction of the α-synuclein segments as defined in Fig. 1. (b) Distribution of solvent-accessible surface area (SASA) of β-hairpins in region 38-53. The distribution is colored green and purple to distinguish buried and exposed β-hairpin conformations, respectively.

To assess further the stability of the long-range contacts, we performed a series of simulations (Table I, InteractionWT, InteractionA30P and InteractionA53T) of α-synuclein as well as of its A30P and A53T mutants starting from the center structure of the conformational ensemble containing the β-hairpins (region 38-53) in contact with the C-terminus (region 118-130, VDPDNEAYEMPSE) (Fig. 1(b)). The final structures that resulted from these simulations are shown in Fig. S8.¹⁰⁰ The interactions between β-hairpin (region 38-53) and C-terminus (region 118-130) are maintained in most cases (WT: 10/10, A30P: 9/10, A53T: 9/10), indicating that the interactions formed between C-terminus and β-hairpin region are not sensitive to the mutations introduced, which is consistent with experimental findings.^39,49

The strong interactions between β-hairpin and C-terminal region may reduce the accessibility of the β-hairpin region for other parts of α-synuclein. To test this possibility, we calculated the solvent-accessible surface area (SASA) of region 38-53 for the β-hairpin-containing ensemble. The SASA distribution of the β-hairpin region, as shown in Fig. 5(c), displays two peaks, one being centered at 280 Ų (green) and the other at 460 Ų (purple). The bimodal distribution suggests that there are at least two types of β-hairpin conformations, each exhibiting different exposure of surfaces. Inspection of the structures containing the less exposed β-hairpins revealed indeed significant interactions formed between C-terminus and region 38-53. Therefore, the C-terminus of α-synuclein appears to reduce the accessibility of formed β-hairpin and, thereby, to prevent an interaction with other α-synucleins during the aggregation processes.

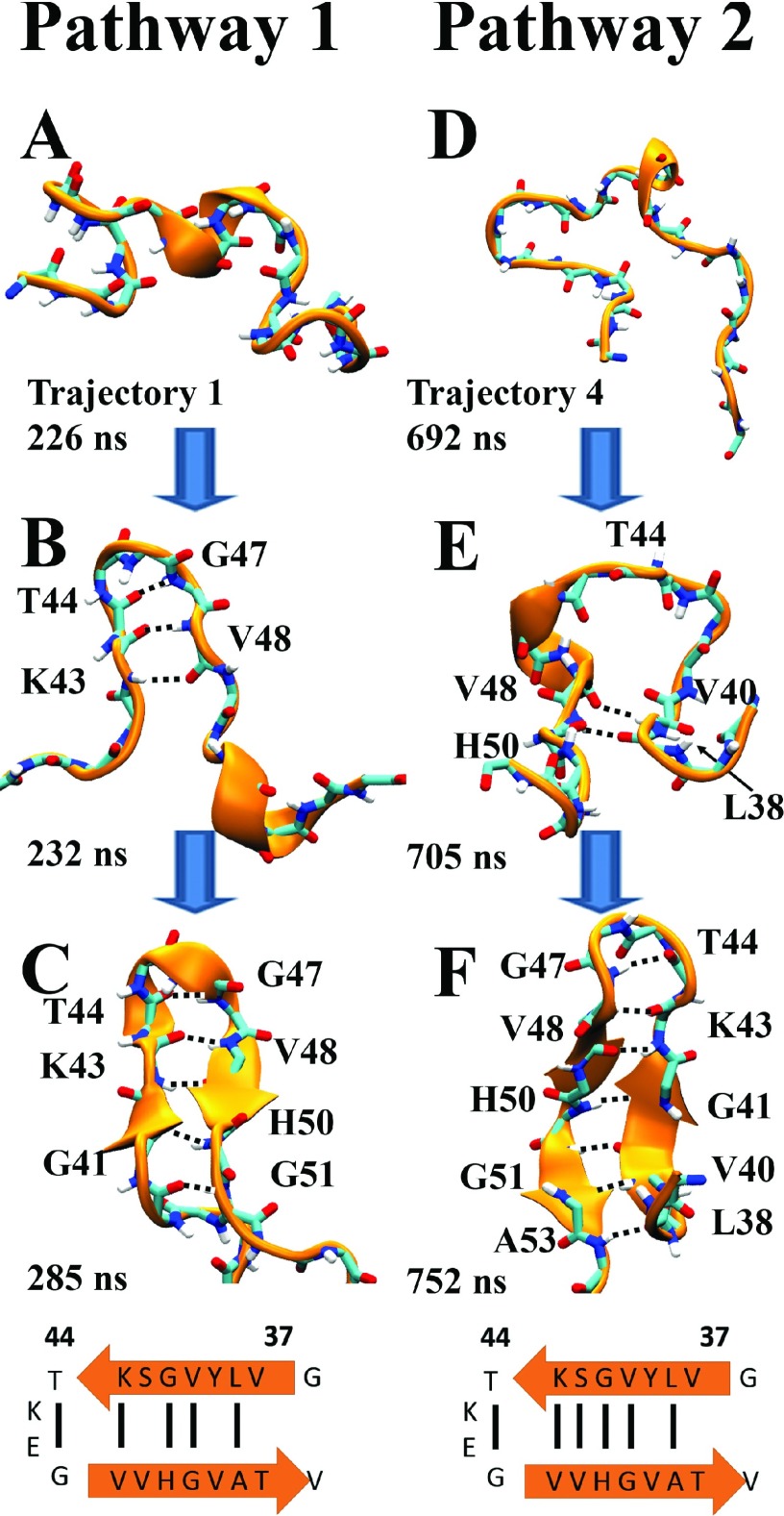
E. α-synuclein achieves β-hairpin conformations via two major pathways

One may wonder whether the formation of β-hairpin conformations in α-synuclein and its mutants follow specific folding pathways. To address this question, we compiled the transition trajectories of β-hairpin folding from all simulations of the isolated β-hairpin region, noting that the large number of observed folding transitions seen in these simulations provides a robust description of the folding process. The analysis of the transition trajectories revealed that there are two major types of pathways through which β-hairpin conformations are achieved. The two pathways are depicted in Fig. 6. In the major pathway (pathway 1), the folding into a β-hairpin initiates near its turn region, often involving HB interactions between backbones of residue pair V43-V48 or T44-G47. Then from the turn region, the HB pattern propagates toward the termini of the β-hairpins, L38 and A53. In a less frequented pathway (pathway 2), HB interactions arise in regions away from the turn region, usually involving backbones of region 38-41 (LYVG) from β1 and region 48-53 (VVHGVA) from β2, at the beginning of the folding processes. The HB interactions propagate then towards the turn region and eventually throughout the β-hairpin structure.

FIG. 6.

Two pathways of β-hairpin formation. Pathway 1 (trajectory 1) follows a fast “zipper out” route, pathway 2 (trajectory 4) follows a “zipper in” route as discussed in the text. Shown are the backbone atoms of the β-hairpin region (region 38-53) in cartoon (gold) and licorice representations (carbon atoms in light blue, nitrogen in dark blue, oxygen in red, and hydrogen in white). Hydrogen bonds are highlighted through black dashed lines between carbonyl oxygen and amine nitrogen atoms. Hydrogen bonded residues are labeled. A cartoon representation of the β-hairpin is shown at the bottom of each pathway to illustrate the hydrogen-bonding pattern.

We next examined in which pathways the β-hairpin conformations in α-synuclein and its mutants arise (Table II). It turned out that for WT α-synuclein, β-hairpins occur only via pathway 1. For the two α-synuclein mutants, β-hairpin folding involves both pathways while pathway 1 is still more favorable.

TABLE II.

Frequencies of two β-hairpin formation pathways. The total numbers of folding events are shown as denominators. The numbers of folding events from pathway 1 and 2 are shown as numerators. The system names are defined as in Table I.

System	Pathway 1	Pathway 2
WT	3/3	0/3
A30P	6/8	2/8
A53T	5/9	4/9
Hairpin	32/50	18/50
HairpinG47V	10/21	11/21

Since pathway 1 is the major pathway of β-hairpin formation, we focused on the turn region that initiates the folding process. Inspection of the observed β-hairpin conformations showed that the turn region (region 43-47) adopts mainly a 4:6 β-turn structure, a turn motif commonly seen in β-hairpins.¹²⁷ In order to form this turn motif, the residue at a key position in the turn region, which corresponds to G47 in α-synuclein, must adopt a left-hand-α-helical (L_α) conformation. It has been shown that a mutation at this position can affect the kinetics of β-hairpin formation by changing the L_α-propensity of the residue at this position and that glycine is one of the amino acids exhibiting the highest L_α-propensity and, thereby, the best fit into this position.^127,128 Thus, to test the influence of the turn region on the β-hairpin formation in α-synuclein, we introduced at residue 47 a valine mutation that is known to lower L_α-propensity.⁹³ Our simulations of the isolated β-hairpin region with the G47V mutation showed indeed that the folding rate becomes reduced by about 2.4-fold (Fig. 4). We examined further the impact of the G47V mutation on the conformational features of residue 47 (Figs. S9 and S10).¹⁰⁰ The analysis revealed that valine at residue 47 exhibits a much smaller chance to adopt L_α-conformations than does glycine at the same position (∼1% vs ∼26%).

IV. DISCUSSION

In the present study, we sought to describe in atomic detail monomeric structures of α-synuclein relevant for fibril formation and Parkinson’s disease. To this end, we performed altogether over 180 μs in aggregated time of unbiased molecular dynamics simulations of α-synuclein monomers to characterize conformational ensembles of α-synuclein and its aggregation-prone mutants, namely, A30P and A53T.^4,81–83 To overcome the difficulties in sampling through MD simulations the large conformational space that α-synuclein can access, we employed a hybrid-resolution model^80,89,90 that can accelerate such simulations significantly. The long-time simulations generated ensembles of heterogeneous structure that agree well with experimental observables regarding overall conformational features, secondary structure content (Fig. 2) as well as residual-level structural features (Fig. 3). The ensembles characterized allow us to identify key β-hairpin conformational states of the α-synuclein monomer and to reveal the role of β-hairpin states in α-synuclein aggregation processes and fibril formation.

The ensembles generated from long-time simulations agree well with multiple experimental observables regarding overall conformational features, secondary structure content (Fig. 2) as well as residual-level structural features (Fig. 3). The radius of gyration of the ensembles is 3.14 ± 0.70 nm, much smaller than those estimated from a random coil model (5.2 nm),⁴² agreeing with previous experimental results that α-synuclein monomer exists as a much more compact structure than random coils.^42,62 The simulation ensembles generated also show long-range contacts between region 38-53 (β-hairpin) and region 118-130 (C-terminus) (Fig. S7).¹⁰⁰ Long-range contacts have been observed in several studies.^36,44,50,55 NMR and EPR methods characterize long-range contacts between C-terminus and N-terminus/NAC regions of α-synuclein, especially between region 40-80 and region 110-130.^36,44,50 With Monte Carlo simulations guided by restraints due to EPR data, long-range contacts were predicted in an earlier study⁵⁵ between multiple segments of region 38-100 and region 104-130, however such model lacks secondary structural information. In the present study, the ensembles generated from long-time simulations identified structure for long-range contacts between region 38-53 (β-hairpin) and region 118-130 (C-terminus) (Fig. 1(b)) and characterized β-hairpin structure involved in the long-range contact.

A general question regarding protein aggregation as observed for α-synuclein is whether particular monomeric conformations of a protein are essential for aggregation. Both prior experimental and computational studies, in seeking such conformations for amyloid-β and amylin peptides, revealed β-hairpin conformations of monomers resembling those of the aggregated forms of the peptides.^{7,38,55,65,67,121,129–131} Although for α-synuclein a similar β-hairpin-like conformation has not been fully characterized, a recent experimental study demonstrated that α-synuclein monomers can be recognized by a peptide targeting specifically β-hairpins, indicating the existence of β-hairpin in monomer structures of α-synuclein.⁶⁷ In the present study, our simulations reveal that conformations containing β-hairpin arise indeed for both α-synuclein and its A30P and A53T mutants (Table II). The observed β-hairpin conformations usually involve two anti-parallel β-strands, namely, β1 (region 38-44) and β2 (region 47-53), that are connected by a turn located at 44-47 (Fig. 1(b)). Our results are consistent with previous computational and bioinformatics studies based on secondary-structure predictions and aggregation index^{7,38,55,65,67,121,129–131} that all showed a high tendency for regions 38-40 and 50-53 of α-synuclein to assume β-strand structures. The results of our simulations agree also closely with β-hairpin structure observed from NMR by peptide sequestration⁶⁷ in structural and hydrogen-bonding pattern (Fig. 6). Indeed, the β-hairpin-forming region identified (region 38-53) are formed by two β-sheet (regions 38-43 and 48-53) connected by a β-turn (region 44-47), the same structure identified in the NMR study.⁶⁷ Three hydrogen bonds in the NMR β-hairpin structure (L38-A53, V40-G51, and S42-V49)⁶⁷ are also observed in our simulations. Interestingly, the β-hairpin-forming region identified (region 38-53) overlaps well with the region (region 37-59) found to form the first strand-loop-strand motif in the core structures of α-synuclein fibrils.⁷ Thus, it is likely that the fibrillar structures may have already been achieved, at least partly, in α-synuclein monomers prior to aggregation (Table II).

Previous experimental and theoretical studies have proposed two possible mechanisms of β-hairpin folding, namely, a “zipper-out” mechanism, by which the folding process starts at the turn of a β-hairpin and propagates toward two termini, and a “zipper-in” mechanism, by which the folding proceeds in the opposite direction.^132–136 In the present study, although both mechanisms were observed (Fig. 6), the majority of β-hairpin folding events followed the “zipper-out” mechanism through which the formation of a critical β-turn in region 44-47 triggers the formation of the entire β-hairpin.

Previous kinetic and mutagenesis studies have proved that the kinetics of β-hairpin folding via the “zipper-out” mechanism is determined largely by formation of the central turn of a β-hairpin.^{17,132–135,137–141} In the present study, our MD simulations reveal that formation of the β-hairpins in α-synuclein can be significantly slowed down by a single mutation, G47V, introduced to eliminate an L_α-conformation at residue 47 that is otherwise needed for formation of a special type of β-turn structure^{132–135,137,142–145} in region 44-47. If the formation of local β-hairpin is indeed essential for α-synuclein aggregation, our finding suggests that the G47V mutation slows down the aggregation processes (Fig. 4). We are unaware of any prior study investigating the effects of a mutation in residue 47 on α-synuclein aggregation. Interestingly, a familial E46K mutant of α-synuclein exhibits increased fibril formation and early-onset Parkinson’s disease,^26,146 indicating the importance of the β-turn region (region 44-47) in aggregation. The aggregation-inhibiting G47V mutation proposed here awaits further experimental tests which could potentially reveal new insights into the mechanism of α-synuclein aggregation.

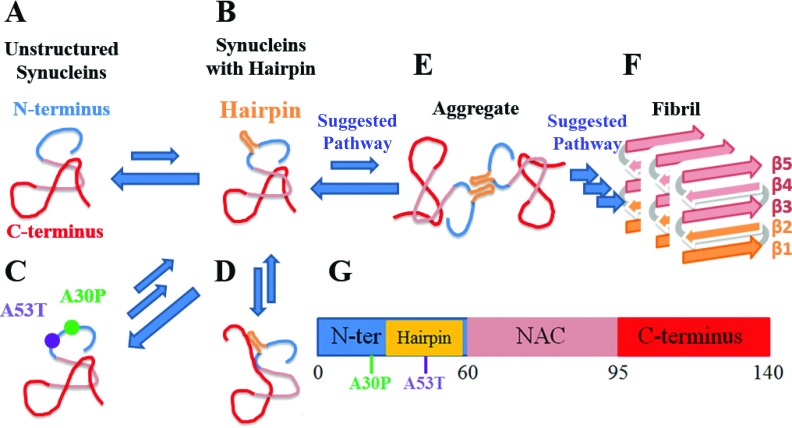
The present study suggests that formation of a β-hairpin precedes α-synuclein aggregation by providing an initiation site for oligomerization (Fig. 7). Our simulations support the key role of β-hairpins in seeding α-synuclein aggregation in three respects. First, the simulations revealed that β-hairpins in region 38-53 are an intrinsic structural feature of both WT α-synuclein and its familial mutants in Parkinson’s disease. The β-hairpin region corresponds to the first two of five β-strand regions constituting the core structures of α-synuclein fibrils⁷ (Figs. 2 and 4 and Table II). In addition, A30P and A53T mutations, which enhance α-synuclein aggregation, accelerate also the formation of β-hairpins (Fig. 4 and Table II). Furthermore, our simulations revealed that the C-terminus of α-synuclein tends to interact with a β-hairpin in region 38-53 and, thus, reduces its accessibility for inter-molecular interactions (Figs. 1(b) and 5). If the β-hairpins are needed for the aggregation process, our simulation results indicate that the C-terminus protects α-synuclein against aggregation, which is indeed consistent with experiments showing that removal of the C-terminus significantly accelerates α-synuclein aggregation.^{34,39,44–49}

FIG. 7.

Role of β-hairpin in possible α-synuclein aggregation. N-terminus, β-hairpin region, NAC region, and C-terminus are shown as blue, gold, pink, and red tubes, respectively. (a)-(f) denote various stages of the aggregation process. (a) α-synuclein monomers assume diverse disordered structures in rapid exchange. (b) Occasionally, region 38-53 of α-synuclein monomers assumes a β-hairpin conformation. (c) The folding to the β-hairpin is accelerated by two aggregation-prone mutations, namely, A30P and A53T. (d) The C-terminus of α-synuclein can interact with the β-hairpin formed and protect α-synuclein against interaction with other α-synuclein molecules. (e) Unprotected (by the C-terminus) β-hairpins participate in intermolecular interactions, particularly with the β-hairpins of other α-synucleins, likely via hydrogen bonds and hydrophobic contacts. (f) Possible α-synuclein aggregate resulting from β-hairpin interactions, the β-hairpins acting as possible nuclei that initiate the formation of a fibril with extended β-sheet structure (β1-β5); fibril formation is irreversible.⁷ (g) Schematic depiction of α-synuclein structure as defined in Fig. 1.

Salt was not modeled in most of the simulations performed in this study. To assess the effect of salt on β-hairpin formation, we have also simulated region 36-55 isolated from α-synuclein at physiological salt concentration (0.15M NaCl).^90,103 We isolated the β-hairpin region (region 38-53) of WT α-synuclein and simulated the segment in the absence and presence of salt. In our simulation, the radius of gyration of the α-synuclein monomer β-hairpin region has been found not to be affected (0.86 ± 0.10 nm without salt vs. 0.85 ± 0.10 nm with 0.15M NaCl), indicating that the compactness of the α-synuclein β-hairpin region is not affected by physiological salt concentration. Both the secondary structural properties (Fig. S11)¹⁰⁰ and the β-hairpin formation rate (Fig. S12)¹⁰⁰ remain largely unchanged (0.60 ± 0.03 μs without salt vs. 0.53 ± 0.10 μs with 0.15M NaCl), indicating salt does not affect the observation of β-hairpin formation. Previous experimental studies suggest that α-synuclein secondary structures are affected by salt.^37,147 It is likely that this salt effect on secondary structure is outside the β-hairpin region and, therefore, imperceptible for our simulation of the folding of the β-hairpin region. To fully investigate, a salt effect requires long time simulations of full-length α-synuclein in the presence of salt, which are presently too demanding computationally. In addition, the MARTINI solvent model¹⁰¹ employed here does not account explicitly for the dielectric property of water and, thus, may not describe properly the outcome of a significant dielectric change in the environment due to salt. Altogether, caution is needed when interpreting the results from the present study in regard to salt effects.

For proteins of the size of α-synuclein, conformational changes occur over a broad range of time scales. The question arises whether 3-μs simulations are long enough to achieve convergence for conformational changes and β-hairpin formation that are of interest in the present study. We examined secondary structure change of α-synuclein by monitoring percentage of secondary structure contents over WT α-synuclein simulations using VMD¹⁰² (Figs. S13, S14, and S15).¹⁰⁰ Neither β-hairpin nor β-sheet conformation is present in starting structures. Secondary structure contents reached equilibrium values within 1 μs of simulation. In addition, we examined large scale conformational changes of α-synuclein through its end-to-end distance. The auto-correlation time of end-to-end distances of the WT was calculated to be 24.9 ± 9.1 ns, suggesting that within the 3-μs simulations, two ends of α-synuclein should have come close to and separated from each other multiple times (Fig. S13).¹⁰⁰

The present study suggests that formation of a β-hairpin precedes α-synuclein aggregation by providing an initiation site for oligomerization. Our simulations support the key role of β-hairpins in seeding α-synuclein aggregation in three respects. First, the simulations revealed that β-hairpins in region 38-53 are an intrinsic structural feature of both WT α-synuclein and its familial mutants in Parkinson’s disease. The β-hairpin region corresponds to the first two of five β-strand regions constituting the core structures of α-synuclein fibrils⁷ (Figs. 1 and 4 and Table II). In addition, A30P and A53T mutations, which enhance α-synuclein aggregation, accelerate also the formation of β-hairpins (Fig. 4 and Table II). Furthermore, our simulations revealed that the C-terminus of α-synuclein tends to interact with a β-hairpin in region 38-53 and, thus, reduces its accessibility for inter-molecular interactions (Figs. 1(b) and 5). If the β-hairpins are needed for the aggregation process, our simulation results indicate that the C-terminus protects α-synuclein against aggregation, which is indeed consistent with experiments showing that removal of the C-terminus significantly accelerates α-synuclein aggregation.^{34,39,44–49}

Taken together, a picture emerges how formation of β-hairpins is possibly involved in α-synuclein aggregation. Fig. 7 shows the process of possible fibril formation assisted by β-hairpins. At physiological conditions, α-synuclein monomers remain as an ensemble of diverse disordered structures in rapid exchange with each other (Fig. 7(a)). Occasionally region 38-53 of α-synuclein monomers assumes a β-hairpin conformation (Fig. 7(b)). The kinetics of the formation of the β-hairpins is accelerated by certain aggregation-prone mutations such as A30P and A53T (Fig. 7(c)). Once the β-hairpins arise, the C-terminus of α-synuclein may interact with the β-hairpins formed and, thereby, prevent a respective α-synuclein monomer from interacting with other α-synuclein molecules (Fig. 7(d)). Without such prevention, the β-hairpins formed can participate in inter-molecular interactions, particularly with the same β-hairpin region of other α-synuclein molecules, likely via hydrogen bonding and hydrophobic contacts (Fig. 7(e)). The pre-complexes resulting from the β-hairpin interactions can serve as possible nuclei to complete the complexes and, thereby, yield a possible fibril with extended β-sheet structures (β1-β5),⁷ the latter rendering the fibril formation irreversible (Fig. 7(f)).

Protein misfolding contributes to degenerative diseases like Parkinson, focused on here, but also Alzheimer’s or diabetes, diseases that emerge very frequently today as human life expectancy has increased. Development of treatments hinges on an understanding of the atomic level relationship between protein misfolding and pathological protein aggregation that likely only a combination of observation and simulation can provide. The challenge for simulations is the long time scale required to reach meaningful results. The best chance to overcome this challenge is coarse-grained molecular dynamics simulations, not as a blind tool simplifying calculations without regard to the physical process that needs to be described, but rather as a tool adjusted to the scientific problem. The PACE^89,91 coarse-grained molecular dynamics approach is well suited to long-time protein folding simulations⁹⁰ as well as to simulation of misfolding as demonstrated in case of fibril elongation in case of Aβ peptides⁸⁰ and, as demonstrated here, in the initial phase of α-synuclein fibril formation. Development of PACE^89,91 and of other coarse-grained methods is both an exciting area of modern chemical physics as well as an extremely relevant area of modern biological physics that holds the promise to prevent human suffering.