Collective Dynamics of Processive Cytoskeletal Motors

Abstract

Major cellular processes are supported by various biomolecular motors that usually operate together as teams. We present an overview of the collective dynamics of processive cytokeletal motor proteins based on recent experimental and theoretical investigations. Experimental studies show that multiple motors function with different degrees of cooperativity, ranging from negative to positive. This effect depends on the mechanical properties of individual motors, the geometry of their connections, and the surrounding cellular environment. Theoretical models based on stochastic approaches underline the importance of intermolecular interactions, the properties of single motors, and couplings with cellular medium in predicting the collective dynamics. We discuss several features that specify the cooperativity in motor proteins. Based on this approach a general picture of collective dynamics of motor proteins is formulated, and the future directions and challenges are discussed.

1 Introduction

Cytoskeletal motor proteins are important classes of biological macromolecules that play crucial roles in major cell biological processes such as transport, transfer of genetic information, synthesis of proteins, signaling, division, and motility.^1–7 At the microscopic scale, competition and coordination of these motors underlie a variety of physiological processes that regulate the internal organization of living cells. Throughout biology, functionally distinct families of motor proteins are programmed to regulate the distributions of organelles, vesicles, and signaling molecules, and to actively participate in cellular processes that require mechanical forces. The collective mechanical behavior of these natural nanomachines results in precise deterministic and macroscopically significant events. It is hard to overestimate the importance of multiple molecular motors for cellular functioning. However, despite extensive experimental and theoretical efforts, our understanding of the cooperative mechanisms in motor proteins remains quite limited.^3,8

In recent years, motor proteins have been investigated by various experimental methods that quantified their dynamic behavior at the single-molecule level with high temporal and spatial resolutions.^2,3,8–13 It was found that many individual motors can efficiently produce large forces while moving long distances along cytoskeletal filaments. Nevertheless, quite surprisingly, multiple experiments also indicate that, in cells, motor proteins usually func tion as groups.^14–19 Frequently, these groups even include motors with antagonistic actions, like kinesins and dyneins that try to pull cellular cargo in opposite directions along the microtubules. Due to revolutionary advances in spectroscopic and structural methods, we understand now much better the dynamic properties of single biomolecular motors.^3,8,11–13 However, the behavior of multiple motor proteins working in teams turned out to be much more complex and difficult to predict purely from single motor properties.^3,8,20 In other words, bringing together several molecular motors leads to new qualitative phenomena that cannot be understood knowing only the features of individual motors. A new physics emerges when several motor proteins start to cooperate while pulling subcellular loads.

This paper provides a brief overview of recent experimental and theoretical investigations that have illuminated mechanisms governing collective dynamic behavior of processive cytoskeletal motors. This covers dynein, a variety of kinesins, and several unconventional non-muscle myosins. We focus on key concepts and ideas that currently exist in the field, and critically analyze them. For this reason, many other important aspects of multiple motor proteins in biological systems will not be discussed. We also focus on transport scenarios involving a relatively small number of motors and do not cover collective phenomena involving very large groups of non-processive muscle myosin motors, for which extensive theoretical treatments have been developed. Our main goal is to highlight an emerging theoretical picture of collective dynamics of cytoskeletal motors which is consistent with experimental observations and fundamental concepts from chemistry and physics.

2 Experimental Studies

Single-molecule biophysical techniques have played a critical role in advancing our understanding of motor mechanochemistry.^{3,8,10–12,21–25} A variety of force-dependent properties, including velocities, unbinding rates, run-lengths, adhesion, and step lengths have been measured for kinesins, cytoplasmic dynein, as well as for processive myosins.^{3,8,22,26–31} Early in vitro investigations of collective motor dynamics^32–34 were also informative, and provided clear evidence that grouping motors together can impact transport behaviors and even cargo transport responses to cytoskeletal filament binding proteins.^32,33

A number of advances also stemmed from the development of new methods to engineer synthetic complexes of motor proteins.^35–50 These approaches typically employ a macromolecule or molecular assembly (protein-DNA linkers,^36,37,41,44 DNA origami scaffolds,^42,51quantum dots,³⁸ or antibody protein complexes.⁴⁷) to template the organization and mechanical coupling of motors. They can provide reliable control over the number, composition, and geometric arrangement of motors (Fig. 1). These complexes can also be viewed as new effective “molecules” for which all existing single-molecule methods can be well applied.

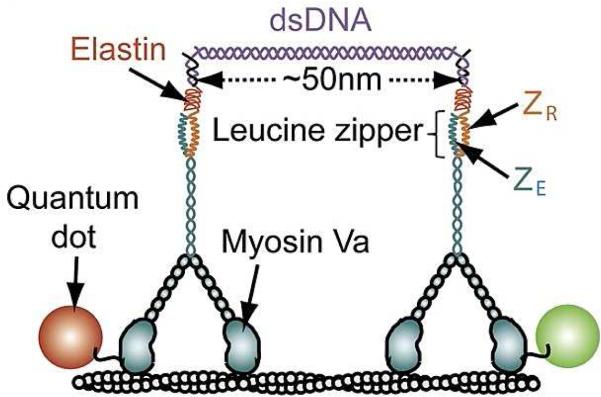
Fig. 1.

A schematic view of synthetically engineered complexes of two myosin V motor proteins. A DNA linker system consisting of a short 50nm segment of double-stranded DNA and polymer connectors at both ends couples two molecular motors. Each motor protein molecule is bound to a quantum dot of different color, which helps to comprehensively monitor the dynamics of the system. Adapted with permission from Ref.⁴¹

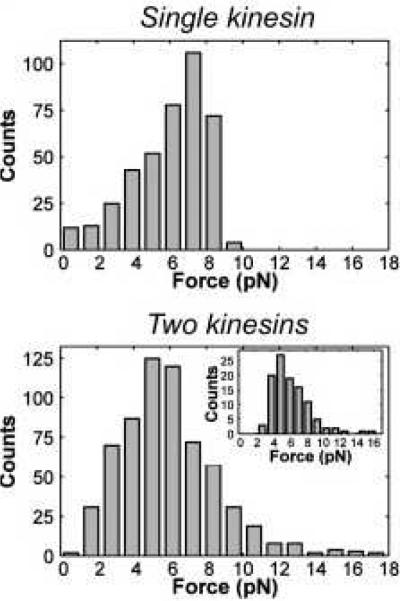
The application of synthetically engineered complexes of motor proteins uncovered many surprising aspects of collective motor behavior.^3,8,20,52 The first important finding was that the degree of cooperativity depends not only on the individual properties of the involved motors, but also on how each modifies the dynamics of its coupled neighbors.^{36–38,40,41,45} While observed with several multiple motor systems, this concept can be illustrated by simply comparing the distributions of detachment forces for single kinesins and for synthetic complexes composed of two kinesins (Fig. 2).³⁷Two-kinesin complexes are found to produce forces that exceed the forces produced by single kinesins, (F_Stall ≃ 7 − 8 pN), yet the average detachment force of single motors and the two-motor complexes are remarkably similar. Mechanical modeling of this behavior has shown that such behavior stems from the applied load on the two-kinesin cargo being shared unequally between the two kinesins. This behavior tends to promote partial cargo-filament detachment at applied loads exceeding single-motor stalling forces, yielding net, sub-additive cooperative behavior.³⁷ Importantly, synthetic complexes composed of two^37,47, four⁴⁴, and as many as seven⁴² kinesin motor proteins are found to exhibit similar effects. Moreover, modulation of the average motor number in vivo also appears to reveal cargo similar transport insensitivity to kinesin copy number.⁵³

Fig. 2.

Distributions of maximal observed forces before the detachment for single kinesins (top) and for two-kinesin assemblies (bottom). Adapted with permission from Ref.³⁷

Different dynamic behavior has been observed for assemblies containing other types of processive motors. For example, collections of processive myosin motors are found to exhibit different behaviors compared to collection of kinesins in the absence of an applied load. The velocities and run distances of DNA-templated myosinVa complexes have been shown to be sensitive to the structural and elastic properties of the assembly.^41,54. Similarly, DNA-origami self-assembly techniques have been used to generate myosinV and myosin VI complexes containing as many as six coupled motors.^51,55 Experimental and theoretical analysis of these systems suggest that the elastic coupling between myosins, and the elasticity of motors themselves can influence the shapes of cargo trajectories within complex actin filament networks. In both cases, cargo velocities are found to decrease with increasing myosin copy number. The difference between the unloaded behaviors of multiple processive myosins and kinesins has been attributed to small stalling force (F_Stall ≃ 2 − 3 pN)^26,56,57 and large step size (d = 36 nm)^26,58 of single myosin motors^41,59. These properties are believed make multiple myosin velocities sensitive to the elasticity of motor linkages since they dictate that complexes will stretch appreciably during asynchronous motor stepping, and since motor stepping rates will be much more sensitive to the resulting strain force (see also similar arguments presented in Ref.⁵⁹).

Optical trapping studies of multiple multiple dynein motor proteins in living cells indicate that these motors are capable of cooperating productively when operating against applied loads.⁴⁶ Although dynein appears to be a weak motor (F_Stall ≃ 1 pN), multiple dyneins are found to generate large collective forces while functioning together as teams. This behavior indicates multiple dyneins can share their load more readily, and thus, stay engaged for long periods of time than multiple kinesins. Interestingly, related behaviors have been observed for non-processive, kinesin-related protein Ncd.⁴⁴ Moreover, similar additive cooperative behavior is expected for collections of processive myosin motors under load. However, this behavior has yet to be tested experimentally.

Even richer, more complex collective dynamics can be found for assemblies of different types of motors, especially for species that transport cargoes in opposite directions.15,18,42,46,52,60–66 These systems are essential for understanding cellular transport processes because in vivo studies routinely find evidence of opposing motors simultaneously bound to each organelle cargo.^60,67,68 Combining molecular motors with antagonistic properties, like dyneins and kinesins, leads to the so-called tug-of-war phenomenon¹⁴ where it is assumed that the strongest team of motors dominates and dictates the direction of transport. The paradigm for this dynamic behavior is schematically illustrated in Fig. 4. Experiments indicate that, despite producing lower forces, in most cases dyneins win this tug-of-war over stronger kinesin motors.^15,42 This unexpected result was explained by the fact that dyneins cooperate with each other additively,^46,69 in stark contrast to the sub-additive behavior of kinesins. In addition, there is some evidence that dyneins may exhibit stronger interactions with microtubules.⁷⁰

Fig. 4.

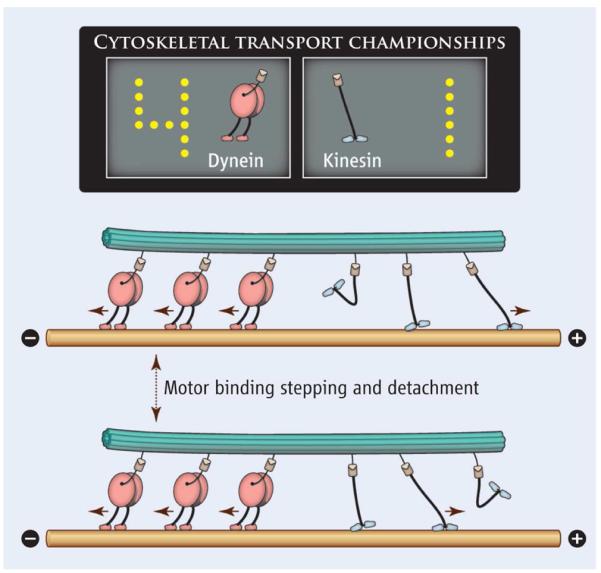
A schematic view of the tag-of-war phenomenon when motor proteins with opposite polarity compete with each other to move the cellular cargo. Dyneins pull the cargo to the “minus” end of the microtubules, while kinesins tend to carry the cargo in the opposite direction. Adapted with permission from Ref.⁵²

Interesting dynamic behavior is also observed for mixed motor ensembles composed of different motors possessing the same polarity but different speeds.^{48,49,71–73} This problem is important for understanding mechanisms of heterozygous genetic disorders where mixtures of mutated and wild type motor proteins function together.^4,74 It may also be relevant for cancer treatments that target motor proteins, that likely produce mixed populations of inhibited and uninhibited motors.⁷⁵ Fast and slow motors of the same polarity also co-transport cargoes in non-pathological cellular contexts.^76,77 Recent synthetic assemblies of same-polarity motors have been studied with in vitro microtubule-gliding assays.^48,73 Experimental results from the gliding assays suggest that force-dependent detachment rates, inherent single-motor properties, govern the dynamics of such complexes. The motor species that binds more strongly to the filaments tends to dominate the overall behavior, unless the number of weaker motors exceeds a critical threshold.^48,49,73 These findings again underscore the importance of inter-motor interactions in the assemblies.

Finally, although the method of synthetically engineered motor protein complexes and related techniques were successful in uncovering many important details of the collective dynamics of molecular motors, there are several limitations in this approach that should be noticed.³ The centerpiece of the method is the use of connecting scaffolds such as DNA, proteins, nanoparticles or other biomacromolecules. One must question which aspects of the observed dynamic phenomena are due to collective motor behavior and which are governed by the properties of the molecular scaffolds and motor-scaffold linkages, such as their rigidity, which is often quite high. The use of engineered membranous vesicles (that mimic the mechanical properties of a large range of natural organelles and vesicular cargoes⁵⁴) will likely be important in resolving these issues. Methods to examine multiple motor behaviors in vivo have also been pursued.^19,49,61 While also seeing important advances, these studies stand to benefit significantly from techniques to control motor cargo coupling and organization. As with the synthetic motor systems, recent attempts to leverage synthetic biology techniques to control motor-cargo coupling, motor density, cargo type and size^19,49,78 have the potential to take these types of experiments in important new directions.

3 Merging Theory with Experiment

The first fully quantitative description of the non-cooperative tug-of-war approach was given in the seminal work of Lipowsky and collaborators in 2005,^20,79 although similar qualitative biological models were explored earlier.⁸⁰ The most basic form of this foundational theoretical framework assumes that motors do not interact with each other except via the geometrical constraint from being connected to the same cargo. Each motor retains the properties of individual protein molecules, and the overall collective dynamics of the assembly is additive.⁷⁹ Applied loads are assumed to be shared equally among all of the filament-bound motors in the complex. Loads are also assumed to be redistributed among motors instantaneously upon the attachment or detachment of motors to and from the filament. Despite the simplicity of these assumptions, the framework allows the relatively straightforward calculation of a number of collective transport parameters, and further, the framework can often be applied to approximate the dynamics of multi-motor complexes that exhibit net additive behaviors.

A problem with modeling multiple motor behaviors is that motor dynamics is rarely purely additive. Again, a number of experimental studies point to elastic strain interactions as an important factor influencing motor cooperation, stimulating the development of new theoretical methods that built upon the Lipowsky framework to explicitly account for motor interference and potential coordination due to these effective interactions^{3,8,39,40,59,81–84} For example, a key adaptation of a method based on a discrete-state modeling approach is the ability to identify the most relevant biochemical states that differ by chemical conformations of the motors (bound or unbound) and by the distances between particles along the cellular tracks.^3,8 Then, using independent single-molecule and mechanical information, a thermodynamically consistent, explicit evaluation of the free energies for each state allows researchers to estimate the transition rates, which, when combined, yield the collective dynamic properties of the assemblies.^8,40

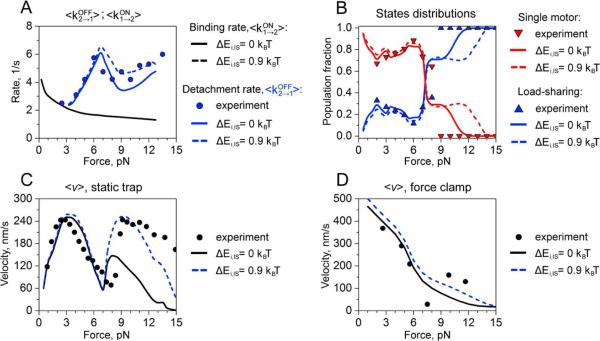
Discrete-state and other similar models have been applied to several experimental studies of engineered multi-motor assemblies.^40,41,81,82 The comparison with experimental observations suggests that this theoretical approach correctly reproduces all experimental trends and it can even quantitatively reproduce many dynamic features. This can be seen in Fig. 6 where the method was utilized for analyzing the dynamics of two-kinesin assemblies in an optical trap.⁸¹

Fig. 6.

Comparison of dynamic properties such as transition rates, velocities and fraction of load-shared states for two-kinesin complexes. Symbols are experimental results, and lines are theoretical predictions from cooperative models with different interactions. Reprinted with permission from Ref.⁸¹. Copyright 2012, American Chemical Society.

The discrete-state stochastic approach can also successfully explain the complex collective dynamics of multiple motor proteins by creating a microscopic picture of the underlying processes.³ Most importantly, it allows us to understand why some motors cooperate while others do not. The main arguments here are based on geometric considerations and on the properties of single motor proteins.^3,8 Again, consider the case of a complex composed of multiple kinesins. Kinesin is a fast and strong processive motor. Single-kinesin velocities are relatively insensitive to loads until they approach the single-motor stalling force. All kinesins in the team therefore move with comparable speeds at moderate applied loads,even when loads are distributed unequally between the motors. This means that multiple kinesin complexes can be trapped kinetically in filament-bound conformations where one motor is required to sustain a dominant portion of the applied load, which, in turn, promotes the detachment of this motor. However, the situation is different for complexes of weaker motors like myosin V or dynein. The velocities of these motors depend more sensitively on external forces. Thus, the leading motors move most slowly, allowing the trailing motors to catch up. These biochemical states with proximally positioned motors usually support equitable load-sharing, and hence, exhibit much more additive, cooperative behaviors.

It should also be noted that, the degree of cooperativity also strongly depends on the strength of interactions between motors and their filament tracks.^3,8 When these interactions are weak, the motors in the complex can easily dissociate from the filament even for small external forces. The probability to reach the states with load sharing is low, which corresponds to weak cooperativity. At the same time, for strong interactions the collective dynamics is much more cooperative because the system has higher chances to reach the load-sharing states. This also implies that in complexes of antagonistic motors, the dynamics depends more on the action of most cooperative species. Thus, it predicts that the changing the number of dynein molecules should affect the cellular transport more strongly than regulating the number of kinesin motors.

While these new methods have helped to clarify several aspects of collective motor behaviors, there are still several problems that remain.^3,8 The main issue is how to obtain a realistic quantitative description for all relevant dynamic transitions in the system, particularly when more than just a few motors are involved in transport. Theoretical calculations frequently rely on several approximations, such as mechanical equilibrium, and simplified chemical-kinetic schemes, that are still not fully tested in experiments or in more advanced theories. In addition, in many cases it is difficult to quantify the interactions in the system. It is expected that further progress in the cooperative approach will be correlated with experimental advances in describing motor proteins.

4 Motor Competition Theory

Considerable attention has also been placed on investigating the dynamics of motor protein complexes composed of multiple antagonistic motors (Fig. 5). A variety of organelles and vesicles are outfitted with multiple copies of opposing kinesins, dyneins, and even myosins, and move bidirectionally within living cells.^{29,45,46,60,85,86} Building upon the general framework established to model teams of similar motors, Lipowsky and collaborators have been able to develop an extension of their stochastic modeling approaches that can provide microscopic descriptions of how antagonistic motors engage in a molecular tug-of-war during bidirectional cargo transport. This framework can also be used to examine how bidirectional transport behaviors depend on the properties of the opposing motor teams.^20,87,88 The method is often used for interpreting various experimental data, and it was supported by many observations, especially for vesicle transport in neurons and for the transport of endosomes.^15,85 One of the biggest advantages of this theoretical approach is the fact that it gives quantitative and experimentally testable predictions of the dynamic behavior for multiple molecular motors.²⁰

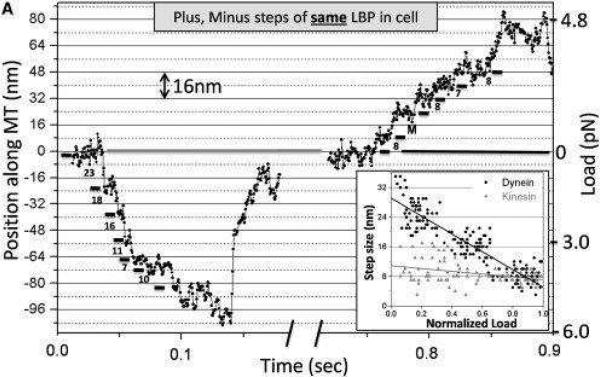
Fig. 5.

Stepping dynamics of the cellular cargo bound to motor protein complexes, which is driven by dyneins (minus direction) or kinesins (plus direction). Adapted with permission from Ref.⁴⁶

The stochastic model framework is also able to capture certain novel transport behaviors that appear to emerge when antagonistic motors function in teams. In particular, it can reproduce the saltatory motions and near-instantaneous reversals in cargo transport directions found during the bidirectional transport of a variety of cargoes. This result is significant since rapid changes in cargo transport direction had long been assumed to signify the existence of cooperative transport mechanisms, that are perhaps mediated by some form of regulatory factor that controlled the mechanical properties of one or both motor teams. The stochastic tug-of-war modeling approach illustrates how this can be a weak dichotomy. It can be used to show that the direction of cargo motion can be determined by the properties of the individual motors, like their unbinding rates and stall forces. Specifically, the nonlinear force-dependence of single-motor detachment rates can give rise to dynamic instabilities in cases where the force-production capabilities of each opposing motor team are similar. Motor systems with these properties can recapitulate the rapid bidirectional-switching, salta-tory trajectories observed in tug-of-wars in vivo⁸⁷

While this modeling approach was successful in clarifying several features of the collective dynamics of motor proteins, there is a large body of experimental observations that are inconsistent with theoretical predictions from this method.^{3,8,61,80,89,90} The model could not describe bidirectional transport of lipid droplets and peroxisomes in vivo.^19,29,80,89 The velocities and run lengths measured for multiple-kinesin complexes, both in vitro and in vivo, differed significantly from theoretical predictions of the non-cooperative model.^{36,37,42,44,47,49} We anticipate that many of these issues could be reconciled by using the discrete-state stochastic approaches, since this adaptation would allow deviations from load sharing behaviors and other forms of inter-motor interactions to be incorporated into the model framework.

Observations of phenomena where inhibition of motors of one polarity actually inhibits or even abolishes transport in both directions^{17,80,91–93} have been presented as evidence against a tug-of-war model of motor antagonism since lowering the mechanical contribution of one type of motor is expected to increase motion in the opposite direction during a tug-of-war. Several intriguing ideas have been presented to reconcile this so-called paradox of codependence.⁸⁰ They include the suggestion that motors might be weakly bound to microtubules when they are inactive, increasing the probability of being bound to the filament track. Another idea is that the forces generated by opposing motors activate the motors out of the inhibited state, and without this activation the transport is much less efficient. Better knowledge and experimental analysis of potential regulatory components are surely needed to sort out this debate. More microscopic, mechanistic, and quantitative models will likely also play an important role. In particular, we expect that the tug-of-war modeling framework can be adapted to account for additional relevant mechanical and biochemical transitions of motors within multi-motor complexes in order to capture these responses. Doing so will likely illuminate a number of presently unknown mechanical principles that allow cells to regulate the integrated functions of coupled motor systems.

5 Future Directions and Challenges

In recent years, our understanding of collective motor protein dynamics has progressed significantly. This is the result of both experimental advances, which allowed researchers to monitor synthetic complexes of motors with controllable geometry and chemical composition, as well as theoretical developments that accounted for mechanical and non-mechanical interactions between motors. However, descriptions of many aspects of multi-motor cooperativity remain incomplete. We list several challenges that currently defer a full understanding of the intricacies of collective motor transport.

One fundamental issue is to resolve the specific role of inter-motor interactions in the collective dynamics. What is more beneficial for transport - attractive or repulsive interactions? Also, what is the strength of these interactions? Can multi-motor complexes tune these interactions to achieve the most efficient transport? There are several recent theoretical studies that tried to address some of these problems.^94–96 They are based on employing multiparticle non-equilibrium models to analyze the motion of interacting molecular motors. However, these models use a very crude and simplified description of cellular transport, and it is not clear how the obtained results can be applied to real biological systems.

The first challenge is to explain why antagonistic motors are involved together in the transport of cellular cargoes. Why is this physical mechanism so universal in eukaryotic cells, from amoebae to humans? Perhaps, it may be associated with the ability of motor protein systems to circumvent traffic jams and crowding in cells, permitting adaptable and efficient distribution of particles. A related issue is to understand the roles that molecular crowding, cytoskeletal filament intersections, and organelle interactions play in transport by motor proteins.^97–99

Perhaps the most serious challenge for the field is to move beyond isolated motor systems and clarify how motor cooperativity connects the influence of spatially heterogeneous environments to transport behavior. When motor proteins move vesicles and organelles in vivo they interact with many components of the cellular medium. Certain chemical and genetic modifications of microtubule tracks – diverse monomer isotypes, post-translational modifications, and decoration by microtubule associated proteins (MAPs)^100–102 – have recently been shown to modulate individual motor dynamics differentially, and hence, these modifications can bias transport by one of several motor species constituting a force-generating team.⁴⁹ Accounting for these effects will progress future theoretical models.

The cytoskeletal network is an important component that influences molecular motors. It is already a highly active dynamical system, and it was also argued theoretically that diverse non-equilibrium structures can arise from the force-dependent properties of motor proteins coupled to the cytoskeleton.^103,104 It will be interesting to investigate how these different structures are impacted by cooperative mechanisms and how they might be realized in real cellular systems.

This last challenge also underlines the importance of development of new quantitative methods for analyzing in vivo processes.^19,105 Synthetic methods that coupled motors with molecular scaffolds greatly improved the understanding of the collective dynamics of motor proteins. However, the coupling of motor proteins in live cells can be quite different compared to current synthetic systems, particularly for vesicular cargoes. In addition, the transport behavior of cellular cargoes will not only depend on how they move on individual filaments. Instead, the dynamics will be strongly affected by cargoes attaching to and dissociating from the new filaments, associating with other regulatory proteins, interacting with the cytoskeleton network. This rich and very complex dynamic behavior is not to easy to recapitulate in in vitro systems. This necessitates the development of new quantitative methods for analyzing collective motor functions in living cells.

Fig. 3.

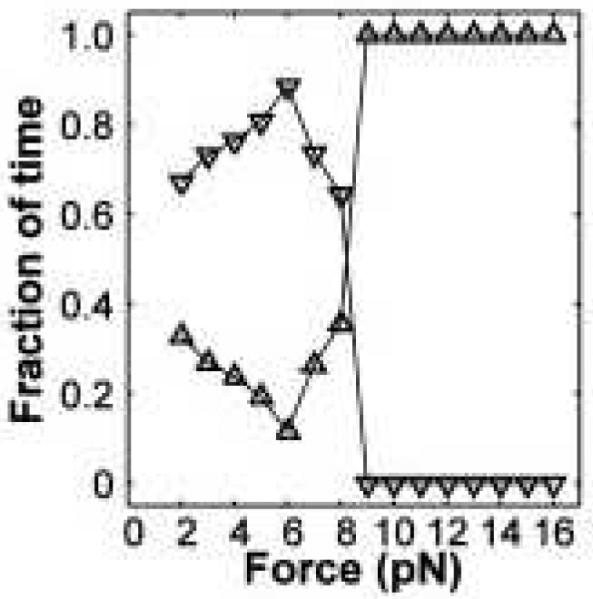
A fraction of time the cellular load is driven by one (downward-pointing triangles) or by two kinesin motors (upward-pointing triangles). Adapted with permission from Ref.³⁷