Imaging based enrichment criteria using deep learning algorithms for efficient clinical trials in MCI

Abstract

The Mild Cognitive Impairment (MCI) stage of AD may be optimal for clinical trials to test potential treatments for preventing or delaying decline to dementia. However, MCI is heterogeneous in that not all cases progress to dementia within the time frame of a trial, and some may not have underlying AD pathology. Identifying those MCIs who are most likely to decline during a trial and thus most likely to benefit from treatment will improve trial efficiency and power to detect treatment effects. To this end, employing multi-modal imaging-derived inclusion criteria may be especially beneficial. Here, we present a novel multi-modal imaging marker that predicts future cognitive and neural decline from [F-18]fluorodeoxyglucose positron emission tomography (PET), amyloid florbetapir PET, and structural magnetic resonance imaging (MRI), based on a new deep learning algorithm (randomized denoising autoencoder marker, rDAm). Using ADNI2 MCI data, we show that employing rDAm as a trial enrichment criterion reduces the required sample estimates by at least five times compared to the no-enrichment regime, and leads to smaller trials with high statistical power, compared to existing methods.

1. Background

Recent clinical trials designed to evaluate new treatments and interventions for Alzheimer’s disease (AD) at the mild to moderate dementia stage have largely been unsuccessful and there is growing consensus that trials should focus on the earlier stages of AD such as mild cognitive impairment (MCI) or even the presymptomatic stage[1, 2], if such stages can be accurately identified in individual subjects[3–5]. However, MCI is a clinical syndrome with heterogeneous underlying etiology that may not be readily apparent from a clinical workup, posing a major challenge in reliably identifying the most probable beneficiaries of a putative effective treatment [6]. For example, MCI patients may have clinical but not biomarker evidence of incipient AD, may have biomarker evidence in some modalities but not others, or may despite biomarker presence not show symptomatic progression during the trial time-period. An efficient MCI trial would ideally include only those patients most likely to benefit from treatment; who possess AD pathology based on a constellation of amyloid, tau and neural injury biomarker assessments, and who are most likely to progress clinically to symptomatic AD. The typical annual conversion rate to dementia among MCI due to AD is 3–20% across several studies [7], where the relatively lower rates are observed in population-based cohorts, and higher rates are in clinical settings. The implication is that over a two year trial, at best only 40% of participants would have naturally progressed and the ability to detect the true efficacy of the intervention is perhaps diminished.

To this end, several ongoing AD trials “enrich” their population by using one or more disease markers as inclusion criteria [2, 8]. The general framework here is to effectively screen out subjects who are weak decliners (i.e., MCI who may not convert to AD) [9]. Unless there is a natural phase change (i.e., an elbow) in the distribution for distinguishing the at-risk and not-at-risk subjects on this scale, a fixed fraction of the total cohort are filtered out based on the study design. Imaging-based markers (e.g., Fluorodeoxyglucose (FDG), hippocampal and ventricular volume) and cerebrospinal fluid (CSF) profiles have been shown to be effective in screening out low-risk subjects, due to the fact that disease manifests much earlier in imaging data compared to cognition [1, 2]. However, these markers are uni-modal while several studies have shown the efficacy of multimodal data [10, 11]. Furthermore CSF cannot be used in practice as a screening instrument because assays typically need to be performed in a single batch and are highly lab specific [12]. To this end, several recent studies have used support vector machines (SVMs) and other machine learning models to design such multimodal markers [8, 13–16]. Although most of these approaches use longitudinal data, a practical enrichment criterion should only use baseline (trial start-point) data. We argue that existing approaches to trial enrichment, including state-of-the-art machine learning based techniques, cannot guarantee the optimal enrichment behavior which is to optimally correlate with the spectrum of dementia with high confidence, while simultaneously ensuring small intra-stage variance.

In this work, we report the design of a novel multimodal imaging marker that is especially tuned to yield accurate predictions of future decline to AD at the level of individual subjects with small intra-stage variance. This new disease marker (which we refer to as randomized denoising autoencoder marker, rDAm) is a machine learning module based on certain extensions of recent ideas in “deep learning” that yield state-of-the-art results in computer vision, natural language processing and machine learning [17, 18]. We provide extensive empirical evidence that this new marker efficiently filters out low-risk subjects from the MCI population and consequently requires much smaller sample sizes per arm (for detecting a given treatment effect at some desired power) compared to any of the existing imaging-based markers. The main contributions of the paper are: (a) We design a novel predictive multimodal imaging-based disease marker, based only on baseline acquisitions, that correlates very strongly with future decline (i.e., disease progression); (b) We show via extensive analyses using imaging, cognitive and clinical data that this new marker results in efficient clinical trials when used as trial inclusion criterion.

2. Methods

2.1 Theoretical approach

Randomized denoising autoencoders (rDA)

Our multimodal imaging marker attempts to capture, i.e., learn from a set of training images, the pattern of differences across different dementia stages. Clearly, in the neuroimaging literature, such an objective has been tackled by numerous studies in the AD setting using well known machine learning methods like SVMs [10, 11, 19]. But using such SVM approaches for clinical trials has limitations (additional details provided below); instead, we present a method that differentiates various stages of AD (i.e., correlates with the dementia spectrum), while simultaneously obtaining a small intra-stage prediction variance (the prediction variance is simply the variance of the predictions given by the trained machine learning model). Such an approach gives results which are competitive with SVM based methods (in terms of accuracy) but aligns much better with our final goal of using these ideas for clinical trials design. The basic statistical behavior of our model is a reduction in the variance at no cost of approximation bias (or accuracy). To do this, we adapt the so-called deep-learning architectures that have been shown to yield state of the art performance in several computer vision and machine learning applications [17, 18, 20, 21]. The main methodological challenge we overcome is to make deep architectures “generalize” well (i.e., yield accurate predictions on previously unseen subjects/images) in this application, which is important due to the high dimensionality of neuroimaging data accompanied by smaller training dataset sizes (at most a few hundred subjects).

We first provide a very brief overview of our model, which we call randomized denoising autoencoders (rDA) [22]. Please refer to the appendix for a complete description and additional mathematical details. Our solution consists of first constructing simple deep learning architectures (referred to as weak learners). Each such weak learner is a neural network learned according to a new deep learning algorithm called stacked denoising autorncoders (SDA) [20]. Since the number of dimensions (voxels) is large, each such weak learner corresponds to inspecting only a small portion (e.g., 3D local neighborhood) of the image and/or using different model hyper-parameters (the network architecture and learning parameters of SDAs [20], refer to Section 2 in the appendix). Although the issue of scaling to high dimensions is handled by learning only small portions of the image, these weak learners by themselves are not useful. However, using a large number of these weak learners, each of which is learned from different portions of the image, we can generate an “ensemble” which is much more expressive in modeling the targets/outputs compared to the weak learners themselves [23]. The ensemble outputs can correspond to uniform or weighted combination of the outputs from this suite of weak learners, and are known to be less sensitive to model hyper-parameters [23]. Such an ensemble learner also comes with guarantees in terms of reducing the variance of model outputs without any loss in approximation bias (i.e., overall output is un-biased whenever the weak learners are un-biased).

Our new model rDA is then constructed by the following procedure. First, the set of voxels are divided into B number of blocks (given a priori) by randomly assigning each voxel to one or more of the B blocks. Second, within each block T different SDAs (again, given a priori) are constructed by randomly sampling T different hyper-parameters. The BxT different SDA outputs are finally combined using ridge regression. This two level “randomization” over voxels and hyper-parameters motivates the name “randomized” denoising autoencoders. The expressive power of deep architectures ensures that rDA can successfully learn complex concepts, which provide the ability to differentiate multiple stages of AD, while forcing the output variance to be as small as possible due to the ensemble structure [23]. The framework of rDA can be extended to multiple modalities by generating weak learners specific to each imaging modality and combining them across all the modalities. The rDA outputs are guaranteed to lie between 0 and 1 [20]. Hence, by training a rDA with healthy controls labeled as 1 and AD subjects as 0, we can project the scale of dementia to [0,1]. These projections then serve directly as imaging-derived continuous predictors of the disease, referred to as rDA markers (rDAm), that provide the confidence of the learning model that a given subject is close to “healthy” or “diseased”. In particular, rDAm values closer to 0, on previously unseen MCI subjects, are expected to convey a stronger sign of dementia than those that are closer to 1. Please refer to the Sections 1–2 in the appendix for additional details about the rDA model (including the required background on SDAs), its training and the calculation of rDAm.

rDAm for sample enrichment

Sample enrichment in AD clinical trials entails filtering out those subjects who are not expected to have a higher risk of progressing to dementia. In other words, enrichment entails including only the strong decliners who are most likely to benefit from the treatment. To formalize the characteristics of a “good” sample enricher, consider the setting where we want to design a 2-year clinical trial on a MCI population using a certain outcome measure. Let δ denote the mean longitudinal change on this outcome measure due to disease. We intend to induce the treatment and reduce this change to ηδ, where η is the hypothesized induced treatment effect. Within this setting, the number of subjects required per arm is computed by applying a two sample t-test which tests for the difference of mean outcome between the treatment and placebo groups[24], as follows,

$$s=\frac{2{(Z_{\alpha }-Z_{1-\beta })}^2{\sigma }^2}{{(1-\eta )}^2{\delta }^2}$$

where σ² denotes the pooled variance of the outcome i.e., average of the variances at baseline and 2-year trial end point. η is the hypothesized induced treatment effect (i.e., 1- η denotes the expected percentage of reduction in the outcome measure). The Null hypothesis then corresponds to no difference between the two groups. For a fixed α and β, the above equation shows that the sample estimates increase with σ² and decrease with a large δ. If the trial cohort includes subjects at low risk of decline (weak decliners), then δ is expected to be small. Enrichment entails removing such weak decliners, thereby increasing δ. However, this might have the undesirable effect of increasing σ², because the latter is the pooled variance of the outcome. Hence, one must ensure that the enriched cohort has smaller variance (with respect to some outcome) but also has large δ i.e., we need to recognize the pool of very strong decliners whose outcomes have smaller variance.

The natural way of ensuring small σ² with large δ, is by designing an outcome with precisely these characteristics. However the trial outcomes are generally cognitive scores, or may be individual image or CSF measures whose statistical properties may not be altered readily. But recall that the multi-modal imaging marker, rDAm, is explicitly designed to ensure smaller variance while yielding prediction scores that correlate well with existing cognitive measures, which are used as the basis for defining multiple stages of dementia: from healthy to early/late MCI to completely demented. Therefore, by using rDAm at baseline (trial start-point) as an inclusion criterion to remove the probable weak decliners, we expect the enriched cohort to have large δ and smaller variance σ² with respect to any outcome measure that may be desired. This directly follows from the ability of rDAm to predict many of these scores (outcomes) with high confidence. Section 3 of the appendix presents more details on reducing sample sizes by designing enrichers with strong correlation to dementia spectrum and small prediction variance. Note that we use the word prediction variance because rDA is trained on ADs and CNs, and offers prediction scores on MCIs. Ideally, and to be practically deployable, this enrichment must be performed only at baseline or the trial start-point. Hence, our first sanity check in terms of the efficacy of rDAm and using it as enricher will focus on whether rDAm computed at baseline correlates with cognitive and other imaging-derived disease biomarkers[25, 26]. If the correlations turn out to be significant, this is evidence of convergent validity, and using baseline rDAm as an inclusion criterion for enriching a clinical trial population is, at minimum, meaningful. Observe that the scale of rDAm (closer to 0 corresponds to higher confidence that a subject will decline) implies that the trial population can be enriched by screening in subjects whose baseline rDAm is smaller than some cut-off. If the enrichment threshold is denoted by t (0 <t< 1), then the enriched cohort would include only those subjects whose baseline rDAm is smaller than t. One way to choose such a threshold t is by comparing the mean longitudinal change of some disease markers (MMSE, CDR and so on) for the enriched cohort as t goes from 0 to 1. An alternative is to include a fixed fraction (e.g., 1/4^th or 1/3^rd) of the whole population whose baseline rDAm is closest to 0.

2.2 Experimental Setup

Participant Data and Preprocessing

Imaging data including [F-18]Florbetapir amyloid PET (AV45) singular uptake value ratios (SUVR), FDG PET SUVRs and gray matter tissue probability maps derived from T1-weighted magnetic resonance imaging (MRI) data, and several neuropsychological measures and CSF values from 516 individuals enrolled in Alzheimer’s disease Neuroimaging Initiative-II (ADNI2)¹ were used in our evaluations. Of these 516 persons (age 72.46± 6.8, female 38%), 101 were classified as AD (age 75.5 ± 5.1), 148 as healthy controls (age 70.75 ± 7), and 131 and 136 as early and late MCI (age 74.3 ±7.1 and 75.9 ± 7.7) respectively at baseline². Among the MCI subjects, 174 had positive family history (FH) for dementia, and 141 had at least one APOE e4 allele. CSF measures were only available at baseline, and three time point data (baseline, 12 months and 24 months) was used for the rest.

The imaging protocols follow the standards put forth by ADNI. MRI images are MP-RAGE/IR-SPGR from a 3T scanner. PET images are 3D scans consisting of four 5-minute frames^3,4 from 50 to 70 minutes post-injection for [F-18]Florbetapir PET, and six 5-minute frames from 30 to 60 minutes post injection for FDG PET. Modulated gray matter tissue probability maps were segmented from the T1-weighted MRI images (other tissue maps are not used in our experiments) using the SPM8 New Segment function. The segmented map was then normalized to MNI space, smoothed using 8mm Gaussian kernel, and the resulting map was thresholded at 0.25 to compute the final grey matter image. All PET images were first co-registered to the corresponding T1 images, and then normalized to the MNI space. Manually constructed masks of pons, vermis and cerebellum were then used to scale these PET maps by the average intensities in pons and vermis (FDG PET SUVR) and cerebellum (florbetapir PET SUVR). All preprocessing was done in SPM8.

Evaluations

We train the rDA model using only baseline imaging data (from all the three modalities, MRI, FDG PET, and florbetapir PET) for AD and CN (cognitively normal) subjects where the AD class is labeled as 0 and the CN class is labeled as 1. When tested on MCI subjects, the trained model outputs a multi-modal rDAm, which is a marker representing the confidence of the learning model that a given MCI subject is (or is not) likely to decline. We only use baseline imaging data for training (hence making the model deployable in practice), while the predictions can be performed on MCIs at baseline or future time-points. Within this setup, our evaluations are two-fold. We first evaluate the premise whether rDAm is a good disease progression marker. We demonstrate this by computing the dependence of well-known outcome measures including Mini Mental State Examination (MMSE), Alzheimer’s Disease Assessment Scale (ADAS Cognition 13), Montreal Cognitive Assessment (MOCA), Rey Auditory Verbal Learning Test (RAVLT), Neuropsychological summary score for Memory (PsyMEM), summary score for Executive Function (PsyEF), hippocampal volume, Clinical Dementia Rating sum of boxes (CDR-SB)), conversion from MCI to AD (0 – no conversion, 1 – conversion; denoted by DxConv hereafter), CSF levels (τ, pτ, Aβ42, τ/Aβ42, pτ/Aβ42⁵), and APOE allelle4 and maternal/paternal Family history (FH), on rDAm computed at baseline. We used the Spearman Rank Order Correlation coefficient to assess these dependencies and accepted as significant those statistics where the p-value was less than 0.05. Note that we are interested in evaluating the predictive power of baseline rDAm, i.e., we report the correlations of baseline rDAm with these markers at say, 12-months and 24-months, and also the longitudinal changes providing evidence that whenever rDAm is closer to 0, the subject’s longitudinal changes are in fact steeper. Once this construct is appropriately validated, it is meaningful to evaluate the use of baseline rDAm for sample enrichment. To this end we compute the sample sizes required when using the above cognitive, neuropsychological, diagnostic and other imaging-based outcome measures with (and without) rDAm based enrichment. We also compute the performance improvement given by rDAm relative to alternative imaging-derived enrichers (including ROI summaries from FDG and florbetapir images⁶), with particular attention to the current state-of-the-art imaging based summary measure which we refer to as MKLm [10]. MKLm is based on Multi-Kernel SVM (MKL) [10], which tries to harmonize contributions from multiple imaging modalities for deriving a maximum margin classifier in the concatenated Hilbert spaces. That is, a linear combination of kernels is used unlike traditional SVMs that use one single kernel, and MKL solves for both the weights on the kernels as well as the normal to the hyper-plane concurrently. Similar to rDA, MKL is trained using AD and CN subjects, and the corresponding predictions on MCIs is referred to as MKL measure (MKLm). Please refer to the appendix (Section 4) for more details. For better interpretation of the estimates from the perspective of a practitioner, we estimate the effect size as a function of rDAm enrichment cut-off for a given (fixed) sample size. Note that all results (correlations and the sample size calculations) only use rDAms from MCI subjects; no AD and CN subjects are included in these calculations since they were used to train the rDA model itself.

3. Results

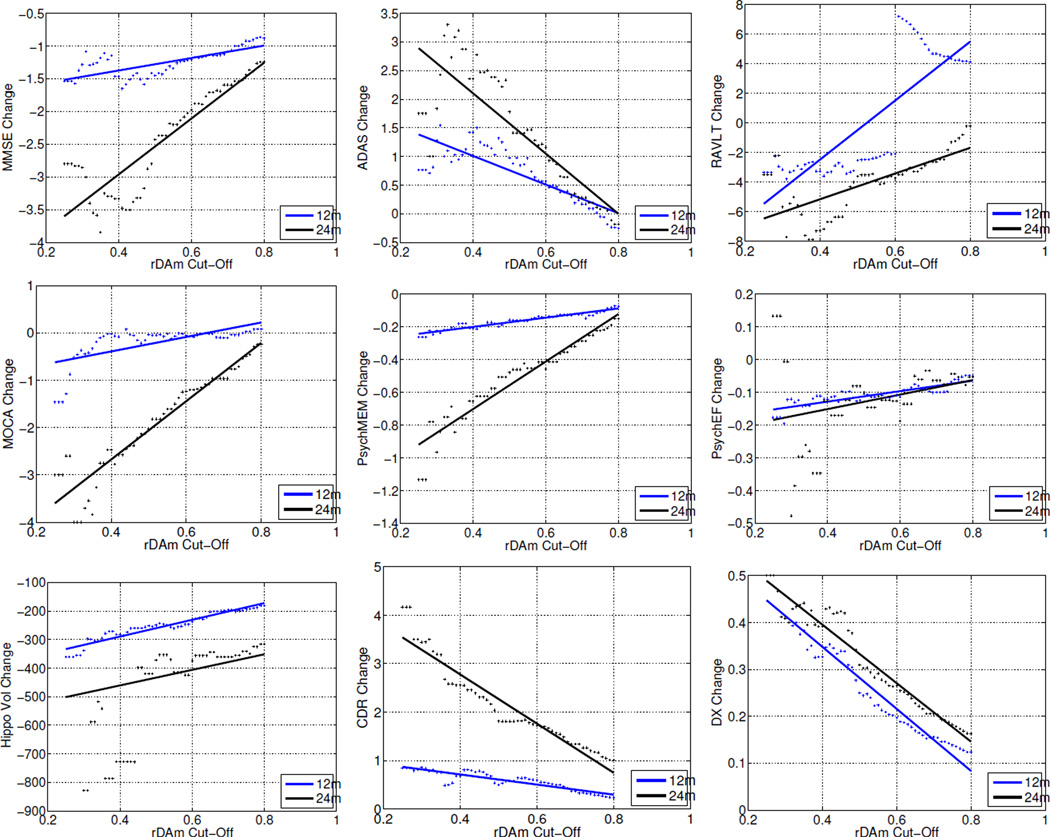
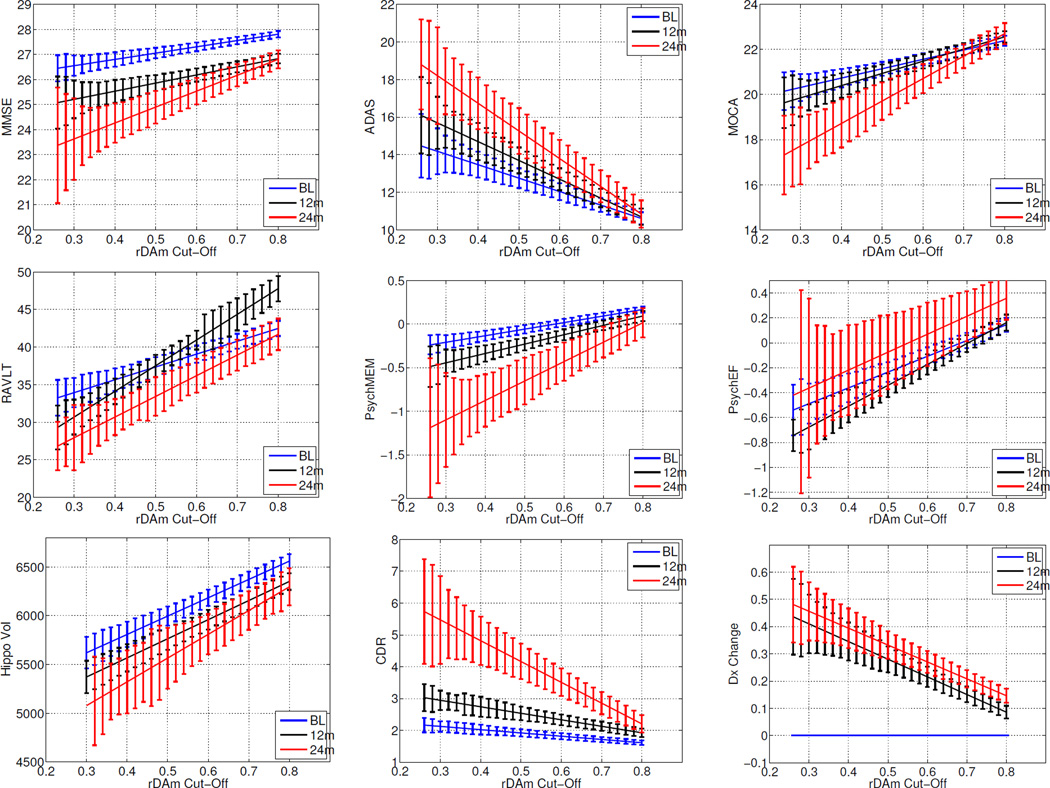
Table 1 corresponds to the predictive power of baseline rDAm. It shows the Spearman correlations and t-statistics of rDAm at baseline with cross-sectional (baseline, 12 and 24 months) scores and longitudinal change (12 and 24 months) in other disease markers. Negative correlations indicate that the corresponding markers (ADAS errors, τ, pτ, τ/Aβ42, pτ/Aβ42) increase with progression of the disease. Large correlations (r>0.5 and p << 10⁻⁴) were observed with baseline summary measures (column 2, Table 1), specifically with ADAS, neuropsychological (memory and executive function) composite scores, hippocampal volume and CSF levels involving Aβ42. FH (t=2.16, p=0.03) had a smaller influence on baseline rDAm compared to APOE (t=3.47, p=0.0006). All the cross-sectional correlations (columns 2– 4, Table I) were significant (r>0.48 and p << 10⁻⁴). The correlations of baseline rDAm with longitudinal change (columns 5 and 6, Table 1) were significant (r>0.21, p < 0.001) for all the measures, except PsyEF and MOCA at 12 months time. Beyond predictive accuracy of baseline rDAm in Table 1, Figure 1 evaluates its relevance for enrichment. Each plot corresponds to the mean longitudinal change of some disease marker after the total MCI population is enriched by removing weak decliners (subjects with baseline rDAm above certain cut-off t, which is shown on the x-axis). The plots show that MMSE, CDR-SB and DxConv have large changes when weak decliners are progressively removed. Specifically, the changes are much steeper for 24 months compared to baseline and 12 months (black and blue colored lines in each plot). RAVLT and PsyEF resulted in irregular changes at different time points. Figure 6 at the end of the Appendix presents the means of the disease markers (in contrast to the mean change as shown in Figure 1), and the trends support the observations in Figure 1.

Table 1.

Predictive associations of baseline rDAm: Testing for dependency of baseline rDAm scores (computed on MCI subjects) on several disease markers at baseline, 12 months and 24 months. Outcomes included cognitive and neuropsychological scores (MMSE – Mini Mental State Examination, ADAS –Alzheimer’s Disease Assessment Scale (Cognition 13 scale), MOCA – Montreal Cognitive Assessment, RAVLT – Rey Auditory Verbal Learning Test, PsyMEM – Neuropsych summary score for Memory, PsyEF – Neuropsych summary score for Executive Function), Hippocampal Volume, CDR-SB (sum-of-boxes), DxConv (Conversion from MCI to AD), CSF levels (τ, pτ, Aβ, τ/Aβ, pτ/Aβ), and APOE and Family history risk factors. Spearman Correlations (coefficient and p–value) and t-test statistic (with its p–value) are reported for continuous and categorical (DXConv, FH, APOE) data respectively.¹

Biomarker	Baseline	Cross-sectional		Longitudinal change
		12 months	24 months	12 months	24 months
MMSE	0.39, p <<10−4	0.49, p << 10−4	0.45, p << 10−4	0.21, p = 0.0008	0.33, p = 0.0003
ADAS	−0.56, p <<10−4	−0.58, p << 10−4	−0.53, p << 10−4	0.21, p = 0.0007	−0.53, p << 10−4
MOCA	0.48, p <<10−4	0.51,p<< 10−4	0.59, p << 10−4	0.06, p > 0.1	0.59, p =10−4
RAVLT	0.49, p <<10−4	0.52, p << 10−4	0.57, p << 10−4	0.13, p = 0.04	0.57, p = 0.0008
PsyMEM	0.56, p <<10−4	0.57, p << 10−4	0.59, p << 10−4	0.28, p <10−4	0.42, p = 0.001
PsyEF	0.52, p <<10−4	0.57,p << 10−4	0.46, p << 10−4	0.15, p = 0.02	0.26, p = 0.05
HippoVol	0.72, p <<10−4	0.74, p << 10−4	0.79, p << 10−4	0.33, p << 10−4	0.47, p << 10−4
CDR-SB	−0.33, p <<10−4	−0.49, p << 10−4	−0.55, p << 10−4	−0.36, p << 10−4	−0.53, p << 10−4
DxConv	-- NA --	21, p << 10−4	31, p << 10−4	21, p << 10−4	31, p << 10−4
τ	−0.39, p <<10−4	-- NA --	-- NA --	-- NA --	-- NA --
pτ	−0.40, p <<10−4	-- NA –	-- NA --	-- NA --	-- NA --
Aβ	0.55, p <<10−4	-- NA --	-- NA --	-- NA --	-- NA --
τ/Aβ	−0.52, p <<10−4	-- NA –	-- NA --	-- NA --	-- NA --
pτ/Aβ	−0.52,p<<10−4	-- NA –	-- NA –	-- NA –	-- NA –
APOE	3.47, p = 0.0006	-- NA --	-- NA --	-- NA --	-- NA --
FH	2.16, p = 0.03	-- NA --	-- NA --	-- NA --	-- NA --

¹Observations with p << 0.0001 are bold, and p < 0.001 are italic. Column 2 shows correlations of baseline rDAm with markers at baseline. Columns 3 and 4 are correlations of baseline rDAm with markers themselves at 12 and 24 months respectively. Columns 5 and 6 are correlations of baseline rDAm with change (i.e. difference) in the markers from baseline to 12 and 24 months. Note that CSF levels, FH and APOE do not have any meaning in column 5 and 6, and hence are marker ‘NA’. Same is the case with DxConv at baseline, since baseline diagnosis of all subjects considered here is MCI.

Figure 1.

Mean longitudinal change of several disease markers as a function of baseline rDAm enrichment threshold. Each plot corresponds to one disease marker (which include MMSE, ADAS, RAVLT, MOCA, PsychMEM, PsychEF, Hippocampal Volume, CDR-SB and DxConv, refer to Section 3.1 for details about these markers). x-axis represents the baseline rDAm enrichment cut-off (t). For each t, the subjects who have baseline rDAm ≫ t are filtered-out, and the mean of within subject change in the disease marker is computed on the remaining un-filtered subjects. Dots represent actual values, and lines are the corresponding linear fit. Blue and black represent changes from baseline to 12 and 24 months respectively.

Figure 6.

Mean of several disease markers as a function of baseline rDAm enrichment threshold. Each plot corresponds to one disease marker (which include MMSE, ADAS, RAVLT, MOCA, PsychMEM, PsychEF, Hippocampal Volume, CDR-SB and Dx Change. x-axis represents the baseline rDAm enrichment cut-off (t). For each t, the subjects who have baseline rDAm ≫ t are filtered-out, and the mean of within subject change in the diseas marker is computed on the remaining un-filtered subjects. Lines are the corresponding linear fit, and the error bars correspond to the stnadard errors. Blue, black and red represent baseline, 12 and 24 months respectively.

Tables 2 and 3 present samples estimated using rDAm as a sample enricher at 80% statistical power (significance level of 0.05) and inducing a treatment effect of 25%. Recall that higher rDAm implies closer to being healthy. Hence, enrichment entails filtering out all subjects with baseline rDAm above some cut-off. Results show that compared to the no-enrichment regime (column 2, Table 2), the sample estimates from rDAm enrichment are significantly smaller, with more than 5 times reduction when using bottom 20% and 25% percentiles (columns 3 and 4, Table 2). In particular, MMSE, CDR-SB and DxConv give consistently smaller estimates (200 to 600) across all columns (the four different percentiles). ADAS and PsychEF still required very large sizes (774 and >2000 respectively) even at 20% enrichment percentile. Using extra covariate information in the form of FH and APOE⁷, in tandem with baseline rDAm, the sample estimates further decrease as shown in Table 3 (last three columns). APOE as a covariate resulted in smallest possible estimates (<350 per arm) across all the outcomes except PsyEF (last two columns in Table 3), although the last column represents using both APOE and FH as covariates. DxConv as an outcome with rDAm + APOE enrichment yields a sample size of 170. Figure 2 shows the detectable effect sizes as rDAm enrichment cut-off is varied, for a fixed sample size of 500 per arm. The detectable effect size (1-η) decreases as more weak decliners are filtered out. This can be seen by the “increase” of η (y-axis) as rDAm cut-offs (x-axis) decrease, specifically for MMSE, CDR-SB and DxConv outcomes. Finally, Table 4 compares rDAm with other imaging-derived inclusion criteria (the cut-off for all the enrichers corresponds to including the strongest 20% decliners in their respective scales). rDAm consistently outperformed other alternatives, with up to 2 times smaller estimates than MKLm (multi-modal generalization of SVM), and much larger reductions compared to uni-modal summaries (hippocampal volume, FDG ROIs and florbetapir ROIs).

Table 2.

Baseline rDAm for sample enrichment: Results of sample enrichment using baseline rDAm (constructed using all the three imaging modalities T1 MRI, FDG and florbetapir) in a 2 year trial with outcome measures being MMSE, ADAS, MOCA, RAVLT, PsychMEM, Hippocampal Volume, CDR-SOB and DxConv. All estimates at significance level of 0.05 and 80% statistical power with treatment effect of 0.25. Second column shows sample estimates with no enrichment (i.e. all clinically-diagnosed MCI subjects included), followed by using MCI subjects from bottom 20%, 25%, 33% and 50% percentiles on rDAm scores respectively. For eachpercentile, the cutoff on rDAm scale is shown and sample sizes smaller than 700 are in bold.

Outcome measure	No enrichment	Bottom 20% rDAm ≤ 0.41	Bottom 25% rDAm ≤ 0.46	Bottom 33% rDAm ≤ 0.52	Bottom 50% rDAm ≤ 0.65
MMSE	1367	200	239	371	566
ADAS	>2000	775	945	>2000	>2000
MOCA	>2000	449	674	960	1919
RAVLT	>2000	591	1211	>2000	>2000
PsyMEM	>2000	420	690	786	1164
PsyEF	>2000	>2000	>2000	>2000	>2000
HippoVol	>2000	543	1504	1560	1675
CDR-SB	1586	281	317	430	433
DxConv	895	230	267	352	448

Table 3.

Baseline rDAm + FH and/or APOE for enrichment: Using already enriched subjects from the bottom 20% percentileon rDAm scale (fourth column from Table III), and further screening out subjects with negative FH and/or APOE. Second column to last columns are results with no enrichment, FH alone, APOE alone, rDAm alone, rDAM + FH, rDAM + APOE and rDAM + both respectively. The best estimates from rDAM + FH and/or APOE are shown in bold.

Outcome measure	No enrichment	FH Only	APOE Only	rDAm only	rDAm + FH	rDAm + APOE	rDAm + both
MMSE	1367	1668	1015	200	182	240	186
ADAS	>2000	>2000	>2000	775	574	328	271
MOCA	>2000	>2000	>2000	449	516	326	334
RAVLT	>2000	>2000	>2000	591	394	484	332
PsyMEM	>2000	>2000	>2000	420	481	310	333
PsyEF	>2000	>2000	>2000	>2000	>2000	1337	721
HipopVol	>2000	>2000	>2000	428	391	274	246
CDR-SOB	1586	1787	763	281	255	217	225
DxConv	895	932	509	230	244	170	192

Figure 2.

Detectable drug effect η as a function of baseline rDAm enrichment cut-off. Recall that η is the hypothesized induced treatment effect where (1−η) denotes the expected percentage of reduction in the outcome measure. Each plot corresponds to using one of the nine disease markers (MMSE, ADAS, RAVLT, MOCA, PsychMEM, PsychEF, Hippocampal Volume, CDR-SB and DxConv, refer to Section 3.1 for details about these markers) as an outcome measure. x-axis represents the baseline rDAm enrichment cut-off (t). For each t, y-axis shows the effect size detectable at 80% power and significance level of 0.05 using 500 samples per arm. As with the results in Table 3, each plot also shows improvements when using FH and/or APOE information in tandem with baseline rDAm enrichment. Blue, green, black and red correspond to rDAm, rDAm + APOE, rDAm + FH and rDAm + APOE + FH enrichment respectively.

Table 4.

Baseline rDAm vs. other imaging-derived sample enrichers. Comparing rDAm's estimates to that of using Hippocampal Volume, FDG ROIs (left temporal, right temporal, left angular, right angular and bilateral cingulum), florbetapir SUVR ROIs (frontal, temporal, parietal, and cingulate gray matter) and MKLm as enrichers. FAH corresponds to linear combination of Hippocampal Volume, FDG and AV45 ROIs. All the estimates correspond at bottom 20% percentiles (i.e., high risk subjects) on the corresponding enricher scale. The best possible estimate per arm is shown in bold.

Sample Enricher	Outcome measure
	MMSE	ADAS	MOCA	RAVLT	PsyMEM	HippoVol	CDR-SOB	DxConv
HippoVol	540	>2000	1005	1606	1009	>2000	389	420
FDG	384	1954	579	>2000	832	752	415	371
AV45	224	>2000	875	>2000	826	698	382	443
FAH	296	>2000	705	>2000	826	722	397	402
MKLm	228	874	827	896	487	877	295	284
rDAm	200	775	449	591	420	543	281	230

4. Discussion

The ability to design clinical trials with smaller sample sizes but sufficient statistical power will enable the implementation of affordable, tractable and hopefully, conclusive trials. Efficiency is seriously compromised in trials where there is poor biomarker specificity of disease progression and when the outcomes contain relatively high amounts of error variance. Determining whether promising treatments are effective in the MCI phase of AD requires accurate identification and inclusion of only those MCI participants most likely to convert to AD and selection of outcomes that are both disease related and possess optimal measurement properties. We have shown that the sample size required to detect a treatment effect can be substantially reduced using the proposed inclusion strategy. The central message of our empirical evaluations is that the baseline rDAm has good predictive power in identifying future disease progression as shown in Table 1 and Figure 1. Together with rDA’s capacity to reduce prediction variance, we see smaller sample estimates compared to existing imaging-derived enrichers as shown in Table 4.

Table 1 supports the general consensus that imaging data captures disease progression [10, 26]. This can be seen from the very strong correlations of baseline rDAm with longitudinal change in several cognitive scores (last four columns in Table 1). It should be noted that high correlations with hippocampal volume (across all time-points) are expected because T1 MRI image at baseline is used in the construction of baseline rDAm. Although hippocampus voxels are used in the rDA model, its inclusion (as an outcome) in our experiments is primarily for completeness. That is, hippocampal volume has been used extensively in previous AD imaging studies [14, 16, 25, 26], and including it ensures continuity with this literature. Interestingly, FH had a lower dependence on rDAm which might be because its influence is superseded by actual neurodegeneration once a subject reaches MCI stage (i.e., FH may play a much stronger role in the asymptomatic phase). Note that we did not correct for age (and other covariates like brain volume) because the markers reported in Table 1 are used directly with no covariate correction in our later evaluations on sample enrichment (Tables 2–4). This is based on the assumption that an actual clinical trial design with randomized treatment assignment would not need to correct for the individual’s age to evaluate eligibility and rDAm is agnostic to all such variables.

Observe that most classification based measures which are used as disease markers are generally unbounded[13]. These include the prediction score from a SVM based classification model on a test subject, or summary measures like S-score, t-score, F-score etc. Unlike these measures, rDAm is bounded to 0 and 1, using which we can visualize its predictive power without any post-hoc normalization (as shown in Figure 1). Except for RAVLT, all other markers used as outcomes (in Table 2 and 3) had steeper changes over time as baseline rDAm decreased, and in none of the cases was there a clear elbow separating weak and strong decliners. This shows that the disease progression is gradual from healthy to AD, and any classifications (like early and late MCI) are mostly artificial. It is interesting to see that rDAm high predictive power for DxConv (Table 1 and Figure 1), implying that subjects with smaller baseline rDAm (closer to 0) have very high likelihood of converting from MCI to AD, providing additional evidence that baseline rDAm is a good predictive disease marker.

Although there is no phase change (since rDAm is lower bounded to 0), we can always select a fixed fraction of subjects that are closest to 0 on the rDAm scale, and claim that they are the strong decliners we should include in a trial. The exact value of such fraction would depend on the logistics and size of the intended trial. This is the reason for the bottom fraction-based enrichment using baseline rDAm as shown in Tables 2–4. Further, note that the high predictive power of baseline rDAm solves an important problem with existing approaches to designing inclusion criteria which use longitudinal data (e.g., Tensor-based morphometry)[8, 13]. Deploying such methods in practice implies that the trial screening time should be at least a year or longer, which is not practical. Although longitudinal signals are much stronger than cross-sectional ones, the results in Table 1 and Figure 1 show that the rDAm marker at trial start-point can still be used with no loss of information, saving trial resources and reducing the cost of trial setup.

The first observation from sample estimates in Table 2 and 3 is that MMSE,CDR-SB and DxConv outperform all other alternate outcomes considered here, even in the no-enrichment regime. This is counter intuitive because of the simplicity of MMSE compared to other composite scores like PsyMEM and PsyEF (neuro-psych memory and executive function composites). It is possible that the composite nature of these measures increases the outcome variance, and thereby increases the sample estimates. Since our population is entirely MCIs, it is expected that the distribution of rDAms is fairly uniform from 0 to 1, which is not the case as shown from rDAm enrichment cut-offs at each percentiles (the top row of last four columns in Table 2). More precisely, the bottom 50% corresponds to a cut-off of 0.65 and 33% corresponds to 0.52, which indicates that more than two-thirds of MCIs in the ADNI2 cohort are healthier (i.e., weak decliners), and also that enrichment is important. This idea has also been identified by others using cognitive characteristics [27]. Ideally, we expect to observe a particular rDAm cut-off (an elbow cut-off) at which there might be the highest decrease in estimates for all outcomes in Table 2 and 3. The elbow cut-off should be a natural threshold point that separates strong and weak decliners on baseline rDAm scale. However, the trends in sample estimates in Table 3(a) do not seem to suggest such a threshold, which is not surprising from Figure 1 and the corresponding discussion above. Specifically, ADAS and RAVLT seem to have an elbow between 25% and 33%, while for MMSE, CDR-SB and DxConv, the elbow is beyond 50%. Since we have 267 MCIs to begin with, a bottom 20% enrichment (third column, Table 2) corresponds to a population size of 52, implying that the estimates might be noisy.

Covariate information (or rather, a preliminary selection based on a factor like Family History) is almost always helpful in estimating group effects, which is observed from Table 3 where using FH and/or APOE details as “filters” prior to rDAm enrichment reduced the estimates further. It has been observed that subjects with positive FH (either maternal or paternal) and/or APOE e4 positive may have stronger characteristics of dementia [28]. This implies that instead of starting off with all MCIs, it is reasonable to include only those MCIs with positive FH and/or positive APOE e4, and then perform the baseline rDAm enrichment on this smaller cohort. Recall that APOE had a higher dependence on baseline rDAm compared to FH (from Table 1), resulting in a higher reduction when using rDAm + APOE or rDAm + APOE + FH (last two columns) than using rDAm + FH (sixth column) for most all the cases except MMSE (row 1 in Table 3). Note that Table 3 corresponds to bottom 20% rDAm enrichment, of which about half were FH and/or APOE positive. The overall strong performance of DxConv resulting in small sample estimates may be because it summarizes the conversion of MCI to AD using longitudinal information, where as rDAm tries to predict this conversion using baseline information alone. Overall, Tables 2 and 3 support the efficacy of rDAm enrichment; however, an interesting way to evaluate the strength of rDAm is by fixing the number of trial-enrolled subjects and computing the detectable treatment size (η). If in fact, rDAm successfully selects strong decliners, then the trial should be able to detect smaller expected decrease in disease (i.e., smaller 1-η or larger η, refer to the sample size equation in Section 2.1 above). Figure 2 shows exactly this behavior, where η (y-axis) increases drastically as rDAm cut-offs (x-axis) are decreased (especially for MMSE,CDR-SB and DxConv). From the practical perspective of a practitioner, this gives a tool for evaluating the minimum treatment effect that can be deemed significant, from a fixed cut-off and sample size.

We discussed in Section 1 that although effective imaging-derived disease markers exist (either based on machine learning models or directly computed from imaging ROIs), they may not lead to the best possible clinical trials. This is supported by the results in Table 4, where rDAm (which is designed to explicitly reduce the prediction variance) is compared to existing markers that have been used as trial inclusion criteria [2, 14, 16]. For example, ROI summaries from multiple imaging modalities have often been used as trial enrichers [1, 2], and rDAm significantly outperforms these baselines (first four rows in Table 4). Further, [14] used SVM models to design effective disease marker and used it as an inclusion criterion in trials. Correspondingly, we compared rDAm to MKLm (which is based on a multi-kernel SVM), and the results in Table 4 show that baseline rDAm as an enricher outperforms MKLm, and the improvements are higher for MOCA, RAVLT and Hippocampal Volume as outcomes. Note that for the current paper, we actually did not adjust any of the parameters relative to the results reports earlier [10]. These were the defaults for the MKL code-base provided on the webpage (http://pages.cs.wisc.edu/~hinrichs/MKL_ADNI/). The necessity of incorporating multi-modal information in designing any disease markers has been reported earlier [10, 11]. This is further supported by the improvement of rDAm estimates over uni-modal measures including hippocampal volume, FDG ROI summaries and florbetapir ROI summaries. These results also build upon the work of [1, 2] where such unimodal imaging summaries are used for enrichment. It is possible to demonstrate that the performance gains of rDAm over [1, 2]is not merely due to using three distinct modalities but also heavily influenced by the underlying machine learning architecture that exploits this information meaningfully. To see this, compare the enricher “FAH” in Table 4 that corresponds to combining the three uni-modal measures, FDG, florbetapir, and hippocampal volume. Its sample estimates are still larger than those obtained from rDAm implying that the reductions are not merely due to multi-modal data or small population size, but due to the efficacy of deep learning methods (i.e., rDAm’s capacity of picking up strong decliners with high confidence with small variance) introduced here.

Overall, these results suggest that rDAm enrichment reduces sample sizes significantly leading to practical and cost-effective AD clinical trials. The rDA model by itself is expressive that scales to very large dimensions, uses only a small number of instances, and can be easily incorporated to design robust multi-modal imaging markers. It should be noted that, the framework can be improved further, particularly in terms of using a richer pooling strategy instead of ridge regression (refer to the appendix) and using other covariate information (like age, CSF levels) in the rDA construction itself. These technical issues are of independent interest and will be investigated in future work. All the implementations used in the paper will be made available at http://pages.cs.wisc.edu/~vamsi/rda upon manuscript acceptance.

Research in Context.

Systematic Review

An efficient trial inclusion criterion should be able to discriminate weak decliners from the strong ones robustly. Further, the screened strong decliners should have less variability if the screening criterion is to result in smaller sample estimates. These two requirements imply that the sample enricher needs to learn complex concepts while reducing the prediction variance. The statistical framework presented here offers both these features and yields substantial improvements over alternative strategies.

Interpretation

First, this work provides strategies for sample enrichment in AD clinical trials. Second, the results show that rDAm predicts strong decliners with high confidence. Third, the findings show that baseline rDAm inclusion criterion is the best available imaging-derived enricher, which leads to smaller trials.

Future Directions

Improving the rDA model by using richer pooling strategies and better ensemble generation. Further, using easily available covariate information (like FH, APOE, age etc.) in the rDA construction (or training) itself.