Abstract
Purpose:
To create a database of highly realistic and anatomically variable 3D virtual breast phantoms based on dedicated breast computed tomography (bCT) data.
Methods:
A tissue classification and segmentation algorithm was used to create realistic and detailed 3D computational breast phantoms based on 230 + dedicated bCT datasets from normal human subjects. The breast volume was identified using a coarse three-class fuzzy C-means segmentation algorithm which accounted for and removed motion blur at the breast periphery. Noise in the bCT data was reduced through application of a postreconstruction 3D bilateral filter. A 3D adipose nonuniformity (bias field) correction was then applied followed by glandular segmentation using a 3D bias-corrected fuzzy C-means algorithm. Multiple tissue classes were defined including skin, adipose, and several fractional glandular densities. Following segmentation, a skin mask was produced which preserved the interdigitated skin, adipose, and glandular boundaries of the skin interior. Finally, surface modeling was used to produce digital phantoms with methods complementary to the XCAT suite of digital human phantoms.
Results:
After rejecting some datasets due to artifacts, 224 virtual breast phantoms were created which emulate the complex breast parenchyma of actual human subjects. The volume breast density (with skin) ranged from 5.5% to 66.3% with a mean value of 25.3% ± 13.2%. Breast volumes ranged from 25.0 to 2099.6 ml with a mean value of 716.3 ± 386.5 ml. Three breast phantoms were selected for imaging with digital compression (using finite element modeling) and simple ray-tracing, and the results show promise in their potential to produce realistic simulated mammograms.
Conclusions:
This work provides a new population of 224 breast phantoms based on in vivo bCT data for imaging research. Compared to previous studies based on only a few prototype cases, this dataset provides a rich source of new cases spanning a wide range of breast types, volumes, densities, and parenchymal patterns.
Keywords: digital phantoms, simulation, segmentation, breast imaging, mammography, CT
1. INTRODUCTION
More than 1 in 8 women who live for 80 years are diagnosed with breast cancer in their lifetime making it the second leading cause of cancer death for women in the United States. Early detection of breast cancer has been found to significantly improve survival rates. This underscores the need for early detection to enable diagnosis and effective treatment. Among other clinically available techniques, screening x-ray mammography is presently the most effective for early detection of breast cancer. Despite the success of mammography, there is still substantial room for improvement.1,2 A major limitation to mammography is that volumetric information is inferred from 2D projection images: the tissues are superimposed on one another making the detection of breast cancer challenging.1 Overall, the breast lesion detection sensitivity of screening mammography falls between 63% and 88% and is dependent upon patient age, family medical history,3 breast density,4 and technical factors (e.g., image acquisition technique factors, dose, and quality of the imaging system) among other factors. To address some of the limitations of mammography, several promising new breast imaging technologies have emerged: digital breast tomosynthesis (DBT),5,6 contrast-enhanced mammography,7,8 and dedicated breast computed tomography (bCT).9,10 However, it can be challenging to fully evaluate each technology, its merits, and its shortcomings, especially in the preclinical phases. While clinical trials still serve as the gold standard for making these evaluations, they are costly, time consuming, and sometimes involve risk to the patient (e.g., radiation dose). In response to these challenges, one proposal is the use of virtual clinical trials involving the use of computerized phantoms in realistic imaging scenarios.
Two main approaches have typically been utilized to create computerized phantoms for breast imaging research: (a) rule-based models where the anatomy is defined by mathematical equations or relationships and (b) voxelized models based upon human imaging data. Rule-based models11–16 utilize a combination of voxel matrices and geometric primitives to create a phantom that may include the breast surface, the duct system, terminal ductal lobular units, Cooper’s ligaments, the pectoral muscle, and breast abnormalities. Because of their mathematical basis, phantoms such as the ones made by Bakic et al. can produce a multitude of variable models for an imaging study.17–19 In spite of their complexity, however, they are limited in their level of realism when compared to actual patient data. Alternatively, voxelized phantoms have been investigated as a means to produce more realistic models. These types of phantoms have been largely based on dedicated bCT data from mastectomy specimens.20,21 However, these specimens do not adequately represent intact breasts. Currently, only a small number of voxelized phantoms using this method exist due to limited access to specimens.
We have taken a different approach to address the limitations of mathematical and voxelized phantoms through the segmentation of in vivo bCT data. Our current work is based on the original work of Li et al.22 and several key improvements to that work contributed by Segars et al.23 Further modification, improvements, and more bCT segmentations have been performed in order to create a larger cohort of over 200 realistic and detailed 3D computational breast phantoms based on in vivo human subject bCT data with the goal of incorporating them into the 4D XCAT suite of phantoms. The phantoms are hybrid models: they are derived from imaging data like voxelized phantoms but like mathematical phantoms, they use geometric surfaces to define the anatomy.24 The anatomical basis provides a foundation for building digital breast phantoms which emulate actual breast anatomy, while the mathematical basis provides flexibility to manipulate and deform the models—a benefit which, for example, allows for realistic breast compression and manipulation for multimodality imaging simulations. Furthermore, previous work has shown that a nearly limitless number of realistic phantoms can be derived by merging and manipulating a small number of 3D computational breast phantoms.25 These methods can be used in conjunction with the larger cohort of phantoms presented in the current work to produce an even larger and more diverse population of digital breast models. Ultimately, the breast phantoms developed in this work will be packaged into a user-friendly software application to distribute for breast imaging research.
2. METHODS
2.A. bCT segmentation
The phantoms produced in this work are based on 231 dedicated bCT datasets obtained through a cooperative agreement with John Boone at the University of California, Davis (UC Davis).26–28 The majority of the women imaged were at a high degree of suspicion for breast cancer (BIRADS 4 or 5), and many were diagnosed with malignant breast cancers; however, all bCT data provided in this study were derived from unaffected breasts. A more detailed description of the bCT dataset demographics is provided by Huang et al.26 Seven of the original 231 datasets received were removed from analysis due to image artifacts, and each of the remaining datasets was segmented using a semiautomated method. Several other authors have developed bCT segmentation algorithms. Notable among them are Chen,29 Nelson et al.,30 and Yang et al.31 Chen used histogram partitioning into five subintervals followed by interval thresholding to decompose the breast into five segmentation classes based on voxel intensity. The methods of Nelson et al. employed a two compartment histogram model to classify adipose, glandular, and skin tissues. This was done using a median filter (to reduce noise) followed by region growing. The methods of Yang et al. made several novel contributions to the (nontrivial) task of bCT segmentation. They corrected adipose nonuniformities with a bias field correction method, denoised the volume using a bilateral filter, and segmented the bCT volume into three classes using a fuzzy C-means (FCM) classification approach. The methods of Yang et al.31 inspired several improvements to the original work of Li et al.22 which were necessary to develop a sufficiently generalized approach capable of adequately segmenting a larger and highly variable data set. Table I provides an overview of the updated segmentation algorithm which can be compared and contrasted with the segmentation steps of Li et al.22 and Yang et al.31 Sections 2.B–2.H explain in detail the major components of the new segmentation routine.
TABLE I.
Overview of steps in the segmentation routine.
| BCFCM3D masking of bCT volume |
| ↓ |
| Noise reduction of reconstructed bCT data |
| ↓ |
| Voxel intensity normalization |
| ↓ |
| 3D nonuniformity (bias field) correction |
| ↓ |
| Conversion to cubic voxels |
| ↓ |
| BCFCM3D bCT segmentation |
| ↓ |
| Skin segmentation |
| ↓ |
| Surface model generation |
2.B. Breast volume masking
Masking of the breast volume to separate it from the background is the first step in the segmentation process. The original volume segmentation method by Li et al. implemented a thresholding scheme that required manual tuning of the threshold value for each breast volume.22 This process was automated through the use of a 3D bias-corrected fuzzy C-means (BCFCM3D) algorithm.32 The standard FCM algorithm objective function was modified to involve the influence of immediate neighbors,33
| (1) |
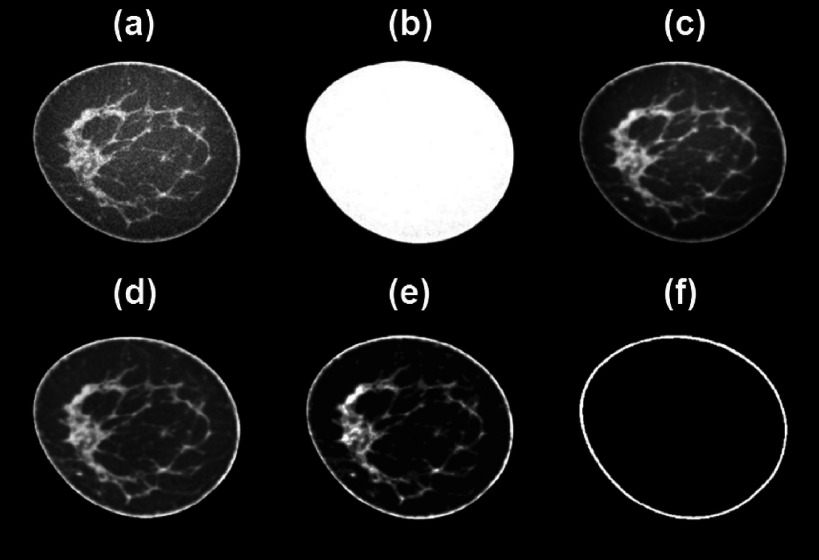
Equation (1) is comprised of two parts—a voxel intensity component and a spatial component. The first intensity-based component involves yk which are the original image voxel values corrected by bias field βk and compared to cluster means vi. is the probability of FCM class membership, and p is a weighting component that determines the “fuzziness” of the resultant classification. The second spatial component of the algorithm serves as a regulizer which biases voxel classification toward that of its neighbors , the set of voxels neighboring yk. α is another weighting term controlling the influence of neighbor classification, and NR is the cardinality of . Bias field estimation and iterative objective function minimization schema are well-described by other authors.32,33 Three voxel intensity values were used to define three cluster means: background, breast, and background/breast average intensities. The third class was used to exclude breast boundary blurring and artifacts due to the partial volume effect and patient motion during bCT data acquisition as depicted in Fig. 1. The breast volume mask was finalized through morphological smoothing with a 3D spherical structuring element with 1 mm radius to smooth the breast mask external boundary.34
FIG. 1.
Breast volume masking. (a) Original bCT coronal slice showing severe motion artifact. (b) BCFCM3D segmentation of (a) depicting three segmentation classes: background (black), breast, and background/breast average (gray). (c) Masked version of (a) with intermediary (blurred) boundary removed.
It should be noted that patient motion may affect both the rendition of the breast boundary and structures internal to the breast. While the methods described in this section are designed to correct motion artifacts affecting the breast external boundary, no attempt has been made to correct artifacts associated with structures within the breast volume. This topic is discussed at length in Sec. 4.
2.C. Denoising
Of the 224 bCT datasets, projection space denoising was previously applied to 53 using partial diffusion equation-based techniques as part of work by Xia et al.35 The remaining 171 datasets were reconstructed without projection space denoising and contained considerable noise due to quantum mottle. This required a postreconstruction denoising method to improve segmentation quality. A 3D bilateral filter was applied to the reconstructed bCT volumes to preferentially smooth the noise while attempting to preserve the sharpness of tissue boundaries and other anatomical structures,36
| (2) |
The bilateral filter works by weighting the influence of both Euclidian distance (governed by the σD term) and radiometric differences (governed by the σR term) between a pixel and its neighbors (within local neighborhood Ω). Doing so increases the amount of denoising (smoothing) in regions with small fluctuations in voxel intensity and decreases the amount of denoising (smoothing) across large intensity gradients (edges). In order to be properly implemented, bCT volume-specific spatial and intensity filtering parameter values must be determined. The intensity parameter is set to the full width at half maximum (FWHM) of the adipose peak of the breast volume histogram. The spatial parameter is set to the average voxel dimension (measured in mm). These parameter values can be multiplied by a scalar before they are implemented to increase or decrease the overall effect of the bilateral filter. Parameter values were manually optimized by one observer on a case-by-case basis in order to maximize noise reduction without compromising the visibility of finer glandular structures.
2.D. Normalization and 3D nonuniformity correction
The cupping artifact in bCT data attributed to scattered radiation is a well-known phenomenon commonly corrected through the use of a second-order polynomial fit and subtraction of the low-frequency artifact from the original data.37 This correction method was used by Li et al. in a slice-by-slice application.22 However, such a method is not necessarily applicable to nonuniformities which are not well-suited to second-order modeling. For example, breasts with ovular or noncircular coronal cross section will not have circularly symmetric cupping artifact due to scatter. Furthermore, breasts with nonconvex surfaces (e.g., teardrop-shaped breasts) can have even more complex nonuniformity throughout the breast volume. Because of this, a simple second-order polynomial fit is not suitable in general for addressing retrospective (i.e., postreconstruction) adipose inhomogeneity correction.
The current segmentation routine considers adipose inhomogeneity as a 3D artifact with neither specific origin nor form:38 Unlike other techniques, it does not explicitly depend on breast symmetry to perform the correction.37 Adipose nonuniformity was corrected in the new protocol using a nonparametric method initially developed for application to the slowly varying, positive, multiplicative bias field in MRI data with additive noise38 and later applied by Yang et al.31 to bCT data,
| (3) |
The above equation describes the Shannon entropy of the normalized intensity gradient joint histogram associated with image X containing L pixels and N1 grey levels. Its gradient magnitude of X is defined by M with N1 distinct grey levels. δ is the delta function. The entropy function is minimized by modeling multiplicative bias in X using B-spline basis functions of iteratively increasing frequency until no noticeable differences were observed between iterations,
| (4) |
Because this method expands on the widely used Shannon entropy homogeneity measurement, it was first necessary to convert the intensity values of the bCT data onto a zero to unity range. Flattening the adipose intensity profile using this uniformity correction prepared the bCT volume for fibroglandular segmentation.
2.E. Resampling and BCFCM3D segmentation
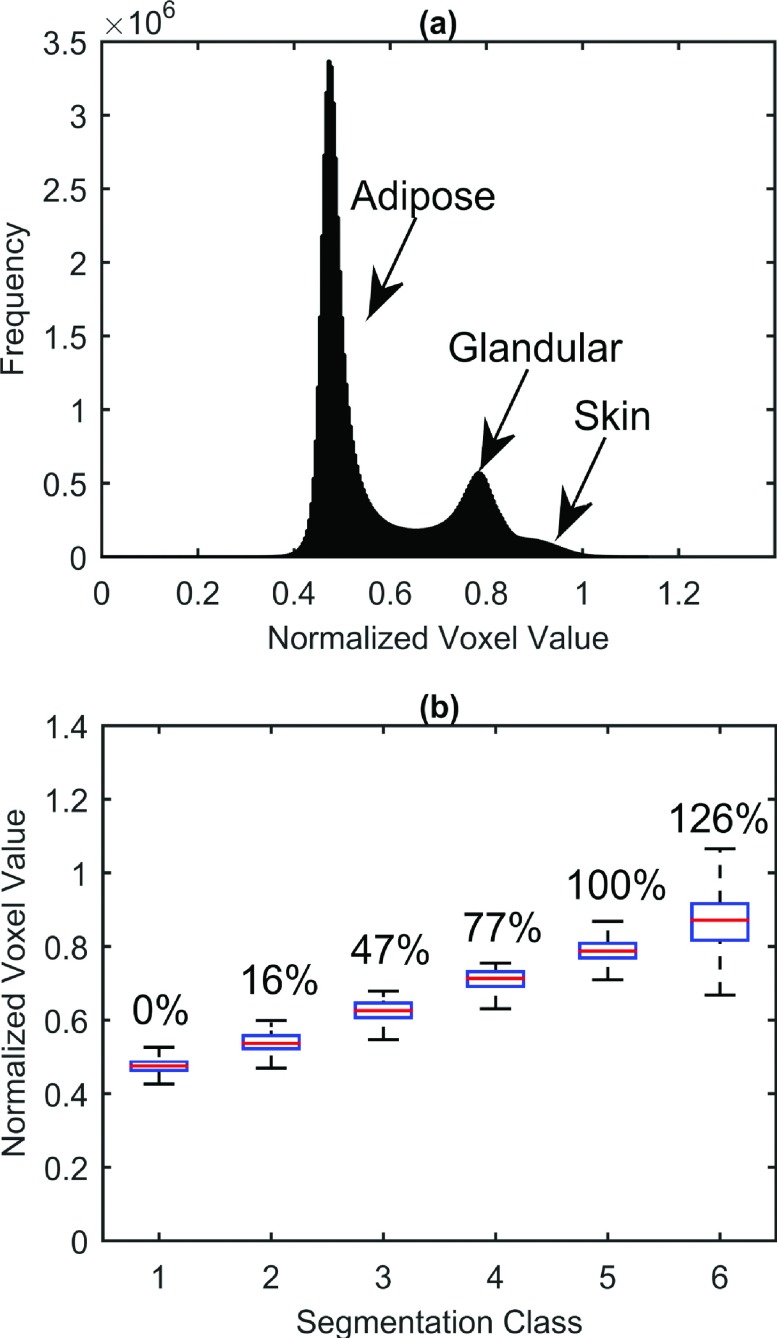
The original bCT data were collected and reconstructed into image matrices with pixel size determined by the diameter of the coronal breast cross section, and slice thickness was determined by the length of the breast. Therefore, prior to segmentation, the bCT volumes were resampled with bicubic interpolation to produce isotropic voxels (with minimum original voxel dimension) to ensure the integrity of the segmentation. Once resampled, the BCFCM3D method of Ahmed et al. was applied a second time to the bCT volume to segment the breast tissue into background, adipose, fibroglandular, and skin classes.32 A total of six tissue segmentation classes were defined to account for the partial volume effect of finite pixel resolution yielding multiple classes with different fractional fibroglandular composition. Six classes were chosen due to a trade-off between fine-structure preservation and computation time. With more classes, computation time and the number low-intensity misclassifications increased; with too few classes, fine glandular structures were improperly classified as fat voxels. The adipose and glandular class means were chosen based on histogram analysis of the breast volume data. The adipose and glandular peaks were automatically detected, and five linearly spaced class means between the peaks were chosen as segmentation seeds corresponding to 0%, 25%, 50%, 75%, and 100% glandular density. However, due to the fuzzy nature of the segmentation routine, the actual resultant class means were subject to change as shown in Fig. 2. The skin intensity peak was used to determine the mean of the final (sixth) tissue segmentation class (if and only if the skin peak was determined to be significantly higher than the glandular peak).
FIG. 2.
Normalized voxel intensity distribution and class assignments from sample bCT dataset. (a) Histogram of voxel intensities clearly shows adipose, glandular, and skin peaks. (b) Box-whisker plot of BCFCM3D segmentation of data into six classes ranging from adipose (0% glandular density—class 1) to glandular (100% glandular density—class 5). Note that skin (class 6) tends to be more dense than glandular tissue making its equivalent glandular density >100%.
2.F. Skin segmentation
The final step in the segmentation algorithm was to accurately locate the internal skin boundary. To maintain the realism of the breast models in this work, it was important to correctly identify the depths at which the glandular and adipose tissues interdigitated with the hypodermal, dermal, and epidermal skin layers. To do this, the external breast boundary was first identified from the perimeter of the breast mask segmentation. Normal vectors were then determined at 50 000–100 000 surface voxels. An iterative approach was then used to make unit-voxel steps toward the breast interior until an adipose voxel was found. A realistic minimum skin thickness limit was set to 0.5 mm, while the maximum skin thickness limit was set to 5 mm.39 Skin thickness estimates were smoothed, and a mask or “skin shell” was formed which contained the external skin surface and the internal breast-skin transition region. The skin was then defined as all nonadipose voxels within this skin shell which contained voxels belonging to the skin class (class 6) in addition to a variety of fractional glandular-equivalent densities (classes 2–5) present at the skin-adipose interface. These glandular-equivalent voxels are attributed primarily to the partial volume effect. The use of a skin shell to define the skin preserved the rough interior surface of the skin while still accurately differentiating the skin from glandular structures and blood vessels internal to the breast. Any voxels classified by the BCFCM3D algorithm as skin-class voxels within the breast parenchyma (e.g., due to microcalcifications or very dense glandular tissue) were forced to assume the highest density glandular class.
2.G. Statistical analysis
The output breast segmentations (8-bit unsigned integer type) along with statistics such as breast volume and volume breast density (VBD) were saved to matlab data (*.mat) files. Breast volume was computed as the total volume of all nonbackground voxels in coronal slices between the end of the pectoral muscle (if visualized) and the nipple. The reported VBD was computed from these same slices using methods similar to those of Yaffe et al.27
| (5) |
| (6) |
where Vfg is the volume of fibroglandular tissue, Vad is the volume of adipose tissue, and Vsk is the volume of skin. VBD without skin (VBDNSk) is computed as the percentage of total breast volume (Vfg + Vad + Vsk) comprised of fibroglandular tissue, whereas VBD with skin (VBDSk) is the percentage of total breast volume comprised of fibroglandular tissue or skin. In a departure from the methods of Yaffe et al. who estimated Vfg, Vad, and Vsk from the total number of voxels identified in fibroglandular, adipose, and skin segmentations, respectively,27 the segmentations in this work contained estimates of the fractional glandular composition of every voxel. Therefore, Vfg, Vad, and Vsk required the following formulae to estimate the respective volumes:
| (7) |
| (8) |
| (9) |
where Vvoxel is the volume of a single voxel, Ffg,i is the fractional glandular composition of segmentation class i, Fad,i is the fractional adipose composition of segmentation class i, Ni is the number of voxels belonging to segmentation class i, and Nsk is the number of voxels.
2.H. XCAT phantom creation
Segmented volumes were used to create a mathematically defined 3D breast phantom in a format congruent with the 4D XCAT suite of phantoms.40 Surface meshes were used to represent the boundaries between fibroglandular classes. Since the intensities of the segmentation correspond to the glandular fraction, increasing from adipose (n1) to skin (nskin), a mesh at the nk+0.5 isosurface creates a boundary between classes nk and nk+1. The resulting meshes created with the Marching Cubes algorithm41 had a nested structure, such that the nk−1 mesh lies completely within mesh nk. Prior to creating the meshes, the background was set to an integer value of nskin + 1. These meshes are capable of representing complicated geometry of arbitrary topology, which are capable of being deformed to model differing patient positions, different states of mechanical compression, and physics of the imaging process.42–45
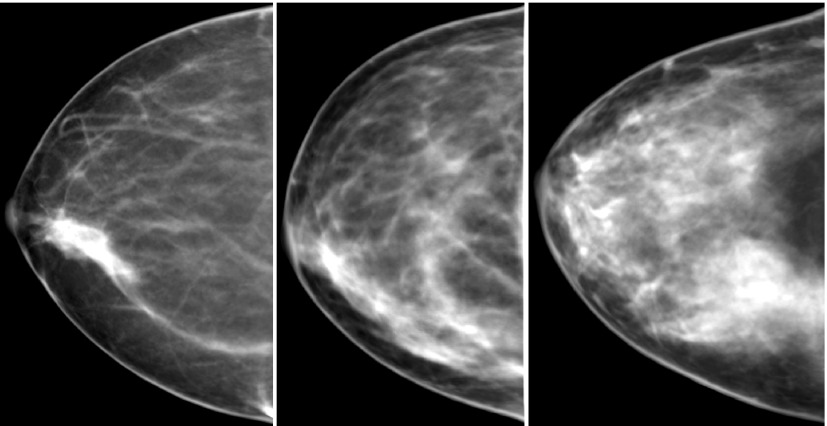
These types of deformations can be solved for using the finite element method, which discretizes a complex domain into a system of smaller simpler elements. Use of the finite element method to model breast deformations and compression has been applied in several applications including multimodality registration,46–48 image-guided surgery,49 and breast augmentation.50,51 Our finite element model uses approximately 60 000 hexahedral elements with six materials of varying stiffness, which are assigned based on the fibroglandular classes within each element. The compression [performed using FEBio (http://mrl.sci.utah.edu/software/febio)] was defined as a displacement constrained problem with a nonlinear contact analysis between the skin surface and the plates (friction neglected), and gravity applied as a body force. The deformation from the finite element model was then applied to the mesh representation of the phantom. A ray-triangle intersection algorithm can be used in conjunction with the resulting deformed meshes to determine the thickness of each material that was intersected by each ray. For the proof-of-concept mammographic images in Fig. 7, a parallel beam projection was performed with the integer of the fibroglandular classes used as a correlate for attenuation.
FIG. 7.
Simulated projection images (with breast compression and ray-tracing). From left to right, VBDSk are 11.8%, 24.7%, and 34.6%, respectively.
3. RESULTS
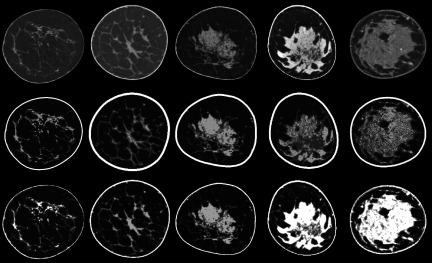
The segmentation algorithm required about 30 min of runtime per case using a 3.4 GHz Intel i7 Processor with 16 GB of RAM running a Windows 7 (64-bit) operating system and matlab R2014a. Refer to Fig. 3 for an illustration of each step in the segmentation routine. Additionally, images from five of the 224 segmented bCT volumes are shown in Fig. 4 to demonstrate how closely our segmented volumes resemble the actual patient data sets with a variety of breast sizes, geometries, glandular distributions, and densities. Our results are also shown alongside segmentations made using the methods of Li et al.22 Based on subjective comparisons, the methods proposed in this paper provide better retention of fine fibroglandular detail and more reasonable skin boundary segmentations.
FIG. 3.
Visual depicition of bCT segmentation processing. (a) Original coronal slice from breast volume. (b) Breast volume mask. (c) Image (a) after masking and denoising with bilateral filter. (d) Image (c) after uniformity correction. (e) BCFCM3D segmentation of (d). (f) Skin mask.
FIG. 4.
(Top) Denoised and nonuniformity-corrected coronal bCT images. (Middle) Phantoms produced with the methods of Li et al. with five integer density classes. (Bottom) Corresponding phantoms from the current work with six segmentation classes shown as integer grayscale levels.
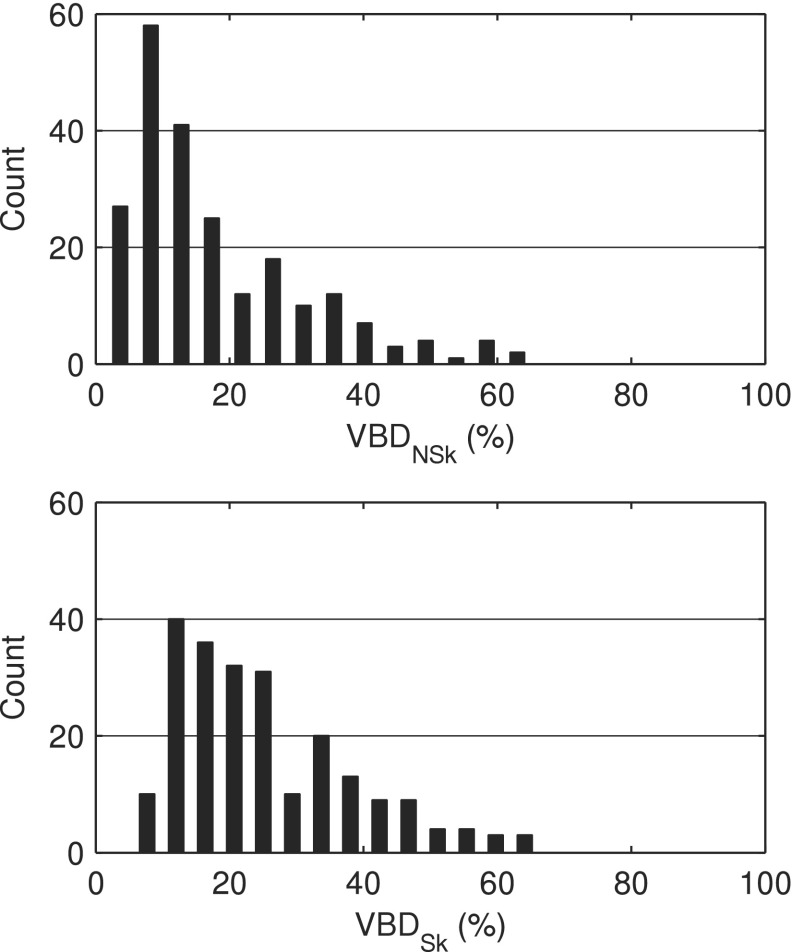
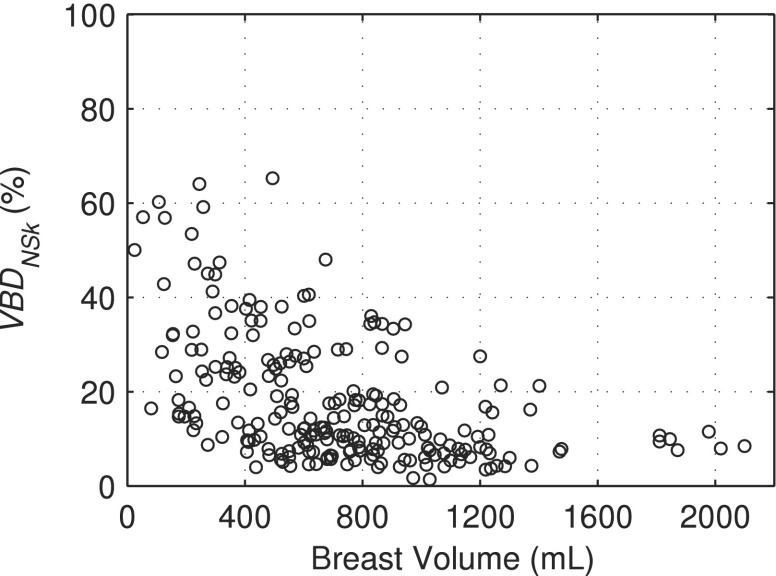
Figure 5 shows the distributions of VBDNSk and VBDSk measured using our methods. The VBDNSk estimates ranged from 1.4% to 65.3% with a mean value of 18.0% ± 13.4% while VBDSk ranged from 5.5% to 66.3% with a mean value of 25.3% ± 13.2%. Segmented breast volumes ranged from 25.0 to 2099.6 ml with a mean value of 716.3 ± 386.5 ml. Figure 5 and the mean and range of breast densities can be compared with the results of Yaffe et al. who found distributions of VBDNSk to be 14.3% ± 10.3% and VBDSk to be 25.6% ± 12.6%. Figure 6 demonstrates the distribution of breast model densities versus breast model volume in the newly available library of phantoms.
FIG. 5.
Volume breast density distributions of the virtual breast phantom library.
FIG. 6.
V BDNSk versus breast volume for 224 bCT subjects.
Figure 7 shows three examples of simulated mammograms after a modeled compression and simple ray-tracing from three different breast phantoms with VBDSk of 11.8%, 24.7%, and 34.6%. The breasts were compressed to 45% of their original diameter resulting in compressed breast thicknesses of 5.5, 4.9, and 5.4 cm, respectively.
4. DISCUSSION
This work has produced a large library of anatomically diverse virtual breast phantoms which, because of their anatomic origins, mirror the natural appearance of breast anatomy and its natural variation in a patient population. This contribution compliments other recent work in the growing field of breast modeling and simulation research. While modifications to prior bCT segmentation methods have resulted in the satisfactory production of over 200 virtual breast phantoms, this approach to breast modeling has several benefits and challenges which merit discussion.
Segmentation of the breast external boundary involved methods which accounted for blur and artifacts attributed to the partial volume effect and patient motion during data acquisition. In Sec. 2.B, it was noted that patient motion may affect both the rendition of the external breast boundary and structures internal to the breast, and that no correction of motion artifacts associated with these internal structures would be attempted. As a result, bCT segmentations derived from cases containing substantial patient motion may be subject to a number of issues depending on the nature of the patient motion. For patients whose breast shifts position during acquisition, a “doubling” of the internal structures may occur due to improper alignment and registration of the internal structures during reconstruction. This doubling would affect the appearance of the glandular architecture and the apparent breast density. In almost all cases involving patient motion, some amount of blurring is involved. Blurring of the fibroglandular structures in the bCT data can cause degradation in the delineation between fibroglandular and adipose tissue in addition to potentially altering assessment of breast attributes such as VGF. Therefore, caution should be exercised when dealing with data potentially contaminated by patient motion, and those data subject to severe patient motion should be screened prior to segmentation and model generation.
The segmentation of 224 bCT volumes presented here has expanded on the earlier work of Li et al.22 In the previous work, the segmentation process was optimized and demonstrated on a single, high-quality breast case. In this work, we have made many modifications to the segmentation algorithm allowing for more reliable and efficient application to hundreds of datasets. One advance was the inclusion of a 3D bilateral filter step to accommodate imaging data that had not been denoised prior to reconstruction. The 3D bilateral filter was used to preferentially smooth the noise while attempting to preserve the sharpness of tissue boundaries and anatomical structures. Another major update to the segmentation routine was the use of a 3D bias-field correction to flatten gross adipose nonuniformities within the breast. This is done to provide more consistent tissue classification across the volume. Compared to the second-order polynomial fit method of Altunbas et al.,37 the new method provided a more generalized approach to nonuniformity correction by not relying on geometric assumptions about the general shape of the nonuniformity. Therefore, nonuniformities due to scatter, beam-hardening, breast positioning, and any incomplete sampling in the bCT data could all be corrected in a single step. A final update to the segmentation routine was the complete revision of the tissue classification algorithm. Previously, iterative histogram classification was applied independently to each axial slice of the bCT data.22 Although this method provided reasonable results in the case of high-quality bCT volumes, it lacked utilization of the 3D voxel neighbor classification information, a characteristic which made the BCFCM3D algorithm more robust, especially when segmenting higher-noise volumes.
Comparing our work to that of Yaffe et al. yielded interesting results. Although the two studies draw on bCT datasets from similar populations, there are key differences between VBD assessments. There are several possible explanations as to why our VBD distributions differ. Yaffe et al. used only the left breast of 191 individuals within their cohort (to maintain independence of the results); our cohort contained bilateral studies from twenty subjects (40 bCT volumes) and 184 unilateral (left or right) breast data from 184 different subjects. Both left and right breast data were used in our study to increase the total number of phantoms produced. It is also possible that our definition of classes with fractional glandularity has positively biased our assessments of VBD. In comparison of our VBDNSk measurements to those of Yaffe, use of classes with fractional granularity may partially explain why our assessment of VBDNSk is 3.7% higher. On the other hand, the average of our VBDSk estimates is only 0.3% lower. This suggests that our methods for segmenting the skin result in lower overall skin density. Although we allowed the skin to assume density which was greater than that of 100% glandular tissue (as Yaffe’s methods also did), our BCFCM3D segmentation algorithm routinely classified voxels at the skin-adipose boundary as mixed glandular + adipose bringing down the overall skin density.
There are some notable limitations to our method of creating phantoms from bCT data. The inherent resolution of the current bCT data is not sufficient to resolve some small anatomical structures (e.g., Cooper’s ligaments and microcalcifications) that are often of interest to researchers and clinicians. The lack of very fine detail structures in turn can negatively impact the realism of the model. To restore these missing data, the work of Lau et al.52 could be used to add detail to our existing models at the high frequencies absent in the bCT data. Their work was specifically developed to enhance existing anthropomorphic breast models. Other authors have taken different approaches to the challenge of simulating realistic breast textures. Elangovan et al.53 have recently demonstrated how breast structure extracted from reconstructed DBT planes can be combined to produce realistic breast tissue background for observer studies in mammography and DBT. Such an approach is attractive since it takes advantage of the high resolution of a digital flat panel detector combined with the quasi-3D resolution of tomosynthesis. Both are interesting works that could be used to improve the realism of the (high-frequency) detail in our population of breast models.
In the same way that microcalcifications and other fine details might be added to enhance the current bCT phantoms, synthetic lesions may also be added to support the utility of these phantoms in virtual clinical trials. This was one motivation for using lesion-free data to produce the initial population of bCT models. The inclusion of lesions in a “healthy” breast model population could affect the outcomes of future virtual clinical trials. Instead, since we elected to start with lesion-free cases, synthetic lesions with controlled size, contrast, shape, etc., can be inserted at will. There is already considerable research on breast lesion modeling,13,54–57 and the feasibility of lesion insertion in our breast model has already been demonstrated in other work suggesting the feasibility of such an approach for virtual clinical trials.58 There is however a caveat to performing virtual clinical trials with a limited (finite) number of available data sets. Previous studies have shown that thousands of models may be required for sufficient statistical power in virtual imaging studies.59,60 While mathematical phantoms have the freedom to create an essentially limitless number of phantoms, our phantoms (based on human subject data) are limited by the number of available bCT datasets. While we recognize this as a potential limitation, bCT data are becoming more readily available to researchers and more common to the clinic. Not only has clinical research involving bCT grown28,61 but the recent FDA approval of the Koning Breast CT system may further increase the availability of clinical cases.62 Additionally, our group has demonstrated the ability to morph between models in order to create a much larger number of phantoms with user-defined anatomical characteristics.25
A second limitation of this segmentation routine is the sensitivity of the algorithm to noise in the bCT data set. As a consequence of using in vivo data, acquisitions are dose-limited and thus limited by the resulting noise which increases the risk of voxel misclassification during segmentation. Our response to this limitation was 2-fold—through the use of a 3D bilateral filter to reduce the noise and through the incorporation of a BCFCM3D segmentation method. With this combined approach to handling image noise, the new segmentation paradigm was successfully applied to produce over 200 digital breast models.
A final limitation and consequence of using the reconstructed bCT images for segmentation is the innate dependence on the reconstruction algorithm. Reconstruction algorithm choice can influence CT image resolution, noise, and artifacts; changes to any of these image quality characteristics may affect the quality of the final segmentation. However, it is important to note that the goal of this work is not necessarily to recreate the exact anatomy of each subject, but rather to generate breast phantoms that portray each bCT dataset with a high degree of realism. Therefore, modest deviations from truth may be tolerable without unduly affecting the utility of the phantom.
5. CONCLUSION
This study provides a new population of 224 breast phantoms for imaging research. As these models are based upon actual human subject bCT imaging data, they offer a degree of realism that may improve the clinical relevance of virtual studies. Compared to previous studies based on only a few prototype cases, this new dataset provides a rich source of cases spanning a wide range of breast types, volumes, densities, and parenchymal patterns. As these phantoms are distributed to the research community, they may be used for a variety of purposes, including virtual clinical trials. Ongoing work seeks to improve the realism of these models as the topics of breast imaging and simulation continue to be subjects of major research and clinical interest.
ACKNOWLEDGMENTS
This work was supported in part by NIH Grant No. RO1-CA134658. The authors thank Dr. John Boone for his gracious collaboration by collecting and making the bCT data available.
REFERENCES
- 1.Jackson V. P., Hendrick R. E., Feig S. A., and Kopans D. B., “Imaging of the radiographically dense breast,” Radiology 188, 297–301 (1993). 10.1148/radiology.188.2.8327668 [DOI] [PubMed] [Google Scholar]
- 2.Yaffe M. J., “What should the burden of proof be for acceptance of a new breast-cancer screening technique?,” Lancet 364, 1111–1112 (2004). 10.1016/S0140-6736(04)17121-3 [DOI] [PubMed] [Google Scholar]
- 3.Kerlikowske K., Carney P. A., Geller B., Mandelson M. T., Taplin S. H., Malvin K., Ernster V., Urban N., Cutter G., Rosenberg R., and Ballard-Barbash R., “Performance of screening mammography among women with and without a first-degree relative with breast cancer,” Ann. Intern. Med. 133, 855–863 (2000). 10.7326/0003-4819-133-11-200012050-00009 [DOI] [PubMed] [Google Scholar]
- 4.Kolb T. M., Lichy J., and Newhouse J. H., “Comparison of the performance of screening mammography, physical examination, and breast US and evaluation of factors that influence them: An analysis of 27,825 patient evaluations,” Radiology 225, 165–175 (2002). 10.1148/radiol.2251011667 [DOI] [PubMed] [Google Scholar]
- 5.Baker J. A. and Lo J. Y., “Breast tomosynthesis: State-of-the-art and review of the literature,” Acad. Radiol. 18, 1298–1310 (2011). 10.1016/j.acra.2011.06.011 [DOI] [PubMed] [Google Scholar]
- 6.Park J. M., E. A. Franken, Jr., Garg M., Fajardo L. L., and Niklason L. T., “Breast tomosynthesis: Present considerations and future applications,” Radiographics 27, S231–S240 (2007). 10.1148/rg.27si075511 [DOI] [PubMed] [Google Scholar]
- 7.Jong R. A., Yaffe M. J., Skarpathiotakis M., Shumak R. S., Danjoux N. M., Gunesekara A., and Plewes D. B., “Contrast-enhanced digital mammography: Initial clinical experience,” Radiology 228, 842–850 (2003). 10.1148/radiol.2283020961 [DOI] [PubMed] [Google Scholar]
- 8.Lewin J. M., Isaacs P. K., Vance V., and Larke F. J., “Dual-energy contrast-enhanced digital subtraction mammography: Feasibility,” Radiology 229, 261–268 (2003). 10.1148/radiol.2291021276 [DOI] [PubMed] [Google Scholar]
- 9.Boone J., Kwan A. C., Yang K., Burkett G., Lindfors K., and Nelson T., “Computed tomography for imaging the breast,” J. Mammary Gland Biol. Neoplasia 11, 103–111 (2006). 10.1007/s10911-006-9017-1 [DOI] [PubMed] [Google Scholar]
- 10.Tornai M. P., McKinley R. L., Bryzmialkiewicz C. N., Madhav P., Cutler S. J., Crotty D. J., Bowsher J. E., Samei E., and Floyd J. C. E., “Design and development of a fully 3D dedicated x-ray computed mammotomography system,” Proc. SPIE 5745, 189–197 (2005). 10.1117/12.595636 [DOI] [Google Scholar]
- 11.Bakic P. R., Zhang C., and Maidment A. D. A., “Development and characterization of an anthropomorphic breast software phantom based upon region-growing algorithm,” Med. Phys. 38, 3165–3176 (2011). 10.1118/1.3590357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bliznakova K., Suryanarayanan S., Karellas A., and Pallikarakis N., “Evaluation of an improved algorithm for producing realistic 3D breast software phantoms: Application for mammography,” Med. Phys. 37, 5604–5617 (2010). 10.1118/1.3491812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen B., Shorey J., R. S. Saunders, Jr., Richard S., Thompson J., Nolte L. W., and Samei E., “An anthropomorphic breast model for breast imaging simulation and optimization,” Acad. Radiol. 18, 536–546 (2011). 10.1016/j.acra.2010.11.009 [DOI] [PubMed] [Google Scholar]
- 14.Näppi J., Dean P. B., Nevalainen O., and Toikkanen S., “Algorithmic 3D simulation of breast calcifications for digital mammography,” Comput. Methods Programs Biomed. 66, 115–124 (2001). 10.1016/S0169-2607(01)00145-6 [DOI] [PubMed] [Google Scholar]
- 15.Pokrajac D. D., Maidment A. D. A., and Bakic P. R., “Optimized generation of high resolution breast anthropomorphic software phantoms,” Med. Phys. 39, 2290–2302 (2012). 10.1118/1.3697523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Taylor P., Owens R., and Ingram D., “Simulated mammography using synthetic 3D breasts,” in Digital Mammography, edited by Karssemeijer N., Thijssen M., Hendriks J., and van Erning L. (Springer, Netherlands, 1998), Vol. 13, pp. 283–290. [Google Scholar]
- 17.Bakic P. R., Albert M., Brzakovic D., and Maidment A. D. A., “Mammogram synthesis using a 3D simulation. I. Breast tissue model and image acquisition simulation,” Med. Phys. 29, 2131–2139 (2002). 10.1118/1.1501143 [DOI] [PubMed] [Google Scholar]
- 18.Bakic P. R., Albert M., Brzakovic D., and Maidment A. D. A., “Mammogram synthesis using a 3D simulation. II. Evaluation of synthetic mammogram texture,” Med. Phys. 29, 2140–2151 (2002). 10.1118/1.1501144 [DOI] [PubMed] [Google Scholar]
- 19.Bakic P. R., Albert M., Brzakovic D., and Maidment A. D. A., “Mammogram synthesis using a three-dimensional simulation. III. Modeling and evaluation of the breast ductal network,” Med. Phys. 30, 1914–1925 (2003). 10.1118/1.1586453 [DOI] [PubMed] [Google Scholar]
- 20.Hoeschen C., Fill U., Zankl M., Panzer W., Regulla D., and Döhring W., “A high-resolution voxel phantom of the breast for dose calculations in mammography,” Radiat. Prot. Dosim. 114, 406–409 (2005). 10.1093/rpd/nch558 [DOI] [PubMed] [Google Scholar]
- 21.O’Connor J. M., Das M., Dider C. S., Mahd M., and Glick S. J., “Generation of voxelized breast phantoms from surgical mastectomy specimens,” Med. Phys. 40, 041915 (12pp.) (2013). 10.1118/1.4795758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Li C. M., Segars W. P., Tourassi G. D., Boone J. M., and Dobbins J. T. III, “Methodology for generating a 3D computerized breast phantom from empirical data,” Med. Phys. 36, 3122–3131 (2009). 10.1118/1.3140588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Segars W. P., Veress A. I., Wells J. R., Sturgeon G. M., Kiarashi N., Lo J. Y., Samei E., and Dobbins J. T., “Population of 100 realistic, patient-based computerized breast phantoms for multi-modality imaging research,” Proc. SPIE 9033, 90331X–90336X (2014). 10.1117/12.2043868 [DOI] [Google Scholar]
- 24.Segars W. P., Ph.D. dissertation, University of North Carolina, 2001. [Google Scholar]
- 25.Hsu C. M. L., Palmeri M. L., Segars W. P., Veress A. I., and Dobbins J. T. III, “Generation of a suite of 3D computer-generated breast phantoms from a limited set of human subject data,” Med. Phys. 40, 043703 (11pp.) (2013). 10.1118/1.4794924 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Huang S.-Y., Boone J. M., Yang K., Packard N. J., McKenney S. E., Prionas N. D., Lindfors K. K., and Yaffe M. J., “The characterization of breast anatomical metrics using dedicated breast CT,” Med. Phys. 38, 2180–2191 (2011). 10.1118/1.3567147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yaffe M. J., Boone J. M., Packard N., Alonzo-Proulx O., Huang S. Y., Peressotti C. L., Al-Mayah A., and Brock K., “The myth of the 50-50 breast,” Med. Phys. 36, 5437–5443 (2009). 10.1118/1.3250863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lindfors K. K., Boone J. M., Nelson T. R., Yang K., Kwan A. L. C., and Miller D. F., “Dedicated breast CT: Initial clinical experience,” Radiology 246, 725–733 (2008). 10.1148/radiol.2463070410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chen Z., “Histogram partition and interval thresholding for volumetric breast tissue segmentation,” Comput. Med. Imaging Graphics 32, 1–10 (2008). 10.1016/j.compmedimag.2007.07.007 [DOI] [PubMed] [Google Scholar]
- 30.Nelson T. R., Cervino L. I., Boone J. M., and Lindfors K. K., “Classification of breast computed tomography data,” Med. Phys. 35, 1078–1086 (2008). 10.1118/1.2839439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yang X., Wu S., Sechopoulos I., and Fei B., “Cupping artifact correction and automated classification for high-resolution dedicated breast CT images,” Med. Phys. 39, 6397–6406 (2012). 10.1118/1.4754654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ahmed M. N., Yamany S. M., Mohamed N., Farag A. A., and Moriarty T., “A modified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data,” IEEE Trans. Med. Imaging 21, 193–199 (2002). 10.1109/42.996338 [DOI] [PubMed] [Google Scholar]
- 33.Bezdek J. C. and Pal S. K., Fuzzy Models for Pattern Recognition (IEEE, New York, NY, 1992). [Google Scholar]
- 34.Nayak D. R., “Image smoothing using fuzzy morphology,” Int. J. Comput. Appl. 1, 43–48 (2012). [Google Scholar]
- 35.Xia J. Q., Lo J. Y., Yang K., C. E. Floyd, Jr., and Boone J. M., “Dedicated breast computed tomography: Volume image denoising via a partial-diffusion equation based technique,” Med. Phys. 35, 1950–1958 (2008). 10.1118/1.2903436 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tomasi C. and Manduchi R., “Bilateral filtering for gray and color images,” in International Conference on Computer Vision (IEEE, Bombay, 1998), Vol. 6, pp. 839–846. 10.1109/ICCV.1998.710815 [DOI] [Google Scholar]
- 37.Altunbas M. C., Shaw C. C., Chen L., Lai C., Liu X., Han T., and Wang T., “A post-reconstruction method to correct cupping artifacts in cone beam breast computed tomography,” Med. Phys. 34, 3109–3118 (2007). 10.1118/1.2748106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Manjón J. V., Lull J. J., Carbonell-Caballero J., García-Martí G., Martí-Bonmatí L., and Robles M., “A nonparametric MRI inhomogeneity correction method,” Med. Image Anal. 11, 336–345 (2007). 10.1016/j.media.2007.03.001 [DOI] [PubMed] [Google Scholar]
- 39.Shi L., Vedantham S., Karellas A., and O’Connell A. M., “Technical note: Skin thickness measurements using high-resolution flat-panel cone-beam dedicated breast CT,” Med. Phys. 40, 031913 (6pp.) (2013). 10.1118/1.4793257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Segars W. P., Sturgeon G., Mendonca S., Grimes J., and Tsui B. M. W., “4D XCAT phantom for multimodality imaging research,” Med. Phys. 37, 4902–4915 (2010). 10.1118/1.3480985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lorensen W. E. and Cline H. E., “Marching cubes: A high resolution 3D surface construction algorithm,” ACM SIGGRAPH Comput. Graphics 21, 163–169 (1987). 10.1145/37402.37422 [DOI] [Google Scholar]
- 42.Li X., Samei E., Yoshizumi T., Colsher J. G., Jones R. P., and Frush D. P., “Experimental benchmarking of a Monte Carlo dose simulation code for pediatric CT,” Proc. SPIE 6510, 65102A–65110A (2007). 10.1117/12.713728 [DOI] [Google Scholar]
- 43.R. S. Saunders, Jr. and Samei E., “A Monte Carlo investigation on the impact of scattered radiation on mammographic resolution and noise,” Proc. SPIE 6142, 61423A–61427A (2006). 10.1117/12.653199 [DOI] [Google Scholar]
- 44.Segars W. P., Mahesh M., Beck T., Frey E. C., and Tsui B. M. W., “Validation of the 4D NCAT simulation tools for use in high-resolution x-ray CT research,” Proc. SPIE 5745, 828–834 (2005). 10.1117/12.595987 [DOI] [Google Scholar]
- 45.Segars W. P., Tsui B. M. W., Frey E. C., and Fishman E. K., “Extension of the 4D NCAT phantom to dynamic x-ray CT simulation,” in IEEE Nuclear Science Symposium, Conference Record (IEEE, Portland, 2003), Vol. 5, pp. 3195–3199. [Google Scholar]
- 46.Han L., Hipwell J., Taylor Z., Tanner C., Ourselin S., and Hawkes D., “Fast deformation simulation of breasts using GPU-based dynamic explicit finite element method,” in Digital Mammography, edited by Martí J., Oliver A., Freixenet J., and Martí R. (Springer, Berlin, Heidelberg, 2010), Vol. 6136, pp. 728–735. [Google Scholar]
- 47.Hopp T., Dietzel M., Baltzer P. A., Kreisel P., Kaiser W. A., Gemmeke H., and Ruiter N. V., “Automatic multimodal 2D/3D breast image registration using biomechanical FEM models and intensity-based optimization,” Med. Image Anal. 17, 209–218 (2013). 10.1016/j.media.2012.10.003 [DOI] [PubMed] [Google Scholar]
- 48.Tanner C., Schnabel J. A., Hill D. L. G., Hawkes D. J., Leach M. O., and Hose D. R., “Factors influencing the accuracy of biomechanical breast models,” Med. Phys. 33, 1758–1769 (2006). 10.1118/1.2198315 [DOI] [PubMed] [Google Scholar]
- 49.Han L., Hipwell J., Mertzanidou T., Carter T., Modat M., Ourselin S., and Hawkes D., “A hybrid fem-based method for aligning prone and supine images for image guided breast surgery,” in IEEE International Symposium on Biomedical Imaging: From Nano to Macro (IEEE, Chicago, IL, 2011), pp. 1239–1242. [Google Scholar]
- 50.del palomar A. P., Calvo B., Herrero J., López J., and Doblaré M., “A finite element model to accurately predict real deformations of the breast,” Med. Eng. Phys. 30, 1089–1097 (2008). 10.1016/j.medengphy.2008.01.005 [DOI] [PubMed] [Google Scholar]
- 51.Roose L., De Maerteleire W., Mollemans W., and Suetens P., “Validation of different soft tissue simulation methods for breast augmentation,” Int. Congr. Ser. 1281, 485–490 (2005). 10.1016/j.ics.2005.03.126 [DOI] [Google Scholar]
- 52.Lau B. A., Reiser I., Nishikawa R. M., and Bakic P. R., “A statistically defined anthropomorphic software breast phantom,” Med. Phys. 39, 3375–3385 (2012). 10.1118/1.4718576 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Elangovan P., Rashidnasab A., Mackenzie A., Dance D. R., Young K. C., Bosmans H., Segars W. P., and Wells K., “Performance comparison of breast imaging modalities using a 4AFC human observer study,” Proc. SPIE 9412, 94121T–94127T (2015). 10.1117/12.2081878 [DOI] [Google Scholar]
- 54.Bliznakova K., Bliznakov Z., Bravou V., Kolitsi Z., and Pallikarakis N., “A three-dimensional breast software phantom for mammography simulation,” Phys. Med. Biol. 48, 3699–3719 (2003). 10.1088/0031-9155/48/22/006 [DOI] [PubMed] [Google Scholar]
- 55.de Sisternes L., Brankov J. G., Zysk A. M., Schmidt R. A., Nishikawa R. M., and Wernick M. N., “A computational model to generate simulated three-dimensional breast masses,” Med. Phys. 42, 1098–1118 (2015). 10.1118/1.4905232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Rashidnasab A., Elangovan P., Yip M., Diaz O., Dance D. R., Young K. C., and Wells K., “Simulation and assessment of realistic breast lesions using fractal growth models,” Phys. Med. Biol. 58, 5613–5627 (2013). 10.1088/0031-9155/58/16/5613 [DOI] [PubMed] [Google Scholar]
- 57.Shaheen E., De Keyzer F., Bosmans H., Dance D. R., Young K. C., and Ongeval C. V., “The simulation of 3D mass models in 2D digital mammography and breast tomosynthesis,” Med. Phys. 41, 081913 (17pp.) (2014). 10.1118/1.4890590 [DOI] [PubMed] [Google Scholar]
- 58.Rashidnasab A., Elangovan P., Mackenzie A., Dance D. R., Young K. C., Bosmans H., and Wells K., “Virtual clinical trials using inserted pathology in clinical images: Investigation of assumptions for local glandularity and noise,” Proc. SPIE 9412, 94122D–94127D (2015). 10.1117/12.2080943 [DOI] [Google Scholar]
- 59.Fukunaga K. and Hayes R. R., “Effects of sample size in classifier design,” IEEE Trans. Pattern Anal. Mach. Intell. 11, 873–885 (1989). 10.1109/34.31448 [DOI] [Google Scholar]
- 60.Young S., Bakic P. R., Myers K. J., Jennings R. J., and Park S., “A virtual trial framework for quantifying the detectability of masses in breast tomosynthesis projection data,” Med. Phys. 40, 051914 (15pp.) (2013). 10.1118/1.4800501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Prionas N. D., Lindfors K. K., Ray S., Huang S.-Y., Beckett L. A., Monsky W. L., and Boone J. M., “Contrast-enhanced dedicated breast CT: Initial clinical experience,” Radiology 256, 714–723 (2010). 10.1148/radiol.10092311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.O’Connell A. M. and Kawakyu-O’Connor D., “Dedicated cone-beam breast computed tomography and diagnostic mammography: Comparison of radiation dose, patient comfort, and qualitative review of imaging findings in BI-RADS 4 and 5 lesions,” J. Clin. Imaging Sci. 2, 1–8 (2012). 10.4103/2156-7514.93274 [DOI] [PMC free article] [PubMed] [Google Scholar]