Procedures for ambient-pressure and tympanometric tests of aural acoustic reflectance and admittance in human infants and adults

Abstract

Procedures are described to measure acoustic reflectance and admittance in human adult and infant ears at frequencies from 0.2 to 8 kHz. Transfer functions were measured at ambient pressure in the ear canal, and as down- or up-swept tympanograms. Acoustically estimated ear-canal area was used to calculate ear reflectance, which was parameterized by absorbance and group delay over all frequencies (and pressures), with substantial data reduction for tympanograms. Admittance measured at the probe tip in adults was transformed into an equivalent admittance at the eardrum using a transmission-line model for an ear canal with specified area and ear-canal length. Ear-canal length was estimated from group delay around the frequency above 2 kHz of minimum absorbance. Illustrative measurements in ears with normal function are described for an adult, and two infants at 1 month of age with normal hearing and a conductive hearing loss. The sensitivity of this equivalent eardrum admittance was calculated for varying estimates of area and length. Infant-ear patterns of absorbance peaks aligned in frequency with dips in group delay were explained by a model of resonant canal-wall mobility. Procedures will be applied in a large study of wideband clinical diagnosis and monitoring of middle-ear and cochlear function.

NOMENCLATURE

AABR

Automated auditory brainstem response

ABR

Auditory brainstem response

CEOAE

Click-evoked otoacoustic emission

CHL

Conductive hearing loss

DFT

Discrete Fourier transform

DPOAE

Distortion product otoacoustic emission

HP

Highpass

IQR

Inter-quartile range

LP

Lowpass

MAD

Median absolute deviation

NHS

Newborn hearing screening

NICU

Neonatal intensive care unit

SNR

Signal to noise ratio

SSOAE

Synchronized spontaneous otoacoustic emission

TM

Tympanic membrane

TPP

Tympanometric peak pressure

TW

Tympanometric width

TWn

Tympanometric half-width towards the negative tail pressure

TWp

Tympanometric half-width towards the positive tail pressure

VRA

Visual reinforcement audiometry

I. INTRODUCTION

Aural acoustic tests of wideband reflectance and admittance provide clinically relevant information on human peripheral auditory function in adults and infants. This report describes extensions and refinements to these tests during the course of a multi-year study on wideband clinical diagnosis and monitoring of middle-ear and cochlear function. Test results are illustrated by measurements in two adult ears with normal hearing, and in one ear each of two infants. These infants were tested at an age close to one month corrected age. One infant test ear was classified as normal hearing and the other as having a conductive hearing loss.

The goal of this study is to describe the procedures underlying the test methodology, with examples of measured results in a small number of test ears. Such test results are used to describe the large reduction in the number of variables in the original test response to a much smaller number that is intended to be used in group analyses of research data described in future reports. The present report does not have the goal of describing the clinical significance of these measurements, which would depend on results in large groups of infant and adult subjects.

A. Reflectance and admittance tests

Clinical measurements of pressure reflectance R(f) as a function of frequency f at a fixed location in the ear canal have focused on reflectance magnitude, or its squared magnitude as energy reflectance. This focus was adopted because reflectance magnitude is insensitive to probe location within the ear canal under the assumptions that the ear-canal wall is immobile and wall losses are small (Stinson et al., 1982). In adult temporal bone measurements, a variation in measurement location resulted in “relatively small effects” on the energy reflectance (Voss et al., 2008).

A complication in reflectance testing of infant ears is that their ear-canal walls are highly distensible in response to changes in air pressure in the ear canal over the tympanometric range, so much so that negative air pressures can cause the collapse of the ear-canal wall in infants between 1 and 5 days of age (Holte et al., 1991). Holte et al. (1991) proposed that the ear-canal walls may vibrate in response to acoustic stimulation and add a resistive component to tympanometric measurements. Keefe et al. (1993) proposed a model or ear-canal wall mobility that explained a low-frequency peak in the acoustic resistance measured at the probe tip in infant ears over the first three months of age.

Wideband acoustic reflectance and admittance tests in this study were performed over a frequency range from 0.2 to 8 kHz. To interpret the admittance data obtained in these tests, an acoustic transmission line model was adopted for sound transmission in an ear canal with an assumed cylindrical shape parameterized by area and length. The tympanic membrane (TM) was represented by an input admittance at a single location in the transmission line. Wideband reflectance and equivalent admittance functions at the TM were measured in individual adult ears, both for ambient and tympanometric pressure conditions in the ear canal. “At the TM” refers to an equivalent reflectance or admittance function first measured at the probe location, and then transformed to a TM location using the transmission line to estimate either transfer function.

In conventional admittance (or impedance) tympanometry, the air pressure in the ear canal is varied, or held constant at some value different from ambient pressure, during the presentation of a sound, and the admittance (or impedance) is measured at one frequency (Metz, 1946), or over a range of frequencies. Admittance tympanometry has often been used to clinically assess middle-ear function. Admittance tympanograms have been transformed into reflectance tympanograms (Keefe and Levi, 1996), which have also been used to clinically assess middle-ear function. Rabinowitz (1981) measured an equivalent acoustic admittance at the TM at ambient pressure for frequencies up to 4 kHz.

The present report describes the first tympanometric measurements in human infants and adults of reflectance group delay over a bandwidth up to 8 kHz. Measurements were obtained in an adult ear at both ambient pressure and over a range of tympanometric pressures of the equivalent admittance at the TM, which was calculated based on acoustic estimations of ear-canal area and length. Wideband tympanograms measured over frequency and pressure form a two-dimensional response with a large number of independent values. The present study represented the data in wideband reflectance and admittance tympanograms using a much smaller set of one-dimensional responses over frequency or pressure. Several approaches were explored to reduce the number of data values in the tympanogram while retaining information that may be clinically relevant. The sensitivity of the ambient equivalent admittance at the TM was measured for a normal adult ear with respect to variations in the estimates of the area and length. A middle-ear model including wall mobility effects in the ears of young infants was applied to explain the presence of a local maximum in absorbance and local minimum in group delay over a range of low frequencies and of varying air pressures during swept tympanograms.

II. GENERAL METHODS

A. Subjects and clinical tests

Adult subjects A and B were tested at Boys Town National Research Hospital (Omaha, NE) according to inclusion criteria for normal hearing. These included a negative history of middle-ear pathology or otological surgery, normal otoscopy, normal 226-Hz tympanometry (GSI Tympstar), air-conduction thresholds (GSI 61) no larger than 15 dB hearing level (HL) at any octave frequency between 0.25 and 8 kHz, and air bone gaps not exceeding 10 dB at any octave frequency between 0.25 and 4 kHz.

Infants received up to three clinical tests assessing a risk for hearing loss. Infants in the well-baby nursery received an initial newborn hearing screening (NHS) at the birthing hospital based on a click-evoked otoacoustic emission (CEOAE) test (Natus Echo-Screen). Well babies referring on this CEOAE screening received an automated auditory brainstem response (AABR) test (Biologic). An infant test ear passed the initial NHS exam based on a pass on either the CEOAE or AABR test; otherwise, the ear was classified as a refer on the initial NHS exam. Infants in the neonatal intensive care unit (NICU) of the birthing hospital received an initial NHS exam based on an AABR test on their release date. Initial NHS exams and research testing were performed at Good Samaritan Hospital (Cincinnati, OH) and Cincinnati Children's Hospital Medical Center.

Infants participated in a follow-up diagnostic hearing exam that was performed on average at a corrected age of one month at Cincinnati Children's Hospital Medical Center. The clinical tests included otoscopy, distortion-product otoacoustic emissions (DPOAE, Vivosonic Integrity), and a tone-burst air and bone conduction auditory brainstem response (ABR) test (Vivosonic Integrity) with two to four test frequencies selected at octave frequencies between 0.5 and 4 kHz (Elsayed et al., 2015).

In a third visit at approximately nine months corrected age at Cincinnati Children's Hospital Medical Center, infants received clinical tests including otoscopy, standard tympanometry, DPOAE, and visual-reinforcement audiometry (VRA). The VRA test used narrow-band noise bursts and speech syllables (da, ba) in an operant head-turn procedure for reinforcement (Widen et al., 2000).

Infant subject N was a white non-Hispanic male who was born premature at gestational age 29 weeks and cared for in a NICU. Subject N was screened in the initial NHS exam on his release date at 36 weeks gestational age, and passed both CEOAE and AABR screenings in both ears at 36 weeks gestational age. The infant had a normal diagnostic ABR and DPOAE at 1.3 months corrected age, and passed the VRA exam in both ears at an age of 9.5 months. The results presented in this report were measured in the left ear of normal subject N at age 1.3 months.

Infant subject C was a white non-Hispanic male full-term newborn, who was cared for in the well-baby nursery and tested in the left ear. The infant subject referred on the initial NHS exam in both the CEOAE and AABR tests, and was classified as having a bilateral conductive hearing loss (CHL) in the follow-up NHS exam at age 0.9 months, which was the age at which data were measured.

B. Measurement system

Measurements were performed using a computer with two-channel sound card (CardDeluxe) and RS-232 serial port using custom software. A Titan ear probe (Interacoustics), which was generally similar in design to that described by Liu et al. (2008), was used for all measurements. This probe had two receiver ports to deliver sound stimuli and one microphone port to measure the acoustical pressure response, although only one of the receivers was used to measure reflectance. The receiver generated sound stimuli under the control of a 24-bit digital to analog converter on the sound card, and a microphone with preamplifier measured acoustic pressure, with the output voltage sent to a 24-bit analog to digital converter on the sound card. The sample rate per channel on the sound card was 22.05 kHz.

An additional port exiting the probe tip communicated air pressure changes delivered by the pump in the tympanometer (AT235, Interacoustics, with modified firmware). A pressure controller circuit matched the actual pressure, which was measured using a pressure sensor within the tympanometer cable, to the desired pressure. During any pressure sweep, air pressure was varied in the ear canal, and the tympanometer communicated the measured air pressure back to the computer using a bi-directional serial port. For ambient-pressure measurements, the air pressure in the ear canal was adjusted to ambient pressure after the probe was fully inserted into the ear canal and prior to any measurements. This adjustment refined the procedure described in Liu et al. (2008), who reported that a leak-free insertion of this type of probe generated a slight excess air pressure within the ear canal that biased the subsequent ambient-pressure absorbance test.

Reflectance and admittance were measured at ambient pressure in the ear canal, and at varying air pressure using down- and up-swept tympanograms. These tests were placed in a battery of multiple research tests. In this battery, a down-swept tympanometry test was first performed followed by an ambient-pressure test and an up-swept tympanometry test. Preliminary testing in infants showed that the testing was more robust by beginning the test battery with the down-swept test rather than the ambient or up-swept test. This is because a down-swept tympanometry test initially pressurized the ear canal to a maximum pressure of 220 daPa. Any leak of the probe within the ear canal was revealed by an inability to pressurize the ear to this maximum pressure.

In contrast, a leaky probe fit would not be so easily revealed in a test at ambient pressure as in a test that varied air pressure in the ear canal, even though a leak test based on Liu et al. (2008) was part of the ambient-pressure test. The up-swept tympanometry test began by pressurizing the ear canal to −315 daPa. Such a negative excess pressure tended to improve the initial goodness of fit of the probe within the ear canal, although a leak might develop later in the sweep when positive pressurization was introduced. Such a case would be identified by an inability to complete a pressure sweep.

III. AMBIENT-PRESSURE REFLECTANCE AND ADMITTANCE

A. Reflectance

The acoustical reflectance and admittance measurement system was calibrated using a calibration-tube procedure (Keefe and Simmons, 2003; Liu et al., 2008) based on responses to a click stimulus. The calibration outputs were the incident pressure spectrum Q(f) at the probe tip and the source reflectance $R^s(f)$ of the probe over frequencies f in the analysis band of the click stimulus (0.25 to 8 kHz). The terms incident pressure and source reflectance are used as in Keefe and Schairer (2011).

After a leak-free insertion of the probe in the ear canal of the test ear, measurements were performed at ambient pressure using synchronous time averaging of the microphone response to the sound stimulus, which had a length of 1024 samples (duration 46.44 ms). After presenting two preliminary buffers to initialize a digital filtering step, the software then acquired 32 synchronous buffers for adult ears (duration 1.49 s) or 16 buffers for infant ears (duration 0.74 s). The filter attenuated sound energy below 0.2 kHz that was noise dominated. Fewer buffers were acquired for infants so that the operator could more easily select a period of time to acquire data in which the infant was quiet. Artifact rejection was performed using a median absolute deviation (MAD) test (Liu et al., 2008).

After calculating the 1024-sample discrete Fourier transform (DFT) of the pressure waveform (with 21.5 Hz bin spacing), an aural acoustic pressure reflectance R(f) was obtained as a function of these calibration outputs and the pressure spectrum P(f) measured at the tip of the probe in the ear canal as follows (Keefe, 1997):

$$R\left(f\right)=\frac{P\left(f\right)-Q\left(f\right)}{R^s\left(f\right)\hspace{0.17em}P\left(f\right)+Q\left(f\right)}.$$ (1)

This reflectance was calculated in terms of a cross-sectional area S_tube equal to the area of a tube in the calibration tube set.

For a particular location in an ear canal with cross-sectional area S, the acoustic admittance Y(f) is related to this pressure reflectance by

$$Y\left(f\right)=Z_c^{-1}\hspace{0.17em}\frac{1-R\left(f\right)}{1+R\left(f\right)},$$ (2)

in which the acoustic characteristic impedance Z_c is the ratio of the product of the equilibrium density ρ and phase velocity c of sound in air to the area $S_{\mathit{t}\mathit{u}\mathit{b}\mathit{e}},$

$$Z_c=\rho c/S_{\mathit{t}\mathit{u}\mathit{b}\mathit{e}}.$$ (3)

The admittance just in front of the probe tip is denoted in the following by $Y_p(f),$ whereas the form of Eq. (2) may be used to solve for an alternative R(f) for any alternative choice of S, e.g., within the ear canal just past the probe tip.

1. Acoustic estimate of ear-canal area

The cross-sectional area of the ear canal was acoustically estimated in Keefe et al. (1992) based on the sum of the measured resistance at the probe across the measurement bandwidth (0.1 to 10.7 kHz). Although the software implementation to calculate area was correct, their published relation for area had an algebraic error that was correctly expressed in Huang et al. (2000) in a study using cat ears. Keefe et al. (1992) reported that the acoustically estimated area was within 2% of the geometrical area for each of six cylindrical tubes used in calibration. This software implementation was used to estimate ear-canal areas in Keefe et al. (1993).

The ear canal had a cross-sectional area S just in front of the probe tip, which would generally differ from tube area $S_{\mathit{t}\mathit{u}\mathit{b}\mathit{e}},$ so that a definition of ear-canal reflectance was needed in terms of the ear-canal area rather than the tube area. The ear-canal area S just past the probe tip was estimated from the specific impedance ζ [see the Appendix, Eqs. (A1)–(A2)] and the average $⟨\text{Re}(Z)⟩$ of the acoustic resistance over all analysis frequencies by the relation in Huang et al.,

$$S=\frac{\zeta }{⟨\text{Re}\left(Z\right)⟩}.$$ (4)

Huang et al. (2000) omitted from the averaging any frequencies at which the resistance was negative. Keefe and Abdala (2007) adjusted the area estimation procedure such that any negative values of probe resistance in the measurement bandwidth were reset to zero but included in the average. Their rationale for this reset was that negative resistance values might be present due to small measurement or calibration errors. They reported that the median difference in estimating areas between their method and that of Huang et al. was zero for infant ears and 1.3% for adult ears. This approach was used in the present study with the averaging in Eq. (4): the resistance was set to zero at any frequency at which the acoustic resistance was negative, but otherwise retained in the average.

2. Absorbance and group delay

The characteristic impedance Z_ce of the ear canal just past the probe tip was calculated using Eq. (3), in which S from Eq. (4) replaced $S_{\mathit{t}\mathit{u}\mathit{b}\mathit{e}}:$

$$Z_{\mathit{c}\mathit{e}}=\frac{\rho c}{S}.$$ (5)

The pressure reflectance $R_e(f)$ in the ear canal is (Keefe and Simmons, 2003)

$$R_e\left(f\right)=\left|R_e\left(f\right)\right|\hspace{0.17em}{e}^{j\varphi \left(f\right)}=\frac{1-Z_{\mathit{c}\mathit{e}}\hspace{0.17em}Y\left(f\right)}{1+Z_{\mathit{c}\mathit{e}}\hspace{0.17em}Y\left(f\right)},$$ (6)

in which the unit imaginary number is j and the reflectance phase is $\varphi (f).$ The reflectances R(f) in Eq. (1) and $R_e(f)$ in Eq. (6) would be equal if $S=S_{\mathit{t}\mathit{u}\mathit{b}\mathit{e}}.$

The energy reflectance ER and absorbance A parameterized the ear-canal pressure reflectance magnitude by

$$\begin{array}{c}ER(f)={\left|R_e(f)\right|}^2,\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}A(f)=1-{\left|R_e(f)\right|}^2.\end{array}$$ (7)

The absorbance is the ratio of acoustic energy (power) that is absorbed by the middle ear and ear canal to the acoustic energy of a transient sound (acoustic power of a steady-state sound) that is directed in the ear canal towards the TM (Liu et al., 2008).

A goal of the multi-year study is to evaluate whether the phase $\varphi (f)$ of the pressure reflectance in Eq. (6) may also convey clinically relevant information, despite the fact that its value varies with location within the ear canal. This phase is represented in terms of reflectance group delay D(f) by

$$D\left(f\right)=-\frac{1}{2\pi }\hspace{0.17em}\frac{d\varphi \left(f\right)}{\mathit{d}\mathit{f}}.$$ (8)

Group delay results were described for adult ears with normal hearing (Keefe et al., 1993; Voss and Allen, 1994; Robinson et al., 2013), but have received scant attention in subsequent studies examining ear-canal or middle-ear dysfunction.¹

Using a cylindrical model of sound propagation in the ear canal, the group delay D₀ at the innermost end of the ear canal was related (in the limit of small ear-canal losses) to the group delay D_p at the probe tip. The length L extended from the probe tip to the innermost end of the ear canal, so that the round-trip delay was $2L/c.$ It follows that the group delay D_p is expressed as the sum of the round-trip delay and D₀ by

$$D_p(f)=D_0(f)+2L/c.$$ (9)

This equation also is given in Keefe et al. (1993) for the special case of a compliant termination at the eardrum.

This approximate equation relies on the assumptions that: (1) sound propagates in the ear canal mainly through one-dimensional acoustics (so that evanescent mode effects can be neglected), (2) viscothermal losses are small, (3) the ear-canal walls are immobile, (4) the ear-canal curvature may be neglected as long as the sound transmission pathway is measured along the mid-line (Khanna and Stinson, 1985), (5) the cross-sectional area of the ear canal is relatively constant along its length, and (6) the location of the ear canal may be identified as a single point in the one-dimensional transmission line representing sound propagation.

The first four assumptions are well satisfied over the frequency range of interest, at least for ear canals of older children and adults in which the ear-canal walls are nearly immobile (except for effects described below related to tympanometry). As described above, reflectance magnitude and phase are influenced by wall mobility effects in young infant ears. This issue is revisited in Sec. VI. Equation (9) is based on the assumption that the canal is rigid-walled so it does not apply for estimating length in young infants. Additional ear-canal curvature effects are small if the radius of curvature of the bend is large compared to the radius of the canal. If the fifth assumption is not adopted but the area is assumed to be slowly varying along the centroid axis (Stinson and Lawton, 1989), then a one-dimensional non-uniform transmission line theory may be introduced which has additional correction terms compared to Eq. (9).² The last assumption has more limited validity: the TM lies at an angle with respect to the longitudinal centroid axis of the curved ear canal, so that different regions of the TM are at slightly different distances when measured in terms of coordinate distance along this centroid axis. This introduces an ambiguity related to the definition of the location of the TM in any one-dimensional transmission line.

3. Acoustic estimate of ear-canal length

A previous estimation procedure for L was based on the pressure-reflectance phase slope, i.e., the group delay, between 6 and 8 kHz in an adult ear, inasmuch as the TM was assumed to be nearly rigid and resistance-dominated at these frequencies (Keefe, 2007). This was based on the property that if the TM were immobile at a particular frequency f₀ so that $D_0(f_0)=0,$ then the group delay at the probe at that frequency in Eq. (9) would equal the round-trip travel time $2L/c.$ The basic idea is that the TM in an adult ear would be highly reflective at these frequencies with a corresponding low value of absorbance.

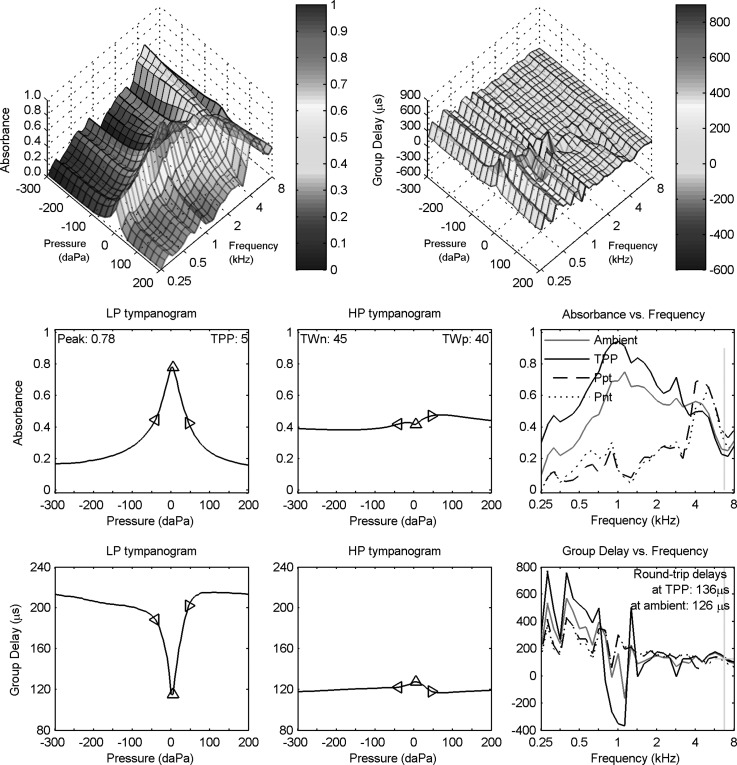
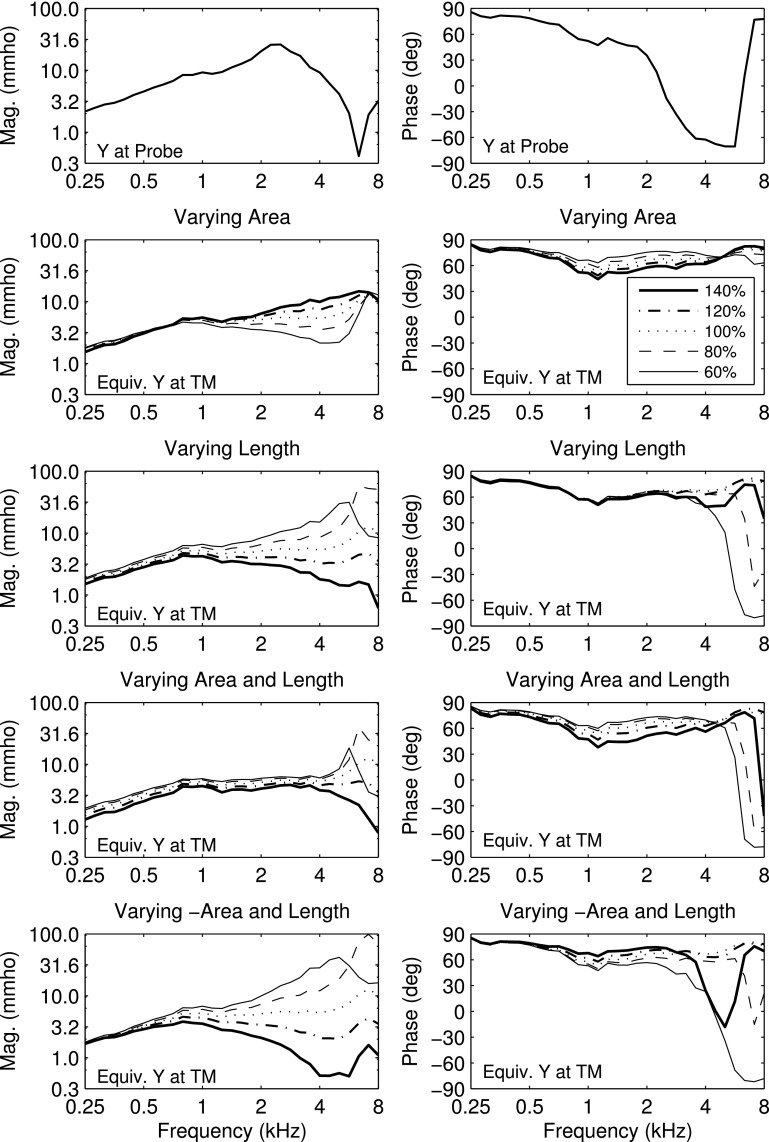
The acoustic estimation of the length L is described by means of an example: the ambient reflectance results shown in the top panel of Fig. 1 for adult subject A. All plotted results for this adult ear use a one-sixth octave smoothing across frequency. The ambient absorbance had a central maximum at frequencies from 1–4 kHz with a relatively narrow, high-frequency minimum near 6.7 kHz. A new estimation procedure for L identified the DFT bin frequency f_min above 2 kHz at which the absorbance was a minimum.

FIG. 1.

(Color online) Normal adult ear A. Top: Ambient absorbance (solid curve, left ordinate) and group delay D_p (dashed curve, right ordinate). A vertical bar identifies a critical frequency f_min above 2 kHz (equal to 6.7 kHz) with minimum absorbance. The group delay value displayed in text is the average $⟨D_p(f_{\mathit{m}\mathit{i}\mathit{n}})⟩$ over the half octave centered at that frequency. A horizontal bar is drawn at this average group delay value over the half octave range centered at that frequency. Bottom: Equivalent TM admittance magnitude (solid line, left ordinate) and phase (dashed line, right ordinate). Acoustic estimates of ear-canal area and length between probe and TM displayed on top of the panel.

The new procedure averaged the group delay D_p over a half-octave centered at $f_{\mathit{m}\mathit{i}\mathit{n}}.$ This average (over values at each DFT bin frequency) was termed $⟨D_p(f_{\mathit{m}\mathit{i}\mathit{n}})⟩.$ The frequency-averaged middle-ear group delay $⟨D_0(f_{\mathit{m}\mathit{i}\mathit{n}})⟩$ in the same range around f_min was assumed to be zero, corresponding to this limit of high reflectivity. It follows from Eq. (9) that the acoustic estimate of length L was

$$L=(c/2)\hspace{0.17em}⟨D_p(f_{\mathit{m}\mathit{i}\mathit{n}})⟩.$$ (10)

The critical property of reflectance at these higher frequencies was that the group delay varied slowly with frequency in the neighborhood of the frequency of minimum absorbance (as in Fig. 1), and the half-octave average of group delay contributed further smoothing to the estimate of L.

Assuming a TM dimension on the order of 8 mm, a mid-TM region was defined at a distance L₀ = 4 mm back from the innermost end of the ear canal. This innermost end was, by default, the location beyond which all sound had been reflected. This mid-TM region would be in the neighborhood of the umbo location but would not coincide with it. The distance L_TM from the probe to the TM was estimated as

$$L_{\mathit{T}\mathit{M}}=L-L_0.$$ (11)

This particular definition is arbitrary in the sense that some other value for L₀ might be selected. The underlying challenge for a one-dimensional description of ear-canal acoustics is that the TM is spatially extended, and no particular value of L₀ is accurate for all measurements that might be performed, especially for measurements close to the TM.

With this definition of $L_{\mathit{T}\mathit{M}},$ the average delay $⟨D_p(f_{\mathit{m}\mathit{i}\mathit{n}})⟩$ was 126 μs, and the corresponding L_TM for subject A was 17.7 mm (based on c = 345 m/s). Because the group delay was slowly varying above 2 kHz in adult subject A and because a half-octave average of group delay was used in Eq. (10) to smooth the length estimate, the estimate was insensitive to the frequency above 2 kHz at which the absorbance was a minimum. Although not shown as a separate plot, the equivalent, or compensated, group delay at the TM would be plotted by subtracting $2L_{\mathit{T}\mathit{M}}/c=$ 103 μs from the group delay in the top panel of Fig. 1. The larger group delay at frequencies below 0.7 kHz in subject A was due to the low-frequency compliance of the TM. The acoustical estimate of ear-canal area S near the probe tip was calculated using Eq. (4) as 21.2 mm² for ear A.

The present procedure to estimate group delay from the pressure reflectance phase gradient differs slightly from that of Keefe (2007). That reference averaged the phase gradient between 6 and 8 kHz, whereas the present procedure using a half-octave around the frequency above 2 kHz of minimum absorbance averaged the phase gradient between 5.6 and 8 kHz for adult subject A. Thus, the procedures would lead to nearly equal results for this ear.

B. Equivalent admittance at the TM

1. Procedures

If the distance between the probe and TM and the ear-canal area are known, a one-dimensional transmission-line model of sound propagation in the ear canal may be used to calculate an equivalent admittance $Y_{\mathit{T}\mathit{M}}(f)$ at the TM in terms of the admittance $Y_p(f)$ at the probe (Rabinowitz, 1981). Rabinowitz described a tympanometric procedure to calculate the length, which is further considered below, and assumed a constant value for ear-canal area derived from mean measurements in adult ears.

The admittance $Y_p(f)$ at the probe was transformed to an equivalent admittance $Y_{\mathit{T}\mathit{M}}(f)$ at the TM by (Rabinowitz, 1981)

$$Y_{\mathit{T}\mathit{M}}\left(f\right)=\frac{Y_p\left(f\right)-j/Z_{\mathit{c}\mathit{e}}\hspace{0.17em}\hspace{0.17em}\text{tan}\hspace{0.17em}k{L}_{\mathit{T}\mathit{M}}}{1-j{Z}_{\mathit{c}\mathit{e}}\hspace{0.17em}{Y}_p\left(f\right)\text{tan}\hspace{0.17em}k{L}_{\mathit{T}\mathit{M}}},$$ (12)

in which the free-space wavenumber is $k=2\pi f/c.$ In the present study, the ear-canal area S was the estimated area at the probe tip using Eq. (4), the Z_ce was calculated using Eq. (5), and the length L_TM was estimated from the probe tip to the mid-TM region using Eq. (11).

This ear-canal model assumes that viscothermal losses in the ear canal can be neglected, which is accurate (Margolis et al., 1999) except for the case of neonatal ear canals with mobile walls. This relation provides a wideband compensation of probe admittance to an equivalent TM admittance. The use of this one-dimensional transmission line model also assumes that the cross-sectional area of the ear canal is relatively constant over the range of possible measurement locations. Voss et al. (2008) estimated the ear-canal area using a similar method to that used in the present study in a set of adult temporal bones, and concluded that the use of a constant area was validated by the area estimates determined over a range of measurement locations with the ear canal.

The magnitude of the equivalent admittance at the TM was expressed in the mmho unit, for which 1 mmho is 0.001/ohm (this ohm is the CGS unit for acoustical impedance); 1 mmho is ${10}^{-8}\hspace{0.17em}{\mathrm{m}}^4\hspace{0.17em}\mathrm{s}/\text{kg}$ in SI units. This mmho unit was adopted because it is commonly used in clinical admittance tympanometry. It is a convenient unit because the admittance magnitude is on the order of 1 mmho in a normal adult ear at frequencies close to 0.25 kHz.

A study (Ravicz et al., 2014) of the pressure field close to the TM referred to the difficulty of defining an input admittance at the TM due to the spatial extent of the TM, the inhomogeneity of the sound field across the TM, and the complex TM motions that are not well correlated to the sound field distribution. The ease of using a one-dimensional description of the sound field is contrasted with the fact that the sound field and the motions on the TM, which forms a part of the boundary of the ear canal, have complex spatial interactions. This is the main reason for referring to Y_TM as an equivalent admittance at the TM. It is at best an approximation using a one-dimensional description of a system that cannot be adequately described near the TM in terms of the long-wavelength approximation. Notwithstanding that limitation, it remains a useful approximation because of the clinical importance of admittance and reflectance measurements.

2. Adult ear measurement of ambient equivalent admittance at the eardrum

The ambient-pressure measurement of the equivalent admittance at the TM for adult subject A is shown in the bottom panel of Fig. 1. The equivalent admittance at the TM was stiffness controlled over all frequencies from 0.25 to 8 kHz with a phase that exceeded 60° except for a slight reduction at about 1.1 kHz. The admittance magnitude increased with increasing frequency up to 1.1 kHz with a slope in level of close to 6 dB/octave. It was relatively constant between 1 and 4 kHz, and increased at higher frequencies to a local maximum near 7 kHz. This local maximum in $\left|Y_{\mathit{T}\mathit{M}}(f)\right|$ occurred close to the critical frequency f_min of minimum absorbance. This equivalent admittance contrasted strongly with the probe admittance, which exhibited maxima and minima associated with standing waves in the ear canal. Probe admittance results over this frequency range have been reported in terms of impedance (Keefe et al., 1993).

Because this property near 7 kHz is reported for only a single adult ear, no conclusions are possible on the behavior in a larger group of adult ears with normal function. The sensitivity in estimating Y_TM to varying estimates of ear-canal length and area is further considered in Sec. VI. This example serves to illustrate the calculation of an equivalent admittance at the eardrum based on measurements at ambient pressure in the ear canal. Such measurements may be used to address clinically relevant questions in groups of ears with normal function and with middle-ear disorders.

IV. TYMPANOMETRIC REFLECTANCE AND ADMITTANCE

A. Preliminary remarks

Following studies of wideband reflectance tympanometry in ears of adults and older children (Margolis et al., 1999; Keefe and Simmons, 2003) and of infants (Sanford and Feeney, 2008), Liu et al. (2008) described a wideband absorbance tympanometry system with results in normal adult ears using a software-controlled pressure pump and pressure controller to perform swept tympanometry tests. This control over air pressure improved over the performance of previous systems. Measurements of absorbance tympanometry and ambient absorbance were applied to detect conductive dysfunction in newborn hearing screening programs (Sanford et al., 2009; Hunter et al., 2010), and to predict the presence of conductive hearing loss in children having otitis media with effusion (Keefe et al., 2012).

Negative middle-ear pressure is a common type of dysfunction. Using an experimental technique to first induce a negative middle-ear pressure and then return to baseline, Shaver and Sun (2013) found that compensation of the ear-canal air pressure to match the negative middle-ear pressure restored energy reflectance to values close to the initial values at ambient pressure prior to pressurization. The tympanometric absorbance measurement corrected for effects of negative middle-ear pressure, which would not be directly possible with ambient absorbance testing. Nevertheless, the tympanometric absorbance slightly increased with retesting due to hysteresis at frequencies below 1.5 kHz, and decreased at some higher frequencies (e.g., 5–6 kHz).

The present report describes refinements of the Liu et al. system that added the ability to measure wideband tympanograms for group delay and equivalent admittance at the TM. Ascending or descending tympanometry sweeps were performed in an overall range between −315 and +220 daPa for infant and some adult tests, in which results were analyzed between extremal pressures of −300 and +200 daPa. The sweep rate used was the nominal rate of 100 daPa/s in normal adult ears described by Liu et al., which was slightly faster than the default rate of 75 daPa/s used by Liu et al.

Air pressure was sampled by the pressure controller every 25 ms whereas clicks were repetitively output by the sound card throughout the tympanometric test with an inter-click interval of 46 ms. The air pressure in the ear canal associated with each click was estimated by linear interpolation, nominally at the time of the peak incident pressure of the click. A failure to achieve the initial extremal pressure within 5 s after pressurizing from ambient, or a failure to complete the pressure sweep within 12 s, triggered a message to alert the operator, who was instructed to check the probe fit for a leak and repeat the test.

The ear-canal pressure P_e during the tympanogram was

$$P_e=P+\Delta P.$$ (13)

This was the sum of atmospheric pressure P and the excess pressure $\Delta P$ produced by the tympanometry pump at the time of a particular click (see the Appendix). The pressure variable P_e was added as an argument of each tympanogram to denote the total pressure associated with each click response. A 1024-sample DFT was calculated for each click response within the tympanogram. The raw values of $R(f,P_e)$ and $Y(f,P_e)$ at the probe tip were calculated from Eqs. (1) and (2), respectively.

A single-frequency admittance tympanogram is often assessed clinically as a function of tympanometric pressure over the sweep range. Such tympanograms are typically used at relatively low frequencies such as 226 and 1000 Hz. It was of potential clinical interest to construct low-frequency averaged reflectance tympanograms that were similarly plotted as a function of tympanometric pressure. In ears of adults (and children of three years and older), absorbance and group delay tympanograms were averaged over all DFT frequency bins in a lowpass (LP) filtered range from 0.376 to 2 kHz, and in a highpass (HP) filtered range from 2 to 8 kHz. This followed the averaging used in Liu et al. (2008) for adult absorbance, excluding the somewhat noisier data below 0.376 kHz. This noise is related to the absence of averaging across click responses during the tympanometric sweep.

Younger children were separated into two sub-groups for purposes of defining the lowpass averaging bandwidth used to calculate the LP absorbance and group-delay tympanograms. For children of ages older than six months up to three years, the lowpass filter bandwidth was 0.354 kHz up to 1.414 kHz (i.e., a half octave below 0.5 kHz to a half octave above 1 kHz). For infants of age six months or younger, the lowpass bandwidth was 0.707 kHz up to 1.414 kHz, i.e., an octave average around 1 kHz. The restriction of including reflectance data only above 0.707 kHz in young infants was because their reflectance tympanometry data were noisier at lower frequencies compared to older children. A HP filter averaging bandwidth was selected as 1.414 kHz up to 2.8 kHz for data from one-month-olds tested in the present study. These averaging bandwidths differed from those previously used for absorbance tympanograms in neonates (Sanford et al., 2009), so as to align the lowpass and highpass filters at the 1 and 2 kHz center frequencies.

B. Procedure

1. Single-click analyses

The ear-canal area of each click was calculated in each DFT bin using Eq. (4), but in which the pressure dependence of the specific impedance $\zeta (P_e)$ was included according to Eq. (A8). By analyzing all recorded clicks in the tympanogram (after rejecting outliers as described below), the ear-canal area $S(P_e)$ was estimated as a function of tympanometric pressure to form an area tympanogram. The ear-canal reflectance $R_e(f,P_e)$ was calculated using Eqs. (5) and (6) in terms of the particular ear-canal area estimated from the main tympanometric sweep when the pressure was closest to ambient pressure, i.e., at P_e = 0 daPa. This procedure is further described below. The tympanometric absorbance $A(f,P_e)$ and group delay $D_p(f,P_e)$ at the probe were calculated in terms of $R_e(f,P_e)$ using Eqs. (7) and (8), respectively.

As in the ambient-pressure analysis of reflectance for the average click response, the tympanometric measurement of reflectance for each click (i.e., at its P_e) was analyzed to determine the critical frequency f_min of minimum absorbance between 2 and 8 kHz, and to calculate the half-octave average $⟨D_p(f_{\mathit{m}\mathit{i}\mathit{n}},P_e)⟩$ of group delay about this critical frequency. By analogy with Eq. (10), the acoustic estimate of length $L(P_e)$ from each click response was

$$L(P_e)=c/2\hspace{0.17em}⟨D_p(f_{\mathit{m}\mathit{i}\mathit{n}},P_e)⟩.$$ (14)

As in Eq. (11), the length $L_{\mathit{T}\mathit{M}}(P_e)$ between the probe and TM was estimated as $L(P_e)-L_0.$

The dependence of a tympanometric transfer function on f and P_e may be explicitly denoted or omitted depending on context. The real and imaginary parts of the tympanometric admittance $Y_t(f,P_e)$ at the probe tip were expressed as the conductance $G_t(f,P_e)$ and susceptance $B_t(f,P_e)$ by $Y_t(f,P_e)=G_t(f,P_e)+j\hspace{0.17em}{B}_t(f,P_e).$

2. Smoothing across multiple clicks

Whereas the ambient-pressure data were first time-averaged before the reflectance and admittance were calculated, the tympanometric processing of reflectance and admittance was performed for each click in a single tympanometric sweep. An additional procedure was performed in each test ear to smooth the tympanometric responses.

Artifact rejection was performed across all clicks presented within the nominal pressure range of the sweep to identify click responses contaminated by environmental, system, or physiological noise. The MAD was calculated over all click responses during the main tympanometric sweep for the peak-to-peak amplitude and the crest factor of the click response. A click response was rejected as an outlier if its peak-to-peak amplitude or crest factor exceeded a criterion value times the MAD of that variable. The click responses varied in waveform morphology during a pressure sweep due to the action of air pressure on the TM, as well as due to any intermittent noise. To accommodate this broader distribution of clicks, an “extreme outlier” was defined as one that would lie outside the interquartile range (IQR) of a hypothetical normal distribution of these response variables by 4.5 times its IQR or more. This increased the criterion from the value 5.92 used in the ambient test (Liu et al., 2008) to a value 8.45.

A two-stage median smoother was used based on Rabiner and Schafer (1978), who described the use of separate median and Hanning filters of equal length in first and second stages. The filter length was three for adults and children of 3 years and older, and five for younger children due to increased noise in younger infants. The filter length of three included the response at the center pressure $P_e,$ and the pair of responses at the nearest-neighbor pressures. Each function of pressure was then re-sampled between the extremal pressures to a uniform pressure grid in 5 daPa steps. Smoothing was again performed by the two-stage median smoother. This resulted in 101 pressure values for a swept tympanogram between −300 and +200 daPa. The present method had somewhat less smoothing of absorbance across pressure than in Liu et al. (2008), which also smoothed over nearby log frequencies.

3. Features of reflectance and admittance tympanograms

Tympanometric features were extracted in all test ears from the LP filter averaged absorbance tympanogram. These included the minimum and maximum absorbance across the range of air pressure, the tympanometric peak pressure (TPP) corresponding to the value of P_e at which the LP absorbance was maximal, and the tympanometric width (TW). The TW was the range of air pressure over which the LP absorbance decreased to half its maximal value on the positive-pressure side and half its maximal value on the negative-pressure side. These features were defined by analogy with features used in the clinical interpretation of compensated admittance magnitude tympanograms at 226 Hz, although the specific definitions differ. Because some infant tympanograms showed an asymmetry in the low-frequency absorbance at pressures above and below the TPP, half tympanometric widths TWp and TWn (which always have non-negative values) were also defined for the half-width on the positive- and negative-pressure side, respectively, of TPP.

C. Assumptions underlying clinical admittance tympanometry

Three commonly adopted assumptions that underlie the use of compensated tympanometry at 226 Hz are as follows.

• (1)Ear-canal volume does not change as air pressure in the ear canal changes.
• (2)The admittance magnitude is zero when the ear canal is pressurized to extremal values in a tympanogram, i.e., for $\left|P_e\right|\ge$ 200 daPa.
• (3)Sound transmission in the ear canal between the probe and TM depends only on ear-canal volume.

Shanks and Lilly (1981) described these assumptions and reported findings that the first two assumptions were inaccurate and the third assumption was not supported by data at 660 Hz. At low frequencies, the volume of air enclosed in the ear canal would have a purely imaginary admittance, so that their phrasing of the third assumption was that the real part of this admittance was zero. The above re-statement of assumption three is more general: it assumes that there are no wall losses in the ear canal and no acoustic standing wave effects between the probe and TM. From this point of view, assumption three is inaccurate at frequencies at and above 660 Hz where standing-wave effects play a role. The admittance compensation results in Shanks and Lilly (1981) were sufficiently general to avoid assumptions (1) and (2), and they reported only results up to 660 Hz so as to avoid adopting assumption (3).

Rabinowitz (1981) described a procedure to calculate an ambient equivalent admittance at the TM up to a maximum frequency of 4 kHz in combination with tympanometric and psychophysical measurements used to estimate ear-canal length. This procedure compensated the admittance to much higher frequencies than in previous research by avoiding the use of assumptions (2) and (3). Rabinowitz (1981) used Eq. (12) based on a model of the ear canal as a “rigid-walled cylinder,” with an area based on mean measurements reported in the literature. Inasmuch as the ear canal was assumed to have rigid walls that did not vary with tympanometric pressurization, this study adopted assumption (1).

Admittance tympanograms were analyzed at low frequencies [i.e., keeping only the terms linear in $k{L}_{\mathit{T}\mathit{M}}$ in Eq. (12) in the low-frequency limit] at ear-canal pressures of ±40 cm H₂0, corresponding to ±392 daPa, relative to ambient pressure. With ear-canal area and length each assumed constant in the pressurized conditions and at ambient pressure, Rabinowitz interpreted changes in the low-frequency admittance with pressurization solely in terms of a pressure-dependent change in the compliance at the TM. This approach resulted in an estimation of the length L_TM to use in Eq. (12).

In contrast to these previous studies, the present study estimated an equivalent admittance at the TM using a procedure that avoided adopting any of the assumptions (1), (2), or (3). As a first step, the area $S(P_e)$ and length $L(P_e)$ were acoustically estimated as a function of air pressure during the tympanogram. These parameterized the acoustic transmission line model of the ear canal that transformed pressure and admittance at the probe to equivalent pressure and equivalent admittance at the TM. Although not needed in this model, the ear-canal volume $V(P_e)$ was estimated as a function of air pressure by

$$V(P_e)=S(P_e)\times L(P_e).$$ (15)

The measurements next described for these ear-canal tympanograms provide new evidence that assumption (1) is inaccurate.

D. Adult ear measurement

1. Area tympanograms

The dependence of air pressure with time is shown in the top row of Fig. 2 for down- and up-swept tympanograms in the test ear of adult Subject A. For the down-swept test (left top panel), the pressure started at 0 daPa at time zero, increased to a starting pressure of 220 daPa at about 1 s, decreased in the main sweep down to −315 daPa at 8 s, and returned to 0 daPa after 8.5 s. The test data were extracted and analyzed over the approximately 6.5 s of the sweep between 200 and −300 daPa. The pressure waveform for the up-swept test (right top panel) took slightly longer (1.5 s) to achieve the initial pressure, while the sweep from −300 to 200 daPa was completed in about 5.8 s, faster than the down-swept test.

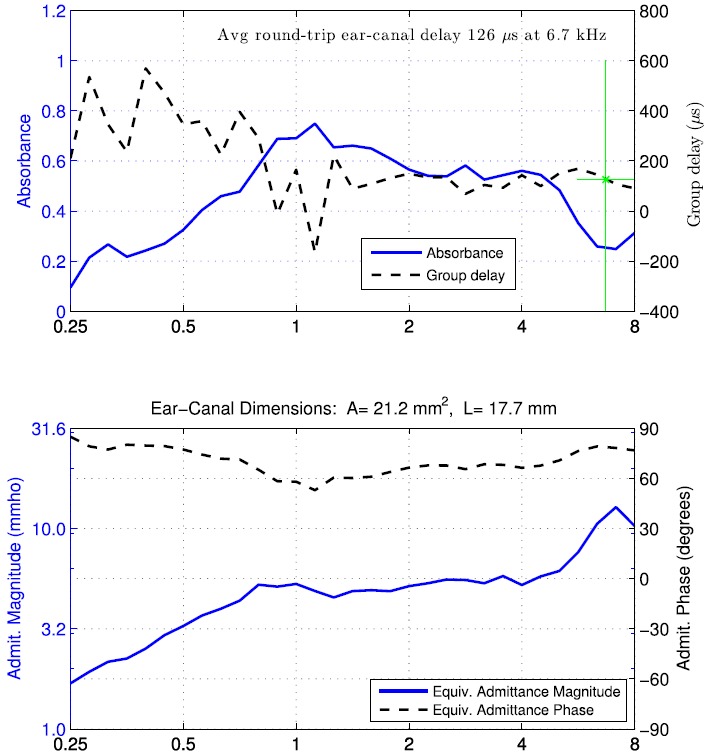
FIG. 2.

(Color online) Pressure and ear-canal dimensions during down-swept (left) and up-swept (right) tympanograms, with arrows increasing directional time course of pressurization. Row 1: air pressure versus time during initial, sweep and final sections of the measurement. Row 2: Ear-canal area versus pressure. Row 3: Ear-canal length versus pressure. Row 4: Ear-canal volume versus pressure.

The admittance tympanogram at the probe tip was measured in the test ear and converted to impedance, and the ear-canal area was estimated for each click in the sweep as a function of air pressure using Eq. (4). This area estimate is shown in row 2 of Fig. 2 for the tympanograms of both sweep polarities. For the down-swept tympanogram starting at the beginning of the test (left panel), the area was about 0.21 cm² at zero pressure; it decreased with increasing pressure to 35 daPa and then increased with increasing pressure up to 220 daPa. The area then decreased with decreasing pressure over the main sweep down to a minimum near 0 daPa, and increased with decreasing pressure from 0 to −80 daPa. The area then decreased to about 0.204 cm² with decreasing pressure down to −315 daPa. In the final ramp back to ambient pressure, the area increased slightly and reached a value at the end of the sweep that was close, but not identical, to the initial value (indicating the presence of hysteresis).

For the up-swept tympanogram (right panel), the area also showed a hysteresis, or path-dependent, value as pressure was varied. The difference between the areas at the beginning and end of the test was slightly larger for the up-swept than the down-swept tympanogram. The areas at the extremal pressures were similar in both tympanograms, as were the areas near 0 daPa (with values close to 0.21 mm²).

The area tympanograms during the main sweep (solid lines in both panels in row 2) showed a maximum area at the maximum pressure, a minimum area at the minimum pressure, and a local minimum in the vicinity of 0 daPa. The latter was close to the TPP (as described below). The maximum area variation across a single sweep ranged from 10% to 20% in adult ears, as exemplified by results in Fig. 2. For example, the range of estimated areas in the down-swept test varied between 0.203 and 0.238 cm², a relative change of about 17%.

2. Tympanometric reflectance

The (smoothed) absorbance and group-delay tympanograms for adult subject A are shown in the top row of Fig. 3 as a function of frequency and air pressure. Each tympanogram had 3031 data values over 31 frequencies and 101 pressures. The absorbance tympanogram had a single-peaked structure at frequencies up to about 2 kHz, and a pair of ridges³ were present at higher frequencies just above 4 kHz. The group-delay tympanogram had spectral maxima and minima at isolated frequencies that were approximately constant with respect to pressure variations.

FIG. 3.

(Color online) Wideband downswept reflectance tympanogram for adult ear A. Row 1: absorbance (left) and group delay D_p (right) tympanograms versus frequency and air pressure. Row 2: LP (left) and HP (middle) filtered absorbance tympanograms versus air pressure, with peak absorbance and TPP values in left panel and half-tympanometric widths TWn and TWp of the LP tympanogram in the middle panel. Row 2 (right): absorbance tympanogram versus frequency at TPP, P_pt, and P_nt compared to ambient absorbance replotted from Fig. 1. Row 3: LP (left) and HP (middle) filtered group-delay tympanograms versus air pressure. Row 3 (right): Tympanometric group delay at TPP, P_pt, and P_nt compared to ambient group delay replotted from Fig. 1 (top). A vertical bar in each right panel of rows 2 and 3 identifies the critical frequency (6.7 kHz) of $A_a.$ The diamond markers in each left and middle panel of rows 2 and 3 show air pressure at TPP, TPP − TWn, and TPP + TWp.

Several approaches have been explored to reduce the number of data values in the tympanogram while retaining information that may be clinically relevant. Row 2 of Fig. 3 shows the frequency-averaged absorbance tympanograms for lowpass (LP) filtered (left panel) and highpass (HP) filtered (middle panel) conditions. These filter bands were defined in Sec. IV A. The maximum absorbance for the low-frequency tympanogram was 0.78 at a TPP of 5 daPa. The triangle markers on the plot show the absorbance values at the pressures TPP + TWp and TPP – TWn on either side of the TPP, such that TWn was 45 daPa and TWp was 40 daPa for this ear (see text in middle panel). The similarity in these values is evidence of the high degree of symmetry of the LP absorbance tympanogram about its peak value (TPP). The absorbance for the high-frequency tympanogram had a more nearly constant value across pressure, although it had a broad maximum at about 80 daPa and a shallow local minimum near the TPP.

An alternative approach to analyzing the absorbance tympanogram plots the absorbance across frequency for a set of fixed tympanometric pressures. This is shown in the right panel of row 2 of Fig. 3 at fixed pressures of TPP, P_pt, and ${\mathrm{P}}_{\mathit{n}\mathit{t}}$, in which P_pt was the positive-tail pressure (+200 daPa) and P_nt the negative-tail pressure (−300 daPa). This panel also shows the absorbance measured at ambient pressure (as contrasted with the absorbance that might be extracted from the tympanogram at 0 daPa). These ambient data are the same data plotted in Fig. 1.

The absorbance at TPP and at ambient pressure were generally similar, although the absorbance at TPP was slightly larger at each frequency below 3 kHz. One would expect a maximum absorbance at the TPP, and the slight deviation of TPP = 5 daPa from ambient pressure may account for this difference. The TPP and ambient measurements of absorbance were both based on the measurement of the ear-canal pressure reflectance R_e in Eq. (6).

The absorbance at P_pt and at P_nt were similar to one another across frequency, and exceeded zero at all frequencies. The latter indicates that there was non-zero eardrum motion at the tail pressures. However, they were much smaller at all frequencies below 4 kHz than the absorbance at TPP. Commonly used clinical variables in single-frequency admittance tympanometry include tip-to-tail ratios of magnitude, in which the tip is the response at the TPP and the tail is the response at either of the positive or negative extremal pressures. An analogous variable in an absorbance tympanogram would be the difference $\Delta A$ in the absorbance at TPP relative to the absorbance at either of the tails. This panel shows each of these absorbances at TPP and at both tails: the absorbance difference is positive at frequencies between 0.25 and about 3 kHz, and negative at higher frequencies. The largest positive $\Delta A$ occurred at about 1–2 kHz.

Row 3 of Fig. 3 shows the group-delay tympanograms for the LP (left panel) and HP (middle panel) averaged conditions. The group delay had a narrow and shallow minimum in the LP tympanogram at the TPP of 5 daPa. This contrasts with a maximum in the LP absorbance tympanogram that occurred at the same pressure (TPP), but with a larger change in relative amplitude. The triangle markers on the group-delay plot show the values at the pressures TPP + TWp and TPP − TWn on either side of the TPP that were derived from the LP absorbance tympanogram. The group delay for the HP tympanogram had a small maximum near 0 daPa.

An alternative approach to analyzing the group-delay tympanogram plots group delay versus frequency for a fixed set of tympanometric pressures. This is shown in the right panel of row 3 at fixed pressures of TPP, P_pt, and ${\mathrm{P}}_{\mathit{n}\mathit{t}}$, along with the group delay from the ambient measurement, which are the same data plotted in Fig. 1. These spectra show narrow maxima and minima occurring at frequencies below 2 kHz that were generally similar across the fixed-pressure conditions. The largest spectral variations in group delay occurred at the TPP, especially with the minimum near 1 kHz, and the next largest variations occurred in the ambient test.⁴ The variations in group delay at the tail pressures were much smaller.

Effects of noise were small in Fig. 3. As described above, the ambient reflectance was measured based on the average over the 32 click presentations, while the tympanometric reflectance was measured using a sequence of clicks during the main sweep across ear pressure. The additional noise present in the tympanometric reflectance might be evident as an additional ripple in the tympanometric absorbance at TPP compared to the ambient absorbance (right panel in row 2), or in the tympanometric group delay at TPP compared to the ambient group delay (right panel in row 3). Despite this difference in the amount of averaging, these pairs of responses were not obviously different in terms of the amount of ripple. This was partially due to the one-sixth octave frequency averaging in these panels.

E. Length and volume tympanograms

The ear-canal length was estimated using the tympanometric group delay near the frequency above 2 kHz at which the absorbance at TPP was a minimum. This critical frequency of about 6.7 kHz is shown in the right panel of row 2 of Fig. 3 by a vertical line intersecting the minimum absorbance at TPP. As expected, the group delay at TPP was slowly varying near this frequency (right panel, row 3), and its half-octave average around this frequency was 136 μs compared to 126 μs for the ambient test (see also Fig. 1). This was converted into an estimate of length at each air pressure using Eq. (14).

This length estimate is shown as a function of air pressure in row 3 of Fig. 2 for the down-swept and up-swept tympanograms. The length varied during the initial portion of the test while pressurizing from ambient pressure to the starting sweep pressure; it varied during the final portion of the test while de-pressurizing from the ending sweep pressure back to ambient pressure. These initial and final segments of the length tympanogram varied smoothly with pressure except for discontinuities during the initial ramp near 200 daPa in the down-swept tympanogram (left panel), and during the initial ramp near −160 daPa and the final ramp near 140 daPa in the up-swept tympanogram (right panel).

Focusing attention on the length during the main sweep of the down-swept tympanogram (left panel) at intermediate times, the length had three pressure ranges over which it was slowly varying separated by discontinuous length changes near 150 and −100 daPa. The length was of an expected tympanometric shape in the inner pressure range from 140 daPa down to −95 daPa, with a local maximum near 0 daPa. The length estimated during the main sweep of the up-swept tympanogram (right panel) had a single large discontinuity near 185 daPa, with more fluctuations than during the down-swept test at pressures from about −110 daPa up to 180 daPa. These discontinuities in length are further described in Sec. VI.

The volume of air enclosed between the probe and TM was calculated as the product of area and length using Eq. (15), and is shown in row 4 of Fig. 2 for down- and up-swept tympanograms. As expected, the volume exhibited a similar qualitative pattern of discontinuities as was observed for the length, whereas the area estimate varied more slowly (in terms of its relative change) in this and other adult ears.

1. Estimating the equivalent admittance tympanogram at the TM

A procedure to measure a compensated wideband acoustic admittance tympanogram in an adult ear, or in a child's ear in which the ear-canal wall was approximately immobile in response to sound, was developed in the present study. This procedure did not require any of the three assumptions in Sec. IV C, and was applicable to both ambient and tympanometric measurements. The procedure assumed a cylindrical model for the ear canal and calculated an equivalent admittance at the TM using Eq. (12).

The tympanometric measurement was more complicated than the ambient measurement because the length and area also varied with pressurization as shown in Fig. 2. An approximation was used in which the values of length and area were sampled at the pressure of 0 daPa during the main sweep, which nominally corresponds to ambient pressure. This fact was introduced in Sec. IV B 1 for the area estimation. The approximation for the length estimation was more critical, because the length tympanograms had large changes at isolated pressures within the main sweep as described above. The zero crossing of pressure is evident in the area and length tympanograms in Fig. 2, which were smoothly varying for this test ear near 0 daPa. This approach avoided calculating the equivalent admittance at the TM over pressures at which abrupt changes occurred in the length tympanogram. However, this introduced a source of error that would perturb the calculation of equivalent admittance. Section VI presents an example of the sensitivity of the estimated equivalent admittance at the TM to variations in ear-canal length and area estimates.

2. Adult-ear example: Equivalent admittance tympanogram at the TM

The resulting equivalent admittance at the TM (Y_TM) for adult subject A is shown in Fig. 4. As a general orientation to the figure, the panels in the top row show Y_TM (magnitude and phase) as a function of frequency for the measurement at ambient pressure, and Y_TM for the tympanometric measurement at the TPP, and at the positive and negative tail pressures. Each panel in the bottom three rows of Fig. 4 shows Y_TM at a single octave frequency from 0.25 to 8 kHz as a function of air pressure. Each such frequency is at the DFT bin frequency that was closest to an octave frequency. Each panel shows a single-frequency Y_TM tympanogram with a circle marker at the frequency-specific TPP, with text providing summary information on Y_TM at that frequency.

FIG. 4.

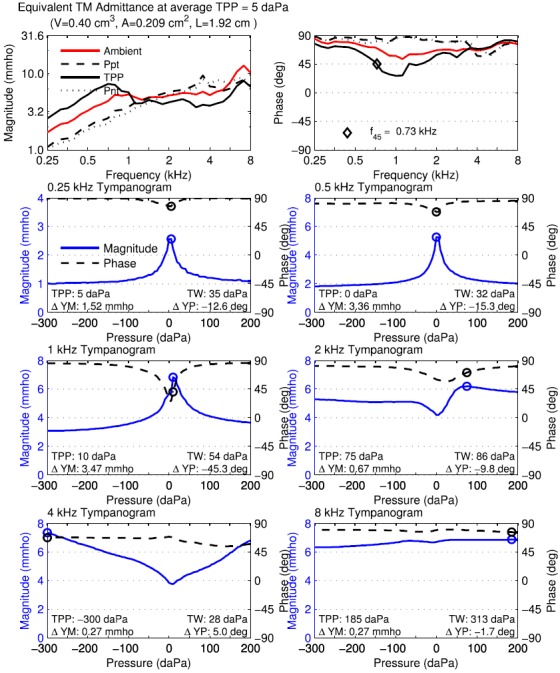
(Color online) Normal adult ear A. Equivalent tympanometric admittance at TM using downwards sweep. Top left: tympanometric magnitude at TPP, P_pt, and P_nt compared to ambient magnitude replotted from Fig. 1 (middle). TPP, S, L, and volume $V=S\times L$ of enclosed ear canal in displayed text. Top right: tympanometric phase at TPP, P_pt, and P_nt compared to ambient phase replotted from Fig. 1 (middle). f₄₅ in displayed text. Rows 2–4: Magnitude and phase of single-frequency tympanograms for equivalent admittance at TM at octave frequencies of 0.25, 0.5, 1, 2, 4, and 8 kHz, with circle symbol at TPP. The legend in the 0.25 kHz tympanogram shows the line styles for magnitude and phase used in the other single-frequency tympanograms. Text in each panel lists values of TPP, TW, ΔYM, and ΔYP.

In the top left panel of Fig. 4, the magnitude of the equivalent admittance at the TM is plotted versus frequency in separate curves parameterized by the fixed pressures of TPP, P_pt, and ${\mathrm{P}}_{\mathit{n}\mathit{t}}$. The magnitude from the ambient-pressure measurement is also plotted in this panel using the same data as in Fig. 1. The equivalent admittance magnitude at TPP increased at frequencies up to 0.75 kHz by 6 dB per octave, and was relatively constant at higher frequencies except for a local maximum value near 7 kHz. The equivalent admittance magnitude at TPP was larger than the ambient equivalent admittance magnitude below 1 kHz, and smaller at higher frequencies. The equivalent admittance magnitude at each tail pressure was smaller than at TPP or ambient pressure below about 1.2 kHz, and of similar magnitude at higher frequencies, except for a narrow peak in the magnitude at P_pt near 3.3 kHz. This showed the effect of the extremal pressures in reducing the TM mobility at frequencies below 1.2 kHz.

The magnitude of the equivalent admittance at the TM in the top left panel would be zero at the tail pressures if assumption (2) underlying the compensation procedure for 226-Hz tympanometry were accurate. However, the top left panel shows that the magnitudes at the tail pressures (P_pt and P_nt) were reduced below 1 kHz compared to the magnitude at TPP, but they remained larger than zero. For example, the Y_TM magnitude at 0.25 kHz was about 3 mmho at TPP and 1 mmho at the tail pressures. The fact that the magnitudes were non-zero at the tail pressures shows that assumption (2) of traditional tympanometry is inaccurate, even at low frequencies. This agrees with Shanks and Lilly (1981) and Rabinowitz (1981).

In the top right panel of Fig. 4, the phase of the equivalent admittance at the TM is plotted versus frequency at the same fixed pressure conditions. The phase was positive at all frequencies and pressures, which corresponded to an equivalent susceptance at the TM that was stiffness controlled. With one exception, the phase was between 45 and 90 degrees at all frequencies and pressures, which corresponded to an admittance that was more stiffness-controlled than conductance-controlled. The exception was that the phase of the equivalent admittance at TPP was less than 45° between 0.73 and 1.3 kHz. This was a resonant region of the equivalent admittance at TPP for which the magnitude was conductance-controlled, which was shown more clearly in the 1.0 kHz tympanograms (left panel of row 3) that is described below.

A summary frequency f₄₅ of the phase response was defined as the frequency at which the susceptance and conductance of the equivalent admittance at TPP were equal, so that the equivalent admittance phase was 45 degrees, with the convention that the phase was larger than 45° just below f₄₅ and smaller just above. The f₄₅ was 0.73 kHz in the test ear of adult subject A. A f₄₅ was defined for the compensated admittance at the probe tip and found to be clinically useful in “distinguishing otosclerotic ears from normal ears” (Shahnaz et al., 2009). That reference reported a 90% range of f₄₅ measurements in normal ears to lie within 0.355 to 0.900 kHz depending on whether their admittances were compensated using the positive or negative tail pressure.

Thus, it may be useful to retain the f₄₅ variable from the current equivalent admittance test for future group analyses. This f₄₅ calculated from the equivalent admittance at the eardrum would differ from a f₄₅ that might be defined and calculated from the admittance at the probe, because this latter admittance would include effects of ear-canal transmission between the probe and TM.⁵

A resonance frequency of the equivalent admittance at the TM was also calculated as the frequency at which the phase of Y_TM was 0° (with positive phase at slightly lower frequencies). In this adult test ear, no such middle-ear resonance frequency at the TM was observed, as the phase never decreased to 0°. With one exception, a “middle-ear resonance frequency” used in multi-frequency tympanometry devices also depends on the effects of sound transmission in the ear canal between the probe and TM, and so may be understood as a combination of ear-canal and middle-ear function. The exception is the Virtual 310 tympanometer,⁶ which, although no longer available, calculated a middle-ear resonance frequency up to 2 kHz from its estimate of Y_TM (Wiley et al., 1999), in which the resonance frequency was similarly defined in terms of the zero-crossing of the phase of Y_TM.

The remaining panels in Fig. 4 show tympanograms of the equivalent TM admittance as a function of air pressure at the six octave frequencies from 0.25 to 8 kHz. Each panel shows the magnitude and phase of $Y_{\mathit{T}\mathit{M}},$ with a circle marker showing the pressure at which the maximum magnitude occurred. At each frequency from 0.25 to 1 kHz, this admittance-based TPP was within 5 daPa of the low-frequency averaged absorbance-based TPP of 5 daPa. The shape of the single-frequency tympanograms at higher frequencies departed from a single-peaked shape, but the effects of the present procedures described in Secs. IV A and IV B to estimate the equivalence admittance at the eardrum mainly avoided the complex tympanometric shapes observed in the uncompensated admittance (Vanhuyse et al., 1975; Van Camp et al., 1986).

Other summary measures of the single-frequency tympanograms are shown in these panels. The TW was defined for each single-frequency $\left|Y_{\mathit{T}\mathit{M}}\right|$ tympanogram by analogy with the definition in Sec. IV B 3 for the LP absorbance tympanogram. The ΔYM was defined as the positive difference in admittance magnitude between its maximum (at the TPP calculated at this frequency) and the average of its tail values. The ΔYP was defined as the difference in admittance phase between its value at TPP relative to the average of the phase at its tail values. For example, ΔYM for the equivalent admittance at the TM was 1.52 mmho at 0.25 kHz. Assuming that $\left|Y_{\mathit{T}\mathit{M}}\right|$ is proportional to frequency at frequencies close to 0.25 kHz, the peak-to-tail difference in $\left|Y_{\mathit{T}\mathit{M}}\right|$ at 0.226 kHz would be reduced from that at 0.25 kHz by $0.226/0.25,$ or about 1.37 mmho.⁷

A ripple in the response is evident in $\left|Y_{\mathit{T}\mathit{M}}\right|$ at 0.25 kHz (left panel in row 2), which is evidence of greater amounts of measurement noise at 0.25 kHz. This ripple is of smaller amplitude at all higher octave frequencies (0.5–8 kHz), which is evidence of reduced noise effects at higher frequencies. In common with all the tympanometric reflectance and admittance results in Figs. 3 and 4, each of the single-frequency tympanograms in Fig. 4 already included the effect of the additional smoothing across pressure described in Sec. IV B 2. This smoothing somewhat reduced the peak amplitude near TPP, but this reduction was offset by an improved signal-to-noise ratio, especially at low frequencies.

V. RESULTS IN TWO INFANT EARS

All infant reflectance data were analyzed as frequency averages within each one-half octave. This provided more frequency averaging than in the adult data, which were averaged over each one-sixth octave frequency band. The larger averaging band in infants was selected because of increased noise levels in infant tests, and to provide a greater reduction in the number of variables characterizing each response (see Sec. VI).

A. Normal infant ear

Measurements of ambient and tympanometric reflectance are described in this subsection for the infant subject N with normal hearing and in the next subsection for the infant subject C with a conductive hearing loss. Infants were tested at a nominal 1 month age.

1. Ambient measurement

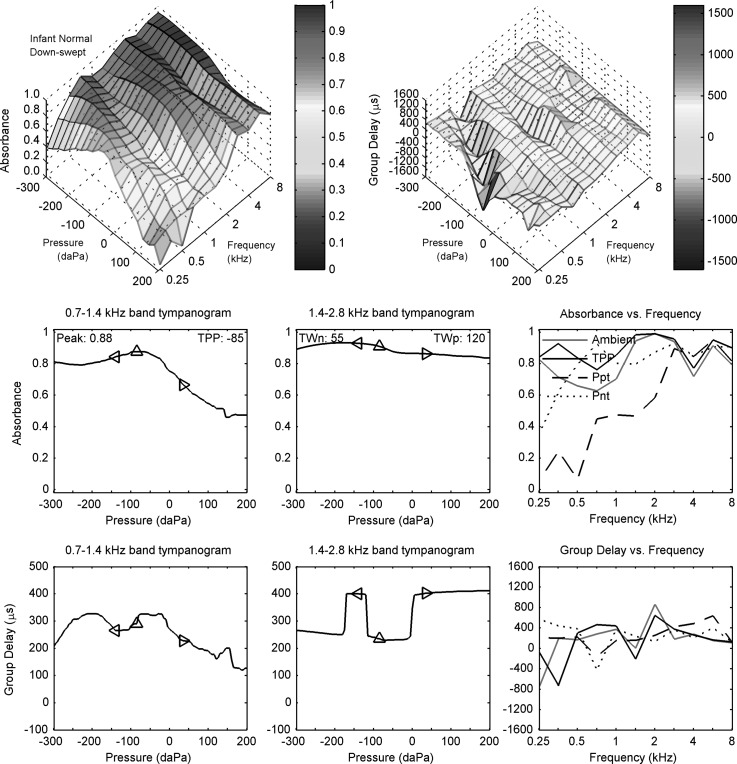
The ambient and down-swept reflectance data are shown for infant subject N in Fig. 5, which has the same plot format as in Fig. 3 for adult subject A. The ambient data are from the separate reflectance test at ambient pressure, but are shown in Fig. 5 (right panels in rows 2 and 3) to facilitate comparisons with the down-swept reflectance tympanogram.

FIG. 5.

(Color online) Down-swept tympanogram for normal infant N. Row 1: absorbance (left) and group delay (right) typanograms D_p versus frequency and air pressure. Row 2: LP (left) and HP (middle) filtered absorbance tympanograms versus air pressure, with peak absorbance and TPP values in left panel and half-tympanometric widths TWn and TWp of the LP tympanogram in the middle panel. Row 2 (right): absorbance tympanogram versus frequency at TPP, P_pt, and P_nt compared to ambient absorbance. Row 3: LP (left) and HP (middle) filtered group-delay tympanograms versus air pressure. Row 3 (right): Tympanometric group delay D_p at TPP, P_pt, and P_nt compared to ambient group delay. The diamond markers in each left and middle panel of rows 2 and 3 air pressure at TPP, TPP − TWn, and TPP + TWp.

The acoustic estimate of ear-canal area, which was based on the use of Eq. (4) with its frequency-averaged acoustic resistance, was 12.3 mm² for infant subject N. This was in the range of area estimates reported at age 1 month (Keefe et al., 1993) and 1.5 months (Keefe and Abdala, 2007). For example, the IQR of areas in the 2007 study extended from about 11 to 16 mm². It is this area that was used to calculate ear reflectance in Eq. (6), and thence the absorbance and group delay.

The ambient absorbance (Fig. 5, row 2, column 3) exceeded 0.6 at all frequencies, with relative maxima occurring at 0.25, 2, and 5.7 kHz. The ambient group delay (row 3, column 3) was positive at all frequencies above 0.25 kHz, with a peak value of about 800 μs at 2 kHz. The absorbance was larger in infant ear N than adult subject A, especially below 1 kHz at which ear-canal wall mobility effects were more pronounced compared to higher frequencies (Keefe et al., 1993).

2. Tympanometric measurement

The down-swept reflectance tympanogram is described for the normal infant ear (subject N) in Fig. 5. The top row of the figure displays contour plots for absorbance (left) and group delay (right) over the pressure-frequency plane. At the lowest frequency (0.25 kHz), the absorbance contour plot had a peak near 0 daPa that shifted to more negative pressures at slightly higher frequencies (e.g., −300 daPa at 0.71 kHz). When compared at the same frequency, the absorbance at more negative pressures was larger than the absorbance at more positive pressures. The group delay response was relatively uniform across the pressure-frequency plane with one exception. This exception was a “valley,” or a line of local minima, along a line extending from a point at about 0 daPa and 0.25 kHz to a point at about −300 daPa and 1 kHz. This line on the pressure-frequency plane tended to lie along a ridge, or a line of local maxima, in the absorbance contour.

The LP absorbance (row 2, left panel), which was filtered over a one octave band centered at 1 kHz, had a single-peaked shape across pressure with a TPP of −85 daPa. The HP absorbance (row 2, middle panel), which was filtered over a one octave band centered at 2 kHz, had only slight variation in the range of 0.8–0.9. The values of the half tympanometric widths TWp relative to the positive tail and TWn relative to the negative tail are plotted on each of these panels with marker symbols at pressures above and below the TPP, respectively. The larger TWp indicates a broader tail on the positive side of the LP absorbance (left panel).

The LP group delay (row 3, left panel) had multiple maxima and minima at pressures that were influenced by the presence of the valley in the contour plot of group delay (top right panel) at the lower frequencies in the LP bandwidth (0.7 to 1.4 kHz). The HP group delay (row 3, middle panel) tended to values around 250 μs at negative pressures and around 400 μs at positive pressures, except for pressures near −150 daPa, at which the group delay was similar to its values at positive pressures. These “steps” in the HP group delay panel were produced by the effects of averaging the group-delay contour (top right panel) over frequencies in the range from 1.4 to 2.8 kHz. This group-delay contour shows another valley of smaller relative depth just below 2 kHz, and another ridge just above 2 kHz, and the width of this valley varied across pressure with a larger width at pressures near −100 daPa. The steps in the HP group delay (row 3, middle panel) were related to a relative dominance of the valley or peak region in the group-delay contour plot across pressure within this one-octave passband at 2 kHz.

The tympanometric absorbance is plotted as a function of frequency at the pressure values of the TPP, Ppt, and Pnt (row 2, right panel). The tympanometric absorbance at TPP had a similar spectral pattern to the ambient absorbance in the same panel (that was described in Sec. V A 1), and their magnitude differences were well within 0.1 at all frequencies between 1.4 and 8 kHz. This is interesting inasmuch as the TPP of −85 daPa was not close to ambient pressure, but the small difference was consistent with the shape of the absorbance contour (top left panel), which was relatively flat for negative pressures across each frequency slice between 1.4 and 8 kHz (although less so at 8 kHz). As would be expected from this property, the tympanometric absorbance at Pnt (row 2, right panel) was similar to the absorbance at TPP and at ambient, except at 0.25 kHz. The tympanometric absorbance at Ppt in the same panel was the most different, with much lower absorbance below 2 kHz. This is also evident in the contour plot of absorbance below 2 kHz. Thus, there was a pronounced asymmetry between positive and negative pressures in the absorbance tympanogram of this normal one-month-old, which was not present in the normal adult ear (see Fig. 3).

The tympanometric group delay is plotted as a function of frequency at the pressure values of the TPP, Ppt, and Pnt (row 3, right panel). The tympanometric group delay at TPP was similar at all frequencies at and above 0.5 kHz to the ambient group delay in the same panel. This is consistent with a physiological response that was not unduly influenced by noise, as these responses were obtained in separate measurements with more averaging in the ambient test. The large minimum at 0.71 kHz in the group delay at Pnt was due to the valley described above in the contour plot of group delay (top right panel). This is one example in which the contour plots may be useful in understanding the peaks and dips in the simpler line plots, which might otherwise be interpreted as noise. The tympanometric group delay at TPP and the ambient group delay (right panel, row 3) were larger than the tympanometric delays at the tail pressures at frequencies near 0.7 and 2 kHz, but not so at other frequencies.

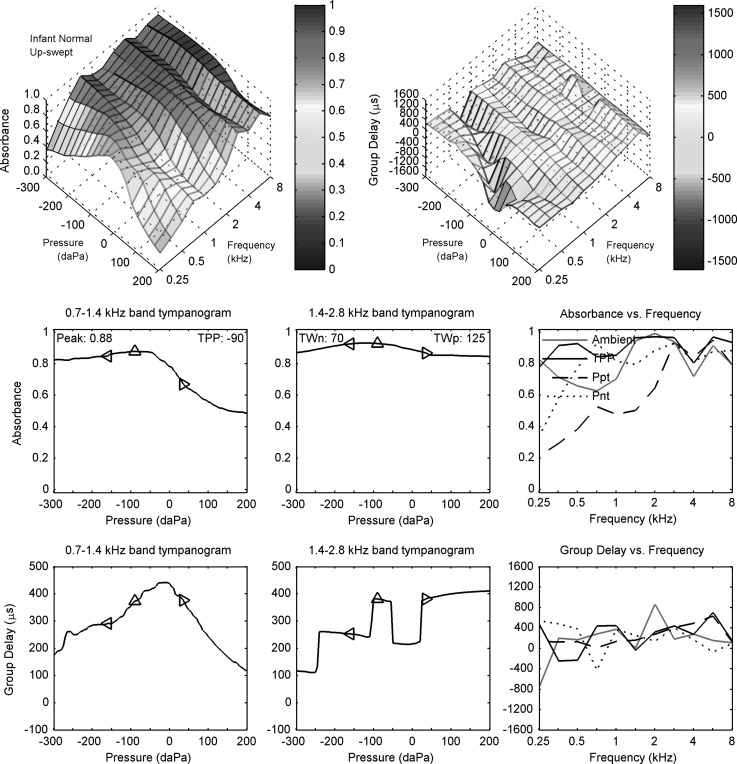
The up-swept reflectance tympanogram for the same normal infant ear (subject N) is shown in a similar manner in Fig. 6. The down- and up-swept reflectance tympanograms shared many similarities. A valley was observed for the group-delay contour plot over a similar line of negative pressures and low frequencies to the ridge observed for the absorbance contour plot. The absorbance functions plotted in row 2 of each figure were similar for both sweep polarities. However, the LP group delay (row 3, left panel) had a pronounced single-peak shape in the up-swept tympanogram at a slightly higher pressure (−20 daPa) than for the LP absorbance at the TPP. This shape was not found in the down-swept tympanogram, although a central maximum in the down-swept group delay (Fig. 5) did also occur at a pressure slightly larger than for the LP absorbance at the TPP. The HP group delay and group delay spectrum at fixed tympanometric pressures (row 3, middle and right panels) also had slightly different patterns in the up-swept test (Fig. 6) relative to the down-swept test (Fig. 5).

FIG. 6.

(Color online) Up-swept tympanogram for normal infant N. Row 1: absorbance (left) and group delay (right) tympanograms D_p versus frequency and air pressure. Row 2: LP (left) and HP (middle) filtered absorbance tympanograms versus air pressure, with peak absorbance and TPP values in left panel and half-tympanometric widths TWn and TWp of the LP tympanogram in the middle panel. Row 2 (right): absorbance tympanogram versus frequency at TPP, P_pt, and P_nt compared to ambient absorbance. Row 3: LP (left) and HP (middle) filtered group-delay tympanograms versus air pressure. Row 3 (right): Tympanometric group delay D_p at TPP, P_pt, and P_nt compared to ambient group delay. The diamond markers in each left and middle panel of rows 2 and 3 air pressure at TPP, TPP − TWn, and TPP + TWp.

This general similarity in down- and up-swept tympanograms observed in this one-month-old ear differs from group tympanometric results in normal newborns (Sanford et al., 2009), in which more asymmetry with sweep polarity was observed. The absorbance in newborn test ears was reduced over a broader range of negative pressures in the up-swept tympanogram, because the initial pressure in the sweep occurred at the most negative pressure (−300 daPa), and this negative pressure acted to collapse the ear-canal walls. This is consistent with Holte et al. (1991). In contrast, the initial pressure in the down-swept test occurred at the most positive pressure (200 daPa), which acted to open the ear canal. The present results are consistent with a reduced mobility of the ear-canal walls over the range of tympanometric pressures in one-month-olds relative to newborns, although group analyses would be required to confirm this finding.

B. Infant ear with CHL

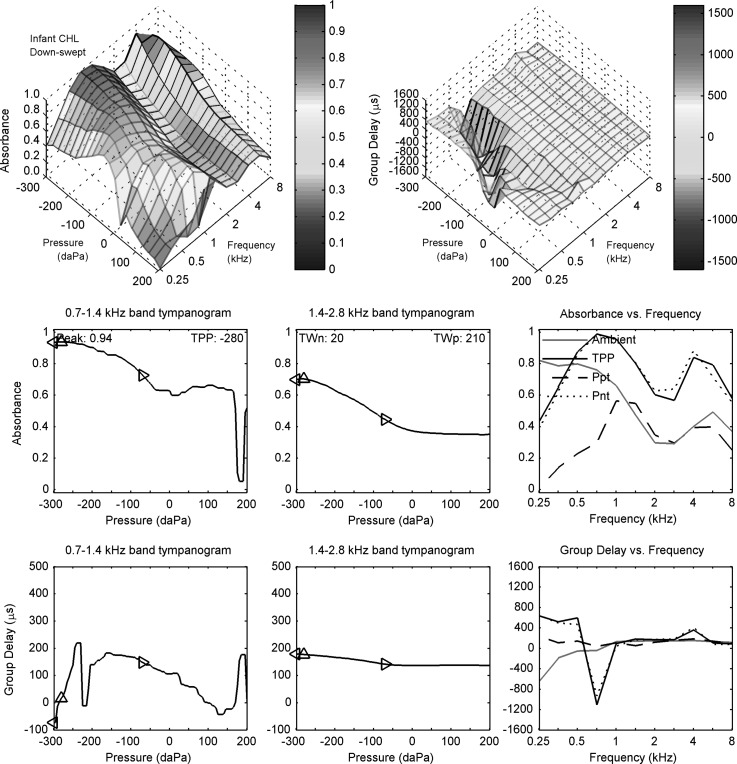
1. Ambient measurements

Measurements of ambient and (down-swept) tympanometric reflectance are next described for the infant subject C with a CHL in Fig. 7 with respect to the corresponding measurements for the normal infant ear (subject N) in Fig. 5 at the same nominal test age of 1 month. The acoustic estimate of ear-canal area was 10.2 mm² for infant subject C with a CHL, or 17% smaller than the area for subject N. This magnitude difference was within the IQR of areas estimated in normal ears at age 1.5 months (Keefe and Abdala, 2007).

FIG. 7.

(Color online) Down-swept tympanogram for infant C with CHL. Row 1: absorbance (left) and group delay (right) tympanograms D_p versus frequency and air pressure. Row 2: LP (left) and HP (middle) filtered absorbance tympanograms versus air pressure, with peak absorbance and TPP values in the left panel and half-tympanometric widths TWn and TWp of the LP tympanogram in the middle panel. Row 2 (right): absorbance tympanogram versus frequency at TPP, P_pt, and P_nt compared to ambient absorbance. Row 3: LP (left) and HP (middle) filtered group-delay tympanograms versus air pressure. Row 3 (right): Tympanometric group delay D_p at TPP, P_pt, and P_nt compared to ambient group delay. The diamond markers in each left and middle panel of rows 2 and 3 air pressure at TPP, TPP − TWn, and TPP + TWp.

The ambient absorbance (row 2, right panel) was similar in the normal and CHL ears at frequencies up to and including 1 kHz. The ambient absorbance in the CHL ear was lower than in the normal ear at all frequencies above 1 kHz. In particular, the ambient absorbance was less than 0.5 at all frequencies at and above 1.4 kHz, with relative maxima occurring at 0.25 and 5.7 kHz. This pair of examples is consistent with results obtained in newborn infants that the absorbance is reduced in ears that refer on an initial NHS exam (Sanford et al., 2009; Hunter et al., 2010), although the present tests were measured in one-month-olds.

The ambient group delay (row 3, right panel) in the CHL ear was negative at frequencies from 0.25 to 0.71 kHz, and was positive with values between 113 and 151 μs at 1 kHz and above. Except for 1.4 kHz, the group delay was smaller in the CHL ear than in the normal ear at all frequencies between 0.5 and 8 kHz.

Suppose that the ear-canal lengths of a normal ear and a CHL ear were the same, that wall mobility may be neglected and that the eardrums were each compliance dominated. Then, a smaller positive group delay in the CHL ear would be associated with a less compliant eardrum. This argument appears consistent with the observed difference in group-delay measurements in this pair of ears, although further studies using groups of infants are needed. This example demonstrates measurement feasibility and suggests interesting directions to pursue in the future.

2. Tympanometric measurements

The down-swept reflectance tympanogram is shown for the infant ear with a CHL (subject C) in Fig. 7. The contour plots (top row) showed a ridge of absorbance and a valley of group delay over a line extending from a point at about 0 daPa and 0.71 kHz to a point at about −300 daPa and 1 kHz. This pattern on the pressure-frequency plane in the infant CHL ear was similar to a pattern observed for the infant normal ears, except with slightly increased frequency. The absorbance had a second ridge of locally maximum values near 4 kHz and at more negative pressures. The group delay was relatively uniform outside of the low-frequency valley. For example, between 1.4 and 8 kHz and across all pressures, the grand mean of the group delay in the infant CHL ear was 148 μs with a grand standard deviation of 26 μs.

The LP absorbance (Fig. 7, row 2, left panel) centered around 1 kHz was largest at the most negative pressures, with a TPP of −280 daPa, with a tapering response at positive pressures, which was characterized by a much larger TWp than TWn. A narrow minimum close to 180 daPa was associated with a general, but non-monotonic reduction in absorbance in the contour plot of absorbance (top row, left) near 1 kHz over pressures near 180 daPa. The HP absorbance (row 2, middle panel) averaged over a center frequency of 2 kHz showed a similar maximum absorbance at the most negative pressures with a slow reduction to a relatively constant value near 0.35 at positive pressure. This HP absorbance value at positive pressures in the CHL ear was much less than the corresponding value in the normal ear, which exceeded 0.8 in Fig. 5.

In Fig. 7, the LP group delay (row 3, left panel) centered at the 1 kHz octave band had a rapid variation near −240 daPa, which was not noise but rather an effect of traversing the valley in group delay in its contour plot in this pressure and frequency range (top row, right panel). This is another example of the value of observing the entire contours of the absorbance and group-delay tympanograms. Otherwise, the LP group delay had a broad relative maximum just below −150 daPa that tapered slowly down to 130 daPa and then rapidly increased to a maximum near 190 daPa. The HP group delay (row 3, middle panel) centered at the 2 kHz octave had a maximum value of about 180 μs at the TPP, slowly decreased to about 130 μs at 0 daPa, and was relatively constant at positive pressures. The LP and HP group delays in the CHL ear were less than the corresponding delays in the normal ear at all pressures (compare to the same panels in Fig. 5).

In Fig. 7, the tympanometric absorbance is plotted as a function of frequency at the pressure values of the TPP, Ppt and Pnt (row 2, right panel); the ambient absorbance is also plotted for ease of comparison. The absorbance at TPP was nearly equal at all frequencies to the absorbance at Pnt, and both were larger at all frequencies than the absorbance at Ppt. The absorbance at TPP was markedly larger than the ambient absorbance at frequencies from 0.7 to 8 kHz, which might be expected because the TPP of −280 daPa was much lower than ambient pressure.

Comparing tympanometric absorbance in the normal infant (Fig. 5) and the infant ear with CHL (Fig. 7), the absorbance at TPP in the CHL ear was reduced at low frequencies (0.25 to 0.5 kHz) and at high frequencies (1.4 to 8 kHz). The reduction in the absorbance at TPP in the CHL ear relative to the normal ear was smaller than the reduction in the ambient absorbance. This factor would be partially explained by the fact that the tympanometric reflectance at TPP controlled for the more negative TPP in the CHL ear relative to the normal ear, while the ambient reflectance did not. However, the absorbance at TPP differed in the two ears, so the presence of CHL appeared to involve more than just a change in TPP. The tympanometric absorbance at Ppt at frequencies from 2 to 8 kHz was much smaller in the CHL ear than the normal ear. For example, this absorbance between 2.8 and 8 kHz exceeded 0.8 in the normal ear but was less than 0.4 in the CHL ear.

In Fig. 7, the tympanometric group delay is plotted as a function of frequency at the pressure values of the TPP, Ppt and Pnt (row 3, right panel) along with the ambient delay for comparison. The group delays at TPP and at Pnt were large up to 0.5 kHz followed by a negative minimum at 0.71 kHz. These delays were consistent with the contour plot of group delay (upper right panel). The group delay for frequencies between 1 and 8 kHz in this ear with CHL were relatively close to zero for all pressure conditions, and were smaller than the corresponding group delays in the normal ear (Fig. 5).

VI. DISCUSSION

A. Length estimation between probe and eardrum

The basic idea underlying the procedure to estimate the length between the probe and the TM was that the group delay would equal twice the round-trip length in a cylindrical ear canal at a frequency at which the TM was immobile. Previous studies have described this idea, and the present procedures emerged from these studies. Wiener and Ross (1946) reported that the pressure ratio at a given location in the ear canal to the pressure at the entrance of the canal occurred at a frequency for which the length L from the location to the eardrum was approximately a quarter-wavelength. Using measurements in couplers with a rigid-wall termination to model an immobile (i.e., hard-wall) eardrum, Shaw and Teranishi (1968) found that the ratio of the pressure at various locations in the ear canal to the pressure at the eardrum had narrow minima occurring at frequencies slightly higher than the frequency for which the quarter wavelength was equal to L. Their pressure ratio measurements in adult human ear canals were qualitatively similar, although the minima near the quarter-wavelength frequency were broader. They concluded that the human eardrum is relatively “hard,” i.e., relatively immobile, at higher frequencies in the range 4–8 kHz. This quarter-wavelength condition is equivalent to a group delay equal to $2L/c,$ as used in Eq. (9).

Gilman and Dirks (1986) confirmed this approximate quarter-wavelength condition in an eardrum simulator (ANSI S3.25) and studied the errors in the approximate equality through a reflectance model of sound transmission through a cylindrical ear canal to an eardrum of variable impedance. They showed that the distance of the lowest-frequency pressure standing-wave minima from the TM was equal to the probe-to-eardrum length L plus a term proportional to the eardrum reflectance phase. After transformation of reflectance phase to group delay, Eq. (9) is analogous to their result. Their experimental results showed the importance of estimating the length L in real ear measurements to measure sound pressure level (SPL) at the TM, or, by extension to the present study, to measure an equivalent admittance at the TM (the present procedures may also be used to estimate an equivalent SPL at the TM).

Based on a model of sound transmission in an ear canal with an assumed cylindrical cross-section, Chan and Geisler (1990) evaluated a novel procedure to estimate the distance L between probe and an “effective reflective plane” of the eardrum using probe SPL measurements at two mid-canal locations separated by a fixed distance of 5 mm. The average optically measured length to the umbo in 14 ears was 3.9 mm further than the optically measured distance to the top of the eardrum. A quarter-wavelength model was used to acoustically estimate $L;$ the average L was 0.7 mm longer than the distance to the top of the eardrum, and shorter than the distance to the umbo. These authors reported that the eardrum effects described in Gilman and Dirks (1986) influencing the length estimate might be on the order of 3 mm or less. These effects are the differences in the eardrum group delay in Eq. (9), in which a 3 mm variation in L corresponds to a 17 μs variation in group delay.

Potential limitations in Chan and Geisler (1990) include: two different mid-canal probe insertions are required with a known 5 mm separation, the 5 mm is a linear distance measurement whereas the centroid axis of the ear canal may have significant curvature, and the contribution of the reflectance group delay at the eardrum, which is termed D₀ in Eq. (9), is unknown. Dirks et al. (1996) characterized the Chan and Geisler procedure as having potential disadvantages for clinical use based on the need for multiple measurements with different probe-to-eardrum distances, which might increase the measurement time.

The present procedure to estimate L used only a single probe insertion and avoided the need to measure a fixed second distance along the curved axis of the ear canal. A feature of the present procedure, following Keefe (2007), was to estimate L near the frequency at which the eardrum would most closely resemble the acoustical effect of an ideal closed end: this was the frequency of minimum absorbance at frequencies between 2 and 8 kHz. Responses below 2 kHz were not analyzed to avoid the frequency range over which the eardrum resonance effects are prominent in adult ears. This approach avoided analyses at the frequencies of minimum SPL in the ear canal, for which the smallness of the plane-wave mode amplitude makes the contributions from evanescent modes more important.

Consistent with Shaw and Teranishi (1968), the eardrum is relatively immobile at high frequencies, and it may be possible to estimate L at other half-octave frequencies within the 2–8 kHz bandwidth. This is consistent with the slow variation in group delay in the adult ear data in Fig. 1 above 2 kHz, although more such data are needed. While this particular ear had a minimum absorbance near 5.7 kHz, group data show a minimum in absorbance (or a maximum in energy reflectance) near 8 kHz (Stinson, 1990; Keefe et al., 1993; Margolis et al., 1999), or a broader minimum absorbance in 6 ears between 6 and 10 kHz (Farmer-Fedor and Rabbitt, 2002). An ear with a minimum absorbance just above 8 kHz would evaluate the group delay in the present procedure by averaging over a quarter-octave band with an upper frequency of 8 kHz, which was the maximum test frequency in the present study.

B. Variability of estimates of ear-canal area and length

The calculations of the ear reflectance using Eq. (6) and the equivalent admittance at the TM using Eq. (12) with Eq. (5) in both ambient and tympanometric tests depended on the estimate of ear-canal area at the probe tip, which was based on Eq. (4). The calculations of the equivalent admittance at the TM in Eq. (12) in both ambient and tympanometric tests also depended on the estimate of ear-canal length between the probe tip and TM. Variability in the area estimate would influence the resulting calculations of reflectance and equivalent admittance, while variability in the length estimate would influence the resulting calculation of equivalent admittance.

An example of this variability is given in Table I for the area and length estimates for adult subject B with normal hearing, who was tested on two dates separated by 49 days (in contrast, adult subject A was tested only once). The ear-canal volume is also calculated in the table. The table lists the percent change of test 2 relative to test 1 for all dimensions. There was larger variability in area and length in the ambient test than in either of the down- or up-swept tympanograms. For all three test conditions, the variability of ear-canal volume was less than that of either the area or length; i.e., the changes in area and length had opposite sign and so were reduced when the volume was calculated as the product of area and length. Except for this linkage of area and length changes on the volume change, it is the magnitude difference between test and retest that is most important. On test date 2, the dimensions estimated from the ambient test were much different from their values on either of the tympanometric tests. Otherwise, the estimated length and area were similar within the ambient, down- and up-swept tympanometric tests performed on the same test date. It is unknown whether the probe fit was adjusted in between each of these three tests on either test date.

TABLE I.

Estimated area, length, and volume repeatability for adult subject B for ambient and tympanometric tests. The column ΔS lists percent change of the estimated area for test 2 relative to test 1, and similarly for the column ΔL for estimated length and ΔV for volume (as product of estimated area and length).

Test type	Test	Area	Length	Volume	ΔS	ΔL	ΔV
	#	(mm2)	(mm)	(mm3)	(%)	(%)	(%)
Ambient	1	32.2	21.5	692
	2	40.5	14.9	603	26	−31	−13
Down-swept tymp.	1	33.7	21.7	731
	2	29.0	22.9	664	−14	6	−9
Up-swept tymp.	1	28.8	21.3	613
	2	24.8	22.5	558	−14	6	−9

The magnitude difference across test dates varied between 14% and 26% for the change in area and between 6% and 31% for the change in length. These results in Table I are illustrative on the order of magnitude of the changes in area and length that might be measured in a normal adult ear, but further research is needed to study the repeatability in groups of normal adult ears. Factors contributing to this difference would include probe depth insertion, which would directly affect the estimated length, the distance of the probe tip from any canal wall surface, which might partially occlude the response to sound measured by the probe microphone, and any other measurement errors and changes in physiological function.

The question arises on the possible relationships between the variabilities in estimating the ear-canal length and area, and the relatively small effects of probe location within the ear canal on the resulting measurements of energy reflectance that Voss et al. (2008) observed in adult cadaver ears. Among the factors that might contribute to the interpretation of a relatively small effect of reflectance on probe location are: the geometry of the receiver and microphone ports of the probe (rotationally symmetrical or otherwise), the material comprising the probe tip (soft plastic or foam), the small effect of viscothermal wall losses on energy reflectance at frequencies below about 1 kHz (Margolis et al., 1999; Voss et al., 2008), the curvature of the ear canal that results in a shift in the local sound field described in terms of the evanescent modes, the test-retest difference in energy reflectance at the same location within the ear canal, biological sources of variability, and any measurement noise.

The probe in the present study used a plastic eartip and its receiver and microphone ports were symmetrically located within the center of the tip, whereas the Etymotic ER 10 C probe used by Voss et al. had a softer foam tip with the receiver port radially offset from the on-axis microphone port. Suppose a probe were positioned at a fixed location in a curved ear canal and the reflectance was measured for the probe in a first configuration and then in a second configuration in which the probe was rotated. With an asymmetrical probe geometry such as that of the Etymotic ER 10C, it is hypothesized that the reflectance would differ in the two probe configurations, in part because the effective distance from the receiver port to the eardrum and back might slightly differ before and after the rotation in a curved ear canal. This effect would be larger at high frequencies and might contribute to slight changes in a reflectance measurement. There might be an additional interaction of the variables describing ear-canal curvature with the relative rotation of the probe, inasmuch as the evanescent modes near the probe tip may vary in a curved ear canal relative to an idealized “straight ear canal.” Given that the ear-canal area does change with distance within the canal, the soft foam is compressed more as the area decreases, which might produce measurable effects on reflectance, inasmuch as it depends on the source reflectance of the probe. More empirical evidence is needed to evaluate the origin of the discrepancies between the prediction of the one-dimensional acoustic theory and the finding of a relatively small effect of $|R_e(f){|}^2$ on probe location.

Notwithstanding these variabilities, the relative insensitivity of energy reflectance on ear-canal measurement location was explicit in Stinson et al. (1982), and motivated the application of energy reflectance to middle-ear testing at higher frequencies as an alternative to impedance or admittance. It is evident from Eq. (9) that the group delay at the probe tip varies with distance L between the probe and the eardrum. The differences between the admittance at the probe and the admittance at the TM are evident above 1 kHz in the responses for Adult A in Fig. 9, and are substantial above 2 kHz. These results agree with previous studies. Whatever may be the magnitude of the small changes in energy reflectance at higher frequencies across varying measurement locations and the explanations for those changes, the more fundamental point is that energy absorbance and energy reflectance convey information about middle-ear function at higher frequencies, while admittance measurements at the probe tip are highly sensitive to probe location. As explained in the present report, the corresponding information at higher frequencies may be obtained from calculating an equivalent admittance at the TM, but that calculation is based on further assumptions and the need to estimate the probe-to-TM length.

FIG. 9.

Sensitivity of Y_TM to changes in estimated ear-canal area and length for Adult A. Admittance measured at the probe tip (row 1). Y_TM for varying ear-canal dimensions: area only (row 2), length only (row 3), length and area varying by the same relative changes (row 4), and length and area varying by relative changes of opposite sign (row 5). For example, in row 5, a change of +20% in length was made with a change of −20% in area. This condition is termed the “−Area and Length” condition in the titles on row 5. These admittances are shown for the estimated area and length (0%) and for percentage increases and decreases relative to these reference dimensions.

C. Repeatability of tympanograms of ear-canal area, length, and volume

Tympanometric measurements of ear-canal area, length and volume were obtained for adult subject B on test dates 49 days apart. Figure 8 shows these ear-canal dimensional tympanograms as measured on the test and retest for the down-swept tympanometric test. The format of these plots is similar to the corresponding results for adult subject A on the down-swept test in the left column of Fig. 2. The top panel shows that the time to complete the sweep was similar for the test and retest.

FIG. 8.

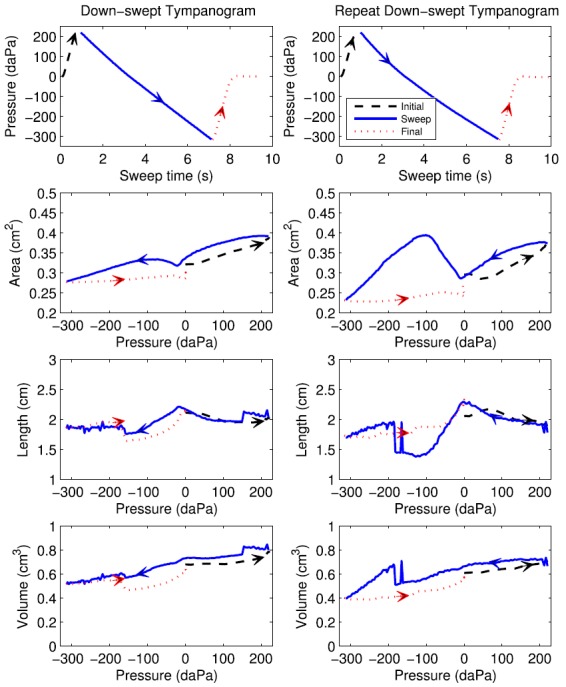
(Color online) Pressure and ear-canal dimensions during down-swept tympanograms on a first test (left) and repeat test (right) 49 days later, with arrows increasing directional time course of pressurization. Row 1: air pressure versus time during initial, sweep, and final sections of the measurement. Row 2: Ear-canal area versus pressure. Row 3: Ear-canal length versus pressure. Row 4: Ear-canal volume versus pressure.

The TPPs measured from the LP absorbance down-swept tympanograms (not shown) were similar in the test and retest, i.e., −15 daPa for the test and −10 daPa for the retest. In Fig. 8 (row 2), the areas estimated during the main sweep were generally similar at the extremal pressures and near ambient pressure, for which the latter result is consistent with Table I. The areas were much more similar during the sweep over intermediary values of positive pressure than the areas over intermediary values of negative pressure, for which the area during the retest was larger near −100 daPa. At the zero-crossing of pressure at which the ear reflectance was calculated for each tympanogram (see Sec. IV E 1), the test area was 33 mm² and the retest area was 29 mm².

The lengths during the main sweep (Fig. 8, row 3) had relatively similar values in test and retest at the extremal pressures and near ambient pressure, for which the latter is quantified in Table I. The lengths in test and retest had a local maximum just below ambient pressure, i.e., these maxima were close to the TPPs given above. The length in the retest was much lower at negative pressures around −100 daPa, which is the pressure range over which the areas were larger in the retest. In the main sweep, the length in the initial test changed over a narrow range of pressure near 150 daPa and again near −175 daPa, and the length in the retest changed twice in the test at pressures between −170 and −200 daPa.

These sudden changes in length were qualitatively similar to those observed for adult subject A in both down-swept and up-swept tympanograms (see Fig. 2). It is possible that these discontinuities were associated with abrupt shifts in the quasi-static configuration of the eardrum and ossicular chain. The inter-click time interval was 46 ms, so that any relative shift in this configuration that occurred over 150 ms or so might affect 3 or 4 click responses, and result in such apparent discontinuities. Another possibility is some unknown source of measurement error. It is highly unlikely that the probe physically moved within the ear canal to any significant extent during the tympanogram. Such a movement would most likely have been associated with a leak, which would be immediately evident in the inability to maintain pressurization during the main sweep. Such leaks were detected by the real-time measurement software (see Sec. II B). The smoothly varying pressures during the main sweep in the top panel revealed that no leaks were present during the test or retest. More research is needed on these discontinuous length changes during swept tympanometry.

D. Equivalent admittance at the eardrum

1. Sensitivity of Y_TM to changes in estimated area and length

A procedure was described to calculate the equivalent admittance at the TM of an adult ear, which involved the calculation of L_TM in Eq. (11) and its use in Eq. (12). The calculated equivalent admittance of the adult ear A was stiffness controlled over all frequencies between 0.25 and 8 kHz in both ambient and tympanometric tests (see Figs. 1 and 4). The positive admittance phase at all frequencies in this single-ear measurement contrasts with group mean measurements of an equivalent impedance at the TM in tests performed at ambient pressure in the ear canal (Rabinowitz, 1981; Margolis et al., 1999).

In Rabinowitz (1981), the mean Y_TM magnitude increased at 6 dB per octave at low frequencies with a local maximum near 1.2 kHz and a local minimum near 2 kHz; this magnitude increased at higher frequencies up to a maximum test frequency of 4 kHz. The mean Y_TM phase was positive at low frequencies and within one standard deviation of zero degrees from about 1.2 kHz up to the maximum test frequency of 4 kHz.

In Margolis et al. (1999), the mean $Y_{\mathit{T}\mathit{M}},$ which was plotted as the corresponding impedance, was similar to the Rabinowitz data, with the largest differences at frequencies between 1 and 2.8 kHz: the reactive components were similar but the resistive component was smaller in the Margolis et al. data. The procedure used by Margolis et al. to estimate Y_TM up to a maximum frequency of 11.2 kHz used a similar uniform transmission line as Rabinowitz for sound transmission in the ear canal between the probe and TM. This model required estimates of ear-canal area and length. The area was estimated based on the size of the plastic eartip of the probe that successfully sealed the probe into the ear canal. The length was estimated as the ratio of a calculated volume to this estimated area. The volume was calculated as the ear-canal volume determined using a clinical compensation procedure of a single-frequency admittance tympanogram at 226 Hz. This estimated volume, and hence the estimated length derived from this volume, was calculated under the assumptions that the ear-canal volume did not change during the tympanogram and the admittance magnitude was zero when the ear canal was pressurized to its extremal values.

The length estimation procedure in Margolis et al. adopted the inaccurate assumptions (1) and (2) described in Sec. IV C, whereas the procedure in Rabinowitz adopted the inaccurate assumption (1). The adult ear example in Fig. 4 showed that none of the three assumptions underlying compensation of 226-Hz admittance tympanograms (in Sec. IV C) was accurate.

This illustrates the need for further research in estimating an equivalent admittance at the eardrum. While the present data were obtained in only a single adult ear, a sensitivity analysis was performed in which the area and length used to estimate the Y_TM for this ear were varied. Each of the area and length was varied by ±20% and ±40% with respect to their estimated values described above to study the resulting effect on $Y_{\mathit{T}\mathit{M}}.$ One additional analysis varied both of these area and length by ±20% and ±40%, which was equivalent to a volume variation of 44% and 96%, respectively. A final analysis varied the length and area to have inverse changes; i.e., when the length change was 20% the area change was −20%, and vice versa. The range of variations of area and length was slightly larger than the magnitude differences in their values listed in Table I for adult subject A.

The results of this sensitivity analysis are shown in Fig. 9, in which the top row shows the admittance at the probe tip given by Eq. (2) in terms of reflectance from Eq. (1). This probe admittance had a maximum magnitude near 2.3 kHz with a sharp notch just above 6 kHz due to the presence of acoustic standing waves in the ear canal between the probe and eardrum. The corresponding probe admittance phase had corresponding regions of positive phase below 2.3 kHz, negative phase up to 6 kHz, and positive phase again at higher frequencies.

In row 2, the estimated Y_TM is shown for the originally estimated area (100% in the legend), and with larger and smaller areas. For the reference 100% condition, the magnitude of Y_TM had a maximum at about 7 kHz (these are the same data as in Fig. 1). The Y_TM magnitude increased monotonically with increasing area between about 1.2 and 7 kHz, with a maximum change of about a factor of 7 just above 4 kHz between the smallest (60%) and largest (140%) areas. The phase did not vary more than 25° with variations in area, and remained positive at all frequencies. The phase decreased with increasing area for frequencies between 0.7 and about 5 kHz, and increased with increasing area above 5 kHz up to 8 kHz. A similar sensitivity of the measured Y_TM to ±10% changes in the estimated area in ears of domestic cats showed a somewhat larger variation of Y_TM phase between 2 and 10 kHz (Huang et al., 2000) than in the present human-ear results. Notwithstanding that difference, the Y_TM estimated in cat and adult human was insensitive to area changes at low frequencies (i.e., below about 1 kHz in row 2).

In row 3, the sensitivity of Y_TM is shown for variations in estimated length. Variations in L_TM had larger effects on the estimated Y_TM than variations in area. For the two smallest lengths (80% and 60%), the magnitude of Y_TM had a maximum at about 6 and 5.2 kHz, respectively, which would converge in the limit of zero length to the probe admittance, whose magnitude was maximal at 2.3 kHz. For the two largest lengths (120% and 140%), the magnitude was reduced compared to the reference condition at all frequencies, but especially above 1 kHz. The corresponding phase of Y_TM was insensitive to the length estimates at frequencies below 4 kHz, but was shifted for the two smallest lengths from positive to negative values at higher frequencies close to the frequencies of the corresponding maxima in the magnitude of $Y_{\mathit{T}\mathit{M}}.$ This analysis would predict that the phase of Y_TM at the reference condition (100%) might vary towards negative values at frequencies just above 8 kHz, but no data were measured in this range.

In row 4, the simultaneous variation of larger area and larger length, or smaller area and smaller length, had only small effects on the magnitude of Y_TM below 4 kHz. The reason for this behavior is most easily observed by comparing the magnitudes of Y_TM in rows 2 and 3. Reducing the area reduced the magnitude, but reducing the length increased the magnitude. Above 4 kHz, the larger effect of varying the length dominated over variations in the area when both were varied, and a maximum in the magnitude of Y_TM was obtained for the smaller variations (60% and 80%). The high-frequency phase of Y_TM in row 4 for co-varying length and area generally followed the phase patterns in row 3 as a function of varying length.

In row 5, the simultaneous variation of area and length with opposite polarity had only small effects on the magnitude of Y_TM below 0.7 kHz, but had large effects at all higher frequencies. This condition followed the trend in the ambient test-retest data in Table I, in which an increased length estimate on a retest occurred in tandem with a decreased area estimate. The combination of an increase in area coupled to a decrease in length (in row 5) led to larger effects on Y_TM than did an increase in area coupled with an increase in length (in row 4).

2. Comparison with procedures of Rabinowitz

None of the predicted Y_TM patterns in Fig. 9 were similar to the estimated mean Y_TM reported by Rabinowitz (1981) [and Margolis et al. (1999)]. For example, none of the estimated Y_TM phase functions were close to 0 degrees between 1.2 and 4 kHz, as reported in these studies. The difference in Y_TM in adult subject A relative to these mean results cannot be explained solely in terms of differences in how the area and length were estimated.

Part of the explanation is that the admittance at the probe tip of adult subject A in the present study (top row of Fig. 9) had a maximum near 2.3 kHz with a change in phase polarity at higher frequencies, whereas the admittance at the probe tip in the two adults shown in Rabinowitz (1981) did not show a clearly defined maximum in magnitude and the phase remained positive at all frequencies up to 4 kHz.

The differing assumptions used in the procedures to calculate Y_TM from the probe admittance may also be involved. Rabinowitz (1981) presented a sensitivity analysis of the effect on Y_TM due to changes in a coefficient $\kappa ,$ which was defined as the ratio of the equivalent volume of the eardrum averaged over the pressurized conditions (±40 cm H₂O or ±392 daPa) to the equivalent volume at ambient pressure. The method to estimate κ was iterative and assumed that (i) the effect of pressurization on the low-frequency admittance was proportional with the same proportionality constant in all ears to the middle-ear transmission assessed in individual ears using a pair of psychophysical tasks (loudness balance and the phase of an aural combination tone), and (ii) the average transfer function of pressure at the TM to pressure at the ear-canal probe in the four ears, which was estimated using the transmission-line model, was assumed equal to the average measured values reported in the literature. The resulting mean value for κ across the estimates in the four ears was 0.57. The value of κ was individually estimated for each ear and used to estimate the ear-canal volume, which was used with the assumption of constant area across ears, to estimate the ear-canal length used in the transmission-line model. These procedures required additional assumptions and psychophysical measurements in order to estimate the ear-canal length between the probe and TM. In contrast, the present procedures estimated the area and length solely from the measured probe admittance and associated ear reflectance.

In the sensitivity analysis of Rabinowitz (1981), a reduction in κ to 0.44 led to a Y_TM phase that was positive at all frequencies up to 4 kHz, with a minimum phase of about 10° near 1.4 kHz. This was the most similar condition in Rabinowitz (1981) to the estimated Y_TM for adult subject A (top panel, Fig. 4), which showed a minimum phase of 23° near 1 kHz.

The present data may be used to estimate $\kappa .$ At the 226 Hz frequency used by Rabinowitz, the ratio of the equivalent volumes is approximately equal to the ratio of the magnitudes of Y_TM at the pressurized conditions relative to the ambient pressure. Using data from the 250-Hz Y_TM tympanogram (left panel in row 2 of Fig. 4), the magnitude of Y_TM was about 1.1 at the pressure extremals and 2.5 at ambient pressure. The resulting κ was 0.44, the same as the reduced κ value considered in the sensitivity analysis in Rabinowitz (1981).⁸

3. Implications

Keefe (2007) described a similarity between acoustic measurements of admittance at the TM to published laser Doppler vibrometry measurements of umbo motion relative to ear-canal pressure just in front of the TM (Goode et al., 1996; Huber et al., 2001; Whittemore et al., 2004). These vibration measurements at the umbo were obtained in tandem with acoustic pressure measurements with a small microphone located 2–4 mm from the umbo. The present study evaluated a new procedure to estimate $Y_{\mathit{T}\mathit{M}}(f)$ from measurements of $Y_p(f)$ based on results obtained in an adult ear. Such umbo measurements and ambient-pressure energy (or power) reflectance measurements have similar diagnostic accuracy in identifying otologic disorders (Nakajima et al., 2012). A comparison between measurements of umbo transfer function and equivalent admittance at the TM would be of clinical interest, as they are transfer functions at the TM of linear velocity and equivalent volume velocity, respectively, relative to the ear-canal pressure. An important detail is the location of the pressure microphone in both the acoustic and LDV measurements. This may be regarded as an alteration in the length from the probe to the location of the measurement, so that the above sensitivity analysis of Y_TM is pertinent to such a comparison.

Because the ear-canal length may vary discontinuously with pressure as in Fig. 2, the resulting tympanogram of the equivalent admittance at the TM may not be as robust as the reflectance tympanogram in studying middle-ear dysfunction. A calculation of the equivalent admittance at the TM also required a transmission-line transformation from the probe to the TM, which was not required to calculate ear reflectance. Because the procedure to estimate ear reflectance in terms of the area is inherently less complicated than the procedure to estimate an equivalent admittance at the TM, the multi-year study in adult and infant ears focused more on the use of reflectance in clinical screening and diagnostic applications.

E. Comments on group delay

The reflectance measurement and analysis procedures described above placed absorbance and group delay representations on a similar basis. One consideration for group delay is whether to analyze responses in terms of the group delay at the probe based on the length defined in Eq. (10), or the equivalent group delay “at the TM” based on the length in Eq. (11).

The adult and infant ear test procedures used the group delay at the probe for two reasons. The first is that the calculation method for the equivalent group delay at the TM depends on the assumption that the ear-canal wall is rigid. This assumption is not valid for young infants as described above.

The second reason is that one goal of the multi-year study is to compare the group delay in ears with a conductive disorder relative to an age-matched group of ears with normal auditory function. Assuming a random variation in ear-canal length with zero mean difference between these normal and impaired groups, the mean difference in group delay at the probe would be the same as the difference in equivalent group delay at the TM. Thus, to investigate the use of group delay as a screening or diagnostic tool for conductive impairment, there appears to be no advantage to using the equivalent group delay at the TM instead of the group delay at the probe. The latter calculation at the probe tip involves fewer assumptions. An exception to such an approach would be if the impaired group included ears with a mean difference in ear-canal length relative to an age-matched normal group. The present method may be used with either definition of group delay.

F. Wall mobility model for local extrema in reflectance tympanograms in infants

The ear-canal volume changes during clinical tympanometry are more complex in neonates due to their more compliant canal walls (Holte et al., 1991). Qi et al. (2006) constructed a nonlinear finite-element model based on the dimensions of a newborn ear canal from a 22-day-old. The model predicted that the newborn ear-canal wall would not be rigid during a tympanometric measurement. In a follow-up study with a finite-element model of ear-canal acoustics during tympanometry in a 22-day-old ear, Qi et al. (2008) concluded that the “canal-wall volume displacement makes a major contribution to the total canal volume change, and may be larger than the TM volume displacement.”

The group delay at the probe can be calculated in a straightforward manner although its interpretation in young infant ears should take into account potential wall-mobility effects. An interesting interpretative problem is the pair of infant responses that showed a ridge in absorbance and a valley in group delay along a line between a point on the pressure-frequency plane at about 0 daPa and 0.25–0.71 kHz to a final point at about −300 daPa and 0.71–1 kHz. This occurred for the pair of infant ears in both the down-swept tympanograms (Figs. 5 and 7) and up-swept tympanograms (Fig. 6 shows results for the normal infant). However, this feature did not occur in the adult down-swept tympanogram (Figs. 3) and up-swept tympanogram (not shown). A model for ear-canal wall mobility was analyzed to explain these features in infant ears.

This model was proposed based on Guelke and Bunn (1981) to account for additional energy losses observed in infant ears at low frequencies (Keefe et al., 1993). The model included circuit parameters for an ear-canal wall admittance based on an inertance $I_w,$ compliance C_w, and conductance $G_w.$ The wall admittance Y_w was defined as a function of radian frequency ω and unit imaginary number j as

$$\frac{1}{Y_w(\omega )}=j\omega I_w+\frac{1}{G_w+j\omega C_w}.$$ (16)

The wall compliance term dominates Y_w at sufficiently low frequencies (in the limit of low damping), and the wall inertance term dominates at sufficiently high frequencies in the limit of a rigid canal wall (for which Y_w approaches zero). The latter limiting condition would explain why canal wall mobility is only important at low frequencies. It is convenient to define a loss-free wall resonance radian frequency ${\omega }_w=1/\sqrt{I_w{C}_w}$ and wall resonance quality factor $Q_w={\omega }_w{C}_w/G_w>1.$ Then Y_w in Eq. (16) is expressed in terms of its real and imaginary parts by

$$Y_w(\omega )=\frac{{\omega }_w\hspace{0.17em}{C}_w\hspace{0.17em}{Q}_w^{-1}+j\omega C_w\left[1-{\left(\omega /{\omega }_w\right)}^2-Q_w^{-2}\right]}{{\left[1-{\left(\omega /{\omega }_w\right)}^2\right]}^2+{\left[\left(\omega /{\omega }_w\right)Q_w^{-1}\right]}^2}.$$ (17)

There is a resonance at frequencies near the wall resonance frequency where the compliance and inertance terms approximately cancel and the admittance magnitude is controlled by damping. Formally, the resonance frequency ω_r is defined as the frequency for which the imaginary part of $Y_w=0.$ It follows from Eq. (17) that

$${\omega }_r={\omega }_w\sqrt{1-Q_w^{-2}}.$$ (18)

The ω_r is slightly reduced from ω_w in the presence of wall loss. The wall admittance magnitude at resonance is

$$Y_w({\omega }_r)=\left|Y_w({\omega }_r)\right|=Q_w{\omega }_w{C}_w.$$ (19)

By analogy with Eq. (6), a pressure reflectance $R_w(\omega )$ for wall motion may be defined by

$$R_w(\omega )=\frac{1-Z_{\mathit{c}\mathit{e}}\hspace{0.17em}{Y}_w(\omega )}{1+Z_{\mathit{c}\mathit{e}}\hspace{0.17em}{Y}_w(\omega )}.$$ (20)

An analytical expression for $R_w(\omega )$ is obtained by substituting Y_w from Eq. (17) into Eq. (20). This relation is parameterized in terms of wall reflectance magnitude $\left|R_w(\omega )\right|$ and phase ${\varphi }_w(\omega ).$ The magnitude is given using Eqs. (19) and (20) under these resonance conditions (for real Z_ce) by

$$\left|R_w\left({\omega }_r\right)\right|=\frac{\left|1-Q_w{\omega }_w{Z}_{\mathit{c}\mathit{e}}{C}_w\right|}{1+Q_w{\omega }_w{Z}_{\mathit{c}\mathit{e}}{C}_w}.$$ (21)

The product $Z_{\mathit{c}\mathit{e}}{C}_w$ is a characteristic time relating the characteristic impedance of the ear canal and the wall compliance. The term ${\omega }_w{Z}_{\mathit{c}\mathit{e}}{C}_w\ll 1$ is dimensionless. In parameter fits to measured data, the term $Q_w{\omega }_w{Z}_{\mathit{c}\mathit{e}}{C}_w\ll 1,$ although it is otherwise increased by the resonant quality factor of wall motion at resonance.

The fact that $\left|Y_w\right|$ has a local minimum at resonance leads to the property that $\left|R_w\right|$ also has a local minimum at resonance. The wall absorbance A_w thereby has a maximum value at resonance given by

$$A_w\left({\omega }_r\right)=1-{\left|R_w\left({\omega }_r\right)\right|}^2=\frac{4Q_w{\omega }_w{Z}_{\mathit{c}\mathit{e}}{C}_w}{{\left[1+Q_w{\omega }_w{Z}_{\mathit{c}\mathit{e}}{C}_w\right]}^2}.$$ (22)

The wall reflectance group delay ${\tau }_w(\omega )$ is defined as the negative gradient of ${\varphi }_w(\omega )$ with respect to ω [as in Eq. (8)]. Using the above equations, the group delay ${\tau }_w({\omega }_r)$ at resonance has a local minimum given by

$${\tau }_w\left({\omega }_r\right)=-\frac{4Q_w^2{Z}_{\mathit{c}\mathit{e}}{C}_w\left(1-Q_w^{-2}\right)}{1-{\left(Q_w{\omega }_w{Z}_{\mathit{c}\mathit{e}}{C}_w\right)}^2}.$$ (23)

The group delay is negative and proportional to $Q_w^2,$ so it is highly negative for more sharply tuned wall resonances.

Because wall mobility effects occur at relatively low frequencies in infant ears and because infant ear canals are short, the low-frequency limit of ear-canal acoustics applies between the probe and the TM. In this limit, the input admittance Y_p at the probe tip is the sum of three admittances (Keefe et al., 1993),

$$Y_p=Y_w+Y_V+Y_{\mathit{T}\mathit{M}},$$ (24)

in which $Y_V=j\omega V_e/\beta$ is the admittance related to the ear-canal volume V_e and bulk modulus of air (see the Appendix), and Y_TM is the admittance at the TM. The wall admittance Y_w has a maximum real value at its resonance frequency ${\omega }_r,$ while $\left|Y_V\right|$ is small at low frequencies. With the assumption that $\left|Y_w\right|\gg \left|Y_{\mathit{T}\mathit{M}}\right|$ at low frequencies, then $Y_p\approx Y_w$ at frequencies close to ${\omega }_r.$ The ear reflectance $R_e,$ which is defined in terms of the admittance Y_p at the probe in Eq. (6), is then approximately equal to the wall reflectance R_w in Eq. (20).

Thus, the predicted ear reflectance is approximately equal to the wall reflectance near the wall resonance frequency ${\omega }_r.$ This is characterized by a local maximum in absorbance and a local minimum in group delay with a negative value.

In the present study, the infant ears N and C were tested at a nominal age of 1 month, which was a similar age to the youngest infants tested at ambient pressure by Keefe et al. (1993), but infant ears N and C were also tested at varying pressure within the ear canal. The more extreme negative (or positive) pressures during a tympanogram would act to stiffen the walls, thereby increasing the resonance frequency ω_r associated with wall mobility. If a wall resonance were present at ambient pressure, then the above model would predict an increased resonance frequency at more negative pressures, and this effect would provide a local maximum in the absorbance and local minimum in the group delay. For the negative tympanometric pressures, this is in agreement with the absorbance ridge and group-delay valley observed in Figs. 5–7. The wall resonant frequency (${\omega }_r/2\pi$) in the model would range from 0.25 to 1 kHz to correspond with the measured frequency range of the ridge and valley in these figures. This would straddle the frequency range of the wall resonances described in Keefe et al. (1993).

At positive pressures in the same frequency range, any corresponding absorbance ridge and group-delay valley are much less evident, if at all, in infant ears C and N (Figs. 5 and 7). Thus, the model has some explanatory power for one normal ear and one ear with CHL, although more research is needed. One possibility is an asymmetry in wall mobility in young infants with larger motions at negative tympanometric pressures compared to positive pressures.

In the presence of wall mobility, the admittance at the probe in Eq. (24) is the parallel combination of the admittance of the walls and the admittance directed towards the tympanic membrane ($Y_V+Y_{\mathit{T}\mathit{M}}$). With such a model, the group delay at the probe does not have the simple relationship to group delay at the eardrum and the round-trip length of the ear canal that is posited in Eq. (9). Thus, it is not possible to acoustically estimate the round-trip length in the ear canal of a young infant using Eq. (10). Moreover, the Y_TM calculation in Eq. (12) would be inaccurate if this additional parallel pathway for wall motion were present. The estimation of an equivalent admittance at the eardrum is more problematical for a young infant than for an adult or older child. An issue for future research is to determine the age at which Y_TM can be estimated in older children (and adults).

In adults, the ear-canal walls are quasi-statically displaced by a change in air pressure during tympanometry, but the walls are effectively rigid during the periodic, higher-frequency fluctuations associated with sound transmission through the ear canal. Despite the limitations in young infants for estimating a response at the eardrum, it is feasible and useful to measure reflectance and admittance at the probe tip in newborn infants. The reflectance responses at the probe tip provide useful data on normal maturation (Keefe et al., 1993; Keefe and Abdala, 2007; Sanford and Feeney, 2008) and on classifying ears that refer on the initial NHS exam to identify an elevated risk for hearing loss (Keefe et al., 2003; Sanford et al., 2009; Hunter et al., 2010).

G. Data reduction

An interpretive issue in the clinical research use of wideband reflectance and admittance data is the large number of variables in the responses, especially in the tympanometric responses. The NHS issues related to a conductive disorder may be investigated in infant ears with less frequency resolution than for detecting some middle-ear disorders in adult ears. For example, an adult ear with an ossicular disarticulation has a narrow frequency region below 1 kHz with a large-amplitude peak in absorbance (Feeney et al., 2003), so that a one-half octave average would make such a narrow-band resonance difficult to detect. Other disorders in adults and older children can be identified using a much broader frequency resolution, even across multiple octaves. For example, the mean absorbance averaged over three octaves between 0.7 and 5.6 kHz in children of age 3–8 years was accurate in detecting a CHL in children with otitis media with effusion (Keefe et al., 2012).

As a practical manner, data need to be acquired with the finest frequency resolution required to diagnose a given type of middle-ear dysfunction—ossicular disarticulation is thusfar the disorder requiring the most resolution. If such a disarticulation is suspected, then the response may be analyzed using a 1/12th octave resolution, or even no averaging beyond the spacing between adjacent DFT frequency bins (22 Hz).

In the context of the multi-year study mentioned in the Introduction, a frequency resolution of one-sixth octave was selected for the summary representations for responses in adults ears, and one-half octave was selected for infant ears. The number of retained variables is described next for reflectance (the counts of admittance variables for Y_TM are generally similar).

The adult ambient reflectance (i.e., absorbance and group delay) each contained data at N = 31 one-sixth octave frequencies between 0.25 and 8 kHz (see Fig. 1), with an additional variable for the estimated area. Thus, the total number of variables in the ambient adult reflectance response was 63.

With 5 daPa spacing in a pressure range from 300 down to −200 daPa (N = 101 pressures), and the same set of one-sixth octave frequencies, there were 6263 variables in a pressure reflectance tympanogram (3131 each for the absorbance and group-delay tympanograms, and one more for estimated area) measured in an adult test. The contour tympanograms in the top panel of Fig. 3 plotted these variables. The tympanometric responses were reduced to a smaller set of variables defined over ranges of pressure or frequency.

As shown by counts for the adult-ear variables plotted in the panels of Fig. 3 in rows 2 and 3, the LP and HP averaged absorbance and group delay responses over pressure included 404 variables, and the absorbance and group delay responses over frequency and three pressures (TPP, P_pt, and P_nt) included 186 variables. The 404 variables over pressure were further reduced to the 18 unique variables indicated by triangle markers on Fig. 3. The retained variables also include the estimated area. Thus, the summary representation of the reflectance tympanogram included 186 + 18+ 1 = 205 variables. This was a 30-fold reduction from the original 6263 variables although about three times more than for ambient reflectance.

An advantage of using one-half octave frequency resolution (N = 11) in infant reflectance tests was the approximately three-fold reduction obtained in the number of variables needed to specify the individual-ear test response compared to using a one-sixth octave resolution. In particular, the representation for ambient reflectance included 23 variables and that for tympanometric reflectance included 85 variables (i.e., 66 + 18 + 1 = 85).

This summary representation of the reflectance tympanogram captured response information that may be clinically relevant for both adult and infant ears. For example, wideband tip-to-tail absorbance (group-delay) differences were defined at each one-sixth octave frequency as the difference between the absorbance (group delay) at TPP in Fig. 3 (row 2, column 3 panel) relative to the absorbance (group delay) at the tail pressures. These generalized the tip-to-tail admittance magnitudes used in clinical applications of 226-Hz tympanometry.

VII. CONCLUDING REMARKS

Procedures were described to measure aural acoustic reflectance and admittance in the ear canals of human adults and infants. The pressure reflectance was represented by absorbance and group delay responses. An equivalent admittance at the tympanic membrane was calculated for adult ears in terms of the measured acoustic admittance at the probe and a one-dimensional acoustic transmission line between probe and tympanic membrane, which was based on acoustic estimates of ear-canal area and length between the probe and the tympanic membrane. This length was defined in adult ears based on the group delay at frequencies above 2 kHz at which the absorbance was a minimum, but was not so defined in infant ears because of the complication of ear-canal wall motion. Illustrative measurements in normal adult ears and in infant ears (age 1 month) with normal hearing and a conductive hearing loss showed distinctive features of reflectance. The data in the three-dimensional reflectance tympanogram were reduced to a smaller set of data as separate functions of frequency and air pressure in the ear canal. The latter representation is intended for use in large-scale clinical studies of reflectance tympanometry in normal and conductive-impaired ears. Features in the infant reflectance tympanograms were analyzed using a dynamical model of ear-canal wall mobility.

APPENDIX: ALTITUDE AND PRESSURE DEPENDENCE OF THERMODYNAMIC CONSTANTS OF AIR

Measurement results for ambient reflectance and admittance vary with the altitude and ambient air pressure at which the test is performed. Results for tympanometric reflectance and admittance vary also with the range of ear-canal air pressures used in the tympanometric sweep. This Appendix summarizes the dependence of the thermodynamic constants on pressure P and altitude z, such that air is assumed to behave as an ideal gas with no water vapor (i.e., it is dry air). The atmosphere is assumed to be isothermal with respect to the altitude z, with sea level at $z_0=0.$

Sound transmission in air is characterized by its phase velocity c and specific impedance $\zeta .$ These are related to the equilibrium density ρ and bulk modulus β of air by

$$c=\sqrt{\beta /\rho },\zeta =\sqrt{\beta \rho }=\rho \hspace{0.17em}c.$$ (A1)

In the limit that viscothermal losses are negligible, the phase velocity in an acoustic transmission line of area S is equal to c in Eq. (A1) and the characteristic impedance Z_c of the transmission line is

$$Z_c=\zeta /S=\rho c/S.$$ (A2)

The adiabatic bulk modulus β and total pressure P are related by

$$P=\beta /\gamma ,$$ (A3)

in which γ is the ratio of the specific heat of air at constant pressure relative to that at constant volume in air. This ratio is constant for air at any altitude.

The reference temperature for all measurements was T₀ = 22 °C, typical of room temperatures in which the calibration was performed. The implementation ignored the slightly larger temperature in the ear canal. At atmospheric pressure and sea level, the values of c, ρ, and γ were calculated at this reference temperature from Benade (1968). A subscript 0 denotes any variable evaluated at the reference temperature T₀ and altitude $z_0=0$ (at sea level). It follows from the equation of state for an ideal gas that the density $\rho (T,P)$ at any temperature T and pressure P is

$$\rho (T,P)={\rho }_0\times (T_0/T)\times (P/P_0).$$ (A4)

Middle-ear tests might be performed at clinics whose altitudes z range from about −400 to 4000 m above sea level. For the nearly constant gravitational acceleration g = 9.80665 m/s² of any mass at the surface of the earth, the atmospheric pressure P(T, z) decreases exponentially with increasing altitude as⁹

$$P(T,z)=P_0\hspace{0.17em}{e}^{-z/H},H=R_g{T}_0/M_{m}g,$$ (A5)

in which M_m = 0.0289644 kg/mol is the molar mass of dry air and R_g = 8.31432 J/(mol × K) is the universal ideal-gas constant. It follows from Eq. (A4) that $P(z)/P_0=\rho (z)/{\rho }_0.$ Hence, the density also decreases exponentially with increasing altitude by the same factor as for pressure. Because the bulk modulus $\beta (z)$ is proportional to P(z) and γ is constant, $\beta (z)$ also decreases exponentially with increasing z according to the same factor as in Eq. (A5). Equation (A1) confirms that c was independent of z. In practice, altitude effects were negligible for $\left|z\right|<100$ m, but should not be ignored for clinical testing above 1500 m.

After accounting for altitude effects, tympanometry adds an external change to the air pressure that influences the air density, and thus the specific impedance. For a tympanometric pressure $\Delta P$ relative to atmospheric pressure, the air pressure P_e in the ear canal at the temperature T₀ is

$$P_e(T_0,z,\Delta P)=P(T_0,z)+\Delta P.$$ (A6)

A tympanogram is measured at a constant (equilibrium) air temperature within the ear canal, i.e., under isothermal conditions. The air density ρ_e in the ear canal during the tympanogram is evaluated using Eq. (A4) under isothermal conditions as follows:

$${\rho }_e(T_0,P_e)=\rho (T_0,P)\times (P_e/P).$$ (A7)

Inasmuch as the phase velocity of sound c is constant under isothermal conditions, Eq. (A1) shows that the bulk modulus β and the specific impedance ζ_e have the same pressure dependence during tympanometry as does the density in Eq. (A7), i.e.,

$$\begin{array}{c}{\beta }_e(T_0,P_e)={\beta }_e(T_0,P)\times (P_e/P),\\ {\zeta }_e(T_0,P_e)={\zeta }_e(T_0,P)\times (P_e/P).\hfill \end{array}$$ (A8)

This shows the desired variation of the bulk modulus and specific impedance of air with changing air pressure during a swept tympanogram performed at a given altitude. Both relations are used in the main body of this report.