A Proposed Theory on Biodynamic Frequency Weighting for Hand-Transmitted Vibration Exposure

Abstract

The objective of this study is to propose a theory on the biodynamic frequency weighting for studying hand-transmitted vibration exposures and vibration-induced effects. We hypothesize that the development of a vibration effect is the result of two consecutive but synergistic processes: biodynamic responses to input vibration and biological responses to the biomechanical stimuli resulting from the biodynamic responses. Hence, we further hypothesize that the frequency-dependency (W) of the effect generally includes two components: a biodynamic frequency weighting (W1) and a biological frequency weighting (W2), or W=W1•W2. These hypotheses are consistent with the stress and strain analysis theory and methods widely used in structural dynamics and biomechanics. The factorization may make it easier to study the complex frequency-dependency using different approaches: the biodynamic frequency weighting depends on the passive physical response of the system to vibration, and it can thus be determined by examining the biodynamic response of the system using various engineering methods; on the other hand, the biological frequency weighting depends on the biological mechanisms of the effects, and it can be investigated by studying the psychophysical, physiological, and pathological responses. To help test these hypotheses, this study reviewed and further developed methods to derive the finger biodynamic frequency weighting. As a result, preliminary finger biodynamic frequency weightings are proposed. The implications of the proposed theory and the preliminary biodynamic frequency weightings are also discussed.

Introduction

Prolonged, intensive exposure to hand-transmitted vibration can result in injury to fingers, hands, and arms. These injuries include dysfunctions of the peripheral vascular and nervous systems, as well as injuries to the musculoskeletal system. Collectively, these symptoms have been referred to as hand-arm vibration syndrome (HAVS). To help determine and reduce the risk of developing HAVS, the International Organization for Standardization (ISO) has established a standard for the measurement, evaluation, and assessment of hand-transmitted vibration exposure¹⁾. Largely because vibration-induced white finger (VWF) has been most studied and considered as a hallmark of HAVS, its exposure-effect relationship proposed in a study²⁾ is adopted in the standard and recommended as a basis for assessing the health effects¹⁾. According to its extrapolated relationship adopted in the standard¹⁾, ten percent of workers exposed daily (8 h) to frequency-weighted acceleration of 2.5 m/s² for 12 yr are predicted to develop VWF. This daily vibration exposure level has been adopted as a major control target in the national standards, guidelines, or regulations of many countries^3–5). Although the results of some studies are consistent with the prediction of this exposure-effect relationship^{2, 6)}, the results of other studies suggest that it may largely over- or under-estimate the incidence of VWF^7–14). This suggests that further studies are required to improve the reliability of the assessment method.

While a number of reasons or factors may contribute to the discrepancies observed in these studies, this study primarily addresses the issues closely related to a critical factor: frequency weighting. In addition to risk assessment, frequency weighting is also important for designing and analyzing tools and vibration-reducing devices. According to the current frequency weighting defined in the standard¹⁾, the vibration frequencies of a tool should be designed as high as possible, well above 12.5 Hz, so that the frequency-weighted acceleration may be minimized. However, this practice may increase the risk of VWF if its actual frequency dependency is largely different from the standardized frequency weighting, as indicated in some studies^{8, 10, 11, 13, 14)}. As stated in the current standard for anti-vibration glove assessment¹⁵⁾, these gloves do not provide significant attenuation in the frequency range below 150 Hz. They are also much less effective for reducing finger-transmitted vibration than for reducing palm-transmitted vibration¹⁶⁾. These observations suggest that such gloves would have little value, especially for finger protection, if the judgment is based on the reduction of frequency-weighted acceleration. Contradicting this judgment, a study suggested that such gloves could reduce some adverse finger effects by approximately 30%¹⁷⁾. While further studies are required to verify this finding, the identification of the actual frequency-dependencies of vibration-induced finger disorders can help find whether such gloves are really effective for protecting the fingers.

The current frequency weighting is not defined based on any direct evidence of the relationship between the exposure frequency and the incidence or prevalence of VWF; instead, it is based primarily on the subjective sensation of the entire hand-arm system in response to different frequencies measured by Miwa^{18, 19)}. In other words, the frequency-dependency of VWF is assumed to be similar to the frequency-dependency of the subjective sensation. This assumption has been questioned by many researchers and some evidence has also suggested that the current frequency weighting is unlikely to be applicable to assess VWF^8–14). However, the standardized frequency weighting remains basically unchanged since it was adopted, except for minor modifications for easier design and construction of measurement instruments¹⁾. This is partially because significant revision of the frequency weighting could greatly influence associated regulations, instruments, and practice, partially because the actual frequency-dependency of VWF has not been clearly identified, and partially because the standard is not established solely for assessing and controlling VWF.

Ideally, the standardized frequency weighting or weightings should be defined based on the frequency dependencies of not only the major components of HAVS but also all major adverse psychological and physiological effects such as discomfort, pain, tingling and numbness during the operation of a vibrating tool or machine. It is possible that the current frequency weighting provides reasonable representations of the frequency dependencies of some of these effects. However, precisely which effects are well-represented remains unclear.

Based on this background, the objective of this study is to propose a theory on the biodynamic frequency weighting for studying hand-transmitted vibration exposures and vibration-induced effects. The proposed theory is based on the general knowledge of biomechanics and some observed phenomena of vibration-induced effects. The major methods for deriving the finger biodynamic frequency weighting are reviewed and further developed. Applying these methods, this study proposes preliminary finger biodynamic weightings for quantifying finger vibration exposures. The implications of the findings are discussed.

A General Hypothesis

A freely falling human body in the air is not usually injured even if the body acceleration is 9.8 m/s² and its velocity is large. This is because free falling does not induce significant dynamic forces or deformations inside the body. However, such a fall could result in severe or fatal injuries upon impact with the ground, because the impact forces could cause large internal stresses and deformations in the body leading to the destruction of body tissues. Severe vibration can injure a human body, but it may not damage the hairs on the head, because vibration can induce little dynamic force within the hairs. These examples demonstrate that it is not the motion/vibration itself but the motion/vibration-induced dynamic forces and deformations that are directly related to the injuries and damage. They also indicate that these biodynamic responses are an intermediate passive process between the input motion/vibration and the motion/vibration-induced injuries; hence, the biodynamic process is an essential component of the injury mechanism.

Although ordinary hand-transmitted vibration exposure rarely causes obvious traumatic injuries, the exposure may cause micro injuries in the tissues and microstructure damage, as observed in some studies^20–22). Similar to traumatic injury, an acute injury is also a passive process. The development of an acute injury may be comparable to the passive processes of material fatigue²³⁾. As the basic stress and strain analysis theory and methods well-established in structural mechanics have been adopted in the general methodology of biomechanics^{24, 25)}, it is reasonable to hypothesize that these theories and methods are also applicable to the study of acute injuries and other acute vibration effects.

In addition to acute injuries, the vibration exposure may also generate some psychophysical responses and other physiological and pathological effects^{26, 27)}. Different from lifeless engineering materials, living tissues or structures can actively respond to injuries and mechanical stimuli. For example, cells and tissues can repair damage and remodel their local structures^28–30). While material fatigue damage at a specific location in an engineering structure is usually directly related to the stress/strain at that location²³⁾, the vibration effects on a living structure may not be limited to the location where the injury or effect originated. For example, major nerve damage at a location within a finger may cause numbness at other parts of the finger. Sympathic effects may also occur at a location without direct vibration exposure^{26, 27)}. Therefore, the entire process toward the development of a chronic vibration disorder is much more complex than the purely passive mechanisms of engineering material fatigue. This may partially explain why the precise mechanisms of HAVS are not well understood^{1, 27)}. However, they all involve the intermediate process – passive physical responses to vibration. As it has been confirmed that the biomechanical loading conditions in living structures are not only directly related to the acute injuries but also closely associated with the growth and remodeling or adaptation of a local structure²⁵⁾, we hypothesize that the vibration biodynamic responses, as components of the biomechanical loading conditions in the hand-arm system, are also directly or indirectly related to various psychophysical, physiological, and pathological processes. The results of some vibration effect studies also support this hypothesis^31–33).

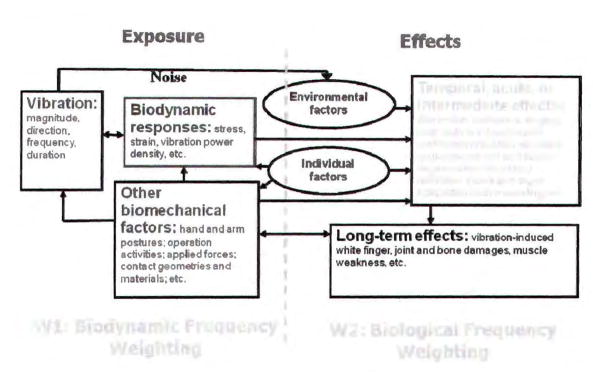
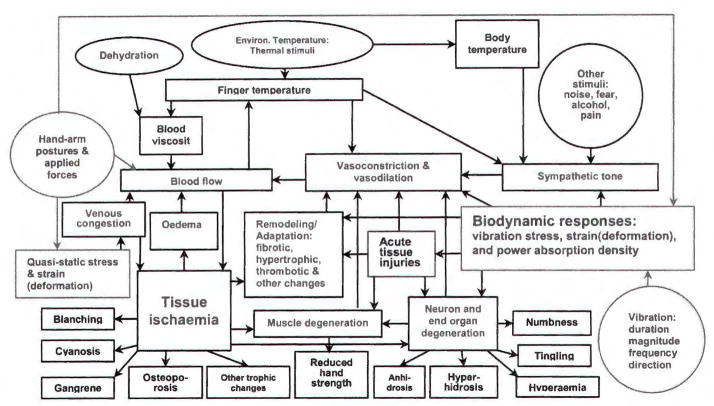
Based on the general hypothesis, a conceptual model of the relationships among various factors and processes is proposed and illustrated in Fig. 1, which is a revision of a previously proposed model³⁴⁾. As an elaboration of the conceptual model, Fig. 2 shows a hypothetical model of the specific relationships among biodynamic responses, vibration intermediate effects, and symptoms of hand-arm vibration syndrome, which is a revised version of the model proposed by Griffin²⁶⁾.

Fig. 1.

A conceptual model of hand-transmitted vibration exposure and the effects.

Fig. 2.

A hypothetical model of vibration-induced vascular disorders – a revision of the model proposed by Griffin ²⁶⁾ by adding essential biodynamic stimuli (vibration stress, strain, and power absorption density, etc.) and additional stimuli (quasi-static stress, strain, etc.) resulting from other biomechanical inputs such as applied hand forces, arm postures, and voluntary dynamic activities of the hand-arm system.

Factorization of the Frequency-Dependency of Vibration Effects

According to the concept shown in Fig. 1, we further hypothesize that the development of any vibration-induced effect can be broadly considered as two consecutive but synergistic processes: biodynamic responses and biological responses of the hand-arm system, as also illustrated in Fig. 1. Their corresponding frequency dependencies are termed as biodynamic frequency weighting (W1) and biological frequency weighting (W2), respectively. In other words, the frequency-dependency (W) of any effect can be factored into two frequency weighting factors:

$$W=W1•W2$$ (1)

For example, mechanoreceptors are primary neurons that respond to mechanical stimuli such as mechanical pressure (stress) and distortion (strain) by firing action potentials or bioelectric signals to the brain³⁵⁾. Hence, the biodynamic responses (stress and strain) must play an essential role in determining the psychophysical effects such as vibration sensation and discomfort. As a result, the frequency-dependencies of vibration sensation and discomfort must include the frequency-dependency of the biodynamic response (W1). If the bioelectric signals at each frequency change approximately linearly with the biodynamic responses, the frequency-dependency of the vibration sensation and discomfort may largely depend on the frequency-dependency of the biodynamic responses, which may be expressed as follows:

$$W_{\mathit{Vibration}\_\mathit{perception}}\approx W1$$ (2)

If the biodynamic responses also vary approximately linearly with the input vibration in a certain range, as observed in some studies^{36, 37)}, the vibration sensation or discomfort contours should exhibit parallel distribution patterns in some ranges of vibration magnitude and frequency. This prediction is consistent with parts of reported results^{18, 19, 38)}.

The reported research also shows some large inconsistences with the predicted linear pattern at some vibration magnitudes and frequencies³⁸⁾. This may be because both the biodynamic responses and the behaviors of the mechanoreceptors are not always linear^{35, 37, 39)} Similar to any man-made sensor, the natural sensors may also be saturated when the stimuli are too strong. Therefore, the frequency-dependency of the biodynamic response alone is generally insufficient to represent the frequency-dependency of any vibration effect, and the biological frequency weighting (W2) should also be considered in determining the overall frequency weighting. The relationships between the mechanoreceptor responses and the input displacement/deformation reported by Martin and Jessell³⁹⁾ may be considered as examples of W2. They demonstrate that the sensitivity of the mechanoreceptor may not only vary non-linearly but also change from one type to another^{35, 39)}. The density of mechanoreceptors may also vary with location ^{35, 40, 41)}; as a result, the same vibration deformation at different locations may cause varied perceptions. This may also be included in W2 or taken into account by quantifying the location-specific weighting.

While the biological weighting primarily depends on the psychophysical, physiological, and pathological processes, the biodynamic weighting primarily depends on the structural properties such as tissue mass, damping, and stiffness, and the boundary/interface conditions such as interface geometries and material stiffness and damping properties. Therefore, these weightings can be studied separately, which may make it easier to investigate and understand the complex mechanisms of many vibration effects.

A Discussion of the Current ISO Frequency Weighting Based on the New Weighting Hypothesis

According to the proposed new weighting concept, the current ISO frequency weighting can be factored into two components: W_ISO = W1_ISO • W2_ISO. An approach for judging the validity of the ISO weighting for assessing VWF is to find whether W1_ISO represents the biodynamic weighting of VWF (W1_VWF) and whether W2_ISO represents the biological weighting of VWF (W2_VWF).

Fig. 3 shows the location-specific vibration perceptions of the hand-arm system at two different frequencies (16 and 125 Hz) reported by McDowell et al.⁴²⁾. Fig. 4 shows the relative frequency weightings of the major substructures of the system derived in the current study from the substructure power absorption data predicted by Dong et al.⁴³⁾. Because the vibration in the low-frequency range (<25 Hz) can be effectively transmitted to the arms, shoulder, neck, and head^44–47), and the power absorption is primarily distributed in these substructures⁴³⁾, the biodynamic frequency weighting of the arms plays the dominant role in determining the overall biodynamic weighting of the entire hand-arm system, as shown in Fig. 4. This explains why stronger vibration perceptions are reported at these substructures at 16 Hz, as shown in Fig. 3. This can also explain why the vibration transmission to the head and its perception could be strongly affected by the arm postures in the low-frequency range⁴⁷⁾. Although workers using low-frequency non-percussive tools could complain of discomfort, VWF occurs at a very low prevalence among these workers^{7, 8)}. These observations suggest that the biodynamic and biological responses in the arms and shoulder are unlikely to be closely correlated with VWF. On the other hand, a much larger prevalence of VWF could be observed among workers using high-frequency tools such as grinders and chainsaws or percussive tools such as chipping hammers and rock drills that generate high-frequency vibration components^{7, 8–14)}. This is likely due to the fact that the stimuli resulting from biodynamic responses at the higher frequencies are primarily concentrated in the hand, especially in the fingers⁴³⁾, as also evident from the distribution of the vibration perception in the hand-arm system at 125 Hz shown in Fig. 3. These observations suggest that VWF is likely to be primarily associated with the biodynamic and biological responses of the hand, especially the fingers. The asymmetrical distribution of VWF symptoms on the fingers ⁴⁸⁾ also suggests that VWF is likely to be primarily related to the finger local biodynamic and biological responses, although the sympathetic response of the biological system could also be part of the mechanisms of VWF, as shown in Fig. 2. Therefore, the frequency-dependency of VWF (W_VWF) is likely to consist primarily of following two components: the frequency-dependency of finger biodynamic response (or W1_VWF ≈ W1_Fingers), and the frequency-dependency of the finger biological responses related to VWF (or W2_VWF ≈ W2_Fingers).

Fig. 3.

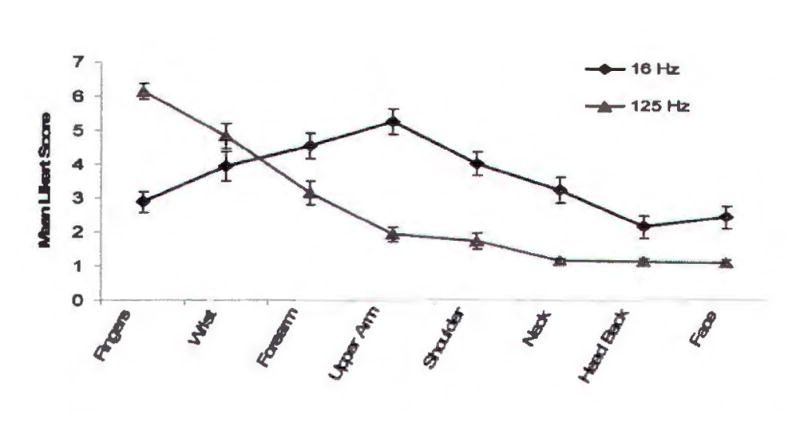
Distributions of vibration perceptions on the hand-arm system at a low-frequency vibration (16 Hz) and a high-frequency vibration (125 Hz) reported by McDowell et al.⁴²⁾. A higher score means a stronger vibration perception.

Fig. 4.

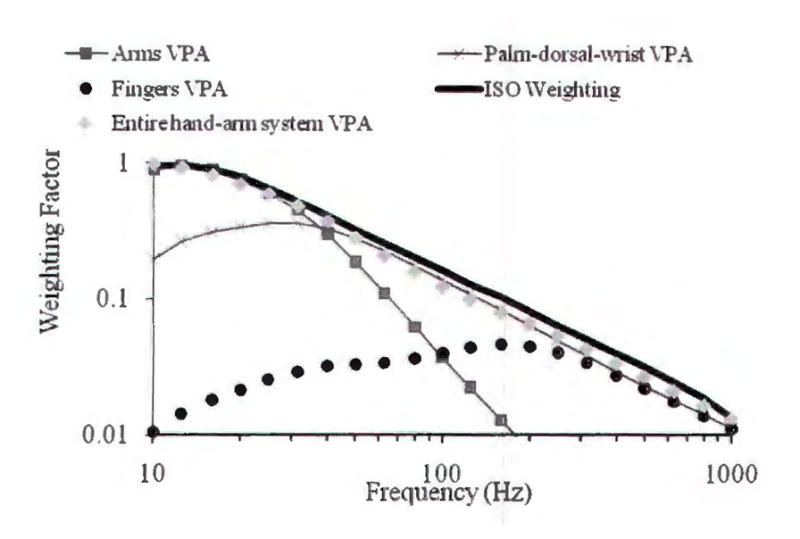
Relative frequency weightings of the vibration power absorptions in the major substructures (arms, palm-dorsal-wrist, and fingers) of the hand-arm system, which are derived from the vibration power absorption data predicted by Dong et al.⁴³⁾. The weightings were normalized with respect to the vibration power absorption of the arms at 12.5 Hz.

Because the subjective sensation contours used for deriving the ISO frequency weighting were measured without differentiating the locations of the vibration perception^{18, 19)}, they represent the frequency-dependency of the overall perception of the entire hand-arm system. Therefore, W1_ISO represents the frequency-dependency of the biodynamic response of the entire system. This has been confirmed from the fact that the frequency-dependency of the total vibration power absorption of the entire system is similar to the ISO frequency weighting, disregarding the vibration direction^49–51). On the other hand, the frequency-dependency of the total VPA (W_VPA) approximately represents the maximum profile of the weightings of the VPAs distributed in the major substructures of the hand-arm system, as also shown in Fig. 4. W1_ISO is representative of W_{VPA_Fingers} or W1_Fingers only in a certain high-frequency range, but W1_ISO is substantially different from W1_Fingers at frequencies below 100 Hz.

As evidenced from the vibrotactile perception tests at different parts of the hand-arm system^{40, 41)}, the subjective sensation generally varies with the measurement location on the system. Therefore, the biological frequency weighting for finger sensation may be different from that for arm sensation; then, the biological weighting for the entire system sensation may not be used to represent the biological weighting for finger sensation. Furthermore, the biological weighting for the sensation may be different from the biological weighting for the physiological and pathological effects that lead to the development of VWF. For these two reasons, W2_ISO is unlikely to be fully representative of W2_VWF or W2_Fingers.

Based on the above discussions, we hypothesize that the ISO frequency weighting is not suitable for assessing VWF. However, the discussions also suggest that the ISO weighting may be acceptable for approximately assessing the vibration perception or discomfort of the entire hand-arm system in certain ranges of vibration magnitude and frequency. Some results of the reported studies also support this hypothesis^{37, 52)}. Another study also reported that the ISO frequency-weighted acceleration was reasonably correlated with neurological disorders in the wrist⁵³⁾. This is at least partially because the frequency-dependency of the biodynamic response in the palm-wrist-forearm system is similar to the ISO frequency weighting in the dominant frequency range of the majority of powered hand tools, as also shown in Fig. 4.

Quantification of Hand-Transmitted Vibration Exposure

While further discussions on the biological frequency weighting are beyond the scope of this study, the following sections focus on discussions primarily of the quantification of hand-transmitted vibration exposure based on the biodynamic responses and the identification of the biodynamic frequency weighting.

Vibration biodynamic stimuli

Vibration biodynamic responses of the hand-arm system have been most frequently studied by measuring and examining functions such as apparent mass, mechanical impedance, dynamic stiffness, and vibration transmissibility⁵⁴⁾. These functions reflect the overall dynamic properties of the system; hence, they can be used to estimate the overall biodynamic responses for a given input vibration or to construct a model of the system to estimate the biodynamic responses distributed in the system.

In principle, the biodynamic responses to be used to quantify the vibration exposure should be those directly associated with the vibration effects. Vibration biodynamic responses include the responding motions (displacement, velocity, and acceleration) of the system, responding forces at the interfaces (driving-point force) and within the system (pressure or stress), dynamic deformation (strain magnitude and rate), and their combinations (vibration power absorption and VPA density). The most studied biodynamic response is the vibration power absorption of the entire hand-arm system, as an integrated measure of the distributed VPA^55–57). Although these biodynamic measures are related to each other, some of them may be more directly related to vibration effects than others. For example, the impact force/stress acting on the joints may be more directly related to the injuries and damage to the joints and bones because such cases were more frequently observed among workers using percussive tools^{58, 59)}. On the other hand, the deformation/strain may be more related to the soft tissue injuries ³¹⁾ and vibration perception³³⁾.

While further studies may help identify the most suitable biodynamic stimulus for evaluating a particular major vibration disorder, the general knowledge of structural mechanics and biomechanics suggests that the vibration stresses and strains are likely to be among the essential biodynamic stimuli directly associated with many vibration effects^{23, 24)}. This hypothesis has also been positively tested in some studies of the vibration effects^31–33). Because vibration power absorption density (VPAD) is a combined measure of the vibration stress and the strain rate⁶⁰⁾, it is considered as a basic biodynamic stimulus for vibration exposure quantification in the following discussion.

Role of biodynamic weighting in the quantification of vibration exposure

The tool or machine vibration input to the hand can be reliably measured using accelerometers. This method has been conventionally used in the measurement of the exposure and adopted in the standard¹⁾. Therefore, the vibration exposure dose quantified based on any alternative mechanical stimulus should also be expressed as a function of the acceleration, similar to the method used in the standards¹⁾. Also similar to the current frequency weighting defined in the standard¹⁾, the biodynamic frequency weighting is actually a transfer function that converts the input vibration and influencing factors into the required biodynamic stimulus for the formulation of the exposure dose. Besides improving the understanding of the mechanisms of vibration-induced disorders, the major purpose for determining the biodynamic frequency weighting is to efficiently quantify the exposure dose based on the selected biodynamic stimulus for workplace applications.

Methods for Deriving Finger VPAD Weighting

The above discussions suggest that the finger VPAD can be used as one of the biodynamic measures to quantify the finger vibration exposure and to derive W1_Fingers. Currently, it is not feasible to directly measure the VPAD. The VPAD has been estimated using some modeling methods. The average finger VPAD weighting may also be estimated from finger vibration transmissibility, which is also explained in this section.

Finger average VPAD

The average VPAD in the fingers can be estimated using a combined experimental and modeling method⁴³⁾. First, the mechanical impedances distributed at the fingers and the palm of the hand can be directly measured. Second, the parameters of a mechanical-equivalent model of the hand-arm system can be determined using the impedance data because the impedance is a measure of the overall dynamic properties of the system. Third, the VPA in the fingers exposed to a given acceleration at each frequency can be estimated from the model. In this averaging method, the finger volume is assumed to be constant at each frequency. Then, the average VPAD is approximately equal to the finger VPA. Then, its normalized frequency weighting (W_VPAD) can be derived using the following formula:

$$W_{\mathit{VPAD}}(\omega )=0.958\sqrt{P(\omega )/P_{\mathit{Max}}}$$ (3)

where ω is the frequency in Rad/sec, P is the average VPAD, and P_Max is the maximum average VPAD in the frequency range of concern, and 0.958 is the maximum value in the current ISO frequency weighting when expressed in one-third octave bands¹⁾.

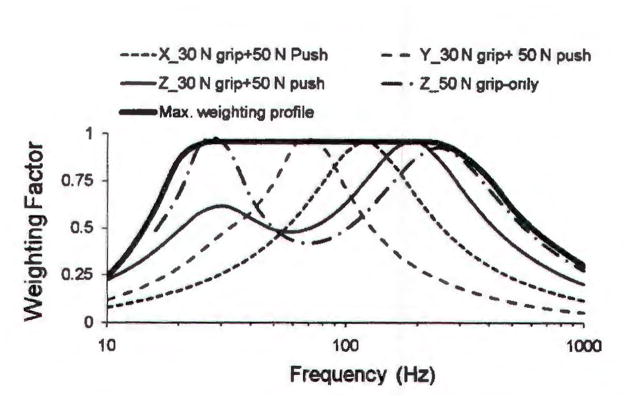
Fig. 5 shows some examples of the average finger VPAD-based frequency weightings in three directions, which were derived from a set of recently reported experimental data measured with the posture and hand forces (50 N push and 30 N grip) required in the standardized anti-vibration glove test¹⁵⁾. The weighting in each direction was normalized with respect to the maximum average VPAD in each direction. The results indicate that the finger average VPAD weighting could vary greatly with different vibration directions.

Fig. 5.

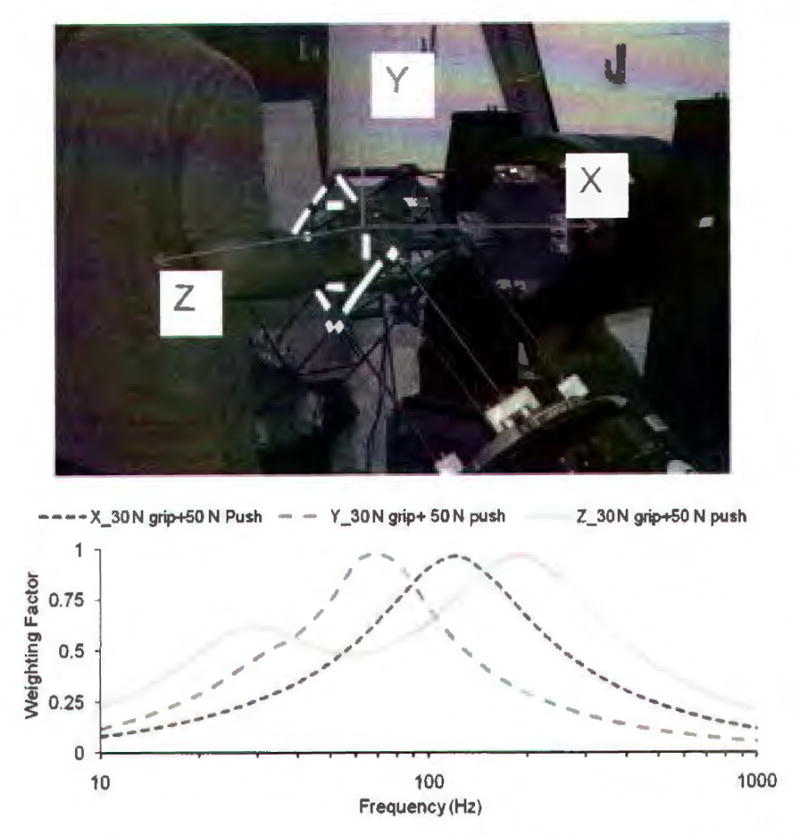
Finger average VPAD frequency weightings in the three orthogonal directions (X, Y, and Z) derived from the mechanical impedance data reported by Dong et al.⁵¹⁾.

Detailed VPAD distribution

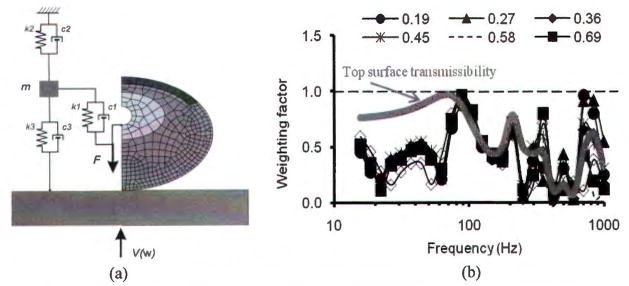
Fig. 6 (a) shows a finite element model of a fingertip reported by Wu et al. ⁶⁰⁾. While the distributed vibration stress and strain can be predicted using the model, the VPAD can be evaluated from the stress and the strain rate. After the VPAD for a given vibration acceleration is estimated, the frequency weighting of the VPAD can be derived with a formula similar to that in Eq. 3⁶⁰⁾.

Fig. 6.

(a) A finite element model of a fingertip⁶⁰⁾; and (b) the frequency dependency of the vibration power absorption density at six locations (0.19, 0.27, 0.36, 0.45, 0.58, 0.69 mm) measured from the line 30° from the bone center in the model⁶⁰⁾.

Fig. 6 (b) shows some examples of VPAD-based frequency weightings at several locations on the cross section of the fingertip model, together with the vibration transmissibility at the top of the fingertip⁶⁰⁾. As expected, the peak VPAD-based weighting at each point is correlated with the resonance of the soft tissue at that point. Below 200 Hz, the tissues of the fingertip vibrate more or less in-phase for the given conditions; hence, their weighting values are similar. At higher frequencies, the peak frequencies vary with location, because the high-frequency responses depend on high-frequency local vibration modes. However, the basic trends in the average VPAD weightings are similar to the transmissibility measured at the top of the fingertip. This observation suggests that, as a crude approximation, the vibration transmissibility can be used to represent the VPAD weighting in a certain frequency range. This also suggests that the basic characteristics of the finger VPAD weighting can be partially understood by examining the characteristics of finger vibration transmissibility.

Basic characteristics of finger vibration transmissibility

The mass of a conventional accelerometer and its installation device could be comparable to or larger than the mass of the finger section where the accelerometer is located. The installation of the accelerometer could also largely change some dynamic properties of the finger due to the fastening stiffness and pressure applied on the finger. These issues can be avoided using a laser vibrometer in the measurement of the finger vibration transmissibility, which is likely to provide more reliable experimental data. Hence, the data measured using laser vibrometers were used as a basis for examining the characteristics in this study.

The reported data indicate the transmissibility is locationspecific^{46, 61–64)}. At the fingertip in the direction vertical to the contact surface (X and Z directions shown in Fig. 5), the transmissibility could be near unity at frequencies up to more than 300 Hz, primarily depending on the applied fingertip force. This is because the fingertip usually has relatively small mass, large damping, and high contact stiffness in this direction due to the larger contact pressure at the fingertip⁶⁵⁾. The resonance frequency generally decreases with the increase in the distance from the fingertip^{46, 66)}. The highest transmissibility on the finger is usually between the first and third metacarpals^{46, 66)}. Because of the nonlinear features of the finger tissues; increasing the finger force increases the contact stiffness and thus the resonance frequency⁶⁶⁾, which is consistent with that observed in the finger VPA study⁴³⁾. The highest transmissibility usually occurs in the range of 50 to 250 Hz. This resonance frequency range is consistent with that observed in finger impedance studies⁴³⁾. However, the frequency of peak transmissibility could be reduced to below 25 Hz in a grip-only action with a low grip force^{52, 58)}. Because the shear stiffness is usually less than the compression stiffness, the resonance frequency in the direction along a handle axial direction is usually less than those in the other directions^{46, 51)}.

Synthesis of Finger Biodynamic Weighting

Ideally, the representative finger biodynamic weighting should be defined based on the biodynamic stimuli measured at critical locations as a function of representative working conditions. However, without a sufficient understanding of the mechanisms of vibration-induced disorders, it is very difficult to identify these critical locations. Furthermore, without sufficient VPAD or transmissibility data, it is also very difficult to define a representative finger weighting function that encompasses all important factors. Therefore, some assumptions and simplifications have to be made in the current study to synthesize the preliminary biodynamic frequency weighting.

Profile of the finger average VPAD weightings

This method is based on the following major assumptions: (1) the average VPAD in each direction is equally important; (2) the major finger resonances are in the range of 25 to 250 Hz; and (3) the fundamental hand resonance (25 to 50 Hz) also affects the finger vibration effects. Based on these assumptions and the available VPAD and transmissibility data, a finger biodynamic weighting is defined as the approximate maximum profile of the average VPAD-based or transmissibility-based weightings, shown in Fig. 7.

Fig. 7.

The finger biodynamic weighting defined as the maximum profile of the finger average VPAD weightings.

Axial VPAD method and total VPAD method

To provide a better assessment of vibration exposure, the frequency weighting should be separately considered for each working condition or defined as a function of the influencing factors. Furthermore, the vibration effects may vary with the vibration direction. The large shear response along the Y direction shown in Fig. 5 may cause some effects different from those in the other two axes. It is also practical to separately consider the Y direction weighting because it is the longitudinal axis of a tool handle. However, it is very difficult to differentiate the X and Z directions shown in Fig. 5 in the vibration measurement at workplaces. A combined frequency weighting for these two directions may be considered.

When the direction effects are identified from further psychophysical or biological studies, the direction-specific frequency weightings can also be combined using direction factors: w_X, w_Y, and w_Z. The combined biodynamic frequency weighting can be derived based on the total VPAD method. This method assumes that finger disorders are associated with the weighted summation (P_Total) of the VPADs in the three directions (P_X, P_Y, and P_Z), which can be generally expressed as follows:

$$P_{\mathit{Total}}=w_X•P_X+w_Y•P_Y+w_Z•P_Z$$ (4)

After P_Total is determined, its weighting (W_VPAD-Total) can be derived from Eq.(3).

Without any effect information on the vibration direction, this study assumes that w_X = w_Y = w_Z = 1. Fig. 8 shows an example of the total VPAD weighting for the unit direction factor, together with the relative VPAD weightings in the three directions. They were derived from the same data used for deriving the average VPAD weightings in each direction shown in Fig. 5. Because the VPAD in the Y direction in the resonance range is much greater than those in the other two directions, W_VPAD-Y plays a dominant role in determining W_VPAD-Total.

Fig. 8.

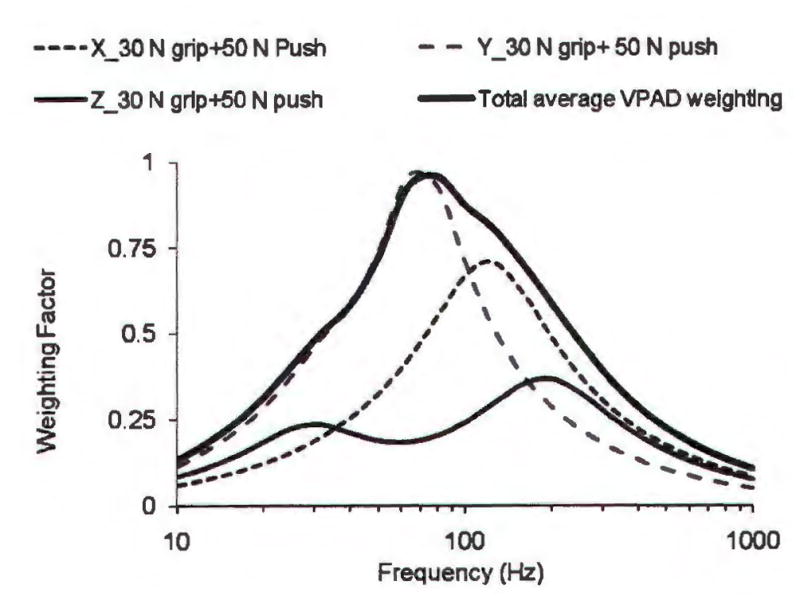
An example of the total VPAD weighting (W_VPAD-Total) for w_X = w_Y = w_Z = 1, together with the relative VPAD weightings in the three directions (W_VPAD-X, W_VPAD-Y, and W_VPAD-Z). They are derived from the finger mechanical impedance data reported by Dong et al.⁵¹⁾.

Three-axis vibration transmissibility method

With a method similar to the three-axis total VPAD weighting method, the three-axis vibration transmissibility weighting (W_Tr-Total) at each frequency can be expressed as follows:

$$W_{Tr-\mathit{Total}}=0.958\frac{\sqrt{{(w_X{T}_{Tr-X})}^2+{(w_Y{T}_{Tr-Y})}^2+{(w_Z{T}_{Tr-Z})}^2}}{\sqrt{3}·T_{Tr-\mathit{Total}}},$$ (5)

where T_Tr-X, T_Tr-Y, and T_Tr-Z are the vibration transmissibility in the three directions, respectively.

Fig. 9 shows an example of the total vibration transmissibility weighting for w_X = w_Y = w_Z = 1, together with the relative transmissibility weightings in the three directions. The transmissibility-based weightings are similar to the VPAD-based weightings shown in Fig. 8. Their similarity also further suggests that the VPAD weighting can be approximately represented using the transmissibility-based frequency weighting.

Fig. 9.

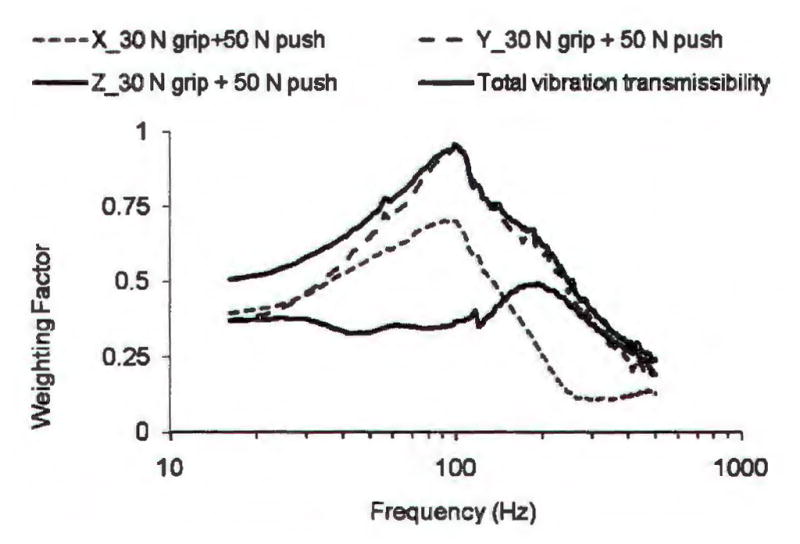
An example of the total vibration transmissibility weighting (W_Tr-Total) for w_X = w_Y = w_Z = 1, together the relative transmissibility weightings in the three directions (W_Tr-X, W_Tr-Y, and W_Tr-Z). They are derived from the finger average transmissibility data reported by Welcome et al.⁴⁶⁾.

Maximum profile of finger vibration transmissibility

While it is difficult to pinpoint the location of the biodynamic response on each finger that is primarily responsible for the development of a particular finger disorder, the average finger VPAD weighting or transmissibility of the fingers may be used to represent the finger biodynamic weighting, as demonstrated in the above subsections. Alternatively, the finger biodynamic weighting may also be represented using the maximum profile of the finger transmissibility functions measured at different locations on each finger. Such a weighting can be derived by replacing the average transmissibility function in Eq.(5) with the maximum profile of the distributed transmissibility functions. An example of the total profile weighting is shown in Fig. 10, together with the profile weightings for each direction. Their basic trends are similar to those shown in Figs. 8 and 9.

Fig. 10.

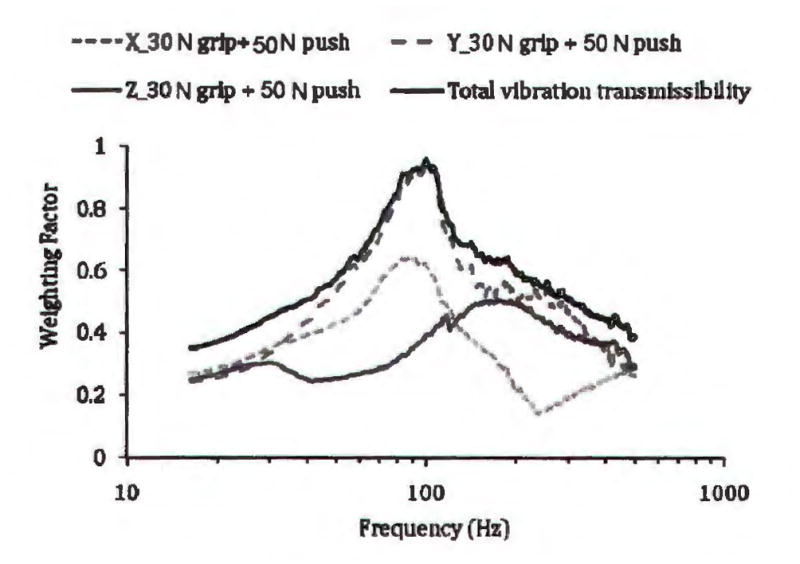
An example of the profile transmissibility weighting (W_{Tr-Total-Profile}) for w_X = w_Y = w_Z = 1, together with the profile transmissibility weightings in the three directions (W_Tr-X-Profile, W_Tr-Y-Profile, and W_Tr-Z-Profile). They are derived from the finger transmissibility measured at several different locations on the fingers⁴⁶⁾.

Major Limitations

Because the synthesized weighting shown in Fig. 7 is the profile of the finger biodynamic weightings, it may not truly represent the frequency-dependency of the finger biodynamic response for a specific working condition. While those shown in Figs. 8–10 may be more representative of some specific working conditions, they may not be applicable to other conditions. Furthermore, they are not applicable for quantifying the vibration exposures of the other substructures of the hand-arm system. It is better to quantify all the major biodynamic responses (stresses, strains, and VPAD) for each substructure of concern for the representative working conditions. In addition to the root-mean-square values of the vibration stresses and strains, some other exposure parameters such as their peak values, impulsiveness measures (like VDV for whole-body vibration), and magnitude-cycle counts (widely used in material fatigue analyses²³⁾) may also be quantified to explore their relationships with the vibration effects. These quantifications require developing a generally-applicable comprehensive finite-element model of the hand-arm system, which remains a formidable research task.