In Vitro Validation of Endovascular Doppler-derived Flow Rates in Models of the Cerebral Circulation

Abstract

This study presents validation of endovascular Doppler velocimetry-based volumetric flow rate measurements conducted in a pulsatile flow loop simulating conditions in both the internal carotid and basilar artery. In vitro models of cerebral vessels, each containing an aneurysm, were fabricated from patient anatomies extracted from 3D rotational angiography. Flow velocity measurements were collected with three different experimental techniques: an endovascular Doppler wire, Particle Image Velocimetry, and a time-resolved ultrasonic flow meter. Womersley’s theory of pulsatile flow in a cylindrical vessel was used to compute time-resolved volumetric flow rates from the endovascular Doppler velocity. The volumetric flow rates computed from the Doppler measurements were compared to those from the Particle Image Velocimetry profile measurements, and the direct measurements from the ultrasonic flow meter. The study establishes confidence intervals for any systematic or random errors associated with the wire-derived flow rates as benchmarked to the other two modalities. There is an approximately 10% random error in the Doppler-derived peak and time-averaged flow rates. There is a measurable uniform bias, about 15% too low, in the time-averaged Doppler-derived flow rates. There is also a small proportional bias in the peak systolic Doppler-derived flow rates. Potential sources of error are also discussed.

1. Introduction

The haemodynamic environment of the cerebral blood vessels is widely thought to influence formation, growth, and rupture of intracranial aneurysms (Sforza et al. 2009). As a result, much activity has been devoted to using computational fluid dynamics (CFD) to calculate haemodynamic stresses and flow features in the intra- and peri-aneurysmal environment (Cebral et al. 2005, Cebral et al. 2011, Miura et al. 2013, Xiang et al. 2011). An important limitation of computational studies of the cerebral circulation, however, is the difficulty in obtaining flow measurements, like velocity or pressure, for the prescription of patient-specific boundary conditions such as the volumetric flow rate at the model inflow boundary.

Despite having detailed anatomical models from patient-specific medical imaging, CFD studies often rely on stereotypical boundary conditions derived from cohorts of volunteers, frequently healthy subjects (Cebral et al. 2008), since phase- contrast magnetic resonance velocimetry in the intracranial vessels or transcranial Doppler ultrasound velocimetry are difficult to collect. CFD calculations based on stereotypical velocity inputs are subject to significant errors based on their sensitivity to pressure and/or flow rate waveform boundary conditions (Karmonik et al. 2010, Jansen et al. 2014, Marzo et al. 2011, McGah et al. 2014, Venugopal et al. 2007). Indeed, recent controversy has originated over the accuracy of CFD using either stereotypical literature-based or patient-specific flow rates for haemodynamic simulations of intracranial aneurysms (Steinman 2011). A robust method for the measurement of cerebral blood flow rates would improve significantly the reliability of computational studies of cerebral aneurysm haemodynamics, particularly for patient- specific treatment planning and prediction of treatment success.

Our group has previously (Levitt et al. 2013, McGah et al. 2014) pioneered the use of a dual-sensor pressure and Doppler velocity endovascular guidewire (Combowire XT Guidewire, Volcano Corp., San Diego, CA) to obtain in situ patient- specific blood pressure and blood flow rates in cerebral vessels. These measurements were used as boundary conditions for computational simulation of blood flow in anatomical models of the intracranial circulation derived from patient-specific 3D rotational angiography images. Additionally, velocity and pressure measurements acquired inside the computational domain, which were not necessary as CFD boundary conditions, were used to validate the computational simulation results. Good agreement was found between the CFD-based and wire-measured velocities and pressure drops. However, considerable scatter, of the order of 20–40%, did exist between the endovascular measurements and CFD predictions.

Widespread use of endovascular Doppler measurements in patient-specific computations for personalized surgical planning and assessment requires extensive validation of the measurements to develop confidence in the technique for the intracranial circulation. Moreover, although the Doppler wire measures velocity, volumetric flow rates are typically derived from the velocity for application as CFD boundary conditions. The wire spectral Doppler processing automatically reports the maximum flow velocity within the sample volume. To obtain the temporal evolution of the flow rate at the measurement location, however, a velocity profile, such as Poiseuille’s law, needs to be assumed to relate the peak velocity to the flow rate (or cross-sectionally averaged velocity). In a Poiseuille parabolic flow profile, for example, the area-averaged velocity (U_ave = Q/A) is half of the peak velocity. Doppler wire flow velocity measurements have been validated, in terms of the estimated volumetric flow rates, against electromagnetic flow meter measurements by previous in vitro studies (Doucette et al. 1992, Labovitz et al. 1993), as well as in vivo in canine coronary arteries (Doucette et al. 1992) and porcine internal carotid arteries (Chaloupka et al. 1994). All of these studies used a Poiseuille velocity profile assumption. Moreover, these studies only compared the mean flow rates (time- averaged), but not the time-resolved measurements of flow rate, which are crucial for accurate estimation of peak shear stresses and for time-dependent CFD simulations and validation (Kono et al. 2012, Shojima et al. 2010).

This study presents validation of the endovascular wire Doppler measurements, compared against ultrasonic flow meter and Particle Image Velocimetry (or PIV) measurements, conducted in patient-specific models of the intracranial circulation created with 3D printing. The guide wire-based technique utilizes Womersley’s theory of pulsatile flow to relate the in situ velocity to a volumetric flow rate. Womersley’s theory accounts for the unsteady acceleration of the fluid, an important effect which is neglected in Poiseuille’s law. The wire-based technique’s accuracy and precision have not been rigorously validated to date. This study quantifies the random error and any systematic bias, with confidence intervals, in the endovascular measurements against two independent standard laboratory techniques.

2. Materials and Methods

All measurements were acquired in an in vitro pulsatile flow loop. The wire-derived volumetric flow rates were compared against two separate and independent techniques: Particle Image Velocimetry and ultrasound transit time flow metrology.

2.1. Experimental Apparatus

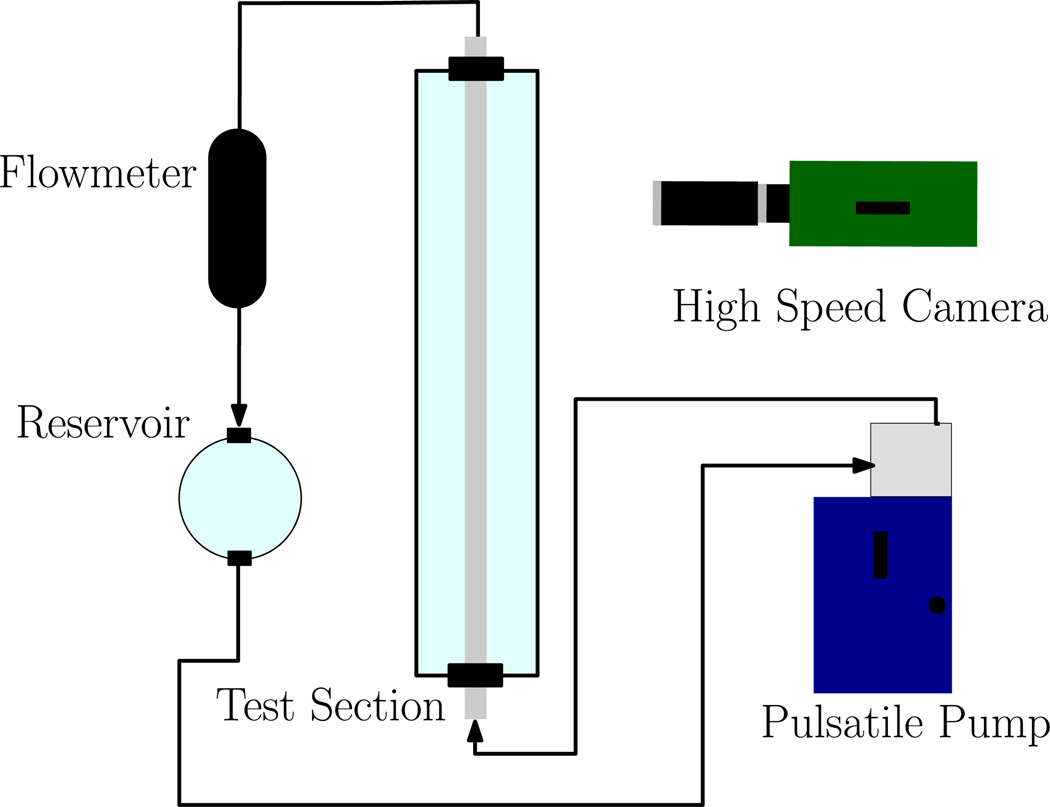
The diagram of the flow loop used to mimic the haemodynamic conditions of the cerebral vasculature is shown in Figure 1. The flow is driven by a computer-controlled pulsatile blood pump (Model 1423, Harvard Apparatus, Holliston, MA) with “heart rate” and “stroke volume” settings adjusted, together with the hydrostatic pressure level, to reproduce the flow waveforms of the intracranial arteries. The test section consisted of two modular components: a section of straight acrylic tube, and a section of flexible vinyl tubing connected to the aneurysm models. The rigid tubing was nominally 1/4″ (measured at 6.47 mm by calipers) inner diameter and the flexible tubing segment, also nominally 1/4″ inner diameter (measured at 6.58 mm by calipers). The loop was filled with a water/glycerol mixture (60/40% by mass at 25°C) to mimic the kinematic viscosity of blood in vivo, with a value of 3.22 cP (Segur & Oberstar 1951). The density of the mixture was 1.097 ± 0.002 g/cm³ as measured by a hydrometer.

Figure 1.

Diagram of the Flow Loop Apparatus. The “test section” is modular: either straight rigid acrylic tubing only, or patient-specific cerebral models.

Experimental conditions matched the patient specific systemic values reported for each of the three aneurysmal cases from which the models were obtained and built. The pump heart rate was set to values between 50–75 beats per minute, while the time-averaged volume flow rates ranged from 2.5–6 mL/s, and peak flow rates range from 5–10 mL/s. These three cases showed conditions typical for the large cerebral vessels (Ford et al. 2005, Hoi et al. 2010). The Womersley numbers inside the cerebral vessel models were ≈ 2.8–3.7, with the mean Reynolds numbers equal to ≈ 150 – 250. The Womersley numbers in the straight tubing segments were ≈ 4.3 – 5.4, the mean Reynolds numbers equal to ≈ 100 – 175.

2.2. Flow Measurement Modalities

Ultrasonic volumetric flow meter (Atrato, Titan Enterprises, Sherborne, Dorset, UK) measurements were conducted just downstream of the test section. Conservation of mass in an incompressible flow ensures that the measured flow rate is valid throughout the experimental flow loop. The flowmeter measurements are based on the ultrasound transit time principle, weighted across the entire cross section of the measurement volume, giving a true volumetric flow rate independent of the shape of the flow velocity profile or the fluid’s density and viscosity. The flowmeter time response is fast enough, 50 ms, to provide a time-resolved measurement of the flow rate waveform during the cardiac cycle.

The endovascular wire Doppler measurements used the Combowire XT Guidewire (Volcano Corp., San Diego, CA). The wire is 0.36 mm in diameter and has a piezoelectric tip that emits pulsed ultrasound waves with a carrier frequency of 12 MHz. The ultrasonic wave insonifies a disk-shaped volume nominally at ≈4 mm in diameter and ≈0.5 mm in depth, centred at 5.2 mm in front of the wire tip. The wire signal is registered and analyzed with the ComboMap (Volcano Corp., San Diego, CA) terminal which automatically outputs the maximum envelope of the Doppler shift frequency spectra at a temporal resolution of 5 ms. The maximum value is derived from the spectral line at a given temporal bin by finding the line’s highest velocity bin whose signal-to-noise strength is above a threshold that is intended to separate velocity information from noise sources. The threshold signal-to-noise strength can be manually set to an integer value from 0 to 5, and the default threshold is 2. A threshold of 2 or 3 was sufficient for all cases reported herein. The system then calculates a velocity based on the maximum spectral envelope assuming a 0° angle of incidence between the ultrasound beam and the flow velocity. Lastly, the system reports the velocity time signal, i.e. u(t), which is smoothed using a three-point moving average filter.

The ComboMap system uses a constant speed of sound equal to 1560 m/s in the conversion from Doppler shifted frequencies to velocity. The speed of sound of a 40% aqueous glycerol mixture at 25°C is 1677 m/s (Slie et al. 1966). We developed a correction, linear with the ratio of sound speed of the working fluid over that of blood, and applied it to the system’s velocity measurements, multiplying them by a factor of 1677/1560 = 1.075. The altered sound speed also changes the distance of the sample volume from 5.2 mm to 5.6 mm and the sample volume diameter from 4 mm to 5 mm.

The PIV technique measures time-resolved velocity vectors on a two-dimensional imaging plane by optically measuring the displacements of many small particles, which follow the motion of the flow, over a small time interval. An argon ion laser (Spectra Physics, Santa Clara, CA) was used to illuminate a plane along the direction of motion and cutting diametrically across the test section vessel. The flow was seeded with small, neutrally buoyant particles that act as flow tracers (lycopodium, Fischer Scientific, Hanover Park, IL). The particles were nominally 30 µm in diameter and were seeded at a concentration of about 100 ppm.

A high-speed camera (Phantom v. 12.1, Vision Research, Wayne, NJ) was oriented perpendicular to the laser plane and recorded the laser light scattered by the particles as they flow along the test section. The imaging settings were: 1000 frames/s, an image exposure time of 100 µs, a field of view of 10 mm×10 mm, and a total acquisition time of 10 s per run.

The velocity field was calculated from the images by processing with the open source code Gpiv (Gerber van der Graaf, Applied Physics, Delft University of Technology, the Netherlands). The resulting streamwise velocities are averaged for all the points equidistant to the vessel axis, resulting in a velocity profile as a function of radial position. The spatial resolution in the radial direction was ≈220 µm. Once the time-dependent velocity profile has been calculated, the volumetric flow rate can be obtained by integrating in the cross section of the vessel, assuming an axi-symmetric velocity field.

2.3. Experimental Procedure

The flowmeter and the PIV were first compared for agreement against each other. For these sets of experiments, the Doppler wire was completely removed from the flow apparatus. The PIV were collected in a straight section of tubing, and flowmeter measurements were taken co-temporally with the PIV.

For the assessment of the Doppler wire, measurements using the wire and PIV were first collected inside the test section where the flow vessels are straight and cylindrical, allowing for assessment of the wire-based endovascular measurement technique under “ideal”, unidirectional flow conditions. The wire was introduced into the flow loop via an entry hole approximately 50 cm upstream to the test section. The wire and the PIV collected velocity measurements in the same vessel segment co-temporally. The wire was positioned about 10 cm proximal to the PIV measurement location. The wire was placed in the centre of the vessel radially and oriented parallel to the vessel axis as best as possible by the operator. The wire position and orientation could be ascertained visually.

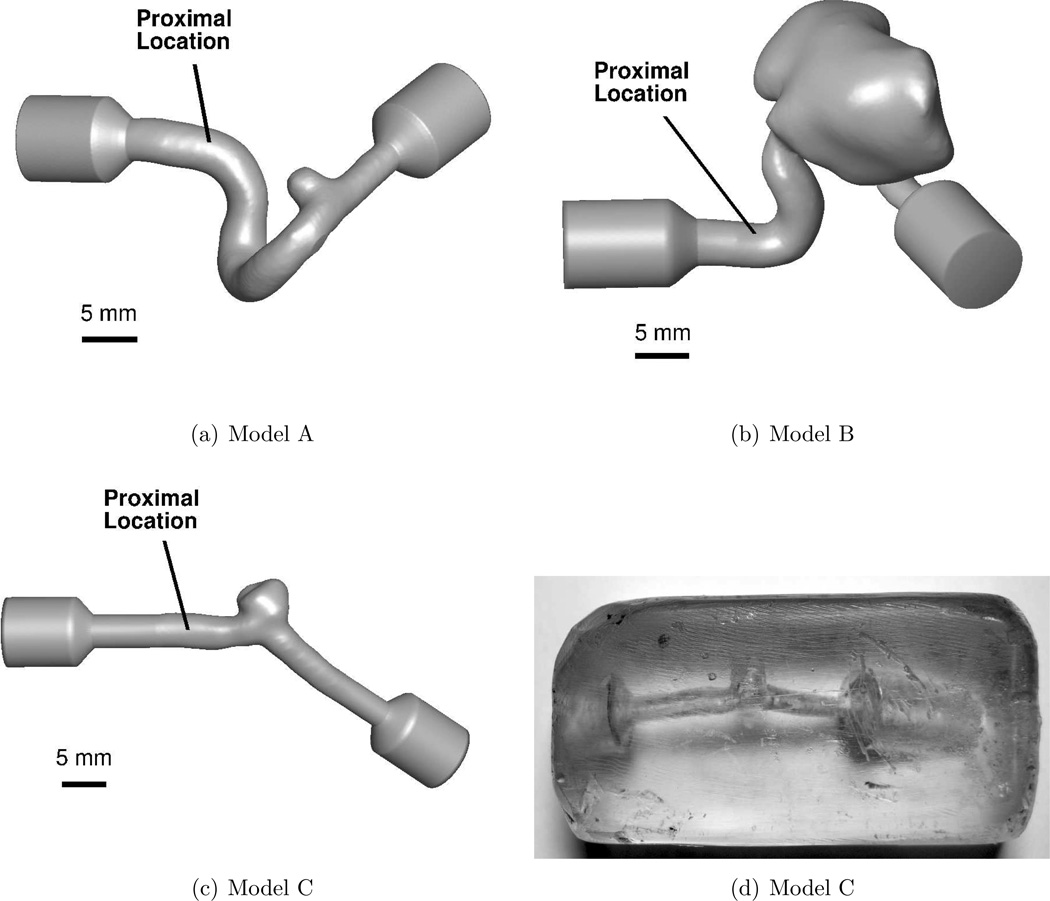
After disabling the PIV setup, additional wire measurements were made in the straight segments of tubing with the flowmeter collecting data co-temporally with each Doppler wire run. Then, Doppler wire measurements were collected inside the cerebral vessel models, allowing for the testing of the wire-based method’s accuracy and robustness in realistic locations where the anatomy differs from the ideal conditions of a straight circular tube. The wire is positioned about 5–10 mm proximally to the location of the aneurysm. The wire is withdrawn from the model and then repositioned and reoriented after each experimental run. the wire was placed in the centre of the vessel radially and oriented parallel to the vessel axis as best as possible in every case. The wire position and orientation could be ascertained visually. The approximate location of the tip of the wire inside the vascular models is denoted by the “proximal location” arrows in Fig. 2. Flowmeter measurements were also recorded co-temporally for each wire run conducted inside a cerebral vessel model. For a given experimental run, the Doppler wire collected data every 5 ms for a total of about 20 seconds. An overview of the different modalities used in each experimental run is presented in Table 1.

Figure 2.

In vitro models. Flow is from left to right in each model. (a)–(c) are CAD representations of the three models. The solid lines labeled “Proximal Location” denote the approximate position of the wire tip when measurements were acquired. (d) is a photograph of model C.

Table 1.

Summary of Experimental Runs.

			Approximate Flow Rate (mL/s)
Modalities	Location	No. of Measurements	Time-averaged	Peak
PIV vs. Flowmeter	Straight Segments	6	8–13a	13–18a
Wire vs. PIV	Straight Segments	4	5–9b	12–17b
Wire vs. Flowmeter	Straight Segments	15	2.5–6a	5.5–10a
Wire vs. Flowmeter	Cerebral Vessels	13	2.5–6a	5.5–10a

^aRange as measured by flowmeter.

^bRange as measured by PIV.

The time-resolved volumetric flow rates are derived from the wire-measured velocities using Womersley’s theory of pulsatile flow (Womersley 1955). The time signal of the wire-measured velocity is assumed to be the streamwise velocity at the centreline of the vessel in Womersley’s theory. This theory can be used to derive a relationship between the centreline velocity and the volumetric flow rate. Womersley’s theory accounts for the unsteady acceleration of the pulsatile fluid which is neglected in Poiseuille flow. The time-averaged and peak flow rate were computed for each pump cardiac cycle, and each reported mean or peak flow rate is the average of 10–20 pump cardiac cycles. The details of the computation are described in the Appendix.

2.4. Cerebral Vessel Model Construction

The cerebral aneurysm models were acquired from human subjects using 3D rotational angiography imaging during an endovascular treatment procedure. A 3D reconstruction of the vascular surface was created by segmenting the images with the software Vascular Modeling Toolkit (vmtk.org). The geometrical characteristics of the aneurysm models are summarized in table 2. CAD representations of the in vitro models used for fabrication are shown in Figure 2.

Table 2.

Aneurysm Characteristics.

Patient	Location	Size (mm×mm)	Parent Vessel Diam. (mm)
A	Posterior Paraclinoid Internal Carotid	4×4.5	4.3
B	Cavernous Internal Carotid	30×30	4.5
C	Basilar Trunk	5.5×5	4.2

The models were extended at the inflow and outflow sections of 9.5 mm diameter to allow integration into the flow loop. A physical “positive” model made of acrylonitrile butadiene styrene (ABS) was created at 1:1 scale by a 3D printer. The ABS model was then cast in a silicone rubber (OOMOO 25, Smooth-On Inc., Macungie, PA). After the silicone cured, the ABS model was cut and removed from the silicone, leaving a “negative” model. The silicone mold was then used to create an additional “positive” model from casting wax (Freeman, Avon, Ohio). The wax model was finally cast in a clear polyester resin (Clear-Lite, TAP Plastics, San Leandro, CA) which cured for 24 hours. The wax was melted away leaving the final “negative” model of the aneurysm and parent vessel. A photograph of one of the completed physical models is shown in Figure 2(d), and photographs of the additional in vitro models are provided in the supplementary materials.

2.5. Data Analysis

The agreement between the different measurement techniques was assessed by the Bland-Altman method. Systematic errors were quantified in terms of the Bland-Altman bias, i.e. the mean of the differences between two methods, and the significance of a bias is determined by two-tailed t-tests. The limits of agreement, which give a measure of random errors, are given as plus or minus twice the standard deviation of the measurement differences, i.e. $\frac{1}{2}\text{Mean}(Q_1+Q_2)\pm 2·s$, where Q₁ and Q₂ are the flow rates determined by two modalities, and s is the standard deviation of (Q₁ − Q₂). The coefficient of variation, CoV, computed as

$$\text{CoV}=\frac{s}{\frac{1}{2}\text{Mean}(Q_1+Q_2)}\times 100\%,$$ (1)

also assesses the limits of agreement between techniques.

Additional ordinary least squares linear regressions were performed to compare the Doppler-based measurements vs. the flowmeter measurements; flowmeter measurements are taken as the regressors and wire-based measurements are taken as the regressands. Confidence intervals of the regressions’ slopes and intercepts are used to assess the significance of any biases, i.e. a slope not equal to 1 is indicative of a bias. Random errors in the linear regression are assessed by the Pearson coefficient of determination, r², and by the standard error of the regression.

3. Results

3.1. PIV and Flowmeter Comparison

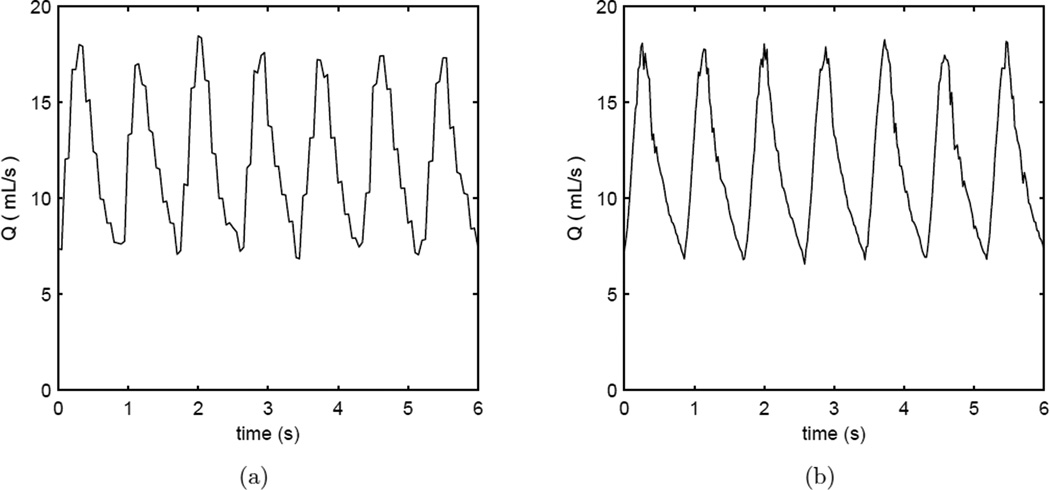
Six flow rate conditions in the flow loop were used to compare between the measurements from the PIV and the flowmeter (see also Table 1). Note that the Doppler wire was completely removed from the apparatus during these 6 experimental runs. Excellent agreement exists between the two methods; the bias is insignificant for the time-averaged (−0.06 mL/s, p > 0.5) or peak (0.09 mL/s, p > 0.5) values (bias reported as PIV minus flowmeter). The CoVs are 3.6% and 2.0% for the time-averaged and peak values, respectively. The standard deviation of the difference is 0.37 mL/s and 0.33 mL/s for the time-averages and the peak values, respectively. Typical time-resolved flow rate measurements with PIV and flowmeter are shown in Figure 3. Descriptive statistics for the agreement between the PIV and the flowmeter are given in the supplementary materials.

Figure 3.

Volumetric flow rate vs. time for a heart rate of 70 bpm in straight vessel segments as measured by (a) flowmeter and (b) PIV. The Doppler wire is is absent from the test section in these examples.

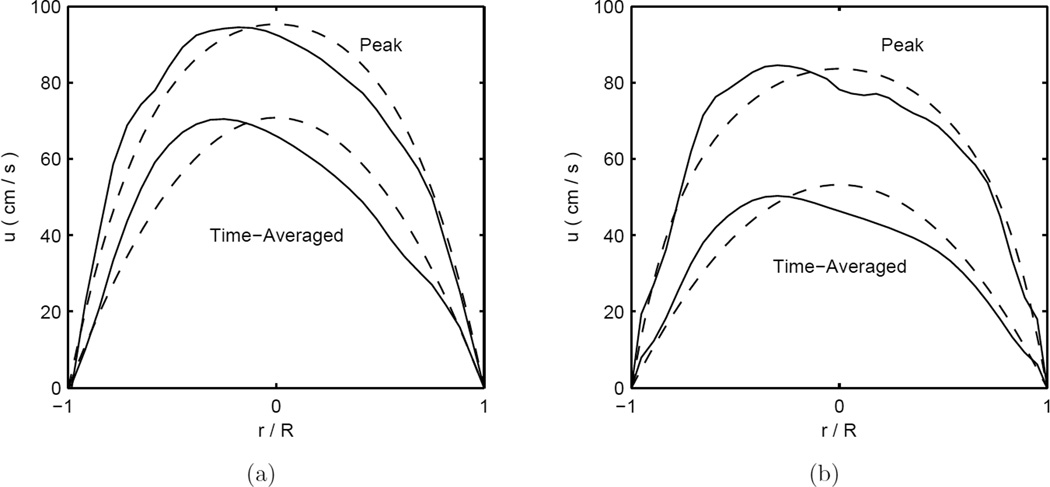
The velocity profiles measured by the PIV when the wire was absent from the apparatus show satisfactory agreement with Womersley flow. The measured ratio of the time-averaged centreline maximum velocity to the area-averaged velocity is 2.024±0.031 (mean±SD) in very good agreement with the theoretical value of 2 for steady flow in a straight cylindrical vessel. An example of PIV-measured velocity profiles and corresponding Womersley profiles (with an equivalent volumetric flow rate) when the wire is absent from the apparatus are shown Figure 4(a).

Figure 4.

Velocity profiles at a heart rate of 70 bpm in straight vessel segments as measured by PIV (solid lines) and Womersley profiles with equivalent volumetric flow rates (dashed lines). Subfigure (a) shows a case where the Doppler wire is absent from the test section and (b) shows a case where the Doppler wire is inside the test section.

3.2. PIV and Doppler Wire Comparison

The wire and the PIV measurements were compared for agreement with respect to both the velocity and the flow rate. Four flow loop conditions, with different velocity and flow rates, were used in the comparison. Typical unsteady velocity waveforms measured by PIV and the Doppler wire are included in the supplementary material. The ratio of the PIV measured time-averaged centreline to area-averaged velocity was 1.912±0.077 (mean±SD) in these cases. PIV-measured velocity profiles and corresponding Womersley profiles (with an equivalent volumetric flow rate) are shown in Figure 4(b) for a run where the wire is present inside the flow apparatus. The Doppler wire measurements are found to be lower than the PIV measurements, in both the velocity and flow rate; these measurement biases are not, however, statistically significant, though the small sample size, N=4, may limit our ability to detect biases. The maximum wire velocities are about 10% lower than those from PIV, and the CoV between the two is ≈ 10–12%. Similar differences are also found with respect to the flow rate agreement analysis. The Bland-Altman analysis for the Doppler wire vs. the PIV is summarized in Table 3. Additional Bland-Altman plots for the PIV and wire Doppler comparison are provided in the supplementary materials.

Table 3.

Doppler Wire vs. PIV Bland-Altman Analysis Statistics.

	Velocity
	r2	Bias* (cm/s) (p value)	Std. Dev. of Differences (cm/s)	CoV (%)
Time Average	.961	−3.32 (> .2)	4.91	12.70
Peak	.960	−6.16 (.16)	6.61	9.64
	Flow Rate
	r2	Bias* (cm/s) (p value)	Std. Dev. of Differences (cm/s)	CoV (%)
Time Average	.883	−.874 (.14)	.863	13.23
Peak	.909	−1.81 (.12)	1.70	12.56

^*Bias is reported as wire value minus PIV value.

3.3. Flowmeter and Doppler Wire Comparison

A total of 15 different conditions were tested to compare the Doppler wire measurements to the flowmeter results in the straight segments of the test section. Typical unsteady flow rate waveforms measured by the flowmeter and the wire are shown in Figure 5. Under these conditions, the measurements with the two methods show some measurable bias. The wire-based mean flow rate measurements are systematically low, while the peak values are systematically high relative to the flowmeter. The bias in the mean flow rate is −0.227 mL/s, 95% CI [−0.348, −0.106], and is 1.29 mL/s, 95% CI [0.98, 1.60], for the peak, with bias reported as wire-derived value minus flow meter value. The CoV is ≈ 6 – 7% indicating high repeatability for both techniques. The agreement analysis in the straight segments of tube is summarized in the first part of Table 4. The Bland-Altman results for the flowmeter vs. wire Doppler comparison in the straight vessel are shown in Figure 6.

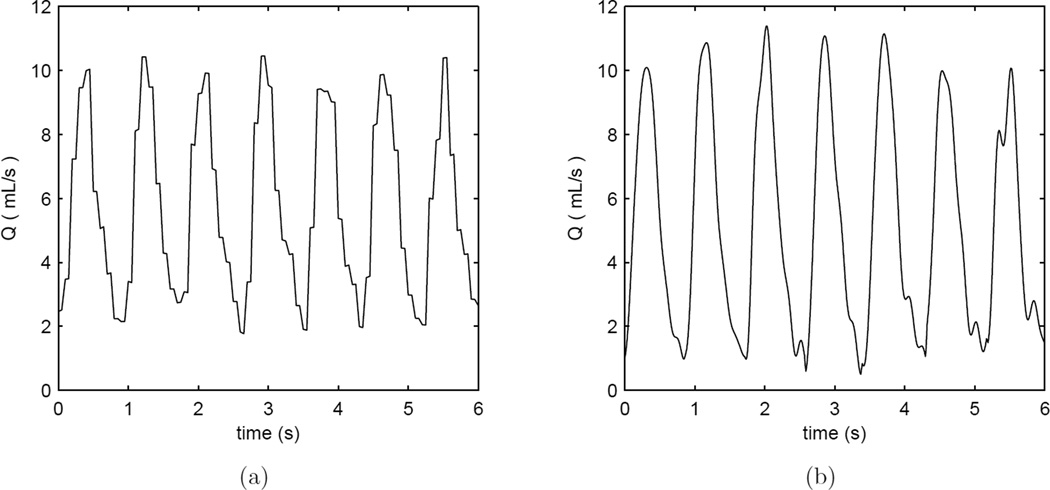
Figure 5.

Volumetric flow rate vs. time for a heart rate of 70 bpm in straight vessel segments as measured by (a) flowmeter and (b) Doppler wire. Since 5 oscillatory Fourier modes are used to reconstruct the Doppler-derived flow rate, the waveform is noticeably more smooth as noise in the higher modes is excluded.

Table 4.

Doppler Wire vs. Flowmeter Bland-Altman Analysis Statistics.

	Straight Segments
	Biasa (mL/s) (p value)	Std. Dev. of Differences (mL/s)	CoV (%)
Time Average	−0.227 (< .01)	.219	6.04
Peak	1.289 (< .0001)	.558	6.97
	Aneurysm Models
	Biasa (mL/s) (p value)	Std. Dev. of Differences (mL/s)	CoV (%)
Time Average	−0.568 (< .0001)	.312	9.29
Peak	−0.053 (> .5)	.747	10.48

^aBias is reported as the wire value minus the flowmeter value.

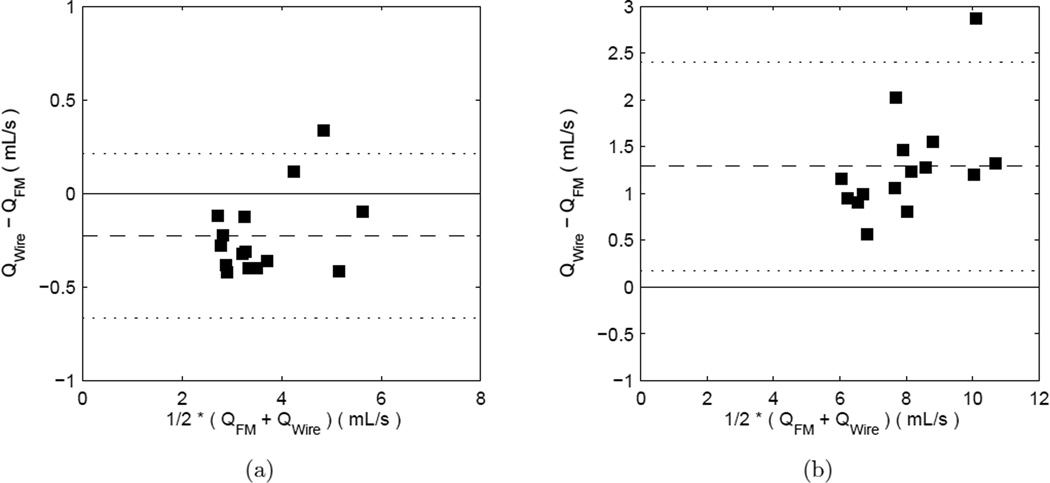
Figure 6.

Bland-Altman plots for flowmeter vs. wire-derived flow rates in straight vessels: (a) time-averaged values (b) peak values. Symbols are data points, dashed line is the mean difference, and dotted lines show the region within ±2 SD of the difference.

At the “proximal location” in the aneurysm models, 13 measurements conditions were used to compare the Doppler wire against the ultrasonic flowmeter. Five different measurements were collected in each one of models A and C, with three conditions tested for model B. The wire-based mean time-average flow rate measurements are systematically low, while the peak values show no detectable bias. The bias in the mean flow rate is −0.568 mL/s, with a 95% CI [−0.757, −0.379] mL/s, computed as wire-derived value minus flow meter value. This is 16% of the flowmeter sample mean of 3.64 mL/s. It is important to note that the Shapiro-Wilk test for normality gives a result of p = .052, so the distribution of the differences may not be normally distributed. Thus, the above confidence interval should only be considered approximate. The random scatter of the measurements inside the cerebral models is larger than that in the straight vessel, ≈ 9 – 10%. The analysis of the comparison of the flowmeter vs. Doppler-wire Bland-Altman analysis for the cerebral models is summarized in the latter part of Table 4, and the corresponding plots are shown in Figure 7.

Figure 7.

Bland-Altman plots for flowmeter vs. wire-derived flow rates in the aneurysm models: (a) time-averaged values (b) peak values. Symbols are data points, dashed line is the mean difference, and dotted lines are ±2SD of the difference.

The linear regression analysis did not discern a significant bias between the wire- based and flowmeter-based volumetric flow rates for the experiments conducted in either the straight segments of the test section or inside the cerebral vessel models. In all cases comparing the Doppler wire against the flowmeter, the slopes are not statistically different from unity, and the line intercepts are not statistically different from zero. The results of the regression analysis are shown in Table 5. Scatter plots of of the measurements and the associated linear regression analyses are shown in the supplementary material.

Table 5.

Doppler Wire vs. Flowmeter Linear Regression Statistics.

	Straight Segments
	r2	Slope 95% CI	Intercept (mL/s) 95% CI	Standard Error of Regression (mL/s)
Time Average	.957	1.07 [.93, 1.21]	−.50 [1.04, 0.03]	.216
Peak	.962	1.15 [.92, 1.39]	.15 [1.61, 1.92]	.539
	Aneurysm Models
	r2	Slope 95% CI	Intercept (mL/s) 95% CI	Standard Error of Regression (mL/s)
Time Average	.900	1.05 [.82, 1.28]	−.76 [−1.63, 0.11]	.322
Peak	.865	1.31 [.97, 1.66]	−2.36 [−4.95, 0.23]	.694

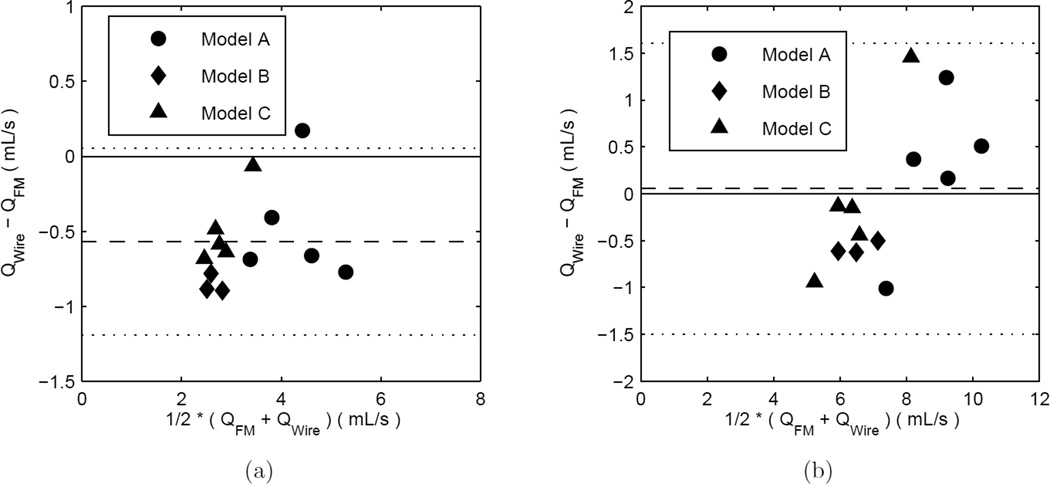
Upon a closer inspection of the Bland-Altman analyses, we found that the there is a proportional bias, i.e. a bias which depends on the magnitude of the measurement, in some cases. A proportional bias can be identified by calculating the strength of the Pearson correlation coefficient for the method differences vs. the method averages, i.e. $(Q_1-Q_2)\text{vs}.\frac{1}{2}(Q_1+Q_2)$. The peak flow rates of the wire vs. flowmeter inside both the straight test section, p < .05, and inside the aneurysm models, p < .01, are found to have statistically significant proportional biases, e.g. Figures 6(b) and 7(b), respectively. No proportional biases are found in the wire vs. flowmeter for the time-averaged flow rates inside either the straight tubing, p = .13, and inside the aneurysm models, p = .29, e.g. Figures 6(a) or 7(a), respectively.

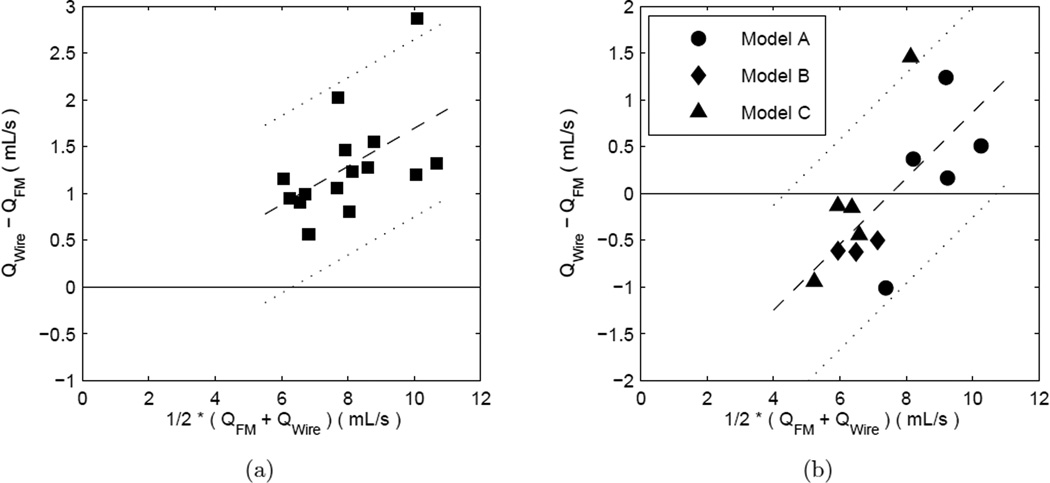
Bland and Altman (1999) themselves suggested that a proportional bias can be quantified by a linear regression of the differences in the methods against the average of the methods. The results of the proportional bias analysis for the case of the peak flow rates of the wire vs. flowmeter inside both the straight tubing and the aneurysm models is presented in Table 6. The table presents the slopes and intercepts (and 95% confidence intervals thereof) for the linear regressions and the standard error of the regression, which represents the mean variation of data around the regression line. The data points with the proportional bias regression line are also plotted in Figure 8.

Table 6.

Doppler Wire vs. Flowmeter Proportional Bias Correction Statistics.

	Straight Segments
	Slope 95% CI	Intercept (mL/s) 95% CI	Standard Error of Regression (mL/s)
Peak	0.20 [.01, 0.40]	−0.34 [−1.94, 1.26]	.47
	Aneurysm Models
	Slope 95% CI	Intercept (mL/s) 95% CI	Standard Error of Regression (mL/s)
Peak	0.35 [.11, 0.60]	−2.66 [−4.51, −0.81]	.56

Figure 8.

Bland-Altman plots for wire-derived vs. flowmeter flow rates in the case of a proportional bias: Subfigure (a) peak values in straight segments. Same data as in Figure 6(b). Subfigure (b) peak values in aneurysm models. Same data as in Figure 7(b). Symbols are data points, dashed line is the linear regression, and dotted lines are ± twice the standard error of the regression.

4. Discussion

The endovascular wire Doppler ultrasound velocimetry technique analyzed in this study is shown to compare positively, albeit imperfectly, against two standard laboratory measurement techniques for in vitro velocity (PIV) and flow rate (ultrasonic transit time). The random scatter in the wire measurements is low, ≈ 9%, representing a satisfactory level of robustness for a clinical in situ measurement. The wire-based measurements inside the aneurysm models show no discernible systematic error in peak flow rate values but an ≈ 16% underestimation in the time-averaged flow rates.

There are three possible sources of error in the wire Doppler flow rate measurements, each of which could systematically lower the wire-derived flow rates: 1) imperfect positioning of the wire and the Doppler sample volume in the centre of the vessel, 2) a non-zero angle of insonation between the flow velocity and the wire orientation, 3) deviation from the ideal Womersley flow velocity profile.

Imperfect positioning of the wire in the vessel cross section could result in the true centreline velocity being outside the Doppler sample volume, and thus, the wire- calculated maximum velocity would be lower than the true maximum velocity inside the vessel. Furthermore, the wire’s own system assumes the angle of insonation is 0°, but any non-zero angle would lower the maximum velocity component in the streamwise direction by a factor equal to the cosine of the angle. For example, a 35° angle of insonation between the ultrasound beam and the flow velocity would cause an 18% downward error in the Doppler-calculated velocity and the calculated flow rate.

The velocity profiles measured by PIV with the wire located just upstream of the imaged region of the test section are slightly more “blunted” than in the absence of the wire. The time-averaged PIV velocity without the wire resulted in good agreement with the Poiseuille flow parabolic profile and a max-to-mean ratio of velocities equal to the theoretical value of 2. In the presence of the wire, the ratio of the time-averaged peak-to-mean velocity is lower, ≈ 1.9. This 5% “bluntedness” in the velocity profile propagates as a 5% downward error in the Doppler-derived flow rates. This evidence shows that the wire contributes a loading error, meaning the velocity profile is altered by the presence of the wire itself. Additionally, the high curvature of the cerebral vessels produces inertial displacement of the maximum velocity away from the centerline, as well as secondary flows, that result in a non- axisymmetric velocity profile. This skewing can, in turn, cause downward errors in our Womersley profile fitting-based flow rate integration technique (Mynard & Steinman 2013).

Although there are measurable biases in the Doppler wire-derived flow rates inside the cerebral vessel models, this does not preclude the wire’s usefulness in providing clinicians physiological information during an angiographic procedure, or supplying patient-specific measurements for CFD boundary conditions. Given the low random errors associated with the measurements, the wire velocity and flow rates can be used to accurately describe the relative haemodynamic environment, for example before and after aneurysm treatment, even if the absolute values are systematically underestimated. To improve its absolute accuracy, a correction factor could be applied to remove either the uniform bias in the time-averaged volumetric flow rates or the proportional bias in the peak volumetric flow rates.

Blood flow velocity can be acquired from other modalities such as transcranial Doppler (TCD) ultrasound (Sun et al. 2012) or phase-contrast magnetic resonance imaging (pcMRI) (Boussel et al. 2008, Karmonik et al. 2010, Marzo et al. 2011). These alternative methods have disadvantages relative to the endovascular technique investigated in the current study. The accuracy of TCD measurements in the vertebrobasilar system, in vessels near the skull base, or small-diameter vessels has been questioned (Sviri et al. 2006, Turner et al. 2003). Insonation of intracranial vessels may not be possible in up to 16% of patients with thick temporal bone windows (Ackerstaff et al. 2005). Flow rates acquired with pcMRA have lower temporal resolution than TCD (Seitz et al. 2001), and they may significantly underestimate systolic peak values; peak systolic velocity in the cerebral vessels as measured by pcMRI can be 30% lower than velocity measured by TCD (Chang et al. 2011) or 12% lower than velocity measured by endovascular Doppler (Schneiders et al. 2012).

The endovascular guidewire, although invasive, offers several advantages over TCD and pcMRA in acquiring patient-specific physiological information. For instance, the wire can be used in nearly any major cerebral blood vessel, including the vertebrobasilar system. The real-time acquisition of velocity eases the integration of such data into the angiographic workflow. This is not possible with pcMRA since it requires interruption of an angiographic procedure for transport to and from the MRI machine. Finally, the peak velocity can be underestimated by pcMRA, which would substantially alter the fidelity of the haemodynamic computations (Karmonik et al. 2010).

There are several limitations of this study. Although the number of individual measurements is high, the measurements are taken in only three anatomic models. A larger dataset would improve the study’s precision. Furthermore, Doppler wire measurements are acquired at only a single anatomic location in each model. Measurements at additional locations could further discern the wire’s accuracy and precision in each of the cerebral vessels, e.g. the middle cerebral vs. the internal carotid artery.

Lastly, an important limitation is that it is not precisely known how this study’s in vitro error estimates agree with those of an in vivo situation. The conditions of an in vivo situation cannot be as carefully controlled as that of an in vitro experiment. For example, the tortuous nature of the internal carotid arteries would likely skew the velocity profiles inside the intracranial vessels even farther away from the ideal Womersley profile. The current study’s error estimates should be considered a lower bound on the expected errors in vivo. Additional studies are certainly needed to quantify this technique’s errors in vivo.

Appendix

The Doppler wire-based flow rate calculation uses Womersley’s theory (He et al. 1993, Womersley 1955) of pulsatile flow in a rigid cylindrical vessel. The theory first assumes that a known temporal velocity signal at the vessel centerline, u(t) is periodic in time and is written as a Fourier series such that

$$u(t)=\sum _{k=0}^{\infty }{û}_k·\text{exp}(\mathrm{i}k\omega t),\text{ where }\omega =\frac{2\pi }{T}$$ (A.1)

and T is the fundamental period of the signal. The theory then states that the volumetric flow rate can be written as a temporally periodic function such that

$$Q(t)=\sum _{k=0}^{\infty }{\hat{Q}}_k·\text{exp}(\mathrm{i}k\omega t)$$ (A.2)

and where the Fourier coefficients Q̂_k are given by

$${\hat{Q}}_k=\pi R^2{û}_k\frac{[J_0({\mathrm{i}}^{3/2}{\alpha }_k)-\frac{2}{{\mathrm{i}}^{3/2}{\alpha }_k}{J}_1({\mathrm{i}}^{3/2}{\alpha }_k)]}{[J_0({\mathrm{i}}^{3/2}{\alpha }_k)-1]}$$ (A.3)

where R is the vessel radius, J₀ and J₁ are the Bessel functions of zeroth and first order, respectively, and α_k is the Womersley parameter at the k-th frequency. The Womersley parameter is defined as

$${\alpha }_k=R\sqrt{\frac{k·\rho \omega }{\mu }}$$ (A.4)

where μ is the fluid viscosity and ρ is the fluid density. The flow rates are reconstructed using 1 mean and 5 harmonic components in the Fourier series.