Assessing and maximizing data quality in macromolecular crystallography

Abstract

The quality of macromolecular crystal structures depends, in part, on the quality and quantity of the data used to produce them. Here, we review recent shifts in our understanding of how to use data quality indicators to select a high resolution cutoff that leads to the best model, and of the potential to greatly increase data quality through the merging of multiple measurements from multiple passes of single crystals or from multiple crystals. Key factors supporting this shift are the introduction of more robust correlation coefficient based indicators of the precision of merged data sets as well as the recognition of the substantial useful information present in extensive amounts of data once considered too weak to be of value.

Introduction

Recent years have seen changes in our understanding of the factors influencing macromolecular crystallographic data quality and in the recommendations for obtaining the highest quality data and selecting an optimal high resolution cutoff for crystallographic refinement. Here, we will focus on three topics related to these changes. First, we discuss the common data quality indicators and their utility. Second, we describe recent results illustrating how high multiplicity¹ can improve data quality. Third, we review recent reports providing evidence that extending resolution limits beyond conventional cutoffs to include weaker high resolution data can improve phasing results, electron density maps, and refined models. Understanding of these aspects of data quality is critically important because the observed diffraction data are typically the sole source of experimental information available for supporting a crystallographic structure determination. Strategic considerations regarding other aspects of data collection (e.g. [1,2]) and data reduction (e.g. [3,4••]) are also important, but are beyond the scope of this review.

Common data quality indicators

In Table 1, we list and comment on the utility of eight common statistical indicators reported by current data reduction software, including the new CC_1/2 and CC* [5••]. The equations for each are in the literature and are not given here. These indicators all report on data precision, so if substantial systematic errors are present the indicators need not reflect the data accuracy [4••]. We have arranged the data precision indicators into three groups according our view of their utility, and we also specify for each one the crucial distinction of whether it reports on the precision of individual or of merged measurements (Table 1).

Table 1.

Common indicators of data precision and their recommended usage. The ‘type’ defines whether an indicator reports on the precision of individual observations or the final merged data

Indicator	Type	Recommended usage
Indicators of first rank
CC1/2	Merged	CC between intensity estimates from half data sets. Primary indicator for use for selecting high resolution cutoff for data processing. Is related to the effective signal to noise of the data (see Box 1).
CC1/2-anom	Merged	Suggested shorthand for CC between anomalous difference estimates from half data sets. (We suggest CCanom be used if datasets rather than between half data sets are compared [7].) Primary indicator for assessing the resolution limit of useful anomalous signal. Analogous to CC*, a ${\mathrm{CC}}_{\text{anom}}^{\ast }$ indicator can be calculated from CC1/2-anom.
CC*	Merged	Calculated from CC1/2. Indicator useful for comparing data and model quality. Provides the potential for a cross-validation independent indication of overfitting [5••]. CC* is undefined for negative CC1/2.
Additional useful indicators
Rmeas (=Rrim)	Individual	Multiplicity independent replacement of Rmerge and Rsym; Useful for assessing space group symmetry and isomorphism of multiple data sets; Should play no role in determining resolution cutoff.
Rpim (~Rmrgd/√2)	Merged	Mainly of value for comparisons with previous practices; Should play no role in determining resolution cutoff, as it rises toward infinity as signal decreases; Also because it is an unweighted sum, if data of varying quality are merged, it will underestimate the quality of the final data. The SFX community's Rsplit = RmrgdI.
〈I/σ〉ind	Individual	Average signal-to-noise ratio of individual observations. The σ for each reflection is calculated according to an ‘error model’ that parameterizes the random and systematic errors. Should play no role in determining resolution cutoff.
〈I/σ〉mrgd	Merged	As 〈I/σ〉ind but for the intensities after a weighted averaging (‘merging’) of equivalent observations. For reflections with multiplicity n, 〈I/σ〉mrgd is at most √n higher than 〈I/σ〉ind, but the increase will be less if reflections to be merged have varying 〈I/σ〉ind. More useful than CC1/2 for assessing quality of low resolution data. If properly estimated data should correlate with CC1/2 values (see Box 1).
ISa	Individual	Also 〈I/σ〉asymptotic; theoretical value of 〈I/σ〉ind for an infinitely strong observation of the dataset calculated from coefficients of error model established during scaling [3,17]. Gives insight into the level of fractional error in the dataset.
Indicators that should not be used
Rmerge = Rsym	Individual	Flawed indicators that have been replaced by Rmeas. We recommend these be removed from all data reduction software.
Overall value	Both	‘Overall’ quantities for statistics are not of general value, because they are highly influenced by the distribution of multiplicity. More informative would be reporting ‘low resolution bin’ and ‘high resolution bin’ values.

With the introduction of CC_1/2, all three key indicators we primarily recommend for assessing the precision of the merged data (for both standard and serial crystallography) are Pearson's correlation coefficients (CC) between independent sets of observations characterized as a function of resolution: CC_1/2, CC_1/2-anom, and CC* (Table 1). CC values range from 1 to –1 for perfectly correlated versus anticorrelated data, but for properly indexed data these indicators should range from near 1 for highly precise data to near 0 for very imprecise data. An advantage of CC-based indicators is that they have well-studied statistical properties so that, for instance, given a CC value and how many observations contributed to it, one can calculate the probability that this value has occurred by chance, i.e. how likely it is that the null hypothesis holds (e.g. http://en.wikipedia.org/wiki/Statistical_significance). CC_1/2-anom, our suggested name for the correlation between independent estimates of the anomalous differences from half data sets [6], was the first of these CC-based indicators to be introduced as an extension of work showing that the CC between anomalous differences of two complete data sets helped define which data would be useful for solving anomalous substructures [7].

Similarly CC_1/2, calculated in resolution shells by correlating the intensity values produced from two half data sets [5••], provides a model-free, empirical measure of the level of discernable signal and is equivalent to the Fourier Shell Correlation statistic used to define resolution in cryo-EM studies (e.g. [8]). In fact, a theoretical relationship between CC_1/2 and the signal-to-noise of the merged data (〈I/σ〉_mrgd) can be derived that helps put CC_1/2 on a familiar footing (Box 1). Typically, CC_1/2 is near 1.0 (or 100%) at low resolution, and drops smoothly toward 0 as the signal-to-noise ratio decreases. Any deviations from this behavior should be scrutinized as possible indicators of anomalies. Since CC_1/2 measures how well one half of the data predicts the other half, it does not directly indicate the quality of the data set after final merging. This, however, is estimated by the quantity CC*.

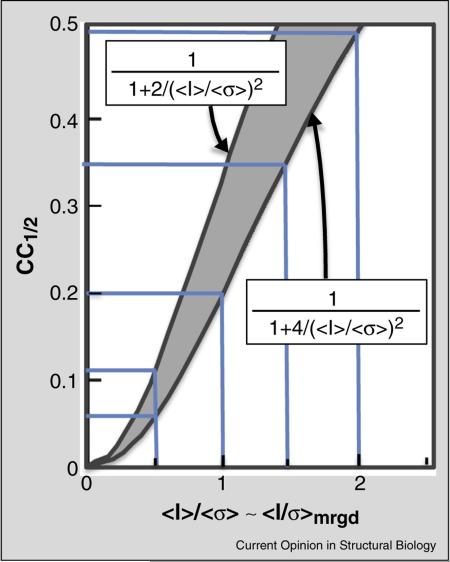
Box 1 Approximate relation between CC_1/2 and 〈I/σ〉_mrgd.

Assuming that the σ = σ_mrgd values obtained from data processing are consistent with the spread of observations around their mean, we can derive an approximate expected relationship between CC_1/2 and 〈I/σ〉_mrgd in a high resolution shell. From the derivation of equation 1 in Karplus and Diederichs [5] we have

$${\mathrm{CC}}_{1∕2}=\frac{{\sigma }_{\tau }^2}{{\sigma }_{\tau }^2+{\sigma }_{\epsilon }^2}=\frac{<I^2>-{<I>}^2}{<I^2>-{<I>}^2+{\sigma }_{\epsilon }^2}$$

where σ_ε denotes the mean error within a half-dataset. Introducing q² 〈I²〉/〈I²〉 – 〈I〉², we can write

$${\mathrm{CC}}_{1∕2}=\frac{1}{(1+q^2{\sigma }_{\epsilon }^2∕{\langle I\rangle }^2)}$$

At this point, we note that for acentric reflections following a Wilson distribution q² = 2 and ${\sigma }_{\epsilon }^2=2{\langle \sigma \rangle }^2$, which lets us write CC_1/2 for acentric reflections as

$${\mathrm{CC}}_{1∕2}^{acentric}=\frac{1}{[1+4∕{(\langle I\rangle ∕\langle \sigma \rangle )}^2]}$$

Then, since 〈I/σ〉 is close to 〈I〉/〈σ〉, in particular at high resolution where σ is approximately the same for all reflections, it is a reasonable approximation that

$${\mathrm{CC}}_{1∕2}\sim \frac{1}{[1+4∕{\langle I∕\sigma \rangle }_{mrgd}^2]}$$

Two factors that may shift this relationship are (1) that real data may include some centric reflections, for which q² = 3/2, changing the 4 in the above equations to a 3, and (2) that at very low 〈I/σ〉_mrgd the measured intensities are dominated by Gaussian noise and will not follow Wilson statistics and q² = 1 applies, which changes the 4 in the above equations to a 2. Thus in resolution shells having weak data, the CC_1/2 versus 〈I/σ〉_mrgd relationship should be fall between the extreme cases of:

$${\mathrm{CC}}_{1∕2}\sim \frac{1}{[1+4∕{\langle I∕\sigma \rangle }_{mrgd}^2]}and{\mathrm{CC}}_{1∕2}\sim \frac{1}{[1+2∕{\langle I∕\sigma \rangle }_{mrgd}^2]}$$

And tending to be closer to the first equation for data with ${\langle I∕\sigma \rangle }_{mrgd}^2$ ≥1 for which Wilson statistics are still relevant. As seen in the figure, this implies that for accurately estimated σ_mrgd values, CC_1/2 between ~0.1 and ~0.4 can be roughly equated to 〈I/σ〉_mrgd values between ~0.5 and ~1.5.

Figure legend: The two curves define limiting relationships for how CC_1/2 relates to 〈I〉/〈σ〉 for low signal data. The upper curve is only valid if Gaussian noise dominates the data; so the lower curve should be considered the more relevant above 〈I〉/〈σ〉 ~0.5. The pale blue lines highlight the corresponding values for 〈I〉/〈σ〉 of 0.5, 1.0, 1.5 and 2.0.

CC* is mathematically derived from CC_1/2 using the relationship CC* = [2 CC_1/2/(1 + CC_1/2)]^1/2 and provides an estimate of the CC that would be obtained between the final merged data set and the unknown true values that they are representing [5••]. This brings a new ability to compare data and model quality on the same scale because one can compare CC* with a CC between $F_{\mathrm{calc}}^2$ and $F_{\mathrm{obs}}^2$ (i.e. CC_work or CC_free) to discover even without cross-validation if overfitting has occurred during refinement [5••]. The calculations have been built into the PHENIX system [9], and already been used in some reports (e.g. [10•, 11••]). While how to best use this information in guiding and validating refinements is not yet clear, it provides a welcome replacement for the practice of comparing refinement R-factors with data reduction R-factors (e.g. [12•]) that is not correct [5••].

In our view (Table 1), no indicators other than CC_1/2 should influence the high-resolution cutoff decisions for data processing. As noted (Box 1), the 〈I/σ〉_mrgd statistic (we use subscripts for the two different 〈I/σ〉 values to avoid confusion and emphasize their distinct information content) is related to CC_1/2, and so is in principle equally useful for defining a cutoff. However, it is not as useful in practice because the 〈I/σ〉_mrgd values obtained during data reduction may not be accurate since they depend on the error model and parameterization used and additional factors such as outlier rejection algorithms and weighting of observations. This causes some irreproducibility across programs as was documented in a report showing that data processed by HKL2000, MOSFLM, and XDS yielded at a certain resolution 〈I/σ〉_mrgd values of 2.7, 3.5, and 5.2, respectively [13].

To illustrate why the other common indicators (besides CC_1/2 and 〈I/σ〉_mrgd) are not useful for guiding the high resolution cutoff decision, we offer the following gedanken experiment. Consider five idealized datasets without radiation damage or systematic errors: ‘Big’ with multiplicity = 2 from a rare large crystal; ‘Tiny’ from a readily grown 100-fold smaller microcrystal; ‘T100’ resulting from the merging of 100 equivalent microcrystal datasets; ‘Big + T100’ resulting from the merging of Big and T100; and ‘Big2’ resulting from the merging of Big with an equivalent dataset from a second large crystal.

Assuming 〈I/σ〉_ind = 2 in the highest resolution bin of Big, and that R_meas ~ 0.8/〈I/σ〉_ind) [4••], that CC_1/2 is related to 〈I/σ〉_mrgd as shown in Box 1, and that n-fold repetition of a measurement reduces its σ by √n, we can generate the following idealized high resolution bin statistics for the five datasets:

Dataset	Big	Tiny	T100	Big + T100	Big2
Multiplicity	2	2	200	202	4
〈I/σ〉ind	2.0	0.2	0.2	0.22	2.0
Rmerge	28%	280%	399%	395%	35%
Rmeas	40%	400%	400%	396%	40%
Rpim	28%	280%	28%	28%	20%
〈I/σ〉mrgd	2.8	0.28	2.8	4.0	4.0
CC1/2	0.66	0.04	0.66	0.80	0.80

Readily apparent is that according to CC_1/2 and 〈I/σ〉_mrgd, Big and T100 are of equivalent quality as are Big + T100 and Big2. The huge differences in the values of 〈I/σ〉_ind, R_merge, and R_meas within these pairs shows why indicators of the precision of individual measurements should never be used for guiding cutoff decisions. Furthermore, a comparison of Big + T100 vs. Big2 shows that even R_pim does not reflect their equivalence. This is because when data of different precision are merged, R_pim and all R-factor based indicators lose relevance because each reflection is weighted equally rather than (as for 〈I/σ〉_mrgd) according to its reliability. The impact of this is even more dramatically seen in the 10-fold different R_meas values of Big + T100 vs. Big2. Also worth noting is that T100 has quite respectable signal in the highest resolution bin even though Tiny does not, emphasizing that high resolution cutoff decisions should only be made after all relevant data have been merged. Finally, the large increase in R_merge for Tiny vs. T100 reveals how tremendously misleading is the overestimation by R_merge of precision at low multiplicity [14,15] — making it appear that the datasets merged in T100 were not isomorphous and should not be merged, even while R_meas correctly indicates the merged data were isomorphous. This is why we recommend (Table 1) that R_merge never be used.

Further, we suggest that publication standards be changed to require low and high resolution shell data quality statistics rather than ‘overall’ and high resolution shell values (Table 1). It has been shown that ‘overall’ statistics are weighted by multiplicity [14], and so depending on how multiplicity varies with resolution, the ‘overall’ number can take on any value from that of the strongest data to that of the weakest data. Selecting a more generous high resolution cutoff (e.g. [11••, 16•]) and/or increasing the multiplicity of the high resolution data (e.g. [14]), makes the ‘overall’ statistics become worse even though the resulting data are better.

Finally, one uncommon indicator we recommend be reported by data reduction programs (but not in structure reports) is 〈I/σ〉_asymptotic or ‘ISa’ ([17]; Table 1). Importantly, 1/ISa provides an estimate of the level of experiment/hardware related systematic (i.e. fractional) error in the data set that limits the precision of strong reflections. For instance, an ISa of near 30, about as high as can be achieved for CCD detector data sets [4••], indicates about a 3.3% (i.e. ~1/30) systematic error. ISa thus has utility as a diagnostic for guiding efforts to improve experimental setups as well as data processing.

Multiplicity can powerfully enhance measurable signal through decreasing noise

A crucial distinction to make regarding data quality is the difference between the level of signal that is measured in a particular data set versus the level of signal that could in principle be measured from that sample (e.g. Figure 1a). Given only random errors, the standard error σ in a measurement is reduced by √n if the measurement is repeated n times. The utility of high multiplicity data sets from single crystals to improve the accuracy of anomalous signal measurements and enable phasing has been powerfully demonstrated many times (e.g. [18,19,20,21]), and it has been recognized that for success sufficient data must be collected before radiation decay degrades the signal (e.g. Figure 1a; [22,23]). Furthermore, theory and practice agree that for a given total crystal exposure time, fractional errors associated with data collection can be minimized and better data produced by collecting higher multiplicity data using shorter exposures [24].

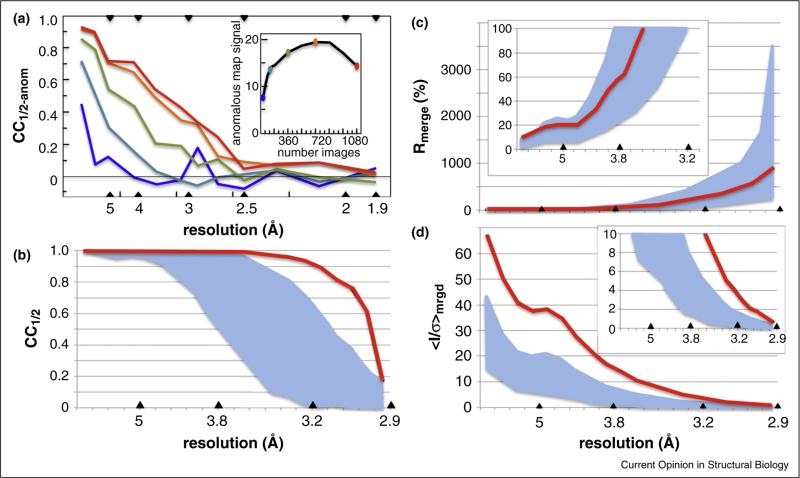
Figure 1.

Averaging multiple measurements can substantially enhance data quality. (a) CC_anom is plotted as a function of resolution for a data set of 1080 18 images in a sulfur-SAD phasing case study [23]. Statistics for data merged from 30 (blue), 120 (cyan), 360 (green), 720 (orange), and 1080 (red) images are shown. Based on 30 images (3.5 fold multiplicity), there is no apparent anomalous signal beyond 4 Å, but with 720 images (75-fold multiplicity) the apparent signal extends beyond 3 Å resolution. Inset shows the quality of the anomalous difference map (maximal r_rms) increases substantially and then, as radiation damage systematically alters the structure, decreases even while CC_anom stays high. (b–d) Behavior of CC_1/2, Rmerge, and 〈I/σ〉_mrgd as a function of resolution for individual crystals (breadth of values indicated by cyan swaths) and for a set of data merged from 18 crystals (red traces) and successfully used for sulfur-SAD phasing and refinement at 2.9 Å resolution [11••]. Insets show close-ups of the low or high resolution regions. According to the authors, the best individual crystal would only have been useful to ca. 3.2 Å resolution, and by the panel C inset, the averaged data would have been truncated at near 3.8 Å based on an R_merge ~ 60% cutoff criterion.

An important recent advance has been the (re)-discovery that high multiplicity can improve signal strength, even for anomalous signal, through combining of data from multiple crystals [25••, 26•, 27] as long as the individual data sets are tested for isomorphism. Building on this work, Akey et al. ([11••]) merged data from 18 crystals to generate anomalous data with 50-fold multiplicity and data for refinement with 100-fold multiplicity thus enabling phasing and a higher resolution refinement than could be accomplished using data from any single crystal. These data illustrate how during merging, the final R_meas becomes roughly the average of the individual R_meas values but the final 〈I/σ〉_mrgd and CC_1/2 values can improve substantially (Figure 1b–d). Recent serial femtosecond crystallography (SFX) results, for which each crystal only provides a single image [28], provide further examples of the power of enhancing data quality through merging data from multiple crystals. In a time-resolved SFX study of the photoactive yellow protein, to obtain sufficient quality difference electron density maps, the workers aimed for a multiplicity of ~1500 in the highest resolution bin [29•].

Evidences that data beyond R_meas ~ 60% and〈I/σ〉_mrgd ~ 2 contain useful information

Until recently, a common and recommended practice has been truncating data at the resolution at which R_meas remains below ~60% and 〈I/σ〉_mrgd is ~2 or higher ([30] and Figure S1 of [5••]). Our report [5••] introducing CC_1/2 also introduced paired refinement tests and showed that, for our test cases, including data out to a CC_1/2 value of between 0.1 and 0.2 led to an improved refined model even though the data at that resolution had R_meas ~ 450% and 〈I/σ〉_mrgd ~ 0.3. We also showed that these weak data improved the quality of difference maps (see Figure S2 of [5••]). This reinforced earlier evidence for the value in refinement of data having 〈I/σ〉_mrgd ~ 0.5 [31,32]. The damage caused by using an R_meas ~ 60% cutoff criterion grows with increasing multiplicity, because the excluded data have a higher and higher 〈I/σ〉_mrgd. For instance, for the 100-fold multiplicity data set of Akey et al. [11••], an R_meas ~ 60% cutoff corresponds to ~3.7Å resolution at which 〈I/σ〉_mrgd is ~ 12 (Figure 2c and d). In another study, extending the resolution from 2.85 Å (R_meas ~ 60%) to 2.1 Å (R_meas ~ 680%; CC_1/2 = 0.22, 〈I/σ〉_mrgd = 0.9) improved the MR-Rosetta [33] solution to a challenging molecular replacement problem from R_free ~ 40% to R_free ~ 31% [34].

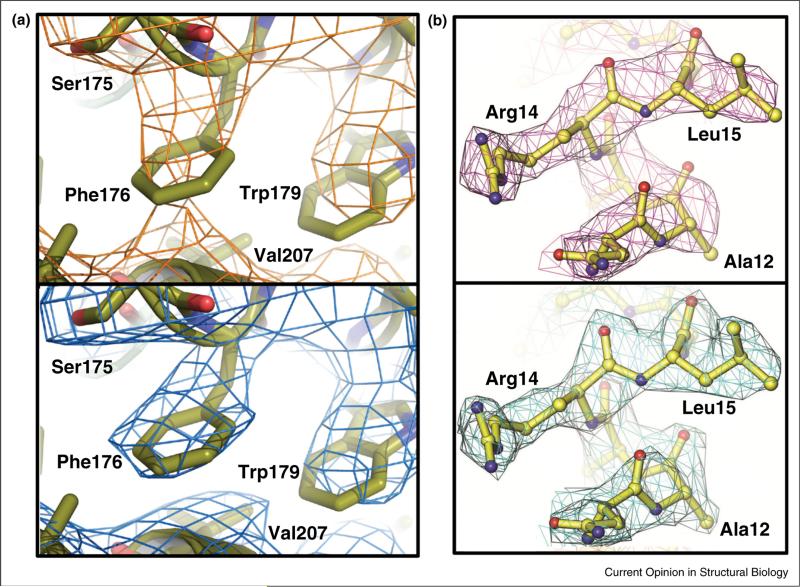
Figure 2.

Examples of tangible electron density map improvement enabled by extending resolution cutoffs. (a) Comparison of the 2Fo–Fc electron density (contoured at 1 ρ_rms) for a region of the prokaryotic sodium channel pore using an 〈I/σ〉_mrgd ~2 cutoff (R_pim = 47%, 〈I/σ〉_mrgd = 1.9, CC_1/2 = 0.78) 4.0 Å resolution (upper panel) versus a more generous CC_1/2 ~ 0.1 based cutoff (R_pim = 213%, 〈I/σ〉_mrgd = 0.3, CC_1/2 = 0.14) 3.46 Å resolution (lower panel). The 4 Å resolution cutoff was already somewhat generous as the R_pim of 47% with a multiplicity of 12 would be expected to correspond to an R_meas value of above 150% (47%*√12). Used with permission from Figure S1 of [48•]. (b). Comparison of the 2Fo–Fc electron density (contoured at 1 ρ_rms) for a region of the E. coli YfbU protein using for the phase extension a fairly conventional cutoff (R_meas = 77%, 〈I/σ〉_mrgd = 3.5, CC_1/2 = 0.85) of 3.1Å resolution (upper panel) versus a more generous 〈I/σ〉_mrgd ~ 0.5 or CC_1/2 ~ 0.1 cutoff R_meas = 302%, 〈I/σ〉_mrgd = 0.5, CC_1/2 = 0.14) of 2.5 Å resolution (lower panel). The additional weak data did not just extend the resolution of the map, but improved the quality of the phases obtained at 3.1 Å resolution. Images used with permission from the International Union of Crystallography from Figure 3 of [40••] (http://dx.doi.org/10.1107/S1399004714005318).

In terms of the value of using data beyond 〈I/σ〉_mrgd ~ 2, one set of systematic refinement tests showed small improvements with no negative impacts by including data out to CC_1/2 between 0.2 and 0.4 corresponding to 〈I/σ〉_mrgd between 0.5 and 1.5 [35••]. Interestingly this correspondence between 〈I/σ〉_mrgd and CC_1/2 roughly matches that expected from theory (Box 1). Another study using distinct tests similarly concluded that useful information is present in reflections out to CC_1/2 between 0.1 and 0.5, and that extending the resolution by ~0.2 Å beyond an 〈I/σ〉_mrgd ~ 2 cutoff provided a marginal benefit and no adverse effects [36••]. A third study showed that the practice of selectively removing weak reflections within a given resolution bin introduced systematic errors into the data and leads to worse refined models [37••].

Also, many analyses are now using the more generous CC_1/2-based cutoffs (with high resolution R_meas values as high as ~1000% and 〈I/σ〉_mrgd values as low as ~0.3) and authors comment on the benefits (e.g. [11••, 16•,38,39•]). One striking example is shown in Figure 2a. Weak data have further been shown to improve the phasing of a crystal with 16-fold non-crystallographic symmetry. Phase extension and automated modeling using data truncated per conventional criteria at 3.1 Å resolution stalled at R_free ~ 35%, whereas using an extended 2.5 Å resolution cutoff produced an excellent model with R_free ~ 24.5% and improved electron density maps (Figure 2b; [40••]). Although the signal per reflection is rather weak for the extended data, the tangible impact on phase extension, refinement, and map quality can be rationalized in that the numbers of added reflections are very large, in some cases doubling the data available and they help to minimize series termination error. Wang [41•] describes a perverse incentive researchers have to truncate datasets to obtain more attractive R/R_free values for any given model, and proposes an intriguing modified Rfactor that emphasizes the value of using more data.

As there is no single ‘correct’ cutoff for every case, using paired refinements [5••] provides a controlled approach to decide for any dataset what resolution cutoff yields the best model. And the PDB-REDO server is now available as a refinement tool that includes a paired refinement option [42•]. Another conservative approach to the cutoff question is to process one's data out to CC_1/2 ~ 0.1, but carry out initial refinements using a self-selected conservative resolution limit until the residual Fo–Fc difference map has no interpretable peaks. Then, one can recalculate the difference map using an extended resolution cutoff, and any interpretable peaks provide evidence of tangible information brought by the newly included weak data. In one project for which this was done, the extended difference map was highly informative, and further refinement improved our 2.6 Å resolution ‘final’ model with R/R_free = 18.9/23.2% to a lower R/R_free = 17.4/22.0% even at the extended 2.3 Å resolution [43•].

Conclusions and outlook

When we pointed out the flawed multiplicity dependence of R_merge and recommended making resolution cutoff decisions based on precision of the data after merging [14], we predicted that this ‘should stimulate a shift in data collection strategies, so that the current bias toward using single crystals for complete data sets whenever possible will shift to favor multiple crystal data sets which have increased multiplicity and hence more accurate reduced structure factors.’ The continued use of R_merge (or even R_meas) to define cutoffs hindered this from occurring, but now, with the introduction of CC_1/2 as a statistically robust indicator of the precision of merged data and with definitive evidence that the inclusion of weak data improves models and that merging data from multiple crystals can be highly beneficial, practices are changing in this direction. Increasing multiplicity is a reasonable strategy to pursue not just to enhance anomalous signals for phasing, but also for obtaining the best high resolution data set for refinement. Important to note, though, is increasing the signal-to-noise of high resolution data occurs by decreasing noise rather than increasing the intensity, so it does not increase the relative contribution of these structure factors to the electron density map. Also worth noting is that obtaining the best high resolution data does not guarantee the best model will be obtained; that depends on care being taken by the crystallographer during model building and refinement.

There obviously need to be changes to what journals require for Table 1 statistics, and we think a useful set would simply be the high resolution bin CC_1/2 and number of reflections it is based on (since the low resolution bin CC_1/2 is always ~1 and not very informative) and 〈I/σ〉_mrgd in the low and high resolution bins, and potentially (for calibration with the past) the resolution at which 〈I/σ〉_mrgd ~ 2. CC_1/2 also needs to be added to the PDB deposition form. In terms of what this does to the meaning of resolution, we are in agreement with Phil Evans [44] that the nominal resolution of a structure has always referred to which reflections are included in the Fourier summation rather than guaranteeing a certain quality in terms of the apparent resolution of the resulting electron density maps.

We also support the ongoing efforts to archive raw diffraction data to maximize the potential benefit of research funds invested by providing maximal flexibility for correcting mistakes and improving existing structures as technologies improve [45–47]. In the meantime, we encourage users to process data out to CC_1/2 ~ 0.1 (after merging of crystals!) even if one is not planning to use it, and to deposit unmerged intensity values together with the merged values. While much is still to be learned about how to obtain the best data, we hope the examples provided here will help crystallographers collect better data and determine better structures.

Highlights.

• Common data quality indicators grouped as primary, secondary, or wrong/misleading.

• A gedanken experiment reveals shortcomings of some common indicators.

• Reviews evidence that massive multiplicity improves data for phasing and refinement.

• Cites examples showing value of extending data past conventional resolution cutoffs.

• A derived relationship between CC_1/2 and 〈I/σ〉_mrgd makes CC_1/2 more intuitive.