Abstract
Transient electronic and vibrational absorption spectroscopy unravel the mechanisms and dynamics of bimolecular reactions of CN radicals with acetone in deuterated chloroform solutions. The CN radicals are produced by ultrafast ultraviolet photolysis of dissolved ICN. Two reactive forms of CN radicals are distinguished by their electronic absorption bands: “free” (uncomplexed) CN radicals, and “solvated” CN radicals that are complexed with solvent molecules. The lifetimes of the free CN radicals are limited to a few picoseconds following their photolytic production because of geminate recombination to ICN and INC, complexation with CDCl3 molecules, and reaction with acetone. The acetone reaction occurs with a rate coefficient of (8.0 ± 0.5) × 1010 M–1 s–1 and transient vibrational spectra in the C=N and C=O stretching regions reveal that both the nascent HCN and 2-oxopropyl (CH3C(O)CH2) radical products are vibrationally excited. The rate coefficient for the reaction of solvated CN with acetone is 40 times slower than for free CN, with a rate coefficient of (2.0 ± 0.9) × 109 M–1 s–1 obtained from the rise in the HCN product v1(C=N stretch) IR absorption band. Evidence is also presented for CN complexes with acetone that are more strongly bound than the CN–CDCl3 complexes because of CN interactions with the carbonyl group. The rates of reactions of these more strongly associated radicals are slower still.
I. Introduction
Reactions in which a cyano (CN) radical abstracts a hydrogen atom from an organic molecule present an unusual opportunity to contrast chemical reaction dynamics under isolated conditions and in the presence of a liquid solvent.1,2 These reactions are exothermic, typically releasing more than 100 kJ mol–1; in contrast to the liquid phase where this energy rapidly transfers to the surrounding solvent, the energy in low-pressure gas-phase reactions can only be distributed among the translational and internal degrees of freedom of the two products. The potential energy surfaces for reactions of the type summarized by eq 1, with R = H, CH3, or other alkyl groups,
| 1 |
have early and low energy barriers, with a flat angular dependence at the transition state.3 Consequently, the energy released by the reaction excites the HCN product mode-specifically in the C–H stretching (v3) and bending (v2) vibrations, as confirmed by infrared (IR) emission and absorption spectroscopy measurements,4−9 as well as trajectory calculations.3 The rates and mechanisms of reactions of cyano radicals with hydrocarbons have been extensively studied at low pressures and temperatures because of their importance in the chemistry of the atmospheres of Titan, Triton, and Pluto.10 Crossed molecular beam studies of CN + alkane reactions, in which the alkyl radical products were ionized without quantum-state specificity, showed that approximately 80–85% of the energy of reaction is deposited in internal modes of the products, which are scattered with angular distributions that indicate direct dynamics.11 Direct H atom abstraction also competes with addition and addition–elimination pathways in reactions of CN radicals with alkenes.12−15
The energy deposited in HCN bending and C–H stretching vibrations persists for reactions in liquid solvents such as chloroform and dichloromethane, although the degree of vibrational excitation is somewhat reduced.1,2,16−19 The reaction mechanism in solution may be modified by factors such as formation of complexes between the CN radical and a solvent molecule,20,21 or coupling of the reaction degrees of freedom with the solvent bath.22 Nevertheless, any shifts in the position of the transition state must be modest, and any solute–solvent couplings must be weak for the gas-phase-like dynamics to persist to such an extent in solution16—at least, for these types of organic solvent.
Velocity map imaging studies of various exothermic bimolecular reactions in the gas phase have shown that measurement of the energy disposal to both products of reaction carries additional insights beyond what can be learned by studying only one of the products.23 These experiments used molecular beam techniques to ensure isolated collisions, and under favorable circumstances could map out the correlated vibrational energy content of both reaction products.24 The correlations were deduced from measurement of kinetic energy release distributions of one product in a specific vibrational quantum state, and application of momentum and energy conservation arguments. No corresponding methodology has yet been developed to observe correlated product energies for reactions in solution, but both products can be independently probed to determine their internal energy content. We illustrate this idea in the current report for the case of the reaction of CN radicals with acetone, eq 2,
| 2 |
in deuterated chloroform (CDCl3) solutions. We used time-resolved vibrational absorption spectroscopy (TVAS) in the infrared region with picosecond time resolution to observe absorption features of the HCN and 2-oxopropyl (or acetonyl) radical (CH3C(O)CH2) products and present evidence that both are vibrationally excited at their point of formation. This excess vibrational energy couples to the solvent bath, flowing from the product molecules on time scales of tens to hundreds of picoseconds. Time-resolved electronic absorption spectroscopy (TEAS) provides complementary information on the interactions of the CN radicals with the solvent and their rates of reactive loss.
Building on pioneering work by Hochstrasser and co-workers,17 Crowther et al. studied the rates of CN radical reactions in solution by TEAS and TVAS.20,21 Their experiments were conducted in CH2Cl2 and CHCl3 solutions, and the proposal was made that CN forms linear and bridged complexes with these chlorinated solvents. In these complexes, the maximum in the CN (B2Σ+ ← X2Σ+) absorption band shifts to shorter wavelength and the band broadens compared to the gas phase. The reactions of CN radicals with organic cosolutes were determined to have bimolecular rate coefficients smaller than the corresponding gas-phase reactions because of the stabilizing effect of the CN–solvent complex. In the current work, we introduce acetone to an ICN/CDCl3 solution, and advances in vibrational probing highlight additional intermolecular interactions between the CN radical and the carbonyl group in the ketone. The results presented here provide evidence for contributions to the observed reactions in solution from both CN–CDCl3 and CN–acetone complexes.
II. Experimental Details
The time-resolved transient-absorption experiments were performed using the ULTRA Facility at the Rutherford Appleton Laboratory.25 The instrumentation has been described previously,16 and a brief summary is provided here of the details of particular relevance to the current study.
Samples were prepared with 0.36 M ICN (Acros Scientific, > 97.5%) in anhydrous CDCl3 (Sigma-Aldrich, 99.96 atom %) or CHCl3 (Sigma-Aldrich, > 99.8%) with acetone (Sigma-Aldrich, ≥ 99.9%) concentrations up to 1.5 M. Solutions were kept at room temperature (294 K) in brown-glass volumetric flasks. All glassware was stored in a drying oven when not in use, and water contamination was minimized by drying the acetone and chloroform over 3 Å molecular sieves. The flow cells used for the experiment were assembled with 0.2 mm PTFE spacers between CaF2 windows and sealed using Kalrez O-rings, which are chemically compatible with acetone and chloroform. Using deuterated chloroform helps isolate any observed HCN as a product of hydrogen abstraction by CN from acetone. The IR spectrum of CDCl3 does not contain any strong spectral features in the C=O and C=N stretching regions that might interfere with transient IR spectroscopy measurements.
ICN was photodissociated at a wavelength of 267 nm by a 1 μJ laser pulse of 50 fs duration and products were probed over time delays of 1–2500 ps by TEAS using a white light continuum (310–700 nm) and by TVAS using tunable broadband (∼500 cm–1 bandwidth) mid-IR light pulses. In both cases, the transmitted probe pulses were dispersed by a grating onto an array detector (512 pixel for TEAS, 128 pixel for TVAS) to measure changes in optical density induced by the UV excitation pulse. Experiments were also conducted on solutions of acetone in CDCl3 without addition of ICN to identify transient features associated with acetone photochemistry that we attribute to triplet states. Samples of CDCl3 without ICN and acetone showed only a weak response in TEAS under our experimental conditions.26
III. Computational Details
Irradiation of a solution of ICN and acetone in CDCl3 at 267 nm induces both ICN dissociation and acetone photochemistry, followed by various possible radical reactions. Multiple intermediate and product species might therefore contribute to the TEAS and TVAS spectra. Hence, calculations were carried out to characterize the harmonic vibrational frequencies and electronic excitations of possible reaction intermediates, reaction products, and acetone photofragments to guide the assignments of bands in the TEAS and TVAS spectra.
DFT calculations of harmonic vibrational frequencies were performed in Gaussian 09 using the B3LYP functional with the 6-311++G(d,p) basis set.27 This method was chosen for its computational efficiency and because of its reliability of calculation of energetics of first row compounds. The diffuse functions were necessary to capture the interactions between π-orbitals in CN radicals and acetone. A polarizable continuum model was applied to mimic chloroform solvent effects, as implemented in Gaussian 09.27 The calculated vibrational band frequencies were offset from their experimental values, so an empirical linear correction factor, fitted to be 0.948 from comparison with an FTIR spectrum of 1.0 M acetone in CDCl3, was applied to all computed frequencies. The calculated wavenumbers of bands that might contribute to the TVAS spectra in the carbonyl stretching region are used as a guide to assignment of spectral features, with the caveat that the continuum model may not capture all solvent effects, such as formation of solute–solvent complexes that require atomistic descriptions of the solvent.
The enthalpy changes (ΔrH0K) associated with H-abstraction from acetone reaction 2 were also computed in Gaussian using various theoretical methods to quantify the reaction exothermicity and to benchmark more computationally efficient techniques against CBS-QB3 calculations.28−31 The results of these calculations are reported in the Supporting Information. The CBS-QB3 calculations predict ΔrH0K = −125.0 kJ mol–1 for the gas-phase reaction, and mimicking the effects of a chloroform solvent using a polarizable continuum model modifies this computed enthalpy change to −134.7 kJ mol–1. For comparison, DFT calculations at the B3LYP/6-31++G(d,p) level incorporating the same treatment of the chloroform give ΔrH0K = −153.5 kJ mol–1 for reaction 2. The similarly exothermic H atom abstraction reactions of CN with propane and cyclohexane were previously shown to be barrierless,3 and we therefore expect facile reaction of CN with acetone to make HCN.
Our group has recently shown that molecular dynamics simulations of CN reactions are helpful as we build atomistic interpretations of the liquid-phase reaction mechanisms.3,18,32 In a computational study of the dynamics of CN radical reactions with propane and cyclohexane in the gas phase and in solution, Glowacki et al. computed structures and energies using DFT with the BB1K functional, modified to have 56% Hartree–Fock exchange.3,32 Trajectory calculations presented in the current study for the CN + acetone reaction, however, sought only qualitative mechanistic insights, so a simpler treatment of the energetics was used. Direct dynamics trajectory calculations for isolated collisions were performed using the VENUS program33−35 with local gradients extracted from NWChem electronic structure calculations.34,36 Trajectories were propagated using potential energy gradients computed by the DFT/B3LYP method with a 6-31++G(d,p) basis set. The CN radicals were initially provided with 2.4 kJ mol–1 of translational energy (corresponding to kBT) and were directed at the acetone with randomly selected initial orientations and with zero-point vibrational energy but no rotational energy. Impact parameters were fixed to values of 0, 1, 2, 4, and 5 Å. Time-step sizes of 0.2 fs were used, and propagation was maintained for up to 1 ps.
IV. Results
The focus of this study is the reaction of CN radicals with acetone in solution in CDCl3. Acetone was chosen as the coreagent because the strong infrared absorption from the C=O stretching mode facilitates detection of possible organic radical reaction products such as 2-oxopropyl, CH3C(O)CH2. Ultraviolet photolysis of ICN dissolved in a solution of acetone in CDCl3 was used to initiate the reaction. The 267 nm wavelength photolysis liberates CN radicals in less than 50 fs,37 and TEAS in the near-UV and visible regions revealed the production of CN radicals, their association with solvent molecules, and their reactive removal. The HCN and 2-oxopropyl products were monitored by TRVS using broadband ultrafast IR pulses.
Acetone absorbs weakly at 267 nm (contributing an absorbance A ≤ 1 for most of our samples) and the photoexcited acetone can undergo Norrish type I photochemistry by cleavage of a C–C bond, or vibrational quenching of the photoexcited state can populate low vibrational levels of the S1 and T1 states of acetone with long lifetimes. TEAS and TVAS of acetone/CDCl3 solutions were therefore used to characterize any contributions by acetone photochemistry to the spectra obtained for ICN/acetone/CDCl3 solutions. Ultraviolet photolysis of ICN in organic solvents and geminate recombination to ICN and INC have been the subject of several previous experimental and computational studies;18,19,37−43 these processes are not discussed here, but both ICN and INC bands appear in our TVAS spectra, as shown below.
This section considers the information obtained from the TEAS experiments and then turns to the TVAS results. Spectral assignments and dynamical deductions are guided by electronic structure calculations of electronic and vibrational band frequencies. We turn first, however, to discuss the outcomes of the trajectory calculations because the insights they provide influence the interpretation of the TEAS and TVAS data.
IV.a. Mechanisms in Trajectory Simulations
The results of our trajectory simulations, which do not include solvent effects, can be separated into the two classes of reaction pathways represented pictorially in Figure 1. Direct abstraction of a hydrogen atom (Figure 1a) appears to be favored by approach of the CN from the side opposite to the carbonyl group. This orientation prevents the CN radical from experiencing an attractive interaction with the carbonyl orbitals. On the other hand, approach of the CN toward the carbonyl group (Figure 1b) results in three types of trajectories; in all cases, the CN is first attracted toward a potential well corresponding to a CN–acetone complex, which we computed to be stabilized by 3600 cm–1. The trajectory may then redistribute the energy of the collision among the internal modes of acetone so that the complex survives longer than the 1 ps simulation time. Alternatively, the CN radical can experience large-amplitude motions on a flat area of the potential surrounding the carbonyl group, after which the two species separate or the CN abstracts a hydrogen atom. The competition between direct abstraction and this addition–elimination pathways is reminiscent of the mechanisms for reactions of gas-phase Cl atoms with propene and other alkenes.44−46 The direct-abstraction mechanism generates simulated HCN products that are internally hot, with up to 3 quanta of excitation in the C–H stretching mode and 8 quanta in the bending vibration. In our measurements, the solvent may quench the energy required to escape from potential energy wells associated with structures like the CN–acetone complex, trapping these solute–solvent adducts and slowing, or preventing further reaction.
Figure 1.
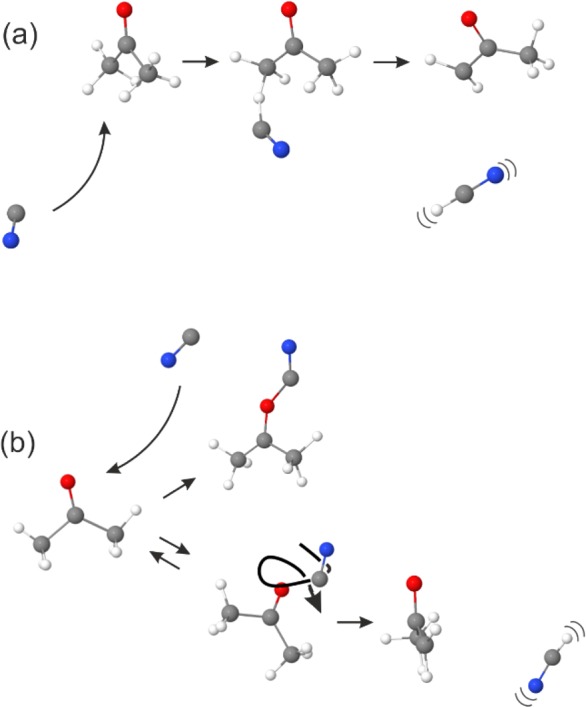
Schematic diagram of the classes of trajectories observed in simulations of isolated collisions of CN radicals with acetone. (a) Direct abstraction pathway making vibrationally hot HCN. (b) Pathways initiated by C=N–carbonyl group interactions, leading to a CN–acetone complex, or large amplitude CN radical motion followed by CN separation from acetone or H atom abstraction.
IV.b. TEAS of Solutions of ICN and Acetone in CDCl3 Following 267 nm Excitation
The B ← X electronic band of the CN radical centered at 389 nm provides a distinctive signature of this species in TEAS spectra. This band evolves with time as the CN radicals form complexes with solvent molecules, and the intensities of transient bands associated with these solvent complexes decay with increasing time delay because of reactive loss of CN radicals. Figure 2 illustrates this behavior following 267 nm excitation of a 0.36 M ICN/1.0 M acetone solution in CDCl3. Decomposition of one illustrative transient spectrum, at a time delay of 2.5 ps, shows the constituent absorptions assigned to uncomplexed (“free”) CN radicals and solvent-complexed (“solvated”) CN radicals, and a long-wavelength feature attributed to I*(2P1/2)-solvent charge transfer (CT).37 The corresponding CT band of ground-state I(2P3/2) atoms underlies the CN–radical features and cannot be distinguished from them but will grow as I* atoms electronically quench to ground-state I. TEAS spectra of separate solutions of acetone in CDCl3 and ICN in CDCl3 are shown in Supporting Information. The spectra support these assignments and identify other contributors; in particular, a transient absorption band assigned to the T1 state of acetone is observed at wavelengths below 400 nm. This triplet state has a lifetime >2 ns in solution in CDCl347 but may be more rapidly quenched in the presence of iodine atoms. Under the conditions of our experiment, the acetone T1 band contributes about 20% of the intensity of spectral features attributed to CN radicals and cannot reliably be separated from the solvated-CN bands.
Figure 2.
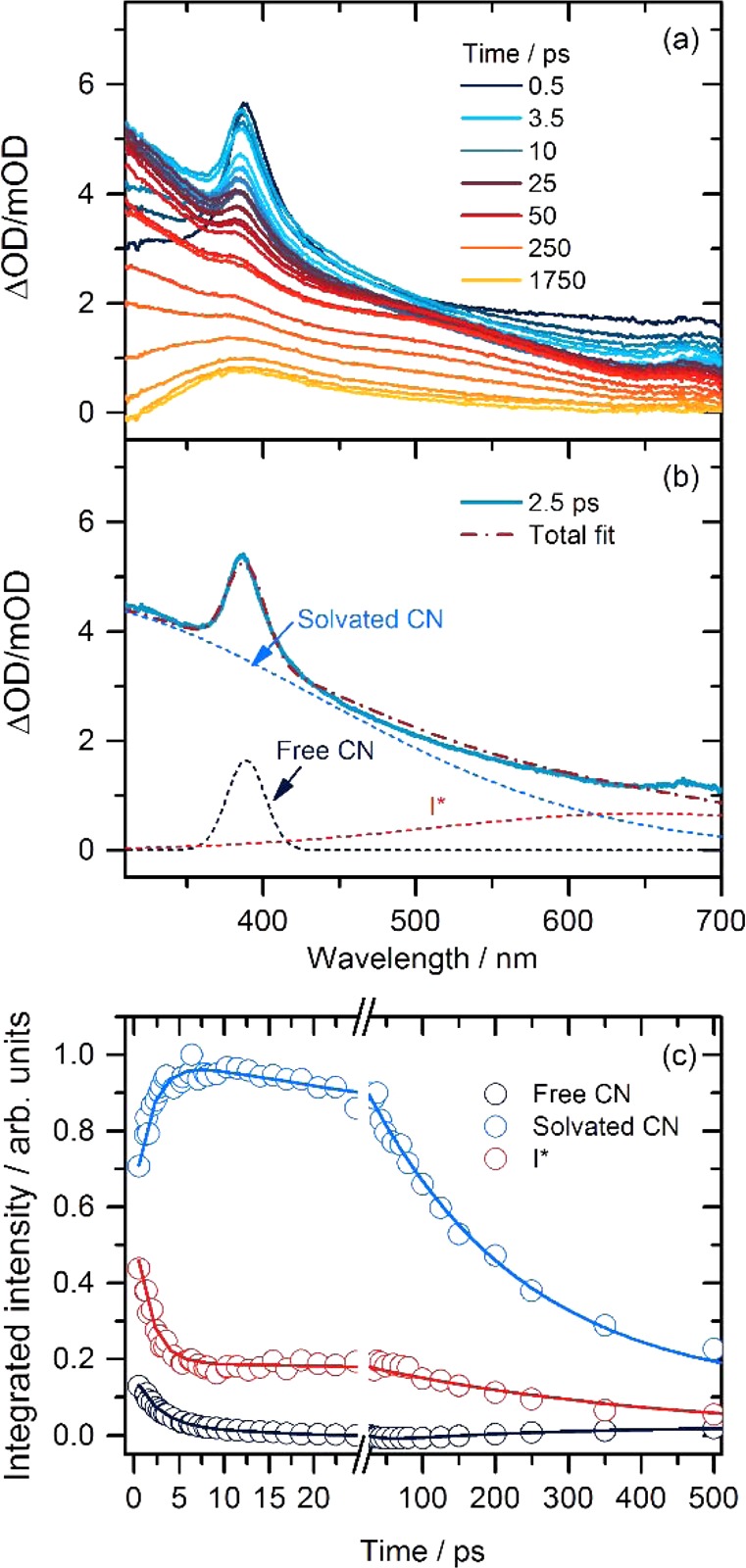
Transient electronic absorption spectra of ICN/1.0 M acetone/CDCl3 solutions and the spectral decomposition into component absorptions. (a) TEAS spectra following 267 nm excitation for times delays from 0 to 1750 ps. (b) Example of decomposition of the spectrum obtained at a time delay of 2.5 ps into its constituent parts. (c) Time dependence of the free and complexed CN and the I* absorption bands obtained from decomposition of TEAS spectra. The solid lines are biexponential fits with time constants and amplitudes reported in Table 1.
Inspection of Figure 2a shows a weak absorption that remains at the longest measurement time of 1.75 ns. This feature is absent without acetone, but the band shape is inconsistent with both the T1 absorption band of acetone, and with CN–CDCl3 complexes. Instead, it may correspond to surviving CN radicals bound to CDCl3 or the carbonyl group of acetone. The latter interpretation is encouraged by TEAS spectroscopy of an ICN solution in acetone, in which a band similar in shape to the long-time feature in Figure 2a was observed. An example is shown in the Supporting Information. This band was not separately fitted in our spectral decomposition because of its similarity to the free CN band; instead, it contributes an apparent growth to the free CN band with a time constant of 263 ± 22 ps.
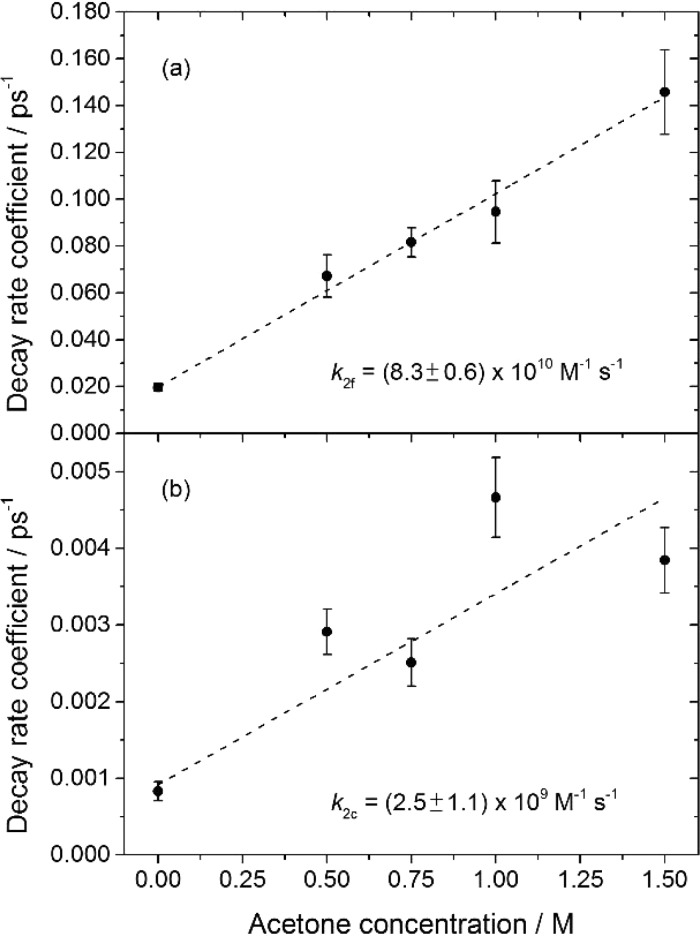
Spectral decomposition produced the time-dependent band intensities for free CN, solvated CN, and I* of the type shown in Figure 2. This decomposition and others presented in this paper all used the KOALA software package.48 Fits to biexponential functions gave the time constants reported in Table 1. The faster decay time scale τ1 of the free CN radicals matches the rise in the solvated CN signal; the time constants for both these processes are controlled by a combination of the cooling of initially rotationally hot CN photofragments,39 complexation with CDCl3 or acetone, geminate recombination to ICN and INC, and reaction with acetone. The time constant τ2, and the relative amplitude of the slower free CN decay component indicate that up to about one-third of these CN radicals avoid complexation, reaction and geminate recombination on an approximately 12 ps time scale. The decay of the solvated CN signal is attributed to reaction with acetone or solvent. The time dependence of the feature assigned to I* is not considered in detail here, but the rapid initial decay is consistent with geminate recombination with CN radicals and is similar to time constants reported by Rivera et al. for I* decay in water and ethanol.37 The longer-time decay may be associated with spin–orbit quenching of I* that has separated from its geminate CN photoproduct or is an artifact of a contribution from CN–acetone complexes to the long wavelength side of the free CN band.
Table 1. Time Constants τ and Amplitudes A for the Biexponential Fits to Time-Dependent Intensity Data Shown in Figure 2 for Free CN, Solvated CN, and I* a.
| τ1/ps | A1 (%) | τ2/ps | A2 (%) | |
|---|---|---|---|---|
| free CN | 2.3 ± 0.4 | 71 ± 6 | 12 ± 4 | 29 ± 6 |
| CN–CDCl3 | 1.9 ± 0.4 | 30 ± 4 | 217 ± 14 | 70 ± 4 |
| I*(2P1/2) | 1.7 ± 0.2 | 66 ± 7 | 410 ± 120 | 34 ± 7 |
Data are for an ICN/1.0 M acetone/CDCl3 solution. Uncertainties are 2 SD from the fits.
Similar measurements were made for other solutions with acetone concentrations in the range 0–1.5 M. The second time constant, τ2, from biexponential fits of the type shown in Figure 2 for both free and solvated forms of CN shows a dependence on acetone concentration because this decay component is associated with the bimolecular reaction between CN and acetone. Under conditions in which the acetone is in excess over CN radicals, the reciprocals of the τ2 time constants correspond to pseudo-first-order rate coefficients for H atom abstraction from acetone reaction 2 by free and solvated CN radicals. Reaction with the CDCl3 may also contribute to CN-radical loss, but it is known to be slow and is unimportant to this analysis.20,21Figure 3 shows pseudo-first-order kinetic plots from which bimolecular rate coefficients for H atom abstraction of k2f = (8.3 ± 0.6) × 1010 M–1 s–1 (for the free CN + acetone reaction) and k2c = (2.5 ± 1.1) × 109 M–1 s–1 (for the solvent-complexed CN + acetone reaction) are determined. Uncertainties are 2 SD from the linear fits. The greater uncertainty in the data for the solvated CN loss may be a consequence of overlapping absorption by the I(2P3/2)-solvent CT band or by acetone (T1) produced by the 267 nm excitation. Fitting of the sharper free-CN absorption band is relatively immune to these interferences from broad underlying features.
Figure 3.
Dependence of the pseudo-first-order rate coefficients on acetone concentration for loss of (a) free CN and (b) solvated and complexed CN radicals. Pseudo-first-order rate coefficients were obtained as the reciprocals of the time constants τ2 from biexponential fits to time-dependent band intensities. Nonzero intercept values indicate reactive loss of CN radicals with species other than acetone, such as the solvent.
The solvent-complexed CN reaction rate coefficient value must be treated with some caution because of possible spectral interferences but is similar in value to bimolecular rate coefficients reported by Crowther et al. for CN radical reactions with various organic solutes in chlorinated solvents.20,21 The lower reaction rate for solvated compared to free CN is consistent with both its stabilization by complexation, and unfavorable orientation of the CN radical for H-abstraction from neighboring molecules. The large value of k2f for the facile bimolecular reaction of free CN with acetone can exceed the diffusion limit expected for a homogeneous solution if the acetone solvates the ICN precursor preferentially over CDCl3.
The estimated rate of growth of the weak, broad absorption band centered just below 400 nm (Figure 2a), and most clearly observable at longer time delays, is similar to the rate of loss of CN–CDCl3 complexes. The band is not observed in the absence of acetone, but a similar feature appears following UV photolysis of ICN in neat acetone (Supporting Information). This evidence suggest assignment to a CN–acetone complex, which can form by transfer of a CN radical from CN–CDCl3.
The TEAS data provide quantitative information on the rates of removal of CN radicals, and distinguish solvated and unsolvated forms. They fail, however, to reveal the products of the reactions. Consequently, TVAS spectra were obtained and analyzed for spectroscopic signatures of reaction products.
IV.c. TVAS of Solutions of ICN and Acetone in CDCl3 Following 267 nm Excitation
Transient IR absorption spectra were obtained with the probe laser spanning 1450–1850 cm–1 to observe carbonyl (C=O), and 2000–2200 cm–1 to observe nitrile (C=N) stretching modes. In the nitrile region, the spectral resolution was improved to ∼1.5 cm–1 per pixel by changing the order of the spectrometer grating to resolve better some overlapping spectroscopic features. In the carbonyl region, the acetone band centered near 1690 cm–1 strongly attenuated the probe light and masked the region from 1670–1720 cm–1.
IV.c.i. TVAS Spectra in the C=N Region
The TVAS spectra measured in the 2000–2200 cm–1 region showed numerous, partially overlapping bands, which were assigned on the basis of previous studies of ICN photolysis and CN–radical reactions in chloroform.16,18,19 A sample set of spectra is shown in Figure 4 together with the band assignments. Typical data sets contained spectra at 50 or more time delays from 0 to 2500 ps, only a few of which are shown in Figure 4 for clarity. The spectral decomposition is illustrated in the Supporting Information. The band centered at 2162 cm–1 is assigned to the C=N stretching mode of ICN and appears in the transient spectra as a negative-going “bleach” feature because the ICN is depleted by the 267 nm photolysis laser. Spectral decomposition suggests there is a broad positive-going feature with a center displaced to higher wavenumber than the ICN bleach; this feature decays rapidly and is tentatively attributed to vibrationally hot ICN formed by I + CN geminate recombination on the ground electronic state. On the basis of this assignment, its decay (with a time constant of 5.5 ± 0.6 ps) is indicative of vibrational cooling by coupling to the solvent bath. Our caution in the assignment stems from the absence of similar signatures of vibrationally hot ICN from I + CN geminate recombination in other solvents.49 The interpretation of this feature is not critical to the main themes of this paper.
Figure 4.
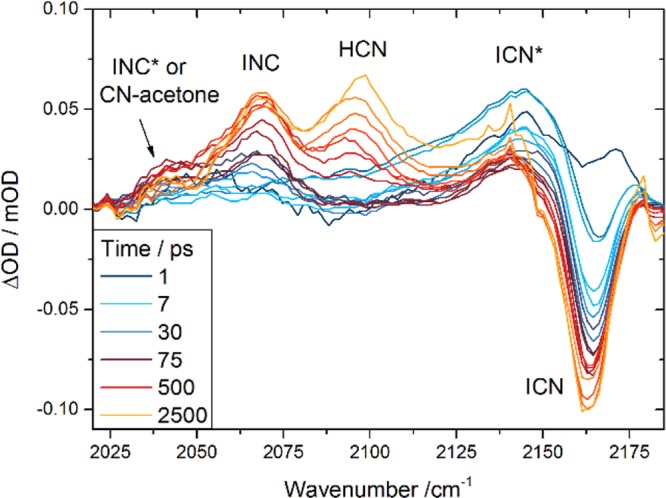
Time-resolved vibrational spectra of 267 nm excited ICN/acetone/CDCl3 solutions in the 2020–2180 cm–1 range. Band assignments are indicated and are discussed further in the main text. The inset key shows the time delays for selected spectra.
A band centered at 2067 cm–1 is assigned to the INC product of in-cage geminate recombination; although a minor channel, it is observed in our spectra because of the large transition dipole moment of the isocyanide group.50 Evidence from our laboratory indicates that the INC also forms vibrationally excited and that the growth rate of the band at 2067 cm–1 is controlled by vibrational relaxation.49
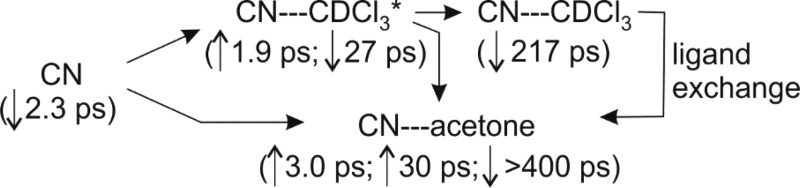
We attributed the weak feature at 2040 cm–1, discernible to the low-wavenumber side of the INC band, to solvated CN radicals in previous work.19 It grows with an initial (few picoseconds) spurt followed by a slower component with a time constant of 27 ± 7 ps (for a solution with 1.0 M acetone). The initial rise can be accounted for by direct complexation of free CN radicals with either CDCl3 or acetone because it is consistent with the 2.3 ps rise of the solvated CN band in the TEAS spectra. The slower time constant for growth of the 2040 cm–1 band depends linearly on the concentration of acetone, and a pseudo-first-order kinetic analysis gives a bimolecular rate coefficient of (2.6 ± 0.8) × 1010 M–1 s–1 (2 SD uncertainties). A plausible assignment of this feature is therefore to CN–acetone complexes of the type discussed earlier, and the observed time constants indicate an indirect route in addition to the direct formation from free CN. We suggest that some fraction of the CN first complexes to the more abundant CDCl3 molecules, then transforms into the more strongly bound acetone complexes.
If this interpretation is correct, we must invoke an intermediate denoted CN–CDCl3* to reconcile the rate coefficient value above with the k2c = (2.5 ± 1.1) × 109 M–1 s–1 value for the loss of CN–CDCl3 complexes deduced from the TEAS data (section IV.b). The CN–CDCl3* intermediate is envisaged to be a higher energy form of CN–CDCl3 such as an isomer or an internally hot complex, in which case it will also contribute to the observed TEAS band. It decays by ligand exchange to produce a CN–acetone complex, or by vibrational energy transfer to the solvent to form thermalized CN–CDCl3. The weakness of the 2040 cm–1 band suggests the branching to CN–acetone is a minor channel. The proposed assignment of the broad UV/visible band centered below 400 nm in TEAS data (Figure 2a) to a CN–acetone complex indicates that these complexes also form from thermalized CN–CDCl3 complexes by CDCl3/acetone exchange on a time scale of a few hundred picoseconds. These various processes are summarized in Scheme 1, with time constants appropriate for 1.0 M acetone solutions and the associated up and down arrows indicating growth and decay, respectively.
Scheme 1.
Further support for the assignment of the 2040 cm–1 band to CN–acetone complexes comes from the carbonyl region TVAS data discussed in section IV.c.ii, where some of the time constants incorporated in Scheme 1 are explained. However, we must consider a second possible explanation based on recent work from our group on ICN photolysis in various solvents:49 as was noted earlier, some fraction of the in-cage geminate recombination of CN + I produces INC, and the nascent molecules are vibrationally excited. Hot bands of the INC are shifted to lower wavenumber than the fundamental N=C stretching band at 2067 cm–1, and their decay rates may be enhanced by vibrational energy transfer to acetone, giving the observed concentration dependence. Because this interpretation requires population to feed from higher vibrational levels into the levels observed via the 2040 cm–1 absorption band to maintain a spectroscopic feature over several hundred picoseconds, we consider it unlikely.
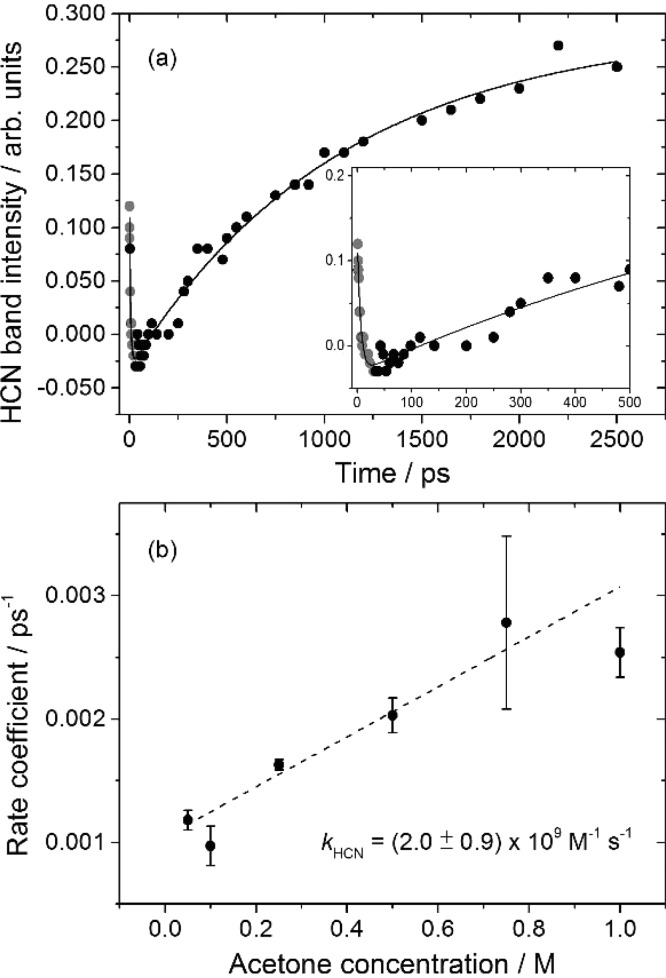
The band of most interest to the current study is centered at 2097 cm–1 and corresponds to the fundamental C=N stretching v1 = 1 ← v1 = 0 absorption of HCN reaction products. The time dependence of the growth of this feature is shown in Figure 5a. An exponential rise in intensity is preceded by an initial decay with time constant of 5.9 ± 0.6 ps that is associated with imperfect separation of the HCN feature from the broad band observed at early times to higher wavenumber (tentatively ICN*). We therefore concentrate on times after 10 ps when this interfering feature has a negligible influence.
Figure 5.
Kinetics of HCN formation. (a) Time dependence of the HCN band shown in Figure 4, with the inset showing an expanded view of the first 500 ps. Gray points are the result of interfering absorptions (see text). (b) A pseudo-first-order plot of the dependence of first-order rate coefficients (obtained as reciprocals of exponential time constants for HCN growth) on acetone concentration.
The spectral decomposition indicates that the HCN band has a negative intensity from 10 to 100 ps. The precise zero of intensity is difficult to identify because of neighboring features, but various different fitting procedures consistently returned negative intensities at early times and a delayed growth of the HCN fundamental band. We have observed these characteristics before: our prior studies of CN radical reactions in solution showed them to be signatures of an initial population inversion in the vibrational levels of HCN.16,18,19 Greater population in vibrationally excited levels than in the vibrational ground state is a consequence of the dynamics of these exothermic reactions with early transition states3 and has also been reported for gas-phase reactions of CN radicals.4−9 We therefore conclude that the CN + acetone reaction produces vibrationally hot HCN, and past precedent suggests that this excitation will be localized in the C–H stretching and bending modes.16
The rate of rise in the intensity of the HCN fundamental band at 2097 cm–1 depends linearly on acetone concentration (Figure 5b) and a pseudo-first-order analysis gives a bimolecular rate coefficient of kHCN = (2.0 ± 0.9) × 109 M–1 s–1 (2 SD uncertainties) that is consistent with the rate coefficient for loss of solvent-complexed CN of k2c = (2.5 ± 1.1) × 109 M–1 s–1 deduced from the TEAS spectra presented in Figure 2. This correspondence indicates that the chemical reaction step is rate determining for production of HCN from solvated CN radicals. In some of our prior studies of CN radical reactions in chlorinated solvents, vibrational relaxation of the internally excited HCN instead controlled the rate of increasing intensity of the fundamental band.16,19 The two different limiting behaviors depend on whether this vibrational relaxation is faster or slower than the chemical production of HCN.18 In the current case, the coupling of vibrationally hot HCN to CDCl3 is weak,16 but acetone appears to be an efficient alternative quencher.
Vibrationally hot HCN from reactions of free CN radicals should give rise to transient absorption bands observable at short time delays to lower wavenumber than the 2097 cm–1 fundamental band. However, we are unable to observe these hot bands directly in the current experiments because the small anharmonicity of the C=N stretch (x11 = −10 cm–1) and weak anharmonic couplings between the C=N stretching mode and the bending (x12 = −3 cm–1) and C–H stretching (x13 = −15 cm–1) vibrations,51 shift the absorptions to regions overlapped by the INC band and the low-wavenumber side of the HCN fundamental band.
IV.c.ii. TVAS Spectra in the C=O Region
There are two important features in the C=O stretching region following ICN photodissociation in acetone/CDCl3 solutions. A representative set of TVAS spectra is shown in Figure 6. In this section, we describe our assignment of the weaker feature at 1640 cm–1 to the CN–acetone complex and the stronger feature at 1550 cm–1 to the 2-oxopropyl reaction product. Both bands are only present in the transient spectra when both acetone and ICN are dissolved in CDCl3, indicating both features involve CN interaction with acetone. Calculated vibrational frequencies and steady-state infrared spectra guided the interpretations we make, and relevant computed frequencies and relative band intensities of candidate species are presented in Table 2 alongside the measured frequencies of the observed absorption bands.
Figure 6.
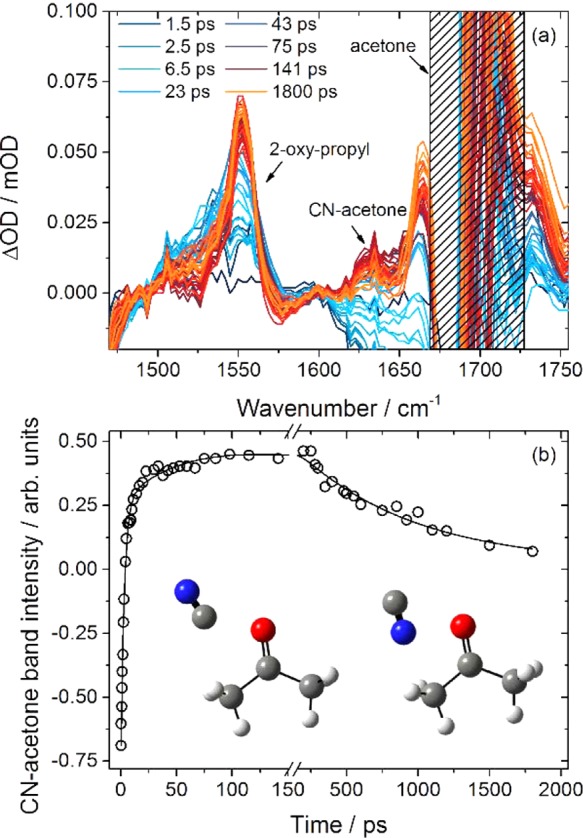
Time dependence of spectral features in the carbonyl stretching region. (a) Time-resolved vibrational spectra spanning 1470–1755 cm–1 after 267 nm excitation of ICN/acetone/CDCl3 solutions. Band assignments are indicated and are discussed in the main text. The gray hatching indicates spectral regions where strong acetone absorption prevents reliable measurement. (b) Time dependence of the weak feature at 1640 cm–1 and computed structures of the CN–acetone complexes to which it is assigned. Negative intensities are a consequence of baseline fluctuations at early times because of the neighboring acetone band.
Table 2. Table of Computed Vibrational Frequencies in the Carbonyl Stretching Region Scaled for Chloroform Solutions.
| chemical species | computed vibrational frequency/cm–1 | relative intensitya | observed vibrational frequency/cm–1 |
|---|---|---|---|
| 2-oxopropyl | 1530 | 2.3 | 1550 |
| acetone–C=N complex | 1608 | 1.1 | 1640 |
| acetone–N=C complex | 1618 | 0.8 | 1640 |
| acetone | 1691 | 1.0 | 1710 |
| acetaldehyde | 1717 | 5.1 | 1714 |
| acetyl | 1833 | 4.2 | 1875 |
Peak intensity specified relative to the acetone band at 1691 cm–1.
Our trajectory calculations indicate that the CN radical can form transiently stable complexes with acetone. (An addition reaction at the carbonyl group may also be possible but was not observed in the trajectory calculations and would lead to a product with a significantly shifted C–O stretching frequency.) The transient complexes were suggested to contribute a band centered just below 400 nm in the TEAS spectra of Figure 2 and a weak feature at 2040 cm–1 that is evident in the C=N stretching region spectra shown in Figure 4. They are stabilized by approximately 3600 cm–1 compared to separated CN and acetone, according to our calculations. Furthermore, these stabilized structures are dynamically decoupled from the H-abstraction pathway, which inhibits further reaction. The CN shifts the acetone C=O stretch down in wavenumber in both our calculations and the spectrum. The calculations predict the band to occur at 1608–1618 cm–1, with the range encompassing two isomers in which the C or N end of the cyano radical is oriented toward the acetone, as shown in Figure 6b. These two isomers cannot be distinguished in the TVAS data. Other potential absorbers in this region include acetaldehyde, CH3CHO, a stable product of the possible radical chemistry. Its fundamental C=O stretch, calculated to be at 1717 cm–1, lies to the higher wavenumber side of the acetone carbonyl band. Similarly, acetyl radical photoproducts of acetone fragmentation have computed IR bands at 1833 cm–1 and are not responsible for the features of interest in Figure 6a. The other features in the spectrum that lie close to the strong acetone fundamental band must be interpreted with caution, but there are indications of time-dependent bands at 1740 and 1770 cm–1; both are observed with and without ICN. We suspect they are associated with the UV photochemistry of acetone and with different solvation environments of acetone in CDCl3. We do not consider them further.
The weak, time-dependent feature at 1640 cm–1 assigned to the CN–acetone complex sits upon a shifting baseline because of proximity to the strong acetone band. Nevertheless, it can be fitted to extract time-dependent band intensities, as shown in Figure 6b. Its growth fits to a biexponential rise with time constants of τ1 = 3.0 ± 0.3 ps and τ2 = 55 ± 25 ps (both for 0.5 M acetone solutions; 2 SD uncertainties). It then undergoes a slow decay (with τ3 = 800 ± 400 ps). The two rise times are consistent with the formation of the complexes directly from unsolvated free CN, which TEAS data show decays on a 2.3 ± 0.2 ps time scale, and from CN–CDCl3* complexes. For the latter process, a time constant of 27 ± 7 ps was suggested from the C=N stretching region TVAS feature at 2040 cm–1, which is approximately half that for the 0.5 M solution but was measured for twice the acetone concentration. We attribute the slow decay to reactive loss of CN–acetone complexes, with a time constant longer than reactive removal of CN–CDCl3 complexes because the former are more strongly bound (we estimate 3600 cm–1 versus 1800 cm–1 for CN–acetone and CN–CDCl3 from our calculations). These various time scales are summarized in Scheme 1.
The remainder of this analysis describes our assignment and interpretation of the temporal evolution of the stronger transient feature at 1505–1575 cm–1. We attribute this band to the 2-oxopropyl product of the H-abstraction reaction of CN with acetone, on the basis of our calculations that place the band center at 1545 cm–1. Several alternative assignments can be quickly discounted because the band lies ∼150 cm–1 below the carbonyl band of acetone. For example, the C=O stretching band of 1-iodoacetone from recombination of I atoms with 2-oxopropyl is expected near 1700 cm–1 (on the basis of the known gas-phase IR spectrum of 1-chloroacetone,52 and our observed solvent shifts in chloroform solutions) and will be masked by the acetone feature.
The band assigned to 2-oxopropyl develops in the TVAS spectra with a center at 1552 cm–1 at late time delays. However, at early times, this feature is broadened to lower wavenumber and coalesces into the sharp 2-oxopropyl feature over a time scale of ∼50 ps. This behavior is suggestive of vibrational cooling of an initially internally hot radical, with broadening and shifting of the absorption to lower wavenumber, because of either vibrational anharmonicity in the C=O stretch or anharmonic coupling to other excited modes. It is less likely to be a consequence of an equilibrating solvent environment around the newly formed radical, which we expect to shift the vibrational frequencies from higher to lower wavenumber with time.53,54 Energy flow from the hot HCN to the 2-oxopropyl radical, an effect we first noted in the reaction of CN radicals with cyclohexane,32 can be ruled out as the cause of the narrowing feature because the vibrationally hot 2-oxopropyl radicals are formed more promptly than the likely time scale for vibrational relaxation of the HCN.
The time dependence of the 2-oxopropyl band was analyzed by fitting to two Gaussian functions with centers x0i and widths σi (both specified in cm–1): x0 = 1552 and σg = 14 for absorptions by ground-state molecules (as determined from fitting the late-time spectra), and x0e = 1533 and σe = 35 for vibrationally excited molecules. The areas of the two Gaussian components were free parameters in the fits, and Figure 7 illustrates the outcomes. The temporal evolutions of the two bands are both satisfactorily modeled with exponential time constants of τ1 = 2.3 ps (fixed to match the faster time constant for loss of free CN radicals from TEAS data) and τ2 = 34 ± 10 ps (determined by simultaneous fits to the time-dependent intensities of both bands; 2 SD uncertainty). The analysis is therefore consistent with production of vibrationally hot 2-oxopropyl radicals from CN reaction with acetone with a time constant of 2.3 ps, and vibrational relaxation with a time constant of ∼34 ps. This cooling may correspond to loss of multiple quanta of vibrational excitation in different modes and is an average time scale. More quantitative information on the vibrational energy content of the nascent 2-oxopropyl radical cannot be deduced from our TVAS data alone.
Figure 7.
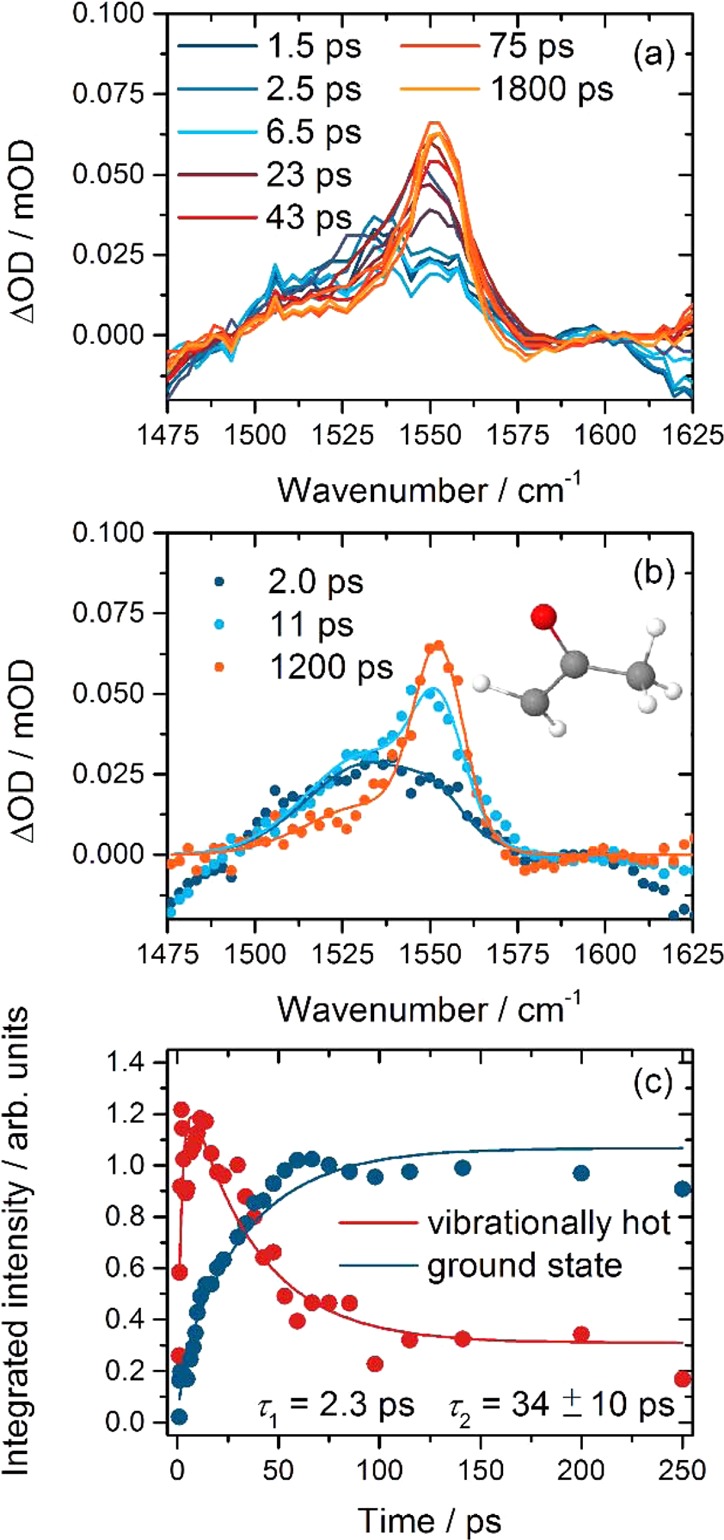
Time dependence of 2-oxopropyl IR bands in an acetone/CDCl3 solution. (a) TVAS data for the wavenumber range from 1475–1625 cm–1. The key shows the time delays for selected spectra. (b) TVAS spectra (dots) and illustrative fits to two Gaussian functions (lines) for time delays of 2.0 ps (dark blue), 11 ps (light blue), and 1200 ps (orange). (c) Time dependences of the feature attributed to vibrationally excited (red) and ground-state (blue) 2-oxopropyl radicals. Solid lines are biexponential fits, as discussed in the main text.
The 2-oxopropyl radical and its coproduct HCN have different long-time kinetics. The band attributed to the C=O stretch of ground-state 2-oxopropyl radicals reaches a steady-state absorbance at ∼50 ps but the HCN absorption continues to grow for time scales up to our experimental limit of 2 ns. The differences in longer time behavior of these two populations hint toward subsequent 2-oxopropyl reactions. This radical is therefore an intermediate in a sequence of steps, which result in a balance between its production and loss. A steady-state (but low) concentration will occur if the rate of removal of the 2-oxopropyl radicals is larger than their rate of production. In addition to the fast reactive production by free CN radicals, a slower contribution to 2-oxopropyl growth will derive from reaction of solvated CN radicals, for which the rate coefficient is ∼2 × 109 M–1 s–1 as determined from HCN growth and CN–CDCl3 loss measurements in section IV.c.i. The time constants for production of the 2-oxopropyl radicals are therefore several hundred picoseconds under our experimental conditions, and assuming that steady-state behavior leads to the effects we see, indicates a decay lifetime of ≤100 ps.
V. Discussion
The analysis of the TEAS and TVAS data obtained for UV-excited ICN/acetone/CDCl3 solutions reveals distinguishable reactivity of free and solvent-complexed CN radicals. The free CN quickly (τCN = 2.3 ps) decays by geminate recombination (to ICN and INC), association with a CDCl3 solvent molecule or acetone cosolute molecule to form complexes, and reaction with acetone to produce HCN. The bimolecular rate coefficient for reaction of acetone with free CN radicals, i.e., for those CN that survive initial loss or complexation to the solvent, is deduced to be k2f = (8.0 ± 0.5) × 1010 M–1 s–1. We suspect that this large reaction rate coefficient results in part from microscopic inhomogeneity that develops in these solutions. Although the reaction itself is facile, preferential solvation of ICN by acetone over CDCl3 will augment the reaction rate.
The bimolecular rate coefficients for the reaction of the CN–CDCl3 complexes with acetone are more than an order of magnitude slower and are controlled by both diffusion and activation: we extracted values of k2c = (2.5 ± 1.1) × 109 M–1 s–1 from the loss of the solvated CN band in the TEAS spectra and k2c = (2.0 ± 0.9) × 109 M–1 s–1 from the rise in the HCN band in TVAS experiments (see sections IV.b and IV.c). Reactions of CN–acetone complexes are slower still because of the greater stabilization deriving from CN–carbonyl interactions. Our calculations show barriers to dissociation of 3600 cm–1 for CN–acetone and 1800 cm–1 for CN–CDCl3 complexes, which support this idea. These CN–acetone complexes form both directly from free CN radicals that happen to have a neighboring acetone molecule when photolytically generated, and by exchange of partner following initial complexation to CDCl3 solvent molecules. The driving force for the CN–CDCl3 to CN–acetone exchange is the greater stabilization energy of the latter complexes.
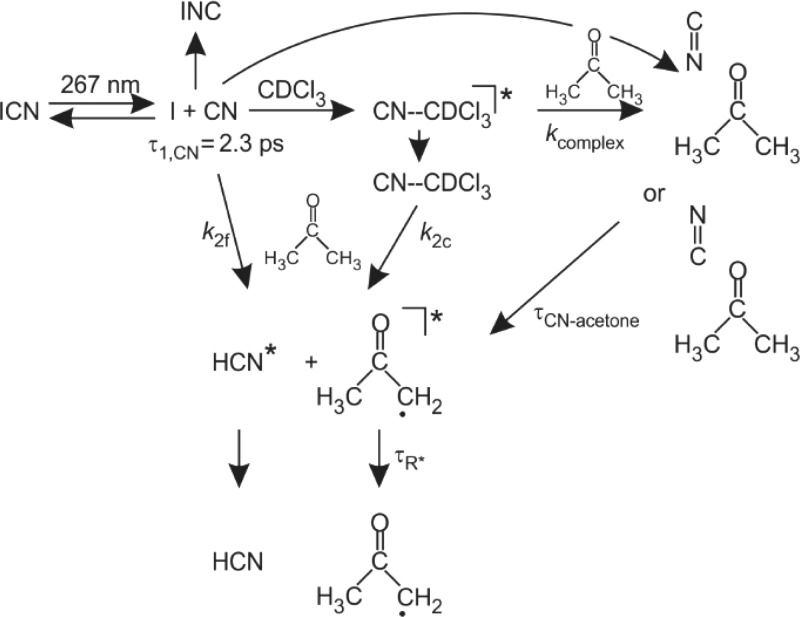
Figure 8 summarizes the various processes that follow UV excitation of ICN in an acetone/CDCl3 solution and the associated time constants (specified for a 0.5 M acetone solution where dependent on the acetone concentration). It extends the initial kinetics of solvation of the free CN radicals with CDCl3 and acetone summarized in Scheme 1 to include the abstraction reaction pathways. The figure excludes the photochemistry that results from 267 nm excitation of acetone molecules. Under the conditions of our experiments, we estimate that fewer than 0.02% of the acetone molecules within the volume of the 266 nm laser beam are photoexcited. Hence excited-state (S1 and T1) acetone molecules and acetone photoproducts (e.g., acetyl radical) are unlikely to react with CN radicals in sufficient numbers to contribute to our observed time-resolved spectra.
Figure 8.
Summary of the photochemical processes involving CN radicals and acetone following UV photolysis of ICN in an ICN/acetone/CDCl3 solution. The rate coefficient values deduced from this work are k2f = (8.0 ± 0.5) × 1010 M–1 s–1 for the slower component of the reaction of the free CN radical with acetone, k2c = (2.5 ± 1.1) × 109 M–1 s–1 for the solvent-complexed CN reaction, and kcomplex = (2.6 ± 0.8) × 1010 M–1 s–1 for formation of the CN–acetone complex. Lifetimes (from decay time constants) are τ1,CN = 2.3 ps for the initial fast-component of the loss of free CN, τCN–acetone = 800 ps for the complex, and τR* = 34 ps for the cooling of vibrationally excited 2-oxypropyl radicals.
Both the HCN and the 2-oxopropyl radical products form with some degree of vibrational excitation greater than expected for thermalized products (see sections IV.c.i and IV.c.ii). In the case of the HCN product, the evidence from the current and our previous studies of CN radical reactions in solution16,18,19 is that there is a vibrational population inversion, with the majority of the HCN formed both C–H stretch- and bend-excited. One quantum of C–H stretching excitation in the HCN corresponds to an energy of 39 kJ mol–1, and each bending quantum adds approximately 8 kJ mol–1 more internal energy. In this regard, the reaction dynamics are similar to those for H atom abstraction reactions by CN in the gas phase.4−9
The extent of vibrational excitation of the 2-oxopropyl radical is less clear-cut, but the evolution from its initially broad to its final, narrow C=O stretching spectrum in Figure 7 shows that a large fraction of the 2-oxopropyl radicals are vibrationally excited. A Franck–Condon type model can be applied to predict a limiting case for the internal excitation of the 2-oxopropyl radical. Sudden abstraction of a hydrogen atom may be a reasonable approximation for the direct dynamics with an early transition state and will leave the 2-oxopropyl radical in a geometry otherwise identical to that of acetone. Electronic structure calculations indicate that relaxation to the equilibrium structure of the 2-oxopropyl radical most significantly involves changes to the C–H bond length in the −CH2 group from 1.098 Å (the C–H bond length in acetone) to 1.083 Å, and a change from tetrahedral to trigonal planar coordination. We estimate from these calculations that the gain in internal energy associated with this structural reorganization is 46 kJ mol–1. The structural changes identified might excite C–H stretching and CH2 wagging and scissoring modes. These arguments suggest that approximately 70% of the available energy may be channeled into product internal motions, which is similar to the fraction reported for CN reactions in the gas phase.11,12
The fast rise time of a few picoseconds of the vibrationally hot 2-oxopropyl radicals, and the concomitant development of the population inversion of vibrational levels of HCN intimate that these products result from reactions of the free CN radicals before they complex to solvent molecules. The CN–CDCl3 and CN–acetone complexes react to form HCN more slowly, with time constants on the order of a few hundred picoseconds (depending on acetone concentration).
We are unable to detect vibrationally excited HCN and 2-oxopropyl radicals from the slower reactions of the complexed forms of CN. This absence may indicate that the complexed reactions exhibit different reaction dynamics, perhaps with later transition states along the reaction pathway, so that the vibrational excitation does not develop in the products. More likely, given the large exothermicity of the reactions (∼140 kJ mol–1) and the relatively small stabilization energies of the complexes (<45 kJ mol–1), is that this product vibrational excitation does develop, but that it relaxes by solvent coupling on faster time scales than the overall buildup of products, so cannot be detected in our experiments.
We have previously shown that exothermic reactions in solution have a propensity to form one vibrationally hot product despite the coupling of the solvent bath to nuclear motions along and orthogonal to the reaction coordinate.1,2,16,53−55 This vibrational excitation mostly appears in the new bond formed from the reaction as a consequence of an early transition state, as predicted by the Polanyi rules for gas-phase reactions.56 The solvent coupling thermalizes the reaction products only after reaction is complete. The current study demonstrates that the coproduct of a bimolecular reaction in solution can also be formed with significant amounts of internal vibrational excitation. Similar behavior is known from gas-phase studies of exothermic reactions of F atoms with methane24 and may also occur for CN–radical reactions with alkanes. In these gas-phase studies, (anti)correlations between the degrees of vibrational excitation of the two products can be established from velocity map imaging measurements. Methodology is lacking to make the corresponding correlated measurements in solution, but our current efforts show that dynamical insights can still be forthcoming from the uncorrelated observations.
VI. Conclusions
Time-resolved absorption spectroscopy of the exothermic reaction of CN radicals with acetone in CDCl3 solutions demonstrates that a significant fraction of the energy released enters vibrational modes of the HCN and the 2-oxopropyl radical coproduct. Transfer of this excess energy to the solvent bath occurs on time scales on the order of 10 ps, leading to thermally equilibrated reaction products. We have previously reported substantial vibrational excitation of one product of a reaction in solution (for exothermic reactions of CN radicals,16 and of F and Cl atoms53,55), but this is our first observation that both nascent products can be vibrationally hot. The CN radicals were generated photolytically from ICN, and take 2.3 ps to equilibrate with the solvent and form CN–CDCl3 complexes. Distinct spectroscopic signatures of complexed and uncomplexed (free) CN radicals allow us to distinguish their reactions. In the reactions with acetone, the complexed CN radicals react more than an order of magnitude more slowly, but the kinetics of reactions of the free CN radicals are partly controlled by in-cage geminate recombination with I atoms, and solvent-complex formation. The CN radicals also complex to acetone molecules, and C=N–carbonyl interactions thermodynamically favor these species over CN–CDCl3 complexes. Evidence from our measurements suggests that the CN radicals complexed with acetone have significantly reduced reactivities. The combination of time-resolved electronic and vibrational spectroscopies allows us to unravel the rates and dynamics of several competing processes that occur following photoinitiation of radical chemistry in solution.
Acknowledgments
The Bristol group thanks the European Research Council (ERC, Advanced Grant 290966 CAPRI) and EPSRC (Doctoral Training Grant studentship for G.T.D.) for financial support. S.J.G. thanks the EPSRC for support via grant EP/J002534/2. Experimental measurements were conducted at the ULTRA Laser Facility, which is supported by the Science and Technology Facilities Council (STFC, Facility Grant ST/501784). We are grateful to Alan Sage (University of Bristol) and Paul Donaldson (Central Laser Facility) for help with collection of the experimental data, and Michael Grubb and Philip Coulter (University of Bristol) for valuable discussions.
Supporting Information Available
All experimental data are archived in the University of Bristol’s Research Data Storage Facility (DOI: 10.5523/bris.85s3r8hlprl11hbx36cg2xvn3). The Supporting Information contains summaries of transient absorption spectroscopy measurements in ICN/chloroform and in acetone/chloroform solutions, spectral decomposition methods, and computational outcomes. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpca.5b05624.
The authors declare no competing financial interest.
Supplementary Material
References
- Orr-Ewing A. J. Bimolecular Chemical Reaction Dynamics in Solution. J. Chem. Phys. 2014, 140, 090901. 10.1063/1.4866761. [DOI] [PubMed] [Google Scholar]
- Orr-Ewing A. J. Dynamics of Bimolecular Reactions in Solution. Annu. Rev. Phys. Chem. 2015, 66, 119–141 10.1146/annurev-physchem-040214-121654. [DOI] [PubMed] [Google Scholar]
- Glowacki D. R.; Orr-Ewing A. J.; Harvey J. N. Product Energy Deposition of CN + Alkane H Abstraction Reactions in Gas and Solution Phases. J. Chem. Phys. 2011, 13421214508. 10.1063/1.3595259. [DOI] [PubMed] [Google Scholar]
- Bethardy G. A.; Northrup F. J.; He G.; Tokue I.; Macdonald R. G. Initial Vibrational Level Distribution of HCN[X1Σ+(v1,0,v3)] from the CN(X2Σ+)+H2→ HCN+H Reaction. J. Chem. Phys. 1998, 109114224–4236 10.1063/1.477028. [DOI] [Google Scholar]
- Bethardy G. A.; Northrup F. J.; Macdonald R. G. The Initial Vibrational-State Distribution of HCN[X1Σ+(v1,0,v3)] from the Reaction CN(X2Σ+)+C2H6→ HCN+C2H5. J. Chem. Phys. 1995, 102207966–7982 10.1063/1.468995. [DOI] [Google Scholar]
- Bethardy G. A.; Northrup F. J.; Macdonald R. G. The Initial Vibrational Level Distribution and Relaxation of HCN[X1Σ+(v1,0,v3)] in the CN(X2Σ+)+CH4→HCN+CH3 Reaction System. J. Chem. Phys. 1996, 105114533–4549 10.1063/1.472537. [DOI] [Google Scholar]
- Copeland L. R.; Mohammad F.; Zahedi M.; Volman D. H.; Jackson W. M. Rate Constants for Cn Reactions with Hydrocarbons and the Product HCN Vibrational Populations: Examples of Heavy-Light-Heavy Abstraction Reactions. J. Chem. Phys. 1992, 9685817–5826 10.1063/1.462681. [DOI] [Google Scholar]
- Morris V. R.; Mohammad F.; Valdry L.; Jackson W. M. Steric Effects on Nascent Vibrational Distributions of the HCN Product Produced in CN Radical Reactions with Ethane, Propane and Chloroform. Chem. Phys. Lett. 1994, 2206448–454 10.1016/0009-2614(94)00212-6. [DOI] [Google Scholar]
- Few J.FTIR Studies of Chemical Processes. D.Phil. Thesis, University of Oxford, 2013. [Google Scholar]
- Morales S. B.; Le Picard S. D.; Canosa A.; Sims I. R. Experimental Measurements of Low Temperature Rate Coefficients for Neutral-Neutral Reactions of Interest for Atmospheric Chemistry of Titan, Pluto and Triton: Reactions of the CN Radical. Faraday Discuss. 2010, 147, 155–171 10.1039/c004219f. [DOI] [PubMed] [Google Scholar]
- Huang C.; Li W.; Estillore A. D.; Suits A. G. Dynamics of CN Plus Alkane Reactions by Crossed-Beam DC Slice Imaging. J. Chem. Phys. 2008, 1297074301. 10.1063/1.2968547. [DOI] [PubMed] [Google Scholar]
- Estillore A. D.; Visger L. M.; Kaiser R. I.; Suits A. G. Crossed-Beam Imaging of the H Abstraction Channel in the Reaction of CN with 1-Pentene. J. Phys. Chem. Lett. 2010, 1152417–2421 10.1021/jz100861t. [DOI] [Google Scholar]
- Gannon K. L.; Glowacki D. R.; Blitz M. A.; Hughes K. J.; Pilling M. J.; Seakins P. W. H Atom Yields from the Reactions of CN Radicals with C2H2, C2H4, C3H6, Trans-2-C4H8, and Iso-C4H8. J. Phys. Chem. A 2007, 111296679–6692 10.1021/jp0689520. [DOI] [PubMed] [Google Scholar]
- Trevitt A. J.; Goulay F.; Meloni G.; Osborn D. L.; Taatjes C. A.; Leone S. R. Isomer-Specific Product Detection of CN Radical Reactions with Ethene and Propene by Tunable VUV Photoionization Mass Spectrometry. Int. J. Mass Spectrom. 2009, 2801–3113–118 10.1016/j.ijms.2008.07.033. [DOI] [Google Scholar]
- Trevitt A. J.; Soorkia S.; Savee J. D.; Selby T. S.; Osborn D. L.; Taatjes C. A.; Leone S. R. Branching Fractions of the CN+C3H6 Reaction Using Synchrotron Photoionization Mass Spectrometry: Evidence for the 3-Cyanopropene Product. J. Phys. Chem. A 2011, 1154613467–13473 10.1021/jp208496r. [DOI] [PubMed] [Google Scholar]
- Greaves S. J.; Rose R. A.; Oliver T. A. A.; Glowacki D. R.; Ashfold M. N. R.; Harvey J. N.; Clark I. P.; Greetham G. M.; Parker A. W.; Towrie M.; et al. Vibrationally Quantum-State-Specific Reaction Dynamics of H Atom Abstraction by CN Radical in Solution. Science 2011, 33160231423–1426 10.1126/science.1197796. [DOI] [PubMed] [Google Scholar]
- Raftery D.; Gooding E.; Romanovsky A.; Hochstrasser R. M. Vibrational Product State Dynamics in Solution-Phase Bimolecular Reactions - Transient Infrared Study of CN Radical Reactions. J. Chem. Phys. 1994, 101108572–8579 10.1063/1.468052. [DOI] [Google Scholar]
- Rose R. A.; Greaves S. J.; Abou-Chahine F.; Glowacki D. R.; Oliver T. A. A.; Ashfold M. N. R.; Clark I. P.; Greetham G. M.; Towrie M.; Orr-Ewing A. J. Reaction Dynamics of CN Radicals with Tetrahydrofuran in Liquid Solutions. Phys. Chem. Chem. Phys. 2012, 143010424–10437 10.1039/c2cp40158d. [DOI] [PubMed] [Google Scholar]
- Rose R. A.; Greaves S. J.; Oliver T. A. A.; Clark I. P.; Greetham G. M.; Parker A. W.; Towrie M.; Orr-Ewing A. J. Vibrationally Quantum-State-Specific Dynamics of the Reactions of CN Radicals with Organic Molecules in Solution. J. Chem. Phys. 2011, 13424244503. 10.1063/1.3603966. [DOI] [PubMed] [Google Scholar]
- Crowther A. C.; Carrier S. L.; Preston T. J.; Crim F. F. Time-Resolved Studies of CN Radical Reactions and the Role of Complexes in Solution. J. Phys. Chem. A 2008, 1124712081–12089 10.1021/jp8064079. [DOI] [PubMed] [Google Scholar]
- Crowther A. C.; Carrier S. L.; Preston T. J.; Crim F. F. Time-Resolved Studies of the Reactions of CN Radical Complexes with Alkanes, Alcohols, and Chloroalkanes. J. Phys. Chem. A 2009, 113163758–3764 10.1021/jp8084099. [DOI] [PubMed] [Google Scholar]
- Nitzan A.Chemical Dynamics in Condensed Phases; Oxford University Press: Oxford, U.K., 2006. [Google Scholar]
- Greaves S. J.; Rose R. A.; Orr-Ewing A. J. Velocity Map Imaging of the Dynamics of Bimolecular Chemical Reactions. Phys. Chem. Chem. Phys. 2010, 12329129–9143 10.1039/c001233e. [DOI] [PubMed] [Google Scholar]
- Lin J. J.; Zhou J. G.; Shiu W. C.; Liu K. P. State-Specific Correlation of Coincident Product Pairs in the F+CD4 Reaction. Science 2003, 3005621966–969 10.1126/science.1083672. [DOI] [PubMed] [Google Scholar]
- Greetham G. M.; Burgos P.; Cao Q.; Clark I. P.; Codd P. S.; Farrow R. C.; George M. W.; Kogimtzis M.; Matousek P.; Parker A. W.; et al. ULTRA: A Unique Instrument for Time-Resolved Spectroscopy. Appl. Spectrosc. 2010, 64121311–1319 10.1366/000370210793561673. [DOI] [PubMed] [Google Scholar]
- Abou-Chahine F.; Preston T. J.; Dunning G. T.; Orr-Ewing A. J.; Greetham G. M.; Clark I. P.; Towrie M.; Reid S. A. Photoisomerization and Photoinduced Reactions in Liquid CCl4 and CHCl3. J. Phys. Chem. A 2013, 1175013388–13398 10.1021/jp406687x. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; et al. Gaussian 09; Gaussian Inc.: Wallingford, CT, 2009. [Google Scholar]
- Montgomery J. A.; Ochterski J. W.; Petersson G. A. A Complete Basis-Set Model Chemistry 0.4. An Improved Atomic Pair Natural Orbital Method. J. Chem. Phys. 1994, 10175900–5909 10.1063/1.467306. [DOI] [Google Scholar]
- Nyden M. R.; Petersson G. A. Complete Basis Set Correlation Energies 0.1. The Asymptotic Convergence of Pair Natural Orbital Expansions. J. Chem. Phys. 1981, 7541843–1862 10.1063/1.442208. [DOI] [Google Scholar]
- Petersson G. A.; Allaham M. A. A Complete Basis Set Model Chemistry 0.2. Open-Shell Systems and the Total Energies of the 1st-Row Atoms. J. Chem. Phys. 1991, 9496081–6090 10.1063/1.460447. [DOI] [Google Scholar]
- Petersson G. A.; Tensfeldt T. G.; Montgomery J. A. A Complete Basis Set Model Chemistry 0.3. The Complete Basis Set-Quadratic Configuration-Interaction Family of Methods. J. Chem. Phys. 1991, 9496091–6101 10.1063/1.460448. [DOI] [Google Scholar]
- Glowacki D. R.; Rose R. A.; Greaves S. J.; Orr-Ewing A. J.; Harvey J. N. Ultrafast Energy Flow in the Wake of Solution-Phase Bimolecular Reactions. Nat. Chem. 2011, 311850–855 10.1038/nchem.1154. [DOI] [PubMed] [Google Scholar]
- Hu X. C.; Hase W. L.; Pirraglia T. Vectorization of the General Monte-Carlo Classical Trajectory Program Venus. J. Comput. Chem. 1991, 1281014–1024 10.1002/jcc.540120814. [DOI] [Google Scholar]
- Lourderaj U.; Sun R.; Kohale S. C.; Barnes G. L.; de Jong W. A.; Windus T. L.; Hase W. L. The Venus/NWChem Software Package. Tight Coupling between Chemical Dynamics Simulations and Electronic Structure Theory. Comput. Phys. Commun. 2014, 18531074–1080 10.1016/j.cpc.2013.11.011. [DOI] [Google Scholar]
- Hase W. L.; Duchovic R. J.; Hu X.; Komornicki A.; Lim K. F.; Lu D.-H.; Peslherbe G. H.; Swamy K. N.; Vande Linde S. R.; Varandas A. J. C.; et al. Venus96: A General Chemical Dynamics Computer Program, 1996.
- Valiev M.; Bylaska E. J.; Govind N.; Kowalski K.; Straatsma T. P.; Van Dam H. J. J.; Wang D.; Nieplocha J.; Apra E.; Windus T. L.; et al. NWChem: A Comprehensive and Scalable Open-Source Solution for Large Scale Molecular Simulations. Comput. Phys. Commun. 2010, 18191477–1489 10.1016/j.cpc.2010.04.018. [DOI] [Google Scholar]
- Rivera C. A.; Winter N.; Harper R. V.; Benjamin I.; Bradforth S. E. The Dynamical Role of Solvent on the ICN Photodissociation Reaction: Connecting Experimental Observables Directly with Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2011, 13188269–8283 10.1039/c1cp20252a. [DOI] [PubMed] [Google Scholar]
- Wan C. Z.; Gupta M.; Zewail A. H. Femtochemistry of ICN in Liquids: Dynamics of Dissociation, Recombination and Abstraction. Chem. Phys. Lett. 1996, 2563279–287 10.1016/0009-2614(96)00443-5. [DOI] [Google Scholar]
- Moskun A. C.; Bradforth S. E. Photodissociation of ICN in Polar Solvents: Evidence for Long Lived Rotational Excitation in Room Temperature Liquids. J. Chem. Phys. 2003, 11984500–4515 10.1063/1.1591726. [DOI] [Google Scholar]
- Moskun A. C.; Jailaubekov A. E.; Bradforth S. E.; Tao G. H.; Stratt R. M. Rotational Coherence and a Sudden Breakdown in Linear Response Seen in Room-Temperature Liquids. Science 2006, 31157691907–1911 10.1126/science.1123738. [DOI] [PubMed] [Google Scholar]
- Benjamin I. Photodissociation of ICN in Liquid Chloroform - Molecular-Dynamics of Ground and Excited-State Recombination, Cage Escape, and Hydrogen Abstraction Reaction. J. Chem. Phys. 1995, 10372459–2471 10.1063/1.470695. [DOI] [Google Scholar]
- Benjamin I.; Wilson K. R. Proposed Experimental Probes of Chemical-Reaction Molecular-Dynamics in Solution - ICN Photodissociation. J. Chem. Phys. 1989, 9084176–4197 10.1063/1.455775. [DOI] [Google Scholar]
- Larsen J.; Madsen D.; Poulsen J. A.; Poulsen T. D.; Keiding S. R.; Thogersen J. The Photoisomerization of Aqueous ICN Studied by Subpicosecond Transient Absorption Spectroscopy. J. Chem. Phys. 2002, 116187997–8005 10.1063/1.1467897. [DOI] [Google Scholar]
- Preston T. J.; Dunning G. T.; Orr-Ewing A. J.; Vazquez S. A. Direct and Indirect Hydrogen Abstraction in Cl + Alkene Reactions. J. Phys. Chem. A 2014, 118305595–5607 10.1021/jp5042734. [DOI] [PubMed] [Google Scholar]
- Joalland B.; Shi Y.; Kamasah A.; Suits A. G.; Mebel A. M. Roaming Dynamics in Radical Addition-Elimination Reactions. Nat. Commun. 2014, 5, 4064. 10.1038/ncomms5064. [DOI] [PubMed] [Google Scholar]
- Joalland B.; Van Camp R.; Shi Y. Y.; Patel N.; Suits A. G. Crossed-Beam Slice Imaging of Cl Reaction Dynamics with Butene Isomers. J. Phys. Chem. A 2013, 117327589–7594 10.1021/jp403030s. [DOI] [PubMed] [Google Scholar]
- Haas Y. Photochemical Alpha-Cleavage of Ketones: Revisiting Acetone. Photoch. Photobio. Sci. 2004, 316–16 10.1039/b307997j. [DOI] [PubMed] [Google Scholar]
- Grubb M. P.; Orr-Ewing A. J.; Ashfold M. N. R. Koala: A New Program for the Processing and Decomposition of Transient Spectra. Rev. Sci. Instrum. 2014, 84, 064104. 10.1063/1.4884516. [DOI] [PubMed] [Google Scholar]
- Grubb, M. P.; Coulter, P. C.; Koyama, D.; Orr-Ewing, A. J.. Dynamics of Solvation, Reaction and Recombination of the Photoproducts of ICN in Solution. Manuscript in preparation.
- Samuni U.; Kahana S.; Fraenkel R.; Haas Y.; Danovich D.; Shaik S. The ICN-INC System - Experiment and Quantum-Chemical Calculations. Chem. Phys. Lett. 1994, 2254–6391–397 10.1016/0009-2614(94)87100-0. [DOI] [Google Scholar]
- Smith A. M.; Coy S. L.; Klemperer W.; Lehmann K. K. Fourier-Transform Spectra of Overtone Bands of HCN from 5400 to 15100 cm–1. J. Mol. Spectrosc. 1989, 1341134–153 10.1016/0022-2852(89)90136-7. [DOI] [Google Scholar]
- NIST Chemistry Webbook, NIST Standard Reference Database Number 69; http://webbook.nist.gov. Website accessed 05/06/2015.
- Dunning G. T.; Glowacki D. R.; Preston T. J.; Greaves S. J.; Greetham G. M.; Clark I. P.; Towrie M.; Harvey J. N.; Orr-Ewing A. J. Vibrational Relaxation and Microsolvation of DF after F-Atom Reactions in Polar Solvents. Science 2015, 3476221530–533 10.1126/science.aaa0103. [DOI] [PubMed] [Google Scholar]
- Dunning G. T.; Murdock D.; Greetham G. M.; Clark I. P.; Orr-Ewing A. J. Solvent Response to Fluorine-Atom Reaction Dynamics in Liquid Acetonitrile. Phys. Chem. Chem. Phys. 2015, 17149465–9470 10.1039/C5CP00774G. [DOI] [PubMed] [Google Scholar]
- Abou-Chahine F.; Greaves S. J.; Dunning G. T.; Orr-Ewing A. J.; Greetham G. M.; Clark I. P.; Towrie M. Vibrationally Resolved Dynamics of the Reaction of Cl Atoms with 2,3-Dimethylbut-2-Ene in Chlorinated Solvents. Chem. Sci. 2013, 41226–237 10.1039/C2SC21267F. [DOI] [Google Scholar]
- Levine R. D.Molecular Reaction Dynamics; Cambridge University Press: Cambridge, U.K., 2005. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.