Optimization and comparison of simultaneous and separate acquisition protocols for dual isotope myocardial perfusion SPECT

Abstract

Dual-isotope simultaneous-acquisition (DISA) rest-stress myocardial perfusion SPECT (MPS) protocols offer a number of advantages over separate acquisition. However, crosstalk contamination due to scatter in the patient and interactions in the collimator degrade image quality. Compensation can reduce the effects of crosstalk, but does not entirely eliminate image degradations. Optimizing acquisition parameters could further reduce the impact of crosstalk. In this paper we investigate the optimization of the rest Tl-201 energy window width and relative injected activities using the ideal observer (IO), a realistic digital phantom population and Monte Carlo (MC) simulated Tc-99m and Tl-201 projections as a means to improve image quality. We compared performance on a perfusion defect detection task for Tl-201 acquisition energy window widths varying from 4 to 40 keV centered at 72 keV for a camera with a 9% energy resolution. We also investigated 7 different relative injected activities, defined as the ratio of Tc-99m and Tl-201 activities, while keeping the total effective dose constant at 13.5 mSv. For each energy window and relative injected activity, we computed the IO test statistics using a Markov chain Monte Carlo (MCMC) method for an ensemble of 1,620 triplets of fixed and reversible defect-present, and defect-absent noisy images modeling realistic background variations. The volume under the 3-class receiver operating characteristic (ROC) surface (VUS) was estimated and served as the figure of merit. For simultaneous acquisition, the IO suggested that relative Tc-to-Tl injected activity ratios of 2.6–5 and acquisition energy window widths of 16–22% were optimal. For separate acquisition, we observed a broad range of optimal relative injected activities from 2.6 to 12.1 and acquisition energy window of widths 16–22%. A negative correlation between Tl-201 injected activity and the width of the Tl-201 energy window was observed in these ranges. The results also suggested that DISA methods could potentially provide image quality as good as that obtained with separate acquisition protocols. We compared observer performance for the optimized protocols and the current clinical protocol using separate acquisition. The current clinical protocols provided better performance at a cost of injecting the patient with approximately double the injected activity of Tc-99m and Tl-201, resulting in substantially increased radiation dose.

1. Introduction

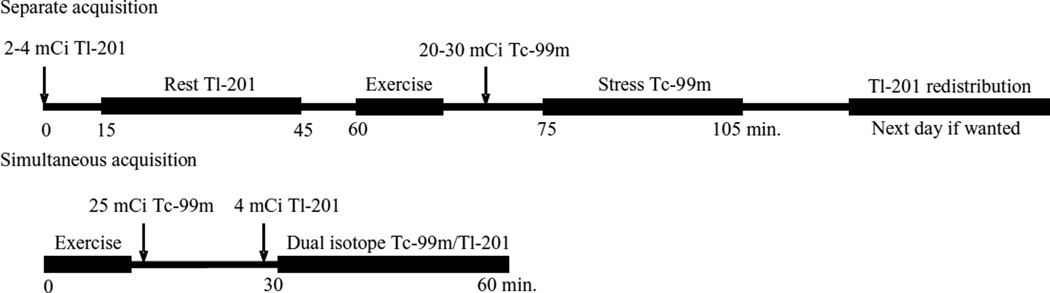
Myocardial Perfusion SPECT (MPS) is a well-established noninvasive method for the detection and characterization of coronary artery disease (CAD). Most myocardial perfusion protocols involve the use of Tl-201 and/or Tc-99m labeled compounds. Single-isotope imaging protocols for tracers using both of these radionuclides as well as dual-isotope protocols with separate acquisition of stress and rest images are well established in routine clinical cardiac imaging (Henzlova et al 2006). Dual-isotope simultaneous-acquisition (DISA) stress Tc-99m/ rest Tl-201 is an appealing cardiac SPECT protocol that allows for simultaneous evaluation and characterization of the stress and rest states of myocardial perfusion (Frey et al 1992, Nakamura et al 1999, Fukushima et al 2005). In addition to providing perfect registration of the rest and stress images in space and time, DISA techniques promise to provide reduced acquisition time, improved patient comfort, and better clinical throughput than single or dual isotope techniques using separate acquisitions (figure 1). In MPS, the stress and rest images are used to classify the patient as being normal (where there is no defect in either image), having a fixed perfusion defect (where there is a defect in both the rest and stress images) or having a reversible defect (where there is a defect in the stress image but not the rest).

Figure 1.

Sample protocols for separate and simultaneous acquisition Tl-201/Tc-99m dual-isotope imaging.

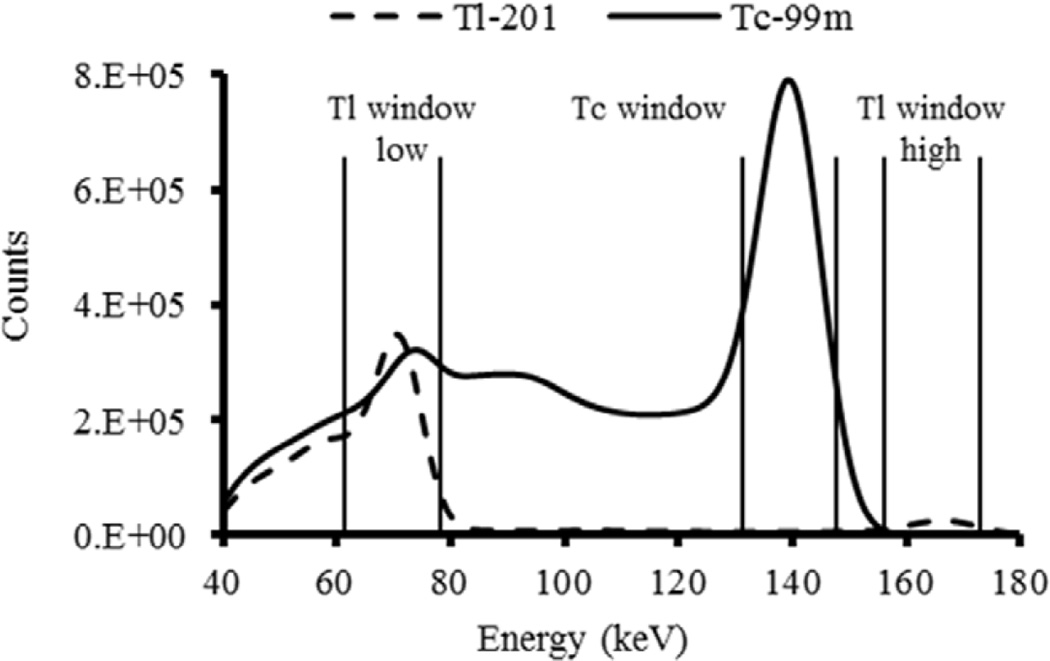
A major image-degrading factor in DISA SPECT is crosstalk, where photons from one radionuclide are detected in the photopeak energy window of the other radionuclide (Kiat et al 1994, Ando et al 1996). Crosstalk results from a number of physical processes, including Compton scatter in the patient, collimator, or crystal or Pb x-ray production in the collimator or simply the inclusion of the 135 keV Tl-201 photopeak in the Tc-99m energy window. There is substantial crosstalk from Tc-99m into the Tl-201 photopeak window, but the contribution of Tl-201 to the Tc-99m energy window is negligible (~2.9%). This is demonstrated by the sample Tc-99m and Tl-201 energy spectra shown in figure 2. The spectra in figure 2 correspond to injected activities of 30 mCi and 3 mCi of Tc-99m and Tl-201, respectively. This crosstalk results in a reduction in image quality that limits both quantitative accuracy and the ability to detect abnormalities and classify patients based on the simultaneously acquired images (Lowe et al 1993, Kiat et al 1994).

Figure 2.

Sample energy spectra indicating detected Tc-99m Tl-201 photons.

Techniques for compensating for crosstalk include estimating and subtracting it prior to reconstruction or reconstruction-based compensation. This can be done either in the spatial domain using crosstalk models (Knesaurek 1994, Kadrmas et al 1997, Kadrmas et al 1999, de Jong et al 2002a, 2002b, Kangasmaa et al 2012) or using measurements in multiple energy windows (Yang et al 1993, Moore et al 1995, Kacperski et al 2011). However, even with an ideal crosstalk estimation method, it is impossible to remove the statistical noise that crosstalk photons contribute and limit image quality. One approach to further improve image quality is to reduce the amount of crosstalk by optimizing the acquisition parameters, such as the relative injected activity, defined as the ratio of Tc-99m to Tl-201 injected activities, and the acquisition energy windows. However, there are a number of tradeoffs involved, as will be discussed in more detail below. It is thus essential to balance these effects in terms of the performance on the task that will be performed with the images. For MPS, the relevant task is the 3-class classification task described above.

The task-based optimization of DISA acquisition parameters requires taking into account the 3-class nature of the diagnostic task because there is an inverse relationship between image qualities for the rest and stress images. For example, if the Tl-201 injected activity is fixed, then decreasing the Tc-99m injected activity decreases the crosstalk contamination of the rest image, and thus improves the rest image quality at the expense of noisier stress images; similarly, increasing the Tc-99m injected activity improves the stress image quality at the cost of more crosstalk contamination in the rest images.

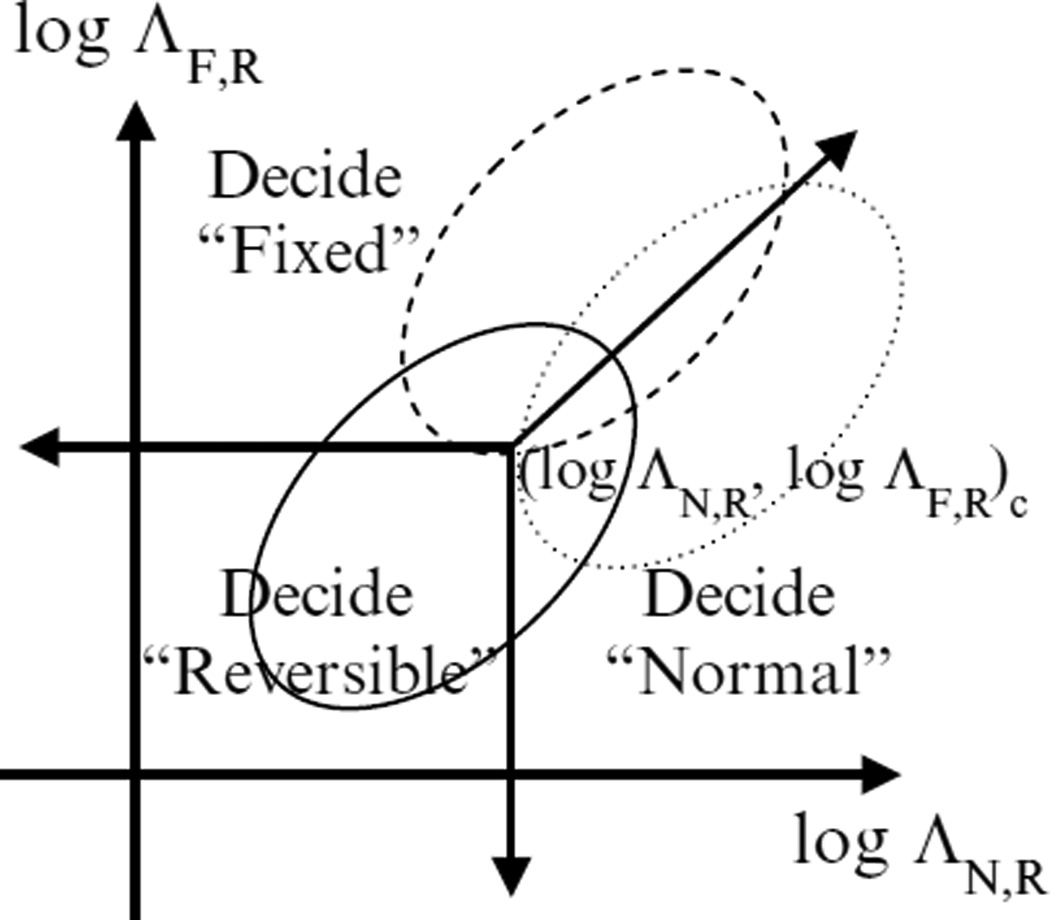
He et al (He et al 2006, He and Frey 2006, 2007, 2008) derived a 3-class ROC analysis method that extends and unifies the decision theory, linear discriminant analysis, and psychophysical foundations of binary ROC analysis in a 3-class paradigm assuming an equal error utility (EEU), i.e. the utilities of making the two possible incorrect decisions are the same for a given class. The decision variable that maximizes the expected utility under the EEU assumption was the log-likelihood ratio; the corresponding decision structure was as shown in figure 3. This is thus the 3-class ideal observer (IO).

Figure 3.

Log likelihood ratio decision plane and the decision structure for the practical 3-class ROC analysis method.

Task performance is characterized by the 3-class ROC surface, obtained by sweeping the decision structure across the log-likelihood decision plane and calculating the triplet (T1F, T2F and T3F), defined as the true class fractions, for every position of the critical point, i.e. the intersection of the 3 rays in the decision structure. The volume under the 3-class ROC surface (VUS) was proposed as a figure-of-merit (FOM) for task performance. We have previously used this 3-class ROC analysis method to investigate the effect of the injected activity of Tc-99m on 3-class diagnostic task performance (He et al 2008). That work investigated a fixed Tl-201 injected activity of 3mCi and Tc-99m injected activities of 8, 16 and 24 mCi and simultaneous and separate acquisition. The energy window was not optimized. The investigation was performed using reconstructed images and a channelized hotelling observer (CHO). This evaluation was very computationally intensive, as it required simulation of full SPECT data, reconstruction of many noise realizations of projection data, and optimization of the number of iterations and post-reconstruction cutoff filter. For separate acquisition, better performance was found for 24 mCi, while for simultaneous acquisition, 16 mCi gave the best performance.

Another protocol parameter that can be varied to optimize the quality of DISA images is the energy window used to acquire projection data for each isotope. Wang et al (Wang et al 2005) studied the optimal energy windows and relative injected activities for Tc-99m/Tl-201 DISA using a signal known exactly (SKE), background know exactly (BKE) task combined with a somewhat ad hoc observer, the no-low-frequency IO. They used the IO signal to noise ratio as the figure of merit summed over 4 projection views of the SPECT data. In that study, they investigated 13 Tc:Tl activity concentration ratios varying from 0.1:1to 5:1 while having Tl-201 activity fixed. They reported that a 22 keV wide Tl-201 acquisition energy window centered at 72 keV was optimal for a Tc:Tl ratio of 1:1. They also observed dependence between the optimal Tl-201 energy window and Tc-99m injected activity. The optimal Tl-201 acquisition energy window was narrower for higher Tc-99m injected activities. Since they used 2-class ROC analysis it was only possible to report the tradeoff between defect detection in the two images and not the overall optimal activities. They also reported that the optimal energy windows for simultaneous and separate acquisition protocols were different. The task in that work did not include background variations, i.e. it was a BKE task. To account for the fact that the IO tends to overestimate the performance of human observers for BKE tasks, they used a no-low-frequency IO. In addition, since they only used two-class ROC analysis it was not possible to estimate task performance.

In this work, we implemented rigorous and practical projection-domain-based optimization methods for performing the requisite 3-class optimization using the IO operating on realistic data generated from a population of phantoms. We have also compared the performance for the dual isotope simultaneous and separate acquisition protocols. We have also compared the observer performances for the optimized protocols and the current clinical protocol using separate acquisition. The IO is an observer that makes optimal use of all the information in the image data about the task. Thus, it has been used to optimize acquisition parameters, based on the logic that it guarantees that there is maximum information in the projection data about the task. In this logic, the role of reconstruction is to then put that information in a form that a human observer can best interpret. In our previous work (Ghaly et al 2015), we demonstrated that sequentially optimizing acquisition parameters in the projection domain and then optimizing the reconstruction algorithm and compensation methods in the image domain yielded similar optimal operating ranges compared to optimizing the acquisition parameters and the reconstruction algorithm jointly, provided that good models of the image formation process were incorporated into the reconstruction algorithm. In that study, we used the IO and an anthropomorphic CHO applied to reconstructed images to optimize Tc-99m acquisition energy window width and evaluate the dual and triple energy window and the effective source scatter estimation (ESSE) scatter modeling methods, in the context of a myocardial perfusion SPECT defect detection task. We found that, when good scatter models, such as the ESSE method, were used in the reconstruction, the optimal energy window for the IO and CHO were similar. In the context of the present study, model based scatter models have previously been applied in a number of SPECT imaging applications for scatter, downscatter, and crosstalk estimation and provided accurate compensation (Kadrmas et al 1999, Du et al 2006). In addition, fast-Monte Carlo downscatter models have also been proposed. Since these are accurate and available, our logic for the present study is that projection domain optimization will provide good predictions of the optimal operating points.

2. Methods

2.1. Phantom population and projection data

We have previously developed a realistic digital phantom population for myocardial perfusion SPECT imaging research (Ghaly et al 2014). In this section, we give a brief overview of the population and the generation of the corresponding Tc-99m and Tl-201 projections. The population is based on the 3D XCAT phantom with organ size parameters sampled from the Emory PET Torso Model Database (Barclay et al 2005). The population consists of 54 phantoms and includes variations in gender, body size, heart size and subcutaneous adipose tissue thickness. Anterolateral and inferior perfusion defects are available for each phantom; in this work we used a defect with 10% extent and 25% severity.

Projections of the XCAT phantoms were simulated using the SimSET Monte Carlo code and angular response functions to model interactions in the body and the collimator detector system (including Pb x-rays, septal penetration and scatter), respectively (Lewellen et al 1998, Song et al 2005). For each phantom, low noise Tc-99m and Tl-201 projection data for the heart, liver and body (including all other organs) are available, to allow modeling of organ uptake variability by post-simulation scaling and summing of the individual sets of projections followed by simulating Poisson noise. Organ uptakes are based on data from a set of 34 patients who underwent sequential-acquisition dual isotope MPS. In the clinical data, patients were injected with 30 mCi of Tc-99m and 3 mCi of Tl-201, corresponding to total effective dose of 25 mSv (Valentin 1998, Strauss et al 1998). The durations at each view for the clinical acquisitions were 26 and 30 s for the Tc-99m and Tl-201 acquisitions, respectively, at a total of 60 projection views. Projection images were simulated at 60 equispaced angles over a 180° acquisition arc extending from 45° right anterior oblique (RAO) to 45° left posterior oblique (LPO) binned in a 128 × 114 matrix with a pixel size of 0.442 cm. We simulated a patient specific non-circular body-contouring orbit. We modeled a GE low-energy high-resolution (LEHR) collimator and a 9.5 mm thick Sodium Iodide (NaI) crystal with a 9% energy resolution at 140 keV and E^−1/2 energy dependence.

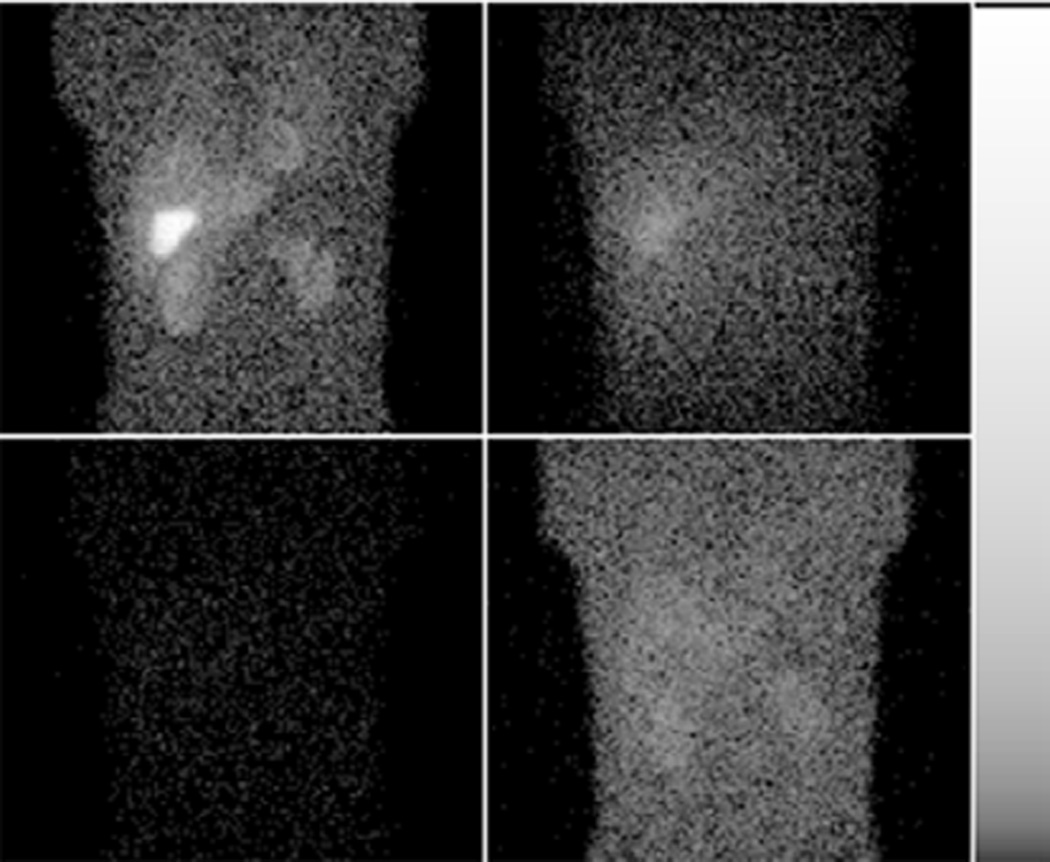
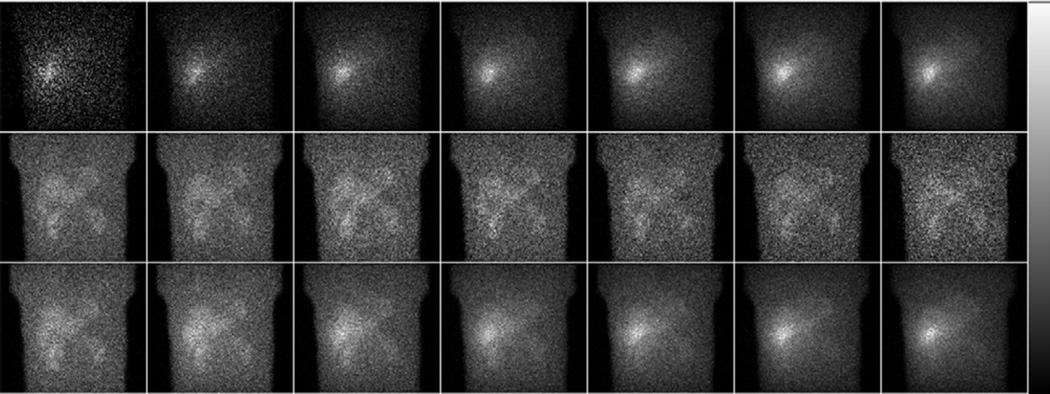
Optimizing relative injected activity and the width of acquisition energy window requires projection data generated in various energy windows and injected activities for both Tc-99m and Tl-201. The flexible design of the projection database in (Ghaly et al 2014) allowed us to rapidly generate projections for various combinations of Tc-99m and Tl-201 injected activities and acquisition windows. To study the effect of the relative injected activity, we varied Tl-201 activity from 1 to 2.5 mCi in increments of 0.25 mCi. We calculated the activity of Tc-99m so that the total effective dose was kept constant at 13.5 mSv (Valentin 1998, Strauss et al 1998). We selected this as the dose level for investigation given current concerns over patient radiation dose. The count levels in this study could also be achieved by a lower dose, e.g. 10 mSv, with longer acquisition duration, e.g. 35% longer than the standard acquisition duration. Table 1 shows the different injected activities of Tc-99m and T-201, labeled as R₁ to R₇, modeled in this study. To study the effects of window widths, we varied the width of the Tl-201 energy window from 4 to 40 keV in 4 keV increments with the window center fixed at 72 keV; these windows are labeled W₁ to W₁₀ as shown in table 2. Also note that, for all the investigated Tl-201 energy windows, we added the detected counts in a 156–180 keV window to the lower acquisition energy window to include the contribution of the 167 keV Tl-201 photopeak. Due to the negligible contribution of Tl-201 to Tc-99m image as illustrated by figure 4, we did not optimize Tc-99m window width. We used a 20% window centered at 140.5 keV, a typical recommended energy window for Tc-99m imaging and one we have found to be in the optimal range in previous work (Ghaly et al 2013, 2015). Sample projections from Tc-99m and Tl-201 acquired in a 20 keV wide Tl-201 energy window for the different relative injected activities are shown in figure 5. Note the increasing amount of Tc-99m downscatter in the Tl-201 window from left to right as well as the decreased noise in the Tl-201 images as the Tl-201 activity increases (from right to left). Figure 6 demonstrates the tradeoff between noise and amount of scatter when increasing the width of the Tl-201 acquisition energy window.

Table 1.

Tl-201 and Tc-99m activities.

	Tc-99m activity (mCi)	Tl-201 activity (mCi)	Relative injected activity (Tc/Tl)
R1	1.7	2.5	0.68
R2	5.9	2.25	2.6
R3	10	2	5
R4	14.1	1.75	8.1
R5	18.2	1.5	12.1
R6	22.3	1.25	17.8
R7	26.5	1	26.5

Table 2.

Investigated Tl-201 energy window settings.

	W1	W2	W3	W4	W5	W6	W7	W8	W9	W10
Lower threshold (keV)	70	68	66	64	62	60	58	56	54	52
Upper threshold (keV)	74	76	78	80	82	84	86	88	90	92
Width (keV)	4	8	12	16	20	24	28	32	36	40
Width (%)	5.5	11.1	16.7	22.2	27.8	33.3	38.9	44.4	50	55.6

Figure 4.

Sample noisy projection images for Tc-99m (top row) and Tl-201 (bottom row) acquired in a 20% wide Tc-99m energy window (left) and 28% wide Tl-201 energy window, W₅ (right). Activities of Tc-99m and Tl-201 correspond to configuration R₃. Images are displayed on a logarithmic gray scale to show more clearly the lower uptake organs.

Figure 5.

Sample noisy Tc-99m (top), Tl-201 (middle) and summed (bottom) projection images acquired in a 20 keV wide Tl-201 energy window (W₅). The Tc-99m and Tl-201 activities correspond to the activity combinations R₁ to R₇ from left to right.

Figure 6.

Sample noisy projection images acquired in Tl-201 energy windows W₁ to W₁₀ from left to right including crosstalk from Tc-99m into the Tl-201 window.

2.2. Three-class ideal observer study

In this section, we review the ideal decision strategy and accompanying ideal observer for the 3-class detection task. In a binary detection task, the goal is to determine whether or not a signal is present based on the measured data. However, for the 3-class MPS detection task the observer is required to classify the patient as being normal (class 1) or having a fixed (class 2) or reversible (class 3) perfusion defect. The 3-class hypotheses to be tested can be represented mathematically by:

• H_N : g = b + n,

• H_F : g = b +s_F + n,

• H_R : g = b + s_R + n,

where g, b, s_F, s_R and n are the noisy projection, background, fixed defect, reversible defect and noise vectors, respectively, and the hypotheses H_N, H_F and H_R mean signal absent, fixed and reversible defects present, respectively.

The ideal observer uses the likelihood ratio, or any monotonic transformation thereof such as the log-likelihood ratio, of defect-present versus defect-absent as the decision variable. To construct the 3-class ROC surface and compute the VUS, it is necessary to calculate the log-likelihood ratios log Λ_N,R(g) and log Λ_F,R(g) defined as,

$$\text{log}{\Lambda }_{\mathrm{N},\mathrm{R}}(\mathbf{g}|\mathbf{b})=\text{log}\frac{\mathit{\text{pr}}(\mathbf{g}|H_{\mathrm{N}})}{\mathit{\text{pr}}(\mathbf{g}|H_{\mathrm{R}})},$$ (1)

$$\text{log}{\Lambda }_{\mathrm{F},\mathrm{R}}(\mathbf{g}|\mathbf{b})=\text{log}\frac{\mathit{\text{pr}}(\mathbf{g}|H_{\mathrm{F}})}{\mathit{\text{pr}}(\mathbf{g}|H_{\mathrm{R}})}.$$ (2)

Although using the IO to optimize the acquisition protocols is theoretically appealing, it is technically difficult to calculate the IO test statistics (log-likelihood ratios) for realistic populations of realistic objects. The expression for the log-likelihood ratio in the case when background variability is included would be the average over the backgrounds with the posterior densities pr(b|g, H_R), a density that is usually complex and unknown and thus hard to sample from (Barrett and Myers 2004). Markov chain Monte Carlo (MCMC) methods have been developed to allow estimating the log-likelihood ratios using Monte Carlo methods (Kupinski et al 2003, Park et al 2003, He et al 2008).

To apply this method, we parameterized the objects, and thus the projection data arising from them, by the object parameter vector, $\stackrel{\rightharpoonup }{\theta }=[m,n,p,q,A_{\text{heart}},A_{\text{liver}},A_{\text{body}}]\stackrel{\rightharpoonup }{\theta }$ is a combination of discrete and continuous parameters: m, n, p and q are integer parameters specifying the object gender, body size, heart size and subcutaneous adipose tissue thickness, and A_heart, A_liver and A_body are scalar parameters representing the total activity in the heart, liver and body, respectively. Thus, the total projection, $\mathbf{b}(\stackrel{\rightharpoonup }{\theta })$, given the object parameter vector, $\stackrel{\rightharpoonup }{\theta }$, can be represented as:

$$\mathbf{b}(\overrightarrow{\theta })=A_{\text{heart}}{\mathbf{\text{prj}}}_{m,n,p,q}^{\text{heart}}+A_{\text{liver}}{\mathbf{\text{prj}}}_{m,n,p,q}^{\text{liver}}+A_{\text{body}}{\mathbf{\text{prj}}}_{m,n,p,q}^{\text{body}},$$ (3)

where prj^heart, prj^liver and prj^body were the projections of the heart, liver and the body (including other organs), respectively, filled with unit activity for the anatomy specified by m, n, p, and q.

We adopted a Metropolis–Hastings approach to draw samples,${\stackrel{\rightharpoonup }{\theta }}^{(0)},{\stackrel{\rightharpoonup }{\theta }}^{(1)},\dots {\stackrel{\rightharpoonup }{\theta }}^{(k)},\dots {\stackrel{\rightharpoonup }{\theta }}^{(N)}$ where N is the number of iterations (N = 50 × 10³), from the posterior distribution $\mathit{\text{pr}}(\stackrel{\rightharpoonup }{\theta }|\mathbf{g},H_{\mathrm{R}})$ for expressions 1 and 2, and computed the ergodic log Λ̃_N,R(g|b) and log Λ̃_F,R(g|b). We discarded the first 20,000 iterations, which are referred to as the burn-in iterations, to ensure the stabilization of each Markov chain. To efficiently apply MCMC IO estimation, we precomputed the noise-free projection images prj^heart, prj^liver and prj^body for each phantom in the population. This constituted a database of 54 different anatomies. For a given parameter vector, ${\stackrel{\rightharpoonup }{\theta }}^{(k)}$, we located the corresponding anatomy using the indexes m, n, p and q and the signal-absent (background) projection image could then be generated by scaling and summing the three organ projections using the scalar activity parameters A_heart, A_liver and A_body.

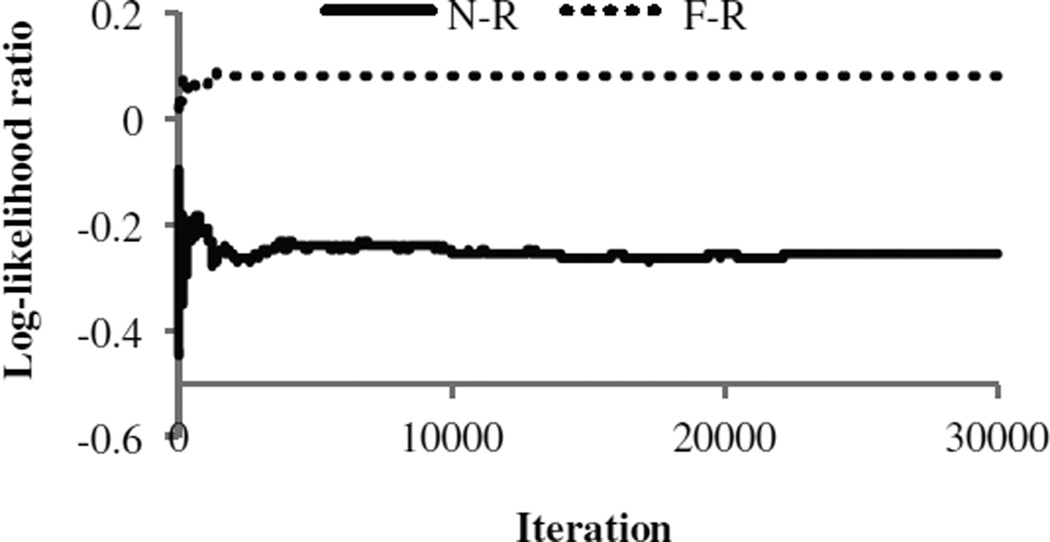
Figure 7 shows the log-likelihood ratios, log Λ_N,R(g) and log Λ_F,R(g) for one sample input projection image as a function of the iteration number after the burn-in process. The input projection image had a fixed perfusion defect in the antero-lateral wall of the heart, i.e. a defect that was present in both the stress and rest images.

Figure 7.

A plot of the log-likelihood ratio versus iteration number for an input projection image with a fixed perfusion defect in the anterolateral wall.

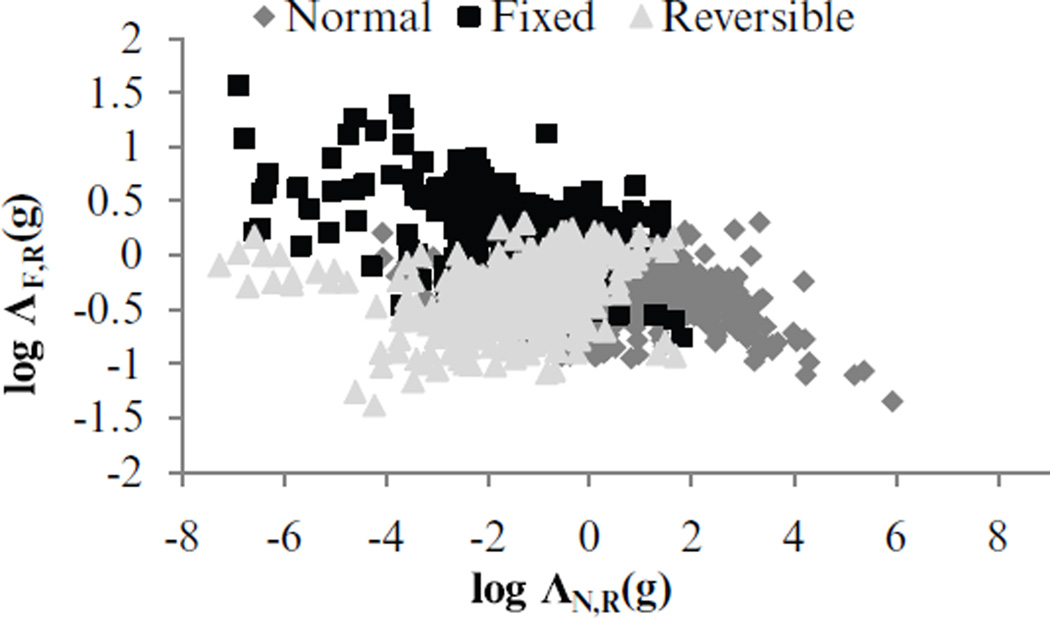
For each combination of energy window and relative injected activity, we computed the IO test statistic using the MCMC method for an ensemble of 1,620 (54 phantoms × 2 defect locations × 15 uptake realizations) triplets of fixed, reversible and normal noisy images, g, modeling variations in anatomical and organ uptake. Figure 8 shows the decision plane with a scatter plot of the pairs of test statistics for each class. Each projection image, g, was comprised of two images, the rest and stress images, stacked together. Each of the stress and rest projection data contained a 64 × 24 × 60 pixel region of interest centered over the heart centroid. This ensured that the whole heart was included inside the region-of-interest. This gave each energy window and injected activity combination that was then analyzed using 3-class ROC methodology to estimate the VUS (He et al 2006, He and Frey 2008). The VUS was estimated using a bootstrap procedure that also provided estimates of the standard deviation of the VUS.

Figure 8.

Decision plane for simulated dual-isotope MPS images for relative injected activity R₃ and acquisition energy window W₅.

3. Results and discussion

3.1. Dual isotope imaging with simultaneous acquisition

In this section, we present results for the case of simultaneous acquisition of the stress and rest images.

3.1.1. Stress Tc-99m and rest Tl-201 image qualities

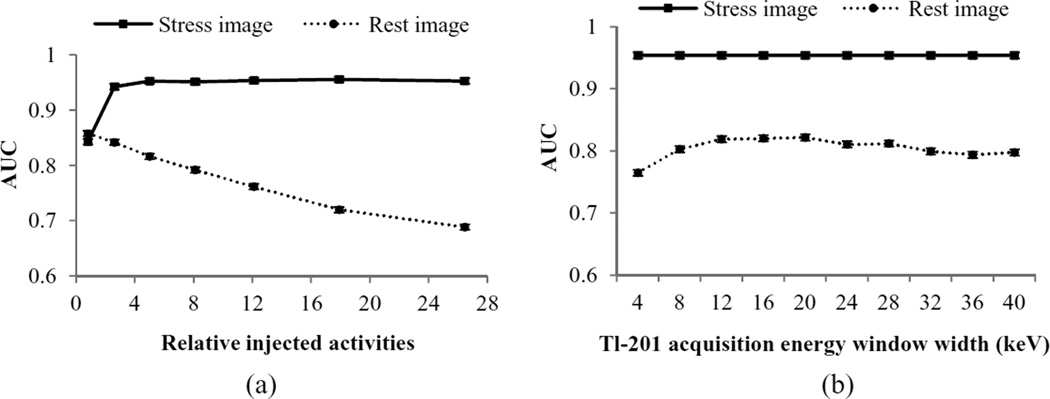
In simultaneous acquisition, the quality of the stress image has a direct relationship to the injected activity of Tc-99m. However, the quality of the rest image degrades with increasing injected activity of Tc-99m due to crosstalk. Thus, there is an inverse relationship between the qualities of the stress and rest images. We performed a binary observer study to assess the quality of each of the stress and rest images with respect to a binary detection task. For the stress image, we pooled the defect-present images from the fixed and reversible classes and used the normal class images as defect-absent. For the rest image, we used the fixed class images as defect-present and pooled the defect-absent images from the normal and reversible classes.

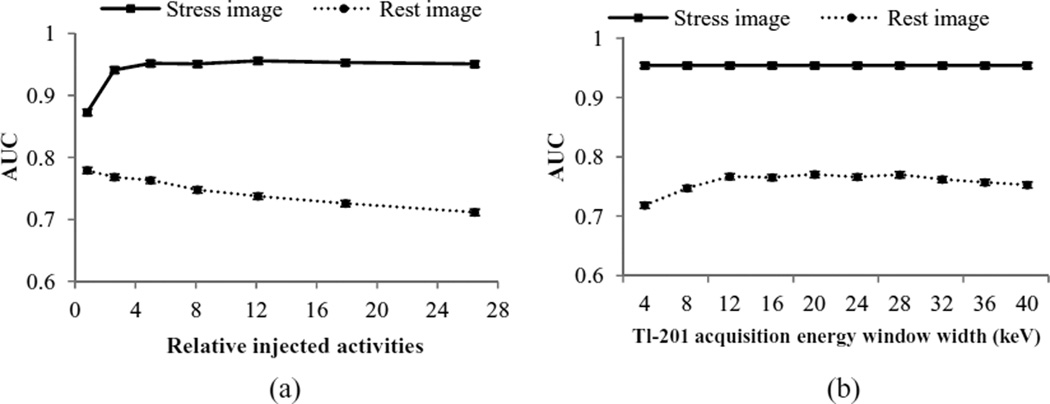
Figure 9 shows the IO performance for the rest and stress images for the different relative injected activities and Tl-201 energy windows. The error bars on the AUC values were small (typically on the order of 5 × 10⁻³). The quality of the stress Tc-99m image improved when the Tc-99m injected activity increased (from left to right). The improvement in performance was small for higher injected activities and was, as expected, independent of the Tl-201 acquisition energy window. This agrees with results previously reported in (He et al 2010). For the rest Tl-201 image, we see that the performance improved as the Tl-201 injected activity increased (from right to left), corresponding to a concurrent reduction of the Tc-99m crosstalk. The rest image detection performance had a broad maximum in the center of the range of investigated Tl-201 energy windows. This is explained by the tradeoff between image noise, which decreases with increasing window width, and the amount of Tl-201 self-scatter and Tc-99m crosstalk, which increase as the width of Tl-201 energy window increases.

Figure 9.

Comparison of IO performances in a binary observer study to assess the qualities of stress Tc-99m and rest Tl-201 images for dual isotope simultaneous acquisition for (a) the different injected activities and energy window W₅ and (b) the Tl-201 energy window widths and relative injected activity R₃. We observed similar patterns for the different energy windows and relative injected activities.

3.1.2. Pairwise comparison of the 3 classes

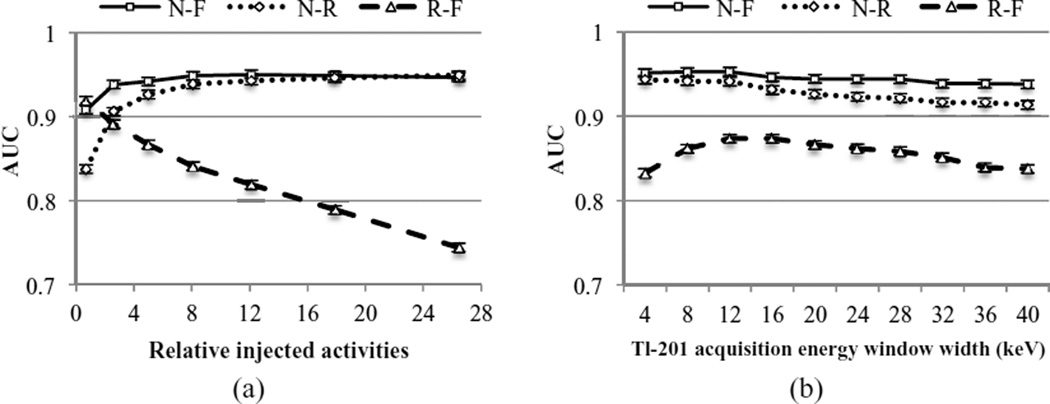
To shed light on the underlying tradeoffs and difficulty of distinguishing the classes, we performed binary observer studies that involved pairwise comparisons of the classes, i.e. normal versus fixed defect (N–F), reversible versus fixed defect (R–F), and normal versus reversible defect (N–R). In all cases, both the rest and stress images were provided to the IO. Figure 10 shows the AUC values for the three pairs of classes for (a) the different relative injected activities and (b) the Tl-201 acquisition energy window widths.

Figure 10.

Comparison of pairwise binary observer performance for dual isotope simultaneous acquisition for (a) the different injected activities and energy window W₅ and (b) the various Tl-201 energy window widths and relative injected activity R₃. We observed similar patterns for the different energy windows and relative injected activities.

To understand the trends in these figures, first consider the effect of the quality of the rest and stress images on these different tasks. Table 3 shows the different defect statuses in the rest and stress images for each pair of classes. Distinguishing between normal and fixed involves a difference in defect status in both the rest and stress images. Distinguishing between normal and reversible involves a change in only the stress image. Distinguishing between reversible and fixed involves only a change in the rest image.

Table 3.

Change in defect status in rest and stress images for the pairs of classes.

Classes (1 versus 2)	Resta	Stressa
Fixed versus Normal	+ ,−	+ ,−
Fixed versus Reversible	+ ,−	+ ,+
Normal versus Reversible	− ,−	− ,+

^aIn these columns the first symbol indicates the presence (+) or absence (−) of a defect in the first class and the second symbol indicates the presence or absence in the second class.

Consider first the effect of relative injected activities. From figure 10(a), performance in distinguishing reversible and fixed defects increased with increasing Tl-201 activity (right to left). This reflects the fact that detecting this difference depends on detecting the defect in the rest image: increasing Tl-201 activity both decreased noise in the Tl-201 image and reduced crosstalk from Tc-99m. Also note that performance for this pair of classes was worse than for the other pairs of classes in the cases where the relative injected activity was less than 2.6. For the cases of normal versus fixed and normal versus reversible, the IO performance decreased as Tl-201 activity increased (from right to left). However, the performance decrease was greater for the case of normal versus reversible, which depends only on the stress image. In this case the reduction in noise and crosstalk in the rest image did not offset the degraded quality in the stress image due to less Tc-99m activity and thus greater noise. However, for the normal versus fixed case, improvement in the rest image quality partially offsets the degraded image quality of the stress image.

Figure 10(b) shows the effects of varying the Tl-201 energy window width on performance for the 3 pairs of 2-class tasks. For the cases of normal versus fixed and normal versus reversible, performance decreased modestly with increasing Tl-201 energy window width, with the decrease somewhat larger for the normal versus reversible case. For the case of reversible versus fixed, there was a range of optimal energy windows (W₃–W₄), indicating that there is a balance between noise, which decreases, and scatter and crosstalk, which increase with increasing Tl-201 energy window width.

The results in figures 9 and 10 confirm that it was impossible to determine the optimal parameters for dual isotope imaging using a 2-class optimization paradigm. For example, in figure 9(a), rest image quality degrades while stress image quality increases with increasing relative injected activity. Similarly, in figure 10(b), discrimination between no defect and fixed defect or no defect and reversible defect is best with the narrowest Tl-201 energy window while discrimination of the reversible versus fixed defects was best for an intermediate energy window width. The optimal tradeoff between these factors is not clear, and it was thus important to consider the 3-class nature of the problem.

3.1.3. 3-Class IO study

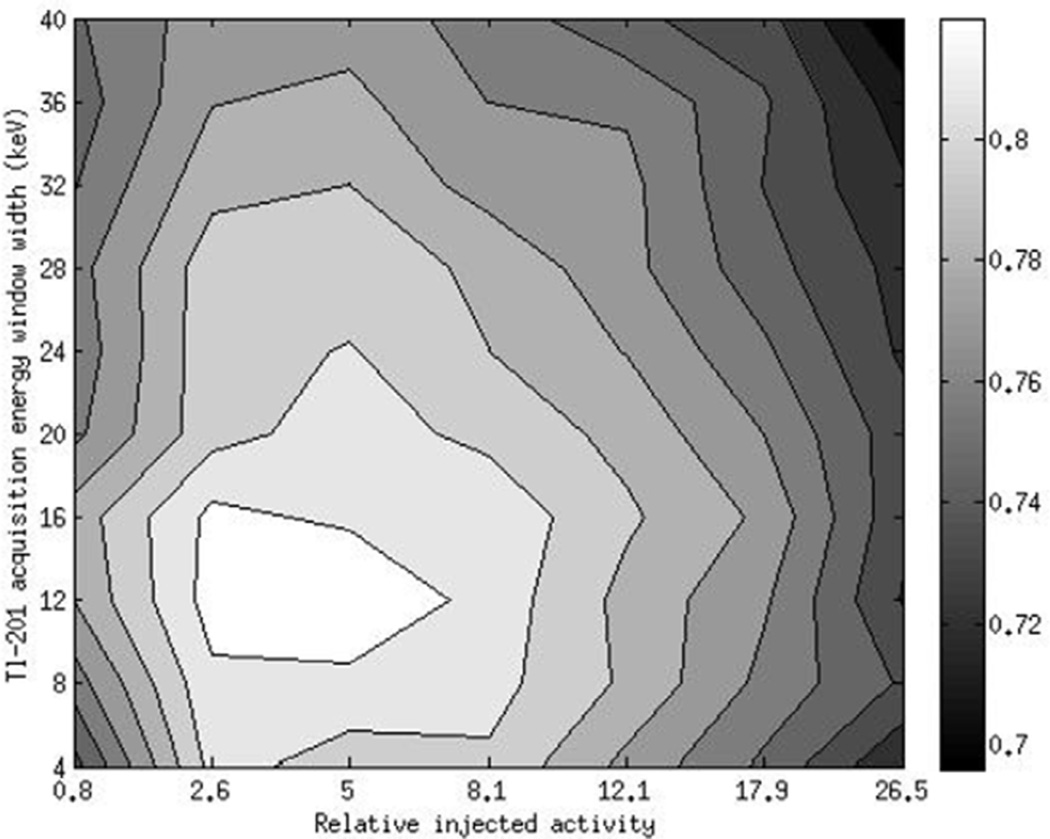
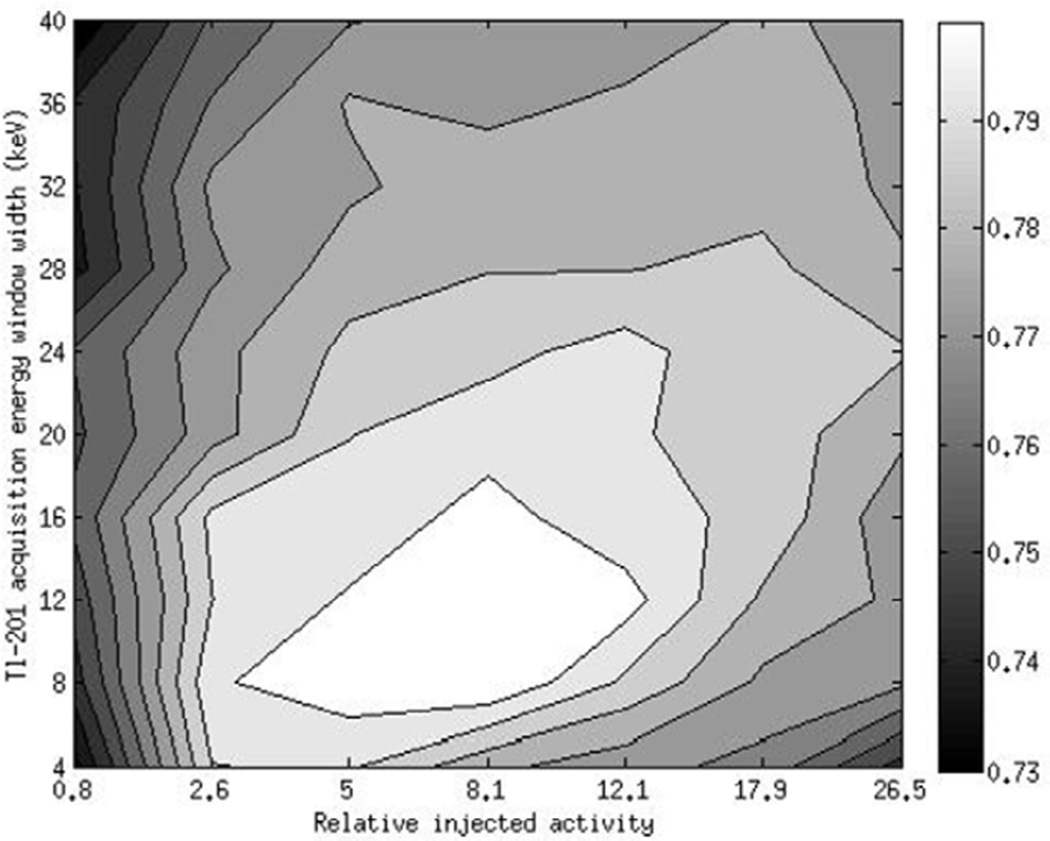
Figure 11 shows a 2D contour plot of the VUS values for the different relative injected activities and Tl-201 acquisition energy windows. The standard deviation of the VUS values was about 0.01. The data suggest that optimal relative injected activities of 2.6–5 (R₂–R₃) and acquisition energy window widths of 8–16 keV (W₂–W₄) were optimal (VUS = 0.806). Also note that the optimal injected activities were the same for the different acquisition windows, as indicated by the shape of the contours. We tested the statistical significance of the differences between the VUS value of the configuration that had the maximum VUS (i.e. a 2.6 relative injected activity and a 12 keV Tl-201 energy window wide) and that of the relative injected activities from 0.68 to 8.1 (R₁–R₄) and acquisition energy windows with widths from 4 to 20 keV (W₁–W₅) on a pair-wise basis. The corresponding p-values, indicating the probability that differences between VUS₁ and VUS₂ were due to chance, are shown in table 4. The boldface values indicate cases where the p-values were > 0.05, implying that the differences between the VUS values were not significant.

Figure 11.

2D contour plot of the VUS values for the different injected activities and acquisition energy windows for dual isotope simultaneous acquisition.

Table 4.

Results of statistical significance tests for the optimal VUS value and the different configurations.

Energy window width (keV)/ Relative injected activity	R1	R2	R3	R4
	0.68	2.6	5	8.1
W1 (4)	1.15E-13	8.41E-04	7.11E-07	9.43E-04
W2 (8)	6.20E-14	9.36E-03	2.89E-01	4.02E-02
W3 (12)	1.55E-09	Max	7.00E-01	3.40E-02
W4 (16)	1.59E-05	4.02E-01	7.03E-02	1.32E-02
W5 (20)	5.54E-11	7.48E-03	4.09E-02	1.79E-06

3.2. Dual isotope imaging with separate acquisition

We studied the case of separate acquisition of the stress and rest images, i.e. where there was no crosstalk between the two images and thus the qualities of the stress and rest images were independent of each other. The goal of this study was to compare the optimal acquisition parameters to the case of simultaneous acquisition and determine if there was significant improvement for using the separate acquisition over the simultaneous acquisition.

3.2.1. Stress Tc-99m and rest Tl-201 image qualities

We performed a binary observer study to evaluate the performance of the IO in assessing the qualities of the rest Tl-201 and stress Tc-99m images interpreted separately. Figure 12 shows IO performance for the different relative injected activities and Tl-201 energy windows. The trends were similar to those for simultaneous acquisition (figure 9). However the degradation in the IO performance for the rest image was greater for the simultaneous acquisition as the Tc-99m injected activity and Tl-201 acquisition energy window width increased.

Figure 12.

Comparison of IO performances in a binary observer study to assess the qualities of stress Tc-99m and rest Tl-201 images for dual isotope imaging with separate acquisition for (a) the different injected activities and energy window W₅ and (b) the Tl-201 energy window widths and relative injected activity R₃. We observed similar patterns for the different energy windows and relative injected activities.

Examining figures 9 and 12 shows that the observer performed better on the rest image in the simultaneous acquisition case (when crosstalk was present) than in the separate acquisition case. This unexpected result can be understood by considering the images used by the observer. For the simultaneous acquisition case, the rest (Tl-201) defect absent images were from both the normal and reversible classes, while the defect present images were from the fixed defect class. The crosstalk in the Tl-201 image is a low-frequency version of the Tc-99m image. Thus, for the defect present case, crosstalk represents the ‘same’ perfusion state and does not degrade the observer’s interpretation of the rest image; indeed, it could theoretically improve it by adding counts. For the defect absent case, the same is true for images from the normal class. That is, it is only for the defect absent case with images from the reversible class where the rest and stress images represented a different perfusion state and thus where crosstalk would have degraded observer performance. Apparently, the fact that crosstalk could actually reinforce the information about defect status in the rest image in two of the three cases was enough to improve overall rest defect detection performance.

3.2.2. Pairwise comparison of the 3 classes

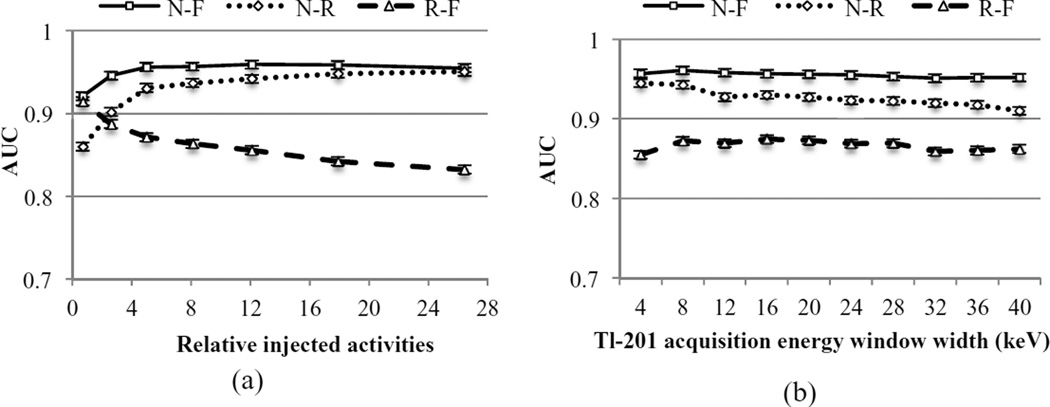
As was the case with simultaneous acquisition, we compared performances for the binary task of distinguishing between the various pairs of classes. Figure 13 shows the IO performance for the three pairs of classes in terms of AUC for the different relative injected activities and Tl-201 acquisition energy windows. The trends were similar to those for simultaneous acquisition, though the degradation in the IO performance for distinguishing between reversible and fixed defects was greater for the simultaneous acquisition as the Tc-99m injected activity and Tl-201 acquisition energy window width increased (left to right).

Figure 13.

Comparison of pairwise binary observer performance for dual isotope separate acquisition.

3.2.3. 3-Class IO study

The optimal injected activity could, in principle, vary as a function of Tl energy window. Figure 14 shows a 2D contour plot of the VUS values for the different relative injected activities and Tl-201 acquisition energy windows. The standard deviation of the VUS values was about 0.01. The plot shows that the IO had a maximum VUS value (VUS = 0.809) when performing on images acquired using a relative injected activity of 8.1 (R₄) and an 8 keV wide acquisition energy window (W₂). However, the differences between the VUS value for the configuration (R₄, W₂) and that of many of the other configurations were not statistically significant at a confidence level of p = 0.05, as shown in table 5 (the boldface cells indicate that the differences between the VUS values were not significant). Therefore, there was a much wider range of near-optimal injected activities and Tl-201 energy windows than for simultaneous acquisition.

Figure 14.

2D contour plot of the VUS values for the different injected activities and acquisition energy windows for dual isotope separate acquisition.

Table 5.

Results of statistical significance tests for the optimal VUS value and the different configurations.

Energy window width (keV) / Relative injected activity	R1	R2	R3	R4	R5	R6
	0.68	2.6	5	8.1	12.1	17.8
W1(4)	3.97E-10	2.08E-03	3.27E-02	1.39E-04	2.34E-07	5.52E-05
W2(8)	4.12E-08	3.09E-01	8.17E-01	Max	5.68E-03	6.18E-04
W3(12)	1.04E-08	2.32E-03	4.97E-01	1.83E-01	8.16E-01	1.05E-04
W4(16)	1.68E-08	1.44E-02	1.10E-02	5.79E-01	1.28E-01	1.96E-03
W5(20)	2.47E-07	3.74E-05	2.00E-03	2.99E-02	2.63E-04	1.82E-03

3.2.4. Comparison between simultaneous and separate acquisition protocols

We compared the optimal parameters that yielded the best performance for both simultaneous and separate acquisition protocols. Table 6 shows the ranges of optimal acquisition parameters for simultaneous and separate acquisitions as well as the observer performance for the binary and 3-class defect detection tasks. The observer favored higher Tc-99m injected activities (less Tl-201) for separate acquisition than simultaneous acquisition. The reduced Tc-99m would reduce the effect of crosstalk on image quality for simultaneous acquisition. As shown in table 6, there was an inverse relation between the stress and rest image qualities for simultaneous and separate acquisitions. The observer performance on the rest image for simultaneous acquisition was better than that for separate acquisition. The inverse was also true for the stress image.

Table 6.

Acquisition parameters and observer performance for the optimized and clinical dual isotope protocols.

	Optimized protocol		Clinical protocol
Acquisition type:	Simultaneous	Separateb	Separate
Acquisition parameters:
(a) Injected activities (mCi):
Tc-99m	5.9–10a	5.9–18.2a	30
Tl-201	2–2.25a	1.5–2.25a	3
Relative injected activity	2.6–5a	2.6–12.1a	10
Total effective dose (mSv)	13.5	13.5	27.5
(b) Energy window width (%):
Tc-99m	20	20	20
Tl-201	16.6–22.2a	11.1–22.2a	27.8
2-class IO performance:
(a) Rest and stress image qualities
Rest Tl-201	0.819	0.751	0.792
Stress Tc-99m	0.938	0.951	0.953
(b) Pairwise comparison between the 3 classes
Normal Versus Fixed	0.949	0.960	0.961
Normal Versus Reversible	0.919	0.944	0.947
Reversible Versus Fixed	0.892	0.862	0.875
3-class IO performance:
VUS	0.805 ± 0.01	0.809 ± 0.01	0.824 ± 0.008

^aRange of optimal acquisition parameter.

^bNote the dependence of optimal Tl-201 injected activity, (and thus Tc-99m activity) and Tl-201 energy window width.

In the simultaneous acquisition case, the optimal injected activities were the same for the different acquisition windows. Similarly, the optimal energy windows were the same for the different injected activities. However, for the separate acquisition case, we observed dependence between the optimal relative injected activity and the acquisition energy window, as indicated by the shape of the contours. That is, when the injected activity of Tl-201 decreased (increasing the relative injected activity and producing better stress images and noisier rest images), the IO tended to perform better with wider Tl-201 acquisition energy windows, i.e. acquired more photons to compensate for the reduction in Tl-201 count level. Similarly, when the injected Tl-201 activity increased (reduced relative injected activity) the IO performed better with narrower energy windows.

We also observed that the degradation in the IO performance as a function of Tl-201 energy window width for simultaneous acquisition was higher than that for separate acquisition, as indicated in figures 11 and 14. This can be explained by the additional negative effect that crosstalk has on observer performance beyond Tl-201 self-scatter. As the energy window width increased, the amount of Tc-99m crosstalk increased, which is an image-degrading factor that only affects image quality in dual isotope imaging with simultaneous acquisition.

Also note that the performance of the observer when operating on images acquired using the optimized separate or simultaneous acquisition protocols was similar (VUS_Simultaneous = 0.806, VUS_Separate = 0.809). We tested the statistical significance of the difference between the VUS values for both protocols and the corresponding p-value at 95% confidence level was equal to 0.92, i.e. the difference was not statistically significant. This suggests that DISA methods can potentially provide image quality as good as that obtained with separate acquisition with a factor of ~2 reduction in total acquisition time, while also providing reduced time for patient positioning and perfect stress and rest image registration.

3.2.5. Comparison between optimized and clinical acquisition protocols

In this paper, we investigated various injected activities of Tc-99m and Tl-201 so that the total effective dose was kept constant at 13.5 mSv. This is about half the effective dose that is currently given to patients undergoing dual isotope imaging with sequential acquisition. We selected this as the dose level for investigation given current concerns over patient radiation dose. In this section, we compare between separate acquisition protocols using the optimal acquisition parameters (i.e. Tl-201 acquisition energy window and Tc-99m/Tl-201 relative injected activity) and the clinical protocols currently used for dual isotope imaging with separate acquisition. The goal of this experiment was to determine if the existing protocols provide better task performance as measured by the IO performance on the binary and 3-class tasks. We measured the performance on images acquired using 30 mCi of Tc-99m and 3 mCi of Tl-201. Stress images were acquired in a 20% acquisition energy window, centered at 140 keV, while rest images were acquired in a 27% wide Tl-201 energy window. These acquisition parameters correspond to those used to acquire the clinical data for patients in a dual isotope imaging protocol with separate stress and rest acquisitions.

As shown in table 6, the clinical protocol provided better task performance for both binary and 3-class tasks. This is because of the improved rest and stress image qualities due to higher injected Tc-99m and Tl-201 activities. However, we observed only modest improvement in the stress image quality, as measured by the observer performance, although the injected activity of Tc-99m was 30 mCi compared to 14 mCi used in the optimized protocol. This can be explained by the fact that the IO performance saturates for high Tc-99m injected activity, as shown in figures 9 and 12. Thus, there was no need to increase Tc-99m activity beyond 14 mCi. This also explains the modest improvement in observer performance in distinguishing normal versus fixed and normal versus reversible defects. These pairs of classes primarily depend on the change of defect status in the stress images, as indicated in table 3. The IO performance on the three-class task for the clinical protocol was substantially better than that for the optimized low-dose protocols. This was mainly due to improvement in the rest image quality.

4. Conclusion

Dual isotope simultaneous acquisition Tc-99m stress/ Tl-201 rest MPS is an appealing protocol that offers a number of advantages over separate acquisition, including reduction in imaging time and an associated increase in patient comfort, inherent registration of the rest and stress images, and an increase in clinical throughput. However, crosstalk contamination, where photons emitted by Tc-99m contribute to the Tl-201 image due to interactions in the patient and gamma camera, degrades image quality. In this work, we optimized the Tl-201 energy window width and relative injected activities, in the context of a 3-class detection task, to reduce the impact of crosstalk. The optimization was performed using the IO and a SKE/BKS task operating on a realistic population of phantoms that included anatomical and background variations. The results indicated that relative injected activities of 2.6–5 and an acquisition energy window width of 8–16 keV centered at 72 keV were optimal. For separate acquisition, we observed a broader range of optimal relative injected activities, 2.6 to 12.1, and acquisition energy window of widths of 8–16 keV. For the separate acquisition case, we observed a negative correlation between Tl-201 injected activity and the width of the Tl energy window within the above-mentioned ranges. The results also showed that, with optimal energy windows and relative injected activities, the IO performance was very similar (VUS = 0.809 and 0.806) for separate and simultaneous acquisition. This indicates that, with appropriate compensation and reconstruction methods, DISA methods can provide equivalent performance compared to separate acquisition while providing the benefits identified above. We have also compared the observer performances for the optimized protocol and the current clinical protocol using separate acquisition. The current clinical protocols provided better performance in the context of binary and three-class defect detection tasks, at a cost of injecting the patient with approximately double the injected activity of Tc-99m and Tl-201, resulting in substantially increased radiation dose.