Abstract
Determining the conditions under which populations may persist requires accurate estimates of demographic parameters, including immigration, local reproductive success, and mortality rates. In marine populations, empirical estimates of these parameters are rare, due at least in part to the pelagic dispersal stage common to most marine organisms. Here, we evaluate population persistence and turnover for a population of orange clownfish, Amphiprion percula, at Kimbe Island in Papua New Guinea. All fish in the population were sampled and genotyped on five occasions at 2-year intervals spanning eight years. The genetic data enabled estimates of reproductive success retained in the same population (reproductive success to self-recruitment), reproductive success exported to other subpopulations (reproductive success to local connectivity), and immigration and mortality rates of sub-adults and adults. Approximately 50% of the recruits were assigned to parents from the Kimbe Island population and this was stable through the sampling period. Stability in the proportion of local and immigrant settlers is likely due to: low annual mortality rates and stable egg production rates, and the short larval stages and sensory capacities of reef fish larvae. Biannual mortality rates ranged from 0.09 to 0.55 and varied significantly spatially. We used these data to parametrize a model that estimated the probability of the Kimbe Island population persisting in the absence of immigration. The Kimbe Island population was found to persist without significant immigration. Model results suggest the island population persists because the largest of the subpopulations are maintained due to having low mortality and high self-recruitment rates. Our results enable managers to appropriately target and scale actions to maximize persistence likelihood as disturbance frequencies increase.
Keywords: Amphiprion percula, long-term monitoring, parentage analysis, self-recruitment, population demography, persistence
1. Introduction
Understanding and identifying biotic and abiotic conditions under which wild populations can persist over space and through time is a formidable theoretical and practical challenge in population ecology [1,2]. Identifying the spatial scale at which populations are influenced by these conditions allows us to define conservation management units and implement appropriately targeted and scaled actions. Wild populations of many species are fragmented and function as metapopulations, comprised of local populations linked by migration [3]. Within metapopulations, local population size is driven by four fundamental demographic rates: recruitment and immigration, which increase the population size, as well as mortality and emigration, which decrease the population size [4]. Local populations within metapopulations can only persist when recruitment and immigration equals or exceeds mortality and emigration [5,6]. However, these demographic rates may equalize as populations approach carrying capacity, a theoretical upper limit on the population size [7,8].
Population models provide a useful way of examining the influence of demographic parameters on population persistence [2,9,10]. These models can be used to generate projections of how the size of a population may change under different environmental conditions, movement patterns of individuals within populations, and mortality rates. Demographic models may also include some level of density dependence, although such processes are hard to estimate in wild populations [11]. However, the reliability of demographic models depends on the accuracy of parameters that are often estimated indirectly due to logistical sampling constraints [12–14]. Evaluating demographic parameters is challenging because it is often difficult or impossible to follow a large number of individuals in situ over a time period sufficiently long enough to accurately estimate rates of population turnover [15]. This is particularly the case for organisms that are not sessile, with complex life cycles that include dispersal, ontogenetic movements, hibernation, or cryptic phases.
Building demographic models is especially challenging for marine species as they often have complex life cycles that may include a dispersive larval phase and/or a mobile adult phase. Consequently, it is often difficult to distinguish between losses due to emigration and losses due to mortality [16]. Many studies have been forced to assume that emigration equals immigration, but it is then impossible to quantify the relative contributions of these two processes to the dynamics of local populations within metapopulations [17,18]. This assumption can bias models towards overestimating the contribution of local populations to the persistence of the metapopulation. Identifying the natal origins of larvae recruiting to marine populations has also represented a significant challenge to the development of accurate demographic models. Larval recruitment to subpopulations comes from two potential sources. Individuals may return to their natal subpopulation (typically termed self-recruitment), or may disperse to other subpopulations within the metapopulation (typically termed connectivity). Both self-recruitment and connectivity may be critical for the persistence of subpopulations, but the means to determine their relative importance has not been available until recently.
The development of several methods to determine the natal origins of juveniles has provided new insights into the spatial scale of larval dispersal (e.g. physical oceanography [19,20], artificial tagging [10], trace-elemental fingerprinting of fish otoliths [21] and invertebrate larval shells [22], and molecular genetics [23,24]). For instance, parentage analysis based on DNA genotyping provides a means to distinguish natal origins as it allows for detection of parent–child relationships [24]. We have used this approach to estimate larval dispersal of orange clownfish in Kimbe Bay from samples collected in 2005 and 2007 [24,25]. When applied regularly to all individuals in a population, DNA fingerprinting using microsatellite loci also provides a powerful tool for measuring mortality and population turnover.
Orange clownfish (Amphiprion percula) form obligate associations with sea anemones, where they remain for the rest of their lives. Mortality and population turnover rates can be quantified by tracking individuals from each subpopulation through time. Previous results from such studies showed a high self-recruitment rate (approx. 50% of recruitment) for the A. percula of Kimbe Island in 2005 and 2007 [24,25] and a very low adult mortality rate (approx. 12.9% per year, [26]) for the same species in Madang, Papua New Guinea. Based on these findings, we hypothesized that levels of self-recruitment may be high enough to ensure the self-persistence of the A. percula population in Kimbe Island without immigration. We test this hypothesis using parentage analysis and DNA identification of all of the individuals in the orange clownfish population in Kimbe Island, Papua New Guinea over an 8-year sampling period. We used the resulting demographic data to parametrize a demographic model of Kimbe Island subpopulations to address a specific question: can the orange clownfish population of Kimbe Island and any of its subpopulations persist in the absence of larval connectivity from other locations in the region?
2. Material and methods
(a). The study system
Amphiprion percula typically lives in groups and occurs in obligate association with sea anemones [27,28]. Groups are usually composed of a dominant breeding pair and between 0 and 6 juveniles [29]. Within each group, there is a size-based dominance hierarchy: the female is largest, the male is second largest and the non-breeders rank progressively lower in the hierarchy as they decrease in size. If the single female adult (i.e. rank 1) of a group dies, then the male (i.e. rank 2) changes sex and the largest juvenile (i.e. rank 3) from the anemone becomes male [30,31]. Reproduction occurs year round, and breeders hatch hundreds of eggs each lunar month but the importance of the lunar cycle on larval settlement is poorly understood [32,33]. Then, eggs hatch into pelagic larvae that spend approximately two weeks in the pelagic environment before settling on an anemone [10,24,34], which may or may not be on the natal reef. Because adult clownfish rarely move among anemones, persistence at the scale of a single anemone (and hence the larger scale) is determined by whether the rate of settling larvae can offset the mortality of juveniles and adults.
(b). Study site and field collections
The study was conducted every two years from 2005 to 2013 during April in Kimbe Island (5°12′22,56″ S, 150°22′35.58″ E), a small island located in Kimbe Bay, Papua New Guinea (electronic supplementary material, figure S1). We subdivided the island into seven geographical areas (A–G). In this study, these geographical areas are described as subpopulations. We located and tagged a total of 210 anemones that were present during the five periods of sampling, all of which were occupied by A. percula (electronic supplementary material, figure S1). All fish at each anemone were captured by divers using hand nets and processed in situ. Individuals were measured using calipers (total length TL, mm), fin-clipped for genetic analysis and then released back on the same anemone. The biggest fish in each anemone was identified as the female, the second largest individual was assumed to be the male and all other individuals were classified as juveniles. In 2005 and 2007, juveniles (non-breeders) with TL > 35 mm were not fin-clipped but were recorded for 2007. The small pieces of fin tissue were preserved in 95% ethanol in 0.2 ml vials. The smallest non-breeders (TL < 35 mm, hereafter referred to as ‘new-recruits') were removed from their anemones and the whole fish were preserved in vials with 95% ethanol. Resident clownfish may prevent recruitment of new individuals at high densities [32]. Therefore, removal of the small individuals homogenized conditions for larval settlement among all anemones. All details related to capture numbers for each stage, subpopulation and year of sampling are provided within the electronic supplementary material, table S1. DNA from a total of 3 890 collected samples (including 1 067 new-recruits) were extracted and screened at 22 polymorphic microsatellite loci (electronic supplementary material, table S2) that satisfied Hardy–Weinberg equilibrium and linkage disequilibrium assumptions.
(c). Demographic parameters
(i). Mortality measurement (biannual)
The package GenAlex v6.5 [35] was used to compare each of the individual genotypes from fish sampled in 2009, 2011, and 2013 (2005 and 2007 are excluded because juveniles with TL > 35 mm were not fin-clipped in those years) to identify all unique multilocus genotypes [36]. The combined probability of identity (i.e. the probability of two samples having the same multilocus genotype by chance) for this set of markers in this population was small (1.7 × 10−24). Therefore, if fin clips from different sampling years had the same genotype, they were assumed to be from the same individual. To account for possible genotyping errors, mismatches of up to two loci between genotypes were allowed in pair-wise genotype comparisons. In this way, we were able to measure mortality for each stage (i.e. average mortality of females, males, and juveniles) for each of the seven subpopulations of Kimbe Island for two time steps (i.e. 2009–2011 and 2011–2013). We used χ2-test to compare the mortality rates observed among the seven subpopulations and between the various life stages (i.e. juvenile, male, and female stages). We then used the Fisher-test to evaluate whether the mortality rate calculated for 2009–2011 was significantly different than the mortality rate calculated for 2011–2013.
(ii). Reproductive success to self-recruitment and to local connectivity, and immigration measurements (biannual)
For every sampling year (2005, 2007, 2009, 2011, and 2013) and for each subpopulation of Kimbe Island (A–G), we used assignment/exclusion tests to estimate an index of reproductive success to self-recruitment, reproductive success to local connectivity, and immigration. Reproductive success to self-recruitment is calculated as the number of juveniles with parents from the same subpopulation divided by the number of females in this population. Reproductive success to local connectivity is calculated as the number of juveniles in a subpopulation that were offspring of parents from another Kimbe Island subpopulation, divided by the number of females in the focal population. Immigration is defined as the number of juveniles that were not assigned to any parent from Kimbe Island. To assign one individual to a breeding pair, we used individual genotypes and the platform FaMoz [37]. We then compared the percentages of self- and local-recruits and immigrants within Kimbe Island among all sampling years using a Kruskal–Wallis test. In this analysis, local-recruitment is the percentage of self-recruitment, defined by Burgess et al. [15] as the fraction of recruitment to a site comprised of individuals born in that site and the percentage of local connectivity. We used the Pettitt homogeneity test to evaluate differences in the presence of connections among subpopulations (i.e. exchange of recruits) and the number of recruits being exchanged among (local recruits) and within (self-recruits) subpopulations among years.
(iii). Carrying capacity
The number of female and male clownfish per anemone cannot exceed one since anemones only host one breeding pair. Therefore, the carrying capacity for adult males and females in a given subpopulation cannot exceed the number of anemones present in that subpopulation. The number of juveniles per anemone may vary between the different subpopulations. We calculated the mean number of clownfish observed per anemone in the seven subpopulations at four sampling periods (2007, 2009, 2011, and 2013, excluding 2005 because non-breeders more than 35 mm were not counted and sampled). For each subpopulation, we obtained a set of four values of mean number of clownfish per anemone and we used the highest values of mean number of clownfish per anemone as the juvenile carrying capacity per anemone. The juvenile carrying capacity per subpopulation is equal to the maximum number of clownfish observed per anemone multiplied by the total number of anemones in that subpopulation.
Mortality rates, and rates for reproductive success to self-recruitment, reproductive success to local connectivity, and immigration are exact measures from the field observations (rather estimation) so are not presented with error bars. All statistical analyses were performed using R v3.0.2 [38] and significance was interpreted using a p-value of >0.05.
(d). Demographic model
The system is based on a loss-input principle using recurrence equations [39]. The number of larvae, juveniles, males, and females in a subpopulation at period t + h (with the time-step resolution of the dynamic) is represented by 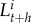 ,
,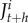 ,
, 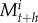 , and
, and 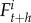 . The dynamics of each subpopulation are described following these four recurrence equations:
. The dynamics of each subpopulation are described following these four recurrence equations:
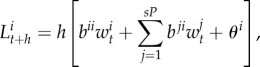 |
2.1 |
| 2.2 |
| 2.3 |
| 2.4 |
where 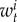 and
and 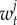 are the number of breeding pairs in the subpopulation i and j at time t and (equation (2.1)),
are the number of breeding pairs in the subpopulation i and j at time t and (equation (2.1)), 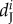 ,
, 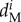 , and
, and 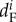 are the mortality rates per capita of juveniles, males and females by unit of time in subpopulation i (equations (2.2)–(2.4)). The parameter bii represents the number per unit of time of self-recruits and breeding pairs (
are the mortality rates per capita of juveniles, males and females by unit of time in subpopulation i (equations (2.2)–(2.4)). The parameter bii represents the number per unit of time of self-recruits and breeding pairs (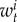 ) in subpopulation i (i.e. reproductive success to self-recruitment), while bji is the number per unit of time of juveniles produced per breeding pair in subpopulation j (
) in subpopulation i (i.e. reproductive success to self-recruitment), while bji is the number per unit of time of juveniles produced per breeding pair in subpopulation j (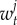 ) at time t that disperse and recruit into subpopulation i (i.e. reproductive success to local connectivity).
) at time t that disperse and recruit into subpopulation i (i.e. reproductive success to local connectivity). 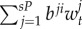 is the sum of the connectivity from the six other subpopulations (sP = 6) j to subpopulation i. The parameter θi denotes the constant number per unit of time of migrants recruiting to subpopulation i who were spawned outside of Kimbe Island. In equation (2.2), sL corresponds to settlement rate per unit of time of larvae arriving at subpopulation i.
is the sum of the connectivity from the six other subpopulations (sP = 6) j to subpopulation i. The parameter θi denotes the constant number per unit of time of migrants recruiting to subpopulation i who were spawned outside of Kimbe Island. In equation (2.2), sL corresponds to settlement rate per unit of time of larvae arriving at subpopulation i.
The number of larvae that can enter the juvenile population on reef i is limited by the amount of free space, 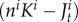 :
:
| 2.5 |
where ni is the maximal number of juveniles per anemone in subpopulation i and Ki is the number of anemones in subpopulation i.
In equations (2.2) and (2.3), tM measures the rate of transition function from juveniles to males per unit of time:
| 2.6 |
where 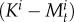 denotes the available space for new males (i.e. male mortality or males changing into females following female mortality) taking into account that we cannot observe more than one adult male per anemone.
denotes the available space for new males (i.e. male mortality or males changing into females following female mortality) taking into account that we cannot observe more than one adult male per anemone.
In equations (2.3) and (2.4), tF corresponds to transition function from males to females per unit of time:
| 2.7 |
where 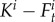 denotes the female turnover due to available space for females in anemones due to female mortality taking into account that we cannot observe more than one adult female per anemone.
denotes the female turnover due to available space for females in anemones due to female mortality taking into account that we cannot observe more than one adult female per anemone.
(e). Hypotheses, model fitting, and simulations
Rates of mortality, self-recruitment, and local connectivity were all assumed to be known parameters, deduced from the parentage analysis, which was entirely independent of the model. The parameters sl, tm, and tf in equations (2.5)–(2.7) appear as adjustment parameters that fit the model to the observed data (electronic supplementary material, figure S2). Their estimated values are obtained by minimizing the least-square criterion measuring the distance between observed data and their values predicted by the model [40], using the procedure outlined by Nelder & Mead [41]. Reproductive success rates of self- and local-recruitment, and immigration used in the demographic model were the averages among all five sampling periods for each subpopulation (table 1). Mortality rates used as inputs to the demography model are the averages between 2009–2011 and 2011–2013 for each life stage of each subpopulation (table 1). Demographic parameters are rescaled to equivalent monthly rates to increase resolution of the model dynamics. The model was initialized from 2007 with a monthly time step. The population dynamics were evaluated considering three different recruitment and immigration scenarios: (i) with all inputs; (ii) removing immigration; and (iii) removing local-recruitment and immigration. The numerical solution for the demographic model was programmed into R v3.0.2 [38].
Table 1.
Demographic parameters from empirical values of a natural population of A. percula. 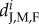 refers to the average biannual mortality rate per capita of juveniles, and adult males and females for each subpopulation between two periods: 2009–2011 and 2011–2013 (see the electronic supplementary material, table S3 for mortality rates for each of the two 2-year periods). ni is the maximal average number of juveniles per anemone in the subpopulation i between 2007 and 2013 and Ki is the total number of anemones in subpopulation i (equal to the maximal number of males or females per subpopulation).
refers to the average biannual mortality rate per capita of juveniles, and adult males and females for each subpopulation between two periods: 2009–2011 and 2011–2013 (see the electronic supplementary material, table S3 for mortality rates for each of the two 2-year periods). ni is the maximal average number of juveniles per anemone in the subpopulation i between 2007 and 2013 and Ki is the total number of anemones in subpopulation i (equal to the maximal number of males or females per subpopulation).
| parameters | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
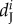 |
0.296 | 0.270 | 0.269 | 0.477 | 0.179 | 0.500 | 0.487 |
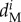 |
0.373 | 0.095 | 0.393 | 0.400 | 0.198 | 0.286 | 0.440 |
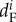 |
0.397 | 0.190 | 0.382 | 0.350 | 0.243 | 0.357 | 0.552 |
| ni | 2.19 | 2.00 | 1.58 | 1.85 | 2.03 | 1.14 | 1.70 |
| Ki | 57 | 21 | 19 | 20 | 56 | 7 | 30 |
(f). Sensitivity analysis
Sensitivity analyses were used to determine which demographic parameters most greatly influence population dynamics and persistence among: mortality rate of females, males, and juveniles, self-recruitment and local-recruitment rates, immigration, and juvenile and adult carrying capacity. We independently varied each parameter by 30% and plotted the resulting trajectory of population size through time.
Further details on the demographic parameters and sensitivity analysis (figure S2b,f) are provided in the electronic supplementary material.
3. Results
(a). Population demography
(i). Mortality measurements (biannual)
In total, 1 706 fins were collected and genotyped between 2009 and 2013. Genetic similarity analyses revealed that 561 individuals were observed only once, 334 individuals were found in two successive sampling years (i.e. 2009 and 2011 or 2011 and 2013) and 159 individuals survived during the three years of sampling. From these data, we calculated the mortality rate between the periods 2009–2011 and 2011–2013 (electronic supplementary material, figure S3 and table S3). We excluded two cases of survival assignments (i.e. similar genotypes with three mismatches on 44 alleles from fins clipped in two consecutive periods) because fins came from females which were sampled in different subpopulations separated by more than 350 m. During the period 2009–2011, the mortality rates differed significantly among the seven subpopulations and for the various life stages (χ2-test, p < 0.001). During the period 2011–2013, the mortality rates among the seven subpopulations and for the various life stages were significantly different only for males and females (χ2-test, pJ = 0.120, pM,F < 0.001). The average mortality rate varied among subpopulations between 0.18 and 0.49 for juveniles, 0.09 and 0.44 for males, and 0.19 and 0.55 for females (table 1). The mortality rates were higher in subpopulation G than in the other subpopulations (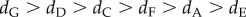 ). However, when all life stages and subpopulations were aggregated, differences in mortality rates between 2009–2011 and 2011–2013 were not significantly different (Fisher's test, p = 0.703). Further, when the development stage and subpopulations were considered separately, differences among mortality rates between the two periods were only significant for males and females from subpopulation A (Fisher's test, p < 0.001).
). However, when all life stages and subpopulations were aggregated, differences in mortality rates between 2009–2011 and 2011–2013 were not significantly different (Fisher's test, p = 0.703). Further, when the development stage and subpopulations were considered separately, differences among mortality rates between the two periods were only significant for males and females from subpopulation A (Fisher's test, p < 0.001).
(ii). Recruitment measurements (biannual)
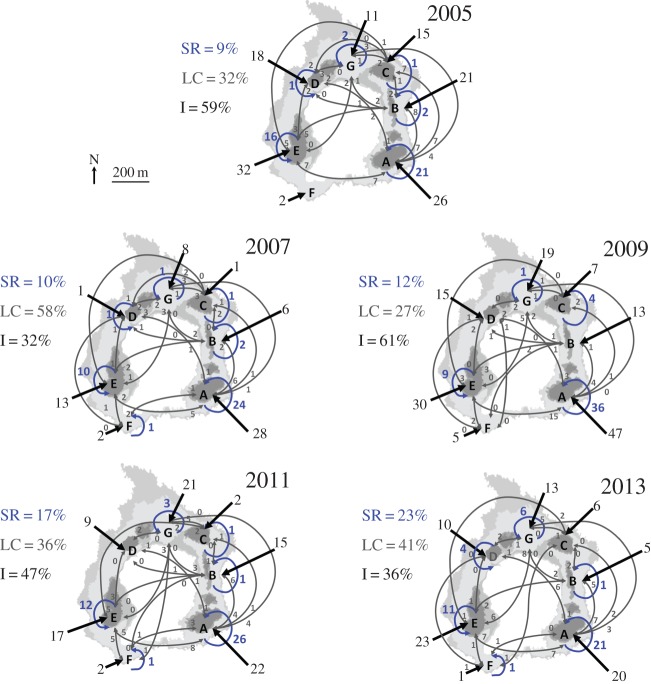
Parentage analysis was used to establish the natal origin of all A. percula offspring spawned by females in the seven Kimbe Island subpopulations. The analysis quantified self-recruitment (fraction of recruitment to a subpopulation comprised of new-recruits born in that subpopulation), local connectivity (fraction of recruitment to a subpopulation comprised of new-recruits born in other Kimbe Island subpopulations), and immigration from other reefs outside Kimbe Island from 2005–2013 (figure 1). From a total of 1 067 new-recruits collected over five sampling events, less than half were immigrants (489 new-recruit immigrants, 45.8%); 222 (20.9%) were self-recruits and 356 (33.3%) were local recruits). The percentages of self-recruits, local-recruits, and immigrants among sampling years did not vary significantly among years (Kruskal–Wallis test, p = 0.877). Further, levels of self-recruitment and local connectivity among subpopulations were all consistent among the five sample years. Differences in the presence of connections among subpopulations (i.e. exchange of recruits) and the number of recruits being exchanged among (local recruits) and within (self-recruits) subpopulations were not significantly different among years (Pettitt homogeneity test, p = 0.702).
Figure 1.
Self-recruitment (SR, blue arrows), local connectivity (LC, grey arrows), and immigration (I, black arrows) calculated on the natural Amphiprion percula populations from parentage analysis from 2005 to 2013 in Kimbe Island, Papua New Guinea. Subpopulations are indicated with letters A–G. The numbers correspond to new-recruits and the arrows show the sources of these inputs (i.e. self-recruitment, local connectivity, or immigration).
The average reproductive success to self-recruitment varied among subpopulations between 0.06 and 0.45 juveniles per female (electronic supplementary material, table S4). The reproductive success to self-recruitment was higher in subpopulation A than in the other subpopulations (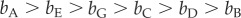 ). The average number of juveniles per female in subpopulation A represented approximately 40% of the total input coming from Kimbe Island.
). The average number of juveniles per female in subpopulation A represented approximately 40% of the total input coming from Kimbe Island.
Further details on the mortality and reproductive success results are provided in the electronic supplementary material.
(b). Modelling population dynamics
The demographic parameters calculated from the field data and used in the model included the reproductive success to self-recruitment, reproductive success to local connectivity, mortality, and the carrying capacity. The carrying capacity is the average number of juveniles per anemone for juveniles and is the number of anemones (K) for adult males and females. Although the number of juveniles per anemone was as high as five (electronic supplementary material, figure S4), the average number of juveniles per anemone varied between 1.14 and 2.19 among subpopulations (table 1). The optimum parameter values for fitting our demographic model to the observed data were sl = 0.196 (larval settlement), tm = 0.310 (transition from juvenile to male), tf = 1.950 (transition from male to female).
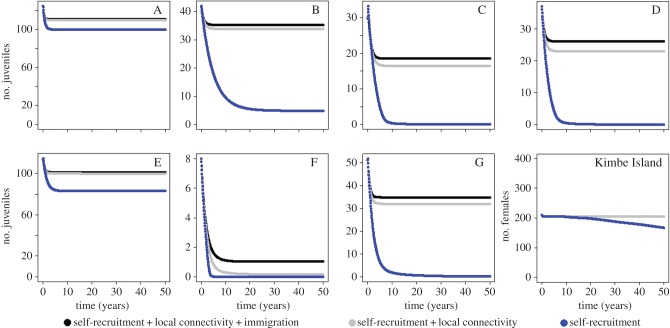
We found that all subpopulations and the Kimbe Island population were stable and persisted when all connections were maintained (self-recruitment, local-recruitment, and immigration, figure 2 black points). The subpopulations A–E and G and the integrated Kimbe Island population were also stable and persisted when immigration was removed (figure 2, grey points). The number of juveniles in subpopulation F was null after 5 years (figure 2, grey points). When immigration was removed, the presence of both a male and female on each anemone were maintained, but the number of recruits/juveniles was halved meaning the available habitat was no longer saturated. The global Kimbe Island population was also stable and persisted if all local connections and immigration were removed, though the habitat became less saturated through a 25% decline in females. In this scenario, only subpopulations A, B, and E persisted (figure 2, blue points), albeit with reductions in juvenile densities of approximately 50% (A and E) and 75% (B). The juvenile stage in subpopulations C, D, F, and G disappeared after approximately five years. Mortality rates for these subpopulations were all higher than for A, B, and E and thus C, D, F, and G were more dependent on local connectivity and immigration. Subpopulations C, D, F, and G were smaller than A, B, and E, which is why the overall Kimbe Island population persisted when only subpopulations A, B, and E persisted. The decline in subpopulations C, D, F, and G started with a reduction in the number of juveniles followed by a decrease in the number of males and then total loss due to the absence of females (electronic supplementary material, figure S5).
Figure 2.
Demographic model projections of numbers of juvenile Amphiprion percula within each of the subpopulations (A–G) and the whole population of Kimbe Island (subpopulations A–G combined) for three different recruitment and immigration scenarios. The model was initialized with data of total juvenile captures during 2007 (set as time[year] = 0). The model temporal resolution is one month and the results are plotted here every six months for 50 years. Self-recruitment and local connectivity refer to reproductive success to self-recruitment and reproductive success to local connectivity, respectively, in the demographic model.
A sensitivity analysis was conducted to determine which parameters most influence subpopulation dynamics. The sensitivity analysis revealed that for subpopulations C, D, and F the time of extinction stayed the same irrespective of whether the other demographic parameters are modified by 30% (electronic supplementary material, figure S6a and b). For these three subpopulations, self-recruitment, local-recruitment, and immigration were equally important. Considering the entire population of females in Kimbe Island, the mortality rate of females and the carrying capacity were the most influential demographic parameters driving persistence (electronic supplementary material, figure S6a and b). The sensitivity analysis demonstrates the robustness of our main finding: the orange clownfish population from Kimbe Island can persist without immigration. In fact, we observed the persistence of the orange clownfish population even after increasing or decreasing by 30% the different demographic parameters.
4. Discussion
We followed an entire population of a coral reef fish through eight years to quantify demographic parameters used in assessments of population dynamics. Our results indicate that the overall Kimbe Island population of clownfish was stable with consistent patterns of self-recruitment and larval immigration, and model results suggest that the population can persist without immigration from other sources. Model results also suggest several smaller lagoonal subpopulations within Kimbe Island were also stable and likely to persist if only populated from self-recruitment. The high level of demographic stability demonstrated at a small spatial scale is a novel and unexpected result for a marine population that includes a dispersive larval stage. The conclusion that the population can be sustained through self-recruitment is likely to be robust for two primary reasons. Firstly, our demographic model was based on genetic identification of every individual and their progeny over an 8-year period. The primary input variables to the model were therefore based directly on sampling of all individuals in the population and parent–offspring relationships, rather than use of indirect methods as is the case in other studies [12,42–44]. Further, the study was long enough to see a near-complete population turnover, with only 18% of adults persisting over the 8-year sampling period. Secondly, mortality, self-recruitment and connectivity patterns were stable over the 8-year sampling period, suggesting that the demographic importance of self-recruitment was not a transitory phenomenon. Although larval connectivity is not necessary for the persistence of relatively undisturbed populations, it is likely to be of great demographic significance via a rescue effect [45] should extrinsic disturbances extirpate a subpopulation.
The power of longitudinal genetic monitoring of each individual was that we can distinguish between death and emigration to generate an accurate estimate of mortality. Our data indicated that a small number of adult individuals moved short distances during the study period from their anemone to another anemone within the same lagoon (approx. 2%), which meant we could adjust mortality rates accordingly and calculate the true mortality rate. We calculated average biannual mortality rates of 31–36% for juveniles, and adult males and females with a global mortality rate that was constant across two 2-year periods. There was no significant difference between the mortality rate of adults (either sex) and juveniles, though most juveniles sampled were large and positioned first in the queue for access to reproduction in the colony hierarchy (juveniles named as ‘rank 3’ by Buston [26,32] represent approximately 83% of total juveniles sampled). Buston [26,32] used visual censuses to estimate mortality for the same species in another part of Papua New Guinea (Madang), and also concluded that adults (named by the authors ‘rank 1 and 2’ to refer to female and male, respectively) and juveniles (named ‘rank 3’) had similar mortality [26]. However, the mortality rate we found was higher (approx. 16.5% versus approx. 12.9%) than Buston [26,32] observed following conversion of our bi-annual and his monthly mortality rates to annual rates. Also, differences among subpopulations were as great as approximately 25%, all of which speaks to the value of longitudinal genetic monitoring of each individual and to the importance of local-scale differences in the environment (abiotic and/or biotic) for survival.
Differences among subpopulations in mortality rates probably reflect a rapid turnover as a result of intense competition for reproductive status on anemones (related to the number of fish in the queue within an anemone), which are clearly a limiting resource. Only the dominant pair of clownfish breeds and non-breeding subordinates queue for breeding positions. The highest-ranking individuals are the most likely to inherit breeding positions so competition for rank may be intense, which results in high stress for some juveniles and competition for food resources within anemones [26,30]. The extent to which competition for rank plays out probably varies among subpopulations resulting in more rapid turnover where competition is most intense, which might be the case for our subpopulations C, D, and G, where mortality rates are highest.
For marine populations, recruitment is often a highly stochastic process with great inter-annual variation [46,47]. In our study, longitudinal genetic monitoring of each individual allowed us to distinguish between individuals that were offspring of parents from Kimbe Island subpopulations and those that were spawned by adults on other reefs (i.e. located more than 10 km from Kimbe Island). We found that local connectivity and self-recruitment combined to provide approximately 50% of recruits each year during the five sampling periods. Importantly, the stability we see through time is a result of several settlement events because new-recruits sampled are between 10 and 281 days old (Salles O.C., 2015) and we are therefore integrating a number of settlement events through the year. Stability in the proportion of local and immigrant settlers over time is likely due to a combination of biological and physical factors. Population numbers are fairly consistent through time with low annual mortality rates (approx. 15%), suggesting that egg production rates were also likely to be relatively stable when averaged over the year in question. Also, the duration of the larval stage for this species is relatively short (10–12 days on average [34]) and therefore capacity for dispersal will be significantly less than for species with longer pelagic larval durations. Larval behaviour may also play a role in stabilizing self- and local-recruitment over time. Coral reef fish larvae are now known to have well-developed sensory systems and reef sounds [48–50] and olfactory cues [51–53] may be used as means to locate and orient towards home to a suitable habitat [54,55]. For instance, Dixson et al. [56] provided evidence that A. percula use olfactory cues to locate their natal reefs, providing a mechanism for the relatively high and consistent levels of self-recruitment documented for Kimbe Island.
Results obtained from our demographic model showed that the three subpopulations with the lowest mortality rates (A, B, and E) are capable of persisting without immigration. Two of these subpopulations (A and E) also have the largest anemone abundance and correspondingly have the highest number of clownfish and the highest self-recruitment rates. Yet, the female reproductive success for self-recruitment was quite different between subpopulations A and E despite their numbers differing by only 2%. The biannual production of self-recruiting juveniles per females from subpopulation A was more than twice that documented for E (approx. 0.38 versus approx. 0.16), perhaps due to local water movement, ability of larvae to sense the shallower anemones here, or a combination of these.
Two different demographic strategies can ensure the persistence of subpopulations in the absence of immigration. The first strategy relies upon high self-recruitment to compensate for high mortality (subpopulation A). The second is the inverse; female mortality rates may be low so self-recruitment rates can be low as well (subpopulations B and E). In contrast to A, B, and E, subpopulations C, D, F, and G disappeared quickly without immigration. Subpopulation F consisted of only seven inhabited anemones in total. For the three other subpopulations (C, D, and G) persistence was not assured once isolated due to higher mortality rates and lower self-recruitment rates in comparison to subpopulations A, B, and E. The persistence of the island population as a whole was driven by the low mortality rates of females and the high self-recruitment rates characteristic of the largest subpopulations at Kimbe Island (i.e. A, B, and E).
In conclusion, longitudinal genetic monitoring of each individual within a population is a powerful approach for understanding the local drivers of population persistence. It can provide accurate measurements of demographic rates that often cannot be reliably estimated by traditional approaches. Our use of longitudinal genetic monitoring is why we are confident it is possible for the Kimbe Island population to persist without immigration; i.e. that our primary result is robust. While we cannot be absolutely certain as to whether the Kimbe Island clownfish population will persist without immigration, all of the evidence presented suggests it is possible. We were also able to reliably determine the demographic parameters driving local-scale spatial variation in persistence likelihood, which, with further work, could be used to examine how and whether local adaptation develops and manifests. The approach outlined here will also be of help to managers in developing appropriately targeted and scaled actions that maximize persistence likelihood in this era of climate change and increasing disturbance frequencies. For example, our results indicate that protecting Kimbe Island may be sufficient to preserve the local A. percula population over time even without immigration from surrounding populations.
Supplementary Material
Acknowledgements
We thank all those that assisted in the field. N. Tolou and S. Baksay assisted with genetic analysis. Mahonia Na Dari R and CC and the crew of M. V. FeBrina provided essential logistic support. We are grateful to the traditional owners of the reefs near Kimbe Island, PNG, for allowing us access to their reefs. To finish, we thank the two anonymous reviewers for their many insightful comments and their contributions to the final draft.
Ethics
The research accomplished in this project was conducted under James Cook University ethics approval number A1264 and followed all guidelines for the country in which it took place.
Authors' contributions
S.P., G.P.J., and S.R.T. conceived the study; O.C.S., P.S.A., G.R.A., G.P.J., M.L.B., S.R.T., and S.P. collected field data; O.C.S. and P.S.A. carried out the molecular laboratory work and parentage analysis; O.C.S., J.A.M., and S.P. drafted the manuscript; G.R.A., S.R.T., G.P.J., and M.L.B. helped to draft the manuscript; O.C.S. carried out the statistical analyses; O.C.S., C.M.B., and M.J. developed and analysed the demographic model. All authors gave final approval for publication.
Competing interests
We declare we have no competing interests.
Funding
This research was supported by LABEX Corail, ERC, CRISP, the GEF CRTR Connectivity Working Group, NSF, the ARC CoE Coral Reef Studies, TNC, Total Foundation, JCU, KAUST, and WHOI.
References
- 1.Levin SA. 1992. The problem of pattern and scale in ecology. Ecology 73, 1943–1967. ( 10.2307/1941447) [DOI] [Google Scholar]
- 2.Hastings A, Botsford LW. 2006. Persistence of spatial populations depends on returning home. Proc. Natl Acad. Sci. USA 103, 6067–6072. ( 10.1073/pnas.0506651103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Austin A, Ovaskainen O, Hanski I. 2011. Size and genetic composition of the colonizing propagules in a butterfly metapopulation. Oikos 120, 1357–1365. ( 10.1111/j.1600-0706.2010.18992.x) [DOI] [Google Scholar]
- 4.Hanski I. 1998. Metapopulation dynamics. Nature 396, 41–49. ( 10.1038/23876) [DOI] [Google Scholar]
- 5.Cowen RK, Sponaugle S. 2009. Larval dispersal and marine population connectivity. Annu. Rev. Mar. Sci. 1, 443–466. ( 10.1146/annurev.marine.010908.163757) [DOI] [PubMed] [Google Scholar]
- 6.White JW, Botsford LW, Hastings A, Largier JL. 2010. Population persistence in marine reserve networks: incorporating spatial heterogeneities in larval dispersal. Mar. Ecol. Prog. Ser. 398, 49–67. ( 10.3354/meps08327) [DOI] [Google Scholar]
- 7.Murdoch WW. 1994. Population regulation in theory and practice. Ecology 75, 271–287. ( 10.2307/1939533) [DOI] [Google Scholar]
- 8.Cappuccino N, Price PW. 1995. Population dynamics: new approaches and synthesis. Amsterdam, The Netherlands: Elsevier Science. [Google Scholar]
- 9.Gerber LR, Botsford LW, Hastings A, Possingham HP, Gaines SD, Palumbi SR, Andelman S. 2003. Population models for marine reserve design: a retrospective and prospective synthesis. Ecol. Appl. 13, S47–S64. ( 10.1890/1051-0761(2003)013%5B0047:PMFMRD%5D2.0.CO;2) [DOI] [Google Scholar]
- 10.Almany GR, Berumen ML, Thorrold SR, Planes S, Jones GP. 2007. Local replenishment of coral reef fish populations in a marine reserve. Science 316, 742–744. ( 10.1126/science.1140597) [DOI] [PubMed] [Google Scholar]
- 11.Hanski I. 1999. Metapopulation ecology. Oxford, UK: Oxford University Press. [Google Scholar]
- 12.Pollock KH. 1991. Modeling capture, recapture, and removal statistics for estimation of demographic parameters for fish and wildlife populations - past, present and future. J. Amer. Stat. Asso. 86, 225–238. [Google Scholar]
- 13.Sandercock BK. 2006. Estimation of demographic parameters from live-encounter data: a summary review. J. Wildl. Manag. 70, 1504–1520. ( 10.2193/0022-541X(2006)70%5B1504:EODPFL%5D2.0.CO;2) [DOI] [Google Scholar]
- 14.Thompson W. 2013. Sampling rare or elusive species: concepts, designs, and techniques for estimating population parameters. Washington, USA: Island Press. [Google Scholar]
- 15.Burgess SC, et al. 2014. Beyond connectivity: how empirical methods can quantify population persistence to improve marine protected-area design. Ecol. Appl. 24, 257–270. ( 10.1890/13-0710.1) [DOI] [PubMed] [Google Scholar]
- 16.Cain ML, Milligan BG, Strand AE. 2000. Long-distance seed dispersal in plant populations. Amer. J. Bot. 87, 1217–1227. ( 10.2307/2656714) [DOI] [PubMed] [Google Scholar]
- 17.Schaub M, Reichlin TS, Abadi F, Kary M, Jenni L, Arlettaz R. 2012. The demographic drivers of local population dynamics in two rare migratory birds. Oecology 168, 97–108. ( 10.1007/s00442-011-2070-5) [DOI] [PubMed] [Google Scholar]
- 18.Pulliam HR. 1988. Sources, sinks, and population regulation. Amer. Nat. 132, 652–661. ( 10.1086/284880) [DOI] [Google Scholar]
- 19.Cowen RK, Lwiza KMM, Sponaugle S, Paris CB, Olson DB. 2000. Connectivity of marine populations: open or closed? Science 287, 857–859. ( 10.1126/science.287.5454.857) [DOI] [PubMed] [Google Scholar]
- 20.Cowen RK, Paris CB, Srinivasan A. 2006. Scaling of connectivity in marine populations. Science 311, 522–527. ( 10.1126/science.1122039) [DOI] [PubMed] [Google Scholar]
- 21.Swearer SE, Caselle JE, Lea DW, Warner RR. 1999. Larval retention and recruitment in an island population of a coral-reef fish. Nature 402, 799–802. ( 10.1038/45533) [DOI] [Google Scholar]
- 22.Carson HS, Cook GS, Lopez-Duarte PC, Levin LA. 2011. Evaluating the importance of demographic connectivity in a marine metapopulation. Ecology 92, 1972–1984. ( 10.1890/11-0488.1) [DOI] [PubMed] [Google Scholar]
- 23.Gilg MR, Hilbish TJ. 2003. The geography of marine larval dispersal: coupling genetics with fine-scale physical oceanography. Ecology 84, 2989–2998. ( 10.1890/02-0498) [DOI] [Google Scholar]
- 24.Planes S, Jones GP, Thorrold SR. 2009. Larval dispersal connects fish populations in a network of marine protected areas. Proc. Natl Acad. Sci. USA 106, 5693–5697. ( 10.1073/pnas.0808007106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Berumen ML, Almany GR, Planes S, Jones GP, Saenz-Agudelo P, Thorrold SR. 2012. Persistence of self-recruitment and patterns of larval connectivity in a marine protected area network. Ecol. Evol. 2, 444–452. ( 10.1002/ece3.208) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Buston PM. 2003. Mortality is associated with social rank in the clown anemonefish (Amphiprion percula). Mar. Biol. 143, 811–815. ( 10.1007/s00227-003-1106-8) [DOI] [Google Scholar]
- 27.Allen GR. 1975. The anemonefishes: their classification and biology. California, USA: T.F.H. Publications. [Google Scholar]
- 28.Fautin DG, Allen GR. 1997. Anemone fishes and their host sea anemones: a guide for aquarists and divers. Perth, Australia: Western Australian Museum. [Google Scholar]
- 29.Buston P. 2004. Does the presence of non-breeders enhance the fitness of breeders? An experimental analysis in the clown anemonefish Amphiprion percula. Behav. Ecol. Sociobiol. 57, 23–31. ( 10.1007/s00265-004-0833-2) [DOI] [Google Scholar]
- 30.Fricke HW. 1979. Mating system, resource defence and sex change in the anemonefish Amphiprion akallopisos. Z. Tierphysiol. Tierer. 50, 313–326. [Google Scholar]
- 31.Hattori A. 1994. Intergroup movement and mate acquisition tactics of the protandrous anemonefish, Amphiprion clarkii, on coral-reef, Okinawa. Jpn. J. Ichthyol. 41, 159–165. [Google Scholar]
- 32.Buston P. 2003. Forcible eviction and prevention of recruitment in the clown anemonefish. Behav. Ecol. 14, 576–582. ( 10.1093/beheco/arg036) [DOI] [Google Scholar]
- 33.Mitchell JS. 2003. Social correlates of reproductive success in false clown anemonefish: subordinate group members do not pay-to-stay. Evol. Ecol. Res. 5, 89–104. [Google Scholar]
- 34.Berumen ML, Walsh HJ, Raventos N, Planes S, Jones GP, Starczak V, Thorrold SR. 2010. Otolith geochemistry does not reflect dispersal history of clownfish larvae. Coral Reefs 29, 883–891. ( 10.1007/s00338-010-0652-z) [DOI] [Google Scholar]
- 35.Peakall R, Smouse PE. 2012. GenAlEx 6.5: genetic analysis in Excel. Population genetic software for teaching and research–an update. Bioinformatics (Oxford, England) 28, 2537–2539. ( 10.1093/bioinformatics/bts460) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Saenz-Agudelo P, Jones GP, Thorrold SR, Planes S. 2009. Estimating connectivity in marine populations: an empirical evaluation of assignment tests and parentage analysis under different gene flow scenarios. Mol. Ecol. 18, 1765–1776. ( 10.1111/j.1365-294X.2009.04109.x) [DOI] [PubMed] [Google Scholar]
- 37.Gerber S, Chabrier P, Kremer A. 2003. FAMOZ: a software for parentage analysis using dominant, codominant and uniparentally inherited markers. Mol. Ecol. Notes 3, 479–481. ( 10.1046/j.1471-8286.2003.00439.x) [DOI] [Google Scholar]
- 38.R-Development-Core-Team. 2007. R: a language and environment for statistical computing., ed computing RFfs Vienna, Austria.
- 39.Hofbauer J, Sigmund K. 1998. Evolutionary games and population dynamics. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 40.Soetaert K, Herman PMJ. 2008. A practical guide to ecological modelling: using R as a simulation platform. Berlin, Germany: Springer. [Google Scholar]
- 41.Nelder JA, Mead R. 1965. A simplex method for function minimization. Comput. J. 7, 308–313. ( 10.1093/comjnl/7.4.308) [DOI] [Google Scholar]
- 42.Nichols JD, Pollock KH. 1990. Estimation of recruitment from immigration versus in situ reproduction using pollocks robust design. Ecology 71, 21–26. ( 10.2307/1940243) [DOI] [Google Scholar]
- 43.Kendall WL, Nichols JD, Hines JE. 1997. Estimating temporary emigration using capture-recapture data with Pollock's robust design. Ecology 78, 563–578. [Google Scholar]
- 44.Pine WE, Pollock KH, Hightower JE, Kwak TJ, Rice JA. 2003. A review of tagging methods for estimating fish population size and components of mortality. Fisheries 28, 10–23. ( 10.1577/1548-8446(2003)28%5B10:AROTMF%5D2.0.CO;2) [DOI] [Google Scholar]
- 45.Kininmonth S, et al. 2011. Dispersal connectivity and reserve selection for marine conservation. Ecol. Model. 222, 1272–1282. ( 10.1016/j.ecolmodel.2011.01.012) [DOI] [Google Scholar]
- 46.Hughes TP, Baird AH, Dinsdale EA, Moltschaniwskyj NA, Pratchett MS, Tanner JE, Willis BL. 1999. Patterns of recruitment and abundance of corals along the Great Barrier Reef. Nature 397, 59–63. ( 10.1038/16237) [DOI] [Google Scholar]
- 47.Hogan JD, Thiessen RJ, Heath DD. 2010. Variability in connectivity indicated by chaotic genetic patchiness within and among populations of a marine fish. Mar. Ecol. Prog. Ser. 417, U263–U289. ( 10.3354/meps08793) [DOI] [Google Scholar]
- 48.Leis JM, Carson-Ewart BM, Hay AC, Cato DH. 2003. Coral-reef sounds enable nocturnal navigation by some reef-fish larvae in some places and at some times. J. Fish Biol. 63, 724–737. ( 10.1046/j.1095-8649.2003.00182.x) [DOI] [Google Scholar]
- 49.Simpson SD, Meekan M, Montgomery J, McCauley R, Jeffs A. 2005. Homeward sound. Science 308, 221 ( 10.1126/science.1107406) [DOI] [PubMed] [Google Scholar]
- 50.Montgomery JC, Jeffs A, Simpson SD, Meekan M, Tindle C. 2006. Sound as an orientation cue for the pelagic larvae of reef fishes and decapod crustaceans. In Advances in marine biology, vol. 51 (eds Southward AJ, Sims DW), pp. 143–196. San Diego, USA: Academic Press. [DOI] [PubMed] [Google Scholar]
- 51.Atema J, Kingsford MJ, Gerlach G. 2002. Larval reef fish could use odour for detection, retention and orientation to reefs. Mar. Ecol. Prog. Ser. 241, 151–160. ( 10.3354/meps241151) [DOI] [Google Scholar]
- 52.Doving KB, Stabell OB, Ostlund-Nilsson S, Fisher R. 2006. Site fidelity and homing in tropical coral reef cardinalfish: are they using olfactory cues? Chem. Senses 31, 265–272. ( 10.1093/chemse/bjj028) [DOI] [PubMed] [Google Scholar]
- 53.Gerlach G, Atema J, Kingsford MJ, Black KP, Miller-Sims V. 2007. Smelling home can prevent dispersal of reef fish larvae. Proc. Natl Acad. Sci. USA 104, 858–863. ( 10.1073/pnas.0606777104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cowen RK, Gawarkiewic G, Pineda J, Thorrold SR, Werner FE. 2007. Population connectivity in marine systems an overview. Oceanography 20, 14–21. ( 10.5670/oceanog.2007.26) [DOI] [Google Scholar]
- 55.Thorrold SR, Zacherl DC, Levin LA. 2007. Population connectivity and larval dispersal using geochemical signatures in calcified structures. Oceanography 20, 80–89. ( 10.5670/oceanog.2007.31) [DOI] [Google Scholar]
- 56.Dixson DL, Jones GP, Munday PL, Planes S, Pratchett MS, Srinivasan M, Syms C, Thorrold SR. 2008. Coral reef fish smell leaves to find island homes. Proc. R. Soc. B 275, 2831–2839. ( 10.1098/rspb.2008.0876) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.