Shear-induced orientational dynamics and spatial heterogeneity in suspensions of motile phytoplankton

Abstract

Fluid flow, ubiquitous in natural and man-made environments, has the potential to profoundly impact the transport of microorganisms, including phytoplankton in aquatic habitats and bioreactors. Yet, the effect of ambient flow on the swimming behaviour of phytoplankton has remained poorly understood, largely owing to the difficulty of observing cell–flow interactions at the microscale. Here, we present microfluidic experiments where we tracked individual cells for four species of motile phytoplankton exposed to a spatially non-uniform fluid shear rate, characteristic of many flows in natural and artificial environments. We observed that medium-to-high mean shear rates (1–25 s⁻¹) produce heterogeneous cell concentrations in the form of regions of accumulation and regions of depletion. The location of these regions relative to the flow depends on the cells' propulsion mechanism, body shape and flagellar arrangement, as captured by an effective aspect ratio. Species having a large effective aspect ratio accumulated in the high-shear regions, owing to shear-induced alignment of the swimming orientation with the fluid streamlines. Species having an effective aspect ratio close to unity exhibited little preferential accumulation at low-to-moderate flow rates, but strongly accumulated in the low-shear regions under high flow conditions, potentially owing to an active, behavioural response of cells to shear. These observations demonstrate that ambient fluid flow can strongly affect the motility and spatial distribution of phytoplankton and highlight the rich dynamics emerging from the interaction between motility, morphology and flow.

1. Introduction

Phytoplankton are a diverse group of photosynthetic microorganisms, many of which are motile [1]. Phytoplankton range in size from hundreds of nanometres [2] to hundreds of micrometres [3], and exhibit an array of morphologies, from spherical to highly elongated [4], from long chains of individual organisms [5] to bodies with long, thin protruding spines [6,7]. Morphology, in turn, affects phytoplankton motion through water, for both motile and non-motile species. For example, spines in non-motile phytoplankton have been suggested to decrease settling rates by enhancing drag [8] and elongated morphologies may alter the organisms' orientational distribution in flow, as recently shown for bacteria [9,10], with consequences for plankton patch formation and foraging abilities [11].

Phytoplankton habitats are frequently characterized by fluid flow, whether in natural aquatic ecosystems such as oceans and lakes or in engineered systems such as algal bioreactors. In marine environments, turbulent fluid motion (‘eddies') generated at large scale cascades to smaller scale until it is dissipated by viscosity [12]. Typical ocean turbulence is characterized by a mean dissipation rate of turbulent kinetic energy, ɛ, between 10⁻⁹ and 10⁻⁵ W kg⁻¹ [13–15]. This corresponds to a Kolmogorov scale—the smallest eddy scale below which flow reduces to a linear spatial variation in fluid velocity—in the range η_K = (ν³/ɛ)^1/4 = 0.5–5 mm (ν ≈ 10⁻⁶ m² s⁻¹ is the kinematic viscosity of water, which varies only modestly with temperature and salinity [16]). Because the majority of phytoplankton are smaller than the Kolmogorov scale, they experience turbulence as an instantaneous, linearly varying fluid velocity across the cell body. The order of magnitude of the associated velocity gradient is given by the Kolmogorov shear rate, S_K = (ɛ/ν)^1/2, which for the turbulent energy dissipation rates, ɛ, mentioned above is in the range 0.03–3 s⁻¹. The inverse of this shear rate yields the characteristic time scale, τ_K = 1/S_K, of fluid velocity fluctuations [12]. Furthermore, because the Stokes number of most phytoplankton is very small [17], there is no net translation (e.g. inertial drift or lift effects) relative to the local, instantaneous flow velocity, except for an additional vertical component of motion owing to positive or negative buoyancy in some species. Typical bioreactor designs, such as raceway ponds or air-lift bioreactors, are also characterized by turbulent flow [18–20], sometimes for the purpose of mixing cultures [18]. These turbulence levels can be much stronger than in the ocean, although actual quantifications are few [21].

Immersed bodies exposed to a velocity gradient, including phytoplankton cells, experience a viscous torque that rotates the body with an angular speed that is proportional to the velocity gradient and depends on shape. For elongated shapes, common to many phytoplankton species [22], the instantaneous rotation rate is a function of the cell orientation relative to the flow direction [23,24]. When cells are oriented with their long axis along the velocity gradient, they experience a greater differential flow velocity along their body (i.e. a higher torque) and thus rotate with a greater angular velocity than when they are aligned with the flow direction. The periodic rotations that a cell undergoes as a result of this orientation-dependent torque are known as Jeffery orbits [24] and can strongly affect cell motility. In the absence of flow, cell motility often results in isotropic, diffusive-like spreading of populations [25]. In contrast, in the presence of flow the preferential flow alignment induced by Jeffery orbits can limit the ability of elongated cells to migrate perpendicularly to the flow direction, resulting in anisotropic transport and driving cell accumulations in the higher-shear regions of the flow, as was recently shown for bacteria [10].

Phytoplankton dynamics in flow can be affected by multiple processes related to cell shape and motility. First, the presence of flagella alters the effective hydrodynamic aspect ratio of the cell compared with the cell body alone. For example, a flagellum protruding along the major axis renders a cell effectively more elongated than its body alone, as was shown for bacteria [10,26]. Second, the drag associated with flagellar beating also impacts a cell's rotational dynamics in flow [27,28]. For example, the waveforms exhibited during a beat cycle by the two flagella of Chlamydomonas, an alga that swims using a breaststroke motion, reduce the organism's effective aspect ratio when compared with the geometrical aspect ratio of the cell body alone [28]. Third, variations in rotational dynamics, arising from desynchronization [29] or asymmetry [30] in flagellar beating, can affect the cell's swimming direction. Rotational noise typically reduces the effective aspect ratio of cells by counteracting the aligning effects of fluid flow (i.e. Jeffery orbits) [31]. Finally, a cell's rotational dynamics may be affected by active behavioural responses to external stimuli, including light [32], chemical gradients [33] or potentially fluid shear. In particular, certain phytoplankton exhibit a non-uniform orientation distribution or a directional persistence in shear flows [34] that is inconsistent with predictions for passive bodies (in particular, with Jeffery orbits). These dynamics may result from the cells actively resisting the viscous torques from the shear flow [35,36], although conclusive evidence for active, behavioural responses by phytoplankton to fluid flow is still lacking.

Here, we present measurements of the trajectories and swimming orientations of single phytoplankton cells in laminar flows for four phytoplankton species, combined with population-scale measurements of spatial cell distributions. Controlled Poiseuille flows were generated in microfluidic devices and spanned a broad range of mean shear rates, = 0.125–25 s⁻¹, where is the mean of the absolute shear rate across the width of the microchannel. These flows exhibit a linear variation of the shear rate across the channel width and thus represent a simple, yet physically relevant, model system for examining the effect of fluid shear on phytoplankton in natural and engineered environments, where flows are often characterized by gradients in the shear rate. We show that the coupling of shear and motility results in different regimes of rotational dynamics and spatial heterogeneity when the mean shear rate exceeds 1 s⁻¹, and we interpret observations in the context of a mathematical model of cell motility in flow.

2. Organisms, motility characterization and microfluidic experiments

2.1. Organisms and culturing

Four species of phytoplankton were examined: Heterosigma akashiwo, Amphidinium carterae, Dunaliella tertiolecta and Chlamydomonas reinhardtii (figure 1a–d), henceforth referred to by the genus name alone, for brevity. Heterosigma and Dunaliella were obtained from the National Center for Marine Algae (strain numbers CCMP 452 and CCMP 1320, respectively). Chlamydomonas was obtained from the Chlamydomonas Resource Center (strain number CC-125). Amphidinium was obtained from Dave Kulis and Don Anderson at the Woods Hole Oceanographic Institute (exact strain information not available). Heterosigma, Dunaliella and Amphidinium are all marine species, where Heterosigma and Amphidinium are both toxic and can form harmful algal blooms [37,38]. Chlamydomonas is a freshwater species that has been studied as a model organism for cell motility [39], flagellar dynamics [40] and phototaxis [41].

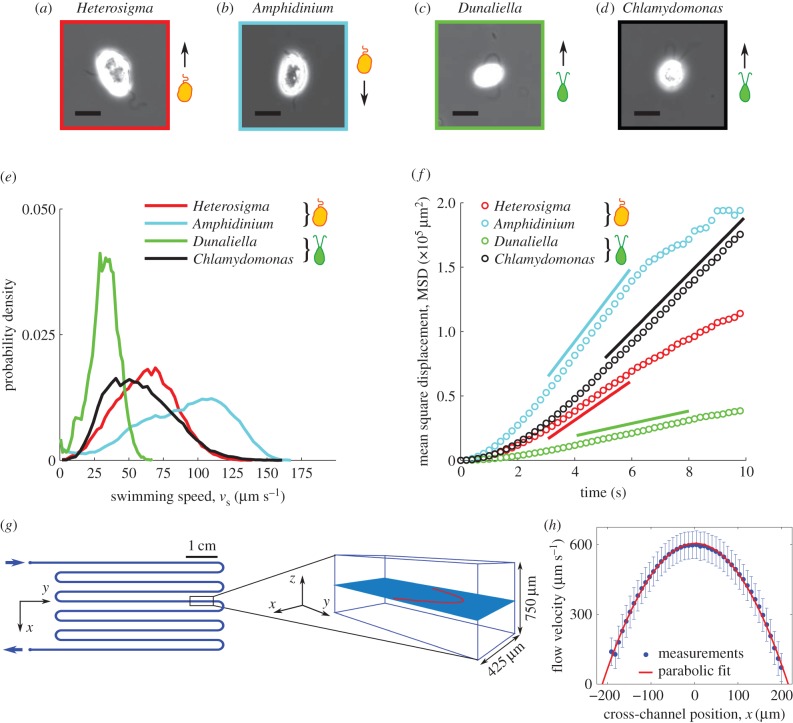
Figure 1.

(a–d) Phase contrast microscopy (40× objective, NA = 0.60) of the four species of phytoplankton investigated: Heterosigma akashiwo, Dunaliella tertiolecta, Chlamydomonas reinhardtii and Amphidinium carterae. All scale bars are 10 µm. (e) Probability density function of measured swimming speeds for each species. (f) Timeseries of the mean square displacement for each species. The solid line represents a linear fit to the diffusive regime, from which the effective translational diffusivity, D, was obtained (reported in table 1). (g) Schematic of the serpentine microfluidic device (left, plan view; right, isometric view, not to scale) showing the imaging plane (light blue) and the flow profile (red) at the channel mid-depth. (h) Flow velocity profiles measured at the mid-depth plane using cells as tracers (blue dots), fitted with a parabolic profile (red line). Error bars correspond to the standard error of the mean.

All four species are biflagellates, but they have markedly different propulsion strategies: Chlamydomonas and Dunaliella swim by pulling themselves forward in a breaststroke-like fashion with their flagella beating synchronously [39], whereas Heterosigma and Amphidinium swim with one flagellum protruding from the cells' anterior (Heterosigma) or posterior (Amphidinium) end, relative to the swimming direction, and a second flagellum wrapped around the body [42,43]. The role played by the protruding and equatorial flagella in propulsion for Heterosigma and Amphidinium is still an open question. For this study, we note that Heterosigma pulls itself forward [42], whereas Amphidinium pushes itself forward with the protruding flagellum [43,44].

All species were grown at 21°C under continuous illumination (75 µmol m⁻² s⁻¹). All marine species (Heterosigma, Dunaliella, Amphidinium) were grown in f/2 media [45], whereas Chlamydomonas was grown in tris–acetate–phosphate media [46]. For propagation of cultures, every three weeks, 25 ml of fresh medium were inoculated with 0.2–1.0 ml of the old culture, depending on the growth rate of the population. All experiments were conducted at room temperature between 5 and 8 days after inoculation.

2.2. Swimming statistics

Measured cell trajectories were used to compute swimming speeds and effective translational and rotational diffusivities for each species. These observations were made in a chamber formed by a coverslip and a silicone gasket (Grace Bio-Labs, JTR20-1.0; 20 mm diameter, 0.8 mm depth). Images were taken at 15 frames per second at mid-depth and in the centre of the chamber over an area of 2.9 mm × 2.9 mm, so that imaged organisms were far from any solid boundaries. Cultures were diluted to a concentration appropriate for reliable tracking. For cells with a tendency to stick to surfaces (Chlamydomonas, Dunaliella, Amphidinium), a small amount of bovine serum albumin (2.5 g l⁻¹ final concentration, consistent with prior studies [29,39]) was added to the media to minimize sticking [47]. For tracking, cell locations were determined by image analysis based on intensity thresholding using Matlab (The MathWorks) routines. Cell trajectories were assembled by linking locations based on proximity and kinematic predictions from previous timesteps.

From trajectories, we obtained the probability density function (PDF) of the swimming speed, v_s, for each species (figure 1e). The mean and standard deviation of v_s are summarized in table 1. The mean square displacement (MSD) as a function of time, t, was computed for each cell trajectory and was then averaged over all trajectories (figure 1f). The regime in which the MSD increases linearly with time is the diffusive regime, and for a random walk in two dimensions, takes the form MSD = 4Dt, where D is the translational diffusivity of the cells. A linear fit to the timeseries of the MSD yielded the translational diffusivity D, which fell in the range D = 1207–7237 µm² s⁻¹ for the four species (table 1). Approximating the diffusive motion of the cells as a continuous-time random walk [25], the rotational diffusivity was computed according to D_R = v_s²/6D. Rotational diffusivities were in the range D_R = 0.15–0.27 rad² s⁻¹ for the four species (table 1).

Table 1.

Summary of swimming statistics for the four phytoplankton species in quiescent conditions.

species	no. trajectories	swimming speed, vs (mean ± s.d.) [μm s−1]	translational diffusivity, D [μm2 s−1]	rotational diffusivity, DR [rad2 s−1]
Heterosigma	5000	62 ± 22	3840	0.25
Dunaliella	1700	32 ± 11	1207	0.21
Amphidinium	4400	89 ± 33	7237	0.27
Chlamydomonas	900	58 ± 24	5576	0.15

2.3. Microfluidic device, video microscopy and flow conditions

To measure the effects of shear, cells were observed in microfluidic Poiseuille flows within a polydimethylsiloxane microchannel fabricated using standard soft lithography techniques [48]. The device (figure 1g) was identical to that used by Rusconi et al. [10] and is thus only briefly described here. To ensure that the dominant velocity gradients occurred in the horizontal observation plane, at the channel mid-depth, the microchannel had an aspect ratio H/W greater than 1 (height H = 750 µm; width W = 425 µm). In the mid-depth plane, the flow velocity profile, v(x) = V[1–4(x/W)²], was parabolic, where V is the flow velocity at the channel centreline. Thus, the shear rate, S(x) = dv/dx = −8xV/W², varied linearly with the distance x across the channel and was zero at the centreline. The flow rate was controlled using a syringe pump (Harvard apparatus, PHD2000) with two 1 ml glass syringes (Hamilton, model 1001 TLL SYR). Luer lock needles (BD precision glide) and polyethylene tubing (Scientific Commodities, ID 0.58 mm) were used to connect the syringes to the inlets of the microchannel. Measurements of the parabolic flow profile were made using live organisms as tracers (figure 1h). We note that although individual cells can move relative to the fluid, the mean velocity of a large population of cells in the flow direction is representative of the underlying fluid velocity. Comparison with flow profiles measured previously in the same device [10] confirmed the present flow measurements.

All imaging was performed with an inverted microscope (Nikon Eclipse Ti-e). Experiments were conducted predominantly with a 4× objective (phase contrast, 0.13 NA) and in some cases with a 10× objective (phase contrast, 0.30 NA). Images were acquired with a digital CMOS camera (Photron FastCam SA3) at 15 frames per second. Exposure times ranged from 40 to 100 µs, to minimize blurring owing to cell motion. A 610 nm long pass filter (Thorlabs, FGL610S) was placed in the microscope illumination path to remove wavelengths for which organisms are known to respond by phototaxis [41,49]. Additionally, stray light was minimized by isolating the microscope with a black felt sheet.

All four species were imaged at the channel mid-depth for the same range of flow rates, 0.25–50 µl min⁻¹, corresponding to mean flow speeds of 20–4000 µm s⁻¹. Specifically, we assayed the mean shear rates = 0 (no-flow control), 0.125, 0.25, 0.5, 1.25, 2.5, 5, 12.5 and 25 s⁻¹, which identify each flow case in the following. After 1 min of flow, image acquisition was initiated and lasted for 6 min (4× objective, for most experiments) or 3 min (10× objective, for selected experiments). To increase the number of cell trajectories for analysis, this process was repeated to collect a minimum of 18 min of imaging data at each shear rate for each species. Data collection for each species occurred on two different days with a separate culture grown for each day. A short video of experiments with Heterosigma for three different flow speeds can be found in the electronic supplementary material, movie S1.

2.4. Spatial distribution of cells, depletion index

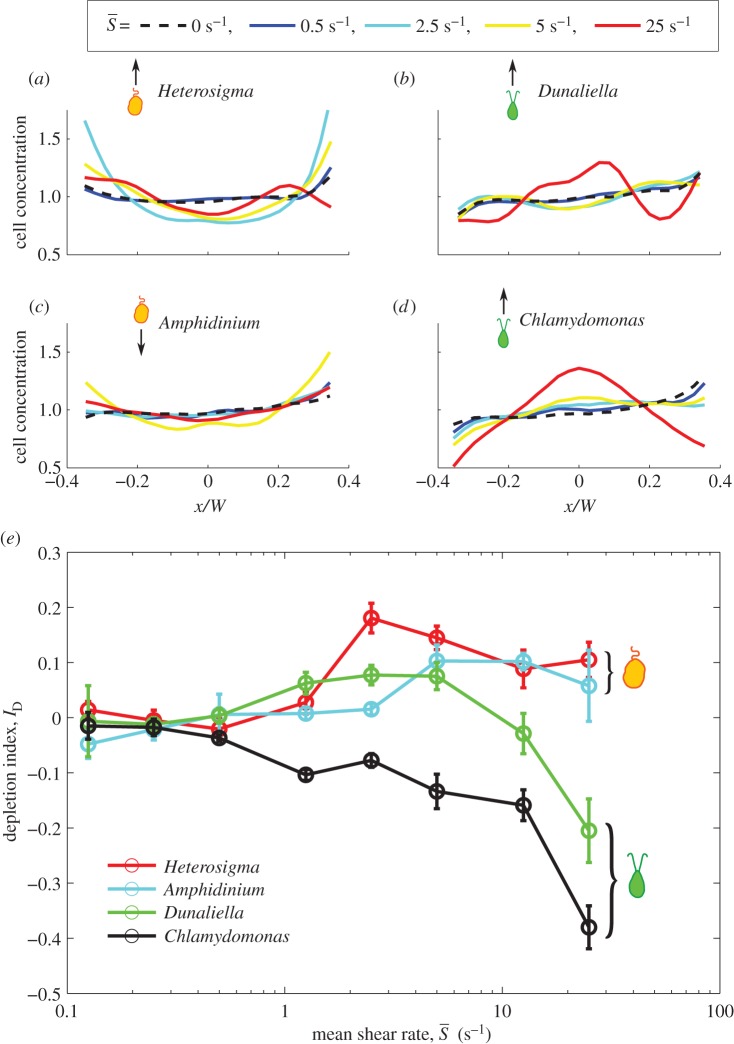
The local cell concentration, C(x), in the cross-channel direction, x, was determined via image analysis of video recordings to measure the dependence of the phytoplankton spatial distribution on the mean shear rate. The lateral positions, x, of all cells within the field of view were discretized in 25 bins of equal width (13 µm). The cell count in each bin, typically larger than 5000 cells, was normalized by the mean count across all bins to compare among different conditions and different species, irrespective of the bulk cell concentration. Local cell concentration measurements obtained in this manner extended across the central approximately 75% of the channel width for all species, because the optical reflections from the walls of the tall microchannel prevented reliable cell identification near the sidewalls.

To quantify deviations of the concentration profile at a given mean shear rate from the no-shear case (i.e. the no-flow case), we computed a depletion index, I_D, from the normalized cell concentration profile, C(x), as

2.1

where C_shear is the mean cell concentration over the central 20% of the channel for the cases with shear and C_{no shear} is the mean cell concentration over the same central region in the no-flow case. A positive (negative) depletion index corresponds to a reduction (increase) in cell concentration in the central part of the channel relative to the no-shear case.

2.5. Measured and predicted orientation distributions

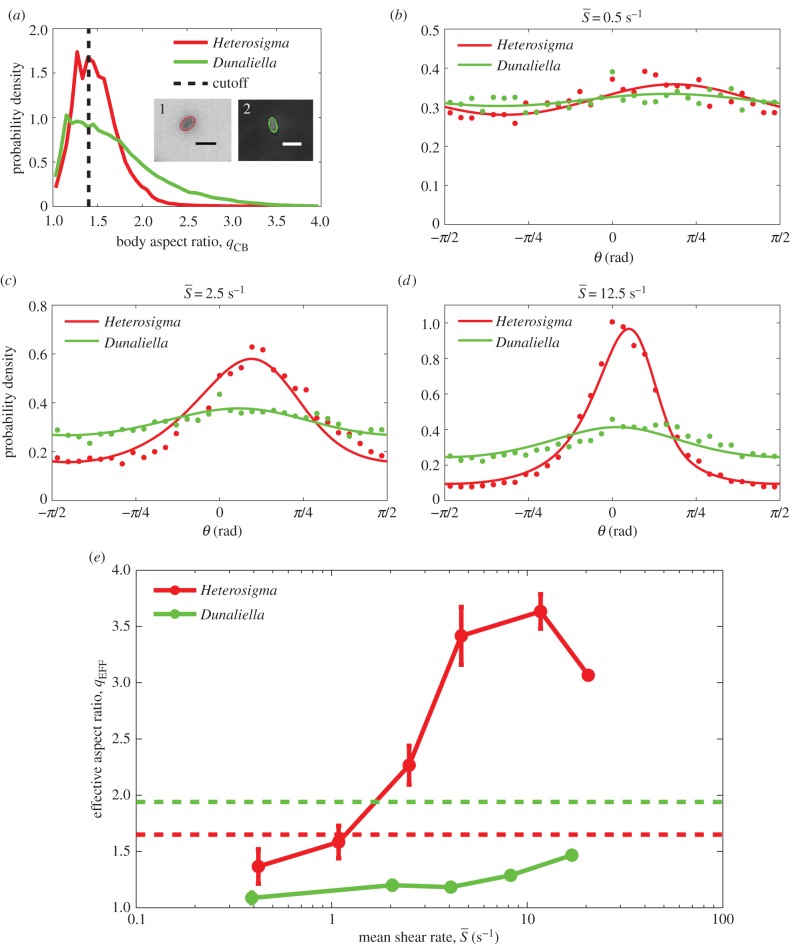
Cell orientation distributions were measured for flow experiments conducted with Heterosigma and Dunaliella and compared with theoretical distributions predicted from Jeffery orbits. Heterosigma was the only organism large enough to clearly identify the body orientation of single cells with a 4× objective. To resolve orientation in Dunaliella, experiments were conducted with a 10× objective. Cell orientations were obtained by first identifying each cell in a frame, as described above, and then using Matlab routines to obtain the area of each cell image in pixels and to fit an ellipse to the identified pixels. The fitted ellipse provided an aspect ratio, q, and an orientation, θ, for each identified cell. Measured orientations (relative to the flow axis, y) ranged from −π/2 to π/2 radians, because the front of the cell could not be differentiated from the back (flagella could not be resolved at the magnifications used). For analyses based on cell orientation, only cells with an imaged aspect ratio greater than 1.4 (approx. 65% of all cells, for both species, across all shear rates) were used, owing to the loss of reliability in capturing the orientation for lower aspect ratios.

Theoretical orientation distributions for ellipsoidal particles with rotational noise in shear flow were computed by solving the steady-state Fokker–Planck equation [10]:

2.2

where p is the probability of occurrence of a given orientation, θ. For each experiment (i.e. each species and each flow rate), equation (2.2) was solved numerically for a range of aspect ratios, q, using the organism-specific measured values of the rotational diffusivity, D_R (table 1), and replacing the local shear rate S with the mean shear rate 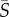. The mean shear rate was used to simplify calculations after it was determined that the distributions based on the channel mean shear rate closely matched those based on the local shear rates integrated across the channel (see electronic supplementary material, figure S1). The experimental distribution was obtained by using orientations from across the entire field of view, where orientations of cells in the left half-width of the channel (x < 0) were reflected to account for the opposite sign of shear compared with the right half-width of the channel (x > 0).

The aspect ratio that corresponded to the theoretical distribution that best fit, via least-squares fitting, the experimental distribution was taken as the effective aspect ratio, q_EFF (sample fits can be observed in figure 5b–d).

Figure 5.

(a) PDFs of the cell body aspect ratio, q_CB, for Heterosigma and Dunaliella. Aspect ratios of individual cells were computed by fitting an ellipse to the cell body as identified by image analysis, as shown in the insets: (1) Heterosigma and (2) Dunaliella (scale bars, 20 and 10 µm, respectively). Cell orientation was only used to compute orientation statistics if the aspect ratio was greater than 1.4 (black dotted line), because smaller aspect ratios were unreliable for determining orientation. (b–d) PDFs of measured orientation distributions across the entire microchannel for Heterosigma (red dots) and Dunaliella (green dots) at mean shear rates of 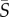= 0.5, 2.5 and 12.5 s⁻¹, respectively. The orientation θ is measured anticlockwise from the flow direction (y-axis). Theoretical predictions of the orientation distribution (solid lines) based on solutions of the Fokker–Planck equation (§2.5) were fitted, via least square fitting, to the measured distributions to determine the effective aspect ratio, q_EFF, for each species at each shear rate. (e) Effective aspect ratios from the Fokker–Planck fits exemplified in (d) as a function of the mean shear rate, for Heterosigma and Dunaliella. Error bars correspond to the standard error of the mean. Red and green dashed lines correspond to the mean body aspect ratio, q_CB, measured for Heterosigma and Dunaliella, respectively (a).

A second, independent measure of cell orientation was obtained from cell trajectories by assuming that cells swam along their main body axis. The procedure for measuring cell orientation from trajectories was as follows. The total cell velocity, measured from video data via central differencing of cell position, comprised the contributions from both swimming and ambient flow. The local flow contribution for each cell at each instant of time was computed using the previously measured, steady-state flow velocity profile in the channel, v(x) (figure 1h), evaluated at the x position of the cell's centroid. Subtraction of this flow velocity from the total cell velocity yielded the cell swimming velocity and thus the cell swimming direction (electronic supplementary material, figure S2). With this approach, we differentiated the anterior from the posterior of the cell (although some of the species studied here can reverse their swimming direction, they do not under typical conditions). The orientation, θ, calculated in this manner ranged from –π to π radians, where 0 corresponds to the flow (y) axis. The cell's angular velocity was then computed as the rate of change of cell orientation.

3. Results

3.1. Cell concentration across the flow

The spatial distribution of cells across the channel width—and thus across the flow velocity gradient—varied with the shear rate and the phytoplankton species, as demonstrated both by the cell concentration profiles (figure 2a–d) and by the corresponding depletion indices (figure 2e). At low mean shear rates (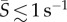), for all species, the distribution of cells across the flow field showed no appreciable departure from the uniform, no-flow case. Accordingly, the depletion index hovered around zero for all four species up to 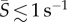, indicating no discernible accumulation or depletion of cells. This confirmed that, by focusing our sampling outside the region where near-field steric interactions are dominant [50], we could safely neglect wall effects in this study.

Figure 2.

(a–d) Phytoplankton cell concentration profiles as a function of the cross-stream position, x, for each species, for selected mean shear rates (see legend). W = 425 µm is the microchannel width. Average cell counts per bin ranged from 5000 to 40 000. (e) The depletion index, I_D, as a function of the mean shear rate, 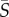, for each species. Error bars correspond to the standard error of the mean for multiple experimental runs conducted at each shear rate.

For medium-to-high shear rates (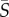 ∼ 1–25 s⁻¹), different swimming styles resulted in strikingly different cell accumulation patterns. Swimmers with a single protruding flagellum, whether pullers (Heterosigma) or pushers (Amphidinium), displayed a marked depletion from the central, low-shear region, as indicated by the positive values of the depletion index. The depletion effect for Heterosigma peaked at medium shear rates (I_D = 0.18 for 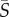= 2.5 s⁻¹) and diminished for higher shear rates. Similarly, the cell distribution for Amphidinium showed maximal depletion for shear rates between 5 and 12.5 s⁻¹, though less pronounced in comparison with Heterosigma (I_D = 0.10). On the contrary, breaststroke-like swimmers (Chlamydomonas and Dunaliella) exhibited a strong accumulation of cells in the central region of the channel, particularly when the shear rate was high ( 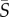≥ 10 s⁻¹). While Chlamydomonas and Dunaliella showed, respectively, slightly negative and slightly positive depletion indices at medium shear rates, they both exhibited their strongest increase in cell concentration in the central region of the channel at the maximum mean shear rate tested, 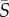= 25 s⁻¹ (I_D = −0.38 for Chlamydomonas and I_D = −0.20 for Dunaliella).

3.2. Cell orientation distributions

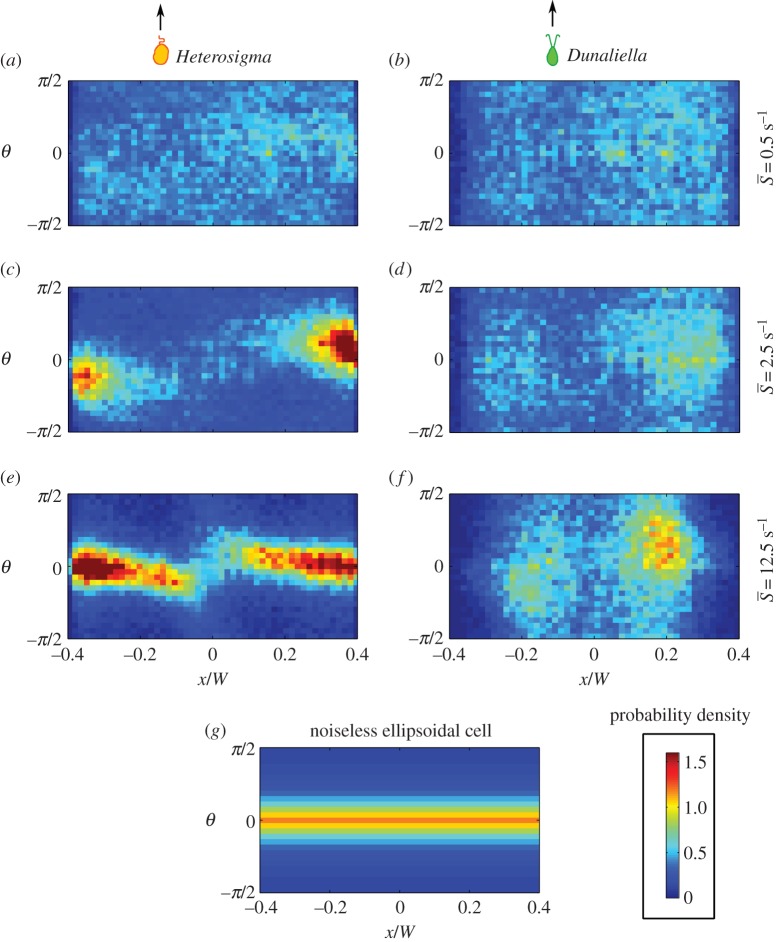
The joint PDFs of the measured cell orientation and concentration across the channel are shown in figure 3 for three mean shear rates (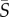 = 0.5, 2.5, 12.5 s⁻¹), for both Heterosigma and Dunaliella. At a low mean shear rate, 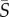= 0.5 s⁻¹, both species show no preferential orientational alignment relative to the flow and the cell distribution is essentially uniform across the channel width (figure 3a,b). At an intermediate mean shear rate, 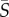= 2.5 s⁻¹, the distribution of orientations for Heterosigma shows preferential alignment with the flow direction (θ = 0; figure 3c) in the regions of high local shear, i.e. closer to the channel walls. At the same mean shear rate, Dunaliella aligned along the flow direction in the presence of high local shear (figure 3d), but to a smaller degree than Heterosigma (the peak probability density was approx. 2.5-fold smaller). For a high value of the mean shear rate, 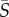= 12.5 s⁻¹, flow alignment was enhanced for both species. For Heterosigma, not only were the cells brought into stricter alignment with the flow (figure 3e), but the region of preferential alignment also extended farther into the channel centre. Dunaliella cells also displayed a greater degree of alignment with the flow at this mean shear rate (figure 3f) compared with the case 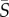= 2.5 s⁻¹ (figure 3b), yet alignment remained weaker compared with Heterosigma (the peak probability density was approximately twofold smaller).

Figure 3.

Joint PDFs of cell orientation and position across the microchannel for (a,c,e) Heterosigma and (b,d,f) Dunaliella at three mean shear rates (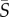 = 0.5, 2.5, 12.5 s⁻¹). Cell orientations were obtained by fitting ellipses to imaged cells (§2.5). The orientation θ = 0 corresponds to the flow orientation, whereas θ =−π/2 and π/2 correspond to the orientations normal to the flow direction. The impact of fluid flow on the orientational dynamics increases as the mean shear rate increases. (g) A theoretical ellipsoidal cell with aspect ratio equal to three rotating in shear with no rotational noise.

Rotational noise (D_R in table 1), which may result from asymmetries in the cell shape or flagellar beating, alters the orientational dynamics of phytoplankton cells in shear, as is revealed by the measured distributions of orientation (figure 3). In the absence of noise, non-motile ellipsoidal cells undergoing Jeffery orbits display an orientation distribution that is only a function of the cells' effective aspect ratio and does not vary with shear rate for any non-zero shear rate [24]. In contrast, despite the elongated shape of most of the phytoplankton species studied here (figure 1a–d), the orientation distribution of all four species is uniform at low mean shear rates and non-uniform at higher mean shear rates (figure 3). The reason is that at low shear rates rotational noise overcomes the weak aligning torque owing to shear, and thus randomizes the cells' swimming direction. This effect is akin to that observed for elongated, micrometre-sized dimers subject to Brownian rotational diffusion: even in shear flow, the dimers exhibit a uniform distribution of orientations as a result of the randomizing effect of rotational diffusion [31]. For phytoplankton, randomization arises predominantly from the non-deterministic nature of the swimming orientation, rather than from thermal fluctuations.

The effect of rotational noise is also evident in the offset in the peak orientation from the flow direction (figure 3). This offset does not occur for deterministic Jeffery orbits (figure 3g) and is, in fact, a hallmark of the competition between rotational diffusion and shear, previously observed in colloidal suspensions [51] and bacteria [10], which is usually expressed by the rotational Péclet number, 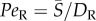. As confirmed by our observations, this offset is stronger at low flow rates 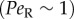and disappears in higher flow regimes 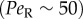, where the cells are tightly aligned with the flow direction in the higher shear regions (most apparent for Heterosigma in figures 3 and 5).

A similar offset in peak orientation also occurred in a previous experiment that tested the response of dinoflagellates to shear rates characteristic of oceanic turbulence in a Couette flow [34]. In line with experiments conducted here at similarly low shear rates, many of the orientation distributions reported in that study were uniform. However, the peak swimming orientation of Alexandrium catenella (a biflagellate with one protruding flagellum) was offset from the flow direction by 0.2–0.5 rad for a shear rate of 1 s⁻¹, which was putatively ascribed to an active behavioural response. Our findings instead suggest that the offset may have resulted purely from the passive interaction between shear and noise. The identification of this offset in phytoplankton gives confidence in the interpretation of their dynamics in terms of the competition between shear-induced aligning torques and orientational noise in the swimming direction.

Heterosigma exhibited both preferential cell alignment with the flow direction and increased cell concentration in regions of high shear, both features that were recently observed for bacteria in shear flows [10]. This agreement is consistent with the similarity in morphology and swimming kinematics: for both Heterosigma and bacteria, the (propulsion-generating) flagellum protrudes along the cell's swimming axis, increasing the cell's hydrodynamic aspect ratio. For Heterosigma, at the mean shear rate corresponding to the peak in the depletion index (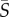 = 2.5 s⁻¹, I_D = 0.18), the orientation distribution is characterized by two distinct regions in the flow (figure 3c): the central, low shear region that exhibited randomly distributed cell orientations and the outer, higher shear regions where cells more strongly aligned with the flow. The torque imparted by shear rotates an elongated swimmer with an orientation-dependent rotation rate, which is considerably slower when the swimmer is parallel to the flow. The swimmer thus spends most of the time aligned with the flow direction. Because propulsion occurs primarily in the direction of the swimmer's orientation, cells lose the ability to migrate across the flow and become ‘trapped’, such that the cell concentration in the high-shear regions of the channel increases. Variations in concentration are therefore not driven by the degree of flow alignment caused by Jeffery orbits per se but rather by the spatial variation in the shear rate and consequently in the degree of alignment of cells with the flow.

Dunaliella cells likewise were depleted from the central, low-shear region of the channel. At a mean shear rate of 2.5 s⁻¹, Dunaliella exhibited a depletion index of 0.08, and the orientation distribution showed some preferential alignment with the flow direction. A clear offset in preferential alignment, however, did not emerge until the mean shear rate increased to 12.5 s⁻¹, and the tendency of the population to align with the direction of the flow remained diffuse in contrast to Heterosigma. Together, these observations suggest Jeffery-like effects in Dunaliella, although to a lesser degree than in Heterosigma. This is qualitatively consistent with the smaller effective elongation of Dunaliella, when the shape and motion of the flagella are taken into account.

3.3. Angular velocity

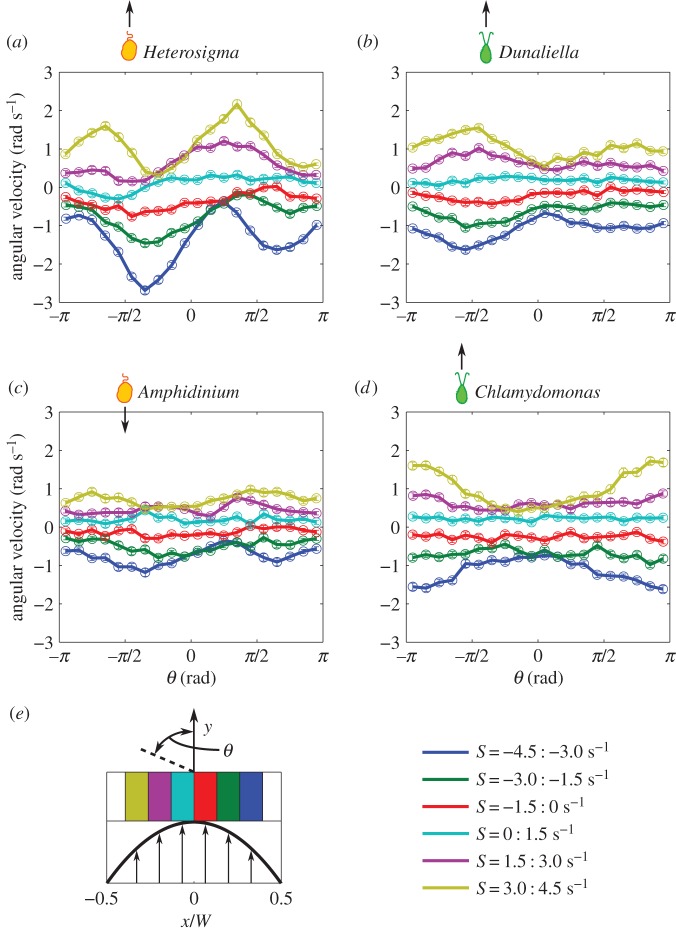
The presence and strength of Jeffery orbits can be assessed by considering the angular velocity of the cells as a function of their orientation, because cells misaligned with the flow are expected to rotate faster than aligned ones. Angular velocity measurements binned based on both the local shear rate and the cell orientation are shown in figure 4 for 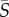= 2.5 s⁻¹. Consistent with the conclusions drawn from the cell concentration and orientation profiles (figures 2 and 3), Heterosigma dynamics exhibited the strongest Jeffery orbit signatures, with the magnitude of the angular velocity in high local shear regions (yellow and blue profiles in figure 4a) being up to threefold higher for flow-misaligned cells compared with flow-aligned ones. We note that the offset of the peaks and troughs of the angular velocity results from the coupling of fluid shear and rotational noise.

Figure 4.

(a–d) Mean angular velocity as a function of cell orientation for each species. Colours correspond to bins of local shear rate as shown in the legend. Error bars correspond to the standard error of the mean. Variations in the magnitude of the angular velocity as a function of orientation are characteristic of Jeffery orbits. (e) A schematic of the microchannel shows where each bin of shear rate is located across the channel width.

The angular velocity of Dunaliella in high local shear regions (yellow and blue profiles in figure 4b) was approximately 1.5-fold larger for flow-misaligned cells compared with flow-aligned ones, confirming the weaker preferential alignment of Dunaliella compared with Heterosigma (figure 3). No coherent deviations from a uniform angular velocity were observed for Amphidinium (figure 4c). More strikingly, Chlamydomonas displayed a mostly uniform angular velocity at all cell orientations (as expected for spherical particles), but exhibited a preference to rotate towards the central, lower-shear region at higher local shear rates (figure 4d). This preference was strong and can be observed in the larger angular velocity of cells oriented in the upstream direction, θ = ±π (yellow and blue profiles in figure 4d). This tendency is incompatible with the Jeffery dynamics of an elongated particle, whether noisy or noiseless, and points to either an active, behavioural response to shear by Chlamydomonas or a complex interplay between the shear and the beating of Chlamydomonas's flexible flagella.

3.4. Effective aspect ratio

Although the observed cell dynamics in flow exhibit signatures of Jeffery orbits and of the coupling between noise and shear, the cell body shape quantified by the aspect ratio of the cell body, q_CB (figure 5a), is not sufficient to predict their rotational motion in shear. The flagellar conformation and kinematics, as well as potentially active behaviour, can also play an important role in cell rotation. To capture the cumulative effect of all processes influencing the cells' rotational dynamics, we computed an effective aspect ratio, q_EFF, as a function of shear rate. This was done by numerically solving the Fokker–Planck equation (equation (2.2)) for each mean shear rate, 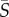, for a range of effective aspect ratios, q, and then determining by a least-square fit which value of q—henceforth referred to as q_EFF—led to the predicted orientation distribution, p(θ), that best approximated the observed distribution. The comparison between predicted and measured orientation distributions is shown in figure 5b–d for Heterosigma and Dunaliella for three mean shear rates ( 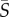= 0.5, 2.5, 12.5 s⁻¹). The comparison shows that this approach leads to a good fit and supports the use of an effective aspect ratio to capture the cells' rotational dynamics.

The effective aspect ratio, q_EFF, is shown across shear rates for both species in figure 5e (solid lines). The effective aspect ratio of Dunaliella is smaller than the population-averaged aspect ratio of its cell body (q_CB = 1.94, green dotted line in figure 5e) for all shear rates. The effective aspect ratio of Heterosigma increases across shear rates; however, in the regime where the mean shear rate is much greater than the rotational diffusivity (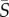 > 2.5 s⁻¹), q_EFF is considerably greater (approx. two- to 2.5-fold) than the aspect ratio of its cell body (q_CB = 1.65, red dotted line in figure 5e). Thus, the strong differences between the two species' rotational dynamics at high shear rates arise despite the fact that they have cell bodies with similar aspect ratios. The low effective aspect ratio at low shear rates, on the other hand, might be influenced by geometrical factors in addition to the effect of rotational noise. Helical swimming patterns, common to phytoplankton cells [52], can make the orientation distribution of the cells appear broadened in regimes where the flow has less impact on cell dynamics. In addition, wall effects can potentially affect a population's orientation distribution if the characteristic time between wall interactions for a given cell is smaller than the time required for the flow to impart a steady (Fokker–Planck) distribution on that population.

4. Discussion

Four species of phytoplankton were examined in a microchannel flow across a range of mean shear rates (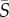 = 0–25 s⁻¹). Concentration profiles of cells across the channel width (figure 2) varied depending on both shear rate and phytoplankton swimming style. At low mean shear rates ( 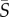< 1 s⁻¹), all species displayed little deviation from the no-flow case. At medium mean shear rates ( 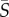= 1–10 s⁻¹), species with a single protruding flagellum displayed reduced concentrations in the central channel region characterized by low local shear, whereas at higher mean shear rates ( 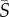> 10 s⁻¹), breaststroke-like swimmers exhibited increased concentrations in the central, low-shear region of the channel. Orientation distributions (figure 3) for Heterosigma and Dunaliella were uniform at low mean shear rates, whereas Heterosigma displayed preferential alignment with the flow direction at the same mean shear rate ( 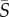= 2.5 s⁻¹) for which its spatial distribution was most heterogeneous. The effective aspect ratio, q_EFF, computed for Heterosigma and Dunaliella (figure 5) showed opposite trends (q_EFF > q_CB for Heterosigma; q_EFF < q_CB for Dunaliella) at medium-to-high mean shear rates ( 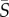> 2.5 s⁻¹), despite the similarity in the aspect ratio of the cell body, q_CB, between the two species. Angular velocity measurements (figure 4) further supported the Jeffery-orbit-like behaviour of elongated swimmers for both Heterosigma and Dunaliella, but not for Chlamydomonas.

Our findings at low shear rates indicate that the most relevant effects of flow on the spatial and orientational distribution of phytoplankton are expected only in the more intense flow conditions in oceans and lakes, as well as in engineered systems such as bioreactors. Indeed, we begin to see effects on concentrations and orientations at 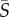> 1 s⁻¹, which is a strong level of shear in most marine environments, although still within the range generated by typical oceanic turbulence in the mixed layer. In this regime of higher shear rates, shear causes alignment with the flow, which, in turn, decreases the cross-stream mobility of cells. The trapping of phytoplankton cells in regions characterized by elevated local shear rates may have behavioural and physiological consequences, for instance by quenching the cells' ability to follow gradients (e.g. of nutrients or light), as previously shown for bacteria [10].

An important consideration for the applicability of these results to turbulent flows is related to the steady conditions in our experiments, whereas in turbulence, conditions are unsteady and organisms are affected by a sequence of eddies. Ideally, this would be approached experimentally by tracking phytoplankton in turbulence, yet the ability to visualize phytoplankton in turbulent flows has remained elusive. Thus, the transition from the demonstration of a mechanism in steady conditions to its testing under unsteady turbulent conditions is currently best achieved using numerical simulations. For example, a recent study of Heterosigma demonstrating the preferential alignment of cells owing to gravitaxis was experimentally conducted in a steady model flow of a turbulent eddy and then extended to the case of unsteady, realistic turbulence using direct numerical simulations [53]. Furthermore, numerical simulations of gravitactic cells swimming in a lattice of counter rotating vortices—often used as a simple proxy for turbulence—yielded a multitude of potential heterogeneity patterns depending on both swimming characteristics and flow strength [54]. This study additionally showed that cells often traversed many vortices before reaching their equilibrium positions, thus demonstrating that vortices can impart a cumulative effect on populations of cells over time scales that exceed the Kolmogorov time scale. Determining the extent to which the mechanisms investigated here impact the heterogeneity of phytoplankton cells in unsteady flows in natural and engineered environments will similarly require careful consideration of the role of unsteadiness, likely through numerical simulations. Initial results in this direction have recently been obtained [55] and suggest that turbulence can quench the accumulation observed in laminar flows, but the diversity of conditions and mechanisms implied by our study suggests that this remains a rich avenue for additional investigation.

Capturing the effective elongation of cells is critical in correctly predicting the depletion of cells from low-shear regions and their orientational dynamics, as previously shown for bacteria [10]. For Heterosigma, the forward-facing flagellum likely acts in concert with the already elongated cell body to increase the hydrodynamic aspect ratio of the cell. In contrast, Dunaliella (like Chlamydomonas) swims in a breaststroke-like manner, so the flagella take on different waveforms throughout the beat cycle. These waveforms include positions where the flagella are out in front of the cell (increasing the effective aspect ratio) and other positions in which the flagella protrude laterally from the cell (decreasing the effective aspect ratio) [56]. A hydrodynamic model of Chlamydomonas swimming in a linear shear flow that included the effect of flagellar beating demonstrated that the net effect of the flagellar beat cycle was to reduce the effective aspect ratio of the cell compared with the geometric aspect ratio of the cell body and that the cells could be adequately modelled as spheres [28]. Despite their similar cell body shape, Heterosigma and Dunaliella exhibit quantitative differences in their effective aspect ratios owing to the presence and configuration of their flagellar appendages, which explains their orientational dynamics in flow (figure 5b–e). Additionally, the effective aspect ratio represents an important parameter to understand their spatial distributions at low and medium shear rates (figure 2) based on a purely passive interplay between shear, cell geometry and rotational noise [10].

Shear-induced trapping of elongated swimmers—which can explain the depletion from low-shear regions for Heterosigma and Amphidinium (figure 2) as well as for bacteria [10]—is inadequate to explain the observed accumulation in low-shear regions of breaststroke-swimming cells—here, Chlamydomonas and Dunaliella (figure 2). Such accumulation in low-shear regions would occur—based on the same physical arguments (Jeffery orbits coupled with motility and noise)—for cells that swim along their shorter axis. By having their long axis preferentially oriented in the flow direction, these cells would primarily swim perpendicular to the flow, and consequently migrate towards low-shear regions. However, this effect appears in conflict with previous predictions of near-sphericity for Chlamydomonas [28], and we do not observe a preference for Dunaliella to align perpendicular to the flow. This leaves open the possibility that shear affects the effective elongation of the cells by deforming their flagella as they beat. Recent analysis of flexible flagella in shear provides initial support for this hypothesis [57], though no experimental evidence exists to date. The coupling between the ambient flow and the local flow field generated by different swimmers (e.g. pushers versus pullers) may also potentially explain the different accumulation patterns, but testing this hypothesis will require more specialized simulation and visualization techniques.

Previous experiments and models have shown that a bias in the motility of phytoplankton, such as that caused by gyrotaxis or phototaxis, is necessary to generate centre-channel accumulation [58–60] at low shear rates (0.1–3 s⁻¹). However, this work shows, unexpectedly, that sufficiently high shear rates (5–25 s⁻¹) can cause breaststroke-like swimmers to accumulate in the lower shear regions without bias. To the best of our knowledge, this manner of accumulation cannot be explained by current mechanistic models and points towards a possible biological response of the swimming cells or a yet-to-be-elucidated physical mechanism.

Given these considerations, we speculate that the observed accumulation of Chlamydomonas and Dunaliella in the low-shear regions could originate from a different effect: active, behavioural responses to fluid shear. Some support for this speculation comes from the peaks in magnitude in the angular velocity of Chlamydomonas (figure 4d), which indicate a tendency to rotate towards the centre of the channel. Conclusive evidence on behavioural responses of phytoplankton to shear and the identification of the physiological mechanisms underpinning such behaviours is still lacking, but some prior evidence exists for active responses to high shear for both of the breaststroke swimmers used in our work. A study of the effective viscosity of Chlamydomonas suspensions speculated that the observed variations in viscosity possibly resulted from behavioural changes, as cells were reported to actively ‘resist the flow rotation’ [36]. In a separate microfluidic study, Dunaliella cells were shown to travel in the direction of the local vorticity vector if the local shear rate exceeded 10 s⁻¹ [35]. The same study presented high-speed videos of cells in a shear flow, showing the bodies of live cells maintaining their orientation over time, whereas dead cells rotated as predicted by Jeffery orbits. The authors proposed that live cells may modify their beat pattern at shear rates above 10 s⁻¹ to counter the flow-induced rotation of the cell, an intriguing hypothesis that remains to be further investigated.

The possibility of active behavioural changes in response to hydrodynamic cues offers both the possibility for an intriguing behavioural adaptation in some species of phytoplankton, and a serious challenge for the experimenter, amidst an already complex set of passive processes governing the fate of phytoplankton in shear, as illustrated here. On the one hand, elucidating these behavioural changes is of particular importance, because models of swimming phytoplankton often rely on a simple, linear superposition of swimming and flow [28,58]. If shear can significantly affect swimming behaviour, such models would either need to account for the modified behaviour or ensure they are only operating in regimes where flow does not alter swimming. On the other hand, a deeper understanding of phytoplankton in flow allows for the possibility of exerting greater control over the organisms in engineered systems. Harvesting biomass, for example, is an energetically costly step in the production of biofuels [59], and behavioural changes in motility that cause cells to self-segregate may potentially help alleviate those costs [60].

5. Conclusion

The environments inhabited by phytoplankton are characterized by dynamic and often turbulent fluid flows, where hydrodynamic shear is prevalent. Our results show that the interactions between shear and motility can result in strongly heterogeneous distributions of motile phytoplankton, and that the nature and origin of these distributions will vary for different species, as they depend on cell morphology, swimming style and, potentially, the ability of cells to actively respond to flow. Our findings further highlight the importance of gaining a deeper understanding of the biophysical mechanisms and potential physiological adaptations governing the interplay between phytoplankton and flow in predicting the fate of different species of phytoplankton in natural and engineered systems.

Data accessibility

Data in Dryad: http://dx.doi.org/10.5061/dryad.2306t.

Author contributions

M.T.B., R.R., J.S.G. and R.S. designed the study. M.T.B. carried out experiments; M.T.B. and R.R. analysed the data. R.R. and J.S.G. fabricated microfluidic channels. All authors wrote the manuscript.

Funding

M.T.B. acknowledges support from an NSF Graduate Research Fellowship. R.S. acknowledges support by NSF grants OCE-0744641-CAREER, CBET-1066566 and CBET-0966000, a Gordon and Betty Moore Marine Microbial Initiative Investigator Award (award number 3783) and support from the MIT-SkolkovoTech Institute joint programme.

Competing interests

We declare we have no competing interests.