Modelling of bone fracture and strength at different length scales: a review

Abstract

In this paper, we review analytical and computational models of bone fracture and strength. Bone fracture is a complex phenomenon due to the composite, inhomogeneous and hierarchical structure of bone. First, we briefly summarize the hierarchical structure of bone, spanning from the nanoscale, sub-microscale, microscale, mesoscale to the macroscale, and discuss experimental observations on failure mechanisms in bone at these scales. Then, we highlight representative analytical and computational models of bone fracture and strength at different length scales and discuss the main findings in the context of experiments. We conclude by summarizing the challenges in modelling of bone fracture and strength and list open topics for scientific exploration. Modelling of bone, accounting for different scales, provides new and needed insights into the fracture and strength of bone, which, in turn, can lead to improved diagnostic tools and treatments of bone diseases such as osteoporosis.

1. Introduction

Bone tissue has an intricate arrangement of material structures at multiple length scales which work in harmony to perform a variety of mechanical, biological and chemical functions such as providing structural support, protection of internal organs and cells, and mineral storage. Bone continuously adapts its structure in response to external mechanical and chemical stimuli. Additionally, it possesses healing and regenerative characteristics enabling repair of microcracks and fractures.

The hierarchical structure of bone significantly contributes to high stiffness, strength, toughness and energy absorption, light weight and other remarkable mechanical properties of bone. There are two main types of bone: cortical (compact or dense) and trabecular (cancellous or spongy). The cortical bone forms a dense, hard outer shell that mostly contributes to bone stiffness and strength. The porous trabecular bone fills interior spaces or ends of long bones and is mainly responsible for energy absorption and load distribution in the body. Bone also serves as a reservoir of minerals such as calcium and phosphorus.

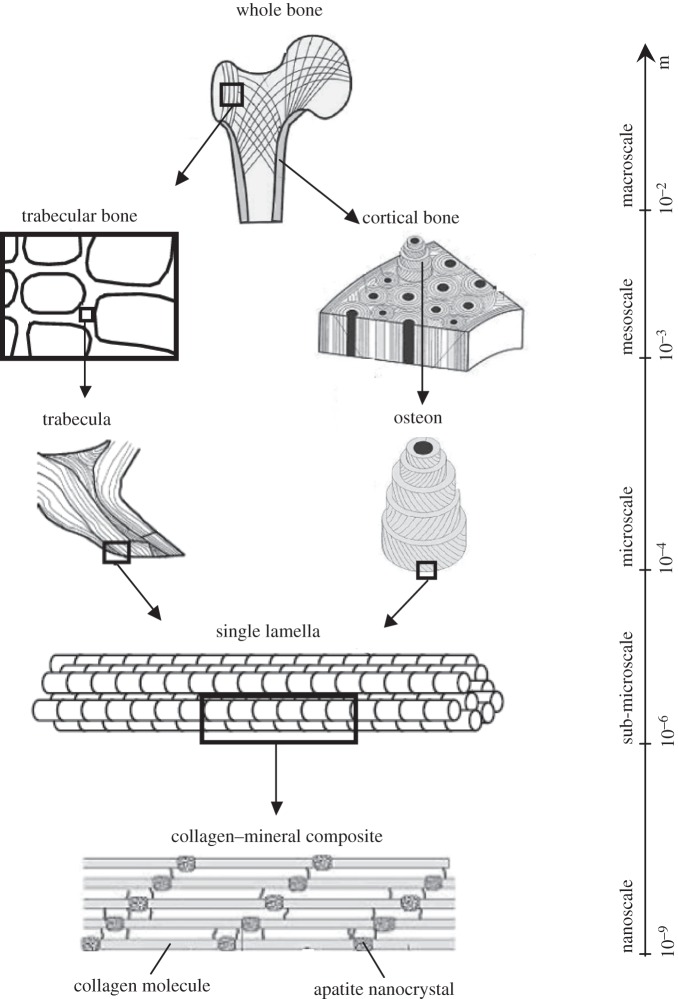
The hierarchical structure of bone, spanning from the nanoscale to the macroscale, is briefly outlined here (figure 1):

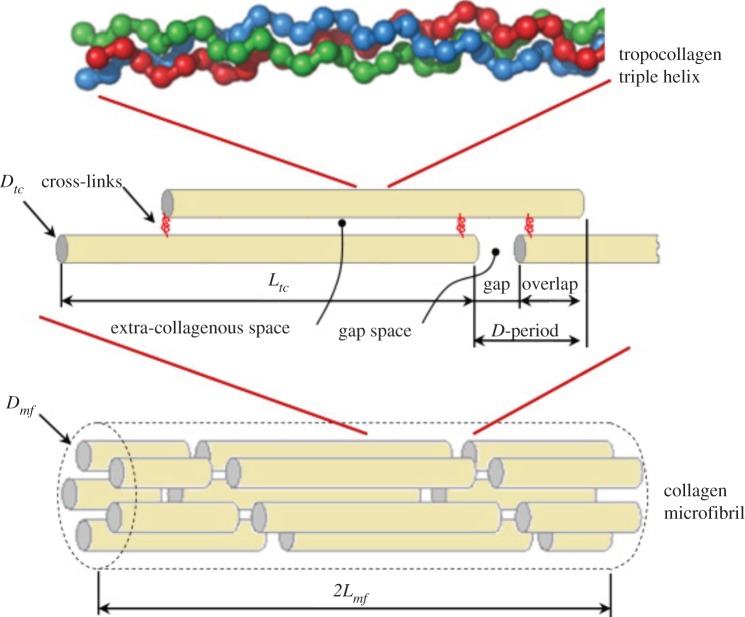
• —Nanoscale. At this level, bone is made of mineralized collagen fibrils which form the basic building blocks of bone. Bone is composed of three major components: an organic matrix (mostly collagen type I), a calcium phosphate mineral in the form of hydroxyapatite (HA) platelets, and water. These constituents constitute, respectively, 32–44%, 33–43% and 15–25% of bone volume [1]. In addition to collagen, the organic matrix contains small amounts of non-collagenous proteins (NCPs) that interact with both collagen and minerals [2]. Collagen molecules, called tropocollagen (TC), self-assemble into collagen fibrils approximately 100 nm in diameter and up to several micrometres in length. The dimensions and formation site of minerals have long been a matter of contention. Early studies using transmission electron microscopy (TEM) and small angle X-ray scattering reported 40–60 nm length, 20–30 nm width and 1.5–4 nm thickness for minerals [3–9]. Atomic force microscopy studies reported larger dimensions for minerals, with widths and lengths of approximately 30–200 nm [10,11]. This discrepancy is partly due to breakage of brittle minerals during TEM sample preparation. More recently, dark-field TEM showed that mineral structures in bone are made of apatite crystals approximately 5–6 nm in thickness, approximately 5.8 nm in width and 28 nm in length [12]. Furthermore, there has not been a consensus on the arrangement of minerals with respect to collagen; some studies stated that bone minerals mostly reside inside collagen fibrils in the gap zones [13–16], while others reported that either the majority or all minerals lie outside the collagen fibrils [12,17–22]. Recent experimental observations on demineralized and deproteinized bone suggested that minerals form a continuum phase in bone [23–26]. In that case, bone can be represented as a composite with interpenetrating phases of collagen and minerals, with some pores filled with water and NCPs, forming a mineralized collagen fibril.
• —Sub-microscale. In this level, the mineralized collagen fibrils assemble into sheet-like structures approximately 3–7 µm thick, called lamellae. Lacunae, which are the hosts to bone cells (osteocytes), reside in the lamellae and are connected with each other through canaliculi (channels about 100 nm in diameter).
• —Microscale. Different assemblies of lamellae give rise to two bone types: cortical and trabecular.

  In cortical bone, lamellae arrange into concentric cylinders forming osteons approximately 200–300 µm in diameter and approximately several millimetres long, which are aligned along the bone's long axis. Each osteon contains a long canal, called a Haversian canal, through which the blood vessels run. Interstitial bone, which consists of remnants of old osteons, lies in between the osteons. It has a similar lamellar structure to osteons but a higher degree of mineralization. The boundary of each (secondary) osteon (formed during bone remodelling) is separated from the interstitial bone by a cement line; primary osteons do not have cement lines.

  In trabecular bone, the lamellae assemble into trabeculae which are in the form of rods or struts. Each trabecula consists of trabecular packets which have a crescent shape and are about 50 µm thick and 1 mm long. Interstitial bone exists at interconnects of trabeculae. Trabecular packets resorb and form during bone remodelling.

• —Mesoscale. This scale represents either cortical bone, which consists of osteons embedded in the interstitial bone, or trabecular bone, which is built up by a porous network of rod-like or plate-like trabeculae.
• —Macroscale. This is the whole bone level, which includes both cortical and trabecular bone types.

Understanding of the damage and fracture of bone is of significant clinical importance. Osteoporosis is a bone disease characterized by low bone mass and deterioration of the microstructure of bone [27], leading to bone fragility and increased risk of fractures [27–29]. Various factors, such as bone disuse, prior history of broken bones and ageing, among others, affect the onset and progression of osteoporosis. This disease manifests itself by one particular symptom: bone fractures, which can further lead to disability or morbidity. Prevention and treatment of osteoporotic and age-related fractures demand an accurate assessment of bone quality and fracture risk. Traditionally, the bone mineral mass or density (BMD) has been used to quantify the bone fracture risk. However, studies have shown that BMD is not the only factor contributing to bone fracture risk and it alone cannot explain the underlying mechanisms of bone fractures in humans [30–34]. Various factors act in combination to increase the bone fracture risk. Burr et al. [30] divided these factors into three general categories: loading conditions, changes in bone structure and changes in bone tissue material properties. Loading factors include the incidence and mechanics of falls [30]. Changes in the trabecular architecture and a decrease in the trabecular connectivity are examples of structural factors contributing to an increased fracture risk. Changes in the tissue material properties can be due to changes in the degree of mineralization, collagen abnormalities, as in the disease osteogenesis imperfecta [35], or accumulation of unrepaired microdamage or microcracks.

Figure 1.

Hierarchical structure of bone, spanning from the nanoscale to macroscale.

Clearly, a cascade of events happening at different length scales affects bone quality and strength, such as changes in the BMD, changes in the collagen quality at the nanoscale, formation of microcracks at the microscale and loss of trabecular connectivity at the mesoscale. Yet, the relationship between the microstructures of bone at different levels of hierarchy and bone's resistance to damage and fracture remain to be fully explored. This provides motivation for the current study. Bone modelling at different structural scales can provide new insights into the failure mechanisms leading to bone fracture.

Several researchers reviewed in detail the composition and structure of bone, its mechanical properties and the relationship between the two [1,2,36–44]. Nevertheless, a complete collection of existing theoretical models on the strength and fracture of bone together with a detailed discussion and comparison of them is still missing. In particular, a standing question is how different models and their predictions at different length scales can be linked to each other to provide a comprehensive, hierarchical picture of bone quality and fracture risk. In this paper, we mainly review developments in the modelling of mechanical properties of bone with a focus on the strength and fracture. To this end, we first identify the dominant fracture and toughening mechanisms taking place at different levels of hierarchy in bone, with a focus on cortical bone. Next, we review different existing models, discuss their assumptions and limitations and compare their findings. Finally, we offer recommendations on future studies in this field. Such discussion sheds light on the structure–property relations in bone and should help in the development of inclusive multiscale models for prediction of bone damage, fracture and strength.

2. Bone toughening mechanisms: a multiscale perspective

2.1. Terminology

Before starting our discussion on the fracture mechanisms in bone and reviewing the existing models to quantify bone strength and fracture, let us first define the terminology.

• —Stiffness (also called elastic or Young's modulus) is a measure of the resistance of a material to elastic deformation and is calculated as the slope of the initial linear portion of a stress–strain curve.
• —Strength is a measure of a material's resistance to failure. Strength can denote the stress at first yield (yield strength) or the maximum stress (ultimate strength) on an engineering stress–strain curve [45].
• —Toughness is a measure of energy absorption capacity up to failure and can be quantified by taking an area under a stress–strain curve.
• —
  Fracture toughness is a measure of the inherent resistance of a material to fracture and can be analysed by fracture mechanics. There are various measurements of fracture toughness, a few of which are briefly summarized next.

  • (1) The fracture toughness K_c, representing the toughness to initiate cracking, is obtained using linear elastic fracture mechanics (LEFM) where a material is considered to be elastic, with a small inelastic region at the crack tip (small-scale yielding). The local stress field, σ_ij, at a distance r from the crack tip is:

    2.1

    where K is the stress intensity factor (SIF), θ is the angle with respect to the crack plane and f_ij are functions that depend on the crack geometry and loading conditions. K can be defined for three modes of crack displacements: K_I for a tensile opening (mode I), K_II for an in-plane shear (mode II) and K_III for an out-of-plane shear (mode III). At fracture, the SIF, K, reaches a critical value, K_c, which is known as the fracture toughness [46].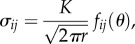
  • (2) Alternatively, one can quantify the energy release rate, G, which is the rate of change in potential energy per unit increase in the crack area. For linear elastic materials, the energy release rate and the SIFs for mixed-mode fracture are related as [46]

    2.2

    where μ is the shear modulus and E* = E (Young's modulus) for the case of plane stress, while E* = E/(1 − ν²) for the case of plane strain with ν being the Poisson ratio. At fracture, G reaches a critical value G_c, which can also be used as a measure of fracture toughness.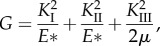
  • (3) The critical value of J integral, J_c, is another measure of the crack-initiation fracture toughness obtained from non-LEFM [47]. Compared with K_c and G_c, it includes additional contributions from plasticity and inelastic deformation.
  • (4) Crack-resistant curves (R-curves) measure the toughness of a growing crack [42,48]. The R-curves represent the measure of the crack driving force, such as K or G, as a function of an extension of a stable crack, Δa.

2.2. Bone toughening mechanisms

As described in the previous section, bone has a hierarchical structure composed of collagen, water and mineral nanoplatelets. Arrangements of these components into different functional units create a light and tough structure that is multi-functional and able to adapt to diverse mechanical environments [32,34,49,50]. The hierarchical structure of bone at each scale is adopted based on local needs to provide required bone functionalities and mechanical properties at that scale, and thus bone strength and fracture toughness are affected by bone structures at all scales [32,34,49,51]. In order to understand the influence of bone quality, characterized by bone's material composition and structural design, on its mechanical properties, we need to investigate how bone resists fracture at different length scales.

As a living tissue, bone has a unique capacity of self-repair through growth and remodelling processes, which gives it a dynamic structure. The remodelling process allows the bone structure to adapt itself to external changes. This continuous process also removes damaged bone tissue and replaces it with a new bone material [32,34,52]. However, excessive remodelling of the microdamage induced by ageing and bone diseases degrades bone quality and increases the possibility of fracture [32,51–57]. Thus, to better understand the fracture phenomena in bone, it is necessary to enhance our understanding of ageing-related changes in structure and composition, which, in turn, influence bone's mechanical properties.

BMD is the parameter that is most commonly used clinically to determine bone deterioration with age and to predict bone's susceptibility to fracture [32,34,51]. However, research has clearly shown that reduced BMD is not the sole factor responsible for an increased fracture risk [31,58–63]. These studies reveal the contributory effects of bone's hierarchical structure on bone quality. Bone resists fracture by different toughening mechanisms at multiple length scales ranging from the nanoscale to the macroscopic scale. A more complete understanding of bone fracture can be achieved by studying active fracture/toughening mechanisms at different structural levels, leading to developments of new and more effective therapeutic treatments [32,34,51,64,65].

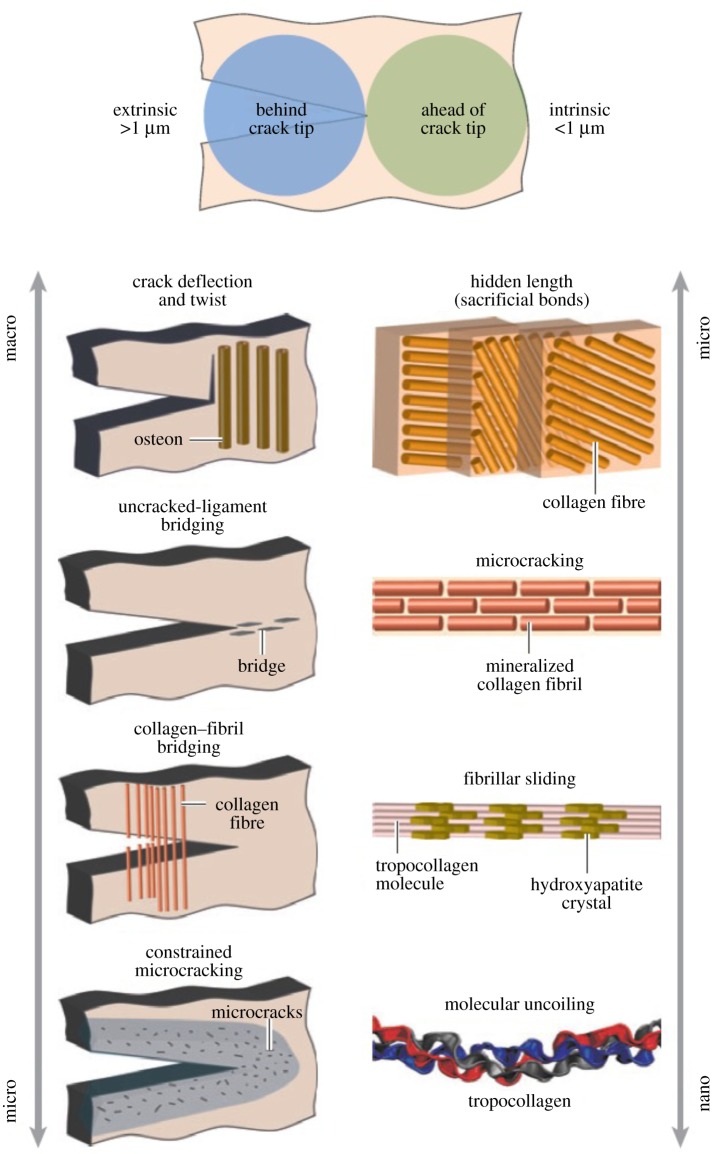
Bone toughness is an important measure of bone quality which can be used to predict the risk of bone fracture. To determine the toughness of bone and to understand the role of different toughening mechanisms, it is crucial to look at the fracture resistance as a hierarchical process. Fracture in bone is a mutual competition between intrinsic damage mechanisms ahead of a crack tip that advance cracking and extrinsic shielding mechanisms, mainly behind the tip, that prevent cracking [32,34]. The former mechanisms increase the structural resistance to the initiation and growth of cracks, whereas the latter mechanisms improve bone toughness by shielding the crack tip from applied driving forces [32].

Figure 2 schematically illustrates various intrinsic (plastic deformation) and extrinsic (crack-tip shielding) toughening mechanisms taking place in the cortical bone [32]. Intrinsic toughening mechanisms such as molecular uncoiling and intermolecular sliding, microcracking and fibrillar sliding act at a sub-microscale level [32,34,49,66]. These mechanisms, which are observed at length scales less than 1 µm, lead to plastic deformation and an increase in the energy dissipation capacity of bone [32,34].

Figure 2.

Bone toughness mechanisms at different levels of hierarchy. The toughness of bone results from a mutual competition between extrinsic (crack-tip shielding) toughening mechanisms and intrinsic (plastic deformation) toughening mechanisms. Molecular uncoiling and intermolecular sliding of molecules are observed at the smallest level of TC molecules and mineralized collagen fibrils. Microcracking and fibrillar sliding are observed at the level of fibril arrays. At larger levels, the breaking of sacrificial bonds contributes to increasing the energy dissipation capacity of bone at the interface of fibril arrays, together with crack bridging by collagen fibrils. At the largest length scales in the 10–100 µm range, the primary sources of toughening are extrinsic and result from extensive crack deflection and crack bridging by uncracked ligaments, both of which are mechanisms that are motivated by the occurrence of microcracking [32]. (Online version in colour.)

As shown in figure 2, at the microscale and above, the main sources of energy dissipation and toughening are the extrinsic mechanisms, involving crack-tip shielding [32]. The interaction of microcracks and bone microstructures at these length scales results in extrinsic shielding mechanisms such as crack deflection and twisting, uncracked ligament bridging, collagen fibril bridging and constrained microcracking [32,34,49,57,67,68]. As opposed to the intrinsic toughening mechanisms that affect both crack initiation and propagation, the extrinsic toughening mechanisms arise during crack growth [32,34]. Bone fracture studies show that active extrinsic shielding mechanisms at the microstructural level influence the toughness of cortical bone by changing the crack growth trajectory [32,34,51].

At the microstructural level, the main structural features that control the cortical bone fracture toughness include osteons, cement lines and extensive discontinuities such as Haversian canals. Such discontinuities could turn out to be stress concentration sites for crack initiation [69]. However, various researchers have shown that microstructural barriers are capable of slowing or hindering crack growth in the osteonal cortical bone [39,70–74]. Therefore, short cracks are encountered more frequently than long cracks in this tissue [75]. Experimental observations showed that microcracks smaller than 300 µm are either deviated in the vicinity of the osteon or stopped at the cement line [69]. Fracture surface studies, on the other hand, indicate that, if microcracks can grow up to a particular length (approx. 300 µm) in a Haversian cortical bone, they can then penetrate osteons [69]. If these cracks continue to grow through the concentric lamellae inside an osteon and have a high enough stress intensity value to break through the Haversian canal, they have a clear pathway with no barriers to further growth, and catastrophic failure is the likely outcome. This could possibly explain the findings of fracture surface studies where failure surfaces tend to show splitting of osteons, often at the centre of Haversian canals. Therefore, both the deviation of a microcrack as it approaches the osteon and its arrest on the cement line boundary cause growth reduction and prevent crack penetration into the osteon. Both of these phenomena enhance cortical bone's resistance to fracture.

Various studies have shown that age-related changes in bone increase the risk of bone fracture [57,76–82]. Even though a loss in bone mass and degradation of bone quality have been pointed out as the main reasons for a reduction in the bone fracture toughness, the importance of the effects of ageing on the bone fracture has not yet been fully understood [32,34,51]. Experimental studies on various types of human cortical bone reported a 5–11% and 12–19% reduction per decade in crack-initiation and crack-growth toughness in the longitudinal direction, respectively [80,83–87]. Other studies indicated that crack-initiation and crack-growth toughness in the transverse direction decrease by 1–4% and 3% per decade, respectively [82,88]. These results show that ageing has a negative impact on the effectiveness of toughening mechanisms and, consequently, reduces the fracture resistance of bone. However, the reasons for these age-related changes in bone are complex and demand more in-depth investigations [32,34,51].

Age-related changes exhibit themselves at multiple structural length scales in bone. At the nanoscale, the ageing process leads to a high cross-link density of collagen molecules, thereby reducing energy dissipation before failure [49,50,66,89–91]. As a consequence, this may cause brittle fracture in older bone [32,34]. At the sub-microscale, ageing degenerates the properties of individual collagen fibrils [32,34].

Finally, at the microscale and above, bone's microstructures and material properties vary with age, which significantly affects the macroscale bone toughness [32,34,51]. The ageing process makes the interstitial bone tissue stiffer [39,92], which was shown numerically to have a profound effect on the bone fracture mechanics [74,93–97]. In addition, ageing leads to changes in the thickness and material properties of cement lines, which are the main sites for microcrack initiation [32,34]. Experimental results showed that cement lines could lead to the death of bone cells by cutting the connecting canals between the interstitial and osteonal bone cells [98]. From the mechanics point of view, modelling results demonstrated a significant impact of material properties of cement lines on microcrack–osteon interactions [74,99]. Quantitative analyses of cortical bone have also reported that the size and density of osteons vary with age [78,100–104]. Because cement lines are prime sites for microcrack formation, an increase in the osteon density could lead to a higher microcrack density, which could reduce the crack-initiation toughness [32,34]. In general, age-related changes in the bone microstructure and material properties at this scale are major causes of the reduction in fracture resistance.

Even though in this review we mainly focus on the fracture of cortical bone, it is worth mentioning that the weakness encountered in the trabecular bone repair mechanism during ageing is one of the main concerns in human bone fractures [76]. For example, hip fractures, which are the most common types of osteoporotic bone fractures, occur usually in the femoral neck, which is mostly made of trabecular bone [32,34]. Although internal changes in trabecular bone's microstructure with age influence bone toughness, trabecular bone's quantitative changes contribute most to the increased bone fracture risk with ageing [105]. For instance, reductions in the density and thickness of the struts in trabecular bone with age [106–110], especially in postmenopausal women, are major reasons for the severe reduction in the bone fracture resistance of the elderly [32,34,105,106,111].

3. Literature review of the existing models of bone strength, fracture and damage

3.1. Models at the sub-microscale and smaller scales

A number of studies have been performed to model strength and fracture of bone at the sub-microscale and smaller scales. However, most of these studies have focused on modelling of bone at the atomic and nanoscale levels, and only a few works have addressed the sub-microscale. The models can be divided into analytical and computational ones.

3.1.1. Analytical models

Mammone & Hudson [112] used a micromechanics approach to obtain the tensile strength of bone. They represented bone as a polymeric composite material containing a collagenous matrix and HA fillers to investigate the role of mineralization, particle shape and orientation on bone strength. In their model, the particle-matrix debonding was assumed as the main mode of bone failure. Jäger & Fratzl [113] proposed a staggered arrangement of HA platelets in a collagen matrix to form the mineralized collagen fibril (figure 3). They employed a shear-lag model to assess the effective elastic modulus and strength of this geometric system for a variety of aspect ratios and distances between mineral platelets. This staggered geometry became the basis for many analytical and computational models of bone that followed.

Figure 3.

A schematic of the shear-lag model proposed by Jäger & Fratzl [113] representing (a) staggered HA crystals embedded in protein matrix and (b) the load-carrying structure of the collagen–mineral composite [113,114]. (Online version in colour.)

Gao and co-workers [115–121] used the geometry suggested by Jäger & Fratzl [113] and addressed several aspects of the mechanical properties of bone and bone-like materials. By using the concepts of fracture mechanics, they suggested a relation for a critical length scale, below which the naturally brittle mineral crystals become insensitive to crack-like flaws. They showed that the critical length scale for HA is in the range of a few nanometres and proposed that this is one of the reasons why the hierarchical structure of bone and many biological materials starts at the nanoscale. By implementing different methods, they also studied stiffness, toughness and strength of bone, in order to shed light on how the bone nanostructure has been designed by nature to optimize bone properties. They estimated the fracture energy and strength of the HA–collagen interface using a tension-shear chain model and showed dependence of the interface strength on the size and geometry of mineral crystals.

Wang & Qian [122] also used a shear-lag model of a mineral–collagen composite to predict stress concentrations around the initial crack to identify the mechanisms of microdamage formation in bone. The focus of their study was on age-related bone fracture mechanisms. They reported that the stress concentration pattern and, consequently, the mode of fracture depend on the nonlinearity of collagen as well as the stiffness and volume fraction of constituents.

Several other biological materials, including nacre, have a ‘brick and mortar’ structure at the nanoscale similar to the structure suggested by Jäger & Fratzl [113] for bone. Thus, researchers have focused on developing models to predict the strength and fracture resistance of such systems regardless of the type of material involved. For example, Barthelat et al. [123] derived a simple analytical model for the prediction of fracture of materials with a brick and mortar structure with a focus on crack bridging and the process zone to capture the toughness amplification observed in experimental studies of such structures. Similarly, Pimenta & Robinson [124] proposed an analytical shear-lag model to predict the tensile response of these systems, which is able to handle a generic piecewise linear constitutive law of the matrix. By performing a parametric study, they found that, for thick inclusions and ductile matrix, the material behaviour is dominated by plasticity, while for slender inclusions and brittle matrix fracture mechanics governs the material's behaviour.

An et al. [125] studied the fracture of materials with a staggered arrangement of hard platelets embedded in a soft matrix. They developed an expanded cohesive zone model under a thermodynamic framework to investigate theoretically the crack growth resistance. Microscopic deformation mechanisms were incorporated into their model considering elastic and plastic deformations and damage. They compared their theoretical results with corresponding experimental results on human dentine and showed a good agreement.

At the scale of collagen fibrils, the effects of sacrificial bonds and hidden lengths on the strength and fracture toughness of bone and other biological materials have also been studied [126–128]. In this regard, a kinetic model was developed [126,127] with random properties assigned to fibrils. The effect of loading rate was studied in this model using classical Bell's theory [129]. Results showed that sacrificial bonds lead to a significant increase in strength and fracture toughness by dissipating large amounts of energy at the molecular level. Moreover, higher loading rates, which drive the system away from equilibrium, result in higher strength and fracture toughness [127].

In summary, the analytical models of bone proposed in the literature have provided several insights into elasticity and fracture of bone at the sub-micro and smaller scales. However, most of these models idealize bone as a two-dimensional collagen–mineral composite material and do not take into account the actual three-dimensional arrangement of collagen fibrils and mineral crystals. Furthermore, it has been challenging to incorporate different failure mechanisms, such as sliding or debonding at interfaces, and various types of material constitutive laws, such as plasticity and viscoelasticity, in analytical models. These challenges can be overcome, to some extent, by using computational models, where one has more control over geometry and material properties. However, it is still not well understood what is the three-dimensional collagen-crystal arrangement, what are the properties of constituents and what are the characteristics of the interfaces. Another challenge is that, although many of the mentioned models predict strength or fracture of bone locally at the smaller scales, they do not explain how these properties are affected by the hierarchical organization of bone at higher scales.

3.1.2. Computational models using a finite-element method

Most of the finite-element method (FEM) analyses of the deformation and failure of bone at the nanoscale used a two-dimensional representation of the staggered arrangement of mineral platelets in a collagen matrix suggested by Jäger & Fratzl [113]. For example, Siegmund et al. [130,131] used a cohesive FEM model with a traction-separation law to study the role of interfaces and collagen cross-linking on the stiffness and strength of a mineralized collagen fibril. They considered two types of cross-links, enzymatic and non-enzymatic, and showed that the latter increase stiffness and decrease toughness of bone, while the former have only minimal effects on the mechanical properties of a mineralized collagen fibril. Luo et al. [132] also used a cohesive FEM model to investigate the effect of mineral–collagen interfacial behaviour on the microdamage progression in bone by considering three types of interfaces: strong, intermediate and weak.

Hambli and co-workers [133–135] suggested a three-dimensional model of a mineralized collagen fibril consisting of five TC molecules, shifted by an interval of 67 nm to form a cylindrical shape, with the space between the TC molecules and NCPs filled with a mineral phase (figure 4). Collagen cross-links were modelled as linear springs, while possible sliding at the interfaces was neglected. The authors investigated the effect of the number of cross-links, Young's modulus of HA, and the HA volume fraction on failure properties, including damping capacity and fracture stress (at crack initiation). They showed that a higher number of cross-links leads to a significantly higher damping capacity and fracture stress for up to 20 cross-links; after that adding more cross-links does not have a significant effect. In addition, as the mineral stiffness increases, the fracture stress increases with no significant change in damping capacity, whereas increasing the HA volume fraction leads to a lower fracture stress and damping capacity. A similar model was used in their earlier studies to extensively investigate the elastic properties of bone [136–139].

Figure 4.

The Hambli & Barkaoui [136] model geometry: five TC molecules shifted by the interval D = 67 nm forming a cylindrical shape, mineral phase filling the gap and extra-collagenous space and cross-links joining two TC molecule ends. (Online version in colour.)

3.1.3. Computational models using molecular dynamics

Experimental studies are most challenging at the level of building blocks of bone: collagen molecules and HA crystals [140–143]. Thus, several atomistic-level simulations were employed to study the deformation mechanisms and failure of a single collagen molecule and bundles of collagen molecules [89,144–147], cross-linked collagen molecules [91,148,149], HA crystals [150] and collagen–HA systems at the nanoscale [90,151–154] using molecular dynamics (MD) simulations.

Buehler and co-workers performed comprehensive studies on bone at the nanoscale. They studied the mechanical properties of a single TC molecule and bundles of TC molecules under different types of loading to evaluate fracture strength, using atomic-scale simulations [89]. Later, they explored cross-linked collagen fibrils under large strain deformations with different densities of cross-links and found that increasing density of cross-links leads to higher strength but the behaviour becomes more brittle [91]. Nair et al. [152] modelled a three-dimensional molecular structure of a mineralized collagen fibril with mineral densities ranging from 0% to 40% to compute its mechanical properties and identify deformation mechanisms. They reported that collagen predominantly contributes to the deformation response, while minerals bear four times higher stresses than collagen. Also, collagen deforms significantly in gap regions, whereas the deformation of mineralized collagen takes places primarily in overlap regions.

Dubey & Tomar [155–161] performed MD simulations of collagen–mineral systems and extensively investigated the strength of these structures. They employed a staggered arrangement of HA crystals embedded in a TC matrix in their simulations and studied the influence of a variety of parameters including the interfacial arrangement of TC–HA, different environments (absence or presence of water and calcium ions), direction of loading, shape of HA crystals and disease [155–161].

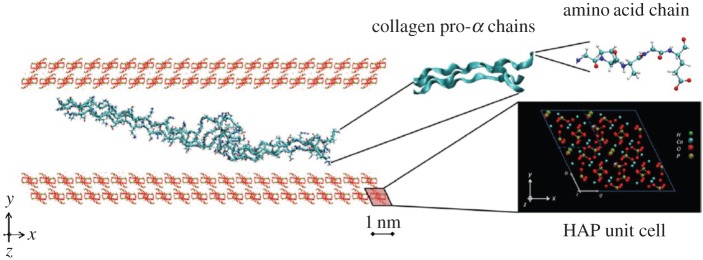
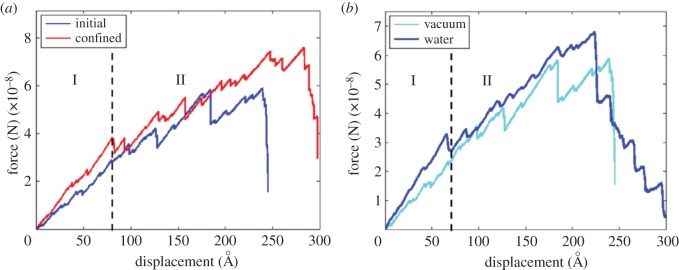
The influence of geometric confinement on the mechanical properties of bone constituents was also studied using MD simulations. Libonati et al. [150] investigated the effect of geometric confinement on strength, fracture toughness, stress field and crack propagation in HA crystals with an edge crack. To investigate the effect of crystal height, they varied the height of crystals, while fixing the width at approximately 30.1 nm and out-of-plane thickness at approximately 2.1 nm. They observed that, for samples with a height of 4.15 nm or smaller, the stress concentration at the crack tip disappears, the failure mode becomes more ductile, and strength approaches that of a flawless section. This observation confirms the earlier predictions of Gao et al. [114] about the existence of an intrinsic length scale that leads to flaw-tolerant behaviour under confinement. In another study, Libonati et al. [151] investigated the effect of confinement and the presence of water on the behaviour of the HA–collagen interface. A schematic of their model is shown in figure 5, while figure 6 shows an example of a force–displacement plot obtained from their simulations. They observed that, in all the studied cases, final failure occurred by breakage of TC molecules rather than by failure at the interfaces. Also, the main deformation mechanisms include breaking of atomic interactions between collagen–collagen and HA–collagen, uncoiling and unfolding of collagen chains as a result of breakage of intramolecular H-bonds (regime I in figure 6), and, at larger displacements, sliding of collagen on the HA surface in a discontinuous way, due to the formation and breakage of H-bonds which increases energy at failure (regime II in figure 6).

Figure 5.

The geometry of the collagen–HA nanocomposite used by Libonati et al. [151]. The building blocks, namely amino acid chains, collagen chains and the HA unit cell, are depicted on the right. (Online vesion in colour.)

Figure 6.

Example of force–displacement curves from [151]. (a) Comparison between the initial structure and the confined one. (b) Comparison between a dry (vacuum) case and wet case: the water causes a general increase in the mechanical properties owing to the interactions with mineral and protein.

In short, computational methods have been employed to study the strength and fracture properties of bone and its constituents, their volume fractions, arrangement and cross-linking. Although three-dimensional realizations of bone at the nanoscale, which represent reality more closely, have been modelled using computational techniques, most of the existing studies assumed idealized two-dimensional representations. In addition, the nature of the arrangement of HA crystals and interfacial interactions between bone's constituents at this scale are still debated, which makes it challenging to select appropriate inputs for computational modelling. It must be noted that most studies have been done on modelling of bone at the nanoscale in the context of elasticity. A comprehensive review of these models can be found in [41].

3.2. Models at the microscale and larger scales

Fracture resistance in different materials could be due to resistance to crack initiation or resistance to crack propagation, depending on the microstructures [162]. In bone, the most important toughening mechanisms are active during crack growth rather than crack initiation [32,34]. Formation of microcracks is an essential process in these toughening mechanisms. Interaction of microcracks with bone microstructure influences the crack paths through the tissue and the resulting frequent changes in crack growth trajectory are the main sources of micro- and macroscopic bone toughness.

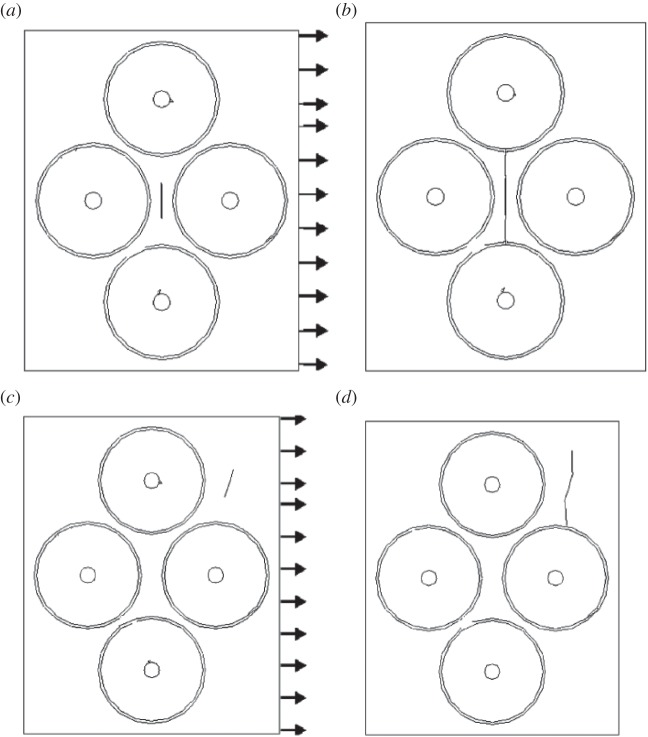
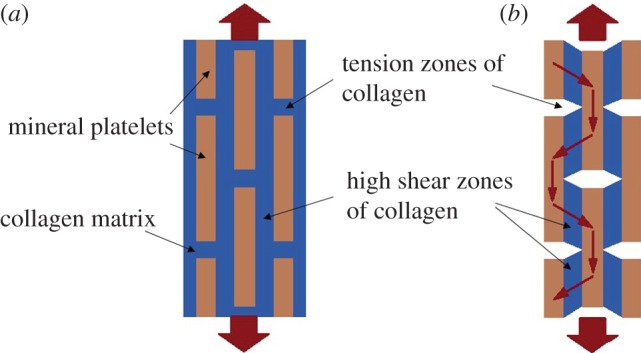
Various computational models were used to investigate microcrack interactions with the bone microstructure. One of the first studies is the work of Advani et al. [99]. They investigated a crack growth seizure by cement lines using a simplified composite beam model. The interaction between a microcrack and an osteon was the subject of Guo et al.'s work [97]. They used LEFM on a composite model of osteonal cortical bone and studied the osteonal effect on a microcrack oriented perpendicular to the external load. This study was later extended by Raeisi Najafi et al. [95,163] to analyse the interaction of arbitrary microcracks in the vicinity of an osteon (figure 7). In those studies, a two-dimensional fibre–matrix composite material model assuming LEFM and a plane strain condition was used to represent a Haversian cortical bone. Osteons were treated as fibres and the interstitial tissue as the matrix. Perfect bonding was assumed at the interface between the osteon and the interstitial tissue, excluding presence of the cement line. Also, this model focused on a single osteon and the interaction among different osteons was not considered. A distributed dislocation technique was adopted to derive an analytical solution from a superposition of two distinct problems. In the first problem, an elastic osteon embedded within an infinite elastic plane of interstitial tissue was considered, with no microcracks. The second problem involved the stress disturbance due to the existence of microcracks in the interstitial bone tissue [95,163]. To solve the second problem, integral equations for the stress disturbance were obtained using an edge dislocation solution [164] as Green's function [165]. These studies showed the effect of microstructure morphology and heterogeneity on the fracture behaviour of cortical bone [95,97,163]. Their results also indicated that the mismatch between the material properties of the osteon and interstitial tissue governs fracture mechanisms: a soft osteon assists microcrack growth towards the osteon, while a stiff osteon repels the microcrack away from the osteon.

Figure 7.

Model of the osteonal cortical bone microstructure with arbitrary oriented microcracks employed by Raeisi Najafi et al. [163].

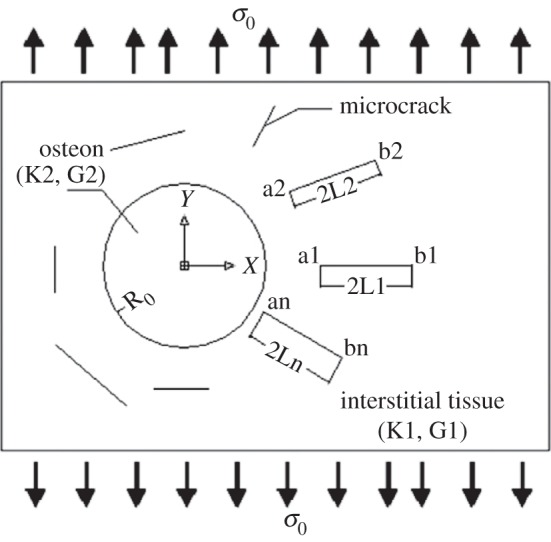
Several computational studies have investigated the role of osteons and cement lines in the crack propagation path and fracture toughness in bone [74,166–171]. For example, Raeisi Najafi et al. [74] studied the crack growth trajectory in cortical bone using an FEM model. Their results show that a microcrack trajectory deviates from the osteon (figure 8). However, the amount of deviation is decreased as the osteon elastic modulus is reduced. These results are in agreement with experimental observations suggesting that microcracks with a length smaller than 300 µm deviate in the vicinity of osteons [69]. Furthermore, Raeisi Najafi et al. reported that osteons act as barriers to microcrack growth (figure 9) and microcracks stop propagating once they enter the bone tissue with high osteonal density [74], which agrees well with experimental observations [69]. They also found that, when a microcrack in the interstitial bone lies in the same direction as the compressive loading, it enters the osteon directly in a direction parallel to the loading [74] (figure 10). These findings are supported by SEM fractography of fracture surfaces of bone subjected to compressive loading [172,173].

Figure 8.

Microcrack propagation trajectory under tension in the Raeisi Najafi et al. [74] model—the propagation trajectory was deviated as approaching the osteon: (a) primary microcrack, (b–d) propagated microcrack with (b) E₀ = 10 GPa, E_i = 26 GPa, E_c = 6 GPa; (c) E₀ = 19 GPa, E_i = 26 GPa, E_c = 6 GPa; (d) E₀ = 19 GPa, E_i = 15 GPa, E_c = 24 GPa.

Figure 9.

Microcrack propagation severely affected by separation of osteons [74]. Close proximity of osteons will not allow microcrack propagation between the osteons. (a,c) Primary microcrack; (b,d) propagated microcrack.

Figure 10.

Microcrack propagation trajectory under compression in the Raeisi Najafi et al. [74] study.

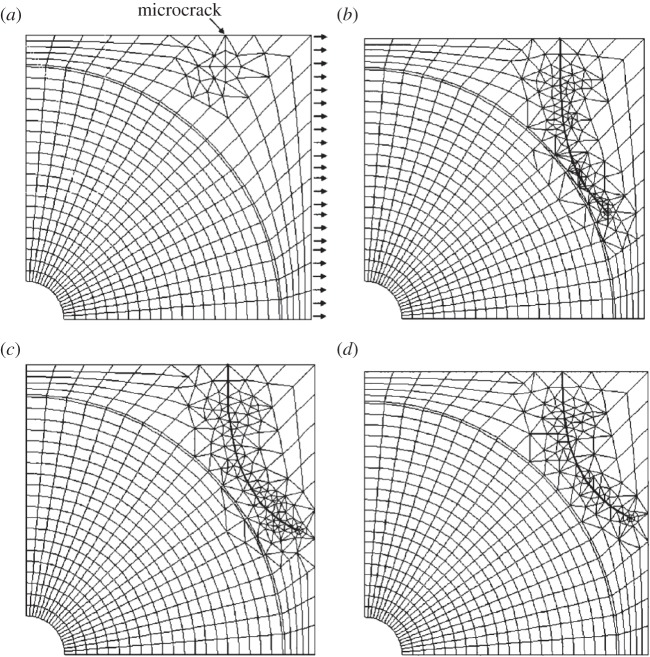
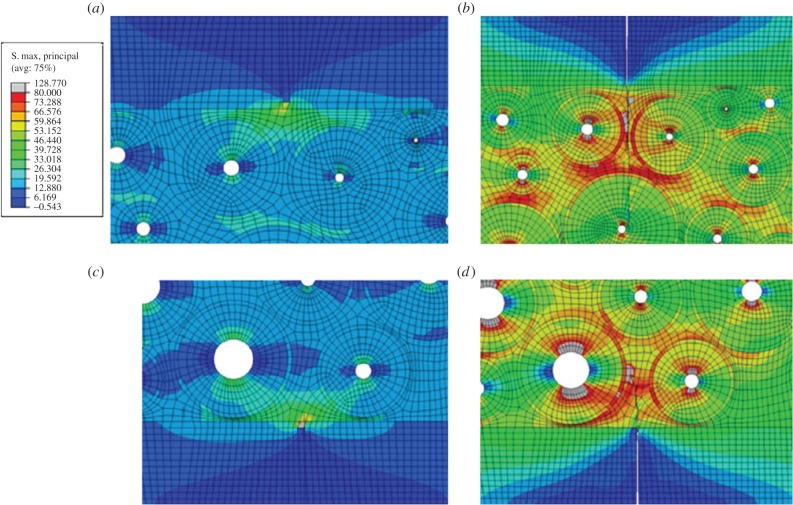
Some studies employed a cohesive FEM technique to model fracture of bone at the microscale [51,170,174–178]. Ural and co-workers used this modelling technique [175] in a two-dimensional idealized model of a single osteon, surrounded by a cement line and an interstitial bone (figure 11) and studied the mechanisms affecting a possible crack deflection and penetration near cement lines. Later, they expanded their study to a model with several osteons which was based on microscopy images of transverse sections of human cortical bone [176,177]. They found that, regardless of fracture toughness of cement lines, low cement line strength facilities crack deflection. Also, they reported that the orientation of a crack with respect to loading affects the crack trajectory.

Figure 11.

The Mischinski & Ural [175] cohesive FEM model of a single osteon. (a) FEM mesh demonstrating crack penetration into an osteon for a 0° crack, (b) stress contours showing the different stages of crack propagation for 0° crack penetration, (c) FEM mesh demonstrating crack deflection into the cement line for a 45° crack, and (d) stress contours showing the different stages of crack propagation for a 45° crack deflection. (Online version in colour.)

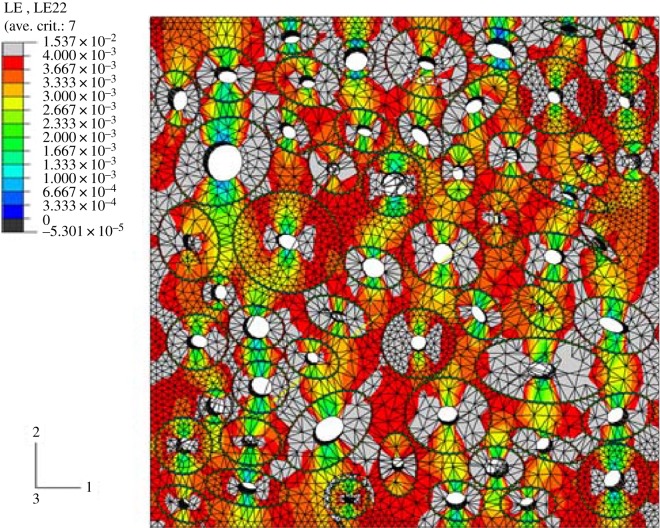
The extended finite-element method (XFEM) has also been used to study the crack growth path in a Haversian cortical bone [166–169,179–182]. Using XFEM, Budyn and co-workers performed extensive studies on cortical bone and investigated the effects of different parameters such as morphology, porosity, ageing and osteoporosis on stress and strain distributions, failure, and fracture of bone [167,168,179–184]. They modelled a multiple crack growth in human cortical bone under tension in order to create a constitutive law at the macroscopic level and investigate the influence of microstructure morphology on bone failure [167,168,182]. Their model consisted of four phases: Haversian canals, osteons, cement lines and matrix. Random position, aspect ratio and orientation were assigned to osteons which were idealized as disjoint elliptical tubes. Randomized mechanical properties were also used in the model to build a statistical microstructure corresponding to actual human bone samples. An example of their model geometry with the corresponding strain distribution is shown in figure 12. In this study [168], a classical FEM analysis was first performed in a three-dimensional transversely isotropic model to find the locations where a critical elastic-damage strain-driven criterion is met. Then, cracks were initiated in those locations and crack growth was modelled in a corresponding two-dimensional geometry. Figure 13 illustrates initiated cracks and crack growth in the model proposed by Budyn et al. [168]. According to this model, the Haversian canal porosity is the source of localization and fracture nucleation for transverse tensile loading, while cement lines are correlated with energy of fracture by isolating osteons from the matrix and causing crack deflection. It was also observed that introducing more inhomogeneity to the model by increasing the osteon density and having a harder matrix leads to an increase in macroscopic strength. Thus, lack of remodelling activity due to ageing that leads to a reduced osteon density lowers fracture strength. In addition, high porosity and large osteons, which contribute to osteoporosis, result in lower macroscopic moduli and fracture strength [168].

Figure 12.

Example of the Budyn et al. [168] model geometry with strain distribution before crack initiation. (Online version in colour.)

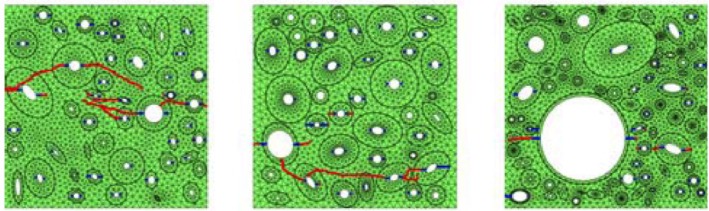
Figure 13.

Examples of the Budyn et al. [168] model with different microstructure showing crack initiation in blue and crack growth in red.

In other studies, Abdel-Wahab et al. [166] and Li et al. [169] investigated the effect of microstructure and material properties of bone on crack propagation, using an XFEM approach, implemented within the FEM software ABAQUS. A two-dimensional fracture model for osteonal bovine cortical bone was developed accounting for its microstructure (figure 14). The topology of bone microstructure was obtained using an optical microscope, and the mechanical properties of microstructural features were measured by a nanoindentation method. Their results confirmed a significant role of bone microstructure on the crack propagation path [166,169].

Figure 14.

The Abdel-Wahab et al. [166] model—distribution of maximum principal stress in the vicinity of (a) upper and (c) lower microcracks at the crack initiation increment, and for increments of (b) arrest of the upper microcrack by void, and (d) arrest of the lower microcrack at the cement line. (Online version in colour.)

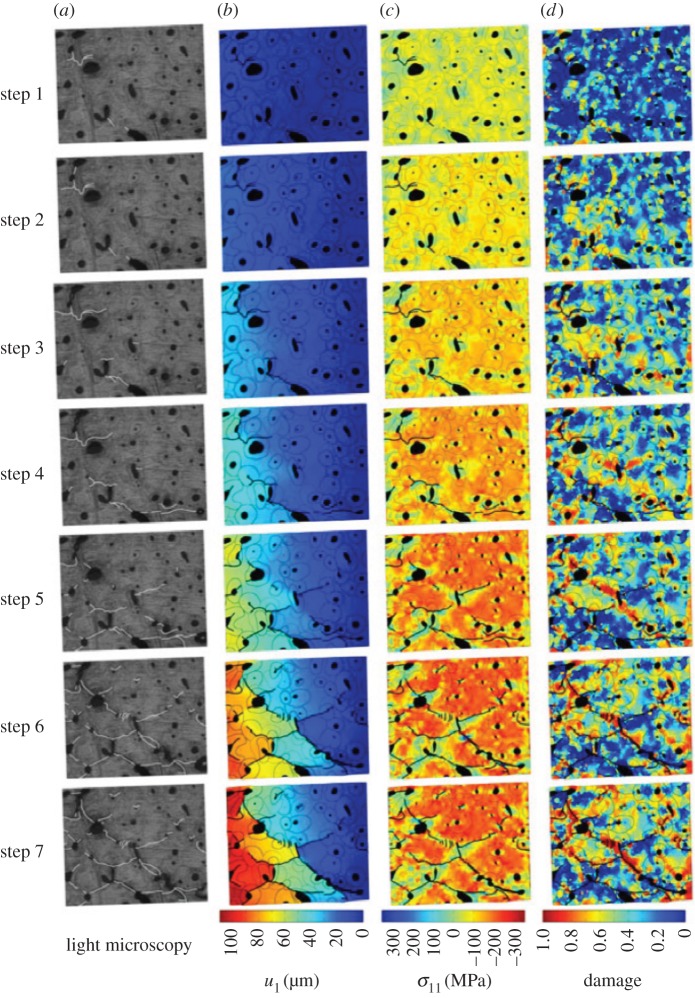
Compared with a relatively large number of models incorporating crack deflection in cortical bone, fewer studies have focused on modelling damage diffusion and crack bridging. Budyn et al. studied micro-fracture and crack bridging in human cortical bone under compression [184] and transverse tension [181] through a coupled experimental/numerical approach. The morphology of the model was based on light microscopy observations of actual bone samples, and crack paths at each step of loading were included explicitly in the model using an extended physical imaging technique. Bone fracture was modelled using LEFM and solved using FEM by implementing a two-level Newton–Raphson scheme in [184] and XFEM in [181]. The authors used a local damage constitutive law so that the global response of the numerical model agreed with experimental measurements. To account for crack bridging due to progressive tearing of collagen fibrils, a cohesive crack opening law in the wake of the crack tip was implemented. When increasing compression, they observed diffused damage in the regions bordering the cracks and also ahead of existing cracks in zones that predicted a new crack initiation, which agreed with experimental observations [185,186]. They also reported the beneficial effects of Haversian canals that help to trap growing cracks and deflect cracks around osteons. Crack propagation in an actual bone sample under compression, compared with displacement, local stress and local damage fields obtained from their FEM simulations, is illustrated in figure 15. Local SIF at the tip of microcracks was also calculated to estimate bone fracture toughness, and it was found that absolute values of mode II SIF were usually at least four times larger than those of mode I, suggesting that mode II is predominant under compression.

Figure 15.

Budyn et al.'s [184] results of human cortical bone modelling under seven steps of applied compression. (a) Light microscopy observations of cracked microstructure, (b) displacement field in the direction of applied compression, (c) longitudinal stress and (d) local damage fields in the FEM solution.

As mentioned earlier, the current review is mainly focused on the strength and fracture models of cortical bone. Next, we will briefly outline several representative studies modelling strength, damage, fracture and softening mechanisms of a single trabecula and trabecular bone. Different approaches have been employed including elastic–plastic constitutive laws and progressive damage evolution by element deletion [187–201]. Due to the complex architecture of trabecular bone, many of the models used micro-computed tomography (µCT) based three-dimensional voxel FEM models, which give an accurate representation of trabecular bone geometry [192–195]. Nevertheless, the complexity of the trabecular bone architecture usually leads to a high computational cost. Consequently, some studies have idealized the geometry of trabecular bone using simpler representations. For example, a collection of rod- and plate-like trabeculae, which is based on µCT or high-resolution peripheral quantitative computed tomography (HR-pQCT) images, has been used as an idealized model for trabecular bone. In this representation, the rod-like structures are modelled as beam elements, while shell elements are used to model plate-like structures. Results of these models are in good agreement with those of the voxel models, while this technique is more efficient computationally [187–189]. Two- or three-dimensional periodic cellular structures have also been used as idealized models of trabecular bone to investigate its mechanical properties [190,191].

Zysset and co-workers [202–204] developed three-dimensional anisotropic constitutive laws for trabecular bone based on a fabric tensor. They discussed several specific cases of material symmetry such as isotropy, cubic symmetry, fabric-based orthotropy and general orthotropy in [204]. Garcia et al. [205] proposed a constitutive law for cortical and trabecular bone under cyclic load that included elastic, plastic and damage aspects. In addition, an anisotropic elastic–viscoplastic damage constitutive model for bone was suggested by Schwiedrzik & Zysset [204]. This model was used in an FEM simulation of nanoindentation in lamellar bone and showed good agreement with experiments.

At the macroscale (whole bone level), FEM models have been extensively used to predict overall behaviour of bone (e.g. [171,196,206–239]). Quantitative computed tomography (QCT)-based FEM analysis was used in the last two decades, mainly for clinical and biomedical purposes, as a non-invasive method to predict strength, fracture load and fracture location in whole bone under different conditions [206–239]. In this technique, a three-dimensional model of whole bone is built using QCT images and bone properties are usually assigned based on mineral density estimates obtained from these images.

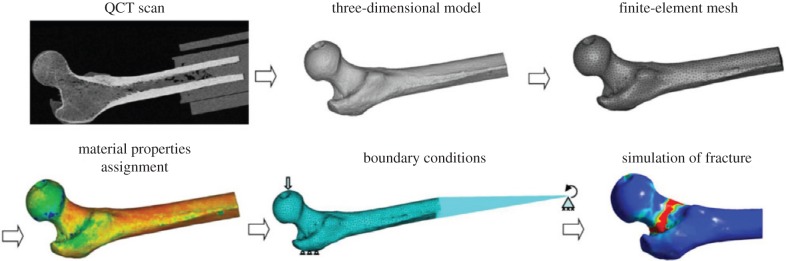
Dragomir-Daescu et al. [208] investigated the fracture of whole femur using QCT/FEM analysis using a nonlinear constitutive law for the bone tissue, while performing parallel experiments on corresponding bone samples (figure 16). Their predicted fracture load and patterns obtained from simulations correlated well with their experimental measurements. Keyak and co-workers [210,212] also used QCT/FEM analysis on the proximal femur to conduct a comparison between performance of different stress- and strain-based failure theories. Using this model, they could successfully predict fracture types. Zysset & co-workers [230–239] implemented anisotropy in their QCT- and HR-pQCT-based FEM analyses by using the modular framework generated in [240]. Using this method, they studied the strength, damage and failure of human femur, vertebral bodies and radius under different loading conditions while conducting corresponding experiments and showed that their results match well with the experiments. Nevertheless, QCT/FEM studies have mostly employed simple uncoupled failure criteria and focused on failure initiation without considering a crack propagation stage [223]. Consequently, these studies are mostly able to predict the ultimate force at fracture rather than providing force–displacement information up to complete fracture.

Figure 16.

Overview of the Dragomir-Daescu et al. [208] QCT/FEA modelling steps, from QCT scan to simulation of fracture. (Online version in colour.)

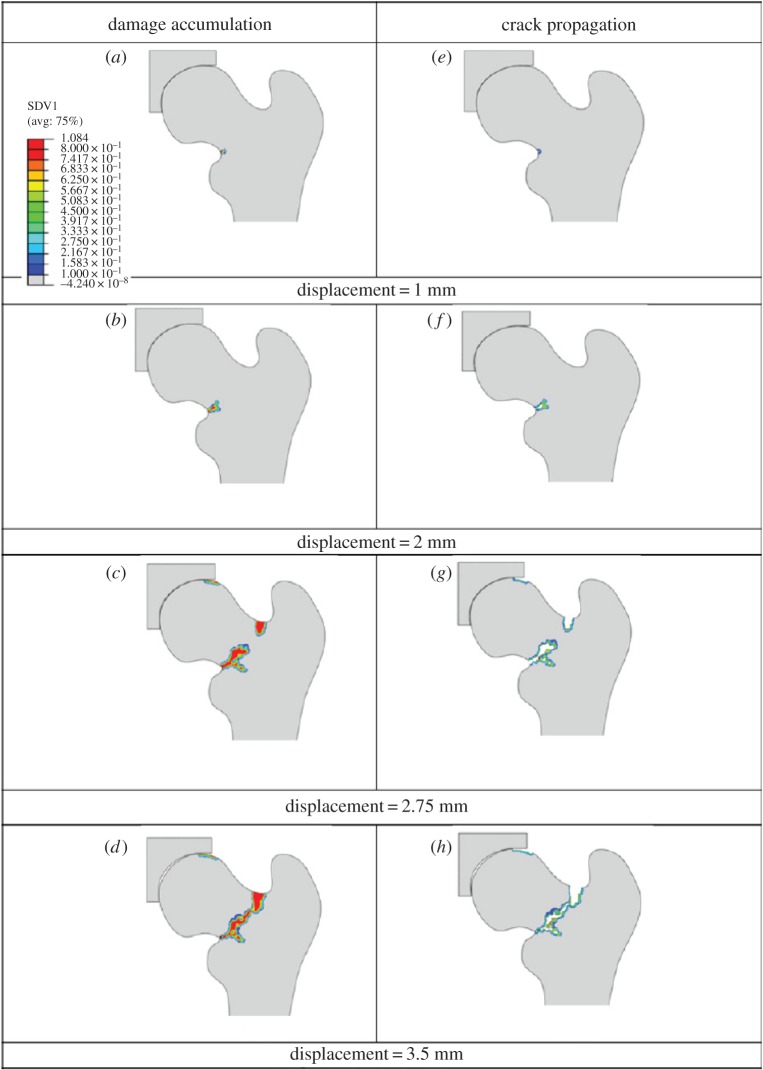
More recently, some studies used fracture mechanics concepts to investigate bone fracture. For instance, Hambli et al. [196,222,223] modelled the behaviour from initiation of a crack up to a total separation of bone. They developed an FEM model of the proximal femur (figure 17) based on continuum damage mechanics to obtain force–displacement curves under a one-leg stance, from the beginning of loading to complete fracture. A damage law, developed based on experimental observations, was implemented in this model. Their simulations predicted that fracture starts at the superior cortex, which was shown to match with experiments.

Figure 17.

Results of the Hambli et al. [223] model. (a–d) Accumulation of continuum damage in the proximal femur; (e–h) corresponding crack propagation. (Online version in colour.)

Cohesive FEM has also been employed to study fracture of bone at the macroscale. Using this technique, Ural and co-workers [171,224–229] investigated crack growth, fracture strength and loss of toughness in human distal radius, considering the effects of ageing, intracortical porosity and strain rate. They reported a decrease of 13% in the R-curve slope per decade, which is in close agreement with the experimentally observed decrease in toughness of 14–15% per decade [80]. In another study [226], they showed that a 4% increase in porosity, while keeping other variables constant, resulted in a 6% decrease in initiation toughness and a 62% decrease in propagation toughness.

It is worth mentioning that an important challenge in modelling bone at this scale (macroscale) is to determine realistic boundary conditions. It has been reported that results of FEM/QCT analysis can vary significantly depending on the applied boundary conditions [223,241,242]. Secondly, assignment of realistic spatially changing constitutive laws is another challenge.

In summary, computational studies reported in the literature illustrate toughening mechanisms which are active at the microscale and larger scales, and results are confirmed by experiments. Numerical models provide deeper understanding of the role of osteons and cement lines in determining crack propagation trajectories. The outcomes of these studies also demonstrate how toughening mechanisms created by microstructural features work during crack growth. At the tissue level, computational techniques such as cohesive FEMs and XFEM were successfully used to capture toughening behaviour of bone and compute fracture toughness of bone under various loading conditions. These results also provide additional insights into the impact of structural morphology, material heterogeneity and porosity on the fracture toughness of bone.

Despite great advances in computational modelling at the microscale and macroscale, as outlined above, there are still key unanswered questions that need to be investigated. One of the important questions is how different toughening mechanisms change the bone fracture risk. At the macroscale, how we can incorporate the role of cortical and trabecular bone microstructures in determining fracture risk. Last, but not least, how we can combine the outcomes of these models into the form that could be used by clinicians to more effectively and accurately assess bone and find solutions to how to prevent fractures in individuals with high fracture risk.

3.3. Multiscale models

As discussed in the previous sections, most of the models incorporating bone strength and fracture focused mainly on one structural length scale rather than employing a multiscale approach. Few studies developed a multiscale model of bone but none of them included all of the scales in the hierarchical structure of bone. In this regard, Fritsch et al. [243] used a multiscale continuum micromechanics model to obtain the strength of bone at the nanoscale and sub-microscale. They suggested that failure occurs by mutual ductile sliding of HA mineral crystals along layered water films followed by rupture of collagen cross-links. Based on that, they extended their previous elastic models to present a micromechanics theory for upscaling of elastoplastic properties.

Structural behaviour at the interface between organic–inorganic materials has also been studied with a multiscale approach [153,244]. As an example, Lau et al. [244] developed a multiscale model based on MD simulations combined with metadynamics methods to quantify the traction-separation behaviour at an organic–inorganic interface to be used as inputs in cohesive FEM analysis at a larger scale.

Hamed & Jasiuk [245] employed a cohesive FEM model to predict the elastic properties and strength of lamellar bone. They considered three levels of hierarchy: the nanoscale, sub-microscale and microscale. The predicted strength at a lower scale was used as inputs to a higher scale. First, a mineralized collagen fibril was studied to assess the role of soft and deformable collagen and stiff but brittle HA minerals on the strength of bone. Then, a single lamella consisting of mineralized collagen fibrils glued together by NCPs was modelled. The model showed that sliding between the neighbouring fibrils and, eventually, the breaking of the bonds between them are the main damage mechanisms at this scale. Finally, the lamellar structure of bone was modelled by varying orientations of lamellae and studying their effects on bone strength at this scale.

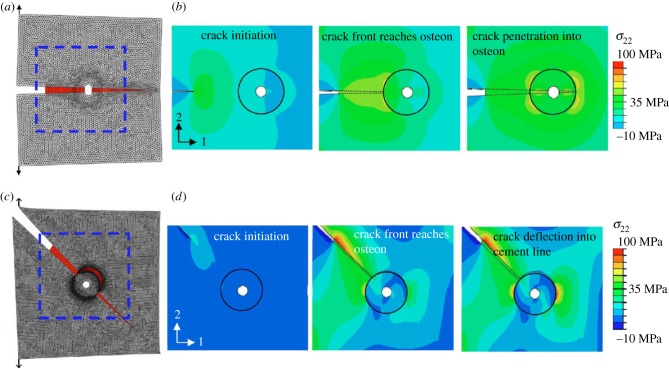
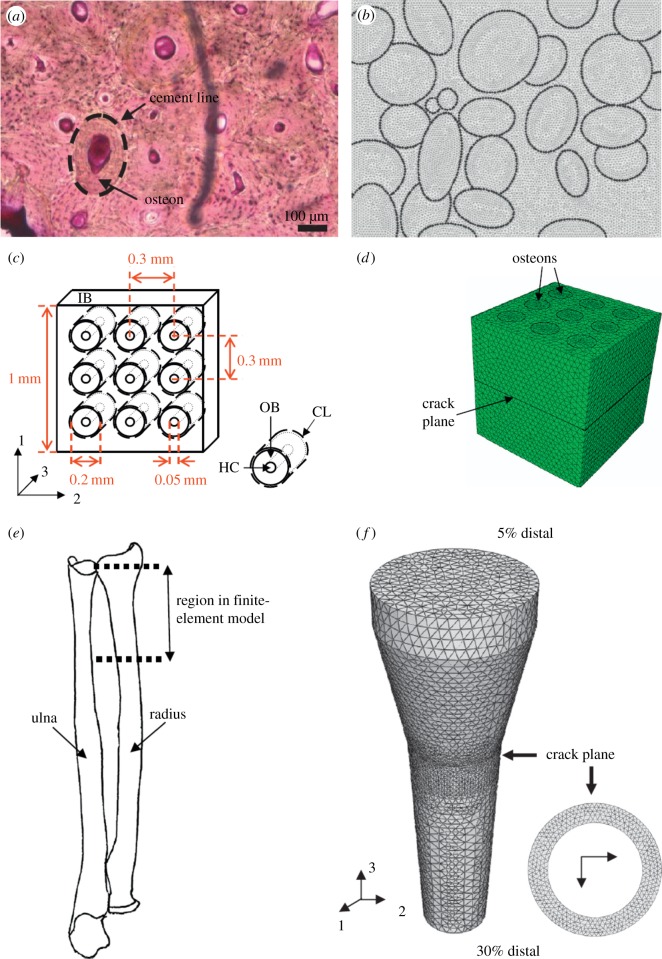
At larger scales, Ural & Mischinski [246] developed a multiscale model using a cohesive FEM approach to simulate fracture of bone at the microscale and macroscale levels. The simulations were carried out in three parts: (i) two-dimensional model of cortical bone based on microscopy images as shown in figure 18a,b, (ii) three-dimensional simplified model of cortical bone with osteons modelled as circular tubes (figure 18c,d) to determine the effect of microscale properties on macroscale fracture toughness, and (iii) three-dimensional idealized model of the distal forearm at the macroscale based on mechanical properties obtained from the microscale model (figure 18e,f). This study illustrated the importance of toughness mechanisms at the microscale on fracture at the macroscale.

Figure 18.

The Ural & Mischinski [246] model geometry: (a) part 1, microscopy image of cortical bone; (b) part 1, FEM model; (c) part 2, schematic of detailed microstructure; (d) part 2, FEM model; (e) part 3, a sketch of the human forearm highlighting the section that was modelled; and (f) three-dimensional FEM model of an idealized human radius bone. (Online version in colour.)

Concluding, there are only limited multiscale models of bone and they do not address all the scales simultaneously. In particular, the link between lower scales and macroscopic fractures is still not well developed. Also, these models are usually hierarchical, addressing each scale separately and using outputs from lower scales as inputs for the next structural scale, rather than considering multiple scales simultaneously. A comprehensive overview of multiscale modelling of materials is given in a recent monograph by Fish [247]. Second, the hierarchical structure of bone changes continuously rather than discretely, thus selection of scales is not unique, with two to seven scales proposed in the literature. Thus, there is no separation of scales, which also leads to open questions about the size (or even existence) of a representative volume element (RVE) of an approximating deterministic continuum and suggests the introduction of a statistical volume element (SVE). Thus, further investigations are needed on the effects of scale and boundary conditions on properties of bone, in particular on the fracture toughness, yield strength and ultimate strength. Finally, since fracture and strength are stochastic phenomena, randomness in microstructure and the resulting properties should be rigorously addressed. These topics are discussed in detail in a recent book by Ostoja-Starzewski [248] in the general context of materials mechanics.

4. Summary

In this paper, we summarized experimental observations on bone fracture and strength and illustrated insights that were gained from modelling. We addressed this problem by focusing on different structural scales in the hierarchical structure of bone and discussing failure mechanisms at the nanoscale, sub-microscale, microscale, mesoscale and macroscale in bone. This review is not comprehensive due to space constraints and it only highlights representative analytical and computational models at these different scales.

Our major observations and findings are as follows:

• —Various studies have investigated microcrack interactions with bone microstructure but they have mainly addressed one or two scales. There are very limited multiscale models of bone addressing more than two scales.
• —Studies at the nanoscale address collagen–HA interactions and provide properties of a mineralized collagen fibril, which is a basic building block of bone. Analytical and computational models show that the mechanical properties of bone at this scale are sensitive to the aspect ratio and arrangement of crystals.
• —There are limited models of bone fracture and strength at the sub-microscale and microscale.
• —At the mesoscale, investigations on cortical bone have been focusing on the effects of osteons and cement lines on the crack growth path. Simulations have shown that osteons act as barriers to microcrack growth. Osteons, as the main features of cortical bone, control bone extrinsic toughening mechanisms such as crack deflection and twisting, and uncracked ligament bridging. In trabecular bone, damage is highly dependent on the complex trabecular architecture and is localized in trabecular struts.

Next, we summarize the main challenges and open issues in modelling bone strength and fracture:

• —Most of the existing models focus on only one scale and very few multiscale models considering two or three scales exist, even though bone fracture is a multiscale phenomenon. Particularly, the link between damage at the nanoscale and whole bone fracture is still missing. No comprehensive multiscale models exist that address the complexity of fracture processes in bone spanning the scales.
• —Most models are hierarchical, addressing one scale at a time, rather than multiscale, incorporating multiple scales simultaneously.
• —Many studies employ idealized, two-dimensional representations of bone. However, since the initiation and growth of cracks are sensitive to microstructures, the use of actual, three-dimensional models would provide more insights into bone behaviour.
• —The effect of size dependence on the predicted results should be highlighted.
• —The transition between different scales is in fact continuous rather than discrete.
• —Do we have an RVE or an SVE for bone mechanics studies?
• —Investigations are needed into the effects of scale and boundary conditions on bone properties, in particular fracture and strength.
• —Natural randomness in properties and geometry is not accounted for in most of the existing models. This is an outstanding issue as fracture is a stochastic phenomenon.
• —The structure and properties are still debated especially at smaller scales. Even for larger scales, a wide range of values is reported for bone properties.
• —More experimental studies are needed on the characterization of bone at the nanoscale. Open issues remain on the locations of HA crystals, their arrangement and interfacial interactions between the collagen and HA. Are the crystals isolated platelets or do the collagen and minerals form interpenetrating phases?
• —Many of the existing models assume isotropic properties for collagen and HA crystals, while the actual behaviour is anisotropic. Anisotropic properties are not readily available. Also, further research is needed on determining accurate constitutive laws of bone's constituents up to failure.
• —Spatial inhomogeneity in bone properties across scales needs to be further characterized to serve as inputs for more realistic computational models.
• —Effects of ageing and bone diseases on bone fracture toughness and strength are still open issues. Modelling of these parameters would provide valuable insights into bone fracture in such conditions and have high clinical impact.
• —There is a close relation between the bone damage (in the form of microcracks and diffuse damage) and bone remodelling. However, only limited models exist that consider this mutual relation in fracture studies.
• —Many of the mechanics models of crack propagation and bone fracture do not take into account the impact of intrinsic toughening mechanisms occurring in bone.
• —The insights gained from various modelling and experimental studies on bone fracture and strength should be linked to clinical practices to design better methods to quantify bone quality and bone fracture risk in humans.

In summary, bone fracture and strength have been studied extensively and significant advances have been made in this area. However, due to the complexity of bone structure and the complexity of fracture processes occurring in bone, numerous challenges remain. These make this clinically important problem challenging and still very open for further scientific investigations.

Competing interests

We declare we have no competing interests.

Funding

We acknowledge funding from the National Center for Supercomputing Applications Faculty Fellows programme and the National Science Foundation (DMR-1507978). The findings, conclusions and recommendations expressed in this manuscript are those of the authors and do not necessarily reflect the views of the NSF.