Tunability of collagen matrix mechanical properties via multiple modes of mineralization

Abstract

Functionally graded, mineralized collagen tissues exist at soft-to-hard material attachments throughout the body. However, the details of how collagen and hydroxyapatite mineral (HA) interact are not fully understood, hampering efforts to develop tissue-engineered constructs that can assist with repair of injuries at the attachments of soft tissues to bone. In this study, spatial control of mineralization was achieved in collagen matrices using simulated body fluids (SBFs). Based upon previous observations of poor bonding between reconstituted collagen and HA deposited using SBF, we hypothesized that mineralizing collagen in the presence of fetuin (which inhibits surface mineralization) would lead to more mineral deposition within the scaffold and therefore a greater increase in stiffness and toughness compared with collagen mineralized without fetuin. We tested this hypothesis through integrated synthesis, mechanical testing and modelling of graded, mineralized reconstituted collagen constructs. Results supported the hypothesis, and further suggested that mineralization on the interior of reconstituted collagen constructs, as promoted by fetuin, led to superior bonding between HA and collagen. The results provide us guidance for the development of mineralized collagen scaffolds, with implications for bone and tendon-to-bone tissue engineering.

1. Introduction

Biologic tissues, such as bones and teeth and their interfaces with tendons and ligaments, achieve high strength and stiffness through a highly mineralized hierarchical composite structure. Although significant variations exist in the micrometre-scale mineral volume fractions and the millimetre-scale shape of the tissues, the basic building block of these tissues is the same: nanometre-scale mineralized collagen fibrils [1]. Collagen molecules (300 nm in length and 1.5 nm in diameter) have triple helical structures that self-assemble into well-organized fibrils. These fibrils contain repeating regions of densely packed collagen (i.e. overlap zones) and regions of loosely packed collagen (i.e. gap zones). During the mineralization process, mineral can deposit either within the gap zones of the fibrils, on the surface of the fibrils or on the surface of the tissue [2–6]. Importantly, the particular location of the mineral relative to the collagen will have significant effects on the mechanics of the collagen fibril; although mineralization occurs at the nanometre scale, it affects the mechanical behaviour at the tissue level [7]. Therefore, proper design and synthesis of mineralized collagen scaffolds with appropriate mechanical properties must finely control the deposition of mineral within the collagen nano- and microstructure.

There is major clinical need to develop partially mineralized collagen matrices with mechanical gradients for the repair of soft-to-hard tissue injuries. For example, rotator cuff tears are common injuries that require tendon-to-bone repair, but have poor clinical outcomes [8]. Successful repair requires reconnecting two materials, tendon and bone, with dissimilar mechanical properties. As with any interface between materials with strongly differing mechanical properties, the transfer of load between the two phases can lead to the formation of stress concentrations. In the healthy rotator cuff, the tendon-to-bone attachment has a variety of structural and biological mechanisms for decreasing stress concentrations, one of which is a gradient in mineral content and location [6,7,9–11]. These mechanisms combine to decrease the risk of failure and increase the toughness and strength of the healthy tendon-to-bone attachment. Unfortunately, after injury and surgical repair, these graded interfacial tissues are not regenerated, and the attachment is prone to failure [12].

Developing a collagen–mineral composite with mechanical gradients similar to those seen at the tendon-to-bone attachment is important for improving repairs [13,14]. Recently, techniques have been developed to make functionally graded materials for replacement of interfacial tissues [15,16]. Many of these techniques focus on synthesizing scaffolds that have gradients in chemical or mechanical properties by modifying polymer-based scaffolds [15]. By applying bone tissue engineering techniques, it has been possible to develop scaffolds of poly(lactic-co-glycolic acid) and polycaprolactone polymers with gradients in mineral [17,18]. These exhibit clear changes in stiffness with mineralization; however, they only employ surface mineralization. Moreover, the use of artificial polymers makes remodelling and resorption of the scaffold more difficult. Some work has been done examining collagen scaffolds with gradients in mineralization chemistry, but not specifically mineral content [19], whereas others have directly created mineral gradients on tendon tissue [20]. These results demonstrate that, although there is a clinical need for controlled mineralization for engineered tissues with functional gradients, there is little research being devoted to this topic.

Spatially tuning the mineral content and mechanical properties of a hydroxyapatite–collagen scaffold would allow for the creation of graded scaffolds for repair of the tendon-to-bone attachment. Addition of a graded scaffold to the repair site would allow for mechanical support of the repair, limiting gap formation while avoiding the negative effects of stress shielding [21]. In addition, cellular responses have been shown to be dependent on the stiffness and mineral content of the substrate [22,23]. The ability to create biomimetic scaffolds with gradients in mechanical properties could greatly increase the cellular response and mechanical integrity of tendon-to-bone repairs. Therefore, the objective of this study was to develop techniques to control the location and quantity of mineral deposition in a collagen matrix in order to make collagen scaffolds with gradients in mechanical properties. Two mineralization methodologies were used: immersion in simulated body fluid (SBF) and immersion in SBF with size-excluding fetuin. The addition of fetuin mineralization was hypothesized to lead to more mineral deposition within (rather than on) the scaffold leading to superior bonding between mineral and collagen. This was expected to result in a greater increase in stiffness and toughness compared with collagen mineralized without fetuin.

2. Material and methods

2.1. Study design

This study compared the influence of two collagen mineralization modalities, mineralization with SBF and mineralization with SBF and fetuin (SBF + Fet), on the mechanical properties of collagen matrices. Collagen and mineral morphology on the matrix surface were assessed using scanning electron microscopy (SEM), and surface chemistry of the matrices was assessed using Raman spectroscopy. Internal collagen and mineral morphology were confirmed using transmission electron microscopy (TEM) and optical microscopy of von Kossa-stained cross sections. To examine mechanical consequences of mineral location and distribution, uniaxial tensile tests were performed on collagen matrices and local strain was analysed. Unmineralized collagen matrices were used as controls.

2.2. Synthesis of mineralized collagen matrices

2.2.1. Collagen matrix

All chemicals were from Sigma-Aldrich, unless otherwise stated. Collagen matrices were produced by mixing 10 mg ml⁻¹ collagen type I from lyophilized calf skin (Elastin Products Company, product no. C857) in 0.005 M hydrochloric acid in deionized water at 4°C. The solution was placed into a syringe under 14 psi vacuum pressure at 4°C for 3–5 days to remove air bubbles. Collagen was then pumped into ring-shaped polypropylene casts (5 mm inner diameter × 7 mm outer diameter by 4 mm in height) in preparation for polymerization (figure 1a). Polymerizing buffer containing 30 mM N-tris(hydroxymethyl)methyl-2-aminoethane sulfonic acid, 30 mM sodium dihydrophosphate and 135 mM sodium chloride, adjusted to a pH of 7.5 by drop-wise addition of 1 M sodium hydroxide was added. A modified collagen polymerization procedure was then performed, as described previously [24,25]. Briefly, cast collagen was submerged in a 30°C bath of polymerizing buffer for 1 h [24,25]. Collagen rings were removed from their casts, incubated in deionized water overnight and then gradually dehydrated in ethanol for 4 h. Dehydrated matrices were then mounted onto 8 mm outer diameter glass rods and air-dried overnight. Dehydrated and dried ring dimensions were approximately 8 mm for the inner diameter and approximately 7 µm thick (figure 1b,c).

Figure 1.

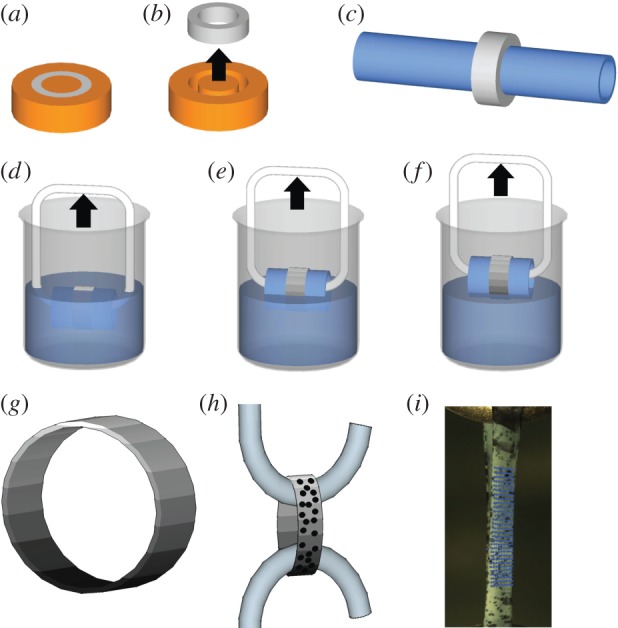
Schematic of collagen casting, polymerization and mineralization. (a) A solution of 10 mg ml⁻¹ of collagen in 0.005 M hydrochloric acid was cast on a plastic mould and incubated in a 30°C bath of polymerizing buffer for 1 h. (b) Polymerized collagen was removed from the mould, soaked overnight in deionized water, serially dehydrated in ethanol and then (c) air-dried around an 8 mm diameter glass tube. (d) SBF mineralization of collagen on glass mounted tubes was generated by incubation in 10× SBF at 37°C. SBF + Fet mineralization was accomplished by incubation in SBF at 37°C supplemented with 5 mg ml⁻¹ fetuin protein. (d–f) A gradient in mineral content was generated by submerging the rings into 10× SBF (with or without fetuin) and slowly drawing them out of the solution. (g) Three-dimensional model of collagen ring with a gradient in mineral is shown (the level of mineral is indicated by the grey scale). (h) To characterize the mechanical properties of the matrices, the rings were sprayed with Verhoeff's stain, removed from the glass tubes and then pulled in tension at a rate of 1% strain per second until failure. (i) A photograph of a collagen matrix under uniaxial tension is shown, with Verhoeff's staining and an overlay field of blue dots representing the region of local strain analysis evident. (Online version in colour.)

2.2.2. Mineralization

In this study, two types of mineralization methods, SBF and SBF + Fet, were compared with unmineralized collagen. For both these methods, homogeneous as well as spatially graded mineral distributions were investigated. Homogeneously mineralized collagen matrices were generated by 1 h incubation at 37°C in 10 times concentrated SBF (10× SBF: 1 M sodium chloride, 0.005 M potassium chloride, 0.025 M calcium chloride, 0.005 M magnesium chloride, 0.01 M sodium phosphate, 0.01 M sodium bicarbonate) for SBF mineralization and 24 h incubation in fetuin-doped SBF for SBF + Fet. SBF mineral gradients were achieved by submerging the tube-mounted rings in 10× SBF and drawing the rings out of the solution at a rate of 8 mm h⁻¹ for 1 h (figure 1d–f). The method of graded SBF mineralization by incubation in a calcium phosphate-rich solution is similar to work previously described for polymer nanofibre mats [17]. SBF + Fet mineralization of collagen fibrils was achieved by submerging the matrices at 37°C in 10× SBF supplemented with 5 mg ml⁻¹ fetuin from fetal calf serum and drawing the matrices out of the solution at a rate of 0.4 mm h⁻¹ for 24 h. The difference in incubation times between the two mineralization methods was necessary to achieve equivalent levels of mineral content (mineral deposition in the presence of fetuin takes substantially longer than mineral deposition by SBF only).

2.3. Material characterization

2.3.1. Scanning electron microscopy

Intact collagen matrices were adhered to glass substrates and then polymerized and mineralized as described above. Mineralized collagen matrices were gold sputter-coated for 60 s and analysed with SEM (FEI Nova 2300; n = 3 per group). Matrices were placed under high vacuum and scanned with a 5 kV electron beam. Images of the surface of the collagen scaffolds were captured every 4 mm along the length of the scaffolds.

2.3.2. Transmission electron microscopy

Dehydrated collagen matrices were fixed overnight in a solution of 2.5% paraformaldehyde/2.5% glutaraldehyde in 1.0 M cacodylate buffer, followed by a 1 h post-fixation in 1% osmium tetroxide in 0.1 M cacodylate buffer (pH 7.3) for 1 h. The matrices were rinsed with 0.1% cacodylate buffer and then dehydrated through a series of ethanol dehydrations: 50% for 10 min, 70% for 30 min, 95% for 45 min with an intervening solution exchange, and 100% for 1 h with two intervening fluid exchanges. The matrices were then washed in propylene oxide for 30 min with an intervening solution exchange. The matrices were then washed in propylene oxide mixed with Epon resin (1 : 1) overnight under vacuum in order to facilitate infiltration. Finally, the matrices were infiltrated with pure Epon for 4 h and then polymerized in Epon resin overnight at room temperature.

Thin sections, approximately 80 nm thick, were cut using a Leica EM UC6 ultramicrotome and then mounted onto carbon-coated TEM grids. Sectioning was done perpendicular to the length of the scaffold such that a cross section of the scaffold could be observed. Collagen and mineral nanostructure were observed using TEM (Hitachi H-7500 transmission microscope, Hitachi High Technologies America, Inc., Schaumberg, IL; n = 3 per group) in high-contrast mode with an 80 kV accelerating voltage. Images were acquired with a digital camera (AMT digital camera, Advanced Microscope Techniques, Woburn, MA).

2.3.3. Raman spectroscopy

Apatite mineral concentration along the lengths of collagen matrices was analysed using Raman spectroscopy, as previously described [26,27]. Collagen matrices were prepared on 10 mm long glass substrates (n = 3 per group). Analysis was performed with a fibre-optically coupled Raman microprobe (HoloLab series 5000 Raman Microprobe, Kaiser Optical System, Inc.). Laser excitation at 532 nm was delivered by an ultra-long-working-distance MSPlan 50× objective, NA = 0.85 (Olympus, Japan). Laser power was 10 mW, as measured at the sample's surface. Spectra were recorded at a spectral resolution of 2.5 Δcm⁻¹ over the region 100–4000 Δcm⁻¹. Reproducibility of the Raman peak position was 0.1 Δcm⁻¹. The typical acquisition time per analysis spot (approx. 1.5 µm diameter) was 32 × 4 s. Individual Raman analyses were conducted at 1 mm intervals along the length of each dry, unfixed matrix. The relative concentration of mineral apatite at each beam spot was determined by comparing the height of the apatite peak at approximately 960 Δcm⁻¹ (the P–O symmetric stretch) with that of a representative collagen band at 1003 Δcm⁻¹ (C–H stretch in phenyl). Owing to the enhancement of light scattering by the nanometre-scale collagen fibrils, most of the acquired Raman signal was obtained from the upper couple of micrometres of the sample.

2.3.4. Histology and optical microscopy

Collagen samples were embedded in optimal cutting temperature compound and frozen to −80°C overnight. The samples were then transversely cryosectioned into 15 µm thick sections such that the infiltration of the mineral within the depth of the scaffold could be observed and placed onto Superfrost microscope slides. The slides underwent von Kossa staining. Specifically, they were stained in 1% silver nitrate solution under a 60 W light bulb until the mineralized regions of the sample turned black. The stained samples were then rinsed thoroughly with deionized water and incubated in sodium thiosulfate for 5 min. After rinsing in deionized water, the samples were dehydrated and cleared in xylene before coverslipping. The stained samples were imaged with bright field microscopy and observed for black staining corresponding to mineral content.

2.4. Mechanical testing

2.4.1. Uniaxial tensile tests

Samples were tested in uniaxial tension to determine bulk and local mechanical properties (n = 10 per group). Prior to mechanical testing, each dry sample was lightly sprayed with Verhoeff's stain to generate a random pattern of dots for strain tracking (figure 1h,i). After 5 min of hydration in 37°C phosphate-buffered solution (PBS) to equilibrate the sample to physiological/testing conditions, a laser displacement sensor was used to measure the thickness of each matrix and optical methods were used to measure sample width. A micrometer was then used to measure the gauge length of the samples held under slight tension using forceps. The cross-sectional area was calculated assuming a rectangular cross section. Engineering stress was calculated by normalizing force measurements to the initial cross-sectional area of each matrix.

Collagen matrices were tested in a PBS bath at 37°C under uniaxial tension using a mechanical testing frame (Instron ElectroPuls model E1000, Norwood, MA). Briefly, the rings were first mounted on hooks connected to the testing frame (figure 1) and preloaded until taut. The matrices were then extended in tension to failure at a rate of 1% per second. Strength, modulus and toughness were determined from the resulting stress–strain curves.

2.4.2. Local strain analysis

Local strain was determined using an image analysis technique that directly determines local deformations using the Verhoeff's stain surface texture [28]. The technique relies on the Lucas–Kanade inverse compositional algorithm, which iteratively minimizes an energy function

2.1

where T(x) is a template image, and I(W(x; p)) is an image, I, warped by a defined warping function W(x; p) whose warping parameter p can be modulated. The warping parameter was defined to be an affine warp with a translation

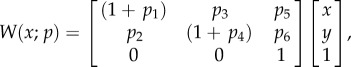2.2

where p₅ and p₆ are the translations in the x- and y-coordinates, respectively. By choosing the warp to be affine, the deformation gradient tensor for the region can be directly extracted from the first four components of the warp

2.3

thereby directly calculating the deformation gradient tensor for each region. Local finite strain was then calculated according to

2.4

where I is the second-order identity tensor.

2.5. Statistical methods

To compare groups, an analysis of variance of the mineralization factors (SBF, SBF + Fet, unmineralized) was performed for mechanical test results followed by a Fisher's protected least-squared difference post hoc test. An alpha level of p < 0.05 was considered statistically significant.

2.6. Multiscale modelling

The effect of mineral on stiffening of the collagen matrices was assessed using homogenization theory and results of multiscale numerical modelling. The central questions assessed were the roles of internal versus surface mineralization, and the role of adhesion between the mineral and the collagen. As a first-order approximation, internal mineral accumulations were idealized as spherical and surface accumulations were treated as uniform sheaths. In both cases, the fractions of mineral accumulations that adhered to collagen were of primary interest.

The stiffening of a matrix by spherical particles is a richly studied problem, with a wealth of models existing for single and multiple phases (cf. [29–32]) and high volume fraction [33]. However, additional structural factors, such as non-random and non-periodic distribution [7] and de-bonding between particles and matrix, are not well modelled by any of these traditional analytical methods [34,35], necessitating the application of multiscale numerical models [36].

Teng [36] found that the degree of stiffening of a matrix by a spherical mineral phase is affected strongly by the nature of the interface between the two phases. He studied the stiffness of composites containing a volume fraction 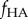of spherical inclusions, a fraction 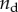of which were debonded from the matrix. For fully debonded particles, the effect of the ratio of the elastic moduli of the inclusions 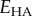and the matrix 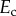was only a few percent for 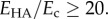Similarly, the effect of Poisson's ration was small. For a composite with inclusion Poisson ratio 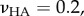matrix Poisson ratio 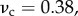and 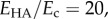the data of Teng could be fitted to within 2% by the following relation:

2.5

where E is the modulus of the composite.

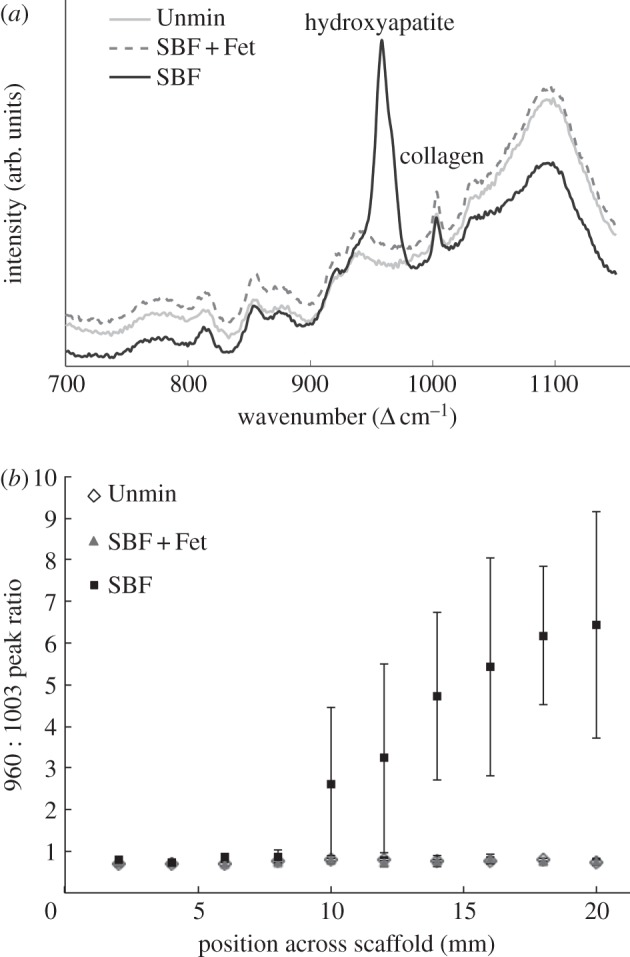
Applying equation (2.5) required relating Raman data (cf. figure 2) to volume fraction. The Raman analysis of mineral content as a function of position (figure 2) showed that mineral content equalled zero for a certain distance along the specimen before increasing. Estimates for the peak volume fraction using energy-dispersive X-ray analysis and von Kossa staining indicated a peak of f_HA ≈ 0.25 for both types of mineralization. In generating homogenization estimates, we therefore used the expression 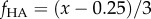for normalized position 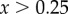along the scaffold.

Figure 2.

Raman microprobe spectroscopic comparison of unmineralized (Unmin), SBF + Fet-mineralized and SBF-mineralized collagen matrices. (a) Superimposed Raman spectra before background correction for the SBF, SBF + Fet and unmineralized samples. Mineral was undetectable on the surfaces of the Unmin and SBF + Fet samples. (b) The graph shows the spectral intensity ratio of mineral-to-collagen matrix as a function of distance along the length of a scaffold. The relative concentration of mineral increased along the length of the SBF-mineralized samples.

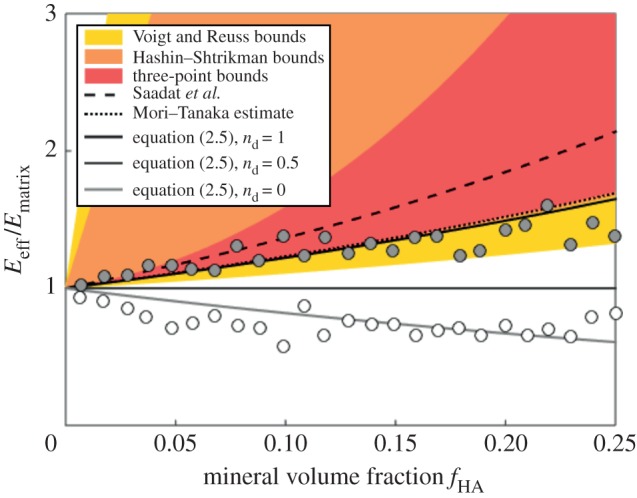
Because mineral accumulated on both the interior and exterior of the scaffolds in specimens prepared without fetuin, this volume fraction was divided into an internal volume fraction, 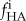and an external volume fraction, 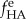The overall modulus was interpreted through the following relation:

2.6

where 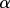determines the degree to which external mineral adheres to the scaffold.

3. Results

3.1. Simulated body fluid produced plate-like mineral crystals on the surface of collagen scaffolds and SFB + Fet produced ellipsoidal mineral inclusions within the collagen scaffolds

Raman spectroscopy was used to examine the surface mineral content of the samples. All collagen matrices exhibited Raman peaks associated with collagen (i.e. 856 Δcm⁻¹ proline, 1003 Δcm⁻¹ phenylalanine, 2940 Δcm⁻¹ C–H stretch). The homogeneous SBF-mineralized samples also exhibited a clear approximately 960 Δcm⁻¹ peak corresponding with apatitic phosphate (figure 2). In the graded SBF samples, the ratio of the 960/1003 peak intensities increases as a function of incubation time along the scaffold. This indicates that, with increased exposure to SBF, the amount of apatitic crystal deposition on the scaffold surface increased. In contrast, the SBF + Fet-mineralized samples, whether homogeneous or graded, did not exhibit any apatite-associated peaks on the sample surfaces.

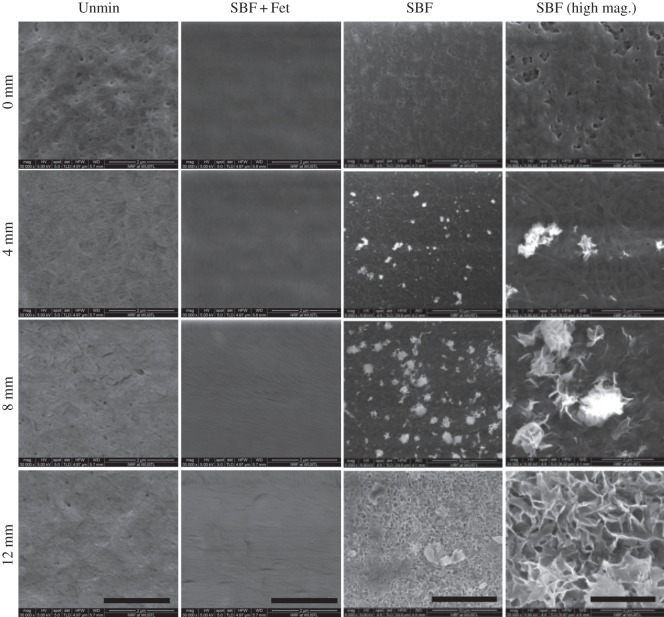
SEM imaging of the unmineralized scaffolds indicated a porous appearance, with collagen fibrils clearly visible on the surface. The scaffolds resemble mats of woven fibrils. Images of the SBF mineralized samples showed a surface layer of crystals (figure 3). These crystals appear plate-like and extend out from the surface of the matrices. In regions of the graded SBF scaffolds with high incubation times, the crystals aggregated into groups and formed rosette-like structures along the entire surface. With decreasing incubation time along the scaffold, the crystals became more dispersed and ultimately reached a crystal-free area where collagen fibrils could be seen. In contrast, the SBF + Fet samples exhibited an irregular surface without evidence of crystalline structures or collagen fibrils.

Figure 3.

Representative scanning electron microscope images of collagen matrices with mineral gradients at different locations along the matrix lengths. The SBF-mineralized scaffolds (two rightmost columns) show an increasing number of mineral deposits on the surfaces with increasing incubation time (e.g. 0 versus 12 mm). Higher magnification shows that the mineral crystals are plate-like and display rosette configurations. There was an absence of mineral on the surfaces of the SBF + Fet samples. The surfaces of these matrices were covered with a morphologically amorphous material (presumably fetuin protein). The unmineralized collagen matrices (left column) appear porous and composed of randomly oriented fibrils. SBF column scale bars = 10 µm. All other scale bars = 2 µm.

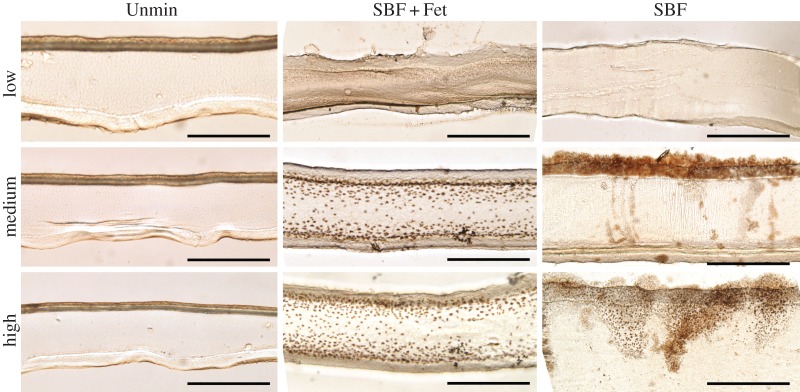
Von Kossa-stained sections confirmed that the SBF and SBF + Fet samples contain mineral compared with the unmineralized scaffolds (figure 4). Staining of the SBF samples revealed mineral at the surface of the collagen scaffolds with little to no mineral at depth within the matrix cross sections. As the incubation time increased along the graded SBF scaffolds, the density and depth of penetration of these surface crystals increased. Mineral in the SBF + Fet samples was absent from the surface but evident as small ellipsoidal inclusions at depth within the matrix cross sections. These inclusions were approximately 2 µm in diameter, denser near the surface and decreased in number towards the centre of the scaffold cross section. In the SBF + Fet-graded scaffolds, both the number and size of the inclusions increased as the incubation time increased. The unmineralized scaffolds did not exhibit any dark staining.

Figure 4.

Bright-field images of scaffold cross sections stained for mineral at equivalent positions for low, medium and high mineral content. Unmineralized (left column), SBF + Fet-mineralized (middle column) and SBF-mineralized (right column) were stained with von Kossa to indicate mineral content in brown. SBF-mineralized collagen shows a sparse population of stained crystals within the collagen bulk but a thick coating of mineral on the outer boundaries of the collagen surface, supporting the expectation that incubation in SBF without fetuin resulted primarily in surface mineralization. In contrast, SBF + Fet-mineralized collagen showed significant staining through the depth of the matrix, suggesting that incubation in fetuin-doped SBF resulted in mineral deposition within the collagen bulk. However, staining in this group was localized to the outer two-thirds of the matrix cross sections with the highest mineral concentration nearest to the outer edges of the scaffold. No positive staining was seen in the Unmin matrices (the dark top surface of the Unmin group is a result of matrix folding during handling and prior to sectioning). Scale bars for bright-field images are 50 µm. (Online version in colour.)

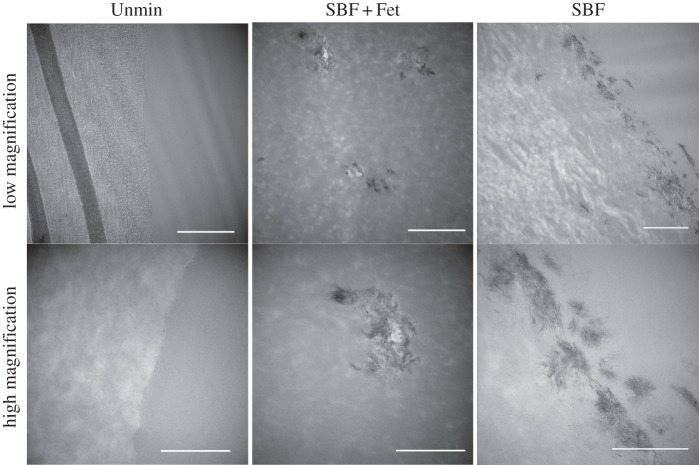
Although TEM images of the scaffolds did not provide us information about the amount of mineral present in the scaffolds owing to mineral pullout during sectioning, they provided additional information about the location of the mineral crystals (figure 5). As seen with the von Kossa staining, the SBF-treated samples revealed mostly surface mineralization. The large, plate-like crystals seen with SEM appeared as aggregates of smaller crystallites when viewed with TEM. These crystals penetrated approximately 1 µm from the surface into the collagen matrix. The mineral inclusions in the SBF + Fet samples were also seen to be aggregates of randomly oriented smaller crystals.

Figure 5.

TEM micrographs of collagen matrices. In SBF + Fet-mineralized collagen matrices, mineral was deposited as small clusters within the collagen matrix (middle column). High magnification shows each mineral inclusion to be composed of many randomly aligned nanocrystals. In SBF-mineralized collagen matrices, mineral deposits were found only on the collagen surface, in some cases penetrating up to 1 µm into the matrix. High magnification showed the formation of clusters of crystals near the matrix surface. Mineral crystals were not observed in Unmin collagen matrices. Scale bars for top row are 1 µm, and scale bars for bottom row are 500 nm.

3.2. The location of mineralization dictated the mechanical behaviour of the collagen matrix

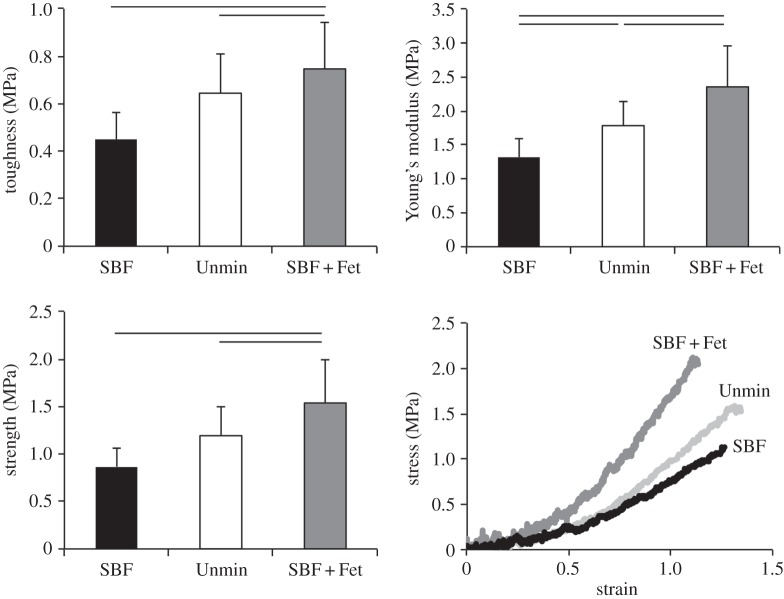
Stress–strain curves acquired from the tensile tests of unmineralized and bulk (i.e. homogeneously) mineralized matrices were analysed to determine matrix modulus, toughness and strength (figure 6). The unmineralized scaffolds had a modulus of 1.78 ± 0.35 MPa, toughness of 0.64 ± 0.16 MPa and strength of 1.91 ± 0.30 MPa. SBF mineralization led to a significant decrease in all of these measures: modulus was 1.32 ± 0.27, toughness was 0.45 ± 0.11 and strength was 0.86 ± 0.20 MPa. SBF + Fet mineralization had the opposite effect, leading to a significant increase in Young's modulus compared with the unmineralized scaffolds. Young's modulus was 2.36 ± 0.6 MPa, toughness was 0.75 ± 0.19 (p = 0.17 compared with unmineralized) and strength was 1.50 ± 0.46 (p = 0.07 compared with unmineralized). In all cases, failure occurred at the interface between the sample and the grip. Regardless of mineralization method, all matrices exhibited high yield strains (unmineralized: 0.55 ± 0.06, SBF: 0.49 ± 0.07, SBF + Fet: 0.53 ± 0.05) and failure strains (unmineralized: 0.62 ± 0.04, SBF: 0.57 ± 0.07, SBF + Fet: 0.59 ± 0.02). Yield and failure strains were significantly lower for SBF-mineralized matrices compared with unmineralized and SBF + Fet-mineralized matrices, indicating more brittle behaviour in those matrices.

Figure 6.

Mechanical properties of collagen matrices. Toughness, modulus and strength were significantly higher in the SBF + Fet group compared with the SBF and Unmin groups. The modulus of the Unmin group was also significantly higher than that of the SBF group. Lines above bars indicate p < 0.05.

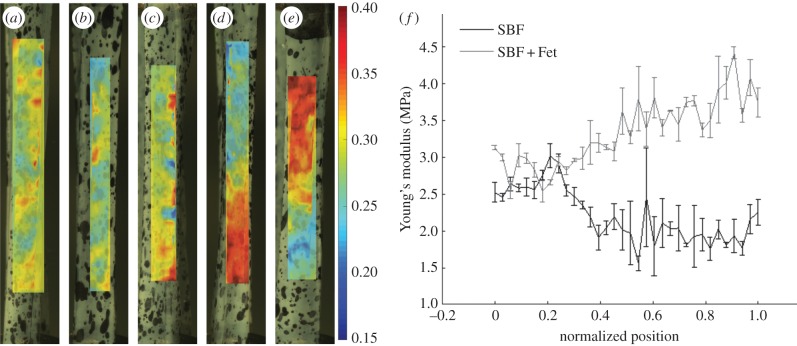
The same patterns among groups were seen in the graded mineralized samples. Local strain analysis was used to obtain strain maps along the surface of the matrices during tensile testing (figure 7). Analysis of samples without gradients in mineral showed consistent levels of strain along the length of the matrices. In contrast, SBF-mineralized graded scaffolds exhibited an increase in local strain with increasing levels of surface mineral. The opposite pattern was seen in the SBF + Fet-mineralized graded samples: local strain decreased with increasing levels of mineralization. For the graded matrices, secant modulus was calculated along the length of each matrix, as described previously [37]. The SBF-mineralized matrices exhibited a nonlinear decrease in modulus as a function of position (and hence as a function of mineral content; figure 7). A relatively constant modulus was observed at low levels of mineralization. At approximately one-third of the way along the length of the mineral-graded matrix, modulus decreased linearly with increased immersion time. Over the latter half of the matrix length, where mineral content was highest, a relatively constant low modulus was observed. The SBF + Fet-mineralized graded matrices showed a constant modulus at low levels of mineralization, followed by a linear increase in the modulus through higher levels of mineralization.

Figure 7.

Local mechanical properties of mineralized matrices. (a–e) Representative strain maps of (a) an unmineralized collagen matrix, (b) an ungraded SBF + Fet-mineralized collagen matrix, (c) an ungraded SBF mineralized collagen matrix, (d) a graded SBF + Fet-mineralized collagen matrix and (e) a graded SBF mineralized collagen matrix. The frames shown for each sample were chosen such that the average strain in the frame was constant. The local strain analysis indicated that ungraded matrices expressed no strain field gradients. Strain was relatively constant along the lengths of unmineralized and ungraded samples. Strain decreased with increasing mineral content in the SBF + Fet group. Strain increased with increasing mineral content in the SBF group. (f) The average secant modulus as a function of position is shown for graded SBF and SBF + Fet scaffolds. Modulus increased with increasing mineral in the SBF + Fet group. Modulus decreased with increasing mineral in the SBF group. (Online version in colour.)

4. Discussion

The past two decades have produced major advances in the development of engineered structural biological materials to replace damaged tissues. Research in mineralized tissue engineering has led to successes that are now reaching the clinical sector [38,39]. Many of these bone replacement materials focused on recreating the mineralized collagen structure and were therefore composites of collagen and hydroxyapatite mineral [3,40–42]. These composites can be assembled in a variety of ways, but the two most common were (i) immersion of collagen scaffolds in a calcium- and phosphate-containing solution [40,43–47] and (ii) mixing of hydroxyapatite nanoparticles with collagen before polymerization [44,48–50]. In the case of the former methodology, a number of mineralization techniques have been employed. These included simply immersing collagen scaffolds in solutions such as SBF or adding proteins, peptides or other chemicals to help control the mineralization process [3,20,51–57]. Simple immersion of collagen leads to surface deposition of mineral either on the surface of fibrils, creating extrafibrillar mineral, or on the surface of dense collagen scaffolds. The addition of components such as fetuin and poly(aspartic acid) (PAsp) inhibits surface mineralization, leading to mineral deposition either within fibrils, i.e. intrafibrillar mineralization, or within dense collagen scaffolds. This, in turn, had significant effects on the mechanical properties of the scaffolds [7]. The goal of this study was to create collagen matrices with gradients in mechanical properties for the repair of tendon-to-bone injuries. The mechanical properties were controlled by controlling the location and quantity of mineral deposited on the surfaces of and within collagen matrices. Tuning the mechanics of these matrices via mineralization may allow for tailored mechanical and cellular responses at interfacial repair sites.

Both SBF and SBF + Fet protocols were successful in mineralizing the collagen matrices. The results showed that mineralization with SBF led to the deposition of mineral onto the surfaces of the collagen matrices (figures 3–5). Extensive prior work has been done on mineralizing collagen scaffolds with calcium- and phosphate-containing solutions. [38,39]. These studies showed similar results to this study, with mineralization occurring primarily on the scaffold surfaces [43,45–47]. SBF mineralization led to rapid deposition of mineral on the surfaces, potentially filling scaffold pores and limiting diffusion of calcium and phosphate ions into the bulk of the scaffold [46]. This deposition of mineral on the surface of the matrix likely resulted in a layered composite of collagen and mineral, arranged in parallel sheets. In contrast, SBF + Fet mineralization did not lead to deposition of mineral on the collagen matrix surfaces, as evidenced by the lack of mineral detected on surfaces by Raman spectroscopy and SEM (figures 2 and 3). Rather, the scaffolds had mineral inclusions within their thickness (figure 4). These micrometre-scale inclusions were denser near the surface of the scaffold and decreased in size and number towards the centre of the cross sections. This result is not surprising, as fetuin protein inhibits calcium phosphate precipitation in solution, preventing deposition of mineral on the matrix surfaces. The fetuin molecule is too large to infiltrate collagen fibrils, so mineralization is inhibited in solution but permitted within the collagen matrix [51,52,58,59]. Mineralization with fetuin and other mineralization inhibitors has been shown to cause intrafibrillar mineralization, meaning that mineral is deposited within the gap zones of collagen fibrils [2,52,56]. This is different from PAsp-induced mineralization, in which PAsp infiltrates the collagen and preferentially binds in the gap zones, promoting intrafibrillar mineralization. Although there is evidence that PAsp may act as an inhibitor when not bound to collagen [60]. Prior studies examining the mineralization of dense collagen scaffolds with fetuin have demonstrated similar results: mineralization occurs preferentially within the matrix, often concentrated near the surface, likely due to diffusion limitations [20,53,61]. Unlike SBF mineralization, which resulted in a two-layer composite, the addition of fetuin led to the formation of micrometre-scale inclusions leading to a particle inclusion composite.

When mechanically tested in uniaxial tension, the SBF + Fet-mineralized matrices exhibited an increased modulus compared with the unmineralized matrices, as expected for a reinforced composite (figure 6). However, the SBF-mineralized matrices showed a decrease in modulus compared with both the unmineralized and SBF + Fet-mineralized scaffolds. In the presence of a mineral coating, a few micrometres thick on the collagen matrix surface, one would expect the modulus of the composite to increase according to the Voigt model (i.e. a parallel arrangement of compliant collagen matrix with a stiff mineral layer). Assuming a mineral volume fraction of approximately 25%, estimated from bright-field images, an increase in modulus of over three orders of magnitude would be expected for the matrices of this study. However, the clear decrease in modulus with SBF mineralization indicates that other factors dominated the mechanical response of these scaffolds.

Several factors could contribute to the initially surprising decrease in the stiffness of the SBF matrices. One possible explanation is that immersion in the SBF solution caused significant degradation of the collagen matrix compared with the SBF + Fet solution. Other than the presence of fetuin, the main differences between the solutions were the pH and the ionic strength, both of which can significantly affect collagen polymerization. In order to evaluate these possible effects, unmineralized scaffolds were treated (i) in deionized water (DiH₂O) at a pH equivalent to that of the SBF solution or (ii) in a saline solution (NaCl) with an ionic strength equivalent to the SBF solution. Mechanical testing of the DiH₂O and saline samples showed no change in the modulus (p = 0.99), which remained significantly higher than those measured for the SBF-mineralized scaffolds (data not shown). This suggests that the decrease in modulus is caused by the mineralization itself.

A second possible explanation for the decreased modulus in matrices with surface mineralization is poor adhesion between the collagen scaffold and the mineral, and possible formation of defects within the collagen owing to mineral growth. SBF mineralization leads to the precipitation of crystallites onto the matrix surface, which then grow into the matrix [40]. SEM, TEM and bright-field images indicated that the mineral formed blade-like crystal aggregates that penetrated approximately 1 µm into the collagen matrix (figures 3–5). Crystal growth may therefore create fissures on the matrix surface, and these local defects have the capacity to weaken the matrix and significantly decrease the strength, toughness and modulus of the matrix.

The stiffening effect was clarified by analysing the data through homogenization bounds and through the multiscale modelling scaling law (equation (2.6); cf. figure 8). The SBF + Fet specimens (filled circles, figure 8) initially stiffened with mineralization at a rate close to the upper bound expected for stiffening by diffuse spheres of mineral, as captured by the estimate of Saadat et al. [33]. However, additional mineral seems to have had markedly less stiffening effect, with higher volume fractions producing stiffening that fell outside of the three-point bounds for randomly distributed spheres (cf. [30]), then below the Hashin–Shtrikman bounds and Mori–Tanaka estimate (cf. [29–31]) that represent the range possible for randomly distributed mineral. At the highest levels of mineralization, the stiffening was at the lower end of the Voigt–Reuss range, indicating that mineral was not well connected to the collagen.

Figure 8.

Interpretation of data through homogenization bounds and multiscale models. The SBF + Fet specimens (filled markers) initially stiffened within mineralization at a rate close to the upper bound expected for stiffening by diffuse spheres of mineral, as captured by the estimate of Saadat et al. [33]. However, additional mineral had markedly less stiffening effect, with higher volume fractions producing stiffening that fell outside of the three-point bounds for randomly distributed spheres (cf. [30]), then below the Hashin–Shtrikman bounds and Mori–Tanaka estimate (cf. [29–31]) that represent the range possible for randomly distributed mineral. At the highest levels of mineralization, the stiffening was at the lower end of the Voigt–Reuss range, indicating that mineral was not well connected to the collagen. The SBF specimens (open markers) led to a reduction of stiffness, consistent with equation (2.5) with 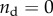(no bonding between the mineral and collagen). The rapid drop in stiffness and the asymptote at high levels of mineralization indicate that mineral coating the fibril must have contributed negligibly to stiffening of the collagen ( 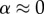in equation (2.6)). (Online version in colour.)

The SBF specimens (open markers, figure 8) led to a reduction of stiffness, consistent with equation (2.5) with 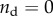(i.e. no bonding between mineral and collagen). The rapid drop in stiffness and the asymptote at high levels of mineralization indicate that mineral coating the fibril must have contributed negligibly to stiffening of the collagen ( 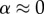in equation (2.6)). This further indicated that mineral was distributed between an external coating and the interior of the collagen at lower volume fractions. At higher volume fractions, the asymptote suggests that all additional mineral was added to the exterior of the specimens, again with negligible contribution to the stiffness of the collagen.

The mineralization characteristics for the graded matrices mirrored those of homogeneously mineralized matrices. The SBF-mineralized scaffolds exhibited mineral crystals on the surface; however, instead of thinning of the mineral coating with decreased immersion time, a decrease in the number of mineralization sites was seen (figure 3). It is expected that, during mineralization in SBF, most of the mineral initially precipitates in solution and subsequently deposits and grows on the matrix surface. Increased immersion time, therefore, leads to an increased number of precipitates, which attach and grow on the surfaces. In the case of the SBF + Fet-graded mineralization, not only the number, but also the size of the mineral crystals within the collagen matrix increased with immersion time (figure 4). This suggests that additional immersion time allowed the calcium and phosphate ions to penetrate into the collagen matrix prior to precipitation.

Functional gradients in mechanical properties were achieved using gradients in mineral content. Matrices with varying mineral content along their lengths showed gradients in strain with applied load along the length of the scaffold. The SBF + Fet-mineralized scaffolds showed a linear gradient in strain along the length of the scaffold, with the strain highest in the unmineralized zone and decreasing with increasing mineral content (figure 7). Mineral inclusions within the matrix acted as particle reinforcement, increasing the modulus in SBF + Fet samples. The linear change in strain is reflected in the measured modulus along the width of the sample. The gradation in the number of small mineral inclusions led to a gradation in mechanical properties, mimicking the structure and mechanics of partially mineralized tissues such as the tendon-to-bone attachment. The smooth gradient in mineral content allowed the stiffness of the matrix to increase gradually, decreasing the risk of forming stress concentrations at abrupt mechanical interfaces and thereby decreasing the risk of failure.

In the case of the SBF-mineralized matrices, the strain increased with immersion time along the scaffold. Although the strain gradient was approximately linear, the scaffold modulus was nonlinear. The modulus quickly dropped with increased mineralization and then plateaued (figure 7). This supports the theory that the degradation in mechanical properties in the SBF-mineralized samples was caused by the presence of mineralization-induced defects. In the regions with low concentrations of mineral, a small number of crystals were deposited and grew on the sample surfaces. As a result, these regions would be expected to have only a small number of defects and slightly decreased mechanical properties. As the immersion time increased so did the number of mineralization sites, and therefore the number of defects. Approximately halfway along the length of the matrix, the entire surface of the scaffold was covered in mineral (figure 3). At this point, there would be a maximum number of defects in the samples. Any additional immersion time would increase only the size of the crystals, which would not add defects to the collagen matrix. As a result, one would expect the mechanical properties to remain constant, even though the mineral content increased.

The methods developed here for controlling the location and amount of mineral deposition have important implications for engineering mineralized tissues (e.g. bone) and interfaces between mineralized and unmineralized tissues (e.g. tendon enthesis). Mineralization of collagen can influence cell attachment, proliferation and differentiation [23]. Presentation of mineral or increased stiffness to mesenchymal stem cells, for example, has the capacity to stimulate differentiation into an osteoblast lineage [22,23]. Controlling mineral concentration spatially can therefore be useful for engineering tissues such as the tendon enthesis, which exhibits spatial gradients in mineral content and cellular phenotypes (tendon fibroblast, fibrochondrocyte, osteoblast/osteocyte). A gradient in mineral concentration in an engineered construct may therefore be useful to promote a gradient in osteogenesis. Controlling the amount and location of the mineral in the collagen scaffold can also be used to tune the mechanical properties and response of biological tissues to the artificial tissues.

There were a number of limitations to this study. The SBF and SBF + Fet mineralization procedures were not identical with regard to mineralization time or rate of gradient formation. These differences were necessary due to the slower mineral nucleation in fetuin-mediated mineralization compared with standard SBF-mediated mineralization. In addition, during SBF + Fet mineralization, a large amount of fetuin was deposited on the surfaces of the matrices. This coating limited the ability of surface techniques such as Raman spectroscopy and SEM to identify small amounts of mineral on the surfaces, as those techniques can only detect a few micrometres into the depth of the matrices. Additionally, formation of mineral gradients was achieved using collagen rings on cylindrical posts, resulting in nonlinear exposure to mineralizing solutions. Lastly, the strength and modulus of mineralized collagen matrices were significantly lower than those in natural bone and tendon-to-bone attachments; further study is needed to engineer tissues that are mechanically more similar to natural tissues.

5. Conclusion

The location and concentration of mineral within collagenous tissue play important roles in the tissue's mechanical properties. We demonstrated that mineral deposition can be finely controlled on collagen matrices with regard to its location relative to the collagen matrix and with regard to its spatial concentration. The location of the mineral had important implications for the mechanics of the matrix: (i) SBF + Fet mineralization led to the deposition of micrometre-scale mineral inclusions within the collagen matrix and enhanced the mechanical properties, whereas (ii) SBF mineralization led to the formation of a layered composite that exhibited degraded mechanical properties. By controlling the immersion time of collagen matrices in SBF and SBF + Fet solutions, spatial gradients in mineral along the length of the scaffold were obtained. These spatial gradients in mineral content led to spatial gradients in matrix modulus. The control of mineralization and matrix stiffness has important implications for control of cell behaviour and for the development of tissue-engineered scaffolds for applications such as tendon-to-bone repair.

Authors' contributions

L.S., A.D., Z.L., and S.L. carried out the laboratory work, participated in data analysis, participated in the design of the study, and helped draft the manuscript; J.B. carried out the strain tracking analysis and helped draft the manuscript; Z.L. and J.P. participated in the Raman characterization and analysis and helped draft the manuscript; Y.X. participated in the design of the study and helped draft the manuscript; G.G. performed the multiscale modelling and helped draft the manuscript; S.T. conceived of the study, designed the study, coordinated the study, and helped draft the manuscript. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

The study was supported by the National Institutes of Health (U01 EB016422 and R01 AR060820) and the National Science Foundation (CAREER 844607).