Measurement of Rat Brain Tumor Kinetics Using an Intravascular MR Contrast Agent and DCE-MRI Nested Model Selection

Abstract

Purpose

Using dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) in a rat glioma model, and nested model selection (NMS), to compare estimates of the pharmacokinetic parameters v_p, K^trans, and v_e for two different contrast agents (CAs)—gadofosveset, which reversibly binds to human serum albumin, and gadopentetate dimeglumine, which does not.

Materials and Methods

DCE-MRI studies were performed on nine Fisher 344 rats inoculated intracerebrally with 9L gliosarcoma cells using both gadofosveset and gadopentetate. The parameters v_p, K^trans, and v_e were estimated using NMS.

Results

K^trans estimates using gadofosveset, compared to gadopentetate, differed in their means (gadofosveset 0.025 ± 0.008 min⁻¹ vs. gadopentetate 0.046 ± 0.011 min⁻¹; P = 0.0039). This difference notwithstanding, the intraclass correlation coefficient (ICC) for the two estimates of K^trans showed nearly perfect linear dependence (ICC = 0.8479 by Pearson’s r). Other estimates, v_e (gadofosveset 22.7 ± 4.7% vs. gadopentetate 23.6 ± 5.6%; P = 0.4258) and v_p (gadofosveset 1.5 ± 0.5% vs. gadopentetate 1.6 ± 0.4%; P = 0.25), were not different in their means between the two CAs, and there was almost perfect agreement for v_e (ICC = 0.8798) and substantial agreement for v_p (ICC = 0.7981) between the two CAs.

Conclusion

Estimates of K^trans were statistically different using gadofosveset and gadopentetate, whereas v_e and v_p were similar with two CAs. NMS produced robust estimates of pharmacokinetic parameters using DCE-MRI that show promise as important measures of tumor physiology and microenvironment.

Dynamic contrast-enhanced T1-weighted magnetic resonance imaging (DCE-MRI) is being increasingly used in various clinical trials involving brain tumors. It allows characterization of the vascular microenvironment in tumors by measurement of a range of parameters, such as K^trans (forward transfer constant), k_ep (reverse transfer constant), v_e (volume of the extravascular extracellular space), and v_p (blood plasma volume) (1,2). These parameters reflect specific physiologic characteristics and hence relate to various aspects of tumor biology. One of the hurdles in obtaining these quantitative metrics is a lack of robust methods for approaching the problem of parametric estimation using multicompartmental pharmacokinetic models (3). Another issue is that current Food and Drug Administration (FDA)-approved extravascular contrast agents (CAs) used for the assessment of vascular parameters in solid tumors are relatively small (molecular weight <1 kDa) (4). Thus, their transfer rates from the vasculature to the extravascular extracellular space (EES) are often very high in solid tumors. This generates a need for rapid sampling of the dynamic behavior of the CA in both tissue and arterial system, and also raises the possibility that the delivery of CA to tissue may be flow-limited in portions of very aggressive tumors.

Intravascular or blood pool CAs are being studied for many clinical applications. For example, gadofosveset has been recently approved by the FDA for MR angiographic application in aorto-iliac disease (5). Gadofosveset is a blood pool agent that binds reversibly to serum albumin, distributes primarily in the intravascular space, exhibiting a prolonged plasma half-life and increased T1 relaxivity at 1.5 T. Since the albumin-gadofosveset compound has an effective molecular weight in excess of 6 kDa, the dynamics of the bound fraction will therefore be slow compared to an extravascular agent, making the delivery of larger CA permeability limited rather than flow-limited. Experience with intravascular or blood pool MR CAs in intracranial tumors is limited. One study by Adzamli et al (6) at 1.5 T demonstrated that small-molecule, albumin-binding blood pool CAs increased dose effectiveness and lengthened contrast enhancement in an intracranial mouse glioma model. A study by Essig et al (7) showed that gadofosveset produced greater, longer-lasting contrast enhancement compared to conventional agents in a variety of human brain tumors.

To our knowledge, gadofosveset has not been used to quantitatively estimate tumor kinetics using a DCE-MRI nested model selection (NMS) procedure in rat gliomas. The purpose of our study was to measure and compare the parameters of vascular physiology such as v_p, K^trans, and v_e in a rat model of human glioma using two different kinds of CAs: a primarily intravascular or blood pool CA (gadofosveset) and an extravascular CA (gadopentetate dimeglumine) using NMS and DCE-MRI.

MATERIALS AND METHODS

9L Gliosarcoma Cells

9L gliosarcoma cells were grown in Dulbecco’s modified Eagle’s medium (DMEM) supplemented with 10% fetal bovine serum (FBS) in 5% CO₂/95% air at 37°C in a humidified incubator. Cells were harvested and resuspended at a concentration of 8 × 10⁷ per mL of serum-free media; 5 μL of the cell suspension containing ~4 × 10⁵ cells was implanted into the rat brain.

Rat Brain Tumor Model

This study was carried out in strict accordance with the recommendations in the Guide for the Care and Use of Laboratory Animals of the National Institutes of Health. The protocol was approved by the Institutional Animal Care and Use Committee of Henry Ford Hospital. Surgery was performed under anesthesia and all efforts were made to minimize suffering. Nine Fisher 344 female rats were inoculated intracerebrally with 9L gliosarcoma cells. Animals were anesthetized with 100 mg/kg ketamine and 15 mg/kg xylazine intraperitoneally. The surgical zone was shaved, swabbed with betadine solution, the eyes coated with Lacri-lube, and the animal was immobilized in a small animal stereotactic device (Kopf, Cayunga, CA). A 1-cm incision was made 2 mm to the right of the mid-line and 1 mm retro-orbitally. The skull was exposed with cotton-tip applicators and an HP-4 dental drill bit was used with a micromanipulator to drill a hole 3 mm to the right of the bregma, taking care not to penetrate the dura. A #2701 10 μL Hamilton syringe with a #4 point, 26-gauge needle containing tumor cells (4 × 10⁵) in 5 μL was lowered to a depth of 3.5 mm, then raised to a depth of 2.5 mm. The tumor cells were injected stepwise at a rate of 0.5 μL/min until the entire volume was injected.

During and after injection, careful note was made of any reflux from the injection site. After completing the injection, the syringe was withdrawn in a stepwise manner. The surgical hole was sealed with bone wax. Finally, the skull was swabbed with betadine before suturing the skin over the injection site. Animals that developed significant symptoms or failed to develop tumors were sacrificed.

MRI Methods: DCE-MRI

A DCE-MRI was performed in each group of animals. An appropriate state of anesthesia was obtained with isoflurane (3% for induction, 0.7% to 1.5% mixed with O₂ for maintenance).

MRI was obtained with a 3T clinical system (Signa Excite, GE Healthcare, Milwaukee, WI) using a Lutz-cage small animal radiofrequency (RF) coil of 50 mm diameter × 108 mm RF rung length (Doty Scientific, Columbia, SC). After positioning using a triplanar FLASH sequence, MR studies were performed using pre-and postcontrast-enhanced T1-weighted MRI scans. The following parameters were used to acquire the images: T1-weighted multislice sequence (TR/TE = 500/12 msec, 256 × 256 matrix, 13–15 slices, 1 mm thick, 40 × 30 mm field of view [FOV], number of excitations [NEX] = 2–4). To generate T1 maps from precontrast images, 3D SPGR images with multiple flip angles 2°, 4°, 8°, 12°, 15°, 20°, 25°, 30°, and 35° were acquired. The following parameters were used to acquire the 3D SPGR images; TR = 5.65 msec, TE = 1.35 msec using a 128 × 128 matrix, FOV = 60 × 60 × 18 mm³, and NEX = 1. Effective slice thickness was 1.5 mm. To obtain dynamic postcontrast 3D-SPGR images for 15 minutes, a fixed flip angle of 30° was used. Acquisition of SPGR images started before the administration of contrast agents to have baseline T1-signals and time interval between image sets was 11.57 seconds.

MRI Methods: Two Different CAs

Tail veins were catheterized using a 24G needle infusion kit. The intravascular agent gadofosveset (t_1/2 elimination phase = 16.3 h) was administered at 0.12 mL/kg (0.03 mmol/kg) over 10 seconds, followed by a saline flush. The extravascular agent gadopentetate (t_1/2 elimination phase = 1.6 h) was administered at 0.2 mL/kg (0.1 mmol/kg) over 10 seconds, followed by a saline flush. MRI was obtained as the injection was administered.

Animals were randomized for the CA used. After tumor implantation (day 0), a contrast-enhanced MRI study was performed on day 13 using either gadofosveset or gadopentetate. On day 14, the remaining CA was used. Of the nine rats, five were scanned with gadofosveset first, followed by gadopentetate and four were scanned with gadopentetate first, followed by gadofosveset.

MRI Methods: DCE-MRI NMS

NMS was performed using our previously described methods (8). First, T1 maps were created using the multiflip angle (2 to 35) fast SPGR 3D images to establish the baseline precontrast T1 values on a voxel-by-voxel basis. Then ΔR1 concentration–time maps were created using the baseline T1 maps, 3D SPGR dynamic sequences, and the ratio of postcontrast to precontrast signal for each voxel. This represented the change in contrast concentration in the tissues over time. A previously reported (9) standard radiological arterial input function (SRAIF) was time-shifted according to the baseline of a manually selected profile of CA concentration in blood (main vessels) from the ΔR1 maps. This allowed us to generate an SRAIF which was temporally matched with the profile of the CA concentration in blood for major vessels in ΔR1 maps. Next, a region of interest (ROI) was manually selected in the white matter area (which was assumed to have about 1% of plasma volume) (10). Then the average time trace of CA concentration in this area was calculated and the area under this curve was used to normalize the adjusted SRAIF. It is notable that this SRAIF was used as an input function for both contrast agents, and was at best an approximation for the unbound fraction of the gadofosveset. Using SRAIF, the concentration–time data in each voxel was fitted to one of the four different nested models, which was best supported by the data. Model 0 represents no contrast filling, model 1 represents contrast filling of normal brain microvasculature without leakage, model 2 represents contrast leakage in abnormal microvasculature without reabsorption, and model 3 represents contrast leakage with reabsorption. The nested models were used to calculate the forward transfer constant K^trans, extracellular extravascular volume v_e, and plasma volume v_p. Further technical details may be found in our previous report (8).

MRI Methods: ROI Analysis

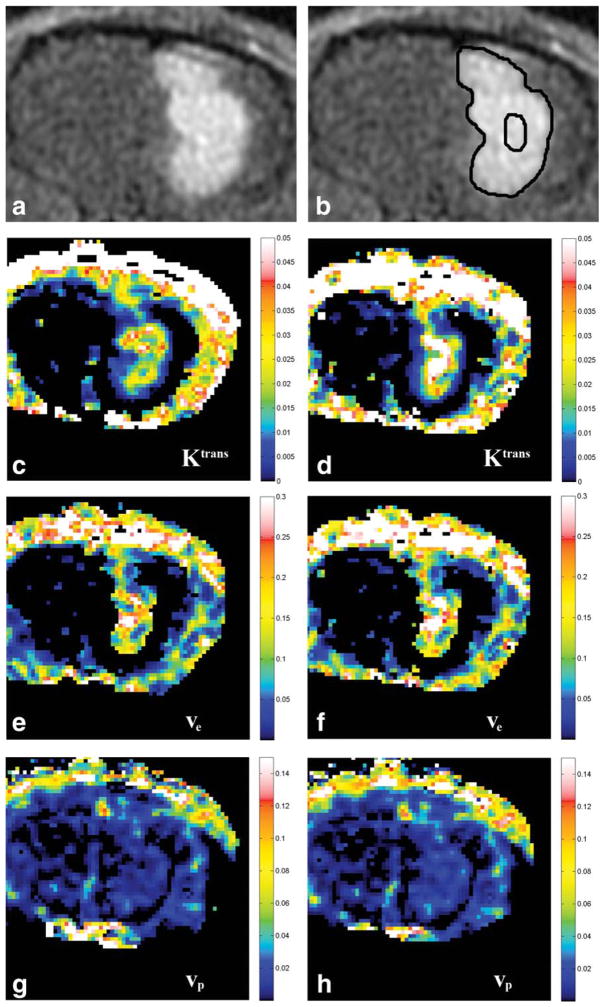
ROIs were drawn manually onto the generated maps of K^trans, v_e, and v_p using ImageJ software (NIH, Bethesda, MD), and the same ROI for each slice was used for each of the parameters measured. For the whole tumor, ROIs were drawn around the entire circumference of the tumor on every section. The mean values for K^trans, v_e, and v_p within each ROI were recorded and normalized to the total area of ROIs for all sections containing tumor. For the central core, a single slice was selected containing the largest area of tumor, and an ROI was drawn around approximately the central third of the tumor diameter. The mean value for K^trans, v_e, and v_p was recorded for this ROI. Examples of MRI images, ROIs, and parametric maps are shown in Fig. 1.

Figure 1.

A: Representative post-contrast T1 image of an animal brain tumor. B: Example of ROIs drawn for the whole lesion and the central core. C–H: Representative parametric maps for each of the vascular parameters using gadofosveset and gadopentetate. C: K^trans map using gadofosveset. D: K^trans map using gadopentetate. E: v_e map using gadofosveset. F: v_e map using gadopentetate. G: v_p map using gadofosveset. H: v_p map using gadopentetate.

Statistical Analysis

Descriptive statistics for the measurements of K^trans, v_e, and v_p were computed for the two CAs, for the whole tumor as well as from the central core of the tumor. Nonparametric Wilcoxon signed rank tests were conducted to compare the results from the gadofosveset and gadopentetate CAs for both the whole tumor and the central core of the tumor, separately. Intraclass correlation coefficients (ICC) were computed to assess the agreement or reliability between the two CAs for v_e and v_p. Landis and Koch (11) used the following cutpoints for interpreting the degree of agreement, which ranges from less than 0 to 1 (<0 representing poor or no agreement, 0.01–0.20 slight agreement, 0.21–0.40 fair agreement, 0.41–0.60 moderate agreement, 0.61–0.80 substantial agreement, and 0.81–1.00 almost perfect agreement). In addition, Bland–Altman plots were done to demonstrate the amount of agreement/disagreement between the CAs for each measurement. These plots represent the difference of the two CAs on the y-axis versus the mean of the two CAs on the x-axis. Because it was anticipated that the K^trans values would differ for the two CAs, statistical methods for agreement were not the appropriate analyses for this measure. Pearson’s correlation coefficients were computed to assess the correlation or association between the two CAs. Landis and Koch’s cutpoints were also used here for interpretation. Scatterplots with regression lines were also done to visually inspect the relationships.

RESULTS

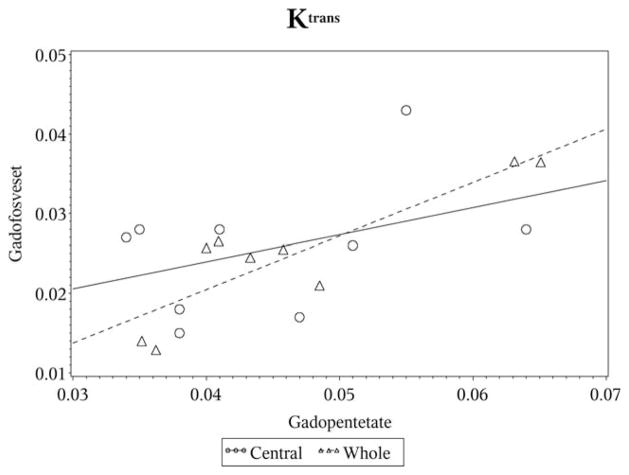
For the whole tumor, K^trans measurements were significantly lower (P = 0.0039) using gadofosveset (mean = 0.025 ± 0.008) compared to gadopentetate (mean = 0.046 ± 0.011). Despite the statistically significant difference in the mean values, the Pearson’s correlation coefficient indicates that there was almost perfect correlation between the two CAs (Table 1, Fig. 2). Estimates of both v_e (gadofosveset: mean = 22.7 ± 4.7, gadopentetate: mean = 23.6 ± 5.6) and v_p (gadofosveset: mean = 1.5 ± 0.5, gadopentetate: mean = 1.6 ± 0.4) as a percentage were not statistically different between the two CAs (P = 0.425 and P = 0.25, respectively). Almost perfect agreement between the two CAs was noted for v_e, while substantial agreement was noted for v_p (Table 1).

Table 1.

Results for the Whole Tumor

	CA	Correlation coefficient	Agreement/association
Ktrans (min−1)	Gadofosveset Gadopentetate	0.879*	Almost perfect
ve (%)	Gadofosveset Gadopentetate	0.880†	Almost perfect
vp (% or ml/100g)	Gadofosveset Gadopentetate	0.798†	Substantial

^*Pearson’s.

^†Intraclass.

Figure 2.

Scatterplot for K^trans.

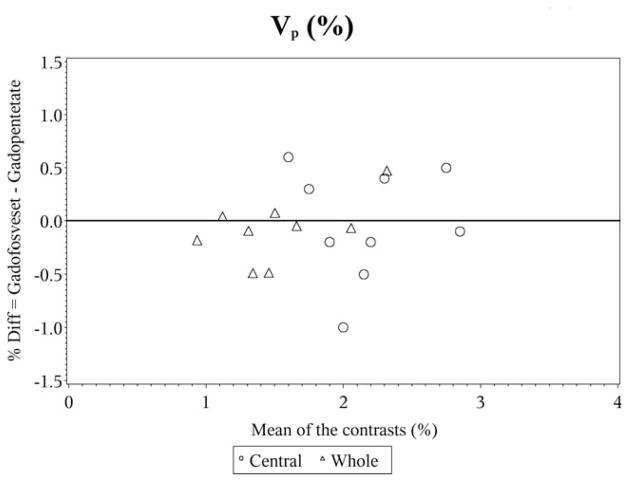
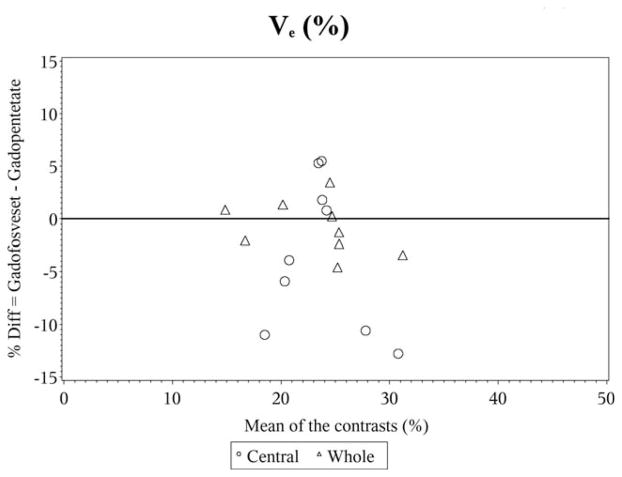
In the Bland–Altman plots for v_p, the differences are scattered and clustered around zero, again showing the almost perfect agreement (Fig. 3). However, for v_e the differences are scattered around zero but appear to become more widespread for higher values of v_e, indicative of substantial agreement (Fig. 4).

Figure 3.

Bland–Altman plot for v_p%.

Figure 4.

Bland–Altman plot for v_e%.

For the central core of the tumor, K^trans measurements were again significantly lower (P = 0.0039) using gadofosveset (mean = 0.026 ± 0.008) compared to gadopentetate (mean = 0.045 ± 0.010). However, the correlation indicates that there was only a fair association between the measurements (Table 2, Fig. 2). No statistically significant differences were observed between the CAs for v_e (gadofosveset: mean = 22.0 ± 4.6, gadopentetate: mean = 25.4 ± 5.7) and v_p (gadofosveset: mean = 2.2 ± 0.5, gadopentetate: mean = 2.2 ± 0.5) (P = 0.25 and P = 0.937, respectively). Moderate agreement was observed for v_p, while v_e only showed slight agreement (Table 2).

Table 2.

Results for the Central Core of the Tumor

	CA	Correlation coefficient	Agreement/association
Ktrans (min−1)	Gadofosveset Gadopentetate	0.411*	Fair
ve (%)	Gadofosveset Gadopentetate	0.063†	Slight
vp (% or ml/100g)	Gadofosveset Gadopentetate	0.442†	Moderate

^*Pearson’s.

^†Intraclass.

In the Bland–Altman plots for v_p, the moderate agreement and lack of statistical differences between the CAs is displayed in the plot by the differences being scattered and clustered around zero (Fig. 3). However, for v_e the differences are scattered around zero and appear to become more widespread for higher values of v_e, showing the slight agreement between the CAs (Fig. 4).

DISCUSSION

In the whole tumor, estimates of v_p, a parameter that is relatively independent of the temporal details of the input function, did not differ for the two contrast agents and showed a substantial agreement. Estimates of v_e, the fractional volume of the interstitial space, a parameter that depends on the ratio of the forward volume transfer constant K^trans and the reverse transfer constant k_ep, did not differ between the two contrast agents and demonstrated a near-perfect agreement. Estimates of both K^trans and k_ep are dependent on the comparative dynamics of the input function and the tissue response function, but since v_e is calculated as the ratio of the two, systematic effects due to an error in the input function tend to cancel.

Estimates of K^trans, a parameter that, as noted, depends substantially on a good estimate of the input function, were highly correlated, but differed between the two CAs in their mean estimates. For the two contrast agents, the estimates for the volume fractions v_p and v_e are well within the range of estimates using other techniques in similar tumors (12), and the estimate for K^trans of gadopentetate in the current study is on the same order of magnitude as that of K^trans for gadopentetate in a U251 glioblastoma model of cerebral tumor (13). Contrariwise, the estimate of K^trans for gadofosveset is an order of magnitude smaller than that of an irreversibly bound Gd-albumin compound (14), but on the same order of magnitude as the estimate for gadopentetate. Significantly, despite gadofosveset’s binding to albumin, and presumably also to external protein sites, most of the model 3 region for gadopentetate, in which measurable reverse transfer of contrast took place, was also a model 3 region for gadofosveset (see Fig. 1E,F, where the nonzero values of v_e mark the extent of the model 3 region). This comparison between the two contrast agents raises the likelihood that it is mainly the unbound fraction of gadofosveset that was leaking from the microvasculature of the tumor. It might be supposed that, since gadopentetate and the unbound fraction of gadofosveset have nearly the same molecular weight, they will have very similar pharmacokinetics in their extravasation from the microvasculature. Once external to the microvasculature, there might have been some binding to interstitial protein pools, but this binding must have saturated fairly quickly in order for significant reverse flux to have occurred. The fact that the estimate of the ratio of K^trans/k_ep for the two contrast agents is nearly identical supports the hypothesis that the two contrast agents exhibit very similar pharmacokinetics, but that the input function of gadofosveset may not be as not well known as that for gadopentetate.

With the foregoing in mind, it appears that, in assessing the absolute value of K^trans for the unbound fraction of gadofosveset, the main problem is that the input function of the unbound fraction is not well known and cannot be determined from an MRI study alone. This is because, even at 3T the longitudinal relaxivities for the bound and unbound fractions differ by a factor of 2, but the only judge of arterial and/or tissue concentration that was available was the change in R1. The bound fraction is concentration-dependent (14), varying from around 40% at high concentrations to 90% at low concentrations. Thus, it can be expected that the first-pass concentration of the unbound fraction is higher than the equilibrium fraction. The bound fraction is also species-dependent, with fractional binding in rat species lying closer to 70% than to 90% (15). This makes for a very complex kinetic picture in the input function, and even a somewhat complex model for the exchange kinetics of the unbound fraction, ignoring to first order the exchange kinetics of the bound fraction. One ameliorating element in this problem is that the time constants (K^trans and k_ep) of even the unbound fraction are on the order of tens of minutes. Since the basic equation of the transfer is that of a low-pass filter, it is probable that those time constants of the input function that are considerably shorter than tens of minutes do not strongly influence the response of the system, and thus do not strongly influence the parametric estimates of the model.

Since the ratio K^trans/k_ep, ie, the parameter v_e, agreed substantially between gadofosveset, which binds to proteins, and gadopentetate dimeglumine, we have noted that the transvascular pharmacokinetics of the two similarly sized CAs were probably similar. There is some complexity in this inference, since it is unknown whether the bound/unbound fractions in the interstitium were substantially the same as that in the plasma. If they were, then the contrast generated from the fraction in the interstitium would have the same relation to the concentration of CA (ie, the same longitudinal relaxivity) in the interstitium as it did in the plasma. Otherwise, the differential relaxivities of the unbound and bound fractions would generate a different relationship between CA concentration and contrast.

Noninvasive and accurate estimation of the volume of the EES (v_e) is another potentially important parameter of tumor microenvironment, which has not gained enough clinical attention and can be measured with dynamic studies. It is related to K^trans and k_ep or k_b (1,16). Increase of EES is known to occur in brain tumors and may further lead to evolution of pathologic tissue composition, such as increased intercapillary and perfusion distances, and formation of hypoxia (17). Transport of a molecule in the EES is dependent on the physiological properties such as interstitial pressure, but also on the physiochemical properties (such as size, charge, structure, composition) of both the EES and the molecule (eg, CA) used (18). v_e estimates in human gliomas range from 20–40% based on the older literature (19) to more recent estimates ranging from 43.8–61.1% using ⁷⁶Br-Bromide and positron emission tomography (PET) examination (17). Hence, we decided to estimate v_e by using two different CAs and DCE-MRI NMS and demonstrated almost perfect agreement when using two different CAs for the whole tumor. However, v_e estimates in the central core of the tumor were in poor agreement with the two different CAs, even though they were within the physiological range. This could be due to the fact that transport of low molecular weight molecules is diffusion dominated, and the transport of the gadofosveset by that modality is probably hindered by its tendency to adhere to interstitial proteins. This could be particularly important in the central core of the tumor, as most of the leaky vasculature is at the periphery of the tumor away from the central core (20–22). Hence, it is perhaps not surprising that in the central portion of the tumor, where delivery of the CA is more likely to be perfusion-limited, estimates of vascular parameters differ for the two CAs.

This insight should be tempered by the uncertainties concerning the interstitial binding of gadofosveset. The sources of uncertainty include the different intervoxel diffusion rates for the two CAs, location-dependent interstitial binding potentials for gadofosveset, and possibly location-dependent relaxivities (depending on the binding potential and bound/unbound fractions) for gadofosveset. Thus, it would be difficult to state with certainty the reason for the lack of agreement in the estimates of pharmacokinetic parameters for the two contrast agents in the central region of the tumor.

In conclusion, both volume of extravascular extracellular space and blood plasma can be measured accurately whether we use currently FDA-approved extravascular CAs or experimental blood pool CAs in preclinical cancer models. K^trans measurements were significantly lower using a blood pool CA due to the much larger size of the albumin-bound CA, but even these were measured accurately using NMS in DCE-MRI. We demonstrated the stability of NMS in DCE-MRI for measurement of these important vascular physiology markers which can provide important information about the tumor microenvironment and, hence, could potentially expand their role into clinical studies as prognostic and/or predictive imaging biomarkers.