Processing time of addition or withdrawal of single or combined balance-stabilizing haptic and visual information

Abstract

We investigated the integration time of haptic and visual input and their interaction during stance stabilization. Eleven subjects performed four tandem-stance conditions (60 trials each). Vision, touch, and both vision and touch were added and withdrawn. Furthermore, vision was replaced with touch and vice versa. Body sway, tibialis anterior, and peroneus longus activity were measured. Following addition or withdrawal of vision or touch, an integration time period elapsed before the earliest changes in sway were observed. Thereafter, sway varied exponentially to a new steady-state while reweighting occurred. Latencies of sway changes on sensory addition ranged from 0.6 to 1.5 s across subjects, consistently longer for touch than vision, and were regularly preceded by changes in muscle activity. Addition of vision and touch simultaneously shortened the latencies with respect to vision or touch separately, suggesting cooperation between sensory modalities. Latencies following withdrawal of vision or touch or both simultaneously were shorter than following addition. When vision was replaced with touch or vice versa, adding one modality did not interfere with the effect of withdrawal of the other, suggesting that integration of withdrawal and addition were performed in parallel. The time course of the reweighting process to reach the new steady-state was also shorter on withdrawal than addition. The effects of different sensory inputs on posture stabilization illustrate the operation of a time-consuming, possibly supraspinal process that integrates and fuses modalities for accurate balance control. This study also shows the facilitatory interaction of visual and haptic inputs in integration and reweighting of stance-stabilizing inputs.

maintaining equilibrium during upright stance is favored by the integration of vestibular, proprioceptive, visual, and haptic sensory inputs (Goodworth and Peterka 2009; Mergner et al. 2002; Peterka 2002; Peterka and Loughlin 2004), which help orchestrate postural muscle activity and produce appropriate corrective torques (Saffer et al. 2008; Sozzi et al. 2013). To cope with daily life environmental and bodily changes, the brain continuously and selectively reweights the fluctuating sensory inputs (Black et al. 1988; Goodworth et al. 2014; Nashner et al. 1982). The integration of sensory input is a nonlinear process (Jeka et al. 2000; Mergner et al. 2003; Teasdale et al. 1991; van der Kooij et al. 2001; van der Kooij and Peterka 2011) whereby the weight given to each sensory input depends on the availability, intensity, and resolution of the other afferent signals (Carver et al. 2006; Hwang et al. 2014; Peterka and Benolken 1995; Peterka 2002). Recent research has evidenced complex dynamic intermodality reweighting so that in particular situations one input can be downweighted while another upweighted (Assländer and Peterka 2014; Assländer et al. 2015; Polastri et al. 2012). This process allows the brain to deal with potential incongruities between the different sensory inputs.

During upright stance, vision and touch both collect information about the outside world that are incorporated in the body reference frame and reduce sway by enhancing body stabilization (Jeka et al. 1997; Nougier et al. 1998; Soechting and Berthoz 1979). For instance, when vision is not available, lightly touching a solid surface is capable of restoring balance (Clapp and Wing 1999; Dickstein et al. 2003; Forero and Misiaszek 2013; Jeka and Lackner 1994; Rogers et al. 2001). Oie et al. (2002) reported the existence of intermodality dependence between vision and touch during standing. They exposed subjects to sinusoidally moving visual and/or haptic inputs and measured sway, which allowed them to calculate gains associated with vision and touch. Their results showed that increasing the amplitude of touch-surface motion resulted in significant increment in gain to visual motion, indicating a strong interaction between visual and haptic processing during stance.

Another problem in addressing the question of sensorimotor integration is related to the time necessary for the brain to integrate new sensory information and make use of it for sway regulation. Measuring sway level and its time course when different combinations of sensory information are added or withdrawn should provide hints about processing time of and weight given to each sensory modality. Rabin et al. (2006) and Sozzi et al. (2011, 2012) found that a finite period of time was required for the brain to incorporate and process sensory changes when vision or touch (henceforth defined as haptic; see Fernandes and Albuquerque 2012 for a recent review) were provided or withdrawn. That time interval was defined as the period after the sensory shift, during which the level of body sway did not yet change despite the newly added sensory information. These latencies from the shift in sensory state to the beginning of balance stabilization were longer for haptic integration (with eyes closed) with respect to visual integration (from eyes closed to eyes open), suggesting a greater difficulty in resolving the haptic integration problem (Sozzi et al. 2012). Latencies were also slightly shorter when the stabilizing input (visual or haptic) was withdrawn with respect to when it was added. Next, sway amplitude began decreasing or increasing exponentially, with a time constant of about 0.5–1.5 s to reach steady-state, a time period during which the reweighting process (accompanying the balance adaptation to the new sensory state) would occur.

Thus, to understand better how the brain integrates both vision and touch for balance stabilization, we measured the time required to incorporate new sensory information in the case of concurrent addition or concurrent withdrawal of vision and touch. The obtained latencies were compared with those required to integrate vision “alone” or touch “alone.” We hypothesized that the concurrent addition of both sensory inputs would enhance the computation required to integrate the new sensory inflow and diminish both latency to the initial change in sway and time course to reach the new steady-state. Our hypothesis would be verified if the latencies following addition of vision and touch simultaneously were shorter than those obtained for vision alone and touch alone. Alternatively, longer latencies would express a computational integration load due to a conflict between visual and haptic processes, and longer time courses to steady-state would express a burden for reweighting. We also investigated whether withdrawal of both vision and touch simultaneously, compelling the body to rely on proprioception and vestibular input, leads to a further reduction of the latencies to increase in sway.

In the same line, we investigated the effects of substituting vision with touch and vice versa to understand how the brain deals with the problem of having one sensory input exchanged with a different sensory input that provides a similar type of stabilizing information. We postulated that when a sensory input is suddenly replaced with another, the brain behaves first as if the former input has been withdrawn. During the “integration period,” the brain then realizes that a different stabilizing input is present and thus starts assigning a weight to it to reduce the level of oscillation accordingly.

METHODS

Participants.

Eleven (4 men and 7 women) healthy subjects participated in the study. Their mean age, mass, and height were 27.8 yr (range 21–41 yr), 62.1 kg (range 49–81 kg), and 1.69 m (range 1.5–1.8 m), respectively. All subjects provided written, informed consent to the experiment as conformed to the Declaration of Helsinki. The local review board approved the research protocol.

Tasks and procedures.

The experiments took place in a normally lit room. Subjects stood on a force platform (Kistler 9286BA) with feet in tandem position (Fig. 1). The contour of the feet was drawn on the platform so that the same feet position was reproduced in subsequent days. Each subject performed four experimental conditions, each in a different day. The order of the conditions was randomized across subjects. Each condition involved addition (In) or subtraction (Out) of a new sensory information during the standing period: 1) vision (V) was added or withdrawn; 2) light touch (T) was added or withdrawn while eyes were closed; 3) vision and touch were added or withdrawn simultaneously (V&T); and 4) vision was replaced with touch or vice versa (V↔T). In the V↔T condition, an extra 1-min-long control trial was performed by the subjects in the absence of vision and touch. This was done to verify that the level of center of pressure (CoP) sway in the absence of vision and touch (control condition) remained largely unchanged in all days in which the different conditions were performed. Under all conditions, vision and/or touch were added or withdrawn in a passive mode without any deliberate action by the subjects.

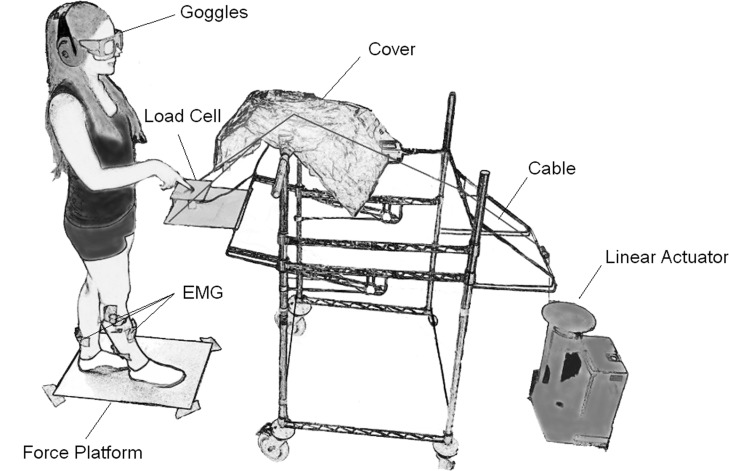
Fig. 1.

Experimental setup. This figure shows a subject standing in the tandem posture on the force platform over which the contour of the feet has been marked. The subject's state of vision was controlled via electronic goggles. A pulley system activated by a linear actuator pulling on a transparent cord (colored black here) allowed the experimenter to lower or raise a load cell, on which a wooden board (15 × 12 cm) was rigidly attached, to produce or withdraw haptic input passively with the index finger. The cord was hidden from the field of view of the subject by covering it with a tissue. Earmuffs were worn at all time to prevent the subjects from hearing any acoustic cues during the experiment. EMG, electromyogram.

All conditions consisted of 60 trials lasting 40 s each. In each trial, a shift in sensory state occurred randomly during a time period ranging from 17 to 22 s with respect to the beginning of the trial. Randomization was adopted to minimize the risk of subjects anticipating the sensory-state shifts and using prediction capabilities to compensate for feedback time delay (Cenciarini and Peterka 2006). Subjects rested following five consecutive trials for as long as they required (normally less than a couple of minutes). Subjects wore earplugs and earmuffs at all times to mask any acoustic cue hinting at the occurrence of the sensory shift (Fig. 1).

Subjects kept their eyes open all of the time. The shift in visual state was achieved passively by means of electronically controlled shutter goggles (PLATO Visual Occlusion Spectacles; Translucent Technologies, Toronto, Ontario, Canada). The goggles allowed subjects to wear corrective eyeglasses if required. A transistor-transistor logic (TTL) signal was used to control the lenses. When eyes were opened, subjects could see the patterned wall of the laboratory at ∼6-m distance. The laboratory was well-illuminated, and luminosity levels were comparable between sessions. The response time to the voltage transient is approximately 1 ms to open and 3–5 ms to close (manufacturer's specification). In the condition where touch was added and withdrawn, subjects kept their right elbow at an angle of ∼120°, the hand in a prone position, and the index finger slightly extended at the metacarpophalangeal joint so that it resulted ∼45° inclined from the vertical. In this way, contact with the touch pad occurred with the palmar surface of the fingertip. The touch pad (15 × 12 cm) was instrumented with a load cell that measured compression forces. The pad was raised slowly by means of a custom-made pulley system attached to a linear actuator (average upward speed = 6 cm/s) to touch the index finger or was lowered quickly (average downward speed = 14 cm/s) so as to leave the finger without support (Fig. 1). The time for the fingertip force to reach plateau or to fall to 0 for addition and withdrawal of touch, respectively, was estimated for each subject by fitting an exponential function to the load cell mean traces. The average time constants of the fitted functions were 0.07 ± 0.02 s for addition and 0.02 ± 0.01 s for withdrawal. Subjects were not specifically instructed to maintain hand position fixed after touching the pad but were allowed to move the index finger on the pad surface if they felt so. The system produced an audible signal when the compression force exerted by the subjects on the touch pad exceeded 1 N to avoid mechanical body support (Kouzaki and Masani 2008). When this occurred, the trial was rejected and a new trial was recorded.

The output signals of the goggles and the load cell were passed in real-time to a computer that in turn controlled both the actuator and the state of the goggles via an analog-to-digital (A/D) board (National Instruments, Austin, TX). The computer was programmed so that the events of touching and releasing the pad could be detected online. The moment at which the subject touched the pad was set when the load cell signal exceeded a force threshold level of 0.15 N with respect to baseline. Exceeding this threshold also blocked the linear actuator to halt the movement of the load cell in ∼30 ms following contact with the finger. The instant of finger release was determined as the moment at which the level of recorded force dropped below a threshold of 0.15 N with respect to the last recorded level before lowering of the load cell. In the V&T and V↔T conditions, the detection of the touch and release of the finger with the load cell triggered the change of state in the TTL signal that commanded the goggles (Fig. 2). Across trials, the actual mean error between touch/release events and triggering of the goggles proved to be 21.4 ± 9.2 ms caused by hardware and software inaccuracies. In the T condition, the same threshold value of 0.15 N was used to detect the onset and offset of touch.

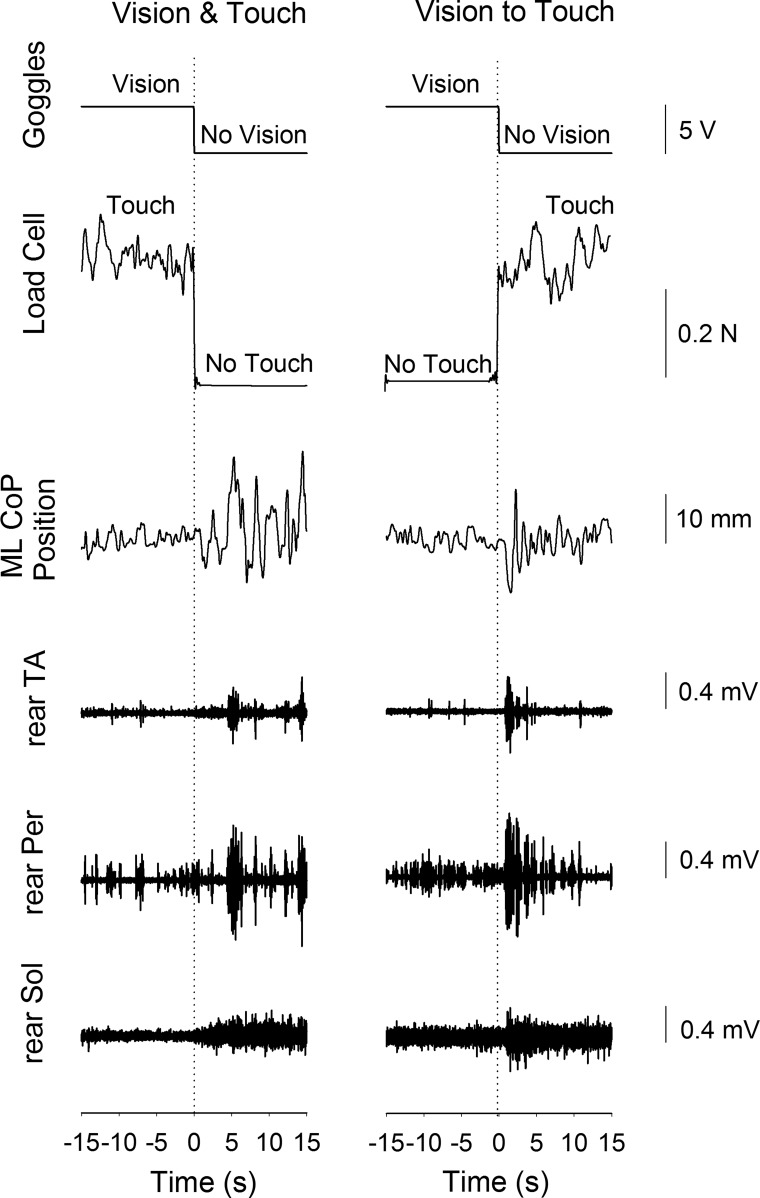
Fig. 2.

Raw recorded signals. This figure illustrates the traces obtained during 1 trial of the Vision & Touch condition (left) and 1 trial of the Vision to Touch condition (right). From top to bottom are the transistor-transistor logic (TTL) signal used to control the goggles, the force measured by the load cell, the mediolateral (ML) position of the center of pressure (CoP), and the activity of tibialis anterior (TA), peroneus longus (Per), and soleus (Sol) of the rear leg, respectively. After a short period following the change in sensory state, ML CoP oscillation and muscle activity increased when vision and touch were withdrawn simultaneously (left) and when vision was replaced with touch (right).

Acquisition of the CoP and EMG signals.

The ground reaction force was measured by the force platform, and the position of the CoP was computed. Bipolar electrodes were employed to record the electromyographic (EMG) activity of tibialis anterior (TA), peroneus longus (Per), and soleus (Sol) of both legs. Preparation of the skin and positioning of the electrodes was performed according to the SENIAM protocol (Merletti and Hermens 2000). The distance between the recording leads was 1.5 cm. The FREEEMG system was employed to record the EMG wirelessly (BTS Bioengineering, Milan, Italy) at a sampling frequency of 1,000 Hz. The CoP position, TTL, and load cell signals were all acquired at a frequency of 560 Hz. All signals were acquired synchronously and saved on the SMART-D system (BTS Bioengineering) for offline analysis using a custom-made MATLAB program (MathWorks, Natick, MA). An example of the raw recorded signals is provided in Fig. 2.

Calculation of mean level of CoP oscillation and EMG activity.

The mediolateral (ML) CoP position signal was band-pass filtered between 0.05 and 5 Hz (Yamamoto et al. 2015) with a no-lag, third-order Butterworth filter and then rectified. EMG signals were rectified and low-pass filtered at a cutoff frequency of 5 Hz (Sozzi et al. 2011) with a no-lag, third-order Butterworth filter. For each subject, CoP oscillation levels and EMG levels were calculated by averaging the respective filtered and rectified signals of all trials collected in a given condition (n = 60; Fig. 3, top). We then calculated the mean levels before and after the instant of the change in sensory state (set as t = 0 s). The level before t = 0 s (L_pre) was calculated as the mean level in a time window from −10 to 0 s, and the mean level after the sensory shift (L_post) was calculated as the mean level from 5 to 15 s. The time windows in which the levels were calculated were selected to ensure that levels referred to steady-state value and were not affected by transient variations that occurred following the shift in sensory state.

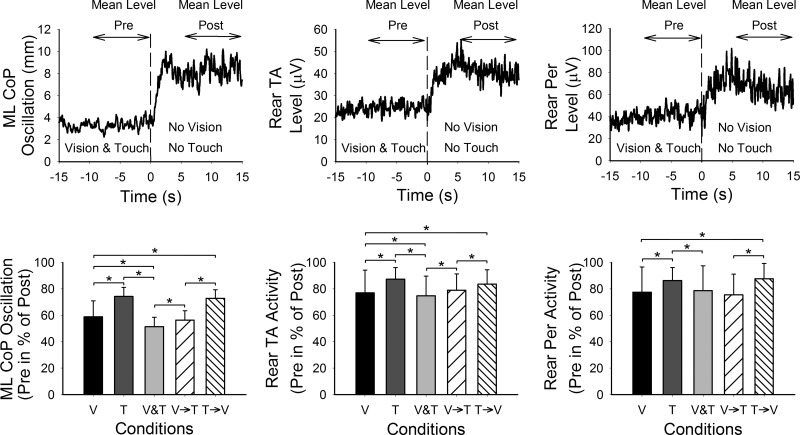
Fig. 3.

Mean levels of CoP oscillation and muscle activity. Top panels show the mean levels (n = 60 trials) of ML CoP oscillation and rear TA and Per (from left to right) of 1 subject during Vision & Touch condition. The mean values were calculated in the time windows indicated by the arrows above the curves. The mean levels in the presence of stabilizing input (Mean Level Pre) were then calculated in percentage of the maximum levels in the absence of vision and touch (Mean Level Post). The bars of the bottom panels show the grand mean plus SD of the levels of CoP oscillation and rear TA and Per activity when vision “alone” (V), touch “alone” (T), vision and touch (V&T), vision to touch (V→T), and touch to vision (T→V) were present. The mean levels of CoP oscillation and muscle activity were reduced in the presence of sensory input. The lowest CoP oscillations were obtained in V&T, and the highest in T. The mean levels of CoP oscillation of V and T conditions are comparable with those obtained during the V→T and T→V conditions, respectively. The asterisks indicate significant differences.

The level of AP CoP oscillation did not enter the analysis since it is known to be nonsignificantly reduced by the presence of touch and/or vision (Sozzi et al. 2012). This is because tandem stance constrains CoP movements in the frontal plane while necessarily increasing ML instability. Furthermore, the reduction in EMG activity due to the presence of vision and/or touch of the front-leg TA and Per muscles was modest with respect to the reduction in the activity of the rear-leg muscles due to the dominant role of the rear leg in controlling equilibrium during tandem stance (Jonsson et al. 2005; Sozzi et al. 2013) and did not enter the analysis. Sol muscle activity (either leg) did not enter the analysis, either, since reduction in Sol activity in the presence of the stabilizing sensory input is elusive in both front- and rear-leg Sol muscles, likely because Sol mainly exerts a body-supporting role whereas ML balance at the ankle level is mainly controlled by TA and Per (Sozzi et al. 2013). Therefore, only ML CoP oscillation and EMG activity of the rear-leg TA and Per have been analyzed in this study.

To compare the effects of the addition or withdrawal of the sensory information recorded in different days, the reduction of sway and EMG levels during the steady-state when vision, touch, or both simultaneously were present has been reported as a percentage of the sway levels obtained in the same day when vision and touch were absent (yielding the highest sway level). This allowed us to avoid problems related to possible minor differences in feet position and impedance levels of the surface electrodes that might be present across the sessions performed in different days.

Estimation of the time period from the sensory-state shift to the onset of changes in sway and muscle activity and of the time to reach the new steady-state.

Following withdrawal or addition of vision or touch, an integration time period is observed before sway and EMG level start varying exponentially until reaching the new steady-state (Sozzi et al. 2011, 2012). To estimate latency and time to reach steady-state, a custom-made fitting algorithm similar to the one used by Assländer and Peterka (2014) was employed. The algorithm fits a time-shifting function composed of a flat line (constant value over time) followed by an exponential function (see Eqs. 1 and 2) to the traces of sway or EMG levels (actually, the averaged traces from all trials).

$$y\left(t\right)=a+b\left(1-e^{\frac{-\left(t-\Delta t\right)}{\hspace{0.17em}\tau }}\right)\hspace{0.17em}\text{for}\hspace{0.17em}\Delta t\hspace{0.17em}\hspace{0.17em}<t<13\left(s\right)$$ (1)

$$y\left(t\right)=a\text{for}\hspace{0.17em}0<t<\Delta t\hspace{0.17em}\left(s\right).$$ (2)

The time of the change in sensory state was set as t = 0 s. The initial values of a and b were set so that the lower and upper bounds of the exponential function would coincide with L_pre and L_post (see Calculation of mean level of CoP oscillation and EMG activity), respectively. The initial value of the time constant τ was set visually. The fitting process employed the least-squares minimization procedure based on the “trust-region-reflective” algorithm provided by MATLAB. The model was allowed to fit a, b, Δt, and τ. Following the fitting procedure, the resulting time shift (or Δt in the equations) was considered to be the duration of the integration time period (henceforth latency), whereas the subsequent τ was the time employed to reach 63% or to fall to 37% of maximum after withdrawal or addition of stabilizing information, respectively. Hence, the time required to reach the plateau of the new steady-state would be about t_steady-state = Δt + 3τ, since 3τ corresponds to ∼95% of the change.

Statistics.

The effect of vision (V), touch (T), and V&T with respect to no vision and no touch on the levels of ML CoP oscillation and rear TA and Per activity was assessed by three separate 2 (presence/absence) × 5 (V, T, V&T, V→T, and T→V) repeated-measures ANOVA. The effects of the presence of the different stabilizing inputs (V, T, V&T, V→T, and T→V) on the reduction in the steady-state levels of oscillation and muscle activity were assessed by three separate repeated-measures ANOVAs. One 2 (withdrawal/addition) × 3 (V, T, and V&T) repeated-measures ANOVA was employed to assess the effect of withdrawal versus addition of sensory information from different modalities on the latencies to change in ML CoP oscillation. One 2 (withdrawal/replace) × 2 (vision and touch) repeated-measures ANOVA was used to compare the latencies of ML CoP oscillation obtained on withdrawal with those on replacement (withdrawal of V and T compared with V→T and T→V). Pearson's method was used to assess the linear relationship between the latencies of rear TA and rear Per and the latencies of ML CoP oscillation. Afterward, separate Student's t-tests compared the β-parameter of the slope of the corresponding best-fit line to the identity line [t = (β − 1)/SE β]. The effect of the level of oscillation before the sensory shift on the latency of the change in CoP oscillation during withdrawal and addition was assessed by a 2 (low/high oscillation level) × 2 (withdrawal/addition) × 3 (V, T, and V&T) repeated-measures ANOVA. A 2 (withdrawal/addition) × 3 (V, T, and V&T) repeated-measures ANOVA was employed to assess the effect of the different sensory conditions and the effect of withdrawal versus addition of sensory information on the time constants to reach the new state. The paired Student's t-test was used to assess differences between the time constants measured during replacement of vision with touch and substitution of touch with vision. All post hoc analyses were made by the Fisher least significant difference test. The level of significance in all tests was set to P < 0.05. The software Statistica (StatSoft, Tulsa, OK) was used.

RESULTS

Steady-state: level of ML-CoP oscillation and EMG activity with or without vision or touch.

The level of ML CoP oscillation and rear-leg TA and rear-leg Per activity was reduced in the presence of stabilizing sensory input, vision alone (V), touch alone (T), or both (V&T). In each condition, the mean levels of oscillation and EMG activity of TA and Per muscles were significantly smaller when vision and/or touch was present than absent [ML CoP: F(4,40) = 17.5, P < 0.0001; rear TA: F(4,40) = 5.2, P < 0.0001; rear Per: F(4,40) = 3.6, P < 0.01]. ANOVA showed that the mean oscillation level in the absence of both vision and touch remained similar in the four conditions V, T, V&T, and V↔T, regardless that each condition was performed on a different day [F(3,30) = 0.65, P = 0.58]. Therefore, since sway level in the absence of vision and touch was similar in all four conditions, we calculated the reduction of oscillation level and EMG activity in the presence of V, T, or V&T as a percentage of the mean levels obtained in the absence of vision and touch. The grand means and SD of the CoP oscillations and EMG of rear-leg TA and Per in the presence of V, T, or V&T in percent of absent vision and touch are shown in Fig. 3. The sensory inputs had a significantly different effect on the level of CoP oscillation and TA and Per activity [ML CoP: F(4,40) = 11.4, P < 0.0001; rear TA: F(4,40) = 2.8, P < 0.05; rear Per: F(4,40) = 2.9, P < 0.05]. Post hoc test showed that the level of oscillation and EMG activity was the highest in the T condition (ML CoP: P < 0.01; rear TA: P < 0.05; rear Per: P < 0.05). The levels of CoP ML oscillation and TA activity were lowest when V and T were present simultaneously (ML CoP: P < 0.05; rear TA: P < 0.05). Moreover, the mean levels of CoP oscillation and EMG activity in the V condition was similar to that in the V condition of V→T (ML CoP: P = 0.4; rear TA: P = 0.14; rear Per: P = 0.21). The mean level of CoP oscillation and EMG activity in the T condition was similar to that in the T condition of T→V (ML CoP: P = 0.3; rear TA: P = 0.3; rear Per: P = 0.26). It is to be noted that, with respect to the level measured in the absence of vision and touch, the reduction in the mean level of CoP oscillation V&T (48.6%) was smaller than the algebraic sum of the effects of V and T [41.1% (V) + 25.8% (T) = 66.9%].

We also checked whether performing 60 tandem-stance trials per condition caused modifications in the level of oscillation with the repetition of the trials. We did so by dividing the trials into 2 groups composed of the 1st 30 and last 30 trials of each subject and measured the mean level of CoP oscillation in both groups (not shown in Fig. 3). There was no difference between the 2 sets in each condition [Student's t-test: P = 0.17 (V); P = 0.34 (T); P = 0.93 (V&T); P = 0.97 (V↔T)]. Thus we concluded that repetition of the trials did not affect sway level, likely because small clusters of successive trials had been intermingled with adequate rest periods.

Latencies of the changes in ML CoP oscillations and muscle activity following addition or withdrawal of stabilizing information.

Figure 4 shows the mean trace of CoP level of one subject following withdrawal (A) and addition (B) of vision. The same plots also show the fitted exponential functions in gray line. The latencies measured for each subject and condition are presented in Fig. 4C. The grand mean and standard deviation of the latencies to the changes of CoP oscillation following addition and withdrawal of V, T, or V&T are provided in Fig. 4D. ANOVA showed a significant effect of sensory modality on the latencies of CoP oscillation [F(2,20) = 42.9, P < 0.0001] and a significantly shorter latency for withdrawal than addition of sensory input [F(1,10) = 23.3, P < 0.001]. A significant interaction between modality and withdrawal/addition was also present [F(2,20) = 8.1, P < 0.01]. Post hoc results confirmed that following addition the longest latencies were obtained when T was provided compared with V and V&T (P < 0.0001 for both comparisons). The shortest latencies were obtained when V and T were added simultaneously compared with V or T (P < 0.0001 for both comparisons). Following withdrawal, relatively longer latencies were obtained when T was removed (P < 0.05 with respect to V; P < 0.001 with respect to V&T). The mean latency following removal of V&T was also shorter than that following withdrawal of V, but the difference did not reach significance (P = 0.07).

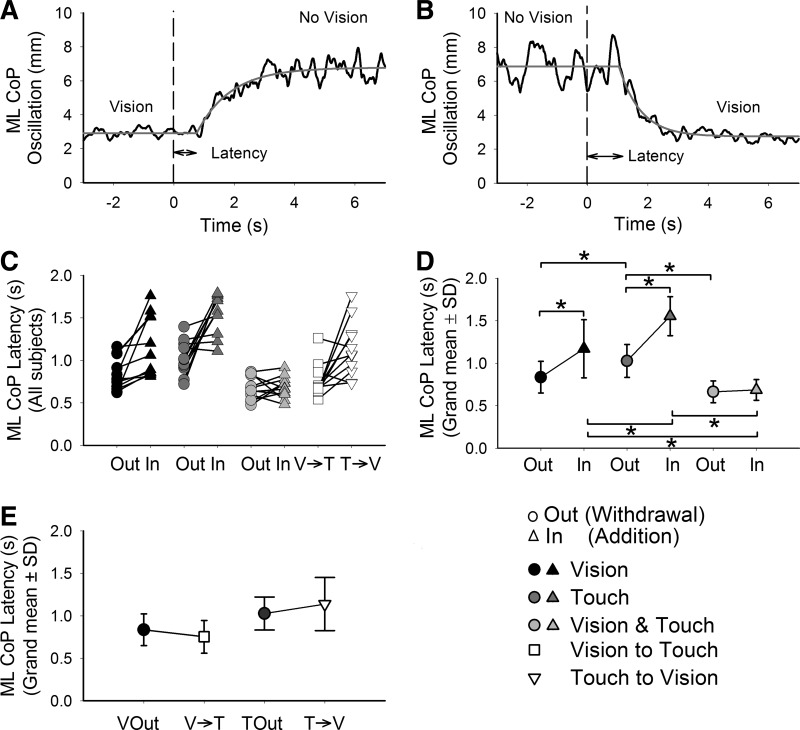
Fig. 4.

Latencies of CoP oscillation following the change in sensory state. The upper panels show the mean curves of CoP oscillation of a representative subject during withdrawal (A) and addition (B) of V (black; at t = 0) and the fitted-exponential function (gray). The segments between the arrowheads under the curves indicate the latencies. In C, the latencies calculated for the CoP oscillation of each subject in all 4 conditions are presented. The grand mean and SD of the latencies in sway for the V, T, and V&T conditions are provided in D. In the labels of the abscissae of C and D, “Out” is used to indicate withdrawal and “In” addition (the symbol key is at the bottom right). The latencies were shorter on withdrawal than addition. They were longest following addition of T and shortest following addition of V&T. In E, the grand mean and SD of the latencies following withdrawal of V, withdrawal of T, and the replacement of V with T and vice versa are provided. The asterisks indicate significant differences.

In Fig. 4E, the grand means and standard deviations of the latencies measured when vision was withdrawn are plotted next to those measured when vision was suddenly replaced with touch (left). On the right, the latencies following withdrawal of touch are plotted next to those measured when touch was suddenly replaced with vision. ANOVA showed no difference in the latencies between withdrawal and replacement [F(1,10) = 0.04, P = 0.85]. The effect of modality was reiterated [F(1,10) = 10.7, P < 0.01; touch longer than vision]. There was no significant interaction between vision/touch and withdrawal/replacement [F(1,10) = 3.7, P = 0.08].

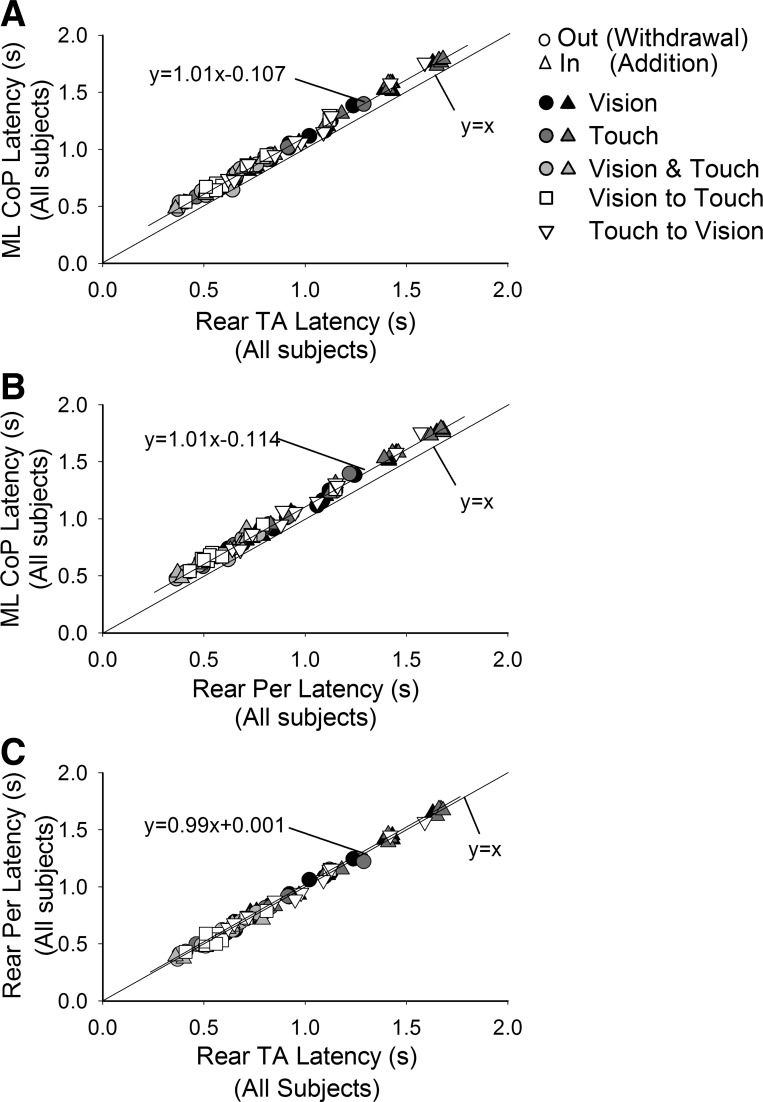
We also wanted to assess that the latency of the changes in leg muscle activity preceded those of the CoP, as already found elsewhere (Sozzi et al. 2011, 2012), and to estimate its extent. The delay between changes in muscle activity and CoP should be compatible with the electromechanical delay from the increase in EMG activity to increase of sway level recorded by the force platform. The latencies of the CoP oscillation are plotted for each subject and condition in Fig. 5, A and B, as a function of the latencies of TA and Per EMG activity. The t-test on the angular coefficient of the best-fit line (all data points collapsed) showed that the slope of the distributions of the data points of TA and Per were parallel to the identity line (P > 0.05 for both plots) and just placed above it. Notably, this was also true for each condition analyzed separately (P > 0.05 for all comparisons, data not shown). The mean latencies of TA and Per preceded the latencies in sway by 114 ± 13.4 and 120 ± 14.7 ms (P > 0.05), respectively (average value of all individual differences between muscle and sway latencies). In Fig. 5C, the latencies of Per and TA were plotted against each other. The slope of the distribution of the data points was not different from the identity line (P > 0.05), and the intercept was negligible, showing that the mean change in latency for both muscles was almost coincident.

Fig. 5.

Latencies of change in muscle activity following change in sensory state. Latencies of CoP oscillation levels are plotted against the latencies of rear TA (A) and rear Per (B) EMG for the different conditions (symbols as in Fig. 4), and the best-fit line is drawn. The identity line (y = x) is also indicated. Changes in muscle activity always preceded those of sway by ∼110 ms. In C, latencies of rear Per are plotted against those of rear TA. The data points sit on the identity line indicating equal mean latency between muscles for each condition.

Entity of CoP oscillation levels before sensory shift and latencies of the change in oscillation.

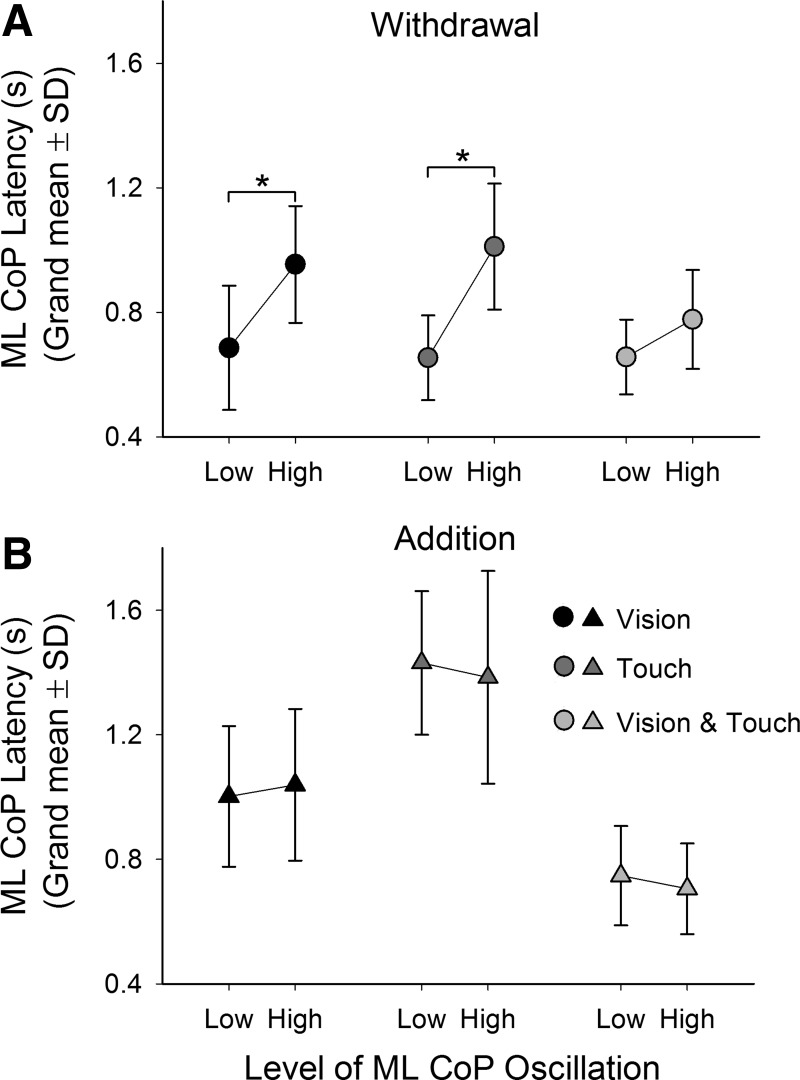
We also investigated whether the integration latency could be affected by the level of CoP oscillation before withdrawal or addition of stabilizing information. To do so, we arbitrarily divided the 60 trials performed by each subject into 2 sets of 30 trials for each sensory condition. The 1st set contained the trials having the lowest-level CoP oscillation, whereas the 2nd set contained the trials with the highest level. Incidentally (see Steady-state: level of ML-CoP oscillation and EMG activity with or without vision or touch), the higher-level oscillation trials did not correspond to the ones last performed. The mean latencies obtained for the low- and high-oscillation data sets (Low and High, respectively, in the figure) are shown in Fig. 6 for both withdrawal and addition and for all sensory conditions.

Fig. 6.

Latency of change in CoP oscillation as a function of the oscillation level before sensory shift. All trials performed by each subject have been divided into 2 sets, 1 composed of low-level oscillation trials, the other of high-level oscillation trials. The grand means and SD of the latencies of each set in each condition (V, black; T, dark gray; V&T, light gray) are provided during withdrawal (A) and addition (B). Following withdrawal, the latencies observed in each condition were longer in the high-oscillation level trials. The same effect did not occur for addition. The asterisks indicate significant differences.

In general, ANOVA showed a main effect of oscillation level [low/high; F(1,10) = 31.1, P < 0.001], withdrawal/addition [F(1,10) = 30.5, P < 0.001], and sensory modality [V, T, and V&T; F(2,20) = 26.9, P < 0.001]. ANOVA also showed an interaction between level of oscillation (low/high) and withdrawal/addition [F(1,10) = 23.8, P < 0.001] and an interaction between withdrawal/addition and modality [F(2,20) = 12, P < 0.001]. No interaction between level of oscillation (low/high) and modality was found [F(2,20) = 1.98, P = 0.16]. Post hoc analysis showed that the levels of oscillation had no effect on the latencies following addition of stabilizing information (V: P = 0.6; T: P = 0.52; V&T: P = 0.57). However, following withdrawal of V or T, the latencies increased when the oscillation level was high with respect to low (V: P < 0.001; T: P < 0.001). The mean latency following removal of V&T was also shorter in the low-oscillation group with respect to the high-oscillation group, but the difference did not reach significance (P = 0.10).

Time required to achieve steady-state following shifts in sensory state.

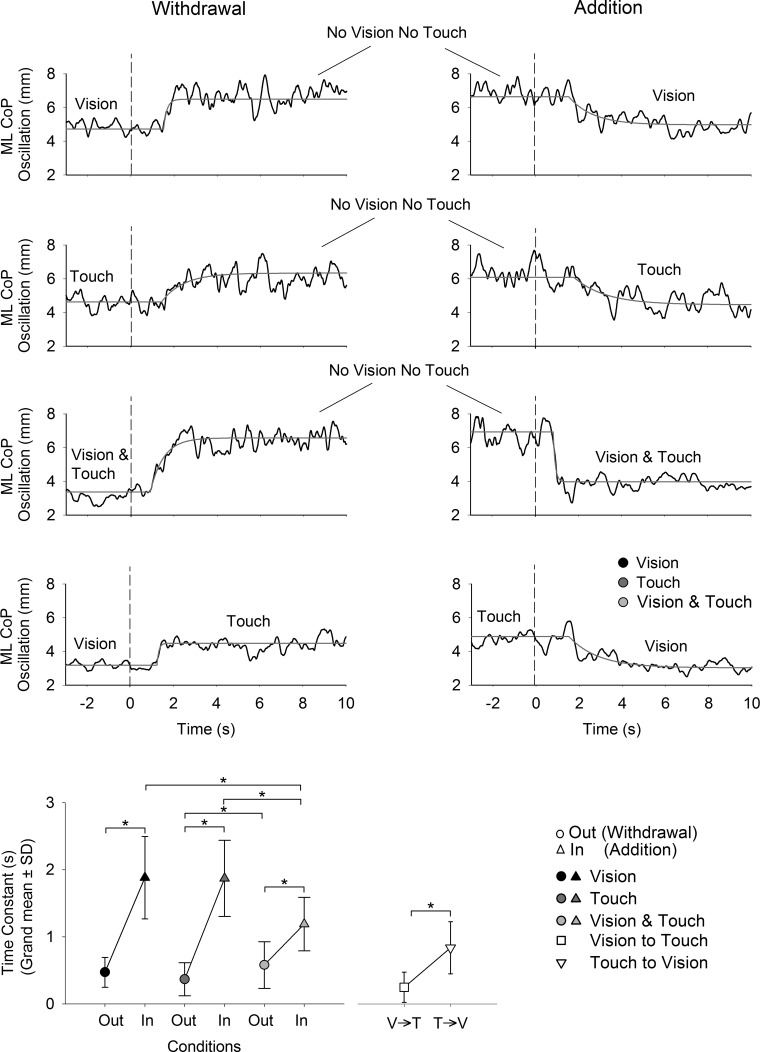
Following the time interval to the estimated onset of changes in sway in response to the sensory shift (the integration time), the level of sway increased or decreased depending on whether the stabilizing input was withdrawn or added, respectively. The transient phases of CoP oscillation levels to reaching the new steady-state (the reweighting time) were fitted with an exponential function for each subject in each condition. The time course of the CoP oscillation levels and the fitted exponential functions are reported for one subject in all conditions in the upper part of Fig. 7. The grand mean and standard deviation of the time constant for the conditions V, T, V&T, and V↔T are provided in the bottom graph of the figure. ANOVA showed effects on the time constants of sensory modality [F(2,20) = 24.3, P < 0.0001] and withdrawal/addition [F(1,10) = 75.2, P < 0.0001]. An interaction between sensory condition (V, T, or V&T) and withdrawal/addition was also found [F(2,20) = 9.7, P < 0.001]. Post hoc analysis confirmed that the time constants were always shorter on withdrawal than addition (P < 0.001 for all comparisons) and shorter when vision and touch were added simultaneously with respect to the addition of V and T (P < 0.0001 for both V&T vs. V and V&T vs. T). In the V↔T condition, the time constants were short, reflecting the rapid change in CoP oscillations when substituting visual and haptic information with one another. Student's t-test showed that the time constants when vision was replaced with touch (i.e., when going from a lower to a higher level of sway) are shorter (P < 0.01) than when T was substituted with V (when going from a higher to a lower level of sway). We estimated the time at which steady-state was effectively reached as the sum of the integration time with the reweighting time or, more precisely, t_steady-state = Δt + 3τ. The grand means and standard deviation of the time to reach steady-state estimated for the conditions V, T, and V&T are reported in Table 1. ANOVA showed significant effects of withdrawal/addition [F(1,10) = 91.4, P < 0.0001] and sensory condition [F(2,20) = 10.4, P < 0.001] on the time to reach steady-state. The interaction between withdrawal/addition and sensory condition was significant [F(2,20) = 19.8, P < 0.001]. Following withdrawal, steady-state was reached at comparable intervals for the three conditions (P > 0.05 for all comparisons). Following addition, steady-state was reached always later than on withdrawal (P < 0.001 for all comparisons). Furthermore, steady-state was reached significantly earlier when V&T was added concurrently with respect to the addition of V and T (P < 0.001 for both comparisons).

Fig. 7.

Time constant of the recovery to steady-state following the sensory shift. Upper panels show the mean curves of the CoP oscillation (black) and the fitted exponential function (gray) in all conditions. The grand mean and SD for the time constant calculated for all subjects in each condition are provided in the bottom graph. The times constants were generally shorter on withdrawal than addition of V and/or T. The time constants were also shorter following addition of V and T simultaneously with respect to the addition of V alone and T alone. The asterisks indicate significant differences.

Table 1.

Time to reach steady-state following the sensory shift

	Withdrawal, s	Addition, s
V	2.2 ± 0.8	6.8 ± 2.1
T	1.8 ± 0.8	7.2 ± 1.8
V&T	2.3 ± 0.9	4.1 ± 1.4*

Values are grand means ± SD of the time to reach steady-state calculated as t_steady-state = Δt + 3τ following addition and withdrawal of vision (V), touch (T), and vision and touch (V&T).

^*Significant difference.

DISCUSSION

The brain continuously incorporates and reweights inputs from vestibular, proprioceptive, visual, and, when applicable, haptic input to maintain equilibrium. An important feature of the human postural control system is the ability to alter its source of sensory orientation cues as environmental conditions change (Assländer and Peterka 2014; Assländer et al. 2015; Hwang et al. 2014; Peterka and Loughlin 2004) or when balance problems ensue, connected to ailments of different nature (Jeka et al. 1996; Kanekar et al. 2013; Zwergal et al. 2012). When a certain sensory information becomes unreliable, such as a rapid shift in the visual flow, vision is quickly downweighted while proprioception is upweighted to reduce the risk of falling (Carver et al. 2006; Jeka et al. 2008; Mahboobin et al. 2009). Inter- and intramodality reweighting schemes may be more complicated than those suggested by current adaptive models of human postural control and should incorporate dynamic and temporal aspects (Polastri et al. 2012). For instance, fast processing of the haptic cues seems to be favored, on the long term, in blind subjects (Schieppati et al. 2014), revealing the potential role of brain plasticity in exploiting haptic inputs for stabilization (Kalaska 1994; Lingnau et al. 2014). Furthermore, the responsiveness to a proprioceptive disturbing input does not immediately change on adding or subtracting vision, but a finite time period must elapse before the postural set defined by vision is fully established (Bove et al. 2009). Vestibular input can also be strongly and selectively modulated by proprioception, and this effect may well outlast the duration of the interactive stimuli (Pettorossi and Schieppati 2014; Pettorossi et al. 2015).

A relatively poorly exploited protocol for tackling the multisensory integration problem is to measure the time period required to observe variations in sway level (latency) following a sudden shift in the sensory state for different sensory modalities (Honeine and Schieppati 2014; Sozzi et al. 2011, 2012). In the present study, subjects stood in tandem stance, which challenges balance mainly in the frontal plane (Sarabon et al. 2013; Sozzi et al. 2013). The level of ML CoP oscillation and of the activity of TA and Per were measured together with the latencies of the changes in these signals in response to the shift in the visual (V) or haptic (T) state. Furthermore, we compared these latencies with those observed when vision and touch were withdrawn or added simultaneously (V&T). In addition, we investigated the latencies to changes in sway when vision was replaced with touch and vice versa to get insight into how shifts between similarly stabilizing inputs from different sensory modalities are processed. Furthermore, we briefly addressed a “second” stage in the process of incorporation of the stabilizing information, i.e., the time course to reach the steady-state level of balance after the latency of the initial changes. This second stage refers to the reweighting (increasing or decreasing) of the feedback from the proprioceptive and vestibular input, necessarily modified by the balance response itself related to the new sensory state (Day et al. 2002; Ferrè et al. 2013; Fitzpatrick et al. 1994).

The role of TA and Per in maintaining equilibrium during tandem stance.

On the average, the latencies of TA and Per changes in response to the changes in sensory state were similar and not differentially affected by modality, indicating that leg muscles are recruited or derecruited at similar intervals in connection to changes in body stabilization. The changes in TA and Per activity on addition or withdrawal of the stabilizing information preceded those observed in ML CoP oscillations by about 100–130 ms, indicating that both together contribute in a similar way to the effects observed in the body sway (Loram et al. 2005). This is in line with Sozzi et al. (2013), who showed that during tandem stance TA and Per cooperate to produce corrective torques across the ankle in the frontal plane. The difference in relative latency between the muscle onset and the neuromuscular output measured through the CoP may be somewhat longer than the true electromechanical delay (∼70 ms under quiet stance condition; Vieira et al. 2010) because of the combined confounding effects of the tandem position, the averaging procedure, the estimation algorithm, and the activity of the muscles of the front leg or of other muscles, the contraction of which would also produce effects on the CoP recorded from the force platform. Sol activity did also increase or decrease with TA and Per activity on removing or adding stabilizing information, but its changes were of minor amplitude. Sol would mainly support the body, as also reported under different balance conditions (Schmid et al. 2011), and participate less in balance control in the frontal plane. On the whole, the strong correspondence between leg muscle and sway across sensory conditions and the stable difference between the latencies in muscle activity and sway regardless of the direction of sensory shifts indicate that the descending command connected with balance stabilization or destabilization in response to the shifts in stabilizing sensory input is directed to both TA and Per muscle and that the measures of the latencies in sway largely reflect the timing of the changes in the nervous command (Saffer et al. 2008).

Integration of visual and haptic information.

The levels of CoP oscillation and EMG activity always decrease when the stabilizing information (vision, touch, or both) is suddenly provided with respect to when vision and touch are both absent and gradually reach the steady-state typical for the new available information. The beginning of this response is not simultaneous with the sensory shift. Following withdrawal or addition of vision, touch, or both, a measureable time period elapses before any changes in EMG activity and sway are observed. During this time period, the brain receives, detects, and incorporates the new sensory state, in a process we refer to here as sensorimotor integration. In line with Sozzi et al. (2011, 2012), the time intervals to the onset of changes in sway and EMG in response to the shift in sensory state, i.e., the latencies, are pretty long, particularly for addition, where they amount on average to between 1.2 and 1.5 s for vision alone and touch alone, respectively. This is in keeping with the interpretation that the integration process occurs at supraspinal or cortical level, since the cortex is certainly involved in controlling critical postures (Maki and McIlroy 2007; Nardone et al. 2008; Obata et al. 2014). Imaging studies in humans and single-cell recordings in primates underscore the prominent role of the premotor and parietal cortices (Fattori et al. 2009; Freund 2003; Hagura et al. 2007; Macaluso and Maravita 2010; Sepulcre 2014) and the striato-pallido-thalamo-cortical circuit (Nagy et al. 2006) as sensorimotor interface. Interestingly, functional inactivation of the right hemisphere prefrontal cortex by continuous theta-burst transcranial magnetic stimulation (TMS) modulated the processing of somatosensory evoked potentials during standing with contact to an earth-fixed reference location (Bolton et al. 2011, 2012). Moreover, disruption of left inferior parietal gyrus by 1-Hz repetitive TMS (Johannsen et al. 2015a) altered the time course of sway following unpredictable contact removal (see Johannsen et al. 2015b).

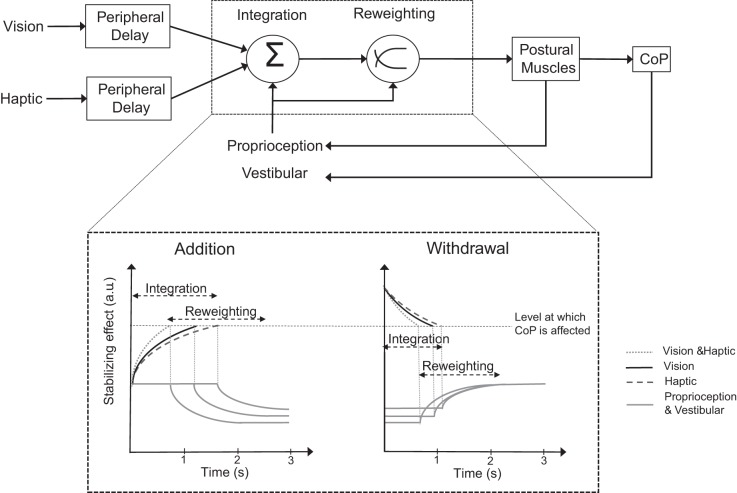
In Fig. 8, we arbitrarily propose a simple model based on our results in the hope of better discussing the main outcome of this study. In the scheme, the integration phase would be followed by the reweighting phase (top), whereby reaching of the new steady-state level of oscillation critically depends on the dynamic treatment of the new input(s) available after the sensory shift (Carver et al. 2006) and on the changing feedback connected to the concurrent change in sway itself. The “level at which CoP is affected” would serve as a threshold for the beginning of the automatic reactions (Mergner 2007), which is kept fixed for simplicity. In the case of addition (bottom, left), the latencies depend on the modality being added. The longest latencies to stabilization onset occur when touch is solely added (dashed curves), hinting at a more complex process in integrating haptic than visual stimuli (solid curves). One possible reason for this longer latency would be that a nonnegligible time period is required before the force of fingertip contact plateaus (see also Rabin et al. 2006), in the assumption that a relatively steady-state in haptic perception is necessary before touch is capable of providing reliable information for maintaining balance. Postural control following addition of touch also requires accurate control of arm and finger (Rabin et al. 2008), which might impose an additional computational cost to the centers coordinating arm and leg posture. However, it should be mentioned that, at least in some subjects, the latency from addition of touch was in the same range as the latency from addition of vision, thereby lessening the importance of the level of exerted force being steady and reliable. An increased attentional cost for haptic with respect to visual input processing (Vuillerme et al. 2006) may be necessary to create the appropriate spatiotopic representation (Azañón et al. 2010), explaining the long processing time required for integrating touch in the control of body sway. Certainly, any additional delay cannot be attributed to a peripheral latency to the cortex, very short and substantially similar for touch and vision (Chiappa 1984; Schieppati and Ducati 1984). Interestingly, in all subjects, the latencies were reduced significantly when vision and touch (dotted curves in the model) were added simultaneously (compared to both vision alone and touch alone). Of note, in this case (vision and touch entering simultaneously), the delay for the force of fingertip contact to reach plateau did not impede to achieve very short latencies to change. We believe that visual and haptic input converge at the integrator level (Ernst and Banks 2002) so that when both are added concurrently the resulting effects promptly reach the threshold (Fig. 8) required to affect the command to the postural muscles. This is in keeping with the conclusion of a recent review paper about the visual enhancement effect for tactile acuity (Eads et al. 2015). Hence, haptic input has the potential to affect balance quickly: however, integration of the stabilizing haptic input, especially in the absence of vision, may be possibly affected by interference with the postural task itself (Lemieux et al. 2014).

Fig. 8.

Simple scheme of the sensorimotor integration and reweighting processes following addition or withdrawal of V and T during standing. Vestibular, proprioceptive, visual, and haptic (T) information are continuously detected and passed to the brain (top). The different modalities converge at an integrator, which incorporates the different stimuli and transforms them into information for maintaining balance. Following sudden shift in visual and/or haptic state, a variable integration time period occurs before any change in sway level is observed (bottom). Following addition of V (solid black), T (dashed), or both simultaneously (dotted), the integration process reaches the threshold (horizontal dashed line) at which the brain modifies the postural muscle activity at different times according to modality. When both V and T are added, the integration time is the shortest. In the case of withdrawal, the “disintegration” process is faster than addition, being the shortest when both V and T are removed. Once the threshold is reached following addition, CoP oscillation starts decreasing exponentially, reflecting the upweighting of the new stabilizing information and the downweighting of the proprioceptive and vestibular inflow (solid gray). Following withdrawal, the remaining proprioceptive and vestibular inputs are upweighted. a.u., Arbitrary units.

Conversely, latencies are in general remarkably and consistently shorter on withdrawal (Fig. 8, bottom, right) than on addition, as if, confronted with the sudden absence of the stabilizing information, the controlling posture of the brain center would entrain a new postural set characterized by large oscillations straightaway. The fast reaction to the withdrawal of the stabilizing information may need no complex intervention by the brain but be produced “by default” at subcortical levels as it happens, for instance, with the startle reaction (Nonnekes et al. 2015; Valls-Solé 2012). It is likely that, when standing in tandem, the sudden withdrawal of the stabilizing information can be particularly “startling” (Sozzi et al. 2012). Subtle differences can be observed, however, since latencies are affected both by the removed modality (just longer for touch than vision) and by the sway level before the sensory shift (see below).

The effect of sway amplitude.

As far as the effect of the sway level present before the shift in sensory state on the latencies to change in sway is concerned, this was expressly considered, since observation of the data hinted at a possible relationship between latency and level of prior body oscillation (slightly longer latencies in the trials in which the sensory withdrawal occurred during larger sway). The outcome of this analysis has shed light on the latency to changes that are connected with the level of oscillation per se and on the effect on the latency due to the stabilizing modality present before withdrawal. Sway was in fact the smallest with vision and touch, medium with vision alone, and largest with touch alone. The presumably larger vestibular and proprioceptive “tonic” inputs related to the current level of sway with touch alone may have interfered with the promptness of changing the postural set.

In principle, this interference might operate either by a disturbing effect (sort of increased entropy; Magnusson et al. 1990) or by furnishing some useful information relevant to the current state of sway (Eikema et al. 2014; Križková and Hlavačka 1994) that is exploited by the brain for sway control. In the former case the latency would increase, and in the latter the integration process would be sped up. As a matter of fact, by dividing into two sets all withdrawal trials, separately for each modality, minor but significant increments in latency were observed for the trials with larger level of sway before the sensory withdrawal. This effect was common to each modality (Day et al. 2002; Hwang et al. 2014; Lackner et al. 2000). Therefore, the larger and noisier vestibular and proprioceptive inputs preceding the sensory shift are, the greater the time required by the brain to integrate the changes. By translating this effect to the different sensory modalities, one would consider that the level of sway before withdrawal is highest when touch is present and lowest when both haptic and visual inputs are provided. Accordingly, the latencies to touch withdrawal were longer than those to withdrawal of vision or V&T, favoring the former of the two possibilities mentioned above, i.e., that higher levels of oscillation are associated with greater sway entropy or noisier vestibular and proprioceptive signals (van der Kooij and Peterka 2011).

Notably, dividing all trials into two groups according to high and low oscillation levels did not influence the latencies in sway following addition of vision and/or touch. Perhaps this is because sway levels are always the highest in the absence of vision and touch, and their perturbing effect saturated. Indeed, the greater vestibular and proprioceptive noise before addition could contribute to the increase in the difficulty of integrating the added inputs resulting in longer latencies for addition with respect to withdrawal.

Integration of touch and vision when these modalities are substituted with each other.

We also investigated the balancing behavior around the time when vision is suddenly withdrawn and substituted with touch and vice versa. We wondered whether any persistence (although vanishing) of the effect of the information from the previous modality could facilitate the integration of another input providing similar stabilizing information. The results, however, do not support this hypothesis. When vision was replaced with touch, the latencies were comparable to those obtained when vision alone was withdrawn altogether. It is possible that once the brain incorporates the removal of vision (mean latency of ∼0.8 s), the level of CoP oscillation starts increasing while the addition of touch is still being independently integrated (haptic addition alone produces a mean latency of ∼1.6 s). When the addition of the haptic input has been completely incorporated, the reweighting process makes the CoP oscillations gradually reach the steady-state level observed in the presence of touch. In an analogous way, when touch is substituted with vision, the latencies are similar to those observed when touch alone is withdrawn. Therefore, no “retention” of the previous state seems to occur and affect the integration timing of the replacing stabilizing information. Furthermore, since the time to incorporate the removal of touch is comparable to that to incorporate the addition of vision (∼1.1 s for both shifts), in T→V the brain seems to process in parallel touch withdrawal and vision addition without interaction between the two processes.

The reweighting phase.

Following the latencies, an exponential rise or decrease in the level of sway is observed depending on withdrawal or addition, respectively. This transient response is referred to as reweighting in the text and in Fig. 6. We believe that during the reweighting process the brain gradually adapts the gain given to each modality, whereby the addition of stabilizing information (be it visual or haptic) would lead to upweighting of the new modality. The conclusions of Carver et al. (2006) were in favor of a downweighting of a disturbing dynamic visual stimulus that suddenly increased and would lead to loss of equilibrium were it not downweighted (as in Oie et al. 2002). A visual stimulus that decreased in amplitude did not pose a threat to upright balance and allowed for slower upweighting of vision without functional consequence. In our case, the (quasi-) static vision and/or touch information enter and stabilize sway. In the reweighting phase, vision and/or touch are likely to be upweighted, whereas the vestibular and proprioceptive inputs would be gradually downweighted [a similar example for haptic effects on stretch reflex excitability is described in Nardone et al. (1990) and Schieppati and Nardone (1995)]. The normal low excitability of the stretch reflex during stance (Baudry and Duchateau 2014; Bove et al. 2006; Chalmers and Knutzen 2002) would in turn contribute to diminish the variations in sway observed after addition of vision or touch.

In the case of withdrawal of vision and haptic input, the brain has to rely solely on proprioceptive and vestibular information while the sway increases: these stabilizing inputs would be upweighted (Bove et al. 2009; Day et al. 2002; De Nunzio et al. 2008; Doumas and Krampe 2010; Rinalduzzi et al. 2011). During the short time period from withdrawal to increase in sway, upweighting of the proprioceptive and vestibular information, which were not manipulated, would start increasing (Assländer et al. 2015; Pasma et al. 2012). Possibly, the fast attainment of the plateau corresponding to the oscillations pertaining to the combined vestibular and proprioceptive feedback depends on the fast reweighting of these two modalities. In passing, recent findings by Eikema et al. (2014; see their Fig. 3) show a longer latency to sway stabilization on adding a visual stimulus, mimicking actual optic flow combined with enhanced proprioceptive stimulation, than to sway increase on withdrawing that stimulation. In the absence of vision and touch, the level of leg muscle activity increases together with corticomotoneural drive (Baudry et al. 2014; Tokuno et al. 2009), possibly in response to the reweighted vestibular and proprioceptive input to supraspinal but not spinal centers for leg muscle control (McIlroy et al. 2003). The time to reach the new plateau after withdrawal of stabilizing information (all conditions collapsed) is about three times shorter (∼2 s) that on adding information (∼6 s). The fast increase in muscle activity and body sway in response to withdrawal seems to instate rapidly a default mode of control, regardless of the nature of the previous stabilizing input, visual, haptic, or both, much as it occurs for the duration of the integration period (latency). The control of balance would be handed over to leg proprioception and partly to the labyrinth (Héroux et al. 2015). We would also note that, owing to their threshold for activation, these inputs would start becoming effective only on the body reaching larger oscillations, and this would occur rapidly, just because the body would very soon attain instability on withdrawing the stabilizing input(s). The default mode of control would be evidently sufficient for preventing falls, since no subject fell over or made a step on withdrawing touch or vision.

Limitations.

A critical point of this investigation is the determination of the latency of the changes in sway. The algorithm used here for estimating the latency, taken from Assländer and Peterka (2014), may introduce errors because it is based on fitting a function to the average trace. We collected a large amount of trials per condition (perhaps close to the largest possible, considering the compliance of the subjects), since the estimation of the latencies based on the mean of a relatively large number of cases increases the reliability of the fitting procedure. Conversely, the smaller the number of the averaged trials was, the less reliable the measurement: this might have made the conclusions on the effect of the level of sway (high vs. low; see 2nd to last paragraph of results) somewhat weaker than expected.

Another point that needs to be taken into consideration is that in the V&T and V↔T condition, for technical reasons, the haptic input was delivered or withdrawn ∼20 ms before the shift in visual input. To account for this error in the touch condition, the same threshold that has been used in V&T and V↔T to trigger the goggles has been used to detect the onset and offset of touch. This allowed to normalize the error in the latencies of touch. In a different context, a study investigating visuotactile integration during cognitive tasks showed that cross-modal congruency effects are consistently observed until the offset between the visual and haptic signal is within a range of ±100 ms (Shore et al. 2006), indicating that our error was probably far from producing effects. It should also be added that no gaps between sensory ins and outs was reported by our subjects during the V&T. All subjects were interviewed after completing the sessions and reported to have perceived both shifts as simultaneous.

Conclusions.

Visual and haptic inputs have been demonstrated to interact strongly in object and motion perception (Pei et al. 2008; Pei and Bensmaia 2014; Yau et al. 2009). For example, the concurrent presence of both visual and haptic information improves perceived speed and direction of moving objects (Bensmaia et al. 2006; Carter et al. 2008), and somatosensory information allows the brain to resolve ambiguous visual input (Blake et al. 2004). Whereas most studies focus on visuohaptic interactions for tactual perception and memory, we have addressed here how these interactions affect a critical task such as equilibrium maintenance. We found that the concurrent addition of haptic and visual input reduces the time necessary to integrate the shift in sensory state during tandem stance and eventually the level of sway during steady-state. This demonstrates that, similar to what has been found in cognitive tasks such as motion perception, haptic and visual signals also strongly interact for maintaining balance.

The values of the latencies in sway following shift in sensory state suggest that the cooperation between the different modalities occurs at a supraspinal level. On one hand, abnormalities at several supraspinal sites in degenerative brain diseases would produce problems at the primary phases of somatosensory integration that might ultimately have an impact on processes of sensorimotor integration, including postural control, fostering further research in selected groups of patients and in more complex balance tasks (Carpenter and Bloem 2011; De Nunzio et al. 2007; Konczak et al. 2012). On the other, the findings reported here could possibly advance the design of robots used to understand and train the operation of human balance and equilibrium mechanisms (Chen et al. 2015; Mahboobin et al. 2009).

GRANTS

This study was supported in part by Ricerca Finalizzata Grants (GR-2009-1471033 and RF-2011-02352379) from the Italian Ministry of Health and by Projects of National Interest (Progetti di Ricerca di Interesse Nazionale, PRIN) Grants (2009JMMYFZ and 2010MEFNF7) from the Italian Ministry of University.

DISCLOSURES

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

AUTHOR CONTRIBUTIONS

J.-L.H. and M.S. conception and design of research; J.-L.H. and O.C. performed experiments; J.-L.H., O.C., S.S., and M.S. analyzed data; J.-L.H. and M.S. interpreted results of experiments; J.-L.H. prepared figures; J.-L.H. and M.S. drafted manuscript; J.-L.H. and M.S. edited and revised manuscript; J.-L.H., O.C., S.S., and M.S. approved final version of manuscript.