Tactile orientation perception: an ideal observer analysis of human psychophysical performance in relation to macaque area 3b receptive fields

Abstract

The ability to resolve the orientation of edges is crucial to daily tactile and sensorimotor function, yet the means by which edge perception occurs is not well understood. Primate cortical area 3b neurons have diverse receptive field (RF) spatial structures that may participate in edge orientation perception. We evaluated five candidate RF models for macaque area 3b neurons, previously recorded while an oriented bar contacted the monkey's fingertip. We used a Bayesian classifier to assign each neuron a best-fit RF structure. We generated predictions for human performance by implementing an ideal observer that optimally decoded stimulus-evoked spike counts in the model neurons. The ideal observer predicted a saturating reduction in bar orientation discrimination threshold with increasing bar length. We tested 24 humans on an automated, precision-controlled bar orientation discrimination task and observed performance consistent with that predicted. We next queried the ideal observer to discover the RF structure and number of cortical neurons that best matched each participant's performance. Human perception was matched with a median of 24 model neurons firing throughout a 1-s period. The 10 lowest-performing participants were fit with RFs lacking inhibitory sidebands, whereas 12 of the 14 higher-performing participants were fit with RFs containing inhibitory sidebands. Participants whose discrimination improved as bar length increased to 10 mm were fit with longer RFs; those who performed well on the 2-mm bar, with narrower RFs. These results suggest plausible RF features and computational strategies underlying tactile spatial perception and may have implications for perceptual learning.

the tactile perception of edge orientation is crucial for grasping and handling objects and presumably for haptic object recognition (Hsiao et al. 2002; Jenmalm and Johansson 1997). Tactile edge stimuli activate diverse neurons in primary (S1) and secondary (S2) somatosensory cortex (Bensmaia et al. 2008a; Fitzgerald et al. 2006a; Hsiao et al. 2002), yet the receptive fields (RFs) on which edge perception is based and the means by which the brain infers the percept from the neural activity are not well understood.

When the edge of an object contacts the skin, it evokes a spatially modulated discharge pattern in populations of underlying mechanosensory afferent fibers (Johnson et al. 2000). By recording from individual afferents, while pressing bars and gratings against the fingers of macaque monkeys, Phillips and Johnson (1981a) found that the slowly adapting type 1 (SA1) population had greater spatial modulation in its response profile than all other afferent types; they concluded that only SA1 afferents could account for the limits of human tactile spatial acuity measured psychophysically (Johnson and Phillips 1981). Rapidly adapting type 1 (RA1) afferents, which are sensitive to low-frequency vibration, are distributed with even higher density than the SA1 afferents but have relatively poor spatial resolution and may, in fact, impede spatial perception (Bensmaia et al. 2006).

Although SA1 afferents, as a population, carry the fine spatial information needed for tactile edge perception, recordings from individual SA1 afferents in monkeys reveal that their orientation selectivity—the modulation of firing rate caused by the successive rotation of a bar stimulus passing through the RF center—is far less than that of orientation-selective S1 cortical neurons (Bensmaia et al. 2008a; Hsiao et al. 2002). It is therefore likely that central processing contributes to the emergence of orientation-selective cortical responses. Two central mechanisms could plausibly shape orientation-selective cortical RFs: convergence of inputs to create an elongated RF and/or anisotropic surround inhibition (e.g., inhibitory sidebands). Evidence exists for both of these mechanisms, although it is presently unclear to what extent edge perception is mediated by elongated RFs compared with RFs that contain inhibitory sidebands.

Consistent with RFs built from convergent input arising from SA1 afferents, the RFs of most cortical area 3b neurons are larger than those of individual SA1s (DiCarlo et al. 1998; Sripati et al. 2006b), yet like SA1s, orientation-tuned cortical neurons tend to have predominantly slowly adapting response properties and indeed, tend to be most orientation selective during their sustained firing period (Bensmaia et al. 2008a). Nevertheless, the extent to which central convergence creates elongated RFs is unclear. SA1 afferents themselves tend to have elliptical RFs (Pruszynski and Johansson 2014; Vega-Bermudez and Johnson 1999) with aspect ratios that are similar, on average, to those of S1 cortical neurons (Sripati et al. 2006b). Elongated RFs, however, seem to be somewhat more prevalent in cortex than in the periphery. Sripati et al. (2006b) reported that 50% of afferents but only 35% of S1 cortical neurons had nearly circular excitatory RF shapes (defined as aspect ratios <1.5) at the time of peak response.

Inhibitory sidebands may plausibly create or further enhance orientation selectivity (Hsiao et al. 2002). However, S1 cortical RF structures are quite diverse, and both the prevalence of spatially offset inhibition and its role in producing orientation-selective responses remain somewhat unclear. A challenge is that RF structures evidently depend, in part, on the stimuli used to characterize them. In response to scanned, raised-dot stimuli, >90% of area 3b neurons showed one or more apparent inhibitory sidebands (DiCarlo et al. 1998), but often, the inhibition was displaced in the direction of the moving stimulus; it was concluded that in many such cases, the inhibition in fact overlapped spatially with the excitatory RF but was temporally lagged, giving rise to an apparent spatial offset (DiCarlo and Johnson 2000, 2002). Consistent with this view, a study using randomly indented punctate stimuli rather than moving dots found surround inhibition in only ∼50% of recorded area 3b neurons (Sripati et al. 2006b). In response to indented bars, approximately one-half of area 3b neurons exhibited significant orientation selectivity; the RF structures of those neurons were better classified as either Gabor spatial filters, which have inhibitory sidebands (67% of neurons), or as two-dimensional (2D)-Gaussian spatial filters, which lack inhibitory sidebands (33% of neurons) (Bensmaia et al. 2008a).

These studies indicate pronounced heterogeneity in the spatial structures of RFs in S1 and raise important questions about the neural underpinnings of orientation perception in the somatosensory system. Which type of somatosensory cortical RF structure is most useful for the discrimination of orientation? Can the RF structures of macaque area 3b neurons account for the perceptual performance of humans tested on a bar orientation task? How many orientation-selective neurons in cortex are required to match human performance? To investigate these and related questions, here we modeled the RF structures of macaque area 3b neurons whose activity was previously recorded extracellularly in response to bars statically pressed against the fingertip (Bensmaia et al. 2008a). We used a Bayesian classifier, which avoids overfitting by penalizing unnecessary model complexity, to assign each neuron a best-fit model RF structure. We incorporated the model RFs into an ideal observer that decoded the activity of simulated cortical neurons to reach a probabilistic inference regarding bar stimulus orientation. We tested the ideal observer on a simulated two-interval, forced-choice (2IFC) orientation discrimination task, involving bars of different orientations and lengths, and compared the results with those from 24 human participants tested on the same task.

MATERIALS AND METHODS

We used RF modeling and an ideal observer analysis to link two empirical data sets: extracellular activity recorded from macaque cortical area 3b neurons in response to oriented bar stimuli (Bensmaia et al. 2008a) and human performance on a bar orientation task (Fig. 1).

Fig. 1.

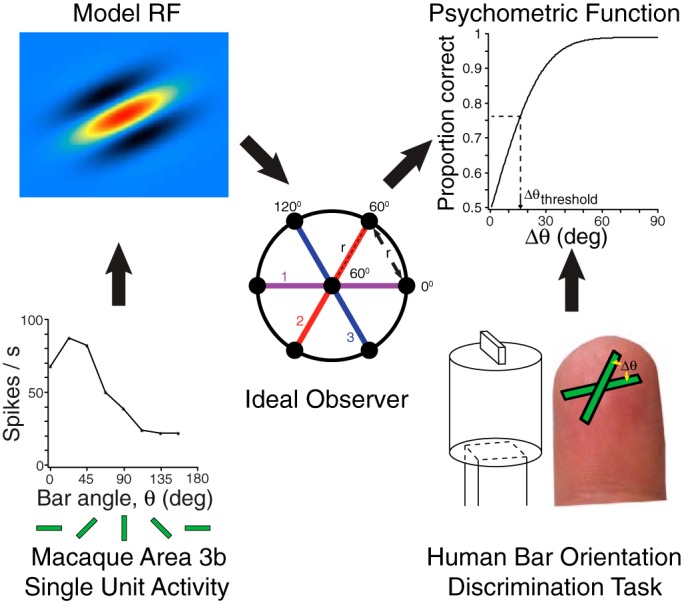
Logic of the study. For each of 42 area 3b neurons, spike activity (bottom left) was fit to a model receptive field (RF) structure (top left), produced from a spatial distribution of weights representing the influence of slowly adapting type 1 (SA1) afferent activity on the cortical neuron. An ideal observer (center) was provided copies of the model RF. Black dots indicate center locations of SA1 RFs in a magnified view of the simulated fingertip. The fixed SA1 RF spacing (r) constrained the number of cortical RF orientations to a maximum of 3 (purple, red, and blue lines). Multiple RF copies were permitted at each orientation. Human and ideal observers performed a 2-interval, forced-choice (2IFC) orientation discrimination task (bottom right). On each trial, 2 bars of equal length, but differing in orientation, sequentially contacted the fingertip. A schematic drawing is shown of 1 of the bars used to stimulate the human fingertip. The observer indicated which bar was perceived to be more horizontal. The psychometric function (top right) related angular difference (Δθ) to the observer's proportion correct, from which a 76% correct performance threshold was extracted (dashed lines; ∼16° in this example). We determined with which RF types and configurations the ideal observer's psychometric function best matched those of the humans.

RF Modeling

We reanalyzed extracellular spike data, collected previously from neurons in cortical area 3b of macaque monkeys in response to raised bars statically indented into the finger (Bensmaia et al. 2008a). Bensmaia et al. (2008a) used a 400-probe array (20 × 20 probes distributed evenly over 1 cm²) (Killebrew et al. 2007) to stimulate the monkey fingertip with bars of 1 mm width indented 500 μm into the skin. They recorded single-unit extracellular spike activity in area 3b in response to 72 stimulus configurations, presenting bars of eight orientations (from 0° to 157.5° in 22.5° increments) at each of nine positions (the bar was stepped orthogonally to its orientation, from −4 to +4 mm from the RF center, in 1 mm increments). Each of the 72 stimulus configurations occurred for 100 ms with 10 repetitions for a total of 1-s stimulation. Each bar extended to the edges of the 400-probe array. From an initial set of 46 neuronal recordings, designated as good or excellent in isolation quality (data generously provided by S. Bensmaia), we eliminated four neurons that responded only weakly to the bar stimuli (evoked firing rate averaged across all stimulus presentations <3 spikes/s above spontaneous), leaving us with 42 neurons in the data set.

The response latency typically varied somewhat as a function of the stimulus configuration (bar position and angle). Therefore, we determined response onset time for each stimulus configuration separately as the first-time poststimulus, starting at which the firing rate in a 5-ms window rose to 10 times the spontaneous activity (we measured spontaneous activity across all trials combined as the average rate in 50 ms preceding the stimulus). The jitter in onset time (SD calculated for each neuron across the 72 stimulus configurations) averaged 4 ms among the 42 neurons. For each trial, we counted spikes occurring within a 100-ms period following the defined response onset. This time period included the stimulus-evoked response while excluding the response evoked by stimulus offset. We summed the spike counts from the 10 separate 100-ms trials for each stimulus configuration to yield the neuron's firing rate in spikes/second.

We represented the RF of an area 3b cortical neuron as a map of weights linking the firing rates of peripheral SA1 mechanoreceptive afferents in the fingertip to the firing rate of the cortical neuron. For simplicity, we modeled the RF as a linear spatial filter, and we did not incorporate response dynamics into the cortical firing rate. We used a skin continuum mechanics model (Sripati et al. 2006a) to predict the steady-state firing rates of SA1 afferents to the statically indented bar stimuli used by Bensmaia et al. (2008a). We populated our model finger with SA1s distributed in a grid with center-to-center RF spacing of 0.86 mm (Darian-Smith and Kenins 1980). We tuned the continuum mechanics model by finding least-squared parameter fits to the maximum and minimum firing rates (R_max and R_min, respectively) recorded from monkey SA1 afferents in response to grating stimuli [the static R_max and R_min curves shown in Fig. 8 of Phillips and Johnson (1981a)]. Because previous research suggested that either SA1s respond to maximum compressive strain (Phillips and Johnson 1981b) or to maximum tensile strain (Sripati et al. 2006a), we considered models with weighted averages of these two strain components. We found that the best-fit settings modeled the SA1 firing rate (spikes/second) as a linear function of maximum tensile strain only, at a depth of 1,147 μm, with threshold 0 and sensitivity 322. Our implementation of the continuum mechanics model used a Poisson ratio of 0.48 (Lesniak and Gerling 2009).

Fig. 8.

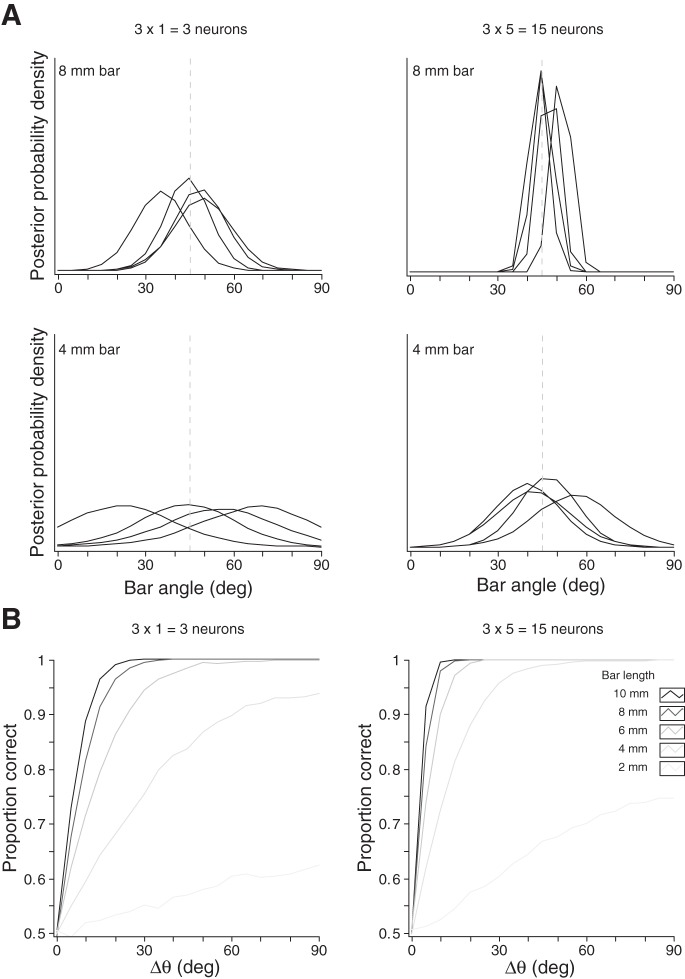
Performance of an ideal observer. Simulations were performed using the best-fitting model RF for area 3b neuron N17 (Symmetric Gabor RF). Left: 3 RF orientations × 1 neuron per orientation; right: 3 RF orientations × 5 neurons per orientation. A: each panel shows the ideal observer's posterior distributions over bar orientation in response to 4 repeated trials with a bar oriented at 45° (vertical dashed lines). Top: 8 mm bar length; bottom: 4 mm bar length. The ideal observer's posterior distributions over bar orientation vary stochastically from trial to trial. However, the observer's confidence increases, and its responses become less variable, when bar length increases (compare bottom and top) or when the observer is endowed with a greater number of cortical RFs (compare left and right). B: psychometric functions show the ideal observer's proportion correct discrimination when tested with 2 sequentially presented bars of equal lengths but differing in angle by Δθ. Bar length is represented by line intensity. Proportion correct increased with Δθ, bar length, and the number of cortical neurons in the ideal observer's pool.

We modeled the RFs of cortical area 3b neurons as linear filters, with the average firing rate (r) of the cortical neuron resulting from a thresholded, rectified, and scaled inner product between the firing rates of the constituent SA1 afferents (SA_i) and the RF weights linking each afferent to the cortical neuron (w_i)

$$r=\alpha {\left[\sum w_{i}S{A}_i-\beta \right]}^{+}$$ (1)

Here, α is the gain, β the threshold, and + represents rectification. In the fitting procedure, we allowed β to take on either positive or negative values. A positive β can be considered a threshold, due, for instance, to untuned inhibitory input, whereas a negative β could reflect untuned excitatory input.

The RF spatial structure was produced by the arrangement of input weights, w_i, that reflect the relative influence of the firing rate of each afferent, SA_i, on the cortical neuron. A primary goal of our modeling was to determine what proportion of area 3b neurons has RFs with inhibitory sidebands and what proportion conversely might achieve orientation selectivity exclusively from the elongated shapes of their RFs. To accomplish this objective, it was necessary to define specific, plausible RF structures that either contained or lacked inhibitory sidebands so that we could quantitatively compare the fit of each recorded neuron with each candidate structure. Accordingly, we considered five candidate RF structures that could give rise to orientation-tuned responses. In order of increasing complexity, these were the following: Spoke, Ellipse, Gaussian, Symmetric Gabor, and Full Gabor. The first three of these structures lack inhibitory sidebands; the final two contain inhibitory sidebands. This approach allowed us to address secondary questions of interest as well, such as whether the simplest possible oriented RF (the Spoke RF) might fit area 3b neuronal responses; whether RFs might have uniform spatial weighting from SA1s (Spoke, Ellipse) or only nonuniform weighting (Gaussian, Symmetric Gabor, Full Gabor); and whether RFs with surround inhibition were best described as having symmetrical sidebands (Symmetric Gabor) or whether the additional complexity of asymmetrical sidebands was required to fit the neuronal response (Full Gabor).

All RF structures were characterized by an orientation (θ) and a central position (x_c, y_c) on the skin. Accordingly, all RFs had five base parameters in common: α, β, θ, x_c, y_c. The RFs were distinguished by their additional free parameter(s). Below, we describe the shape of each canonical RF type, as it appears when centered at the origin (x_c = 0, y_c = 0) and with horizontal orientation (θ = 0°). In the equations below, x_i and y_i refer to the x and y locations of the i^th SA1 afferent, and the superscript above the weight refers to the RF type. Each RF was populated with SA1 inputs at 0.86 mm spacing, with an SA1 always occupying the central position (0,0); the SA1 positions were subsequently rotated by θ and shifted by (x_c, y_c) to acquire their final orientation and center location.

The Spoke RF consisted of a series of SA1 afferents aligned linearly along the finger, all with equal input weight to the cortical neuron. This RF type has just one free parameter beyond the base five parameters: the length of the spoke, l. The RF formula is the following

$$w_i^S=1\hspace{0.17em}\text{for}\hspace{0.17em}\left|x_i\right|\le l/2,y_i=0$$

$$w_i^s=0\hspace{0.17em}\hspace{0.17em}\text{otherwise}$$

The Ellipse RF consisted of a group of SA1 afferents that populated an elliptical region on the finger. As with the Spoke RF, the SA1s in the Ellipse RF have equal input weight to the cortical neuron. This RF type has two free parameters beyond the base five: a diameter in each dimension (l_x and l_y). The RF formula is

$$w_i^E=1\hspace{0.17em}\text{for}\hspace{0.17em}{\left(\frac{x_i}{l_x/2}\right)}^2+{\left(\frac{y_i}{l_y/2}\right)}^2\le 1$$

$$w_i^E=0\hspace{0.17em}\hspace{0.17em}\text{otherwise}$$

The Gaussian RF consisted of a 2D bell-shaped distribution of synaptic weights. Like the Ellipse RF, this RF type has two free parameters beyond the base five: a SD in each dimension (σ_x and σ_y). The RF formula is

$$w_i^G=e^{-(\frac{x_i^2}{2{\sigma }_x^2}+\frac{y_i^2}{2{\sigma }_y^2})}$$

The Symmetric Gabor RF consisted of a Gaussian envelope multiplied by a cosine function to achieve symmetric inhibitory sidebands straddling a central excitatory lobe. This RF type has three free parameters beyond the base five: a SD in each dimension (σ_x and σ_y) and a cosine spatial period (λ). The RF formula is

$$w_i^{SG}=e^{-(\frac{x_i^2}{2{\sigma }_x^2}+\frac{y_i^2}{2{\sigma }_y^2})}\cos \left(\frac{2\pi x_i}{\lambda }\right)$$

The Full Gabor RF consisted of a Gaussian envelope multiplied by a cosine function with adjustable phase to allow for asymmetric inhibitory sidebands. This RF type has four free parameters beyond the base five: a SD in each dimension (σ_x and σ_y), a cosine spatial period (λ), and a cosine phase (φ). The RF formula is

$$w_i^{FG}=e^{-(\frac{x_i^2}{{2\sigma }_x^2}+\frac{y_i^2}{{2\sigma }_y^2})}\cos (\frac{2\pi x_i}{\lambda }+\varphi )$$

With the use of a differential evolution algorithm to minimize mean-squared error (Global Optimization, LabVIEW; National Instruments, Austin, TX), we separately fit each of the five RF types to each of the 42 area 3b neurons' firing rates evoked by the 72 stimulus configurations. We then implemented a Bayesian classifier to assign each neuron's RF to one of the five canonical types. Our Bayesian classifier avoided overfitting by considering both goodness of fit and model complexity. For each neuron, for each RF type, we computed a Bayesian information criterion (BIC) (Wagenmakers 2007)

$$BI{C}_{RF}=72\ln \left(1-r^2\right)+q\hspace{0.17em}\ln \left(72\right)$$

Here, r² is the coefficient of variation between the 72 firing rates of the model RF and those of the recorded neuron, and q is the total number of free parameters for the RF type (q = 6, 7, 7, 8, and 9 for the Spoke, Ellipse, Gaussian, Symmetric Gabor, and Full Gabor, respectively). For each neuron, we converted the BICs into Bayes factors (BF_kj; the likelihood ratio comparing any two RF types k and j) and then into posterior probabilities over RF type, p(RF_j|d), under the assumption of a uniform prior distribution, according to the formulae

$$B{F}_{kj}=\frac{p\left(d|R{F}_k\right)}{p\left(d|R{F}_j\right)}\approx \exp \left(\frac{BI{C}_{R{F}_j}-BI{C}_{R{F}_k}}{2}\right)$$

$$p\left(R{F}_j|d\right)=\frac{1}{\sum _{k=1}^{5}B{F}_{kj}}$$

Here, d refers to the neuron's spike data collected over the 72 stimulus configurations. We assigned each neuron to the RF type with the greatest posterior probability.

We next wished to incorporate the modeled RF for each neuron into an ideal observer that could be tested with bars of any length and any indentation (following section). This raised the following question: could the same RF parameters be used to predict the response of a neuron to any stimulus bar? A crucial observation suggests that the threshold parameter, β, in fact depends on the stimulus. Bensmaia et al. (2008a) reported that the orientation tuning of S1 cortical neurons was indentation-depth invariant, similar to the contrast-invariant tuning of visual cortical neurons (Skottun et al. 1987). Specifically, a neuron's orientation index (OI) changed little, if at all, with stimulus indentation depth. Following Bensmaia et al. (2008a), we defined OI as

$$OI=\frac{\sqrt{{\left(\underset{\theta }{\mathrm{\Sigma }}r\left(\theta \right)\sin \left(2\theta \right)\right)}^2+{\left(\underset{\theta }{\mathrm{\Sigma }}r\left(\theta \right)\cos \left(2\theta \right)\right)}^2}}{\underset{\theta }{\mathrm{\Sigma }}r\left(\theta \right)}$$

Here, r(θ) is the neuron's firing rate when stimulated with a bar at angle θ. OI ranges from 0 (a completely untuned neuron that responds equally to all bar angles) to 1 (a maximally orientation-selective neuron that responds to one bar angle only).

It is clear from this formula that OI will be indentation-depth invariant, provided that the adjustment of the indentation depth of a bar stimulus scales the firing rate of the neuron at every angle, θ, by the same factor. We note that according to our implementation of the skin continuum mechanics model (above), the scaling of the indentation depth of any bar stimulus by some factor, c, will cause the firing rate of each SA1 to scale as well by the same factor, c; with reference to Eq. 1, the term ∑w_iSA_i will scale by c. Consequently, indentation depth-invariant orientation tuning will be achieved provided that β also scales by c. Therefore, to generalize Eq. 1 for use with bar stimuli indented to any depths, we scaled the threshold according to the stimulus strength. Threshold scaling has been proposed as a means to achieve contrast-invariant tuning in visual cortical neurons (Troyer et al. 2002) and may result from untuned inhibitory input (Lauritzen and Miller 2003). We implemented threshold scaling by calculating β for any bar stimulus as follows

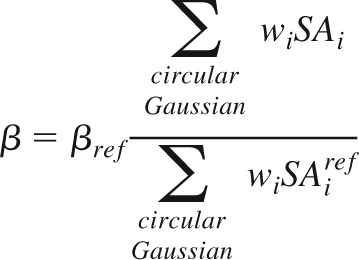Here, β_ref is the β parameter fit to the data of Bensmaia et al. (2008a) (i.e., in response to a nominal reference bar of 10 mm length indented by 500 μm; above), and β is the threshold parameter for use with any new bar stimulus. The formula adjusts for stimulus strength by calculating the firing rate of an untuned neuron—a circular Gaussian RF with SD (σ_x = σ_y) equal to the length of the long axis of the neuron's RF—in response to the new stimulus, relative to the firing rate of the same untuned neuron in response to the reference bar. Thus stimuli that evoke a greater number of input spikes from SA1s, such as those indented more deeply into the skin, will cause a proportionate growth in the magnitude of β. We used this formula in all subsequent tests of our Bayesian ideal observer in which we applied stimuli of various indentation depths and bar lengths ranging from 2 to 10 mm.

To display a model RF graphically, we show either the spatial distribution of its input weights (w_i in Eq. 1) or the summed firing rates of its inputs (∑w_iSA_i in Eq. 1) in response to a simulated punctate probe of surface area 250 μm² indented 300 μm into the skin (the punctate RF map). We defined the full width at half maximum of the longitudinal and transverse cross-sections through the punctate RF map as the length and width of the RF. We computed the aspect ratio of the RF as its length divided by its width.

Ideal Observer Simulations

To determine the maximal perceptual acuity conferred by each of the modeled cortical RFs, we constructed a series of Bayesian ideal observers that made optimal inferences regarding bar orientation based on the firing rates of a pool of cortical neurons. For simplicity of interpretation, we furnished each ideal observer with one or more copies of a single model cortical RF (one of the 42 model RFs; previous section). The ideal observer's RFs were centered, as was the bar stimulus, at the center of the simulated finger pad. The RFs had identical spatial structure but could be rotated to occupy different orientations. Because each model cortical RF was fully populated by input from SA1 RFs, the minimum angular increment between cortical RFs of different orientations was constrained to 60° (Fig. 1). Specifically, our ideal observers were configured with RFs at just one orientation, at two orientations separated by 90°, or at three orientations separated by 60°. Divergence of projections in ascending pathways from periphery to cortex permits multiple cortical neurons to share the same inputs. Accordingly, we configured ideal observers with up to 50 cortical neurons situated at each of the occupied orientations. Consequently, our ideal observers had a minimum of 1 and a maximum of 150 cortical neurons (3 RF orientations × 50 neurons per orientation). We refer to an ideal observer's total complement of cortical neurons as its neuronal pool.

The ideal observer consisted of an encoding module and a decoding module. In response to a bar stimulus (always of an angle between 0° and 90°, in 5° increments), the encoding module calculated the expected firing rate, r_i, of each of the ideal observer's cortical neurons (Eq. 1). The encoding module ignored any spike-rate dynamics (e.g., adaptation) that might occur during the stimulation period, producing an expected spike count simply as the product of the modeled firing rate [determined from the responses to 100-ms stimulation periods used by Bensmaia et al. (2008a); see previous section] and the stimulus duration.

To simulate trial-by-trial spike-count variability, the encoding module stochastically sampled an observed firing rate, n_i, from a Poisson distribution with mean r_i. A hallmark of Poisson firing is that the variance in spike-count over-repeated trials is equal to the mean count. Consistent with Poisson-like variability in area 3b neuronal firing, Sripati et al. (2006b) reported a Fano factor (ratio of response variance to mean response) of 0.86. To test the Poisson assumption in our data set, for each of the 42 recorded neurons, we used linear regression to fit the firing-rate variance against the mean rate over the 10 repeated trials at each of the 8 bar orientations (RF centered on the bar stimulus). Consistent with Poisson-like firing statistics, the regression slopes (mean 0.73; SE 0.30) and intercepts (mean 0.58; SE 1.2) did not differ significantly from one and zero, respectively (one-sample t-tests: slope, P = 0.4; intercept, P = 0.6). As mentioned, we did not model spike-rate dynamics; nevertheless, to facilitate future modeling studies, we note that the early response (from 0 to 25 ms after firing onset) was considerably less variable than the following response (25–100 ms after firing onset; mean regression slopes: early response, 0.39; following response, 1.27).

From the observed firing rates of the cortical neurons, the decoding module produced a posterior probability distribution over stimulus orientation. The decoder assumed a uniform prior probability distribution from 0° to 90° and conditional independence among the cortical neurons, given the stimulus. The posterior probability distribution was accordingly calculated over 0–90° (discretized in 5° increments) via Bayes' rule

$$p\left(\theta |\left\{n_i\right\}\right)=\frac{p\left(\left\{n_i\right\}|\theta \right)}{\sum _{\theta }p\left(\left\{n_i\right\}|\theta \right)}$$

where

$$p\left(\left\{n_i\right\}|\theta \right)=\mathrm{\prod }_{i}p\left(n_i|\theta \right)=\mathrm{\prod }_i\frac{e^{-r_i}{r}_i^{n_i}}{n_i!}$$

In a simulated 2IFC bar orientation experiment, we stimulated the ideal observer sequentially with two bars separated by an angular difference, Δθ, ranging from 0° to 90° in increments of 5°. The model reported which interval was perceived to have the lower (i.e., more horizontal) θ. To arrive at this inference, it made optimal use of the full information available to it by comparing the posterior distributions from the two intervals (demarcated below with subscripts 1 and 2) as follows

$$p({\theta }_1<{\theta }_2{|\left\{n_i\right\}}_1,{\left\{n_i\right\}}_2)=\sum _{{\theta }_1=0°}^{90°}\left(p\left({\theta }_1|{\left\{n_i\right\}}_1\right)\sum _{{\theta }_2={\theta }_1+5°}^{90°}p\left({\theta }_2{\left|\right\{n_i\}}_2\right)\right)$$

$$p({\theta }_2<{\theta }_1{|\left\{n_i\right\}}_1,{\left\{n_i\right\}}_2)=\sum _{{\theta }_2=0°}^{90°}\left(p\left({\theta }_2|{\left\{n_i\right\}}_2\right)\sum _{{\theta }_1={\theta }_2+5°}^{90°}p\left({\theta }_1{\left|\right\{n_i\}}_1\right)\right)$$

The ideal observer responded that the first stimulus was more horizontal whenever p(θ₁ < θ₂|{n_i}₁,{n_i}₂) > p(θ₂ < θ₁|{n_i}₁,{n_i}₂); it responded that the second interval was more horizontal whenever p(θ₂ < θ₁|{n_i}₁,{n_i}₂) > p(θ₁ < θ₂|{n_i}₁,{n_i}₂).

We simulated bars of width 1.3 mm and lengths ranging from 2 to 10 mm, applied with 50 g force (as in our experiments on human participants; below). To input these bar stimuli into the continuum mechanics model, we required the depth of their indentation into the skin, which we determined using a nominal value of 126 kPa for the Young's modulus of elasticity of skin, the average of proximodistal and mediolateral values reported by Wiertlewski and Hayward (2012). This resulted in indentation depths of 992, 611, 441, 345, and 284 μm for bars of 2, 4, 6, 8, and 10 mm, respectively.

For each bar length, we ran the ideal observer on 10,000 trials at each Δθ and calculated its proportion correct. On each trial, we randomly chose a pair of bar orientations (each one between 0° and 90°) that produced the desired Δθ, and while maintaining the fixed angular separation between the ideal observer's RF orientations, we randomly selected the RF orientation phase. For instance, a separation of 60° between adjacent RF orientations was equally likely to be implemented as (0, 60, 120°), (1, 61, 121°), (15, 75, 135°), or any other triplet with 60° increments.

Human Psychophysical Experiments

Participants.

Twenty-four undergraduate participants (12 men, 12 women; 18.0–22.7 yr old; median 18.7 yr old) were recruited from McMaster University. All participants were free of cuts, calluses, and scars on their dominant index finger, and none identified as having diabetes, dyslexia, or neurological disorders. These conditions were exclusion criteria, because they may adversely affect neural transduction and/or tactile acuity (Grant et al. 1999; Hyllienmark et al. 1995). All participants were tested on the index finger of the hand that they identified as dominant (right hand: n = 17; left hand: n = 7). The McMaster University Research Ethics Board approved all procedures.

Tactile stimulation.

A fully automated, precision-controlled tactile stimulator (Goldreich et al. 2009) moved raised bars to contact the distal pad of the stationary index finger. The stimulus set comprised 40 custom-machined, 1.3 mm-wide acetal plastic bars (Fig. 1, bottom right) in all combinations of five lengths (2.0, 4.0, 6.0, 8.0, and 10.0 mm) and eight orientations (from 0° to 90°, in 12.9° increments). We defined the 0° orientation to be transverse to the long axis of the finger and referred to this orientation as “horizontal.” We referred to the 90° orientation as vertical.

The participant, comfortably seated, rested the dominant hand palm-side down on a table, with the index finger covering the top of a tunnel through which a stimulus bar rose from below. The bar contacted the finger with onset velocity 4 cm/s and then rested on the finger with 50 g force for a duration of 1 s. Small, plastic barriers placed on both sides of the tested finger prevented lateral scanning movement, and a force sensor positioned on the fingernail monitored upward and downward finger movement. A computer-generated voice alerted the participant to the presence of any sensor-detected finger movement, and trials with finger movement were automatically discarded from analysis.

2IFC discrimination task.

We used a 2IFC task to assess participants' tactile orientation discrimination. On each trial, two bars with equal lengths but different orientations contacted the participant's finger pad successively (2-s interstimulus interval). The participant was instructed that the bars would have orientations somewhere between horizontal and vertical (inclusive). The task was to indicate which of the two intervals had the more horizontally oriented bar. The participant answered by pressing one of two response keys with the nondominant hand.

Before sensory testing, the participant completed 20 practice trials, during which the computer provided auditory feedback tones to indicate correct and incorrect answers. During the subsequent testing, no feedback was provided. The experiment comprised five testing blocks, one block per bar length, each consisting of 80 trials. The first block always contained the longest bar stimulus (i.e., 10 mm), whereas subsequent blocks were counterbalanced across participants (each of the 24 participants completed 1 of the 24 possible permutations of the remaining 4 bar lengths). To ensure that participants rested periodically, the program paused for 30 s after the first 40 trials of a block and for 60 s following the completion of each block. Participants could take longer breaks as desired.

Adaptive procedure and psychometric function estimation.

Within each testing block, Δθ (the difference in orientation between the bars presented in the two intervals) was varied from trial to trial following a version of the Bayesian adaptive Ψ-procedure (Kontsevich and Tyler 1999). On each trial, the Ψ-procedure chose to present the Δθ that was expected to yield the greatest information gain (entropy reduction) regarding the shape of the curve describing the participant's proportion correct as a function of Δθ [f(Δθ)]. Following completion of the experiment, we fit each participant's f(Δθ) separately on each of the five testing blocks to a mixture of a cumulative, normal psychometric function [Ψ(Δθ)] and a lapse-rate (ε) term

$$f\left(\Delta \theta \right)=\frac{\epsilon }{2}+\left(1-\epsilon \right)\psi \left(\Delta \theta \right),\text{where}\hspace{0.17em}\psi \left(\Delta \theta \right)=\frac{1}{\sqrt{2\pi }}\underset{-\infty }{\overset{\frac{\Delta \theta }{a\sqrt{2}}}{\int }}\exp (-\frac{y^2}{2})dy$$

The a-parameter is the Δθ that the participant was able to discern with 76% correct probability, corresponding to d′ = 1 on this 2IFC task (Gescheider 1997). We defined this value as the orientation discrimination threshold. Beginning with uniform prior probabilities over ε (0.01–0.05) and a (0-180°), we entered the participant's responses on the testing block to calculate the joint (a, ε) posterior distribution. To obtain a best estimate of the a-parameter and thereby the participant's psychometric function, we marginalized the joint posterior distribution over ε and read out the mode of the resulting a-posterior distribution.

RESULTS

The Fitting of Model RFs to Area 3b Neuronal Responses

We fit five candidate RF models to the firing rates of 42 neurons, recorded previously from macaque area 3b in response to bars pressed against the fingertips, placed at different positions and orientations (Bensmaia et al. 2008a). The RF models represented a logical progression of increasing structural complexity. We used a Bayesian classifier to assign one of the five RF structures to each recorded neuron, thereby capturing the RF features that best replicated the neuronal responses while avoiding overfitting.

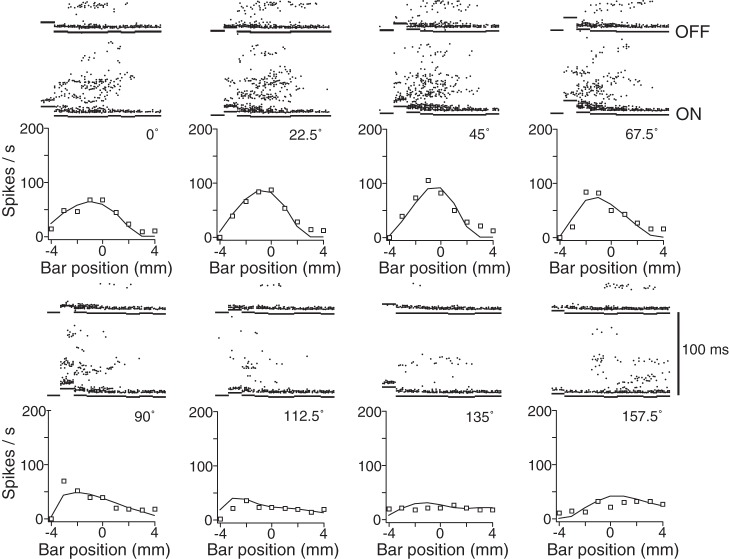
To illustrate the five RF models and the fits they provided, we first focus on a single neuron (N17; see Figs. 2–4). Figure 2 shows raster plots and mean responses of N17 to all 72 stimulus configurations (8 bar orientations × 9 positions). This neuron preferred orientations around 45° and became unresponsive to stimuli positioned 4 mm away from the approximate RF center. Our Bayesian classifier assigned N17 to the Symmetric Gabor RF type; the responses of the best-fit Symmetric Gabor RF to simulated bar stimuli closely matched those of the neuron (Fig. 2).

Fig. 2.

Responses to the 72 stimulus configurations for area 3b neuron N17. For each of 8 bar orientations (22.5° increments), Bensmaia et al. (2008a) applied the bar at 9 positions, ranging ±4 mm from the nominal RF center (here defined as position 0) in a direction orthogonal to the bar's long axis. Graphs show the neuron's responses (squares) and RF model fit (curves). Above each x-axis position are the raster plots for 10 stimulus repetitions at that position and orientation (note: time runs vertically in these raster plots, and repeated trials are separated horizontally). ON and OFF line segments demarcate times estimated to just precede response onset and (100 ms later) response offset, between which the spike count was summed. Note that N17 preferred stimuli oriented at ∼45°.

Fig. 4.

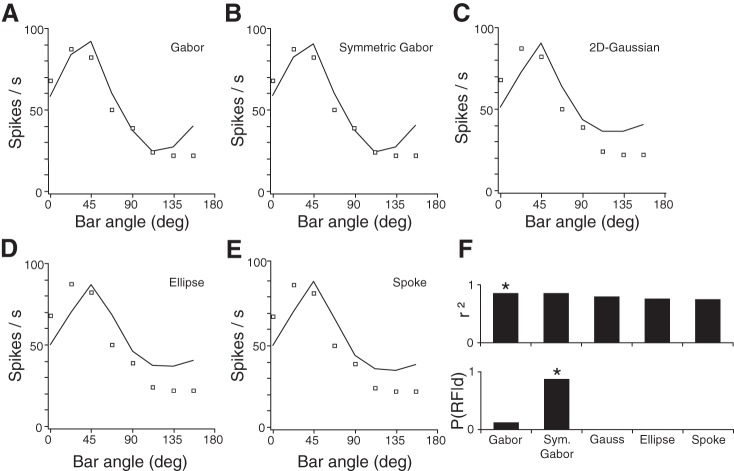
Goodness of fit of model RFs and Bayesian classifier decision for neuron N17. Squares display the observed response of N17 to each bar orientation, with the bar centered on position 0 mm, along with the responses of the best-fit RF model (curves): Full Gabor RF (A); Symmetric Gabor RF (B); 2-dimensional (2D) Gaussian RF (C); Ellipse RF (D); Spoke RF (E). F, top: histogram of the coefficient of determination (r²) values for each RF model's best fit to the responses of N17 to all 72 stimulus configurations (not shown). Bottom: posterior probability of each RF model [P(RF|d)]. *, modal RF.

Figure 3 displays the best-fit RF shapes for N17 provided by each of the five candidate RF models. The five model RFs that we used ranged in complexity from simplest (Spoke RF: one spatial dimension, uniform excitatory input weights, six free parameters) to most complex (Full Gabor RF: two spatial dimensions, spatially graded excitatory and inhibitory input weights with phase freedom, nine free parameters). Note that all five fits to N17 share in common a thin, excitatory, central region, oriented at ∼45°, bestowing a response selectivity for that orientation.

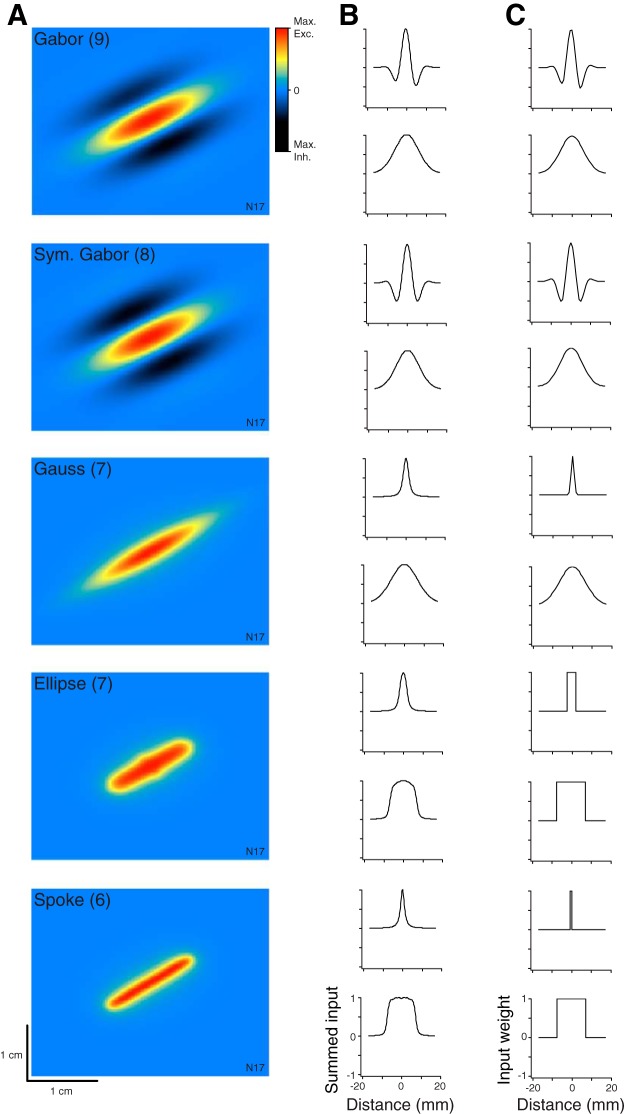
Fig. 3.

Canonical RF models fit to neuron N17. A: punctate RF maps showing the summed firing-rate input to the cortical neuron (∑w_iSA_i in Eq. 1), predicted from the indentation of a 250-μm² probe tip at each location. Red, maximum excitatory input (Max. Exc.); blue, no input; black, maximum inhibitory input (Max. Inh.). B: transverse (top) and longitudinal (bottom) cross-sections through the punctate RF map (RF center position defined as 0). C: SA1 input weights (w_i in Eq. 1) plotted along transverse and longitudinal sections through the RF center. Input weights reflect the strength and sign of connection between each SA1 afferent and the cortical neuron. For illustration purposes, we normalized each RF map and cross-section to a maximum of 1.

Figure 4 shows the best fit of each RF model to the neuronal responses at each orientation with the bar positioned over the approximate RF center (i.e., the 0-mm shift data points at each of the 8 angles; see Fig. 2). Each of the five model RFs fits these neural data (and, indeed, all 72 recorded data points) reasonably well. However, when the Bayesian classifier factored in model complexity, the Symmetric Gabor RF model emerged as the clear winning RF type for this neuron (posterior probability = 0.88). The best-fit Full Gabor RF explained only slightly more of the neuron's firing-rate variance [compare coefficient of determination (r²) values in Fig. 4F: Full Gabor r² = 0.8575; Symmetric Gabor r² = 0.8567], yet it has one additional free parameter (the sideband phase parameter, φ). Note also that the best-fit Full Gabor RF had nearly symmetrically distributed inhibitory sidebands (Fig. 3A). For these reasons, the Bayesian classifier could not justify the increased complexity of the Full Gabor RF for N17 and instead assigned the neuron to the Symmetric Gabor RF class.

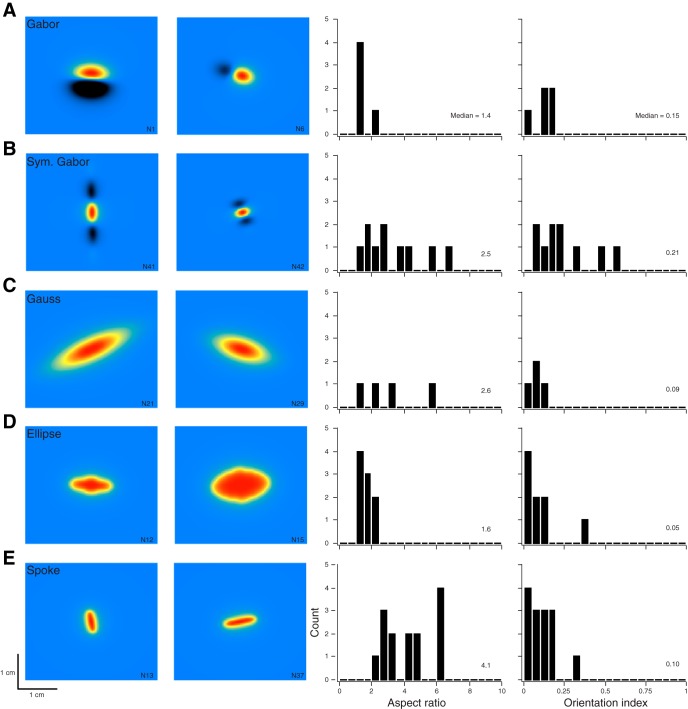
We used the Bayesian classifier to assign each of the 42 area 3b neurons a best-fit RF structure. The number and percentage of neurons assigned to each RF class, in order of increasing RF complexity, were: Spoke (14, 33%), Ellipse (9, 21%), Gaussian (4, 10%), Symmetric Gabor (10, 24%), and Full Gabor (5, 12%). Thus 36% of neurons were assigned RFs with inhibitory sidebands (Symmetric or Full Gabor RFs), and nearly as many neurons were assigned the simplest RF type (Spoke).

The Bayesian classifier assigned RFs with reasonably high confidence ratings. For most neurons, the classifier's confidence in the winning model far exceeded its confidence in the runner-up and lower-ranked models (Fig. 5). The classifier moved from an initial uniform confidence (prior probability) of 0.2 for each candidate RF shape for each neuron to a median final confidence (posterior probability) of 0.70, 0.51, 0.54, 0.77, and 0.76 for the Spoke-, Ellipse-, Gaussian-, Symmetric Gabor-, and Full Gabor-assigned RFs, respectively. Thus neurons were classified as having the simplest RF structure (Spoke) and the two most complex RF structures (Symmetric Gabor and Full Gabor) with greatest confidence.

Fig. 5.

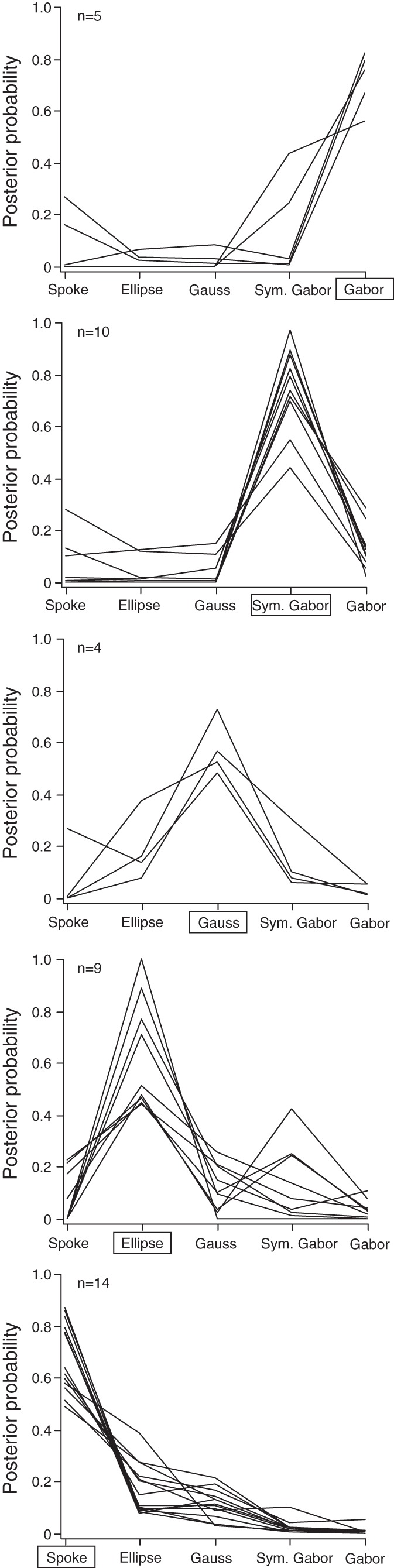
Confidence of the Bayesian classifier. Plots show the posterior probability distributions over the 5 models for neurons assigned to each RF type. Rectangles around x-axis labels indicate the model that was favored.

A diversity of best-fit RF shapes and sizes was present within each RF category. Figure 6 shows best-fit RF assignments for 10 different neurons (displayed as punctate stimulation maps). Interestingly, whereas the Spoke RFs had the highest aspect ratios, the Symmetric and Full Gabor RFs, owing presumably to their inhibitory sidebands, had the highest orientation selectivity indices (Fig. 6). A one-way ANOVA confirmed that aspect ratio differed significantly by RF type [F(4, 37) = 6.938, P < 0.001]. Post hoc comparisons [Tukey honest significant difference (HSD)] revealed that Spoke RFs had significantly greater aspect ratios than Ellipse RFs (P = 0.001) or Gabor RFs (P = 0.003). A one-way ANOVA confirmed that orientation selectivity also differed significantly by RF type [F(4, 37) = 5.191, P = 0.002]. Post hoc comparisons (Tukey HSD) revealed that neurons assigned Symmetric Gabor RFs had significantly higher orientation selectivity than those assigned Spoke RFs (P = 0.004) or Ellipse RFs (P = 0.003).

Fig. 6.

Model RF variability. Punctate RFs are shown for 2 sample area 3b neurons best fit by each RF model (columns 1 and 2). Histograms plot the aspect ratios (column 3) and orientation selectivity indices (column 4) of all neurons best fit by the corresponding RF model. The number displayed in each plot is the median value. Full Gabor RF (A); Symmetric Gabor RF (B); 2D Gaussian RF (C); Ellipse RF (D); Spoke RF (E).

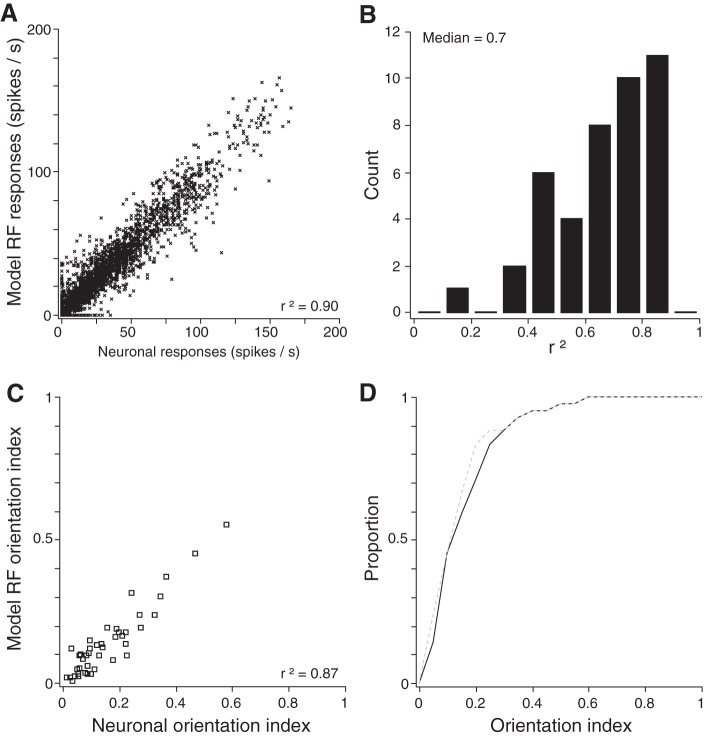
The fit between the model RF responses and neuronal responses was strong, with r² = 0.90 across the total neural data set (72 stimulus configurations per neuron × 42 neurons = 3,024 data points; Fig. 7A). On a neuron-by-neuron basis, the median r² value, relating the firing rates of the best-fit model RF (across the 72 stimulus configurations) to those of the corresponding area 3b neuron, was 0.7 (Fig. 7B). Finally, the orientation indices of the model RFs corresponded closely to those computed directly from the neuronal responses (r² = 0.87; Fig. 7, C and D). To three significant digits, the median OI of the 42 recorded area 3b neurons was the same as that of the 42 best-fit model RFs: 0.113.

Fig. 7.

Goodness of fit between the model RF assigned each neuron by the Bayesian classifier and the neuron's physiologically observed responses. A: scatter plot showing the best-fit model RFs' firing rates and the observed neuronal firing rates across the entire data set (72 responses × 42 neurons = 3,024 data points). B: histogram of r² values obtained individually for each neuron, relating the neuron's best-fitting model RF to the observed responses from the neuron (across all 72 stimulus conditions). C: scatter plot showing the orientation index (OI) of each best-fit model RF and that of the corresponding area 3b neuron. D: cumulative distribution of orientation indices for the area 3b neurons (solid black curve) and their best-fitting model RFs (gray dashed curve).

Ideal Observer Performance Predictions

Having fit the neural data to model RFs, we next constructed an ideal observer for perceptual bar orientation tasks. The ideal observer's complement of cortical RFs—its neuronal pool—could, in principle, consist of any number, type, and arrangement of RFs. For simplicity of interpretation, we centered the ideal observer's RFs on the center of the simulated fingertip and populated the entire pool with copies of the same model RF, allowing only the RF orientations to vary. Given this geometric arrangement of cortical RFs and the fact that each RF was constructed from SA1 RF inputs, the maximum allowable number of RF orientations was three (Fig. 1, center). We permitted up to 50 RF copies at each orientation, and we assumed that each cortical neuron was subject to Poisson firing-rate variability (Sripati et al. 2006b).

We simulated a 2IFC task in which two oriented bars (whose centers coincided with that of the fingertip) of equal length but differing in orientation were pressed against the fingertip. The ideal observer used Bayesian decoding of the firing rates of its cortical neurons to infer which bar was more horizontally oriented. We tested the ideal observer with differences in bar orientation (Δθ) ranging from 0 to 90° and with bars of lengths ranging from 2 to 10 mm. Owing to the unpredictable trial-by-trial Poisson variability in firing rates, the ideal observer experienced unavoidable uncertainty regarding bar orientation on any trial. The observer's uncertainty is reflected in the width of the posterior density, and the observer's confidence in its percept is reflected in the height of the posterior density at the mode. When the ideal observer used fewer neurons and when it was tested with shorter bars, it experienced more uncertainty and more trial-to-trial perceptual variability (Fig. 8A). In such cases, it required greater Δθ to reach the same proportion correct responding (Fig. 8B).

For most RF types and configurations, the ideal observer's performance was poor with the shortest bar; performance improved sharply as bar length was increased from 2 to 4 mm and showed little or no further improvement as bar length increased from 4 to 10 mm. The ideal observer simulations thus predicted a nonlinear and often saturating improvement in bar orientation discrimination with increasing bar length.

Human Performance and Ideal Observer Fits

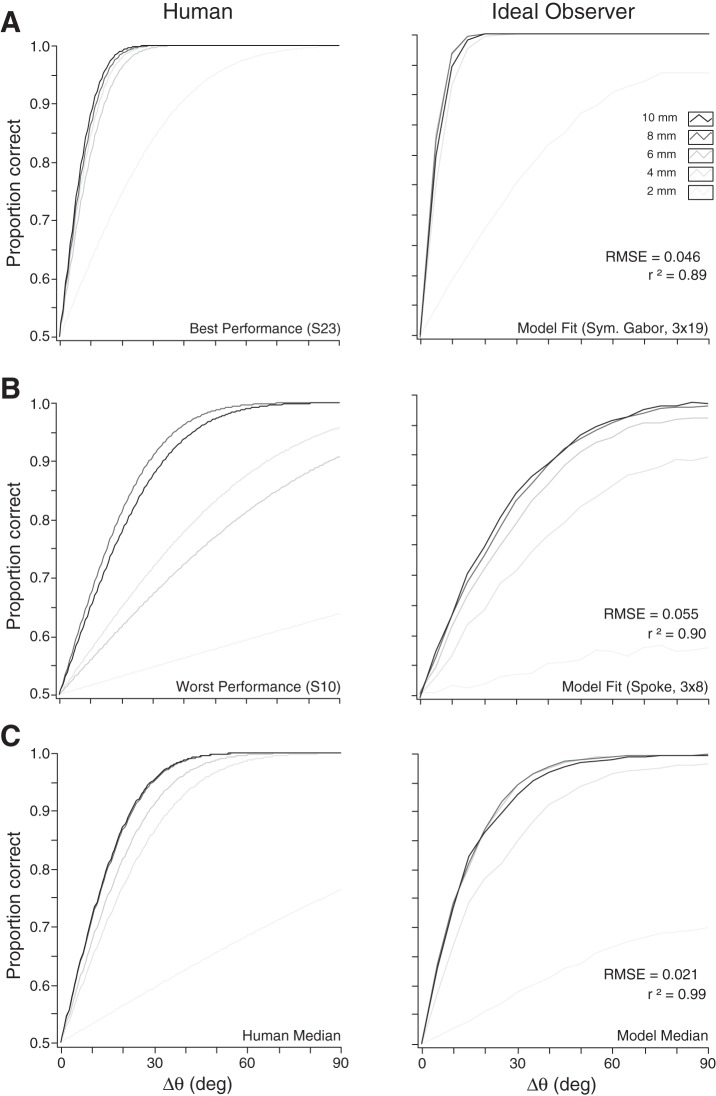
We tested 24 human participants on a precision-controlled 2IFC bar orientation task. Two oriented bars of equal length but differing in orientation were pressed sequentially against the stationary index fingertip, and the participant reported which was more horizontally oriented. The effect of bar length on human performance was consistent with that predicted by the ideal observer, with relatively poor performance at 2 mm bar length, followed by an abrupt improvement at 4 mm with little or no further improvement from 4 to 10 mm. This trend was observed in most human participants; it is apparent in the plots of the best, worst, and median of the 24 participants' performance (Fig. 9).

Fig. 9.

Psychometric functions of human (left) and ideal observers (right) on a 2IFC bar orientation discrimination task. A: human performance and ideal observer fit for the participant with best performance. This participant was best fit by the ideal observer using area 3b neuron N42 (Symmetric Gabor) with 3 RF orientations and 19 neurons per orientation. B: human performance and ideal observer fit for the participant with worst performance. This participant was best fit by the ideal observer using area 3b neuron N38 (Spoke) with 3 RF orientations and 8 neurons per orientation. C. median heights of the psychometric functions for the 24 human observers (left) and corresponding ideal observers (right). Right: includes root mean square error (RMSE) and r² values between human and ideal observer psychometric function heights at each angle.

To determine whether the ideal observer could capture the range of performance observed among the human participants and to gain insights into the types and numbers of RFs that humans might be using to perceive tactile orientation, we ran the ideal observer repeatedly on a simulated version of the same 2IFC task completed by the human participants. We furnished the ideal observer separately with each of our 42 best-fit model RFs. In each case, we made copies of the RF to produce a pool of identical RFs that differed only in orientation. We then determined with which RF and in which configuration (number of RF orientations and number of neurons per orientation) the ideal observer best fit each human's performance.

The ideal observer was able to fit the data of the 24 individual human participants rather closely, with a median r² value of 0.96 between ideal observer and human psychometric function heights at each bar angle across all bar lengths and a median root mean square error (RMSE) of just 0.03 proportion correct. Figure 9 shows the fits of the ideal observer to the best, worst, and median of human performance.

Investigating Individual Variability in Human Performance

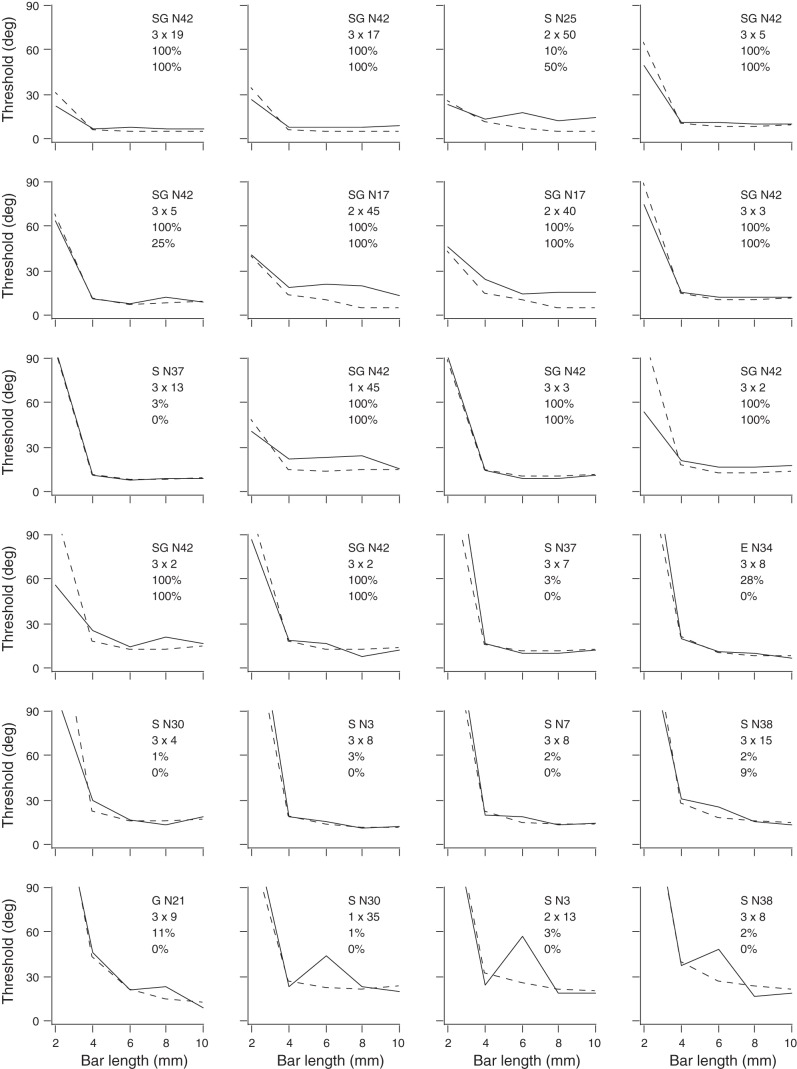
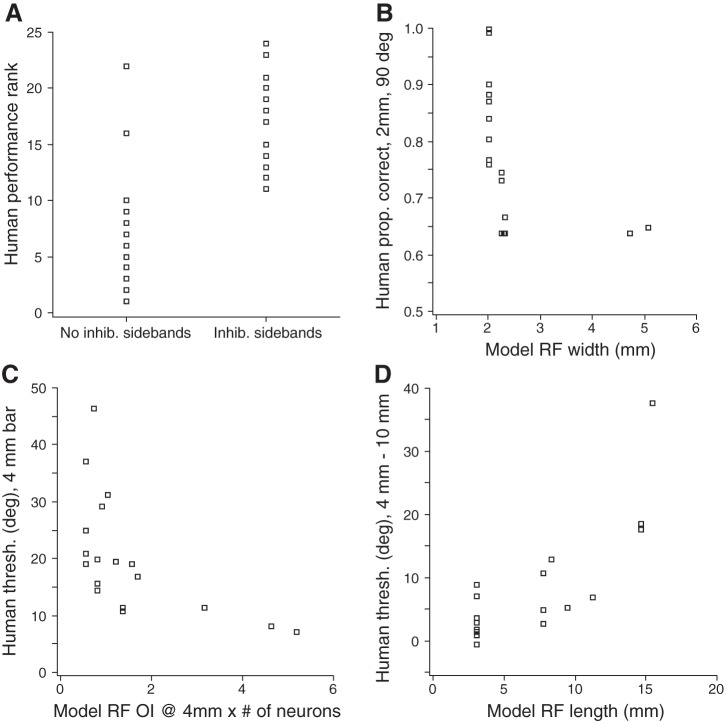
Figure 10 plots the difference in bar angle associated with 76% correct performance (the orientation discrimination threshold) at each bar length for each of the 24 human participants and for the best-fit ideal observer. The plots, displayed in order from the best to worst performing human participant, reveal a clear trend in most participants of dramatic threshold reduction from 2 to 4 mm bar lengths, followed by a flattening of the curve from 4 to 10 mm bar lengths.

Fig. 10.

Thresholds of the 24 human participants (solid curves) and corresponding best-fit ideal observer (dashed curves) vs. bar length, arranged in order of best (top left) to worst (bottom right) human performance. Each panel lists the best-fit ideal observer's RF type (S, Spoke; G, Gaussian; E, Ellipse; SG, Symmetric Gabor) and individual neuron identification (line 1 inset), the number of RF orientations × neurons per orientation (line 2 inset), the posterior probability that the best-fit RF had inhibitory sidebands (line 3 inset), and the percentage of top fits that involved RFs with inhibitory sidebands (line 4 inset).

As indicated in Fig. 10, the performance of most participants was best fit by the ideal observer with RFs positioned at the maximum allowable three orientations (n = 18); however, some participants were best fit using only two (n = 4) or just one (n = 2) of the orientations. The best-fitting number of neurons per orientation ranged from 2 to 50 (median = 8). The product of the number of RF orientations and the number of neurons per orientation was the total number of neurons in the ideal observer's pool. This ranged from 6 to 100 neurons (median 24). Some RF types fit the performance of more human participants than did other RF types. The number of humans whose performance was best fit by each RF type was: Spoke (10), Ellipse (1), Gaussian (1), Symmetric Gabor (12), and Full Gabor (0). Thus one-half of the participants had performance indicative of RFs without inhibitory sidebands, and one-half had performance indicative of RFs with inhibitory sidebands.

Interestingly, when participants were arranged in order of their performance ranking (Fig. 10), a stark contrast became apparent in the neuronal types that best fit the data from participants with lower and higher acuity. Participants with poorer orientation discriminability tended overwhelmingly to be fit best by RFs lacking inhibitory sidebands, whereas participants with better orientation discriminability tended overwhelmingly to be fit best by RFs containing inhibitory sidebands (Fig. 11A). Of the 10 lower-performing participants, all 10 (100%) were best fit by the ideal observer using RFs that lacked inhibitory sidebands (8 participants were fit with Spoke, 1 with Gaussian, and 1 with Ellipse RFs). Of the 14 higher-performing participants, 12 (86%) were best fit by the ideal observer using RFs that contained inhibitory sidebands (Symmetric Gabor RFs). The difference in performance ranking between participants best fit by the ideal observer with RFs containing or lacking inhibitory sidebands was highly significant (Mann-Whitney U-test, P < 0.001).

Fig. 11.

Factors that may influence human performance, as revealed by the ideal observer. A: the presence of inhibitory sidebands strongly associates with better overall performance among the human participants. Participant ranking (y-axis) is from worst (1) to best (24). B: RF width correlates inversely with performance on the 2-mm bar. We plot proportion correct at 90° rather than the performance threshold, because many participants did not reach 76% correct on the 2-mm bar. C: the product of RF OI and number of neurons in the pool correlate with performance on the 4-mm bar. D: RF length correlates with the degree of performance improvement (threshold reduction) from the 4- to 10-mm bar. All 24 participants displayed (A); 18 participants fit with 3 RF orientations displayed (B–D).

To characterize further the confidence with which each human's performance could be described as fit best by RFs with or without inhibitory sidebands, we undertook two additional analyses. First, we calculated the posterior probability, according to our Bayesian RF classifier, that the best-fit RF for each human had inhibitory sidebands: the sum of posterior probabilities of the Symmetric and Full Gabor RF models for the neuron. These probabilities, listed as percentages in each panel in Fig. 10, show that the classifier was generally very confident. N42, for instance, had 100% probability of containing inhibitory sidebands (its posterior probability was 71.17% for Symmetric Gabor, 28.81% for Full Gabor, and negligible for the other RF types). Second, in addition to showing the single best-fit neuron and configuration for each participant, we obtained the top 10 best fits in order of increasing RMSE and asked what percentage of those fits (up to 10 fits total or until the RMSE was 5% greater, i.e., worse, than that of the best fit) was made by RFs with inhibitory sidebands. As can be seen, each of the 10 lower-performing participants was well fit exclusively by RFs lacking inhibitory sidebands, and 11 of the 14 higher-performing participants were well fit exclusively by RFs containing inhibitory sidebands. Together, these two analyses indicate a robust association between better human performance on the bar orientation task and an ideal observer that bases inferences on RFs containing inhibitory sidebands.

Figure 10 reveals that participants showed marked heterogeneity in their ability to discriminate the orientation of the shortest bar. Some participants were unable to discriminate even the 90° angular difference with high probability. Our ideal observer simulations suggest an explanation for this heterogeneity: the width of the best-fit RF for each participant influenced performance. As RF width exceeded 2 mm, performance on the 2-mm bar worsened considerably (Fig. 11B). This effect presumably occurs because an RF wide enough to encompass the length of the bar will receive nearly equal excitation at all bar angles. The best-fit RF width was a significant predictor of participants' proportion correct at 90° on the 2-mm bar [inverse curve fit, F(1,16) = 8.396, P = 0.010]. Thus those participants who performed poorly on the 2-mm bar may have been basing their perception on the activity of wider RFs. In light of this observation, it may seem paradoxical that many lower-performing participants were fit with Spoke RFs, which are narrow. We note, however, that RFs with inhibitory sidebands can be somewhat narrower even than Spoke RFs (see, for instance, Symmetric Gabor RF N42 in Fig. 6).

Although performance on the 2-mm bar was the most heterogeneous, considerable variability across participants was evident as well for other bar lengths. The ideal observer analysis again provides a plausible explanation: as might be expected, the number of neurons in the ideal observer's pool, together with their orientation selectivity, predicted perceptual performance. For example, participants' angular threshold on the 4-mm bar was an approximately inverse function of the product of these two factors [Fig. 11C; inverse curve fit, F(1, 16) = 8.317, P = 0.011]. Thus better-performing participants may have based their perception on the activity of a greater number of neurons and/or neurons that were more sharply tuned for orientation.

Interestingly, whereas the curves relating angular thresholds to bar length tended to be nearly flat for most participants, from 4 to 10 mm bar lengths, some participants showed large and consistent threshold reductions over the same interval (Fig. 10). Again, our ideal observer analysis suggests an explanation: those participants whose performance improved from 4 to 10 mm bars tended to be fit by neurons with long RFs, whereas those whose performance remained nearly flat were fit by neurons with shorter RFs (Fig. 11D). This effect presumably occurs because an RF will receive similar excitation as a function of bar angle from any bar whose length exceeds that of the RF. Best-fit RF length was a significant predictor of the magnitude of threshold decrease from 4 to 10 mm [linear regression, F(1, 16) = 26.512, P < 0.001]. Thus the shape of the performance threshold vs. bar length curves may reflect, in part, the length of the RFs used by participants to make a tactile orientation judgment.

Finally, we note that participants' performance on 2 mm bars did not correlate with their performance on 6, 8, or 10 mm bars (Table 1). Thus participants who performed better than others on the shortest bars did not also tend to perform better on the longer bars. This finding argues against explanations for interindividual performance differences based primarily on cognitive factors (e.g., motivation on the task), as such explanations would predict a consistency in relative performance across bar lengths. Rather, in keeping with our analysis above, the performance dissociation observed between 2 mm bars and longer bars suggests that performance on the shortest bar length may have been influenced by specific RF features, e.g., RF width, that differed from the RF features that influenced performance on the longer bars.

Table 1.

Threshold correlations

	4 mm	6 mm	8 mm	10 mm
2 mm	0.53*	0.39	0.08	0.12
4 mm		0.53*	0.65*	0.44†
6 mm			0.57*	0.70*
8 mm				0.58*

Pearson's r correlations (n = 24 participants) between 2-interval, forced-choice orientation thresholds (degree) for bars of lengths 2, 4, 6, 8, and 10 mm.

^*P < 0.01; ^†P < 0.05. Self-correlations (r = 1) and duplicate cells are left unfilled.

Comparison of the RFs That Fit and Did Not Fit Human Performance

Lastly, we were interested in understanding which characteristics, if any, distinguished the area 3b neurons that best fit human performance from those that did not. Notably, the ideal observer fit the 24 human participants' data using just 10 of the total 42 area 3b neurons in our sample (Fig. 10). This occurred because some individual neurons were chosen as best fits for several human participants. The neuron that fit more (n = 10) participants than any other was N42, a small Symmetric Gabor RF (see Fig. 6B). By comparison, N17, the large Symmetric Gabor RF featured in Figs. 2–4, fit two participants. The assignment of just 10 or fewer neurons to 24 participants would occur by chance (sampling with uniform probability 24 times with replacement from a set of 42 neurons) with a probability of only 1.7 × 10⁻⁶. Evidently, the 10 selected neurons formed a highly nonrandom sample from the group of recorded area 3b neurons; we wondered which characteristics, if any, might set them apart. To that end, in an exploratory analysis, we compared the two groups of neurons with respect to several RF properties.

We found that the RFs of the 10 neurons selected as best fits for human participants (referred to subsequently as Group A neurons) tended to be smaller, more elongated, and more orientation selective than the RFs of the 32 other neurons (Group B neurons). The surface area of the central excitatory RF lobe was much smaller in neurons that fit human performance than in the other neurons [median surface area: Group A, 23.6 mm²; Group B, 40.1 mm²; unpaired t-test, t(2.8) = 39.620, P = 0.007]. This difference was explained primarily by the smaller RF widths of the neurons that fit human performance [median width: Group A, 2.3 mm; Group B, 4.7 mm; unpaired t-test, t(36.8) = 3.536, P = 0.001]; RF lengths in the two groups were equivalent (median length: Group A, 10.4 mm; Group B, 10.4 mm). Because their RF lengths were the same, but their widths were smaller, the neurons that fit human performance had more elongated RFs (median aspect ratio: Group A, 3.5; Group B, 2.1), although this difference did not reach statistical significance. Interestingly, the orientation indices of the neurons that fit human performance were equivalent to those of the other neurons (median OI: Group A, 0.11; Group B, 0.11).

We noted one additional, intriguing characteristic that distinguished the two groups of neurons: the RF constant, β (see materials and methods), was negative for all 10 of the neurons that best fit human performance, whereas β was negative for only 17 of the 32 other neurons (53%). This difference was statistically significant (Fisher's exact test, P = 0.007). A negative β value is indicative of untuned excitatory input, that is, an excitatory input to the cortical neuron that is independent of the bar stimulus orientation. Such input could, in principle, be stimulus evoked, or it could be due to constitutive excitatory drive onto the cortical neuron. The latter possibility, however, would be expected to increase the neuron's spontaneous activity, and we did not observe a significant difference in the spontaneous activity levels between the neurons that fit human performance and the other neurons. Therefore, we cautiously interpret a negative β as indicative of a significant orientation-untuned component within the stimulus-evoked excitatory input to the neurons that fit human performance.

DISCUSSION

Here, we undertook an information-theoretic investigation of tactile orientation perception. With the use of a Bayesian classifier to assign model RF structures to previously recorded macaque area 3b neuronal responses (Bensmaia et al. 2008a), we found, in general agreement with empirical studies, that area 3b neurons are heterogeneously distributed with respect to RF size, shape, and input weighting, with some RFs showing clear evidence of surround inhibition and others not (DiCarlo and Johnson 2000, 2002; DiCarlo et al. 1998; Sripati et al. 2006b). By furnishing an ideal observer with the resultant model RFs, we found that RFs with inhibitory sidebands carry information sufficient to provide close fits to the perceptual acuity of the more discriminating human participants and that neurons lacking inhibitory sidebands, which obtain their orientation preferences exclusively from the aspect ratios of their RFs, carry information that is sufficient to match the performance of the less discriminating human participants. Our ideal observer analysis further suggested that the human angular threshold vs. bar length curve may provide information about the widths, lengths, and numbers of RFs used by humans in orientation discrimination. In particular, worse performance on a 2-mm bar may indicate the use of wider RFs, and thresholds that remain nearly constant as bar length increases beyond 4 mm may indicate the use of shorter RFs.

We subscribe to the view that insights into brain function are gained not only by characterizing the average perceptual acuity of humans, but also by investigating the causes of interindividual variation in perceptual acuity (Kanai and Rees 2011). Tactile spatial acuity varies widely among humans, and in recent years, several attempts have been made to elucidate the causes of this interindividual variation (Peters et al. 2009; Stevens and Patterson 1995; Vega-Bermudez and Johnson 2004). Both peripheral and central factors plausibly influence tactile spatial acuity; of these, the role of peripheral factors has been far better characterized (Gibson and Craig 2006; Peters and Goldreich 2013; Peters et al. 2009; Vega-Bermudez and Johnson 2004). Even when peripheral factors are statistically controlled, however, considerable interindividual variability remains (Peters et al. 2009; Vega-Bermudez and Johnson 2004), suggesting the influence of unknown central differences among individuals. Our study contributes toward the understanding of these central differences—albeit in a preliminary fashion—by showing close matches between the performance of distinct human participants and that of an ideal observer operating upon RFs with distinct characteristics. The results of our analysis suggest plausibly that the widths, lengths, orientation tuning, and numbers of RFs used by individual participants may explain much of the interindividual differences in orientation discrimination. We emphasize again that these conclusions, although intriguing, should be seen as preliminary and that additional research—physiological, psychophysical, and modeling—remains to be done.

Comparison with Previous Studies

Our RF modeling results are broadly consistent with previous literature that has emphasized the considerable heterogeneity of RF structures, shapes, and sizes in cortical area 3b. Among neurons previously recorded in area 3b, RFs have been reported to vary in excitatory and inhibitory area by over an order of magnitude, to have aspect ratios ranging from 1 to 3.6, and to differ in the spatial arrangement of inhibitory regions, if any, around a central excitatory core (DiCarlo and Johnson 2000, 2002; DiCarlo et al. 1998; Sripati et al. 2006b). This RF diversity is qualitatively consistent with our findings (see Fig. 6).

Although quantitative comparison between studies is made difficult by differences in the stimuli used, such comparisons also reveal a general consistency with the previous literature. We found that 15 of 42 area 3b neurons were classified as having RFs containing inhibitory sidebands. This is a lower proportion than reported by Sripati et al. (2006b), who found that 17 of 33 area 3b neurons had substantial surround inhibition, but the two proportions do not differ significantly (Fisher's exact test, P = 0.24). Among neurons classified with inhibitory sidebands, Symmetric Gabor RFs outnumbered Full Gabor RFs by a factor of two (10 neurons compared with 5). This result is generally consistent with the findings of DiCarlo et al. (1998). That study reported inhibition on just one side of the RF to be common in the distal direction, which corresponded to the movement direction of the stimulus; however, this apparently spatially offset inhibition was later attributed largely to inhibition that overlapped the RF center but was staggered temporally (DiCarlo and Johnson 2000, 2002). When such responses are discounted, the results of DiCarlo et al. (1998) indicate truly one-sided inhibition in ∼16% of neurons, which in our sample of 42 neurons, would be 6 or 7 neurons; they reported two-sided straddling inhibition (15%) or indeed three-sided inhibition (14%) in nearly twice that number of neurons. Our Bayesian classifier would identify one-sided inhibition as a Full Gabor RF and two-sided straddling inhibition as a Symmetric Gabor RF. Because we did not construct a model RF with three-sided inhibition, such responses would plausibly be assigned to the Symmetric Gabor category as well in many cases.

Our results indicate that orientation selectivity in cortical neurons can emerge from an elongated RF shape and/or from inhibitory sidebands. Of these two mechanisms, however, inhibition appears to be the more powerful. We found that model RFs with inhibitory sidebands tended to fit the responses of the more orientation-selective area 3b neurons (and the higher-performing human participants), whereas RFs lacking inhibitory sidebands fit less orientation-selective neurons (and lower-performing human participants; Figs. 6 and 11A). Indeed, the RFs with inhibitory sidebands tended to be more orientation selective, despite being less elongated, than the spoke RFs, which lack inhibitory sidebands. This result is generally consistent with the report of Bensmaia et al. (2008a)—that a BIC favored Gabor over Gaussian RFs more frequently among the most highly orientation-selective area 3b neurons.

A difference in approach to the modeling of RFs in our study and that of Bensmaia et al. (2008a) is that our RF structures explicitly represent the input weights characterizing the influence of each SA1 afferent on the cortical neuron. An interesting observation that emerges from our approach is that even when the input weights are made to be uniform throughout an excitatory RF region (e.g., the Spoke and Ellipse RFs; Fig. 3C), the stimulus-evoked RF map is characterized by a smooth falloff from the center of the RF (Fig. 3, A and B). This occurs because the strain under the skin evoked by a punctate stimulus is not restricted to the stimulus position but rather, is strongest there and falls off with distance. Therefore, a physiologically measured smooth falloff in firing rate as a function of stimulation distance from an RF center should not alone be taken as evidence that the more eccentrically located mechanoreceptors are more weakly coupled to the cortical neuron.

We found that a median of 24 cortical neurons (range 6–100 neurons) is sufficient to account for human performance on a bar orientation discrimination task. This is in reasonable accord with estimates of the number of neurons required to match perceptual performance on other tasks, although it is lower than some values reported in the literature. For instance, ideal observers match psychophysical visual motion direction thresholds using hundreds of middle temporal neurons (Purushothaman and Bradley 2005; Shadlen et al. 1996). The number of cortical sensory neurons on whose activity a percept is based will presumably vary by task and by individual.

The median orientation discrimination threshold of our human participants on 10 mm-long bars was 12.5°. This is lower than that reported previously. Bensmaia et al. (2008b), testing participants on a battery of tactile orientation tasks involving 10 mm-long bars, found thresholds of ∼20°. The reasons for this discrepancy are unclear, but we note that the standard stimulus duration used in that study (0.4 s) was shorter than that used in the current study (1 s). Bensmaia et al. (2008b) reported that participants performed significantly better when tested with the 0.4-s stimulus than when tested with a 0.1-s stimulus; it is plausible that our even longer 1-s stimulus, resulted in additional improvement.

We found that tactile orientation discrimination thresholds tended to fall rapidly as bar length increased from 2 to 4 mm and that the decline slowed or even vanished in some participants with further increases in bar length (Fig. 10). This finding is qualitatively consistent with the effect of bar length reported in visual orientation discrimination (Makela et al. 1993). Both vision and touch extract spatial form from the activity of receptors arrayed on a 2D sheet, and the two systems may process spatial information in similar ways (Yau et al. 2009). However, as pointed out by Bensmaia et al. (2008a), S1 neurons tend to have poorer orientation selectivity than the primary visual cortex (V1) neurons. The 42 area 3b RFs that we studied had a median OI of 0.11, whereas Ringach et al. (2002) reported a median circular variance for macaque V1 neurons of 0.61, corresponding to an OI of 0.39.

Orientation Processing in the Somatosensory System

Our results are consistent with the hypothesis that orientation selectivity emerges via the central convergence of spatially aligned inputs to create elongated RF shapes and/or via the inclusion of inhibitory sidebands. The presence of these features in cortical RFs does not necessarily implicate intracortical processes in their origin. Ascending somatosensory projections show considerable divergence/convergence in the brain stem, thalamus, and cortex [for review, see Jones (2000)]. Further research is needed to elucidate the extent to which convergence in each of these areas contributes to the elongated RF shapes of some of the orientation-selective cortical neurons. The enhancement in tuning via inhibitory sidebands is apparently, at least in part, of cortical origin, because tuning varies by cortical layer. DiCarlo and Johnson (2000) found that neurons in supragranular layers tend to have greater inhibitory-to-excitatory mass ratios and to be significantly more orientation selective than neurons in layer IV.

Orientation-tuned neurons in areas 3b and 1 (Bensmaia et al. 2008a) may participate in an early stage of a cortical shape perception hierarchy, whereby local orientation information extracted in these areas is subsequently assembled into more global contour information within area 2 and S2 (Yau et al. 2013). A key aspect of feature-extracting neurons is that they remain tuned to their target stimulus feature, as concomitant extraneous features vary; that is, they show invariance to nontarget features. Orientation-sensitive area 3b neurons show several such invariance properties: their tuning is invariant to stimulus-indentation depth, their preferred orientations tend to be similar for statically indented and for scanned bars, and their tuning is invariant to bar scanning speed (Bensmaia et al. 2008a).

Area 3b sends projections to several other areas, including area 2 and S2 (Jones and Wise 1977). Intriguingly, RFs in the S2 hand representation are much larger than those in S1, often encompassing multiple pads on several digits (Fitzgerald et al. 2004). Twenty-three percent of neurons in the S2 hand representation had RFs that were orientation selective on at least one finger pad (Fitzgerald et al. 2004). In neurons that had orientation tuning on two or more pads, the preferred orientations on different pads tended to be the same (Fitzgerald et al. 2006b). These observations are consistent with the hypothesis that some S2 RFs result from convergence of inputs from similarly oriented but spatially separated S1 RFs, such as the area 3b RFs that we have studied here. Orientation-tuned responses that span the fingerpads and palm may be crucial for haptic recognition of objects held in the hand (Hsiao et al. 2002).

In addition to their perceptual role, it is likely that orientation-tuned somatosensory cortical neurons play a crucial role in the successful grasping and manipulation of objects during haptic exploration. The grasping forces applied by humans vary with an object's edge orientations and in the absence of vision, depend critically on sensory feedback from the hand (Jenmalm and Johansson 1997). Evidence suggests that somatosensory cortical neurons provide sensory feedback during object grasping, both to primary motor cortex and to posterior parietal areas that mediate prehension (Gardner et al. 2007a–c).

Assumptions and Caveats: RF Modeling

Here, we discuss several assumptions underlying our RF modeling approach. Most obviously, we have assumed that macaque and human somatosensory processing are sufficiently similar that the structure of cortical RFs in one species can be fruitfully applied toward an understanding of perception in the other. The practice of relating neural data recorded from nonhuman primates to psychophysical data recorded from humans dates to the seminal work of Mountcastle and colleagues (Mountcastle et al. 1969; Talbot et al. 1968). Many similarities in somatosensory anatomy and physiology have been demonstrated across primate species, including similarities in peripheral receptors, and cortical organization and topography (Gelnar et al. 1998; Johnson et al. 2000). Notably, by testing trained monkeys on a tactile letter discrimination task, Hsiao et al. (1993) showed that tactile spatial acuity is also similar in monkeys and humans. One difference between the species is that nonhuman primates apparently lack SA2 afferents (Johnson et al. 2000). More subtly, the spacing between SA1 afferent RFs is reportedly slightly greater in humans (Johansson and Vallbo 1979) than in monkeys (Darian-Smith and Kenins 1980), although the difference may not be statistically significant (Johnson et al. 2000). Whereas tactile spatial processing in the periphery has been well characterized physiologically in both humans (Johansson 1978; Phillips et al. 1992; Pruszynski and Johansson 2014) and nonhuman primates (Bensmaia et al. 2008a; Phillips and Johnson 1981a; Sripati et al. 2006b), few recordings have been made from somatosensory neurons in the human central nervous system (Weiss et al. 2009). The assumed similarity of area 3b RFs in human and macaque then is an untested assertion.

Our model cortical RFs linked SA1 firing rates to the cortical neuronal response via a spatial structure of input weights. We used a skin continuum mechanics model to predict the SA1 firing rates from the stimulus-induced tensile strain (Sripati et al. 2006a). The continuum mechanics model is computationally tractable and provides satisfactory fits to afferent firing in response to a broad array of stimuli (Sripati et al. 2006a), but it ignores both inhomogeneities in the skin and the fine structure of SA1 RFs, which typically show multiple sensitive zones (Johansson 1978; Phillips et al. 1992; Pruszynski and Johansson 2014). In a recent microneurographic study of human SA1 afferents, Pruszynski and Johansson (2014) showed that the spatial arrangement of multiple sensitive zones confers a degree of orientation selectivity to the SA1 response, and they propose that the primary afferents themselves take part in orientation feature decoding. This intriguing hypothesis will provide a focus for future modeling studies. An SA1 RF microstructure consisting of multiple sensitive zones could be incorporated into our cortical RF models as an earlier stage of convergence, preceding the central convergence of SA1 inputs. Another topic for future investigation is the effect of individual variability in SA1 RF density within the fingertip, which has been proposed as a possible explanation for the influence of finger size on tactile spatial acuity (Peters et al. 2009).

We fit the firing-rate profiles of each recorded area 3b neuron in response to 72 bar stimulus configurations (e.g., Fig. 2) to one of five canonical linear RF filters that could plausibly serve orientation discrimination. The assumption of linearity is a useful simplification that is known to provide only an approximate representation of actual area 3b neuronal RFs (DiCarlo et al. 1998; Thakur et al. 2012). We do not suggest that any of the five canonical RF structures exactly matches that of a cortical neuron but only that to the extent that the Bayesian classifier prefers one structure over the others for a particular neuron, the essence of that neuron's response is best captured by that idealized structure.

We supplied the ideal observer with a group of radially arranged RFs, identical except for their orientations and centered (together with the bar stimulus) at the midpoint of the simulated fingertip. Of course, in any perceptual task, the brain presumably relies on a mixture of RF types and quite plausibly on RFs with diverse center locations. We centered the ideal observer's RFs at the location of the bar stimulus to ensure that the ideal observer's ability to perform the bar discrimination task depended only on the shapes and other orientation-specific properties of its cortical neurons (as well as the numbers of those neurons). This allowed us to draw conclusions regarding the perceptual acuity conferred by RFs with different shapes and tuning properties. Had we allowed the ideal observer to make perceptual judgments based on RFs whose centers occupied arbitrary locations throughout the finger, we would have been faced with a situation that was both less tractable computationally and much more difficult to interpret. For instance, a sufficiently large number of even completely untuned neurons, distributed at sufficiently high density in the finger, could convey information regarding bar orientation. In humans, the perceptual contribution made by area 3b neurons—tuned or untuned—whose RFs are not centered on the bar stimulus, remains an open question.

Assumptions and Caveats: Stimulus Encoding and Decoding

Our ideal observer made the simplifying assumption that the activity of cortical sensory neurons is conditionally independent, given the stimulus. That is, the model assumes, in both the encoding and decoding stages, that the firing rate of each of its cortical neurons depends (stochastically) only on the stimulus and is not influenced by the firing of the other cortical neurons in the pool. The assumption of conditional independence greatly simplifies the mathematical calculations that the observer must perform. Many real cortical neurons, however, influence one another's firing rates to varying degrees via mono- or polysynaptic connections. This results in noise correlations that tend to reduce the useful perceptual information contributed by each neuron (Shadlen et al. 1996; Zohary et al. 1994). For this reason, our estimate of the number of neurons required to replicate human bar orientation perception should be viewed as a lower estimate.

We restricted our ideal observer to the analysis of stimulus-epoch spike counts, even though additional information is often available from spike timing (Mackevicius et al. 2012; Pruszynski and Johansson 2014). Indeed, in primary afferents, first spike latency alone has been shown to encode accurately the direction of forces applied to the skin (Johansson and Birznieks 2004). We do not rule out the relevance of spike timing in the active tactile perception of surface microgeometry (e.g., discrimination among fabrics), which is a spatial property that cannot be resolved via the static stimuli that activate SA1 receptors. Only when we actively scan fabrics do they become discriminable. Scanning elicits a unique spectral signature of vibration across the skin surface (Bensmaia and Hollins 2005; Manfredi et al. 2012), which may be captured primarily by rapidly adapting receptor classes—Pacinian and RA1 afferents—via the precise timing of action potentials (Mackevicius et al. 2012). Nevertheless, for the static bar orientation task used here, a spatially modulated spike-count code appears to be adequate to replicate human performance, and to the extent that the area 3b neurons we have modeled receive input from slowly adapting receptors (Bensmaia et al. 2008a), our ideal observer's use of stimulus-epoch spike counts seems a reasonable first approach.

Our ideal observer made inferences based on simulated spike counts occurring over a 1-s span, during which the bar stimulus remained in contact with the finger in the human experiments. Because the neural data (Bensmaia et al. 2008a) were obtained over 10 repeated, 100-ms stimulus intervals for each bar angle, we took the simple approach of modeling spikes per 1 s of stimulation as the sum of the spike counts across these 10 repeated, 100-ms intervals. This method is reasonable to first approximation, but it ignores the dynamics of the neural response. Area 3b neurons typically show a high-frequency onset discharge, followed by a reduction in firing rate (e.g., raster plots in Fig. 2) that occurs with a time course that varies by neuron (Pei et al. 2009). Furthermore, orientation tuning tends to be lower during the onset discharge and higher during the firing period that follows (Bensmaia et al. 2008a). Therefore, our simulated spike counts presumably overestimated the actual spike counts and somewhat underestimated the orientation tuning that many area 3b neurons would show during a continuous, 1-s interval in which a bar statically contacts the skin. Future investigations are needed to incorporate response dynamics into area 3b tactile perceptual models.

Research is needed as well to characterize the time period over which humans actually integrate neural input to arrive at a perceptual inference. Although the stimulus contacted the finger during 1 s in our human experiments, human observers might integrate information over a shorter time period before finalizing a perceptual inference. If humans base their perceptual inference on a spike-count code, then shorter time windows will require the use of more neurons to achieve the same perceptual acuity. This can be illustrated by analogy to our ideal observer. The ideal observer's perceptual acuity increases in proportion to the number of stimulus-evoked spikes it processes. It will reach the same perceptual inference if, for example, it bases perception on a pool of 10 identical neurons that fire at a particular rate for 100 ms or on just one of those neurons that fires (at the same rate) for 1 s. Therefore, we can state that our ideal observer matched human performance with a median of 24 model neurons firing throughout 1 s or more generally, with 24 neuron-seconds; for instance, the ideal observer would achieve the same performance with 240 neurons firing for 100 ms or with 120 neurons firing for 200 ms. Although the same will not hold strictly for human observers, because actual neurons, unlike our model neurons, show response dynamics, we expect the same trend to hold, namely, that performance will depend on the number of neurons on which the inference is based and the time window over which spikes are integrated. An intriguing possibility is that humans might not use a fixed time window at all but rather integrate sensory information until they are able to reach a decision at a fixed confidence threshold or until the trial ends, whichever occurs first (Mazurek 2003). An equally intriguing possibility, not incompatible with the previous one, is that participants' attention might be drawn to the stimulus by the onset response, but they might base perception exclusively on the following response. This strategy could be useful, as the onset response is less well tuned, as noted.

Perception as Probabilistic Inference

Cortical sensory neurons, including those in S1, typically respond stochastically to an identical, repeated stimulus, showing trial-by-trial, Poisson-like firing-rate variability (Sripati et al. 2006b). Because the same stimulus can produce different patterns of neural activity, it follows that a given pattern of neural activity could have been caused by different stimuli. Nevertheless, the nervous system must decode the neural activity on a single trial to reconstruct a percept of the external world. Perception thus involves the challenging “inverse problem” of inferring a cause from its stochastically generated effects (Pizlo 2001). This notoriously difficult problem is optimally approached via Bayesian probabilistic reasoning (Knill and Richards 1996).

The ideal observer that we used here makes optimal probabilistic judgments regarding bar orientation, based on the spike counts it experiences in a population of simulated cortical neurons. Ideal observers are tools used to quantify the information content in a signal (in the present study, the spike counts of model area 3b neurons) that is relevant to performance on a particular task (bar orientation discrimination), but ideal observer modeling can also suggest hypotheses for how nervous systems may actually attempt to solve perceptual tasks (Geisler 2011). Indeed, a growing body of research supports the exciting hypothesis that the nervous system implements Bayesian or Bayesian-like calculations. Bayesian inference models replicate many perceptual phenomena (Knill and Pouget 2004; Knill and Richards 1996), including in the tactile spatiotemporal domain (Goldreich 2007; Goldreich and Tong 2013), and researchers have begun to consider plausible mechanisms for the neural implementation of Bayesian calculations (Beck et al. 2008).

The close fits between the performance of the ideal observer—appropriately configured—and that of the human participants support the possibility that humans use probabilistic inference to discern tactile orientation. However, we caution that our results do not allow us to infer the processing that humans undertake on a bar orientation task. We can only state that if humans were performing the probabilistic perceptual inference that we have implemented in our ideal observer, with RF structures and configurations similar to those we have used, then their performance on the bar orientation task would match that which we have observed.

Our finding that the performance of many humans was best fit by an ideal observer using few neurons and/or with neurons that were not among the sharpest tuned raises interesting speculations regarding the potential for and mechanisms underlying tactile perceptual learning (Harrar et al. 2014; Harris et al. 2001; Wong et al. 2011, 2013). In particular, perceptual improvement might arise as the brain selects better-tuned neurons to support the task at hand (Jacobs 2009). Under this scenario, the brain already has neurons with RFs that are particularly well suited to the task, and performance improves when the brain manages to access and use those neurons. Alternatively, or in addition, perceptual improvement may occur as the brain sharpens the tuning of individual neurons (Schoups et al. 2001). Finally, improvement could occur if the brain simply recruits a greater number of neurons into the inference process, even if those neurons are not better tuned individually for the task. Any of these mechanisms would reduce the uncertainty and variability of an optimal perceptual inference, thereby enhancing task performance.

GRANTS

Support for this research was provided by an Individual Discovery Grant to D. Goldreich from the Natural Sciences and Engineering Research Council of Canada (NSERC).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: R.M.P. and D.G. conception and design of research; R.M.P., P.S., and D.G. analyzed data; R.M.P., P.S., and D.G. interpreted results of experiments; R.M.P. and D.G. prepared figures; R.M.P., P.S., and D.G. drafted manuscript; R.M.P., P.S., and D.G. edited and revised manuscript; R.M.P., P.S., and D.G. approved final version of manuscript; P.S. performed experiments.