Abstract
Intermanual transfer, i.e., generalization of motor learning across hands, is a well-accepted phenomenon of motor learning. Yet, there are open questions regarding the characteristics of this transfer, particularly the intermanual transfer of dynamic learning. In this study, we investigated intermanual transfer in a force field adaptation task concerning the direction and the coordinate frame of transfer as well as the influence of a 24-h consolidation period on the transfer. We tested 48 healthy human subjects for transfer from dominant to nondominant hand, and vice versa. We considered two features of transfer. First, we examined transfer to the untrained hand using force channel trials that suppress error feedback and learning mechanisms to assess intermanual transfer in the form of a practice-dependent bias. Second, we considered transfer by exposing the subjects to the force field with the untrained hand to check for faster learning of the dynamics (interlimb savings). Half of the subjects were tested for transfer immediately after adaptation, whereas the other half were tested after a 24-h consolidation period. Our results showed intermanual transfer both from dominant to nondominant hand and vice versa in extrinsic coordinates. After the consolidation period, transfer effects were weakened. Moreover, the transfer effects were negligible compared with the subjects' ability to rapidly adapt to the force field condition. We conclude that intermanual transfer is a bidirectional phenomenon that vanishes with time. However, the ability to transfer motor learning seems to play a minor role compared with the rapid adaptation processes.
Keywords: motor learning, motor memory, interlimb transfer, reaching movements, force field adaptation
interlimb transfer refers to a generalization of motor learning from one limb to another. This transfer is a well-documented phenomenon and is of high interest for both practical and theoretical reasons (Magill 2007). Most frequently, interlimb transfer is investigated for arm movements (i.e., intermanual transfer). Thereby, subjects usually adapt their reaching movements to either kinematic or dynamic perturbations and are subsequently checked for transfer to the contralateral untrained arm. Yet, it is assumed that adaptations to kinematic and dynamic perturbations at least partly involve different memory systems (Donchin et al. 2012; Krakauer et al. 1999) and that transfer of kinematic and dynamic features follows different principles (Sainburg 2002). Previous research mostly concentrated on intermanual transfer following kinematic adaptation (e.g., Mostafa et al. 2014; Sainburg 2002; Sainburg and Wang 2002; Taylor et al. 2011). In contrast, fewer studies investigated intermanual transfer of learned dynamics (e.g., Criscimagna-Hemminger et al. 2003; Joiner et al. 2013). Yet, basic characteristics regarding intermanual transfer of dynamic adaptation are far from clear. In this article, we focus on intermanual transfer of dynamic learning.
For instance, there are open questions on (a)symmetry and magnitude of this transfer. Previous studies that investigated intermanual transfer in force field adaptation tasks reported a unidirectional transfer, asymmetric in particular, only from the dominant to the nondominant arm (Criscimagna-Hemminger et al. 2003; Galea et al. 2007; Wang and Sainburg 2004). However, it remains unclear why transfer should be exclusively unidirectional. It was assumed that force field adaptation with the dominant arm yields a more proficient internal model compared with the nondominant arm and that this internal model is fundamental for the transfer to the contralateral arm (Wang and Sainburg 2004). In contrast to this elaborate internal model formation of the dominant arm controller, the nondominant arm controller was suggested to rely more on an impedance control rather than feedforward motor control (Duff and Sainburg 2007; Schabowsky et al. 2007). Hence, the nondominant arm controller lacks “knowledge” that could be transferred to the contralateral arm. However, the detailed connection between internal model formation during adaptation and intermanual transfer remains unclear.
Moreover, there are diverging results when the coordinate frame of transfer is considered. Transfer could occur in an extrinsic (Cartesian based) coordinate frame, meaning that for a certain movement, the forces on the left and the right hand should be similar. Transfer might also occur in intrinsic (joint based) coordinates. Thereby, if the workspace is near the midline, transfer would lead to the same joint torques, resulting in mirror symmetric force profiles (for details, see Criscimagna-Hemminger et al. 2003). Criscimagna-Hemminger et al. (2003) as well as Malfait and Ostry (2004) found transfer within an extrinsic coordinate frame. On the contrary, Wang and Sainburg (2004) as well as Galea and colleagues (2007) found transfer within an intrinsic coordinate frame. From a theoretical point of view, knowledge about the coordinate frame of transfer offers valuable information about the internal representation of motor actions and might help to improve computational models of motor control and learning.
After a motor task is learned, the motor memory formed is stabilized by processes of consolidation (Robertson et al. 2004). For force field adaptation tasks, plenty of studies have demonstrated such motor memory consolidation on a behavioral level (Brashers-Krug et al. 1996; Caithness et al. 2004; Focke et al. 2013; Overduin et al. 2006; Stockinger et al. 2014). Moreover, functional imaging has shown that after practice, the brain engages new regions to perform the task, suggesting a change of newly formed neural representations (Shadmehr and Holcomb 1997). In particular, sleep seems to play a major role in memory formation and consolidation (Rasch and Born 2013). Accordingly, sleep supports generalization processes by structural reorganization and consolidation of more general motor memory representations (Censor 2013; Rasch and Born 2013). However, it is still unclear whether consolidation processes may also facilitate intermanual transfer of dynamic adaptation.
The aim of this study was to investigate intermanual transfer characteristics in a force field adaptation task. First, we hypothesized that motor adaptation is more elaborate with the dominant compared with the nondominant hand. We further hypothesized that intermanual transfer only occurs from dominant to nondominant hand. For this purpose, we considered two distinct features of transfer (practice-dependent bias and interlimb savings). Moreover, we examined the coordinate frame of this transfer. Finally, we hypothesized that processes of consolidation (including nocturnal sleep) facilitate intermanual transfer.
MATERIALS AND METHODS
Participants
A total of 48 healthy human subjects (18–29 yr; 10 women, 38 men) participated in the study. All subjects gave written informed consent, and the test protocol was reviewed and approved by the Karlsruhe Institute of Technology ethics committee. All subjects were right-handed (Edinburgh Handedness Inventory; Oldfield 1971) and were naive to the experimental procedure (apparatus, paradigm, and purpose of the study). They were instructed to sleep at least 6 h in the nights before the test sessions and asked not to consume any alcohol or drugs during the test days.
Apparatus
We used a robot-assisted experimental paradigm (Shadmehr and Mussa-Ivaldi 1994). Thereby, subjects grasped the handle of a robotic device (Kinarm End-Point Lab, BKIN Technologies, Kingston, Canada) that could exert forces. The subjects' arms were not supported, and motion of the robot's handle was restricted to the horizontal plane. Subjects had clear view of their hand throughout the whole experiment. They received full visual feedback of the targets as well as the cursor corresponding to the position of the handle on a vertical monitor, approximately centered at eye level. Subjects sat on a chair such that they were able to comfortably grasp the handle with either hand and reach all target positions. The robot was centrally positioned in front of the subjects such that the center position of the robot handle was located in the subjects' midsagittal plane. Position and force at the handle were recorded at a sampling rate of 200 Hz.
Task
Subjects were asked to perform accurate goal-directed two-dimensional point-to-point reaching movements using the robot handle. Starting from a center point, subjects had to reach for one of three peripheral target points that appeared in a pseudorandomized order. The subsequent movement was initiated from this peripheral point back toward the center point. Therefore, the end point of each movement was the starting point for the subsequent movement. The peripheral target points appeared at a 10-cm distance from the center point in the forward (0°), forward-leftward (45° left of straight line), or forward-rightward (45° right of straight line) direction (Criscimagna-Hemminger et al. 2003). If a target had to be reached, it appeared as a light gray circle (1-cm diameter) on a black background. The cursor representing the position of the handle was displayed as a white circle (0.35-cm diameter).
We defined a set of movements as six trials (3 outward and 3 inward movements) in which each peripheral target point occurred exactly once, and thus each of the possible six movements had to be performed once. All learning blocks were constructed as concatenation of such movement sets and were equal for all subjects. This ensured the same amount of practice toward each target direction.
Subjects were requested to perform each movement within 500 ± 50 ms. Subjects were told that reaction time was not important; i.e., after appearance of the new target they could wait as long as they wanted before initiating the movement. After completion of each movement, subjects received visual feedback about movement time on the screen. If the subjects reached the target within the required time, its color changed to green. If they moved too slowly, it became red, and if moving too fast, it became blue. This visual feedback was provided throughout the whole experiment to ensure consistent movement speed.
Experimental Design
To test for transfer in both directions, participants were divided into two main groups [left to right (LR) and right to left (RL); Table 1]. To assess the influence of a consolidation period on transfer, we further subdivided the groups. One half was tested for transfer immediately after the training block (immediate transfer groups: LRi and RLi). The other half was tested for transfer after a consolidation period of 24 h (consolidation transfer groups: LRc and RLc). Thus there were four different groups to which subjects were randomly assigned (LRi, RLi, LRc, RLc; 12 subjects per group). Note that each pair of groups that were tested for the same transfer direction (LRi and LRc; RLi and RLc) followed the same basic timetable but differed only in the break between force field training and transfer test. Similarly, the groups that were tested for different transfer directions but the same transfer test type (LRi and RLi; LRc and RLc) followed the same basic timetable but differed only in the hand used to perform each block. In particular, the target sequences for the groups were mirrored and therefore similar with reference to the body midline. Thus, for instance, when the LRi and LRc groups had to perform a forward-leftward movement, the RLi and RLc groups had to perform a forward-rightward movement.
Table 1.
Subject groups and experimental setup
| Transfer |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Familiarization |
Baseline |
Training |
Bias |
Savings |
|||||||||||
| [NF] |
[NF, EC, FFCT]* |
[NF] |
[EC] |
[NF] |
[EC] |
[FF, EC]† |
[EC] |
[FF, EC]‡ |
|||||||
| Transfer Direction | Group | 54 | 54 | 54 | 54 | 54 | 54 | 6 | 6 | 6 | 6 | 168 | Break | 6 | 168 |
| LR | LRi | L | R | L | R | L | R | R | R | L | L | L | R | R | |
| LRc | L | R | L | R | L | R | R | R | L | L | L | 24 h | R | R | |
| RL | RLi | R | L | R | L | R | L | L | L | R | R | R | L | L | |
| RLc | R | L | R | L | R | L | L | L | R | R | R | 24 h | L | L | |
Subjects were randomly assigned to 4 different groups, with 2 groups in each transfer direction (LR, left to right; RL, right to left) subdivided for transfer testing immediately after the training block (LRi, RLi) or after a 24-h consolidation period (LRc, RLc). Trial types (NF, null field trail; EC, error-clamp trial; FF, force field trial; CT, catch trial) and no. of trials (numbers above columns) are indicated for familiarization, baseline, training, and transfer blocks, with breaks indicated where applicable. L, left hand; R, right hand.
Baseline block consisting of 2 cycles of 54 trials per hand contained mainly NF but also 6 randomized EC and 6 randomized FFCT (1 per hand and direction).
Training block consisted mainly of FF but also contained ∼10% EC; subjects were given a 30-s break after 84 trials.
Transfer block trials testing for interlimb savings consisted mainly of FF but also contained ∼10% EC; subjects were given a 30-s break after 84 trials. See text for details.
During the experiment, three different trial types were used: null field trials (no perturbing forces), force field trials (perturbing forces), and error-clamp trials (force channel trials). On null field trials, the subjects could reach without perturbing forces because the robot's motors were turned off.
On force field trials, the robot generated a velocity-dependent force field that applied forces to the subjects' hand via the robot handle. A clockwise-directed curl force field pushed the handle perpendicular to the direction of movement (F = [Fx; Fy] = [0, k; −k, 0] · [ẋ; ẏ], where Fx and Fy are the robot-generated forces, k = 15 Ns/m is the force field viscosity, and ẋ and ẏ are the components of hand velocity). This force field was used to alter the dynamic conditions of the movements and therewith provoke subjects' adaptation of reaching movements (Shadmehr and Mussa-Ivaldi 1994).
On error-clamp trials, the robot generated a virtual force channel (wall stiffness 6,000 N/m, wall viscosity 25 Ns/m) that restricted the movement to a straight line toward the target point, thus counteracting all movements perpendicular to the target direction (Joiner et al. 2013; Scheidt et al. 2000). These trials were used to measure the forces at the handle that subjects produced perpendicularly to the movement direction. These forces served as an indicator for predictive force field compensation. Because on these trials the motor errors were clamped to zero and the force field that had to be learned was not present, these trials allowed measurement of motor adaptation with respect to feedforward adaptation without overlapping error feedback or learning mechanisms (Joiner et al. 2013; Scheidt et al. 2000).
The experiment consisted of a familiarization block, a baseline block, a force field training block, and a transfer test block (Table 1). The familiarization block consisted of 54 null field trials for each hand.
The baseline block consisted of 2 cycles of 54 trials per hand, which consisted mostly of null field trials but also contained 6 pseudorandomly interspersed error-clamp trials and force field catch trials per hand (1 trial per movement direction and hand). The baseline block finished with another set of null field trials followed by a set of error-clamp trials for each hand, respectively (1 trial per movement direction and hand). The error-clamp trials during the whole baseline block (2 error-clamp trials for each hand and each movement direction) served as baseline trials. The force field catch trials (1 trial for each hand and each movement direction) served as force field baseline to assess the arm stiffness and the impact of the force field to the arms.
The force field training block (168 trials) consisted mainly of force field trials that were performed with the training hand only. To assess performance, error-clamp trials were randomly interspersed with a probability of ∼10%.
In the transfer test block, we tested for two different features of transfer: practice-dependent bias and interlimb savings (Table 1). First, we defined practice-dependent bias as a change in the prediction of the environmental conditions when reaching with the untrained hand caused by the previous contralateral force field adaptation. To assess this practice-dependent bias, we used six error-clamp trials (1 trial per movement direction) (Joiner et al. 2013). Second, we considered whether force field adaptation with the training arm facilitated subsequent force field adaptation with the transfer arm. For this purpose, subjects also performed a force field training block (168 trials) with their transfer hand equivalent to the initial force field training block (Criscimagna-Hemminger et al. 2003). We refer to this kind of transfer as interlimb savings (Joiner et al. 2013). Note that both features refer to the ability to transfer learning. The practice-dependent bias would lead to changes in the prediction about the dynamics, whereas interlimb savings would lead to the ability to adapt faster when the previously experienced learning stimulus is presented.
Throughout the whole experiment, there were short breaks of 30 s each time subjects had to change the reaching hand, as well as after 84 trials (14 sets) in the force field training blocks.
Data Analysis
Preprocessing.
All data were processed using the custom-made software application ManipAnalysis (Stockinger et al. 2012). Thereby, raw data were filtered using a fourth-order Butterworth low-pass filter with a cutoff frequency of either 6 (positional data) or 10 Hz (force data). Movement velocities were numerically computed using the central difference method. Next, data sets were segmented. Movement start (or end) was defined as the time point at which hand speed exceeded (or fell below) 10% of maximal speed of that movement. Finally, data sets were time-normalized using cubic spline interpolation.
Performance measurement.
Subjects had to learn to compensate forces in the perpendicular direction because the force field was acting perpendicularly to the movement direction. Therefore, we concentrated on the analysis of forces (on error-clamp trials) and deviations (on force field trials) in the perpendicular direction.
As a dynamic performance measure, we considered the forces that subjects produced against the virtual channel wall during error-clamp trials. During the baseline block, we recorded two such force profiles for each hand and each movement direction. By averaging these force profiles, we assessed a baseline force profile for each hand and each movement direction, respectively. As a performance measure, we computed a force field compensation factor (Joiner et al. 2013). This factor was found by linear regression of the actually measured perpendicular force profile on the error-clamp trial and the ideal perpendicular force profile (forces necessary to cancel the force field if it had occurred, determined by Fideal = [Fideal,x; Fideal,y] = [0, 15 Ns/m; −15 Ns/m, 0] · [ẋactual; ẏactual]) according to
where ε is an additive error term, a0 is the intercept, and the parameter a1 serves as the force field compensation factor (Joiner and Smith 2008; Joiner et al. 2013).
In addition, we calculated the midmovement force as the average perpendicular force produced against the channel wall during error-clamp trials within a time window ranging from 70 ms before to 70 ms after maximum speed of that movement (Joiner et al. 2013). The statistical analyses performed using this measure yielded results similar to the force field compensation factor; thus these results are not presented in this article.
The performance measurement obtained using error-clamp trials is a good indicator of the performance of the feedforward controller, because it is not confounded by error feedback and learning mechanisms. This allows analyses of the adaptation of the feedforward controller by formation of an internal model of the task.
As a kinematic performance measure, we considered force field trials and computed the perpendicular displacement of the hand path from a straight line joining the start and target points at maximum hand speed (PDVmax) (Mattar and Ostry 2007; Pekny et al. 2011). The hand path produced results from the superposition of several control mechanisms (feedforward control, feedback control, and impedance control) and therefore reflects net motor performance. In addition, we fit the adaptation curves obtained by the kinematic error (PDVmax) to an exponential function:
(mean R2 value across all subjects was 0.65), whereby we analyzed the time constant τ, which represents the rate of adaptation (e.g., Davidson and Wolpert 2004).
To evaluate magnitude and direction of forces or deviations, all measures were computed as signed values. Thereby, for outward (inward) directed movements, a positive sign indicates force compensation or perpendicular deviation in the counterclockwise (clockwise) direction.
Statistics.
Normal distribution of the data was checked using the Kolmogorov-Smirnov test. Homoscedasticity was checked using Levene's test. Results of these tests were not in conflict with the respective parametric statistical tests used. If ANOVAs revealed significant differences, Tukey's honestly significant difference (or the Tukey-Kramer method in unbalanced cases) post hoc tests were used.
For all statistical tests, the level of significance was set a priori to P = 0.05. When multiple analyses were conducted addressing the same research question, the Holm-Bonferroni procedure (sequentially rejective Bonferroni test; Holm 1979) was used to adjust the level of significance. All results that are reported as statistically significant comply with this α-level adjustment. Effect sizes were determined using partial η2 (ηp2; small effect: ηp2 = 0.01; medium effect ηp2 = 0.06; large effect: ηp2 = 0.14) or Cohen's d (small effect: d = 0.20; medium effect: d = 0.50; large effect: d = 0.80; Cohen 1988). All data are mean values and 95% confidence intervals. All statistical analyses were conducted using IBM SPSS software (v.22).
RESULTS
Adaptation to the Force Field Condition
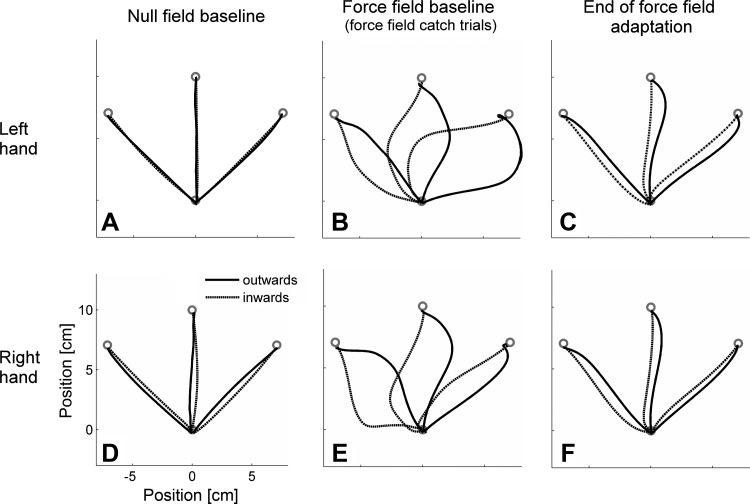
The subjects' hand paths reflected the typical adaptive behavior (Fig. 1). Under null field conditions, hand paths were unperturbed and almost straight-lined (Fig. 1, A and D). When exposed to the force field, hand paths initially showed high deviations (Fig. 1, B and E) but straightened with training (Fig. 1, C and F).
Fig. 1.
Mean plots of reaching movements with the left (LR group; A–C) and right hand (RL group; D–F): null field baseline (A and D), force field catch trials (B and E), and movement trials at the end of the training block under force field conditions (C and F). Compared with those of the right hand, left hand movements are straighter under null field conditions but are more deviated by the force field. (Note: all illustrations are in extrinsic coordinates.)
We used two different approaches to assess adaptation to the force field condition. We calculated a dynamic performance measure that represents subjects' predictive behavior and a kinematic end-point error measure that represents net motor performance (Fig. 2).
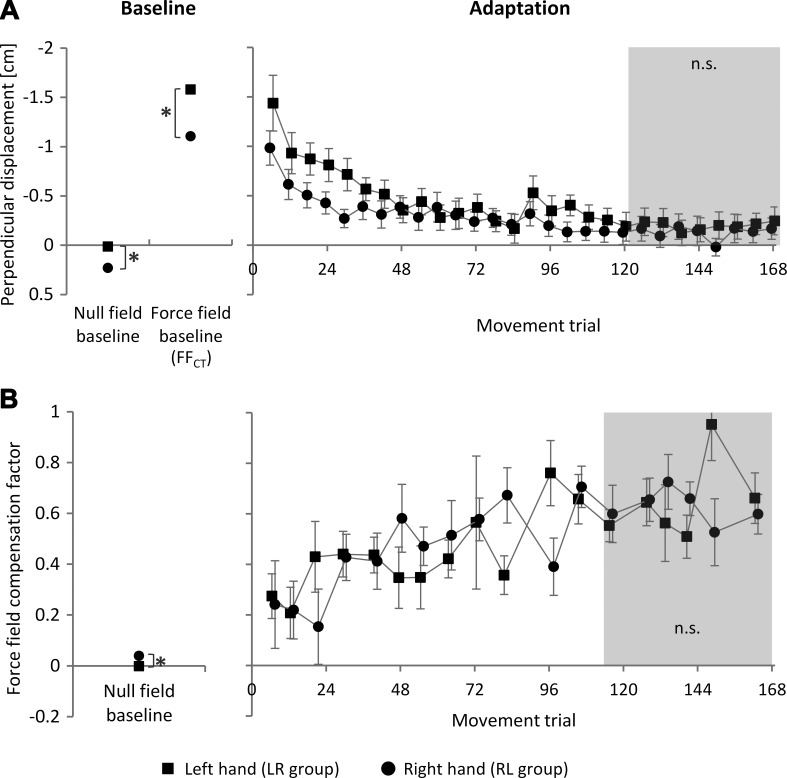
Fig. 2.
Baseline measurements and adaptation progression for the left and right hand as measured by the kinematic end-point error (perpendicular displacement; A) and the force field compensation factor (B). After 84 trials, a break of 30 s was given. Values are means ± 95% confidence intervals (CI). Asterisks indicate statistically significant differences (P < 0.05); n.s., not significant.
Before performing the analysis of adaptation to the force field condition, we considered the impact of the force field on the subjects' arms before any learning occurred. Therefore, we analyzed motor performance under null field conditions and on force field catch trials, i.e., null field and force field baseline (Fig. 2A, left). A repeated-measures ANOVA [condition (null field baseline, force field catch trial); hand (L, R)] of these baseline values revealed a significant effect of hand [F(1,46) = 84.8, P < 0.001, ηp2 = 0.65], a significant effect of the force field condition [F(1,46) = 1,918.2, P < 0.001, ηp2 = 0.98], and a significant interaction of hand and force field condition [F(1,46) = 14.8, P < 0.001, ηp2 = 0.24]. Under null field conditions, movements of both arms tended to be curved inward (as indicated by the positive sign of the deviations). Thereby, the left arm produced significantly lower deviations [t(47) = 8.22, P < 0.001, d = 1.81]. On force field catch trials, the left arm showed significantly higher deviations compared with the right arm [t(47) = 10.85, P < 0.001, d = 2.07]. Thus the force field had significant impact on both hands. However, the impact of the force field on the left hand was higher than on the right hand.
To preclude that the assessed differences in force field catch trials are due to dissimilar error feedback mechanisms of the two hands (which might occur earlier than the time point of maximum speed at which the hand path was evaluated), we conducted the same analysis comparing the perpendicular displacement 80 and 150 ms after movement onset. Thereby, we found qualitatively similar results indicating a larger impact of the force field to the left hand compared with the right hand (P < 0.001 in both cases).
Consideration of the adaptation to the force field condition revealed that subjects were able to reduce the kinematic end-point error during force field training until reaching a performance plateau for both hands (Fig. 2A, right). When the degree of performance improvement between hands was compared using a repeated-measures ANOVA [time (force field catch trials, end of adaptation); hand (L, R)], the results showed a significant effect of time [F(1,46) = 880.8, P < 0.001, ηp2 = 0.95] and hand [F(1,46) = 43.0, P < 0.001, ηp2 = 0.48], as well as a significant interaction of time and hand [F(1,46) = 18.0, P < 0.001, ηp2 = 0.28]. This indicates significantly higher overall error reduction of the left hand compared with the right hand (caused by the initial differences). Consideration of the motor performance at the end of adaptation (mean of last 8 sets) revealed no significant difference between the left and right hands [t(46) = 1.04, P = 0.304, d = 0.54]. Thus motor adaptation ended up on a similar performance level for both hands. Moreover, consideration of the time constants of adaptation revealed no significant differences between the left and right hands [τL = 3.9, τR = 4.9; t(46) = 1.52, P = 0.223, d = 0.32], indicating similar adaptation capacities for both hands.
Consideration of the force field compensation factor yielded similar results for the adaptation to the force field condition (Figs. 2B and 3). A repeated-measures ANOVA [time (baseline, end of adaptation), hand (L, R)] revealed a significant effect of time [F(1,46) = 999.5, P < 0.001, ηp2 = 0.96]. The effect of hand [F(1,46) = 0.6, P = 0.447, ηp2 = 0.01] and the interaction of time and hand [F(1,46) = 3.1, P = 0.086, ηp2 = 0.06] were not statistically significant. Under null field baseline conditions, we found significantly higher forces produced against the channel wall for the right hand compared with the left hand [t(47) = 4.27, P < 0.001, d = 0.89; Fig. 2B, left]. This is in line with the aforementioned higher deviations of right hand paths under null field conditions. When exposed to the force field, subjects adapted their motor output by producing additional perpendicular forces. At the end of the training block (last 6 error-clamp trials, 1 per movement direction), subjects learned to produce additional compensating perpendicular forces to counteract the force field. At the end of the training block, subjects compensated, on average, 64.8 ± 4.5% (left hand) and 62.8 ± 5.3% (right hand) of the force field. This did not differ between hands [t(46) = 0.56, P = 0.580, d = 0.16]. Therefore, the left and right hands showed a similar ability to adapt their motor output by predicting the force field.
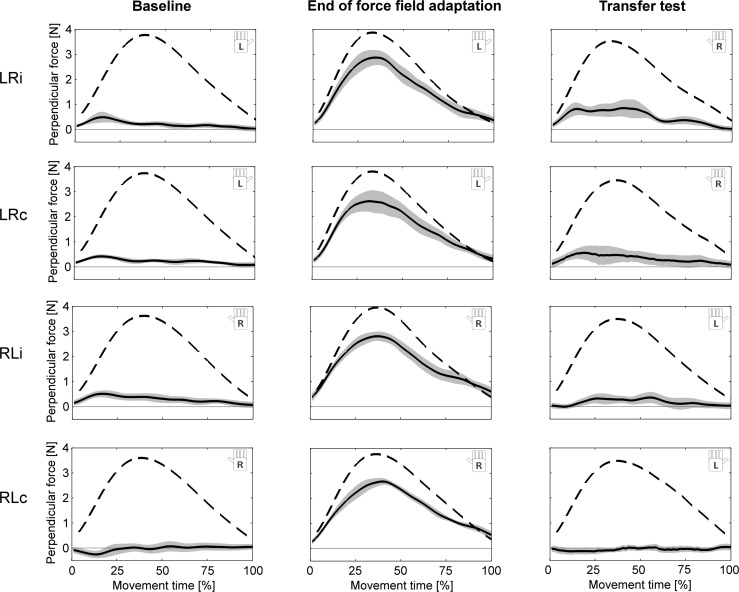
Fig. 3.
Ideal (dashed lines) and measured (solid lines) perpendicular force profiles on error-clamp trials during baseline, at the end of force field adaptation, and in the transfer test block. Values are means ± 95% CI. At the end of the training phase, all subject groups learned to produce additional compensatory forces in the perpendicular direction. On the transfer tests, the groups LRi, LRc, and RLi show transfer in the form of increased perpendicular forces compared with baseline conditions (practice-dependent bias). Immediate transfer groups (LRi and RLi) were tested immediately after the transfer training block; consolidation transfer groups (LRc and RLc) were tested after a 24-h consolidation period.
Combining the results of kinematic and dynamic measures of performance shows that both the left and right hands were able to adapt to the changed dynamic conditions by predicting the force field, resulting in reduced kinematic reaching error. The applied force field had a higher impact on the left hand, causing a higher overall reduction of motor error during the training block. However, the motor error progression indicated a comparable rate of adaptation between hands. Similarly, feedforward motor adaptation was comparable between hands.
Transfer of Learning
To assess transfer of learning, we considered two different transfer features. First, we considered the practice-dependent bias as measured on error-clamp trials. This allowed analysis of the subjects' predictions about the dynamic conditions with the transfer hand without previously being exposed to the force field with that hand (Joiner et al. 2013). Second, we considered the interlimb savings, i.e., subjects' ability to adapt to the force field condition with their transfer hand when exposed to the contralaterally experienced force field (see materials and methods).
Practice-dependent bias.
Figure 3 illustrates the perpendicular forces on error-clamp trials applied by the subjects at the end of adaptation as well as in the transfer test immediately after training (LRi, RLi) and after a 24-h consolidation period (LRc, RLc). As shown in Fig. 4, transfer occurred in extrinsic coordinates as indicated by the positive sign of the force field compensation factor (which was defined relative to the forces necessary to counter the force field).
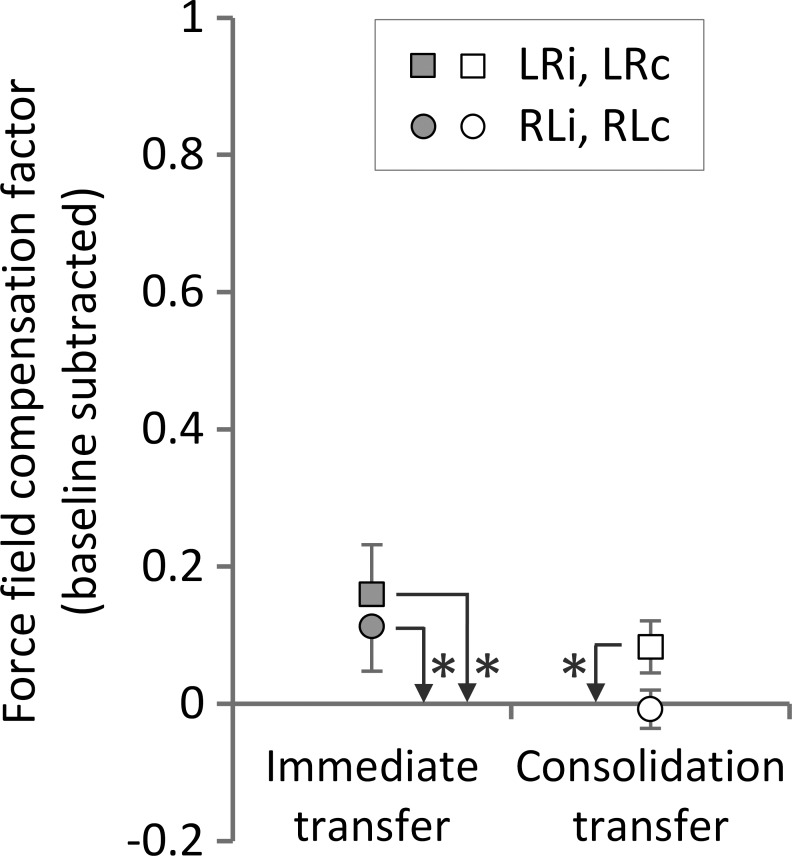
Fig. 4.
Transfer of learning by means of practice-dependent bias as measured by the force field compensation during error-clamp trials for all 4 groups. Values are means ± 95% CI. Asterisks indicate statistically significant differences (P < 0.05) vs. zero (baseline).
To simplify presentation of the results and make the two hands comparable, all further reported results of the force field compensation factor are based on baseline-subtracted force profiles. To assess whether transfer in terms of a practice-dependent bias occurred, we considered error-clamp trials immediately after adaptation. Thereby, we found transfer of learning both from left to right arm [1-sample t-test vs. 0; LRi: t(11) = 4.33, P = 0.001] and from right to left arm [RLi: t(11) = 3.39, P = 0.006] as indicated by an increased lateral force compared with baseline (i.e., zero value; Fig. 4). On average, this corresponded to 23.7% (LRi) and 20.0% transfer (RLi). After the 24-h consolidation period, only the LRc group showed significant transfer to the contralateral arm of, on average, 12.8% [LRc: t(11) = 4.27, P = 0.001; RLc: t(11) = 0.55, P = 0.592].
To test if the amount of transfer differed between transfer conditions, we conducted a 2 × 2 ANOVA [transfer direction (LR, RL), transfer type (immediate, consolidation)]. Thereby, we found a significant effect of transfer direction [F(1,44) = 6.22, P = 0.016, ηp2 = 0.12] and transfer type [F(1,44) = 12.79, P = 0.001, ηp2 = 0.23] but no significant interaction of these two factors [F(1,44) = 0.64, P = 0.43, ηp2 = 0.014].
Altogether, immediately after adaptation, transfer of learning in terms of practice-dependent bias occurred in both directions. After the consolidation period, these transfer effects declined and only occurred from the left to the right hand.
Interlimb savings.
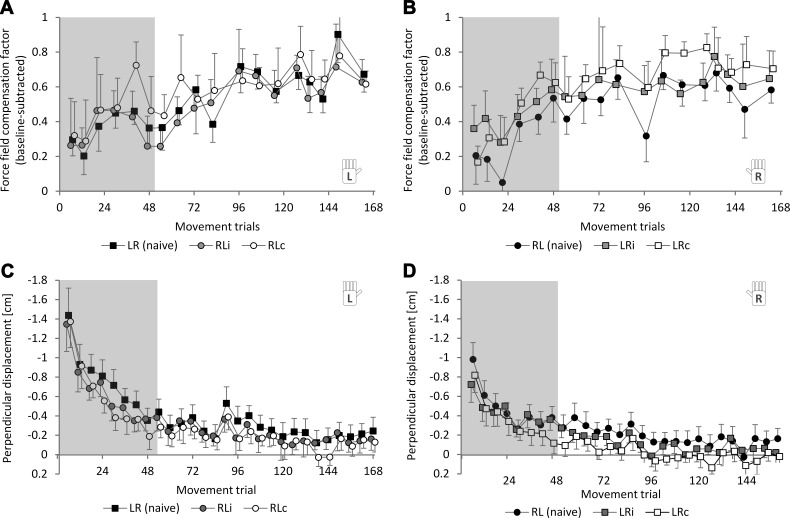
To assess interlimb savings, subjects were exposed to the force field with their transfer hand. Consideration of the randomly interspersed error-clamp trials during the force field block allowed analysis of subjects' predictive behavior. The progression of the force field compensation factor for naive subjects and transfer subjects is shown in Fig. 5, A and B, for each hand, respectively. Accordingly, the progression of net motor performance as quantified by the perpendicular displacement is depicted in Fig. 5, C and D.
Fig. 5.
Intermanual transfer by means of interlimb savings as a comparison of adaptation progression between novices (black symbols) and transfer groups (gray and white symbols) on error-clamp trials (A and B) and the kinematic end-point error on force field trials (C and D). A and C: left-hand novices (LR naive) vs. right-to-left transfer groups (RLi, RLc). B and D: right-hand novices (RL naive) vs. left-to-right transfer groups (LRi, LRc). After 84 trials, a break of 30 s was given. Values are means ± 95% CI.
For statistical analyses, we considered the first eight sets of movement trials (48 movements, containing 6 error-clamp trials) because these comprise the initial adaptation phase before performance reaches plateau. Within this time window, we compared performance between transfer and control subjects using one-way ANOVAs. For instance, for the transfer groups LRi and LRc, i.e., transfer from left to right hand, the pooled RL group (RLi and RLc) served as a control group because its subjects were naive to the force field when reaching with their right hands. Moreover, to assess differences in the rate of adaptation, we compared the time constants of adaptation between groups as assessed by fitting to exponentials (see materials and methods).
For the right-to-left direction [group (LR, RLi, RLc); Fig. 5, A and C], there were no statistically significant differences between groups. This holds for the force field compensation factor measured on error-clamp trials [F(2,45) = 2.56, P = 0.088, ηp2 = 0.10] as well as for the mean values of perpendicular displacement measured on force field trials [F(2,45) = 1.75, P = 0.185, ηp2 = 0.07] and for the time constants of adaptation [τLR = 3.9, τRLi = 3.0, τRLc = 3.9; F(2,45) = 0.85, P = 0.433, ηp2 = 0.04].
For the left-to-right direction [group (RL, LRi, LRc); Fig. 5, B and D], there were differences between groups [F(2,45) = 4.05, P = 0.024, ηp2 = 0.153] when the force field compensation factor was considered. Thereby, the control group tended to show less force field compensation compared with the transfer groups. However, after α-level adjustment using the Holm-Bonferroni method, these differences were not statistically significant. Similarly, the performance assessed by the perpendicular displacement did not reveal any statistically significant differences between groups when the mean values [F(2,45) = 2.00, P = 0.146, ηp2 = 0.082] or the time constants of adaptation [τRL = 4.4, τLRi = 5.2, τLRc = 5.8; F(2,45) = 0.93, P = 0.401, ηp2 = 0.04] were considered.
Even when considering only the forces measured during the first randomly interspersed error-clamp trial (which occurred on the seventh trial), we did not detect any differences between groups. This holds both for the right-to-left transfer direction [1-way ANOVA: group (LR, RLi, RLc); F(2,45) = 0.19, P = 0.829, ηp2 = 0.01] as well as the left-to-right transfer direction [1-way ANOVA: group (RL, LRi, LRc); F(2,45) = 1.17, P = 0.320, ηp2 = 0.05].
Taking all results together, for all considered measures of performance, we failed to detect clear transfer effects by means of interlimb savings immediately after adaptation as well as after the consolidation phase in either direction. Thus transfer effects were quite weak compared with the fast initial performance improvements caused by adaptation mechanisms.
DISCUSSION
This study revealed three main findings: 1) the ability to adapt to the force field condition did not differ between hands; 2) intermanual transfer in the form of a practice-dependent bias occurred both from dominant to nondominant hand and vice versa in extrinsic coordinates; and 3) a consolidation phase (including nocturnal sleep) after adaptation did not foster but rather weakened transfer effects.
Adaptation Does Not Differ Between Hands
Our results showed that subjects are able to adapt their reaching movements to a changed dynamic environment with either hand. During training, the left hand reduced motor error more than the right hand when absolute values were considered. This, however, was mainly attributed to the higher impact of the force field on the left hand and therewith to higher deviations at the beginning of force field exposure. Accordingly, the adaptation rate did not differ between hands. Most interestingly, we did not detect differences between hands in the ability to predict the force field at the end of adaptation when considering the force field compensation factor, which is a measure of feedforward control mechanisms. Thus we did not detect better adaptation competence of the dominant right hand compared with the nondominant left hand. We rather assume that both the dominant and nondominant arm controllers are able to form an elaborate internal model of the task dynamics.
This result is in contrast to the findings of Duff and Sainburg (2007). In their study, only the dominant, not the nondominant, arm showed increased motor errors during aftereffect trials following the adaptation to an attached inertial load (Duff and Sainburg 2007). This was taken as evidence for a more elaborate predictive control during dominant compared with nondominant arm movements. On the other hand, Sainburg (2002) found aftereffects for both dominant and nondominant arm movements following adaptation to an inertial load. However, these initial aftereffects were not statistically evaluated for potential differences but appear to be of similar magnitude for either hand (see Fig. 2B in Sainburg 2002). Similarly, a closer look at the results of Criscimagna-Hemminger et al. (2003) indicates that their subjects did not show a better adaptation competence when using the dominant compared with the nondominant arm (consider control groups in their Figs. 3B vs. 4B or Fig. 5, A vs. B). Unfortunately, Criscimagna-Hemminger et al. did not statistically test for this issue either, because this was not part of their research question. Thus one can only speculate about this disparity. Yet, our findings contradict the assumption that the nondominant arm controller is generally less proficient in forming an appropriate internal model for feedforward control (Sainburg 2002; Wang and Sainburg 2004). Likewise, we cannot support the idea that the nondominant arm controller relies more on an impedance control than on feedforward control during reaching under changed dynamic conditions (Sainburg 2002; Schabowsky et al. 2007). Moreover, the left hand's higher deviations during force field catch trials challenge the assumption that the nondominant arm generally relies more on impedance control and therefore makes use of higher arm stiffness (Schabowsky et al. 2007).
Intermanual Transfer of Dynamic Learning is Bidirectional
Our second main finding is that dynamic learning can transfer both from dominant to nondominant hand, and vice versa. Former research reported only unidirectional transfer from dominant to nondominant hand (Criscimagna-Hemminger et al. 2003; Galea et al. 2007; Wang and Sainburg 2004). This unidirectional transfer was explained by the above-discussed potential different abilities of the dominant and nondominant arm controllers to form an appropriate internal model of the task dynamics (Wang and Sainburg 2004). Accordingly, the formation of such an internal model is critical for intermanual transfer. However, for methodological reasons, the aforementioned studies were not able to measure solely internal model formation without overlap of learning or feedback mechanisms or increased arm stiffness due to impedance control. Therefore, in these studies, effector specific differences in the attained feedforward adaptation level and acquired motor memory were not specifically assessed. Nevertheless, we also suggest that the formation of an internal model is mandatory for intermanual transfer. However, we propose that this can be accomplished for either arm in comparable quality and serve as the basis for bidirectional transfer.
We found that subjects learned, on average, 63% (right) and 65% (left) of the force field, and we found intermanual transfer of 20% (right to left) and 24% (left to right) immediately after adaptation in the form of a practice-dependent bias. For a similar learning schedule and the same performance measure, Joiner et al. (2013) found that subjects learned, on average, 77% of the force field, and they assessed intermanual transfer of 9% (right to left). Maybe the small differences in the attained adaptation level and amount of transfer are attributed to slight differences in the experimental setup (arm support, amount of targets). In any case, our quantitative results are more similar to those of Joiner et al. (2013) than to the 50% intermanual transfer reported by Malfait and Ostry (2004). These quantitative differences might be explained by the performance measure used, as discussed previously by Joiner et al. (2013). They argued that the feedforward adaptation, which is of interest, is overlapped by feedback control and increased stiffness when transfer was measured using force field trials. Moreover, measuring transfer with the use of force field trials also induces learning processes as the learning stimulus is presented. It becomes apparent that learning the considered task proceeds at a very high rate when our results on practice-dependent bias and interlimb savings are compared. We found significant transfer in the form of practice-dependent bias on error-clamp trials. In contrast, we did not detect this clear transfer when subjects were exposed to the force field and their initial performance was compared with that of naive subjects (interlimb savings). In our opinion, this is attributed to the rapid initial learning processes induced by force field exposure, which complicates detection of transfer. Maybe former studies were subject to this methodical issue, and thus potential bidirectional transfer remained hidden. However, note that we only found clear bidirectional transfer in terms of practice-dependent bias; we did not detect such clear transfer in terms of interlimb savings. At this point, we were not able to replicate the findings of Criscimagna-Hemminger et al. (2003), who detected interlimb savings in the direction from dominant to nondominant hand, which suggests that the aforementioned methodical issues (e.g., feedforward adaptation overlapped by feedback control, measuring transfer while adapting to the force field) may not be the only reason for the asymmetrical transfer observed in previous studies.
We found that transfer occurred in extrinsic coordinates. This is in line with findings of Criscimagna-Hemminger et al. (2003) as well as Malfait and Ostry (2004) and contrasts the findings of Wang and Sainburg (2004) and Galea et al. (2007), who found transfer within an intrinsic (joint based) coordinate frame. It is possible that intermanual transfer (in terms of interlimb savings) would have occurred in intrinsic coordinates if we specifically tested it by presenting a counterclockwise force field in the transfer test. However, it is unlikely that subjects who showed the reported transfer (practice-dependent bias) in extrinsic coordinates on error-clamp trials would immediately afterward switch their prediction and show transfer by means of interlimb savings in intrinsic coordinates.
These diverging results on the coordinate frame of transfer indicate that the internal representation of movements is highly specific to the task and the experimental setup. For instance, the coordinate frame of transfer might depend on whether the same object is handled with both arms (e.g., 1 robot handle; Criscimagna-Hemminger et al. 2003; Malfait and Ostry 2004) or whether two different objects are handled (e.g., 2 robotic handles; Galea et al. 2007) or additional loads are attached to either hand (Wang and Sainburg 2004). When one single object is handled with both hands (present study; Criscimagna-Hemminger et al. 2003; Malfait and Ostry 2004), transfer may occur preferentially in extrinsic coordinates because the changed dynamics are linked to the external object rather than to the limb dynamics. In the latter cases (Galea et al. 2007; Wang and Sainburg 2004), transfer may have occurred preferentially in intrinsic coordinates. This would match findings by Cothros et al. (2006), who suggested the acquisition of a distinct internal model of the dynamics of an object separate from internal models used to control limb dynamics. Another influencing factor might be the workspace in which movements are performed. Research suggests that reaching near or across the midline implies different motor control features compared with reaching in the ipsilateral hemispace (e.g., Bryden et al. 2011). Potentially, intermanual transfer might also be influenced by the workspace in which the original task is learned. Practice near the midline, as in our study, preferentially yielded to transfer in extrinsic coordinates (Criscimagna-Hemminger et al. 2003; DiZio and Lackner 1995), whereas movements that were performed in ipsilateral hemispace were rather shown to be transferred in intrinsic coordinates (Wang and Sainburg 2004). Furthermore, visual feedback of one's own arm or the cursor representing the end point being controlled, as well as whether the visual feedback is aligned vs. nonaligned, might influence the internal representation of a task and therewith the coordinate frame of transfer (Parmar et al. 2015). Moreover, as supposed by Galea et al. (2007), the coordinate frame of transfer might also be attributed to the type of observed motor error and the visual cues providing this information.
Presumably, the internal representation of movements, and therefore the coordinate frame of intermanual transfer, is a combination of different coordinate frames that is modulated by diverse task specifications. Recent investigations suggest such a mixture of internal representations underlying both intramanual (Berniker et al. 2014; Parmar et al. 2015) and intermanual generalization (Parmar et al. 2015).
Taking these findings together, we found bidirectional intermanual transfer in terms of practice-dependent bias that occurred in extrinsic coordinates. Yet, the magnitude of transfer and the coordinate frame of transfer appear to be influenced by diverse task specifications. However, the observed transfer effects seem to play a minor role compared with the fast initial adaptation processes. Because transfer characteristics are of high interest from a theoretical point of view and give insights to fundamental motor learning mechanisms, future studies should account for the methodical difficulties in detecting transfer. Moreover, further research should examine whether transfer in more complex motor tasks has more robust features, giving transfer subjects a substantial advantage in performance compared with naive subjects.
Intermanual Transfer Effects Weaken with Time
Despite the observed bidirectional intermanual transfer of motor memory immediately after adaptation, transfer of motor memory declined with time. After the 24-h consolidation period, transfer from nondominant to dominant hand decreased and, in the case of dominant to nondominant hand, even vanished. Considering the initially mentioned importance of consolidation and sleep on motor memory formation (Censor 2013; Rasch and Born 2013), this finding is surprising.
Transfer in terms of practice-dependent bias decreased with the consolidation period. On error-clamp trials following the consolidation period, we only detected a small amount of transfer from the nondominant to the dominant hand (LRc group). Generally, a decrease of motor performance and therewith a decrease of transfer effects after a consolidation period could be caused by a warm-up decrement. This phenomenon refers to a decrement in performance caused by temporary factors rather than memory loss, e.g., loss of internal states that are critical for the motor action (Kantak and Winstein 2012; Schmidt and Lee 2011). Yet, potential transfer should have been detectable in our interlimb savings test block despite warm-up decrement because the internal set was reinstated. However, even when exposed to the force field, subjects did not show interlimb savings. Thus processes of consolidation did not facilitate intermanual transfer in the considered task, but rather weakened transfer effects. Plenty of former studies found consolidation of motor memory for this specific task when the retest was performed with the training hand (Brashers-Krug et al. 1996; Caithness et al. 2004; Focke et al. 2013; Overduin et al. 2006; Shadmehr and Holcomb 1997; Stockinger et al. 2014). This indicates that motor memory underlying the considered task is, in principle, sensitive to consolidation. Possibly, the consolidation period only fosters the stabilization of an effector-specific internal representation rather than a more generalized internal representation.
Neural Processes and Models of Intermanual Transfer
Previous research proposed several potential neural processes underlying transfer and generalization of motor memory. In the context of intermanual transfer, the most common explanations are the cross-activation model and the bilateral access model (for review, see Ruddy and Carson 2013). According to the cross-activation model, unilateral practice causes bilateral adaptation by increasing motor activity not only in the contralateral hemisphere, which controls the arm, but also in the ipsilateral hemisphere. Thereby, during adaptation, an inferior motor program is built in the contralateral hemisphere, which is used on the transfer test. The bilateral access model states that motor adaptation occurs in neural regions that are involved in the control of the trained hand but also are accessible to the untrained hand (Anguera et al. 2007; Ruddy and Carson 2013). Regarding the bidirectional transfer in our experiment, both models may account for our findings. However, our study was not designed to examine intermanual transfer on a neural level. For the purpose of a more elaborate theory of neural processes underlying the transfer, further studies using functional imaging techniques are needed.
GRANTS
Young Investigator Group “Computational Motor Control and Learning” received financial support from the “Concept for the Future” of Karlsruhe Institute of Technology within the framework of the German Excellence Initiative.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
C.S., B.T., A.F., and T.S. conception and design of research; C.S. performed experiments; C.S. analyzed data; C.S., B.T., and T.S. interpreted results of experiments; C.S. prepared figures; C.S. drafted manuscript; C.S., B.T., A.F., and T.S. edited and revised manuscript; C.S., B.T., A.F., and T.S. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Matthias Pöschl for technical support as well as Simon Renner and Thomas Kaib for their aid in data acquisition.
REFERENCES
- Anguera JA, Russel CA, Noll DC, Seidler RD. Neural correlates associated with intermanual transfer of sensorimotor adaptation. Brain Res 1185: 136–151, 2007. [DOI] [PubMed] [Google Scholar]
- Berniker M, Franklin DW, Flanagan JR, Wolpert DM, Kording K. Motor learning of novel dynamics is not represented in a single global coordinate system: evaluation of mixed coordinate representations and local learning. J Neurophysiol 111: 1165–1182, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brashers-Krug T, Shadmehr R, Bizzi E. Consolidation in human motor memory. Nature 382: 252–255, 1996. [DOI] [PubMed] [Google Scholar]
- Bryden PJ, Mayer M, Roy EA. Influences of task complexity, object location, and object type on hand selection in reaching in left and right-handed children and adults. Dev Psychobiol 53: 47–58, 2011. [DOI] [PubMed] [Google Scholar]
- Caithness G, Osu R, Bays P, Chase H, Klassen J, Kawato M, Wolpert DM, Flanagan JR. Failure to consolidate the consolidation theory of learning for sensorimotor adaptation tasks. J Neurosci 24: 8662–8671, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Censor N. Generalization of perceptual and motor learning: a causal link with memory encoding and consolidation? Neuroscience 205: 201–207, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J. Statistical Power Analysis for the Behavioral Sciences. Hillsdale, NJ: Erlbaum, 1988. [Google Scholar]
- Cothros N, Wong JD, Gribble PL. Are there distinct neural representations of object and limb dynamics? Exp Brain Res 173: 689–697, 2006. [DOI] [PubMed] [Google Scholar]
- Criscimagna-Hemminger SE, Donchin O, Gazzaniga MS, Shadmehr R. Learned dynamics of reaching movements generalize from dominant to nondominant arm. J Neurophysiol 89: 168–176, 2003. [DOI] [PubMed] [Google Scholar]
- Davidson PR, Wolpert DM. Scaling down motor memories: de-adaptation after motor learning. Neurosci Lett 370: 102–107, 2004. [DOI] [PubMed] [Google Scholar]
- DiZio P, Lackner JR. Motor adaptation to Coriolis force perturbations of reaching movements: endpoint but not trajectory adaptation transfers to the nonexposed arm. J Neurophysiol 74: 1787–1792, 1995. [DOI] [PubMed] [Google Scholar]
- Donchin O, Rabe K, Diedrichsen J, Lally N, Schoch B, Gizewski ER, Timmann D. Cerebellar regions involved in adaptation to force field and visuomotor perturbation. J Neurophysiol 107: 134–147, 2012. [DOI] [PubMed] [Google Scholar]
- Duff SV, Sainburg RL. Lateralization of motor adaptation reveals independence in control of trajectory and steady-state position. Exp Brain Res 179: 551–561, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Focke A, Stockinger C, Diepold C, Taubert M, Stein T. The influence of catch trials on the consolidation of motor memory in force field adaptation tasks. Front Psychol 4: 479, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galea JM, Miall RC, Woolley DG. Asymmetric interlimb transfer of concurrent adaptation to opposing dynamic forces. Exp Brain Res 182: 267–273, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm S. A simple sequentially rejective multiple test procedure. Scand J Statist 6: 65–70, 1979. [Google Scholar]
- Joiner WM, Brayanov JB, Smith MA. The training schedule affects the stability, not the magnitude, of the interlimb transfer of learned dynamics. J Neurophysiol 110: 984–998, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joiner WM, Smith MA. Long-term retention explained by a model of short-term learning in the adaptive control of reaching. J Neurophysiol 100: 2948–2955, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kantak SS, Winstein CJ. Learning-performance distinction and memory processes for motor skills: a focused review and perspective. Behav Brain Res 228: 219–231, 2012. [DOI] [PubMed] [Google Scholar]
- Krakauer JW, Ghilardi MF, Ghez C. Independent learning of internal models for kinematic and dynamic control of reaching. Nat Neurosci 2: 1026–1031, 1999. [DOI] [PubMed] [Google Scholar]
- Magill RA. Motor Learning and Control: Concepts and Applications (8th ed). New York: McGraw-Hill, 2007. [Google Scholar]
- Malfait N, Ostry DJ. Is interlimb transfer of force-field adaptation a cognitive response to the sudden introduction of load? J Neurosci 24: 8084–8089, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattar AA, Ostry DJ. Neural averaging in motor learning. J Neurophysiol 97: 220–228, 2007. [DOI] [PubMed] [Google Scholar]
- Mostafa AA, Salomonczyk D, Cressman EK, Henriques DY. Intermanual transfer and proprioceptive recalibration following training with translated visual feedback of the hand. Exp Brain Res 232: 1639–1651, 2014. [DOI] [PubMed] [Google Scholar]
- Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychololgia 9: 97–113, 1971. [DOI] [PubMed] [Google Scholar]
- Overduin SA, Richardson AG, Lane CE, Bizzi E, Press DZ. Intermittent practice facilitates stable motor memories. J Neurosci 26: 11888–11892, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parmar PN, Huang VC, Patton JL. Evidence of multiple coordinate representations during generalization of motor learning. Exp Brain Res 233: 1–13, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pekny SE, Criscimagna-Hemminger SE, Shadmehr R. Protection and expression of human motor memories. J Neurosci 31: 13829–13839, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasch B, Born J. About sleep's role in memory. Physiol Rev 93: 681–766, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson EM, Pascual-Leone A, Miall RC. Current concepts in procedural consolidation. Nat Rev Neurosci 5: 576–582, 2004. [DOI] [PubMed] [Google Scholar]
- Ruddy KL, Carson RG. Neural pathways mediating cross education of motor function. Front Hum Neurosci 7: 397, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL. Evidence for a dynamic-dominance hypothesis of handedness. Exp Brain Res 142: 241–258, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Wang J. Interlimb transfer of visuomotor rotations: independence of direction and final position information. Exp Brain Res 145: 437–447, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schabowsky CN, Hidler JM, Lum PS. Greater reliance on impedance control in the nondominant arm compared with the dominant arm when adapting to a novel dynamic environment. Exp Brain Res 182: 567–577, 2007. [DOI] [PubMed] [Google Scholar]
- Scheidt RA, Reinkensmeyer DJ, Conditt MA, Rymer WZ, Mussa-Ivaldi FA. Persistence of motor adaptation during constrained, multi-joint, arm movements. J Neurophysiol 84: 853–862, 2000. [DOI] [PubMed] [Google Scholar]
- Schmidt RA, Lee TD. Motor Control and Learning: A Behavioral Emphasis (5th ed). Champaign, IL: Human Kinetics, 2011. [Google Scholar]
- Shadmehr R, Holcomb HH. Neural correlates of motor memory consolidation. Science 277: 821–825, 1997. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi F. Adaptive representation of dynamics during learning of a motor task. J Neurosci 14: 3208–3224, 1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stockinger C, Focke A, Stein T. Catch trials in force field learning influence adaptation and consolidation of human motor memory. Front Hum Neurosci 8: 231, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stockinger C, Pöschl M, Focke A, Stein T. ManipAnalysis - a software application for the analysis of force field experiments. Int J Comput Sci Sport 11: 52–57, 2012. [Google Scholar]
- Taylor JA, Wojaczynski GJ, Ivry RB. Trial-by-trial analysis of intermanual transfer during visuomotor adaptation. J Neurophysiol 106: 3157–3172, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Sainburg RL. Interlimb transfer of novel inertial dynamics is asymmetrical. J Neurophysiol 92: 349–360, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]