Dynamics of visual receptive fields in the macaque frontal eye field

Abstract

Neuronal receptive fields (RFs) provide the foundation for understanding systems-level sensory processing. In early visual areas, investigators have mapped RFs in detail using stochastic stimuli and sophisticated analytical approaches. Much less is known about RFs in prefrontal cortex. Visual stimuli used for mapping RFs in prefrontal cortex tend to cover a small range of spatial and temporal parameters, making it difficult to understand their role in visual processing. To address these shortcomings, we implemented a generalized linear model to measure the RFs of neurons in the macaque frontal eye field (FEF) in response to sparse, full-field stimuli. Our high-resolution, probabilistic approach tracked the evolution of RFs during passive fixation, and we validated our results against conventional measures. We found that FEF neurons exhibited a surprising level of sensitivity to stimuli presented as briefly as 10 ms or to multiple dots presented simultaneously, suggesting that FEF visual responses are more precise than previously appreciated. FEF RF spatial structures were largely maintained over time and between stimulus conditions. Our results demonstrate that the application of probabilistic RF mapping to FEF and similar association areas is an important tool for clarifying the neuronal mechanisms of cognition.

the receptive fields (RFs) of frontal eye field (FEF) neurons are often mapped using reduced stimulus parameters outside of the context of the main experimental task (Bruce and Goldberg 1985; Ferrera et al. 2009; Mayo and Sommer 2008; Phillips and Segraves 2010; Stanford et al. 2010; Thompson and Schall 1999). This conventional approach is generally restricted to localizing RF centers for subsequent stimulus presentation. Coarse maps of RFs seemed sufficient given the history of finding little visual selectivity in FEF visual responses (but see Barborica and Ferrera 2003; Mohler et al. 1973; Xiao et al. 2006) and the general hypothesis that the FEF and similar association areas, such as lateral intraparietal cortex, engage more in spatial operations, “pointing” to locations for perisaccadic vision or motor planning, than in featural analyses (e.g., Cavanagh et al. 2010; Mayo and Sommer 2010). However, conventional RF mapping limits broader studies of visuomotor capabilities across FEF neurons such as RF interactions and task-dependent changes in RF sensitivity.

Our understanding of FEF RFs is therefore impoverished except for some efforts to examine their spatial structure (Cavanaugh et al. 2012; Schall et al. 2004). One concern about the lack of detail is that it may contribute to misinterpretations of data. The study of presaccadic remapping provides one possible example. The RFs in FEF and other regions of visual cortex can shift their retinal positions just before a saccade (Duhamel et al. 1992; Sommer and Wurtz 2006; Umeno and Goldberg 1997). Such shifts are usually measured by characterizing RF centers, leaving open the possibility that apparent differences in RF dynamics across studies could stem from trivial experimental differences. For example, large RFs may appear to shift continuously, as opposed to jump discretely, because the “original” and “future” RFs overlap but could not be measured simultaneously. Thus improved RF measures with better spatial precision could help to elucidate the role of FEF in vision.

Improvements in the temporal precision of FEF RF measurements are also needed. The majority of previous work on RF dynamics probed the RF location once or twice per trial (Joiner et al. 2013; Sommer and Wurtz 2006; Umeno and Goldberg 1997; Zirnsak et al. 2014). Even though some studies used brief stimuli, around 25–50 ms in duration, a more complete understanding of active vision may require temporally precise knowledge about the dynamics of neuronal responses to multiple, repeated stimuli. However, it is unclear whether FEF visual responses maintain their fidelity at fast stimulus presentation rates. More precise measures of temporal sensitivity would therefore help clarify the role of FEF in dynamic cognitive processing.

As a first step in characterizing FEF RFs in detail, we focused on their spatiotemporal organization during steady fixation. We mapped the extent of FEF RFs with high temporal precision using sparse, stochastic dot stimuli. We used a probabilistic approach to measure the relationship between visual stimuli and spiking activity in FEF neurons using a generalized linear model (GLM; Kelly et al. 2010; Pillow et al. 2008). Probabilistic mapping provided a richer measure of FEF RFs from a comparable amount of data obtained using conventional methods. FEF neurons had reliable responses to repeated stochastic dots shown as briefly as 10 ms if only one or a few dots were present on the screen simultaneously. Our findings characterize the time course of visual sensitivity in FEF neurons and provide a foundation for studying the neuronal circuitry underlying stable visual perception and motor planning during natural behavior.

MATERIALS AND METHODS

Surgical preparation.

Two adult rhesus macaques, one female and one male (Macaca mulatta; monkeys L and U), were surgically implanted with headposts and an FEF recording chamber (stereotaxic coordinates: 25 mm anterior, 20 mm lateral) using sterile surgical techniques under isoflurane anesthesia. All procedures were approved by the Institutional Animal Care and Use Committee of the University of Pittsburgh and complied with guidelines set forth in the National Institutes of Health (NIH) Guide for the Care and Use of Laboratory Animals.

Experimental setup.

Stimuli were displayed on a 21-in. cathode-ray-tube (CRT) monitor with a resolution of 1,024 × 768/768 × 384 pixels and a refresh rate of 60/100 Hz at a distance of 36/43 cm (monkey L/U). All stimuli were white dots (104 cd/m²) on a black background (0.0 cd/m²). Stimuli were generated using the Rex real-time system (Hays et al. 1982) for monkey L and custom software written in MATLAB (MathWorks, Natick, MA) including Psychophysics Toolbox extensions (Brainard 1997; Kleiner et al. 2007) for monkey U. Stimulus timing and alignment was confirmed using a photodiode. Eye position was monitored via infrared eye tracking (monkey L: ISCAN, Woburn, MA; monkey U: EyeLink 1000, SR Research, Mississauga, Canada). We acquired data with the Rex real-time system for monkey L and a Grapevine recording system (Ripple, Salt Lake City, UT) for monkey U.

Electrophysiological methods.

Extracellular recordings were made with tungsten microelectrodes (300-kΩ to 1-MΩ impedance at 1 kHz; FHC, Bowdoin, ME) advanced with an NIH-designed mechanical microdrive (Laboratory for Sensorimotor Research, Bethesda, MD). Recordings were aligned using a plastic grid placed inside of the recording chamber (Crist Instruments, Hagerstown, MD). FEF was visually identified on the anterior bank of the arcuate sulcus and physiologically verified as the chamber grid holes where we could evoke fixed-vector saccades reliably (>50% of the time) using low-current (≤50 μA for 70 ms) microstimulation (Bruce et al. 1985) and grid holes immediately adjacent to those sites. Isolation of single neurons was performed online using time-amplitude window discrimination and later refined offline using custom software in MATLAB (Kelly et al. 2007). We typically recorded one isolated neuron per recording session but occasionally isolated two units.

Conventional RF mapping.

The conventional RF of each neuron was mapped using a memory-guided saccade (MGS) task (Hikosaka and Wurtz 1983). The trial began when the monkey fixated a central blue circle (0.5° diameter). After maintaining fixation within 1.8° for 200 ms, a peripheral target (1.8° diameter) was flashed for 50 ms at one of eight locations (cardinal and orthogonal directions, typically 10° from fixation). The animal was required to maintain fixation for another 250 or 400 ms until the fixation point was extinguished. If the animal made a saccade to the previously cued (remembered) location within 200 ms and maintained gaze within 2.7° of that location for 150 ms, it received a liquid reward. One block consisted of pseudorandomized presentations of all eight directions, and typically ten blocks were acquired per neuron. Visually guided saccades (VGS) were occasionally used instead of the MGS task to map RFs.

Characterization of classic RFs.

The location of the classic RF of each neuron was determined using vector averaging of neuronal responses across radial stimulus positions in the MGS or VGS task. A tuning bias vector was calculated (Leventhal et al. 1995) to determine the direction of the conventional RF relative to fixation (Fig. 1A). Mean visual responses at a range of amplitudes (e.g., 3–30°) during a second series of saccades at or near the preferred direction were fitted with a Gaussian function (MATLAB function: lsqcurvefit). The peak of that function defined the best amplitude for a given neuron.

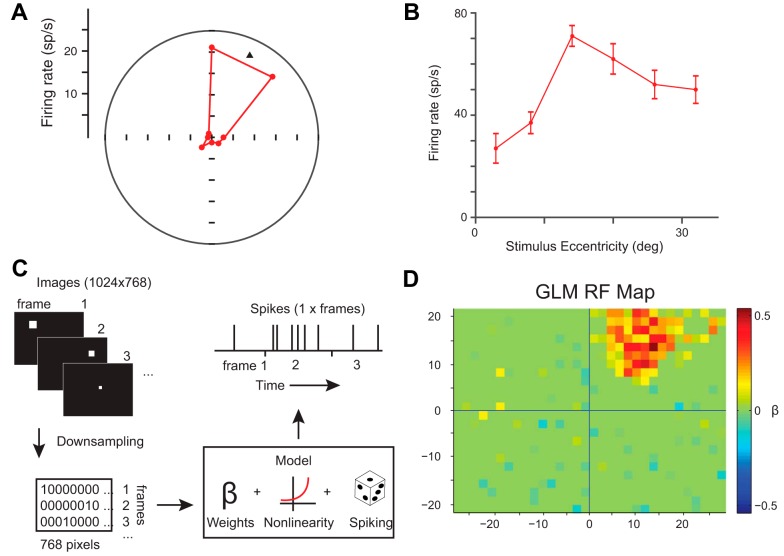
Fig. 1.

Conventional and probabilistic (glmRF) receptive field (RF) mapping for an example neuron. A: polar plot illustrating direction tuning of the visual response (50–150 ms after target onset) during the memory-guided saccade task. The black triangle indicates the vector fit of the preferred direction. sp/s, Spikes per second. B: tuning of the visual response at 6 eccentricities along the preferred direction. deg, Degrees. C: schematic illustrating the generalized linear model (GLM); see materials and methods for details. D: resulting glmRF for this neuron.

Visuomotor and sustained-transient indices.

Following identification of the direction and amplitude of the RF, we used the same responses to determine the relative strength of the visual and motor components of a neuron. The visual response was defined as 50–150 ms after stimulus onset, and the motor response was defined as −50 to 50 ms around saccade onset. Baseline firing rate was also calculated from the 100 ms preceding stimulus onset. The number of spikes within each epoch across all directions was used to calculate a visuomotor index (VMI) for each neuron [(visual − motor)/(visual + motor); Bruce and Goldberg 1985]. VMI ranges from −1 for neurons with purely movement responses to 1 for neurons with purely visual responses.

A similar procedure was used to estimate the relative amount of sustained and transient activity to produce a transient-sustained index (TSI) per neuron. We defined the transient component as the firing rate 0–50 ms after the time to half of the maximum of the initial visual response (half max.) and the sustained component as the firing rate 50–100 ms after time to half max., where (transient − sustained)/(transient + sustained). TSI ranged from −1 for neurons with only sustained responses to 1 for neurons with only transient responses.

A signal-to-noise ratio (SNR) was calculated for units recorded on the Grapevine system to estimate neuronal isolation. The SNR was determined as the ratio of the amplitude of the average waveform to the standard deviation of the noise (Kelly et al. 2007).

Probabilistic RF mapping.

After conventional RF mapping, we used stochastic dot stimuli to map the same RF probabilistically. Animals were trained to fixate on a central blue circle (3 s for monkey U, 2 s for monkey L). During this time, white square dots were presented at random locations over the entire screen, and each dot was scaled to increase in size with eccentricity to match approximately the magnification factor in V1 RFs (Dow et al. 1981). At the extremes, a dot shown at fixation was ∼0.16° in diameter, and a dot at the rightward edge of the screen at the vertical midpoint (∼28° eccentric) was ∼0.95° in diameter. A single trial consisted of many dot stimulus images that were refreshed many times. The passive fixation task reduced the influence of saccade planning on neuronal activity and increased the number of possible stimulation presentations per trial. If the monkey broke fixation or made a saccade to one of the RF-probing stimuli, the trial was aborted and no reward given. Dots were flashed briefly (10–167 ms per image), and animals quickly learned not to respond to them. All analyses were performed on correctly completed trials.

To probe the spatial and temporal sensitivity of FEF neurons, we varied 1) the number of dots presented per stimulus image (“dots task”), or 2) the duration of each stimulus image per frame (“dwell task”). For monkey U, we varied parameters across randomly interleaved trials in one of three ways: one, two, or eight dots per image at 70-ms image duration; one dot per image at 30-, 70-, or 150-ms image durations; or one dot per image at 10- or 70-ms image durations. For monkey L, we used one dot per image at 167-ms image duration. In all cases, the number of dots per image and the image durations were fixed within a trial. We varied at most 1 parameter (number of dots or image duration) per recording session. We recorded 535 ± 38 SE (range: 96-1,590) trials per condition per session. Because of issues inherent in maintaining neuronal isolation, we were not able to record conventional and probabilistic RFs for every neuron; for this reason, we provide the sample sizes in Figs. 2, 4, and 5.

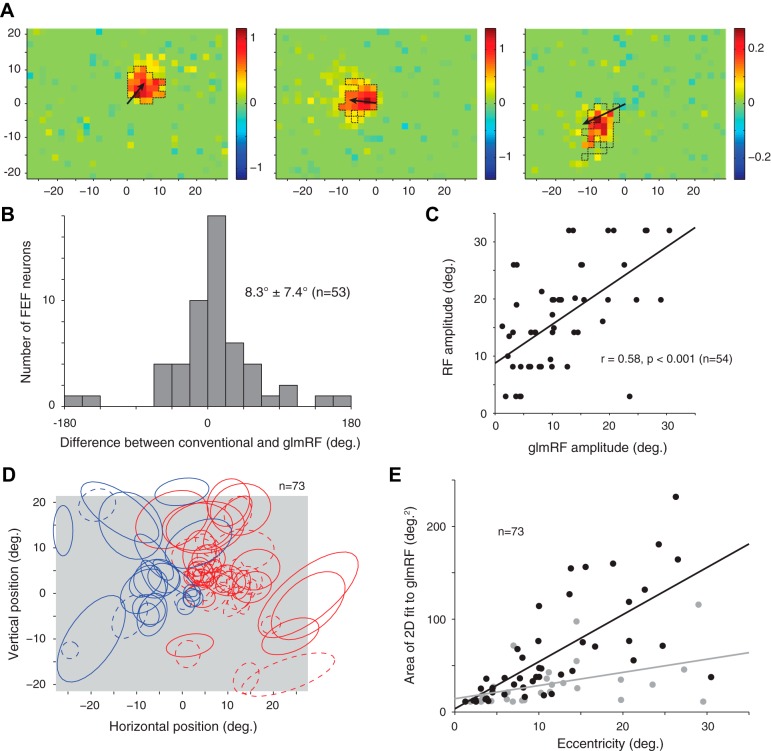
Fig. 2.

A: 3 additional example glmRFs with an arrow indicating the direction and amplitude of the preferred visual stimulus using conventional RF mapping. Thin, dashed black lines outline the significant contiguous pixels as determined by permutation test. B: distribution of angular differences between the preferred direction from conventional RF mapping and the peak of the glmRF [from a 2-dimensional (2-D) Gaussian fit]. FEF, frontal eye field. C: scatterplot of the amplitude or eccentricity of the RF as determined by conventional RF mapping and the glmRF. Note that the extra data point in this panel represents a neuron for which we measured amplitude but not direction tuning. D: ellipsoids representing the 2-D Gaussian fit are plotted here for all neurons with a significant glmRF. Each ellipse is drawn with its major and minor axis radius equal to 1 SD of the corresponding axis of the best-fit Gaussian. Red represents neurons recorded from the left hemisphere and blue represents neurons recorded from the right hemisphere for the glmRFs for neurons that passed the cross-validation test (solid lines) or that failed the cross-validation but passed the resampling test (dashed lines). E: scatterplot of the RF area as a function of RF eccentricity for the glmRFs for neurons that passed the cross-validation test (black dots and line) or that failed the cross-validation but passed the resampling test (gray dots and line).

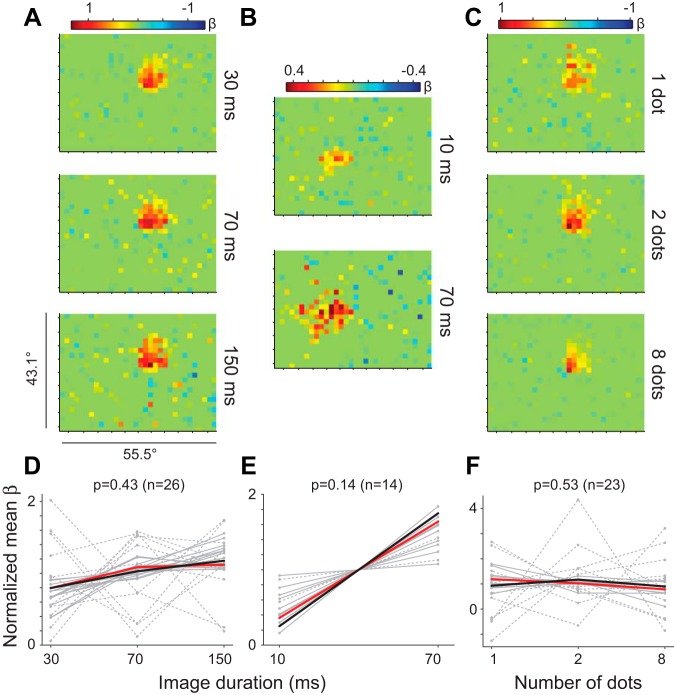
Fig. 4.

A: population-averaged temporal kernels for the neurons tested at image durations of 30 ms (blue line) and 10 ms (red line). The shading indicates ±1 SE. B: average of the r value matrices for all neurons at the optimal condition for each neuron (n = 73).

Fig. 5.

Spatiotemporal tuning by task. A–C: example glmRFs for 3 neurons (1 for each task). D: image duration task where a dot was held on the screen for 30, 70, or 150 ms before a new dot location was chosen. E: image duration task with each dot held on the screen for 10 or 70 ms. Note that 1 outlying neuron was removed for display purposes (although it followed the same trend). F: dot density task with image duration held at 70 ms while the number of dots per image was 1, 2, or 8. Dashed lines represent cells that failed the cross-validation test. Each panel (D–F) shows the normalized mean β for each of the recorded neurons (gray lines) in all conditions, with the mean across neurons shown by a thick black line. Red lines represent example neurons.

GLM for probabilistic RF mapping.

For each neuron, we formulated a GLM to predict the spiking activity (Y) as a linear combination of the pixel values (X) and noise: Y = Xβ + e, where β are the coefficients or weights fit by the GLM and e is an error term. For computational expediency, we downsampled the screen by a factor of 32 to create “superpixels,” each ∼1.9° square. Each superpixel was assigned a value of 1 if it contained an illuminated pixel in the full image and 0 if it did not. A value between 0 and 1 was assigned if a dot stimulus fell on the border, based on the proportion of its area in each superpixel. This process resulted in a 32- × 24-element matrix (a 768-element vector) for each dot image shown in experiments with monkey U. We used a 24- × 16-element matrix and a 384-element vector for monkey L, but the analysis was otherwise identical. This vector became a row in the design matrix X, and the number of rows in X was determined by the number of dot images shown (concatenated across fixation trials). For each row in X, we counted spikes occurring within a time window of Δt to Δt + d (in milliseconds) relative to the dot image onset. Δt and d account for the visual onset latency and the duration of the impulse response for each neuron. Solving the GLM produces a coefficient matrix β with 768 values representing the coefficients that predict spiking from the visual stimulus at the location on the screen of each superpixel, a “probabil-istic RF” (glmRF).

GLM fits were obtained using the “glmnet” toolbox in MATLAB (Friedman et al. 2010). We set the maximum of the nonzero λs to 20% of the pixel values and used an α-value of 1 (lasso regression, an L1-norm). Our results were not sensitive to the particular parameters of the GLM within a wide range of options, and ridge regression (L2-norm) produced qualitatively similar results.

We used fivefold cross-validation to compare GLMs across conditions. Additionally, conditions with faster frame rates (e.g., 10 and 30 ms per image) consisted of more stimulus presentations than slower frame-rate conditions (e.g., 150 ms per image). The difference in total stimuli presented in each condition could lead to differences in the quality of GLM fits between conditions, so we subsampled the number of trials in the dwell task such that the total number of stimulus presentations was equal across conditions. For nonoverlapping sets of 80% of these trials, we obtained a GLM fit. For each of these five sets of β-values, we evaluated the fit equation of the GLM to produce estimated spike trains in response to images from the training trials in all conditions. In this way, we could ensure that GLMs were not specific to the conditions in which they were built. For each model and cross-validation iteration, we computed the Pearson correlation between the predicted and observed spike counts, giving us a correlation value (r) and P value. The mean of these five values was used to evaluate the predictive power of the RF model for each cell in each condition (see Statistical evaluation of probabilistic RFs below).

To estimate the ideal spike window latency and duration for each neuron, we 1st fit the spiking activity with 624 different GLMs (26 latencies, 0–250 ms in 10-ms steps × 24 durations, 10–250 ms in 10-ms steps) for each condition, spanning the range of plausible FEF response latencies and durations (Mayo and Sommer 2013). The 624 GLMs were fit to the equivalently sampled data. A 2-dimensional (2-D) Gaussian was fit to the resulting GLM matrix (Fig. 3C), and the location of its peak was selected as the optimal spike window latency and duration. Cross-validation was always used when comparing GLMs between conditions or with different spike alignments. Once the optimal condition and spike window were chosen, we fit a 2-D Gaussian to the GLM built on all trials with those parameters to determine the glmRF position and size.

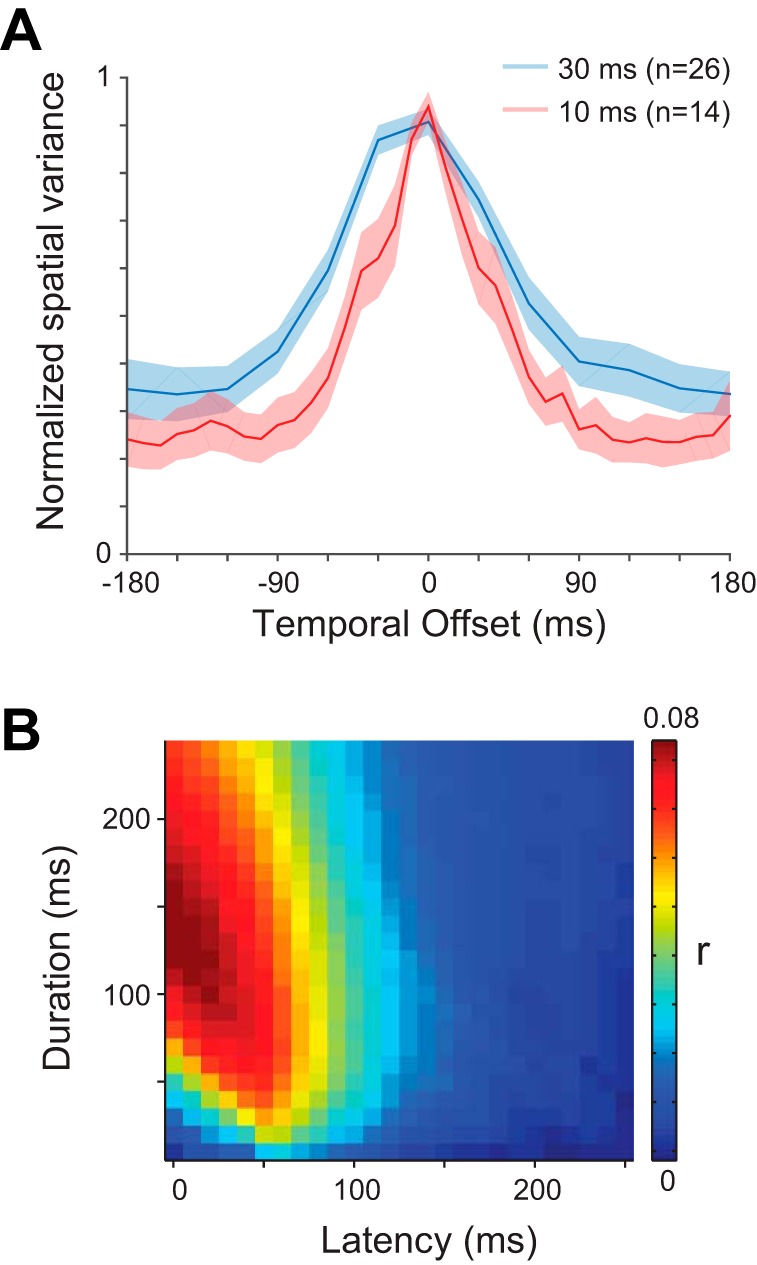
Fig. 3.

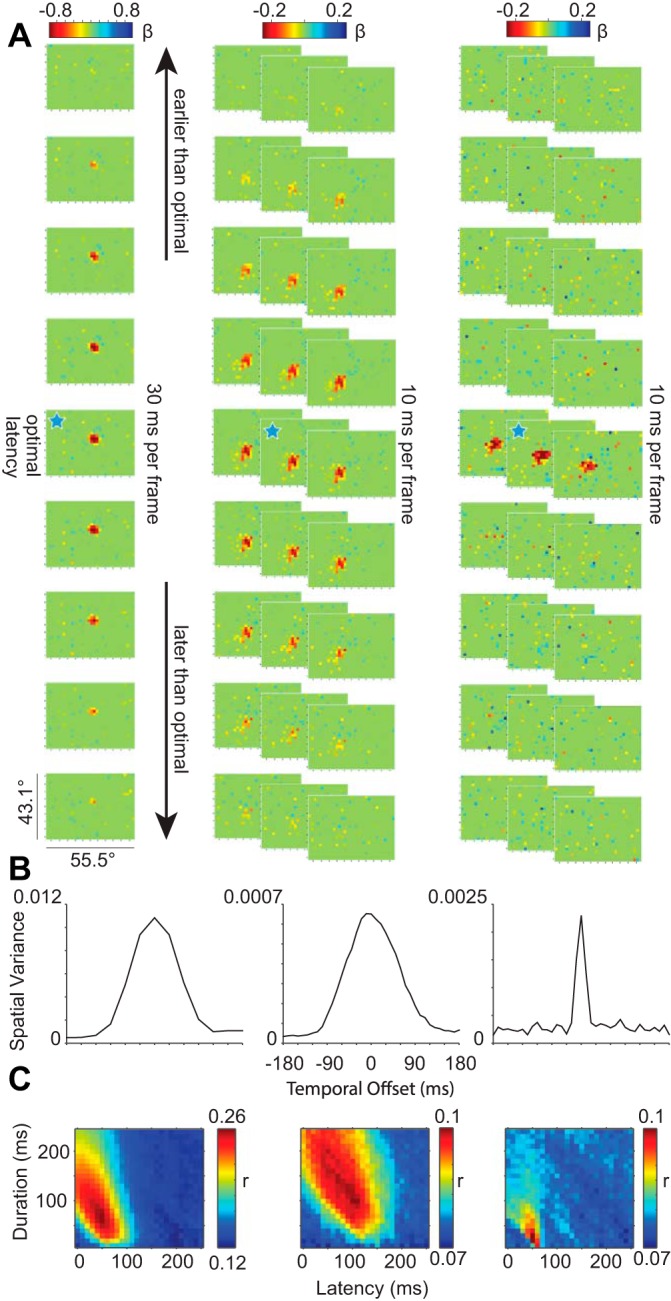
A: spatial plots of glmRFs over time for 3 example neurons with 30-ms image duration (left column) and 10-ms image duration (middle and right columns). In all 3 panels, the ticks on the color bars represent a step of 0.2 in the β-value of the GLM, and the vertical and horizontal ticks on each frame represent steps of 5° as in Figs. 1D and 2A. Ten-millisecond frames in the middle and right columns are stacked so that each row across columns represents a 30-ms progression in time over a total latency range of 270 ms. The blue stars indicate the optimal window delay and width for each of the 3 neurons. B: temporal kernels for the same 3 neurons showing the spatial variance at each temporal offset. C: matrices of the r values of the GLM at each window delay and window width tested.

Statistical evaluation of probabilistic RFs.

For each spatial β-map, we used a resampling test to determine significance. First, we calculated the mean and standard deviation of the β-values and found the area of the largest contiguous set of β-values that were 2 SD away from the mean. Next, we randomly shuffled the β-values 1,000 times and recalculated the largest contiguous area each time. If the area from the original, unshuffled map was at least 3 superpixels (2.7 square degrees per superpixel) large and fell outside of the 99% confidence interval of the shuffled map values, we declared that map as having a significant glmRF. We included any neuron with a significant glmRF on any β-map in further analyses. Three neurons had significant inhibitory RFs without accompanying excitatory RFs, and we did not correct for RFs on the edge of the screen (see elongated RFs in the periphery in Fig. 2D). An identical resampling procedure was used to determine the significance of cross-validation by resampling the contiguous, significant P values (<0.01) of the Pearson r values in the GLM matrices (Fig. 3C). We also included neurons that exhibited clear glmRFs by eye and yielded a significant glmRF after resampling all trials but failed cross-validation (n = 28). These files tended to have fewer trials overall. We found no difference between the cross-validated and “significant by resampling but not cross-validated” cells, but for clarity we represent each population by different symbols in Figs. 2 and 5.

RESULTS

We recorded from 186 neurons in FEF in 2 monkeys (26 from monkey L). We mapped the RFs of FEF neurons using both conventional and GLM-based methods, which yielded the conventional RF and glmRF for each neuron. Mapping RFs and glmRFs allowed us to validate our approach, quantify the accuracy of glmRFs, and measure the relatively stable RF dynamics in FEF.

RFs were mapped conventionally using VGS or MGS. Visual responses to stimuli presented during conventional mapping yielded RF estimates such as those in Fig. 1. The RF of this neuron was located up and to the right (Fig. 1A) and most responsive ∼15° from the fixation point (Fig. 1B).

To address the limitations of conventional mapping, we also measured FEF RFs using probabilistic mapping, which samples the full visual field in an unbiased manner. While the monkey fixated on a central target, they were presented with visual stimuli at pseudorandom locations and rewarded for maintaining fixation. Monkeys learned to ignore the peripheral stimuli within a single training session. In contrast to conventional mapping, which tests a single location per trial, probabilistic mapping permitted us to test dozens to hundreds of stimulus locations per trial. We varied the number of stimuli or the stimulus presentation rate during a recording session to measure the spatial or temporal sensitivity of FEF neurons. Neuronal responses were analyzed as a function of visual stimuli in the sequential video frames using a GLM (with an L1-norm for regularization to produce a sparse model) and statistical analyses (Fig. 1C) to generate the glmRF in space and time. For the same example neuron, we used conventional RF mapping (Fig. 1, A and B) as well as probabilistic mapping using stimulus frames presented every 70 ms during trials consisting of 3 s of fixation. The resulting glmRF (Fig. 1D) matched the conventionally obtained RF well but provided much more detail.

Comparisons of conventionally obtained RFs and glmRFs for 3 other example neurons are summarized in Fig. 2A. We ran the GLM analysis on all 186 FEF neurons and found significant glmRFs for 73 of them (39%), matching proportions found previously (Mohler et al. 1973). For the majority of these (53/73), we obtained conventional RFs as well as glmRFs. Responsiveness to conventional stimuli and noise stimuli was almost identical, such that noise stimuli did not reveal responsivity that was otherwise overlooked in the conventional RF mapping task. We quantified the similarity between the radial directions of the RFs by measuring the angular difference relative to fixation (Fig. 2B). The distribution of differences was not significantly different from 0 (8.3 ± 7.4°; t-test, P = 0.27); more generally, 72% of the RFs and glmRFs of the neurons were within 45° of each other, and 47% were within 20°. We compared this distribution against a bootstrap data set composed of randomly paired RF and glmRF data from different neurons and found that the angular differences we observed were significantly smaller than the chance expectation from this bootstrap test (P < 0.001).

The eccentricities of RFs and glmRFs for each neuron were likewise similar (Fig. 2C). Conventional RF mapping included large amplitude saccades (20–40°) across the full extent of the monitor, whereas probabilistic mapping used fixation in the center of the screen. Conventional mapping therefore tested a larger range of eccentricities than probabilistic mapping and may have led us to underestimate the eccentricity of RFs that overlapped the edge of the display. We fit the conventional RF mapping data with a log Gaussian (Bruce and Goldberg 1985). RF and glmRF amplitudes were highly correlated (Spearman ρ = 0.61, P < 0.001), but conventional RF amplitudes were significantly larger (signed-rank test, P = 0.002). More importantly, probabilistic mapping yielded RFs that were highly consistent with those determined by conventional methods while far exceeding their spatial and temporal resolution.

Given the consistency between conventional and probabilistic RFs, the remaining analyses focus on the more spatially detailed glmRFs. For each neuron, we selected the spike window parameters that provided the best description of its glmRF. The largest area of significant, contiguous screen pixels defined the glmRFs and was fit with a 2-D Gaussian. (Better fits may be achievable with a more complex mixture of Gaussians; this is an avenue for future research.) We recorded from both hemispheres, and glmRFs consequently spanned the full visual field (Fig. 2D, each ellipse drawn with a radius equal to 1 SD of the 2-D Gaussian fit). With one exception, glmRFs were centered in the visual field contralateral to the recording hemisphere. We used the ellipses in Fig. 2D as an estimate of the area of each glmRF. As in other parts of visual cortex and consistent with previous reports (Cavanaugh et al. 2012), glmRFs increased in size as they became more eccentric (Fig. 2E). The relationship between the size of the glmRF and its eccentricity was, as expected, even more pronounced for the best-fit glmRFs (Fig. 2E, black symbols and line). Thus the location, eccentricity, and extent of glmRFs are an excellent match to conventionally derived measures.

We explored the possibility that probabilistic mapping could be biased to yield glmRFs for neurons with certain firing characteristics. We computed four metrics for each neuron (mean ± SE): 1) its baseline firing rate (17.2 ± 1.9 spikes per second); 2) the relative strength of its visual- and saccade-related responses, as measured by the VMI (0.13 ± 0.05); 3) the relative strength of its transient and sustained response components, as measured by the TSI (0.2 ± 0.03); and 4) the quality of single-neuron isolation, as quantified by the SNR of the recording (3.02 ± 0.14). We found no significant correlations between these four metrics and the glmRF goodness of fit (Spearman ρ-values = 0.15, 0.07, −0.12, and 0.12; P > 0.2 for all 4 correlations). We expected more visually responsive neurons (VMI ≈ 1) to yield better glmRFs, but this was not the case. We suspect that this is because the VMI is derived from a saccade task and therefore more susceptible to preparatory motor activity than the passive fixation task and a less sensitive measure of visual responsiveness. Overall, probabilistic mapping was relatively unbiased in its ability to reveal glmRFs in terms of these four distinguishing features.

Probabilistic mapping allows for viewing RF changes over time, and such measurements of the “temporal impulse” of a neuron are essential for determining whether FEF neurons can track stimulus changes on a fine time scale. This issue is related to but distinct from most previous work that measured the responses of FEF neurons to a single brief stimulus presentation. Above, we selected the optimal conditions for each neuron that yielded the best glmRF. To determine the shape of the temporal impulse, we can also shift the spiking activity relative to the time of stimulus presentations to understand the temporal sensitivity of an individual neuron. Figure 3A illustrates the evolution of glmRFs for three neurons each in a 270-ms epoch surrounding the optimal response. For this analysis, all of the image and spiking data were fed into a single GLM run across all temporal offsets, such that the βs were only fit once for the entire temporal kernel. The left column illustrates 9 frames of a glmRF measured at 30-ms resolution, whereas the right 2 columns illustrate 27 frames each of glmRFs measured at a 10-ms resolution. In all cases, there is a smooth transition from no relationship between spikes and stimuli (green), to a punctate, ellipsoidal ideal alignment (red), and back again to baseline (green). An important commonality is that all of them show a surprisingly strong and spatially consistent response even though the stimuli that evoked the responses were brief, rapidly flashed, and stochastic.

The duration of each glmRF clearly differed between individual neurons (optimal spike window duration: 118 ± 5.5 ms, mean ± SE; range: 30–190 ms; n = 63). The dynamics of the glmRFs in Fig. 3A are summarized by their temporal kernels in Fig. 3B. Temporal kernels are created by sliding a fixed-duration spike window over a range of spiking latencies and visual stimulus offsets. They capture changes in visual sensitivity over time, centered on the best-fit spike-stimulus alignment, and summarize the spatial variance of each frame (Yeh et al. 2009). One-dimensional temporal kernels can be expanded to 2-D temporal matrices by allowing the spike window duration also to vary (Fig. 3C). In our analyses, the temporal matrix of a cell covers a broad range of spike window delays and durations and represents the results for 624 independent GLMs per neuron (26 latencies × 24 durations). Correlations between observed and model-predicted spike trains were relatively weak when the spike window was short and immediately followed stimulus onset (bottom left corners of matrices). As the spike window increased in duration, the spiking activity of the GLM was a better match to the actual spike trains (transition from blue to red along left vertical axis). The combination of frame-by-frame plots of visual space (Fig. 3A) and broader descriptions of temporal sensitivity (Fig. 3, B and C) illustrate that the three representative neurons responded well to visual stimuli presented every 10–30 ms.

Because temporal sensitivity varied across individual neurons, we again asked whether factors such as the degree of visual responsiveness or neuronal isolation could account for the variability. We found no significant correlations between spike window latency or duration with VMI, SNR, or baseline firing rate (all comparisons P > 0.1). However, we found a significant correlation between TSI and spike window duration such that neurons with more sustained responses (TSI < 0) were associated with longer spike windows (Spearman ρ = −0.29, P < 0.05). This confirms that our analysis appropriately adapted to the firing characteristics of individual neurons. Also, spike window latency and width were each significantly correlated with the goodness of fit of glmRFs across neurons (ρ = −0.39 and 0.48, respectively; both P < 0.001), although not with each other (P = 0.68), such that neurons with relatively short-latency responses and a longer response to each dot image tended to yield the best-fit glmRFs.

Independent populations of FEF neurons, recorded using different stimulus presentation rates, showed similarly broad temporal sensitivity as stimulus-spike alignment was shifted away from optimal. The population-averaged temporal kernels for neurons in conditions with 30 and 10 ms per stimulus are shown in Fig. 4A. Regardless of the stimulus presentation rate, FEF neurons were roughly half as responsive when using their optimal spike window durations and offsetting the spike-stimulus alignment by 30–45 ms. These results suggest that spatiotemporal integration may be relatively brief for visually responsive FEF neurons.

The population-averaged temporal matrix shown in Fig. 4B is made by averaging the normalized matrices from each cell. The peak predictive value of our glmRFs, when assayed across the entire population, corresponded to a window delay of ∼50 ms with a window width of ∼125 ms. These values correspond to previous estimates of FEF latency and response duration to a brief flash (Mayo and Sommer 2013; Pouget et al. 2005). More importantly, the smooth variation of this population average indicates that our glmRFs were able to predict spikes well when the temporal kernel of each cell was considered, and predictive power fell off rapidly as the spikes and images were poorly aligned.

Although FEF neurons clearly responded to sparse stimuli at rapid presentation rates (Figs. 3 and 4), their responses only marginally improved, if at all, when using slower frame rates or more visual stimuli. To illustrate this point, for each neuron we averaged the β-values within a 5-pixel radius centered on the optimal spike window for each condition. (Results were similar for radii 1-10.) We then normalized each neuron to its average β across conditions so that the relative sensitivity to image durations/number of dots could be visualized by its deviation from 1. Figure 5 shows representative single neurons for each combination of stimulus presentation rates (Fig. 5, A and B) and number of dots (Fig. 5C) tested. Population results are illustrated in Fig. 5, D–F. Despite the trend for preferring longer image durations, spatiotemporal tuning was not significantly different across conditions in each of the 3 subtasks (1-way ANOVA, P > 0.13 in all tasks). Differences in optimal spike window latency and duration across conditions for the population were likewise not significant (1-way ANOVA, P > 0.16 in all tasks for both latency and duration). It is important to note that because of the subsampling of image presentations at shorter image durations (see materials and methods), glmRFs with equivalent predictive power were acquired more rapidly at faster stimulus presentation rates (i.e., it took 20% of the time to acquire the glmRFs at 30 ms compared with 150 ms). Thus the goal of acquiring the best RF per unit time (i.e., most predictive of spiking response) was best served with faster stimulus presentation, even if the trend was slightly in the opposite direction in Fig. 5, D and E.

We did see spatial interactions in a few single neurons, such as evidence for a suppressive surround based on negative β-values outside of the excitatory RF. Spatial integration in FEF has been explored previously (Cavanaugh et al. 2012; Schall et al. 2004). Given that our sample of neurons varying the number of dots was small (n = 23), we did not explore this issue in detail. Initial measurements of dot interactions over time (e.g., the distance between dots on consecutive frames) and spiking activity also did not yield notable effects. However, our method of mapping RFs using stochastic stimuli could easily be adapted to test specific predictions about spatial integration in FEF.

DISCUSSION

We measured the RFs of visually responsive FEF neurons using sparse noise stimuli and regressed the spike trains and images using a GLM (Fig. 1). Independent measures of probabilistic and conventional RFs produced well-matched estimates of RF locations, eccentricities, and sizes (Fig. 2). Although conventional RF mapping remains a useful way of estimating RF centers, probabilistic mapping provides a richer estimate of the RF's extent, substructure, and changes in those features over time (Fig. 3). We used brief, task-irrelevant stimuli. Nonetheless, we found that FEF neurons responded robustly and consistently to sparse dot stimuli presented as briefly as every 10 ms and to many dots on the screen simultaneously (Figs. 4 and 5).

Stochastic approaches to measuring RFs have been widely implemented throughout the visual system, ranging from linear spike-triggered averaging approaches (Churan et al. 2012 in superior colliculus; Jones and Palmer 1987 in V1; Livingstone et al. 2001 in MT; Reid and Alonso 1995 in lateral geniculate nucleus; Sakai and Naka 1987 in retina) to more sophisticated methods for recovering nonlinear neuronal RFs such as spike-triggered covariance (Rust et al. 2005) and nonlinear RF models (David et al. 2004). Recently, a few studies have employed GLMs as a means of probabilistically determining neuronal responses based on the visual stimulus (Calabrese et al. 2011; Hartmann et al. 2011; Kelly et al. 2010; Park et al. 2014; Pillow et al. 2008). These models are convenient because they naturally fit into a statistical framework, allowing for simple assessment of the RF model's significance and implementation of methods like regularization to constrain model outcomes. They are also easily extensible to incorporate additional signals that may influence neuronal activity such as the activity of nearby neurons (Kelly et al. 2010; Pillow et al. 2008) or specific metrics extracted from the visual stimulus (Fernandes et al. 2014). Finally, the usefulness of probabilistic approaches will only increase as computational resources advance, for example, obviating downsampled visual stimuli and allowing more model parameters to be tested simultaneously.

Despite the potential advantage of probabilistic approaches to measure neuronal RFs, they have been rarely utilized in prefrontal cortex. Coarser RF measures have been sufficient for a number of important studies of the role of FEF in oculomotor control, attention, and visual stability (Noudoost et al. 2010; Schall 2004; Sommer and Wurtz 2008). A complete understanding of the dynamic nature of vision, however, will require increased spatial and temporal sensitivity. A prime example of this comes from recent contrasting results in spatial RF dynamics around the time of a saccade (Sommer and Wurtz 2006; Wurtz 2008; Zirnsak et al. 2014). The application of probabilistic approaches to higher-order cortical neurons, along with expansion beyond passive fixation into more detailed experimental tasks, will permit the study of RF dynamics in more naturalistic contexts.

We found that FEF contains neurons with surprisingly exquisite sensitivity to visual stimuli, roughly an order of magnitude more temporally precise than previous estimates. Specifically, Fig. 5, D–F, suggests that optimal data collection (i.e., minimizing reward rates and maximizing RF sampling), given the parameter ranges that we tested, can be achieved using eight stimuli, each 0.16° in size when near fixation (see materials and methods), simultaneously and stochastically presented every 10–30 ms. We used an L1-norm, lasso regression to normalize our GLM, tested a range of spike window latencies and durations, and downsampled the raw pixel data for computational expediency, but these modifications were not necessary to obtain viable data. Our results are consistent with the role of FEF as a visual area, driven by visual inputs from the superior colliculus and extrastriate visual cortex (Schall et al. 1995). Perisaccadic vision and mechanisms of visual stability likely require high precision because eye movements cause frequent disruptions of visual input. Our results add to the growing literature on the role of FEF in rapid and temporally precise cognitive processing (Stanford et al. 2010).

Improvements in the measurement of RF dynamics can help resolve longstanding issues regarding perisaccadic vision. Indeed, previous work shows that coarse RF estimates can hide the fine dynamics of RFs, possibly obscuring what happens perisaccadically (Sommer and Wurtz 2006; Zirnsak et al. 2014). Increasing the spatial and temporal precision of RF measurements has proved fruitful in elucidating circuits in a number of settings: the computation of pattern motion selectivity in area MT (Pack and Born 2001; Smith et al. 2005), understanding suppressive phenomena in V1 (Bair et al. 2002; Smith et al. 2006, 2007), and the dynamic shifts of RFs with attention in MT (Anton-Erxleben et al. 2009; Womelsdorf et al. 2006). The prefrontal cortex has been notably absent from these types of advances in RF measurement despite the need for such precision in measuring RF dynamics during the brief and turbulent perisaccadic period. The detail provided by increasing the spatial and temporal resolution of RF measurements around the time of an eye movement is critical to revealing the neural circuitry of perisaccadic vision.

Taken together, our results highlight two previously unreported aspects of the responses of FEF neurons: 1) rapid temporal integration; and 2) reliable responses to repeated, briefly presented stimuli that are behaviorally irrelevant. Although FEF neurons varied in their responses to our stochastic stimuli, as a population there was no evidence that these findings were confined to a specialized FEF population. Instead, this appears to represent the profile of visually responsive FEF neurons. These findings suggest a reappraisal of the conventional view of FEF and demonstrate new experimental approaches to test the role of FEF neurons in active vision.

GRANTS

J. P. Mayo was supported by National Eye Institute (NEI) Fellowship F32-EY-022529. M. A. Sommer was supported by NEI Grant R01-EY-017592. M. A. Smith was supported by NEI Grants R00-EY-018894, R01-EY-022928, and P30-EY-008098, a Research to Prevent Blindness Career Development Award, an unrestricted award from Research to Prevent Blindness, and the Eye and Ear Foundation of Pittsburgh.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

J.P.M. and M.A. Smith conception and design of research; J.P.M., A.R.D., and M.A. Smith performed experiments; J.P.M. and M.A. Smith analyzed data; J.P.M. and M.A. Smith interpreted results of experiments; J.P.M. and M.A. Smith prepared figures; J.P.M. and M.A. Smith drafted manuscript; J.P.M., M.A. Sommer, and M.A. Smith edited and revised manuscript; J.P.M., A.R.D., M.A. Sommer, and M.A. Smith approved final version of manuscript.