Parallel updating and weighting of multiple spatial maps for visual stability during whole body motion

Abstract

It is known that the brain uses multiple reference frames to code spatial information, including eye-centered and body-centered frames. When we move our body in space, these internal representations are no longer in register with external space, unless they are actively updated. Whether the brain updates multiple spatial representations in parallel, or whether it restricts its updating mechanisms to a single reference frame from which other representations are constructed, remains an open question. We developed an optimal integration model to simulate the updating of visual space across body motion in multiple or single reference frames. To test this model, we designed an experiment in which participants had to remember the location of a briefly presented target while being translated sideways. The behavioral responses were in agreement with a model that uses a combination of eye- and body-centered representations, weighted according to the reliability in which the target location is stored and updated in each reference frame. Our findings suggest that the brain simultaneously updates multiple spatial representations across body motion. Because both representations are kept in sync, they can be optimally combined to provide a more precise estimate of visual locations in space than based on single-frame updating mechanisms.

the brain uses spatial maps in different formats to organize its sensory inputs and motor outputs. For example, processing of visual stimuli occurs in eye-centered maps (Wurtz 2008), and vestibular signals are coded in head-centered coordinates (Clemens et al. 2012; Li and Angelaki 2005), while movements are generated based on body-centered maps (Crawford et al. 2011; Medendorp 2011).

Neurophysiological evidence and computational modeling suggest that these neural maps are mutually connected to perform multisensory integration and sensorimotor control (Cohen and Andersen 2002; Stein and Stanford 2008), thereby weighting each representation according to its reliability (Pouget et al. 2002). In support, McGuire and Sabes (2009) showed that reaching to targets consisting of simultaneous visual and proprioceptive signals is based on a distribution of reference frames, which leads to a lower end point variability than could be expected by using a single modality (Van Beers et al. 1999).

This network perspective on brain computation not only accounts for feed-forward sensorimotor transformations but could also permit the reverse transformation: the prediction of sensory consequences of motor action (Wolpert and Flanagan 2001). Bolstering this notion, it has been shown that representations in eye-centered maps are predictively updated to maintain a stable visual world across eye movements, emphasizing the pathways that run in the reverse direction (Hallett and Lightstone 1976; Duhamel et al. 1992; Henriques et al. 1998; Medendorp et al. 2003; Sommer and Wurtz 2006; Dash et al. 2015).

However, whether this reverse process acts to update the respective sensory representation only or also works on the parallel representations based on the conversion of this input remains an open question. Because body-centered maps are invariant to eye movement, here we applied a combination of eye and body motion to study visual updating in the context of multiple reference frames (Baker et al. 2003). Based on optimal integration theory (Shadmehr and Mussa-Ivaldi 2012), we hypothesize that updating relies on remapped representations in all rather than a single reference frame to achieve the most reliable estimate of the visual world after the motion.

Our hypothesis is illustrated in Fig. 1. When an observer looks at a scene, the visual system processes the spatial information of the attended objects. This information is stored in an eye-centered reference frame, i.e., the location of each object is stored relative to the line of fixation. By taking gaze position into account, this representation can be transformed into a body-centered representation in which objects are encoded relative to observer's body position. To account for self-motion, vestibular and other extra-retinal information is used to update both representations. These maps are combined into an updated representation of the scene, thereby taking the appropriate coordinate transformations into account. If this updating process operates flawlessly, the updated scene is equal to the original scene.

Fig. 1.

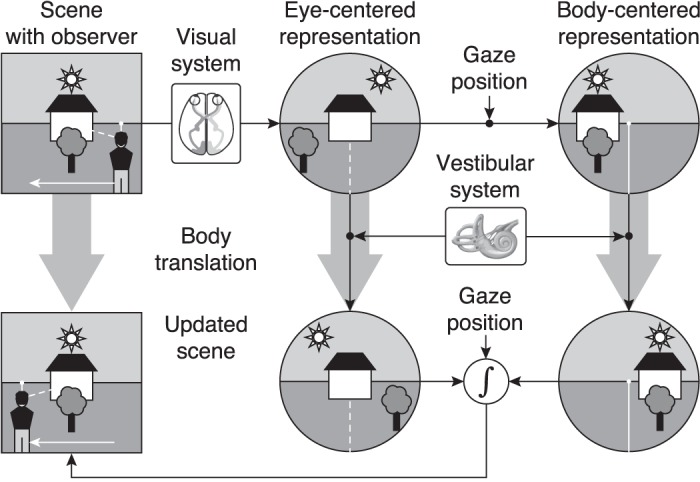
Schematic of our hypothesis. An observer is looking at a scene while maintaining fixation (dashed line) at an object. The visual system stores spatial information of the scene in an eye-centered representation, relative to the point of fixation (indicated by the dashed line). By using gaze position, this representation is transformed into a body-centered representation where objects in the scene are stored relative to observer (indicated by the solid line). Vestibular (and other extra-retinal information) is used to update both representations across body translation (white arrow). Since the location of the observer has changed, each representation should be updated to account for the current eye/body position. Both maps are optimally combined (optimal integration) by taking into account the reliability of the spatial information in each reference frame and the appropriate coordinate transformations between reference frames.

We implemented a statistical approach to model the updating of spatial representations during passively induced body translations in combination with eye rotations. In this scheme, a visual scene is initially stored in an eye-centered map and transformed into a body-centered map. During the motion, the sensory system provides inaccurate and imprecise estimate of the body displacement (Angelaki and Cullen 2008). Because the noise on this signal is direction specific (i.e., the uncertainty will be largest along the axis of motion), it will affect the update of both representations differently for different directions in space. The reason is that, due to the geometry, updating of the body-centered map requires an internal translation of the target locations, whereas for the eye-centered map, target locations require an internal rotation about the fixation point to remain veridical. The model integrates these two spatial estimates according to their reliability, which involves a reference frame transformation, to yield an optimal estimation of the scene after updating. For comparison we also modeled updating in either an eye-centered or body-centered reference frame.

We tested this model using a psychophysical approach. Participants had to remember a target location, taken from a virtual grid of locations in the horizontal plane, during linear sinusoidal whole body motion, while keeping their gaze fixed on a stationary point, at the center of the grid. An update in body-centered coordinates predicts a translation of the target grid along the body motion axis, whereas a model based on updating eye-centered coordinates predicts this grid to be rotated around the fixation point, because of parallax geometry (Medendorp et al. 2003). Modeling the updating of both representations, weighted according to the reliability of the signals involved, predicts a slight translation combined with a parallax effect (i.e., targets in front of and behind the eye's fixation point shift in opposite directions).

Our results were in agreement with the latter prediction, suggesting that the brain keeps spatial information coded in different reference frames up-to-date. Because both representations are kept in sync, they can be optimally combined to provide the most precise estimate of object locations in space after the motion.

METHODS

Subjects.

Nine human subjects (6 male) with ages between 20 and 31 yr participated in this study. All subjects had normal or corrected-to-normal visual acuity and none of them had any known neurological or vestibular disorder. The study conformed to the institutional guidelines of and was approved by the Ethics Committee Faculty of Social Sciences of the Radboud University, Nijmegen, The Netherlands. All subjects gave written informed consent before the start of the experiment.

Setup.

We used a chair mounted on a sled to passively translate subjects. The sled had a linear motor (TB15N; Technotion) to move the chair along a linear track. Sled motion was controlled by a Kollmorgen S700 drive (Danaher) with an accuracy better than 0.034 mm, 2 mm/s, and 150 mm/s². Subjects were seated with their interaural axis aligned with the motion axis, such that they underwent lateral translation. They were restrained using a five-point seat belt and the head was firmly fixed by an ear-fixed mold and a chin rest, such that the subject's cyclopean eye was aligned with the center of the sled. Subjects used the thumb stick of a handheld gamepad (Logitech Dual Action) to respond. Valid responses were followed by a short beep tone of 100 ms. Eye movements were recorded using an EyeLink II eye tracking system (SR Research). We used the raw EyeLink signal to verify whether subjects maintained fixation, under the assumption that they fixated at the fixation point when no other visual stimuli were present.

A world-fixed 27-inch LCD monitor (Iiyama Prolite T2735MSC), with screen dimensions of 40.4 × 30.3 cm and a refresh rate of 60 Hz, was placed in front of the sled, such that the midpoint of the screen was aligned with the center of the linear track. The monitor was tilted by 90°, such that the screen pointed towards the ceiling, and was mounted on a height adjustable table. The position of the screen was adjusted such that the vertical distance between the cyclopean eye and the plane of the screen was 20 cm, and the horizontal distance between the cyclopean eye and the center of the screen was 50 cm. A white fixation cross (5 × 5 mm; 0.5° visual angle) and a flashed target (6 × 6 mm white square; 0.6 to 0.4° for near and far targets, respectively) were presented on the screen with a timing resolution better than 16.7 ms.

Paradigm.

We tested subjects in a dynamic and a stationary condition. In total, we tested eight different target locations, which were arranged in a square grid with a spacing of 10.5 cm and aligned to the center of the screen (Fig. 2A). The fixation cross was presented within the center of this grid. Each block of 112 trials (8 target locations × 14 repetitions) started with switching off the room lights and ramping the sled motion to a steady sinusoidal translation with an amplitude of 20 cm and a period of 3.0 s (Fig. 2, bottom). At the same time, the fixation cross was displayed, and subjects had to maintain fixation during the entire block. After one cycle, steady-state motion was reached, and the target was flashed for 50 ms when the chair was in its rightmost position, i.e., when the direction of body motion reversed (Fig. 2A). At the next reversal point, when the chair reached its leftmost position, the probe was flashed for 50 ms (Fig. 2C).

Fig. 2.

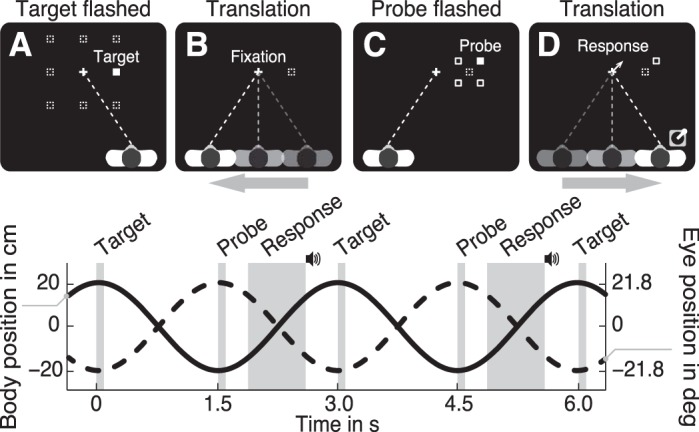
A–D: top view of the paradigm showing the consecutive events. A: at the right reversal point (body position equals 20 cm) 1 (filled square) of 8 targets (dashed squares) was briefly flashed while the participant maintained fixation (dashed line) on the fixation marker (cross). B: next, the participant had to remember the (invisible) target's location (dashed square) while maintaining fixation and moving to the left reversal point (translation of 40 cm in 1.5 s). C: then, at the left reversal point (−20 cm) a probe was briefly flashed. For the 1st trial, the probe appeared at one (filled square) of 4 predefined locations (open squares) around the (invisible) target location. D: subsequently, the participant reported the perceived location of the probe relative to the memorized target location by pointing a thumb stick into the corresponding direction, followed by an auditory cue. Visual feedback of the response was given by displaying an arrow at the center of the screen. Images not to scale. Bottom: timing of the consecutive events. Solid and dashed line represent body and eye position, respectively.

The memorized target location was obtained by applying an adaptive staircase procedure with fixed intervals (Kingdom and Prins 2010), extended to two dimensions. In this procedure, subjects had to indicate in which direction they perceived the probe relative to the remembered target location by pointing the thumb stick in the perceived direction. For example, if the subject remembered the target position at the location indicated by the dashed square in Fig. 2D and perceived the probe at the location indicated by the open square, he or she would point the thumb stick 45° clockwise from straight ahead. This value was stored and used to compute the location of probe when the same target was selected (see below). Once the thumb stick was released, a short beep tone was played and visual feedback was given by displaying an arrow at the center of the screen (duration of 83 ms), pointing into the response direction.

The next target was pseudorandomly selected from one of the eight target locations (dashed squares in Fig. 2A). When a novel target was selected, the initial probe location was pseudorandomly set to one of four initial locations, defined as one of the corners of a 4-cm square centered at the target location, as indicated by the open squares (Fig. 2C). When a recurring target was selected, we updated the probe location based on the response in the previous trial for the same target. More specifically, the probe location was displaced by 1.2 cm (fixed interval) with respect to the previous probe location into the direction of the remembered target position, which was given by the subject's previous response.

Trials were divided into four blocks of 10 min each, such that each target was tested with all four initial probe locations. After 112 trials, when all 8 targets were probed for 14 times, sled motion stopped and the lights were switched on. To obtain baseline performance, the paradigm was also performed without sled motion. In this stationary condition, the sled remained aligned with the fixation cross, i.e., the sled position was zero throughout the experiment. Each of the 8 targets was probed 10 times. All other parameters were equal to the dynamic condition.

Model description.

We used a two-dimensional geometric model to predict the updated memorized target locations (Fig. 3). During target presentation, an estimate of the target location, represented by the center (mean) and shape (covariance) of the gray ellipses in Fig. 3, bottom, is stored in an eye-centered reference frame and subsequently transformed into a body-centered reference frame. Even though this transformation adds noise (Burns and Blohm 2010; Schlicht and Schrater 2007), we assume it to be negligible compared with the noise arising during the encoding, updating and response phase and therefore did not incorporate noise between reference transformations. We return to this point in the discussion.

Fig. 3.

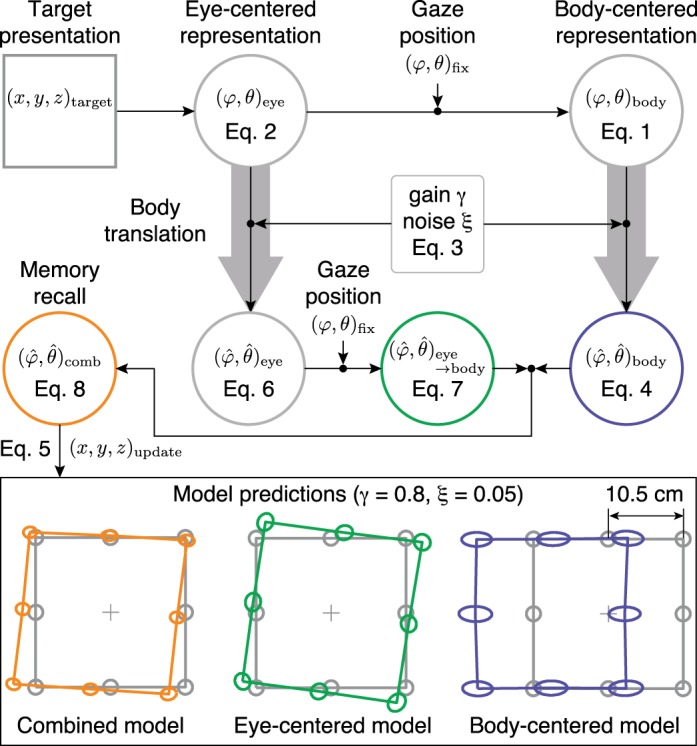
Schematic of the model. During target presentation, an estimate of the target location, represented by the center (mean) and shape (covariance) of the gray ellipses in the bottom panels, is stored in an eye-centered reference frame (φ, θ)_eye (Eq. 2) and subsequently transformed into a body-centered reference frame (φ, θ)_body, by taking eye position (φ, θ)_fix into account (Eq. 1). Both representations are updated across body translation, where the perceived update is modeled with a gain parameter γ and noise parameter ξ (Eq. 3). The updated target estimate in eye-centered coordinates ${\left(\widehat{\phi }\stackrel{}{},\hat{\theta }\stackrel{}{}\right)}_{\text{eye}}$ (Eq. 6) is then transformed into body coordinates ${\left(\widehat{\phi }\stackrel{}{},\hat{\theta }\stackrel{}{}\right)}_{\text{eye}\to \text{body}}$ (Eq. 7) and is optimally combined with the updated target estimate in body coordinates ${\left(\widehat{\phi },\widehat{\theta }\right)}_{\text{body}}$ (Eq. 4). The combined map (Eq. 8) is used for target recall, from which the updated target location (x, y, z)_update can be computed (Eq. 5). As an example, the orange ellipses show the updated target locations for γ = 0.8 and ξ = 0.05, as predicted by the combined model. The green and blue ellipses show the prediction when the model only uses the eye-centered or body-centered representation, respectively.

The world-fixed scene (i.e., fixation point, target and probe) is constrained to the horizontal (x, y, 0) plane, see Fig. 4. Therefore, each point in that plane can be represented by a vector (φ, θ) having its origin at the midpoint between the eyes (i.e., the “cyclopean eye”) of the observer, as indicated by the eyeball in Fig. 4. If we set the center of the observer's body reference system (x, y, z)_body equal to the cyclopean eye, the direction of the target with respect to the body is given by

$${\left[\begin{array}{c}\phi \\ \theta \end{array}\right]}_{\text{body}}=\left[\begin{array}{c}{\tan }^{-1}\left(\frac{x_{\text{target}}-x_{\text{body}}}{y_{\text{target}}-y_{\text{body}}}\right)\\ {\tan }^{-1}\left(\frac{z_{\text{target}}-z_{\text{body}}}{\sqrt{{\left(x_{\text{target}}-x_{\text{body}}\right)}^2+{\left(y_{\text{target}}-y_{\text{body}}\right)}^2}}\right)\end{array}\right],$$ (1)

with (x, y, z)_target and (x, y, z)_body the target and body location in world-fixed coordinates (origin at the fixation point, see Fig. 4), respectively. At target onset, x_body = 20 cm, which equals the sled amplitude; y_body = −50 cm; z_body = 20 cm; and z_target = 0 throughout the experiment. We will call this vector the target location in body coordinates, denoted by (φ, θ)_body in Fig. 3.

Fig. 4.

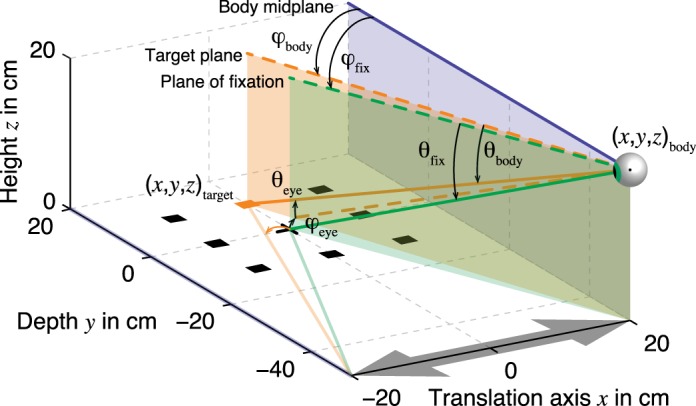
Geometry of experiment and model. At target onset, the cyclopean eye of the observer is located at (x, y, z)_body = (20, −50, 20) cm, indicated by the eyeball icon. The body and head are restrained such that the body midplane (blue) runs parallel to the y-axis and perpendicular to the translation axis (x-axis, gray arrow). The observer maintains fixation at location (0, 0, 0) and therefore, the line of fixation (green line) is rotated counterclockwise and downward with respect to straight ahead (blue line), coinciding with the plane of fixation (green). Since the targets (squares) are constrained to the horizontal plane, each target (x, y, z)_target can be represented by a vector (orange line), with an azimuth (φ) and elevation (θ) component, with its origin at the cyclopean eye. This vector can be expressed relative to the body (blue line) to obtain body-centered coordinates (φ, θ)_body. Alternatively, the same vector can be expressed relative to the line of fixation (green line) to obtain eye-centered coordinates (φ, θ)_eye. The fixation direction is denoted by (φ, θ)_body and is expressed relative to the body. Note that the target marked in orange is located slightly to the right with respect to the fixation direction. After translation, the cyclopean eye is located at (−20, −50, 20) cm (not shown). Now, the same target is located to the left with respect to the line of fixation, as indicated by the orange arrow.

We have chosen to define body-centered coordinates as a vector with an azimuth (φ) and elevation (θ) component to simplify the coordinate transformation between body-centered and eye-centered coordinates, which is given by

$${\left[\begin{array}{c}\phi \\ \theta \end{array}\right]}_{\text{eye}}={\left[\begin{array}{c}\phi \\ \theta \end{array}\right]}_{\text{body}}-{\left[\begin{array}{c}\phi \\ \theta \end{array}\right]}_{\text{fix}}$$ (2)

with (φ, θ)_eye the target location in eye-centered coordinates. The eye position (φ, θ)_fix is computed from Eq. 1, where (x, y, z)_target = (0, 0, 0) represents the location of the fixation marker, indicated by the black cross in Fig. 4. Thus (φ, θ)_eye represents the target location relative to the line of fixation, i.e, in eye-centered coordinates.

For example, the target at location (0, 10.5, 0) cm, marked in orange in Fig. 4, is located right with respect to the plane of fixation (green) at (3.5, 2.9)° in eye-centered coordinates (Eq. 2). The same target is located left with respect to the body midplane (blue), at (−18.3, −17.4)° in body-centered coordinates (Eq. 1). For simplicity, we compute the body-centered representation directly from the world-fixed location, which implies that the coordinate transformation from the eye-centered to the body-centered reference frame is veridical.

When the observer is translated along the x-axis, the perceived target location has to be updated to account for the displacement. In the model (Fig. 3), both representations are updated across body translation, which may not necessarily be perceived veridically (Van Pelt and Medendorp 2007). Instead, this estimate could be systematically under- or overestimated (inaccurate) and noisy (imprecise). We modeled this uncertainty as a Gaussian distribution $\mathcal{N}$ with mean γ (gain parameter, dimensionless) and standard deviation ξ (noise parameter, dimensionless). Since the observer's body moved along the x-axis, symmetrically about x = 0 (gray arrow in Fig. 4), the estimated body position from memory (denoted by the hat symbol) is given by

$${\hat{x}\stackrel{}{}}_{\text{body}}=x_{\text{body}}\left(2\stackrel{\stackrel{}{}}{\hat{\gamma }}\stackrel{}{}-1\right),\hspace{0.17em}\text{with}\hspace{0.17em}\hat{\gamma }\stackrel{}{}=\mathcal{N}\left(\gamma ,{\xi }^2\right).$$ (3)

With the use of Eq. 1, the memorized target location estimate in body coordinates is given by

$${\left[\begin{array}{c}\widehat{\phi }\stackrel{}{}\\ \hat{\theta }\stackrel{}{}\end{array}\right]}_{\text{body}}=\left[\begin{array}{c}{\tan }^{-1}\left(\frac{x_{\text{target}}-{\hat{x}\stackrel{}{}}_{\text{body}}}{y_{\text{target}}-y_{\text{body}}}\right)\\ {\tan }^{-1}\left(\frac{z_{\text{target}}-z_{\text{body}}}{\sqrt{{\left(x_{\text{target}}-{\hat{x}}_{\text{body}}\right)}^2+{\left(y_{\text{target}}-y_{\text{body}}\right)}^2}}\right)\end{array}\right],$$ (4)

Following up on the previous example, consider that the observer's body displacement estimate is veridical (γ = 1, ξ = 0). In that case, ${\hat{x}}_{\text{body}}$ = −20 cm, which is equal to the left reversal point of the sled (see also Fig. 2). The target location, which was initially to the body's left, has been moved to the right side of the body, which means that the horizontal component (azimuth) of the body-centered target representation should flip sign. Indeed, by using Eq. 4, we find that the observer remembers the target at an angle ${\left(\widehat{\phi }\stackrel{}{},\hat{\theta }\stackrel{}{}\right)}_{\text{body}}$ = (18.3, −17.4)°.

Next, assume that the observer underestimates his or her body displacement such that the perceived body position after translation is −16 cm instead of −20 cm (γ = 0.8, ξ = 0). In this case, the observer remembers the target at an angle of (11.2, −18.0)° relative to the body and will erroneously report that the target was shifted to the left with respect to the veridical location. Similar errors will occur for the other targets. This becomes evident when we express the memorized location of all targets in world-fixed coordinates using

$${\left[\begin{array}{c}x\\ y\\ z\end{array}\right]}_{\text{target}}=\left[\begin{array}{c}{x}_{\text{body}}+z_{\text{body}}\text{sign}\widehat{\phi }\frac{\tan \widehat{\phi }\stackrel{}{}}{\tan \widehat{\theta }\sqrt{1+{\tan }^2\widehat{\phi }\stackrel{}{}}}\\ y_{\text{body}}+z_{\text{body}}\frac{1}{{\tan }^2\widehat{\theta }\sqrt{1+{\tan }^2\widehat{\phi }}}\\ 0\end{array}\right].$$ (5)

Figure 3, bottom right, shows the memorized locations in world-fixed coordinates for all targets (blue) relative to the veridical target locations (gray) if the observer would only rely on a body-centered representation of space and would underestimate his or her body displacement. In that case, the targets seems to have moved towards the left, into the direction of motion. Note that adding noise to the body displacement estimate (ξ = 0.05) results in a larger variability along the motion axis (i.e., the gray circles become blue ellipses with the semimajor axes parallel to the x-axis).

Equations 4 and 5 demonstrate that because of a misestimation of body position, the perceived target locations change. Since the fixation point can be considered as a target at position (0, 0, 0), the perceived fixation location changes as well. This results in biased estimates of the memorized target locations in eye-centered coordinates, given by

$${\left[\begin{array}{c}\widehat{\phi }\stackrel{}{}\\ \hat{\theta }\stackrel{}{}\end{array}\right]}_{\text{eye}}={\left[\begin{array}{c}\widehat{\phi }\\ \hat{\theta }\end{array}\right]}_{\text{body}}-{\left[\begin{array}{c}\widehat{\phi }\\ \hat{\theta }\end{array}\right]}_{\text{fix}},$$ (6)

where is the perceived fixation location computed from Eq, 4 with (x, y, z)_target = (0, 0, 0). When applying this equation to the example above, we find that the memorized target, located

$${\left(\widehat{\phi }\stackrel{}{},\hat{\theta }\stackrel{}{}\right)}_{\text{fix}}$$

at (0, 10.5, 0) cm in gaze-centered coordinates becomes (−3.5, 2.9)° if the observer correctly perceived his or her displacement to be 40 cm to the left (i.e., ${\hat{x}\stackrel{}{}}_{\text{body}}$ = −20 cm, γ = 1, ξ = 0). This is an example of motion parallax, since initially, the target was represented 3.5° to the right with respect to the fixation point, but due to body motion, the target shifted to the opposite side, 3.5° to the left of the fixation point, as illustrated by the orange arrow in Fig. 4. By using the same equation, the eye-centered representation for = 0.8 is equal to (−2.9, 3.1)°. Thus the observer will perceive the target rightward and upward of the veridical location. To express this error in world-fixed coordinates, we first transform the eye-centered representation into a body-centered representation using

$${\left[\begin{array}{c}\widehat{\phi }\stackrel{}{}\\ \hat{\theta }\stackrel{}{}\end{array}\right]}_{\text{eye}\to \text{body}}={\left[\begin{array}{c}\widehat{\phi }\\ \hat{\theta }\end{array}\right]}_{\text{eye}}+{\left[\begin{array}{c}\phi \\ \theta \end{array}\right]}_{\text{fix}}.$$ (7)

Then, we transform this representation into a world-fixed representation by applying Eq. 5. The result is shown in Fig. 3, bottom middle, where the green ellipses represent the estimated target locations when body displacement is inaccurate (γ = 0.8) and imprecise (ξ = 0.05). Thus, if the observer would rely on an eye-centered representation to remember the target locations, and underestimate his or her body displacement, he or she will perceive the targets as being rotated around the fixation point.

However, instead of using either an eye-centered or body-centered reference frame, we hypothesize that the observer uses the estimates of both spatial representations, combining them in a statistically optimal fashion. Therefore, one of the representations needs to be transformed into the other one before it can be combined. For simplicity, we assume that the transformations between reference frames are noise free. Therefore, combining the spatial information in either an eye-centered or a body-centered representation will yield the same results.

Here, the eye-centered representation ${\left(\widehat{\phi }\stackrel{}{},\hat{\theta }\stackrel{}{}\right)}_{\text{eye}}$ is transformed into a body-centered representation ${\left(\widehat{\phi },\hat{\theta }\right)}_{\text{eye}\to \text{body}}$ using Eq. 7, after which it is combined with the updated target estimate in body coordinates ${\left(\widehat{\phi }\stackrel{}{},\hat{\theta }\stackrel{}{}\right)}_{\text{body}}$. If we assume that both estimates are normally distributed, the statistically optimal estimate is given by

$${\left[\begin{array}{c}\widehat{\phi }\stackrel{}{}\\ \stackrel{}{\hat{\theta }}\end{array}\right]}_{\text{comb}}={\sum }_{\text{comb}}\left({\sum }_{\text{eye}\to \text{body}}^{-1}{\left[\begin{array}{c}\widehat{\phi }\\ \hat{\theta }\end{array}\right]}_{\text{eye}\to \text{body}}+{\sum }_{\text{body}}^{-1}{\left[\begin{array}{c}\widehat{\phi }\\ \hat{\theta }\stackrel{}{}\end{array}\right]}_{\text{body}}\right)$$ (8)

with ∑_comb = (∑_eye→body⁻¹ + ∑_body⁻¹)⁻¹ and ∑ is the covariance matrix (see Model fits for details).

Figure 3, bottom left, shows the predicted responses in world-fixed coordinates (using Eq. 5 with ${\left(\widehat{\phi },\hat{\theta }\right)}_{\text{body}}={\left(\widehat{\phi },\hat{\theta }\right)}_{\text{comb}}$) for the combined model, with γ = 0.8 and ξ = 0.05. If the observer optimally combines the information stored in both maps, the model predicts that the memorized targets are slightly shifted to the left and show a parallax effect relative to the fixation point (Fig. 3, bottom left).

For comparison, if the observer would rely only on the body-centered map, the model predicts a translation of the targets but no rotation (Fig. 3, bottom right). If only eye-centered information would be used, the model predicts the a rotation of the targets around the fixation point (Fig. 3, bottom middle). We will refer to these two alternatives as the body-centered and eye-centered model, respectively, to distinguish them from the combined model.

Model fits.

To investigate whether the proposed model correctly explains the observed behavior, we fitted the two free parameters, gain γ and noise ξ, to the subject's responses. For each subject, 600 model simulations were run, starting with randomly drawing 100 data points (with replacement) per target from a bivariate normal distribution. The distribution's mean and covariance were obtained from the recorded location estimates in the stationary condition by the following procedure. Each target was tested in four blocks. The last 4 responses of each block were used for further analysis, yielding 16 location estimates per target. Next, for each target we subtracted the mean from each of the 16 values. The variability of each target location estimate was expressed as a single covariance matrix computed across all mean-corrected values (16 values × 8 targets). Pooling the data across all targets yields a more reliable estimate than using a single estimate per target. The mean was set to the presented target location to provide the model with an unbiased estimate of the initial target position.

These 100 data points were fed into the model, updated, and transformed (Eqs. 1–8). For each target in the eye-centered and body-centered map we computed the mean and covariance across the 100 data points and then computed the optimally combined estimate. Next, for each target we generated 100 data points from the combined distribution (model), and drew 16 data points (with replacement) from the recorded location estimates in the dynamic condition (data).

We defined an error function as the Mahalanobis distance between each of the 100 model predictions and the data, averaged across targets. The Mahalanobis distance d_i defines how many standard deviations the prediction ${\left({\widehat{\phi }}_i,{\widehat{\theta }}_i\right)}_{\text{comb}}$ is from the mean of the data (μ_φ, μ_θ)_data, and is given by

$$d_i=\sqrt{\left({\left({\widehat{\phi }}_i,{\hat{\theta }}_i\right)}_{\text{comb}}-{\left({\mu }_{\phi },{\mu }_{\theta }\right)}_{\text{data}}\right)\times {\sum }_{\text{data}}^{-1}{\left({\left({\widehat{\phi }}_i,{\hat{\theta }}_i\right)}_{\text{comb}}-{\left({\mu }_{\phi },{\mu }_{\theta }\right)}_{\text{data}}\right)}^{\text{T}}},$$ (9)

with ∑_data the covariance matrix of the estimated target locations in the dynamic condition. For each subject, values for γ and ξ were obtained by minimizing this error function.

RESULTS

Sequence of responses.

In each trial, subjects had to remember a briefly presented stimulus, the target, while they were being translated sideways. The memory recall was tested by recording thumb stick responses representing the direction of the remembered target relative to a second stimulus, the probe. In the next trial where the same target was tested, the probe was displaced into the response direction. As a result, the sequence of probe locations reflects the convergence toward the remembered target location in two-dimensional space.

Figure 5 shows these probe trajectories for the stationary (Fig. 5A) and the dynamic condition (Fig. 5B) for a representative subject (S5). Each of the eight targets (Fig. 5, black squares) was tested in four blocks (Fig. 5, colored lines) with different initial probe locations (Fig. 5, open circles). For the first trials, the trajectories are fairly straight, indicating that the subject is certain about the direction of the memorized target location relative to the probe. However, when the distance between memorized target and probe decreased, the variability increased and the trajectory becomes more noisy towards the final probe location (Fig. 5, filled circle).

Fig. 5.

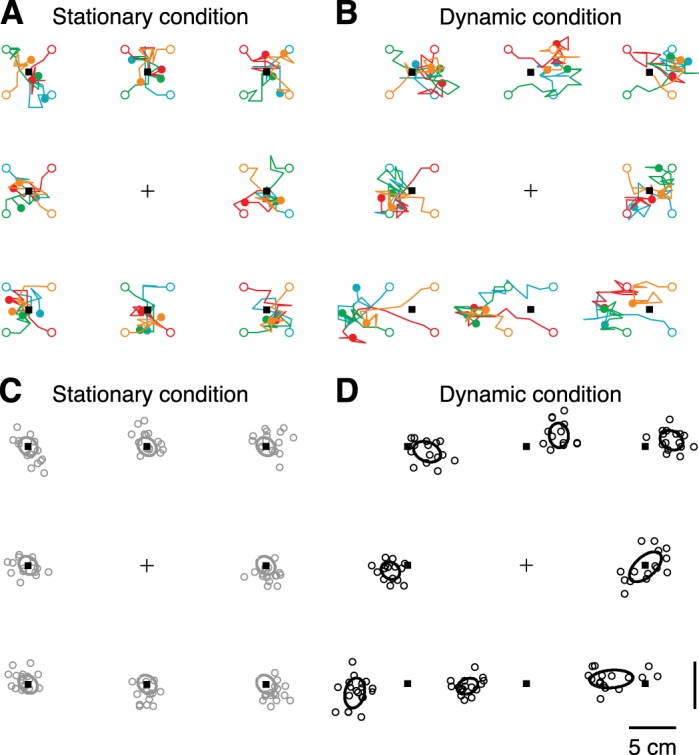
A: top view of target and probe locations in the stationary condition for subject 5 (S5). For each of the 8 target locations (black squares), each colored line represents subsequent probe locations (n = 10) for each of the 4 blocks. Open circles represent initial probe location; filled circles represent final probe location; cross indicates fixation marker. B: same as A for the dynamic condition (n = 14 probe locations). C: visualization of the location estimates used in the model for S5. For each target, the last 4 probe locations of each block were taken as the location estimate, resulting in 16 data points (open circles). Ellipses indicate covariance, computed across all mean-corrected data points (16 × 8 values). In the stationary condition, the mean target estimate (center of the ellipse) was set to the presented target location (black squares). D: same as C for the dynamic condition, but for each target the mean and covariance was computed across the n = 16 target estimates (open circles).

The last four probe locations of each block lack any dominant direction and were therefore used to obtain an estimate of the target location after body displacement (see Fig. 5D, where the mean and covariance are represented by the center and outline of the ellipses, respectively). Since both conditions were identical except for the body translation, systematic differences between responses in Fig. 5, C and D, are caused by updating the remembered target locations across body motion. For this particular subject, the arrangement of target responses revealed a parallax effect, that is, responses for targets closer than the fixation point were shifted towards the left (Fig. 5, C and D, bottom row) and targets further away were shifted towards the right (Fig. 5, C and D, top row). Response behavior is also more variable in the dynamic condition than in the stationary condition.

Model fits.

We used a model that combines eye-centered and body-centered estimates of the remembered target locations to predict the observed spatial pattern in the updating of the memorized targets. Figure 6 compares the fit of the combined model (orange ellipses) with memorized target locations after updating (black). The responses in the stationary condition (gray) served as input for the model. The ellipses are connected to show the spatial arrangement of the target locations to ease the comparison between the data and the model predictions.

Fig. 6.

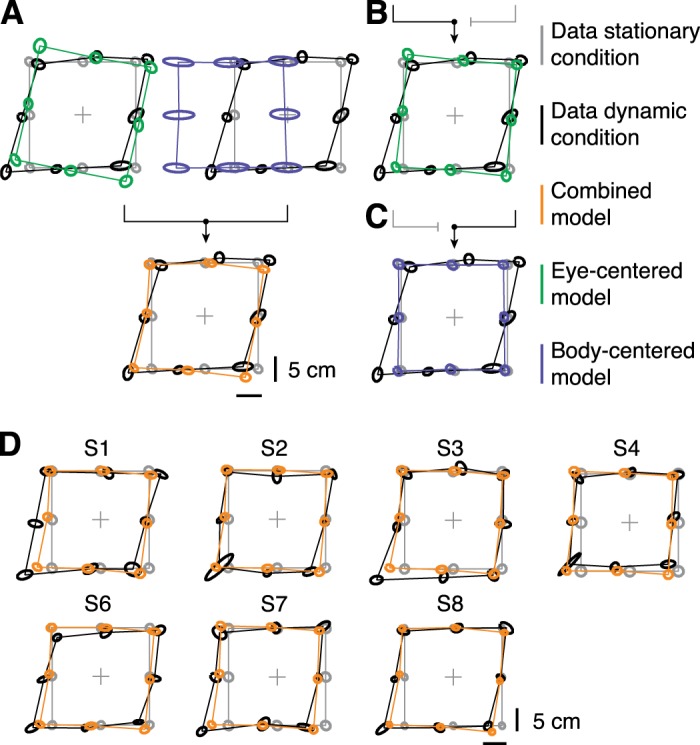
Top view of measured and predicted memorized target locations. Ellipses represent target location estimates from the stationary condition (gray), dynamic condition (black), and model fit (orange). Center and outline of the ellipses represent mean and covariance across 16 data points, respectively. A: an eye-centered (green) and body-centered representation (blue) are optimally combined (orange) and fitted to the responses of S5 (black). B and C: the fits when the model only uses the eye-centered (green) or body-centered (blue) representation, respectively, for S5. D: data (black) and fits of the combined model (orange) for the remaining participants.

For S5 (Fig. 6A), the combined model correctly predicts the arrangement of target locations as illustrated by the overlap of the orange and black ellipses for the majority of target locations. That is, the combined model can account for the both the translation of the targets to the left as well as the parallax effect. The key feature of our model is the combination of an eye-centered and body-centered estimate into a combined location estimate. The blue and green ellipses in Fig. 6A show these maps before they are optimally combined. Note that neither the body-centered representation (blue) nor the eye-centered representation (green) alone could predict the observed behavior. Instead, only after combining the individual estimates (blue and green) into a “merged” representation (orange) the model prediction is in agreement with the data (black).

To demonstrate that integrating both maps is necessary to account for the observed results, we refitted the model without combining the two representations (Fig. 6, B and C). The blue and green ellipses show the predictions if only the eye-centered (Fig. 6B) or the body-centered map (Fig. 6C) was used, respectively. The eye-centered model predicts a rotation of the target locations around the fixation point. Therefore, by using only the eye-centered updates (green), the model can neither capture the translation nor the parallax that is observed. Also, the model cannot predict the observed behavior (black) based on only body-centered location updates (blue). In agreement with subject S5, the observed update errors for the remaining subjects can be characterized by a translation into the direction of motion and a parallax effect (black ellipses in Fig. 6D).

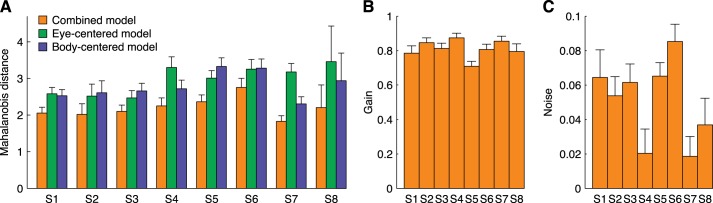
We tested the goodness-of-fit of the combined model and its two alternatives by comparing the fit error, which was defined as the Mahalanobis distance between model and data, averaged across targets. For all subjects, the distance was smallest for the combined model, compared with the two alternatives, and this difference was significant [Fig. 7A; ANOVA, F_(2,1797) > 370, P < 0.0001 for each subject; post hoc Bonferroni comparisons, P < 0.0001 for each model comparison within a subject]. For the combined model, the Mahalanobis distance across subjects was 2.2 ± 0.3 (means ± SD), compared with 3.0 ± 0.4 and 2.8 ± 0.4 for the eye-centered and body-centered model, respectively. These results indicate that updating the visual targets in either an eye-centered or a body-centered representation alone does not result in a better prediction compared to the combined representation.

Fig. 7.

A: model fit errors (orange), computed as the Mahalanobis distance, compared with the fit errors when only eye-centered (green) or body-centered (blue) location estimates are used. Bars show mean values, and error bars show SD obtained by boot-strapping (n = 600). B: gain parameter for the combined model. C: noise parameter for the combined model.

Translation estimate.

Our model used two parameters to quantify the body translation estimate. The gain parameter quantified γ the perceived update. If γ = 1 the subject's perceived displacement equals the veridical displacement. An underestimation or overestimation is reflected by a gain smaller or larger than 1, respectively. All subjects underestimated their displacement, which is reflected by an overall gain of 0.81 ± 0.05 (means ± SD; see Fig. 7B). The noise parameter ξ quantified the precision of the translation estimate. For example, if γ = 0.75 and ξ = 0.05, the means and SD are 30 and 2 cm, respectively, since the total displacement is 40 cm. Overall, we found ξ values between 0.020 and 0.085 (across subjects: 0.051 ± 0.024).

DISCUSSION

It has remained an open question whether the brain updates multiple spatial representations in parallel to predict the sensory consequences of motor actions or it restricts its updating mechanisms to a single reference frame from which other representations are constructed. This study is the first to provide evidence for such a parallel mechanism, by showing that the input of a single sensory modality (i.e., vision) is stored in eye-centered and body-centered representations, which are simultaneously updated across body motion, using vestibular and other extra-ocular information, and integrated in a reliability-dependent manner to create spatial constancy.

We took the following approach. Based on previous computational work and neurophysiological evidence, a statistical model was developed to simulate the updating of visual targets across body motion in multiple reference frames, assuming an inaccurate estimate of body displacement (Fig. 3). To test this model, subjects had to remember the location of briefly presented targets while being translated sideways. The model correctly predicted the spatial arrangement of remembered target locations that was observed in all individual subjects (Fig. 6), without making any a priori assumptions on the geometry of these update errors. However, the model failed to predict these errors if it updated only an eye-centered or only a body-centered representation, suggesting that parallel updating of spatial information in both reference frames in necessary to account for the observations. Fit errors, computed as the Mahalanobis distance between model and data, confirmed these results (Fig. 7A). Moreover, for each subject the model quantified the perceived body displacement, which revealed that subjects underestimate their body translation (Fig. 7, B and C).

Several studies have investigated the update of space across whole body motion. Clemens et al. (2012) used a similar paradigm in which targets were presented either in front or behind a fixation point. Participants were translated sideways and had to judge whether a probe stimulus occurred left or right from the memorized target. Their results implied that an eye-centered reference frame was involved. However, since they only tested an eye-centered or body-centered model, it cannot be ruled out that a combination of the two would have significantly improved the model predictions. In addition, for the majority of subjects they found larger fit errors for the body-centered model compared with the eye-centered model, which is in agreement with our results (Fig. 7A).

We found that subjects underestimate their translation in the updating process, reflected by a gain value of 0.81 across subjects. This value was in agreement with update performance across transient passively induced body translation of the same amplitude as used in our study (Gutteling et al. 2015). For active body translations, subjects overestimate their translation (Van Pelt and Medendorp 2007), whereas Clemens et al. (2012) found considerably smaller gain values compared with our results. These differences could be explained by an erroneous attribution of visual motion to either self-motion or object-motion, which has been found during passive translation and darkness (Dyde and Harris 2008). In addition, it is likely that the depth perception of a small visual stimulus, briefly presented in a dark environment, is compromised. The targets that we presented (small squares of ∼0.5°) contain more depth information than point targets (e.g., LEDs), which could account for a better depth percept and thus a better update performance.

Previous studies on reaching to visual and proprioceptive targets have shown that optimal integration models can explain direction-dependent (Van Beers et al. 2002) and gaze-dependent errors (McGuire and Sabes 2009). Importantly, both studies did not simulate updating processes but reach behavior to stationary targets. In the present study, an estimate of self-motion was used to update the spatial maps. Our results showed that the localization errors could be explained by a misestimation of self-motion. Could our results also be explained by biases in reference transformations, as proposed by Schlicht and Schrater (2007) and McGuire and Sabes (2009)? McGuire and Sabes simulated the reach errors by assuming that gaze direction is biased towards the reach target during reference transformations. If we adopt the same transformation bias (i.e., gaze direction is biased towards the target), then targets to the right of the fixation point will be biased to the right, and vice versa, after transformation to body-centered coordinates. Therefore, if the self-motion estimate would be unbiased, the memorized target locations to the right of the fixation point will be shifted to the right and left targets to the left. We found that all targets were shifted to the left, and therefore, a bias in gaze direction alone cannot explain our observations.

The present model uses a single estimate (Eq. 3) of body translation, which is used to update both the eye-centered and body-centered maps simultaneously. However, each map might use its own estimate of self-motion to update its content. For example, the body-centered map could rely more on vestibular information whereas the eye-centered map could rely more on (efferent) eye position and velocity signals. However, with this paradigm we could not separate the individual contributions of the sensory signals to the self-motion estimate. More specifically, the observed variance in the stationary condition (represented by the gray ellipses in Figs. 5 and 6) was a combination of noise in the visual system, noise in initial encoding in memory, noise originating from maintaining the target location in memory during the movement, and response noise. Added to that, noise in vestibular and eye movement signals contributed to the variance in the dynamic condition (black ellipses). Importantly, the mean estimate of updated target locations depended on the covariance of the locations kept in memory (see Eq. 8). Therefore, the sensory signal pertaining to the update could be estimated from the mean responses, without the necessity to make direct comparisons between variances in the stationary and dynamic conditions.

One could argue that the visual fixation point, available during the body motion, was a biasing factor for the eye-centered representation. However, Van Pelt and Medendorp (2007) showed that eye-centered effects still arise in the absence of a visual fixation point during the translation, which would rule out this explanation. Alternatively, one could propose that the visual fixation point serves as an allocentric anchor for the target representations. We cannot exclude this possibility. However, since we did not manipulate the position of the fixation point during the motion, updating of such an allocentric representation would not be needed and cannot explain the systematic errors that we observed. In future work, it would be interesting to examine whether moving the fixation point, which will elicit smooth pursuit eye movements as in the present study, could reveal a contribution of such representations, optimally weighted in combination with the eye- and body-centered representations that we have probed here.

Neurophysiological data provide evidence for the underlying neural mechanisms of spatial updating across body motion. Recently, in a task very similar to ours, it has been shown that this remapping is reflected in occipito-parietal alpha-band activity, suggesting that the neural computations take place in the posterior parietal cortex (PPC) (Gutteling et al. 2015). If so, this brain area should be able to perform reference transformations and should have access to an internal estimate of body displacement. It has been shown that the PPC receives input from the vestibular system (Kaufman and Rosenquist 1985; Meng et al. 2007; Shinder and Taube 2010) and eye position signals (Andersen et al. 1985; Chang and Snyder 2010; Gnadt and Mays 1995; Prevosto et al. 2009), allowing for integrating the different sensory contributions to estimate self-motion. This estimate could be used to update both eye-centered and body-centered maps of visual space, provided that these representations exist in the PPC. Indeed, monkey single-unit recordings have shown that the processing in the PPC involves a mixture of reference frames, including eye-centered, body-centered and, intermediate coordinates (Avillac et al. 2005; Chang et al. 2009; Chang and Snyder 2010; Mullette-Gillman et al. 2005, 2009; Stricanne et al. 1996). This neural architecture provides the PPC with a mechanism to implicitly create multiple modes of representation at the population level, with each reference frame weighted and updated by context and sensorimotor input (Buchholz et al. 2013; Pouget et al. 2002). We believe that this is what we have probed.

To summarize, this study suggests that the brain encodes spatial information in different reference frames, even when this information originates from one sensory modality, and keeps these representations up-to-date. Because both representations are kept in sync, they can be optimally combined to provide an accurate estimate of object locations in space during self-motion.

GRANTS

This work was supported by EU-FP7-FET SpaceCog Grant 600785, the European Research Council (EU-ERC-283567), and the Netherlands Organization for Scientific Research (NWO-VICI: 453-11-001).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.J.T. and W.P.M. conception and design of research; J.J.T. performed experiments; J.J.T. analyzed data; J.J.T. and W.P.M. interpreted results of experiments; J.J.T. prepared figures; J.J.T. and W.P.M. drafted manuscript; J.J.T. and W.P.M. edited and revised manuscript; J.J.T. and W.P.M. approved final version of manuscript.