Comparison of Vocal Vibration-Dose Measures for Potential-Damage Risk Criteria

Abstract

Purpose

Schoolteachers have become a benchmark population for the study of occupational voice use. A decade of vibration-dose studies on the teacher population allows a comparison to be made between specific dose measures for eventual assessment of damage risk.

Method

Vibration dosimetry is reformulated with the inclusion of collision stress. Two methods of estimating amplitude of vocal-fold vibration are compared to capture variations in vocal intensity. Energy loss from collision is added to the energy-dissipation dose. An equal-energy-dissipation criterion is defined and used on the teacher corpus as a potential-damage risk criterion.

Results

Comparison of time-, cycle-, distance-, and energy-dose calculations for 57 teachers reveals a progression in information content in the ability to capture variations in duration, speaking pitch, and vocal intensity. The energy-dissipation dose carries the greatest promise in capturing excessive tissue stress and collision but also the greatest liability, due to uncertainty in parameters. Cycle dose is least correlated with the other doses.

Conclusion

As a first guide to damage risk in excessive voice use, the equal-energy-dissipation dose criterion can be used to structure trade-off relations between loudness, adduction, and duration of speech.

Prolonged speaking, shouting, or singing may expose the larynx to excessive tissue vibrations. It is well known that excessive hand vibration in industrial tool use can cause deleterious effects on vascular and neural function of the hands (Griffin, 1990) and that whole-body vibration can negatively affect various organs and tissues (Murfee et al., 2005). However, small amounts of vibration of tissues can also be healthy in that they promote bone generation (LaMothe & Zernicke, 2004; Rubin, Turner, Bain, Mallinckrodt, & McLeod, 2001), wound healing (Verdolini Abbott et al., 2012), and general body health (Dahlin, Necking, Lundström, & Lundborg, 1992; Khalil & Qassem, 1996; Mester, Kleinöder, & Yue, 2006). Thus, as with exposure to sunlight and other electromagnetic radiation, the risk associated with exposure to sonic tissue vibration is a matter of degree.

Whenever vibration is involved in any transfer of energy to tissues, the degree of exposure is usually expressed as a vibration dose, calculated from three metrics: amplitude, frequency, and duration. These metrics are the basis for calculating vocal dose in ambulatory phonation monitoring (Cheyne, Hanson, Genereux, Stevens, & Hillman, 2003; Popolo, Švec, & Titze, 2005). Of the three metrics, voicing duration (Watanabe, Shin, Fukaura, Nakaaki, & Tsuda, 1985) and voicing frequency (Švec, Titze, & Popolo, 2005) are the easiest to obtain nonintrusively. Vibrational amplitude is the most difficult to obtain. It can be measured directly with optical methods (Popolo & Titze, 2008; Schuberth, Hoppe, Döllinger, Lohscheller, & Eysholdt, 2002), but this measurement is not feasible for ambulatory and on-the-job situations.

To address this issue, we previously estimated vibrational amplitude (Titze, Švec, & Popolo, 2003) from radiated mouth pressure (dB SPL) using a combination of empirical rules from laboratory observations and a range of assumptions. An alternative indirect method is to estimate vibration amplitude from skin acceleration (Švec et al., 2005). From such estimates of vocal-fold vibration amplitude, dose calculations are performed in ambulatory phonation monitoring devices and voice dosimeters (e.g., VoxLog, http://www.sonvox.com; KayPentax's APM, http://www.kaypentax.com; VocaLog, http://www.vocalog.com).

In an initial article (Titze et al., 2003), we defined a time dose, a frequency dose, a distance dose, and an energy-dissipation dose for the purpose of setting out an investigation on schoolteachers, a population of people who are at risk of damage from vocal vibration due to long hours of talking. With the doses defined, a vocal dosimeter was constructed and tested (Popolo et al., 2005), and adequate software for online processing was developed (Švec, Popolo, & Titze, 2003). In addition, some protocol challenges in long-term monitoring of public-school teachers were addressed (Hunter, 2012; Nix, Švec, Laukkanen, & Titze, 2007). Using the time-dose data from 57 teachers, voicing periods and silence periods were quantified in terms of duration at work and not at work (Titze, Hunter, & Švec, 2007). Using frequency dose and SPL data, intensity and fundamental frequency for the same group of teachers were reported (Hunter & Titze, 2010). Teachers also learned to produce an autoperceptive rating of prolonged speaking effects on their voice (Halpern, Spielman, Hunter, & Titze, 2009; Hunter, 2008). Instabilities in the voice were described separately in terms of nonlinear dynamic bifurcation analysis (Popolo, Titze, & Hunter, 2011). As a further test of the device, children have been monitored (Hunter, 2009; Hunter, Halpern, & Spielman, 2012), as have professional vocal performers (Carroll et al., 2006).

The purpose of this article is to develop damage-risk trade-offs between duration, amplitude, vocal-fold contact, and fundamental frequency in prolonged speech. Measurement of amplitude is revisited in terms of a small set of calibrated digital vocal-fold images and corresponding skin acceleration levels (SALs) obtained at the jugular notch. In addition, vocal-fold collision stress is built into the energy-dissipation dose formulation. The following primary questions in the current study are: (a) How do the four vibration-dose calculations (time dose, cycle dose, distance dose, and energy dose) correlate in capturing duration, fundamental frequency (f ₀), and vocal loudness in a corpus of 57 teachers? and (b) How can these measures be used to quantify trade-offs between duration, loudness, vocal-fold contact, and f ₀ in terms of an equal-energy-dissipation (EED) dose criterion? Answers to these questions will allow practitioners in preventive voice care to design strategies for lowering damage risk in populations with high voice use.

Review of Vibration-Dose Calculations

A review of vibration-dose calculations is in order as a starting point toward new theoretical investigations that include collision between opposing vocal folds in the energy-dissipation dose.

In any vibration-dose calculations, it is assumed that vocal-fold vibration amplitude, frequency, and duration can be measured or estimated. Following the definitions described previously (Švec et al., 2003; Titze et al., 2003), we begin with a unit step function as follows:

$$\begin{array}{cc}\hfill k_{\mathrm{v}}=1.0\hfill & \hfill \mathrm{when}\mathrm{voicing}\mathrm{is}\mathrm{on}\hfill \\ \hfill =0.0\hfill & \hfill \mathrm{when}\mathrm{voicing}\mathrm{is}\mathrm{off}\text{.}\hfill \end{array}$$ (1)

The on/off voicing decision is made on the basis of an energy threshold level (Popolo et al., 2005). The unit step function is a multiplication factor in all dose calculations.

Time Dose

Time dose (in units of seconds) is the total voicing time over some selected duration of measurement; it quantifies the total time the vocal folds are vibrating. In mathematical terms, the time dose is simply the integral of the voicing step function,

$$D_{\mathrm{t}}=\int k_{\mathrm{v}}dt=d{T}_{\mathrm{e}}\text{,}$$ (2)

where the limits of integration can be taken over any reasonable exposure period T _e (hours, days, weeks, etc.). The unit of D _t is the second, but when normalized to T _e it becomes d, the mean duty ratio, sometimes expressed as a percentage of voicing over the exposure period.

Cycle Dose

An important extension of the time dose is the cycle dose. Cycle dose (measured in number of accumulated cycles) was originally introduced under the name vocal loading index (Vilkman, Lauri, Alku, Sala, & Sihvo, 1997); it quantifies the total number of oscillatory periods completed by the vocal folds over the exposure time and is obtained as follows:

$$D_{\mathrm{c}}=\int k_{\mathrm{v}}{f}_0\left(t\right)dt\text{,}$$ (3)

where f ₀(t) is the short-term fundamental frequency of voicing. When normalized to the exposure time T _e, D _c becomes the average rate at which cycles are accumulated. The integration includes silence periods, where no cycles are accumulated. When D _c is normalized to the time dose dT _e, silences are eliminated and the cycle dose becomes the mean fundamental frequency over the exposure time. The cycle dose contains two of the three metrics of exposure, frequency and duration, whereas the time dose in Equation 2 contains only one, duration. Neither of the measures contains amplitude. Hence, two more definitions of vocal dose were introduced (Titze et al., 2003).

Distance Dose

Distance dose (with the unit of meters) is the approximate distance a tissue particle in the vocal folds travels in a cyclic trajectory over many cycles. The trajectory may be complex (Berry, Montequin, & Tayama, 2001), involving both medial–lateral and inferior–superior motions. If we assume the fundamental component of this path to be a time-dependent circle of radius A(t), then 2πA(t) is the distance per cycle and the distance dose becomes

$$D_{\mathrm{d}}=\int k_{\mathrm{v}}2\pi A\left(t\right)f_0\left(t\right)dt\text{,}$$ (4)

where A(t) and f ₀(t) are both short-term time functions. Note that this dose involves all three metrics: vocal-fold amplitude, frequency, and duration. When normalized to the exposure period T _e, it becomes the rate at which distance is accumulated. When normalized to the time dose dT _e, the distance dose becomes the mean tissue-particle velocity in meters per second.

Dissipated-Energy Dose per Unit Volume of Tissue

Dissipated-energy dose per unit volume of tissue is derived from the energy dissipated by friction in vocal-fold tissues during vibration. As tissue particles travel in cyclic motions, they rub against one another and create friction. In terms of continuum mechanics (Titze et al., 2003), the dissipated-energy dose has been derived as

$$D_{\mathrm{e}}=\mathrm{\int }\mathrm{½}{k}_{\mathrm{v}}\eta {\omega }^2{\left(\frac{A}{T}\right)}^{2}dt\text{,}$$ (5)

where η is the tissue viscosity, ω is the angular frequency of vibration, A is the amplitude of vibration of a shear mode (upper and lower out-of-phase movement along the medial surface), and T is the thickness of tissue over which this shear mode occurs. The ratio A/T is known as the shear strain of the tissue in this mode of vibration. Equation 5 applies to simple shear (shear strain being constant throughout vocal folds), but boundary conditions on anterior, posterior, and lateral surfaces of the vocal folds do not allow simple shear to take place. All deformations are nonuniform (Titze, 2006, chapter 4); nevertheless, the deformations are based on shear properties because there is negligible tissue compression at sonic frequencies. In addition, collision between vocal folds involves highly complex shear. Hence, Equation 5 is an order-of-magnitude estimate of frictional energy loss.

The unit of the energy dose is joules per cubic meter of tissue, which is also the unit of vibrational shear stress, expressed in pascals. For vocal-fold dimensions, a unit of millijoules per cubic centimeter is more workable, which is equivalent to 1 kPa of vibrational shear stress. When divided by the exposure time T _e, the energy-dissipation dose becomes the mean frictional power dissipated in a volume of tissue (expressed in milliwatts per cubic centimeter), or the mean shear stress per second.

Inclusion of Vocal-Fold Contact in the Energy-Dissipation Dose

Vocal-fold collision occurs over a fraction of the vibration cycle. This fraction is expressed as the contact quotient Q _c, which ranges from 0.0 (no contact) to 1.0 (contact throughout the cycle). For sinusoidal vocal-fold vibration of the form Asin(ωt), tissue velocity v is proportional to ωA. The kinetic energy per unit volume of tissue is therefore proportional to ½ρω² A ², and the power dissipated in collision can be expressed in terms of the proportion

$$P_{\mathrm{d}}\sim \frac{1}{2}\rho {\omega }^2{A}^2\frac{1}{T_0}\text{,}$$ (6)

where T ₀ is the period of oscillation. If all kinetic energy were lost during collision, Equation 6 would be an equality rather than a proportionality. There is a rebound kinetic energy, however, which means that only a fraction of the impact kinetic energy is lost. The fraction is directly proportional to Q _c. We can therefore write

$$P_{\mathrm{d}}=C{Q}_{\mathrm{c}}\frac{1}{2}\rho {\omega }^2{A}^2{f}_0\text{,}$$ (7)

where C is an empirical constant to be determined, and the substitution f ₀ = 1/T ₀ was made. (Note that the dissipated power is proportional to $f_0^3$ because ω = 2πf ₀.)

The units of P _d are watts per cubic meter, which can be expressed alternatively as pascals per second. This alternative unit suggests a direct connection to impact stress, which has been calculated and measured. By theoretical reasoning, Titze (1994) estimated an impact stress of 2.6 kPa at an f ₀ of 200 Hz and a vibrational amplitude of 1 mm. Jiang and Titze (1994) measured peak contact stress to be in the range of 0.5–5 kPa in excised larynges under self-sustained oscillation. The variation was due to controlled changes in subglottal pressure, degree of adduction, and location of contact along the medial surface of the vocal folds. Direct measurements on human subjects (Gunter, Howe, Zeitels, Kobler, & Hillman, 2005; Hess, Verdolini, Bierhals, Mansmann, & Gross, 1998; Verdolini, Hess, Titze, Bierhals, & Gross, 1999) also yielded a range of 1–5 kPa. Li et al. (2013) calculated values as high as 9 kPa from indirect measurement (glottal area and electroglottography). The linear relation between contact stress and contact quotient in Equation 7 was demonstrated in the data of Verdolini et al. (1999).

Horáček, Laukkanen, Šidlof, Murphy, and Švec (2009) suggested that collision stress should be included as a vocal loading factor. In our formulation, this can be accomplished easily by adding Equation 7 to the integrand in Equation 5. Prior to this addition, however, it is important to obtain a good estimate of the empirical constant C. The data of Jiang and Titze (1994) suggested a pulse-like impact stress, the duration of which was only about one quarter to one third of the contact period. Verdolini et al. (1999) showed raw data for which the stress waveshape was triangular, lasting over more than half of the contact period. Given that the mean value of a triangular pulse is half of its peak value, and that the duration is on the order of 40% of the contact period from the combined studies, it can be assumed that the mean stress over the entire contact period is about 20% of the peak value. This would indicate a value of about 1 kPa for a 5-kPa peak value. For a mean male–female f ₀ of 160 Hz, a mean amplitude of vibration of 1.0 mm, and a mean contact quotient Q _c of .5, Equation 7 yields a value of C of 0.02.

The total energy-dissipation dose is now written as

$$D_{\mathrm{e}}={\displaystyle \int k_{\mathrm{v}}}\left[\frac{1}{2}\eta {\omega }^2{\left(\frac{A}{T}\right)}^2+0.02Q_{\mathrm{c}}\frac{1}{2}\rho {\omega }^2{A}^2{f}_0\right]dt\text{.}$$ (8)

When normalized to exposure time T _e, this dose expresses either the mean power dissipated (in watts per cubic millimeter) or the mean combined shear and contact stress per second of vibration.

The Problem of Amplitude Estimation

Vibrational amplitude is difficult to measure in vivo. Our original estimate of vibrational amplitude was based on the following empirical relation (Titze et al., 2003):

$$A=0.05L_0{\left[\left(P_{\mathrm{L}}-P_{\mathrm{t}\mathrm{h}}\right)/P_{\mathrm{t}\mathrm{h}}\right]}^{1/2}\text{,}$$ (9)

where L ₀ is the preadductory vocal-fold length (Nishizawa, Sawashima, & Yonemoto, 1988), P _L is lung pressure, and P _th is threshold lung pressure. The threshold lung pressure was measured on human subjects as

$$P_{\mathrm{t}\mathrm{h}}=0.14+0.06\left(f_0/f_{0\mathrm{N}}\right)\text{,}$$ (10)

where f _0N is a nominal speaking f ₀ (120 Hz for male subjects and 190 Hz for female subjects). The lung pressure above threshold was expressed in terms of sound pressure level (SPL),

$$P_{\mathrm{L}}-P_{\mathrm{t}\mathrm{h}}={10}^{(\mathrm{S}\mathrm{P}\mathrm{L}-83)/27.3}\text{,}$$ (11)

where SPL was measured 0.5 m from the mouth (Titze & Sundberg, 1992) but converted to 0.3 m for SPL calibrations in our measurement protocols on teachers.

A new attempt to estimate vibration amplitude from skin acceleration measured on the neck is based on more recent work by Popolo and Titze (2008). An experiment was designed to measure absolute amplitude with a two-point laser projection system while simultaneously measuring skin acceleration on the neck. The two-point laser projection provided a known distance in the video image field, using a ridged endoscope to capture the vocal-fold movement. Details of the design and construction of the two-point laser projection device are reported by Popolo and Titze. Recognizing a priori that acceleration in tissue vibration is proportional to frequency squared, we propose here a regression equation that relates vibrational amplitude to SAL and ${\omega }_0^2$:

$$A=648\left(\mathrm{SAL}/{\omega }_0^2\right)+0.357\mathrm{mm}$$ (12)

for a male subject, with a correlation coefficient R = .84, and

$$A=119\left(\mathrm{SAL}/{\omega }_0^2\right)+0.324\mathrm{mm}$$ (13)

for a female subject, with a correlation coefficient R = .64.

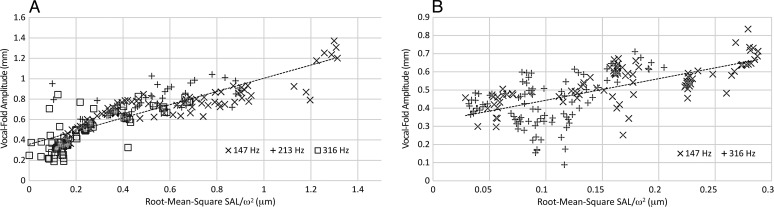
Figure 1 shows the measured data for several hundred observations at a variety of pitch and loudness conditions for a male subject (A) and a female subject (B). The units of $\left(\mathrm{root-mean-square}\mathrm{SAL}\right)/{\omega }_0^2$ are micrometers on the horizontal axis, whereas A is in millimeters on the vertical axis. This suggests that the tissue displacement at the neck is on the order of 1/1,00 of the tissue displacement at the vocal folds. The slightly greater scatter for the female subject (and the correspondingly smaller correlation coefficient for a linear regression) is due to a smaller amplitude being resolved with the same number of pixels on the video images. The experiment was very tedious, so that repetition with many subjects (e.g., teachers) was impossible with existing resources.

Figure 1.

Scatter plot of A in mm versus SAL/ω² in μm for (A) a male and (B) a female subject, showing all vocal loudness and frequency data points and the linear regression line (data from Popolo, 2007).

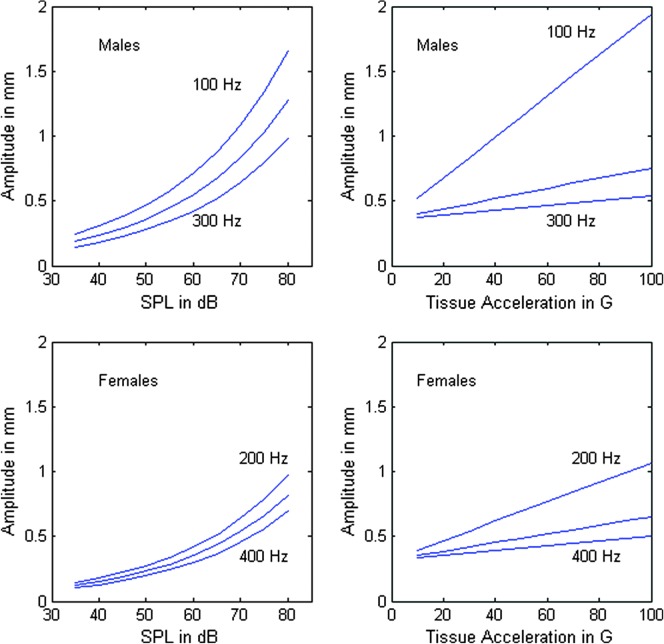
For later comparisons between vibration-dose calculations, the exact relation between A and SAL is less important than the range of amplitudes encountered. This range, on the order of 0.2–1.5 mm, determines how important amplitude variation is relative to frequency, contact quotient, and duration variation. Figure 2 shows a comparison of amplitude estimation from SPL measurement (left panels, on the basis of Equations 9 –11) and from tissue acceleration (in units of gravity acceleration G) from visual and SAL measurements (right panels, on the basis of Equations 12 and 13). Note that although the exact variations with f ₀ are not the same (spacing between the curves and the curvatures themselves), the ranges of amplitude obtained from SPL and optical measurement are similar (0.2–1.6 mm for SPL and 0.5–1.9 mm for optical in men; 0.1–1.0 mm for SPL and 0.3–1.1 mm for optical in women). In the dose calculations to follow, we used the SPL formulas because the optical data were not available at the outset of our 10-year study on teachers. The optical data are presented here to confirm the validity of the range of amplitudes used, but variation with f ₀ may have been on the conservative side with SPL estimates.

Figure 2.

Estimation of vocal-fold amplitude from (left) sound pressure level (SPL) measurement at 30 cm and (right) from tissue acceleration measurements in units of G (gravity acceleration).

Variation of Dose Calculations With Amplitude, Frequency, and Integration Time

For completeness, we restate two auxiliary relations given earlier (Titze et al., 2003). The energy-dose calculation in Equation 8 introduced tissue viscosity η and vibrational vocal-fold thickness T as parameters. Some empirical relations were given for gender and frequency dependence of these parameters. For viscosity, Chan and Titze (1999) estimated

$$\eta =5.4/f_0\mathrm{Pa}·\mathrm{s}$$ (14)

for male subjects and

$$\eta =1.4/f_0\mathrm{Pa}·\mathrm{s}$$ (15)

for female subjects. Measurements were made on excised tissue, however, which are questionable for in vivo conditions. Thus, refinement of tissue-viscosity measurement is a high priority for future energy-dose calculations.

Vocal-fold thickness is also frequency and gender dependent. Previous estimates (Titze et al., 2003) were

$$T=\left(15.8\right)/\left[1+2.15{\left(f_0/120\right)}^{1/2}\right]$$ (16)

for male subjects and

$$T=\left(10.63\right)/\left[1+1.69{\left(f_0/190\right)}^{1/2}\right]$$ (17)

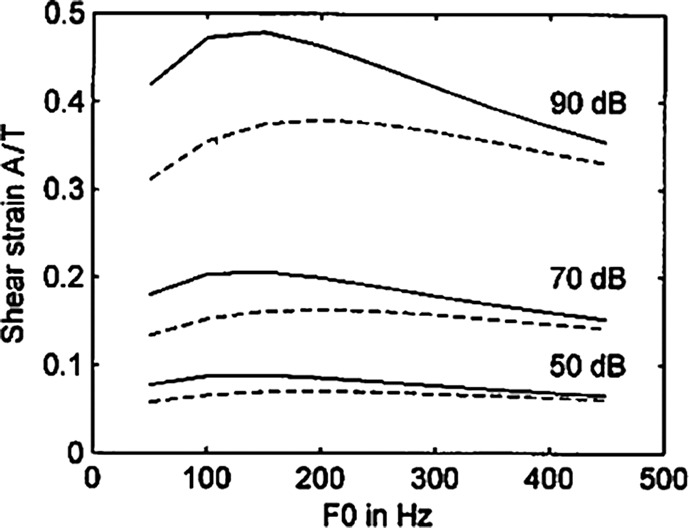
for female subjects. These relations also need further validation. However, some new insights are given here. When the ratio A/T is taken in the energy-dose calculation in Equation 8, imprecision in the inverse relation between T and f ₀ is partially canceled by a similar inverse relation between A and f ₀. Figure 3 shows the dependence of A/T on gender and f ₀. Here A/T is plotted for values of 50, 70, and 90 dB SPL at 30 cm from the mouth, corresponding to a range of amplitude of 0.3–1.5 mm. Solid lines are for male subjects and dashed lines are for female subjects. Note that the A/T ratio, which is the shear strain for a uniform shear mode in the tissue, is only mildly sensitive to f ₀ in a large f ₀ range (50–450 Hz). The greatest variation with f ₀ is 20% for male subjects at 90 dB. Likewise, variation with gender is at most about 30%, again for loud phonation (90 dB).

Figure 3.

Shear strain A/T plotted against f ₀. Solid lines are for geometries for male subjects, and dashed lines for female subjects.

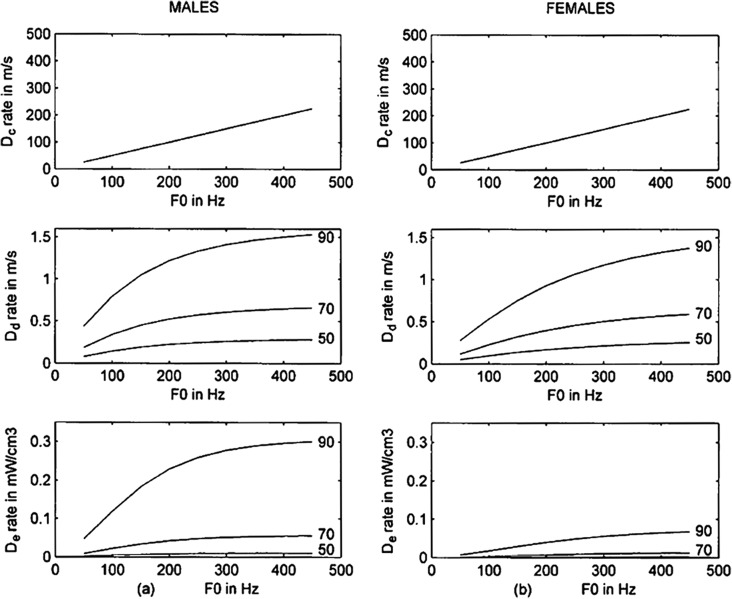
Figure 4 shows how vibration-dose rates (doses per unit time) vary with f ₀ and amplitude (plotted in terms of SPL at 30 cm). Time dose D _t, obviously, is not included because it does not change with either f ₀ or A. Cycle-dose rate D _c (top row) is simply proportional to f ₀, with the proportionality factor being the duty ratio (chosen to be .5 here). Rates of D _d and D _e (middle and bottom rows) have a square-root-like relation with f ₀, increasing more at lower values of f ₀ than at higher values. No vocal-fold collision is included in the D _e rate here; it will be discussed later. The large male–female difference in the D _e rate (bottom row, comparing left and right) is attributed entirely to the large difference in tissue viscosity (Equations 14 and 15), for which there is as yet not a high level of confidence. In later computations, an average value of tissue viscosity will be taken across genders. With respect to dose rates' dependence on SPL, note that a change from 70 to 90 dB increases D _d and D _e rates much more than a change from 50 to 70 dB. Loud speech (90 dB at 30 cm or greater) tends to dissipate a disproportionate amount of energy in vocal-fold tissues.

Figure 4.

Vocal dose-rate variation with f ₀ and SPL at 30 cm (changing vibrational amplitude) for male (left) and female (right) subjects.

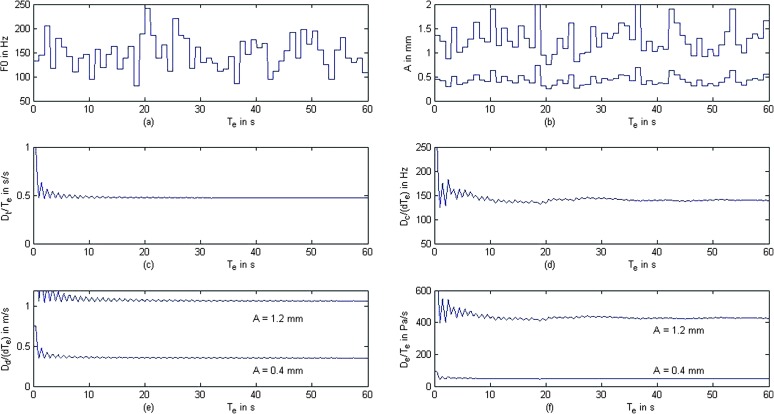
All dose calculations involve an integration over time. The voice turns on and off according to the step function k _v (Equation 1). An important question is: How long does the integration time need to be for the dose calculations to stabilize? Figure 5 shows simulated time series and dose-rate calculations following the empirical rules presented here for amplitude, tissue viscosity, and vocal-fold thickness in male subjects. A voicing step function with a duty ratio of .5 was chosen. In other words, voicing was on for 0.5 s and off for 0.5 s, repeatedly. The time sampling interval was 0.03 s, which is the sampling interval used in our dosimeter. Figure 5a shows a randomized f ₀ contour with a mean f ₀ value of 120 Hz and a coefficient of variation of 25%. Figure 5b shows two corresponding levels of vibrational amplitude, one for low (A = 0.4 mm) and one for high amplitude (A = 1.2 mm). The amplitude fluctuations are a result of the f ₀ fluctuations in Figure 5a, determined by the covariations of A and f ₀ in our mathematical model. When f ₀ goes up, A goes down in Equations 12 and 13. The mean amplitudes are in the range measured optically and predicted from SPL (recall Figure 2).

Figure 5.

Simulation of time sequences for (a) randomized fundamental frequency, (b) corresponding vibrational amplitude (two levels), (c) time dose normalized to integration time T _e, (d) cycle dose normalized to time dose dT _e, (e) distance dose normalized to time dose dT _e, and (f) energy (shear stress) dose normalized to integration time T _e.

The lower four panels of Figure 5 show the dose-rate calculations according to Equations 2 –5. Note that after the first few voicing episodes, the dose rates stabilize, even though the f ₀ and amplitude fluctuations continue. Thus, short-term variability in amplitude and f ₀ appear to be inconsequential when integration is over a period of 1 min or more. They are integrated out in the dose calculations, suggesting that only long-term changes in mean values of f ₀ and A matter. We will see later that hourly drifts in f ₀ throughout the day are observable in teachers.

Of major significance, however, is the overall level of vibrational amplitude after stabilization. Distance-dose rate is scaled directly in proportion to amplitude (3:1 in Figure 5e), whereas energy-dose rate is scaled to the square of amplitude (9:1 in Figure 5f). In contrast, time- and cycle-dose rates are insensitive to vibrational amplitude. Time-dose rate asymptotes to the duty ratio d = .5 (Figure 5c), whereas cycle-dose rate (Figure 5d) asymptotes to the mean f ₀ when it is normalized by the time dose dT _e.

Having shown the predicted differences in dose-rate calculations on theoretical grounds, we now present measurements from a corpus of 57 teachers.

Four Vocal-Dose Calculations Computed on 57 Schoolteachers

The National Center for Voice and Speech teacher dosimetry data bank was the primary resource for the current study. It contains 2-week data that have been captured as described previously (Hunter & Titze, 2010; Titze et al., 2007). For completeness, we summarize the methods of acquisition here.

Subjects

After consent under the approval of the local institutional review board, 57 teachers completed the 2-week study, which began (whenever possible) on a Saturday morning and ended 2 weeks later on Friday evening. The teachers (all K–12 teachers from more than a dozen schools in the Denver [CO] metropolitan area) comprised 45 women and 12 men with an average age of 44 years (median = 55; SD = 10).

The breakdown by teaching grade was: K–fourth grade, 59%; fifth–eighth grade, 16%; and ninth–12th grade, 25%. Breakdown by teaching topic was: general classroom instruction, 71%; music/theater instruction, 16%; physical education instruction, 9%; and other (e.g., library instruction, special education), 4%. The results from this moderate-size corpus were powerful enough to draw conclusions about doses across work hours versus nonwork hours, but no specific comparisons between the teachers' teaching topics were conducted.

Recordings

Dosimeter recording was calibrated for each teacher's voice in order to relate SPL (at 30 cm) to skin acceleration (Švec et al., 2003, 2005). During this calibration session, each teacher was taught how to attach and use the dosimeter. No daily calibration was necessary because preliminary testing showed little variation with reattachment of the accelerometer at the same location (the sternal notch). A laboratory technician was on call at all hours, however, to provide technical support or to answer general questions.

The device recorded data every 30 ms, with each data record time-stamped so that it could be searched by date and time for analysis. Because each dosimeter was individually set up for a specific teacher, data files were also categorized by dosimeter, using a unique identification number. For each teacher who completed the 2-week dosimetry study, a complete data set contained approximately 108,000 data records per hour, nearly 2 million records per day (18 hours), or 27 million records per 14-day period.

Analysis and Statistics

MATLAB scripts were written that could search all of the teacher dosimeter data by date and time. Using these scripts, average voicing measures were calculated in 15-min increments throughout all the days. If there was at least 30 s of voicing within a 15-min increment, the data were utilized for further statistical analysis. Data were compiled first into weekday and weekend groupings and also by a time-day grouping: at-work times (9 a.m.–2:30 p.m.) and not-at-work times (4:30–10:00 p.m.). Averages were also calculated in a sliding hour-long window in 20-min steps. This compilation tracked the number of teachers contributing to a specific interval of the day, separated by weekdays or weekends (e.g., 7:00–8:00 a.m. weekdays). For the two weekends, some teachers could contribute only up to 4 hr of observational voice data (7:00–8:00 a.m. for two Saturdays and two Sundays). Because all of the dose measures are dependent on basic measures such as f ₀ and SPL, we present those data first with the accompanying statistics.

From the 15-min increment averages, treating each increment as one of many voice samples from a subject, linear mixed-effects models (fitted by maximum likelihood) were implemented using R (Version 3.1.2, lme4; http://www.r-project.org) and were used to compare the at-work and not-at-work values for both weekdays and weekends. Semitones and log(f ₀) were used so that f ₀ values in the long recording had a more normal distribution. Using the dose equations already given (but not including the contact-stress term in Equation 8, which is a new development), the doses per hour of exposure were calculated. The analysis window moved in 20-min steps, resulting in some analysis overlap. Dose calculations were divided by 3,600 s to be expressed as an average dose rate, as in the theoretical results. For the 57 teachers, data were collected from 769 days of 798 possible days, and usable voice data consisted of 8,451 hr (weekdays: 6,106 hr; weekends: 2,345 hr). Unusable data resulted from teachers temporarily removing the device or from temporary equipment malfunction (e.g., an electrical short in the accelerometer cable). The four dose-measure averages were analyzed for correlation using Pearson product–moment correlations. An equivalent of analysis-of-variance effect sizes was calculated for the linear mixed-effects models by regressing the observed values in the model on the corresponding fitted values and extracting the coefficient of multiple determination (R ²).

Teacher Results

Averages of f ₀ and dB in the 15-min increments for all subjects (male and female) and for weekdays and weekends are presented in Figure 6 and displayed in those increments for the at-work and not-at-work times. For the female subjects, comparing at-work and not-at-work f ₀ showed that f ₀ was significantly lower for not-at-work—log(f ₀): t = −2.02, df = 6247, p < .05, R ² = .35; f ₀ in semitones: β = −.3, t = 3.78, df = 6246, p < .001, R ² = .38. It is not surprising that there was a difference in log(f ₀) between weekday and weekend periods, but the difference was greater during the at-work hours, not during the not-at-work hours. Similar but larger effects were shown in terms of the dB values, with the not-at-work weekday and weekend values significantly lower than the weekday at-work time, t = 18.32, df = 6242, p < .0001, R ² = .61.

Figure 6.

Notched box plots for the male (upper) and female (lower) teachers showing compiled weekday and weekend data for times between 9 a.m. and 2:30 p.m. (at-work) and 4:30 p.m. and 10:00 p.m. (not-at-work).

The male teachers also showed a significant difference for at-work time compared to not-at-work times for dB changes, t = −9.6, df = 2081, p < .0001, R ² = .6). However, where female teachers lowered their f ₀ outside of work times, male teachers raised their vocal pitch—log(f ₀): t = 3.94, df = 2079, p < .0001, R ² = .52; f ₀ in semitones: β = .21, t = 2.8, df = 2081, p < .01, R ² = .58. The statistical models also reveal another gender difference. For the male teachers, there was no interaction of time of day and weekday and weekend, yet for the female teachers there was a significant interaction—log(f ₀): t = 2.4, df = 6240, p < .05; f ₀ in semitones: t = 3.59, df = 6245, p < .001; dB: t = 11.43, df = 6242, p < .0001. This implies that in the evening, even after a day of work, the male teachers behaved much the same on both weekdays and weekends. This difference may have implications for the reported gender differences between men and women.

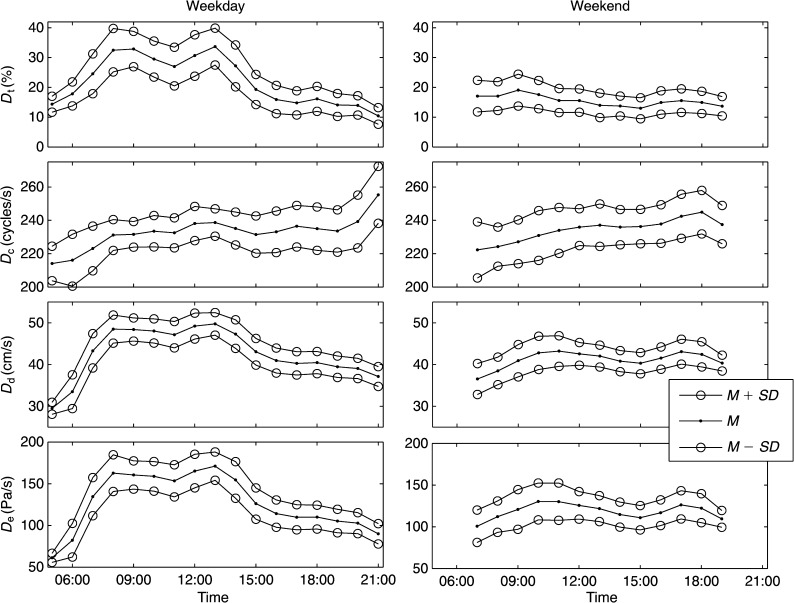
The time-course of average dose rates and standard deviations across all 45 female subjects are shown in Figure 7. Time-, distance-, and energy-dose rates (top left, bottom two left) are seen to reach a peak twice in the middle of the workday hours. One peak occurs in early morning and one in early afternoon. The same dose rates D _t, D _d, and D _e fall dramatically after 3:00 p.m. during workdays, whereas cycle-dose rate D _c (second from top) does not. The dramatic fall is partially the result of the change in the underlying quantities of f ₀ and dB SPL just discussed. The cycle-dose rate (or mean f ₀ with duty-ratio normalization) rises gradually over the entire day, on both weekdays and weekends. On weekends, there are smaller peaks in D _t, D _d, and D _e around 10 a.m. and 6:00 p.m., which are likely to be domestic conversation and social times, respectively. It is visually obvious that cycle dose does not correlate well with the other three doses. Correlation coefficients will be given later.

Figure 7.

Dose rates from 45 female teachers across an entire day, both weekdays (left) and weekends (right). SDs (circles) bracket the mean values.

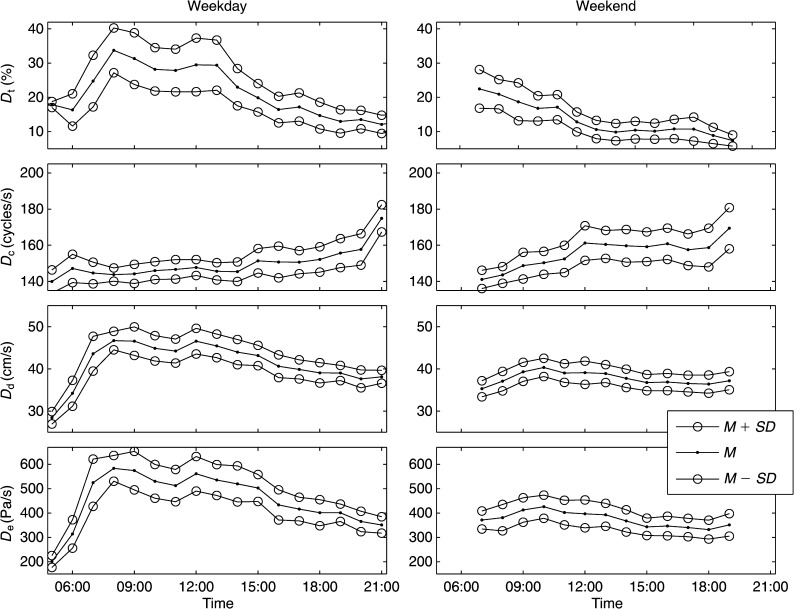
Similar data for the 12 male teachers are shown in Figure 8. Except for the lack of a 6:00 p.m. rise of D _d and D _e on weekends (perhaps male teachers are less talkative or speak more softly during those hours), no major differences are noticed in the trends. Again, the time-, distance-, and energy-dose rates appear highly correlated visually.

Figure 8.

Dose rates from 12 male teachers across an entire day, both weekdays (left) and weekends (right). SDs (circles) bracket the mean values.

Taking the average dose measures per hour, Pearson product–moment correlations for paired samples were conducted (see Table 1). For all teachers, time dose D _t correlates well with D _e and D _d on weekdays (.76 and higher for both genders, top row, marked with three asterisks) but less well on weekend days (fifth row). The best correlations are categorically between D _d and D _e, which is understandable, because they both contain amplitude and frequency variation. The most striking difference between the dose measures is the negative correlation between D _t and D _c, especially for the male teachers on weekend days. Female teachers also exhibit this negative correlation, but not as significantly. When both speaking times and f ₀ vary a lot for unstructured conversation or recreational activities, D _t and D _c are poorly correlated. Similar to the interaction results presented earlier for f ₀ and SPL, gender difference in duration and f ₀ for weekend speech could underlie increased occupational vocal risks for women.

Table 1.

Correlation coefficients between average dose rates for female and male teachers during weekdays and weekend days.

Dose	Female teachers (see Figure 6)				Male teachers (see Figure 7)
	D t	D c	D d	D e	D t	D c	D d	D e
Weekday
D t	—	−.06	.86***	.92***	—	−.63**	.76***	.80***
D c		—	.35	.25		—	−.19	−.30
D d			—	.99***			—	.99***
D e				—				—
Weekend
D t	—	−.66*	−.16	.18	—	−.95***	.07	.56**
D c		—	.70**	.41		—	.04	−.43
D d			—	.92***			—	.84***
D e				—				—

Note. For female teachers, see Figure 7; for male teachers, see Figure 8. D _t = time dose; D _c = cycle dose; D _d = distance dose; D _e = dissipated-energy dose.

^* p < .05.

^** p < .01.

^*** p < .001.

The gender differences are further clarified in Table 2. Correlations across gender were categorically high for D _d and D _e on weekdays (> .96), but only modest on weekend days (.57 and .42), suggesting different duration, amplitude, and f ₀ patterns for male versus female teachers. The cross-gender correlation for D _t was higher than for D _c (.97 vs. .75) but lower and similar for weekends (.82 vs. .81), indicating that the general patterns for speech duration and f ₀ vary with the loss of structured speaking.

Table 2.

Dose rates for female teachers compared to those for male teachers via correlation coefficient.

Part of the week	D t	D c	D d	D e
Weekday	.97***	.75***	.97***	.96***
Weekend	.82***	.81***	.57*	.42

Note. D _t = time dose; D _c = cycle dose; D _d = distance dose; D _e = dissipated-energy dose.

^* p < .05.

^*** p < .001.

On the basis of the shape of the dose-rate curves of Figures 7 and 8, it could be argued that weekday D _d and D _e are predictable from the time dose D _t. One might question, therefore, if frequency and amplitude are even relevant in the dose calculations. Shape does not predict the overall level of the dose, however, which can vary greatly with f ₀ and A. Furthermore, it will be demonstrated in the next section that collision stress alters the energy dose. Therefore, there may not be redundancy between any of the dose measures.

Retroactive Inclusion of Vocal-Fold Collision

The dosimeter software for our 10-year study on teachers did not include collision-stress calculations in the energy dose. The second term under the integral in Equation 8 was missing. Given that this term involves a new measurement, namely the contact quotient Q _c, it is impossible to produce a new data set from the existing one. New measurements would need to include an electroglottograph or some type of inverse filtering of an acoustic signal to obtain the closed quotient. These options are currently not feasible for an ambulatory device. Hence, some postprocessing and mathematical prediction are the only way to address the dependency of energy-dissipation dose on vocal-fold collision.

We offer here an EED criterion, with and without the contact quotient Q _c. Table 3 shows nominal benchmark parameters gleaned from the teacher data for at-work vocalizations. Mean values of amplitude, f ₀, viscosity, duty ratio, vocal-fold strain, and closed quotient are tabulated. The stark gender contrast in tissue viscosity mentioned earlier was eliminated so that more subtle differences in parameters with greater accuracy could be highlighted. A mean value of η = 3/f ₀ for both genders was chosen as a current benchmark. With these values, an 8-hr energy-dissipation dose is on the order of 8–10 J/cm³ (see last column of Table 3).

Table 3.

Nominal parameters for equal energy dissipation for teachers at work.

Gender	A	f 0	η	k v	A/T	Q c	8-hr D e
Male	0.8 mm	150 Hz	3/f 0 Pa-s	.4	0.20	.4	8.1 J/cm3
Female	0.5 mm	230 Hz	3/f 0 Pa-s	.4	0.17	.4	10.0 J/cm3

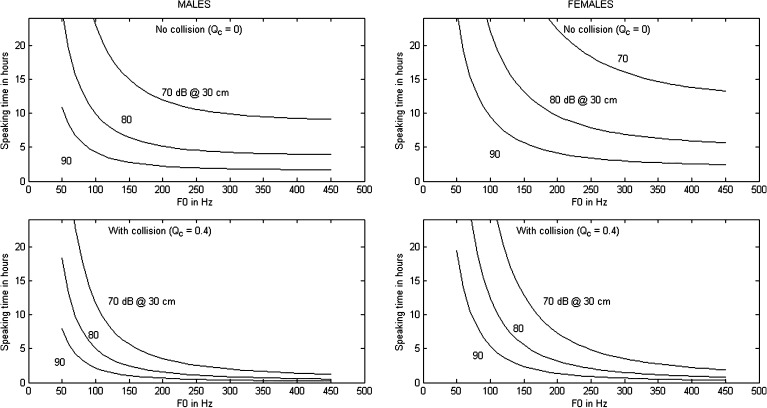
Trade-offs between A, f ₀, Q _c, and duration of speaking with the same EED are captured in Figure 9. Speaking time in hours is on the vertical axis, f ₀ is on the horizontal axis, and amplitude (expressed in dB SPL at 30 cm for ease of clinical application) is defined by separate curves. The upper two panels are for no vocal-fold collision (Q _c = 0), and the lower two panels are for typical collision (Q _c = .4; Holmberg, Perkell, Hillman, & Gress, 1994). As an example from the top right panel, without collision a female teacher with f ₀ = 230 Hz could speak at 90 dB for 4 hr, at 80 dB for 8 hr, and at 70 dB for 20 hr with EED. With collision at the same f ₀, the speaking times reduce to 1 hr at 90 dB, 2.5 hr at 80 dB, and 6 hr at 70 dB for EED. If a risk factor can be assigned to vocal injury or fatigue in the teaching profession (e.g., Verdolini & Ramig, 2001, reported a risk factor 4.67 times higher for teachers than for the nonteaching population), then Figure 9 could become a damage-risk criterion for trade-offs in loudness, pitch, adduction, and duration.

Figure 9.

Equal-energy-dissipation curves for male (left) and female (right) teachers. The top row is for no vocal-fold collision, and the bottom row is for a contact quotient Q _c = .4.

Discussion

Four vocal-dose calculations, originally developed over a decade ago, have been applied to the speaking load of schoolteachers. A new energy-dose calculation now includes vocal-fold collision. The first question posed was: How do the four doses compare in capturing duration, f ₀, and loudness in a corpus of 57 teachers? Time dose quantifies only one important exposure variable, duration. The time-dose rate (duty ratio) peaked at about 33% and averaged about 25% during work hours. Before and after work, the duty ratio dropped into the 10%–20% range, with an average of 15%. These data corroborate previous findings, which report the voicing percentages of teachers to be in the range of 15%–25% (Masuda, Ikeda, Manako, & Komiyama, 1993; Södersten, Granqvist, Hammarberg, & Szabo, 2002). It is interesting to note that the time-dose rate pattern (variation over a day) is very predictive of the pattern of distance and energy dose during work days, suggesting that duration of voicing governs hourly variations at work, with amplitude and f ₀ being somewhat regulated. We attribute two peaks in the dose rate to a “first-hour” effect—that is, more speech in monologue style in the first hour in the morning and the first hour in the afternoon. The teachers' total accumulation of voicing time with the 25% duty ratio at work was about 2 hr in an 8-hr workday.

Cycle dose serves mainly to determine long-term f ₀ drifts. Cycle-dose rate did not peak at any specific time in the middle of the day, but rose gradually and peaked in late evening hours, from 240 to 260 Hz for female teachers and from 150 to 170 Hz for male teachers. The gradual increasing trend of f ₀ over the day has been reported previously (Laukkanen & Kankare, 2006) and is hypothesized to be related to lack of muscle relaxation when the larynx remains primed all day for speech. The gradual increases in f ₀ during the day partially negate a reduced mean duty ratio in evening hours, making cycle-dose rate the least variable in terms of range. Weekend cycle-dose rates were similar to those on weekdays. The integrated cycle dose ranged between 150,000 and 300,000 cycles/hr for female teachers and 70,000 and 170,000 cycles/hr for male teachers. Total at-work cycle dose was approximately 1.2 million cycles for male teachers and 2.0 million cycles for female teachers in an 8-hr teaching day. The not-at-work cycle dose was about half that for at-work, weekdays, or weekends.

The at-work distance-dose rate for female teachers was about 0.17 m/s, or about 0.5 m/s when normalized to the duty ratio. Accumulated distance was 620 m/hr, with a total of 5 km in an 8-hr teaching period. For male teachers it was only about 5% less, owing to the trade-off between f ₀(t) and A(t) in Equation 4. The not-at-work distance dose was an additional 2 km on weekdays. Distance dose was 3–4 km over weekend days. Assuming the teachers' not-at-work dose to be comparable to those of nonprofessional voice users (75% of the U.S. workforce), normal daily distance doses are 3–4 km.

Dissipated-energy-dose rate showed a greater range of variation than the other dose rates. The maximum/minimum ratio was about 3:1 (both genders), compared to about 2:1 for time-dose rate and 1.5:1 for distance-dose rate. Thus, although the pattern of variation for D _e was similar to the patterns for D _t and D _d on teaching days, the range of variation favors D _e in terms of sensitivity to biomechanical parameters. In female teachers, D _e peaked at about 0.17 mW/cm³ (170 Pa/s) around 1:00 p.m. from a rate of 0.06 mW/cm³ (60 Pa/s) around 6:00 a.m. It decreased dramatically after 3:00 p.m. The accumulated energy dissipation during 8 working hours was on the order of 10 J/cm³ of vocal-fold tissue. (As a note of interest, caloric calculations show that this energy dissipation would raise the temperature of 1 cm³ of tissue by 2.4°C if no heat were removed from the vocal folds by air and fluid circulation, which is of course not the case.)

A retrospective analysis that included energy loss from vocal-fold collision revealed that speech duration for EED with typical vocal-fold collision (Q _c = .4) is only one third of that without any vocal-fold collision (Q _c = 0.0). Some collision is necessary, however, because collision is effective in the production of source harmonics.

The second question in this study concerned the trade-off relations between amplitude, f ₀, and speaking duration. The EED criterion showed that every 10-dB reduction in SPL allows the speaking duration to be increased by a factor of 2. Reduction in closed quotient from .4 to .2 allows speaking duration to be increased by another factor of about 1.5.

Conclusions

Teachers have been used as a benchmark for quantifying the amount of vibration exposure that individuals can inflict upon themselves by talking (Roy et al., 2004; Södersten et al., 2002). This benchmark will hopefully be useful for similar studies on telephone workers, counselors, public speakers, actors, singers, or any other vocally active population.

An EED criterion was established to quantify the trade-offs between f ₀, loudness, adduction, and speaking duration. Lowering any one of the four variables allows another to be raised for EED. A cautionary note is offered, however, about lowering f ₀. Clinical wisdom is that muscular and biomechanical stresses on the larynx may increase with artificially lowered f ₀. Thus, the gain in reduction of vibration dose may be negated by an increase in mechanical stresses in muscles and connective tissues. The best trade-offs, therefore, are between amplitude (loudness), collision, and duration of speech. The combination of loudness and voice-quality training (less adduction) may have a significant impact on longevity in the teaching profession, lowering the risk of vibration overexposure. In addition, speech duration can also be managed by building more pauses and dialogue into daily vocal activities.

Among the four dose calculations that were investigated (time, cycle, distance, and energy), energy dose showed the greatest numerical range and the greatest sensitivity to vibrational amplitude. It varies with amplitude squared for shear stress and amplitude cubed for collision stress, whereas distance dose varies with amplitude to the first power. Only energy dose can accommodate vocal-fold collision as a potential risk factor. However, energy dose is highly dependent on tissue viscosity, a quantity not yet well known under live conditions. This quantity is worthy of intense pursuit because it is also highly relevant for phonation threshold pressure, a measure of “ease” of phonation (Titze, 1988). Hence, although energy-dissipation dose is predicted to have the greatest diagnostic value, more work is needed to refine the empirical relations for viscosity, amplitude, and vocal-fold thickness in vibration and collision.

Female teachers report a higher instance of voice disorders than male teachers (Roy et al., 2004). Our dose calculations at typical speaking conditions do not predict this. On the basis of the empirical data available, there seems to be a natural trade-off between amplitude and f ₀ between men and women. Women speak at higher f ₀ but with lower amplitude of vibration, and often with a smaller contact quotient. Thus, other factors need to be included to explain the higher incidences of voice disorders in female teachers, as Roy et al. have suggested and Hunter, Tanner, and Smith (2011) further explored.

As a final note, given that the benchmark teacher population exhibits a risk factor for voice disorders nearly five times greater than nonteacher populations, the proposed EED criterion may be useful in predicting the likelihood of voice disorders in other populations. A critical next step will be to show that a potential 3:1 reduction in EED with electronic amplification and therapy can in fact reduce the risk factor in teachers from 5:1 to a smaller ratio.

Funding Statement

This work was supported by National Institute on Deafness and Other Communication Disorders Grant 5R01 DC004224, awarded to Ingo R. Titze, Principal Investigator.