Abstract
BiFeO3 based MIM structures with Ti-implanted Pt bottom electrodes and Au top electrodes have been fabricated on Sapphire substrates. The resulting metal-insulator-metal (MIM) structures show bipolar resistive switching without an electroforming process. It is evidenced that during the BiFeO3 thin film growth Ti diffuses into the BiFeO3 layer. The diffused Ti effectively traps and releases oxygen vacancies and consequently stabilizes the resistive switching in BiFeO3 MIM structures. Therefore, using Ti implantation of the bottom electrode, the retention performance can be greatly improved with increasing Ti fluence. For the used raster-scanned Ti implantation the lateral Ti distribution is not homogeneous enough and endurance slightly degrades with Ti fluence. The local resistive switching investigated by current sensing atomic force microscopy suggests the capability of down-scaling the resistive switching cell to one BiFeO3 grain size by local Ti implantation of the bottom electrode.
Nonvolatile resistive switching has been observed in many material systems within a simple structure consisting only of a metal-insulator (or semiconductor)-metal (MIM) sandwich stack.1 The engineering of resistive switching has attracted great attention due to the potential application of MIM structures in the next generation of nonvolatile memory1,2,3, reconfigurable nonvolatile logics4,5 and data encryption6. Recent intensive investigations have provided a deep understanding of the resistive switching mechanisms in oxides. There is a general agreement on the role of the ion migration (oxygen vacancies migration) within an applied electric field, which induces the formation and rupture of conductive filaments inside the filamentary-type oxide resistive switches7,8,9,10, and which induces a reversible change of the barrier heights at the interfaces inside interface-type oxide resistive switches5,11,12,13,14. It is reported that the ion migration is related to the thermal diffusion of the metallic atoms from the active bottom/top metallic electrodes, e.g. Cu15,16, Ag16,17, Ni18, and Al19, or even from the adhesion layer under the bottom electrodes, e.g. Ti20,21,22. The diffused metallic atoms can be oxidized and incorporated into the oxide thin films23, and the created cations can either induce oxygen vacancies which are mobile in the oxide thin films20,21,22 or itself migrate within an applied electric field15,16,17,18,19. In other words, the diffused metallic atoms seed the nanoscale switching centers in the resistive switches20. However, technically, the metallic diffusion from the bottom electrodes or the adhesion layer is often poorly controlled and restrains the options of metallic materials used for the bottom electrodes. In addition, the metallic diffusion often occurs over the whole wafer chip which is in contradiction with the complementary metal-oxide-semiconductor (CMOS)-compatible technology.
BiFeO3 (BFO) has been intensively investigated as an oxide resistive switch24,25,26,27,28,29 thanks to its fascinating physical properties, e.g., ferroelectric effect and photovoltaic effect30,31, which offers the possibility to integrate multi-functionality into one single device. In our previous works2,32,33,34,35,36, BFO thin films on Pt/Ti/Sapphire or Pt/Ti/SiO2/Si substrates show excellent bipolar resistive switching performances such as electroforming free, multi-level states, long retention time, and stable endurance, in which the Ti diffusion from the bottom electrodes during BFO thin film deposition plays an important role. A model based on modifiable Schottky barrier heights was proposed to explain the bipolar resistive switching in BFO thin films, in which the ionized oxygen vacancies (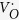 ) and diffused Ti act as mobile and fixed donors, respectively. The mobile
) and diffused Ti act as mobile and fixed donors, respectively. The mobile 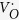 donors are redistributed by a writing bias which changes the Schottky barrier height at the bottom interface, and the fixed Ti donors can trap the mobile
donors are redistributed by a writing bias which changes the Schottky barrier height at the bottom interface, and the fixed Ti donors can trap the mobile 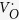 donors after the writing process to stabilize the resistive switching. In this work, we show that the Ti diffusion can be engineered before the BFO thin film deposition by Ti implantation of the Pt bottom electrode on Sapphire substrates. This offers a deeper understanding on the role of the fixed Ti donors in the resistive switching of BFO thin films.
donors after the writing process to stabilize the resistive switching. In this work, we show that the Ti diffusion can be engineered before the BFO thin film deposition by Ti implantation of the Pt bottom electrode on Sapphire substrates. This offers a deeper understanding on the role of the fixed Ti donors in the resistive switching of BFO thin films.
Methods
The Ti implantation of Pt(100 nm)/Sapphire substrates was carried out at room temperature with an ion energy of 40 keV and a series of Ti fluences. Subsequently, BFO thin films with a thickness of 460 nm were deposited on the Ti-implanted Pt/Sapphire substrates by pulsed laser deposition (PLD). For the PLD process, the nominal laser energy density, laser repetition rate, oxygen ambient pressure, and growth temperature were 2.6 J/cm2, 10 Hz, 0.013 mbar, and 650 °C, respectively. After the PLD process, the BFO thin films were in-situ annealed at 390 °C with the oxygen ambient pressure of 200 mbar for 60 minutes. Following the deposition, circular Au top contacts with an area of 0.045 mm2 and a thickness of 110 nm were prepared by DC magnetron sputtering at room temperature using a metal shadow mask. Thus, Au-BFO-Pt MIM structures with a series of Ti fluences were fabricated. The schematic sketches of the sample fabrication process and the sample structure are indicated in Figure S1 in supplementary information.
Electrical measurements were carried out using a Keithley source meter. For the time-of-flight secondary ion mass spectrometry (Tof-SIMS) measurements we used an IONTOF TOF-SIMS 5 equipment with an O2 sputtering beam (2000 eV) and a Bi analysis beam (25000 eV). The crater size was 300 μm × 300 μm. Atomic force microscopy (AFM) topography and current-sensing AFM (CsAFM) measurements were carried out with an Agilent Technologies 5420 Scanning Probe Microscope.
Results and Discussions
Ti distribution and morphologies of films
The Ti distribution in the Pt/Sapphire after the Ti implantation was estimated by the Stopping and Range of Ions in Matter (SRIM) 2013 code37,38. The predicted concentrations of implanted Ti ions as a function of depth in Pt/Sapphire with different Ti fluences are shown in Figure S2 in supplementary information. It can be seen that Ti ions distribute within 50 nm below the surface of Pt layer and a concentration peak forms at the depth of ~10 nm. Note that SRIM as a static Monte Carlo program can only estimate the Ti distribution under the assumption that the initial stoichiometry of Pt/Sapphire is preserved. A sputtering yield of 9.36 for Pt was calculated by SRIM 2013, which suggests that around 15% of Pt atoms could be sputtered away at the Ti concentration peak with Ti fluence of 5 × 1016 cm−2. Experimentally, the Pt layer was completely removed when the Ti fluence was further increased, e.g. 1 × 1017 cm−2. The Ti implantation effect on the surface morphology of Pt/Sapphire was investigated by AFM as shown in Fig. 1. Pt grains with a typical size of 80 nm randomly distribute over the pristine Pt/Sapphire, and the mean arithmetic roughness (Ra) is 3.98 nm. After Ti implantation at low fluence of 5 × 1015 cm−2, the roughness is reduced to 2.24 nm. By further increasing the fluence to 1 × 1016 cm−2, the roughness is reduced to 1.15 nm, which may be due to the strain relaxation between the grains caused by the energy deposited by the implanted Ti ions. However, by further increasing the Ti fluence to 5 × 1016 cm−2, the typical Pt grain size dramatically increases to 170 nm, which may be due to the appearance of the disordering induced agglomeration of grains. Consequently, the roughness is increased to 4.99 nm. A comparable dependence of surface roughness on ion fluence has also been observed for ZnO thin films irradiated by Au ions39.
Figure 1.
Three-dimensional AFM topography images of the pristine Pt/Sapphire (a) and the Ti-implanted Pt/Sapphire with Ti fluence of 5 × 1015 cm−2 (b), 1 × 1016 cm−2 (c), and 5 × 1016 cm−2 (d).The scanning size is 3 × 3 μm2. The mean arithmetic roughness (Ra) is 3.98 nm, 2.24 nm, 1.15 nm, and 4.99 nm, respectively. The AFM color scale (right side) indicates the height information.
It is expected that the Ti migration into BFO layer is more efficient along the BFO grain boundaries and occurs during the PLD process at 650 °C40. Figure 2 shows the Tof-SIMS intensity-time profiles of the BFO thin film on Ti-implanted Pt/Sapphire with Ti fluence of 5 × 1016 cm−2, depicting Au, Bi, Fe, Ti, Pt, and Al ion intensities as a function of sputtering time. It is clear that the Ti intensity profile exhibits a broader shoulder compared to that of other metallic elements, which indicates that Ti diffused into the BFO thin films during the PLD process and that a Ti concentration gradient was created along the BFO growth direction. The Ti diffusion into BFO was also observed in the BFO thin films on Pt/Ti/Sapphire or Pt/Ti/SiO2/Si substrates in our previous works, which plays a crucial role for the resistive switching in BFO thin films36,40. In these MIM structures, Pt layer serves not only as a bottom electrode but also as a diffusion suppressing layer to prevent a strong Ti diffusion into BFO layer during the BFO deposition at 650 °C. Therefore, an optimized concentration of fixed Ti donors is realized and a tunable Schottky barrier can be formed at the BFO/Pt/Ti interfaces. It is expected that less Ti diffuses into the BFO layer in MIM structures with Pt bottom electrodes which have been implanted with a smaller Ti fluence. The surface morphology of the BFO thin films on Ti-implanted Pt/Sapphire was characterized by AFM measurements with a scanning size of 3 × 3 μm2 (Supplementary information, Figure S3). The mean arithmetic surface roughness of BFO thin films is 12.5 nm, 9.54 nm, and 13.1 nm for the Ti fluence of 5 × 1015 cm−2, 1 × 1016 cm−2, and 5 × 1016 cm−2, respectively.
Figure 2. Tof-SIMS intensity-time profiles of the metallic elements in the MIM structure with Ti fluence of 5 × 1016 cm−2.
Resistive switching characteristics
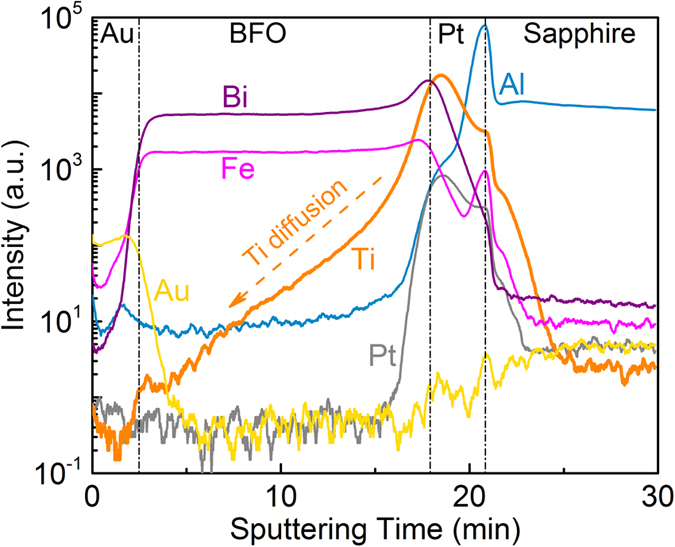
The current-voltage (I-V) measurements were carried out with a Keithley 2400 source meter. The schematic sketch of the electrical measurement configuration is indicated in Figure S1 in supplementary information, in which the bias voltage was applied on Au top electrode and the Ti-implanted Pt bottom electrode was grounded. As shown in Fig. 3, the shape of the I-V characteristics obtained from the BFO on Ti-implanted Pt/Sapphire is quite similar to that reported in our previous works2,32,33,34,35,36,40. The I-V characteristics were measured by sweeping the voltage in sequence of 0 V → +8 V → −8 V → 0 V (black curve) and 0 V → −8 V → +8 V → 0 V (red curve) on two pristine cells of the MIM structures, respectively. In both cases, a distinct I-V hysteresis exists in the positive bias range and no significant difference in the I-V characteristics is observed, which suggests that the electroforming process is not required for the resistive switching. Initially, the pristine MIM structures show high resistance state (HRS), and the low resistance state (LRS) is set by a positive bias while the HRS is reset by a negative bias. This indicates a bipolar resistive switching without an electroforming process for the MIM structures with different Ti fluences. Note that BFO thin films deposited on non-implanted Pt/Sapphire substrates do not show distinct resistive switching behavior (Supplementary information, Figure S4)34,36,40. Within the same applied bias range (between −8 V and +8 V) there is no obvious current difference in the negative bias range for the MIM structures with different Ti fluences, while the current in the positive bias range and the on/off current ratio at +2 V increase with increasing Ti fluence (Supplementary information, Figure S5).
Figure 3.
Typical I-V characteristics with different voltage sweeping sequences measured at two pristine cells on the MIM structures with Ti fluence of 5 × 1015 cm−2 (a), 1 × 1016 cm−2 (b), and 5 × 1016 cm−2 (c).The insets show the I-V characteristics with the same voltage sweeping sequences but different maximum voltage measured at the same cell on the MIM structures. Note that to avoid a hard breakdown of the devices, the maximum current was limited to be 100 μA. The sets of the maximum voltages are [8.0 V, 9.0 V, 10.0 V], [8.0 V, 8.5 V, 9.0 V] and [6.0 V, 7.0 V, 8.0 V] for the MIM structures with Ti fluence of 5 × 1015 cm−2, 1 × 1016 cm−2, and 5 × 1016 cm−2, respectively. The numbers (1)–(4) and the arrows indicate the voltage sweeping sequences and the voltage sweeping directions, respectively.
The work function of Au and Pt amounts to 5.1 eV and 5.3 eV, respectively. The band gap of BFO is taken as 2.8 eV and the electron affinity is 3.3 eV41, and then the work function of n-type BFO should be less than 4.7 eV, which suggests an upward band bending in BFO at top Au/BFO and bottom BFO/Pt interfaces. Therefore, a Schottky barrier can be formed at both top and bottom interfaces. The observed resistive switching characteristics in BFO based MIM structures can be explained by a model of modifiable Schottky barrier height at bottom interface which can be tuned by the mobile  acting as the mobile donors (Supplementary information, Figure S6)36. With lower Ti fluence, a larger Schottky barrier height is expected to form at the bottom interface which will be discussed later. Therefore, a larger electric field is required to move the
acting as the mobile donors (Supplementary information, Figure S6)36. With lower Ti fluence, a larger Schottky barrier height is expected to form at the bottom interface which will be discussed later. Therefore, a larger electric field is required to move the 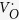 to the bottom interface to reduce the Schottky barrier height to fully set the structures to LRS. The insets in Fig. 3 show the I-V characteristics with different maximum voltages. The paths for the I-V curves in negative bias range (branches (3) and (4)) and the HRS branch of the I-V curve in positive bias range (branch (1)) are nearly the same which are independent of the maximum voltage. While the LRS branch of the I-V curve in positive bias range (branch (2)) are well separated from each other with different maximum voltage, indicating different LRS can be achieved depending on the applied maximum voltages. This multilevel LRS behavior offers an opportunity for designing multi-bit memories/logics33.
to the bottom interface to reduce the Schottky barrier height to fully set the structures to LRS. The insets in Fig. 3 show the I-V characteristics with different maximum voltages. The paths for the I-V curves in negative bias range (branches (3) and (4)) and the HRS branch of the I-V curve in positive bias range (branch (1)) are nearly the same which are independent of the maximum voltage. While the LRS branch of the I-V curve in positive bias range (branch (2)) are well separated from each other with different maximum voltage, indicating different LRS can be achieved depending on the applied maximum voltages. This multilevel LRS behavior offers an opportunity for designing multi-bit memories/logics33.
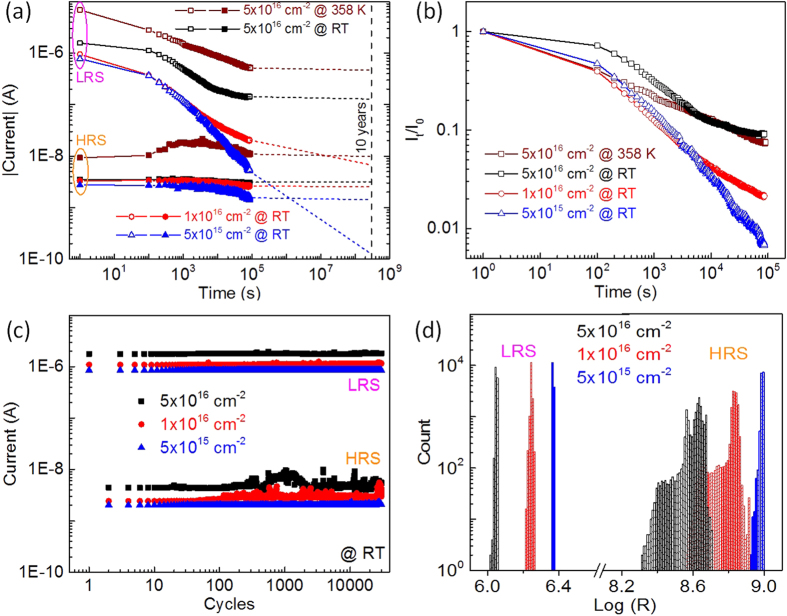
As shown in Fig. 4(a), the retention tests were carried out by first setting/resetting the MIM structures to LRS/HRS at room temperature, and then detecting the current with a small reading bias of +2 V every 2 min at room temperature (for the MIM structure with Ti fluence of 5 × 1016 cm−2, the current detection was performed at 358 K as well). In order to fully set/reset the MIM structures to LRS/HRS, the set/reset bias of +10 V/−10 V, +9 V/−9 V and +8 V/−8 V with pulse length of 100 ms were used for the MIM structures with Ti fluence of 5 × 1015 cm−2, 1 × 1016 cm−2, and 5 × 1016 cm−2, respectively. At room temperature, the HRS for all MIM structures are relatively stable, while degradation is observed during the LRS tests. The LRS of the MIM structures with low Ti fluences (both 5 × 1015 cm−2 and 1 × 1016 cm−2) decreases continuously during the retention tests, and the current ratio ILRS/IHRS of the MIM decreases below 10 within 24 hours, while the LRS of the MIM structure with high Ti fluence (5 × 1016 cm−2) becomes stable after around 15 hours. The extrapolated current ratio ILRS/IHRS can be well-kept at around 50 for more than 10 years as indicated by the dashed lines in Fig. 4(a). The change of LRS is more visible with the linear time axis (Supplementary information, Figure S7). Even at an elevated temperature of 358 K, the LRS of the MIM structure with Ti fluence of 5 × 1016 cm−2 can be stabilized within 24 hours and a current ratio ILRS/IHRS larger than 30 can be obtained for more than 10 years. The HRS at elevated temperature initially exhibits a small decay. The similar effect was also observed in Au-BFO-Pt/Ti/Sapphire MIM structures, which was possibly due to the redistribution of 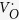 in HRS at elevated temperature36.
in HRS at elevated temperature36.
Figure 4.
(a) Retention test results of the MIM structures with different Ti fluences. The extrapolated 10-years HRS/LRS retention time can be expressed by the dashed lines. (b) Normalized current of LRS vs. retention time. The current values taken at different time (It) are normalized by the initially measured current value (I0). (c) Endurance test results of the MIM structures with different Ti fluences. (d) Statistics histograms of LRS/HRS in the endurance test results.
Figure 4(b) shows the normalized current in LRS, which suggests that the degradation in LRS becomes more pronounced with decreasing Ti fluence. In LRS the 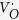 migrate to the bottom interface and then are trapped by the diffused Ti from the substrates during the BFO deposition, which consequently increases the doping concentration at the bottom interface and lowers the bottom Schottky barrier height36. The degradation in LRS is possibly due to the back diffusion of
migrate to the bottom interface and then are trapped by the diffused Ti from the substrates during the BFO deposition, which consequently increases the doping concentration at the bottom interface and lowers the bottom Schottky barrier height36. The degradation in LRS is possibly due to the back diffusion of 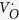 after the application of a positive writing voltage pulse which partially decreases the doping concentration at the bottom interface and partially starts to rebuild the bottom Schottky barrier. With lower Ti fluence, during the PLD process less Ti can diffuse from the hot Pt bottom electrode into the BFO layer. Therefore, not enough
after the application of a positive writing voltage pulse which partially decreases the doping concentration at the bottom interface and partially starts to rebuild the bottom Schottky barrier. With lower Ti fluence, during the PLD process less Ti can diffuse from the hot Pt bottom electrode into the BFO layer. Therefore, not enough 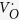 can be effectively trapped by Ti and the LRS is badly maintained (Supplementary information, Figure S6). The degradation of LRS in MIM structure with Ti fluence of 5 × 1016 cm−2 is stronger at an elevated temperature of 358 K because of the increasing diffusivity of
can be effectively trapped by Ti and the LRS is badly maintained (Supplementary information, Figure S6). The degradation of LRS in MIM structure with Ti fluence of 5 × 1016 cm−2 is stronger at an elevated temperature of 358 K because of the increasing diffusivity of 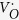 with increasing temperature. This suggests that a certain minimum amount of Ti in the BFO MIM structures is required to trap the mobile
with increasing temperature. This suggests that a certain minimum amount of Ti in the BFO MIM structures is required to trap the mobile 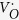 in the bottom interface in order to stabilize the resistive switching into LRS.
in the bottom interface in order to stabilize the resistive switching into LRS.
As shown in Fig. 4(c), the endurance tests were carried by repeating the process of set/read/reset/read for more than 3 × 104 times at room temperature. Figure 4(d) shows the statistics histograms of the LRS/HRS in the endurance test results. In endurance tests, all MIM structures with different Ti fluences possess a relatively stable LRS and a narrow distribution of the resistance values in LRS. The relative fluctuation (standard deviation divided by mean value)42 of LRS is 0.20%, 0.91%, and 0.82% for the MIM structures with Ti fluence of 5 × 1015 cm−2, 1 × 1016 cm−2, and 5 × 1016 cm−2, respectively. However, the distribution of the resistance values in HRS is much broader than that in LRS. The relative fluctuation increases with the Ti fluences, i.e., 1.11%, 3.95%, and 12.34% for the MIM structures with a Ti fluence of 5 × 1015 cm−2, 1 × 1016 cm−2, and 5 × 1016 cm−2, respectively. The endurance can be improved by structuring the bottom electrodes or by local Ti implantation into the bottom electrodes36,42,43.
Dependence of Schottky barrier height on the Ti fluence
The temperature-dependent I-V characteristics (from −2 V to +2 V) were measured by Keithley 2636A source meter (with a theoretical current resolution of 0.1 fA) after the MIM structures were fully set/reset to LRS/HRS (Supplementary information, Figure S8). The current increases with the temperature increasing from 253 K to 353 K. In HRS, the current is small in both positive and negative bias range showing head-to-head diode behavior as the Schottky-like barriers form at both top and bottom interface36. The reversed diode current can be governed by Poole-Frenkel emission44, Schottky emission44 or modified Schottky emission mechanisms45. The corresponding emission coefficients (Supplementary information, Figure S9-S10 and Table S1) suggest that electric conduction under reverse bias condition is consistent with the modified Schottky emission which is described by the modified Richardson-Schottky equation45:
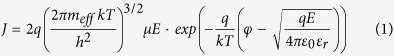 |
where J, E, meff, μ, φ, and εr represent the current density, the electric field, the effective mass, the electron mobility, the potential barrier height, and the dielectric constant, respectively. The other symbols have their usual meaning. From equation (1), the Schottky-Simmons graphic representation can be obtained at a constant voltage (electric field) as follows:
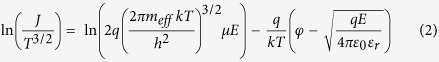 |
The apparent potential barrier for the respective constant voltage (electric field) can be estimated from the slope of the representation of ln (J/T3/2)~1/T which gives a straight line. The temperature dependent I-V characteristics of the MIM structures with different Ti fluences were replotted in the Schottky-Simmons representation of ln (J/T2/3)~1/T at voltages of ±0.8 V, ±1.0 V, ±1.2 V, ±1.4 V and ±1.6 V. A linear fitting was obtained in both negative and positive bias range (Supplementary information, Figure S11). Figure 5(a) shows the apparent potential barrier height (φHRS) calculated from the slope of the linear fitting in the plotting of ln (J/T2/3)~1/T as a function of |V|1/2. The barrier height at top interface can be obtained from the plotting in the negative voltages range (V<0 V) as the top Schottky barrier is reversed and dominates the current under the negative bias, and similarly the barrier height of reversed bottom Schottky barrier corresponds to the plotting in positive bias range (V>0 V). As shown in Fig. 5(a), with increasing reverse bias both top and bottom Schottky barrier heights decrease in the MIM structures with low Ti fluence (5 × 1015 cm−2 and 1 × 1016 cm−2), while the barrier heights of the MIM structure with Ti fluence of 5 × 1016 cm−2 increase. The Schottky barrier height depends on the doping concentration and the applied reverse bias, i.e. the Schottky barrier height decreases with increasing reversed bias in the case of low doping concentration but increases in the case of high doping concentration46. With larger Ti fluence, more Ti diffuses into BFO during the PLD process and the as-prepared BFO thin film possesses a higher doping concentration. Therefore, different changes of the Schottky barrier heights are presented. The potential barrier at zero bias can be extracted from the intercept of the linear fitting in the apparent potential barrier height as a function of |V|1/2. The top Schottky barrier height (φt-HRS) is deduced to be 0.47 eV, 0.43 eV, and 0.30 eV for the MIM structures with Ti fluence of 5 × 1015 cm−2, 1 × 1016 cm−2, and 5 × 1016 cm−2, respectively, and the corresponding bottom one (φb-HRS) is 0.57 eV, 0.46 eV and 0.26 eV, respectively.
Figure 5.
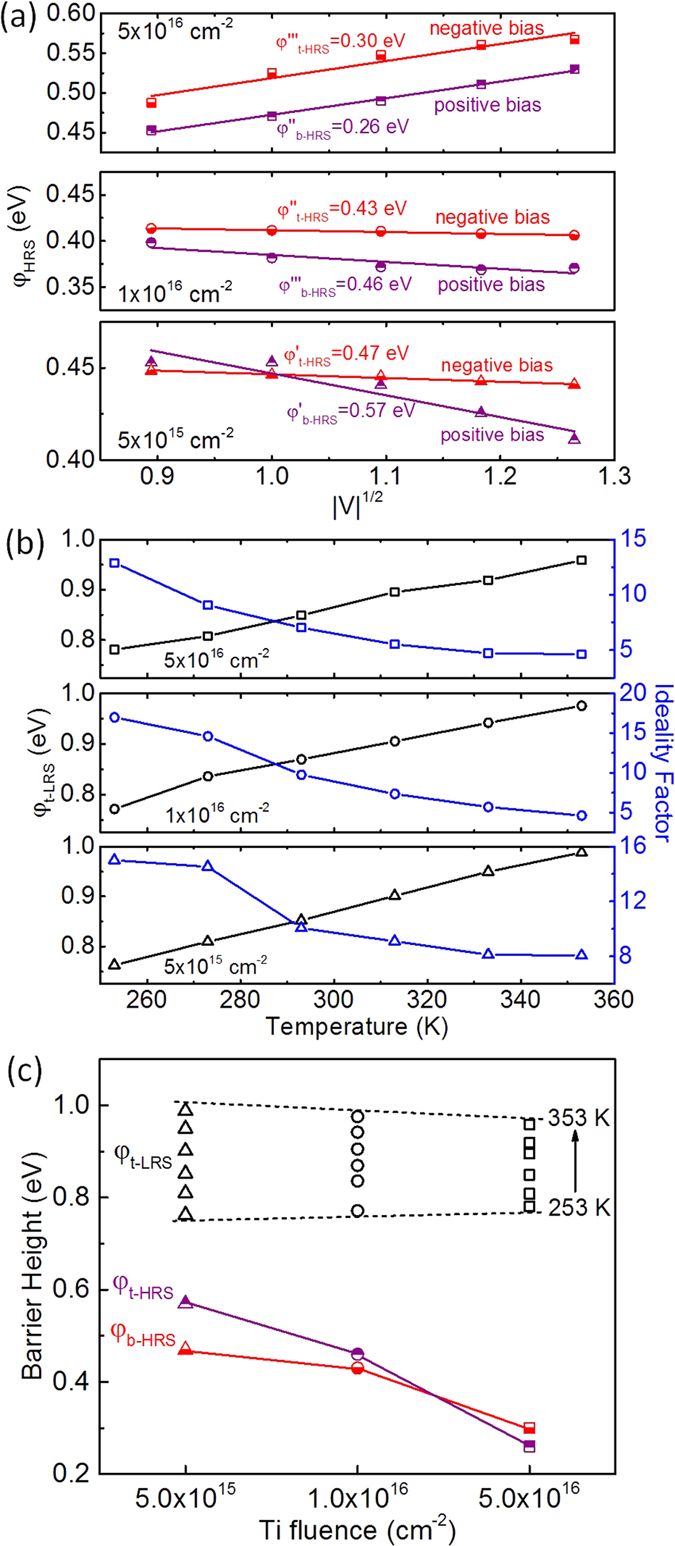
(a) Bias dependent Schottky barrier heights in HRS. The zero-bias Schottky barrier height can be extracted by a linear fitting. (b) Temperature dependent zero-bias Schottky barrier heights and ideality factors in LRS. (c) Change of the top and bottom Schottky barrier heights in LRS and HRS for the MIM structures with different Ti fluences.
In LRS, the I-V characteristics exhibit forwarded diode behavior due to the Schottky contact at top interface and Ohmic contact at bottom interface, and the current is mainly dominated by the Schottky barrier at top interface36. As shown in Fig. 5(b), the temperature dependent zero bias Schottky barrier height and ideality factor were fitted from the temperature dependent I-V curves by using the Shockley equation as follows:
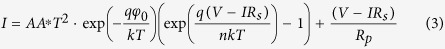 |
where A, A*, φ0, Rs, Rp and n represent the area of the diodes, the effective Richardson constant, the zero bias barrier height, the series resistance, the parallel resistance and the ideality factor, and the other symbols have their usual meaning. The obtained Schottky barrier height (φt-LRS) at the top interface decreases with the increasing temperature, while the ideality factor increases. The relatively large ideality factor may be due to the large series resistance in the order of several mega-ohm. By comparing the top and bottom Schottky barrier heights of the MIM structures in LRS and HRS as shown in Fig. 5(c), it is clear that the Schottky barrier height at top interface is greatly increased when the MIM structures are set to LRS as most of the 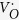 are drifted to the bottom interface, which is in agreement with the result in our previous report36. In HRS, the Schottky barrier height at both top and bottom interface (φt-HRS and φb-HRS) decreases with the increasing Ti fluence because donors including the fixed Ti donors and mobile
are drifted to the bottom interface, which is in agreement with the result in our previous report36. In HRS, the Schottky barrier height at both top and bottom interface (φt-HRS and φb-HRS) decreases with the increasing Ti fluence because donors including the fixed Ti donors and mobile 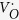 donors distribute relatively homogenously over the BFO layer in HRS36, and the Schottky barrier height is in inverse proportion to the doping concentration12,13. As the resulting Ti concentration in the BFO layer increases with the Ti fluence during Ti implantation into the underlying Pt bottom electrode, a larger Ti fluence causes a lower Schottky barrier height in HRS. However, as expected from the negligible Ti concentration close to the top electrode there is no significant difference between the top Schottky barrier height in LRS (φt-LRS) for the MIM structures with different Ti fluence which varies between 0.76 eV and 0.99 eV. Most of the mobile
donors distribute relatively homogenously over the BFO layer in HRS36, and the Schottky barrier height is in inverse proportion to the doping concentration12,13. As the resulting Ti concentration in the BFO layer increases with the Ti fluence during Ti implantation into the underlying Pt bottom electrode, a larger Ti fluence causes a lower Schottky barrier height in HRS. However, as expected from the negligible Ti concentration close to the top electrode there is no significant difference between the top Schottky barrier height in LRS (φt-LRS) for the MIM structures with different Ti fluence which varies between 0.76 eV and 0.99 eV. Most of the mobile 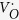 are drifted to the bottom interface to lower the bottom Schottky barrier height in LRS and the donor concentration at the top interface is very low. Thus, the top Schottky barrier height in LRS is independent of the Ti fluence. The relationship of the Schottky barrier height in LRS and HRS and the Ti fluence in turn is a good evidence for the model of modifiable Schottky barrier height for the resistive switching mechanism proposed in our previous publication36.
are drifted to the bottom interface to lower the bottom Schottky barrier height in LRS and the donor concentration at the top interface is very low. Thus, the top Schottky barrier height in LRS is independent of the Ti fluence. The relationship of the Schottky barrier height in LRS and HRS and the Ti fluence in turn is a good evidence for the model of modifiable Schottky barrier height for the resistive switching mechanism proposed in our previous publication36.
Local Resistive Switching
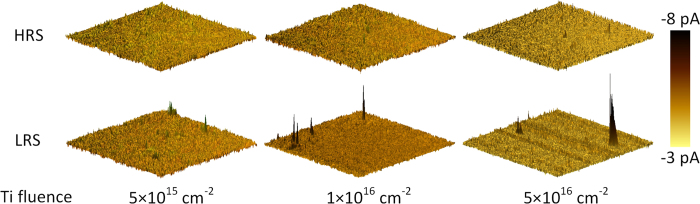
The local resistive switching characteristics of the deposited BFO without Au top electrode were investigated by CsAFM measurements. A 3 × 3 μm2 large area on the BFO was switched to HRS and LRS by scanning a grounded conductive tip over the BFO surface while a constant voltage bias of +10 V and −10 V was applied to the Pt bottom electrode, respectively. Note that the voltage polarity is opposite to that in I-V measurements as indicated by the schematic sketch shown in Figure S1 in supplementary information. After that the current maps were measured by scanning the conductive tip over the same 3 × 3 μm2 large area with a small constant reading voltage of −4 V applied to the Pt bottom electrode as shown in Fig. 6. In HRS, only some small leakage current was detected which homogeneously distributes over the local area. Furthermore, there is no significant difference for the MIM structures with different Ti fluences. The maximum absolute value of the current in HRS is 5.79 nA, 5.64 nA and 5.50 nA with increasing Ti fluences. However, 2–4 conductive spots were observed in LRS. We expect that due to the nonuniform Ti distribution in BFO grains and BFO grain boundaries during the BFO deposition at 650 oC and due to the nonuniform voltage drop over the polycrystalline BFO between CsAFM tip and large scale bottom electrode, the Schottky barrier height at bottom BFO/Pt/Ti interface is laterally inhomogeneous after scanning the CsAFM tip with writing bias. The current preferentially flows through the potential barrier minima and conductive spots can be observed47. Possibly, the highly resistive areas can be switched with a writing bias with larger magnitude or longer pulse length36. The maximum absolute value of the current in LRS increases with the increasing Ti fluences, i.e., 6.41 nA, 9.96 nA, and 12.81 nA for the MIM structures with Ti fluence of 5 × 1015 cm−2, 1 × 1016 cm−2, and 5 × 1016 cm−2, respectively. This is in agreement with the I-V characteristics and the calculated Schottky barrier heights. The local resistive switching suggests the possibility to scale down the nonvolatile resistive switching cell volume which is a function of the Ti distribution in the BFO thin films and of the film thickness dependent voltage drop.
Figure 6. 3D CsAFM current maps acquired with a reading bias of −4 V applied on the Pt bottom electrode for the MIM structures with different Ti fluences in HRS (upper) and LRS (lower).
Conclusions
In conclusion, we have demonstrated the influence of Ti implantation of Pt bottom electrodes on Sapphire substrates on the resistive switching characteristics of the subsequently deposited BFO thin films. With decreasing Ti fluence the bottom Schottky barrier height increases, and a larger writing bias is required to fully set/reset the MIM structure. The retention performance can be improved while the endurance slightly degrades with increasing Ti fluence. This work provides a deeper understanding of the resistive switching in BFO thin film switches with a focus on the role of the diffused Ti. Resistive switching in BFO MIM structures can be engineered by Ti implantation of the bottom electrodes. Additionally, ion implantation as a microelectronic compatible process can be scaled down for generating the local resistive switching via defining a Ti pattern, which will allow to control the nonvolatile resistive switching cell volume in a CMOS/memristor hybrid chip.
Additional Information
How to cite this article: You, T. et al. Engineering interface-type resistive switching in BiFeO3 thin film switches by Ti implantation of bottom electrodes. Sci. Rep. 5, 18623; doi: 10.1038/srep18623 (2015).
Supplementary Material
Acknowledgments
The authors acknowledge Karthikeyan Loganathan Manga and Dr. Feng Zhu for assistance during the temperature-dependent I-V measurements. T.Y. acknowledges the China Scholarship Council (201206970006) and the Initiative and Networking Fund of the Helmholtz Association (VI MEMRIOX VH-VI-422), X.O. acknowledges the One Hundred Talent Program of CAS and Pujiang Talent Program of Shanghai (15PJ1409700), X.W. acknowledges the Creative Research Groups of National Science Foundation of China (61321492), D.B. and H.S. acknowledge the Deutsche Forschungsgemeinschaft (BU 2956/1-1, and SCHM 1663/4-1, 2).
Footnotes
Author Contributions T.Y. and X.O. designed the work, T.Y., X.O., D.B. and I.S. fabricated the samples, G.N. and F.B. made the Tof-SIMS measurements, T.Y., G.L. and N.D. made the electrical measurements, T.Y. and G.L. performed the CsAFM measurements, T.Y., X.O., G.N., F.B., G.L., Q.J., W.Y. and H.S. discussed the results, T.Y. wrote the manuscript, X.O., G.L. and H.S. revised the text, and all the authors reviewed and approved the manuscript. X.W., O.S. and H.S. supervised the research.
References
- Sawa A. Resistive switching in transition metal oxides. Mater. Today 11, 28–36 (2008). [Google Scholar]
- Shuai Y., Zhou S., Bürger D., Helm M. & Schmidt H. Nonvolatile bipolar resistive switching in Au/BiFeO3/Pt. J. Appl. Phys. 109, 124117 (2011). [Google Scholar]
- Waser R. & Aono M. Nanoionics-based resistive switching memories. Nat. Mater. 6, 833–840 (2007). [DOI] [PubMed] [Google Scholar]
- Borghetti J. et al. ‘Memristive’ switches enable ‘stateful’logic operations via material implication. Nature 464, 873–876 (2010). [DOI] [PubMed] [Google Scholar]
- You T. et al. Exploiting Memristive BiFeO3 Bilayer Structures for Compact Sequential Logics. Adv. Funct. Mater. 24, 3357–3365 (2014). [Google Scholar]
- Du N. et al. Novel implementation of memristive systems for data encryption and obfuscation. J. Appl. Phys. 115, 124501 (2014). [Google Scholar]
- Celano U. et al. Filament observation in metal-oxide resistive switching devices. Appl. Phys. Lett. 102, 121602 (2013). [Google Scholar]
- Pearson C. et al. Focused ion beam and field-emission microscopy of metallic filaments in memory devices based on thin films of an ambipolar organic compound consisting of oxadiazole, carbazole, and fluorene units. Appl. Phys. Lett. 102, 213301 (2013). [Google Scholar]
- Chen C. et al. Conductance quantization in oxygen-anion-migration-based resistive switching memory devices. Appl. Phys. Lett. 103, 043510 (2013). [Google Scholar]
- Sun H. et al. Direct Observation of Conversion Between Threshold Switching and Memory Switching Induced by Conductive Filament Morphology. Adv. Funct. Mater., 24, 5679–5686 (2014). [Google Scholar]
- Jiang W. et al. Mobility of oxygen vacancy in SrTiO3 and its implications for oxygen-migration-based resistance switching. J. Appl. Phys. 110, 034509 (2011). [Google Scholar]
- Yang J. J., Borghetti J., Murphy D., Stewart D. R. & Williams R. S. A family of electronically reconfigurable nanodevices. Adv. Mater. 21, 3754–3758 (2009). [Google Scholar]
- Yang J. J. et al. Memristive switching mechanism for metal/oxide/metal nanodevices. Nat. Nanotechnol. 3, 429–433 (2008). [DOI] [PubMed] [Google Scholar]
- Xu Z. T. et al. Evidence for a Crucial Role Played by Oxygen Vacancies in LaMnO3 Resistive Switching Memories. Small 8, 1279–1284 (2012). [DOI] [PubMed] [Google Scholar]
- Lee D. et al. Resistance switching of copper doped MoOx films for nonvolatile memory applications. Appl. Phys. Lett. 90, 122104 (2007). [Google Scholar]
- Lee C. B. et al. Effects of metal electrodes on the resistive memory switching property of NiO thin films. Appl. Phys. Lett. 93, 042115 (2008). [Google Scholar]
- Tsunoda K. et al. Bipolar resistive switching in polycrystalline TiO2 films. Appl. Phys. Lett. 90, 113501 (2007). [Google Scholar]
- Lee C. B. et al. Electromigration effect of Ni electrodes on the resistive switching characteristics of NiO thin films. Appl. Phys. Lett. 91, 082104 (2007). [Google Scholar]
- Hou J., Nonnenmann S. S., Qin W. & Bonnell D. A. Size Dependence of Resistive Switching at Nanoscale Metal-Oxide Interfaces. Adv. Funct. Mater. 24, 4113–4118 (2014). [Google Scholar]
- Yang J. J. et al. Diffusion of adhesion layer metals controls nanoscale memristive switching. Adv. Mater. 22, 4034–4038 (2010). [DOI] [PubMed] [Google Scholar]
- Hwan Kim G. et al. Schottky diode with excellent performance for large integration density of crossbar resistive memory. Appl. Phys. Lett. 100, 213508 (2012). [Google Scholar]
- Xia Q. Nanoscale resistive switches: devices, fabrication and integration. Appl. Phys. A 102, 955–965 (2011). [Google Scholar]
- Maeder T., Muralt P., Sagalowicz L. & Setter N. In-situ sputter deposition of PT and PZT films on Platinum and RuO2 electrodes. Microelectron. Eng. 29, 177–180 (1995). [Google Scholar]
- Guo Y., Guo B., Dong W., Li H. & Liu H. Evidence for oxygen vacancy or ferroelectric polarization induced switchable diode and photovoltaic effects in BiFeO3 based thin films. Nanotechnology 24, 275201 (2013). [DOI] [PubMed] [Google Scholar]
- Hong S. et al. Large Resistive Switching in Ferroelectric BiFeO3 Nano-Island Based Switchable Diodes. Adv. Mater. 25, 2339–2343 (2013). [DOI] [PubMed] [Google Scholar]
- Jiang A. Q. et al. A Resistive Memory in Semiconducting BiFeO3 Thin‐Film Capacitors. Adv. Mater. 23, 1277–1281 (2011). [DOI] [PubMed] [Google Scholar]
- Kim W.-H., Son J. Y. & Jang H. M. Confinement of Ferroelectric Domain-Wall Motion at Artificially Formed Conducting-Nanofilaments in Epitaxial BiFeO3 Thin Films . ACS Appl. Mater. Interfaces 6, 6346–6350 (2014). [DOI] [PubMed] [Google Scholar]
- Wu L., Jiang C. & Xue D. Resistive switching in doped BiFeO3 films. J. Appl. Phys. 115, 17D716 (2014). [Google Scholar]
- Yin K. et al. Resistance switching in polycrystalline BiFeO3 thin films. Appl. Phys. Lett. 97, 042101 (2010). [Google Scholar]
- Yang C.-H. et al. Electric modulation of conduction in multiferroic Ca-doped BiFeO3 films. Nat. Mater. 8, 485–493 (2009). [DOI] [PubMed] [Google Scholar]
- Choi T., Lee S., Choi Y., Kiryukhin V. & Cheong S.-W. Switchable ferroelectric diode and photovoltaic effect in BiFeO3. Science 324, 63–66 (2009). [DOI] [PubMed] [Google Scholar]
- Ou X. et al. Forming-Free Resistive Switching in Multiferroic BiFeO3 thin Films with Enhanced Nanoscale Shunts. ACS Appl. Mater. Interfaces 5, 12764–12771 (2013). [DOI] [PubMed] [Google Scholar]
- Shuai Y. et al. Nonvolatile Multilevel Resistive Switching in Irradiated Thin Films. IEEE Electron Device Lett. 34, 54–56 (2013). [Google Scholar]
- Shuai Y. et al. Substrate effect on the resistive switching in BiFeO3 thin films. J. Appl. Phys. 111, 07D906 (2012). [Google Scholar]
- Shuai Y. et al. Control of rectifying and resistive switching behavior in BiFeO3 thin films. Applied Physics Express 4, 095802 (2011). [Google Scholar]
- You T. et al. Bipolar electric-field enhanced trapping and detrapping of mobile donors in BiFeO3 memristors. ACS Appl. Mater. Interfaces 6, 19758–19765 (2014). [DOI] [PubMed] [Google Scholar]
- Jin K. et al. Electronic stopping powers for heavy ions in SiC and SiO2. J. Appl. Phys. 115, 044903 (2014). [Google Scholar]
- Ziegler J. F., Bierszck J. P. & Littmark U. The Stopping and Range of Ions in Solids. Pergamon. (2013) Available at: http://www.srim.org. (Accessed: 3rd May 2015).
- Agarwal D. et al. SHI induced modification of ZnO thin film: Optical and structural studies. Nucl. Instr. Meth. Phys. Res. B 244, 136–140 (2006). [Google Scholar]
- Shuai Y. et al. Key concepts behind forming-free resistive switching incorporated with rectifying transport properties. Sci. Rep. 3, 2208 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark S. J. & Robertson J. Band gap and Schottky barrier heights of multiferroic BiFeO3. Appl. Phys. Lett. 90, 132903 (2007). [Google Scholar]
- Wang Z. et al. Performance improvement of resistive switching memory achieved by enhancing local-electric-field near electromigrated Ag-nanoclusters. Nanoscale 5, 4490–4494 (2013). [DOI] [PubMed] [Google Scholar]
- Yoon J. H. et al. Highly improved uniformity in the resistive switching parameters of TiO2 thin films by inserting Ru nanodots. Adv. Mater. 25, 1987–1992 (2013). [DOI] [PubMed] [Google Scholar]
- Tomer D., Rajput S., Hudy L., Li C. & Li L. Carrier transport in reverse-biased graphene/semiconductor Schottky junctions. Appl. Phys. Lett. 106, 173510 (2015). [Google Scholar]
- Simmons J. Richardson-Schottky effect in solids. Phys. Rev. Lett. 15, 967 (1965). [Google Scholar]
- Latreche A. Reverse bias-dependence of schottky barrier height on silicon carbide: influence of the temperature and donor concentration. Inter. J. Phys. Res. 2, 40–49 (2014). [Google Scholar]
- Werner J. H. & Güttler H. H. Barrier inhomogeneities at Schottky contacts. J. Appl. Phys. 69, 1522–1533 (1991). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.