Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Dec 22;5:18647. doi: 10.1038/srep18647

Electronic Structure of Oxide Interfaces: A Comparative Analysis of GdTiO3/SrTiO3 and LaAlO3/SrTiO3 Interfaces

Hrishit Banerjee 1, Sumilan Banerjee 2, Mohit Randeria 3, Tanusri Saha-Dasgupta 1,a
PMCID: PMC4686895  PMID: 26689360

Abstract

Emergent phases in the two-dimensional electron gas (2DEG) formed at the interface between two insulating oxides have attracted great attention in the past decade. We present ab-initio electronic structure calculations for the interface between a Mott insulator GdTiO3 (GTO) and a band insulator SrTiO3 (STO) and compare our results with those for the widely studied LaAlO3/SrTiO3 (LAO/STO) interface between two band insulators. Our GTO/STO results are in excellent agreement with experiments, but qualitatively different from LAO/STO. We find an interface carrier density of 0.5 e−/Ti, independent of GTO thickness in both superlattice and thin film geometries, in contrast to LAO/STO. The superlattice geometry in LAO/STO offers qualitatively the same result as in GTO/STO. On the other hand, for a thin film geometry, the interface carrier density builds up only beyond a threshold thickness of LAO. The positive charge at the vacuum surface that compensates the 2DEG at the interface also exhibits distinct behaviors in the two systems. The compensating positive charge at the exposed surface of GTO charge disproportionates due to correlation effect making the surface insulating as opposed to that in LAO which remains metallic within band theory and presumably becomes insulating due to surface disorder or surface reconstruction.

Following the pioneering work by Ohtomo and Hwang1 on LAO/STO, there has been much effort on understanding the interface (IF) between two different insulating ABO3 perovskites. The [001] stacking consists of AO and BO2 layers, which are charge neutral in one of the oxides like the (SrO)0 and (TiO2)0 layers in STO, but have charge +1/−1 in the other oxides, like (LaO)+1 and (AlO2)−1 in LAO. This creates a polar discontinuity at the interface of the two types of oxides and a build up of electrostatic potential, which can only be averted by a transfer of charge to the interface. The 2DEG that results from this simple polar catastrophe picture should lead to an interface carrier density of 0.5 e−/Ti, corresponding to 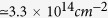Inline graphic, much larger than that achieved in conventional semiconductor hetero-structures.

The n-type interface in LAO/STO heterostructures is the most studied of all oxide interfaces2,3,4,5. It exhibits gate-tunable superconductivity and in addition shows signatures of local moments and possible ferromagnetism6,7,8,9 coexisting with the superconductivity. The density of itinerant carriers at the interface, however, is consistently found to be an order of magnitude smaller10,11,12 than 0.5 e−/Ti, the value expected from the polar catastrophe model. In addition, the interfaces are insulating, rather than being metallic, below a certain critical thickness of LAO layers12.

A more recent development is the study of the n-type interface between the Mott insulator GTO and the band insulator STO grown by molecular beam epitaxy13,14,15. Note, GTO with Ti ions in 3+ state, is in d1 state as opposed to Al states of LAO which are empty. This hints towards the crucial role of Ti d electrons and potential correlation effects in making a difference between GTO/STO and LAO/STO. Remarkably, the GTO/STO samples give rise to 2DEGs with carrier densities of 0.5 e−/Ti, exactly as expected from the ideal polar catastrophe scenario. Furthermore, the GTO/STO interface is found to be conducting irrespective of layer thickness of GTO, so that there is no thickness threshold for metallic behavior. In both these respects GTO/STO seems to be qualitatively different from LAO/STO. The 2DEG at the GTO/STO interface also shows many other interesting properties13,14,15, including possible transport signatures for magnetism16 and strong correlations17.

Motivated by these developments, we present here a detailed electronic structure study of the GTO/STO interface and contrast our results with those obtained for LAO/STO. While the LAO/STO interface has been thoroughly studied by electronic structure calculations18,19,20,21, much less is known about GTO/STO. The specific problem of single SrO layer in a GTO matrix in the superlattice geometry has been studied22,23,24 by a variety of techniques, first-principles, model Hamiltonian as well as combined density functional theory (DFT) and dynamical mean field theory. There have been some suggestions25 about the origin of the differences between the LAO/STO and GTO/STO systems, but to the best of our knowledge, no first principles electronic structure study exists which compares the LAO/STO and GTO/STO interfaces on same footing in different heterostructure geometries. Gaining insight into GTO/STO and into the differences and similarities with LAO/STO is very important for the advancement in the field of oxide interfaces. We provide a simple, intuitive understanding of our detailed DFT results at the end of the paper, summarized in terms of a schematic diagram and the associated discussion.

We conclude the introduction by summarizing our main results for n-type interfaces in GTO/STO and LAO/STO in two different geometries: (a) a superlattice and (b) a thin film on an STO substrate with vacuum on top. (1) Both GTO/STO and LAO/STO show essentially similar behavior in the superlattice geometry, despite differences in details of the orbital character of the carriers due to different structural distortions. The key result is that both GTO/STO and LAO/STO superlattices have an interfacial charge density of 0.5 e−/Ti, and there is no critical thickness of GTO or LAO for conductivity in the superlattice geometry. (2) The behavior of the two systems is very different in the thin film-substrate geometry. We find that GTO/STO conducts even for GTO thickness of 1 unit cell, the minimum thickness possible, while LAO/STO conducts only beyond a critical thickness of 5 unit cells of LAO. (3) In the thin film-substrate geometry, GTO/STO has an interface carrier density of 0.5 e−/Ti independent of GTO thickness. In contrast, the carrier density in LAO/STO is about a factor of four smaller just beyond the threshold for conductivity, and rises slowly with increasing LAO thickness. (4) We find that, in the thin film geometry, the surface layers facing the vacuum have very different electronic structures in LAO/STO and GTO/STO. The holes at Ti sites on the top GTO layer charge disproportionate making the surface insulating, while the holes on top LAO layer are metallic within band theory.

Results

Heterostructure Geometries

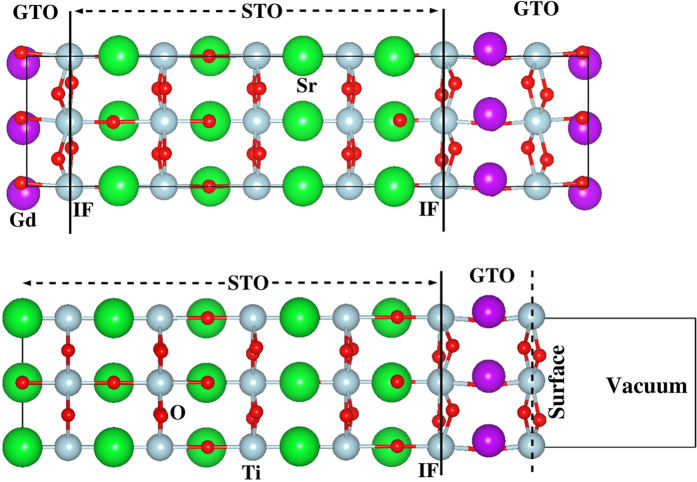
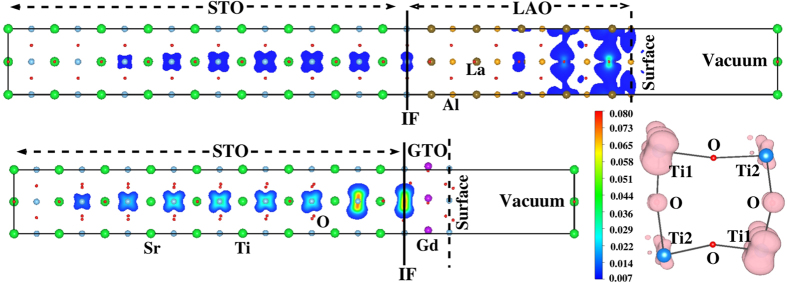
A study of both experimental and theoretical literature1,2,3,13,14,15,26,27,28 shows that the oxide interfaces have been investigated in two different geometries, (i) superlattice geometry with periodic repetition of alternating layers of STO and, LAO or GTO, and (ii) thin film of LAO or GTO grown on a STO(001) substrate. Most experimental studies on LAO/STO are carried out in a thin film-substrate geometry, while both geometries have been investigated in GTO/STO experiments. Since we would like to have a comparative study of the two systems with an aim to arrive at a common understanding, in the present study we consider both the geometries, as shown in Fig. 1. Following the experimental literature on GTO/STO13,14,15, we consider only n-type IFs formed between GdO layer from GTO and TiO2 layer from STO in GTO/STO, and between LaO and TiO2 in LAO/STO. In the superlattice geometry, we consider two symmetric n-type interfaces in the cell which result in non-stoichiometric supercells with an additional TiO2 layer in STO and an additional GdO layer in GTO (LaO layer in LAO). This results in superlattices with the formula (LAO)p.5/(STO)q.5 or (GTO)p.5/(STO)q.5. Calculations are carried out for p = 1, 2, 3, 4 and q = 4 and 9.

Figure 1. The two geometries used in the present study: superlattice (upper panel) and thin film-substrate (lower panel).

Figure 1

Open in a new tab

We show the representative cases of (GTO)1.5/(STO)4.5 superlattice and (GTO)1/(STO)5 thin film-substrate geometry. The various atoms are: Gd (purple), Ti (grey), O (red), and Sr (green). The interfaces (IFs) formed between GdO from GTO and TiO2 from STO are marked.

The thin film-substrate geometry, shown in the bottom panel of Fig. 1, creates a single n-type interface and a surface of TiO2 (in case GTO/STO) or AlO2 (in case of LAO/STO) facing the vacuum. Within the periodic set-up of DFT calculations, this amounts to having periodic copies of STO/(LAO or GTO) heterostructures separated by a vacuum layer. The general formula of the thin film-substrate systems is (LAO)p/(STO)q or (GTO)p/(STO)q. Calculations are carried out for p = 1, 2, 3, 4, 5, 6 and q = 9.

The in-plane dimension of the simulation cell is expanded by Inline graphic creating two Ti or Al atoms in the BO2 layers of the unit cell to take into account the GdFeO3-type orthorhombic distortion characterized by tilt and rotation of the TiO6/AlO6 octahedra. This becomes specially important for the GTO/STO system, as we will see in the following.

Structure

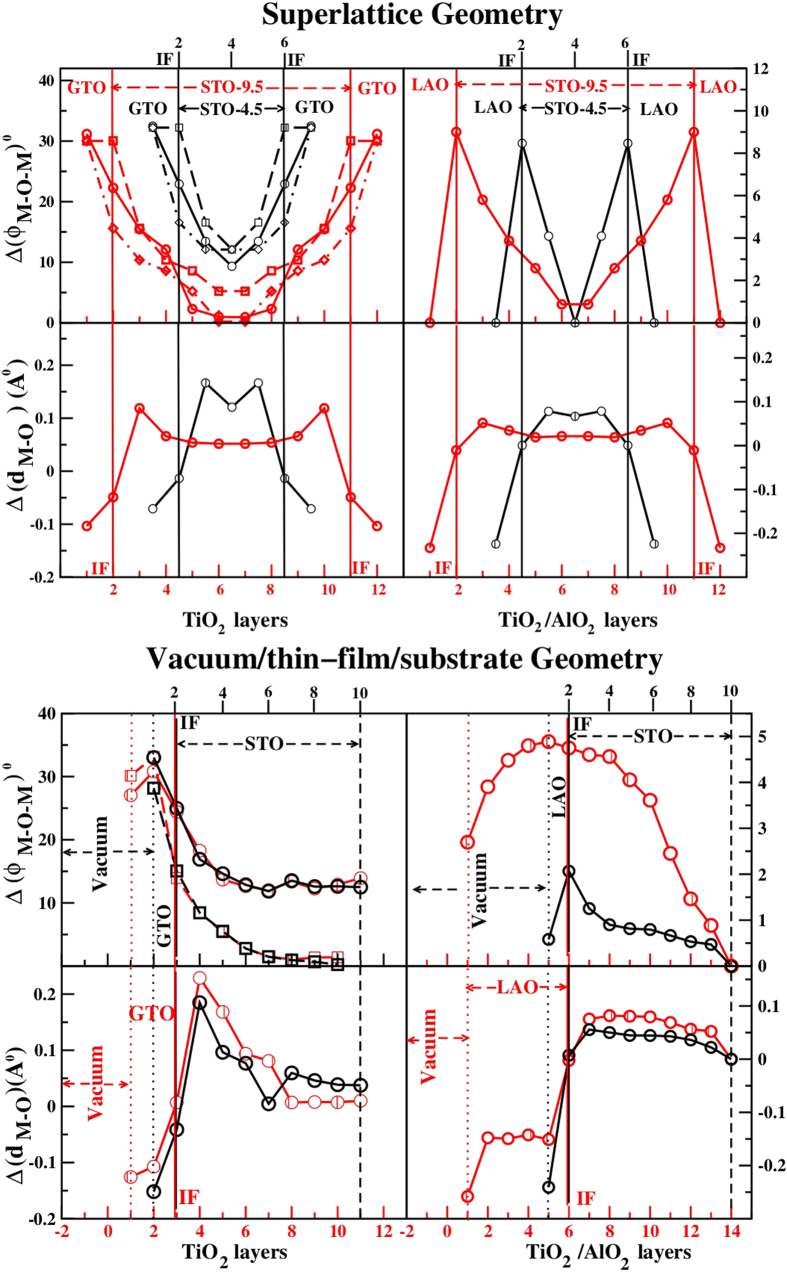
We first start with discussion of the structural properties of the studied heterostructures. As already mentioned, the presence of GdFeO3-type orthorhombic distortion is an important structural aspect of GTO. This distortion in bulk GTO makes the structural properties of the optimized GTO/STO systems rather different compared to LAO/STO. Structural distortions observed include the tilt and rotation of the metal (M) - oxygen(O) octahedra as well as the compression or elongation of the individual MO6 octahedra. Figure 2 shows the plots of the deviation of M-O-M bond angle from 180°, as well as the difference between out-of-plane and in-plane M-O bond lengths. The former quantifies the tilt/rotation of MO6 octahedra, while the latter quantifies the compression (for negative sign) or elongation (for positive sign) of MO6 octahedra. The top panels of the figure show the result for the superlattice geometry while the bottom panels are for the thin film-substrate geometry. The qualitative behavior is similar between the two geometries.

Figure 2. The deviation of M-O-M angles from 180°, Δ (ϕM−O−M) and the difference of M-O lengths in the out-of-plane and in-plane directions, Δ (dM−O).

Figure 2

Open in a new tab

On the right we show results for LAO/STO and on the left for GTO/STO. For superlattices (upper panels), we show results for (LAO or GTO)4.5/(STO)1.5 (black symbols) and (LAO or GTO)9.5/(STO)1.5 (red symbols). For the thin film-substrate geometry (lower panels), results are shown for (GTO)1/(STO)9 (black symbols), (GTO)2/(STO)9 (red symbols), and (LAO)1/(STO)9 (black symbols), (LAO)5/(STO)9 (red symbols). The x-axis labels for the red curves are marked in red at the bottom of the figures, while those for the black curves are marked in black at the top. For GTO/STO, we show the rotations (circles) and the asymmetric tilts in +c (squares) and -c (diamonds) directions; see text. For LAO/STO only the rotation angles are shown as circles, the tilt angles being zero.

For the GTO/STO systems, the deviation of the Ti-O-Ti bond angle from 180° is as high as 30° or so in the GTO side. This decreases systematically and reaches a value of about 5°–10° within the interior of STO block. For thin film-substrate geometry the tilt/rotation attains a constant value within the interior of STO, which is found to be substantial for rotation. The TiO2 layer at the IF faces the SrO layer on one side and GdO on the other. This makes the tilt angle in the 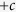Inline graphic and Inline graphic directions with respect to the TiO6 octahedra to be different (c-axis is the [001] direction that is perpendicular to the IF). This effect is found to percolate to other TiO2 layers as well, specially in the case of GTO/STO. At the interfaces, the highly asymmetric out-of-plane tilt angles vary between about 15° and about 25–30°. The in-plane and out-of-plane Ti-O bondlengths become unequal in GTO layers, with maximum difference of 0.1–0.2 Å, indicating distortion of the TiO6 octahedra. This distortion becomes smaller at IF and inside the STO block it attains a value of ≈0.1 Å or smaller. The MO6 octahedra are compressed in GTO layers, and are elongated in STO block. For the thin film-substrate geometry, the distortion of TiO6 attains more or less a small constant value inside the interior of STO block.

In comparison, in LAO/STO, the deviation of M-O-M bond angle from 180° occurs only for rotation, which is much smaller in magnitude compared to GTO/STO. The rotation angles are only significant at the IFs or close to them with values of about 5–9°. The tilt angles are found to be zero. Like in GTO/STO, the metal-oxygen octahedra are compressed in LAO side and elongated in STO side. The structural differences between GTO/STO and LAO/STO, specially in terms of tilt and rotation of MO6 octahedra, has important bearing on the orbital character of the conducting electrons at different layers, as will be elaborated in the following.

Electronic Structure

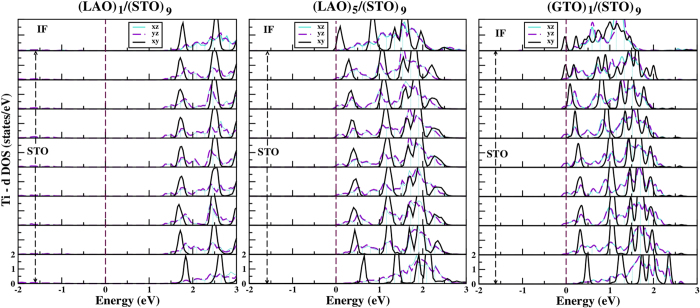
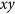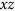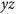We analyze the electronic structure of the optimized GTO/STO and LAO/STO heterostructures in both superlattice and thin film-substrate geometry in terms of density of states, charge and orbital populations. Figure 3 shows the layer-wise density of states (DOS) projected to Ti Inline graphic, Inline graphic and Inline graphic states in (GTO)1.5/(STO)4.5 and (LAO)1.5/(STO)4.5 superlattices. Qualitatively similar results are obtained for (GTO)1.5 or (LAO)1.5/(STO)9.5 superlattices, proving that the physics in the superlattice geometry is independent of the STO thickness. First, we find both GTO/STO and LAO/STO superlattices are metallic with non-zero density of states at the Fermi level (EF). Since the layer thickness of GTO or LAO of 1.5 layers is the minimum possible within the superlattice geometry, we conclude that for both LAO/STO and GTO/STO superlattices, there is no minimum thickness for conductivity. As expected, calculations with larger thickness of GTO and LAO (checked with thicknesses of 2.5, 3.5 and 4.5 unit cells), are also found to be metallic.

Figure 3. The density of states projected to xy, xz, yz orbitals of Ti, in different TiO2 layers of (LAO)1.5/(STO)4.5 (right panels) and (GTO)1.5/(STO)4.5 (left panels) superlattices.

Figure 3

Open in a new tab

The top panel corresponds to TiO2 in GTO on the left, and to AlO2 layer in LAO on the right (for which there are no states in the energy range shown). The subsequent panels from top to bottom (both on the left and right) refer to TiO2 at 1st IF, 1st, 2nd and 3rd TiO2 layers in STO block, and TiO2 at the 2nd IF in the cell. The cell is symmetric about the 2nd TiO2 layer in STO. The zero of the energy is the Fermi energy.

We find that in both superlattices, the conducting electronic charge is not strictly confined to the IF, and spreads out into several layers of the STO block. This is in agreement with experimental findings29, and previous theoretical studies18 of LAO/STO. We note, however, that the nature of the conduction electrons is different in the two superlattices, as seen from the DOS in Fig. 3. We find that, while the carriers at the IF are predominantly of 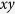Inline graphic character for both GTO/STO and LAO/STO, the situation is different in two systems in the TiO2 layers in STO, specially those adjacent to IF. The orbital characters of the carriers in these layers are mixed in case of GTO/STO, and 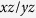Inline graphic type in case of LAO/STO. This is further corroborated by the plots of conduction electron charge densities, as shown in Fig.S1 of the supplementary information (SI) for (LAO)1.5/(STO)4.5 and (GTO)1.5/(STO)4.5. This difference stems from the structural differences between GTO/STO and LAO/STO.

To obtain the layer-wise contribution to the conduction electron, we integrate the layer projected DOS from 0.5 eV below EF to EF. For GTO/STO system this corresponds to integrating from the upper edge of the lower Hubbard band of Ti d in insulating GTO layer to EF. The electron from Ti3+ ion in GTO layer in its 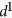Inline graphic charge state occupies the localized lower Hubbard band and does not contribute to conduction. Table 1 shows the layer-wise contribution to the conduction electron for 1.5/4.5 as well as 1.5/9.5 superlattices. We find the total conduction charge in the LAO/STO as well as in GTO/STO superlattices to be 1 e− irrespective of the thickness of STO layers. This is fully consistent with the presence of two symmetric interfaces each with a carrier density of 0.5 e−/Ti. Interestingly we find Ti d states at the IF of GTO and STO are spin-polarized, with Ti d states within STO layers adjacent to IF inheriting this spin-polarization, as shown in Fig. S2 in SI. Moving further away from the IF, the spin-polarization decreases and finally vanishes deep inside the STO block. The calculated magnetic moments at Ti sites are found to be ≈0.15 μB, ≈0.12 μB in the STO layer next to IF, ≈0.02 μB in the following layer, and vanishingly small in other layers. The Ti moments are found to be aligned in a ferromagnetic arrangement, consistent with experimental results30.

Table 1. The layer-wise contribution of the conduction electron in GTO/STO and LAO/STO in superlattice and thin film-substrate geometries.

LAO/STO
 GTO/STO
Superlattice
 Thin film-substrate Superlattice
 Thin film-substrate
(LAO)1.5/(STO)4.5 (LAO)1.5/(STO)ub (LAO)5/(STO) (GTO)1.5/(STO)ub (GTO)1.5/(STO)ub (GTO)1/(STO)
Layer: Charge Layer: Charge Layer: Charge Layer: Charge Layer: Charge Layer: Charge
2 : 0.185 (1st IF) 2 : 0.200 (1st IF) 6 : 0.062 (IF) 2 : 0.181 (1st) IF 2 : 0.163 (1st )IF 2 : 0.185 (IF)
3 : 0.184 3 : 0.104 7 : 0.050 3 : 0.203 3 : 0.101 3 : 0.108
4 : 0.260 4 : 0.070 8 : 0.006 4 : 0.231 4 : 0.058 4 : 0.034
5 : 0.184 5 : 0.066 9 : 0.007 5 : 0.203 5 : 0.082 5 : 0.045
6 : 0.185 (2nd IF) 6 : 0.060 10 : 0.005 6 : 0.181 (2nd IF) 6 : 0.096 6 : 0.049
  7 : 0.060 11 : 0.004   7 : 0.096 7 : 0.044
  8 : 0.066 12 : 0.002   8 : 0.082 8 : 0.029
  9 : 0.070 13 : 0.001   9 : 0.058 9 : 0.006
  10 : 0.104 14 : 0.000   10 : 0.101 10 : 0.000
  11 : 0.200 (2nd IF)     11 : 0.163 (2nd IF)  
Total Charge: 0.999 Total Charge: 1.000 Total Charge: 0.137 Total Charge: 0.999 Total Charge: 1.000 Total Charge: 0.500
Open in a new tab

In case of superlattices, results for both (LAO or GTO)1.5/(STO)4.5 and (LAO or GTO)1.5/(STO)9.5 are shown. For thin film-substrate geometry, we show the results for LAO (5 u.c.) and GTO (1 u.c.), the minimum thicknesses in each case at which the 2DEG is formed.

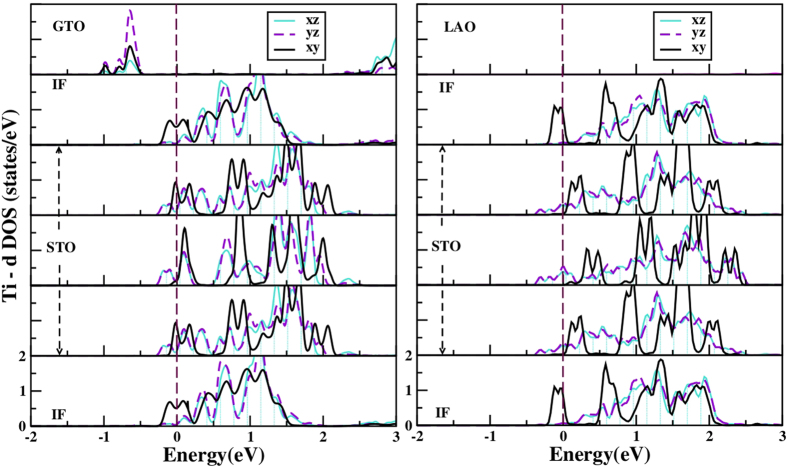
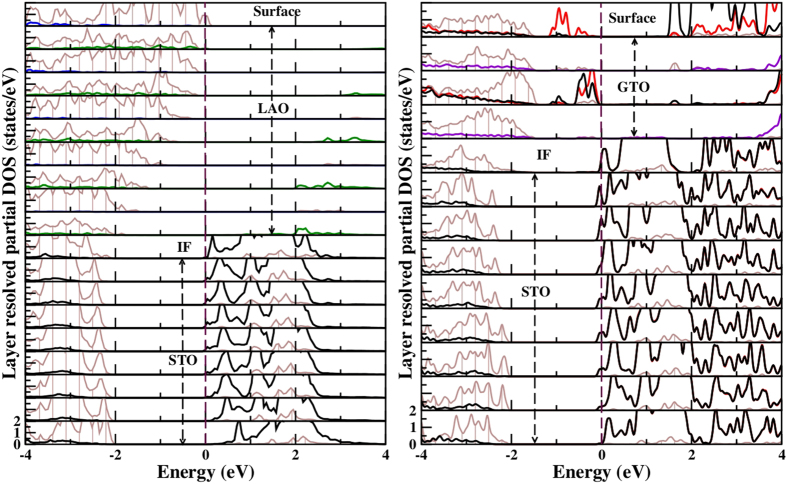
A similar analysis in the thin film-substrate geometry shows dramatically different behavior. The left and middle panels in Fig. 4 show the DOS in different TiO2 layers of LAO/STO in thin film-substrate geometry with two different thicknesses of LAO layers, 1 and 5 unit cells, respectively. We find that the IF in 1 unit cell of LAO on STO is insulating with a large gap between the valence and conduction states, and no states at EF. On the other hand, 5 unit cell of LAO on STO is barely metallic, setting a critical LAO thickness of 5 unit cell for the conductivity. This behavior is significantly different from that of LAO/STO in superlattice geometry for which IFs are found to be conducting for any thickness of LAO. This difference in conduction properties of LAO/STO, depending on the system geometry has been pointed out previously in literature20,21.

Figure 4. The density of states projected to xy, xz, yz orbitals of Ti, in different TiO2 layers of LAO/STO and GTO/STO in thin film-substrate geometry.

Figure 4

Open in a new tab

From top to bottom, different panels refer to TiO2 at IF, TiO2 layers belonging to STO block. The zero of the energy is set at EF.

A markedly different picture is obtained for GTO/STO system. The right most panel of Fig. 4, shows the plot of density of states of GTO/STO in thin film-substrate geometry with 1 unit cell thickness of GTO. We find the solution to be metallic even in the limit of 1 unit cell thickness of GTO. This is in sharp contrast to LAO/STO case, but in excellent agreement with experimental reports on GTO/STO13. The calculation of total conduction charge by integrating the layer wise density of states from −0.5 eV below EF to EF gives a charge of 0.5 e− (see Table 1) for GTO/STO in thin film-substrate geometry with 1 unit cell thickness of GTO. This is in complete accordance with a single n-type interface in the unit cell, and the expectation from polar catastrophe model. In contrast, the total conduction charge for the LAO/STO in thin film-substrate geometry with 5 unit cell thickness of LAO, which is at the critical thickness of metallicity, is found to be about 0.14 e−/Ti, almost a factor of 4 smaller than 0.5 e−/Ti expected from the ‘ideal’ polar catastrophe scenario. Increasing the LAO thickness beyond 5 u.c., the carrier concentration is found to slowly increase, for example for (LAO)6/(STO)9 the conduction charge is found to be 0.18 e−. This is expected to reach the asymptotic value of 0.5 e− for very large thickness of LAO, as discussed below. Similar to the observation in superlattice geometry, we find the Ti d states to be spin-polarized at the IF of GTO and STO, with spin-polarization of Ti d states percolating down in the STO block (cf Fig. S2 in SI). The estimates of the magnetic moments are found to be similar to that in case superlattice geometry, with parallel alignment of spins.

The analysis of orbital population of the conduction electron shows the carriers at the IF are predominantly of 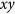Inline graphic character, while that within the STO block to be predominantly of 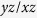Inline graphic character in LAO/STO with LAO thickness beyond the critical thickness of conductivity. For GTO/STO, the IF is of significant 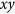Inline graphic character, the subsequent layers being of mixed character which converts to predominant 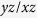Inline graphic character in the interior of STO block. We thus find that the orbital characters in LAO/STO and GTO/STO are quite similar in the superlattice and thin film-substrate geometries, as might be expected given the similarities in the structural distortions in the two geometries.

Another pertinent issue in the context of thin film-substrate geometry is the fate of the surface layer facing the vacuum, which is AlO2 in LAO, or TiO2 in GTO. By simple charge balance, the uppermost surface layer should be hole doped to compensate for the electrons at the n-type interface. For instance, the surface layer in GTO should have Ti in a 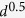Inline graphic state, rather than the 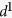Inline graphic state in bulk GTO. This simple picture, of course, does not take into account the disordering effects like oxygen vacancies and cation disorder, or the effect of surface reconstruction, which are reported to be important in the context of LAO/STO31,32. 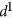Interestingly, our DFT calculation which allows for possible structural reconstruction only within the scope of Inline graphic cell, shows the topmost AlO2 surface in LAO to be metallic, while the topmost TiO2 surface in GTO to be insulating. This is seen in the plot of charge density contributed by a narrow energy window around EF, for (LAO)5/(STO)9 and for (GTO)1/(STO)9 (cf Fig. 5). While the surface reconstruction in reality can be complex, which undoubtedly needs further exploration both from experimental and theoretical side, the stabilization of the insulating solution at the topmost TiO2 surface layer of GTO doped with 0.5 hole is interesting. We find this to be triggered by charge disproportionation between two Ti atoms at the top layer. With the choice of U = 7 eV on Ti atoms (see Methods for further discussion), this charge disproportionation becomes complete leading to insulating solution with nominal charge of Inline graphic on one Ti atom and 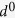Inline graphic on the other, maintaining an average charge of 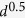Inline graphic per Ti at the top layer. This is evident from the charge density plot focused on the energy window around the occupied lower Hubbard band (LHB) of Ti d states (see inset in Fig. 5), which shows significantly large charge on one set of Ti atoms and a significantly smaller on the other. We find this disproportionation to be triggered by the strong correlation effect which together with small differences in local environment of two Ti atoms, make the charges on two Ti’s significantly different. The associated magnetic moments at two charge disproportionated Ti sites are found to be ≈1 μB and ≈0 μB, with spins of magnetic Ti ions feromagnetically aligned.

Figure 5. Conduction electron charge density for (LAO)5/(STO)9 (upper panel) and (GTO)1/(STO)9 (lower panel) in thin film-substrate geometry, integrated over an energy window from 0.1 eV below EF to EF.

Figure 5

Open in a new tab

The color of different contours corresponds to the values shown in the scale bar. The topmost AlO2 surface layer in LAO is metallic, while the topmost TiO2 layer in GTO is insulating. Inset: We also show the charge disproportionation with two inequivalent Ti sites on the top layer of GTO which drives the surface insulating. The charge density in this plot is obtained from integration over the lower Hubbard band in GTO; see text for details.

We show the DFT layer-resolved density of states, projected onto O p, Ti d and Gd d states, for (GTO)2/(STO)9 in the thin film-substrate geometry in the right panel of Fig. 6. To clearly show the charge disproportionation in this plot, we plot the DOS contributions for the two inequivalent Ti atoms at the surface using two different colors in Fig. 6. The disproportionation weakens as we move away from the vacuum surface towards the interface and is absent at the IF. We note that the charge disproportionation found at the surface does not lead to an additional translational symmetry breaking, associated with the opening of the charge gap, given that a Inline graphic structural distortion is already present in bulk GTO.

Figure 6. The layer decomposed DFT density of states for (LAO)5/(STO)9 (left panel) and (GTO)2/(STO)9 (right panel) in thin film-substrate geometry, projected onto O p (brown line), Al p (green line), Ti d (black/red line) and Gd d (magenta) and La d (blue line) states.

Figure 6

Open in a new tab

For GTO/STO, the projection to two charge disproportionated Ti atoms are shown as black and red lines, respectively, while for LAO/STO projection to Ti d is shown as black line. EF is set at zero. From top to bottom, various panels show the surface layer, the LAO or GTO block, the IF and the STO block.

Electronic Reconstruction

Our DFT results described above lead to the following conclusions.

  1. Both GTO/STO and LAO/STO show essentially similar behavior in the superlattice geometry, despite differences in details of the orbital character of the carriers due to differences in the structural distortions. The central result is that both GTO/STO and LAO/STO superlattices have the full interfacial charge density of 0.5 e−/Ti and there is no critical thickness of GTO or LAO for conductivity.

  2. The behavior of the two systems differs qualitatively in the thin film-substrate geometry. We find that GTO/STO conducts with an interfacial carrier density of 0.5 e−/Ti, independent of GTO thickness. In contrast, LAO/STO conducts only beyond a critical thickness of 5 unit cells of LAO, and the interfacial carrier density is still almost a factor of four less than 0.5 e−/Ti just beyond threshold.

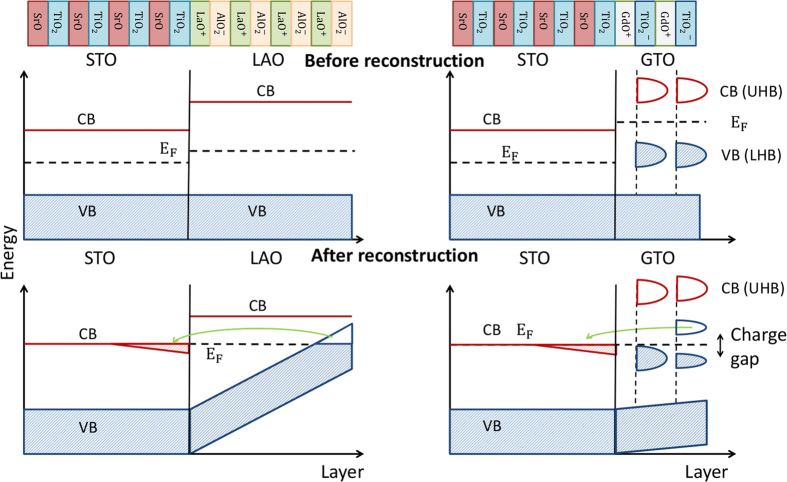
We now address the question: What are the driving mechanisms behind the similarity and differences between the two geometries in the two systems? In the superlattice geometry, we need an extra GdO or LaO layer with a charge of +1, as emphasized by Chen et al.21. This is then directly responsible for doping the two (symmetric) n-type interfaces with 0.5 e−/Ti each. In effect, there is no polar catastrophe (potential divergence) that is averted in this geometry; rather one simply obtains a fixed interface carrier concentration, independent of the thickness of GTO or LAO, as demanded by charge neutrality.

However, in the film-substrate geometry with a single interface, we find that band alignment, band bending and electronic reconstruction play a crucial role. As a result, there are striking differences between LAO/STO and GTO/STO. To understand these differences, it is useful to look at the DFT results for the density of states (DOS) in the thin film geometry.

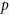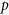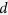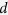The left panel in Fig. 6 shows the density of states plotted over a wide energy window, projected onto O Inline graphic, Al Inline graphic, Ti Inline graphic and La Inline graphic states for (LAO)5/(STO)9 in the thin film-substrate geometry. This provides the picture after electronic reconstruction as given by DFT. We see that the upper edge of the oxygen valence band (VB) in LAO bends progressively towards EF, moving from the interface to the surface. We see that the surface AlO2 layer next to vacuum is hole doped into a metallic state with electrons transferred from the surface to the conduction band (CB) of Ti d-states at the IF. This can be seen schematically in the lower left panel of Fig. 7.

Figure 7. Schematic plot of the band offset (top panels) and electronic reconstruction (bottom panels) that summarizes some of the important DFT results described in the text.

Figure 7

Open in a new tab

The left panels show results for LAO/STO, while GTO/STO results are shown on the right. Prior to electronic reconstruction in LAO/STO, the top of the valence band (VB) in LAO is widely separated in energy from the bottom of the conduction band (CB) in STO. Thus electronic reconstruction requires a large band bending, which is responsible for the threshold in LAO thickness for the polar catastrophe to set in. In contrast, the VB in GTO is the Ti-d lower Hubbard band, which is already close in energy to the CB in STO prior to reconstruction. Thus only a modest band-bending is required for a conduction electron density of 0.5e per interface Ti. We also see in the reconstructed GTO/STO electronic structure the charge gap due to the correlation-induced charge disproportionation in the top TiO2 layer next to vacuum.

The band alignment before electronic reconstruction can be derived from the bulk band structure of LAO and STO shown schematically in the upper left panel in Fig. 7. The experimentally measured bulk band gap of STO is 3.3 eV, while that of LAO is 5.6 eV. In LAO/STO, the valence band offset is small, and the VB maxima of LAO and STO, which is the upper edge of filled O 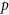Inline graphic bands, are almost aligned. For the electronic reconstruction, therefore a large band bending with VB maxima of LAO at the surface aligning with conduction band minima of STO is needed, as observed in DFT results presented in Fig. 6 and schematically in left lower panel of Fig. 7.

The necessary band bending in LAO/STO is estimated to be about the same as band gap 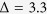Inline graphic eV of STO. One can make a simple estimate20,33 of the critical thickness 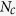Inline graphic of LAO layers for charge transfer from the surface to the interface as follows. The potential difference between the surface and interface is 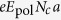Inline graphic, due to the polar field 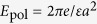Inline graphic (where ε is the dielectric constant of LAO arising from both electronic and ionic screening) should be equated to the gap Δ. Using the bulk dielectric constant of LAO, 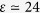Inline graphic, and the in-plane lattice constant of 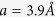Inline graphic, the critical thickness could be estimated to be 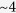Inline graphic layers, consistent with experiment and the DFT result. 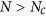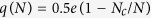For thickness Inline graphic, when an amount of charge Inline graphic is transferred to the interface the potential difference Inline graphic stays pinned at Δ. This leads to an estimate of Inline graphic, that approaches the asymptotic value of 0.5 e for 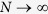Inline graphic. For 5 LAO layers, one obtains 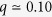Inline graphic, roughly consistent with the DFT result of Table 1.

The electronic reconstruction scenario is quite different for GTO/STO. Bulk GTO is a Mott insulator and the relevant valence band is the Ti d lower Hubbard band (LHB), which lies far above the O p derived VB of the STO, as shown schematically in the right upper panel in Fig. 7. The Ti d LHB lies only 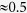Inline graphic eV below the conduction band of STO. Electrostatic considerations, similar to the ones discussed above for LAO/STO, with the bulk dielectric constant of 30 for GTO imply that a minimum thickness of 1 u.c. of GTO is sufficient to allow for required band bending and charge transfer. This would suggest the charge is transferred to the interface independent of the thickness of the GTO layers, consistent with our DFT results and also with the experimental observations13,14. Apart from the usual upward bending of the GTO VB approaching the surface, the Ti d LHB in GTO also bends upward near the interface to connect with the Ti d derived conduction band in the STO side, as seen in Fig. 6 (right panel).

Finally, we stress again the fate of the holes on the top surface layer next to vacuum, that must exist to counterbalance the electrons at the interface. Unlike LAO, which is a band insulator, GTO is a correlation driven Mott insulator in the bulk. As described above, we find a rather strong correlation-induced charge disproportionation on the topmost TiO2 layer of GTO at the surface. We thus find the LHB of Ti d states at the top layer of GTO, which would naively have been partially filled (average filling of d0.5) and metallic, splits into occupied and unoccupied bands due to opening of a charge gap due to the charge disproportionation. This is clearly seen in the DFT result of Fig. 6 (right panel) and shown schematically in the lower right panel of Fig. 7. Our theoretical observation of charge disproportionation in top TiO2 layer in GTO/STO in thin film-substrate geometry should be explored experimentally.

Discussion and Outlook

In this work we have carried out a detailed first-principle DFT study of LAO/STO and GTO/STO heterostructures, focusing on their essential similarities and differences in two experimentally well-studied geometries, namely the superlattice and thin film-substrate geometry. While the two systems behave quite similarly in the superlattice set up, e.g. in terms of the total 0.5 e−/Ti transfer of charges to the interface, very different pictures emerge in case of thin film-substrate geometry due to the differences in electronic reconstructions in the two systems, even though, in both the cases, the reconstructions are driven by the same underlying electrostatic mechanism, namely the need to avert the ‘polar catastrophe’. We find a full 0.5 e−/Ti conducting charge at the interface even for 1 u.c. thick GTO on STO substrate, consistent with experiments13,14. On the other hand, in case of LAO on STO, the transferred charge only increase gradually with thickness from a small value of ~0.14 e−/Ti above a critical thickness of about 4.

Additionally, in the thin film-substrate case, we find the fate of the surface layers, which host the neutralizing charges for the interface carriers, to be quite distinct. The electronic states derived from O p orbitals at the surface LAO layer turn out to be metallic within DFT but are experimentally31 found to be localized, possibly due to disorder or surface imperfections like oxygen vacancies32. On the other hand, the Ti d states at the top most layer of GTO/STO correspond to a doped Mott insulating layer of GTO and stays insulating by opening a charge gap via an interesting correlation driven charge disproportionation. Such a correlation induced phenomenon could be a robust feature, at least within a short length scale, even in the presence of surface disorder and, in principle, could be probed experimentally. This also pertains to the experimental verification of the polar catastrophe mechanism by detecting the counter charges at the surface of the heterostructure. The presence of conducting charges at the interface by itself does not ambiguously establish the polar catastrophe mechanism for the polar oxide interfaces as there could be other possible sources of interfacial charge carriers, e.g. oxygen vacancies1.

A few interesting future directions for theoretical study would be to investigate in detail the sub-band structures, that is relevant for quantum oscillation measurements15, and spin-orbit coupling in the GTO/STO interface. Our structural analysis indicates substantially larger polar distortions of the Ti-O-Ti bonds at the GTO/STO interface compared to that in LAO/STO. This could potentially lead to much larger Rashba spin-orbit coupling for GTO/STO heterostructure. The magnetic property of the interface 2DEG in GTO/STO should also be investigated by DFT. GTO/STO shows signature of ferromagnetism that could be an intrinsic correlation driven phenomenon, independent of the proximity to magnetic GTO layer16.

Methods

Our first-principles calculations are based on plane wave basis as implemented in the Vienna Ab-initio Simulation Package (VASP)34,35 with projector-augmented wave (PAW) potential36. The exchange-correlation functional is chosen to be that given by generalized gradient approximation (GGA)37. Correlation effects beyond GGA are taken into account through an on-site Hubbard U correction in form of GGA +U38. Since we are not interested in the magnetism of Gd spins in the present study, in the plane-wave calculations for the results reported here, the Gd f electrons are considered to be part of the core orbitals. The use of GGA +U turn out to be crucial for the correct description of the Mott insulating behavior of GTO. The GGA+U implementation in the plane wave code of VASP with PAW potential needed a U value of 7 eV applied on Ti d states, for the bulk GTO to be insulating. The Hund’s coupling parameter JH is chosen be 1 eV. We have thus consistently used U = 7 eV and JH = 1 eV on Ti d states throughout our calculations. We found a smaller U value (≈4 eV) within the linear muffin tin orbital (LMTO) basis calculation to be sufficient to drive bulk GTO insulating, a value more consistent with spectroscopic considerations39. The fact that different U values are needed in different basis set implementations of DFT has been appreciated in the literature (see, e.g., ref. 40). We found in our LMTO calculations of bulk GTO that taking into account the effect of U on both Ti d and Gd f states, with choice of UTi = 4 eV and UGd = 9 eV, and JH = 1 eV, resulted into a ferrimagnetic ground state with antiparallel alignment of the Ti and Gd spins, consistent with experiment.

The in-plane lattice constants of the simulation cells are fixed at the experimental lattice constant of STO with a value of 3.91 Å, while the out-of-plane lattice constant is allowed to relax. The relaxed out-of-plane lattice constants for GTO/STO is found to be ≈2% larger than that of LAO/STO. The consideration of tilt and rotation of metal-oxygen octahedra becomes rather important for GTO with significant orthorhombic distortion. In order to take into account of that, the in-plane dimension of the simulation cell is expanded by Inline graphic. Internal positions of the atoms are allowed to relax until the forces become less than 0.01 eV/Å.

For the calculations carried out on thin film geometry, the thickness of vacuum layer is chosen to be 16 Å. The effect of the artificial electric field in the vacuum due to periodic boundary condition is taken into account through dipole correction, as implemented in VASP. The effect of this artificial electric field is however small, as shown in the detailed calculation by Chen et al.21 in Appendix B1 of their paper. Considering the dielectric constants of STO and that of LAO and GTO, as shown by Chen et al.21 the field in STO is found to be only about 0.3% of that in LAO or GTO for a vacuum thickness of 16 Å. Further to establish the convergence of our calculations in terms of vacuum layer thickness, we have carried out additional calculations considering an increased thickness of vacuum layer (30 Å). We found our conclusions concerning the carrier density, minimum thickness of conductivity to remain unchanged, justifying physical soundness of our calculations. The situation becomes different in presence of external electric field which is not considered in the present study.

Additional Information

How to cite this article: Banerjee, H. et al. Electronic Structure of Oxide Interfaces: A Comparative Analysis of GdTiO3/SrTiO3 and LaAlO3/SrTiO3 Interfaces. Sci. Rep. 5, 18647; doi: 10.1038/srep18647 (2015).

Supplementary Material

Supplementary Information
srep18647-s1.pdf (495.6KB, pdf)

Acknowledgments

HB and TSD would like to thank Thematic Unit of Excellence on Computational Materials Science, funded by Department of Science and Technology for computational facility used in the present study. M.R. would like to acknowledge the support of the CEM, an NSF MRSEC, under grant DMR-1420451, which also made possible the collaboration with TSD.

Footnotes

Author Contributions H.B. did the theoretical calculations. The figures were made by H.B. and S.B. The results were analyzed by T.S.-D., M.R., S.B. and H.B. T.S.-D. and M.R. wrote the manuscript. H.B., S.B., M.R. and T.S.-D. finalized the manuscript.

References

  1. Ohtomo A. & Hwang H. Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature (London) 427, 423–426 (2004). [DOI] [PubMed] [Google Scholar]
  2. Mannhart J. et al. Two-Dimension Electron Gases at Oxide Interfaces. MRS Bull. 33, 1027–1034 (2008). [Google Scholar]
  3. Huijben M. et al. StructureProperty Relation of SrTiO3/LaAlO3 Interfaces. Adv. Mater. 21, 1665–1667 (2009). [Google Scholar]
  4. Zubko P. et al. Interface Physics in Complex Oxide Heterostructures. Annu. Rev. Cond. Mat. Phys. 2, 141–165 (2011). [Google Scholar]
  5. Sulpizio A., Ilani S., Irvin P. & Levy J. Nanoscale Phenomena in Oxide Heterostructures. Ann. Rev. of Mater. Res. 44, 117–149 (2014). [Google Scholar]
  6. Brinkman A. et al. Magnetic effects at the interface between non-magnetic oxides. Nat. Mater. 6, 493–496 (2007). [DOI] [PubMed] [Google Scholar]
  7. Reyren N. et al. Superconducting Interfaces Between Insulating Oxides. Science 317, 1196–1199 (2007). [DOI] [PubMed] [Google Scholar]
  8. Bert J. A. et al. Direct imaging of the coexistence of ferromagnetism and superconductivity at the LaAlO3/SrTiO3 interface. Nature Phys. 7, 767–771 (2011). [Google Scholar]
  9. Li L., Richter C., Manhart J. & Ashoori R. C. Coexistence of magnetic order and two-dimensional superconductivity at LaAlO3/SrTiO3 interfaces. Nat. Phys. 7, 762–766 (2011). [Google Scholar]
  10. Siemons W. et al. Origin of Charge Density at LaAlO3 on SrTiO3 Heterointerfaces: Possibility of Intrinsic Doping. Phys. Rev. Lett 98, 196802 (2007). [DOI] [PubMed] [Google Scholar]
  11. Basletic M. et al. Mapping the spatial distribution of charge carriers in LaAlO3 /SrTiO3 heterostructures. Nat. Mater. 7, 621–625 (2008). [DOI] [PubMed] [Google Scholar]
  12. Thiel S. et al. Tunable Quasi-Two-Dimensional Electron Gases in Oxide Heterostructures. Science 313, 1942–1945 (2006). [DOI] [PubMed] [Google Scholar]
  13. Moetakef P. et al. Electrostatic carrier doping of GdTiO3/SrTiO3 interfaces. Appl. Phys. Lett. 99, 232116 (2011). [Google Scholar]
  14. Cain T. A., Moetakef P., Jackson C. A. & Stemmer S. Modulation doping to control the high-density electron gas at a polar/non-polar oxide interface. Appl. Phys. Lett. 101, 111604 (2012). [Google Scholar]
  15. Moetakef P. et al. Quantum oscillations from a two-dimensional electron gas at a Mott/band insulator interface. Appl. Phys. Lett. 101, 151604 (2012). [Google Scholar]
  16. Moetakef P. et al. Carrier-Controlled Ferromagnetism in SrTiO3. Phys. Rev. X 2, 021014 (2012). [Google Scholar]
  17. Moetakef P. et al. Toward an artificial Mott insulator: Correlations in confined high-density electron liquids in SrTiO3. Phys. Rev. B 86, 201102 (R) (2012). [Google Scholar]
  18. Popovic Z. S., Satpathy S. & Martin R. M. Origin of the Two-Dimensional Electron Gas Carrier Density at the LaAlO3 on SrTiO3 Interface. Phys. Rev. Lett, 101, 256801 (2008). [DOI] [PubMed] [Google Scholar]
  19. Zhong Z. & Kelly P. J. Electronic-structureinduced reconstruction and magnetic ordering at the LaAlO3|SrTiO3 interface. Eur. Phys. Lett. 84, 27001 (2008). [Google Scholar]
  20. Pentcheva R. & Pickett W. Avoiding the Polarization Catastrophe in LaAlO3 Overlayers on SrTiO3(001) through Polar Distortion. Phys. Rev. Lett. 102, 107602 (2009). [DOI] [PubMed] [Google Scholar]
  21. Chen H., Kolpak A. & Ismail-Beigi S. First-principles study of electronic reconstructions of LaAlO3/SrTiO3 heterointerfaces and their variants. Phys. Rev. B 82, 085430 (2010). [Google Scholar]
  22. Chen R., Lee S. & Balents L. Dimer Mott insulator in an oxide heterostructure. Phys. Rev. B 87, 161119(R) (2013). [Google Scholar]
  23. Bjaalie L., Janotti A., Himmetoglu B. & Van de Walle C. G. Turning SrTiO3 into a Mott insulator. Phys. Rev. B 90, 195117 (2014). [Google Scholar]
  24. Lechermann F. & Obermeyer M. Towards Mott design by δ-doping of strongly correlated titanates. arXiv:1411.1637v2
  25. Janotti A., Bjaalie L., Gordon L. & Van de Walle C. G. Controlling the density of the two-dimensional electron gas at the SrTiO3/LaAlO3 interface. Phys. Rev. B 86, 241108(R) (2012). [Google Scholar]
  26. Kim J. S. et al. Nonlinear Hall effect and multichannel conduction in LaTiO3/SrTiO3 superlattices. Phys. Rev. B 82, 201407(R) (2010). [Google Scholar]
  27. Zhang J. Y. et al. Correlation between metal-insulator transitions and structural distortions in high-electron-density SrTiO3 quantum wells. Phys. Rev. B 89, 075140 (2014). [Google Scholar]
  28. Zhang J. Y. Symmetry Lowering in Extreme-Electron-Density Perovskite Quantum Wells. Phys. Rev. Lett. 110, 256401 (2013). [DOI] [PubMed] [Google Scholar]
  29. Dubroka A. et al. Dynamical Response and Confinement of the Electrons at the LaAlO3/SrTiO3 Interface. Phys. Rev. Lett. 104, 156807 (2010). [DOI] [PubMed] [Google Scholar]
  30. Moetakef P. et al. Carrier-Controlled Ferromagnetism in SrTiO3. Phys. Rev. X 2, 021014 (2012). [Google Scholar]
  31. Huijben M. et al. Structureâ Property Relation of SrTiO3/LaAlO3 Interfaces. Adv. Mater. 21, 1665–1677 (2009). [Google Scholar]
  32. Yu L. & Zunger A. A polarity-induced defect mechanism for conductivity and magnetism at polarnonpolar oxide interfaces. Nature Commun. 5, 5118 (2014). [DOI] [PubMed] [Google Scholar]
  33. Millis A. J. Oxide Interfaces and Heterostructures (2012) http://phys.columbia.edu/~millis/MillisOxideInteraceLecture1.pdf (accessed 29/01/2014)
  34. Kresse G. & Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558(R) (1993). [DOI] [PubMed] [Google Scholar]
  35. Kresse G. & J. Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996). [DOI] [PubMed] [Google Scholar]
  36. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994). [DOI] [PubMed] [Google Scholar]
  37. Perdew J. P., Burke K. & Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett., 77, 3865 (1996). [DOI] [PubMed] [Google Scholar]
  38. Dudarev S. L. et al. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 57, 1505 (1998). [Google Scholar]
  39. Imada M., Fujimori A. & Tokura Y. Metal-insulator transitions. Rev. Mod. Phys. 70, 1039 (1998). [Google Scholar]
  40. Zhang Y., Jeschke. H. O. & Valenti R. Microscopic model for transitions from Mott to spin-Peierls insulator in TiOCl. Phys. Rev. B 78, 205104 (2008). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep18647-s1.pdf (495.6KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES