Bayesian model selection methods in modeling small area colon cancer incidence

Abstract

Purpose

Many types of cancer have an underlying spatial incidence distribution. Spatial model selection methods can be useful when determining the linear predictor that best describes incidence outcomes.

Methods

In this paper, we examine the applications and benefits of using two different types of spatial model selection techniques, Bayesian model selection and Bayesian model averaging, in relation to colon cancer incidence in the state of Georgia, USA.

Results

Both methods produce useful results that lead to the determination that median household income and percent African American population are important predictors of colon cancer incidence in the Northern counties of the state while percent persons below poverty level and percent African American population are important in the Southern counties.

Conclusion

Of the two presented methods, Bayesian model selection appears to provide more succinct results, but applying the two in combination offers even more useful information into the spatial preferences of the alternative linear predictors.

Introduction

Colon cancer (ICD-9-CM code: 153), accompanied by rectum cancer (ICD-9-CM code: 154.1), is ranked as the third most common tumor type in the United States, with colon cancer being the more frequent of the two. Routine screening for this cancer, particularly after the age of 50, is encouraged since a good prognosis typically accompanies an early diagnosis. Important risk factors of colon cancer include: nutritional inclinations, age, smoking status, inflammatory bowel diseases, previous incidence of malignant disease, and some genetic traits (1-3). Research examining the geography of some of these risk factors suggests that there may be an underlying spatial structure to the incidence of colon cancer (4, 5).

The data of interest in this study is the 2003 colon cancer incidence for the 159 counties in the state of Georgia, USA. The Area Health Resource Files (AHRF) (6) dataset provides ecological predictors useful for explaining the variation in this outcome. The chosen predictors are as follows: median household income (in thousands of dollars), percent persons below poverty level (PPBPL), unemployment rate of those aged 16 or greater (UER), and percent African American (AA) population. Other studies indicate that poverty and race are associated with colon cancer incidence (1, 7). Of the chosen variables, there is evidence to suggest that median income and PPBPL may be correlated (see section titled Data and Linear Predictor Alternatives). This same evidence could also be an indicator of the underlying spatial effect that we believe may play a role in colon cancer incidence. The age cut off associated with the unemployment variable may be criticized since much of the younger population in this age range may not hold steady jobs as they are full time students. In the individual level data used to create this county level variable, ‘student’ is an option as an employment status.

Selecting appropriate linear predictors is one of the most important aspects of data analysis, and this can become very challenging when spatial structures are present in the data. Many methods, such as variable selection, transformation selection, model selection, model averaging, and other model uncertainty methods, have been proposed and explored to achieve these goals (8-12). In this paper, we discuss the application of two types of spatial model selection techniques, Bayesian model selection (BMS) and Bayesian model averaging (BMA) (12-14), in modeling small area cancer incidence. This is achieved by assigning prior probability distributions to each of the possible linear predictors. For BMS, we simply choose the linear predictor associated with the largest posterior probability as the true model. This type of inference works well when a single model stands out, but if that is not the case, BMA is a more appropriate alternative method that can produce a model that blends the alternative linear predictors. In the BMA method, an average posterior mean and variance are calculated based on the posterior model probabilities. However, this posterior mean and variance can be quite difficult to interpret (15). An additional statistical issue involving these types of models revolves around the correlated spatial effect, and there have been several studies examining the issues related to this (16-18). Our models, however, do not involve the correlated spatial random effect in this same way. Rather than using the effect as add additive component in the separate linear predictors, we only use this element as a structure within the model weights and probabilities produced with the model selection techniques.

This paper is developed as follows. First, we describe the available data and the linear predictors of interest. Second, we explain the BMS and BMA methods to be applied. Next, we display the results of employing these methods to the colon cancer data using these different model selection techniques. Finally, we discuss the results and draw conclusions.

Materials and Methods

Our data for this study involves measures of incidence of colon cancer for each of the 159 counties in the state of Georgia, USA and predictors from the AHRF dataset. Since our outcome of interest is the incidence of colon cancer, a conditionally independent Poisson distribution is a reasonable model for these data. This is a commonly assumed model for small area counts in disease mapping (19) and is appropriate because the Poisson distribution is a discrete frequency distribution that provides the probability of events occurring in a given area.

Data and Linear Predictor Alternatives

The colon cancer data comes from the online analytical statistical information system (Oasis) of the Georgia Department of Public Health. For the 1332 diagnosed colon cancers across the state in the year 2003, there was approximately a mean incidence of 8.38 cases per county where the minimum county level value was 0 and the maximum value was 102. In these data, there are no missing values at the county level.

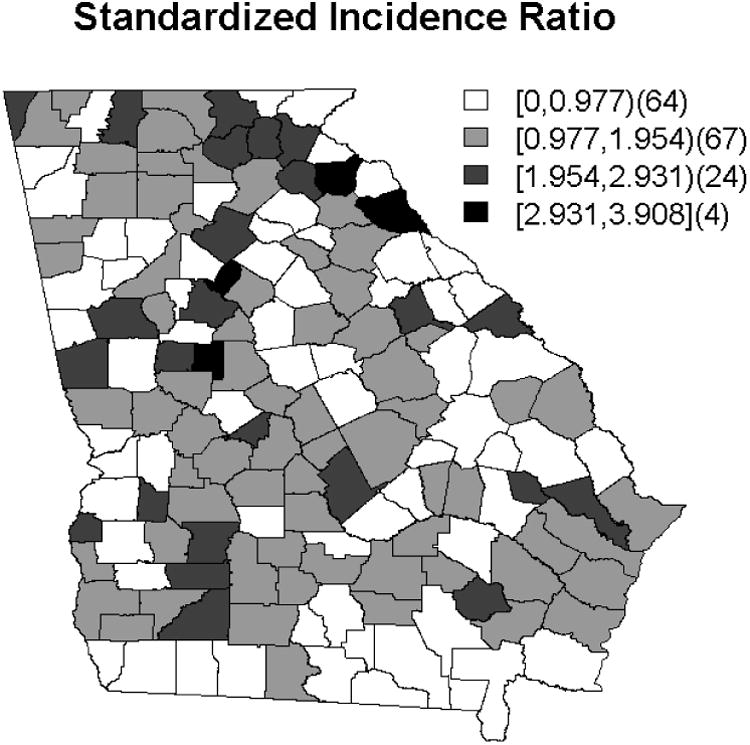
The geographical distributions of the chosen predictors is displayed in Figure 1 and suggests some spatial clustering. An additional indicator of the underlying spatial structure is made evident by the pattern of standardized incidence ratios (SIR) displayed in Figure 2. The SIR is calculated as the ratio of the observed colon cancer incidences to the expected rates for each of the 159 counties and can be useful as a first step in data analysis (20). Qualitatively, for these data, there does appear some spatial structure.

Figure 1.

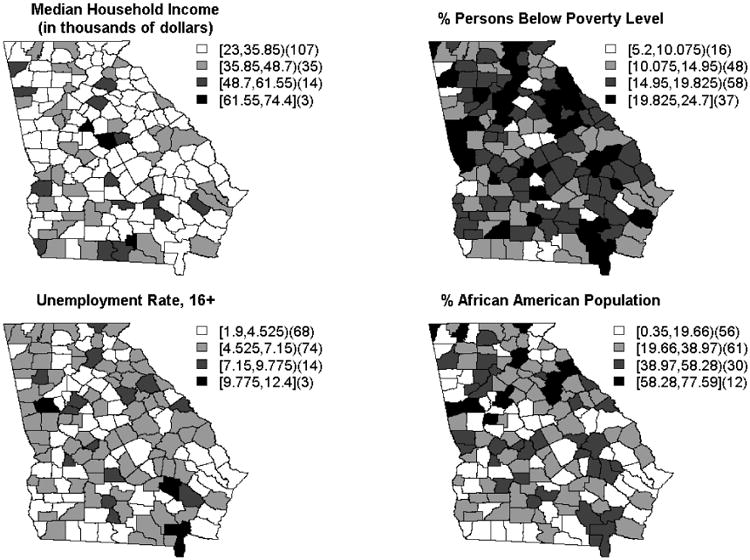
Geographical distribution of predictors from the AHRF dataset.

Figure 2. Map of the Standardized Incidence Ratio for the 2003 colon cancer data.

Based on the chosen predictors (median income in thousands - x₁, PPBPL - x₂, UER - x₃, and percent AA population - x₄), we have employed three possible linear predictors for use with both the BMS and BMA methods. Table 1 displays these alternative predictor options. The first linear predictor (Alt1) includes all of the covariates. The second (Alt2) includes only income and percent AA population. The third and final linear predictor (Alt3) includes PPBPL and percent AA population. Note that all of our possible linear predictors contain an uncorrelated random effect to aid in accounting for any uncontrolled for parameters or extra noise present in the data, and they differ by the predictors included. Additionally, for all of these linear predictor alternatives, the prior distributions are such that:

Table 1. Alternative linear predictor contents.

Model	Contents
Alt1	α0 + α1x1 + α2x2 + α3x3 + α4x4 + ui
Alt2	α0 + α1x1 + α4x4 + ui
Alt3	α0 + α2x2 + α4x4 + ui

$$u_{id}~\mathit{\text{Norm}}(0,{\tau }_u),{\tau }_u~\mathit{\text{Gam}}(1,0.5),\text{and}{\alpha }_{jd}~\mathit{\text{Norm}}(0,1)$$

where i = 1,…,159, d = 1,…, D such that D is the number of linear predictors to be selected between, and j = 0,…, J such that J is the number of predictors for the d^th model.

We alternate income and PPBPL in the second two linear predictors because there is evidence to suggest that they may be correlated. This is not an uncommon assumption as, typically, when income is higher, poverty is lower, as shown in Table 2. This table illustrates, through individual Poisson model fits, that median income and PPBPL are collinear with respect to the incidence of colon cancer outcome because PPBPL becomes well estimated when median income is removed from the model. We also note some changes in percent AA population when PPBPL is used in place of median income. These individual model fits were performed using Bayesian approximation techniques by way of the R package INLA (21, 22).

Table 2.

Individual fits of possible linear predictors. Posterior mean and standard deviations are displayed.

	Alt1 Mean (SD)	Alt2 Mean (SD)	Alt 3 Mean (SD)
Intercept	1.49 (0.08)*	1.49 (0.08)*	1.48 (0.09)*
Median income (x1) (in thousands)	0.69 (0.19)*	0.65 (0.09)*	---
PPBPL (x2 )	0.10 (0.23)	---	-0.69 (0.11)*
UER (x3 )	-0.14 (0.10)	---	---
% AA population (x4 )	0.28 (0.13)*	0.26 (0.09)*	0.41 (0.12)*

^*Indicates that a predictor is well estimated or ‘significant’ and SD stands for standard deviation.

In addition to collinearity, the changes seen in the parameter estimates could also indicate that some of these predictors may be more important in certain regions of the county map. This indication will be further explored with the application of the BMS and BMA techniques. The covariates were standardized prior to fitting the models.

Statistical Methods

In what follows, we describe the methodology associated with the BMS and BMA techniques which are implemented using the R package BRugs which calls OpenBUGS (23, 24).

Bayesian Model Selection

To evaluate a number of alternative linear predictor models, we adopt a method which fits a variety of models, and the selection of weights allows each model to be evaluated for its appropriateness. In general, for d = 1,…., D models, the following structure applies:

$$y_i|{\mu }_i~\mathit{\text{Poi}}({\mu }_i)$$

$${\mu }_i=e_i{\theta }_i$$

$$log({\theta }_i)=\sum _d{w}_{id}{\phi }_{id}$$

$$logit(p_{id})~\mathit{\text{Norm}}(\frac{1}{n_i}\sum _{i~1}logit(p_{id1}),\frac{1}{n_i{\tau }_{id}});{\tau }_{id}^{-1/2}~\mathit{\text{Unif}}(0,10)$$

$$w_{id}~\mathit{\text{Bern}}(p_{id})$$

where φ_id is our d^th model's suggested linear predictor for the i^th county complimented with a possible uncorrelated random effect. In general, we write φ_id as $x_i^T{\beta }_d{\psi }_{dj}+u_i{\psi }_{d,J+1}$ with $x_i^T$, the vector of J possible covariates (j = 1,…,J), and ψ_dj an indicator for if the j^th predictor or random effect is to be included in the linear predictor of the d^th model. Hence, for a variable not included in the d^th model, ψ_dj would be zero, otherwise it would be one. Further, w_d is a model indicator, equal to 1 if the d^th model is selected and zero otherwise. The model selection probability for the d^th model in the i^th county is given by the probability p_id. Additionally, in the equations, i ≠ 1 , n_i is the number of neighbors for county i, and i ∼ 1 indicates that the two counties i and 1 are neighbors. This is an intrinsic CAR (23) model, which adds the desired spatial structure to the model selection process.

Following the application of BMS, we re-fit the selected linear predictors to the appropriate counties to gain interpretable results. Following that, to explicitly interpret the results in terms of the regression coefficients, we must back-transform the estimates because we standardized the data prior to the model fits.

Bayesian Model Averaging

Bayesian model averaging is similar to the BMS technique described in the previous section (14). This method averages over the D possible models, M₁,…, M_D to find the posterior distribution of θ as follows:

$$P(\theta |y_1,\dots ,y_{159})=\sum _{d=1}^{D}P({\theta }_i|y_1,\dots ,y_{159},M_{d,i})P(M_{d,i}|y_1,\dots ,y_{159})$$

where P(M_di| y₁,…,y₁₅₉) is the prior model probability for model d in county i, and P(θ| y₁ ,…,y₁₅₉, M_d,i) is determined by marginalizing the posterior of the model parameters. The posterior probability for model M_d,i is given by (11, 14):

$$\begin{array}{c}P(M_{d,i}|y_1,\dots ,y_{159})=P(y_1,\dots ,y_{159}|M_{d,i})P(M_{d,i})/C\\ \text{where}C=\sum _{1=1}^{D}P(y_1,\dots ,y_{159}|M_{1,i})P(M_{1,i})\\ \text{and}P(y_1,\dots ,y_{159}|M_{d,i})=\int P(y_1,\dots ,y_{159}|{\theta }_{d,i},M_{d,i})P({\theta }_{d,i}|M_{d,i})d{\theta }_{d,i}\end{array}$$

Here, a spatial structure is imposed on P(M_d,i) by way of the CAR model as we saw with the BMS method. Furthermore, following this method, we must re-fit the selected linear predictors and back-transform the parameter estimates in the same way as indicated in the BMS technique to gain interpretable, comparable results.

Results

The results below illustrate the application of BMS and BMA as described above. Following the application of the model selection techniques, we re-fit the selected linear predictors to the appropriate counties.

The results from fitting these models with the real data using the BMS method are displayed in Figure 3 and suggest that it may be beneficial to use the second alternative linear predictor option in the Northern and Western counties of the state as the weights produced for those counties are fairly large. By the same guidelines, the third alternative linear predictor option may be optimal for the Southern and Western counties. Given the fact that there is some overlap in these results, this indicates that either predictor could be appropriate for these counties. Thus, there is not a clear best alternative linear predictor for those counties. From these results, we also see that it is beneficial to place correlated covariates in separate linear predictors and allow the BMS process to determine which is most appropriate across the county map. Additionally, we note that the distribution of the county weights across the county map for p₁ and p₂ are very similar to each other as were the parameter estimates, α_j1 and α_j2, associated with the initial individual model fits shown in Table 2. This indicates that median income may have a more palpable relationship with colon cancer incidence compared to PPBPL. Furthermore, these results do suggest that there is a spatial relationship between these predictors and colon cancer incidence.

Figure 3.

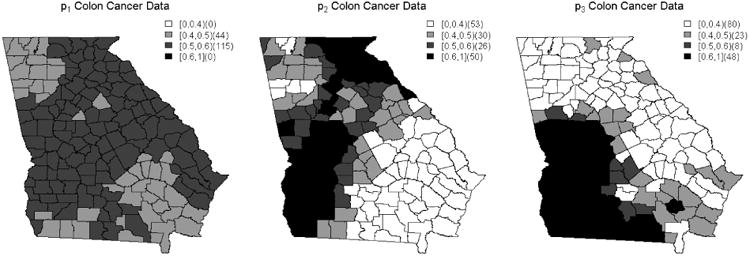
County-specific model selection probabilities corresponding to Alt1, Alt2 and Alt3, based on the BMS procedure.

This application of the BMA method produced different results from those obtained using the BMS method. We use the 0.3 cut off to determine model significance in this instance because in a situation where there is no most appropriate model, the model probabilities would equal 0.3. This value is determined by summing across the three county weights produced by simulation, dividing by 3, and taking the mean of the summed values across all counties. Thus, the BMA model probability results shown in Figure 4 suggest that the second alternative linear predictor option should be used for the Northern counties while the third linear predictor option seems appropriate for the majority of the county map, particularly the Southern and Western counties. Additionally, the first alternative linear predictor appears important in some of the central counties. Again, we see that there is some overlap in the appropriate linear predictors, but in the case of BMA, the differences are trivial for the majority of counties. This suggests that the BMA method designates all of the linear predictors as interchangeable across the county map. We also continue to see some similarities between the distributions produced for p₁ and p₂ . These similarities are not as distinct as they were in the BMS method results, however. Additionally, the results below do still suggest that there is a spatial relationship present for colon cancer incidence.

Figure 4.

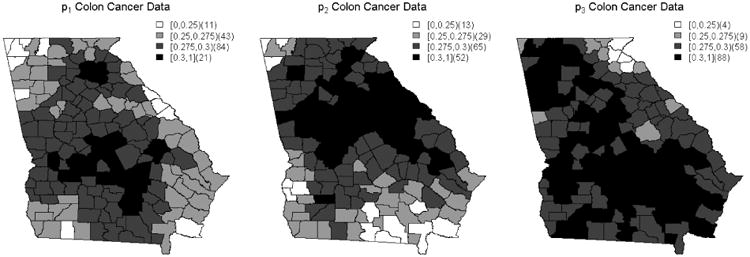
County probabilities based on the BMA procedure.

Table 3 illustrates individual model re-fits for the appropriate counties with the selected linear predictors based on both the BMS and BMA results. From the results above, first we chose to fit the 53 most Northern counties with the second linear predictor and the remaining Southern counties with the third alternative linear predictor. In comparison to the initial individual model fits in Table 2, in Table 3 we observe increases in the magnitudes of the parameter estimates for Alt2 while Alt3 stays roughly the same.

Table 3.

Selected linear predictor re-fits.

Counties included (number)	North (53) Mean (SD)	South (106) Mean (SD)	A2 (50) Mean (SD)	A3 (48) Mean (SD)
Linear Predictor	Alt2	Alt3	Alt2	Alt3
Intercept	1.50 (0.15)*	1.49 (0.10)*	1.51 (0.11)*	1.52 (0.11)*
Median Income (in thousands)	0.87 (0.17)*	---	0.51 (0.13)*	---
PPBPL	---	-0.63 (0.13)*	---	-0.43 (0.18)*
% AA population	0.28 (0.15)*	0.36 (0.14)*	0.08 (0.12)	-0.01 (0.19)

^*Indicates that a predictor is well estimated or ‘significant,’ SD stands for standard deviation, and the definitions of A2 and A3 are as follows: The appropriate counties selected for Alt2 are considered to be in area A2 while the area for the counties selected with Alt3 is named A3.

Next, we consider applying the linear predictors based exactly on the BMS results. Here, if BMS produced a weight greater than 0.5, that county was included in the model re-fit for the associated alternative linear predictor. This is not a strict cutoff for the BMS method, it is simply what seemed appropriate for these data as this is the value that all weight would acquire if there were no true model. This value is determined in the same way as the BMA 0.3 cutoff value described above. The appropriate counties selected for Alt2 are considered to be in area A2 while the area for the counties selected with Alt3 is named A3. Based on these definitions and in comparison to their respective initial model fits (Table 2), the estimates associated with Alt2 and Alt3 decrease in magnitude as well as value. Here, for both linear predictors, the parameter estimates associated with percent AA population are no longer well estimated.

Discussion

Our results present evidence suggesting that there is a spatial structure in the distribution of colon cancer incidence. These results also show that the model selection techniques are useful in determination of the appropriate linear predictors for different areas of the county map. Additionally, there are many reasons why some of the selected linear predictors may not perform as well as expected. These include: 1) the larger size and more separation among the Southern counties; 2) the limited number of counties selected when restricting the included counties to those with a weight of 0.5 or more; and 3) the strength of association in the data: in general, these predictors may not have a very strong relationship with colon cancer incidence. Thus, they are difficult to first select and then fit to produce well estimated parameter estimates.

Based on the results above, both techniques suggest that median income and percent AA population are useful in predicting colon cancer incidence in the Northern counties of Georgia. Alternatively, these results also suggest that PPBPL and percent AA population are useful in predicting incidence of colon cancer in the Southern counties of the state of Georgia. After applying the appropriate transformations defined in the Statistical Methods section titled Bayesian Model Selection, the explicit interpretations of the parameter estimates from the individual model re-fits are as follows. For the Northern counties, every $1000 increase in median income indicates that 1.09 times as many incidences of colon cancer occur, and each 1% increase in AA population indicates that 1.02 times as many incidences of colon cancer occur. For the Southern counties, every one unit increase in PPBPL indicates 0.87 times as many incidences of colon cancer occur, and every one percent increase in percent AA population indicates that 1.02 times as many incidences of colon cancer occur. These estimates are not very large in magnitude because they are incremental, continuous increases per unit of the parameter of interest; they are also displayed in Table 4.

Table 4.

Transformed mean parameter estimates for linear predictor re-fits.

Counties included (number)	North (53)	South (106)	Predictor Standard Deviation
Linear Predictor	Alt2	Alt3	---
Median Income (in thousands)	exp (0.87 / 9.75) = 1.09	---	9.75
PPBPL	---	exp (-0.63 / 4.58) = 0.87	4.58
% AA population	exp (0.28 /17.47) = 1.02	exp (0.36 /17.47) = 1.02	17.47

For BMS, we receive very clear indications that the linear predictors which include either PPBPL or median income are preferred over the linear predictor that includes both. We also see that these two linear predictors are clustered in specific areas, with some overlap, of the county map. Once we look into re-fitting the selected models, we see that the second linear predictor seems to have a slightly stronger relationship with colon cancer incidence than the third in their appropriately selected counties. Furthermore, A1 and A2 produce even less substantial results. These losses in substantiality may be due to the limited number of counties selected or the smaller size and closer proximity to each other involved with the counties in the Northern part of the state, or both.

Some of our simulation studies have suggested that the BMA technique does not perform as well in detecting smaller levels of association in the data (25). The results here also suggest that this may be an issue for these data. Our predictors are not among the most important risk factors mentioned previously, thus they are not considered of high association with incidence of colon cancer. BMA does not appear to choose one linear predictor clearly over the other, though it does seem to have a slight preference of the second two alternatives in comparison to the first. In general, BMA will not produce probabilities of the same magnitude as the weights produced by BMS because they are scaled such that they add to 1. This leads to slightly more interpretable results produced with BMA. Regarding measures of goodness of fit measures, because in BMA each of the linear predictors are fit individually then averaged to create the averaged posterior, this method offers the ability to examine how well each of the alternative linear predictors perform, while BMS does not.

Both BMS and BMA techniques illustrate the importance of keeping collinear variables in separate alternative linear predictors. In both sets of results, we see that the first alternative linear predictor, which contains two collinear predictors, is somewhat under-stimulated in comparison to the other two alternatives. This is most distinguished in the BMS results. Additionally, the results given here indicate the importance of using these spatial models for incidence of colon cancer. We received meaningful, important results when performing the initial individual, non-spatial model fits, but we gain even more information by allowing the model selection techniques to determine the appropriate linear predictor for each individual county. Furthermore, the model re-fits illustrate how these techniques perform better when the regions of interest are smaller and closer together. This issue has been noted in our simulation studies as well. Both model selection techniques suggested that Alt2 was a good choice for the Northern counties, and when we re-fit that linear predictor for only those Northern counties, we saw the parameter estimates become even more substantial. For the A1 and A2 counties, however, this was not as clear even though we still gain some meaningful results for these counties.

Conclusion

Based on this exploration of the spatial structure of colon cancer incidence, our findings suggest that there is much information to gain by employing spatial model selection techniques to determine the appropriate linear predictor that best explains the variation in the data. Through the application of these techniques, we determined the important predictors for the different areas of the county map, and these indicate that median income and percent AA population are important predictors of colon cancer incidence in the Northern counties of the state while PPBPL and percent AA population are important for the Southern counties of the state. By employing these two methods in combination, we were able to detect some interesting and important aspects of these data.

Abbreviations

AHRF

Area Health Resources Files

AA

African American

PPBPL

percent persons below poverty level

UER

unemployment rate of those age 16+

SIR

standardized incidence ratio

BMS

Bayesian model selection

BMA

Bayesian model averaging

CAR

conditional autoregressive