Genetics in geographically structured populations: defining, estimating and interpreting F_ST

Abstract

Wright’s F-statistics, and especially F_ST, provide important insights into the evolutionary processes that influence the structure of genetic variation within and among populations, and they are among the most widely used descriptive statistics in population and evolutionary genetics. Estimates of F_ST can identify regions of the genome that have been the target of selection, and comparisons of F_ST from different parts of the genome can provide insights into the demographic history of populations. For these reasons and others, F_ST has a central role in population and evolutionary genetics and has wide applications in fields that range from disease association mapping to forensic science. This Review clarifies how F_ST is defined, how it should be estimated, how it is related to similar statistics and how estimates of F_ST should be interpreted.

Nearly every plant or animal species includes many partially isolated populations. As a result of genetic drift or divergent natural selection, such populations become genetically differentiated over time. For example, recent analyses based on more than 370 short tandem repeat loci¹ (microsatellites) and 600,000 SNPs² suggest that only 5–10% of human genetic diversity is accounted for by genetic differences among populations from major geographical regions. These results indicate that there are far more similarities among geographically distinct human populations than differences. But what does it mean to say that 5–10% of diversity is accounted for by differences among populations, and how is this figure derived? The short answer is that the estimate of F_ST among human populations sampled from these regions is 0.05 for the microsatellite data and 0.10 for the SNP data. However, this answer helps only if one understands what F_ST is, how it is estimated from data and what it means to get two different estimates for the same set of populations when different genetic markers are used.

Working independently in the 1940s and 1950s, Sewall Wright³ and Gustave Malécot⁴ introduced F-statistics as a tool for describing the partitioning of genetic diversity within and among populations. In a paper published in 1931 (REF. 5), Wright had already provided a comprehensive account of the processes that cause genetic differentiation among populations. He showed that the amount of genetic differentiation among populations has a predictable relationship to the rates of important evolutionary processes (migration, mutation and drift). For example, large populations among which there is much migration tend to show little differentiation, whereas small populations among which there is little migration tend to be highly differentiated. F_ST is a convenient measure of this differentiation, and as a result F_ST and related statistics are among the most widely used descriptive statistics in population and evolutionary genetics.

But F_ST is more than a descriptive statistic and a measure of genetic differentiation. F_ST is directly related to the variance in allele frequency among populations and, conversely, to the degree of resemblance among individuals within populations. If F_ST is small, it means that the allele frequencies within each population are similar; if it is large, it means that the allele frequencies are different. If natural selection favours one allele over others at a particular locus in some populations, the F_ST at that locus will be larger than at loci in which among-population differences are purely a result of genetic drift. Genome scans that compare single-locus estimates of F_ST with the genome-wide background might therefore identify regions of the genome that have been subjected to diversifying selection^6–8. Alternatively, if the demographic history of populations affects the genetic variation on sex chromosomes in a different way from the genetic variation on autosomes, the estimates of F_ST derived from sex chromosome markers might be different from those derived from autosomal markers⁹.

Estimates of F_ST are also important in association mapping of human disease genes and in forensic science. The same evolutionary processes that increase differentiation among populations also increase the similarity among individuals within populations. Therefore, F_ST must be considered when allele frequencies are compared between cases and controls to ensure that the differences between them are greater than expected by chance. Similarly, the probability of a match between a suspect and a crime scene sample is specific to the set of people who might reasonably be expected to be sources of the sample. However, defining this set is difficult, so a ‘θ correction’ is applied to population frequencies to accommodate variation among subpopulations. The θ correction depends on the value of F_ST.

In this review, we discuss how F_ST is defined, describe approaches for estimating it from data and illustrate several ways in which analysis of F_ST can provide insights into the genetic structure and evolutionary dynamics of populations. In addition, we discuss four statistics that are related to F_ST (G_ST, R_ST, Φ_ST and Q_ST), clarify the differences among them and recommend when each should be used.

These additional statistics partition genetic diversity into within- and among-population components. of the four, G_ST is most closely related to F_ST, and it has been widely used as a measure of genetic differentiation among populations. However, as we describe below, G_ST is an appropriate measure of genetic differentiation only when the contribution of genetic drift to among-population differences is not of interest. As a result, the contexts in which it is useful are limited. By contrast, R_ST (for microsatellite data) and Φ_ST (for molecular sequence data) are useful in a wide range of contexts in which it is important to account for the mutational ‘distances’ among alleles, and Q_ST is useful in the analysis of continuously varying traits.

Definitions

Wright introduced F_ST as one of three interrelated parameters to describe the genetic structure of diploid populations³. These parameters are: F_IT, the correlation between gametes within an individual relative to the entire population; F_IS, the correlation between gametes within an individual relative to the subpopulation to which that individual belongs; and F_ST, the correlation between gametes chosen randomly from within the same subpopulation relative to the entire population. We describe here how these parameters are defined in terms of the departure of genotype frequencies from Hardy–Weinberg proportions.

Deriving measures of genetic diversity

As an example of how to calculate genetic diversity, consider two populations that are segregating for two alleles at a single locus. The frequency of allele A₁ in the first population is labelled as p₁ and its frequency in the second population is labelled as p₂. The frequency of genotype A₁A₁ in the first population is labelled as x_11,1, the frequency of genotype A₁A₂ in the first population is labelled as x_12,1, and so on. The genotype frequencies in the two populations are given by the following set of equations:

$$x_{11,1}=p_1^2+f_1{p}_1(1-p_1)$$

$$x_{12,1}=2p_1(1-p_1)(1-f_1)$$

$$x_{22,1}={(1-p_1)}^2+f_1{p}_1(1-p_1)$$

$$x_{11,2}=p_2^2+f_2{p}_2(1-p_2)$$

$$x_{12,2}=2p_2(1-p_2)(1-f_2)$$

$$x_{22,2}={(1-p_2)}^2+f_2{p}_2(1-p_2)$$ (1)

In this context, f₁ and f₂ are often referred to as the within-population inbreeding coefficients, but this term can be misleading. In practice, f is a measure of the frequency of heterozygotes compared with that expected when genotypes are in Hardy–Weinberg proportions. Inbreeding leads to a deficiency of heterozygotes relative to Hardy–Weinberg expectations, so when there is inbreeding in both populations, f₁ and f₂ will have positive values. But if individuals avoid inbreeding or if there is heterozygote advantage, then heterozygotes will be more common than expected under Hardy–Weinberg expectations, and f₁ and f₂ will be negative. In short, f₁ and f₂ are measures of how different the genotype proportions within populations are from Hardy–Weinberg expectations, and positive values of f indicate a deficiency of heterozygotes, whereas negative values indicate an excess.

Now consider the genotype frequencies in a combined sample that consists of a proportion c of individuals from the first population and a proportion 1 – c of individuals from the second population. Similar to the way in which the genotype frequencies in each population differ from Hardy–Weinberg expectations based on the allele frequency in each population, genotype frequencies in the combined sample differ from Hardy–Weinberg expectations based on the average allele frequency. The allele frequencies are given by:

$$x_{11}={\pi }^2+F\pi (1-\pi )$$

$$x_{12}=2\pi (1-\pi )(1-F)$$

$$x_{22}={(1-\pi )}^2+F\pi (1-\pi )$$ (2)

in which π = cp₁ + (1 – c)p₂ is the average allele frequency for A₁ in the combined sample and F is the total inbreeding coefficient¹⁰. F can be expressed as:

$$(1-F)=(1-f)(1-\theta )$$ (3)

in which f = cf₁ + (1 – c)f₂ is the average within-population departure from Hardy–Weinberg expectations and θ is a measure of allele frequency differentiation among populations (see BOX 1 for a summary of the mathematical notation used in this review). We can define θ as:

$$\theta =\frac{{\sigma }_{\pi }^2}{\pi (1-\pi )}$$ (4)

in which ${\sigma }_{\pi }^2$ is the variance in allele frequency among populations. π(1 – π) is the variance in the allelic state for an allele chosen randomly from the entire population, so it can be regarded as a measure of genetic diversity in the entire population. θ can therefore be interpreted as the proportion of genetic diversity that is due to the differences in allele frequency among populations.

Box 1. Mathematical notation.

In this box, we provide definitions for the mathematical symbols used throughout the Review.

Parameter	Definition
Among-population allele frequency distribution
π	Mean allele frequency
${\sigma }_{\pi }^2$	Variance in allele frequency
Wright’s F-statistics and Cockerham’s θ-statistics
FIS	Correlation of alleles within an individual relative to the subpopulation in which it occurs; equivalently, the average departure of genotype frequencies from Hardy–Weinberg expectations within populations
FST	Correlation of randomly chosen alleles within the same subpopulation relative to the entire population; equivalently, the proportion of genetic diversity due to allele frequency differences among populations
FIT	Correlation of alleles within an individual relative to the entire population; equivalently, the departure of genotype frequencies from Hardy–Weinberg expectations relative to the entire population
f	Co-ancestry for alleles within an individual relative to the subpopulation in which it occurs; equivalent to FIS
θ	Co-ancestry for randomly chosen alleles within the same subpopulation relative to the entire population; equivalent to FST
F	Co-ancestry for alleles within an individual relative to the entire population; equivalent to FIT
Φ-statistics and RST*
ΦIS	Excess similarity of alleles within an individual relative to the subpopulation in which it occurs; analogous to FIS
ΦST	Excess similarity among randomly chosen alleles within the same subpopulation relative to the entire population; equivalently, the proportion of genetic diversity (measured as the expected squared evolutionary distance between alleles) due to differences among populations; analogous to FST
ΦIT	Excess similarity of alleles within an individual relative to the entire population; analogous to FIT
RST	Excess similarity among randomly chosen alleles within the same subpopulation relative to the entire population; equivalently, the proportion of genetic diversity (measured as the expected squared difference in repeat numbers between alleles) due to differences among populations; analogous to FST
Measuring genetic differentiation among populations in quantitative traits
${\sigma }_{\mathrm{G}\mathrm{I}}^2$	Additive genetic variance within populations
${\sigma }_{\mathrm{G}\mathrm{P}}^2$	Additive genetic variance among populations
QST	Proportion of additive genetic variation in the entire population due to differences among populations; analogous to FST

^*Φ_ST from analysis of molecular variance (AMOVA) is used for haplotype data (for example, nucleotide sequence data or mapped restriction site data) and requires a measure of evolutionary distance among all pairs of haploytpes. R_ST is used for microsatellite data and requires that alleles are labelled according to the number of repeat units that they contain.

Wright first developed these ideas in the context of a model of discrete populations, in which each population is the same size and receives immigrants from all other populations at the same rate⁵. However, the same statistical argument can be applied to any partitioning of genetic diversity in which the populations differ in allele frequency, whether or not those populations are discrete¹¹. Therefore, when we use θ as a purely descriptive statistic that describes the partitioning of genetic diversity among ‘populations’, we do not need to make assumptions about whether the ‘populations’ we sample are discrete or about the evolutionary processes that might have led to differences among them. Nonetheless, other methods of analysis could be more informative in continuously distributed populations^12–14.

Linking f, θ and F to Wright’s F-statistics

Using a different approach, Cockerham^10,15 showed that f, θ and F can also represent intraclass correlation coefficients. He showed that f is the correlation between alleles within individuals relative to the population to which they belong, θ is the correlation between alleles within populations relative to the combined population and F is the correlation between alleles within individuals relative to the combined population. These are the definitions that Wright gave for F_IS, F_ST and F_IT, respectively. In short, f and F_IS can be thought of either as the average within-population departure from Hardy–Weinberg expectations or as the correlation between alleles within individuals relative to the population to which they belong. θ and F_ST can be thought of either as the proportion of genetic diversity due to allele frequency differences among populations or as the correlations between alleles within populations relative to the entire population. F and F_IT can be thought of either as the departure of genotype frequencies in the combined sample from Hardy–Weinberg expectations or as the correlation between alleles within individuals relative to the combined sample.

In Wright’s notation, subscripts refer to a comparison between levels in a hierarchy: _IS refers to ‘individuals within subpopulations’, _ST to ‘subpopulations within the total population’ and _IT to ‘individuals within the total population’¹⁶. The hierarchy in equation 1 can be extended indefinitely to accommodate such structures. For example, Wright¹⁶ describes variation in the frequency of the Standard chromosome in Drosophila pseudoobscura in the western United States at the level of demes (D; local populations), regions (R; groups of several demes), subdivisions (S; groups of several regions) and the total range (T). The corresponding F-statistics are related in the same multiplicative way as f, θ and F:

$$(1-F_{\mathrm{D}\mathrm{T}})=(1-F_{\mathrm{D}\mathrm{R}})(1-F_{\mathrm{R}\mathrm{S}})(1-F_{\mathrm{S}\mathrm{T}})$$ (5)

In this scheme, F_DR measures the differentiation among demes within a region, F_RS measures the differentiation among regions within subdivisions and F_ST measures the differentiation among subdivisions within the total range.

If we return to the examples of genetic differentiation among human populations that were mentioned at the beginning of this review, we can now see that an estimate for F_ST or θ of 0.05 (from microsatellites) and 0.10 (from SNPs) suggests that only 5–10% of human genetic diversity is a result of genetic differentiation among human populations. What might be surprising is that the two estimates are derived from the same set of populations — this indicates that the amount of genetic differentiation among human populations is greater at SNP loci than at microsatellites.

Estimation

Statistical sampling

When Wright and Malécot introduced F-statistics, they did not distinguish between the parameters defined in the preceding section and the estimates of those parameters that we make from data. Not making this distinction is similar to confusing the mean height of the human population with an estimate of the mean height calculated from a sample of the population. Estimates of height must account for the variation associated with taking a finite sample from a population. New samples from the same population will have different characteristics. We refer to this variation as statistical sampling¹⁷ (BOX 2). In the context of F-statistics, statistical sampling refers to the variation associated with collecting genetic samples from a fixed set of populations that have fixed but unknown genotype frequencies. The magnitude of variation associated with statistical sampling can be reduced by increasing the size of within-population samples.

Box 2. Genetic sampling versus statistical sampling.

Genetic drift leads to differences among populations that are described by the distribution of allele frequencies among those populations. The variance of this distribution is directly related to F_ST (see equation 2), but in a typical study only a subset of populations is sampled. Therefore, in addition to accounting for the variation associated with sampling from populations, estimates of F-statistics must account for the variation associated with sampling sets of populations from the allele frequency distribution.

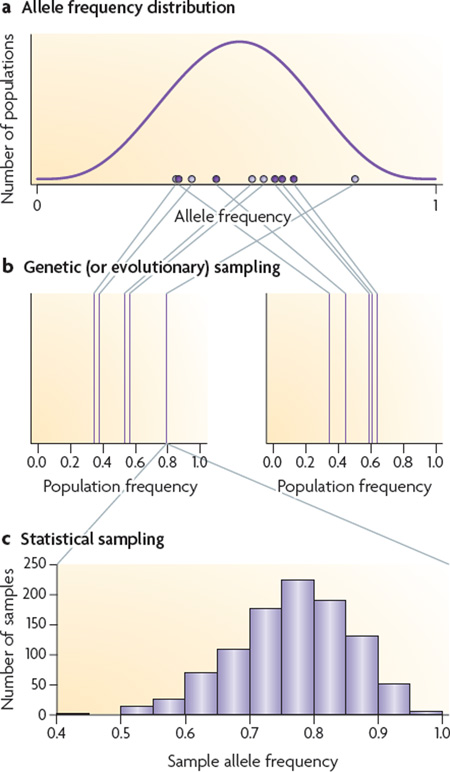
Genetic (or evolutionary) sampling

Part a of the figure shows the distribution of allele frequencies among populations corresponding to a mean allele frequency of π = 0.5 and F_ST = θ = 0.1. If two sets of populations (represented by dark and light circles) are sampled from this distribution, the allele frequencies in the first set of populations (light circles) will differ from those in the second set (dark circles). Part b provides an example in which two different sets of five population frequencies are drawn randomly from the distribution of allele frequencies shown in part a.

The variation in allele frequencies illustrated in part a reflects the effect of genetic or evolutionary sampling. The differences between the sets of samples in part b reflect the effect of sampling particular populations from the distribution of allele frequencies in part a and are analogous to the results that would be expected in an empirical study if it were repeated on a different set of populations.

Statistical sampling

Part c illustrates the more familiar idea of statistical sampling. It shows the distribution of sample allele frequencies obtained in 1,000 samples of 20 individuals from the population with the largest allele frequency in the population sample on the left in part b. Statistical sampling refers to the variation in sample composition that is expected when alleles are repeatedly sampled from a population with a particular allele frequency.

Investigators can control the amount of variation associated with statistical sampling by increasing the number of individuals sampled within populations: the larger the number of individuals sampled, the less that the sample allele frequencies will differ from the underlying population frequencies. By contrast, investigators cannot control the amount of variation associated with genetic sampling: the variation associated with genetic sampling is an intrinsic property of the underlying stochastic evolutionary process that contributes to the differentiation among populations.

The relationship between F_ST and G_ST

Nei introduced the statistic G_ST as a measure of genetic differentiation among populations³³. It is defined in terms of the population frequencies in part b, not the allele frequency distribution in part a. By contrast, estimates of F_ST account for genetic sampling and they are intended to reflect the properties of the allele frequency distribution in part a. As a result, F_ST and G_ST measure different properties. Therefore, G_ST will be an appropriate measure only when interest focuses on characteristics of the particular samples illustrated in part b. In a typical population study, θ will be a more appropriate measure of differentiation.

It might seem that similar arguments should apply to exact tests of population differentiation¹⁰² because they also use permutations of sample configurations to determine whether populations are differentiated from one another. However, the permutation test is equivalent to determining whether the allele frequency distribution in part a has a variance greater than zero, so exact tests implicitly consider both statistical and genetic sampling effects.

Genetic sampling

There is an important difference between estimates made by F-statistics and estimates of height. In addition to accounting for statistical sampling, F-statistics must account for differences among the sets of populations that have been sampled. These differences might arise either because the populations that are sampled are only a subset of all of the populations that could be sampled (statistical sampling of populations rather than statistical sampling of genotypes within populations) or because the populations that are sampled represent only one possible outcome of an underlying stochastic evolutionary process. even if we could take the set of sampled populations back to a previous point in time and re-run the evolutionary process under all of the same conditions (the same population sizes, mutation rates, migration rates and selection coefficients), the genotype frequencies in the new set of populations would differ from those in the populations that were actually sampled¹⁸. This genetic sampling¹⁷ is an unavoidable consequence of genetic drift. The magnitude of variation associated with genetic sampling cannot be reduced by increasing either the number of individuals sampled within populations or the number of populations sampled. Indeed, the characteristics of genetic sampling are shown by estimates of F-statistics.

In simple cases, it might make sense to estimate statistical parameters using simple functions of the data, such as the sample mean. In more complicated cases, such as those presented by F-statistics, it is useful to have well-defined approaches for constructing estimates. Statisticians have developed several different approaches for estimating parameters from data¹⁹. Three widely used approaches are the method of moments, the method of maximum likelihood and Bayesian methods.

Approaches to estimating F_ST: method-of-moments estimates

The method of moments produces an estimate by finding an algebraic expression that makes the expected value of certain sample statistics equal to simple functions of the parameters that are being estimated (as explained in more detail below)¹⁹. Method-of-moments estimates are designed to have low bias in the sense that if samples are taken repeatedly from the same population, the average of the corresponding sample estimates will be close to the unknown population parameter. These estimates have the additional advantages that they are easy to calculate and do not require any assumptions about the shape of the distribution from which the sample is drawn, other than that it has a mean and variance.

For F-statistics, method-of-moments estimates^17,20,21 are based on an analysis of variance (ANOVA) of allele frequencies. ANOVA is a statistical method that tests whether the means of two or more groups are equal and can therefore be used to assess the degree of differentiation between populations. Briefly, if the variance among populations is the same as the variance within populations, there is no population substructure. ANOVA calculations are framed in terms of mean squares. Therefore, in practice, one calculates the expected mean square among populations (that is, the variance of sample allele frequencies around the mean allele frequency over all populations) and the expected mean square within populations (that is, the heterozygosity within populations when genotypes are in Hardy–Weinberg proportions) averaged over all possible samples (statistical sampling) from all possible populations with the same evolutionary history (genetic sampling). These expected values are then equated to the observed mean squares that are calculated from a sample, and the resulting set of equations is solved for the corresponding variance components. Following the work of Cockerham^10,22, F-statistics are defined in terms of these variance components (BOX 3).

Box 3. Comparing methods for estimating F_ST.

To illustrate the differences among calculating method-of-moments, maximum-likelihood and Bayesian estimates of F-statistics, we use data from a classic study on human populations that investigated the allele frequency differences at blood group loci (see the table). We use a subset of the data that were originally reported by Workman and Niswander¹⁰³. Their data consist of genotype counts at several loci in Native American Papago and were collected from ten political districts in south-western Arizona. Estimates of F_IS, F_ST and F_IT derived from the MN blood group locus suggest that there is little departure of the genotype frequencies from Hardy–Weinberg expectations within each district and little genetic differentiation among the districts.

Method-of-moments analysis

Analysis of variance on the indicator variable y_ij,k, in which y_ij,k = 1 if allele i in individual j of population k is M, gives moment estimates for the variance components of ${\sigma }_{\mathrm{G}}^2=0.16,{\sigma }_{\mathrm{I}}^2=0.00511$, and ${\sigma }_{\mathrm{P}}^2=0.0000667$, in which _G stands for genotypes (alleles within individuals), _I stands for individuals (individuals within populations) and _P stands for populations (among populations). Following Cockerham¹⁰:

$$F=\frac{{\sigma }_{\mathrm{P}}^2+{\sigma }_{\mathrm{I}}^2}{{\sigma }_{\mathrm{P}}^2+{\sigma }_{\mathrm{I}}^2+{\sigma }_{\mathrm{G}}^2}$$

$$\theta =\frac{{\sigma }_{\mathrm{P}}^2}{{\sigma }_{\mathrm{P}}^2+{\sigma }_{\mathrm{I}}^2+{\sigma }_{\mathrm{G}}^2}$$

$$f=\frac{{\sigma }_{\mathrm{I}}^2}{{\sigma }_{\mathrm{I}}^2+{\sigma }_{\mathrm{G}}^2}$$

Therefore, the moment estimates are F = 0.0348, θ = 0.00402 and f = 0.0309. As expected for human populations, there is little evidence that the genotype proportions within each political district differ from Hardy–Weinberg expectations (f ≈ 0). Similarly, there is little evidence of genetic differentiation among political districts (θ ≈ 0).

Bayesian and likelihood analysis

By contrast, current implementations of a Bayesian approach to analysing these data typically assume independent uniform (0,1) prior distributions for both f and θ. The posterior mean of f and θ for these data are 0.0503 and 0.0189, respectively. The posterior distribution of f has a mode near 0 but is broad (with a 95% credible interval of 0.0033–0.123), which causes the posterior mean of f to be larger than the method-of-moments estimate. Similarly, the estimates of allele frequencies within each population are uncertain and the estimate of θ takes this uncertainty into account, suggesting that there is slightly more among-population differentiation than detected with moment estimates. For comparison, the maximum-likelihood estimates are F = 0.0408, θ = 0.00640 and f = 0.0346 (obtained by estimating the variance components in a Gaussian mixed model applied to the indicator variables and by using Cockerham’s definitions of F, f and θ in terms of the variance components).

Parameter	Method of moments	Maximum likelihood	Bayesian
f	0.0309	0.0346	0.0503
θ	0.00402	0.00640	0.0189
F	0.0348	0.0408	0.0683

To extend the method-of-moments approach to multiple alleles and multiple loci, calculations are done separately for every allele at every locus and the sums of squares are combined^17,27. To extend the likelihood or Bayesian approaches, we make the assumption that f and θ have the same value at every locus and that genotype counts are sampled independently across loci and populations^104,105.

Approaches to estimating F_ST: maximum-likelihood and Bayesian estimates

In contrast to method-of-moments estimates, likelihood and Bayesian estimates are difficult to calculate and require the specification of the probability distribution from which the sample was drawn. Once this probability distribution is specified, we can calculate a quantity called the likelihood, which is proportional to the probability of our observed data given those parameters. A maximum-likelihood estimate for the parameters is obtained by finding the values of the unknown parameters that maximize that likelihood¹⁹. In most cases, maximum-likelihood estimates are biased. Nonetheless, they typically have a smaller variance and deviate less from the unknown population parameter than the corresponding method-of-moments estimates¹⁹. For these and other reasons, the method of maximum likelihood is the most widely used technique for deriving statistical estimators^23,24.

Bayesian estimates share many of the advantages associated with maximum-likelihood estimates because they use the same likelihood to relate the data to unknown parameters. However, they differ from maximum-likelihood estimates because the likelihood is modified by placing prior distributions on unknown parameters, and estimates are based on the posterior distribution, which is proportional to the product of the likelihood and the prior distributions. Both maximum-likelihood and Bayesian methods suffer the disadvantage that simple algebraic expressions for the estimates are rarely available. Instead, the estimates are obtained through computational methods. Because the Markov chain Monte Carlo methods (MCMC methods) used for analysis of Bayesian models do not require a unique point of maximum likelihood to be identified, Bayesian estimates can be obtained even in complex models with thousands or tens of thousands of parameters, for which numerical maximization of the likelihood would be difficult or impossible²⁶.

For F-statistics, the likelihood approach^27,28 specifies a probability distribution that describes the variation in allele frequencies among populations and a multinomial distribution that describes genotype samples within populations. θ is related to the variance of the probability distribution that describes the among-population distribution of allele frequencies, and the genotype frequencies are determined by the allele frequencies in each population and f. Estimates are obtained by maximizing the likelihood function with respect to θ, f and the allele frequencies. The Bayesian approach uses the same likelihood function, and after placing appropriate prior distributions on f, θ and allele frequencies, MCMC methods are used to sample from the posterior distributions of f and θ.

Comparing the methods

With more than 5,000 citations, the moments method described by Weir and Cockerham²⁰ has been widely used, partly because of its robustness and partly because it is simple to implement. The maximum-likelihood methods also give simple equations when the distribution of allele frequencies among populations is assumed to be normal²⁷, but only if the sample sizes are equal²⁹. Bayesian methods allow probability statements to be made about F-statistics, and extensions of these methods allow the relationship between F-statistics and demographic or environmental covariates to be explored in the context of a single model³⁰. However, implementations of Bayesian methods may be computationally demanding.

A simple data set is used in BOX 3 to illustrate the slightly different estimates obtained from each approach. Estimates of F_ST using moments and Bayesian methods have not been extensively compared, but our experience suggests that the differences in estimates are small when the average number of individuals per population is moderate to large (>20), when the number of populations is moderate to large (>10–15) and when most populations are polymorphic. When differences arise, they reflect differences in the treatment of allele frequency estimates when alleles are rare or sample sizes are small. The Bayesian approach ‘smooths’ population allele frequencies towards the mean²⁴ and does so more aggressively when alleles are rare or sample sizes are small. The moments approach treats the sample frequencies as fixed quantities without such smoothing. The simulation results in REF. 31 are consistent with this interpretation, although they compare Bayesian estimates with estimates of G_ST³², which does not account for genetic sampling.

Related statistics

Population geneticists have proposed several statistical measures that are related to F_ST. Here, we describe four of them: G_ST, R_ST, Φ_ST and Q_ST. Nei³³ introduced G_ST as a measure of population differentiation. We discuss its relationship to F_ST in BOX 2. Haplotype and microsatellite data contain information not only about the frequency with which particular alleles occur but also on the evolutionary distance between them. Statistics such as Φ_ST (for haplotype data) and R_ST (for microsatellite data) are intended to take advantage of this additional information and to provide greater insight into the patterns of relationships among populations. Whereas F_ST, Φ_ST and R_ST all apply to discrete genetic data, Q_ST is an analogous statistic for continuously varying traits. If the markers used to estimate F_ST can be presumed to be selectively neutral, comparing an estimate of Q_ST with an estimate of F_ST can provide investigators with evidence that natural selection has shaped the pattern of variation in the quantitative trait.

R_ST, Φ_ST and AMOVA

The methods for estimating f, θ and F described above are appropriate for multi-allelic data when the alleles are regarded as equivalent to one another. However, when the data consist of variation at microsatellite loci or of nucleotide sequence (haplotype) information, related methods that allow mutation rates to differ between different pairs of alleles might be more appropriate. Excoffier et al.³⁴ introduced analysis of molecular variance (AMOVA) for analysis of haplotype variation. AMOVA is based on an analysis-of-variance framework that is analogous to the one developed by Weir and Cockerham²⁰. The mean squares in an AMOVA analysis are based on a user-specified measure of the evolutionary distance between haplotypes, and AMOVA leads to quantities that are analogous to classical F-statistics (BOX 1). Similarly, the mean squares used to calculate R_ST^35,36 are based on differences in the number of repeats between alleles at each microsatellite locus. Although the result of both analyses is a partitioning of genetic variance into within- and among-population components analogous to F_ST, neither has a direct interpretation as a parameter of a statistical distribution. Instead, they estimate an index that is derived from two different statistical distributions: the distribution of allele (haplotype or microsatellite) frequencies among populations and the distribution of evolutionary distances among alleles. Nonetheless, such measures may be thought of as estimating the additional time since the common ancestry of randomly chosen alleles that accrues as a result of populations being subdivided^37,38, provided that the measure of evolutionary distance between any two alleles is proportional to the time since their most recent common ancestor. Extensive simulation studies have shown that estimates of R_ST may be unreliable unless many loci are used^39–41, but unlike F_ST the expected value of R_ST does not depend on the rate of mutation. Estimates of Φ_ST or R_ST may be useful when mutations have contributed substantially to allelic differences among populations, but their usefulness may be limited by the extent to which the mutational model underlying the statistics matches the actual mutational processes occurring in the system³⁹.

Q_ST and polygenic variation

Spitze⁴² noted that another quantity analogous to θ can be estimated for continuously varying traits. Specifically, we can define:

$$Q_{\mathrm{S}\mathrm{T}}=\frac{{\sigma }_{\mathrm{G}\mathrm{P}}^2}{{\sigma }_{\mathrm{G}\mathrm{P}}^2+2{\sigma }_{\mathrm{G}\mathrm{I}}^2}$$ (6)

in which ${\sigma }_{\mathrm{G}\mathrm{P}}^2$ is the additive genetic variance among populations and ${\sigma }_{\mathrm{G}\mathrm{I}}^2$ is the additive genetic variance within populations. ${\sigma }_{\mathrm{G}\mathrm{P}}^2$ can be estimated from between-population crosses, and ${\sigma }_{\mathrm{G}\mathrm{I}}^2$ can be estimated from within-population crosses. Because the total variance in between-population crosses is ${\sigma }_{\mathrm{G}\mathrm{P}}^2+{\sigma }_{\mathrm{G}\mathrm{I}}^2$, Q_ST is the proportion of additive genetic variance in a trait that is due to among-population differences. If the trait is selectively neutral, if all genetic variation is additive and if the mutation rates at loci contributing to the trait are the same as those at other loci, we expect Q_ST and F_ST to be equal^43,44. Comparing the magnitude of Q_ST and F_ST may therefore indicate whether a particular trait has been subject to stabilizing selection (Q_ST<F_ST) or diversifying selection (Q_ST>F_ST). However, because of the uncertainties associated with estimates of Q_ST and F_ST, such comparisons are likely to be useful only when they are available for a moderately large number of populations (>20)⁴⁵. Furthermore, caution is necessary when suggesting that a comparison of Q_ST and F_ST provides evidence for stabilizing selection because non-additive genetic variation tends to change Q_ST, even for a neutral trait⁴⁶.

Applications

F-statistics include both F_ST, which measures the amount of genetic differentiation among populations (and simultaneously the extent to which individuals within populations are similar to one another), and F_IS, which measures the departure of genotype frequencies within populations from Hardy–Weinberg proportions. Here, we focus on the applications of F_ST for several reasons (BOX 4).

Box 4. Why focus on F_ST?

We focus here on F_ST for several reasons. First, F_IS is easier to interpret. It is defined with respect to the populations that are included in the sample, either through population-specific estimates or through the average of those estimates. By contrast, F_ST is defined and interpreted with respect to the distribution of allele frequencies among all populations that could have been sampled, not merely those that have been included in the sample. As a result, estimates of F_ST must account for genetic sampling, which introduces a level of complexity and subtlety that requires extra attention.

Second, the application of F-statistics to problems in population and evolutionary genetics often centres on estimates of F_ST. For example, when interpreting aspects of demographic history, such as sex-biased dispersal out of Africa in human populations⁹, detecting regions of the genome that might have been subject to stabilizing or diversifying selection^8,58,61 or correcting the probabilities of obtaining a match in a forensic application for genetic substructure within populations¹⁰⁶, estimates of F_ST often play a crucial part in interpretations of genetic data. Estimates of F_IS reveal important properties of the mating system within populations, but estimates of F_ST reveal properties of the evolutionary processes that lead to divergence among populations.

Finally, in many populations of animals, and in human populations in particular, within-population departures from Hardy–Weinberg proportions are small. Where they are present, such departures may reveal more about genetic substructuring within populations than about departures from random mating. Moreover, although estimates of F_IS may provide insights into the patterns of mating in inbred populations of plants or animals, the direct analysis of mother–offspring genotype combinations is usually more informative and reliable^107,108.

Estimating migration rates

Wright⁵ showed that if all populations in a species are equally likely to exchange migrants and if migration is rare, then:

$$F_{\mathrm{S}\mathrm{T}}\approx \frac{1}{4N_{\mathrm{e}}m+1}$$ (7)

in which m is the fraction of each population composed of migrants (the backward migration rate)⁴⁷ and N_e is the effective population size of local populations⁴⁸. Because of this simple relationship, it is tempting to use estimates of F_ST from population data to estimate N_em.

Unfortunately, it has been recognized for many years that this simple approach to estimating migration rates might fail⁴⁹. The most obvious reason for this failure is that populations are rarely structured so that all populations exchange migrants at the same rate, which causes some populations to resemble one another more than others. If differentiation between populations is solely a result of isolation by distance⁵⁰, for example, then the slope of the regression of F_ST/(1 – F_ST) on either the logarithm of between-population distance (for populations distributed in two dimensions) or the between-population distance alone (for populations in a linear habitat) is proportional to D_eδ², in which D_e is the effective density of the population (D_e = N_e/area) and δ² is the mean squared dispersal distance⁵¹. However, if differentiation is the result not only of isolation by distance but also of natural selection or if the drift–migration process has not reached a stationary point, the slope of this relationship cannot be interpreted as an estimate of migration. Moreover, a pure migration–drift process, a pure drift–divergence process or a combination of the two could produce the same distribution of allele frequencies. Indeed, migration–drift, drift–divergence or a combination of the two can account for any pattern of allele frequency differences among populations⁵². Therefore, although pairwise estimates of F_ST (or Φ_ST or R_ST) provide some insight into the degree to which populations are historically connected^37,38, they do not allow us to determine whether that connection is a result of ongoing migration or of recent common ancestry.

There are additional difficulties with interpreting estimates of F_ST. Different genetic markers may give different estimates of F_ST for many reasons, and to derive an estimate of migration rates from F_ST, one must assume that the particular set of markers that are chosen have the expected relationship with N_em. This may often be problematic. For example, differences between F_ST estimates from human microsatellites (0.05) and SNPs (0.10) cannot reflect differences in migration rate because both estimates are derived from the same set of individuals and the same set of populations — the Human Genome Diversity Project–Centre d’Étude du Polymorphisme Humain sample^1,2,53. The use of coalescent-based approaches (see later section) that incorporate models of the mutational process is one method of overcoming this difficulty^54–56.

Inferring demographic history

Population-specific or pairwise estimates of F_ST may provide insights into the demographic history of populations when estimates are available from many loci. For example, Keinan et al.⁹ reported pairwise estimates of F_ST for 13,600–62,830 autosomal SNP loci and 1,100–2,700 X chromosome SNP loci in human population samples from northern Europe, East Asia and West Africa. Because there are four copies of each autosome in the human population for every three copies of the X chromosome, one would expect there to be greater differentiation at X chromosome loci than at autosomal loci. Specifically, for two populations that diverged t generations ago, one might expect:

$$1-F_{\mathrm{S}\mathrm{T}}={(1-\frac{1}{2N_{\mathrm{e}}})}^t$$ (8)

in which N_e is the effective size of the local populations. Therefore, if Q is defined as:

$$\text{ln}(1-F_{\mathrm{S}\mathrm{T}}^{\text{auto}})/\text{ln}(1-F_{\mathrm{S}\mathrm{T}}^{\mathrm{X}})$$ (9)

Q is approximately:

$$N_{\mathrm{e}}^{\mathrm{X}}/N_{\mathrm{e}}^{\text{auto}}=0.75$$ (10)

Q is approximately 0.75 for comparisons between East Asians and northern Europeans (Q = 0.72 ± 0.05), but it is substantially smaller for comparisons between West Africans and other populations in the sample (Q = 0.58 ± 0.03 for the comparison with northern Europeans and Q = 0.62 ± 0.03 for the comparison with East Asians). These results suggest either sex-biased dispersal (long-range immigration of males from Africa after non-African populations were initially established) or selection on X chromosome loci after the divergence of African and non-African populations.

Identifying genomic regions under selection

Similarly, locus-specific estimates of F_ST may identify genomic regions that have been subject to selection. The logic is straightforward; the pattern of genetic differentiation at a neutral locus is completely determined by the demographic history of the populations (that is, the history of population expansions and contractions), the mutation rates at the loci concerned and the rates and patterns of migration among the populations^6,57–60. In a typical multilocus sample, it is reasonable to assume that all autosomal loci have experienced the same demographic history and the same rates and patterns of migration. If the loci also have similar mutation rates and if the variation at each locus is selectively neutral, the allelic variation at each locus represents a separate sample from the same underlying stochastic evolutionary process. loci showing unusually large amounts of differentiation may indicate regions of the genome that have been subject to diversifying selection, whereas loci showing unusually small amounts of differentiation may indicate regions of the genome that have been subject to stabilizing selection⁵⁸. Several groups have used such genome scans to examine patterns of differentiation in the human genome.

By comparing locus-specific estimates of F_ST with the genome-wide distribution, Akey et al.⁶ identified 174 regions (out of the 26,530 examined) that showed what they called ‘signatures of selection’ in the human genome. of these loci, 156 showed unusually large amounts of differentiation (suggesting diversifying selection) and 18 showed unusually small amounts of differentiation (suggesting stabilizing selection). By contrast, when Weir et al.⁷ examined the high-resolution Perlegen (~1 million SNPs) and phase I HapMap (~0.6 million SNPs) data sets in humans to examine locus-specific estimates of F_ST, they also found large differences in F_ST among loci, but their analyses suggested that the very high variance associated with single-locus estimates of F_ST precluded using these estimates to detect selection. Both sets of investigators noted a particular problem with single-locus estimates when using high-resolution SNP maps: the high correlation between F_ST estimates when loci are in strong gametic disequilibrium makes it difficult to determine whether the F_ST at any particular SNP is markedly different from expectation.

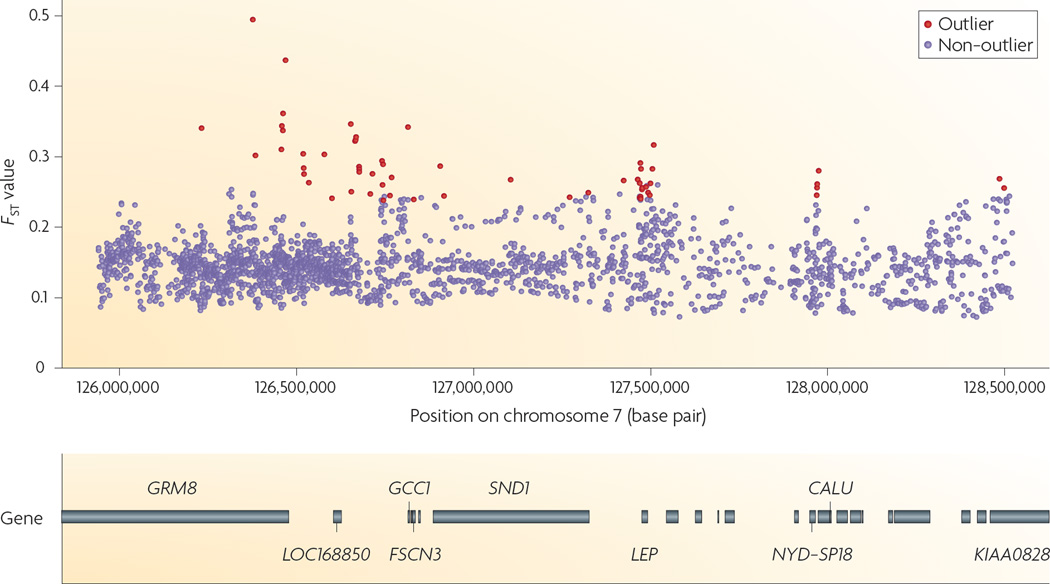
Although single-locus estimates of F_ST are highly uncertain, simulation studies suggest that when loci are inherited independently, background information about a few hundred loci is sufficient to allow the reliable identification of loci that are subject to selection when a suitable criterion for detecting ‘outliers’ is used^8,58,61. Although few loci are falsely identified as being subject to selection when they are neutral, genome scans using F_ST may often fail to detect selection when it is present. For example, when a single allele is strongly favoured in all populations, not only is F_ST expected to be nearly zero but variation is also expected to be nearly non-existent, rendering estimates of F_ST either highly unreliable or unobtainable. Similarly, when selection is weak, data from many loci are needed to recognize that the estimate of F_ST at the locus involved is unusual. More importantly, as mentioned above, high-resolution genome scans must account for the statistical association between closely linked loci. Guo et al.⁸ used a conditional autoregressive scheme to identify 57 loci that showed unusually large amounts of among-population differentiation in a sample of 3,000 SNP loci on human chromosome 7 separated by only 860 nucleotides on average. Sixteen of these markers are associated with LEP, a gene encoding a leptin precursor that is associated with behaviours that influence the balance between food intake and energy expenditure⁶² (FIG. 1). Moreover, association studies in one French population had previously suggested a relationship between one of the SNPs identified as an outlier in this study and obesity⁶³.

Figure 1. Locus-specific estimates of F_ST on human chromosome 7.

Estimates are as inferred from the phase II HapMap data set⁹⁵. Horizontal bars indicate the locations of known genes. The red circles are posterior means for SNPs with estimates that are detectably different from the genomic background (purple circles). All ‘outliers’ show significantly more differentiation among the four populations in the sample than is consistent with the level of differentiation seen in the genomic background. The excess differentiation suggests that these SNPs are associated with genomic regions in which loci have been subject to diversifying selection among populations. CALU, calumenin; FSCN3, ascin homolog 3; GCC1, GRIP and coiled-coil domain containing 1; GRM8, glutamate receptor, metabotropic 8; LEP, leptin; SND1, staphylococcal nuclease and tudor domain containing 1. Figure is modified, with permission, from REF. 8 © (2009) American Statistical Association.

Forensic science and association mapping

In forensic science, matching a genetic profile taken from a suspect with a profile taken from a stain left at a crime scene serves as evidence linking the suspect to the crime. To quantify the strength of this evidence, it is useful to determine the probability of a random match — that is, the probability that the genetic profile at the crime scene matches that of the suspect if the suspect was not the source of the stain. In some cases, two people, the suspect and the person who left the crime sample, may belong to a subpopulation for which there is no specific allele frequency information. In such a case, we can use a θ correction⁶⁴ to calculate the probability of a match based on allele frequency information from a larger population of which the subpopulation is a part. The probability of a random match takes into account the allele frequency variation among subpopulations within the wider population for which allele frequencies are available. For example, if the matching profile consisted of a homozygote AA at a single locus and if p_A is the population frequency of allele A, the probability that the crime profile is AA given that the suspect is AA and the suspect is not the source of the stain is (REF. 65):

$$P(\mathrm{A}\mathrm{A}|\mathrm{A}\mathrm{A})=\frac{(3\theta +(1-\theta )p_{\mathrm{A}})(2\theta +(1-\theta )p_{\mathrm{A}})}{(1+\theta )(1+2\theta )}$$ (11)

There is a similar equation for heterozygotes, and these θ-correction results are multiplied over loci. The 1996 National research Council report⁶⁶ recommended using θ = 0.01 except for small isolated subpopulations, for which they suggested that a value of θ = 0.03 was more appropriate. The practical effect of the θ correction is that the numerical strength of the evidence against a suspect is reduced. If p_A = 0.01, for example, the uncorrected probability of a match is 0.0001. However, with θ = 0.01, the probability of a match is an order of magnitude larger — 0.0012. With θ = 0.03, it is even larger — 0.0064. Therefore, it is much less surprising to see a match when we take account of the population substructure than when we ignore it.

In association mapping, case–control studies compare the allele frequencies at genetic markers (generally SNPs) between groups of people with a disease and groups who do not have the disease. When frequencies at a marker locus differ between the groups, it is interpreted as evidence for gametic disequilibrium between the marker and a disease-related gene. This in turn suggests that the marker and disease-related genes are in close proximity on the same chromosome. However, as many authors have pointed out, population substructure unrelated to disease status could cause the same kind of allele frequency difference^67–70. The genomic control method is one way to account for population substructure. It uses background estimates of F_ST to control for subpopulation differences that are unrelated to disease status^67,68. If cases and controls have different marker allele frequencies for reasons unconnected with the disease, as would be shown by frequency differences across the whole genome, an uncorrected case–control test would give spurious indications of marker–disease associations.

Relationship to coalescent-based methods

When Kingman introduced the coalescent process to population genetics just over 25 years ago^71,72, it revolutionized the field. Many approaches to the analysis of molecular data, particularly molecular sequence and SNP data, now take advantage of the conceptual, computational and analytical framework that coalescent-based methods provide^73–79. For example, whereas F-statistics provide only limited insight into the rates and patterns of migration, statistics based on the coalescent process can provide insights into the rates of mutation, migration and other evolutionary processes. Coalescent analysis is based on maximizing the likelihood of a given sample configuration or sampling from the corresponding Bayesian posterior distribution. The likelihood is constructed from the genealogical histories for the sample that are consistent with the unknown evolutionary parameters of interest; for example, the size of the population or populations from which the sample was taken, or the history of population size changes, mutation rates, recombination rates or migration rates^55,80–86. Coalescent analyses are likely to provide precise estimates of effective population size, mutation rates and migration rates when certain conditions are met — that is, when the model used for analysis is consistent with the demographic history of populations from which samples are collected, with the migration patterns among populations in the sample and with the mutational processes that generated allelic differences in the sample, and also when it is reasonable to presume that the drift–mutation–migration process has reached an evolutionary equilibrium^54,73. When these assumptions are not met it may not be reasonable to estimate the related evolutionary parameters, and the examples presented above show that analyses based on F-statistics may still provide substantial insights.

Conclusions

Sewall Wright⁵ provided a comprehensive account of the processes leading to genetic differentiation among populations nearly 80 years ago, but he did not provide the tools that empirical population geneticists needed to apply his insights to understanding variation in wild populations. During his work on isolation by distance in the plant Linanthus parryae in the 1940s^50,87, the theory of F-statistics that he and Gustave Malécot later developed^3,4,16,88 began to emerge. Because of the insights that F-statistics can provide about the processes of differentiation among populations, over the past 50 years they have become the most widely used descriptive statistics in population and evolutionary genetics. From the time population geneticists first began to collect data on allozyme variation^89–94 to recent analyses of SNP variation in the human genome^2,9,95–97, F-statistics, and F_ST in particular, have been used to investigate processes that influence the distribution of genetic variation within and among populations. Unfortunately, neither Wright nor Malécot distinguished carefully between the definition of F-statistics and the estimation of F-statistics. In particular, until Cockerham introduced his indicator formalism^10,22, few if any population geneticists understood that estimators of F-statistics must take into account both statistical sampling and genetic sampling.

The statistical methodology for estimating F-statistics is now well established. With the availability of methods to estimate locus- and population-specific effects on F_ST^{7,8,27,58,61,98}, geneticists now have a set of tools for identifying genomic regions or populations with unusual evolutionary histories. Through further extensions of this approach, it is even possible to determine the relationship between the recent evolutionary history of populations and environmental or demographic variables⁹⁹. The basic principles of how population size, mutation rate and migration are related to the genetic structures of populations have been well understood for nearly 80 years. Analyses of F-statistics in populations of plants, animals and microorganisms have broadened and deepened this understanding, but these analyses have mostly been applied to data sets that contain a small number of loci. The age of population genomics is now upon us^100,101. The 1,000 Genomes project and the International HapMap Project give a hint of what is to come. Despite the scale of these projects, much of the data can be understood fundamentally as allelic variation at individual loci. As a result, we expect F-statistics to be at least as useful in understanding these massive data sets as they have been in population and evolutionary genetics for most of the past century.

Glossary

Genetic drift

The random fluctuations in allele frequencies over time that are due to chance alone.

Short tandem repeat loci

Loci consisting of short sequences (2–6 nucleotides) that are repeated multiple times. Alleles at short tandem repeat loci differ from one another in their number of repeats.

Variance

A measure of the amount of variation around a mean value.

Diversifying selection

Selection in which different alleles are favoured in different populations. It is often a consequence of local adaptation (in which genotypes from different populations have higher fitness in their home environments owing to historical natural selection).

Hardy–Weinberg proportions

When the frequency of each diploid genotype at a locus equals that expected from the random union of alleles. That is, the genotypes AA, Aa and aa will be at frequencies p², 2pq and q², respectively.

Heterozygote advantage

A pattern of natural selection in which heterozygotes are more likely to survive than homozygotes.

Likelihood

A mathematical function that describes the relationship between the unknown parameters of a statistical distribution — for example, the mean and variance of the allele frequency distribution among populations or the allele frequency in a particular population — and the data. It is directly proportional to the probability of the data given the unknown parameters.

Prior distribution

A statistical distribution used in Bayesian analysis to describe the probability that parameters take on a particular value before examining any data. It expresses the level of uncertainty about those parameters before the data have been analysed.

Posterior distribution

A statistical distribution used in Bayesian analysis to describe the probability that parameters take a particular value after the data have been analysed. It reflects both the likelihood of the data given particular parameters and the prior probability that parameters take particular values.

Markov chain Monte Carlo methods

Methods that implement a computational technique that is widely used for approximating complex integrals and other functions. In this context, these methods are used to approximate the posterior distribution of a Bayesian model.

Multinomial distribution

A statistical distribution that describes the probability of obtaining a sample with a specified number of objects in each of several categories. The probability is determined by the total sample size and the probability of drawing an object from each category. The binomial distribution is a special case of the multinomial distribution in which there are two categories.

Additive genetic variance

The part of the total genetic variation that is due to the main (or additive) effects of alleles on a phenotype. The additive variance determines the degree of resemblance between relatives and therefore the response to selection.

Stabilizing selection

Selection in which either the same allele or the same genotype is favoured in different populations.

Effective population size

Formulated by Wright in 1931, the effective population size reflects the size of an idealized population that would experience drift in the same way as the actual (census) population. The effective population size can be lower than the census population size owing to various factors, including a history of population bottlenecks and reduced recombination.

Coalescent-based approaches

Approaches that use statistical properties of the genealogical relationship among alleles under particular demographic and mutational models to make inferences about the effective size of populations and about rates of mutation and migration.

Conditional autoregressive scheme

A statistical approach developed for analysis of data in which a random effect is associated with the spatial location of each observation. The magnitude of the random effect is determined by a weighted average of the random effects of nearby positions. In most applications, the weights of the averages are inversely related to the spatial distance between two sample points.